Gene regulatory network inference as relaxed graph matching

Abstract

Bipartite network inference is a ubiquitous problem across disciplines. One important example in the field molecular biology is gene regulatory network inference. Gene regulatory networks are an instrumental tool aiding in the discovery of the molecular mechanisms driving diverse diseases, including cancer. However, only noisy observations of the projections of these regulatory networks are typically assayed. In an effort to better estimate regulatory networks from their noisy projections, we formulate a non-convex but analytically tractable optimization problem called OTTER. This problem can be interpreted as relaxed graph matching between the two projections of the bipartite network. OTTER’s solutions can be derived explicitly and inspire a spectral algorithm, for which we provide network recovery guarantees. We also provide an alternative approach based on gradient descent that is more robust to noise compared to the spectral algorithm. Interestingly, this gradient descent approach resembles the message passing equations of an established gene regulatory network inference method, PANDA. Using three cancer-related data sets, we show that OTTER outperforms state-of-the-art inference methods in predicting transcription factor binding to gene regulatory regions. To encourage new graph matching applications to this problem, we have made all networks and validation data publicly available.

Introduction

Bipartite networks are studied across disciplines ranging from machine learning (Yamanishi 2009), ecology, and economics to biology. They focus on the interaction of different types of nodes like vertices in different graphs, pollinators and plants, countries and products, or compounds and proteins. Another prominent example are gene regulatory networks consisting of transcription factors (TFs) and genes (see Fig. 1). These are fundamental objects of study in molecular biology and their analysis provides insights into mechanisms underlying the progression of various diseases, including cancer (Lopes-Ramos et al. 2018; Burkholz and Quackenbush 2021; Lopes-Ramos et al. 2020).

Figure 1:

Gene regulation. A. Transcription factors (TFs) are represented by green, blue, and yellow objects that bind to the genome (gray band) in vicinity of the start site of a gene (black arrow) to regulate its expression. B. Representation of A as bipartite gene regulatory network.

Often, we do not observe the bipartite network W (e.g. representing TF–gene interactions) directly but instead have information about its two associated projections WW^T (TF–TF cooperation) and W^TW (gene–gene interactions, see Fig. 2). The general objective of this work is to infer W based on noisy observations of its projections P ≈ WW^T and C ≈ W^TW. We formulate this task as a non-convex optimization problem, OTTER (Optimize to Estimate Regulation). It is related to inexact graph matching, as it seeks agreement between two graphs P and C. W could be interpreted as relaxed permutation matrix that matches nodes in P (TFs) with nodes in C (genes). As relaxed graph matching, OTTER is theoretically tractable but the solutions are non-unique, since information about W is lost as a consequence of projecting. To select a solution, we need a good initial guess W₀ of the bipartite network as input in addition to P and C.

Figure 2:

The unknown bipartite network W is inferred from its observed projections P and C.

Our first contribution is to fully characterize OTTER’s solution space, which depends on the spectral decomposition of C and P. Hence, two natural choices to solve OTTER are (1) a spectral algorithm and (2) gradient descent. For both, we provide theoretical network recovery guarantees. While the spectral method is robust to small noise, gradient descent is more reliable in higher noise settings, which are common in biological applications. As we show on three benchmark data sets related to gene regulation and cancer, optimizing OTTER using gradient descent outperforms state-of-the-art gene regulatory network inference techniques. Among these techniques is PANDA (Passing Attributes between Networks for Data Assimilation (Glass et al. 2013)), an established GRN inference method. OTTER gradient descent resembles the corresponding message passing updates, and it can therefore be interpreted as simplified, theoretically tractable formulation of PANDA. This formulation enables us to provide network recovery guarantees and analyze the effects of noise on the network reconstruction.

Gene regulation

Next generation genome sequencing technology has revolutionized biomedical research and provides data at an unprecedented scale and speed. The low cost of this technology facilitates large, genome-scale studies which provide new insights into gene regulation. The human genome encodes about 25,000 genes, but not all genes are activated, or ”expressed,” in every cell type. Gene expression distinguishes tissues from each other can make the difference between health and disease, as it controls the production of proteins. These proteins influence higher level cellular functions, which are often altered during the development and progression of different diseases, including cancer. To gain an understanding of the gene regulatory mechanisms perturbed by a disease, it is common practice to infer and compare associated gene regulatory networks (GRNs) (Lao et al. 2015; Lopes-Ramos et al. 2018; Qiu et al. 2018; Yung et al. 2019). In many cases, these networks are weighted, bipartite, and have a representation as matrix W. W consist of two types of nodes – transcription factors (TFs) and genes. A TF is a protein that can bind to the DNA in the vicinity of a gene and regulate its expression. When this occurs, the TF and target gene are linked in the gene regulatory network, see Fig. 1. TFs are also known to cooperatively regulate target genes. One actively studied mechanism by which TFs cooperate is through the formation of protein complexes which then go on to bind to DNA. These TF-TF interactions are an area of active study, and public databases with such information are actively maintained. In this work, we denote the TF-TF cooperativity matrix as P.

Genes that are co-regulated are frequently correlated in their expression levels. We can estimate this co-regulation using a gene-gene co-expression matrix C estimated from gene expression data. This is especially attractive because gene expression is widely available and is context-specific, i.e., it depends on the tissue type, disease, etc. A more detailed explanation of gene regulation is given in the supplement. We also recommend the review article by Todeschini et al. (Todeschini, Georges, and Veitia 2014)).

GRN inference is central to deepening our understanding of diseases on the molecular level, but it is a notoriously difficult problem. Contributions by researchers working in different domains like graph matching could therefore have a great impact. For this reason, we provide benchmark data sets for three human tissues in the cancer domain (Guebila et al. 2020). Their use does not require expertise in molecular biology.

Related work

The OTTER objective is inspired by a state-of-the-art GRN inference method, PANDA (Glass et al. 2013). PANDA integrates multiple data sources through a message passing approach, which is similar to the gradient descent of OTTER. A derivation is given in the supplement. PANDA has been used to investigate gene regulatory relationships in both tissue specific (Sonawane et al. 2017) as well as several disease contexts, including chronic obstructive pulmonary disease (Lao et al. 2015), asthma (Qiu et al. 2018), beta cell differentiation (Yung et al. 2019), and colon cancer (Lopes-Ramos et al. 2018). OTTER can be seen as a theoretically tractable simplification of PANDA, which is amenable to modern optimization techniques and draws connections to graph matching.

Many methods try to infer regulatory relationships solely based on gene expression with two possible (non-exclusive) objectives: structure learning and gene expression prediction. Usually, gene expression prediction makes indirect statements about the interaction structure of variables as well and thus forms an hypothesis about which TFs regulate which genes. TFs are proteins that are created from the mRNA expressed by their corresponding genes. Hence, predicting target gene expression from the expression of the genes coding for the TFs assumes a biologically reasonable structure. The most common and basic approach is to analyse the Pearson correlation (COR) matrix or, if feasible, partial correlations (PARTIAL COR). Spearman correlations usually lead to similar conclusions. Another popular approach is Weighted Gene Co-expression Network Analysis (WGCNA) (Zhang and Horvath 2005; Langfelder and Horvath 2008), in particular the TOM subroutine. It also starts from a gene expression correlation matrix but down-weighs connections if they are not consistent with neighborhood information. Other pruning heuristics take also different types of node similarities resulting from graph embeddings into account (Pio et al. 2020). Alternatives are based on mutual information, where ARACNe (Lachmann et al. 2016) is one of the most commonly used representatives. Among graphical models, mainly Gaussian graphical models are used because the learning algorithms have to scale to a large number of genes. The GLASSO (Friedman, Hastie, and Tibshirani 2008) method is among the best performing candidates and uses LASSO regularization to enforce sparsity. However, it still does not scale to our setting (approximately 20,000–30,000 genes for human tissue), so that we had to omit it from the benchmarks in our experiments. Linear models (Haury et al. 2012) and random forests (Huynh-Thu et al. 2010) have been used for a similar purpose, where TIGRESS (Haury et al. 2012) and GENIE3 (Huynh-Thu et al. 2010) were top scorers at the DREAM5 challenge (Marbach et al. 2012) (although the challenge was somewhat different from the GRN modeling we study here). Both methods have high computational requirements and are less suitable for the human genome. An alternative approach is to treat the binding of TFs to the promoter region of a gene as supervised learning problem (Karimzadeh and Hoffman 2019; Yuan and Bar-Joseph 2019). While such models can be quite accurate, they are limited to the small number of TFs for which the relevant data is available, which is provided by ChIP-seq experiments. Hence, supervised approaches cannot discover new gene regulatory relationships. Transfer learning algorithms can utilize more data from different domains, for instance, GRNs related to mice (Mignone et al. 2019), but might also inherit unrealistic biases. Note that, in contrast, the data required to define OTTER are widely available, related to the relevant domain, and include a much larger set of known TFs.

In addition, OTTER is related to established problems in graph matching (Yan et al. 2016), which have strong theoretical foundations (Jiang et al. 2017; Barak et al. 2019). The quadratic assignment problem (QAP) (Aflalo, Bronstein, and Kimmel 2015) and its variants (Maron and Lipman 2018) have a direct link to OTTER and can support a similar biological theory. Graph matching has broad applications in computer science ranging from machine learning (Cour, Srinivasan, and Shi 2007), pattern matching (Zhou and De la Torre 2016), vision (Berg, Berg, and Malik 2005; Zhou and De la Torre 2013), and protein network alignment (Singh, Xu, and Berger 2008) to social network analysis (Fan 2012). However, it has not been applied to gene regulatory network inference to the best of our knowledge. As we show, simple relaxed graph matching techniques are competitive with established GRN inference methods.

Contributions

1) We pose a novel optimization problem, OTTER, for the inference of bipartite networks in general and gene regulatory networks (GRNs). Importantly, OTTER is analytically tractable. 2) We gain insights into a state-of-the-art GRN inference method, PANDA (Glass et al. 2013), as OTTER gradient descent resembles the related message passing equations. 3) We characterize OTTER’s solution space and derive a spectral algorithm on its basis, for which we give network recovery guarantees. 4) We solve the gradient flow dynamics associated with gradient descent for OTTER. 5) We draw a connection from OTTER to relaxed graph matching and open a new application area for related algorithms. 6) We show that OTTER gradient descent outperforms the current state of the art in GRN inference on three challenging biological data sets related to cancer. 7) We make the processed data publicly available to ease the use for researchers without a computational biology background and to foster further innovation in relaxed graph matching and GRN inference.

OTTER

Biological motivation

Our objective is to infer a gene regulatory network (GRN) represented by a matrix W. Entries w_ij with larger values indicate a higher probability that TF i regulates gene j. OTTER and PANDA refine an initial guess W₀ of a GRN by increasing its consistency with protein-protein interactions P and observed gene expression with correlation matrix C. In our experiments, a TF–gene edge exists in W₀ if the sequence motif for that TF is present in the promoter region of the target gene. This information depends only on the human reference genome and provides a reasonable estimate of where TFs bind. Yet, it is context agnostic. TF binding changes between different tissues, allowing cells to assume their specific functions, and can become disrupted by diseases like cancer.

To estimate condition specific GRNs, we solve the OTTER objective. In doing so, we assume that P and C agree partially with the projections of the actual gene regulatory network W. We do not require perfect equality of WW^T = P and W^TW = C but improve W₀ according to the following three central elements of gene regulation: (1) TFs that can bind to the promoter region of a gene are more likely to regulate that gene (W ≈ W₀) (Spitz and Furlong 2012; Lambert et al. 2018; Ouyang, Zhou, and Wong 2009), (2) genes that are correlated in their expression are more likely to be co-regulated by similar TFs (W^TW ≈ C) (Lambert et al. 2018; Shi, Fornes, and Wasserman 2018; Hobert 2008), and (3) TFs that interact (for example, by forming complexes) are more likely to target the same genes (WW^T ≈ P). TF cooperation is often mediated through protein-protein interactions (Spitz and Furlong 2012; Morgunova and Taipale 2017; Deplancke, Alpern, and Gardeux 2016). For example, the TFs Msn2 and Msn4 bind together to form a complex before binding to the DNA of their target genes (Chapal et al. 2019).

This reasoning motivates our general study of bipartite network inference based on observed noisy projections (P and C). As we will show, a considerable amount of information is lost by projecting. This explains partially why GRN inference is challenging. Central to our success is a good initialization W₀ and the choice of algorithm that picks a solution among the many different options. Specifically, we study two approaches: (a) a spectral algorithm and (b) a gradient descent variant optimizing the OTTER objective, which we introduce formally in the next section. As we show, the spectral approach has excellent recovery guarantees in low noise settings, while gradient descent is more reliable in high noise applications, which is common in high throughput sequencing data in biology. Gradient descent also has the advantage that it allows us to stay closer to the initial W₀ with early stopping. For this reason, it enables us to outperform the state of the art in GRN inference.

Theoretical framework

In this section, we analyse the general problem of learning a bipartite and weighted network with matrix representation $W\in {ℝ}^{n_p\times n_c}$ from its symmetric projections $P\in {ℝ}^{n_p\times n_p}$ and $C\in {ℝ}^{n_c\times n_c}$. By analogy with our motivation of GRN inference, we call the nodes of one type transcription factors (TFs) and of the other type genes. We have n_p TFs and n_c genes, where the number of genes is usually much larger (n_p ≪ n_c). Minimizing the following OTTER objective

$$\begin{gathered} f\text{(}W\text{)=} \\ \frac{(1-\lambda )}{4}{\Vert W{W}^T-P\Vert }^2+\frac{\lambda }{4}{\Vert W^{T}W-C\Vert }^2+\frac{\gamma }{2}\Vert W{\Vert }^2 \end{gathered}$$ (1)

with respect to W seeks agreement between the projections of W and P and C. λ ∈ [0, 1] denotes a tuning parameter that moderates the influence of P versus C, and γ corresponds to a potential regularization. As we will see later, this choice of regularization compensates for a bias that noise in P and C introduces. In principle, we could choose any matrix norm but limit our following discussion to the Frobenius norm $\Vert A{\Vert }^2:={\sum }_{i=1}^n{\sum }_{j=1}^m{a}_{ij}^2=\mathrm{tr}\left(A^{T}A\right)$ for a matrix A = (a_ij). For this choice, gradient descent resembles most closely the related message passing equations of PANDA and we can derive the solutions of the minimization problem.

These solutions depend on the spectral decomposition of $P=U_p{D}_p{U}_p^T$ and $C=V_c{D}_c{V}_c^T$, which exist with respect to orthogonal U_p and V_c, as P and C are symmetric. Otherwise, the same results hold for the spectral decomposition of (P + P^T)/2 and (C + C^T)/2. D_p and D_c are diagonal matrices containing the eigenvalues of the respective matrix. In a slight abuse of notation, we denote with D_p a matrix $D_p\in {ℝ}^{n_p\times n_p}$ and, if convenient, a matrix $D_p\in {ℝ}^{n_c\times n_c}$, which is padded with zeros accordingly. Furthermore, let $M^{\left[n_p\right]}={\left(m_{ij}\right)}_{i\le n_p,j\le n_p}$ denote a submatrix of a larger matrix M with dimension n_p × n_p. Without loss of generality, we assume that the eigenvalues d_p,ii of P are indexed in descending order; d_p,ii ≥ d_p,jj for i < j. For C however, we require a good matching with P. We therefore assume implicitly that the distance of D_c to D_p is minimized with respect to permutations of the eigenvalues of C, that is ${\Vert D_c-D_p\Vert }^2={\min }_{\pi \in \mathrm{P}}{\Vert D_{c,\pi }-D_p\Vert }^2$, where P denotes the set of permutations of {1, · · · , n_c} and D_c,π the corresponding ordering of eigenvalues on the diagonal. If D_p and D_c show little discrepancy, this will result in the eigenvalues of C being in descending order as well. Now, everything is in place to characterize the solution space 𝒮.

Theorem 1.

For given $P\in {ℝ}^{n_p\times n_p}$ with P = P^T and $C\in {ℝ}^{n_c\times n_c}$ with C = C^T, for any spectral decomposition $P=U_p{D}_p{U}_p^T$ and $C=V_c{D}_c{V}_c^T$, λ ∈ [0, 1] the minimization problem (1) has solutions $W^{*}\in \mathrm{S}$ with singular value decomposition $W^{*}=U_p{D}_w{V}_c^T$, where

$$d_{w,ii}=\sqrt{\max \left((1-\lambda )d_{p,ii}+\lambda d_{c,ii}-\gamma ,0\right)}$$ (2)

for i ≤ n_p. For d_w,ii = 0, the corresponding columns of U_w and V_w are not restricted to the eigenvectors of P and C. The eigenvalues of C are ordered such that D_c = D_c,π, where the permutation solves the minimization problem

$$\begin{gathered} \pi ={\mathrm{argmin}}_{{\pi }^{\prime }\in \mathrm{P}}(\frac{\lambda (1-\lambda )}{2}{\Vert {\text{D}}_{\text{p}}-{\text{D}}_{\text{c},{\pi }^{\prime }}^{\left[{\text{n}}_{\text{p}}\right]}\Vert }^2 \\ -\frac{\lambda }{2}{\Vert D_{c,{\pi }^{\prime }}^{\left[n_p\right]}\Vert }^2+(1-\lambda )\gamma \mathrm{tr}\left(D_{c,{\pi }^{\prime }}^{\left[n_p\right]}\right)). \end{gathered}$$ (3)

For $\mathrm{\Delta }:=D_c^{\left[n_p\right]}-D_p$, we further assume that

$$\frac{1}{{\lambda }^2}\left(\Vert P{\Vert }^2+\frac{1}{n_p}\mathrm{tr}{(P)}^2\right)+\frac{1}{n_p}{(\mathrm{tr}(\mathrm{\Delta }))}^2>\Vert \mathrm{\Delta }{\Vert }^2.$$ (4)

Condition (4) is usually met and it is a minor technicality to exclude alternative global minima of Objective (1) that defy our intuition. The nature of these alternatives is discussed in detail in the proof of Thm. 1 in the supplement.

According to Thm. 1, OTTER (Eq. (1)) has at least $2^{n_p}$ different solutions. Each column u_:i of U_p has two optional signs that do not alter the spectral decomposition of P but can lead to a different solution W*. The same applies to columns v_:i of V_c. Only the product of corresponding columns (u_:i and v_:,i) determines the respective solution W*, as we have $w_{ij}^{*}={\sum }_k{d}_{w,kk}{u}_{ik}{v}_{jk}$. This leaves us with $2^{n_p}$ alternatives. If the (non-zero) spectra are not simple, such that some eigenspaces have multiple choices of basis functions, we have additional degrees of freedom in constructing the solutions.

As a consequence, we face a model selection problem and require additional information to make an informed decision. In the following, we propose two natural algorithmic choices to identify a solution: (a) a spectral approach based on Thm. 1 and (b) gradient descent minimizing OTTER.

Both rely on additional input $W_0\in {ℝ}^{n_p\times n_c}$, an initial guess of a gene regulatory matrix. The choice of W₀ is crucial for the performance of both algorithms. To understand some of their advantages and limitations, we provide theoretical recovery results when W₀ is a random perturbation of the correct W and compare both algorithms on synthetic data with increasing levels of noise.

A spectral method for solving OTTER

Assuming that W₀ provides good evidence, our first proposal for a network inference algorithm selects the closest solution $(\widehat{W}\in \mathrm{S})$ to W₀ in a spectral approach: $\widehat{W}={\min }_{W\in \mathrm{S}}{\Vert W-W_0\Vert }^2$. If P and C have simple spectra so that the non-zero eigenvalues correspond to 1-dimensional eigenspaces, the solution to this minimization problem can be computed easily. Note that this assumption is satisfied in our applications. From our previous derivation of the solution space, we know that the only ambiguity lies in the sign of the eigenvectors or, equivalently, the singular eigenvalues. Essentially, for fixed spectral decomposition $P=U_p{D}_p{U}_p^T$ and $C=V_c{D}_c{V}_c^T$, our candidate solutions are of the form $W=U_p{D}_w{D}_s{V}_c^T$, where D_s contains the unknown sign information. D_s is a diagonal matrix with entries d_s,ii ∈ {−1, 1} on the diagonal. These are our only degrees of freedom. Hence, our problem turns into

$$\underset{W\in \mathrm{S}}{\min }{\Vert W-W_0\Vert }^2=\underset{d_{s,ii}\in \{-1,1\}}{\min }{\Vert D_w{D}_s-U_p^T{W}_0{V}_c\Vert }^2$$ (5)

For simplicity, we write $M_0=U_p^T{W}_0{V}_c$. The solution $\widehat{W}$ is unique and given by $\widehat{W}=U_p{\widehat{D}}_w{V}_c^T$ with ${\widehat{d}}_{w,ii}=d_{w,ii}\mathrm{sign}\left({\text{m}}_{0,\text{ii}}\right)$, where d_w,ii is defined as in Thm. 1 and sign(x) = 1 for x ≥ 0 and sign(x) = −1 for x < 0.

An important question in many applications is how well this approach performs under noise. First, we study a simplified scenario, in which only W₀ is noise corrupted so that we know the singular values D_w, as we can deduce them from the correct P and C. Even in this simplified case, perfect recovery of W is unlikely for large-scale problems, as the next proposition states. Let Φ denote the cumulative distribution function (cdf) of a standard normal and X ∼ Ber(p) a Bernoulli random variable with success probability p.

Proposition 2.

Assume that we observe P = W^*TW*, C = W*W^*T, and W₀ = W* + E for a true underlying $W^{*}\in {ℝ}^{n_p\times n_p}$ and noise $E\in {ℝ}^{n_p\times n_p}$ with independent identically normally distributed components $e_{ij}~\mathrm{N}\left(0,{\sigma }^2\right)$. Further assume that P and C have a simple spectrum $\left\{d_1,\dots ,d_{n_p}\right\}$. Then, for the spectral approach $\widehat{W}={\mathrm{argmin}}_{\text{W}\in \mathrm{S}}{\Vert \text{W}-{\text{W}}_0\Vert }^2$ with γ = 0, the recovery loss is distributed as ${\Vert \widehat{W}-W^{*}\Vert }^2=4{\sum }_{i=1}^{n_p}{d}_i^2{R}_i$, where R_i ∼ Ber(Φ(−d_i/σ)) for d_i > 0 and R_i = 0 for d_i = 0 are independent. For any ϵ > 0, the following holds with the usual Chernoff bound:

$$\mathbb{P}\left({\Vert \widehat{W}-W^{*}\Vert }^2\le ϵ\right)\ge 1-\exp \left(ϵ-\mu -\frac{ϵ}{4}\delta \log \left(\frac{ϵ}{\mu }\right)\right),$$

where $\mu ={\sum }_i{p}_i$ and $\delta =\frac{1}{{\max }_i\left(d_{w,ii}^2\right)}$ for ϵ ≤ μ and $\delta =\frac{1}{{\min }_i\left(d_{w,ii}^2\right)}$ otherwise.

The proof is given in the supplement. The insight that R_i ∼ Ber(Φ(−d_i/σ)) allows us also to analyze the probability of perfect recovery (ϵ = 0). We have $\mathbb{P}\left(\widehat{W}=W^{*}\right)={\prod }_{i=1}^{n_p}\left(1-\mathrm{\Phi }\left(-d_i/\sigma \right)\right)$. In our examples, n_p = 1636 and d_min ≈ 0.0001. To achieve a probability of at least 0.5, we could allow for a noise variance of σ ≈ 3 · 10⁻⁵. In many applications, this would be a reasonable range, considering that we have n_pn_c ≈ 4.4 · 10⁷ matrix entries.

Yet, biological data is known to be very noisy. In addition, we also expect high noise in P and C. To compensate for this additional noise, we need regularization.

Regularization

To motivate the need for regularization (γ > 0), we show that, depending on the source of the noise, the spectrum of P and C becomes biased. Typical noise matrices E_p and E_c have iid entries with zero mean, variance ${\sigma }_{p/c}^2$, and a symmetric distribution. They could distort the true projections W*W^*T and W^*TW* as P = (W* +E_p)(W* +E_p)^T and C = (W* +E_c)^T(W* +E_c) or $P=W^{*}{W}^{{*}^T}+E_p{E}_p^T$ and $C=W^{*T}{W}^{*}+E_c^T{E}_c$, respectively. In both cases, P and C become biased as $\mathbb{E}(P)=W^{*}{W}^{*T}+{\sigma }_p^{2}I$ and $\gamma =\lambda {\sigma }_c^2+(1-\lambda ){\sigma }_p^2$, where I denotes the respective identity matrix. The choice $\gamma =\lambda {\sigma }_c^2+(1-\lambda ){\sigma }_p^2$ in Eq. (1) can compensate for this spectral shift.

It should be noted that, Thm. 1 states that such a l2-regularization alters the solutions to Problem (1) in two ways. Not only are the singular values of W* shifted by −γ to compensate for the biases introduced by the noise, also the matching of the eigenvalues of P and C is influenced by the additional penalty $\gamma (1-\lambda )\mathrm{tr}\left(D_{c,\pi }^{\left[n_p\right]}\right)$ in Eq. (3). Consequently, it may be optimal to pair the eigenvalues of P with smaller eigenvalues of C rather than larger ones if γ is large.

The spectral method can be powerful in a setting in which noise is well controlled such that our assumptions are met approximately. Our second solution proposal, gradient descent, however, gives us more tuning options, including the step size and early stopping, that will allow us to stay closer to the initial guess W₀.

Gradient descent for solving OTTER

The message passing equations of PANDA resemble a gradient descent procedure minimizing Objective (1). We explain this relationship in detail in the supplement. In our experiments, we used the ADAM method (Kingma and Ba 2014) for gradient descent, but alternatives are equally applicable. To better understand the approach from a theoretical perspective and reason about its response to noisy data, we take the continuous time approximation (corresponding to infinitesimally small step size) and study the corresponding gradient flow:

$$\begin{gathered} \tau \frac{dW}{dt}=-\nabla f(W) \\ =-W{W}^{T}W+(1-\lambda )PW+\lambda WC-\gamma W, \end{gathered}$$ (6)

where we set the time unit τ = 1 in the following for simplicity. If the initial W₀ has a similar singular value decomposition as a solution, the differential equation decouples and we can solve the resulting one-dimensional ordinary differential equations for the diagonal elements explicitly.

Proposition 3.

For initial $W_0=U_p{D}_0{V}_c^T$ with $U_p{D}_p{U}_p^T$ and $V_c{D}_c{V}_c^T$, the solution of the gradient flow (6) is given by $W(t)=U_p{D}_t{V}_c^T$ with

$$\begin{array}{l}{d}_{t,ii}=\mathrm{sign}\left({\text{d}}_{0,\text{ii}}\right){\text{d}}_{\text{w},\text{ii}}\\ \times \sqrt{\frac{1}{2}h\left(d_{w,ii}^{2}t+h^{-1}\left(2d_{0,ii}^2/d_{w,ii}^2-1\right)\right)+1},\end{array}$$

where h(x) = tanh(x) if $d_{0,ii}^2<d_{w,ii}^2$ and h(x) = coth(x) otherwise.

The proof is provided in the supplement. Note that the square root factor converges to 1 for t → ∞ in both cases. Hence, the final solution inherits the signs sign(d_0,kk) of the initialization, which is similar to our spectral approach. Thus, if we start from a reasonable guess W₀ that diagonalizes with respect to the same U and V as the global minima, gradient descent will converge to the closest global minimum (for small enough learning rate). For general W₀, however, it is important to keep in mind that gradient descent can converge to different solutions, since it optimizes a non-convex objective (Kingma and Ba 2014; Burkholz and Dubatovka 2019). It does not necessarily stay close to our initialization and can even get stuck in local minima. But it also provides us with additional tuning options and early stopping, which will enable us to outperform the state of the art in GRN inference.

Relation to inexact graph matching

As we show in this section, OTTER can also be interpreted as relaxed graph matching. If W solves the OTTER objective for γ = 0 perfectly (f(W) = 0), P and C are its projections, i.e., P = WW^T and C = W^TW. It follows that P, C, and W also fulfill the relation PW = WW^TW = WC. Hence, it would also be reasonable infer a bipartite network from its projections by minimizing the objective

$$g_1(W)=\frac{1}{2}\Vert PW-WC{\Vert }^2+\frac{\gamma }{2}\Vert W{\Vert }^2$$ (7)

(with additional l2-regularization). This is the well known quadratic assignments problem (QAP), a standard objective in graph matching (Aflalo, Bronstein, and Kimmel 2015). In this setting, P and C are usually assumed to have the same dimension (n_P = n_C). The dimensions can differ for inexact graph matching, but the smaller network is then supposed to be similar to a subgraph of the bigger one. Thus, the minimization is performed under the constraint that W is a permutation matrix. In contrast, we are not interested in a permutation matrix, but in a weighted network $W\in {ℝ}^{n_p\times n_c}$ that solves the relaxed QAP. As OTTER, QAP has different solutions and thus solution techniques. Gradient descent and spectral approaches are common choices.

In particular, GRAMPA (Fan et al. 2019a,b) is a variant of QAP with strong recovery guarantees. It adds the term −δ1^TW1 to the QAP objective (7), where 1 denotes a vector with all entries equal to one:

$$g_2(W)=\frac{1}{2}\Vert PW-WC{\Vert }^2+\frac{\gamma }{2}\Vert W{\Vert }^2-\delta 1^{T}W1$$ (8)

As a consequence, the GRAMPA minimization problem has a unique solution and becomes explicitly solvable by a spectral approach.

As for OTTER, the spectral approach performs worse in estimating GRNs than the optimization by gradient descent. We therefore only report the latter in our experiments, where we explore the utility of graph matching techniques for GRN inference in comparison with OTTER. The precise gradient descent algorithms minimizing QAP or GRAMPA are detailed in the supplement.

Graph matching can also be studied within the optimal transport framework (Peyré, Cuturi, and Solomon 2016; Titouan et al. 2019). We could formulate the OTTER objective with respect to a nonstandard metric and regularization term. Since we are not searching for stochastic matrices W, this does not serve our purpose and we leave the transfer of related methods to gene regulatory network inference to future explorations.

Experiments

Experiments on synthetic data

To showcase the performance of OTTER for cases in which our assumptions are met and to study the influence of noise, we create synthetic data based on a ground truth W* that we try to recover from noise corrupted inputs W₀ = W* + E₀, P = (W*+E_p)(W*+E_p)^T, and C = (W*+E_c)^T(W*+ E_c). All noise entries are Gaussian and independently distributed with $e_{0,ii}~\mathcal{N}\left(0,{\sigma }_0^2\right)$, $e_{p,ii}~\mathcal{N}\left(0,{\sigma }_p^2\right)$, and $e_{c,ii}~\mathcal{N}\left(0,{\sigma }_c^2\right)$. To obtain a realistic ground truth for which we can repeat each experiment 10 times conveniently, we sub-sample (in each repetition) the ChIP-Seq network for the liver tissue to n_p = 100 and n_c = 200. (See the next section for more details.) As this is unweighted, we draw the weights iid from $\mathrm{N}\left({10}^{-5},1\right)$. For each network, we use the spectral and the gradient descent version of OTTER and report the obtained recovery error ∥|W − W*∥².

We align the eigenvalues of P and C by arranging them in descending order in the spectral approach. ADAM gradient descent for the OTTER objective is run for 10⁴ steps with the default ADAM parameters, as detailed in the supplement. For both the gradient decent and the spectral approach, we use parameters $\gamma ={\sigma }_{p/c}^2={\sigma }_p^2={\sigma }_c^2$ and λ = 0.5.

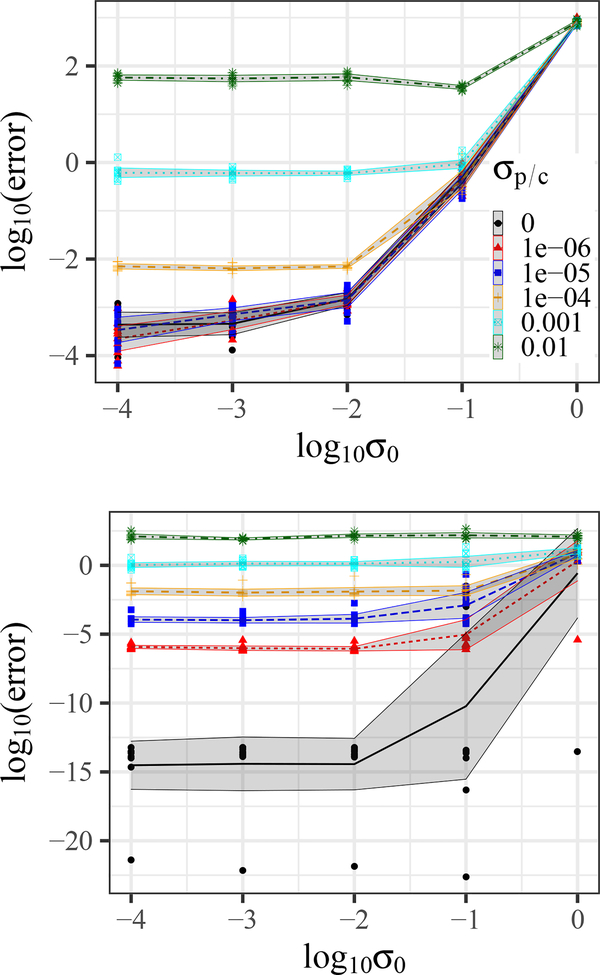
The results are shown in Fig. 3. For small levels of noise in P and C, the spectral approach performs reliably and better than gradient descent. However, for high ${\sigma }_{p/c}^2$ gradient descent outperforms the spectral method. Since biological data is inherently noisy, gradient descent seems to be the method of choice. Furthermore, it provides us with additional tuning options that we can leverage to outperform state-of-the-art methods.

Figure 3:

OTTER recovery error using (top) gradient descent and (bottom) spectral decomposition for artificial networks of size n_p = 100, n_c = 200 and Gaussian noise with variance ${\sigma }_{p/c}^2$ for P and C and ${\sigma }_0^2$ for W₀. Shaded regions correspond to the 0.95 confidence interval and lines to the average over 10 repetitions. The legend applies to both figures.

Experiments on cancer data

The most abundant data source for studying gene regulation is gene expression data. These data are often measured using bulk RNA-sequencing (RNA-seq) with samples corresponding to different individuals.

Datasets and experimental set-up

We obtained bulk RNA-seq data from the Cancer Genome Atlas (TCGA) (Tomczak, Czerwińska, and Wiznerowicz 2015). The data is downloaded from recount2 (Collado-Torres et al. 2017) for liver, cervical, and breast cancer tumors and normalized and filtered as described in the supplement. The corresponding Pearson correlation matrix defines the gene-gene co-expression matrix C consisting of n_c = 31,247 genes for breast cancer, n_c = 30,181 for cervix cancer and 27,081 for liver cancer. The protein-protein interaction matrix P is derived using laboratory experiments and represents possible interactions; we use the version of (Sonawane et al. 2017) and fill unavailable information with zeros. P consists of n_p = 1,636 potential TFs. Our initial guess of a gene regulatory network, W₀, is derived from the human reference genome. It is almost identical across tissues. It only varies slightly according to the number of genes (n_c) included after filtering and normalization. W₀ is a binary matrix with w_0,ij ∈ {0, 1} where “1” indicates a TF sequence motif in the promoter of the target gene. Sequence motif mapping was performed using the FIMO software (Grant, Bailey, and Noble 2011) from the MEME suite (Bailey et al. 2009) and the GenomicRanges R package (Lawrence et al. 2013). Note that neither W₀ or P carry sign information about edge weights so that we cannot infer whether TFs inhibit or activate the expression of a gene. We therefore focus on the prediction of link existence with the understanding that the type of interaction can be estimated post hoc.

Validation of gene regulatory networks is a major challenge. Data from chromatin immunoprecipitation followed by sequencing (ChIP-seq) experiments, which measure the binding of TFs to DNA in the genome, provide a validation standard against which to benchmark our results. Each ChIP-seq experiment assays only one TF. Because of the assay’s relatively high cost, there are only few data sets that have ChIP-seq data for many TFs from the same cells. We used ChIP-seq data from the HeLa cell line (cervical cancer, 48 TFs), HepG2 cell line (liver cancer, 77 TFs) and MCF7 cell line (breast cancer, 62 TFs) available in the ReMap2018 database (Chèneby et al. 2018), a database collection of publicly available ChIP-seq datasets from available studies. This database contains identified ChIP-seq peaks, representing our target TF binding sites. Further details are given in the supplementary material. Based on this data, we measure the performance of link classification on the subnetwork in each tissue that is constrained to the available TFs and report the AUC-ROC (area under the receiver operating characteristic curve) and AUPR (or AUC-PR) (area under the precision recall curve).

Hyperparameter tuning of OTTER was assisted by MATLAB’s bayesopt function utilizing a Gaussian process prior to maximize the joint AUC-PR for breast and cervix cancer, max AUPR_breast · AUPR_cervix. Breast and cervix data serve therefore as training data while the liver cancer data is an independent test set. The parameters of all compared methods are reported in the supplementary information.

Results

Table 1 compares the feasible GRN inference and relaxed graph matching methods based on comparison with experimental ChIP-seq binding data. Note that we also report the performance of our initialization W₀, which is based on motif data. OTTER GRAD, PANDA, QAP GRAD, and GRAMPA GRAD greatly improve this initial guess and make it tissue specific. Overall, OTTER gradient descent (OTTER GRAD) achieves the best performance on all tissues, in particular, on the liver test set. An enrichment analysis of Gene Ontology terms between networks for healthy and cancerous liver tissue in the supplement provides additional evidence that OTTER GRAD is biologically meaningful.

Table 1:

TF binding prediction for different cancer tissues.

	AUC-ROC (AUC)
Method	Breast	Cervix	Liver
COR	0.5900	0.5758	0.5637
Partial COR†	0.5366	0.5209	0.5175
ARACNE	0.6150	0.5234	0.5636
GENIE3	0.4818†	0.4832	0.4846
TIGRESS†	0.4945	0.4808	0.5018
OTTER spectral	0.5787	0.5420	0.5345
GRAMPA grad	0.6301	0.6328	0.6072
QAP grad	0.6373	0.6287	0.6081
WGCNA TOM	0.6146	0.5842	0.5946
W0	0.6282	0.6261	0.5982
PANDA	0.6739	0.6642	0.6211
OTTER grad	0.6936	0.6833	0.6600
	AUC-PR (AUPR)
COR	0.2772	0.2247	0.3057
Partial COR†	0.2361	0.1952	0.2525
ARACNE	0.2858	0.2027	0.2986
GENIE3	0.2064†	0.1836	0.2437
TIGRESS†	0.2088	0.1845	0.2523
OTTER spectral	0.2555	0.2024	0.2614
GRAMPA grad	0.3162	0.2763	0.3223
QAP grad	0.3215	0.2637	0.3425
WGCNA TOM	0.2834	0.2229	0.3140
W0	0.2865	0.2523	0.3045
PANDA	0.3481	0.2960	0.3503
OTTER grad	0.3752	0.3179	0.3746

The symbol † indicates that binding predictions were made only for TFs with ChIP-seq data due to high computational demands. The highest score for each data set is shown in bold.

Interestingly, ADAM gradient descent solving alternative graph matching problems, i.e., QAP GRAD and GRAMPA GRAD, achieve better results than established GRN inference algorithms, even though they were not originally designed for this purpose. They succeed based on similar hyperparameters as OTTER GRAD.

In general, we observe better performance for the methods that incorporate additional biological evidence such as (transformed) protein-protein interactions and binding motifs, even though P and W₀ are not tissue-specific. A reason for this is that correlations in gene expression can be caused by many factors. Many TFs are expressed at very low levels but strongly activate their target genes, obscuring correlations between TFs and their targets. Hence, graph matching approaches are a promising alternative to models that make predictions based on gene expression alone.

Discussion

We formulated the inference of a bipartite network from its two projections as a non-convex but analytically tractable optimization problem, OTTER. The projections alone do not provide enough information for network inference, as OTTER has multiple solutions that we derived explicitly. We proposed two natural inference algorithms for model selection, a spectral approach and gradient descent, and derived sufficient conditions for network recovery. Both rely on an additional initial guess of the bipartite network, W₀, which has to be close to the correct network to guarantee good network recovery. We find the spectral approach to be more reliable in low noise settings, while gradient descent seems to be more robust with respect to higher amounts of noise and therefore more suitable for our application of interest: gene regulatory network inference.

As we have shown, gradient descent also resembles in part an established gene regulatory network inference method, PANDA. OTTER can therefore be interpreted as a theoretically tractable simplification of PANDA that provides an intriguing connection to relaxed graph matching. OTTER also outperforms state-of-the art gene regulatory network inference approaches on real world data sets corresponding to three human cancer tissues. We make these data sets publicly available to benchmark the use of general graph matching algorithms for gene regulatory network inference (Guebila et al. 2020). As highlighted, relaxed graph matching approaches apply to this setting and achieve competitive performance. They have the advantage that they can integrate additional information about a gene regulatory network in the form of W₀ and protein interactions P. We therefore see great potential in transferring other graph matching techniques to gene regulatory network inference in future investigations.

Data and code availability

OTTER is available in R, Python, and MATLAB through the netZoo packages: netZooR v0.7 (https://github.com/netZoo/netZooR), netZooPy v0.7 (https://github.com/netZoo/netZooPy), and netZooM v0.5 (https://github.com/netZoo/netZooM).