Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2021 Oct 18;6(43):29223–29232. doi: 10.1021/acsomega.1c04842

Remote Learning of COVID-19 Kinetic Analysis in a Physical Chemistry Laboratory Class

Kelle D Hart 1, Chelsea Thompson 1, Clay Burger 1, Dylan Hardwick 1, Amanda H Michaud 1, Abdul HM Al Bulushi 1, Cole Pridemore 1, Carson Ward 1, Jixin Chen 1,*
PMCID: PMC8547164  PMID: 34723043

Abstract

graphic file with name ao1c04842_0009.jpg

The COVID-19 pandemic has affected many in-person laboratory courses across the world. The viral spreading model is complicated but parameters, such as its reproduction number, Rt, can be estimated with the susceptible, infectious, or recovered model. COVID-19 data for many states and countries are widely available online. This provides an opportunity for the students to analyze its spreading kinetics remotely. Here, we reported a laboratory set up online during the third week of the spring semester of 2021 to minimize social contacts. Due to the wide interest in developing online physical chemistry and analytical laboratories during the pandemic, we would like to share this laboratory design. The method, technique, procedure, and grading are described in this report. The student participants were able to apply the kinetic techniques learned in physical chemistry to successfully analyze an ongoing real-world problem through a remote learning environment and prepare this report.

Introduction

This laboratory targets students who are taking physical or analytical chemistry laboratory courses and have studied or are in the process of studying kinetics. The pandemic has rapidly affected chemistry and promoted remote teaching and learning globally.1,2 Significant long-term changes in chemistry laboratory courses have been suggested in the COVID-19 special issue of the Journal of Chemical Education.1 Since learning data analysis techniques are critical for students in physical chemistry laboratories, the co-authors of this report performed a project remotely to analyze kinetic data at the beginning of the spring semester of 2021. During the laboratory period, the instructor generated or provided kinetic data and instructed the students on how to go about analyzing that data. This instruction included finding key parameters, drawing useful conclusions, and predicting the kinetics under new conditions.3 The laboratory allowed the students to apply the kinetic analysis method to the COVID-19 pandemic situation and draw relevant conclusions that will give them a better understanding of the spreading character of the COVID-19 virus.

COVID-19 is a novel virus that the whole world has encountered. It is a new coronavirus strain labeled as SARS-CoV-2.4 This specific strain is an upper respiratory virus that is somewhat like the flu but foreign to human immune systems.5,6 This newest coronavirus was first identified in December of 2019 and propelled the development of new virus detecting methods.5,6 The list of possible symptoms associated with this virus is incredibly long due to people responding to it differently. The most common symptoms include cough, fever/chills, body aches, and difficulty breathing after doing normal tasks.7 The severity of the virus ranges from a typical cold to intense respiratory problems. Unfortunately, this virus is a deadly one and has led to the deaths of over three million people worldwide from the first infection to April 2021.8 Currently, this virus is known to spread through droplets released into the air when a person who is infected coughs or sneezes. These droplets normally do not travel more than a couple of feet. There has also been evidence that aerosol that travels much further may contribute to the spread.9 Because of this information, social distancing is one of the ways that the CDC recommends mitigating the spread of the virus.10

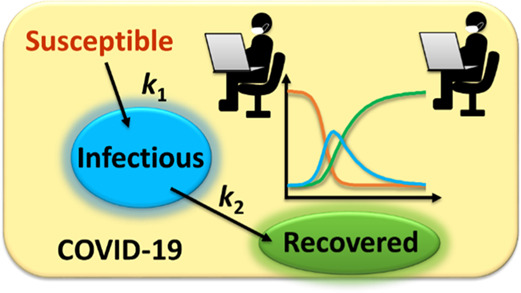
With the unfortunate introduction and proliferation of COVID-19 worldwide, many questions were raised by the scientific community. The most important question that this laboratory activity aims to answer is, how fast does this virus spread? This question can be answered using a kinetic model. Kinetic models help understand, explain, and forecast the rate at which a virus spreads. Many disease-spreading models have been published in the literature.11−16 The kinetic model that was used in this experiment is the susceptible–infectious–recovered (SIR) model,17−19 which is widely used in the academic literature and general public,16,20,21 and has been introduced to the chemistry teaching practice very recently.22,23 In this model, a two-dimensional plot that contains the number of infected individuals on the y-axis and time on the x-axis is used to visualize how fast a virus truly spreads.16−19 Many alternative models that have been reported in the literature are used to investigate the spreading of infectious disease, a common feature of most is using the reproduction/replacement number Rt as a key parameter, whose initial value is called basic reproduction number R0.11,12,21 We chose the SIR kinetic model due to its dependence on the Rt value which correlates to the ease at which the virus spreads. This factor was then studied as to how it related to the effect of mitigating factors like social distancing and other governmental regulations. We also chose the SIR model for analysis due to its relevance to the material taught in class. This laboratory class was the first laboratory class taught in the semester, and it allowed for students to become proficient in modeling kinetic trends, Microsoft Excel skills, and advanced plotting techniques. These skills were used throughout the rest of the semester on examinations and homework.

The R0 and Rt values of an infectious disease are indicators of how contagious a disease is and how easily it spreads from person to person.24 The main purpose of this laboratory, besides investigating the kinetic model of COVID-19, was to analyze this Rt parameter of the virus and how social events or limitations affect its value. The Rt is defined as the average number of people that one infected person could infect. For example, the Rt value for the seasonal flu is around 1.30. This means that for every person that is infected, they have the chance on average to infect one and a third person.25 When the Rt value approaches one, the number of infectious people remains the same over time.10 The Rt value can be brought below one with social restrictions and herd immunization.26−28 These aspects would allow for the virus infections to come to a gradual halt. Since the immunization for COVID-19 is in the infant stages, the Rt value of COVID-19 is still ever-changing and is a value above one across the globe.29 During this experiment, data from different states within the United States were analyzed, and the Rt values were assigned to peaks and dips on the curves of the infected cases. It is still ongoing research in the literature on the causes of the variation on Rt with a lot of efforts in correlating with governmental policies and more recently also on vaccination.30−33 Thus, the students were encouraged to associate these peaks and dips with social events, mass gatherings, or regulations such as social distancing depending on the value of Rt. Note that the students should be instructed that these correlations are just hypothetical practices based on the simple social distancing rationale. More evidence such as contact tracking is needed to conclude with higher confidence.

Before introducing the SIR model to the students, we started analyzing compound interest and payment balance models of a typical mortgage loan to engage and prepare the students. The mortgage model has been used in the United States and most countries to pay off homes and take loans from the bank. The mortgage model uses variables of time, balance, compound interest, and payment to function,34 while the SIR model uses time, susceptible people, infectious people, recovered people, and Rt to function. When setting up the SIR model, the key variable to study is the Rt value as it describes the rate of infection among citizens. The key variable to study within the mortgage model is the payment as it determines the amount of principal and interest to be paid. If the payment value is changed in the mortgage model, the interest amount and balance amount fluctuate accordingly.35 If the Rt value is changed in the SIR model, the amount of infectious and recovered people changes. The parallel examination encouraged the students to find the similarities between these two models. Even though the students found similarities between the two models, it must be noted that the mortgage model is somewhat disconnected from the SIR model. It is provided to the students as a warmup experience of manual regression using Excel. If the students have learned the general consecutive reaction model in the lecture class, it can be used to replace the mortgage model.

As for the laboratory techniques, the widely available software Microsoft Excel was heavily used in the modeling and fitting, and all interactions with students were held via Microsoft Teams. This format is similar to the literature reported teaching physical chemistry courses remotely during the pandemic.1,2 Solving simple kinetics without integrals is educationally beneficial to high school and college students.36,37 We are interested in using this technique to analyze the SIR model. For this relatively complicated consecutive reaction model, computer programing is ideal to teach the kinetics without the steady-state approximation.38−41 Excel has been reported as an efficient tool to teach kinetics.36,37 We have been using Excel very intensively for our physical chemistry course. The free software Google Sheets can be used if there is an accessibility issue with Excel. In this laboratory, we first introduced the mortgage model of loans and explained the analytical and numerical solutions of the kinetic model. We then introduced how to use Excel to implement these calculations. The students then downloaded statewide COVID-19 data and analyzed it to find Rt values over time in a randomly chosen state in the United States. The major goal is to teach the students the kinetic models and the regression method for data fitting.

Our laboratory design is complementary to the kinetic analysis laboratories reported in the literature for chemical reactions and COVID-19. Kinetic analysis for chemical reactions is a common practice in various chemistry courses.42−44 Right after the first outbreak of the epidemic, the SIR model has been compared to a second-order autocatalytic chemical reaction system, and the data have been fitted using a programming language during a physical chemistry class.23 This report is targeting the early stage of the spreading by fitting a single set of parameters including the Rt value. Our model has complementary targets fitting longer-term variations on the Rt value such as detection, quarantining, social distancing, and vaccination. The SIR model has also been compared to the collision theory that explains the connection between the rate constants with the social interactions within the society.22 Combining others and our practices, we believe the COVID-19 kinetics analysis has the potential to go beyond the laboratory courses. It can be taught in the physical chemistry lecture courses as an example application of the consecutive reaction model of the kinetic theory. At the same time, we may consider teaching kinetics without the steady-state approximation with the help of numerical simulation using Excel or computer programming.

Results and Discussion

The online laboratory is carried out with a brief introductory lecture, demonstration, active discussion, and hands-on calculations. The major goal for the students is to use the common principles in kinetic modeling and learn the numerical regression method to fit kinetic data.

Mortgage Analysis

The students are instructed to compare the analytical and numerical solutions of fixed monthly payment mortgages. The mortgage model is not directly connected to the SIR model. It is provided to the students as a warmup experience of manual regression using Excel. If the students have learned the general consecutive reaction model in the lecture class, it can be used to replace the mortgage model. All calculations are carried out with Microsoft Excel or Google Spreadsheet. Microsoft Excel is available for free at many American Universities, and Google Spreadsheets are free for anyone to use. In the analytical solution, the equation used to solve for monthly payment is given by34,35,45

graphic file with name ao1c04842_m001.jpg 1

where P is the monthly payment, r is the interest rate per month, PV is the principal, and n is the number of payments. The student is given the equation and instructed to find a solution for a set of given parameters and experiment with any parameters they want to try. For example, PV = $100,000, n = 360 months (30 years), and r = 0.4869% (annual rate 6%), yield P = $589.37 per month. One major concept comes from the annual compound interest rate which is used to calculate the monthly compound interest rate

graphic file with name ao1c04842_m002.jpg 2

where ra is the annual compound interest rate or annual percentage rate.

The students then carry out the same analysis in Excel using the numerical simulation with a manual regression strategy (Table 1, Figure 1). Most students are familiar with Excel, but step-by-step instruction is given to avoid difficulties and confusion in the next steps due to this regression method being used to analyze the COVID-19 data later. An example Excel sheet has been attached to the Supporting Information section. Then, fixed parameters are placed in column H (Table 1). Four columns in Excel A, B, C, D are set for four vectors, time, balance, interest, and payment (Table 1). The first row lists these column names. The first column, column A, contains the time vector, months from 0 to 400. In the second row, the cell of B2 is set to =$H$4, the same as the analytical example. The interest is then set to 0, and the payment is set to 0. The “=” sign is used in Excel to type in an equation, and the “$” sign is an operator to lock the citation cell during a vector calculation. Excel uses aEb to represent the scientific notation of the number a × 10b. Row 3 initializes the vector calculation with the equations shown, which can be dragged by the corners of the cells to the bottom row to automatically implement a vector calculation in Excel. This operation finalizes the creation of the “software.”

Table 1. Part of the Excel Sheet for the Numerical Mortgage Calculationsa.

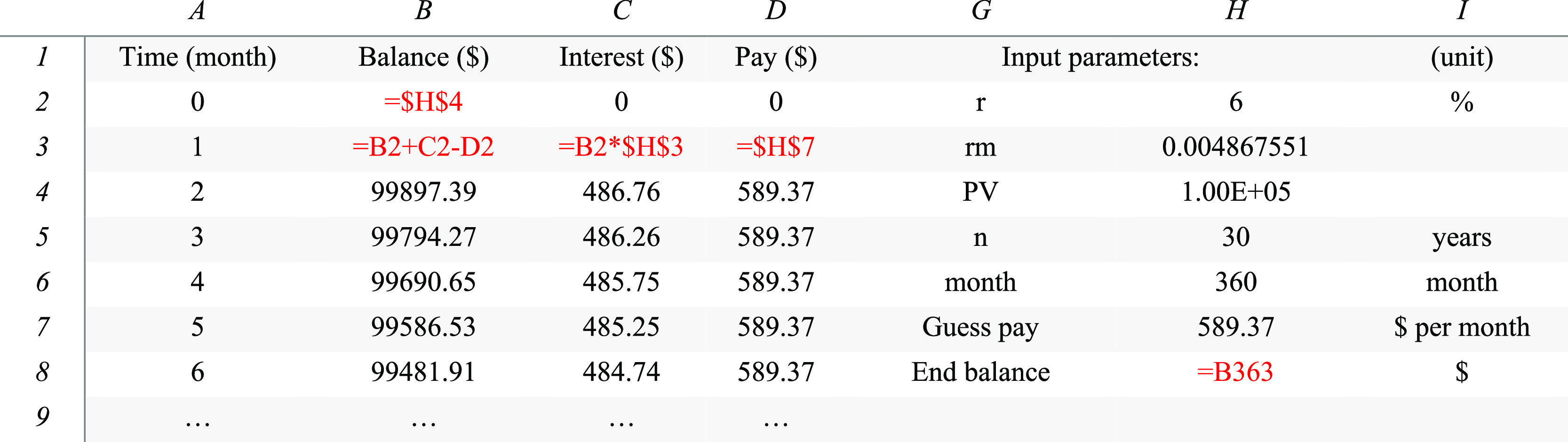
graphic file with name ao1c04842_0008.jpg

Open in a new tab
a

Note: red color showing the formula to type in Excel. Cell H8 value = 0.4. Significant figures are from Excel default and have not been corrected.

Figure 1.

Figure 1

Open in a new tab

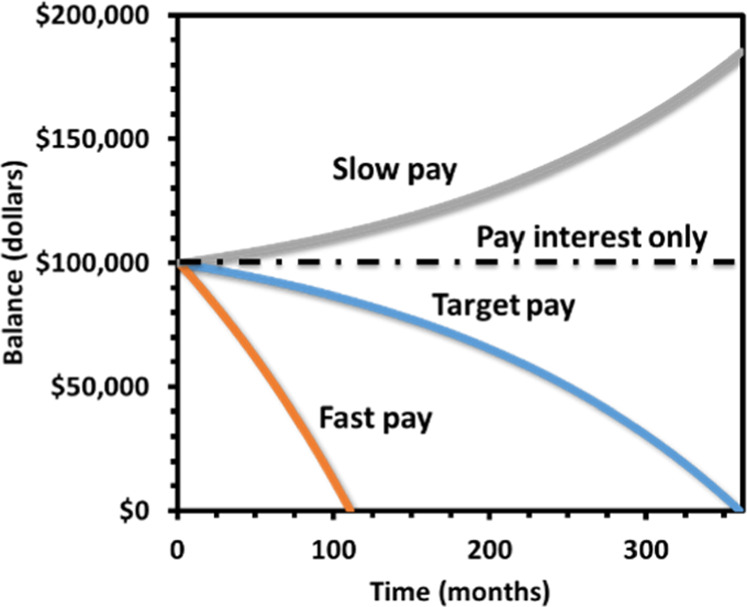
Overlay of a few plots of the balance over time modified from a student’s laboratory report. Part of the Excel sheet is shown in Table 1.

In the next step, the students manually change the monthly payment to find a condition indicated by reaching a 0 balance at the end month, a root-finding problem. This value can be monitored in the reporting cell, H8 (Table 1). The balance versus time curve is also plotted in the Excel spreadsheet (Figure 1). The students are instructed to play with the monthly payment value manually. Typically, less than 10 guesses are needed for a regression convergence with three significant figures. The students are then free to change the initial parameters to practice a few random calculations using their “software” creation.

SIR Model Analysis

The standard SIR model is then introduced to the students. The students should have a general knowledge of physical chemistry kinetics or should be learning it within the course to understand this model. It should be noted that the SIR model of kinetics and the standard consecutive reactions kinetic model hold a significant difference. The significant difference is that the rate constants are expressed in different ways. The rate constant for the SIR model is expressed in terms of the Rt, while the consecutive reaction model uses k as the rate constant. The students are instructed to create a numerical simulation on the SIR model like the mortgage simulation. This simulation should contain a rate of growth and a rate of reduction. The subsequent curve represents a logistic function that the students may have seen before. The primary purpose of the simulation is to introduce the concept of the Rt value to the students and should be correlated as being complementary to the consecutive kinetic model the students have studied during the lecture class. For a SIR model14,16,19,46

graphic file with name ao1c04842_m003.jpg 3

where susceptible (S) is the total non-infected people in the state, infectious (I) is the active carriers that can infect others, recovered (R) is the people who are neither susceptible nor infectious (immune or dead), N is the total population in the state, β is the average infection frequency of one carrier infecting a susceptible person per period with the unit of day–1, and γ is the frequency of removing a carrier with the unit of day–1. It is important to note that as soon as a person is infected, he/she can begin infecting others, and the probability of this person infecting others is related to the γ value which is discussed further in this report.

The following differential equations of the SIR epidemic model are used for the students to numerically fit the COVID spreading data.13,14,16,19,47

graphic file with name ao1c04842_m004.jpg 4
graphic file with name ao1c04842_m005.jpg 5
graphic file with name ao1c04842_m006.jpg 6

The reproduction number, the average number of people infected by an infectious person is

graphic file with name ao1c04842_m007.jpg 7

The basic reproduction number, R0, is defined as the initial replacement number when one infectious individual is introduced into an all-susceptible population with initial parameters β0 and γ0, 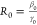Inline graphic.16 We can define time-dependent reproduction number

graphic file with name ao1c04842_m009.jpg 8

Rt remains constant at R0 over time if no action is taken. When actions such as social distancing, detection, protection, quarantine, and better treatment are taken which change β and γ, then Rt changes over time.

We can further assume an effective reproduction number from eq 5 to incorporate the effect of the “dilution” of the susceptible population on spreading into the effective reproduction number13,26,47

graphic file with name ao1c04842_m010.jpg 9

where S(t) is the non-immune susceptible population and N(t) is the total population. We can see that when Re > 1, eq 5 has a positive value, and the number of infectious people exponentially grows; when Re < 1, eq 5 has a negative value, and the number of infectious people exponentially decay; and when Re = 1, eq 5 equals 0, and the curve of infectious people reaches a “steady state.”

Comparing Rt and Re, Rt is correlated to β and the second-order spreading rate constant (eq 8), and Re is correlated to the quasi-first-order rate constant with respect to the infectious population (eq 9).

The students are then instructed to use a set of parameters to create a simulated trajectory of the SIR model of an epidemic example in Excel. An example is shown in (Table 2, Figure 2), and an in-class demonstration file is shown in the Supporting Information.Equations 4–6 are numerically approximated by calculating the changes in the number of people ΔS, ΔI, and ΔR within time Δt. The simulation is more accurate with a smaller time spacing Δt. Δt is set to 1 day in this laboratory, but it can be a variable for the student to change to check the convergence of the simulations. The students create their own Excel files and debug their formulas and then can play with changing the parameters such as the size of population N, recovery rate γ, and spreading rate β/N to check the trend of the trajectories. In this model, the Rt, β, and γ remain constants, and the two reactants, S and I, change over time (Table 2, Figure 2). We can see for a constant Rt, S goes down, R goes up over time, and I goes up at the early stage and then goes down at the later stage when assuming the recovered population gains immunity in the SIR model (Figure 2A). This is because the “concentration”/fraction of the susceptible people (S/N) drops over time, becomes significant, and then dominates at the middle to late stages of the outbreak, which reduces the probability of an infectious individual reacts with a susceptible individual. Rt maintains constant over time in this simulation, while Re decays from R0 to zero over time and equals 1 at the peak of the I curve, a “steady-state” (Figure 2B). It is scaled from the curve of the number of susceptible populations.

Table 2. Excel Sheet of a Simulated SIR Model.

time Rt Re(t) β γ S I R
0.0 3.0 3.00 0.375 0.125 1000.0 1.0 0.0
1.0 3.0 3.00 0.375 0.125 999.6 1.3 0.1
2.0 3.0 3.00 0.375 0.125 999.2 1.6 0.3
3.0 3.0 3.00 0.375 0.125 998.6 2.0 0.5
4.0 3.0 2.99 0.375 0.125 997.8 2.4 0.7
Open in a new tab

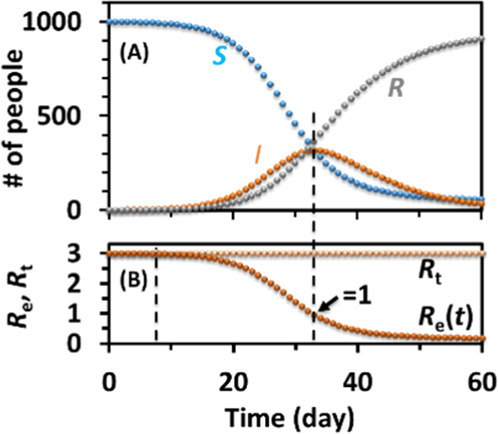
Figure 2.

Figure 2

Open in a new tab

Corresponding SIR curves of the numerical simulation of the SIR model in Excel with N = 1000. Part of the Excel sheet is shown in Table 2. (A) Changes of populations over time. (B) Changes of reproduction number and effective reproduction number over time.

To simplify the analysis in this laboratory class, we assume that the total population of interest N(t) remains the same N over time and are all-susceptible at the beginning, and the recovered or vaccinated population is immune

graphic file with name ao1c04842_m011.jpg 10

where V is the number of people who are vaccinated. Because the data we had in the laboratory was at the early stage of the COVID-19 outbreak when S(t) ≈ N(t) (Figure 2B, left part of the dashed line on the left), following an approximation in the literature,47 we further simplified eq 9 to

graphic file with name ao1c04842_m012.jpg 11

Future laboratories can consider including the vaccination and recovery data in the analysis, suggesting to assume S(t) = (1 – pR – pV)N(t), where pR is the fraction of the population that has been recovered (assuming people gain immunity after recovery) and pV is the fraction of non-infected people who are vaccinated. Therefore

graphic file with name ao1c04842_m013.jpg 12

If there are populations who are naturally immune, it can be further removed from the susceptible population. One can see that, for example, R0 = 3, >67% vaccination rate is enough to bring the Re to <1 to guarantee the value I to exponentially decay when eq 5 has a negative value. At this vaccination ratio, the society achieves “herd immunity”26 without any change in β and γ (and thus a constant Rt), that is, under the same social and clinical conditions before the breakout.

Obtaining the COVID Data

The students are then instructed to obtain and analyze COVID-19 data from two states within the United States, with the state of residence being mandatory and the other state being the student’s choice. The students are instructed to download the COVID spreading data. Some data sites contain Excel files of the spreading data, while some do not. The instructor should suggest that the students pick a website that uses a downloadable data format,48 whose consistency has been checked with official sources such as the US CDC and WHO. This laboratory was done in February 2021, so most of the data are from around March 2020 to February 2021 for a US state. Only the time (date) and the accumulated positive viral test values are used for this data analysis laboratory.

An example of the data and the pre-analysis data treatment is shown in Figure 3. The date are ordered backward in the original data file found online, with the most recent dates at the top of the document and the later dates at the bottom of the document. Before analysis, the data should be resorted to have the most recent dates at the bottom and later dates at the top using the sorting function in Excel. The daily number of people who tested positive can be obtained by subtracting a day’s positive test value from the day before (−ΔS). If the daily positive cases are plotted, the curve is consistent with the curves from the CDC or other websites such as Google (Figure 3B). This daily positive curve is then smoothed using a moving-average method in Excel. This is carried out by creating a new column and calculating the average cases in 5–7 days. An example of a moving average would be that the day 1 value is the average positive cases of day 1–6, the day 2 value is the average positive cases of day 2–7, the day 3 value is the average positive cases of days 3–8, and so on. This smoothing allows the students to identify waves at the noisy parts of the data which signify inclines or declines in positive cases. For the simplicity of this laboratory, the waves in the smoothed daily cases are divided into pieces of incline periods and decline periods manually. Students divide the pieces very differently depending on where they think the incline and decline periods are located. Some students divide the periods, as shown in Figure 3B, into many more pieces, especially for the areas around markers 6 and 7. Some students may only divide the smoothed graph into a few pieces for analysis. For simplicity, each piece will be fitted with one average Rt value. This procedure is explained in the next section.

Figure 3.

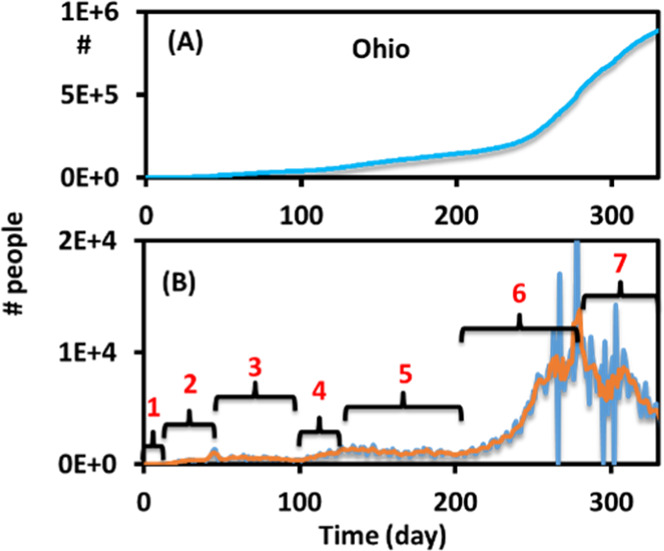
Figure 3

Open in a new tab

(A) Example raw data (state of Ohio) of the accumulated positive test cases (N–S) vs time. (B) Tested positive cases per day (−ΔS) and an overlay of the smoothed data in orange. The time is divided manually into seven pieces for the further fitting of Rt.

COVID Data Analysis

First, the students will use the first 2 weeks of state Covid-19 data to find an initial R0 value of the state using the manual regression method under direct instructor demonstration. For this section, students will need to create several columns to calculate the SIR values each day using the model, as shown in Figure 2, and then compare the (I + R) values to the accumulated cases. The instructor should have fixed all parameters for a given state, except for the Rt value, which is the only parameter that is left to adjust during the manual regression data fitting. All people within a state are assumed to be susceptible at the beginning of the spread.

The value γ(t) is difficult to determine in each state. In the SIR model (eqs 4–8), each infectious individual randomly infects βS/N people per day, and the infected person recovers or dies with the probability of γ per day. The γ value is dependent upon the inverse of the recovery time.16,46 Both β and γ values should change over time. When the two parameters have the same value, the number of infected people I drops because the rate in eq 5 is negative. It drops faster and faster over time because the fraction of the susceptible population S/N in eq 5 decays. The β(t) and γ(t) values are affected by detection, self and mandatory quarantine, treatment, vaccination, and even seasonal changes. Given similar conditions, γ(t) should be relatively stable. Literature sources also reported the median incubation time (time to show symptoms) for COVID-19 being 5.1 days,49,50 and the individual is suspected already infectious during this period.49 The United States CDC reported average infectious time, the time between infection and loss of infectiousness, of COVID-19 being 5–7 days.51 After that, the person may stay infectious but does not infect others due to the factors of quarantining, or recovery, or death. We fixed the average γ(t) value to be 1/5 day–1 in this laboratory to simplify the analysis. This γ value is consistent with the values adopted in the literature.11

The students can then manually guess the Rt value that changes the β(t) to quickly get a good fit signified by an overlay between the raw data and the simulated curve (Table 3, Figure 4). As listed in Table 3, the first column is the day, the second column is the accumulated positive raw data, the Rt value is guessed, and β is calculated from eq 7 with the guessed Rt and fixed γ value equaling 0.2 day–1. S, I, and R are calculated using eqs 4–6 with Ohio’s population, N, equaling 1.16 × 107 and an initial guess of I0 equaling 1. The last column is the simulated total positive cases I + R. Please see the Supporting Information in the Excel sheet for the procedure. The simulated curves with different guesses on Rt are shown in Figure 4. Fitting by eye is used in this laboratory for the time concern, and students with extra time can be instructed to use the least-square residual criteria for fittings with better goodness. The students found that it was easy to guess an Rt with two significant figures that fit the data well by eye. The initial R0 value at Ohio is 2.8, which is consistent with the literature reported value of an average initial R0 value of about 2– 4 in many places of the United States,12 and consistent with the initial R0 of other countries.23

Table 3. Part of the Excel Sheet in Fitting the R0 Value of the State of Ohio.

day case R0 β γ S I R simu.
0 0 2.8 0.56 0.2 1.16 × 107 1 0 1
1 0 2.8 0.56 0.2 1.16 × 107 1.36 0.2 1.56
2 0 2.8 0.56 0.2 1.16 × 107 1.85 0.5 2.32
Open in a new tab

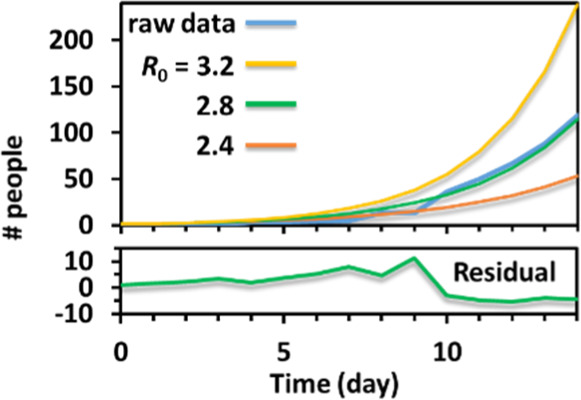
Figure 4.

Figure 4

Open in a new tab

Example simulation for the student to fit the average R0 values in the first 2 weeks of COVID-19 data of the state of Ohio. Overlap of the data with three different guesses of R0. Part of the Excel sheet is shown in Table 3. The fitting precision is adjusted by eyes. Students with extra time can create a square deviation column (square residual) to minimize the sum of the square deviation for better precision (Supporting Information, Excel sheet). The residual from the R0 = 2.8 fitting is shown in the figure.

The last step of the fitting is just to repeat the process for the other smoothed graph wave periods one by one. Students must start at the beginning dates and progress chronologically through wave periods because the fitting of each period is dependent on the fitting of the period before it (Figure 5). A few guesses of Rt values for each period are typically sufficient to obtain a reasonable fit of the curve (Figure 5A). Once all the pieces are fitted, one can also estimate the daily Rt′ values using eq 7 (Figure 5B). One can also overlap the daily positive cases with the fitted values to check the accuracy of the fitting (Figure 5C). This curve can be linked to the daily interest parameter of the mortgage model.

Figure 5.

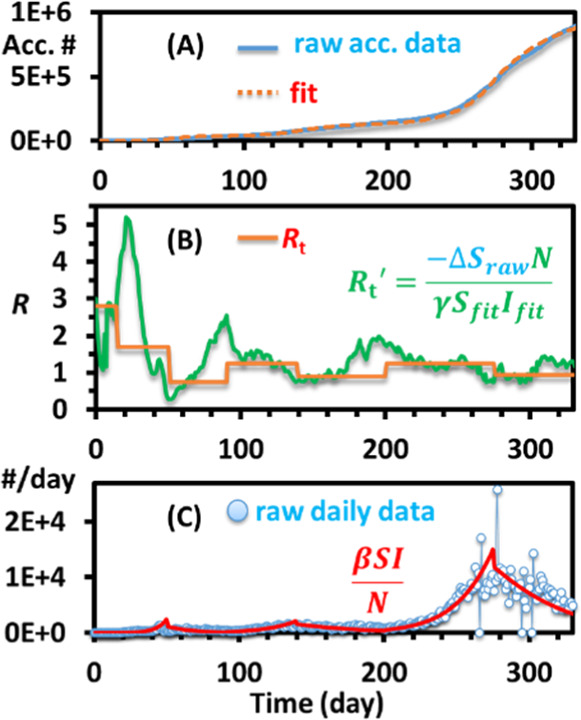
Figure 5

Open in a new tab

(A) Manually fitted cumulative positive cases of the state of Ohio with the piecewise guesses of Rt, as shown in (B). (B) Averaged Rt and an estimated daily value Rt′ using the equation shown. (C) Overlay of daily positive cases raw data and the piecewise fitted curves calculated with the equation modified from eq 4.

After fitting all the data, some students will have free time to play with the Rt values and predict a trajectory in the future based on different social activities such as fully open social activities, social distancing, reducing social activities, lockdown, and vaccination. Each event will affect the current Rt values, and the students will use the different social activities to project the future Rt values using the SIR model.

The students should be encouraged to fit at least one other state’s data. The states chosen by this class include West Virginia, Florida, Texas, Michigan, Tennessee, and New York. A few examples fitted by the students are shown in Figure 6.

Figure 6.

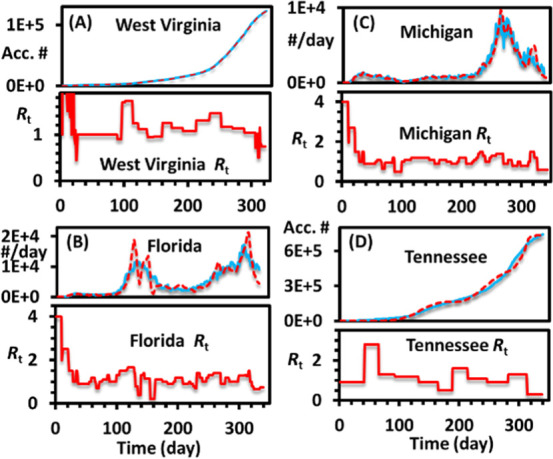
Figure 6

Open in a new tab

Example fittings by the students. The accumulated data are plotted in (A,D), and the daily positive data are plotted in (B,C), as preferred by different students.

Relating Rt Values to Social Events

The students are instructed to search for hypothetical correlations to the inclines or declines of positive cases indicated by the waves on the smoothed graph. The correlations are to be reported in their laboratory reports. These waves are not associated with the change in the fraction of the susceptible population (<10%), which maintains in small change at the early stage of outbreak and vaccination. Rather it is mainly attributed to the change in the reproduction probability β upon changes in social activities. The effect of a social event on the Rt value is assumed to show up after 1–2 weeks, which is consistent with a recent contact tracing study.30 For example, several students correlated the drop of the Rt value within the first month in Ohio with the stay-at-home order announced on day 18. A further drop in the value is associated with the mask mandate on day 53. A small incline wave around 60 days could be caused by the partial reopening of stores. After the reopening, the social distancing regulations allowed the Rt value to flatline over a long period. On day 150, the mask order was implemented in schools which correlated to seeing a dropped wave after about a week. The incline spikes after day 240 are correlated to the beginning of the holiday season, such as Halloween, Thanksgiving, Christmas, and New Year. It should be noted that this practice can be harmful if the students are not told that the guessing and associating of Rt is not scientifically rigid. Correlation with higher confidence can be found via contact tracing and statistical analysis with a few examples cited.30−33 There are inherent dangers with allowing students to be open with guessing the effects of the social mandates, and readers should use caution when allowing students to do so. It is ultimately up to the reader whether this practice is followed, but the reader may also implement guidelines for the students. For example, if the reader knows where the peaks and dips are in a certain state’s Rt kinetic model, they may be able to tell students that there are six peaks and the students must find what mandates they correlate to. Similar correlations are observed for other states with an example from a student, as shown in Table 4.

Table 4. Possible Correlation between COVID-19 Cases and Social Events in Texas was Modified (Formatting) from a Student’s Laboratory Report.

days Rt value CDC cases SIR cases % errora events
0–14 2.60 82 73 11.26 testing begins in Texas
14–50 1.81 21 944 19 856 9.51 (stay home order day 30)
50–90 0.93 66 568 66 271 0.45 schools go online
90–140 1.27 351 618 344 725 1.96 businesses can operate at 50% occupancy
140–200 0.90 688 534 687 486 0.15 bars close again
200–275 1.15 1 350 542 1 350 006 0.04 college football
275+ 1.07 2 574 194 2 611 607 1.45  
Open in a new tab
a

This student reports % errors between the confirmed cases in the state of Texas and the simulated data (the absolute value of 1 – simulated/confirmed) as a measure of the goodness of the manual simulations. These correlated events are hypothetical that may or may not be among the major causes.

Relating Rt to Reaction Rate Constant k

The students are then instructed to connect the Rt value to a typical reaction rate constant, k, that they have studied in the lecture class. In a typical kinetic analysis in physical chemistry, the β/N value and γ value will be presented as rate constants k1 and k2, while the Rt value is the total susceptible population times the ratio between the two individual reactions involving k1 and k2 (see eq 8).52 The students strengthen this connection in this laboratory and understand the exponential growth or decay models determined by the Rt value. The change in Rt upon social behaviors can be correlated to the change in the rate constant in a reaction. For example, social distancing is like the temperature of a heat-favor reaction suddenly drops; mask order is like a sudden rise of the reaction energy barrier; and vaccination is like a change in the reactant concentration on susceptible people.

When the effective reproduction number Re is introduced in future laboratories with later stages of the epidemic, the difference between Rt and Re should be discussed. Re is better correlated with the quasi-first-order rate constant of the number of infectious population than Rt. It is easier to be used to measure the spreading rate and predict the future trajectory of the epidemic. Rt is better correlated with the second-order reaction rate constant of the same reaction and the intrinsic properties of the disease than Re. It is easier to be used to compare the different mutations of the same disease or among different contiguous diseases. These simplifications (could be too naive) can help the undergraduate students establish a connection between the SIR model and the kinetic models learned in the textbook, especially for those who have just started learning kinetics.

Take-Home Questions and Report Grading

There are additional take-home questions for the student to think about within this laboratory, with one example being the discussion of the similarity between the mortgage model and the SIR model, that is, Rt = 1 is equivalent to paying just the interest in the mortgage, so the balance is flat. Additional questions include, what one can do to stop or slow down the spreading of the virus? What can the government do to help stop the spreading? What will a vaccination of 50% of the population do to slow down the spreading?

The laboratory report is written in a standard ACS style like this manuscript, with each section graded for both structural and merit points. Reports are due ∼2 weeks after the laboratory. Instruction is given to the students on the grading of the report and is also attached in the Supporting Information section of this report.

Conclusions

Numerical simulation of kinetics has its value in teaching kinetics and addressing complicated kinetic models. It also carries an additional advantage to explain or bypass the steady-state approximation for some models in the textbook. This form of teaching could also be positively impacted by the learning of a computer programming language, for example MATLAB that has been used in the author’s laboratory for research projects. As a rethinking of our chemistry curriculum has been suggested,1 we may consider adding the learning of a computer language as a mandatory requirement to overcome possible technical challenges. While this laboratory does not contain the learning of a computer language, this skill could aid students in becoming familiar with the premises of numerical simulations without the steady-state approximations. Start from this training, several sophisticated and free software packages of numerical simulation can be used for their later projects, such as Acuchem,53 Kinsim,40 and COPASI.9

By comparing the Rt value between states and their correlation with social events, we believe that social regulations such as lockdown, facemask, and social distancing orders are effective ways to slow down the spreading speed. However, we are aware that there are limitations on such analysis due to uncertainty on the data and the over-simplicity of the model.

From Rt analysis, we can see that its value is more sensitive to the changing of the spreading speed rather than the confirmed cases or accumulated confirmed cases. A very large number of positive cases does not necessarily associate with a large Rt value. This is because the Rt value is more connected to the slope of the increase rate rather than the absolute value of the confirmed cases. As such, it is a better parameter to investigate the total number of cases in a state. The change in the Rt value provides fast feedback on the evolution of the virus, the degree of the effect of the social regulations, events, and vaccination on the early stage. Bringing the effective reproduction number Re below 1 will see a turning point of the number of infectious people which is the goal of the disease control. We approximate Re to Rt for the early outbreak data in this laboratory (eq 8). Re can be calculated using eq 9 from Rt, which should be analyzed for future laboratories when infection and vaccination rate are significant. Although Re can be less than 1 with many different strategies, one would hope it to be realized via a large number of the vaccinated population rather than a large number of the infected population.

The manual regression method that the students learned in this laboratory can be employed in many other data analysis projects. Through learning these practices, students gain a hands-on feeling about how to adjust a fitting parameter to influence a larger set of data. Students also learn how to establish a software package in Excel dealing with complicated kinetic models. It is also crucial that the students create all the spreadsheets themselves. This can be carried out through direct demonstration by the instructor or brief demonstration by the instructor. The students should create the template because knowing the principles and using an established template are very different than creating a bug-free version of the template by themselves. The skill of applying an “eye-ball fit” by overlaying curves and checking differences is also adapted in this laboratory. The least-squares regression method and the accuracy of the fitting, such as the R(2) value, have also been introduced in the lecture but are not practiced in this experiment due to time restrictions. Convergence tests run by changing the independent variable spacing, Δt (which is reasonably set = 1 day now), have been discussed during the lectures and mentioned during the laboratory but are not practiced due to the time constraints. This laboratory class is important because students are to use these techniques for data analysis in later laboratories during the semester. We hope the knowledge of data fitting will be acquired and will provide the students with strategical data analysis experience in their future careers.

Acknowledgments

We thank all university and department teams that make the online teaching and in-person laboratory feasible during the pandemic. We also thank the National Human Genome Research Institute of the National Institutes of Health (award number R15HG009972) for supporting undergraduate teaching.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c04842.

  • Prelaboratory assignment, laboratory report instruction, and grading criteria (PDF)

  • Mortgage simulation and COVID-19 simulation and fitting (XLSX)

The authors declare no competing financial interest.

Supplementary Material

ao1c04842_si_001.pdf (413.4KB, pdf)
ao1c04842_si_002.xlsx (280.3KB, xlsx)

References

  1. Holme T. A. Introduction to the Journal of Chemical Education Special Issue on Insights Gained While Teaching Chemistry in the Time of COVID-19. J. Chem. Educ. 2020, 97, 2375–2377. 10.1021/acs.jchemed.0c01087. [DOI] [Google Scholar]
  2. Quezada R. L.; Talbot C.; Quezada-Parker K. B. From Bricks and Mortar to Remote Teaching: A Teacher Education Program‘s Response to COVID-19. J. Educ. Teach. 2020, 46, 472–483. 10.1080/02607476.2020.1801330. [DOI] [Google Scholar]
  3. Koc Y.; Doymuş K.; Karaçöp A.; Şimşek Ü. The Effects of Two Cooperative Learning Strategies on the Teaching and Learning of the Topics of Chemical Kinetics. J. Turk. Sci. Educ. 2010, 7, 52–65. [Google Scholar]
  4. Velavan T. P.; Meyer C. G. The COVID-19 Epidemic. Trop. Med. Int. Health 2020, 25, 278. 10.1111/tmi.13383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Pascarella G.; Strumia A.; Piliego C.; Bruno F.; Del Buono R.; Costa F.; Scarlata S.; Agrò F. E. COVID-19 Diagnosis and Management: A Comprehensive Review. J. Intern. Med. 2020, 288, 192–206. 10.1111/joim.13091. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Pokhrel P.; Hu C.; Mao H. Detecting the Coronavirus (COVID-19). ACS Sens. 2020, 5, 2283–2296. 10.1021/acssensors.0c01153. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Wu Y.-C.; Chen C.-S.; Chan Y.-J. The Outbreak of COVID-19: An Overview. J. Chin. Med. Assoc. 2020, 83, 217–220. 10.1097/jcma.0000000000000270. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. WHO . WHO Coronavirus (COVID-19) Dashboard. https://covid19.who.int/ (accessed April 17, 2021).
  9. Hoops S.; Sahle S.; Gauges R.; Lee C.; Pahle J.; Simus N.; Singhal M.; Xu L.; Mendes P.; Kummer U. COPASI—a COmplex PAthway SImulator. Bioinformatics 2006, 22, 3067–3074. 10.1093/bioinformatics/btl485. [DOI] [PubMed] [Google Scholar]
  10. Lotfi M.; Hamblin M. R.; Rezaei N. COVID-19: Transmission, Prevention, and Potential Therapeutic Opportunities. Clin. Chim. Acta 2020, 508, 254–266. 10.1016/j.cca.2020.05.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ferretti L.; Wymant C.; Kendall M.; Zhao L.; Nurtay A.; Abeler-Dörner L.; Parker M.; Bonsall D.; Fraser C. Quantifying SARS-CoV-2 Transmission Suggests Epidemic Control with Digital Contact Tracing. Science 2020, 368, eabb6936 10.1126/science.abb6936. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Ives A. R.; Bozzuto C. Estimating and Explaining the Spread of COVID-19 at the County Level in the USA. Commun. Biol. 2021, 4, 60. 10.1038/s42003-020-01609-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cooper I.; Mondal A.; Antonopoulos C. G. A SIR Model Assumption for the Spread of COVID-19 in Different Communities. Chaos, Solitons Fractals 2020, 139, 110057. 10.1016/j.chaos.2020.110057. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Wikipedia . Compartmental models in epidemiology. https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology (accessed March 23, 2021).
  15. Canini L.; Perelson A. S. Viral Kinetic Modeling: State of the Art. J. Pharmacokinet. Pharmacodyn. 2014, 41, 431–443. 10.1007/s10928-014-9363-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Simon C. M. The SIR Dynamic Model of Infectious Disease Transmission and Its Analogy with Chemical Kinetics. PeerJ Phys. Chem. 2020, 2, e14 10.7717/peerj-pchem.14. [DOI] [Google Scholar]
  17. Ross R. An Application of the Theory of Probabilities to the Study of a Priori Pathometry.—Part I. Proc. R. Soc. London, Ser. A 1916, 92, 204–230. 10.1098/rspa.1916.0007. [DOI] [Google Scholar]
  18. Ross R.; Hudson H. P. An Application of the Theory of Probabilities to the Study of a Priori Pathometry.—Part II. Proc. R. Soc. London, Ser. A 1917, 93, 212–225. 10.1098/rspa.1917.0014. [DOI] [Google Scholar]
  19. Kermack W. O.; McKendrick A. G.; Walker G. T. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. London, Ser. A 1927, 115, 700–721. 10.1098/rspa.1927.0118. [DOI] [Google Scholar]
  20. Rhodes C. J.; Anderson R. M. Contact Rate Calculation for a Basic Epidemic Model. Math. Biosci. 2008, 216, 56–62. 10.1016/j.mbs.2008.08.007. [DOI] [PubMed] [Google Scholar]
  21. Baldé M. A. M. T.Fitting SIR Model to COVID-19 Pandemic Data and Comparative Forecasting with Machine Learning. 2020, medRxiv:2020.04.26.20081042. [Google Scholar]
  22. Fernández-Terán R.; Sucre-Rosales E.; Echevarría L.; Hernández F. E. Social Distancing During the COVID-19 Pandemic: An Analogy to Explain Collision Cross-Sections in Chemical Kinetics. J. Chem. Educ. 2020, 97, 4540–4544. 10.1021/acs.jchemed.0c01010. [DOI] [Google Scholar]
  23. Sucre-Rosales E.; Fernández-Terán R.; Carvajal D.; Echevarría L.; Hernández F. E. Experience-Based Learning Approach to Chemical Kinetics: Learning from the COVID-19 Pandemic. J. Chem. Educ. 2020, 97, 2598–2605. 10.1021/acs.jchemed.0c00698. [DOI] [Google Scholar]
  24. Diekmann O.; Heesterbeek J. A. P.; Metz J. A. J. On the Definition and the Computation of the Basic Reproduction Ratio R 0 in Models for Infectious Diseases in Heterogeneous Populations. J. Math. Biol. 1990, 28, 365–382. 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
  25. Pellis L.; Ball F.; Trapman P. Reproduction Numbers for Epidemic Models with Households and Other Social Structures. I. Definition and Calculation of R0. Math. Biosci. 2012, 235, 85–97. 10.1016/j.mbs.2011.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Fox J. P.; Elveback L.; Scott W.; GATEWOOD L.; Ackerman E. Herd Immunity: Basic Concept and Relevance to Public Health Immunization Practices. Am. J. Epidemiol. 1971, 94, 179–189. 10.1093/oxfordjournals.aje.a121310. [DOI] [PubMed] [Google Scholar]
  27. Frederiksen L. S. F.; Zhang Y.; Foged C.; Thakur A. The Long Road toward COVID-19 Herd Immunity: Vaccine Platform Technologies and Mass Immunization Strategies. Front. Immunol. 2020, 11, 1817. 10.3389/fimmu.2020.01817. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Britton T.; Ball F.; Trapman P. A Mathematical Model Reveals the Influence of Population Heterogeneity on Herd Immunity to SARS-CoV-2. Science 2020, 369, 846–849. 10.1126/science.abc6810. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Jentsch P. C.; Anand M.; Bauch C. T. Prioritising COVID-19 Vaccination in Changing Social and Epidemiological Landscapes: A Mathematical Modelling Study. Lancet Infect. Dis. 2021, 21, 1097–1106. 10.1016/s1473-3099(21)00057-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Woskie L. R.; Hennessy J.; Espinosa V.; Tsai T. C.; Vispute S.; Jacobson B. H.; Cattuto C.; Gauvin L.; Tizzoni M.; Fabrikant A.; et al. Early Social Distancing Policies in Europe, Changes in Mobility & COVID-19 Case Trajectories: Insights from Spring 2020. PLoS One 2021, 16, e0253071 10.1371/journal.pone.0253071. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Vokó Z.; Pitter J. G. The Effect of Social Distance Measures on COVID-19 Epidemics in Europe: An Interrupted Time Series Analysis. GeroScience 2020, 42, 1075–1082. 10.1007/s11357-020-00205-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Buckee C. O.; Balsari S.; Chan J.; Crosas M.; Dominici F.; Gasser U.; Grad Y. H.; Grenfell B.; Halloran M. E.; Kraemer M. U. G.; et al. Aggregated Mobility Data Could Help Fight COVID-19. Science 2020, 368, 145–146. 10.1126/science.abb8021. [DOI] [PubMed] [Google Scholar]
  33. Leung K.; Wu J. T.; Leung G. M. Real-Time Tracking and Prediction of COVID-19 Infection Using Digital Proxies of Population Mobility and Mixing. Nat. Commun. 2021, 12, 1501. 10.1038/s41467-021-21776-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Garriga C.; Kydland F. E.; Šustek R. Mortgages and Monetary Policy. Rev. Financ. Stud. 2017, 30, 3337–3375. 10.1093/rfs/hhx043. [DOI] [Google Scholar]
  35. Koijen R. S. J.; Van Hemert O.; Van Nieuwerburgh S. Mortgage Timing. J. Financ. Econ. 2007, 93, 292–324. 10.3386/w13361. [DOI] [Google Scholar]
  36. Loyson P. Teaching Kinetics Using Excel. J. Chem. Educ. 2010, 87, 998. 10.1021/ed1005739. [DOI] [Google Scholar]
  37. Vitz E. Conceptualizing Kinetics with Curve Fitting. J. Chem. Educ. 1998, 75, 1661. 10.1021/ed075p1661. [DOI] [Google Scholar]
  38. Pavlis R. R. Kinetics without Steady State Approximations. J. Chem. Educ. 1997, 74, 1139–1140. 10.1021/ed074p1139. [DOI] [Google Scholar]
  39. Hanson R. M. Mechanism-Based Kinetics Simulator. J. Chem. Educ. 2002, 79, 1379. 10.1021/ed079p1379.3. [DOI] [Google Scholar]
  40. Peng Z.; Jimenez J. L. KinSim: A Research-Grade, User-Friendly, Visual Kinetics Simulator for Chemical-Kinetics and Environmental-Chemistry Teaching. J. Chem. Educ. 2019, 96, 806–811. 10.1021/acs.jchemed.9b00033. [DOI] [Google Scholar]
  41. Potratz J. P. Making Enzyme Kinetics Dynamic via Simulation Software. J. Chem. Educ. 2018, 95, 482–486. 10.1021/acs.jchemed.7b00350. [DOI] [Google Scholar]
  42. Birk J. P.; Gunter S. K. Water Dipping Kinetics. A Physical Analog for Chemical Kinetics. J. Chem. Educ. 1977, 54, 557–559. 10.1021/ed054p557. [DOI] [Google Scholar]
  43. Martín O.; Mendicuti F.; Tarazona M. P. Use of a Reliable Homemade Dilatometer To Study the Kinetics of the Radical Chain Polymerization of PMMA: An Undergraduate Polymer Chemistry Laboratory Kinetics Experiment. J. Chem. Educ. 1998, 75, 1479–1481. 10.1021/ed075p1479. [DOI] [Google Scholar]
  44. Prigodich R. V. A Stopped-Flow Kinetics Experiment for the Physical Chemistry Laboratory Using Noncorrosive Reagents. J. Chem. Educ. 2014, 91, 2200–2202. 10.1021/ed500206k. [DOI] [Google Scholar]
  45. Wikipedia . Mortgage calculator. https://en.wikipedia.org/wiki/Mortgage_calculator (accessed March 23, 2021).
  46. Liao Z.; Lan P.; Liao Z.; Zhang Y.; Liu S. TW-SIR: Time-Window Based SIR for COVID-19 Forecasts. Sci. Rep. 2020, 10, 22454. 10.1038/s41598-020-80007-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Dehning J.; Zierenberg J.; Spitzner F. P.; Wibral M.; Neto J. P.; Wilczek M.; Priesemann V. Inferring Change Points in the Spread of COVID-19 Reveals the Effectiveness of Interventions. Science 2020, 369, eabb9789 10.1126/science.abb9789. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Atlantic . The COVID Tracking Project. https://covidtracking.com/data/download (accessed March 21, 2021).
  49. Lauer S. A.; Grantz K. H.; Bi Q.; Jones F. K.; Zheng Q.; Meredith H. R.; Azman A. S.; Reich N. G.; Lessler J. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Ann. Intern. Med. 2020, 172, 577–582. 10.7326/m20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. He W.; Yi G. Y.; Zhu Y. Estimation of the Basic Reproduction Number, Average Incubation Time, Asymptomatic Infection Rate, and Case Fatality Rate for COVID-19: Meta-Analysis and Sensitivity Analysis. J. Med. Virol. 2020, 92, 2543–2550. 10.1002/jmv.26041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. CDC . Interim Clinical Guidance for Management of Patients with Confirmed Coronavirus Disease (COVID-19). https://www.cdc.gov/coronavirus/2019-ncov/hcp/clinical-guidance-management-patients.html. The incubation period forCOVID,from exposure to symptoms onset. (accessed March 23, 2021).
  52. de Jong M. C. M.; Diekmann O.; Heesterbeek H.. How Does Transmission of Infection Depend on Population Size. In Epidemic Models: Their Structure and Relation to Data; Mollison D., Ed.; Cambridge University Press Cambridge, 1995; pp 84–94. [Google Scholar]
  53. Braun W.; Herron J. T.; Kahaner D. K. Acuchem: A Computer Program for Modeling Complex Chemical Reaction Systems. Int. J. Chem. Kinet. 1988, 20, 51–62. 10.1002/kin.550200107. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c04842_si_001.pdf (413.4KB, pdf)
ao1c04842_si_002.xlsx (280.3KB, xlsx)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES