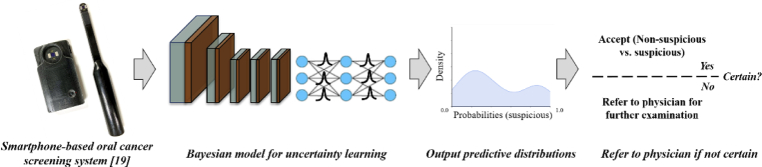
Abstract
In medical imaging, deep learning-based solutions have achieved state-of-the-art performance. However, reliability restricts the integration of deep learning into practical medical workflows since conventional deep learning frameworks cannot quantitatively assess model uncertainty. In this work, we propose to address this shortcoming by utilizing a Bayesian deep network capable of estimating uncertainty to assess oral cancer image classification reliability. We evaluate the model using a large intraoral cheek mucosa image dataset captured using our customized device from high-risk population to show that meaningful uncertainty information can be produced. In addition, our experiments show improved accuracy by uncertainty-informed referral. The accuracy of retained data reaches roughly 90% when referring either 10% of all cases or referring cases whose uncertainty value is greater than 0.3. The performance can be further improved by referring more patients. The experiments show the model is capable of identifying difficult cases needing further inspection.
1. Introduction
Deep neural networks have gained attention in the field of medical imaging and diagnosis [1] and have been proven to be successful in detecting skin cancer [2], breast cancer [3], lung cancer [4] and oral cancer [5]. These methods are now being considered for integration into diagnostic systems [6], especially for disease screening in resource-limited settings where there is a severe shortage of trained doctors and specialists [7,8]. The reliability of automated decisions must be high for practical clinical applications [9]. However, despite the promising performance, traditional deep learning-based classification still lacks the ability of human physicians to quantify decision uncertainty. Without uncertainty measurements, clinicians cannot rely on decisions from deep learning based automatic systems in practical clinic routines. No matter how powerful a deep learning classifier is, difficult diagnostic cases are inevitable and may lead to potentially severe consequences for patients if the model does not refer them for further inspection.
Machine learning based automatic oral cancer diagnostic systems are typically evaluated by accuracy, sensitivity, specificity, receiver operating characteristic (ROC) curve, and area under ROC curve (AUC) [10–12], but less attention has been paid to assessing confidence in neural network decisions. Previous models fail to know how confident the model is about a specific output. In this work, we propose a deep learning oral cancer image classification framework that can quantify the model’s output uncertainty and suggest that difficult cases with high uncertainty value be referred for further examination. This deep learning classifier with uncertainty estimations could be integrated to assist and accelerate traditional clinical workflows, not replace them. Deep learning approaches are often seen as a ‘black-box’, but the methods could become more reliable and trustable by providing uncertain information and potentially increasing overall performance. If so, the automatic classifier could be considered as a tireless front-line doctor that needs no rest, directly providing diagnoses when confident and referring difficult cases to experienced specialists when uncertain.
Bayesian deep learning integrates deep learning with Bayesian probability theory. Bayesian neural networks provide a prediction and an uncertainty value by imposing prior distributions on the model parameters (weights) to obtain a posterior distribution of these parameters [13]. The uncertainty is estimated through a probability density over outcomes, while traditional deep learning only produces a deterministic output. Bayesian neural networks (BNN) have been studied for a long time [14,15] but are not widely used because of massive training times and implementation difficulties. Gal et al. [16] proposed a new framework that takes Monte Carlo samples of the prediction by training a dropout network that approximates Bayesian inference in deep Gaussian processes. This approach produces the posterior distribution of the network weights and estimates uncertainty in a more straightforward way. Some pioneering works in the emerging field of Bayesian deep learning in imaging systems [17,18] demonstrate that uncertainty analysis is necessary for scientific imaging and diagnosis where critical assessment is essential.
Oral cancer is one of the most common cancers, especially in low- and middle-income countries like India [19]. Early detection is the most effective way to reduce the mortality rate [20], but unfortunately, most high-risk populations lack healthcare infrastructure and doctors. Therefore, there is an urgent need for a reliable automatic detection system for large-scale, high-risk population screening. In this work, we developed a Bayesian deep neural network for oral cancer detection and trained it using our intraoral image dataset collected from a high-risk population in India. The results show that meaningful uncertainty information can be obtained and used to identify difficult cases in need of further examination effectively. By referring these cases for review, the overall detection performance of the trained network can be further improved.
2. Material and methods
Bayesian deep learning is an effective method to add uncertainty handling in deep learning models. It combines Bayesian probability theory with deep learning to extend standard neural networks by assigning distributions to their weights. Traditional deep networks have fixed weights, while the weights of Bayesian networks are assigned a probability distribution. Therefore, a standard deep network with fixed weights will always give the same outputs, but a Bayesian neural network will deliver stochastic outputs.
When conventional deep neural networks trained with cross-entropy loss classify N instances with corresponding labels to K classes using the Softmax model, cross-entropy minimizes the distance between the true class label distribution and the approximating distribution from the model, resulting in a single best set of parameters ω and a network function φ correlated with those parameters. The probability that the instance xi belongs to class k is calculated as:
| (1) |
The probability value generated by softmax could be considered as the multiplication of features extracted by the convolutional layers and the weight for the features of each category. The result compares how many features are found within each category, and the sum of all probability values is 1.
Bayesian deep neural networks consider a distribution over network parameters instead of a single best set. The predictive posterior probability distribution calculated using the Bayesian deep learning model for a new instance is:
| (2) |
The probability that a case belongs to a specific class is a single value produced by Eq. (1), while the predictive posterior defined by Eq. (2) is a distribution that describes all possible predictions given the network weights and test instance . The width of the predictive posterior distribution would be able to reflect the model’s confidence about a specific prediction.
Dropout is a well-established procedure to regularize a deep learning model and reduce overfitting by randomly dropping neurons in a neural network layer. Since this technique can also be interpreted as a Bayesian approximation of a Gaussian process, model uncertainty can be obtained from dropout neural network models. This approach, called Monte Carlo (MC) dropout, mitigates the problem of representing uncertainty in deep learning without sacrificing either computational complexity or test accuracy. By running the Monte Carlo dropout model multiple (ρ) times to obtain several stochastic outputs, the final prediction on a test instance (predictive mean) can be calculated using a Monte Carlo integration over ρ samples:
| (3) |
The variance of the distributions from the ensembles will be considered as the model uncertainty on the prediction:
| (4) |
The intraoral dataset used in this study contains 2350 cheek mucosa images that were captured using a smartphone-based intraoral screening device we developed [21], and among patients attending the outpatient clinics of the Department of Oral Medicine and Radiology at KLE Society Institute of Dental Sciences, Head and Neck Oncology Department of Mazumdar Shaw Medical Center (MSMC), and Christian Institute of Health Sciences and Research (CIHSR), India. Oral oncology specialists from MSMC, KLE and CIHSR labeled all the dual-modality image pairs and separated them into two categories: A) ‘Normal’ which contains normal and benign mucosal lesion images, and B) ‘suspicious’ which contains OPML and malignant lesion images. In a previous study, we show that oral oncology specialists’ interpretation of classifying normal/benign vs. OPML/malignant has high accuracy with biopsy-confirmed cases [22]. The intraoral cheek mucosa dataset (normal/benign: 1510; suspicious: 840) were randomly split to training, validation, and standalone test. We used 1979 (normal/benign: 1272; suspicious: 707) images for training and validation (randomly split where 75% was allocated to training and 25% was allocated to validation) and another 371 (normal/benign: 238; suspicious: 133) images for the standalone test. The proposed Bayesian deep learning model for oral cancer detection is shown in Fig. 1.
Fig. 1.
The proposed Bayesian deep learning model for oral cancer detection.
3. Experiments and results
We trained the Bayesian deep neural network for oral cancer images using VGG19 as a base network; the initial weights of the network were obtained from training the ImageNet dataset. Two dropout layers with a 0.5 rate were applied to the fully connected layers, which means half of the units in these layers were turned off during training and inference. The dropout in the network not only can be treated as a Bayesian approximation of a Gaussian process, but also as a means to reduce overfitting. Data augmentation was applied to the training set to over-sample the dataset based on the ratios of imbalanced classes by flipping horizontally and vertically, random rotating, and shearing. Our augmentation strategy increased the instances number of minority classes and could reduce the model bias toward the majority groups.
Adam optimizer was used to minimize the Focal loss function. Focal loss can reduce the class imbalance problem and hard sample issues. The initial learning rate was 1e-4 and decay 5 times by every 20 epochs. The experiment was run for 300 epochs, and the batch size was set to 32. The model with the best validation accuracy was saved. The model was trained on the high-performance computing platform of the University of Arizona [23]. The predictive means calculated by Eq. (3) will be used as final predictions by the Bayesian neural network. The predictive standard deviation calculated by Eq. (4) is the associated uncertainty value; we set ρ as 50 in our experiments. The structure of our proposed architecture and was shown in Fig. 2.
Fig. 2.
Structure of our BNN architecture (VGG19 as baseNet).
We evaluated the Bayesian deep neural network's intraoral cancer image classification accuracy using a standalone dataset containing 371 intraoral cheek mucosa images in the test set. The results were compared with a conventional network with standard dropout. The BDNN achieved 85.6% accuracy, while the accuracy of the traditional network with standard dropout was 85.1%. The result shows good classification performance of the Bayesian network and indicates the BNN didn’t sacrifice accuracy but slightly improved the performance by ensemble learning.
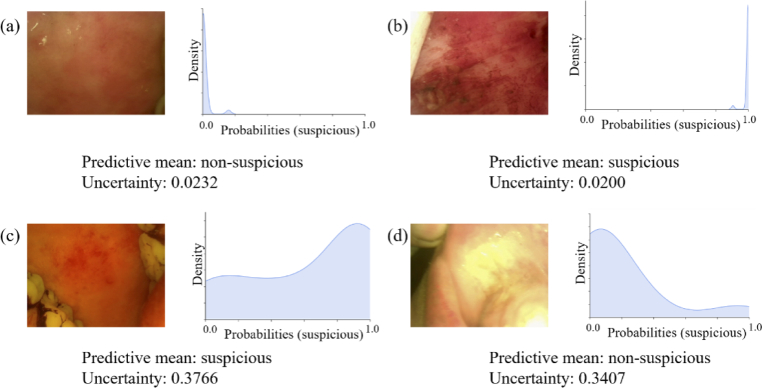
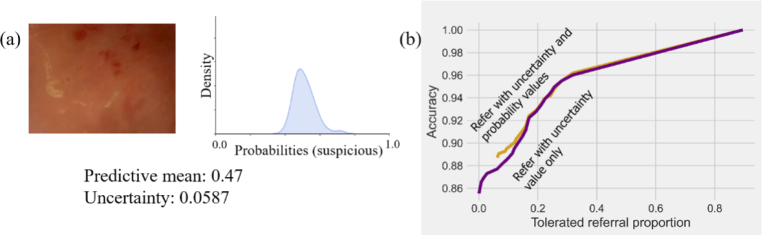
Figure 3 shows examples of the BNN prediction with uncertainty estimation. For a specific input case, the network can be certain (Fig. 3(a) and 3(b)) or uncertain (Fig. 3(c) and 3(d)) about its prediction, as indicated by the standard deviation of the predictive posterior distribution calculated with Eq. (4). The image of Fig. 3(a) was confidently classified as non-suspicious by the BNN since all the sampled probability (suspicious) predictions are near 0.0, and the uncertainty value (standard deviation) is 0.0232. The image of Fig. 3(b) was confidently classified as suspicious by the BNN since all the sampled probability (suspicious) predictions are near 1.0, and the uncertainty value is 0.0200. Whereas Fig. 3(c) shows an example of the model is uncertain: the predicted label (predictive mean) is correct, but with wider posterior distribution, and the uncertainty value is 0.3766, which may be because the lesion is not obvious in this case. Figure 3(d) shows another example where the BNN is highly uncertain: the uncertainty value is 0.3407, caused by image quality (over-exposed). These examples indicate the BNN can produce informative uncertainty estimation.
Fig. 3.
Examples of intraoral images and corresponding approximate predictive probability (suspicious) posteriors distribution produced by the Bayesian neural network. (The density (vertical axis) is based on Gaussian kernel density estimates.)
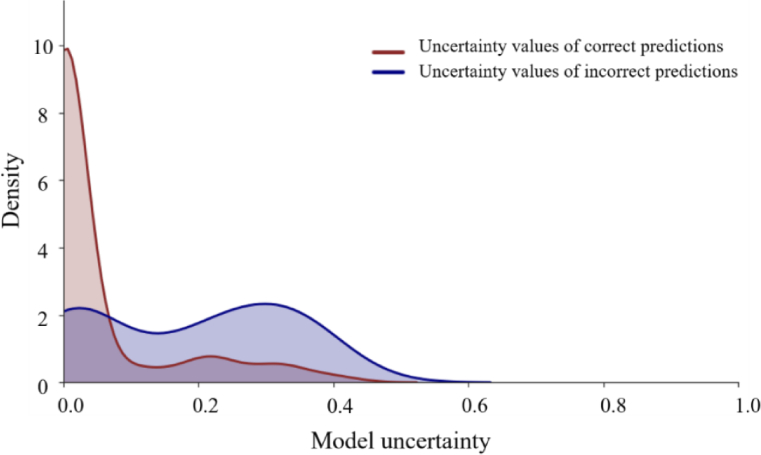
We were also curious if most misclassified cases have higher model uncertainty values than correct predictions, in which case they could be flagged for further inspection. The uncertainty values for all 371 standalone test images were plotted using Kernel Density Estimation with a Gaussian kernel and grouped by correct and incorrect predictions (see Fig. 4). The result shows incorrect cases have higher model uncertainty. Therefore, the correlated uncertainty value could be used to find difficult cases in need of further examination to improve the overall accuracy. The results also indicate the BNN model has the potential to mimic the human clinical workflow and be integrated into diagnostic systems.
Fig. 4.
Distribution of uncertainty value for all test data grouped by correct and incorrect model predictions. (The density (vertical axis) is based on Gaussian kernel density estimates.)
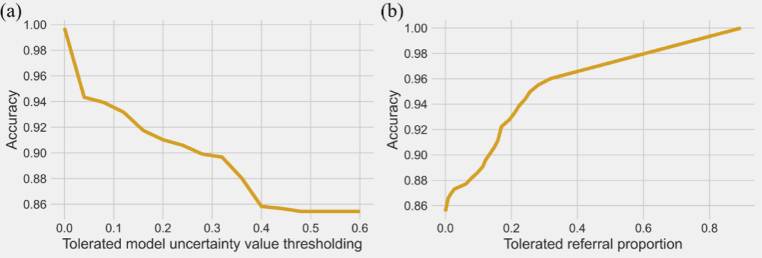
We then sorted the predictions of the test images according to the uncertainty value from high to low and measured the change of accuracy when referring cases with uncertainty values higher than a specific level. By switching the level of uncertainty thresholding, we plotted the change of accuracy in Fig. 5(a). We used this experiment to test whether the proposed method could refer uncertain patients for further inspection and therefore mimic the clinic workflow. From the figure, we can see a continuous increase of accuracy in response to a decrease of uncertainty thresholding. The accuracy will be around 90% if the model refers cases with uncertainty higher than 0.3. We wanted to verify this increase in accuracy was not simply due to the model referring too many cases, which would render it effectively useless. Therefore, we monitored the change of accuracy when referring different proportions of cases (cases with larger uncertainty values were referred first). With the increase of referral proportion thresholding, we also observed an increase in prediction performance (see Fig. 5(b)). The figure shows the accuracy will be around 90% if the model refers 10% of the cases.
Fig. 5.
The change of accuracy correlated to the tolerated (a) model uncertainty value, (b) referral proportion.
In addition, we noticed that there are cases where the probability value is distributed around 0.5 with low uncertainty, indicating that the network has extracted features correlated to both categories (See Fig. 6(a)). Although the network is certain about the result (low uncertainty value), it cannot provide a precise diagnosis (probability value around 0.5). Therefore, we tried to combine the uncertainty and mean probability values for the referral strategy and re-drew Fig. 5(b). We tried to refer cases with high uncertainty values and mean probability values between 0.4 to 0.6, and monitored the change of accuracy by referring varying proportions of cases. The results (Fig. 6(b)) show that this new referral strategy achieves higher accuracy for the same referral proportion. But no difference was observed with increasing proportion, because the cases referred due to the mean probability value are included in the uncertainty value referral.
Fig. 6.
(a) Example of intraoral image and corresponding approximate predictive probability (suspicious) posteriors distribution with low uncertainty value and probability values are distributed around 0.5. (b) The change of accuracy correlated to the tolerated referral proportion with two referral strategies.
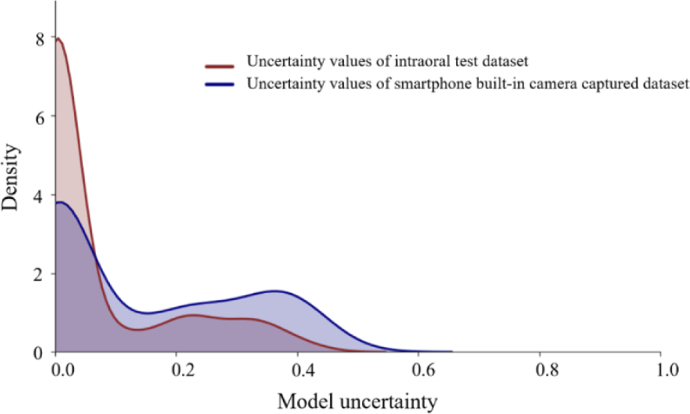
Theoretically, the Bayesian neural network should produce higher uncertainty values on unfamiliar data. The model uncertainty should be able to identify data different from the training dataset to sort out abnormal or unusable data. We ran the model trained with intraoral cheek mucosa images on another cheek mucosa test dataset which was captured using a smartphone’s built-in camera (n=351). The uncertainty values for both the intraoral cheek mucosa test dataset and the dataset captured with smartphone built-in camera were plotted using Kernel Density Estimation with a Gaussian kernel in Fig. 7. We can see the intraoral cheek mucosa test dataset had lower average uncertainty. This result indicates the model was more confident with a familiar dataset.
Fig. 7.
Distribution of uncertainty value for familiar intraoral probe test dataset and unfamiliar test data captured with smartphone built-in camera. (The density (vertical axis) is based on Gaussian kernel density estimates.)
4. Conclusion
We have presented a Bayesian deep learning-based framework to estimate model uncertainty for intraoral cancer images. The classification accuracy achieved by the proposed model was about 85% on the standalone test dataset, which is comparable to results from a traditional deep learning framework. The model was able to measure the uncertainty of each prediction and identify difficult cases in need of further examination. In other words, the reliability of BNN predictions could be assessed. Therefore, the reliability and overall performance of the model were improved. Our experimental results show that this model produced higher uncertainty values on incorrect predictions and achieved higher accuracy by referring cases with low confidence. We have monitored the change of accuracy with different levels of tolerated model uncertainty and different levels of referral proportion. In this process of imitating traditional medical workflow, we have observed a continuous improvement. In addition, we have shown that the model can sort out unfamiliar and difficult data. The method enables users to know when they can trust the output of a network. We believe this framework is a step forward in establishing accurate and reliable deep learning-based oral cancer detection and increasing the acceptance of deep learning integration into clinical practice in high-risk population screening.
Funding
National Institute of Biomedical Imaging and Bioengineering10.13039/100000070 (UH2EB022623); National Institute of Cancers (UH3CA239682); National Institute of Dental and Craniofacial Research10.13039/100000072 (R01DE030682) of the National Institutes of Health (NIH).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
References
- 1.De Fauw J., Ledsam J. R., Romera-Paredes B., Nikolov S., Tomasev N., Blackwell S., Askham H., Glorot X., O’Donoghue B., Visentin D., van den Driessche G., Lakshminarayanan B., Meyer C., Mackinder F., Bouton S., Ayoub K., Chopra R., King D., Karthikesalingam A., Hughes C. O., Raine R., Hughes J., Sim D. A., Egan C., Tufail A., Montgomery H., Hassabis D., Rees G., Back T., Khaw P. T., Suleyman M., Cornebise J., Keane P. A., Ronneberger O., “Clinically applicable deep learning for diagnosis and referral in retinal disease,” Nat. Med. 24(9), 1342–1350 (2018). 10.1038/s41591-018-0107-6 [DOI] [PubMed] [Google Scholar]
- 2.Esteva A., Kuprel B., Novoa R. A., Ko J., Swetter S. M., Blau H. M., Thrun S., “Dermatologist-level classification of skin cancer with deep neural networks,” Nature 542(7639), 115–118 (2017). 10.1038/nature21056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ehteshami Bejnordi B., Veta M., Johannes van Diest P., van Ginneken B., Karssemeijer N., Litjens G., van der Laak J. A. W. M., and C. C. and the, “Diagnostic assessment of deep learning algorithms for detection of lymph node metastases in women with breast cancer,” JAMA 318(22), 2199–2210 (2017). 10.1001/jama.2017.14585 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Coudray N., Ocampo P. S., Sakellaropoulos T., Narula N., Snuderl M., Fenyö D., Moreira A. L., Razavian N., Tsirigos A., “Classification and mutation prediction from non–small cell lung cancer histopathology images using deep learning,” Nat. Med. 24(10), 1559–1567 (2018). 10.1038/s41591-018-0177-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Song B., Sunny S., Uthoff R. D., Patrick S., Suresh A., Kolur T., Keerthi G., Anbarani A., Wilder-Smith P., Kuriakose M. A., Birur P., Rodriguez J. J., Liang R., “Automatic classification of dual-modalilty, smartphone-based oral dysplasia and malignancy images using deep learning,” Biomed. Opt. Express 9(11), 5318–5329 (2018). 10.1364/BOE.9.005318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang F., Casalino L. P., Khullar D., “Deep learning in medicine—promise, progress, and challenges,” JAMA Intern Med 179(3), 293–294 (2019). 10.1001/jamainternmed.2018.7117 [DOI] [PubMed] [Google Scholar]
- 7.Hu L., Bell D., Antani S., Xue Z., Yu K., Horning M. P., Gachuhi N., Wilson B., Jaiswal M. S., Befano B., Long L. R., Herrero R., Einstein M. H., Burk R. D., Demarco M., Gage J. C., Rodriguez A. C., Wentzensen N., Schiffman M., “An observational study of deep learning and automated evaluation of cervical images for cancer screening,” JNCI: Journal of the National Cancer Institute 111(9), 923–932 (2019). 10.1093/jnci/djy225 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.de Haan K., Ceylan Koydemir H., Rivenson Y., Tseng D., Van Dyne E., Bakic L., Karinca D., Liang K., Ilango M., Gumustekin E., Ozcan A., “Automated screening of sickle cells using a smartphone-based microscope and deep learning,” npj Digit. Med. 3(1), 76 (2020). 10.1038/s41746-020-0282-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kermany D. S., Goldbaum M., Cai W., Valentim C. C. S., Liang H., Baxter S. L., McKeown A., Yang G., Wu X., Yan F., Dong J., Prasadha M. K., Pei J., Ting M. Y. L., Zhu J., Li C., Hewett S., Dong J., Ziyar I., Shi A., Zhang R., Zheng L., Hou R., Shi W., Fu X., Duan Y., Huu V. A. N., Wen C., Zhang E. D., Zhang C. L., Li O., Wang X., Singer M. A., Sun X., Xu J., Tafreshi A., Lewis M. A., Xia H., Zhang K., “Identifying medical diagnoses and treatable diseases by image-based deep learning,” Cell 172(5), 1122–1131.e1129 (2018). 10.1016/j.cell.2018.02.010 [DOI] [PubMed] [Google Scholar]
- 10.Zheng X., Yao Z., Huang Y., Yu Y., Wang Y., Liu Y., Mao R., Li F., Xiao Y., Wang Y., Hu Y., Yu J., Zhou J., “Deep learning radiomics can predict axillary lymph node status in early-stage breast cancer,” Nat. Commun. 11(1), 1236 (2020). 10.1038/s41467-020-15027-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wentzensen N., Lahrmann B., Clarke M. A., Kinney W., Tokugawa D., Poitras N., Locke A., Bartels L., Krauthoff A., Walker J., Zuna R., Grewal K. K., Goldhoff P. E., Kingery J. D., Castle P. E., Schiffman M., Lorey T. S., Grabe N., “Accuracy and efficiency of deep-learning–based automation of dual stain cytology in cervical cancer screening,” JNCI: Journal of the National Cancer Institute 113(1), 72–79 (2021). 10.1093/jnci/djaa066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Aubreville M., Knipfer C., Oetter N., Jaremenko C., Rodner E., Denzler J., Bohr C., Neumann H., Stelzle F., Maier A., “Automatic classification of cancerous tissue in laserendomicroscopy images of the oral cavity using deep learning,” Sci. Rep. 7(1), 11979 (2017). 10.1038/s41598-017-12320-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ghahramani Z., “Probabilistic machine learning and artificial intelligence,” Nature 521(7553), 452–459 (2015). 10.1038/nature14541 [DOI] [PubMed] [Google Scholar]
- 14.Denker J. S., LeCun Y., “Transforming neural-net output levels to probability distributions,” in Proceedings of the 3rd International Conference on Neural Information Processing Systems, (Morgan Kaufmann Publishers Inc., 1990), pp. 853–859. [Google Scholar]
- 15.MacKay D. J. C., “A practical Bayesian framework for backpropagation networks,” Neural Computation 4(3), 448–472 (1992). 10.1162/neco.1992.4.3.448 [DOI] [Google Scholar]
- 16.Yarin G., Zoubin G., “Dropout as a Bayesian approximation: representing model uncertainty in deep learning,” PMLR, pp. 1050–1059.
- 17.Xue Y., Cheng S., Li Y., Tian L., “Reliable deep-learning-based phase imaging with uncertainty quantification,” Optica 6(5), 618–629 (2019). 10.1364/OPTICA.6.000618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu R., Cheng S., Tian L., Yi J., “Deep spectral learning for label-free optical imaging oximetry with uncertainty quantification,” Light: Sci. Appl. 8(1), 102 (2019). 10.1038/s41377-019-0216-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Petersen P. E., “Oral cancer prevention and control–the approach of the World Health Organization,” Oral Oncology 45(4-5), 454–460 (2009). 10.1016/j.oraloncology.2008.05.023 [DOI] [PubMed] [Google Scholar]
- 20.Zygogianni A. G., Kyrgias G., Karakitsos P., Psyrri A., Kouvaris J., Kelekis N., Kouloulias V., “Oral squamous cell cancer: early detection and the role of alcohol and smoking,” Head Neck Oncol 3(1), 2 (2011). 10.1186/1758-3284-3-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ross D. U., Bofan S., Sumsum S., Sanjana P., Amritha S., Trupti K., Keerthi G., Kimberly W., Vishal G., Mary E. P., Anurag K. S., Petra W.-S., Moni Abraham K., Praveen B., Rongguang L., “Small form factor, flexible, dual-modality handheld probe for smartphone-based, point-of-care oral and oropharyngeal cancer screening,” J. Biomed. Opt. 24, 1–8 (2019). 10.1117/1.JBO.24.10.106003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Birur N., Gurushanth K., Patrick S., Sunny S., Raghavan S., Gurudath S., Hegde U., Tiwari V., Jain V., Imran M., Rao P., Kuriakose M., “Role of community health worker in a mobile health program for early detection of oral cancer,” Indian J Cancer 56, 107–113 (2019). 10.4103/ijc.IJC_232_18 [DOI] [PubMed] [Google Scholar]
- 23. https://it.arizona.edu/service/high-performance-computing.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.