Active Cell Appearance Model Induced Generative Adversarial Networks for Annotation-Efficient Cell Segmentation and Identification on Adaptive Optics Retinal Images

Abstract

Data annotation is a fundamental precursor for establishing large training sets to effectively apply deep learning methods to medical image analysis. For cell segmentation, obtaining high quality annotations is an expensive process that usually requires manual grading by experts. This work introduces an approach to efficiently generate annotated images, called “A-GANs”, created by combining an active cell appearance model (ACAM) with conditional generative adversarial networks (C-GANs). ACAM is a statistical model that captures a realistic range of cell characteristics and is used to ensure that the image statistics of generated cells are guided by real data. C-GANs utilize cell contours generated by ACAM to produce cells that match input contours. By pairing ACAM-generated contours with A-GANs-based generated images, high quality annotated images can be efficiently generated. Experimental results on adaptive optics (AO) retinal images showed that A-GANs robustly synthesizes realistic, artificial images whose cell distributions are exquisitely specified by ACAM. The cell segmentation performance using as few as 64 manually-annotated real AO images combined with 248 artificially-generated images from A-GANs were similar to the case of using 248 manually-annotated real images alone (Dice coefficients of 88% for both). Finally, application to rare diseases in which images exhibit never-seen characteristics demonstrated improvements in cell segmentation without the need for incorporating manual annotations from these new retinal images. Overall, A-GANs introduce a methodology for generating high quality annotated data that statistically captures the characteristics of any desired dataset and can be used to more efficiently train deep-learning-based medical image analysis applications.

I. Introduction

DEEP learning-based methods have quickly become mainstream in medical image analysis, but the performance of most approaches is contingent upon having large amounts of training data together with high quality annotations. However, extensive medical imaging datasets are often difficult and costly to generate, and in the case of most rare diseases, are sometimes not attainable. Moreover, manual annotation is a tedious process, especially for tasks such as cell segmentation due to the need to annotate a high number of cells within a single image, let alone an entire dataset. To enlarge training data without resorting to additional manual annotation, data augmentation is a routine strategy used to create artificial training data through operations such as rotation, shearing, translation, flipping, or blurring of images and annotations together [1]. Unfortunately, these artificially created images are not always realistic in appearance due to distortions introduced by these operations that also cause potential deviations from the range of data statistics observed in the real world. Image retrieval has also been proposed to add more consistent data by searching for only those unannotated images that are similar to annotated ones [2]. A more direct approach for realistic data augmentation can be achieved through generative adversarial networks (GANs) [3].

GANs can produce realistic-looking images from random noise through a competition between discriminator and generator networks [3]. Indeed, utilizing GANs to create larger training datasets has quickly been popularized in many medical imaging applications [4], especially for generating prognostic images since many lesion classification problems suffer from imbalanced training data due to the relative lack of lesion examples, such as for breast [5], liver [6], and gastric [7] cancer. Although GANs can readily generate images belonging to a certain class or tag, they are not inherently able to control generated images based on additional input masks (e.g. object regions or contours, relevant for segmentation).

Conditional generative adversarial networks (C-GANs) [8] were introduced to address this issue by combining images and masks as inputs for the discriminator network, instead of images alone as used in the original GANs [3]. Since data generated by C-GANs include both images and masks, C-GANs are useful for data augmentation in applications beyond image classification. For example, C-GANs can improve vessel segmentation accuracy in retinal fundus images by generating artificial training data that contains images and vessel masks [9]. Similar strategies have also improved segmentation accuracy in chest X-ray, brain MRI, and abdominal CT images [10], as well as classification accuracy in breast images paired with breast masks [11].

Moving beyond images paired with masks, image style has become increasingly relevant for higher order control of C-GANs. For example, Med-GAN was developed as an improvement over C-GANs for transferring image style from one image modality to another, with promising results already demonstrated on PET-CT translation, MRI motion correction, and PET denoising [12]. However, image style transfer with C-GANs require paired input images, which can be restrictive. CycleGAN [13] addresses this difficulty by reconstructing an input image’s pair through a series of generator networks without the need for an image pair in the first place. CycleGAN has been used for transferring image style across modalities [14], [15] or for sharing feature spaces across image modalities [16]–[18]. Examples of higher-order control over image characteristics that can be achieved using CycleGAN include transfering fine textural details [21] or shape consistency between masks [22], or for improving contrast without changing to another modality [19], [20]. Recently, C-GANs and CycleGAN were combined to improve cell segmentation. In this case, C-GANs were either directly chosen as the cell segmentation framework [23] or used to refine the training data [24].

Although image style transfer strategies have greatly improved C-GANs and CycleGAN for image synthesis, fine control over image characteristics have mostly been focused on global image style transfer, with little or no control over local object details such as individual cells within images. For example, retinal cells imaged using adaptive optics (AO) vary in appearance and shapes (Fig. 1B). Moreover, these approaches rely on a prerequisite of already having masks. It is often nontrivial to create a large set of high quality masks, such as cell contour masks. In this work, exquisite control over local variation is introduced. First, to measure local variation, active appearance models (AAM) [25] are explored to statistically model cell shape and appearance variation locally (i.e. on a cell by cell basis). AAM is commonly used as shape and appearance priors for image segmentation, such as segmenting the prostate [26], heart [27], and anterior visual pathway [28] in MRI images. In this work, a cell-based AAM (active cell appearance model, ACAM) plays the role of generating a set of cell contours with shape and appearance satisfying real-world statistical distributions from actual training data. The masks composed of cell contours from ACAM not only preserve local cell details, but also ensure automatically created cells fall within a statistically-specified distribution of shape and appearance.

Fig. 1.

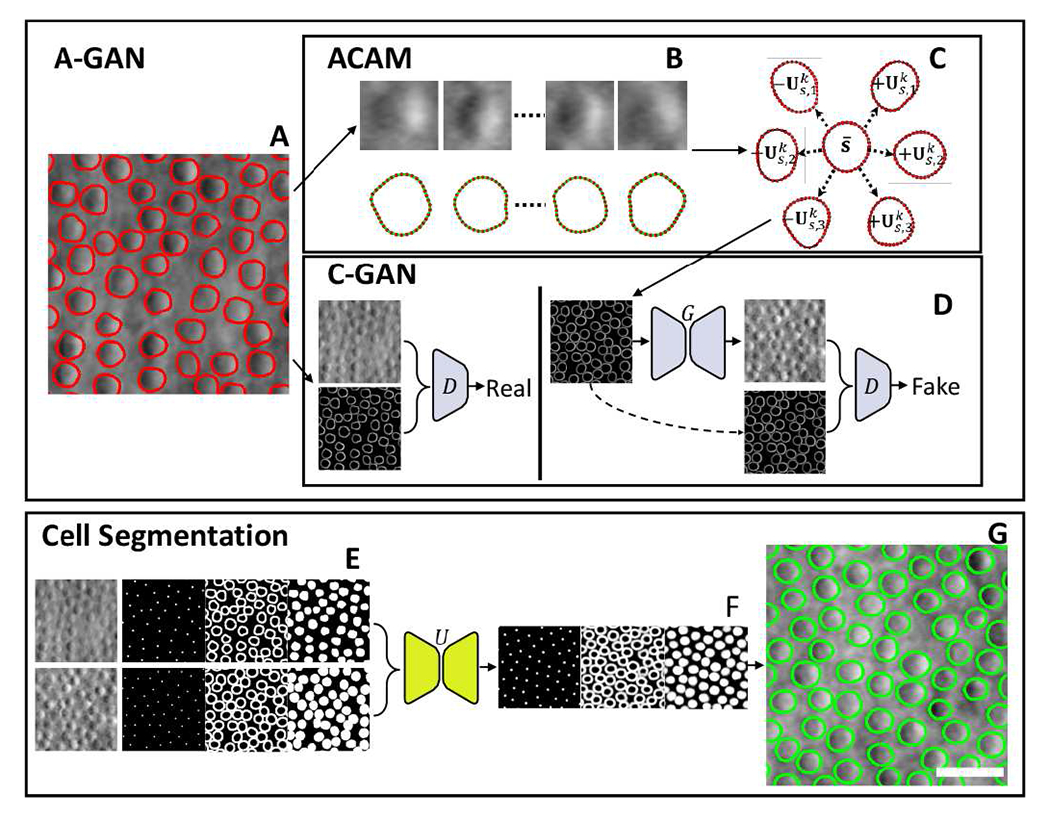
Overview of active cell appearance induced generative adversarial networks (A-GANs) for cell segmentation on (A) adaptive optics retinal images. A-GANs consist of three main steps, including (B) individual cell sample extraction from manual annotations (red contours), (C) active cell appearance model (ACAM), and (D) conditional generative adversarial networks (C-GANs) to create adaptive optics images. (E) The cell segmentation model takes both real and generated adaptive optics images as well as centroid, contour, and region masks as the training data for a U-Net model. The trained U-Net model predicts (F) centroid, contour, and region masks on test images. All of these predicted masks are imported into a level-set segmentation framework to obtain (G) the final cell segmentation (green contours). Scale bar, 20 μm.

Building upon ACAM, this work further improves C-GANs so that the C-GANs can utilize masks from ACAM to efficiently generate high quality images that not only match their input contours in position (for the purposes of generating an already-annotated dataset) but also in local image style (to capture cell to cell variation).The combination of ACAM with C-GANs is called A-GANs. A-GANs were demonstrated to be a more effective controllable data augmentation strategy over C-GANs [29], with initial promising results shown on adaptive optics retinal images. Adaptive optics is an imaging technique that can visualize retinal cells directly in the living human eye [30], [31]. Since retinal cells have varying densities and local packing arrangements in different retinal regions [32], it can be difficult to generate training datasets that represent the images of interest for cell segmentation. Existing cell analysis methods on adaptive optics images have mainly focused on cell detection, utilizing approaches ranging from conventional image analysis [33] to deep learning, such as convolutional neural networks [34]–[36], recurrent neural networks [37], transfer learning [38], U-Net [39], and LinkNet [40]. Cell segmentation is a much more complex problem than cell identification [41], [42]. In this paper, we build upon our earlier results by substantially expanding both A-GANs and cell segmentation on adaptive optics images as introduced in our previous conference papers [29], [42] with the following contributions: 1) efficient data annotation achieved using A-GANs combined with a multi-channel U-Net cell segmentation method, which also helps to simplify the level-set cell segmentation method; 2) a novel training strategy for A-GANs to remove the process of manual fine-tuning of parameters and the development of a sequential level-set framework to accurately extract cell contours; 3) a systematic analysis to empirically determine the influence of incorporating training images from A-GANs on cell segmentation accuracy which ultimately enables efficient data annotation with only a very small set of manual annotations; and 4) extension of the proposed techniques to never-seen images of cells in rare genetic eye diseases, demonstrating superior results with A-GANs compared to the traditional method of only using manually-annotated real world images.

II. Methodology

The image generation framework consists of two main components, as shown in Fig. 1. The overall active cell appearance-induced generative adversarial networks (A-GANs) are designed to take manually annotated adaptive optics images (Fig. 1A) and use them to generate additional annotated adaptive optics images that are statistically representative of real data. The first component is established as an active cell appearance model (ACAM) (Fig. 1B), where $\overline{\text{s}}$ represents the average contour shape captured from real data that can be adjusted according to a set of possible contours. The second component incorporates C-GANs which use pairs of real images and manually created contour masks with actual intensity values embedded within the cell contours to set up the discriminator in the C-GANs (Fig 1D). At the same time, generated contours that are initiated by ACAM are used to set up the generator in the C-GANs. Together, these networks generate realistic adaptive optics images that are faithful to their generated input contours. The resulting output is a realistic generated image that is pre-annotated with a high quality contour mask.

To establish the cell segmentation model, a set of binary cell centroid, contour, and region masks are used together with their corresponding adaptive optics images to form training data for a multi-channel U-Net (Fig. 1E). Importantly, training data can come from either the set of real adaptive optics images or from A-GANs generated images, or a combination of both. After training the multi-channel U-Net, cell centroid, contour, and region prediction masks can be generated (Fig. 1F). The final cell segmentation result is achieved using all of these prediction masks in a level-set segmentation method (Fig. 1G). Details of these major components follow.

A. Active Cell Appearance Model Induced Generative Adversarial Networks (A-GANs)

1). Active Cell Appearance Model (ACAM):

The goal of ACAM is to build a statistical model that captures the actual variation of cell shapes and intensity values along cell boundaries in real data. A small set of 64 annotated adaptive optics images (e.g. red contours, Fig. 1A) is used to establish ACAM (Fig. 1B). Collectively, the images contain a large number of cells, each with local variations in shape, size, and intensity distribution. For each cell contour, polar coordinates centered at the cell centroid are established. Along the contour, N evenly-angular landmarks (outlines, bottom row of Fig. 1B) are used for sampling and then catalogued as a one-dimensional vector s = (x₁, ⋯ , x_N), with N = 36 used in this paper. A collection of M contour shape vectors $\mathcal{S}=\{{\mathbf{s}}_1,\cdots ,{\mathbf{s}}_M\}$ from all the cells sampled is used to derive the active shape model on $\mathcal{S}$ as $\left\{\overline{\mathbf{s}},{\mathbf{\text{U}}}_s^K\right\}$. Here, $\overline{\mathbf{s}}$ is the mean shape vector of $\mathcal{S}$ and ${\mathbf{\text{U}}}_s^K$ is an orthonormal basis of the first K eigenvector using principal component analysis (PCA). The matrix ${\mathbf{\Lambda }}_s^K$ is composed of the corresponding K eigenvalues. A new cell shape instance can be created as $\mathbf{s}\left(\mathbf{\text{p}}\right)=\overline{\mathbf{s}}+{\mathbf{\text{U}}}_s^K·\mathbf{p}$, where p = (p₁, ⋯, p_K) is a shape parameter vector. As an example, Fig. 1C illustrates the mean shape $\overline{\mathbf{s}}$ (center contour) together with contour shape variations $\overline{\mathbf{s}}-{\mathbf{\text{U}}}_{s,i}^K$ and $\overline{\mathbf{s}}+{\mathbf{\text{U}}}_{s,i}^K$ for i ∈ [1, 4].

In addition to modeling the statistical description of contour shape variation, ACAM also captures a statistical description of the local intensity appearance variation along cell contours. Following a similar procedure as was carried out for contour shape variation, for each adaptive optics image I_i, we can sample a set of sub-image patches J_i = {J_i,1, ⋯ , J_i,N} around all contour points of s_i. Here, $\mathcal{J}=\{I_1,\cdots ,I_M\}$ is the set of cell images (top row, Fig. 1B). Vectoring J_i as a_i and applying PCA again leads to $\left\{\overline{\mathbf{a}},{\mathbf{\text{U}}}_a^K\right\}$, where $\overline{\mathbf{a}}$ is the mean appearance vector and ${\mathbf{\text{U}}}_a^K$ is an orthonormal basis of the first K eigenvector. Similar to before, ${\mathbf{\Lambda }}_a^K$ contains the corresponding K eigenvalues. New cell intensity profiles can be created as $\mathbf{\text{a}}\left(\mathbf{\text{t}}\right)=\overline{\mathbf{\text{a}}}+{\mathbf{\text{U}}}_a^K\cdot \mathbf{t}$, where t = (t₁, ⋯ , t_K) is an appearance parameter vector.

The two components of ACAM, s(p) and a(t), are used together to create new cells with realistic shapes and appearances (i.e. local intensity distributions) according to the parameters p and t. A key feature of this approach is that ACAM creates cell contours with locally-varying intensity values, unlike the binary masks that are typically used for C-GANs [8]–[12]. As we will show, this intensity information is a key factor for stabilizing C-GANs. We found that using the first four eigenvectors for both shape and appearance models gave satisfactory results (K = 4) because $\text{Tr}\left({\mathbf{\Lambda }}_s^{K=4}\right)/\text{Tr}\left({\mathbf{\Lambda }}_s\right)=95.4\%$ and $\text{Tr}\left({\mathbf{\Lambda }}_a^{K=4}\right)/\text{Tr}\left({\mathbf{\Lambda }}_a\right)=96.9\%$ [45], where Tr is the matrix trace operator. In other words, the first four shape and appearance eigenvalues (Λ_s and Λ_a) preserve over 95% of the information. Therefore, utilizing the first four eigenvectors can generate realistic cell contours. p and t are randomly sampled between $\left[-{\mathbf{\Lambda }}_s^K,{\mathbf{\Lambda }}_s^K\right]$ and $\left[-{\mathbf{\Lambda }}_a^K,{\mathbf{\Lambda }}_a^K\right]$, respectively. This enables the rapid creation of new cell instances with variations in shape and intensity values that are based on actual measurements from real data. To seed cells, we pseudorandomly assign a set of points on an image plane according to a separation distance parameter that determines how densely packed cells are. The placement of cells is determined according to a brute-force process in which a new point is iteratively placed in the image plane if its distances to all existing points are less than the separation distance. This process continues until a preset number of points is reached or no new points could be inserted. These points are used as cell centroids, with new cell instances attributed to each of these points, thereby providing a systematic way to create contour masks, $F_c^a$, for image generation (bottom image, right panel of Fig. 1D). The separation distance parameter is critical for controlling cell spacing in the generated masks so as to simulate the characteristics of varying cell densities in different retinal regions; the value of this parameter is informed by previous studies [32], [33], [41]. When multiple contours cover the same image region, the average intensity value of all corresponding contours within an overlapping region is used.

2). Improved Conditional Generative Adversarial Networks:

The overall goal of this step is to take contour masks $F_c^a$ from ACAM to induce C-GANs [8] to create realistic images that respect the contours and intensity distributions suggested by ACAM. The combination of ACAM with C-GANs is denoted as A-GANs. Here, U-Net [46] is used as the generator network and PatchGAN [8] as the discriminator network. The key improvements of this approach over C-GANs is in the objective function to optimize the networks as contour masks of A-GANs carry intensity information for image generation. Another important technical improvement over our earlier work [29] is the development of a novel training strategy to avoid manual fine-tuning of ACAM parameters, which could cause A-GANs to yield some unrealistic cells.

Alongside the contour masks $F_c^a$ from ACAM, the C-GANs also use pairs of real images I and their manually obtained contour masks $F_c^r$ with actual intensity values within contour regions (left images, Fig. 1D). To eliminate the need for obtaining a second set of manual annotations, these image pairs are taken from the set of 64 annotated adaptive optics images used for establishing ACAM. Similar to C-GANs [8], A-GANs also attempt to learn a mapping from $F_c\in \left\{F_c^a,F_c^r\right\}$ and a random noise vector n to I; i.e., G : {F_c, n} → I. After convergence, the generator network G produces realistic appearing images that are indistinguishable from the real images used by the adversarial discriminator network D. The first term of the objective function of A-GANs is defined as

$$\begin{gathered} L_{GAN}\left(G,D\right)={\mathbb{E}}_{F,I}\left[\log D\left(F_c,I\right)\right] \\ +\gamma {\mathbb{E}}_{F,\mathbf{n}}\left[\log \left(1-D\left(F_c^a,G\left(F_c^a,\mathbf{n}\right)\right)\right)\right] \\ +\left(1-\gamma \right){\mathbb{E}}_{F,\mathbf{n}}\left[\log \left(1-D\left(F_c^r,G\left(F_c^r,\mathbf{n}\right)\right)\right)\right] \end{gathered}$$ (1)

As an improvement over our previous implementation [29], we added a small portion of contour masks $F_c^a\left(\gamma =0.2\right)$ from ACAM during training to improve the robustness of the generated images I to variations in p and t. Previously [29], p and t were manually fine-tuned to ensure that the contour appearance was consistent over the $F_c^a$. In contrast, here, since $F_c^a$ is included in Eq. 1, the generator network can directly obtain consistent results without manual tuning. Fig. 2 illustrates that the addition of contour masks to A-GAN training improves the generation of cell images. Here, the same contour mask (Fig. 2A) is input to A-GAN. When ACAM parameters are fine-tuned, some cells (white arrows, Fig. 2B) are still not visually realistic because they are either too dark or saturated. The appearance of these cells are improved (white arrows, Fig. 2C) with the addition of contour masks, which teach A-GAN to recognize these cells as fake.

Fig. 2.

Addition of contour masks from ACAM improves cell image generation. (A) Input contour mask. (B) Generated image without the addition of contour masks to A-GAN training [42]. (C) Generated image with the addition of contour masks. Note that some unrealistic cells with extreme low and high intensity values (white arrows) were generated due to improper selection of ACAM parameters, but are improved through the addition of contour masks in A-GAN training without additional parameter adjustment. Scale bar, 20 μm.

The second term in the objective function is used to prevent blurring of the generated image, and is given by

$$L_{L1}\left(G\right)={\mathbb{E}}_{F,I,\mathbf{n}}\left[{\Vert I-G\left(F_c^r,\mathbf{n}\right)\Vert }_1\right]$$ (2)

Finally, the last term in the objective function incorporates the partial intensity information from F_c:

$$L_F\left(G\right)={\mathbb{E}}_{F,\mathbf{n}}\left[{\Vert F_c-G\left(F_c,\mathbf{n}\right)\Vert }_1\right],\mathrm{where}{F}_c\ne 0$$ (3)

Here, F_c ≠ 0 indicates that Eq. 3 only considers nonbackground image points. Otherwise, it is discarded for the calculation of the combined loss function. Combining Eqs. 1–3 yields the objective function for optimizing A-GANs.

$$L\left(G,D\right)=L_{GAN}\left(G,D\right)+L_{L1}\left(G\right)+L_F\left(G\right)$$ (4)

The expected G is G* = arg min_G max_D L(G, D). The final result of this approach is that artificially-created, realistic training data for cell segmentation can be systematically generated by utilizing ACAM to create contour masks and importing them to G*.

B. Cell Segmentation

The goal of this step is to develop a deep learning-based level-set cell segmentation method for adaptive optics retinal images by using images of cells together with their annotations. For the purposes of training this cell segmentation model, images can be real (with manual annotations) or generated (with ACAM-generated annotations). The proposed segmentation model combines three visual cues to improve segmentation accuracy: centroids, cell contours, and cell region masks (Fig. 1E). All of these binary masks can be easily extracted from F_c for both real and generated datasets. Finally, a sequential level-set method is developed to replace the multi-phase level-set approach [42] in our early work to avoid oversegmentation of densely-packed cells.

A multi-channel U-Net is utilized to train the segmentation model, which has the same network structure as U-Net [46], except that it takes multi-dimensional masks that combine centroid, contour, and region masks. Therefore, the loss function consists of the sum of centroid, contour, and region components, each based on Eq. 5, which is the sum of binary cross entropy and Dice coefficient loss. B and $\widehat{B}$ represent the binary mask and predicted mask, respectively. Unlike our preliminary implementation of this network [42] that models contour boundaries with Gaussian distributions, the segmentation model in this paper only utilizes binary masks to reduce computational cost.

$$\begin{gathered} L_{mask}=-\frac{1}{2}\sum _{i=1}^{2}B\left({\mathbf{\text{x}}}_i\right)\log \widehat{B}\left({\mathbf{\text{x}}}_i\right) \\ -\frac{2{\sum }_{i=1}^{2}B\left({\mathbf{\text{x}}}_i\right)\widehat{B}\left({\mathbf{\text{x}}}_i\right)}{{\sum }_{i=1}^2{B}^2\left({\mathbf{\text{x}}}_i\right)+{{\sum }_{i=1}^2\widehat{B}}^2\left({\mathbf{\text{x}}}_i\right)} \end{gathered}$$ (5)

After training, the multi-channel U-Net predicts centroid, contour, and region masks for a test image, as illustrated in Fig. 1F. After binarization, the centroid map can be used as watershed markers; in addition, binarized region masks can be used to approximately subdivide images into cell regions. These cell regions might be connected with each other in the case of high cell density. Thus, cell regions are separated based on the four-color theorem [47], which states that any 2D planar graph can be labeled with as few as four colors such that no neighbors have the same color. This is implemented as a greedy coloring algorithm to separate cell regions [42].

Level-set segmentation is used to improve segmentation results from the multi-channel U-Net, similar to Hatamizadeh’s work [43]. Instead of utilizing a multiphase level-set segmentation framework to extract all cell contours at the same time [42], here, we utilize a single level-set function to sequentially extract cell contours from each color group to avoid the possibility of adjacent cells merging across different color groups. Note that the level set is propagated on the predicted cell region map (right image, Fig. 1F), instead of on the original cell image. The predicted cell region map is close to a binary map except near cell boundaries, which mitigates any negative effects on the level set function from image noise. Given that cell regions are disconnected within each color group and assuming that actual cell contours are in the vicinity of their boundaries, it is reasonable to use these cell regions as shape priors to constrain level-set propagation to protect against oversegmentation of cells (similar to localizing level set propagation [44], except that our shape prior controls the speed function while localized level set is only allowed to propagate in predefined image regions). Given a binary image C_i containing all cell regions associated with the ith color (i ∈ [1, 4]), with cell regions represented as 1 and background as 0, a signed distance function ψ can be calculated on C_i. Normalizing ψ yields the shape prior term:

$$\overline{\psi }=\{\begin{array}{cc}0& C_i=0\\ \psi /\max \left(\psi \right)& \text{otherwise}\end{array}$$ (6)

To ensure that the level-set propagation speed slows near the predicted contours in the contour map B_c, the speed function of the level-set is defined as $P=\overline{\psi }+B_c$. Then, geodesic active contour method [48] is used to propagate level sets and extract cell contours:

$$\frac{\partial \varphi }{\partial \tau }=P\left|\nabla \varphi \right|\text{div}\left(\frac{\nabla \varphi }{\left|\nabla \varphi \right|}\right)-\nabla P\cdot \nabla \varphi$$ (7)

Here div(·) is the divergence operator, and the initial contour ϕ at τ = 0 is initialized with ψ. Iterative evolution of ϕ leads to the identification of cell boundaries pertaining to the current C_i (100 iterations in all our experiments). After combining all segmentation results over all remaining colored regions (up to 3 additional colored regions based on four-color theorem [47]), the final cell segmentation result is generated (Fig. 1G).

C. Data Collection and Validation Methods

Research procedures were approved by the Institutional Review Board of the National Institutes of Health. Written, informed consent was obtained from all participants after the nature of the research and possible consequences of the study were explained. A custom-built adaptive optics retinal imager [30], [49] was used to acquire images from twenty eyes of twenty healthy subjects (age: 24.9±5.3 years) as well as from four eyes of two patients with two different rare genetic eye diseases (age: 41 and 25). A total of 312 images from the healthy eyes and 20 images from the diseased eyes (each 333×333 pixels) were manually annotated by two experienced graders. From these images, 248 images from sixteen healthy subjects were selected as the training data, and the remaining 64 images from the remaining four healthy subjects were used as the test data. The full training dataset (248 images) was further reduced to only 64 randomly selected images (≈25%) to explore whether efficient data annotation could be achieved using the proposed A-GANs strategy (relying on ACAM to generate any missing gaps in the training dataset). Importantly, we note that A-GANs can be stably trained with 64 training images due to the fact that each image contains numerous cells. For the groundtruth dataset, in addition to the 64 real test images, we also generated an additional 64 artificial images from A-GANs to further evaluate cell segmentation accuracy. Specifically, for the real images in the test dataset, manually-annotated cell contours are considered to be groundtruth; for the generated images from A-GANs, cell contours generated from ACAM are considered to be groundtruth. When measuring segmentation accuracy, corresponding segmented contours and groundtruth contours were paired if the distance between contour centroids is less than 8 pixels (cell diameters are expected to be approximately 20 pixels, which is within 6.5-7.5 μm [41]). Six metrics were used to quantify segmentation accuracy: area overlap (AP), Dice coefficient (DC), area difference (AD), average symmetric contour distance (ASD), symmetric RMS contour distance (RSD), and maximum symmetric absolute contour distance (MSD) [41], [42].

First, we evaluated the robustness of A-GANs. A set of contour masks with varying cell spacings of (9.8 μm-32.9 μm) were generated using ACAM, capturing a wider range of cell spacings than what has been reported for healthy eyes at different retinal regions [32] (Fig 3). For comparison, conventional C-GANs [8] was taken to be the baseline method for benchmarking against the improved C-GANs. Here, the inputs to the C-GANs were the same contour masks, except that intensity values were withheld from contour masks for conventional C-GANs which only accepts binary masks. The goal of this comparison was to determine whether intensity values in masks improved local intensity distributions and to evaluate whether this additional information improved the stability of GANs training.

Fig. 3.

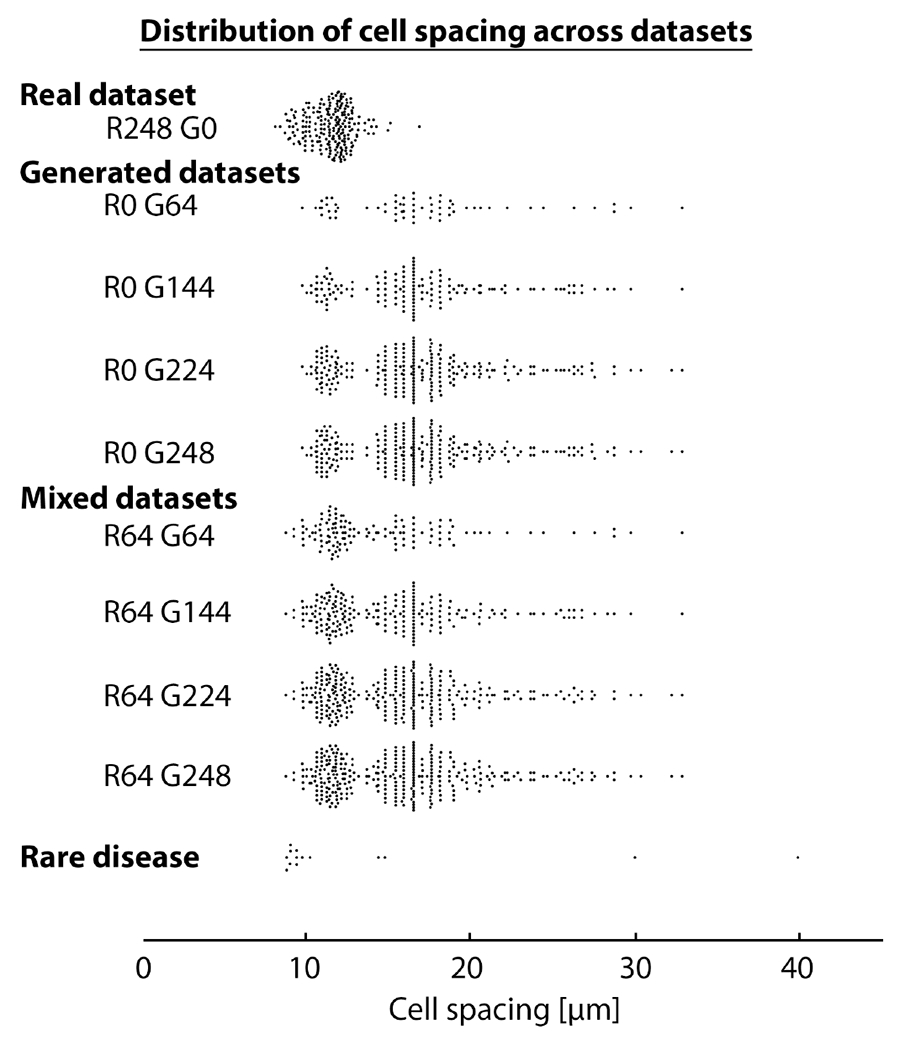
Distribution of cell spacing in datasets. The “Real dataset” includes images used for training and testing and matches the natural variation in cell spacing in healthy eyes based on expected histologic values [32] and in vivo measurements [33], [41]. R#G# denotes the number of real and generated images, respectively. The “Generated datasets” contain only generated images, while the “Mixed datasets” contain both real and generated images; both cover a larger range of cell spacings than the “Real dataset”. The “Rare disease” dataset is based on the images from diseased eyes in this paper.

Second, we evaluated the accuracy of generated images from A-GANs. We utilized cell contours from the 64 real test images and input them to A-GAN to re-generate new images. The relative image difference between the generated and real images was used to evaluate A-GAN. Here, the intensity range was normalized to [0, 1]. In addition, all cells on both real and generated images were segmented for comparison.

Third, we sought to characterize the relationship between the number of training images (considering both real and generated images) and final cell segmentation accuracy. If the performance hit associated with using a reduced training dataset of only real images could be recovered by augmenting the training dataset with generated images, then this would suggest that the proposed approach is an effective annotation-efficient training strategy. In particular, we derived a set of cell segmentation models which were evaluated on the test dataset with 64 real adaptive optics images. As a baseline, we used the complete training dataset (248 images) to create randomly selected subsets of training data consisting of 144 (≈58%) and 224 (≈90%) real images to evaluate the influence of the number of real adaptive optics images on the segmentation accuracy. Next, we created datasets of different numbers of generated images (64, 144, 224, and 248) for direct comparison to cell segmentation results obtained using the same numbers of real images. Here, three smaller datasets are created by randomly selecting images from the one with 248 images. All four datasets contain the same ratio of 60% densely-packed cells (≈ 14.8 ± 2.7 μm) and 40% sparsely-packed cells (≈ 23.1 ± 3.8 μm). They are used in all experiments with generated images in this paper. Finally, after evaluating the segmentation models established purely on generated images, we gradually mixed real and generated images together to evaluate if the strategy of using A-GANs to generate adaptive optics images was useful as an annotation-efficient strategy for data augmentation from the perspective of improving cell segmentation accuracy.

Fourth, we aimed to understand the technical improvements of A-GANs through comparison with our early version of A-GANs with fine-tuning of ACAM parameters [29], a multi-channel U-Net in which the level-set segmentation step is removed, and a C-GANs based cell segmentation method [23] to explore the efficacy of A-GANs for improving data augmentation by locally controlling each individual cell mask. Similar to above, all three comparisons were performed with 64 training images. Except for the comparison with the C-GANs based method [23], the other two comparisons also utilized additional generated images.

Fifth, we wanted to determine if the addition of real images improved cell segmentation on generated images using the generated test dataset containing A-GANs generated images with ACAM generated contours. Whereas the previous evaluation considered the accuracy of cell segmentation on real images, here, for symmetry, we consider the opposite situation in which increasing numbers of real images are added to a training dataset of generated images. If the real and generated images are indeed similar to each other, then we expect consistent results between this configuration and its symmetric counterpart from the previous section. As a baseline for comparison, we used the full dataset of 248 real images to evaluate whether we could further improve performance. In addition to using the test dataset with only generated images, we also compared results on the test dataset with only real images, to evaluate whether results were consistent across both a real and synthetic (generated) test dataset.

Finally, we considered the case of rare genetic eye diseases that have limited data available. Whereas the cells in healthy eyes tend to follow a range of expected cell spacings of (8.2 μm-16.9 μm) [29], [32], [33], in these two patients, the distribution of cells is fundamentally very different. In the first patient, cone photoreceptor cells are very sparse, and in the second patient, cell spacing is non-uniform. Although it is possible to train deep learning algorithms with manually-annotated disease-specific patient datasets [35], these datasets are not publicly available and it is difficult to recruit a large number of patients (estimated prevalence of the first case is 1 in 30,000 individuals; the second case is a previously-undescribed congenital maculopathy. As the second case has not been reported yet, there is little or no available information and therefore performance improvements that can be realized using an annotation-efficient method are truly needed.). Therefore, we wanted to see if we could improve performance without using any real data from these patients in the training dataset simply by using A-GANs. Here, we anticipated that A-GANs could generate a more diverse set of cells to complement the training dataset containing images with cells that are individually similar to some found in patient images but distinct in terms of packing arrangement. If so, then A-GANs can potentially be used to improve segmentation accuracy in a disease-specific manner without needing to explicitly train a new dataset tuned to a specific disease (and importantly, eliminating the need to invest in additional manual annotations on new datasets). Evaluation on these patient examples will help to establish whether A-GANs are a potential solution for annotation-efficient cell segmentation in rare diseases.

Both A-GANs and the multi-channel U-Net were implemented using Keras with a Tensorflow backbone and trained with 2,500 epochs using mini-batch (batch size = 32) stochastic gradient descent and Adam optimization with an initial learning rate of 0.001. Training data for the multi-channel U-Net was augmented with standard geometric transformations (rotation, translation, zooming, and shearing). It took less than an hour to train the A-GANs on 64 images, and 1-8 hours to train the multi-channel U-Net with the number of training data ranging from 64 to 496 images. All training experiments were performed on a desktop computer with Microsoft Windows 7, Intel(R) Core(TM) i7-6850K CPU, and dual NVIDIA GeForce GTX 1080 Ti GPUs. After training, it took less than a second to generate an adaptive optics retinal image from A-GANs, and 15 seconds to segment an adaptive optics retinal image.

III. Experimental Results

A. Incorporation of Local Intensity Information into Contour Masks Stabilizes Image Generation

Fig. 4 illustrates three examples of generated adaptive optics images with varying cell spacings after different training epochs. Figs. 4A1–4E1 show the results from conventional C-GANs using binary contour masks (Fig. 4A1). After 50 epochs, many cells are created incorrectly, with their intensity information on the opposite sides (dark areas are always on the left side of cells in real data, not the right side; white arrows, Fig. 4B1). Training with additional epochs does not correct the problem and sometimes results in further deterioration of the generated cells (Figs. 4C1–4E1). In contrast, using contour masks that include local intensity information from ACAM quickly stabilized the training process of A-GANs. Even after as few as 50 epochs, cells appear to be reasonable with correct shading (dark areas on the left, bright areas on the right; Fig. 4B2), with further improvements in cellular detail added after training with more epochs. Similar results are obtained as the cell to cell spacing is increased (Figs. F1/F2-J1/J2 and K1/K2-O1/O2). These results demonstrate that the additional information transferred from ACAM is a key factor for stabilizing A-GANs in order to faithfully generate adaptive optics retinal images. As a direct benefit, A-GANs can generate images with densely-packed cells (Figs. 4A2–4E2) or sparsely-packed cells (Figs. 4K2–4O2) that may not be readily obtainable in training datasets derived from real data alone. We will show that this is very beneficial for augmenting training data for application to rare genetic eye diseases that introduce never-seen data for cell segmentation.

Fig. 4.

Comparison of generated adaptive optics retinal images with varying cell spacings after different training epochs from conventional C-GANs and the proposed C-GANs. (A1-E1) shows the results of conventional C-GANs, in which a binary contour mask (A1) is used. Due to lack of local intensity information in these binary input contour masks, generated cells often contain the incorrect (opposite) intensity distribution (dark/bright areas reversed; white arrows), both after 50 epochs, as well as after 2,500 epochs. For many cells, image quality further degrades after additional epochs. In contrast, the proposed C-GANs which incorporates local intensity information into the input contour masks quickly achieves stable results with correct shading. More cellular details were added as the number of epochs increased. Similar results were observed as the cell spacing was increased (F1/F2-J1/J2) and (K1/K2-O1/O2). Scale bar, 50 μm.

B. Realistic Image Generation Using A-GANs

Direct comparison between real and generated images was performed by comparing 64 real images (Fig. 5A) with their corresponding 64 generated images (Fig. 5B) that are based on input contours extracted from the real images. There is little difference observed within cell regions, with most differences arising at non-cell regions (Fig. 5C). An annotation-efficient cell segmentation model (trained using a combination of 64 real images and 248 generated images) is used to segment cells on both real (Fig. 5D) and generated (Fig. 5E) images. Nearly all cell contours matched with each other well, indicating that A-GANs could accurately generate realistic images. Further evaluation also showed an average symmetric contour distance of 1.2 pixels (Table I). Overall, these results validate that A-GANs can accurately generate images for the purposes of enlarging training data.

Fig. 5.

Fidelity of image generation process. Cell contours from real images are used to re-generate new images. The two images are compared using relative image difference and cell segmentation. (A) Real image. (B) Generated image. (C) Relative image difference between real and generated images. (D) Cell segmentation on real image. (E) Cell segmentation on generated image using the same annotation-efficient cell segmentation model as (D). (F) Overlay of segmentation results from real and generated images. Segmentation results match except for one cell (white arrows). Scale bar, 50 μm.

TABLE I.

Evaluation of image generation comparing real and generated images.

AP (%)	DC (%)	AD (%)	ASD (Pix)	RSD (Pix)	MSD (Pix)
81±10	89±7	16±18	1.2±0.9	1.5±1.1	2.9±2.5
Average Relative Image Difference (%)				6.2±1.4

AP: Area overlap; DC: Dice coefficient; AD: Area difference; ASD: Average symmetric contour distance; RSD: Symmetric RMS contour distance; MSD: Maximum symmetric absolute contour distance.

C. Augmenting Real Images with Generated Images Improves Cell Segmentation Accuracy

The improvement in cell segmentation that is realized by incorporating generated images from A-GANs into the cell segmentation model is illustrated in Fig. 6. For testing, only real images are used for each of the different segmentation models (Table II). As expected, cell segmentation improved as the number of real images used for training was increased from 64 to 248. Whereas the segmentation model trained with only 64 real images seems to yield under-segmentation (white arrows, Fig. 6A3–D3), the model trained with all 248 real images achieved the best segmentation accuracy (Fig. 6A4–D4). In comparison, the models trained using only generated images seemed prone to over-segmentation (white arrows, Fig. 6A5/A6–D5/D6). However, the addition of only 64 real images to a set of generated images successfully steered the segmentation model to reduce over-segmentation (Fig. 6A7–D7), with the combination of 64 real images and 248 generated images achieving a segmentation accuracy similar to that of the highest accuracy of models that use real images alone. There was no statistically significant difference between the six pairs of cell segmentation accuracy metrics from these two models (Table II) (p = 0.11, two-tailed paired t-test). Detailed segmentation results are presented in Table II. These results demonstrate that A-GANs can be used as a sophisticated method for data augmentation. With A-GANs, the performance hit attributed to using a smaller than ideal training dataset can be recovered (as small as 25% of an annotated training dataset can be used).

Fig. 6.

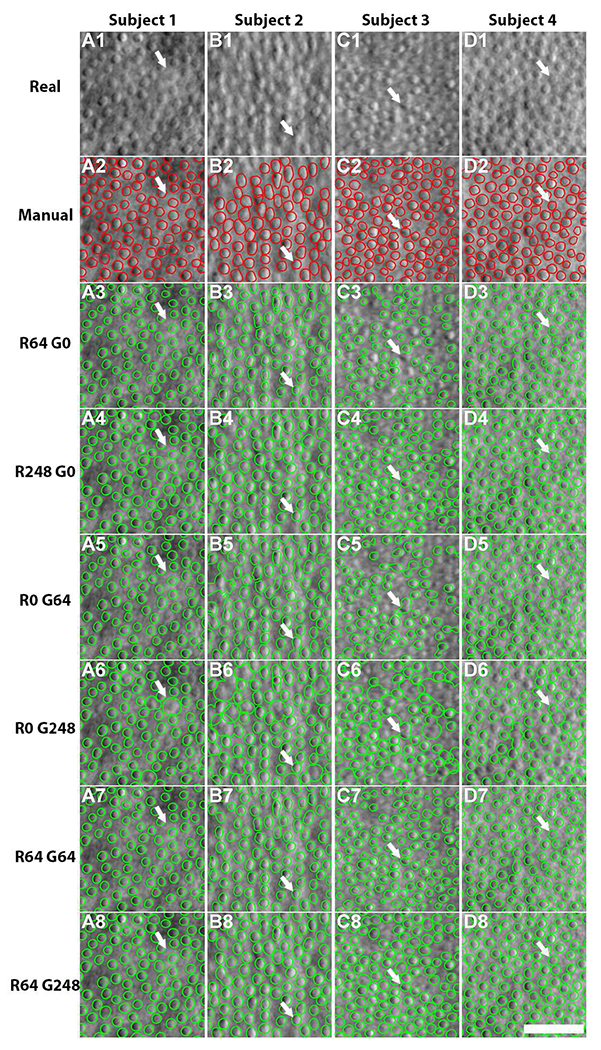
Comparison of cell segmentation results from segmentation models trained with different numbers of real and generated images using real test data from four healthy subjects (R#G# denote the number of real and generated images used for training). (A1-A4) Input data, (A2-D2) manually-annotated cell contours, (A3-D8) segmentation results the various models. Note that the R64 G0 model seems to either under-segment cells (white arrows, A3, B3, D3) or fails to identify cells (C3). Cell segmentation tested on real images achieves the highest accuracy with the R248 G0 model (A4-D4). In contrast, both segmentation models trained on generated images yielded over-segmentation (white arrows, A5/A6-D5/D6). However, combining generated images with 64 real images to train the segmentation model is efficacious in improving accuracy, despite some instances of under-segmentation (white arrows, A7-D7). The R64 G248 model achieved similar segmentation accuracy compared to the models trained using all real images (A8-D8). Scale bar, 50 μm.

TABLE II.

Cell segmentation accuracy with varying amounts of real and generated images.

R(#)/G(#)	AP (%)	DC (%)	AD (%)	ASD (Pix)	RSD (Pix)	MSD (Pix)
64/0	65±10	78±8	31±13	2.4±0.9	2.7±1.0	4.7±2.0
144/0	69±9	81±7	27±13	2.0±0.8	2.3±0.9	4.2±2.0
224/0	78±10	87±7	17±15	1.4±0.8	1.7±0.9	3.4±1.9
248/0	79±11	88±7	16±17	1.4±0.8	1.7±1.0	3.4±2.0
0/64	69±12	81±10	25±51	2.1±1.1	2.5±1.3	5.1 ±3.1
0/144	70±11	82±10	23±27	2.0±1.1	2.4±1.5	4.8±3.7
0/224	74±12	84±9	24±65	1.8±1.4	1.2±1.6	4.4±3.6
0/248	73±14	83±12	33±96	2.1±2.0	2.4±2.2	4.8±4.2
64/64	69±10	81±8	26±17	2.0±0.8	2.3±1.0	4.2±2.1
64/144	78±11	87±7	17±20	1.4±0.9	1.7±1.0	3.5±1.9
64/224	78±10	87±10	17±18	1.5±0.8	1.8±0.9	3.6±2.0
64/248	79±11	88±8	17±21	1.4±0.9	1.7±1.0	3.5±2.0

D. Accurate Cell Segmentation Achieved by Locally Controlled Data Augmentation

This experiment aims to understand the technical contributions of A-GANs through comparison with our earlier version of A-GANs with fine-tuning of ACAM parameters [29], a multi-channel U-Net without level-set segmentation, and a C-GANs-based cell segmentation method [23]. All experiments utilized 64 real images as the training data because the same number of images was also employed by A-GANs in this work. Except for the comparison with the C-GANs-based cell segmentation method, 248 generated images were used to enhance training data, either created by the early version of A-GANs or by the model in this paper for multi-channel U-Net cell segmentation.

Table III shows the segmentation accuracy of four different methods, where only area overlap, Dice coefficients, and area difference were reported for the C-GANs-based method for nuclei segmentation on histopathology images [23] because it only yields segmentation masks, not individual cell contours. Cell segmentation accuracy dropped slightly using the early version of A-GANs [29], which suggests that our segmentation framework is robust to the presence of some unrealistic cells with extreme intensity values (Fig. 2) as long as the majority of cells are within the normal intensity ranges. These results also show that level-set segmentation is a necessary step for improving cell segmentation accuracy (effectively relocating cell contour boundaries). The deep adversarial segmentation method performed poorly on our images, possibly due to crowded cells or lack of image textural features compared to histopathological images. Importantly, in contrast to the deep adversarial segmentation method that globally creates segmentation masks, A-GANs could control the shapes, appearances, and locations of individual cells, giving the user more control over the augmentation of training data.

TABLE III.

Comparison of cell segmentation accuracy among four different methods.

Method	AP (%)	DC (%)	AD (%)	ASD (Pix)	RSD (Pix)	MSD (Pix)
1	74±11	84±9	23±49	1.8±1.3	2.2±1.8	4.7±4.4
2	63±10	77±8	34±12	2.4±0.9	2.7±1.0	4.9±1.9
3	33±4	50±5	46±23	-	-	-
4	79±11	88±8	17±21	1.4±0.9	1.7±1.0	3.5±2.0

1: Early version of A-GANs with fine-tuning parameter adjustment [29].

2: Multi-channel U-Net without the level-set segmentation.

3: C-GANs-based method [23].

4: A-GANs (R64 G248 from this paper).

E. Symmetric Results Obtained Using Real and Generated Test Datasets

The experiment in section III-C showed that similar segmentation accuracy could be achieved using either the R64 G248 model or the baseline R248 G0 model. This section symmetrically evaluates the segmentation model on test data with real as well as generated images. Here, we fixed the training data with 248 generated images, gradually adding real images to evaluate its influence on segmentation accuracy.

Two real images (left two columns, Fig. 7) and two generated images (right two columns, Fig. 7) were chosen for evaluating segmentation accuracy. Interestingly, similar segmentation results are observed between segmentation models trained with 248 real images (Fig. 7A5–D5) and with 64 real + 248 generated images (Fig. 7A4–D4). We noticed that the baseline model trained on real images alone generated many extra false positives (white arrows, Fig. 7D3), possibly because sparsely-packed cells are observed to a lesser degree in real images. In contrast, the segmentation models that incorporate generated images successfully address this issue.

Fig. 7.

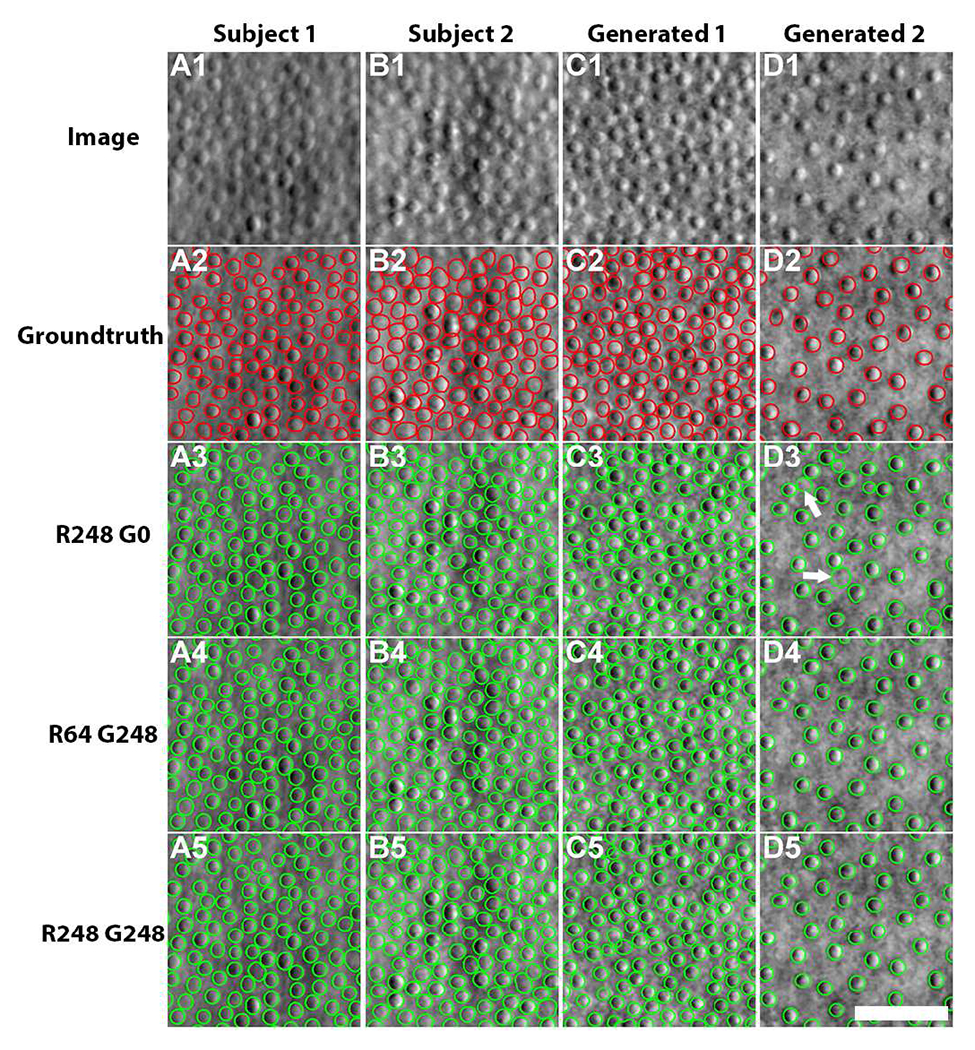
Comparison of cell segmentation results on two healthy subjects and generated images. (A1-B1) Real images, (C1-D1) generated images, (A2-D2) groundtruth cell contours from (A2-B2) manual annotations and (C2-D2) ACAM-generated annotations, (A3-D3) segmentation results from the model trained with 248 manually-annotated real images, (A4-D4) results from the model with 64 real images and 248 generated images, and (A5-D5) results from the model with 248 real images and 248 generated images. Note that some false positives (white arrows, D3) are observed in the segmentation results from the model trained on manually-annotated images, likely because sparsely-packed cell images are less commonly observed in the real training dataset. Scale bar, 50 μm.

Table IV shows the full segmentation results evaluated on test dataset of generated images. Segmentation models trained with generated images fared well either with or without real images and were similar or slightly better in performance when compared to the baseline model trained on real images alone. understandably, the segmentation accuracy of the test dataset is coupled with the selection of training dataset. The model training on 248 real images yielded the highest accuracy on the test dataset with real images, while it dropped in accuracy on the test dataset with generated images. Symmetrically, the model trained on the dataset with generated images achieved better performance on the generated test images. These results confirmed that augmentation using A-GANs can enhance the segmentation model by covering cell distributions that are less commonly found in the training dataset.

TABLE IV.

Cell segmentation accuracy on generated test images.

R(#)/G(#)	AP (%)	DC (%)	AD (%)	ASD (Pix)	RSD (Pix)	MSD (Pix)
248/0	72±12	83±8	12±10	2.1±1.0	2.4±1.1	4.3±1.9
0/248	74±11	85±8	9±8	1.8±0.9	2.2±1.1	4.0±1.9
64/248	74±12	85±8	10±11	1.9±1.0	2.2±1.1	4.0±2.0
248/248	74±11	85±8	10±9	1.8±1.0	2.2±1.1	4.0±2.0

F. Annotation-Efficient Improvement in Cell Segmentation in Never-Seen Rare Genetic Eye Diseases

Thus far, experimental data consisted of images from healthy eyes. Here, we applied cell segmentation models to two rare genetic eye diseases that contain never-seen images in which the cells exhibit a very different arrangement than what is typically seen in healthy eyes (Fig. 8). We tested the two best performing cell segmentation models (Table V).

Fig. 8.

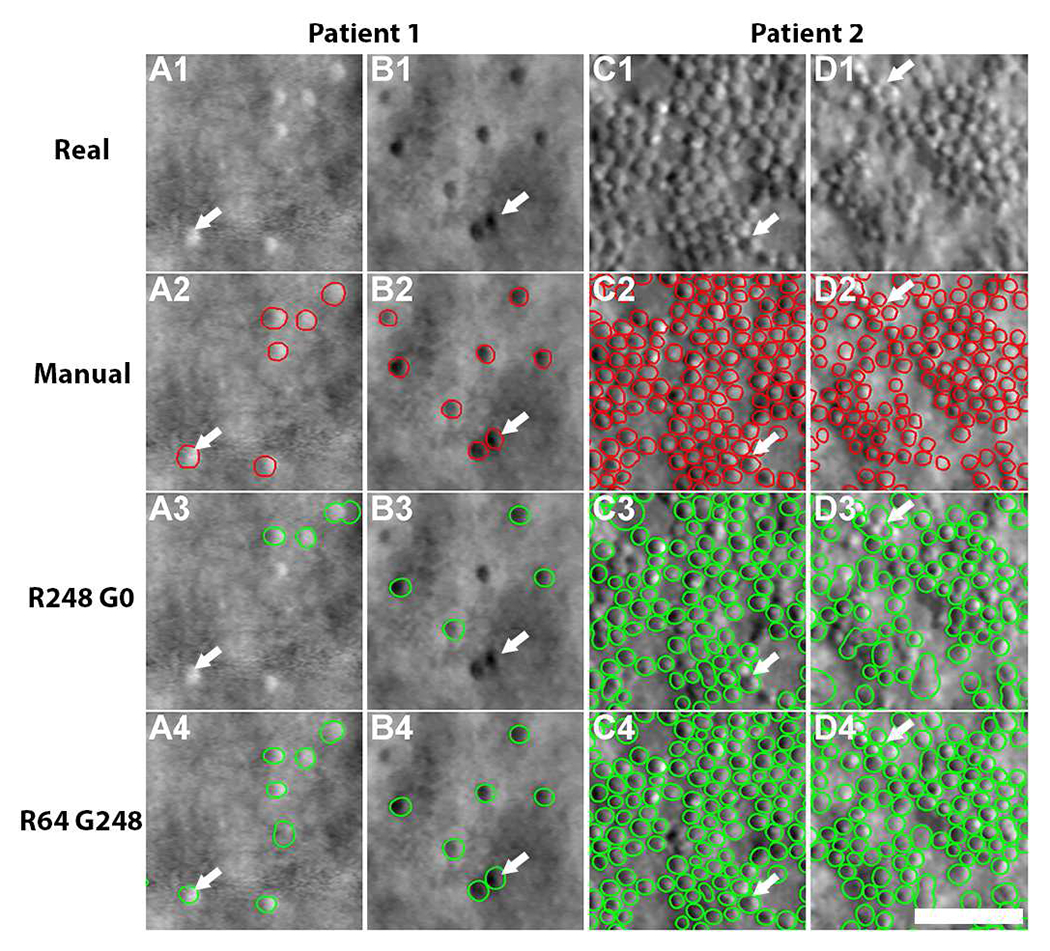
Comparison of cell segmentation results in four eyes from two patients: achromatopsia (patient 1) and a previously-undescribed congenital maculopathy (patient 2). (A1-D1) Real images, (A2-D2) annotated cell contours, (A3-D4) segmentation results from the R248 G0 and R64 G248 models. In patient 1 (sparsely packed cells), the model trained from real images alone fails to identify some brighter appearing cells (e.g. arrow, A3) and some darker appearing cells (e.g. arrow, B3) but these cells are successfully segmented using the model that combined both real and generated images (A4, B4). In patient 2 (non-uniformly packed cells), the model trained from real images only was prone to over-segmentation (arrows, C3-D3). In contrast, the combined model was successful in segmenting these cells (C4-D4). Scale bar, 50 μm.

TABLE V.

Cell segmentation accuracy on patient images.

R(#)/G(#)	AP (%)	DC (%)	AD (%)	ASD (Pix)	RSD (Pix)	MSD (Pix)
248/0	69±13	81±11	38±72	2.2±1.5	2.4±1.8	4.9±3.7
64/248	69±12	81±9	32±38	1.9±1.1	2.3±1.3	4.6±2.8

The baseline model (training with all real images from healthy eyes) failed to identify many cells that had local intensity values which were sufficiently different from “typical” cells observed in healthy eyes (arrows, Fig. 8A3 and B3). In contrast, the cell segmentation model based on both real and generated images successfully extracted nearly all of the cell contours in achromatopsia (Fig. 8A4 and B4). This is likely due to the ability of A-GANs to generate cells that have a more balanced distribution of cell spacing, including both sparsely-packed and densely-packed cell mosaics (Fig. 4). similar improvements in cell segmentation were also observed in previously-undescribed congenital maculopathy. The baseline model often resulted in over-segmentation errors (arrows, Fig. 8C3–D3), due to the close proximity of some cells. The proposed model incorporating both real and generated images successfully reduced over-segmentation (Fig. 8C4–D4), likely because it was enhanced during training with generated examples of densely-packed cells (Figs. 4A2–4E2). Table V compares the segmentation accuracy using the two different models and shows that the cell segmentation model that incorporates generated images was better than the baseline model (real images only).

IV. Discussion and Conclusion

This paper demonstrates the application of A-GANs to cell segmentation for adaptive optics images. A multi-channel U-Net trained on both real and generated images can predict cell centroid, contour, and region cues. All these visual cues are then imported into a level-set segmentation framework and combined with four-color theorem to improve cell segmentation. There are several key advantages with respect to annotation efficiency. First, the generation of realistic images based on ACAM is effectively a sophisticated method for data augmentation. We show that the training dataset size can be reduced to as much as 25% of the original size without suffering a loss in performance, as long as A-GANs are used. Second, since A-GANs can be used to generate pre-annotated datasets, A-GANs are valuable for augmenting traditional groundtruth datasets used for testing or for generating surrogate test datasets for alternate purposes. Such datasets would not be subject to the variability that is associated with manual annotation. Finally, adopting an annotation-efficient strategy is particularly important when working with rare diseases so that the number of diseased images reserved for testing is maximized. Results on two never-seen rare genetic eye diseases show that cell segmentation in these images is further improved using the proposed approaches.

A fundamental element for generating realistic images is our use of ACAM to statistically capture the range of cell contour shapes and local intensity patterns from real data, so that new cells that vary in shape and appearance can be generated in a manner that mimics the characteristics of real data. The first four components from PCA were used for both cell shape and appearance models (over 95% of the shape and appearance information were contained in these terms [45]). Figs. 4 and 5 illustrated that realistic cell images could be generated with only four model components. Consistently across all our experiments, we show that the addition of generated images from ACAM to existing training datasets improves cell segmentation accuracy. The advantage to this de novo synthesis of data is that local manipulations to cells can be realized which cannot be easily achieved using conventional data augmentation methods [1], [2] that globally transform images. Table III showed that level-set segmentation is a necessary step to achieve further improvements in cell segmentation accuracy from multi-channel U-Net. In addition to the characteristics of individual cells, ACAM also allows for different cell spacings to be easily achieved to better represent the range of cell packing that exists across different retinal regions [32]. Fig. 7 and Fig. 8 demonstrated that the proposed approach can achieve improved segmentation accuracy without the need for large amounts of training data. All in all, ACAM provides an annotation-efficient strategy to enrich training datasets with both a broader and deeper range of examples that may not be readily available for incorporation into training.

Incorporation of local intensity values in contour masks is key for stabilizing GANs. By combining ACAM with the improved C-GANs, we present a strategy for systematically creating pre-annotated data with exquisite control over the parameters of the generated data. In short, by using ACAM as an input into the improved C-GANs, we avoid having to adjust parameters within the GANs to control cell shapes and appearance [29]. Our results suggest that even the addition of a very small set of real images alongside generated images can improve cell segmentation results. Depending on the application, titrating the relative amount of real and generated images may be important (Fig. 6). Other future applications include extending A-GANs to situations where capturing the real-world variations are desired, such as for retinal vessels [10], spines [50] with elongated shapes, irregular liver shapes across individuals [17], and when there is substantial variation in the appearance of neighboring cells [40], [51].

Specific improvements to the cell segmentation model realized by incorporating A-GANs include improvements to false positives, false negatives, and over- and under-segmentation. In the case of a sparsely-packed cell mosaic, the baseline model resulted in numerous false positives (Fig. 7D3). In contrast, the segmentation models that incorporate additional generated images address this issue. Similarly, in patients with rare diseases, the baseline model either misses some cells (Figs. 8A3–8B3) or over-segments others (Figs. 8C3–8D3), which is understandable since neither sparsely-packed cells nor non-uniformly and densely-packed cells are present in high numbers in the training data from healthy subjects. Enhancing the real dataset with generated images that capture a range of sparse and dense packing led to the best results. Although A-GANs can accurately generate cell regions, it sometimes produces errors in non-cell regions, especially in situations where there are other types of structures present, such as blood vessels. Developing a controllable augmentation method on non-cell image regions could benefit cell segmentation as well as other applications in which realistic image generation may be needed.

All in all, this work describes a set of strategies to improve the efficiency of data annotation for establishing training and test datasets for deep learning as well as for improving the training of deep-learning based models such as cell segmentation. We demonstrate a 75% reduction in the amount of manual annotation needed (248 to 64 images) while still achieving robust cell segmentation results. Results in healthy subjects can be extended to never-seen images from patients with rare diseases, an important step towards applying machine learning to medical images in which disease-based training datasets are difficult or expensive to obtain.