ATP Can Efficiently Stabilize Protein through a Unique Mechanism

Abstract

Recent experiments suggested that ATP can effectively stabilize protein structure and inhibit protein aggregation when its concentration is less than 10 mM, which is significantly lower than cosolvent concentrations required in conventional mechanisms. The ultrahigh efficiency of ATP suggests a unique mechanism that is fundamentally different from previous models of cosolvents. In this work, we used molecular dynamics simulation and experiments to study the interactions of ATPs with three proteins: lysozyme, ubiquitin, and malate dehydrogenase. ATP tends to bind to the surface regions with high flexibility and high degree of hydration. These regions are also vulnerable to thermal perturbations. The bound ATPs further assemble into ATP clusters mediated by Mg²⁺ and Na⁺ ions. More interestingly, in Mg²⁺-free ATP solution, Na⁺ at higher concentration (150 mM under physiological conditions) can similarly mediate the formation of the ATP cluster on protein. The ATP cluster can effectively reduce the fluctuations of the vulnerable region and thus stabilize the protein against thermal perturbations. Both ATP binding and the considerable improvement of thermal stability of ATP-bound protein were verified by experiments.

Introduction

Adenosine 5′-triphosphate (ATP) can provide energy for biochemical reactions within cells. ATP consists of an adenine base, a ribose sugar, and triphosphate with high energy phosphate bonds. As an energy currency, ATP at ∼100 μM concentration is sufficient for most ATP-utilizing enzymes, while the physiological concentration (1–10 mM) of ATP is 10- to 100-fold higher.^1,2 Besides, ATP synthesis varies remarkably during cell cycle: it decreases by ∼50% in early mitosis as compared to the G2 level.³ Both imply that ATP has other essential physiological functions. As indicated in a recent study, ATP can act as an effective cosolvent that stabilizes protein structure, improves protein solubility, and inhibits liquid–liquid phase separation.⁴ The proteome-wide study about the effect of ATP on protein thermal stability further demonstrated the global role of ATP in stabilizing proteins under cellular environment.⁵ More strikingly, the thermal stability of protein pervasively changes throughout the cell cycle and exhibits a notable correlation with ATP synthesis: it reduces in mitosis and recovers in interphase.⁶ Protein solubility and stability, especially thermal stability, are crucial for its activity.^6,7 The pervasive variation of protein thermal stability and activity are related to the regulation of transcription and metabolism.⁶ In the intracellular environment, the structural stability of protein may be compromised by nonspecific interaction with other biomacromolecules and inner membranes.⁸⁻¹⁰ In addition, it is also affected by considerable thermal fluctuations^11,12 and substantial temperature gradients in biological systems; e.g., the temperature of mitochondria is considered to be several degrees higher than ambient temperature.¹³⁻¹⁶ The stabilizing effect of ATP may be vital for protein to maintain its structure in these conditions.

The ability of cosolvent to improve protein stability and solubility has been well characterized. To date, the mechanisms of natural cosolvent can be roughly categorized into two types. The first is osmolyte, e.g., trimethylamine N-oxide (TMAO), which indirectly enhances protein stability by altering the bulk water structure.¹⁷⁻¹⁹ The other is hydrotrope, e.g., sodium xylene sulfonate (NaXS), which forms complete micellar assembly to encapsulate protein to improve its solubility.^4,20 For both types of mechanisms, a high cosolvent concentration of up to ∼1000 mM is required to effectively solubilize proteins. By contrast, ATP at concentrations of less than 10 mM can effectively stabilize proteins. The ultrahigh efficiency of ATP strongly suggests that it stabilizes protein via a novel mechanism that is fundamentally different from previous models of cosolvents.

The behavior of protein under thermal perturbation and the impact of cosolvent have been widely studied by molecular dynamics (MD) simulations.²¹⁻²⁸ It was revealed through MD simulations that the unfolding process of lysozyme induced by high temperature begins in the highly flexible interdomain loop region.^29,30 As indicated in previous works, the osmolyte TMAO enhances the stability of lysozyme by altering the structure of bulk water.^17,31 A high concentration of TMAO (∼1000 mM) is required to sufficiently strengthen the hydrogen-bond network of aqueous solutions, thereby stabilizing protein. However, there has been limited work on the interactions between ATP and protein, leaving the molecular mechanism underlying how ATP enhances the protein stability with such great efficiency largely obscure. Being a highly negatively charged molecule, ATP is usually complexed with cation, especially Mg²⁺ under physiological conditions.³²⁻³⁵ Cations may take part in the interactions of ATP with protein. Therefore, a comprehensive understanding on the interactions of ATP and cations with proteins and their effects on the protein stability may substantially advance our knowledge on the physiological roles of ATP.

In this work, we combined MD simulations with experiments to study the interactions of ATP with three proteins (i.e., lysozyme, ubiquitin, and malate dehydrogenase) and its effect on the protein thermal stability. We found that ATP molecules accumulate around and partially cover the protein and that the surface regions with higher degree of hydration and larger structural flexibility are more susceptible to ATP binding. Both Mg²⁺ and Na⁺ ions mediate the interaction between the bound ATPs and facilitate the formation of the ATP cluster. It should be mentioned that the regions susceptible to ATP cluster, which possess high flexibility and degree of hydration, are also vulnerable to thermal perturbation. For example, in the case of lysozyme, the ATP cluster binds to the flexible interdomain loop and thus reduces its structural fluctuation. In this way, the binding of the ATP cluster effectively prevents these vulnerable regions from loosening due to thermal perturbation, thereby improving the overall thermal stability of lysozyme. More strikingly, in Mg²⁺-free ATP solution, Na⁺ at significantly higher concentration (150 mM under physiological conditions) can likewise mediate the formation of the ATP cluster on lysozyme, increasing the thermal stability of lysozyme to a similar extent. Similar phenomena including ATP cluster formation and the improved protein thermal stability are also observed in ubiquitin and malate dehydrogenase. We verified the binding of the ATP cluster to protein by ANS fluorescence and NMR spectroscopy and confirmed the enhancement of thermal stability of the ATP-bound protein using thermal shift assay and circular dichroism spectroscopy. Our results suggest ATP can efficiently stabilize protein through a unique nonspecific binding mechanism which is distinct from the previous models of cosolvents.

Results and Discussion

Accumulation of ATP around Protein

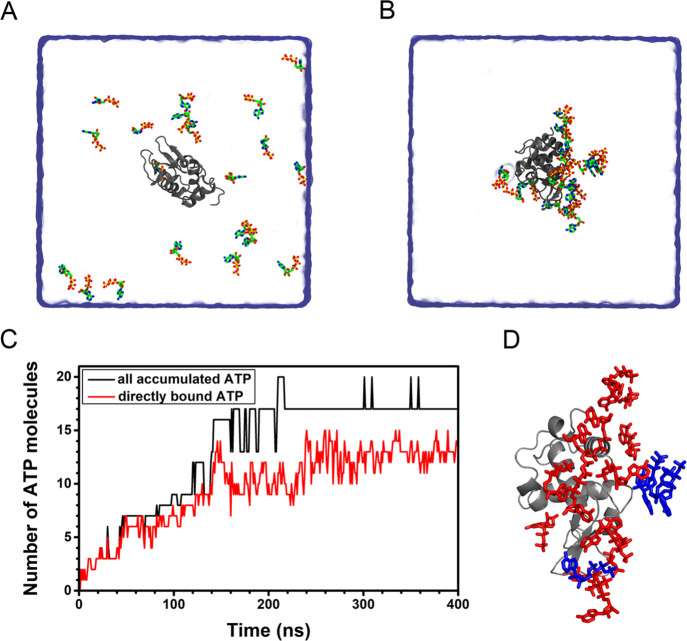
We first studied the interaction of ATP with lysozyme. There were 20 ATP–Mg complexes (Figure S1, ATP tends to coordinate with intracellular Mg²⁺ ion^34,35) in a cubic box with a side length of 12.6 nm, corresponding to a 16.6 mM concentration. Initially, all ATP–Mg complexes were at least 9 Å from lysozyme (Figure 1A). Five independent simulations were performed for 400 ns each. A representative trajectory was chosen to be studied in detail. ATP exhibits a considerable tendency to accumulate around lysozyme (Figure 1B). As the adsorption reaches equilibrium, most of the ATPs accumulate around the protein. We notice that the ATPs accumulating around lysozyme can be roughly divided into two groups (Figure 1D): the ATPs that directly contact with protein (in red) and the ATPs that accumulate around protein through contact with the directly bound ATPs (in blue).

Figure 1.

Binding and accumulation of ATP around lysozyme. (A, B) Initial and final configurations of the ATP binding to protein. (C) The number of ATPs accumulated around protein. (D) ATPs in direct (in red) and indirect (in blue) contact with protein.

The numbers of the total accumulated ATPs (N_A) and the directly bound ATPs (N_D) were calculated separately (Figure 1C). At the beginning (before t = 140 ns), almost all of the accumulated ATPs were directly bound to lysozyme. As the accumulation proceeded, the newly adsorbed ATPs accumulated around and primarily indirectly bound to the protein. After t = 240 ns, the adsorption of ATPs became saturated. The average N_A and N_D were 17.1 and 12.7 (based on the last 160 ns trajectory), respectively. In other words, most ATP molecules (17 out of 20) accumulate around protein by the aforementioned two approaches and 74.3% of the accumulated ATPs directly contact with protein. Similar phenomena of ATP adsorption were also found in all other independent simulations: ATPs first accumulate around and directly bind to lysozyme and at equilibrium ∼70% of the accumulated ATPs are in direct contact with the protein (Figure S2). To explore the prevalence of ATP accumulation on protein, we also studied the interaction of ATP with other proteins, namely ubiquitin and malate dehydrogenase. ATPs can similarly accumulate around these proteins in a mixed mode of direct and indirect contact. The average N_A and N_D values were 10.0 and 6.4 for ubiquitin (based on the last 50 ns trajectory) and 24.7 and 16.6 for malate dehydrogenase (based on the last 140 ns trajectory), respectively. ATP exhibits a considerable tendency to bind to these two proteins (Figures S3 and S4). Moreover, in all simulations of these three proteins, a part of the accumulated ATPs (∼70%) were in direct contact with protein. In other words, adequate binding of ATP may be realized at a concentration even lower than the physiological concentration we studied, whereas the indirectly bound ATPs could be redundant for maintaining adequate contact with protein. It is worth noting that all these three proteins do not have specific ATP binding sites. To put it another way, such a strong accumulation can be attributed to the somewhat nonspecific interaction of ATP with protein.

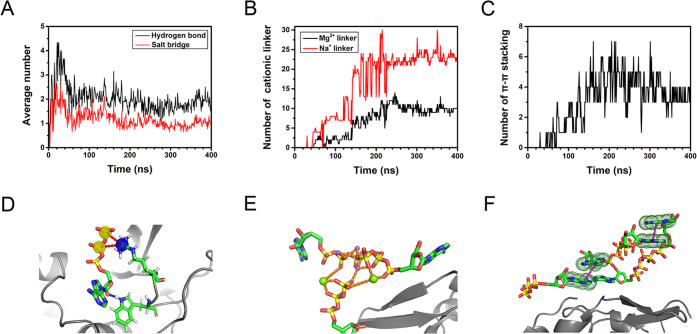
To investigate the mechanism by which ATP accumulates around protein, the interaction between directly bound ATP and lysozyme was analyzed in detail. ATP mainly interacts with the surface residues via salt bridges and hydrogen bonds, with the corresponding numbers of 12.6 and 22.2, respectively. It should be noted that most of the directly bound ATPs simultaneously form hydrogen bonds and salt bridges with lysozyme. Each directly bound ATP can form 1.0 salt bridge and 1.7 hydrogen bonds on average (Figure 2A,D). The salt bridge plays a significant role in the ATP binding process. When ATP approaches the protein, its phosphate groups tend to interact with the positively charged residue to form salt bridges. For example, the average interaction energy of ATP and the positively charged residue ARG was as high as ∼−247 kJ/mol. A previous experiment also showed that ATP binding depends on the properties of surface residues, especially charged residues.³⁶ In other words, although the interaction of ATP with protein is generally nonspecific, ATP exhibits a clear tendency to accumulate around certain surface region enriched with charged residues, such as the interdomain loop (residues 33–70, Table S1 and Figure S5) of lysozyme. In addition, all three parts (i.e., adenine, ribose, and triphosphate) of the directly bound ATP can form hydrogen bonds with protein, which further promotes the binding of ATP. Besides, the interactions of ATPs with lysozyme may also affect the coordination state of ATP–Mg (Figures S6 and S7). Based on the binding tendency of ATP, lysozyme can be divided into “ATP-susceptible” (with contact probability greater than 50%) and “ATP-neutral” regions (Figure 3A and Table S1). There are 42 residues in the ATP-susceptible region (Table S1), corresponding to ∼46% of the surface residues (92 in total).^37,38 The ATP-susceptible region contains most of the aforementioned interdomain loop of lysozyme. In other independent simulations, ATPs also appear to bind to the loop region enriched with charged residues, and more than 40% of the surface residues are covered with ATPs (Figure S8). In other words, given the extensive binding of ATP, the flexible loop region enriched with charged residues is likely to be covered with ATPs, despite the somewhat different distributions of the ATP-susceptible region (Figure 3A and Figure S8).

Figure 2.

Detailed analysis of ATP accumulated around lysozyme. (A) Average number of salt bridges and hydrogen bonds of the directly bound ATP with protein. (B) Number of Mg²⁺ (black) and Na⁺ linkers (red) between accumulated ATPs (the separations of linking ion with both phosphate oxygens are less than 5 Å). (C) The number of π–π stacking interactions between the accumulated ATPs (the COM distance between two adenine bases is less than 5 Å). (D) Representative snapshots of the directly bound ATPs. Salt bridges and hydrogen bonds are shown in red and blue dash lines, respectively. (E) Representative snapshots of the cationic linkers between accumulated ATPs. Mg²⁺ linkers and Na⁺ linkers are shown as green and purple spheres, respectively. (F) Representative snapshots of π–π stacking interactions between the adenine bases of accumulated ATPs and π–π stacking interactions are shown in purple dash lines.

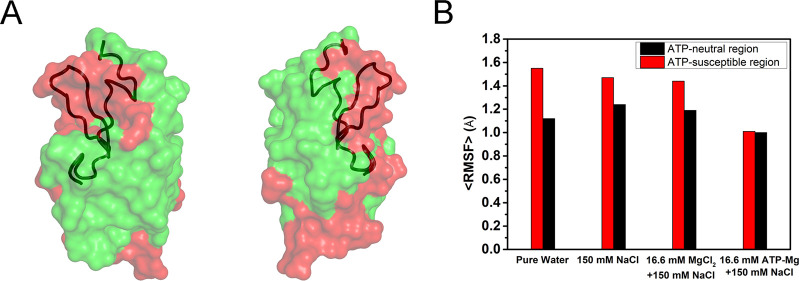
Figure 3.

ATP binding reduces the structural fluctuations of lysozyme. (A) ATP-susceptible (red) and ATP-neutral (green) regions of lysozyme; the interdomain loop is shown in tube representation. (B) Average RMSF of the residues in the ATP-susceptible and ATP-neutral region.

Similarly, ATPs tend to bind to a prominent fraction of surface region of ubiquitin and malate dehydrogenase (Figures S9A and S10A). These ATP-susceptible regions share similar features, e.g., highly flexible, enriched with charged residues (Tables S2 and S3). On the other hand, the sequence identities of the ATP-susceptible regions of lysozyme, ubiquitin, and malate dehydrogenase are rather low (Figures S11), indicating the lack of unique sequence feature for ATP-susceptible region. Because of the extensive binding of ATP (Figure 3A and Figures S8–S10), the bound ATPs can still cover most of the protein flexible loops, regardless of the differences in the size, shape, and residue distribution of these three proteins. In other words, ATPs exhibit the tendency to bind to a broad spectrum of proteins characterized by the loops enriched with charged residues.

When the number of directly bound ATPs reaches ∼10 (t = 140 ns, Figure 1C), the subsequently adsorbed ATPs tend to interact with the directly bound ATPs and accumulate around lysozyme in an indirect manner. We note that the accumulation of these ATPs is mainly mediated by cations (Mg²⁺ and Na⁺) in solution (Figure 2B,E). As shown in Figure 2E, divalent Mg²⁺ can simultaneously link the triphosphates of two ATPs: Mg²⁺ mainly links with β- and γ-phosphate oxygens of different ATPs to form a Mg²⁺ linker between these ATPs. The average number of Mg²⁺ linkers between the accumulated ATPs was up to 10.0. In addition, the adenine bases of adjacent ATPs can pack together via π–π stacking (Figure 2C,F), which further enhances the interaction between the accumulated ATPs. The average number of the π–π stacking interactions within the ATP cluster was 3.7 (based on the last 160 ns trajectory). Previous experimental studies also observed the self-stacking of ATPs and the formation of oligomers in solution.³⁹⁻⁴² Our results further suggest that protein can serve as a substrate to support and stabilize the complex of ATPs, i.e., ATP cluster. More interestingly, monovalent Na⁺ can also link two ATPs and form a Na⁺ linker. As indicated in previous studies, Na⁺ can simultaneously link with the electronegative groups of different molecules to form a Na⁺ linker, allowing these molecules to form a stable complex.⁴³⁻⁴⁵ Since the concentration of Na⁺ ions (150 mM, the physiological concentration) was much higher than that of Mg²⁺ ions (16.6 mM), the number of Na⁺ linkers (22.9) between the surrounding ATPs was ∼2.3 times the Mg²⁺ linkers. These cationic linkers effectively promote the interactions between ATPs, facilitating the efficient accumulation of these ATPs around protein.

As mentioned above, ATPs tend to accumulate around certain regions of proteins, e.g., the interdomain loop of lysozyme. ATPs can interact with the surface residues by forming salt bridges and hydrogen bonds. The accumulated ATPs can readily form clusters through the cationic (both Na⁺ and Mg²⁺) linkers and π–π stacking interactions. Taken together, the accumulation and clustering of ATPs are attributed to the sufficient interaction of protein with ATPs. In other words, our results suggest Mg²⁺ ions may be not indispensable for ATP binding.

To validate this hypothesis, we studied the system of ATP and lysozyme in 150 mM NaCl solution, i.e., Mg²⁺-free ATP solution. We first investigated the binding process of ATPs on lysozyme. Strikingly, ATPs still exhibit a considerable tendency to accumulate around lysozyme (Figure S12). Na⁺ ions can effectively mediate the interaction of accumulated ATPs and the formation of ATP cluster. The average number of Na⁺ linkers was up to 64.3, much more than that of the cationic linkers in the case of ATP–Mg solution (10.0 Mg²⁺ linkers and 22.9 Na⁺ linkers). On the other hand, the average number of π–π stacking interactions was 3.1 (Figure S13) and less than that in 16.6 mM ATP–Mg solution (3.7), suggesting that the strong coordination of divalent Mg²⁺ to phosphate groups promotes ATP stacking around protein. It agrees with previous experimental results that Mg²⁺ enhances the π–π stacking between ATPs.⁴² Nevertheless, both the accumulation of ATP and the cation-mediated ATP interaction around lysozyme can be realized by abundant Na⁺ ions in solution.

Effect of ATP-Cluster on Structural Fluctuation

As mentioned above, the accumulated ATPs further form clusters on the protein via cationic linkers. In the system of lysozyme and 16.6 mM ATP–Mg, accumulated ATPs are roughly organized into two ATP clusters, containing 11 (cluster-1) and 6 ATPs (cluster-2) separately. It can be seen that most of the flexible interdomain loop of lysozyme is covered with ATP clusters (red region in Figure 3A; see also Figure S8 for the other four independent trajectories). Moreover, the conformational fluctuation of the ATP-bound protein is largely suppressed. The average root-mean-square fluctuations (RMSF) of residues was only 1.00 Å (based on the last 160 ns trajectory). It was notably smaller than the case of pure water and 150 mM NaCl solution, wherein the average RMSF values of residues were 1.26 and 1.31 Å, respectively.

The structural fluctuations of ATP-susceptible and ATP-neutral regions were further analyzed separately. As mentioned above, the charged residues are enriched in the ATP-susceptible region including most of the flexible interdomain loop. The proportion of the charged residues in the ATP-susceptible region is twice as high as in the ATP-neutral region (33% vs 15%, Table S1). Because of the elevated degree of hydration of the charged residues, the disturbance of hydration water on the structure of these regions should be profound.⁴⁶⁻⁴⁸ Together with the high inherent structural fluctuation of the interdomain loop itself, the RMSF of the ATP-susceptible region (1.55 Å for pure water, 1.47 Å for 150 mM NaCl solution) was considerably higher than that of the ATP-neutral region (1.12 Å for pure water, 1.24 Å for 150 mM NaCl solution, Figure 3B) in the case of free protein. When the protein was partially covered with ATP clusters, the RMSF of the ATP-susceptible region significantly dropped to 1.01 Å—only ∼69% of that of the free protein (150 mM NaCl solution) and close to that of the ATP-neutral region (1.00 Å). In other words, the flexibility of the ATP-susceptible region is notably decreased after the covering of ATP cluster and its fluctuation amplitude is now comparable to ATP-neutral region. In order to elucidate the possible interference of Mg²⁺, 16.6 mM MgCl₂ was added to an ATP-free NaCl solution. In this solution, the RMSF of ATP-susceptible region (1.44 Å) was also considerably higher than that of ATP-bound protein (1.01 Å, Figure 3B). Moreover, the RMSF of the ATP-susceptible region in the Mg²⁺-free ATP solution was significantly decreased (Figure S12), similar to the case of ATP–Mg solution. Thus, the suppression of protein structure fluctuations can be largely attributed to the ATP cluster covering on the ATP-susceptible region, which is insensitive to the presence of Mg²⁺ ion.

Dynamical cross-correlation matrices (DCCM) analyses were performed to investigate the effect of ATP–Mg on the structural fluctuations of lysozyme. In the case of free lysozyme, the internal motion of the segment containing residues 42–81 exhibited considerable positive correlations (Figure S14A), and it largely overlaps with the interdomain region (residues 33–70). On the other hand, residues 66–74 in this segment (the protruded loop in this region) had negatively correlated motions with the other parts of this segment (Figure S15). The relative movement within the interdomain region caused the structural loosening of this segment and may result in the penetration of water molecules. Hence, the considerable structural fluctuations of the interdomain region should influence the structural stability of protein. Interestingly, such correlation largely vanishes in ATP-bound lysozyme (Figure S14B), suggesting a reduction of the local fluctuation of the interdomain region and the resulting stabilization of protein structure. The results based on DCCM analysis are in line with the discussion on RMSF that ATP–Mg can effectively suppress the structural fluctuation of the vulnerable regions (Figure 3).

The impact of ATP binding on the structural fluctuation was also studied for ubiquitin and malate dehydrogenase. As indicated above, ATP also tends to bind to the loop regions with considerable flexibility. We also observe the formation of ATP cluster mediated by cations. Moreover, the formation of ATP cluster can significantly suppress the structural fluctuations of these two proteins, especially in their respective ATP-susceptible regions (Figures S9B and S10B).

Although the interaction of ATP with protein is generally nonspecific, it has a clear binding preference to certain regions of the protein; i.e., ATP tends to bind to the regions with high flexibility and a high degree of hydration. It should be noted that these regions are usually vulnerable to perturbation, e.g., thermal fluctuation. As illustrated by previous MD studies, protein unfolding is often initiated in the regions with large structural flexibility and accompanied by the penetration of water molecules.⁴⁹⁻⁵² Thus, the ATP-susceptible region (Figure 3A and Figures S8–S10) of protein which has higher degree of hydration and larger structural fluctuation should be vulnerable to stress conditions. As suggested by our results, the stable binding of ATP and the subsequent formation of considerable ATP clusters on protein surface can significantly reduce the flexibility of these vulnerable regions, and their fluctuation amplitude then becomes comparable to the other surface regions (Figure 3A and Figures S8–S10). Consequently, the covering of ATP clusters strengthens these vulnerable regions and improves the structural stability of the overall protein.

Effect of ATP-Cluster on Thermal Stability

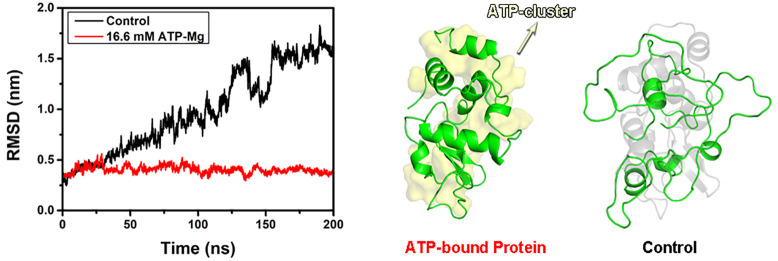
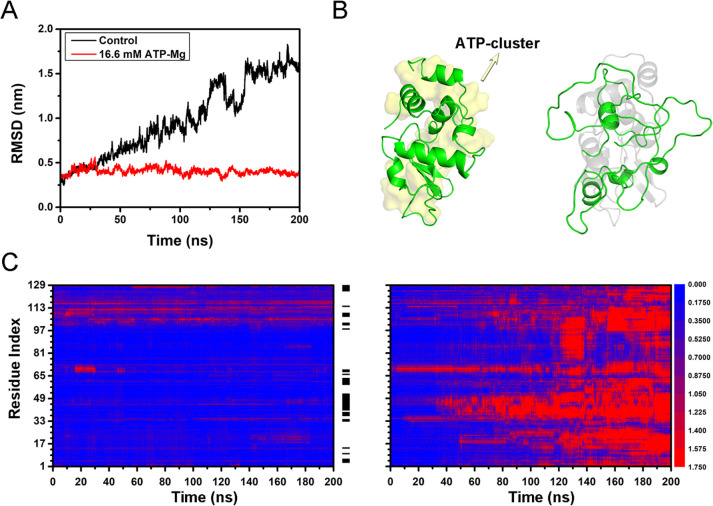
We further analyzed the effect of ATP binding on the thermal stability of protein. The RMSD of both the free lysozyme (in 150 mM NaCl) and ATP-bound lysozyme (in 16.6 mM ATP–Mg solution) at room temperature (300 K) remained below 3 Å (Figure S16), indicating the structure of the overall protein is relatively stable under room temperature. The final configuration of both the free lysozyme and ATP-bound lysozyme (300 K) was then adopted for the following simulation at high temperature (430 K). The free protein progressively unfolded at high temperature. After t = 30 ns, the RMSD continuously increased to ∼16 Å at t = 200 ns. On the other hand, the RMSD of the ATP-bound protein kept less than 5 Å (Figure 4A). The final configurations of both free protein and ATP-bound protein are shown in Figure 4B. It can be seen that the free protein almost loses its native structure (right panel), while the ATP-bound protein largely sustains its structure (left panel). In other words, the binding of ATP significantly enhances the thermal stability of protein. Similar phenomena can be found in Mg²⁺-free ATP solution, the ATP-bound lysozyme in the solution without Mg²⁺ ion exhibits similar thermal stability (Figure S17). We also studied the effects of ATP binding to the thermal stability for ubiquitin and malate dehydrogenase. In both cases, the structural stability of ATP-bound proteins at high temperature is considerably higher than their free counterparts (Figures S18 and S19). Our results suggest that the binding of ATP can effectively enhance the thermal stability of a variety of proteins and that ATP may serve as a generic stabilizer to maintain protein structure, which is consistent with previous high-throughput experiments.^5,53

Figure 4.

Structural characterization of free lysozyme and ATP-bound lysozyme at T = 430 K. (A) RMSD of free protein and ATP-bound protein with respect to the crystal structure. (B) Representative snapshot of the free protein (right panel, the native structure is shown in shaded gray) and ATP-bound protein (left panel, ATP clusters are shown in shaded yellow). (C) RMSD of residues of the free protein (right panel) and ATP-bound protein (left panel). The black stripes between two panels represent the distribution of ATP, and the color scale represents the range of RMSD.

The behaviors of ATP-bound protein and free protein were further compared in detail by calculating the RMSD evolution for each residue of lysozyme (Figure 4C). In the initial unfolding stage of free protein (right panel, t < 50 ns), the most profound structural changes took place in the finite region (residues 33–48 and 61–70, accounting for 20% of the sequence) which largely overlaps with the interdomain loop. These results are in line with the previous simulation studies on the thermal unfolding of lysozyme: the region of interdomain loop is most prone to unfold.^29,30 Besides, for the denaturation caused by other perturbations such as pH and chemical denaturants, these regions are also first to unfold.⁵⁴ It should be pointed out that even at room temperature the structure of these regions (i.e., residues 33–48 and 61–70) fluctuates considerably with the average RMSF up to 1.44 Å. Moreover, these regions have high exposure to water with SASA (18.5 nm²) accounting for 26% of the total (70.4 nm²) and a high proportion of charged residues (7 residues) accounting for 26% of the total residues (27 residues). A high degree of hydration should naturally be expected in these regions. Therefore, these highly flexible and strongly hydrated surface regions are the most vulnerable regions, which determine the thermal stability of lysozyme. As mentioned above, the extensive binding of ATP cluster (accounting for more than 40% of the surface residue, Table S1) can cover most residues in these vulnerable regions. The covering of ATP cluster significantly suppresses the local unfolding under high temperature by reducing their structural fluctuation and inhibiting the possible penetration of water molecules.

Although ATP only binds to a fraction of the protein surface, it can significantly enhance the overall thermal stability of protein. The impact of ATP binding thus shares some features with the behavior of ligand binding to stabilize protein structure,⁵⁵⁻⁵⁸ even though the binding of ATPs is generally nonspecific. This mechanism is apparently distinct from the hydrotrope action which requires formation of micellar assembly to encapsulate protein.²⁰ Moreover, the effects on the structural stability of the vulnerable region should be mainly attributed to the directly bound ATPs (∼70% of the accumulated ATPs), while the indirectly bound ATPs seems to be redundant. Thus, a lower than physiological concentration of ATPs may be sufficient to realize protein protection.

Experimental Verification

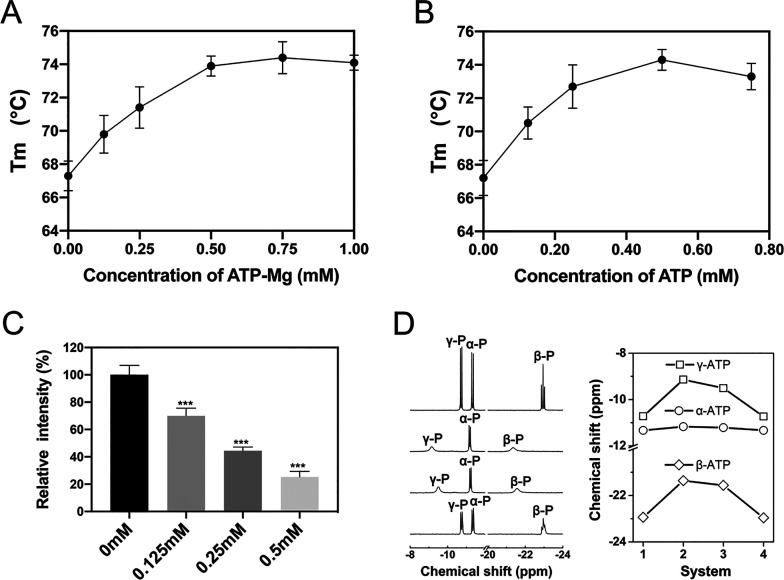
Possible impacts of ATP binding to the thermal stability of protein were further investigated by using fluorescence-based thermal shift assay (TSA) to determine the melting temperature (T_m) of a protein.⁵⁵⁻⁵⁸ With rising temperature, the degree of protein unfolding increases, and the fluorescence intensity is gradually enhanced. The T_m of protein is then acquired by fitting the inflection point of the fluorescence intensity curve.⁵⁹ The T_m values of lysozyme in both ATP–Mg solution and Mg²⁺-free ATP solution (both solutions contain 150 mM NaCl) were investigated separately (Figure S20). The average Tm of lysozyme in 0.25 mM ATP–Mg solution was 71.4 °C, which was significantly higher than that of the control system (67.3 °C, Figure 5A). With higher ATP–Mg concentration, theT_m can reach up to 74.4 °C (0.75 mM). Therefore, the addition of ATP–Mg considerably promotes the thermal stability of lysozyme. More interestingly, in Mg²⁺-free ATP solution, ATP still has a comparable effect on protein thermal stability. The average T_m rose to 72.7 °C when 0.25 mM ATP was added to the lysozyme solution. As the concentration of ATP further increased, T_m reached as high as 74.3 °C (0.5 mM, Figure 5B). In addition, circular dichroism (CD) spectroscopy was employed to assess the conformational change and the thermal denaturation of lysozyme. Similarly, the melting temperature increases as the ATP–Mg concentration escalates (Figure S21).

Figure 5.

Thermal shift assay, ANS fluorescence, and NMR spectroscopy of lysozyme. (A) Relationship of the melting temperature with ATP–Mg concentration. (B) Relationship of the melting temperature with ATP concentration in Mg²⁺-free ATP solution. (C) Summarized ANS fluorescence intensity for lysozyme in Mg²⁺-free ATP solution. (D) Liquid-state ³¹P NMR spectrum of ATP for four systems (left panel, from top to bottom), i.e., ATP without Mg²⁺ ions and lysozyme (system-1), ATP–Mg without lysozyme (system-2), ATP–Mg and lysozyme (system-3), ATP and lysozyme in the absence of Mg²⁺ ions (system-4). The chemical shifts of α-P, β-P, and γ-P of ATP (right panel).

We also investigated the impact of ATP on the thermal stability of malate dehydrogenase. The average Tm of malate dehydrogenase considerably increased from 48.2 °C (control system) to 54.9 °C after the addition of ATP (16 mM ATP–Mg, Figure S22). It is worth mentioning that recent studies have shown that the working temperature of mitochondria is several degrees higher than ambient temperature.¹³⁻¹⁶ As an ATP producing organelle, high ATP concentration of mitochondria should be essential for proteins like malate dehydrogenase to persist in its high temperature environment and maintain their structural and functional integrity, e.g., regulating the citric acid cycle. The TSA results of both lysozyme and malate dehydrogenase illustrate that the addition of ATP (even without the accompanying of Mg²⁺) can effectively stabilize proteins, which agrees with our simulation results that ATP can suppress the thermal unfolding of both proteins.

The ANS-binding experiments were performed to verify the covering of ATP cluster on lysozyme surface. The intensity of ANS fluorescence in 0.25 mM ATP–Mg solution was only half of the intensity for control system (Figure S23). These results suggest ATP can directly bind to protein and suppress ANS binding. Similar phenomena can be found for lysozyme in Mg²⁺-free ATP solution, the intensity of ANS fluorescence in this solution was also much weaker than the control system (Figure 5C). The decrease in ANS fluorescence intensity indicates that ATP can effectively bind to protein, consistent with our simulation results.

To fully characterize the interaction of ATPs with protein, ³¹P NMR experiments were conducted to investigate the spatial proximity of ATP’s triphosphate to protein. We first studied the ³¹P NMR spectrum of ATP in a buffer solution without Mg²⁺ ions (8 mM ATP and ∼150 mM NaCl, system-1). The resonance peaks of ATP’s triphosphate are well resolved, and the chemical shift signals at −11.3, −22.9, and −10.7 ppm can be assigned to α-P, β-P, and γ-P, respectively (Figure 5D). When divalent Mg²⁺ ions (8 mM MgCl₂) were further added to the buffer solution (system-2), Mg²⁺ effectively coordinated to the triphosphate of ATPs and formed stable ATP–Mg complex. The resonances of triphosphate thus suffered significant shifts relative to system-1: the peaks of β-P and γ-P shifted downfield to −21.4 and −9.1 ppm, which should be attributed to the strong deshielding effect of divalent Mg²⁺. This result shows that Mg²⁺ ions are tightly bound to ATPs, which is in line with previous NMR studies.^33,34 The changes in chemical shifts of β-P and γ-P further indicate that Mg²⁺ ions are mainly coordinated with β- and γ-phosphate groups, which is also consistent with our simulation results (Figure S1).

More interestingly, after addition of lysozyme (1 mM) to the ATP–Mg solution (system-3), the peaks of the β-P and γ-P of ATP shifted upfield to −21.6 and −9.5 ppm. This indicates that the protein weakens the coordination interaction between Mg²⁺ and ATP, resulting in the loss of the deshielding effect. The phenomena of the weakened coordination interaction between Mg²⁺ and ATP upon their binding to the protein are also captured by our simulation. When ATPs accumulate around protein, the protein can serve as a substrate to foster the formation of ATP cluster. Within ATP cluster, Mg²⁺ links the phosphate groups of two ATPs wherein the interaction between Mg²⁺ and each ATP becomes weaker. For example, the average interaction energy of Mg²⁺ with ATP in solution is ∼−1267 kJ/mol. On the other hand, the average interaction energy of Mg²⁺ with bound ATP on lysozyme (mostly in the form of ATP cluster) decreases to ∼−788 kJ/mol. For Mg²⁺-free ATP solution (ATP and lysozyme in 150 mM NaCl solution, system-4), it can be seen that the peaks of the β-P and γ-P of ATP notably shifted upfield. In other words, the deshielding effect of monovalent Na⁺ on ATP’s phosphate group is remarkably weaker than that of divalent Mg²⁺, in agreement with previous NMR studies.^60,61 This also agrees with our simulation results: the average interaction energy of Na⁺ with ATP is only ∼−327 kJ/mol (in solution) and ∼−262 kJ/mol (ATP cluster on lysozyme). In short, adding lysozyme induces the Mg²⁺ mediated clustering of bound ATPs, which in return makes the interaction of Mg²⁺ with bound ATP weaker than that with solution ATP. Meanwhile, Na⁺ ions with considerably higher concentration can also mediate the binding and clustering of ATP despite their weaker interaction with ATP.

Conclusions

In this work, the ATP binding and its impact on protein thermal stability were studied in three proteins—lysozyme, ubiquitin, and malate dehydrogenase. We find ATPs can extensively bind to the surface of these proteins (e.g., ∼40% of surface residues of lysozyme) and that the regions with high flexibility and high proportion of charged residues are favorable for ATP binding. Thus, the extensive ATP binding can cover most flexible regions vulnerable to thermal perturbation. It should be noted that both Mg²⁺ and abundant Na⁺ mediate the interaction between the bound ATPs and facilitate the formation of ATP cluster on protein surface. ATP cluster considerably reduces the fluctuations of these vulnerable regions to a level comparable to the rest of the surface region. Therefore, the nonspecific binding of ATP can effectively prevent the structural loosening of these vulnerable regions caused by high temperature and the following intrusion of water molecules, thereby improving the overall thermal stability of the protein.

Our results show that ATP improves protein thermal stability by forming ATP cluster and covering a fraction of the protein surface, especially the vulnerable regions. This stabilizing mechanism is not only different from the ligand-induced protein stabilization effect but also apparently distinct from the hydrotrope action on proteins and other biomacromolecules which involves formation of micellar assembly to encapsulate the biomacromolecule. It is interesting to note that a mechanism of the classical hydrotrope on small molecule solute was proposed as the aggregation of hydrotropes around the small molecule solute and the formation of a complex with the molecule.⁶² Our finding about the mechanism of ATP to improve protein stability by forming aggregates on part of the protein surface thus shares some characteristics with the classical hydrotrope to solubilize small molecule even though the minimum effective concentration of ATP is lower than ∼2 order of magnitude. This is also the reason why ATP can efficiently stabilize proteins at a significantly lower minimum effective concentration. More interestingly, both the binding of ATP cluster and its stabilizing effect can be realized by abundant Na⁺ even without the presence of Mg²⁺. The binding of ATP to protein is verified by ANS fluorescence and NMR spectroscopy, and the considerable promotion of protein thermal stability is validated by TSA and CD experiments. We argue that the mechanism proposed here may be applied to a wide spectrum of proteins characterized by the loops enriched with charged residues that may interact with ATPs in a similar manner. This impact of ATP may be relevant to the structural stability of protein in the intracellular environment. For example, the stabilizing effect of ATP should be related to the pervasive regulation of thermal stability and activity of protein during the cell cycle. This effect may also be linked to the stability of proteins in mitochondria (the main site of ATP synthesis) where the temperature is considerably higher. Taken together, our findings provide insights into the role of ATP in biological systems from the perspective of protein stability. For protein in some extreme conditions, e.g., industrial enzyme, the stabilizing effect of ATP may also be exploited to improve the performance of such protein. Moreover, the unique behaviors of ATP binding and its role in suppressing structural fluctuation of protein should further affect the interprotein interaction and the relevant biological process. Therefore, our results can shed new light on the design of molecules to modulate protein behavior like liquid–liquid phase separation, without involving in energy transfer.

Methods

Computational Details

The initial structures for proteins of lysozyme, ubiquitin and malate dehydrogenase were obtained from the protein data bank, with PDB IDs 1IEE, 1UBQ, and 4MDH, respectively. ATP consists of an adenine base, a ribose sugar, and a triphosphate. As indicated by previous work, ATP tends to coordinate with intracellular Mg²⁺ ion and form a stable ATP–Mg complex.³²⁻³⁴ We performed a 100 ns simulation of 20 ATP–Mg in 150 mM NaCl solution. In most of the trajectory, ATP–Mg complexes adopted the coordination mode that Mg²⁺ simultaneously binds to two phosphates (i.e., β-P and γ-P) of the same ATP (Figure S1), in agreement with previous simulation results.⁶³⁻⁶⁶ Such a conformation was then adopted for the following simulations.

Each protein was initially placed in a cubic box; the box side length was chosen according to the protein size, namely 10.0, 12.6, and 14.4 nm for ubiquitin, lysozyme, and malate dehydrogenase, respectively. ATP–Mg complexes were placed at least 9 Å from the protein. The number of ATP–Mg complexes corresponded to the concentration of 16.6 mM (10, 20, and 30 for ubiquitin, lysozyme, and malate dehydrogenase, respectively). Each box was then solvated with TIP3P water molecules.⁶⁷ Requisite numbers of sodium and chloride ions were then added to the system to neutralize the system and mimic physiological conditions (150 mM NaCl). The solvated systems were then subjected to 10000 steps of energy minimization. For lysozyme, five independent simulations were performed to investigate the interaction of ATP–Mg with protein, and ATP–Mg can accumulate and cluster around the protein in all the trajectories. In addition, the interaction between ATP and lysozyme in the absence of Mg²⁺ was also investigated by constructing the Mg²⁺-free ATP solution, i.e., ATP and lysozyme in 150 mM NaCl solution. ATP can also accumulate and cluster around lysozyme in this system. For each of ubiquitin and malate dehydrogenase, three independent simulations were performed separately, and ATP–Mg can also accumulate and cluster around the protein in all the trajectories. The final configurations of ATP-bound proteins in above-mentioned systems (300 K) were adopted for the following simulation to study the thermal stability of ATP-bound protein at high temperature (430, 450, and 490 K for lysozyme, malate dehydrogenase, and ubiquitin respectively), where each system was gradually heated from 300 K to the setting temperature in 100 ns before the constant temperature production run. The structure and thermal stability of free protein at high temperature was also investigated for comparison. The details of all these simulated systems were summarized in Table S4.

All MD simulations were performed in the NPT ensemble at 1 atm. The pressures of the system were maintained using Parrinello–Rahman barostat,⁶⁸ and the temperatures were maintained by velocity-rescaled Berendsen thermostat.⁶⁹ The CHARMM36 force field was adopted to describe the interactions of the proteins and ATP,⁷⁰ and the parameters developed by Allnér et al. were employed for Mg²⁺ ion.⁷¹ The periodic boundary conditions were applied in all directions.⁷² The particle-mesh Ewald (PME) method was employed to compute the long-range electrostatic interactions,⁷³ whereas a typical 12 Å cutoff distance was used for short-range electrostatic interactions and van der Waals interactions. The LINCS algorithm was used to constrain the bond vibrations involving hydrogen atoms,⁷⁴ and a time step of 2 fs was adopted. All simulations were carried out using the GROMACS 2018 package,⁷⁵ and snapshots were rendered using PyMol molecular graphics system⁷⁶ and visual molecular dynamics (VMD) program.⁷⁷

Experimental Details

All materials and reagents were purchased from Sigma-Aldrich and used without further purification. For the nuclear magnetic resonance (NMR) spectroscopy, the protein and ATP samples were prepared in Dulbecco’s phosphate buffered saline buffer (DPBS, pH = 7.5), and D₂O was added in the H₂O/D₂O ratio of 8:2. The ³¹P NMR measurements were performed with a Bruker 600 M NMR spectrometer at 25 °C, using a cryoprobe. The ³¹P NMR spectra were recorded with a spectral band of 96153 Hz, 65536 data points, and 2 s relaxation delay.

Fluorescence-based TSA was performed using differential scanning fluorimetry following a previously described method.⁷⁸ Unless otherwise specified, 150 mM NaCl was added to all protein solutions to simulate the physiological environment and ensure comparable ionic strength. The protein sample (1 mg/mL, i.e., 0.069 mM for lysozyme or 0.013 mM for malate dehydrogenase) was mixed with ATP and incubated in the assay vessels (20 min, 25 °C) with 5 μL (25×) SYPRO Orange (Sigma S5692) added as a fluorescent indicator. The temperature was increased from 25 to 95 °C at an incremental rate of 0.3 °C every 5 s. The change of fluorescence intensity during temperature ramping can reflect the process of protein denaturation, which was monitored by a Rotor-Gene quantitative real-time PCR (Q-RT-PCR) machine (QIAGEN). All samples were excited at 470 nm, and the emission at 555 nm is recorded for analysis.

ANS (8-anilinonaphthalene-1-sulfonic acid) fluorescence spectra were measured by a Hitachi F-4600 spectrofluorometer using a 10 mm path-length cuvette. After lysozyme was incubated with ATP, ANS probes were added to the solution. The resulting solution (1 mg/mL lysozyme, 1 mM ANS) was further incubated for 20 min. The ANS fluorescence was excited at 380 nm, and the emission spectra were collected from 400 to 600 nm.

The circular dichroism (CD) spectra were measured using a Chirascan V100 spectropolarimeter (Applied Photophysics Ltd., UK) with the parameters previously described.^79,80 Lysozyme samples (0.2 mg/mL) were incubated with ATP at room temperature for 20 min before the CD measurement. The temperature was gradually increased from 42 to 90 °C, and the ellipticities at 222 nm were measured to monitor the structural changes of protein.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.1c00316.

• Details of simulated systems; coordination state of ATP–Mg; schematic representation of the interdomain loop; binding and accumulation of ATPs around lysozyme, ubiquitin, and malate dehydrogenase and their impacts on protein stability; experimental characterizations of protein stability (including TSA, CD spectra, ANS fluorescence) (Tables S1–S4 and Figures S1–S23) (PDF)

Author Contributions

^# X.O., Y.L., and J.X. contributed equally. J.L. designed the study. X.O. and Y.L. performed molecular dynamics (MD) simulations and analysis. Y.L. and X.O. collected and analyzed the NMR spectra. X.C. and J.X. performed the thermal shift assay (TSA), ANS fluorescence spectroscopy, and circular dichroism (CD) spectroscopy and related data analysis. All authors discussed the results and contributed to the writing of the manuscript.

The authors declare no competing financial interest.