Cation- and pH-Dependent Hydrogen Evolution and Oxidation Reaction Kinetics

Abstract

The production of molecular hydrogen by catalyzing water splitting is central to achieving the decarbonization of sustainable fuels and chemical transformations. In this work, a series of structure-making/breaking cations in the electrolyte were investigated as spectator cations in hydrogen evolution and oxidation reactions (HER/HOR) in the pH range of 1 to 14, whose kinetics was found to be altered by up to 2 orders of magnitude by these cations. The exchange current density of HER/HOR was shown to increase with greater structure-making tendency of cations in the order of Cs⁺ < Rb⁺ < K⁺ < Na⁺ < Li⁺, which was accompanied by decreasing reorganization energy from the Marcus–Hush–Chidsey formalism and increasing reaction entropy. Invoking the Born model of reorganization energy and reaction entropy, the static dielectric constant of the electrolyte at the electrified interface was found to be significantly lower than that of bulk, decreasing with the structure-making tendency of cations at the negatively charged Pt surface. The physical origin of cation-dependent HER/HOR kinetics can be rationalized by an increase in concentration of cations on the negatively charged Pt surface, altering the interfacial water structure and the H-bonding network, which is supported by classical molecular dynamics simulation and surface-enhanced infrared absorption spectroscopy. This work highlights immense opportunities to control the reaction rates by tuning interfacial structures of cation and solvents.

Introduction

Catalyzing water splitting, specifically water reduction to produce molecular hydrogen, is central to achieving high efficiency of chemical transformations for carbon-free or carbon-neutral energy carriers. Significant efforts have been focused on design principles or activity descriptors of catalysts by tuning the covalent adsorbate–surface interaction using surface electronic structure features,^1,2 which have greatly aided mechanistic understanding of the reactions and discovery of new catalysts with enhanced activity.^1,3 For example, tuning the d-band center relative to the Fermi level^4,5 of metals can control the binding energy of surface adsorbates such as adsorbed hydrogen (H_ad) or hydroxyl (OH_ad) and consequently dictate the catalytic activity of reactions such as the hydrogen oxidation/evolution reaction (HER/HOR).⁶⁻¹⁰ Recently, there are many examples of catalysts that show cation-dependent¹¹ and pH-dependent^9,12 catalytic activity, which can result from noncovalent interactions associated with water molecules, spectator ions, surface adsorbates, and electrified interfaces.¹³ For example, the exchange current density of HER/HOR normalized to the electrochemical surface area (ECSA) on platinum group metals in acid^14,15 is about 2 orders of magnitude higher than that in base,¹⁶ where the activity decreases linearly with increasing pH.^8,9 Moreover, the catalytic activity of HOR, oxygen reduction reaction (ORR), and methanol oxidation on platinum measured at 0.9 V versus the reversible hydrogen electrode (RHE) is cation-dependent, increasing with spectator cations in the order of Li⁺ < Na⁺ < K⁺ < Cs⁺.¹¹ Furthermore, spectator cations have been shown to alter the selectivity of aqueous CO₂ reduction¹⁷ on Cu from H₂ for Li⁺ to C₂H₄, C₂H₅OH with Cs⁺;¹⁷ and CO reduction toward C₂H₄ relative to CH₄ from Li⁺, Na⁺, and K⁺ to Rb⁺ and Cs⁺.¹⁸ All of these observations point to the possibility that the chemical physics of electrolytes offers promising opportunities to significantly change catalytic activity and selectivity by tuning noncovalent interactions and solvation environments at the electrified interface. However, the physical origin about how cation and pH modify the solvation environment at the electrified interface is not fully understood. Below, we focus on the state-of-the-art understanding for cation-dependent and pH-dependent HER/HOR kinetics.

Unfortunately, the physical origin of cation- and pH-dependent HER/HOR kinetics is still under debate. Generally speaking, HER/HOR kinetics (2H⁺ + 2e^– ↔ H₂ in acid and 2H₂O + 2e^– ↔ H₂ + 2OH^– in base) involve dissociative adsorption/desorption of H₂ without electron transfer (Tafel step, 2H_ad ↔ H₂ + 2*)^9,15,19 or with simultaneous electron transfer (Heyrovsky step, H_ad + H⁺ + e^– ↔ H₂ + * in acid and H_ad + H₂O + e^– ↔ H₂ + OH^– + * in base)^9,15,19 and the formation/oxidation of adsorbed hydrogen (Volmer step, H₃O⁺ + e^– + * ↔ H_ad + H₂O in acid and H₂O + e^– + * ↔ H_ad + OH^– in base),^15,19 whereby the asterisk represents an adsorption site on Pt. The Volmer step has been proposed as the rate-determining step (RDS) for HER/HOR kinetics on polycrystalline Pt surfaces based on some previous work by Gasteiger et al.,^15,19 Tang et al.,²⁰ Liu et al.,²¹ and Koper et al.¹⁰ On the other hand, other studies such as Chan et al.²² have shown that the activation energy of the Heyrovsky reaction was higher than that of the Volmer reaction on Pt(111) via density functional theory calculation, indicating that the Heyrovsky step is the RDS in HER. Thus, we are not able to exclude the possibility of the Heyrovsky step being the RDS.

There have been two schools of thought to explain the electrolyte-dependent activity for HER/HOR.^23,24 First, the binding energy of surface absorbates^8,9 has been reported to govern the kinetics of HER/HOR, which can be cation-^11,25,26 and pH-dependent.^8,9 For example, hydrogen binding energy (HBE)^8,9 on precious metals (e.g., Pt, Ir, Pd, and Rh) has been estimated from hydrogen underpotential deposition regions of cyclic voltammograms (CVs), which is shown to increase linearly with increasing pH over a broad pH range (0–13) and is correlated with decreasing HER/HOR kinetics. Later, Zheng et al.²⁷ suggested to consider the disruption of water structure inevitably occurred during the Volmer step and thus proposed the concept of apparent HBE, HBE_app = HBE+ ΔG_IW⁰, where HBE is determined from the H adsorption/desorption peak in the CV and ΔG_IW represents the Gibbs free energy change of the interfacial water during HER/HOR. Recent studies^20,28 have questioned the extraction of HBE from peak shifts in the hydrogen underpotential deposition regions using CV measurements and thus raised questions regarding the applicability of the first school of thought. For example, cation-dependent peak shifts associated with hydrogen underpotential deposition on Pt(110) in base have been attributed to slow kinetics of H_ad adsorption but not changes in the HBE.²⁰ In addition to H_ad, OH_ad is reported recently to be coadsorbed with alkali cations on stepped Pt surfaces in the conventional hydrogen underpotential deposition region (0–0.4 V_RHE),²⁸ where the adsorption energy of OH_ad is shown to increase in the order of Li⁺ > Na⁺ > K⁺ > Cs⁺.¹¹ The coadsorption of H_ad and OH_ad in a low potential region (0–0.4 V_RHE) implies that the peak shifts from hydrogen underpotential deposition regions^8,14 might not be appropriate to extract the binding energy of H_ad as the observed peak shifts can arise from coadsorption and interactions of alkali cations and OH_ad on the step sites of Pt(553) instead of pH-dependent HBE.²⁸ The second school of thought has attributed such pH-dependent kinetics to pH-dependent reorganization energy of interfacial water molecules on Pt(111),¹² where faster kinetics in acid are associated with higher entropy with less ordered structure in acid as a result of lower potential of zero charge (PZC) and lower reorganization energy for interfacial water than those in base. This argument is in agreement with recent computational findings on pH-dependent proton transfer barriers for HER/HOR kinetics,²⁹ where greater pH is correlated with larger entropic barrier of proton transfer across the outer Helmholtz layer and thus lowered HER/HOR kinetics. Further support to the role of solvation environment on the reaction kinetics comes from our recent work,³⁰ which shows that the kinetics of aqueous outer-sphere electron transfer [Fe(CN)₆]^3–/[Fe(CN)₆]^4– reaction can be increased by 2 orders of magnitude by tuning noncovalent interactions associated with alkali cations in the electrolyte. Such cation-dependent kinetics have been attributed to cation-dependent coordination environments of the redox species at the electrified interface, whereby cations of lower charge density such as Cs⁺ (compared to Li⁺) in the redox solvation shell are associated with lower effective static dielectric constant at the interface, smaller reorganization energy, and greater kinetics. Therefore, it is of great interest to examine cation- and pH-dependent HER/HOR kinetics using the Marcus–Hush–Chidsey (MHC) framework and surface-enhanced infrared absorption spectroscopy (SEIRAS), from which new insights into the role of noncovalent interactions and/or interfacial solvation environments on the HER/HOR kinetics can be obtained.

In this study, we employed a series of structure-making/breaking cations in aqueous electrolytes of pH 1 to 14 to perturb the interfacial structure at polycrystalline Pt and investigate the kinetics of HER/HOR. Classical molecular dynamics (MD) simulation showed that structure-making cations (e.g., Li⁺ and Na⁺) retained their solvation shell at the electrified interface, while structure-breaking cations (e.g., Rb⁺ and Cs⁺) exhibited a tendency to partially desolvate and segregate to the surface, where such a cation-dependent interfacial structure was more significant at pH 13 than at pH 1 due to higher negative surface charge at pH 13 as a result of higher PZC (1.1 V_RHE for the Pt(111) surface) at pH 13 than that at pH 1 (0.3 V_RHE for the Pt(111) surface).³¹ The exchange current density of HER/HOR increased by up to 2 orders of magnitude with greater structure-making tendency in the order of Cs⁺ < Rb⁺ < K⁺ < Na⁺ < Li⁺, which was accompanied by decreasing reorganization energy extracted from MHC analysis. Such cation-dependent exchange current density and reorganization energy trends became more pronounced with increasing pH. We propose that partial desolvation and concentration of cations with increasing structure-breaking tendency (such as Cs⁺) at the electrified interface results in higher static dielectric constants at the interface, greater reorganization energy and higher entropic barrier associated with the formation of H_ad from H₂O, and reduced HER/HOR kinetics. Such molecular-level understanding sheds new insights on electrolyte engineering as an alternative pathway to control electrochemical reaction kinetics.

Methods

Classical Molecular Dynamics Simulations

To isolate the effect of pH on the cation–electrode binding affinity, we set up a series of simulations of an aqueous electrolyte solution of Cl^– and alkali ions (Li⁺, Na⁺, K⁺, Rb⁺, Cs⁺) confined between platinum electrodes at constant potential of −0.3 V and at −1.1 V relative to PZC for the Pt(111) surface, corresponding to 0 V_RHE at pH 1 and pH 13, respectively. As we study the negative charged Pt(111) surface, cations were expected to interact with the surface by Coulombic interaction. Due to limited validation of the force field parameters of ClO₄^– and OH^– anions, Cl^– anions were considered to replace ClO₄^– for simulating acidic solutions and OH^– for simulating alkaline solutions. All of the simulations were performed in LAMMPS. A simulation box with dimensions of 30.43 × 28.75 × 89.23 Å was periodically replicated in x,y-directions, while a fixed boundary condition was employed for the z-direction containing the platinum electrode. The simulation box contained 792 Pt atoms, 2293 water molecules, and 42 alkali ions with an equal amount of Cl^– anion as their counterions, approximately corresponding to a 1 M concentration of cations. Due to the lack of appropriate force field parameter to describe proton and hydroxyl in the literature, Cl^– ions were used as counterions to balance the charge of alkali metal cations for both pH 1 and pH 13. The long-range electrostatic interactions³² were calculated using a particle-mesh Ewald algorithm with a real-space cutoff value of 9 Å. An NVT ensemble with a Langevin thermostat was employed to keep the system at 300 K. A Langevin thermostat was used here as we were only concerned with the static properties of the system at equilibrium. Furthermore, the Shake algorithm³³ was used to constrain the bonds and angles of SPC/E water. The system was equilibrated for 0.1 ns before performing the final production runs of 1 ns with a time step of 2 fs using the SPC/E force field for water. Lennard-Jones (LJ) parameters were used along with the scaled ionic charge model for alkali ions in order to account for electronic polarization effects in a classical nonpolarizable force field. Lorentz–Berthelot mixing rules were employed to derive the mixed LJ parameters. The Pt(111) electrode atoms were modeled using the LJ force field from ref (34). The charges on each platinum atom were calculated at each time step to satisfy the imposed voltage across the cell (either 0.3 or 1.1 V) by the constant potential fix in LAMMPS developed by Wang et al.³⁵ All of the parameters used are summarized in Table S1. Note that our MD simulation system did not include the presence of H_ad on the Pt surface at 0 V_RHE. As a result, the simulations are of limited quantitative value. However, we assume that qualitative trends that emerge when changing cation identity are physically meaningful. While our simulations did not include the potential difference in the relative surface hydrophobicity, or the associated changes in the double layer water structure, the free energy differences in the cation desolvation responsible for the cation-dependent trends in interfacial structure were expected to be similar for both hydrophilic (without H_ad) and hydrophobic (with H_ad) surfaces as a cation-dependent interfacial water structure on a hydrophobic surface (CO-covered Pt) has also been reported previously.³⁶ While the exact interfacial water structure in our MD simulation might be different from the realistic condition, our MD simulation results via the simplified model are supported by our reorganization energy, reaction entropy, and in situ SEIRAS experiments. Further study by considering H_ad on the Pt surface in MD simulations is needed to provide more quantitative information.

Electrochemical Measurements and Electrolyte Preparation

A Biologic SP-300 potentiostat and a three-electrode electrochemical system³⁷ were employed for all electrochemical measurements. A Pt rotating disk electrode (RDE) (Pine Instrument) was used as the working electrode. Potentials were recorded versus a mercury sulfate (Hg/HgSO₄) reference electrode in acidic and buffer solutions and to a mercury oxide (Hg/HgO) reference electrode in alkaline electrolytes. All potentials were converted to the RHE scale. The effects of pH and cations on H/OH adsorption/desorption and the kinetics of HER/HOR were examined by CV measurements at a scan rate of 50 mV s^–1 in Ar-saturated electrolytes and 10 mV s^–1 in H₂-saturated solutions at 293 K. The normalized current density was obtained using the geometric surface area of RDE (0.196 cm²), and the reported potentials were iR corrected. For temperature-dependent measurements, the cell temperature was controlled by a thermal bath circulator (Thermo Neslab RTE 7) and increased from 293 to 323 K in increments of 10 K. Buffer solutions and acidic and alkaline electrolytes were prepared from deionized water (Millipore, > 18.2 MΩ.cm). For cation-dependent measurements, 0.1 M perchlorate salt of Li⁺, Na⁺, or 0.08 M perchlorate salt of K⁺, Cs⁺ or 0.05 M perchlorate salt of Rb⁺ were added to electrolyte at pH 1 and pH 2 prepared by diluting HClO₄ (Sigma-Aldrich 70 wt %). Alkaline electrolytes at pH 12–14 were prepared with aqueous solutions of 0.01–1 M lithium hydroxide (Sigma-Aldrich 99.9%), sodium hydroxide (Sigma-Aldrich 99.9%), potassium hydroxide (Sigma-Aldrich 99.95%), rubidium hydroxide (Sigma-Aldrich 99.95%), and cesium hydroxide (Sigma-Aldrich 99.95%). The purity of cesium hydroxide was further analyzed by inductively coupled plasma (Table S2). Buffer solutions were prepared by adding different amounts (e.g., 1 and 2 mL) of 4 M hydroxide of Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺ into 50 mL of 0.2 M solution of phosphoric acid (Sigma-Aldrich 80 wt %), citric acid (Sigma-Aldrich 99.9%), acetic acid (Sigma-Aldrich 99.9%), bicarbonate (Sigma-Aldrich 99.9%), and carbonate (Sigma-Aldrich 99.9%).

For the extraction of kinetic current density, we measured HER/HOR polarization curves with Pt RDE at rotation speeds from 400 to 2500 rpm, as shown in Figure S1a–c. Kinetic current density could be estimated from rotation speed dependent HOR polarization curves using the Koutechy–Levich equation.³⁸ (Further details can be found in Supporting Information and in our previous work.³⁰)

To extract kinetic parameters, including the exchange current density and reorganization energy, from kinetic current density, the Butler–Volmer equation and MHC formalism^39,40 were employed. The MHC formalism, widely employed to accurately predict activity trends of numerous Faradaic reaction kinetics, including inner-sphere and outer-sphere reactions, for example, PCET reactions (HER/HOR on nickel-based molecular electrocatalyst⁴³ and the reduction of water–superoxide ion complex on a glassy carbon electrode⁴⁴), interfacial ET on the metal surfaces,³⁰ lithium electrodeposition/stripping,⁴⁵ and lithium-ion intercalation at solid–solid interfaces,^40,46 considers the reactant–solvent interactions but not the reactant–electrode interactions (Appendix S1), which can be used to describe the HER/HOR kinetics on Pt as the hydration energy of the proton (−11.5 eV)⁴⁷ is 2 orders of magnitude larger than that with HBE on Pt (−0.1 eV).⁴⁸ This hypothesis is supported by the fact that the values of exchange current density extracted by MHC formalism (Figure S2a,c) are comparable to those extracted via the Butler–Volmer equation (Figure S2b,c). Further support comes from the fact that the value of the reorganization energy of the Volmer reaction on a metal surface has been reported to be ∼0.4 eV,⁴⁹ which is comparable to the cation-dependent reorganization energy found in this work, 0.6–1.2 eV. Therefore, based on our understanding from the literature^44,50−52 and the consistency between our results and previous work,^8,49 we propose that the kinetics of HER/HOR on Pt RDE can be described by the MHC formalism. (More details can be found in Supporting Information and in our previous work.³⁰)

In Situ Surface-Enhanced Infrared Absorption Spectroscopy

A hemispherical Si prism (radius 22 mm, Pier Optics) deposited with Pt was mounted in a spectro-electrochemical three-electrode cell. The reference electrode used was a mercury oxide electrode, and a platinum wire was used as the counter electrode. A Fourier transform infrared (FTIR) Vertex 70 (Bruker) spectrometer equipped with an MCT detector was used to record SEIRAS spectra. Additional experimental details for the in situ SEIRAS measurements can be found elsewhere.^54,55 For in situ SEIRAS measurements during HER/HOR in electrolyte at pH 13, electrolytes consisting of 0.1 M hydroxide of Li⁺, K⁺, and Cs⁺ were saturated with H₂ by purging H₂ gas. Before in situ SEIRAS measurements, the prism surface was cleaned by cycling the potential between 0.05 and 1.1 V_RHE. SEIRAS spectra were collected at a potential from 1.1 to −0.3 V_RHE at room temperature. The reference spectrum I₀ was measured at 1.1 V_RHE. All spectra are shown in absorbance units defined as log(I₀/I), where I₀ and I represent the spectra at the reference and sample potentials, respectively. We note that the same Pt surface was used for measurements in 0.1 M LiOH, KOH, and CsOH to ensure a similar surface enhancement effect.

Results and Discussion

pH-Dependent and Cation-Dependent Solvation Environments at the Electrified Interface from MD

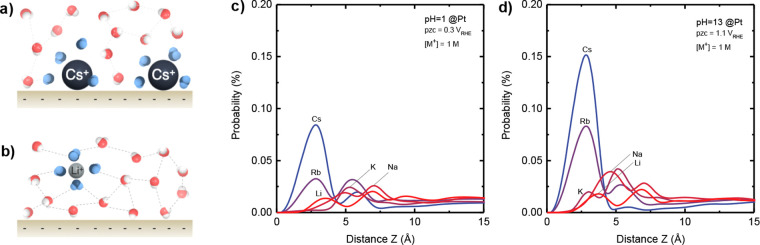
Our MD simulation results show that the solvation environment of redox anions and cations at the electrified interface induced by noncovalent interactions is cation dependent. With larger cations (e.g., Cs⁺), there are fewer surface water molecules (having been replaced by cations), as illustrated in Figure 1a, whereby with smaller cations (e.g., Li⁺), the surface layer is primarily water molecules, as illustrated in Figure 1b. The z-axial probability distribution functions (ZDF) for surface cations from classical MD simulations for pH 1 (Figure 1c) and pH 13 (Figure 1d) revealed increasing peak intensity in the order of Li⁺ < Na⁺ < K⁺ < Rb⁺ < Cs⁺, corresponding to more structure-breaking cations (Cs⁺) in the vicinity of the electrified interface than structure-making cations (Li⁺). In addition, the peak center for larger cations such as Cs⁺ and Rb⁺ was found to be 2.8 Å compared to ∼4 Å for that of smaller cations such as Li⁺ and Na⁺, indicating that Rb⁺ and Cs⁺ are partially desolvated at the electrified interface, whereas Li⁺ and Na⁺ (assembled >3 Å from the surface) retain their solvation shell at the electrified interface. This difference can be attributed to stronger Coulombic interactions with the negatively charged surface with larger cations (e.g., Cs⁺) having less tightly bound water in the solvation shell^36,56 (Figure 1a) than those of smaller cations (e.g., Li⁺) with tightly bound hydration shells (Figure 1b). Moreover, Pt(111) exhibits higher PZC (∼1.1 V_RHE at pH 13)^31,57 in base than in acid (∼0.3 V_RHE at pH 1);^31,57 consequently, the electrified interface could electrostatically attract more cations to its surface in base than in acid. In addition, the findings are in agreement with our previous observations that cations only exerted short-range effects on the water structure in their solvation shells and could not affect the hydrogen-bonding network in the bulk solution of 0.6 M chloride with Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺,³⁰ unlike those reported for superconcentrated electrolytes such as 21 M LiTFSI water-in-salt electrolyte.⁵⁸ Further support comes from surface X-ray scattering results on the Pt(111) surface in the presence of Ba²⁺ ions, which show that, relative to the Pt(111) surface, Ba²⁺ is found to be located at a distance larger than its ionic radii but smaller than the corresponding hydrated radii, suggesting that Ba²⁺ is partially dehydrated and immobilized at the interfaces by noncovalent interaction between Ba⁺ and OH_ad.⁵⁹ In the next section, we discuss the HER/HOR kinetics measured near equilibrium (0 V_RHE), where the surface is dominant by H_ad with OH_ad coverage⁶⁰ significantly lower than that in the OH adsorption region related previously to cation-dependent HOR kinetics.¹¹ We further correlate HER/HOR kinetics with interfacial solvation environment changes induced by cations in the electrolyte.

Figure 1.

Tuning the outer Helmholtz layer (OHL) structure at the electrode/electrolyte interface by spectator ions contained in the electrolyte. Schematic illustration showing the interactions among interfacial water molecules, cation, and the interface where (a) water molecules are removed from the interface by larger cations (Cs⁺) due to strong ion-surface interaction and (b) stable interfacial water layer in the presence of smaller cations (Li⁺). Strongly H-bonded (ice-like) and asymmetric H-bonded (solvating ion) water molecules are represented in red and blue, respectively. The z-axial probability distribution function (ZDF) of the surface cation in a classical MD simulation of Pt(111) for (c) pH 1 at 0 V_RHE, 0.3 V lower than the potential of zero charge (PZC) and (d) pH 13 at 0 V_RHE, 1.1 V lower than PZC, where the unit cells contain 2293 water molecules, 42 cations, 42 Cl^– anions, corresponding to 1 M cation in water.

pH- and Cation-Dependent Exchange Current Density of HER/HOR

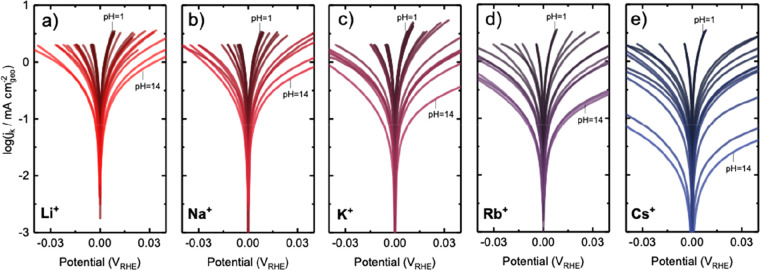
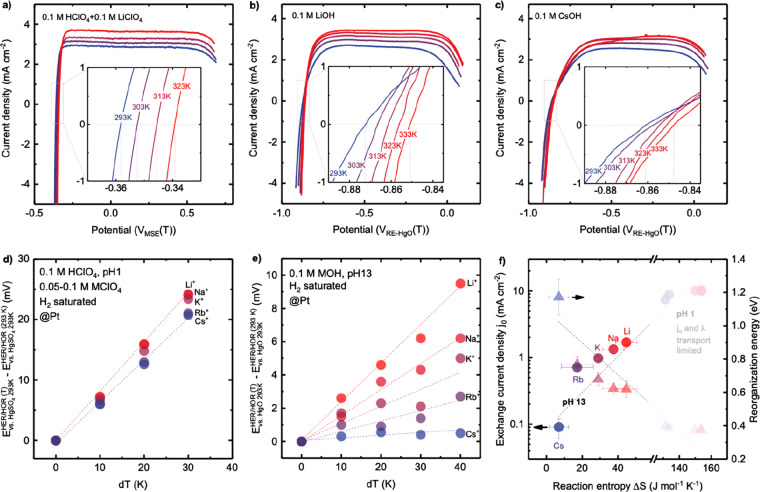
RDE measurements showed that the HER/HOR kinetic current densities were strongly dependent on pH (Figure 2), decreasing considerably with increasing pH, and cation-dependent, decreasing in the sequence of Li⁺ > Na⁺ > K⁺ > Rb⁺ > Cs⁺ in base, as shown in Figure 2. CVs of H₂-saturated 0.1 M LiOH collected from Pt RDE revealed a well-defined kinetics-limiting regime (overpotential of ±30 mV) and a linear increase in transport-limiting currents with increasing rotation speeds from 400, 900, 1600 to 2500 rpm at 293 K in Figure S1a,d, from which kinetic currents were extracted using the Koutecky–Levich method. The kinetic current densities normalized by the geometric surface area (0.196 cm²) of Pt RDE are shown in Figure 2. Similar cation dependency was also observed for kinetic current densities normalized by the ECSA (Figure S3). Comparable exchange current densities were obtained from fitting kinetic current densities, (j₀) using the Butler–Volmer (Figure S2b,c) or the MHC formalism^39,52 (Figure S2a,c). The extraction of kinetics current in acid is not accurate as the HOR kinetics on Pt are too fast to be separated from the hydrogen diffusion overpotential in RDE measurements.^9,16 The measurements of HOR kinetics at pH 0 has shown to be ∼2 orders of magnitude higher than that at pH 13 from the RDE measurement.¹⁴ The measured HOR current density at 2500 rpm and 293 K after iR correction and the calculated Nernstian diffusion overpotential (η_diff)¹⁶ were compared at different pH with various cations in Figure S4, where the HER/HOR kinetics current densities in electrolytes at pH < 6.9 for Li⁺ (Figure S4d) and pH < 3.9 for Cs⁺ (Figure S4i) are indistinguishable from the Nernstian diffusion overpotential. Therefore, we focus on the HER/HOR kinetic data with exchange current density j₀ below 6 mA cm_geo^–2 from RDE measurements, which are not limited by diffusion.

Figure 2.

Cation-dependent and pH-dependent HER/HOR kinetics on Pt RDE electrode in H₂-saturated aqueous electrolytes of 0.01–0.1 M HClO₄ with 0.05–0.1 M perchlorate salts of Li, Na, K, Rb, and Cs (pH 1–2), buffer solutions consisting 0.2 M of acetic acid (pH 2–4), citric acid (pH 1–3), phosphoric acid (pH 1–13), bicarbonate (pH 8–10), carbonate (pH 11–12) with 0.2 M MOH (M = Li, Na, K, Rb and Cs), and aqueous solutions of the hydroxide of Li, Na, K, Rb, and Cs for pH 12–14. Kinetic current density of HER/HOR on Pt RDE electrode in aqueous electrolytes containing (a) Li⁺, (b) Na⁺, (c) K⁺, (d) Rb⁺, and (e) Cs⁺ at pH from 1 to 14.

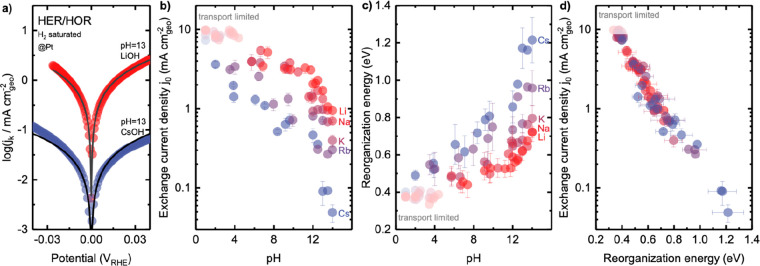
The exchange current density j₀ was found to decrease sharply with increasing pH by 2 orders of magnitude, where the dependence on pH became more pronounced in the order from Li⁺, Na⁺, K⁺, Rb⁺, to Cs⁺. The highest exchange current density (9.9 ± 0.6 mA cm_geo^-2) was obtained for Li⁺ at pH 1 whereas the lowest (0.05 ± 0.01 mA cm_geo) was found for Cs⁺ at pH 14 (Figure 3b). The values of exchange current density were in agreement with a previous RDE study,^9,16 for example, ∼8.2 ± 0.6 mA cm_geo^–2 at pH 2 in citrate buffer with K⁺ (∼6 mA cm_pt⁹) and ∼0.9 ± 0.1 mA cm_geo^–2 at pH 13 in 0.1 M KOH (0.7 mA cm_geo¹⁶). The exchange current density at pH 13 was strongly cation-dependent, having 1.6 ± 0.2 mA cm_geo^–2 in 0.1 M LiOH to 0.1 ± 0.03 mA cm_geo in 0.1 M CsOH (Figure 3a,b and Figure S5 for cation-dependent kinetic current density). The extracted exchange current density at pH 1 was not significantly cation-dependent (Figure 3b and Figure S5), which can be attributed to the mass transport limitation as mentioned above. These differences can be attributed to the interaction of cations with water molecules around them, where smaller cations with higher charge density (e.g., Li⁺ and Na⁺) tend to interact strongly with neighboring water molecules,^56,61 while larger ions (e.g., Cs⁺ and Rb⁺) impose weaker constraints on their solvation shells.^56,61

Figure 3.

Extraction of reorganization energy of HER/HOR on Pt electrode from MHC formalism 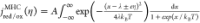, where λ is reorganization energy, k_B is the Boltzmann constant, T is temperature, η is the overpotential, A is the pre-exponential factor, accounting for the electronic coupling strength and the electronic density of states (DOS) of the electrode, and x accounts for the Fermi statistic of electron energies distributed around electrode potential. (a) Fitting of kinetic currents of HER/HOR measured on the Pt surface in 0.1 M LiOH (pH 13, red circle) and in 0.1 M CsOH (pH 13, blue circle) by MHC formalism (black lines). Cation-dependent and pH-dependent (b) exchange current density and (c) reorganization energy extracted by MHC formalism. (d) Exchange current density plotted against reorganization energy. Mass transport limitation in RDE measurements underestimates the exchange current density >∼6 mA cm_geo^–2, which is shaded. Error bars were obtained from the standard deviation of 2–3 independent measurements. Full data points are available in Figure S6.

In this work, we assign the cation-dependent exchange current density of HER/HOR kinetics to the cation-dependent Volmer^15,19 or Heyrovsky²² step, where having larger cations at the electrified interface compared to smaller cations impedes water dissociation associated in the Volmer or Heyrovsky step in a base. Having a Volmer rate-determining step is supported by the experimental values of the Tafel slope being ∼120 mV dec^–1 (Figure S7), which is in agreement with that estimated from 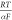(62) (with α = 0.5). Further support comes from fitting kinetic current densities to the Butler–Volmer or the MHC formalism with α_a + α_c = 1, suggesting that HER/HOR reactions undergoes the Tafel–Volmer mechanism but not the Heyrovsky–Volmer mechanism having α_a + α_c = 2.¹⁹ On the other hand, Intikhab et al.²⁰ showed that the kinetics of water dissociation (Volmer reaction) were slower in LiOH than in KOH electrolyte, whereas HER/HOR was faster in LiOH than in KOH electrolyte,⁶⁰ indicating that the Volmer reaction was not the RDS and either the Heyrovsky or Tafel step should be limiting. We attributed the cation dependence of exchange current densities to changes in the solvation structure at the electrified interface associated with noncovalent interactions among cations, water molecules, and Pt, which is supported by cation-dependent interfacial structure from MD simulation shown in Figure 1. Specifically, cations could alter the interfacial solvation structure and its reorganization, and the energetic barrier associated with proton-coupled electron transfer in the Volmer or Heyrovsky step, which would lead to cation-dependent HER/HOR kinetics. In the next section, we further extracted the reorganization energy of HER/HOR kinetics using the MHC formalism and discussed its physical origin and implication.

pH- and Cation-Dependent Reorganization Energy

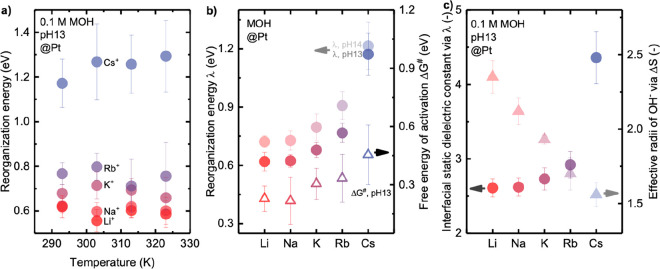
The reorganization energy for the HER/HOR kinetics was found to be cation-dependent, increasing with larger cations or greater structure-breaking tendency, as shown in Figure 3c. The reorganization energy was found to increase from 0.46 ± 0.06 to 0.72 ± 0.03 eV for Li⁺ with increasing pH from 6.9 to 14, while a greater increase from 0.52 ± 0.04 to 1.22 ± 0.12 eV was noted for Cs⁺ with increasing pH from 3.9 to 14. Similar trends were observed for the other cations. The exchange current density predicted by the MHC formalism (eq S5) was found to decrease linearly with increasing reorganization energy (Figure 3d).

Fitting temperature-dependent kinetics of HER/HOR at pH 13 with increasing temperature from 293 to 323 K (Figure S8a–e) using the MHC formalism revealed that the reorganization energy was temperature-independent (Figure 4a). Moreover, the free energy of activation obtained from the Arrhenius analysis of temperature-dependent exchange current densities of HER/HOR (Figures S8f–j) was found to be cation-dependent, increasing from 0.23 ± 0.11 eV for Li⁺ to 0.46 ± 0.25 eV for Cs⁺ (Figure 4b), which could be approximated as 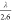. This ratio is in agreement with those reported previously (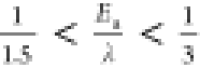) for outer-sphere electron transfer of [Fe(CN)₆]^3–/[Fe(CN)₆]^4– redox on a Au electrode.³⁰ Both temperature-independent reorganization energy and the proportionality between the free energy of activation and the reorganization energy suggest that the HER/HOR kinetics can be described by the MHC formalism.

Figure 4.

Fitting temperature-dependent kinetics of HER/HOR on Pt RDE in alkaline electrolytes using the MHC formalism: (a) reorganization energy measured at pH 13 in 0.1 M hydroxide of Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺ for a temperature range from 293 to 323 K; (b) comparison of reorganization energy of HER/HOR at pH 13 and pH 14 by the MHC formalism, and the free energy of activation ΔG^⧧ for HER/HOR at pH 13 obtained by Arrhenius analysis; (c) cation-dependent interfacial static dielectric constant of water extracted by Born model of reorganization energy and effective radii of OH^– fitted using Born model of reaction entropy. Error bars were obtained from the standard deviation of 2–3 independent measurements. Full data points of reorganization energy at pH 13 are available in Figure S9.

We further calculated the static dielectric constant at the electrified interface using the Born model 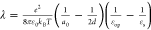,^38,40 where ε₀ is the permittivity of free space, a₀ is the effective radius of the reactant, d is the distance from the redox center to the surface of the electrode, ε_op is the optical dielectric constant, and ε_s is the static dielectric constant of the electrolyte near the electrified interface. Note that the Born model of reorganization energy is a simple dielectric continuum model, which does not allow to identify which elementary reaction is the RDS during HER/HOR. For Volmer step being the RDS, using the O–H bond length of water molecule (1 Å)⁶³ as the radius of redox species for a₀, the distance d between redox (interfacial water molecules) and the electrode being the same as a₀, the optical dielectric constant of water 1.8,^64,65 the cation-dependent reorganization energy in Figure 4b gave rise to cation-dependent static dielectric constants at the electrified interface in the order of Li⁺ (2.6) ∼ Na⁺ (2.6) < K⁺ (2.7) < Rb⁺ (2.9) < Cs⁺ (4.3) (Figure 4c). Assuming that Pt–H_ad bond length is not affected by the cation due to weak interaction between H_ad and the cation (relative to water–cation interaction), the cation-dependent trend in the interfacial dielectric constant can also be found for the Heyrovsky being the RDS. Therefore, both Volmer and Heyrovsky pathways suggest a cation-dependent interfacial static dielectric constant on the Pt surface at HER/HOR relevant potential region. These estimated static dielectric constants at the electrified interface are significantly lower than that of bulk water (78.2)⁶⁶ and 1 M solutions of chloride salts of Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺ (∼70),^66,67 which could originate from different cation/water molecule distributions at the electrified interface from MD simulations in Figure 1. The difference in the interfacial hydrogen-bonding structure induced by different cations has been revealed by in situ surface-enhanced infrared absorption spectroscopy in our previous work³⁰ and in this work. These results are in agreement with previous MD simulation, showing that the static dielectric constant of water molecules can be significantly reduced to 2.1 at a planar hydrophobic interface from 80 in bulk.⁶⁵ Further support comes from much reduced static dielectric constants of water confined at planar surfaces (2–5),^65,68 spherical cavities (40–60),⁶⁹ and spherical curvatures (3–9)⁷⁰ due to different interfacial water structures from bulk and cation concentrations at the electrified interface that can be greatly different from bulk.^71,72

pH- and Cation-Dependent Entropy Changes of HER/HOR

We examined the pH and cation dependence of the HER/HOR reaction entropy change ΔS from temperature-dependent potential measurements of HER/HOR, as shown in Figure 5a–c. Greater HER/HOR reaction entropy changes were found in acid (Figure 5a,d) than base (Figure 5b,c,e), regardless of the cations present, which suggests higher disorder in acid, in agreement with previous work by Ledezma-Yanez et al.¹² The reaction entropy (131–154 J mol^–1 K^–1 for pH 1 in 0.1 M HClO₄ and 0.1 M perchlorate of Li⁺/Na⁺ or 0.08 M perchlorate of K⁺/Cs⁺ or 0.05 M perchlorate of Rb⁺) is approximately 1 order magnitude higher than that at pH 13, with 0.1 M hydroxide of Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺ (7–45 J mol^–1 K^–1), as shown in Figure 5f. Moreover, while the HER/HOR entropy was found to be weakly cation-dependent in acid (Figure 5f), cation dependence was significant in base, increasing in the sequence of Cs⁺ < Rb⁺ < K⁺ < Na⁺ < Li⁺, as shown in Figure 5f. The trend can be attributed to the fact that the adsorption of cations in the decreasing order of Cs⁺ > Rb⁺ > K⁺ > Na⁺ > Li⁺ at the electrified interface (Figure 1) could alter the hydrogen-bonded water structure and solvation environment configurations at the interface. This hypothesis is supported by cation-dependent static dielectric constants extracted by the Born analysis of measured reaction entropy.

Figure 5.

Cation- and pH-dependent reaction entropy change of HER/HOR on Pt RDE, determined by 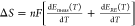(Appendix S2). Temperature-dependent CV of HER/HOR measured on Pt at pH 1 in H₂-saturated 0.1 M HClO₄ electrolyte (a) with 0.1 M LiClO₄. Temperature-dependent CV of HER/HOR measured on Pt at pH 13 of H₂-saturated (b) 0.1 M LiOH and (c) 0.1 M CsOH. Insets show the zoom-in of zero overpotential region. Temperature-dependent HER/HOR potential vs the potential of reference electrode (Hg/HgSO₄ for pH 1 and Hg/HgO for pH 13) at 293 K (d) at pH 1 and (e) at pH 13. (f) Cation dependence of the exchange current density j₀ and reorganization energy, as a function of reaction entropy, ΔS, of HER/HOR at pH 1 and pH 13. Note that the kinetics (j₀ and λ) of HER/HOR on Pt RDE at pH 1 was limited by mass transport (Figure S4) and cannot be separated from diffusion current density, thus the exchange current density at pH 1 shown in Figure S5c does not reflect the pure HER/HOR kinetics at pH 1. The thermodynamic HER/HOR entropy changes were found to increase in the sequence of Cs⁺ < Rb⁺ < K⁺ < Na⁺ < Li⁺, where adsorbed Cs⁺ and Rb⁺ could expel interfacial water molecules and weaken the hydrogen-bonding network of surrounding water molecules at OHL, which leads to an increase in molar entropy of interfacial water molecules S_H2O(l) and interfacial hydronium S_H3O⁺(aq), and a corresponding decrease in HER/HOR reaction entropy, ΔS = S_H2(g) – 2 × S_H3O⁺(aq) in acid (2H_(aq)⁺ + 2e^– ↔ H_2(g)) or ΔS = S_H2(g) + 2 × S_OH^–(aq)) – 2 × S_H2O(l) in alkaline electrolytes (2H₂O_(l) + 2e^– ↔ H_2(g) + 2OH_(aq)). Error bars were obtained from the standard deviation of 2–3 independent measurements. Full data points are available in Figure S10.

We further extracted the interfacial static dielectric constant of water using the Born model of reaction entropy 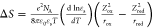,^37,73 where T is temperature, e is elementary charge, and N_A is the Avogadro constant. ε₀ is permittivity of free space; ε_s is static dielectric constant of solvent; Z and r are the charge and ionic radii of redox species, and compared to that extracted from Born model of reorganization energy (Figure 4b). Assuming the overall HER/HOR reaction in alkaline electrolyte 2H₂O + 2e^– ↔ H₂ + 2OH^–, where the effective radius and charge of H atom in a H₂O molecule are r_H2O = 1.4 Å and Z_H2O = +1, r_H2 = 1 Å, and Z_H2 = 0 for H atoms in H₂ molecule, whereas Z_OH^– = +1 for H atom in OH^– anion. By fitting experimental data to Born model of reaction entropy with interfacial static dielectric constant obtained from reorganization energy (Figure 4c) and considering that the temperature dependence term, 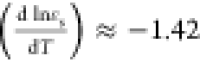,⁷⁴ being the same as pure water for approximation (identical for all cation), the effective radii of OH^–, r_OH^–, was found to decrease in the order of Li⁺ (2.4) < Na⁺ (2.1) < K⁺ (1.9) < Rb⁺ (1.7) < Cs⁺ (1.6), as shown in Figure 4c. The cation-dependent trend in the effective radii of OH^– is supported by the short-range effect of cations on the water structure in their solvation shell, where structure-breaking cations (e.g., Cs⁺) could decrease the effective radii of OH^– by weakening the solvation structure of OH^–, whereas structure-making cations (e.g., Li⁺) maintain their hydration shell and do not impact on the solvation structure of OH^–. Using Davies equation,⁷⁵ the activity coefficient of OH^– (γ_OH^–) at the Pt interface was found to increase with cation radii from 0.21 for Li⁺ and 0.48 for Cs⁺ (Appendix S4), where the cation-dependent trend is consistent with that reported by Harned and Swindells.⁷⁶

We further estimated the Gibbs free energy of the reaction ΔG (ΔG = ΔG_OH– – ΔG_H2O), where the change of the Gibbs free energy, ΔG, of OH^– for Li⁺ and Cs⁺, which should change by a factor of −2.303·R·T·log(γ_OH–) according to Nernst equation. The values of 2.303·R·T·log(γ_OH–) can be estimated to be −0.038 eV for Li⁺ and −0.018 eV for Cs⁺. Between the two extreme cations (Li⁺ and Cs⁺), the Gibbs free energy of the reaction ΔG varies by 0.02 eV, whereas the free energy of activation ΔG^⧧ increases 0.23 eV (from 0.23 eV for Li⁺ to 0.46 eV for Cs⁺, Figure 4b). The comparison of the Gibbs free energy of the reaction ΔG and the free energy of activation ΔG^⧧ shows that the barrier of kinetics can be 1 order of magnitude larger than the thermodynamic driving force, the Gibbs free energy of the reaction ΔG. The proportionality between the Gibbs free energy of the reaction ΔG and the free energy of activation ΔG^⧧ indicates that the linear free energy relationship holds and could explain the cation-dependent HER/HOR kinetics at pH 13 in this work.

We further showed that enthalpic contribution to the free energy of HER/HOR was small. For example, the entropic term of HER/HOR, TΔS, differed 0.11 eV from Li⁺ to Cs⁺ (with ΔS varies from 7 to 45 K mol^–1 K^–1 from Cs⁺ to Li⁺), whereas the reaction enthalpy (peak potential of H/OH exchange peaks) was almost cation-independent (Figure S15). This observation suggests that the entropic term is much more important in the free energy of the reaction than the enthalpic term in our case. Thus, the linear relationship between reaction entropy ΔS and activation entropy ΔS* can be expected as enthalpic terms are small. Therefore, we try to examine the correlation between reaction entropy change ΔS (thermodynamic quantity) and kinetic quantities (e.g., exchange current density and reorganization energy) and understand the physical origin of such a correlation, as the activation entropy ΔS* could not be quantified from experimental approaches or from reorganization energy in the MHC formalism. However, the reaction entropy change ΔS can be obtained from temperature-dependent potential (Appendix S2). From our previous work,³⁰ we demonstrated that the kinetics (exchange current density and reorganization energy) correlated strongly with the reaction entropy of [Fe(CN)₆]^3–/4– redox (an outer-sphere electron-transfer reaction), which was associated with the disordering/ordering of the solvation environment of the redox centers at electrode surface. In this work, the HER/HOR reaction entropy is a measure of the disordering of solvation structures at electrified interface and can be used to extract the interfacial dielectric constant, suggesting that cation-dependent reaction entropy is associated with cation-dependent interfacial solvation structure. Furthermore, our studies demonstrated that the exchange current density (kinetics) increased with increasing reaction entropy change ΔS for proton-coupled electron transfer (HER/HOR in this work, as shown in Figure 5f) and for outer-sphere electron transfer ([Fe(CN)₆]^3–/4– redox in our previous work³⁰).

Cation-Dependent Water Structures at the Electrified Interface

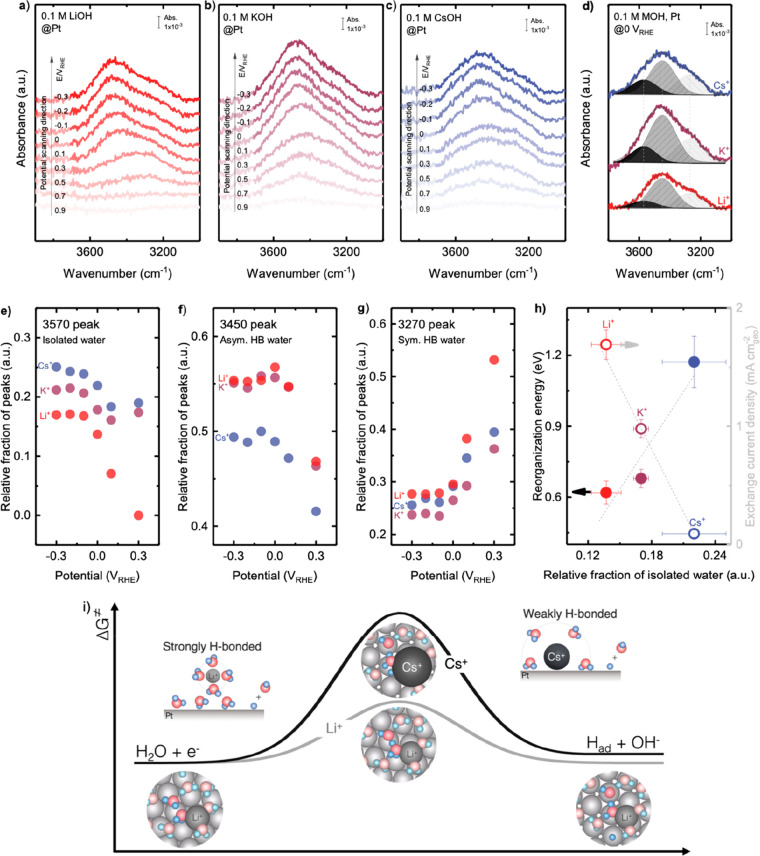
We employed in situ SEIRAS to probe interfacial water structures on Pt during HER/HOR as a function of voltage from 1.1 to −0.3 V_RHE in the electrolyte containing 0.1 M hydroxide of Li⁺, K⁺, and Cs⁺, where OH stretching (∼3600–3200 cm^–1) and HOH bending (∼1700–1600 cm^–1) were probed (Figures 6 and S12). Figure 6a–c shows the OH stretching features of in situ SEIRAS spectra measured in the presence of Li⁺, K⁺, and Cs⁺, respectively. It should be noted that the PZC of Pt(111) at pH 13 was at the potential of 1.1 V_RHE, where the reference spectrum of SEIRAS was measured. Note that the PZC of Pt does not change drastically with surface facets (Appendix S3). The Pt electrode surface was negatively charged at potentials below PZC, and the surface charge increased with decreasing potentials, which could result in the increase of the intensity of OH stretching peak when the potential decreased from 0.9 to −0.3 V_RHE. The OH stretching peaks were further deconvoluted into three components: weakly H-bonded water at 3570 cm^–1,^36,77 asymmetric H-bonded water molecules at 3450 cm^–1 (water–cation interaction, i.e., water molecules solvating cations),^36,77 and symmetric H-bonded water molecules at 3270 cm^–1 (water–water interaction, i.e., ice-like water or bulk water),^36,77 as shown in Figure 6d for 0 V_RHE and Figure S13 for other potentials. The potential-dependent relative fractions of deconvoluted peaks for weakly H-bonded water, asymmetric, and symmetric H-bonded water molecules are shown in Figure 6e–g. The relative fraction of weakly H-bonded water at the electrified interface was found to increase with decreasing potential (Figure 6e), which was attributed to the increase in Pt–water dipole interaction due to higher surface charge. The relative fraction of asymmetric H-bonded water molecules was shown to increase with decreasing potential (Figure 6f), which can be attributed to the increase of hydrated cations at the electrified interface when Pt surface charge was more negative at lower potential. The relative fraction of symmetric H-bonded water molecules decreased with decreasing potential (Figure 6g), which can be due to the replacement of symmetric H-bonded water by hydrated cations. At a given potential, such as 0 V_RHE, the relative peak fraction of weakly H-bonded water at the interface was shown to increase in the order from Li⁺ to K⁺ to Cs⁺ (Figure 6e), whereas that of strongly H-bonded (asymmetric and symmetric) water decreased (Figure S14). The observation agrees with more cations and less water molecules at the electrified interface for Cs⁺ compared to Li⁺, as shown schematically in Figure 1a,b, which is consistent with HOH bending features. The HOH bending vibration peak (Figure S12) also showed similar trends for the hydrogen-bonding network of interfacial water molecules, where the peaks at ∼1605 and ∼1626 cm^–1 correspond to weakly H-bonded and strongly H-bonded water molecules, respectively.^77,78 In the presence of Li⁺, the Pt surface was mainly covered by strongly (symmetric and asymmetric) H-bonded water, which increased its intensity with decreasing potential (Figure S12a). In the case of Cs⁺, the intensity of the peak at ∼1610 cm^–1 (weakly H-bonded water) was more significant (Figure S12c) compared to that of Li⁺, resulting in an increased fraction of weakly H-bonded water. Note that although a spectroscopic technique such as in situ SEIRAS could probe the interactions between cations and interfacial water molecules, further techniques are needed to quantify the adsorption energy and identify whether this adsorption involves electron transfer to the cation and how it depends on the nature of the cations.

Figure 6.

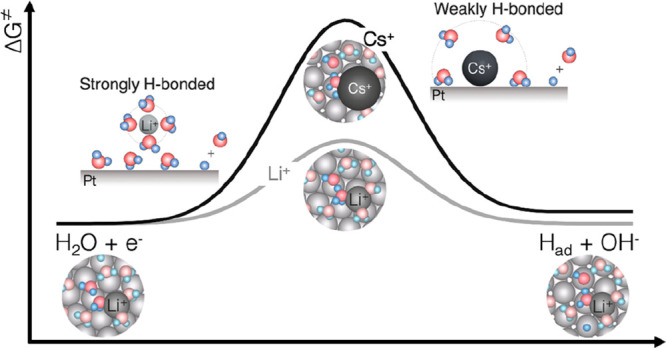
Altering interfacial structure at the Pt surface in aqueous electrolytes through noncovalent interactions associated with the hydrated cations, water molecules, and negatively charged Pt surface. The potential-dependent OH stretching features of in situ SEIRAS spectra of HER/HOR measured from 0.9 V_RHE to −0.3 V_RHE in a H₂-saturated aqueous solution of 0.1 M of (a) LiOH, (b) KOH, and (c) CsOH, where the reference spectrum was taken at 1.1 V_RHE. Full spectra before and after subtracting by reference spectrum (at 1.1 V_RHE) are available in Figure S11. (d) Deconvolution of the OH stretching peak at 0 V_RHE into three components: 3570 cm^–1 (weakly H-bonded/isolated water), 3450 cm^–1 (asymmetric H-bonded water), and 3270 cm^–1 (symmetric H-bonded water). The potential dependence of the relative fractions of (e) isolated water, (f) asymmetric H-bonded water, and (g) symmetric H-bonded water. (h) Reorganization energy and exchange current density of HER/HOR measured on Pt RDE in 0.1 M hydroxide of Li⁺, K⁺, and Cs⁺ as a function of the relative fraction of isolated water. Error bars were obtained from the standard deviation of 2 independent measurements. (i) Scheme summarizing the proposed mechanisms of cation dependent kinetics of HER/HOR, where Li⁺ ions retain their solvation shell intact and promote strongly hydrogen-bonded interfacial water layer, enhance proton-coupled electron transfer rate of the Volmer or Heyrovsky step by facilitating interfacial water molecule reorganization. Cs⁺ ions partially desolvate and attach to the negatively charged Pt surface, promoting weakly H-bonded interfacial water molecules, leading to an increase of the barrier of proton transfer during the Volmer or Heyrovsky step in HER/HOR on the Pt surface.

Relating HER/HOR Kinetics to Surface Chemistry and Solvation Environments at the Electrified Interface

We further examine and correlate the peak potential determined from CVs (the peaks of H/OH exchange on Pt(110) and Pt(100) facets)^28,79,80 with the HER/HOR kinetics, as it has been suggested to govern the HER/HOR activity in a wide range of electrolyte with pH from 0 to 13 on platinum group metals, e.g., Pt,^8,9,14 Ir,^9,14 Pd,^8,9,14 and Rh.⁹ The peak potentials were extracted from CV measured in Ar-saturated electrolytes on polycrystalline Pt in a base (Figure S15a) and in an acid (Figure S15b) following previous work,^8,9 where the peaks at ∼0.25 and ∼0.32 V_RHE correspond to the potentials of the H desorption peak at Pt(110) and Pt(100) facets, respectively.^8,9 Increasingly, peak potential from 0.12 to 0.27 eV for the Pt(110) facet and from 0.25 to 0.39 eV for the Pt(100) facet was observed for increasing pH from 1 to 14 (Figure S15c,d), in agreement with previous work.^8,9 Note that the peaks of Pt(110) and Pt(100) of CVs measured on polycrystalline Pt result from a competitive H/OH exchange, therefore convoluting HBE and OH binding energy (OHBE).^28,79,80 Interestingly, the experimental values of peak potential determined from CV at a given pH were almost independent of cations (Figure S15), whereas the exchange current density normalized by the geometric surface was changed by 1–2 orders of magnitude from Cs⁺ to Li⁺ (Figure S15c,d). Therefore, our result indicates that the experimentally measured peak potential from the CV cannot explain the cation-dependent HER/HOR kinetics, which could arise from the coadsorption of H_ad, OH_ad, and cations in low potential region (0–0.4 V_RHE),²⁸ and consequently, the peak shifts from hydrogen underpotential deposition regions might not be appropriate to extract the binding energy of H_ad.²⁸

We further showed that the HER/HOR exchange current density normalized by geometric surface j₀ correlated strongly with reaction entropy change ΔS, where the exchange current density increased with increasing reaction entropy (Figure 5f). In addition, smaller reorganization energy of HER/HOR kinetics is associated with greater reaction entropy change (Figure S16a). Such correlation has also been observed for outer-sphere electron-transfer reaction in our previous work.³⁰ These results suggest that having more disordered solvation environments at the electrolyte/electrode interface with greater solvating configurations can increase the exchange current density and reduce reorganization energy during electron transfer³⁰ or proton-coupled electron-transfer processes (Figure 5f and Figure S16).

Our in situ SEIRAS experiments further revealed that solvation environments at the electrified interface can be altered by spectator cations in the electrolyte, where structure-breaking cations (such as Cs⁺) could expel interfacial water molecules (Figure 1a) and reduce the interfacial H-bonding network and promote weakly H-bonded water molecules at the electrified Pt surface (Figure 6e and Figure S14). A similar cation effect on interfacial water structures on the Au surface during outer-sphere electron transfer has been observed in our previous work.³⁰ The weakly H-bonded interfacial environment was shown to enhance the reaction rate of outer-sphere electron-transfer processes. Unlikely, the weakly H-bonded interfacial solvation environment could increase the barrier of proton-coupled electron transfer from water in the Volmer step (H₂O + e^– + * ↔ H_ad + OH^–) or Heyrovsky step (H_ad + H₂O + e^– ↔ H₂ + OH^– + *) during HER/HOR (Figure 6h,i). In addition, as the HER/HOR potential on the RHE scale differs on the SHE scale for electrolytes of different pH,^12,81 different water dipole orientation,^6,12,77 solvation, and adsorption of cations at the electrified interface as a function of pH can influence the energetics of water adsorption/desorption at Pt(111) during HER/HOR.⁸² Specifically, larger alkali metal cations can adsorb more easily on the metal surface in alkaline electrolytes, due to stronger Coulombic interactions associated with hydrated cations and Pt surface induced by the higher surface charge at pH 13 than at pH 1.^31,57 The negative charge of the Pt surface in base attracts cations and hydrogen dipole of interfacial water molecules, leading to an ordered interfacial structure at the electrified interface. In the acidic electrolytes, the Pt surface becomes less negatively charged,^31,57 which interacts more weakly with both water and cations to induce a more disordered interfacial layer, rendering greater reaction entropy (Figure 5f). Going beyond the PZC-dependent interfacial water structure descriptor of HER/HOR kinetics,¹² which does not explain the asymmetrical effect of the shift in PZC on HER and HOR activity,⁸⁰ we propose that the difference in HER/HOR kinetics in acid and in base can be attributed to the adsorbed cations on Pt surfaces at the HER/HOR potential region.

The proposed mechanism in this work (Figure 6i) is in agreement with previous work,¹² suggesting pH-dependent interfacial water structure as the HER kinetics descriptor, where faster kinetics in acid are associated with higher entropy with less ordered structure in acid and lower reorganization energy for interfacial water than those in the base. In addition, the trends in the HER/HOR kinetics and proposed explanation is consistent with recent computational findings²⁹ on pH-dependent proton transfer barriers for HER/HOR kinetics, where greater pH is correlated with a larger entropic barrier of proton transfer across the outer Helmholtz layer and thus lowered HER/HOR kinetics. This work highlights promising opportunities to control the reaction rates by tuning the solvation environments at the electrified interface. Further experimental and computation fundamental studies are needed to understand how these solvation environments at the electrified interface can alter water adsorption and dissociation and proton transfer kinetics in details.

Conclusions

Classical MD simulation of electrolytes containing 1 M cation of Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺ at pH 1 and pH 13 at the Pt(111) interface has shown that the local solvation environment at the electrified interface is cation-dependent. Electrolytes containing larger (more structure-breaking) cations yield more surface-bound cations than those containing smaller (more structure-making) cations. These differences can result in a cation-dependent interfacial hydrogen-bonding network, which was probed by in situ SEIRAS measurements. The cation-dependent interfacial water structure can further alter the effective dielectric and fluctuations that determine solvent reorganization energy. The contribution to the HER/HOR kinetics on the Pt RDE surface from the interfacial structure change induced by redox-inactive structure-making/breaking cations and pH of electrolytes was systematically probed. We show that the HER/HOR exchange current density j₀ decreases with increasing pH by 2 orders of magnitude, where the cation dependence becomes more pronounced in the order of Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺. We further show that the exchange current density of HER/HOR increases with increasing reaction entropy. Using the Born model of reorganization energy (extracted by MHC formalism) and reaction entropy (experimentally measured), the interfacial static dielectric constant has been estimated to be significantly lower than that in bulk electrolyte and increases in the order of Li⁺ < Na⁺ < K⁺ < Rb⁺ < Cs⁺ on negatively charged Pt RDE. The findings of this study can have broader implications for the chemical physics of electrolytes on electron transfer and proton-coupled electron-transfer reactions at the electrified interface, which can be leveraged to tune the kinetic rates and selectivity of electrochemical reactions for achieving the decarbonization of sustainable fuels and chemical transformations.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.1c00281.

• Cyclic voltammograms; Koutecky–Levich analysis; cation-dependent kinetics current density per ECSA and per geometric surface; Tafel slope; calculated Nernstian diffusion overpotential; temperature-dependent kinetics current density; in situ SEIRAS spectra; deconvolution of OH stretching peak; force field parameters of classical MD simulation (PDF)

Author Present Address

^▽ University of Michigan–Shanghai Jiao Tong University Joint Institute, Shanghai Jiao Tong University, Shanghai, 200240, People’s Republic of China

Author Contributions

B.H., K.X., and Y.S.-H. designed the experiments. B.H. carried out electrochemical measurements and in situ SEIRAS experiments and performed analysis. K.H.M. and Y.W. performed classical MD simulations. B.H. prepared the initial manuscript. All authors contributed to the discussion and revision of the manuscript.

The authors declare no competing financial interest.