Abstract
Background
An accurate estimation of athletes’ energy needs is crucial in diet planning to improve sport performance and to maintain an appropriate body composition. This study aimed to develop and validate in elite athletes new equations for estimating resting energy expenditure (REE) based on anthropometric parameters as well as bioimpedance analysis (BIA)-derived raw variables and to validate the accuracy of selected predictive equations.
Methods
Adult elite athletes aged 18–40 yrs were studied. Anthropometry, indirect calorimetry and BIA were performed in all subjects. The new predictive equations were generated using different regression models. The accuracy of the new equations was assessed at the group level (bias) and at the individual level (precision accuracy), and then compared with the one of five equations used in the general population or three athletes-specific formulas.
Results
One-hundred and twenty-six male athletes (age 26.9 ± 9.1 yrs; weight 71.3 ± 10.9 kg; BMI 22.8 ± 2.7 kg/m2) from different sport specialties were randomly assigned to the calibration (n = 75) or validation group (n = 51). REE was directly correlated with individual characteristics, except for age, and raw BIA variables. Most of the equations from the literature were reasonably accurate at the population level (bias within ±5%). The new equations showed a mean bias −0.3% (Eq. A based on anthropometric parameters) and −0.6% (Eq. B based on BIA-derived raw variables). Precision accuracy (individual predicted-measured differences within ±5%) was ~75% in six out of eight of the selected equations and even higher for Eq. A (82.4%) and Eq. B (92.2%).
Conclusion
In elite athletes, BIA-derived phase angle is a significant predictor of REE. The new equations have a very good prediction accuracy at both group and individual levels. The use of phase angle as predictor of REE requires further research with respect to different sport specialties, training programs and training level.
Keywords: Athletes, Energy expenditure, Predictive equations, BIA, Phase angle, Accuracy
Background
Total energy expenditure of most athletes is expected to be greater compared to general population because of training, and changes in metabolism and body composition [1]. At the same time, estimating energy needs is crucial in diet planning to improve sport performance and manage body mass in weight-category sports [2, 3]. Further, under- or over-estimating athletes’ energy requirements might result in unwanted changes in fat-free mass (FFM), and/or fat mass (FM), impaired performance and health concerns, for instance increased risk of injuries or cardiovascular diseases [1, 2, 4].
Energy requirements may be assessed based on resting energy expenditure (REE) [5], which is the amount of energy expended at rest by a fasted individual in a thermoneutral environment, representing 60–70% of total energy expenditure in normal-weight healthy adults and variable percentages in athletes [6]. In human nutrition REE is commonly estimated by using predictive equations based on easily available variables such as age, stature, body weight, etc. Most of the widely used equations for estimating REE in the general population (Harris and Benedict (HB) [7], Schofield [8], FAO/WHO/UNU [9], Mifflin [10] and Owen [11]) have been developed based on minimally active or sedentary individuals. Taking into account different physical activity level and body composition (i.e. higher FFM and body cell mass with lower FM) relative to general population [12–14], the equation used for estimating REE in the general population may be not appropriate for athletic individuals. As a consequence, few specific predictive equations for REE have been developed for athletes, [15–18], indeed exhibiting some limitations. The study by De Lorenzo et al. included a small sample size (n = 51) [15] whereas the one by ten Haaf et al. involved recreational athletes exercising on average 9.1 ± 5 h a week [17]. Wong et al. studied Asiatic athletes only [16] and Watson et al. [18] only females. Finally, Jagim et al. [5] determined the accuracy of selected predictive equations for REE, but they did not propose a validated formula.
REE is expected to be associated with FFM, which is a reasonable surrogate body composition marker for oxidatively active tissues [19]; in other word, FFM might be used for predicting REE, and from a practical point of view this is even more credible if field techniques are employed. In this perspective, bioelectrical impedance analysis (BIA) is widely used for assessing body composition in athletes [20], but the interpretation of BIA results depends to a large extent on the equation used to estimate FFM [21]. Interestingly, raw BIA variables such as bioimpedance index (BI-Index = stature2/impedance at 50 kHz) and phase angle (PhA) might be taken into account as possible predictors of REE. In fact, while BI-index is strictly related to FFM, PhA is thought to be a proxy of both water distribution (i.e. the ratio between extracellular water-ECW and total body water-TBW) [22], body cell mass and cellular integrity [23]. So far, a relationship between REE and BI-index and/or PhA has already been observed in normal-weight or overweight subjects [24] as well as in patients with obesity [25] and Crohn’s disease [26]. Not surprisingly, the results of these studies suggest that raw BIA variables may improve the prediction power under physiological conditions [24], but only to a limited extent in subjects with altered body water distribution [25, 26].
Based on this background, the primary aim of this study was to develop and validate new predictive equations of REE in elite athletes, considering not only anthropometric measures, but also raw BIA variables. The accuracy of new equations, as well as the one of selected predictive equations of REE used in the general population or in athletes, was evaluated at the group level (bias) and at the individual level (precision).
Methods
Study design and subjects
In the present study we have retrospectively analysed routine data collected between January 2012 and December 2019 in elite athletes defined as those who have previously competed as regional and/or national players [27].
Subjects were selected for this study according to the following inclusion criteria: (1) both sexes, (2) age between 18 and 45 yrs and (3) at least 24 h/week of training. Subjects affected by overt metabolic and/or endocrine diseases and/or regularly taking any medications or using any drugs affecting energy metabolism, were excluded. This study was conducted in accordance with the Declaration of Helsinki and was approved by the Federico II University Ethical Committee.
All measurements were performed early in the morning (8.30 a.m.) after an overnight fast (10–12 h) according to standardized conditions, i.e. abstention from alcohol, caffeine or other thermogenetic substances, smoking and any physical activity for 24 h (in most cases 36 h) prior to the assessment.
Anthropometry and bioelectrical impedance analysis
Body weight was measured in duplicate to the nearest 0.1 kg using a platform beam scale and stature was measured in triplicate to the nearest 0.5 cm using a stadiometer (Seca 709; Seca Hamburg, Germany). The subject wore light clothes and no shoes. Body mass index (BMI) was calculated as body weight (kg) divided by squared stature (m2).
BIA was performed by phase-sensitive device (Human IM Touch, DS Medica S.r.l., Milan, Italy). Measurements were carried out with empty bladder, in a supine position for at least 10 min before starting the measurement). After cleaning skin surface, patients were asked to lay with upper and lower limbs slightly abducted, so there was no contact between the extremities and trunk. The measuring electrodes were placed on the anterior surface of the wrists and ankles, and the injecting electrodes were placed on the dorsal surface of the hands and the feet, respectively (overall, eight electrodes). Data for impedance and PhA from the non-dominant side of the body, measured at 50 kHz, were considered. BI-index was calculated as the ratio stature2/resistance (cm2/ohm).
Before each test the analyser was calibrated with the calibration considered successful if resistance value was between 382 and 385 Ω and reactance was 44–46 Ω, as indicated by the manufacturer guidelines. The test-retest coefficient of variation (CV) (as determined in ten subjects) was always less than 3%.
Resting energy expenditure
REE was measured (MREE) by indirect calorimetry [28] using a canopy system (Vmax® Encore system, CareFusion Corporation, U.S.). The instrument was routinely checked by burning ethanol, whereas oxygen and carbon dioxide analysers were calibrated on the test day using nitrogen and standardized gases (mixtures of nitrogen, carbon dioxide and oxygen).
Measurement conditions for by indirect calorimetry were defined following the suggestions made by Compher et al. [29] and Fullmer et al. [30]. In addition to the standardized conditions already mentioned, REE was measured with the subject laying down, but awake, on a bed in a quiet environment. After a 15-min adaptation period, oxygen consumption and carbon dioxide production were measured for 45 min. Only steady state periods of measurement were selected according to the procedures for the ventilated hood system (< 5% CV). The first 5 min were discarded. Also, the inter-day CV (as determined in 10 subjects on subsequent days) was always less than 4%. The flow throughout the canopy was modified in order to maintain the CO2 between 0.6–0.8%.
Energy expenditure was calculated using the abbreviated Weir’s formula, neglecting protein oxidation [31]. Data were excluded from analysis if the respiratory quotient was outside the expected range (0.71–1.00) and when measured REE was ±3 standard deviations outside the mean REE.
Predictive equations
In the validation group REE was predicted (PREE) using five equations that are widely mentioned with respect to the general population (Harris & Benedict [7], Schofield [8], FAO/WHO/UNU [9], Mifflin [10] and Owen [11]), and three athletes-specific formulas from the literature (De Lorenzo [15], Wong [16] and ten Haaf [17])(Table 1).
Table 1.
Resting energy expenditure predictive equations in their original unit (kcal/day, except Schofield and FAO/WHO/UNU (MJ/day))
| Equation | Formula |
|---|---|
| Harris and Benedict [7] | Males 13.75 × Weight (kg) + 5 × Stature (cm) – 6.76 × Age (yrs) + 66.47 |
| Schofield [8] |
Males (18–30 yrs) 63 × Weight (kg) – 42 × Stature (m) + 2953 Males (30–60 yrs) 48 × Weight (kg) – 11 × Stature (m) + 3670 |
| FAO/WHO/UNU [9] |
Males (18–30 yrs) 15.3 × Weight (kg) – 27 × Stature (m) + 679 Males (30–60 yrs) 11.6 × Weight (kg) – 16 × Stature (m) + 879 |
| Mifflin [10] | 9.99 × Weight (kg) + 6.25 × Stature (cm) – 4.92 × Age (yrs) + 166 × Sex (M = 1, F = 0) – 161 |
| Owen [11] | Males 10.2 × Weight (kg) + 879 |
| De Lorenzo [15] | 9 × Weight (kg) + 11.7 × Stature (cm) − 857 |
| Wong [16] | 13 × Weight (kg) + 192 × Sex (M = 1, F = 0) + 669 |
| Ten Haaf [17] | 11.936 × Weight (kg) + 587.728 × Stature (cm) – 8.129 × Age (yrs) + 191.027 × Sex (M = 1, F = 0) + 29.279 |
Statistical analysis
Statistical analyses were performed using IBM SPSS (version 26). All data are presented as mean ± standard deviation (SD), unless otherwise specified, and significance was defined as p < 0.05. The Kolmogorov-Smirnov Test and the Shapiro-Wilk Test were used to assess if variables were normally distributed.
As presented in Table 2, subjects were randomly assigned to either a calibration or a validation group.
Table 2.
Characteristics of the study sample for the calibration and validation groups
| All (n = 126) |
Calibration group (n = 75) |
Validation group (n = 51) |
|
|---|---|---|---|
| Age, yrs | 26.9 ± 9.1 | 26.8 ± 9.0 | 27.1 ± 9.5 |
| Weight, kg | 71.3 ± 10.9 | 71.4 ± 11.3 | 71.1 ± 10.6 |
| Stature, cm | 177 ± 7 | 177 ± 7 | 177 ± 7 |
| BMI, kg/m2 | 22.8 ± 2.7 | 22.8 ± 2.8 | 22.8 ± 2.6 |
| MREE, kcal/die | 1831 ± 250 | 1834 ± 261 | 1826 ± 234 |
| RQ | 0.821 ± 0.07 | 0.832 ± 0.07 | 0.822 ± 0.07 |
| BI-index, cm2/Ω | 65.9 ± 9.6 | 65.9 ± 9.8 | 66.0 ± 9.4 |
| PhA, degrees | 7.76 ± 0.76 | 7.79 ± 0.74 | 7.73 ± 0.78 |
Data are expressed as mean ± standard deviation
BMI body mass index, MREE measured resting energy expenditure, RQ respiratory quotient, BI-index bioimpedance index, PhA phase angle
As far as statistical power is concerned, in the calibration group for alpha level = 0.05 and beta = 0.20 a sample size of 75 subjects is requested to reach a p < 0.05 for r = 0.330 (R2 = 0.10). In the validation group a sample size of 51 subjects is adequate to identify a significant between-groups difference of 50 kcal with a standard deviation of 125 kcal.
Linear correlation was applied for evaluating associations between variables. Multivariate linear regression analysis was performed to develop the new predictive equations, with REE measured by indirect calorimetry as dependent variable. We generated models as follows: in Model 1, age, sex, weight, stature and BMI were set as predictors, while in Model 2 we added the raw BIA variables (BI-index and PhA). Coefficient of determination (R2) and standard error of the estimate (SEE) were considered for assessing the predictive power of formulas. The regression equations, derived from the calibration subset, were applied to the validation group.
Differences between PREE and MREE as well as bias, i.e. the mean percent difference, were both used as a measure of accuracy at the population level. Bias was found acceptable if within ±5% [32, 33]. The percentage of patients with a PREE within 90–110% of MREE was used as a measure of accuracy at the individual level (precision accuracy). Values lower than 90% were classified as underprediction, while values higher than 110% as overprediction. The root mean squared error (RMSE) was used to define the predictions obtained with these models. Finally, comparisons of PREE-MREE differences vs mean PREE-MREE values were performed by Bland and Altman plots to estimate the limits of agreement [34].
Results
One hundred and twenty-six male elite athletes from different sport specialties were included in the analysis. As mentioned above, data on anthropometric measures, raw BIA variables and MREE are reported for the calibration and validation groups in Table 2. Athletes from seven sports were recruited, practicing masters swimming (n = 24, 19%), cycling (n = 22, 17.5%), running (n = 21, 16.7%), karate (n = 17, 13.5%), water polo (n = 16, 12.7%), ballet dance (n = 15, 11.9%) and boxing (n = 11, 8.7%). Individual characteristics for each sport specialty are reported in Table 3. BMI was the highest in water polo players (25.9 ± 1.8 kg/m2) and the lowest in runners (20.6 ± 1.2 kg/m2). MREE was the highest in water polo players (2195 ± 244 kg/day) and the lowest in ballet dancers (1567 ± 107 kg/day) in line with the differences in body weight. Mean value of PhA varied between 8.57 ± 0.65 degrees in boxers and 6.96 ± 0.54 degrees in master swimmers, being higher in boxers, cyclists and water polo players (Table 3).
Table 3.
Characteristics of the study sample according to sport specialty
| Cycling | Water polo | Masters swimming |
Karate | Ballet Dance | Boxing | Running | |
|---|---|---|---|---|---|---|---|
| (n = 22) | (n = 16) | (n = 24) | (n = 17) | (n = 15) | (n = 11) | (n = 21) | |
|
Age (yrs) |
27.0 ± 2.7cdef | 24.2 ± 6.6c | 40.4 ± 4.5abdefg | 18.8 ± 2.7aceg | 19.1 ± 1.1acg | 20.7 ± 2.7aeg | 29.0 ± 9.9cdf |
|
Weight (kg) |
69.2 ± 5.2bcg | 88.8 ± 4.9acdefg | 76.6 ± 10.0abdeg | 69.5 ± 10.4bcg | 64.1 ± 5.2bc | 70.0 ± 5.2bg | 61.1 ± 6.3abcdg |
|
Stature (cm) |
181 ± 6defg | 185 ± 3cdefg | 176 ± 5bf | 176 ± 7ab | 175 ± 4ab | 169 ± 5abc | 172 ± 5ab |
|
BMI (kg/m2) |
21.2 ± 1.3bcf | 25.9 ± 1.8adeg | 24.6 ± 2.8adeg | 22.5 ± 2.7bcg | 20.9 ± 0.9bcf | 24.7 ± 0.6aeg | 20.6 ± 1.2bcdf |
|
MREE (kcal/die) |
1866 ± 142beg | 2195 ± 244acdefg | 1766 ± 188bde | 1928 ± 207bceg | 1567 ± 107abcdf | 1946 ± 127beg | 1641 ± 120abdf |
| RQ | 0.785 ± 0.031beg | 0.865 ± 0.046a | 0.815 ± 0.081 | 0.804 ± 0.049g | 0.850 ± 0.049a | 0.807 ± 0.082 | 0.870 ± 0.070ad |
|
BI-index (cm2/Ω) |
65.4 ± 8.0bg | 78.8 ± 8.3acdefg | 67.6 ± 7.7bg | 64.0 ± 8.7bg | 67.7 ± 6.3bg | 65.9 ± 5.7bg | 55.2 ± 5.0abcdef |
|
PhA (degrees) |
8.31 ± 0.79cdg | 8.11 ± 0.49c | 6.96 ± 0.54abdefg | 7.59 ± 0.60acf | 7.75 ± 0.53cf | 8.57 ± 0.65cdeg | 7.60 ± 0.38acf |
Data are expressed as mean ± standard deviation.
BMI body mass index, MREE measured resting energy expenditure, RQ respiratory quotient, BI-index bioimpedance index, PhA phase angle.
acycling; b water polo; c master swimming; d karate; e ballet dance; f boxing; g running
p < 0.05
Developing new predictive equations
Linear correlations showed that MREE of the athletes directly correlated with individual characteristics and raw BIA variables, except for age (r = − 0.124, p = 0.290). Actually, a strong correlation was found between MREE and body weight (r = 0.768, p < 0.001), followed by BMI (r = 0.623, p < 0.001), BI-index (r = 0.606, p < 0.001) as an index of FFM, stature (r = 0.489, p < 0.001) and PhA (r = 0.327, p = 0.004).
Then, multiple regression analysis was performed to assess the relationship between MREE and different sets of potential predictors. Basic anthropometric measures (weight, stature and BMI) and age (although not significant in bivariate analysis) were considered first in Model 1 to generate the following Eq. A:
| REE (kcal/day) = |
17.2 × Weight (kg) (1.5) 0.794 |
− 5.95 × Age (yrs) (1.9) − 0.218 |
+ 748 (117.9) |
(unstandardized regression coefficients with SE in brackets and beta coefficients in italics)
R2 = 0.637; SEE = 150 kcal/day.
When raw BIA variables (BI-index and PhA) were added to the Model 2, PhA was included whereas age was excluded from the model, developing the following Eq. B:
| REE (kcal/day) = |
16.3 × Weight (kg) (1.5) 0.755 |
+ 95.4 × PhA (degrees) (22) 0.291 |
− 93 (197) |
(unstandardized regression coefficients with SE in brackets, and beta coefficients in italics)
R2 = 0.675; SEE = 141 kcal/d.
Validation of predictive equations
To assess the accuracy of the new predictive equations, as well as of those selected from the literature, 51 athletes were randomly assigned to the validation group. Prediction accuracy at the population level was evaluated by PREE-MREE difference, mean bias and RMSE in kcal/day (Table 4).
Table 4.
Evaluation of new and selected predictive equations in athletes (validation group)
| REE predictive equations | Difference PREE-MREE kcal/d Mean (SD) |
Bias§, % | RMSE kcal/d |
|---|---|---|---|
| Equations for normal-weight subjects | |||
| HB | − 82 (146)* | − 3.9 | 107 |
| Schofield | − 93 (142)* | − 4.4 | 108 |
| FAO/WHO/UNU | − 92 (140)* | − 4.4 | 107 |
| Mifflin | − 141 (156)* | − 7.0 | 164 |
| Owen | − 222 (140)* | − 11.3 | 225 |
| Equations for athletes | |||
| De Lorenzo | 21 (173) | 2 | 94 |
| Wong | − 41 (153)* | −1.4 | 104 |
| Ten Haaf | 60 (152)* | 4 | 98 |
| Equation A | − 17 (134) | − 0.3 | 88 |
| Equation B | − 20 (124) | − 0.6 | 76 |
Average REE measured with indirect calorimetry = 1826 ± 234 kcal/d
REE resting energy expenditure, MREE measured resting energy expenditure, PREE predicted resting energy expenditure, RMSE root mean square error, HB Harris and Benedict, FAO Food and Agriculture Organization
§ Mean percentage error between predicted and measured REE; * p < 0.05
The new developed predictive formulas showed a mean bias < 1% (Eq. A − 0.3%; Eq. B − 0.6%) with the lowest RMSE values of 88 kcal (Eq. A) and 76 kcal (Eq. B); while REE seemed to be underestimated by most of the other equations, with the exception of those by De Lorenzo and ten Haaf (Table 4). Overall, the PREE-MREE difference was < 100 kcal/day for the HB, FAO, Schofield, De Lorenzo, Wong and ten Haaf equations. The mean bias was as follows: HB − 3.9%; Schofield + 4.4%; FAO − 4.4%; De Lorenzo + 2%; Wong − 1.4% and ten Haaf + 4%), and greater for the Mifflin (− 7%) and Owen (− 11.3%) equations.
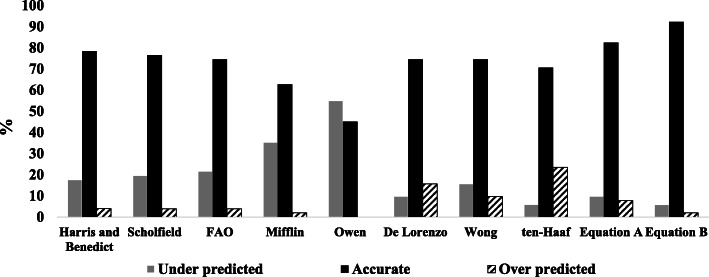
(As shown in Fig. 1) the precision accuracy at the individual level (percentage of athletes with a PREE within ±10% of MREE) was higher for the new equations (Eq. A 82.4%, Eq. B 92.2%) compared to those selected from the literature (~ 45% for the Owen, ~ 65% for the Mifflin and ~ 75% for the Harris-Benedict, FAO, Schofield, De Lorenzo, Wong and ten Haaf equations).
Fig. 1.
Accuracy of prediction equations for measurements of resting energy expenditure within ±10%
Bland-Altman plots of PREE-MREE differences
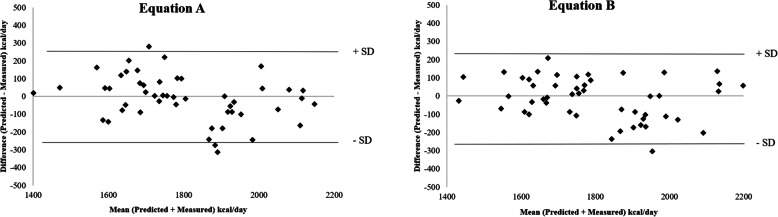
Lastly, the Bland-Altman method was used to quantify the agreement between PREE and MREE. Figure 2 shows that the best agreement was found for the new formulas. For the other equations, the 95% limits of agreement were wider (+/− 200–300 kcal/d) with the largest values observed for the Mifflin and Owen equations.
Fig. 2.
Bland - Altman plots between differences and mean predicted-measured resting energy expenditure using new equations
Discussion
The primary purpose of this study was to develop and cross-validate new equations for estimating REE in a group of elite male athletes of different sport specialties, and then to compare them with existing formulas. The new equations provide the best prediction of REE in the validation group, with the use of BIA-derived PhA significantly improving the prediction power of the equation.
Meeting energy requirements is a priority of athletes. Inadequate energy intake might compromises performance and reduces the benefits of training [1, 2]. Energy needs are usually estimated by REE multiplied by the appropriate activity factor. To date, only a few number of predictive equations for REE have been specifically developed for athletes [15–18]. De Lorenzo formula [15] was derived in a sample of 51 male athletes (22 water polo, 12 judo, 17 karate) who exercised at least 3 h/day; in that paper REE was underestimated by most of the seven equations selected from the literature. Later, Wong et al. [16] proposed sex-specific predictive formulas for elite Malaysian athletes in most cases practicing combat sports. Of note, Malaysian population seemed to have relatively low body frames and size and, therefore, low REE [16]. They found that mean resting energy expenditure measured by indirect calorimetry were similar in males to values predicted using the HB [7], FAO [9] and De Lorenzo [15] equations; indeed the accuracy of the predictive formulas was not evaluated. Also, ten Haaf et al. [17] developed two predictive equations for recreational athletes practicing > 3 h/day two times a week, the first formula being based on weight, the second one on FFM (determined using pletismography). Authors pointed out that the weight-based equation had a higher precision accuracy (83% for males) compared to the De Lorenzo formula (77.4% for males). Finally, Watson et al. [18] derived two formulas in a sample of 66 collegiate female athletes from eleven different sports; the first equation was based on weight, the second one on FFM (estimated by skinfold thickness). Authors stated that both equations were more accurate for resting metabolic rate estimation in their population but did not evaluate bias or precision accuracy. Jagim et al. [5] did not derive new formulas but determined the accuracy of several predictive equations for REE in both male and female athletes; most of the five equations selected from the literature underestimated REE in both sexes. Of the previous studies, only the one by Watson et al. [18] described the relationships between REE and age or different anthropometric variables, showing that age was not related to REE while the best predictor was body weight (r = 0.590). These results are confirmed in our study since body weight was the best predictor (r = 0.768) while there was no association with age. Some authors also introduced FFM as predictor, with no increase in the prediction power [17, 18].
In the present study, first we developed an equation based on age and main anthropometric variables (weight, stature, and BMI) (Model 1, Eq. A). In addition to age, weight emerged as the only significant predictor. Two of the existing formulas for athletes identified also stature as predictor [15, 17] while in the athletes we studied, REE was correlated to stature in univariate analysis, but not in multiple regression analysis, p = 0.374).
Instead of using BIA-derived body composition (strictly dependent on the BIA formula used), we opted for including raw BIA variables (BI-index and PhA) in the regression model (Model 2, Eq. B).
BI-index is directly related to FFM and quite always included as predictor in the BIA equations to predict FFM. More recently, attention has been focused on the role of PhA as a biomarker of body cell mass and muscle quality as well as of water distribution (ratio between extracellular water-ECW and intracellular water-ICW) [22]. Thus, high PhA indicates greater cellularity (e.g. more body cell mass relative to FFM), cellular integrity and cell functions [22]. It may represent a proxy parameter of muscle quality in athletes, being significantly associated with physical activity and muscle strength [35, 36]. A recent systematic review showed that PhA was higher in athletes vs controls whereas it was still uncertain to what extent PhA differs among various sports [37]. In addition, PhA may help in detecting low muscle quality and identifying sarcopenia [38]. In previous studies, we also found that both BI-index and PhA improved the prediction power of REE under physiological conditions [24]. The findings of the present paper confirmed that PhA was as a significant predictor along with weight, with R2 increasing from 0.637 to 0.675 and SEE decreasing from 150 to 141 kcal/day. On the contrary, BI-index was not recognized as a stronger predictor than weight, possibly because of low body fat percentage and low BMI. In general, for those with no access to BIA, only age and weight values are sufficient for predicting REE in male elite athletes.
As additional aim, we validated the two new equations and eight formulas selected from the literature (5 for the general population and 3 for athletes), at both population and individual level. On the average, the accuracy was very good for our new formulas, since bias ranged within ±1%. Similarly, most of the selected equations, except the Mifflin and Owen ones, showed an acceptable prediction accuracy (bias ±5%).
From a practical point of view, evaluating the accuracy of predictive equations at individual level (within ±10%) is crucial for the nutritional management of the single athlete. This study shows that precision was high for the new formulas, especially for Eq. B (~ 92%) including PhA in the model while it was lower, being close to 75%, for most of the other formulas (with the exception of the Mifflin and Owen ones for which it was much lower). Looking at the Bland-Altman plots, most of the prediction equations were more accurate at lower ranges of MREE and less accurate with the higher REE values. The new formulas gave the narrowest limits of agreement and the lowest bias.
To the best of authors’ knowledge, this is the first study that developed and cross-validate equations for elite athletes to predict REE based not only on anthropometric measures, but also on raw BIA variables. Overall, we conducted this study in a reasonable large sample of individuals, using recognized and well-documented methods and in line with similar previous studies in healthy subjects. Furthermore, the assessment of BIA with the same device has limited the device-related changes in PhA. Nevertheless, these findings are subject by a number of limitations. Since this is a retrospective study, our findings need to be confirmed in larger samples and in different sports disciplines. Additionally, we studied elite athletes mostly practicing endurance sports. Lastly, female athletes were excluded from the analysis due to the small number of potential participants (n = 27); therefore, we have developed new athlete-specific predictive equations for estimating REE in elite male athletes only.
Conclusions
As main finding, in elite athletes BIA-derived PhA is a significant predictor of REE and improved the prediction power of the model. The new equations exhibited a very good accuracy at population level, while precision at the individual level was markedly higher compared to that reported by previous studies in the general population as well as athletes. However, the use of PhA as predictor of REE requires further research with respect to different sport specialties, training programs and training level.
Acknowledgements
Not applicable.
Abbreviations
- BI-Index
Bioimpedance Index
- BIA
Bioelectrical Impedance Analysis
- BMI
Body Mass Index
- ECW
Extracellular Water
- FAO
Food and Agriculture Organization
- FFM
Fat-Free Mass
- FM
Fat Mass
- HB
Harris and Benedict
- ICW
Intracellular Water
- MREE
Measured Resting Energy Expenditure
- PhA
Phase Angle
- PREE
Predicted Resting Energy Expenditure
- REE
Resting Energy Expenditure
- TBW
Total Body Water
Authors’ contributions
MM and ODV formulated the study concept and design. MM, ODV and RS acquired data used in the study and assisted in the interpretation of this data. MM, LS and ODV interpreted data, drafted the manuscript, and completed the data analysis and interpretation. IC, RS and DM helped advise the direction of the manuscript and made substantial revisions. Each author has read and approved the final manuscript prior to submission.
Funding
Not applicable.
Availability of data and materials
All data pertaining to the conclusions of the study are found within the article. The corresponding data set used is available under reasonable requests.
Declarations
Ethics approval and consent to participate
This study was conducted in accordance with the Declaration of Helsinki and was approved by the Federico II University Ethical Committee.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Maurizio Marra and Olivia Di Vincenzo contributed equally to this work.
References
- 1.Thomas DT, Erdman KA, Burke LM. American College of Sports Medicine joint position statement. Nutrition and athletic performance. Med Sci Sports Exerc. 2016;48(3):543–568. doi: 10.1249/MSS.0000000000000852. [DOI] [PubMed] [Google Scholar]
- 2.Rodriguez NR, DiMarco NM. Langley S, American dietetic association, dietitians of Canada, American College of Sports Medicine: nutrition and athletic performance. Position of the American dietetic association, dietitians of Canada, and the American College of Sports Medicine: nutrition and athletic performance. J Am Diet Assoc. 2009;109(3):509–527. doi: 10.1016/j.jada.2009.01.005. [DOI] [PubMed] [Google Scholar]
- 3.Trexler ET, Smith-Ryan AE, Norton LE. Metabolic adaptation to weight loss: implications for the athlete. J Int Soc Sports Nutr. 2014;11(1):7. doi: 10.1186/1550-2783-11-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Melin AK, Heikura IA, Tenforde A, Mountjoy M. Energy availability in athletics: health, performance, and physique. Int J Sport Nutr Exerc Metab. 2019;29(2):152–164. doi: 10.1123/ijsnem.2018-0201. [DOI] [PubMed] [Google Scholar]
- 5.Jagim AR, Camic CL, Kisiolek J, Luedke J, Erickson J, Jones MT, Oliver JM. Accuracy of resting metabolic rate prediction equations in athletes. J Strength Conditioning Res. 2018;32(7):1875–1881. doi: 10.1519/JSC.0000000000002111. [DOI] [PubMed] [Google Scholar]
- 6.Marra M, Montagnese C, Sammarco R, Amato V, Della Valle E, Franzese A, et al. Accuracy of Predictive Equations for Estimating Resting Energy Expenditure in Obese Adolescents. J Pediatr. 2015;166:1390–1396.e1. doi: 10.1016/j.jpeds.2015.03.013. [DOI] [PubMed] [Google Scholar]
- 7.Harris JA, Benedict FG. A biometric study of human basal metabolism. Proc Natl Acad Sci U S A. 1918;4(12):370–373. doi: 10.1073/pnas.4.12.370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schofield WN. Predicting basal metabolic rate, new standards and review of previous work. Hum Nutr Clin Nutr. 1985;39(Suppl 1):5–41. [PubMed] [Google Scholar]
- 9.Energy and protein requirements Report of a joint FAO/WHO/UNU Expert Consultation. World Health Organ Tech Rep Ser. 1985;724:1–206. [PubMed] [Google Scholar]
- 10.Mifflin MD, St Jeor ST, Hill LA, Scott BJ, Daugherty SA, Koh YO. A new predictive equation for resting energy expenditure in healthy individuals. Am J Clin Nutr. 1990;51(2):241–247. doi: 10.1093/ajcn/51.2.241. [DOI] [PubMed] [Google Scholar]
- 11.Owen OE, Holup JL, D’Alessio DA, Craig ES, Polansky M, Smalley KJ, Kavle EC, Bushman MC, Owen LR, Mozzoli MA. A reappraisal of the caloric requirements of men. Am J Clin Nutr. 1987;46(6):875–885. doi: 10.1093/ajcn/46.6.875. [DOI] [PubMed] [Google Scholar]
- 12.Ribeyre J, Fellmann N, Montaurier C, Delaître M, Vernet J, Coudert J, Vermorel M. Daily energy expenditure and its main components as measured by whole-body indirect calorimetry in athletic and non-athletic adolescents. Br J Nutr. 2000;83(4):355–362. [PubMed] [Google Scholar]
- 13.Poehlman ET, Melby CL, Badylak SF. Resting metabolic rate and postprandial thermogenesis in highly trained and untrained males. Am J Clin Nutr. 1988;47(5):793–798. doi: 10.1093/ajcn/47.5.793. [DOI] [PubMed] [Google Scholar]
- 14.Melby CL, Schmidt WD, Corrigan D. Resting metabolic rate in weight-cycling collegiate wrestlers compared with physically active, noncycling control subjects. Am J Clin Nutr. 1990;52(3):409–414. doi: 10.1093/ajcn/52.3.409. [DOI] [PubMed] [Google Scholar]
- 15.De Lorenzo A, Bertini I, Candeloro N, Piccinelli R, Innocente I, Brancati A. A new predictive equation to calculate resting metabolic rate in athletes. J Sports Med Phys Fitness. 1999;39(3):213–219. [PubMed] [Google Scholar]
- 16.Wong JE, Poh BK, Shanita SN, Izham MM, Chan KQ, Tai MD, et al. Predicting basal metabolic rates in Malaysian adult elite athletes. Singapore Medical Journal. 2012;53:744–9. [PubMed]
- 17.ten Haaf T, Weijs PJM. Resting Energy Expenditure Prediction in Recreational Athletes of 18–35 Years: Confirmation of Cunningham Equation and an Improved Weight-Based Alternative. Alemany M, editor. PLoS One. 2014;9:e108460. [DOI] [PMC free article] [PubMed]
- 18.Watson AD, Zabriskie HA, Witherbee KE, Sulavik A, Gieske BT, Kerksick CM. Determining a resting metabolic rate prediction equation for collegiate female athletes. J Strength Conditioning Res. 2019;33(9):2426–2432. doi: 10.1519/JSC.0000000000002856. [DOI] [PubMed] [Google Scholar]
- 19.Gallagher D, Visser M, Wang Z, Harris T, Pierson RN, Heymsfield SB. Metabolically active component of fat-free body mass: influences of age, adiposity, and gender. Metabolism. 1996;45(8):992–997. doi: 10.1016/S0026-0495(96)90269-3. [DOI] [PubMed] [Google Scholar]
- 20.Campa F, Toselli S, Mazzilli M, Gobbo LA, Coratella G. Assessment of body composition in athletes: a narrative review of available methods with special reference to quantitative and qualitative bioimpedance analysis. Nutrients. 2021;13(5):1620. doi: 10.3390/nu13051620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kyle UG, Bosaeus I, De Lorenzo AD, Deurenberg P, Elia M, Manuel Gómez J, et al. Bioelectrical impedance analysis-part II: utilization in clinical practice. Clin Nutr. 2004;23(6):1430–1453. doi: 10.1016/j.clnu.2004.09.012. [DOI] [PubMed] [Google Scholar]
- 22.Lukaski HC, Kyle UG, Kondrup J. Assessment of adult malnutrition and prognosis with bioelectrical impedance analysis: phase angle and impedance ratio. Curr Opin Clin Nutr Metab Care. 2017;20(5):330–339. doi: 10.1097/MCO.0000000000000387. [DOI] [PubMed] [Google Scholar]
- 23.Norman K, Stobäus N, Pirlich M, Bosy-Westphal A. Bioelectrical phase angle and impedance vector analysis--clinical relevance and applicability of impedance parameters. Clin Nutr. 2012;31(6):854–861. doi: 10.1016/j.clnu.2012.05.008. [DOI] [PubMed] [Google Scholar]
- 24.Marra M, Sammarco R, Cioffi I, Morlino D, Di Vincenzo O, Speranza E, Pasanisi F. New predictive equations for estimating resting energy expenditure in subjects with normal weight and overweight. Nutrition. 2021;84:111105. 10.1016/j.nut.2020.111105. [DOI] [PubMed]
- 25.Marra M, Cioffi I, Sammarco R, Santarpia L, Contaldo F, Scalfi L, et al. Are raw BIA variables useful for predicting resting energy expenditure in adults with obesity? Nutrients. 2019;11(2). 10.3390/nu11020216. [DOI] [PMC free article] [PubMed]
- 26.Marra M, Cioffi I, Morlino D, Vincenzo OD, Pagano MC, Imperatore N, Alfonsi L, Santarpia L, Castiglione F, Scalfi L, Pasanisi F. New predictive equations for estimating resting energy expenditure in adults with Crohn’s disease. J Parenter Enter Nutr. 2020;44(6):1021–1028. doi: 10.1002/jpen.1790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Swann C, Moran A, Piggott D. Defining elite athletes: issues in the study of expert performance in sport psychology. Psychol Sport Exerc. 2015;16:3–14. doi: 10.1016/j.psychsport.2014.07.004. [DOI] [Google Scholar]
- 28.Elia M, Livesey G. Theory and validity of indirect calorimetry during net lipid synthesis. Am J Clin Nutr. 1988;47(4):591–607. doi: 10.1093/ajcn/47.4.591. [DOI] [PubMed] [Google Scholar]
- 29.Compher C, Frankenfield D, Keim N, Roth-Yousey L. Evidence analysis working group. Best practice methods to apply to measurement of resting metabolic rate in adults: a systematic review. J Am Diet Assoc. 2006;106(6):881–903. doi: 10.1016/j.jada.2006.02.009. [DOI] [PubMed] [Google Scholar]
- 30.Fullmer S, Benson-Davies S, Earthman CP, Frankenfield DC, Gradwell E, Lee PSP, et al. Evidence analysis library review of best practices for performing indirect calorimetry in healthy and non-critically ill individuals. J Acad Nutr Diet. 2015;115:1417–1446.e2. doi: 10.1016/j.jand.2015.04.003. [DOI] [PubMed] [Google Scholar]
- 31.Weir JB de V. New methods for calculating metabolic rate with special reference to protein metabolism. J Physiol. 1949;109(1-2):1–9. doi: 10.1113/jphysiol.1949.sp004363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Frankenfield DC, Rowe WA, Smith JS, Cooney RN. Validation of several established equations for resting metabolic rate in obese and nonobese people. J Am Diet Assoc. 2003;103(9):1152–1159. doi: 10.1016/S0002-8223(03)00982-9. [DOI] [PubMed] [Google Scholar]
- 33.Frankenfield D, Roth-Yousey L, Compher C. Comparison of predictive equations for resting metabolic rate in healthy nonobese and obese adults: a systematic review. J Am Diet Assoc. 2005;105(5):775–789. doi: 10.1016/j.jada.2005.02.005. [DOI] [PubMed] [Google Scholar]
- 34.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–310. doi: 10.1016/S0140-6736(86)90837-8. [DOI] [PubMed] [Google Scholar]
- 35.Di Vincenzo O, Marra M, Sammarco R, Speranza E, Cioffi I, Scalfi L. Body composition, segmental bioimpedance phase angle and muscular strength in professional volleyball players compared to a control group. J Sports Med Physical Fitness. 2020;6:870–874. doi: 10.23736/S0022-4707.20.10548-6. [DOI] [PubMed] [Google Scholar]
- 36.Marra M, Di Vincenzo O, Sammarco R, Morlino D, Scalfi L. Bioimpedance phase angle in elite male athletes: a segmental approach. Physiol Meas. 2020;12(12):125007. doi: 10.1088/1361-6579/abcb5c. [DOI] [PubMed] [Google Scholar]
- 37.Di Vincenzo O, Marra M, Scalfi L. Bioelectrical impedance phase angle in sport: a systematic review. J Int Soc Sports Nutr. 2019;16(1):49. doi: 10.1186/s12970-019-0319-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Di Vincenzo O, Marra M, Di Gregorio A, Pasanisi F, Scalfi L. Bioelectrical impedance analysis (BIA) -derived phase angle in sarcopenia: a systematic review. Clin Nutr. 2021;40(5):3052–3061. doi: 10.1016/j.clnu.2020.10.048. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data pertaining to the conclusions of the study are found within the article. The corresponding data set used is available under reasonable requests.