Effect of different preconditioning protocols on the viscoelastic inflation response of the posterior sclera

Abstract

Preconditioning by repeated cyclic loads is routinely used in ex vivo mechanical testing of soft biological tissues. The goal of preconditioning is to achieve a steady and repeatable mechanical response and to measure material properties that are representative of the in vivo condition. Preconditioning protocols vary across studies, and their effect on the viscoelastic response of tested soft tissue is typically not reported or analyzed. We propose a methodology to systematically analyze the preconditioning process with application to inflation testing. We investigated the effect of preconditioning on the viscoelastic inflation response of tree shrew posterior sclera using two preconditioning protocols: (i) continuous cyclic loading-unloading without rest and (ii) cyclic loading-unloading with 15-min rest between cycles. Posterior scleral surface strain was measured using three-dimensional Digital Image Correlation (3D-DIC). We used five variables of characterizing features of the stress-strain loop curve to compare the two preconditioning protocols. Our results showed protocol-dependent differences in the tissue response during preconditioning and at the preconditioned state. Incorporating a resting time between preconditioning cycles significantly decreased the number of cycles (10.5 ± 2.9 cycles vs. 3.1 ± 0.5 cycles, p<0.001) but increased the total time (15.8 ± 4.4 min vs. 51.2 ± 8.3 min, p<0.001) needed to reach preconditioned state. At the preconditioned state, 2 of 5 characteristic variables differed significantly between protocols: hysteresis loop area (difference=0.023 kJ/m³, p=0.0020) and elastic modulus at high IOP (difference=24.0 MPa, p=0.0238). Our results suggest that the analysis of the preconditioning process is an essential part of inflation experiments and a prerequisite to properly characterize the tissue viscoelastic response. Furthermore, material properties obtained at the preconditioned state can be impacted by the resting time used during preconditioning and may not be directly compared across studies if the resting time varies by 15 min between studies.

1. Introduction

In the mechanical characterization of soft biological tissues, it is common practice to apply repeated cyclic loads to obtain a steady and repeatable response that can be used to measure the mechanical properties of the tissue and objectively compare the obtained results across studies [1]. The practice of applying to the tissue loading-unloading cycles before the actual mechanical test is referred to as preconditioning. The effect of preconditioning typically involves changes in the viscoelastic response including a rightward shift (softening) of the stress-strain response towards higher strains, increased stiffness, decreased hysteresis loop area (area included between loading and unloading curves), and an accumulation of residual strains [1]. The goal of preconditioning is to reach, after a transient stage, a preconditioned or steady state, where the mechanical response becomes repeatable [1–4]. Though this procedure is commonly performed, the mechanical response during preconditioning or briefly preconditioning response, is often excluded from the mechanical characterization of the tissue. Mechanical testing protocols vary greatly in scleral biomechanics. Viscoelastic properties were measured immediately after the tissue preconditioning cycles [5–7], after recovery periods of 10 sec [8], 60 sec [9], 360 sec [10,11], 15 min [12–14], 30 min [15,16] or unspecified [5,17]. The number of the loading-unloading cycles varies greatly even among studies that used the same mechanical testing scheme: 9 [7], 10 [6,9,10], 50 [18,19], and 10-cycle preconditioning repeated twice [20] for uniaxial test; two-stage preconditioning protocol [21] or unreported [13] for biaxial test; and 5 [11,15], 9 [22], 10 [14,23], 20 cycles [16,17,24] were used for inflation tests.

A commonly accepted methodology to analyze the preconditioning response by defining characteristic features of the viscoelastic response does not exist, along with a definition of when the response reaches preconditioned state. Grytz et al. [18] analyzed the preconditioning response of scleral strips taken from juvenile tree shrews using the strain at the maximum load (peak strain) and the change of that strain from one loading cycle to the next. The authors used the cycle-dependent change of only one strain variable (incremental peak strain) to define the cycle at which a preconditioned state was reached. The authors found that, in physiological loading conditions (IOP < 60 mmHg), the preconditioning response did not stabilize during 50 cycles. By a polynomial regression model, they estimated that the sclera strips would be reached a preconditioned state after 135 cycles which is over the 50 cycles applied. Additionally, at supraphysiological loading conditions (IOP < 600 mmHg), the response never reached a preconditioned state. In both cases, strain measurement uncertainty was not included in the analysis to define a repeatable response. This could lead to overestimating the number of cycles at which the response reaches a preconditioning state. Furthermore, using only one variable to analyze the preconditioning process does not ensure that all features of the stress-strain response (i.e. hysteresis or elastic modulus) reach a repeatable state and may result in an underestimated number of cycles needed to reach a fully preconditioned state. The same method was applied to compare the preconditioning responses of scleras obtained from tree shrews with experimental myopia and after scleral crosslinking [19]. A cycle-dependent change of less than 2% in maximum strain was used in [22] to define the cycle at which the preconditioned state was reached, but no consideration of statistical significance was incorporated. All the aforementioned studies applied continuous cyclic loads to precondition scleral tissues without rest between cycles.

An alternative preconditioning protocol consisting of repeated loading cycles with a 15-min rest period between cycles was applied by Myers et al. [25], Coudrillier et al. [26], and Tonge et al. [27] and largely investigated by Tonge et al. [28]. Tonge et al. [28] have shown that the viscoelastic response of inflated porcine and bovine scleras (as well as human skin and bovine cornea) exhibited minimal changes during a 3-cycle preconditioning protocol by graphically comparing the stress-strain loop curves and quantifying the differences between the strain peaks at the maximum load. Thus, the authors showed that a repeatable response can be achieved by applying a rest period between cycles, reporting that 15 min were sufficient to completely recover the viscoelastic properties after each loading-unloading cycle. Moreover, in some follow-up studies [29–31], scleral specimens were not preconditioned based on the minimal preconditioning effect reported by Tonge et al. [28]. However, the results of Tonge et al. were not confirmed, and it remains unclear if these effects were negligible in these studies. The analysis presented in [28] was limited to one specimen for each species, leaving the question open of whether or not the applied rest period for the full viscoelastic recovery of the response can be generalized to other species and if the preconditioning effects can be minimized by applying a 3-cycle protocol. Thus, we have included this protocol in our investigation to test its reported minimal preconditioning effect and to compare it to a commonly used protocol. In conclusion, a standardized preconditioning protocol and a systematic analysis strategy of the preconditioning process are missing. This standardization is difficult to be accomplished because of the complexity and variety among mechanical testing methodologies (uniaxial, biaxial, inflation), species, age, disease, analysis purpose, and loading protocols (i.e. upper and lower limits, loading rate, the rest period between cycles or no rest). Furthermore, to the best knowledge of the authors, the effect of using different preconditioning protocols on the mechanical response at the preconditioned state in inflation testing has never been investigated. In this study, we propose an objective methodology to analyze the preconditioning process. We applied our proposed methodology to compare two preconditioning protocols: continuous cycling preconditioning (CCP) and rested cycling preconditioning (RCP). The two protocols were performed on five juvenile tree shrew posterior scleras undergoing inflation testing with scleral surface deformations measured by three-dimensional Digital Image Correlation (3D-DIC). We investigated the effect of the two protocols on the mechanical response during preconditioning and at the preconditioned state.

2. Materials and methods

2.1. Animal model and specimen preparation

We used tree shrews (Tupaia glis belangeri) that were bred and raised in a colony at the University of Alabama at Birmingham in accordance with The American Association for the Advancement of Laboratory Animal Care guidelines. The presented work is part of a larger study on scleral remodeling in myopia that involved the use of tree shrews as a translational animal model of myopia [18,19,32]. The overall goal of this investigation is to identify the mechanisms that underlie scleral remodeling and biomechanical weakening in myopia and to evaluate and develop novel treatment strategies that target the sclera for myopia control. Five juvenile animals (35 days after eye opening) were euthanized with a lethal injection of xylazine anesthesia, and both eyes were enucleated and stored in phosphate buffered saline (PBS) at 4°C. Each eye was tested under both preconditioning protocols, performing the first test within 48 hours after enucleation and the second after another 24 hours to allow full mechanical recovery [33]. As pointed out by Carew et al. [33], the strain history could affect the estimations of the material properties if adequate recovery time were not allowed or if permanent deformations were introduced during the first mechanical test. The testing order was randomly assigned to the specimens. A total of n=10 eyes were tested, 5 left and 5 right eyes. Of the 10 samples, 5 eyes underwent both protocols, 2 eyes were tested only with the CCP protocol (n_CCP=7), 1 only with the RCP protocol (n_RCP=6), and 2 were excluded because of failure occurring during the first test (leakage from the scleral surface or the ONH). In terms of eye pairs, 3 pairs were tested by CCP, 2 pairs by RCP, and 2 by both protocols. For inflation testing, each eye was set in a conical hole of a metal disk (washer) that was designed to hold the eye sample at the limbus-anterior sclera region with minimal boundary effects, with the largest diameter of the conical hole (7 mm) being smaller than that of the eyeball’s equatorial diameter (~ 9 mm). The eye specimen was set to have its optical axis perpendicular to the washer’s plane. The specimen was held in place by carefully gluing it onto the washer in that region with a clamping length of ~ 2.2 mm (Fig. 1a,b). After gluing, the cornea was trephined through the washer’s hole (3 mm diameter, ~1 mm depth of cut), the lens and vitreous removed – allowing the scleral shell to be pressurized by PBS in-flow – and the washer mounted on the pressurization chamber. These procedures were conducted by a trained operator using a surgical microscope. After completion of the first protocol, the specimen was stored at 4°C while remaining mounted to the pressurization chamber, with PBS filling the inside of the shell and a gauze pad soaked in PBS covering the outside of the specimen.

Fig. 1.

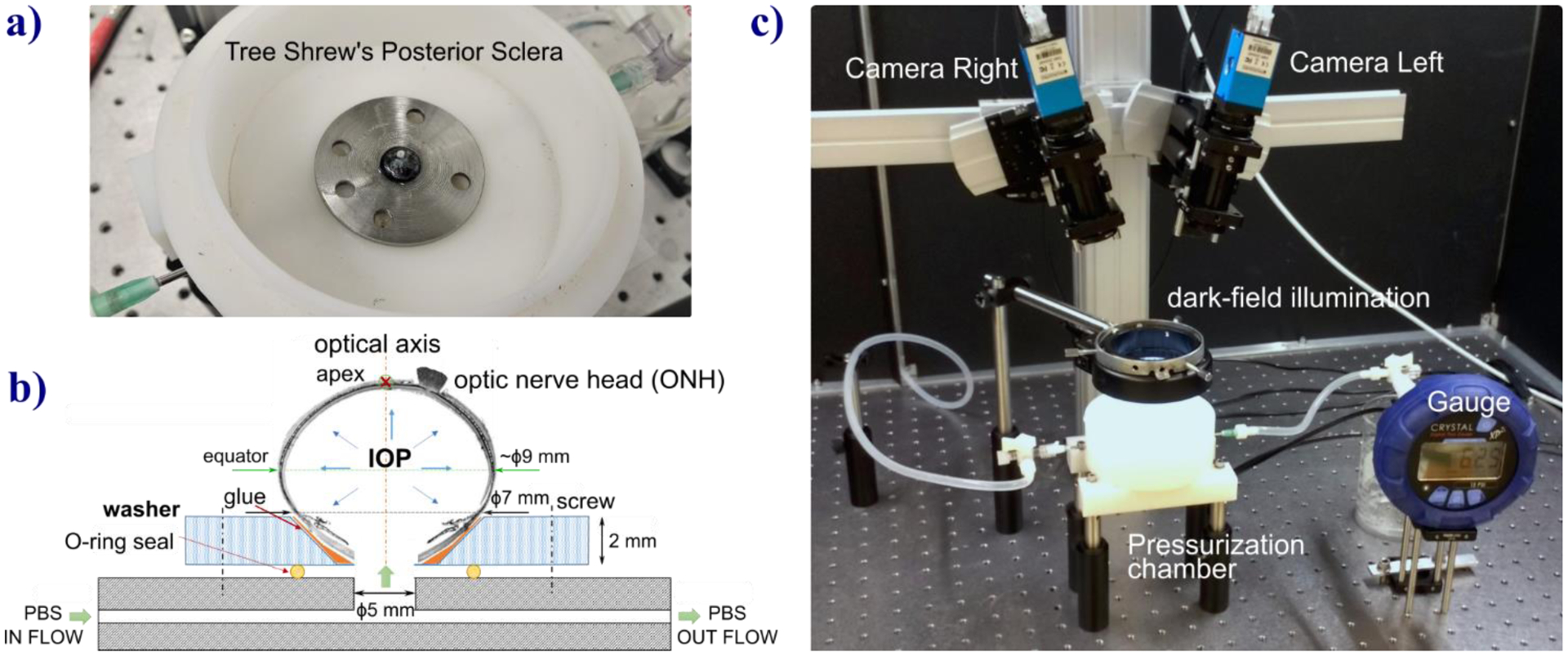
Setup for inflation testing of tree shrew scleral shells. a) Tree shrew sclera shell glued to stainless steel washer and placed into the pressurization chamber. b) Scheme of the PBS flow used to pressurize the scleral shell. c) The optical stereo system used to apply 3D-DIC method that images the sclera surface illuminated by a LED ring for dark-field illumination. A pressure gauge is connected to the chamber and used for continuous IOP recording during the experiment.

2.2. Preconditioning protocols and inflation testing

During the CCP protocol, scleral shells underwent 20 continuous loading-unloading cycles without rest (Fig. 2a). 20 cycles were chosen as it is the highest number of cycles proposed in the literature for inflation testing [16,24,34]. For the RCP protocol, we followed a variant of the rested cycling preconditioning protocol proposed by Tonge et al. [28], which included a 15-min rest period between cycles. In contrast to the 3-cycle protocol used by Tonge et al. [28], we applied 2 additional cycles (5 cycles in total) with the same resting time (Fig. 2b) to evaluate the persistence of the minimal preconditioning effects demonstrated by the authors. Some preliminary tests have been conducted to set the loading parameters. After some preliminary tests, the baseline pressure was set under the physiological IOP of ~12 mmHg measured in anesthetized tree shrews [32] to 5 mmHg to avoid buckling of the scleral shell; maximum pressure was set to 50 mmHg in order to measure the typical J-shaped response of biological tissues, obtaining a linear region at high IOPs that allows accurate measurement of the elastic modulus, as reported in detail in Section 3.1. Although 50 mmHg is a higher value than that which can occur during physiological conditions such as blinks, saccades, and ocular pulses (14 mm Hg above baseline [35]), it is much lower than 300 mmHg that can occur during eye rubbing [36]. Furthermore, similar or higher IOP levels have been commonly used throughout existing studies [23–25,37] that performed ex vivo mechanical test on scleral tissues. Pressure was changed at a rate of 1 mmHg/sec during loading and unloading resulting in a total testing time of 30 min for the CCP and 82.5 min for the RCP protocol. Pressure inside the shell was measured using a Crystal XP2i pressure gauge (0.1% reading accuracy, Fig.1c) connected to the pressurization chamber placed at the same level as the center of the shell and was controlled via hydrostatic pressure applied by a reservoir mounted on a motorized vertical stage. During the preconditioning protocols, the deformation of the scleral surface was measured by 3D-DIC method that allows for prolonged imaging protocol providing micrometric accuracy of the deformation [38]. For this purpose, a stereo camera system (The Imaging Source - DMK 23G445 GigE, 1280×960 pixel, monochrome 1/3 inch Sony CCD sensor) was built (Fig. 1c), configuring the cameras with a 30° pan angle, 10 × 12 mm field of view and ~5mm depth of field. The scleral shell was illuminated by an LED ring placed near the shell to provide dark-field illumination for taking high-contrast images with uniform illumination of the surface. The scleral surface was painted with a thin mixture of cosmetic oil and titanium dioxide powder. The mixture served two purposes: the oil prevented tissue dehydration during mechanical testing, and the titanium dioxide enhanced image contrast of the surface. Activated charcoal powder was sprayed on the scleral surface to create a speckled texture required by the 3D-DIC method [39] (see Fig. 3a). A sequence of stereo-pair images was captured at 1 Hz during each protocol. Humidity and room temperature were kept stable at 50% and 22°C during testing, respectively.

Fig. 2.

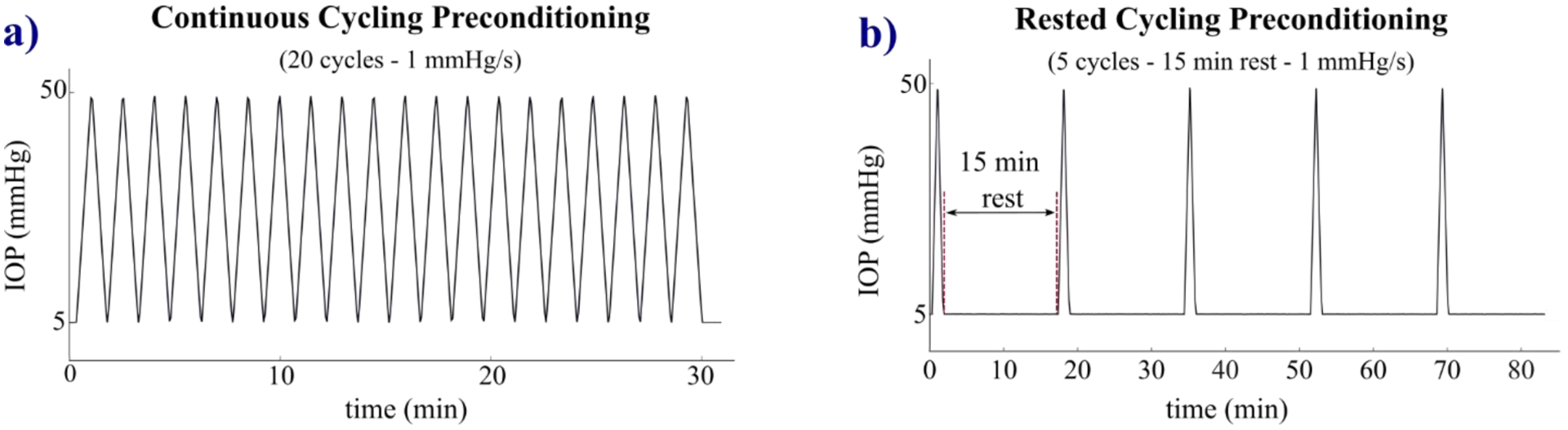
The two loading protocols used to precondition the tree shrew sclera shells. a) continuous cycling preconditioning consisting of 20 cycles without rest periods between cycles; b) rested cycling preconditioning consisting of 5 cycles with 15-min rest between cycles to allow the recovery of the response.

Fig. 3.

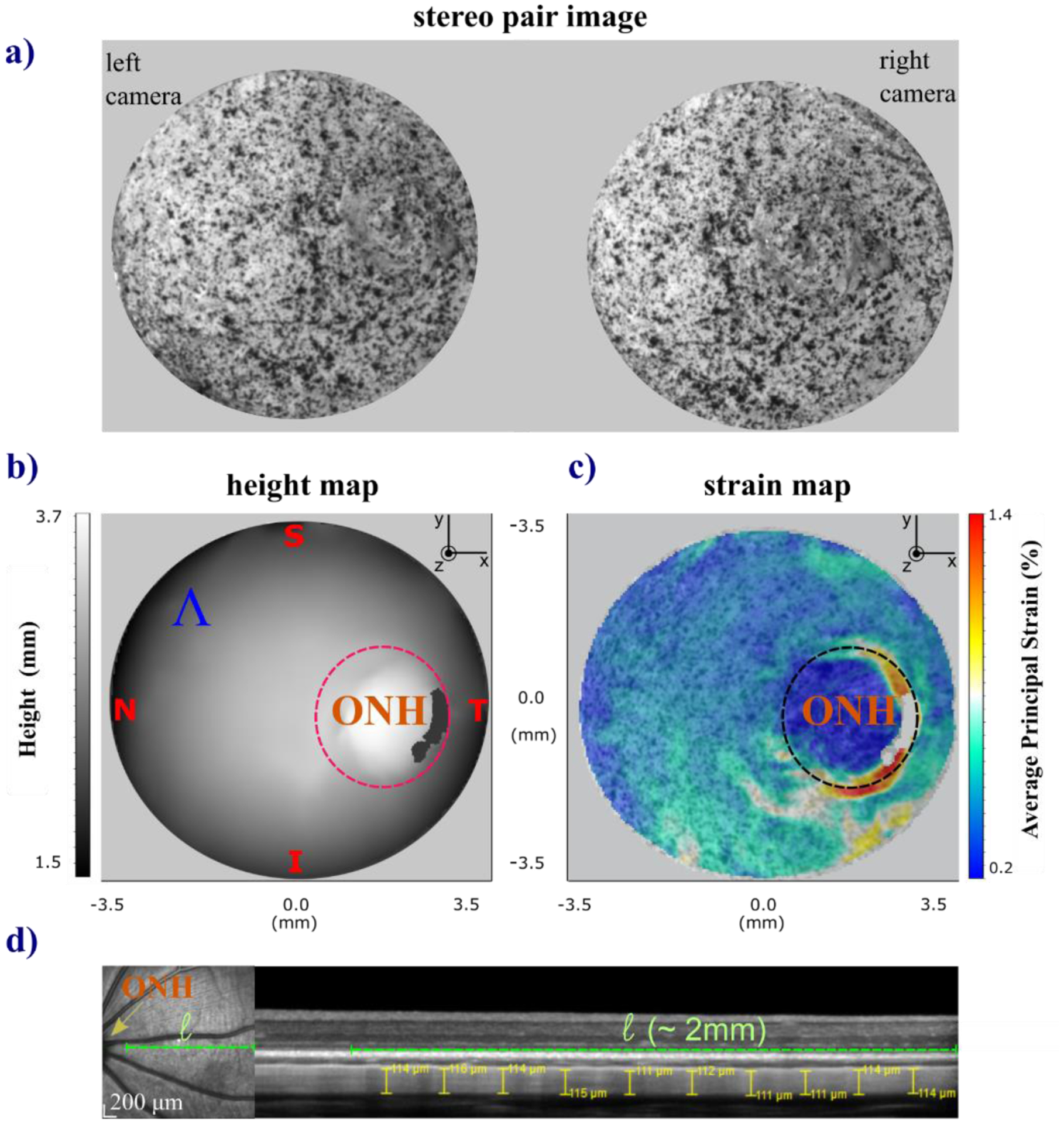
Schematic of the 3D-DIC images collected and calculated measures of the tree shrew scleral shells during inflation testing and OCT scan for scleral thickness measurement. One representative case, the scleral shell of a right eye is shown. The shell was placed on the pressurization chamber by orienting the ocular regions (T=temporal, N=nasal, S=superior, and I=inferior) along the coordinate axes. From a sequence of paired stereo images of the sclera surface with painted speckled texture (a) the LaVision-DaVis software calculates the height (b) and average principal strain maps (c). The ONH area was excluded from the best-fitting sphere to calculate the mean radius (R) of each shell and from the average strain (ε) calculation. (d) En-face scanning laser ophthalmoscopy image (on the left) showing the location of the OCT B-Scan (dashed green line). The ONH and posterior pole are near the left and right hand side of the image, respectively. 30 degree wide OCT scan using enhanced depth imaging (on the right). Ten thickness measurements near the posterior pole were obtained using the manual measurement tool of the Heidelberg Spectralis software.

The overall acquisition procedure during each testing protocol was controlled by custom code written in Labview (National Instruments, Austin, TX). Validation of the scleral surface preparation, IOP, and 3D-DIC measurements is presented in the Appendix.

2.3. Average strain and stress calculation of scleral surface

The sequences of stereo-pair images taken during the preconditioning-inflation tests were processed by LaVision-DaVis software (vs8.4, Göttingen, Germany) to calculate strain maps (Fig. 3c) of the reconstructed 3D scleral surface, shown in Fig. 3b as a height map. The DaVis software provided strain maps of the maximum and minimum principal strains (ε_Max, ε_Min) on the reconstructed surface [40]. Strain maps calculated at each stereo frame used the first frame of the image sequence as the initial reference. Because this study is focused on the overall mechanical response of the posterior sclera, we calculated the average principal strain maps ε_Ave [41] on the scleral surface (Ʌ) excluding the region of the optical nerve head (ONH) (Fig. 3c). The ONH region was visually identified by an experienced operator that first identified the center of the ONH in the stereo images then applied a 2.4 mm circle mask. This diameter was chosen based on preliminary evaluations of the strain distribution around the ONH, where the region was characterized by large strain variations compared to peripheral scleral regions. By doing so, we removed this region that cannot be fully imaged, properly matched, and reconstructed with an optical stereo system due to optical occlusions (shadowing from the ONH stump) and complex-shaped areas with abrupt geometric changes affecting the regularity and accuracy of the deformation maps [23]. Then, we averaged each map across the reconstructed sclera surface (${\overline{\epsilon }}_{Ave}$):

$${\overline{\epsilon }}_{Ave}=\frac{1}{\Lambda }{\int }_{\Lambda }\frac{{\epsilon }_{Max}+{\epsilon }_{Min}}{2}d\Lambda =\frac{1}{\Lambda }{\int }_{\Lambda }{\epsilon }_{Ave}d\Lambda$$ (1)

In the rest of this manuscript, we will refer to the average scleral surface strain (${\overline{\epsilon }}_{Ave}$) with the symbol ε. For mechanical stress (σ) computation, we applied Laplace’s law for a thin-walled shell [42], assuming the scleral shell was approximated by a spherical vessel with radius (R) and thickness (T):

$$\sigma =\frac{\text{ IOP R}}{2T}$$ (2)

The radius of each shell was estimated by CloudCompare software 2.10.2 [43] on the best-fit sphere obtained from the reconstructed surface Λ. For both strain and stress data of the preconditioning response, the state at baseline pressure was used as the zero deformation and zero load references, respectively. Scleral thickness was calculated by averaging thickness measures as visible by optical coherence tomography (OCT) in-vivo at ten different locations of the posterior pole. OCT images were obtained using a Spectralis OCT (Heidelberg Engineering, Inc., Heidelberg, Germany) one day before the animal was euthanized. Mean and standard deviation of radius and thickness for all the eyes were R=4.7 ± 0.2 mm and T=0.11 ± 0.01 mm, respectively. Using these values, the tree shrew scleral shells satisfied the Laplace’s law for thin shells condition [42]:$\frac{T}{2*R}=\frac{0.107}{2*4.701}\approx 0.01\ll 1$.

2.4. Characteristic features of the viscoelastic stress-strain response

In Fig. 4 we depicted a typical loop curve of the stress-strain response (σ(ε)) of soft biological tissue during a loading-unloading cycle [44]. Five variables, characterizing some features of the σ(ε) curve, have been proposed in this study to analyze the effect of the preconditioning process: 1) The hysteresis loop area, h, defined as the area between the loading and unloading curves, representing the energy dissipated by the tissue during one cycle and calculated by numerical integration; 2) The elastic modulus at high IOPs, E = Δσ/Δε, was calculated as the slope of the best-fitting line of the stress-strain data points on the loading curve for IOPs greater than 35 mmHg [45]; 3) The residual strain, ε_res, defined as the difference in strain from zero at the end of the cycle representing the remaining strain in the tissue at the end of the cycle, calculated after the rest period of 15 min for the RCP protocol; 4) The peak strain, ε_peak, is the strain at the maximum IOP (50 mmHg); 5) The variation of the strain limits at each cycle, Δε_L=ε_peak − ε_res.

Fig. 4.

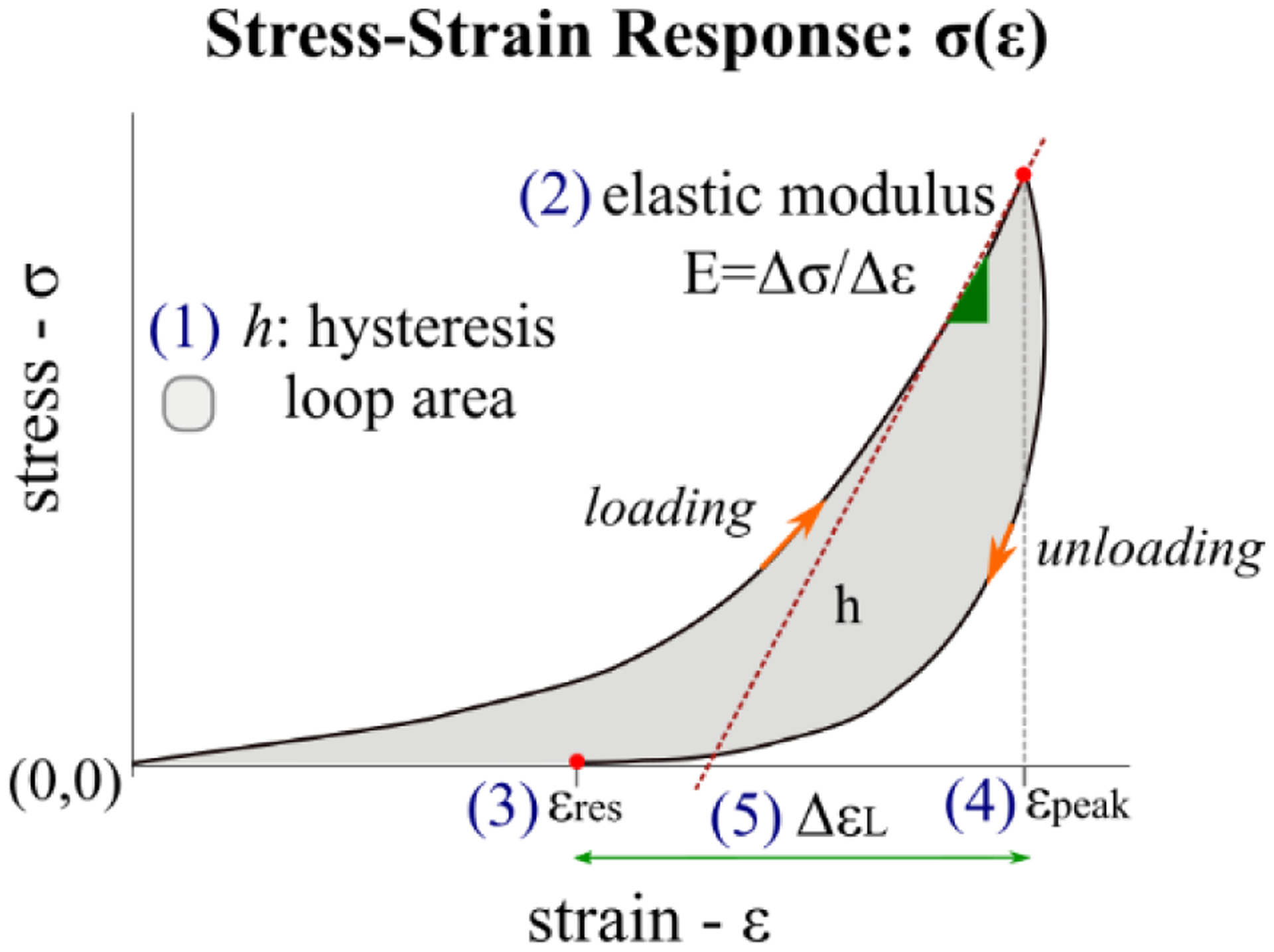
Five variables characterizing the stress-strain loop response σ(ε) obtained during a loading-unloading cycle of soft biological tissue.

2.5. Exponential regression function to model cycle-varying variables of the preconditioning response

Data of the five variables used to characterize features of the stress-strain response at each loading-unloading cycle was analyzed following a two-stage analysis approach for repeated measures [19,46]. First, we modeled each of the five variables’ variation over cycle using the exponential function:

$$f(N)=\text{A }{e}^{[-B(N-1)]}+C$$ (3)

where f(N) is an exponential function of the cycle number, N, for a given variable. f(N) depends on three coefficients – A, B, and C – that are graphically illustrated in Fig. 6a. Each coefficient assumed a specific role [47] in modeling the preconditioning response considered as the set of all consecutive cyclic stress-strain responses. A is the span coefficient, representing the difference between the value of f(N) at the first cycle (N=1) and the asymptote C (N→∞). This represents the change in value the variable undergoes from the beginning to the end of the preconditioning process. The sign of A models the decay (A>0) or the growth (A<0) of the function. The rate constant, B, models the stabilization rate, quantifying how rapidly the variable moves toward the asymptote C (B<1 slow rate; B>1 fast rate). Thus, C is the asymptotic value to which f(N) gradually converges (plateau), defining the preconditioned state of the tissue. Second, statistical analysis was performed on the regression coefficients A, B, and C. The proposed regression model followed a simplified version of the exponential functions used to model the transient response of brain tissues [48], ligament [49], and vocal fold lamina propria [50] during cyclic mechanical loads. Data analysis was implemented in Mathematica (Wolfram Research, Urbana, USA).

Fig. 6.

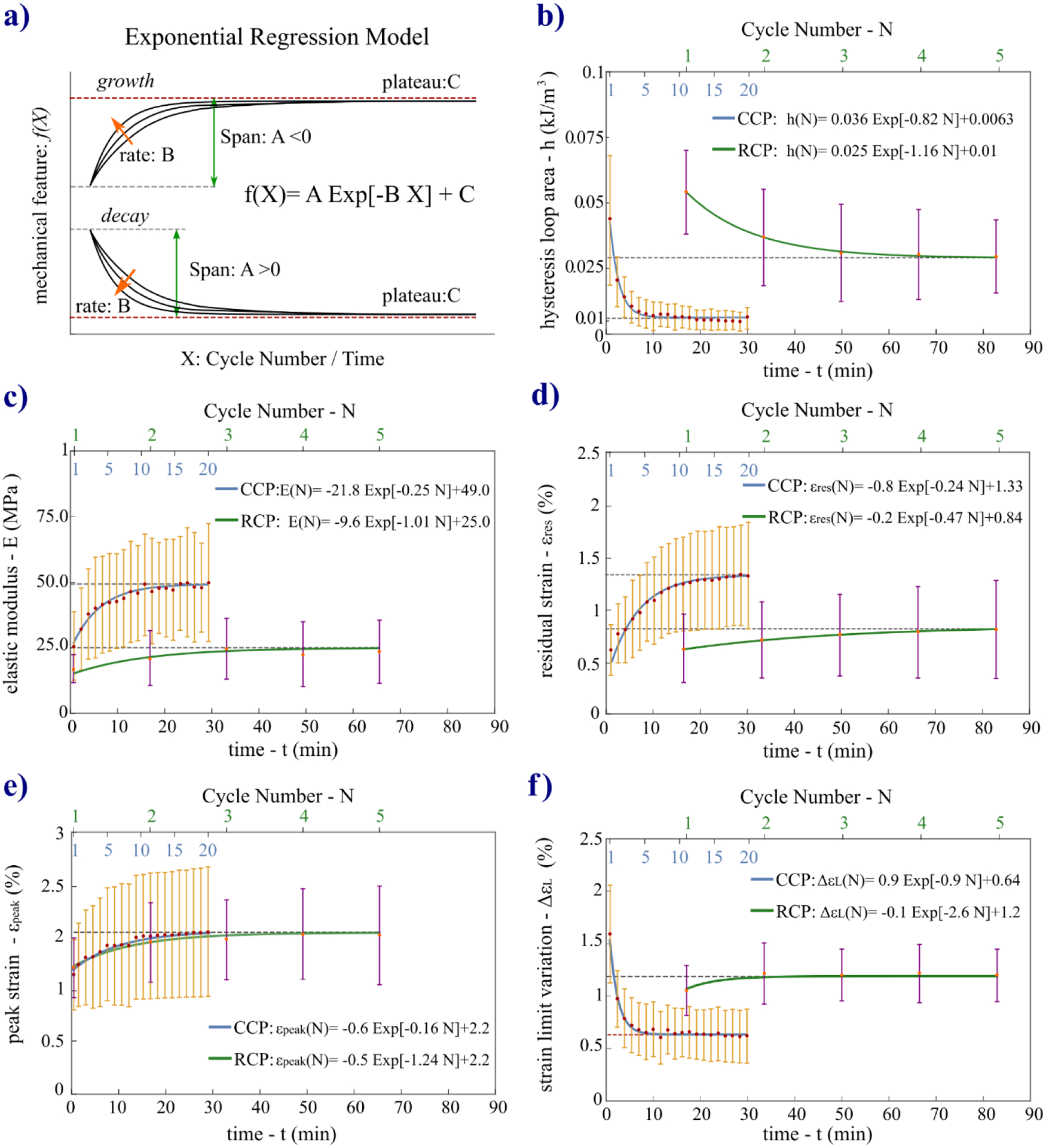
a) Illustration of the coefficients (A, B, C) of the exponential regression function used to fit the data of the mechanical variables characterizing the evolving preconditioning response over cycles. Orange arrows indicate direction of magnitude increase for B. b-f) Experimental data of the five variables plotted along with the mean curves (h(N), E(N), ε_res(N), ε_peak(N), Δε_L(N)) obtained with the mean coefficients. The mean curves are plotted over time t and over cycle number N for both protocols to provide an easier graphical comparison.

2.6. Statistical analysis

To assess the independence of the viscoelastic responses and the full recovery of the tissue’s mechanical properties from the order of the two preconditioning testing protocols, the variables h, E, and ε_peak of the stress-strain curve obtained at the first load-unload cycle of each protocol were compared using a paired t-test. Note that the first load-unload cycle represents an identical component (excluding the 15-min rest for RCP) of both preconditioning protocols and can, therefore, be used to investigate the potential effects of the testing order, resting time, and permanent deformations during the first test. Then, the calculated coefficients of the exponential function (Eq. (3)) for all variables of the data grouped by the respective protocol were analyzed by linear mixed-effects models in RStudio (Version 1.1.463) [51]. Additionally, the metrics used to define the number of cycles needed to reach preconditioned state were analyzed using this same model, outputting means, and standard deviations for each mechanical variable. The models were run to account for sources of random variability, including individual specimen, animal, and measurement conditions. Potential correlation between left and right eyes belonging to the same animal was also taken into account in the models. Then, unpaired t-tests were performed on the calculated coefficients to analyze the difference between the two protocols, while paired t-tests were used for the pairwise multiple comparisons of the cycle number needed to reach the preconditioned state estimated for the five variables for each protocol. Data are plotted as means with error bars indicating the standard deviation. Statistical significance was indicated by p-values (*: p<0.05; **: p<0.001) while not significant differences (p>0.05) were indicated by “n.s.”.

3. Results

3.1. Preconditioning response

Strain-time ε(t) and stress-strain σ(ε) curves of the preconditioning response of one representative sclera shell tested by both protocols are plotted in Fig. 5. Observing ε(t) and σ(ε) curves, both protocols showed typical preconditioning effects: a gradual accumulation of residual strains – due to cyclic softening accompanied by the rightward shifting of the peak strain – and a decrease of the hysteresis loop area. The strain-time curves showed the largest deformation during the first cycle when the tissue was initially inflated to the maximum IOP. Both loading stress-strain curves show the typical J-shaped nonlinear hyperelastic response of biological tissues [52]. As illustrated in Fig. 5c,d, three stages can be identified within the first cycle: an initial linear behavior at low strains (I) becomes nonlinear at the intermediate toe region (II) and finally linear again at high strains (III).

Fig. 5.

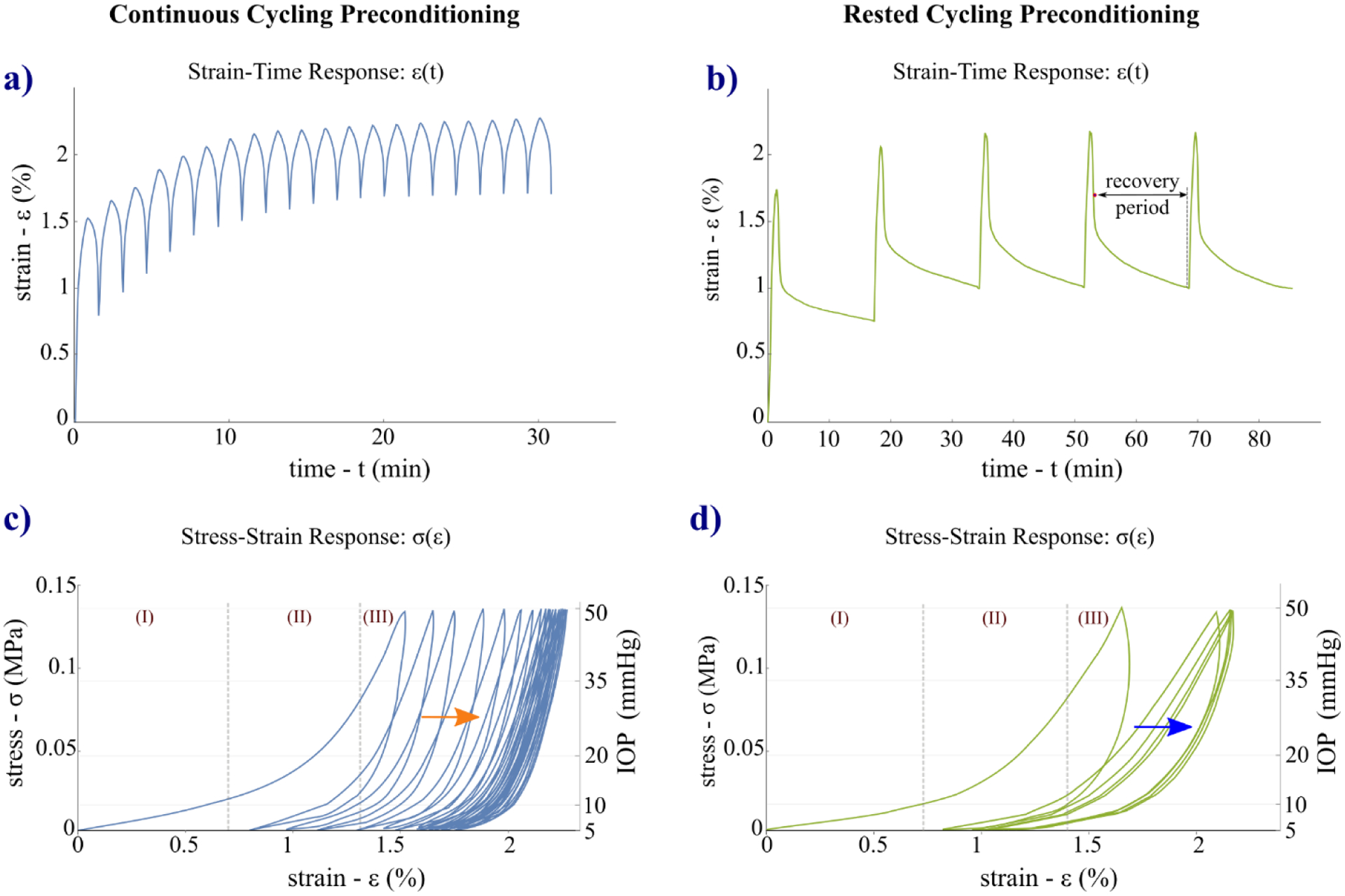
Strain-time ε(t) (a, b) and stress-strain σ(ε) (c, d) responses of one representative sclera specimen tested by the CCP (left column) and RCP (right column) protocols. On the RCP’s strain-time ε(t) curve is indicated (b) the recovery period of 15 min applied between cycles. The stress-strain σ(ε) curves show a gradual rightward shifting (softening) toward higher strains in both protocols (c, d, arrows). Looking at the loading stress-strain curves of the first cycle, tree shrew sclera showed the typical J-shaped nonlinear response of biological tissues, where 3 stages can be distinguished: an initial linear behavior at low strains (I) becomes nonlinear at the intermediate toe region (II) and finally linear again at high strains (III).

3.2. Exponential regression models of the characteristic variables of the preconditioning response

In Fig. 6b–f we plotted the mean curves for each coefficient (p<0.05 for all coefficients) of the exponential regression models (Eq. (3)) for both protocols. The curves are plotted over time (t, principal x-axis) and cycle number (N, secondary x-axis) to simplify graphical comparison of the two protocols. The plots highlight the different timing necessary to reach a preconditioned state of the tissue during cycling loads applying the two protocols and also allowed for comparing the different behavior of the five variables. The comparison of h, E, and ε_peak measured at the first load-unload cycle for the five scleras tested sequentially by the two preconditioning protocols with a resting time of 24h between them, revealed no significant differences (p>0.05). This result suggests the independence from the sequential order of testing, confirms the full recovery of the viscoelastic properties after 24h as suggested by Carew et al. [33], and shows that no permanent deformations were introduced during the first testing protocol.

3.3. Comparison within and between protocols

A numerical comparison between the two protocols is provided in Fig. 7 reporting the statistical analysis conducted on the coefficients of the exponential regression models for all five variables used to characterize the preconditioning response that we discuss in detail as follows.

Fig. 7.

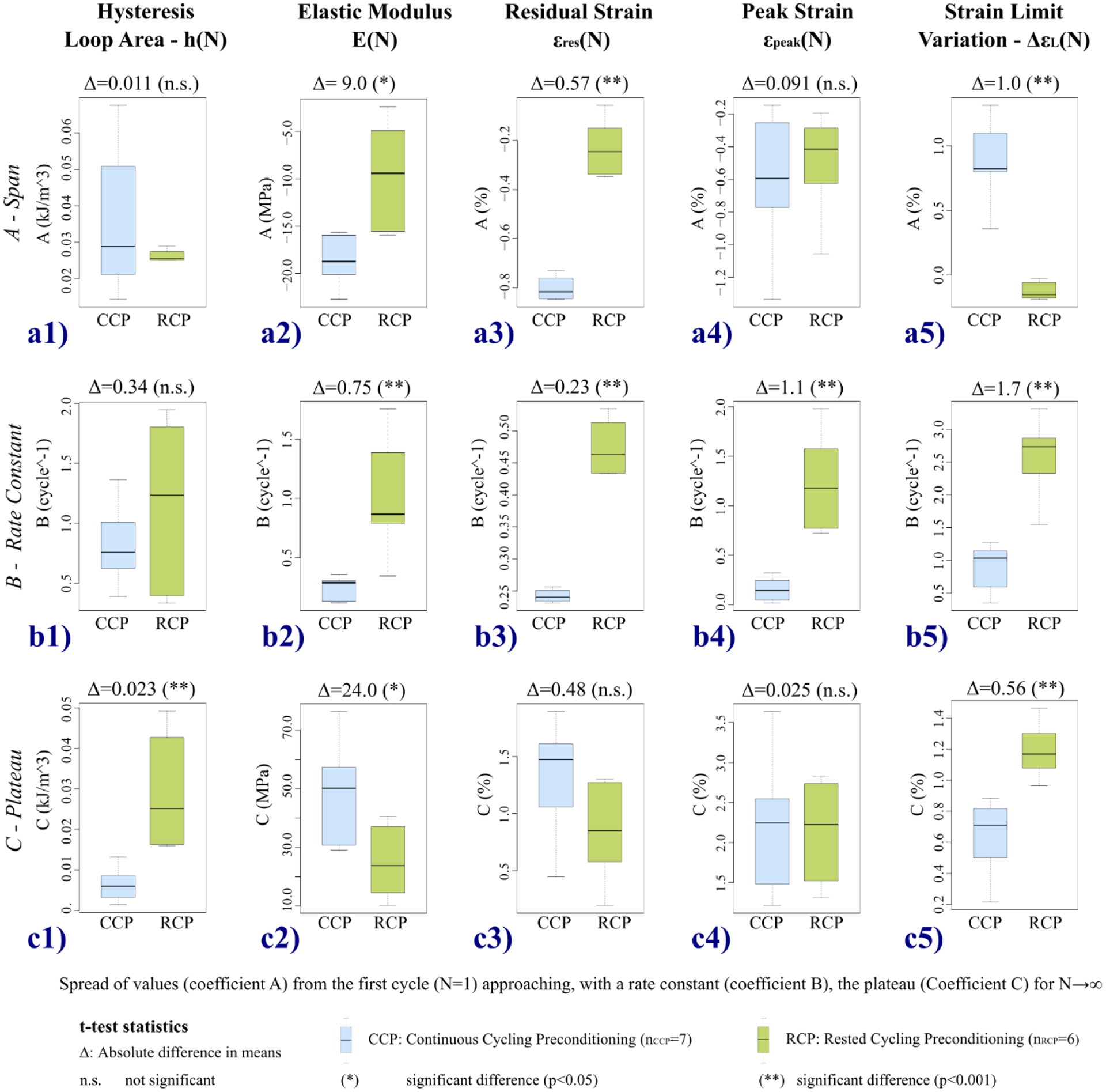
Statistical analysis for the comparison between continuous cycling preconditioning and rested cycling preconditioning protocols. Box plots of the three coefficients A, B, C of the exponential regression model (Eq. (3)) for the five variables used to characterize the preconditioning response. Unpaired t-tests were used for the statistical comparison, reporting the absolute difference Δ between the means.

3.3.1. Span of the variable – Coefficient A

The spread of values of the characteristic variables from the first cycle (N=1) to the plateau C (N→∞) varied between the two protocols. The span coefficient (A) estimated by the regression model (Eq. (3)) is a metric of the overall variation of the variable across the preconditioning cycles. The results of the statistical comparison of the span coefficients between protocols for each characteristic feature are illustrated in Fig. 7a1–a5. No significant difference (Δ=0.011 kJ/m³, p=0.2574) was found between the spans of the hysteresis loop area (Fig. 7a1). The CCP protocol induced a remarkable decrease of 85.3% from the first cycle to the preconditioned state, while the RCP response recovery between cycles was nearly half that of the CCP, at a 46.3% decrease. The CCP protocol also induced higher variation of the tissue stiffness (E) at high IOPs with a significant absolute difference Δ=9.0 MPa (p=0.01531) (Fig. 7a2). With respect to the hysteresis, a lower difference was found comparing the percentage variations of the elastic moduli: 80.1% (CCP) and 62.3% (RCP). A similar overall reduction was observed between h and E for the CCP protocol. The value found for the RCP’s elastic modulus represents the highest variation induced by the RCP protocol while the largest percentage variation for CCP was found for ε_res (152.8%). The rest periods used in RCP reduced significantly (p<0.001) the variation of ε_res to 37.0% with an absolute difference Δ=0.57% strain between protocols. Conversely, ε_peak was unaffected by the recovery showing no significant difference between protocols (Δ=0.091 %, p=0.6698) with similar percentage variations (36.9% for CCP, 29.9% for RCP). Finally, Δε_L was the feature most affected by the resting periods, with only 11.2% variation; this was 58.6% for CCP, making the difference between them significant (p<0.001), with the absolute difference equal to Δ=1.02% strain.

3.3.2. Rate of the transient variable – Coefficient B

The cyclic transient response during preconditioning was analyzed through the rate-constant coefficients B of the variable’s regression model. Comparing the boxplots in Fig. 7b1–b5, we observe that the response stabilized significantly more quickly in terms of cycle number in all features for the RCP protocol, significantly so (p<0.001) for all variables except hysteresis loop area (p=0.1834), likely due to the large variability in the RCP’s B coefficients. The CCP protocol induced smaller variations of the B coefficients in all variables, on average. The comparison within the CCP protocol revealed that h (0.8 ± 0.2 cycle⁻¹) and Δε_L (0.9 ± 0.3 cycle⁻¹) had similar and the highest rates suggesting a correlation between the variables that globally characterize the mechanical response at each cycle during the transient preconditioning response. Similar rates were also found between E and ε_res (0.25 ± 0.07 cycle⁻¹ and 0.242 ± 0.008 cycle⁻¹, respectively), though slower than those of h and Δε_L, while the slowest rate (0.16 ± 0.08 cycle⁻¹) was found in ε_peak. Similarly for the RCP protocol, the fastest change toward the preconditioned state was found in Δε_L (2.6 ± 0.5 cycle⁻¹), while the recovery periods between cycles made ε_res the slowest feature (0.42 ± 0.09 cycle⁻¹). Finally, h, E, and ε_peak showed similar rates in the intermediate range (1.2 ± 0.5 cycle⁻¹; 1.0 ± 0.3 cycle⁻¹; 1.2 ± 0.4 cyle⁻¹, respectively).

3.3.3. Plateau of the stabilizing variable – Coefficient C

The numerical comparison of the preconditioned states reached by applying the two protocols was conducted through the analysis of the plateau coefficients (C) (Fig. 7c1–c5). Among the five variables, only ε_peak showed similar plateaus in the two protocols (2.2 ± 0.6 % for CCP and 2.2 ± 0.4 % for RCP), with no significant difference (Δ=0.03 %, p=0.9538, Fig. 7c4). Also for ε_res, no significant difference was found (p=0.1117) likely due to the high variability within both protocols (1.3 ± 0.4 % and 0.8 ± 0.3 %) but showing a relevant absolute difference of Δ=0.48 %. The effect of such a variability was attenuated for Δε_L finding a significant difference (Δ=0.56 %, p<0.001) between protocols, with the difference of Δ=0.56 % representing the overall relaxation of the tissue during the recovery periods. The two hysteresis loop areas were significantly different (Δ=0.023 kJ/m³; p=0.0020) as expected because of the progressive decrease induced by CCP. This significant difference between the two hysteresis loop areas could explain the insignificant difference found between the two A-span coefficients (Fig. 7a1) because of the large variability of CCP’s data. A relevant difference of the preconditioned states was found comparing the elastic moduli at high IOPs (Δ=24.0 MPa; p=0.02383), where the highest stiffness of the tissue was measured for the CCP protocol. Thus, the rest periods applied in the RCP protocol allowed not only for a significant strain relaxation of the tissue but also a partial recovery of the h and E.

3.4. Method to define the number of cycles needed to reach preconditioned state and uncertainty of the repeatable preconditioning response

To quantify at what cycle the five variables of the preconditioning response of the CCP and RCP protocols reaches a stabilized and repeatable state, we propose a method based on the 95% confidence band. The point of stability was calculated by the intersection of the 95% confidence band estimated by the exponential regression model with the relative plateau line. Two representative cases of the intersection were plotted in Fig. 8 that occurred with the growth and decay models. In Table 1, we reported mean and standard deviation of the cycle at which starts the preconditioned state N*. In Fig. 9 we reported the statistical results of the pairwise multiple comparisons of N* between the five variables. Comparing the N* values within each protocol we found that the five variables reached stability at different cycles. For the CCP protocol, we found no significant difference between N* of h and Δε_L (p=0.9733) or between E and ε_peak (p=0.3809). The residual strain ε_res showed significant differences from h (p=0.01533), Δε_L (p=0.04574), and ε_peak (p=0.03838) but not from E (p=0.7578). The hysteresis h was significantly different from E (p=0.001895) and ε_peak (p<0.001), and no significant difference between Δε_L and E (p=0.005351) or between Δε_L and ε_peak (p<0.001). By calculating the average N* across all features and all scleras for the CCP protocol, we determined that the preconditioning response started to stabilize after 15.8 ± 4.4 min at cycle number of 10.5 ± 2.3 (p<0.001). For the RCP protocol, all features stabilized between the second and the fourth cycle (Table 1), but no significant differences (p>0.05) were found between all pairwise comparisons. On average, the RCP’s response started to stabilize after 51.2 ± 8.3 min at cycle number 3.1 ± 0.3 (p<0.001). As metrics of the uncertainty of the repeatable response at the preconditioned state, in Table 1 we reported the percent error (e_N*) of the C coefficients per number of cycles (see ΔN_S in Fig. 8) over which the response was considered stabilized based on the proposed method. For example, for the CCP protocol, the hysteresis started to stabilize after ~5 cycles, and for the remaining ~15 cycles can be considered repeatable. Comparing the values within each protocol, the greatest e_N* was found in ε_peak for both protocols revealing the highest instability in deformation measurements at the maximum load. The overall comparison between the two protocols (CCP: 3.0 ± 1.2 % cycle⁻¹, p=0.0029; RCP: 8.2 ± 3.0 % cycle⁻¹, p=0.0023) showed that CCP provided more accurate repeatability of all variables.

Fig. 8.

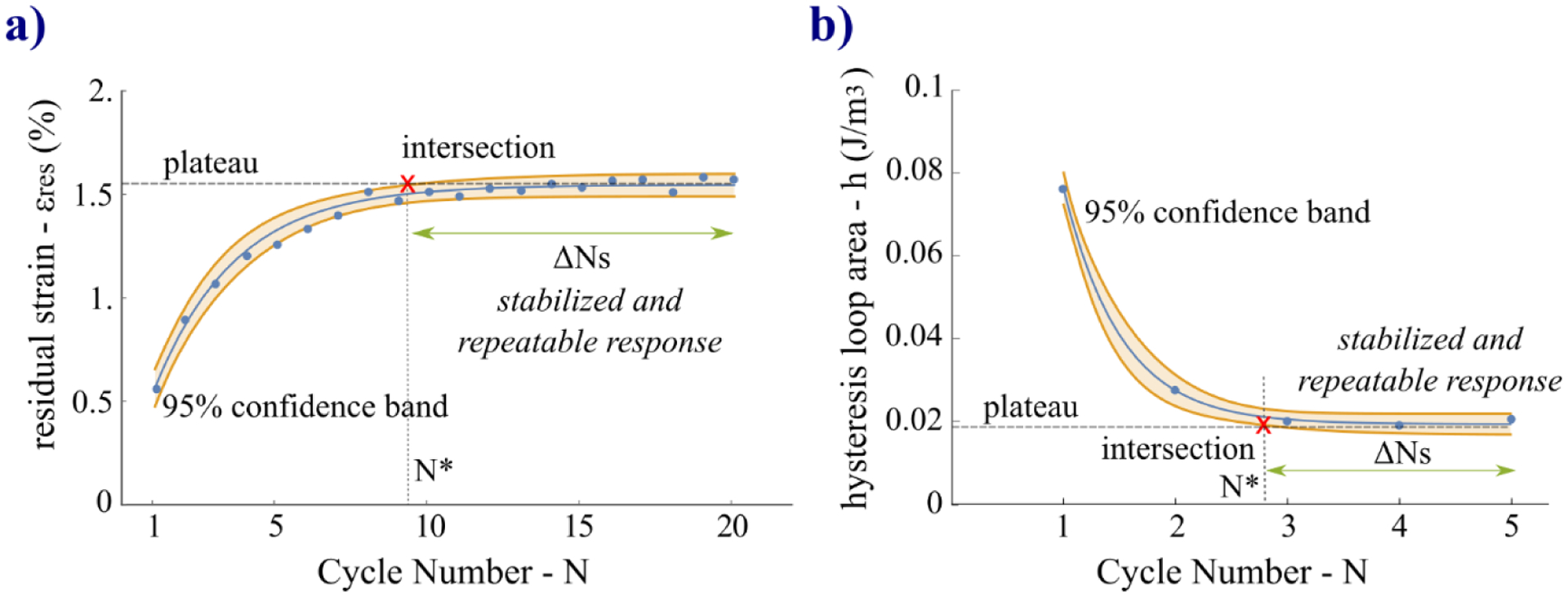
Illustration of the method proposed to define the cycle number (N*) at which the response stabilizes becoming repeatable over a range of cycles ΔN_s. The method is based on the intersection of the 95% confidence band with the plateau line. Two representative cases of growth (a) and decay (b) tendencies are illustrated for the CCP and RCP protocol, respectively, as examples of the two different cases of intersection.

Table 1.

Metrics to define the cycle number from which the five variables characterizing the preconditioning response reach a steady and repeatable state obtained by the CCP and RCP protocols. Mean and standard deviation (M±SD) (p<0.001 for all variables) of the cycle number N* corresponding to the intersection between the 95% confidence band and the plateau line. Uncertainty of the repeatable response is measured by the percent error per number of cycles e_N* where the variables were considered preconditioned.

	cycles needed to reach preconditioned state - N* (cycle)		uncertainty per number of cycles - eN* (% cycle−1)
	CCP	RCP	CCP	RCP
Hysteresis loop area h	4.9 ± 1.5	3.5 ± 0.6	2.9	7.0
Elastic modulus E	10.5 ± 5.1	2.7 ± 0.6	2.7	7.8
Residual strain ε res	11.1 ± 2.9	4.0 ± 0.7	2.4	7.1
Peak strain ε peak	14.9 ± 1.2	2.3 ± 0.9	5.2	13.7
Strain limit variation Δε L	6.0 ± 2.9	2.9 ± 0.3	2.1	5.4

Fig. 9.

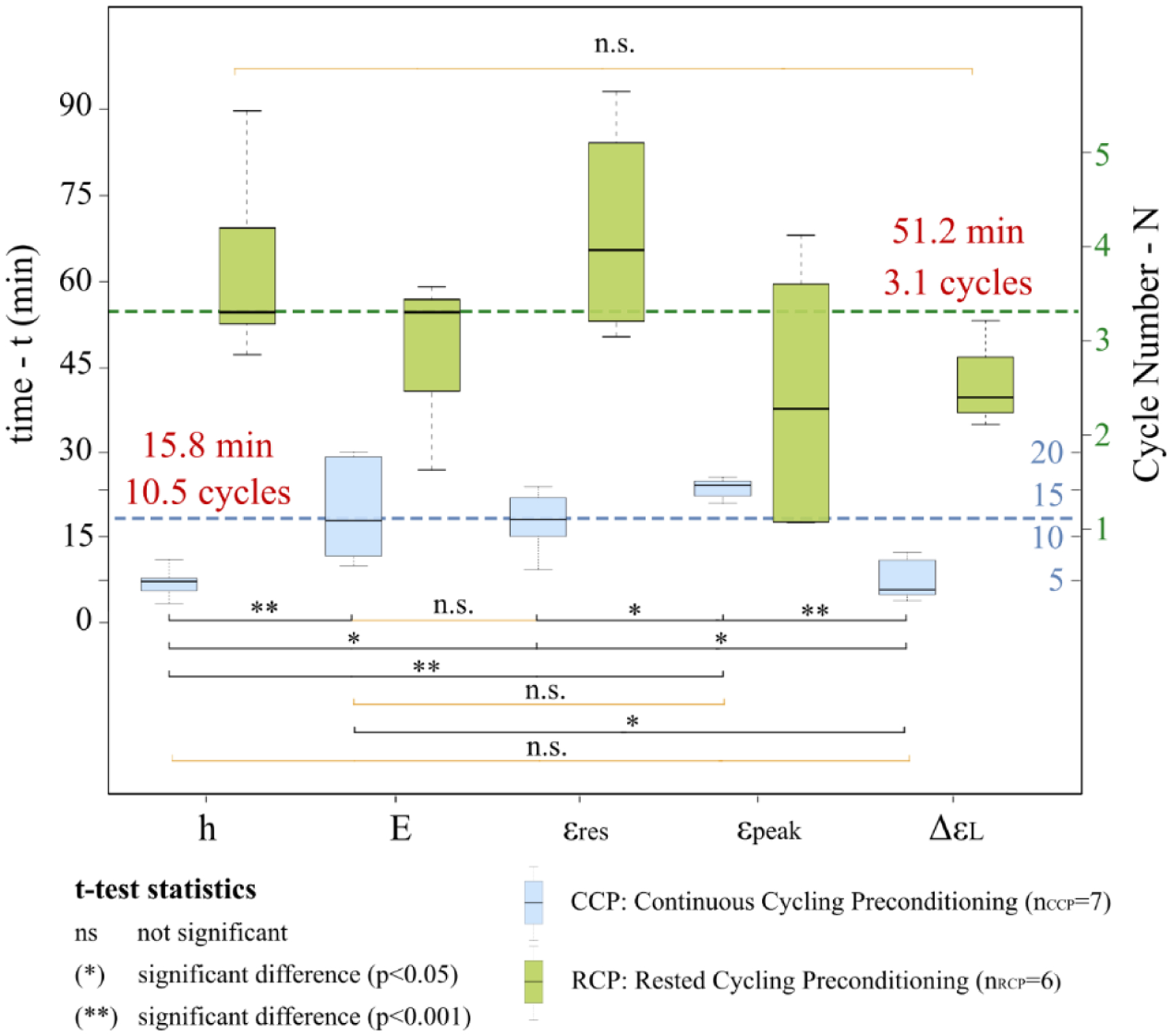
Pairwise multiple comparisons of the cycles N* obtained by the proposed method between the five variables investigated (hysteresis loop area h, elastic modulus E at high IOPs, residual strain ε_res, peak strain ε_peak, and strain limit variation Δε_L) in the CCP and RCP protocols to characterize the preconditioning response. N* defines the number of cycles needed to reach preconditioned state. Paired t-tests were used for the statistical comparison.

4. Discussion and conclusions

We analyzed and compared the responses obtained by two different preconditioning protocols used for inflation testing of ocular tissues based on continuous and rested cyclic loads. Scleras from five tree shrews were preconditioned by 20 loading-unloading cycles without rest and 5 cycles with 15-min rest between cycles. The scleral surface strain response was obtained by averaging the average principal strain maps measured by 3D-DIC method and the stress was calculated by applying the Laplace’s law for thin-walled shells. Strain-time and stress-strain curves from both protocols appeared remarkably different, however both revealed typical preconditioning effects: gradual accumulation of residual strains, increased cyclic softening and stiffness, and decreased hysteresis loop area. Such effects have been attenuated for the RCP protocol because of the viscoelastic recovery at each rest period between cycles. The CCP’s stress-strain response showed the typical rightward shifting towards higher strains in agreement with uniaxial strip test results presented by Grytz and Levy [18,19]. However, the RCP’s response showed substantial preconditioning effects contrary to those results reported by Tonge et al. [28] on porcine and bovine scleras. Our results revealed that the tree shrew sclera did not fully recover its viscoelastic properties within these same rest periods. To analyze and compare the preconditioning responses obtained by the CCP and RCP protocols, we proposed a new methodology based on modeling the cycle-dependent change of five variables characterizing some features of the stress-strain loop curve by exponential regression. Thus, we investigated the preconditioning response through: 1) hysteresis loop area, 2) elastic modulus at high IOPs, 3) residual strain, 4) peak strain at the maximum IOP, and 5) strain limit variation. Using exponential regression models with three coefficients (span, rate constant, and plateau) allowed us to study each variable in terms of the total change during preconditioning, the cycle-dependent stabilization rate at which a repeatable “plateau” region is approached. Finally, a method based on the intersection between the 95% confidence band (Fig. 8) obtained by the exponential regression of each specimen’s feature data and the relative plateau, was proposed to define the cycle number when the response starts to stabilize and becomes also repeatable. The results showed large differences of the preconditioning features within and between protocols. The CCP protocol induced overall the highest variations of the variables from the initial state to the preconditioned state while they were more attenuated for RCP. The RCP protocol induced the highest stabilization rates with significant differences between protocols for all variables (p<0.05) except for the hysteresis loop area. No significant differences in the plateaus were found for ε_peak, while h, E, and Δε_L were significantly different between protocols. This last results along with that found for Δε_L and ε_peak, suggest that the 15-min rest periods allowed for a partial but substantial recovery of the residual strains. Interestingly, for CCP we found a similar behavior between the two global features (h and Δε_L) and between two of the local features (E and ε_peak). In both protocols, the largest variability of data was found in measuring the strain at the maximum load, ε_peak which showed the lowest repeatability. Thus, using only the peak strain as a variable to analyze the preconditioning response – as reported previously by Grytz et al. [18] and Wong et al. [22] – by applying continuous cycling protocols could ensure the lowest uncertainty of the repeatable response in the others variables.

The two preconditioning protocols analyzed in this work have pros and cons. The CCP protocol provides more data points through an increased number of cycles for robust statistics and stabilizes a sample in a shorter time frame. Additionally, the transition to stability and final steady state of CCP are both characterized by higher precision than that of RCP. The capability to absorb/dissipate mechanical energy (damping) as related to the hysteresis loop area [53] undergoes a consistent reduction (85.3%) for CCP from the first cycle to the final cycles at the preconditioned state. This finding suggests studying the damping capability of a soft biological tissue only by cross-sectional analysis measuring the hysteresis at the first cycles.

The RCP protocol requires a longer testing time with a lower number of cycles, and it should require to preliminarily design the rest period between cycles for the full recovery of the response between cycles. RCP can induce a repeatable steady state of the tissue where the hysteresis is not substantially lost, allowing for a characterization of the tissue undergoing partial decrease of its viscoelastic properties. It also allows to study the behavior of the preconditioning features during the recovery. It should be pointed out that applying only the CCP or the RCP protocol a biomechanical characterization of tissue can be performed. In fact, in [19] the inelastic properties of tree shrew sclera induced by experimental myopia and inhibited by crosslinking were studied by a CCP protocol. As we demonstrated in our work, a preconditioning protocol can provide measurements of the transient and steady-state responses. In addition, being normally the first testing stage of a testing protocol the integrity of the tissue is more preserved and the risk of irreversible damage during prolonged loading test is reduced.

The mechanisms of the preconditioning effects are still not well understood as related to the composition and the species-specific fiber arrangement of the tissue. Tree shrew sclera consists primarily of networks of fibers (mainly collagen fibers type I and elastin) embedded in a hydrated interfibrillar amorphous gelatinous material (ground substance) of proteoglycans and glycoproteins [32,54]. The fibers are packed in a non-uniform crimped architecture at rest becoming gradually uncrimped and straight if subjected to loading with consequent increase of the tissue stiffness. Collagen fibers being viscoelastic are determinant in the loading history of the tissue [4] and are thought to contribute to the tissue response especially at high strains (linear region III, Fig. 5c,d), while elastin contributes mainly to the scleral stiffness at low loads (initial linear region and toe region I-II, Fig. 5c,d), having a nearly elastic and non-dissipative behavior [1,52]. Proteoglycans and glycoproteins are believed to inhibit collagen and elastin fiber sliding and maintain tissue hydration [31,44]. In view of the scleral structure, we can speculate that partial deformation due to the elastic fibers is recovered rapidly at each unloading cycle of the tissue. Another portion of the deformation is recovered slowly after 15 min rest likely due to the combined interaction of the ground substance matrix and the fibers, while the recovery to the virgin state that is obtained after ~24h rest and it is thought to involve the reorganization of the collagen architecture. This finding agrees with the hypothesis that the recovery from the viscoelastic effects is rapid and completed within minutes while the recovery from the preconditioning effects may be partial or require several hours [3,4].

In our study, an increase of the stiffness at high IOPs and a decrease in the hysteresis loop area were found as the tissue stabilized in both protocols. We believe this suggests these two features are inversely correlated without full recovery during cycling loads. We hypothesized that the increased stiffness occurred because of the progressive uncrimping and increased recruitment of collagen fibers with each subsequent loading cycle [55]. A gradual loss of hydration in the tissue (water) during the repetitive stretching of the tissue may have affected the ground substance [56] with progressive decreasing of the capability to absorb/dissipate mechanical energy (hysteresis) as observed in the CCP protocol. The similar maximum deformation obtained in both protocols at the preconditioned state (Fig. 7c4) suggests that the tissue had a memory of the deformation undergone during previous loads independently by the recovery of the response. We think that some sliding pathways in the collagen fiber architecture are established primarily during the first load cycle when the tissue shows the largest changes of its mechanical properties as it is stretched to the maximum load from its initial state. A new organization of the fiber architecture may have formed with an increase of the internal inertia that mostly opposes further changes resulting in a decreasing variation of the properties. The tissue stiffness was recovered more slowly compared to the hysteresis in both protocols, suggesting that the realignment of the collagen fibers in recovering the original state took longer than the re-hydration of the tissue. For an easier interpretation of this finding, in Fig. 10 we plotted two idealized stress-strain responses representing the equivalent mechanical behavior at the preconditioned state obtained by the mechanical features (h, E, ε_res, ε_peak) measured in both protocols. Although the tissue reaches the same peak strain level, the different stress-strain curves for the two protocols suggest the loading history impacts the steady state response.

Fig. 10.

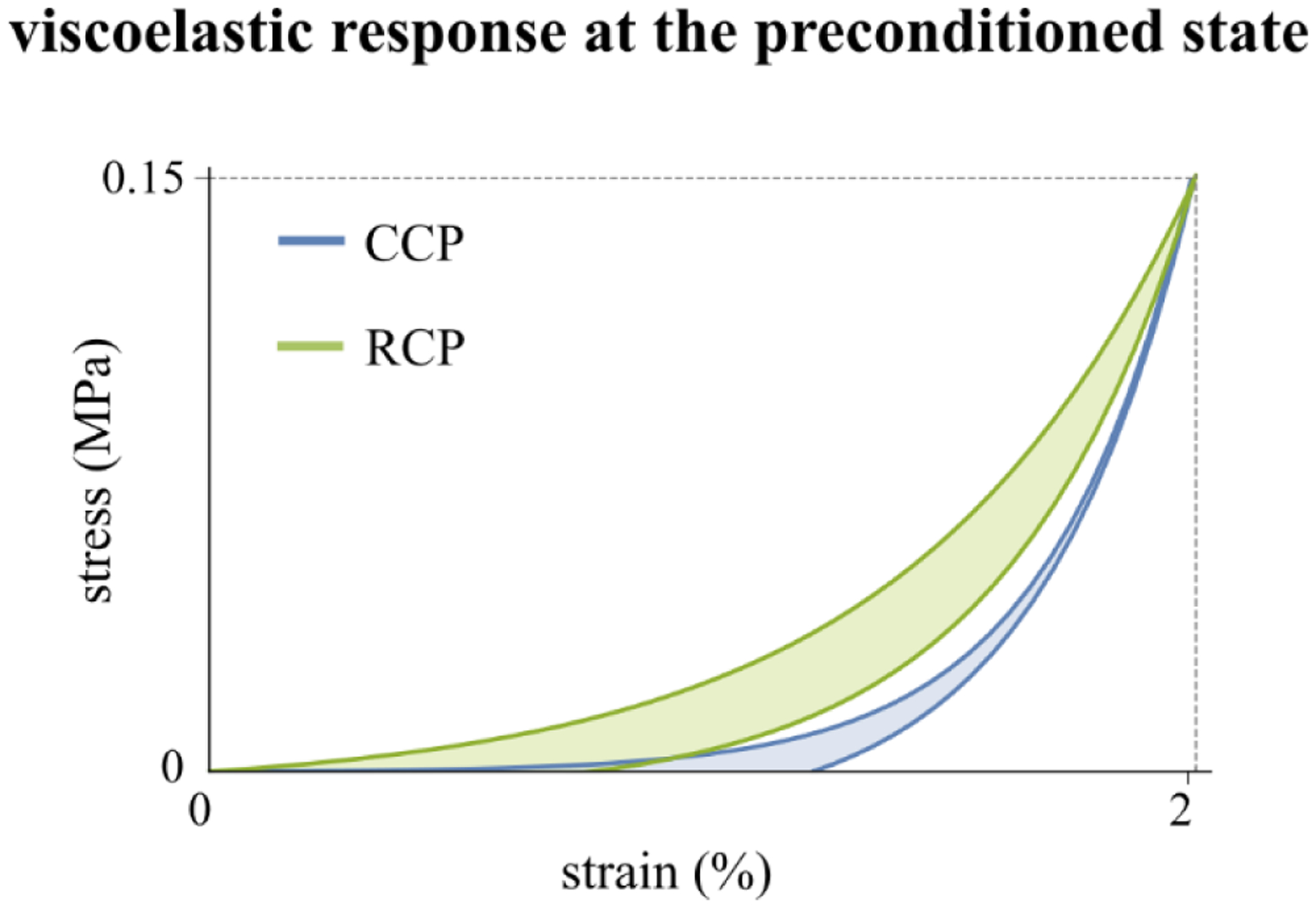
Idealized representation of the equivalent mechanical behavior showed by tree shrew sclera at the preconditioned state induced by continuous and rested cycling preconditioning (CCP, RCP).

In inflation tests of porcine and bovine scleras using a 3-cycle RCP protocol, Tonge et al. [28] reported small differences in peak strains – less than 1.15% between the first and second and between the second and third cycles. In these 5-cycle RCP tests of tree shrew scleras, we found substantial changes in peak strain (ε_peak): 21.30% between the first and the second cycle, 5.06% between the second and the third cycle, 1.39% between the third and the fourth cycle, and 0.39% between the fourth and the fifth cycle. Such differences between the two studies could be explained by several factors: species- and age- specific differences in the composition of the scleral tissues, the region of sclera used for measuring the deformation, the kind of strain used to quantify the deformation (meridional and circumferential strain by Tonge et al. [28] and average principal strain in the present work), and the loading limits of the testing protocol. These differences suggest that the results obtained in one or two species cannot necessarily be directly applied to others.

We also compared the results of the incremental strain at the maximum load (Δε_peak) with those found by Grytz et al. [18] by polynomial regression (Δε_peak(ΔN) = −0.0066 + 0.8934/ΔN) in case of uniaxial testing of tree shrew sclera strips at physiological loads (0–60mmHg [19]) with that resulting from the exponential regression model proposed in our work obtained by the function (ε_peak(N) = −0.589 + Exp[−0.155 N] + 2.187). We can observe in Fig.11 a remarkable different behavior of the evolving response over cycles during preconditioning. The softening effect is more reduced in the case of inflation testing likely due to the integrity of the tissue that lowered the progressive recruitment-alignment of the fibers. A significant difference was also observed in porcine sclera by comparing whole globe inflation and uniaxial testing [57], finding a more compliant hyperelastic response in the scleral strips.

Fig. 11.

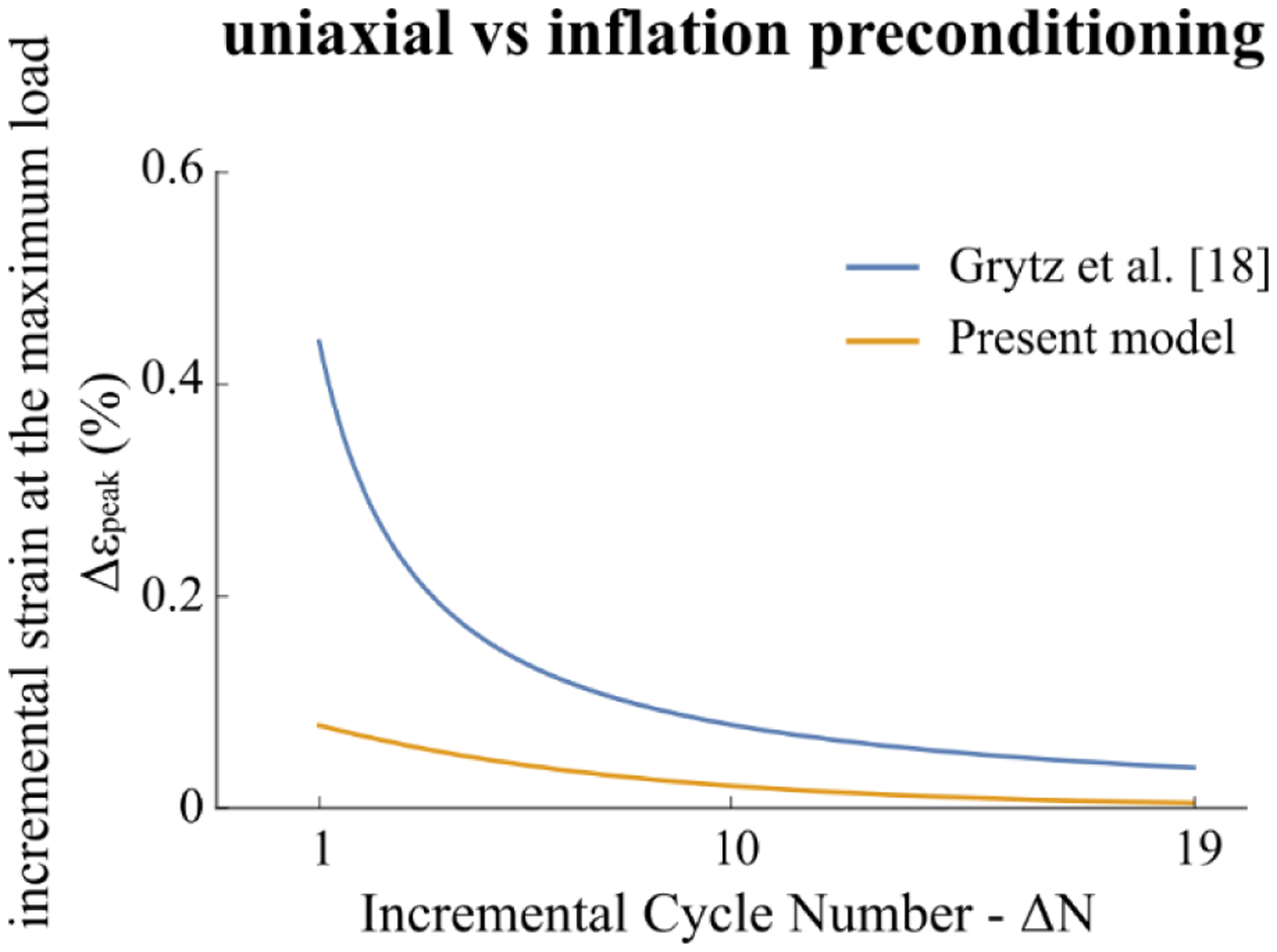
Comparison between the polynomial regression model of the incremental strain at the maximum load Δε_peak(ΔN) obtained by Grytz et al. [18] on tree shrew sclera strips by uniaxial testing and the model calculated in the present work from the exponential regression of ε_peak(N) as reported in Fig. 6d1 obtained for inflation testing.

The limitations of this work concern mainly the generalizability of the results of the preconditioning features obtained in both protocols. In fact, the complexity of the preconditioning mechanism as related to mechanical testing (uniaxial, biaxial, inflation), species, tissue condition (age, disease, treatment), and loading parameters (load limits, load rate, rest period) makes difficult to extend our findings to other case studies. However, even with a small number of specimens, we demonstrated the effectiveness of the proposed methodology to analyze the preconditioning response based on exponential regression modeling of the mechanical features. This exponential model, as well as the method used to establish preconditioned state and repeatability, can be applied across the different sectors/regions of the sclera (peripapillary and anterior sclera). Another limitation of our work concerns the global characterization of the sclera’s response by using the average principal strain across the scleral surface. This approach neglects the local/regional behavior of the tissue that, due to its intrinsic anisotropy, varies across the posterior sclera [24]. The usage of Laplace’s law (Eq. (2)), widely used in ocular biomechanics to calculate the stress distribution across corneoscleral shells [58], represents a limitation in our study because it is based on some assumptions that can be violated in real cases. Even if Laplace’s law has been formulated for stress calculation in thin-walled pressure vessels [42] – which is a valid assumption in the case of posterior scleral shells of tree shrews (T/2 R = 0.1 << 1) – it assumes that the pressure vessel is a hollow sphere with a uniform thickness. Furthermore, Laplace’s law does not account for complex mechanical properties (anisotropy, viscoelasticity, heterogeneity, nonlinearity) of the tissue. As carefully evaluated by Chung et al. [58], the violation of the geometrical assumptions and the lack of information of the scleral material properties can lead to locally erroneous stress estimates when using Laplace’s law. Inverse finite element models [59–62] can provide local and eye-specific estimations of the scleral shell stress field with less restrictive assumptions. However, the intent of our study was not to accurately characterize the local stress field of the sclera but to compare the overall mechanical response of the sclera across two preconditioning protocols. To mitigate the limitations of using Laplace’s law, regions with high anisotropic material properties such as the optic nerve head region have been excluded from the analysis. Also, the loading-unloading cycles were conducted at a constant rate to avoid viscoelastic rate-dependency. Scleral thickness values have been measured by OCT along a small region near the posterior pole showing only small variations in thickness (T = 0.11±0.01 mm), which are consistent with previously reported values [19] (T = 0.117±0.006 mm) measured by microscopy in a larger sclera region. To evaluate the deviation of the investigated scleral shell region from a perfect sphere, we estimated the best-fitting sphere for each reconstructed scleral shell using the 3D point cloud obtained by the LaVision-DaVis software [40]. Then, we calculated the mean and standard deviation of the absolute distances between the reconstructed point cloud and the best-fitting sphere (error). We found through all specimen shells that the error was equal to 26.4±41.2 μm, which is consistent with the estimation of the error (25.6 ± 36.2 μm) obtained for a ball bearing used to validate the 3D shape reconstruction method [63] as presented in the Appendix. Based on these assessments, the use of Laplace’s law seems appropriate and sufficient for the proposed study. In our analysis, we excluded the elastic modulus at low IOPs, further characterizing feature of the load–unload stress–strain diagram [44], because the camera frame rate of 1 Hz was unable to capture sufficient data to fit the initial linear region (I, see Fig. 5) in case of the CCP protocol. Since the preconditioning effects of tissue response exhibited during cyclic loads are phenomena strictly related to ex vivo lab testing [1], the experiments were conducted under conditions that are typical for ex vivo inflation testing [23–25], which mimic the in vivo loading condition but vary in other aspects from the in vivo condition such as temperature, hydration, boundary conditions, and interactions with intraocular tissues. In absence of in vivo mechanisms to maintain tissue integrity, testing at the physiological temperature would have accelerated tissue degradation [25]. Hydration of the scleral shells during testing was maintained by internal PBS in-flow, while dehydration from the outer surface of the sclera shell due to the humidity gradient from the shell to the lab environment was prevented by coating the surface with a mixture of cosmetic oil and titanium dioxide powder. While the use of the oil does not replicate in vivo conditions, it avoids the need for a humidity chamber (setting humidity at 90 %) [31] that could affect the texture-speckled surface during testing with the formation of some micro droplets of water (with humidity and temperature equal to 90% and 24°C, respectively, the dew point is 23°C). Our method to prepare the scleral surface for 3D-DIC method provides high-accurate deformation measurements as preliminarily validated and presented in the Appendix, and it allows for beginning testing once the surface has been coated, on the contrary, the use of Indian ink [23,25] requires waiting for the ink to dry before testing. Scleral shells were clamped below the eyeball equator avoiding boundary effects that could affect strain maps of the reconstructed shell surface. Removing the intraocular tissues has likely changed the mechanical response of the eyeball from the in vivo condition. This said, our goal was not to perfectly mimic the in vivo condition but to compare two preconditioning protocols. As we processed each scleral shell in the same way, our conclusions related to the different preconditioning protocols should remain valid.

To the best of our knowledge, this is the first work to propose a systematic methodology for analyzing the preconditioning response. This comparison of two common preconditioning protocols serves as a first attempt at suggesting a common framework for standardized analysis, allowing the comparison of results obtained by different labs. Additionally, this work presented useful information for designing a preconditioning protocol with a measurable and repeatable response. Our study demonstrated that the analysis of the preconditioning response is necessary to induce a well-defined and measurable preconditioned state for tissue analysis purposes (like pseudo-elasticity) or to reach a reference state for the tissue, reducing bias in cross-sectional studies. The proposed method can be applied in the analysis of the preconditioning response in cross-sectional studies, in preliminarily investigations to design a preconditioning protocol (i.e. cycle number), and in measuring the repeatability of the pseudo-elasticity in a longitudinal study.

Future work is needed in this topic to expand the proposed methodology to characterize the preconditioning response of other ocular tissues and develop a finite element model to provide eye-specific local estimations of the stress incorporating also tissue material properties. More research is also required to expand the regression model based on a specific constitutive model [64], which would expand our understanding of the viscoelastic and preconditioning roles of the various structural components of the sclera. In summary, our results suggest that the analysis of the preconditioning response is an essential part of any mechanical testing experiment and a prerequisite to induce a well-defined and objective preconditioned state. Also, the preconditioned state cannot be directly compared across studies with different preconditioning protocols.

Appendix

Setup validation

The inflation testing setup was preliminarily validated regarding: (i) the optical setup to apply the 3D-DIC method, (ii) the relative LaVision-DaVis software’s ability to reconstruct the 3D shape of and calculate the strain on the scleral shell surface, (iii) IOP measurements taken by the pressure gauge, and (iv) the method of applying a speckled texture to the scleral surface (described in Section 2.1) as required by DIC methods [38]. Thus, to quantify the accuracy of the 3D shape reconstruction, we adopted the method proposed previously [62]. We measured the ball bearing’s diameter (8.03 ± 0.01 mm) with a digital caliper with 10-μm resolution and then created a CAD (computer-aided design) model of the sphere (Fig. A1a) to be used as the “true” model. By computing the absolute distances between the surfaces of the 3D reconstructed point cloud and the CAD model of the ball bearing, CloudCompare calculated the mean ± standard deviation accuracy of the system to be 25.6 ± 36.2 μm, respectively.

The resulting strain is a measure of the accuracy of the 3D-DIC strain measurement. By averaging the maximum principal strain maps (Fig. A1b) obtained during five stereo frames of the ball bearing, we found the strain accuracy equal to 0.0017 ± 0.0009%. IOP measurements by the Crystal pressure gauge were validated utilizing a Millar Mikro-Tip® SPR-407 piezoelectric pressure catheter with PCU-2000 pressure control unit, PowerLab 35 Series data acquisition system, and LabChart Pro analysis module. The sensor of the piezoelectric pressure catheter was placed in the chamber (Fig. 1a) immediately below the washer holding the sclera shell, and IOP was changed during 10 cycles – using the same protocol settings as those reported in Section 2.2 – and recorded by the gauge and the pressure sensor. We have found high agreement between the two measurements with a correlation equal to 0.998 (Fig. A1c). Finally, we validated the surface preparation method for the scleral surface. After cutting a 3-mm-wide × 15-mm-long strip from a sclera shell, the strip was fully clamped at each end as illustrated in Fig. A1d. The strip was deformed like in a punch test by vertically translating (Z-axis) the spindle of a micrometer (resolution 10 μm) with a 4-mm diameter semi-spherical head. Initially, the position of the spindle was set in order to shape the strip by the spherical head of the spindle. Then, the displacements at each 10 μm Z-increment from 0–250 μm were measured, taking 5 repeated measurements at each step. We evaluated the error of the measured displacements (v_z) along the Z-axis using the DaVis software. This experiment was repeated with 4 scleral strips, and no slips or detachments of the speckle coating were observed in any case. We found that the displacement accuracy was equal to 0.8 ± 0.1 μm, confirming the reliability of the method to prepare the speckled texture of the scleral shells.

Fig. A1.

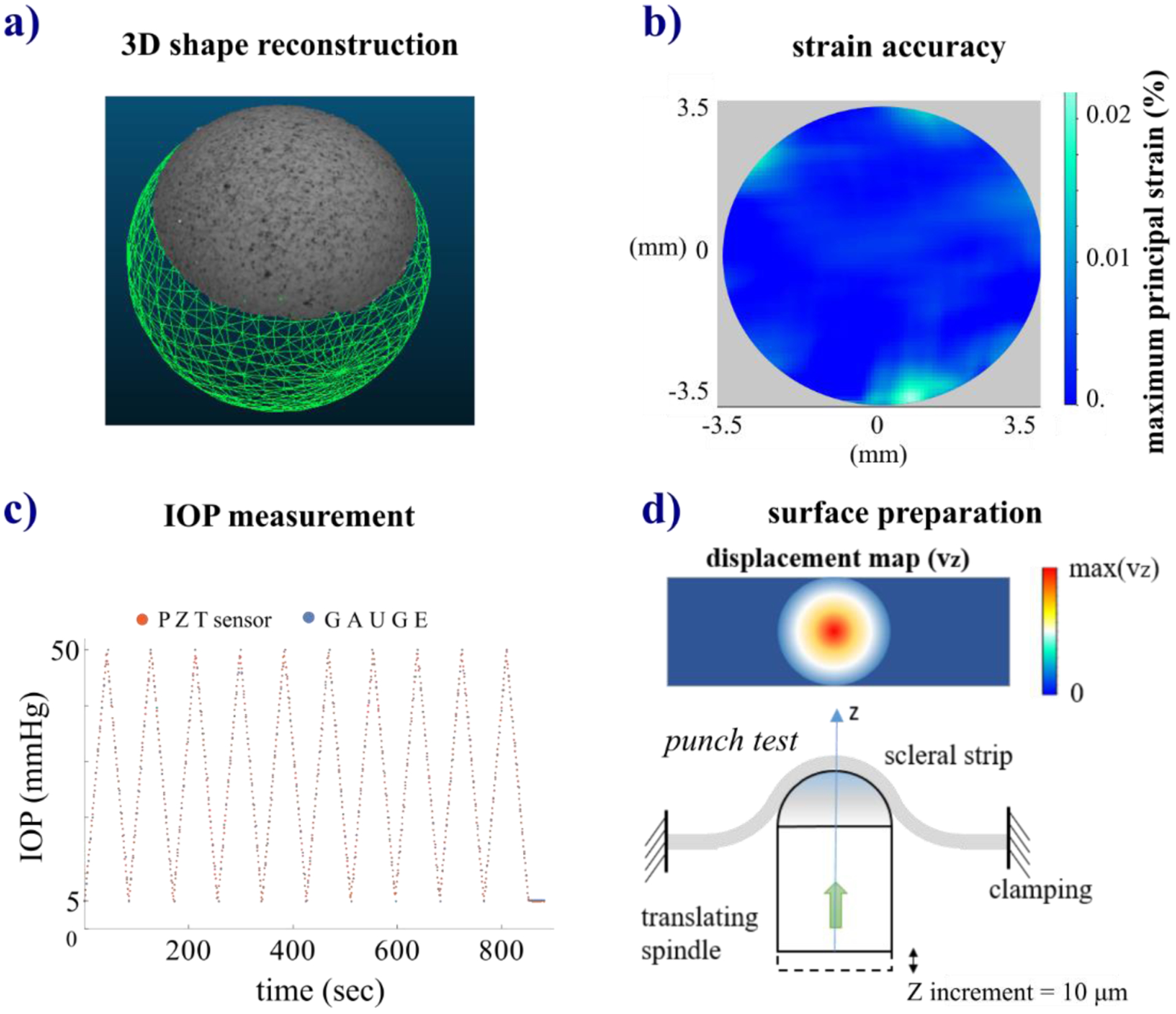
Validation of the inflation testing setup: a) 3D shape reconstruction of a ball bearing performed by DaVis software visualized as a textured 3D point cloud and comparison with a reference CAD model of the ball bearing used as “true” model; b) map of the maximum principal strain measured during a null strain test of a ball bearing to quantify the strain accuracy of the 3D-DIC system; c) comparison of the IOP measurements taken by a pressure gauge and a PZT sensor; d) illustration of the punch test used to assess the method proposed for the scleral surface preparation method by measuring the displacement accuracy of a scleral strip.