The Transition Metal Catalyzed [π2s + π2s + σ2s + σ2s] Pericyclic Reaction: Woodward–Hoffmann Rules, Aromaticity, and Electron Flow

Abstract

We have shown that the fundamental step responsible for enantioinduction in the inner-sphere asymmetric Tsuji allylic alkylation is C–C bond formation through a seven-membered pericyclic transition state. We employ an extensive series of quantum mechanics (QM) calculations to delineate how the electronic structure of the Pd-catalyzed C–C bond forming process controls the reaction. Phase inversion introduced by d orbitals renders the Pd-catalyzed [π2s + π2s + σ2s + σ2s] reaction symmetry-allowed in the ground state, proceeding through a transition state with Craig–Möbius-like σ-aromaticity. Lastly, we connect QM to fundamental valence bonding concepts by deriving an ab initio “arrow-pushing” mechanism that describes the flow of electron density through the reaction.

The fundamental step responsible for enantioinduction in the inner-sphere asymmetric Tsuji allylic alkylation is C–C bond formation through a seven-membered pericyclic transition state (TS1) (Figure 1A).¹ Since the original computational reports by our groups² and others,³ the relationship between this class of seven-membered transition states to those of the canonical pericyclic reactions as described by Woodward and Hoffmann is underexplored.⁴ Exemplifying the peculiar nature of the reaction, an analogous transformation in a system comprised of main group elements remains elusive.⁵ Given the key role of this seven-membered pericyclic process in asymmetric catalysis, we sought to delineate the underlying reactivity paradigm that enables this unique reactivity.

Figure 1.

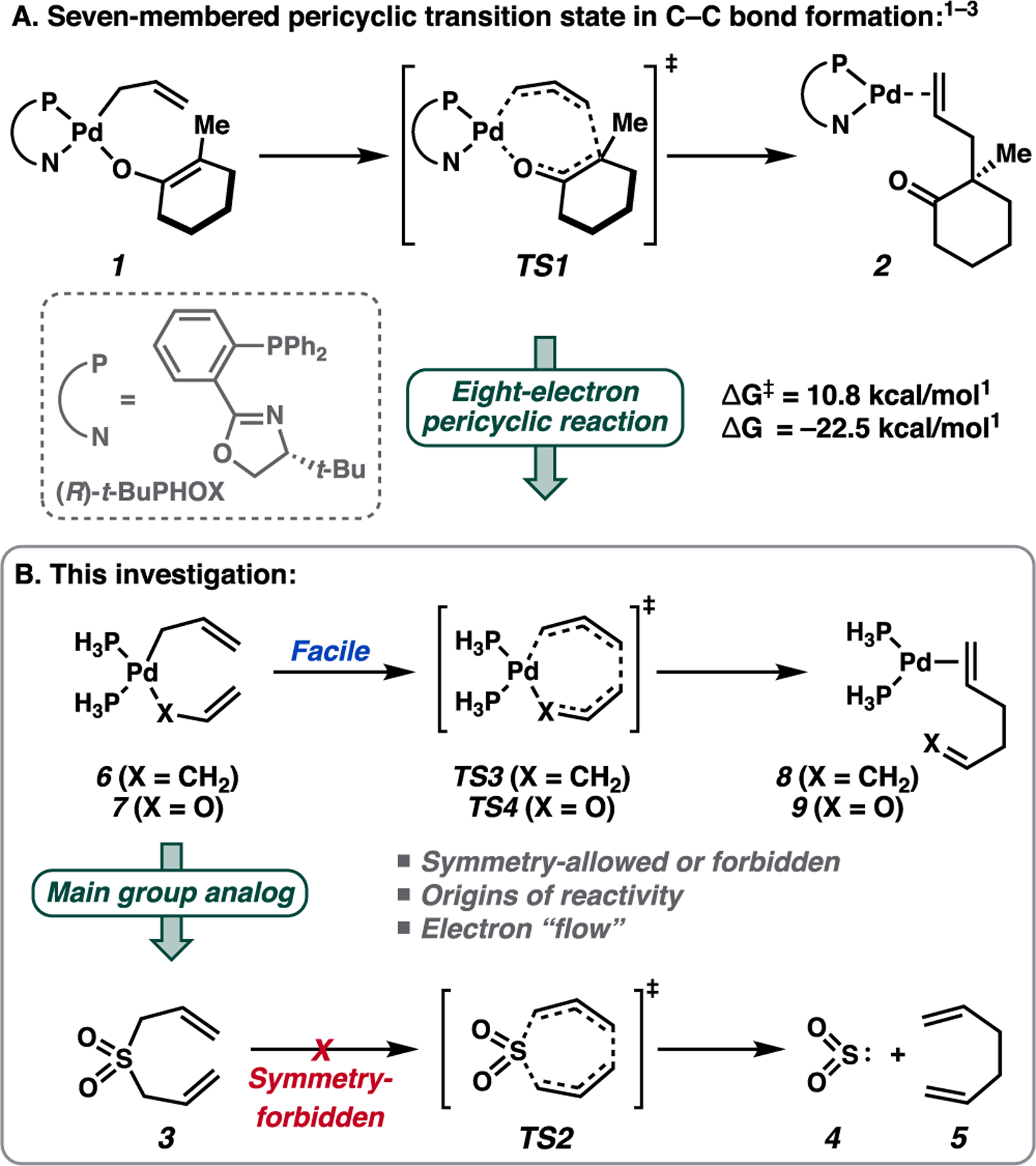
Inner-sphere C–C bond formation in the Pd-catalyzed asymmetric allylic alkylation reaction.^1–3

To obtain a general understanding of this bond forming event, we first examined an analogous system comprised of main group elements, namely, the reaction of diallyl sulfone 3 to sulfur dioxide (4) and 1,5-hexadiene (5) (Figure 2). If the geometry of the seven-membered quasi-cheletropic transition state (TS2) is constrained to match that of TS1, then a suprafacial relationship among the eight correlating orbitals with linear departure of the chelefuge is mandated. Thus, the transformation of 3 to 4 + 5 is designated [π2s + π2s + σ2s + σ2s], and the reverse is designated as [ω2s + π2s + π2s + σ2s].

Figure 2.

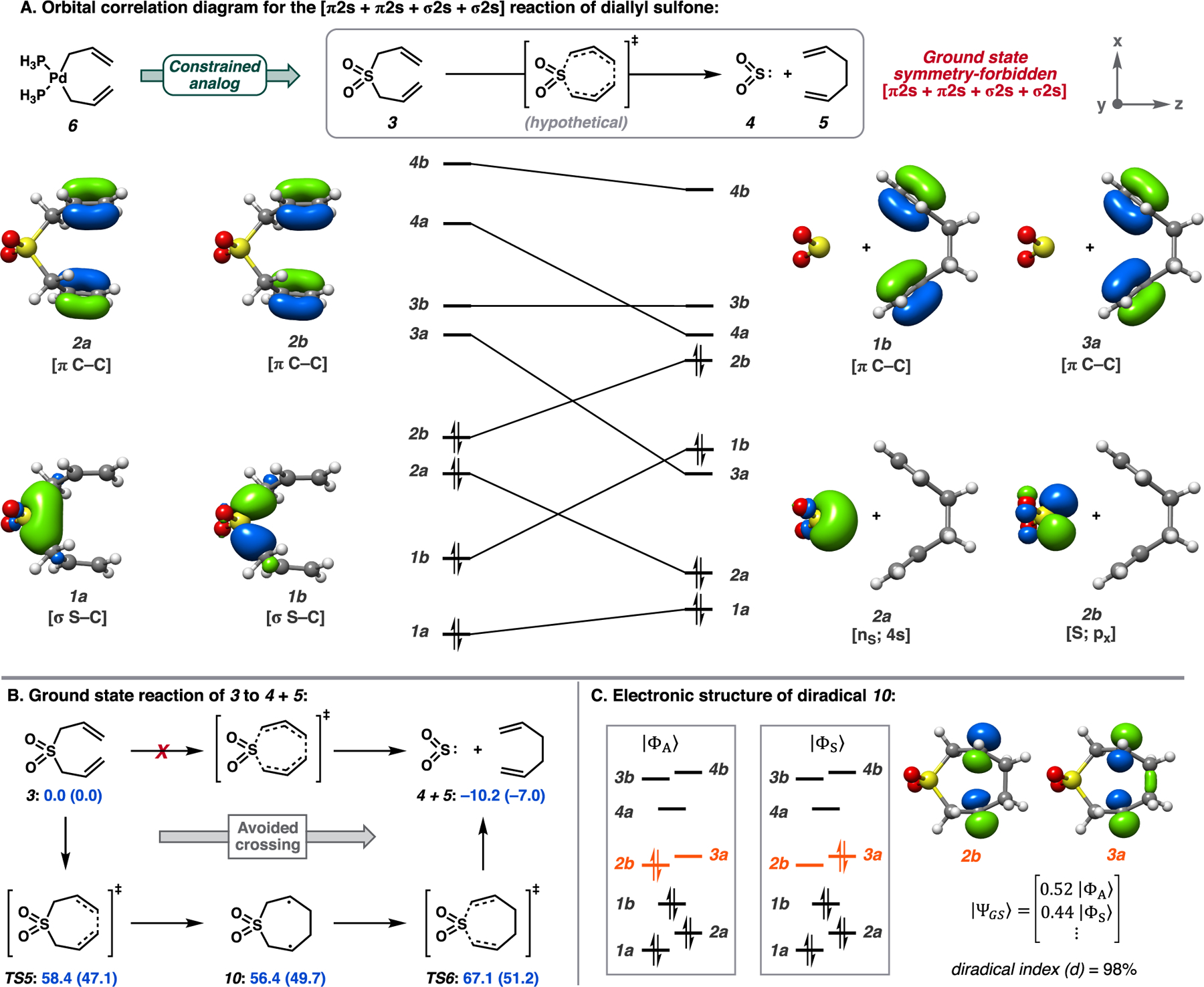
(A) Orbital correlation diagram for the [π2s + π2s + σ2s + σ2s] quasi-cheletropic reaction of diallyl sulfone. Select natural orbitals from the CAS(8,8) active space shown. (B) Symmetry-forbidden C–C bond formation from diallyl sulfone 3. CASSCF-based free energy estimates in kcal/mol with the NEVPT2-corrected values in parentheses. (C) Relevant orbitals in the (8,8) active space of diradical 10 and ground-state CI vector fractional composition.

With four suprafacial two-electron terms, the ground-state [π2s + π2s + σ2s + σ2s] pericyclic reaction of 3 to 4 + 5 is anticipated to be symmetry-forbidden by the generalized Woodward–Hoffmann rules.⁴ An identical conclusion is reached for chelefuges such as CO and N₂ in the ground state.⁶ Given the low thermal barriers with which the Pd-catalyzed transformations proceed (ΔG^⧧ = 10–20 kcal/mol),¹ we became curious as to whether the transformation is similarly forbidden for a L_nPd⁰-like chelefuge.

To uncover the electronic origins that enable the transition metal-mediated pericyclic processes, we turned to ab initio quantum mechanics (QM) calculations. Calculations were carried out with the ORCA ab initio package (see the Supporting Information for full computational details).⁷ Complete active space self-consistent field (CASSCF) theory is utilized to capture the multiconfigurational nature of the potential energy surface (PES), where the (8,8) active space is defined to be the eight valence electrons in eight correlating orbitals as described by orbital correlation diagrams. Dynamical correlation is accounted for via N-electron valence state perturbation theory⁸ (NEVPT2) single-point calculations on the CASSCF wave functions. All geometry optimizations and frequency calculations were carried out with the triple-ζ quality def2-TZVP basis set⁹ on all atoms (with the small core ECP28MWB pseudopotential¹⁰ on Pd, i.e., 18 explicit electrons including the 4s and 4p core electrons). For transition metal complexes with insignificant multiconfigurational character, geometries were obtained with density functional theory (DFT) (PBE0-D3(BJ)/def2-TZVP)¹¹ followed by CASSCF/NEVPT2 single-point calculations with the def2-TZVPP basis set. Solvation was accounted for in single-point calculation with the SMD model for THF.¹² All energies reported are solvated free energies at 298.15 K.

Beginning with main group analog diallyl sulfone (3), generation of symmetry-adapted linear combinations of correlating valence orbitals under approximate C₂ symmetry affords symmetric (a) and antisymmetric (b) sets of σ/σ*(C–S) and π/π*(C–C) orbitals (Figure 2A). Correlating these orbitals to those of the product implies an avoided crossing along the ground-state potential energy surface (PES) as the diabatic state describing 3, |Φ_A⟩, corresponds to a doubly excited state of the products. A single transition state connecting 3 to 4 + 5 was not found on the CASSCF potential energy surface. Rather, a stepwise process involving singlet diradical intermediate 10 was found (Figure 2B).¹³ At this point, the ground-state configuration interaction (CI) vector possesses nearly equal contributions of configurations |Φ_S⟩ and |Φ_A⟩, leading to a diradical index d = 98.0% (Figure 2C).¹⁴ Calculations with multireference iterative difference-dedicated CI (IDDCI) theory provide d = 95.4% and a singlet/triplet exchange coupling constant (J) of 83 cm⁻¹.¹⁵

In summary, the required crossing of the starting material (3) and product (4 + 5) diabatic ground states renders the concerted [π2s + π2s + σ2s + σ2s] reaction symmetry-forbidden. The ground-state PES of 3 → 4 + 5 is characterized by a stepwise mechanism involving weakly coupled diradical 10, with an overall ΔG^‡ of >50 kcal/mol, contrasting the low thermal barriers of Pd-catalyzed transformations (ΔG^‡ = 10–20 kcal/mol).¹ Given this, we became curious as to whether the Pd-catalyzed transformation is similarly symmetry-forbidden, proceeding through a low-energy diradical intermediate, or whether a unique set of symmetry elements describes the transformation that conserves orbital symmetry through the reaction.

In order to probe this hypothesis, we first considered the case of a simplified bis(η¹-allyl)Pd^II complex, 6. Contrary to 3, we find a single low-energy transition state (TS3), with ΔG^‡ = 13.4 kcal/mol, on the spin-restricted DFT (PBE0-D3(BJ)/def2-TZVP) PES connecting 6 to 8 (Figure 3B). We obtain a similar result for (η¹-allyl)Pd^II enolate 7. We find that the ground-state wave function along the PES is stable with respect to symmetry breaking, suggesting that a single closed-shell singlet (CSS) configuration is dominant. This suggests that simple DFT geometries should be reliable for these palladium complexes and will be used in the following.

Figure 3.

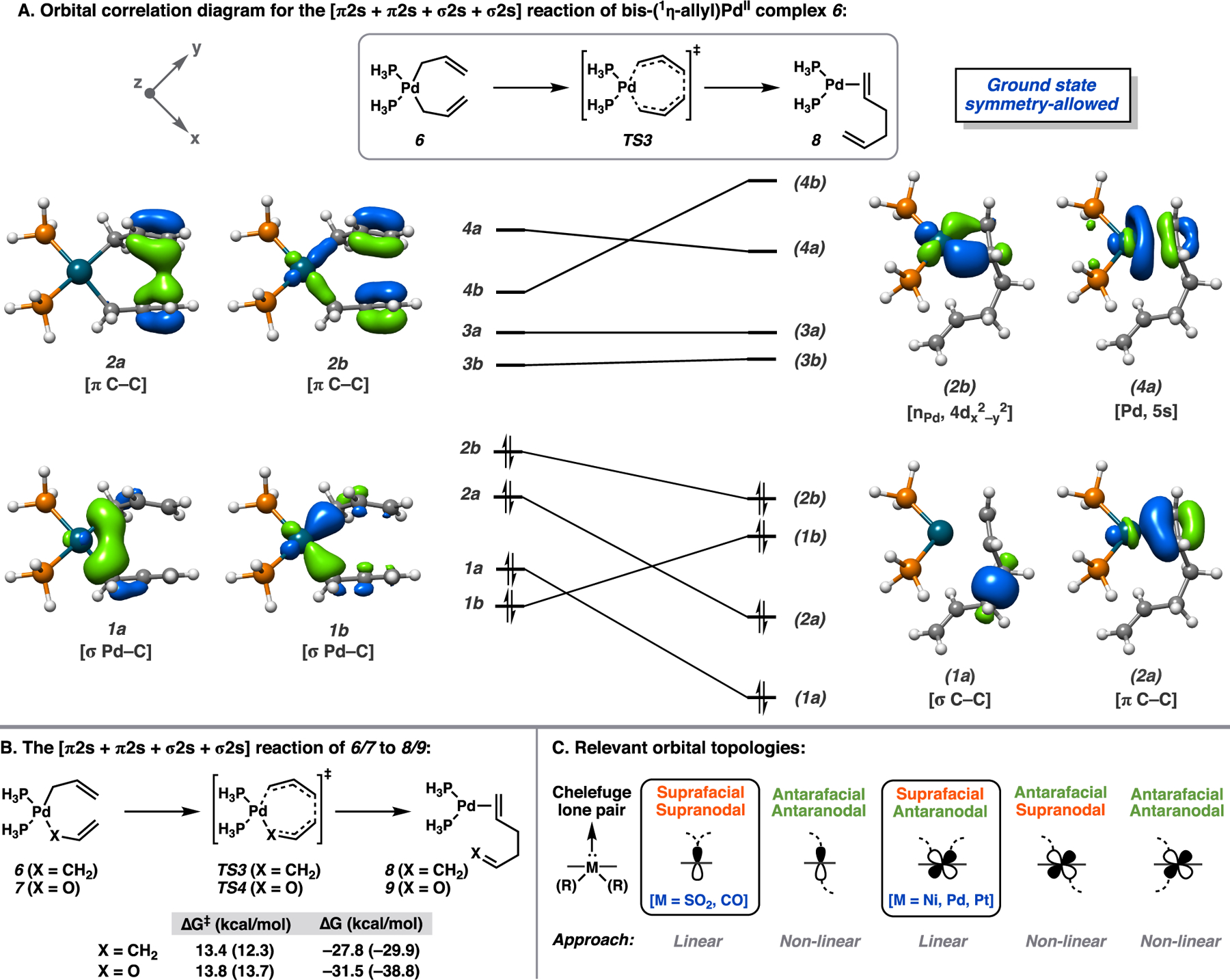
(A) Orbital correlation diagram for the pericyclic reaction of 6 to 8. Select natural orbitals of CAS(8,8) wave function shown. (B) DFT (PBE0-D3(BJ)) free energies with NEVPT2 [using DFT geometries and thermodynamical corrections] free energy estimates in parentheses. (C) Orbital topologies.

For comparison to the symmetry-forbidden transformation of 3 to 4 + 5, we construct the corresponding orbital correlation diagram for the conversion of 6 to 8 (Figure 3A). The four occupied correlating orbitals of starting complex 6 are identical in symmetry to those of diallyl sulfone 1. However, unlike the products of the thermally-forbidden reaction (4 + 5), complex 8 maintains the orbital symmetries of ground-state minimum 6. This is further evident in the composition of the ground-state CASSCF wave function at TS3, with weights of 0.86 and 0.02 for the dominant CSS configuration and second largest contributor, respectively. Hence, the Pd-catalyzed transformation is symmetry-allowed. The symmetry of the lone pair-like orbital of the chelefuge differentiates between the thermally-allowed and forbidden scenarios. In ground state SO₂, the lone pair occupies a symmetric sp² valence orbital (2a in Figure 2A), whereas in 8/9, this corresponds to the antisymmetric Pd-based ${\text{d}}_{x^2-y^2}$ orbital (2b in Figure 3A). Thus, the eight-electron seven-membered pericyclic transition is thermally-allowed in the cases of Pd complexes 7, 9, and 1 by virtue of the parity of the ${\text{d}}_{x^2-y^2}$ orbital involved in σ bonding with the organic scaffold.¹⁶

From the perspective of frontier molecular orbital (FMO) theory, the transformation is readily interpreted as the (in)ability of the chelefuge HOMO/donor to constructively interact with the antisymmetric LUMO/acceptor of the 1,5-hexadiene in the appropriate geometry (Figure 4). If constructive overlap is achieved, then net bonding is preserved through the transition state, and the reaction is thermally-allowed.^16a,b This is the case for the Pd-catalyzed transformation as the Pd-based ${\text{d}}_{x^2-y^2}$ HOMO of hypothetical L₂Pd⁰ chelefuge σ bonds with the diene in a suprafacial/antaranodal fashion (Figure 3C), that is, with phase inversion, constructively mixing with the diene LUMO (Figure 4C).¹⁷ This is not the case for the symmetric nucleophile lone pair orbitals of SO₂ and CO.⁶

Figure 4.

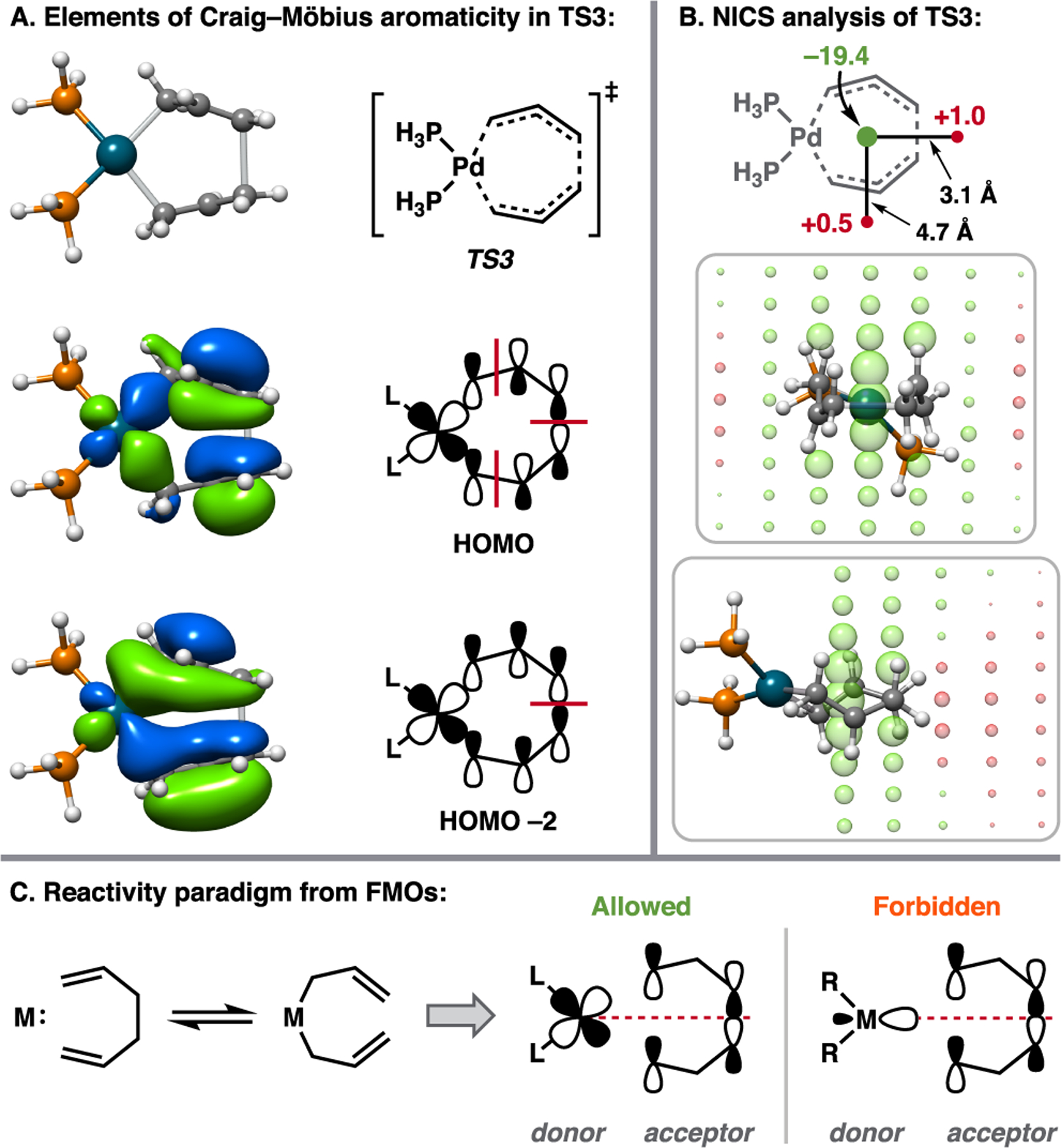
(A) Relevant MOs from the CAS(8,8) active space that contribute to the aromaticity of TS3. (B) NICS analysis of TS3. NICS values in ppm. For grid points, green and red spheres denote negative and positive NICS values, respectively, with the sphere radius depicting the magnitude of the shift (r = (|δ_ppm|)^1/3). (C) FMO perspective of the [π2 + π2 + σ2 + σ2] reaction.

It is well-understood that concerted, symmetry-allowed pericyclic reactions preferentially proceed through aromatic transition states.¹⁸ Thus, if the Pd-catalyzed [π2s + π2s + σ2s + σ2s] reaction of 6 to 8 is indeed thermally-allowed, then TS3 should be aromatic in nature. From analysis of the active space MOs at TS3 we find elements of Craig–Möbius-like aromaticity within the σ bonding framework.¹⁹ Particularly interesting is that the HOMO and HOMO–2 conform to a Möbius topology with the Pd ${\text{d}}_{x^2-y^2}$ generating a phase inversion and an odd number of nodes (1 and 3) along the ring (Figure 4A).²⁰ To probe this suspected aromaticity, we employ the nucleus-independent chemical shift (NICS) method of Schleyer and co-workers.²¹ A NICS(0) of −19.4 ppm is calculated at the geometric center of the 7-membered ring of TS3, indicating aromaticity.²² Likewise, a positive NICS is found at various points along the external periphery. For enhanced visualization, the NICS at points along 2D grids are displayed in Figure 4B.

A principal objective of our investigation is to relate electronic structure to intuitive concepts in chemical bonding. As such, we sought to explore whether the Pd-catalyzed [π2s + π2s + σ2s + σ2s] transformation could be properly described by valence bonding concepts such as the ubiquitous “arrow-pushing” mechanisms of Robinson and Ingold.²³ Given the single-configurational nature of the ground state density, the concept of electron flow is addressed through analysis of intrinsic bonding orbitals (IBOs) as described by Knizia and co-workers.²⁴ Previously, IBO analysis was implemented to highlight electron flow through transition states, discern between classes of mechanisms, and evaluate synchronicity of bond making/breaking in these events.²⁴ Generation of IBOs proceeds through a Pipek–Mezey-style localization where orbital charge contribution to an atomic center is measured by Intrinsic Atomic Orbital (IAO) charge.^24a,b At no point in the localization are empirical concepts of valence bonding introduced, thus the ensuing insight is purely ab initio to the extent of the preceding calculation.

IBO analysis was carried out with the full (PHOX)Pd enolate system (Figure 5). Four IBOs (ϕ_i) undergo significant displacement along the intrinsic reaction coordinate (IRC) through 1 → TS1 → 2.²⁵ The first of these, ϕ₁, corresponds to the localized π(C–C) bond of the enolate fragment, which smoothly progresses to encapsulate the density of the newly formed σ(C–C) bond of the product (Figure 5). Likewise, ϕ₂, ϕ₃, and ϕ₄ track the transformations of π(C–C) → π(C–C)′, $\sigma (\text{Pd}-\text{C})\to \text{n}\left(\text{Pd};{\text{d}}_{x^2-y^2}\right)$,²⁶ and σ(Pd–O) → π(C–O), respectively. Considering these transformations together reveals an intrinsic directionality to the flow of electron density in the Pd-catalyzed [π2s + π2s + σ2s + σ2s] reaction. Inspection of the relative magnitudes of net orbital displacement along the IRC further suggests synchronicity in the bond making/breaking events of the [π2s + π2s + σ2s + σ2s] process (Figure 5). In accord with the initial reports of Knizia and co-workers, we also find the localized IBOs obtained from the ground-state densities closely resemble valence orbitals as portrayed in simple Lewis structures. Thus, tracking the net flow of electron density is carried out in the same valence bonding framework. The result is a mechanism described by the synchronous movement of valence bonding electron pairs, or more precisely, a first-principles-derived “arrow-pushing” mechanism that accounts for the net change in bonding along the reaction coordinate in a chemically intuitive orbital basis (Figure 5).^24b,c

Figure 5.

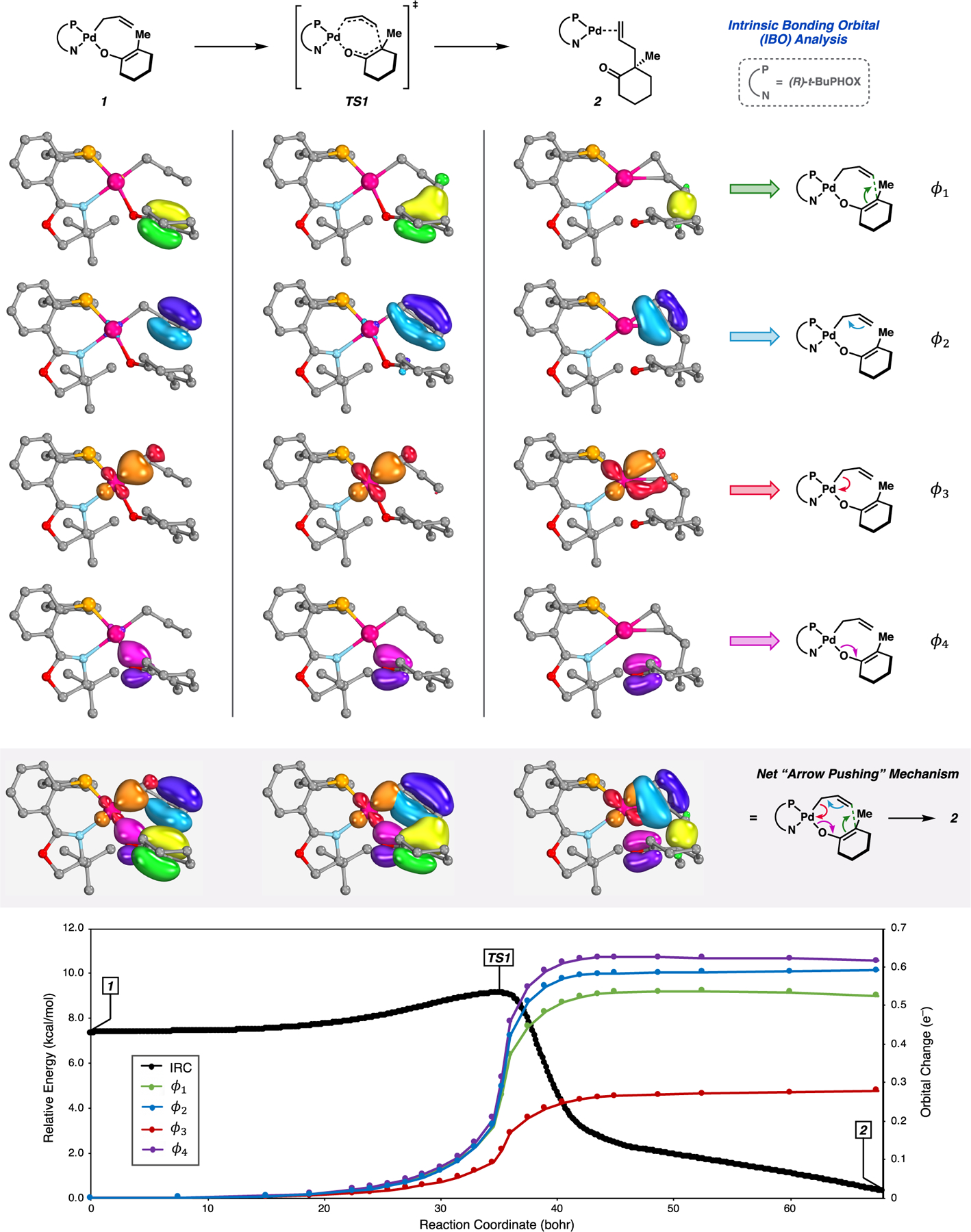
Transformation of four IBOs (ϕ₁−ϕ₄) along the IRC connecting palladium enolate 1 to 2 via TS1. Orbital change is defined in accordance with ref 24. Select atoms of PHOX ligand omitted for clarity.

In conclusion, we find the Pd-catalyzed [π2s + π2s + σ2s + σ2s] reaction to be symmetry-allowed in the ground state owing to the phase-inverting role of the Pd ${\text{d}}_{x^2-y^2}$ orbital in the σ bonding framework of the transition state. Insights from this investigation are contextualized within the frameworks of the Woodward–Hoffmann rules, orbital correlation diagrams, and FMO theory. As with prototypical thermally-allowed pericyclic reactions, we find the Pd-catalyzed [π2s + π2s + σ2s + σ2s] reaction proceeds through an aromatic transition state. Finally, we describe a first-principles-derived “arrow-pushing” mechanism from analysis of the flow of electron density through the transformation by means of IBOs. These efforts highlight the connection between ab initio electronic structure calculations and empirical bonding concepts, thus facilitating a natural conceptualization of chemical bonding in these unique systems.