Inference of the Local Interstellar Spectra of Cosmic-Ray Nuclei Z ⩽ 28 with the GalProp–HelMod Framework

Abstract

Composition and spectra of Galactic cosmic rays (CRs) are vital for studies of high-energy processes in a variety of environments and on different scales, for interpretation of γ-ray and microwave observations, for disentangling possible signatures of new phenomena, and for understanding of our local Galactic neighborhood. Since its launch, AMS-02 has delivered outstanding-quality measurements of the spectra of $\overline{p}$, e^±, and nuclei: ₁H–₈O, ₁₀Ne, ₁₂Mg, ₁₄Si. These measurements resulted in a number of breakthroughs; however, spectra of heavier nuclei and especially low-abundance nuclei are not expected until later in the mission. Meanwhile, a comparison of published AMS-02 results with earlier data from HEAO-3-C2 indicates that HEAO-3-C2 data may be affected by undocumented systematic errors. Utilizing such data to compensate for the lack of AMS-02 measurements could result in significant errors. In this paper we show that a fraction of HEAO-3-C2 data match available AMS-02 measurements quite well and can be used together with Voyager 1 and ACE-CRIS data to make predictions for the local interstellar spectra (LIS) of nuclei that are not yet released by AMS-02. We are also updating our already-published LIS to provide a complete set from ₁H–₂₈Ni in the energy range from 1 MeV nucleon⁻¹ to ~100–500 TeV nucleon⁻¹, thus covering 8–9 orders of magnitude in energy. Our calculations employ the GalProp–HelMod framework, which has proved to be a reliable tool in deriving the LIS of CR $\overline{p}$, e⁻, and nuclei ₁H–₈O.

1. Introduction

The past decade has brought impressive advances in astrophysics of cosmic rays (CRs) and γ-ray astronomy. Launches of new missions that are employing forefront detector technologies were followed by a series of remarkable discoveries¹⁰ even in the energy range that is deemed as well studied. Many of those missions have the discovery of dark matter (DM) as one of their primary goals (Porter et al. 2011; Hooper et al. 2020).

Among those missions are the Payload for Antimatter Matter Exploration and Light-nuclei Astrophysics (PAMELA; Picozza et al. 2007; Adriani et al. 2014), the Fermi Large Area Telescope (Fermi-LAT; Atwood et al. 2009), the Alpha Magnetic Spectrometer—02 (AMS-02; Aguilar et al. 2013), the NUCLEON experiment (Atkin et al. 2018, 2019; Grebenyuk et al. 2019a, 2019b), the CALorimetric Electron Telescope (CALET; Adriani et al. 2019; Torii et al. 2019; Maestro et al. 2020), the DArk Matter Particle Explorer mission (DAMPE; Chang et al. 2017; DAMPE Collaboration et al. 2017; An et al. 2019), and the Cosmic-Ray Energetics and Mass investigation (ISS-CREAM; Seo et al. 2014). Outstanding results have also been delivered by more mature missions, such as the Cosmic Ray Isotope Spectrometer on board the Advanced Composition Explorer (ACE-CRIS; Binns et al. 2016; Israel et al. 2018) operating at the L1 Lagrange point for more than two decades, and by the grandparents of the current instrumentation, the Voyager 1, 2 spacecraft (Stone et al. 1977), which were built with the technology of the 1970s and launched in 1977 at the dawn of the space era. The latter are providing unique data on the elemental spectra and composition at the interstellar reaches of the solar system (Stone et al. 2013; Cummings et al. 2016; Stone et al. 2019), currently at 149 and 124 au from the Sun, respectively. The modern technologies employed by many of these missions have enabled measurements with unmatched precision, which allow for searches of subtle signatures of new phenomena and DM in CR and γ-ray data, e.g., the claimed precision of AMS-02 data is 1%–3%.

Indirect observations of CR acceleration sites and CR propagation in the Galaxy and beyond are made by γ-ray telescopes covering the range from MeV to multi-TeV. Among these instruments are the International Gamma-Ray Astrophysics Laboratory (Bouchet et al. 2008, 2010, 2011), Fermi-LAT (Ackermann et al. 2012), the High-Altitude Water Cherenkov γ-ray observatory (HAWC; Abeysekara et al. 2017, 2019), the Large High Altitude Air Shower Observatory (LHAASO; Bai et al. 2019) currently under construction, and three atmospheric Cherenkov telescopes: the High Energy Stereoscopic System (H.E.S.S.; Hinton & Hofmann 2009; H.E.S.S. Collaboration et al. 2018), Major Atmospheric Gamma-ray Imaging Cherenkov Telescopes (MAGIC; Aleksić et al. 2016), and the Very Energetic Radiation Imaging Telescope Array System (VERITAS; Holder et al. 2006; Humensky & VERITAS Collaboration 2019). Construction of the next-generation Cherenkov Telescope Array¹¹ (CTA) began in 2017 (Acharya et al. 2013; see also the CTA Consortium of 2019). High-resolution data in the microwave domain are provided by the Wilkinson Microwave Anisotropy Probe (Bennett et al. 2003, 2013) and the Planck mission (Tauber et al. 2010; Planck Collaboration et al. 2016b).

Recent technological advances in astrophysics of CRs and γ-ray astronomy and the reached level of precision imply that we are on the verge of major discoveries. Meanwhile, disentangling faint signals of new physics from the conventional astrophysical processes requires a high degree of sophistication, including a proper description of all variety of interactions of CR species in the interstellar medium (ISM), a description of the detailed properties of the ISM itself, and understanding of the propagation of energetic particles in the Galaxy and in the heliosphere. Such a description has to be self-consistent, i.e., account for the interrelationships between CR species and their associated photon emissions (radio to γ-rays), and compare well with available data. Understanding the conventional astrophysical backgrounds and having the most up-to-date knowledge of physics of the ISM—these are the keys to extracting weak signals of new physics. If the signatures of DM were too obvious, we would have discovered them long ago.

The direct precise measurements of spectra of CR species in the wide energy range form a basis for propagation models, for interpretation of γ-ray and microwave observations, and for disentangling possible hints of new phenomena. Composition and spectra of CR species are vital for studies of galactic nucleosynthesis and high-energy processes in a variety of environments, from CR sources to properties of the ISM and the Milky Way galaxy as the whole, and they are equally important for understanding our local Galactic environment. Since the beginning of its operation, AMS-02 has delivered outstanding-quality measurements of the spectra of CR protons, $\overline{p}$, e^±, and nuclei ₂He–₈O, ₁₀Ne, ₁₂Mg, and ₁₄Si (Aguilar et al. 2014, 2015a, 2015b, 2016a, 2016b, 2017, 2018b, 2018c, 2019a, 2019b, 2020). These measurements have already resulted in a number of breakthroughs. However, the spectra of heavier nuclei and especially low-abundance nuclei, such as ₉F, ₁₁Na, ₁₃Al, and ₁₅P–₂₈Ni, are expected to be available only later in the mission. Meanwhile, a comparison of published AMS-02 results with data from earlier experiments, such as HEAO-3-C2 (Engelmann et al. 1990), indicates that earlier data may be affected by significant undocumented systematic errors (see Boschini et al. 2018b, 2020). Therefore, we found ourselves in an awkward position: we are keen to use new data to move forward, but we cannot do it because the new data are still incomplete. At the same time, using the old data to make up for the lack of AMS-02 measurements could lead to significant errors.

In this paper we are using the existing AMS-02 data to test HEAO-3-C2 results (Engelmann et al. 1990). We show that the local interstellar spectra (LIS) built with available AMS-02 measurements match well some part of the HEAO-3-C2 data when modulated appropriately to the solar activity observed during the HEAO-3-C2 flight. This part of the HEAO-3-C2 data can be used together with Voyager 1 (Cummings et al. 2016; Stone et al. 2019) and ACE-CRIS data to make predictions for the LIS of nuclei that are not yet released by the AMS-02 collaboration. We are also updating our already-published LIS to provide a complete set of LIS from ₁H–₂₈Ni in the kinetic energy range from 1 MeV nucleon⁻¹ to ~100–500 TeV nucleon⁻¹, thus covering 8–9 orders of magnitude in energy. Our calculations employ the GalProp–HelMod framework, which has proved to be a reliable tool in deriving the LIS of CR species: $\overline{p}$, e⁻, and nuclei from ₁H to ₈O.

2. CR Transport in the Galaxy and the Heliosphere

Here we provide short descriptions of the two dedicated codes that are used in the present work and that complement each other: GalProp,¹² for description of the interstellar propagation, and HelMod,¹³ for description of the heliospheric transport. More details can be found in the referenced papers.

2.1. GalProp Framework for Galactic CR Propagation and Diffuse Emissions

Our main research tool is the state-of-the-art fully numerical GalProp code that describes propagation of Galactic CRs and production of the associated diffuse emissions (radio, X-rays, γ-rays). It has about 23 yr of development behind it (Moskalenko & Strong 1998; Strong & Moskalenko 1998). Over these years, the GalProp code has proven to be invaluable tool in sophisticated analyses in many areas of astrophysics, including numerous searches for DM signatures (e.g., Ackermann et al. 2012, 2015; Vladimirov et al. 2012; Ajello et al. 2016; Cummings et al. 2016; Planck Collaboration et al. 2016a, 2016b; Achterberg et al. 2017; Karwin et al. 2017, 2019; Cholis et al. 2019; Abdollahi et al. 2020).

The GalProp code uses information from astronomy, particle, and nuclear physics to predict CRs, γ-rays, synchrotron emission, and its polarization in a self-consistent manner. The key concept underlying the GalProp code is that various kinds of data, e.g., direct CR measurements, $\overline{p}$, e^±, γ-rays, synchrotron radiation, and so forth, are all related to the same Galaxy and hence have to be modeled self-consistently (Moskalenko et al. 1998). It provides the modeling framework unifying results of many individual experiments in physics and astronomy spanning in energy coverage, types of instrumentation, and the nature of detected species. The goal for the GalProp-based models is to be as realistic as possible and to make use of available information with a minimum of simplifying assumptions (Strong et al. 2007). The range of physical validity of the GalProp code extends from sub-keV to PeV energies for particles and from 10⁻⁶ eV to PeV energies for photons.

The GalProp code solves a system of about 90 time-dependent transport equations (partial differential equations in 3D or 4D: spatial variables plus energy) with a given source distribution and boundary conditions for all CR species: ${}_1^1\text{H}-{}_{28}^{64}\text{Ni}$, $\overline{p}$, e^± (Strong & Moskalenko 1998; Strong et al. 2007, 2009). This includes convection, distributed reacceleration, energy losses, nuclear fragmentation, radioactive decay, and production of secondary particles and isotopes. The numerical solution is based on a Crank–Nicholson implicit second-order scheme (Press et al. 1992). The spatial boundary conditions assume free particle escape. For a given halo size the diffusion coefficient, as a function of rigidity and propagation parameters, is determined from secondary-to-primary nuclei ratios, typically ₅B/₆C, [₂₁Sc+₂₂Ti+₂₃V]/₂₆Fe, and/or $\overline{p}/p$. If reacceleration is included, the momentum-space diffusion coefficient D_pp is related to the spatial coefficient D_xx = βD₀R^δ (Seo & Ptuskin 1994), where β = v/c is the particle velocity, R is the magnetic rigidity, δ =1/3 for a Kolmogorov spectrum of interstellar turbulence (Kolmogorov 1941), or δ = 1/2 for an Iroshnikov–Kraichnan cascade (Iroshnikov 1964; Kraichnan 1965), or it can also be arbitrary. Also arbitrary can be the spatial dependence of the diffusion coefficient, but for calculations in this paper it is assumed to be uniform throughout the Galaxy. For more details and fitted parameter values see Section 3 and Table 1.

Table 1.

Best-fit Propagation Parameters for I- and P-Scenarios

Parameter	Units	Best Value	Error
z h	kpc	4.0	0.6
D0(R = 4 GV)	cm2 s−1	4.3 × 1028	0.7
δ a		0.415	0.025
V Alf	km s−1	30	3
dVconv/dz	km s−1 kpc−1	9.8	0.8

Note.

^aThe P-scenario assumes a break in the diffusion coefficient with index δ₁ = δ below the break and index δ₂ = 0.15 ± 0.03 above the break at R = 370 ± 25 GV; see the text for details.

Distributions of CR sources and gas components can be customized at the user’s discretion. Their configurations are defined with an XML file (using the galstruct library distributed with the galtoolslib package), where each entry is a single component that can be added to the aggregate distribution. Possible components include an axisymmetric disk, spiral arms, various central bulges, and other structures. Each basic component can be further split up and fine-tuned with different radial profiles, allowing for a very flexible description of a galaxy.

In this work we are using a standard pulsar distribution for all CR species:

$$S(r)\propto {\left(\frac{r}{R_{\odot }}\right)}^{\alpha }\text{exp}\left(-\beta \frac{r-R_{\odot }}{R_{\odot }}\right),$$ (1)

where r (kpc) is the distance from the Galactic center, and the parameter values α = 1.9, β = 5.0, R_⊙ = 8.5 kpc correspond to the C-model from Lorimer et al. (2006). Meanwhile, the results are not sensitive to the used CR source distribution, and other parameterizations, such as the supernova remnant (SNR) distribution (Case & Bhattacharya 1998) or another pulsar distribution (Yusifov & Küçük 2004), work as well. The total injected CR power does not vary at most more than a few percent over these similar 2D, or more detailed 3D, CR source distributions (Strong et al. 2010; Porter et al. 2017). The injection spectra of CR species are parameterized by the rigidity-dependent function:

$$q(R)\propto {\left(R/R_0\right)}^{-{\gamma }_0}\prod _{i=0}^2{\left[1+{\left(R/R_i\right)}^{\frac{{\gamma }_i-{\gamma }_{i+1}}{s_i}}\right]}^{s_i},$$ (2)

where γ_i = _0,1,2,3 are the spectral indices, R_i = _0,1,2 are the break rigidities, and s_i are the smoothing parameters (s_i is negative/positive for $|{\gamma }_i|\lessgtr |{\gamma }_{i+1}|$).

The GalProp code computes a complete network of primary, secondary, and tertiary isotope production starting from input CR source abundances. Since the decay branching ratios and half-lives of fully stripped and hydrogen-like ions may differ, GalProp includes the processes of K-electron capture, electron pickup from neutral ISM gas, and formation of hydrogen-like ions, as well as the inverse process of electron stripping (Pratt et al. 1973; Wilson 1978; Crawford 1979). Meanwhile, the fully stripped and hydrogen-like ions are treated as separate species. Also included are knock-on electrons (Abraham et al. 1966; Berrington & Dermer 2003) that may significantly contribute to hard X-ray–soft γ-ray diffuse emission through inverse Compton scattering and bremsstrahlung (Porter et al. 2008).

The nuclear reaction network is built using the 64 volumes of Nuclear Data Sheets (see Nuclear Data Sheets 2018, for Cumulated Index to A-Chains for A = 1 − 64 nuclei). Included are multistage chains of p, n, d, t, ³He, α, β^±-decays, and electron K-capture, and, in many cases, more complicated reactions. This accounts for up to four stages of three decay branchings (ℬ) each in any of the decay channels, i.e., up to 3⁴ = 81 total daughter nuclei in the final state for each fragment produced in spallation of the initial target nucleus plus an unlimited number of p, n, and β^±-decays. For example, for a neutron-deficient fragment ${}_{12}^{20}\text{Mg}$ we have a two-stage decay chain with three daughter nuclei in the final state:

$$\begin{array}{lll}{}_{12}^{20}\text{Mg}\hfill & \to {}_{10}{}^{19}\text{N}\text{e}(ℬ=0.03)\stackrel{{\beta }^{+}}{\to }\hfill & {}_9{}^{19}\text{F}\hfill \\ \hfill & \searrow {}_{11}{}^{20}\text{N}\text{a}(ℬ=0.97)\stackrel{{\beta }^{+}}{\to }\hfill & {}_{10}{}^{20}\text{N}\text{e}(ℬ=0.80)\hfill \\ \hfill & \hfill & \searrow {}_8{}^{16}\text{O}(ℬ=0.20).\hfill \end{array}$$

Another example is a neutron-rich fragment ${}_4^{14}\text{Be}$, where we have a two-stage decay chain with four daughter nuclei in the final state:

$$\begin{array}{lll}{}_4{}^{14}\text{B}\text{e}\hfill & \to {}_5{}^{14}\text{B}(ℬ=0.14)\stackrel{{\beta }^{-}}{\to }\hfill & {}_6{}^{14}\text{C}\stackrel{{\beta }^{-}}{\to }{}_7{}^{14}\text{N}\hfill \\ \hfill & \searrow {}_5{}^{13}\text{B}(ℬ=0.81)\stackrel{{\beta }^{-}}{\to }\hfill & {}_6{}^{13}\text{C}\hfill \\ \hfill & \searrow {}_5{}^{12}\text{B}(ℬ=0.05)\stackrel{{\beta }^{-}}{\to }\hfill & {}_6{}^{12}\text{C}(ℬ=0.97)\hfill \\ \hfill & \hfill & \searrow 2\times {}_2{}^4\text{H}\text{e}(ℬ=0.06).\hfill \end{array}$$

Here we have two α-particles with branching ℬ = 0.03, and thus the branching of this chain is ℬ = 0.06. The individual branchings in the consequent decay chains are multiplied to obtain the yields of the final products.

The routines for the isotopic production cross sections are built using a systematic approach tuned to all available data extracted from Los Alamos (LANL) and Experimental Nuclear Reaction Data (EXFOR) databases, as well as from an extensive literature search. To account for different measurement techniques that were introduced in experimental nuclear physics over decades of research since the 1950s, the distinction was made between the individual, direct, decaying, charge-changing, cumulative, differential, total, and isobaric cross sections, or reactions with metastable final states, with the target that could be a particular isotope, a natural sample with mixed isotopic composition, or a chemical compound. Often, experimental cross sections for the same reaction published by various groups were found to differ by a significant factor. A (tough) decision on which set to be used was based on examination of the descriptions of particular experimental setups in the original papers.

One example is a hard-to-find 26-page document PRVCAN-58-074812-24, which is a supplement to a paper by Webber et al. (1998) detailing the secondary beam quality used for measurements of individual charge-changing and isotopic production cross sections, along with the cross-section values themselves measured with the 1.52 g cm² thick hydrogen target at SATURNE. For many secondary beams the quality is marked as >90%, which means the percentage of the desired isotope in the beam. This may be acceptable given the accuracy of CR measurements at that time. However, many other secondary beams have a much smaller fraction of the isotope in question, such as ${}_{11}^{22}\text{Na\hspace{0.17em}}(72\%)$, ${}_{15}^{30}\text{P\hspace{0.17em}}(57\%)$, ${}_{16}^{33}\text{S\hspace{0.17em}}(61\%)$, ${}_{17}^{34}\text{Cl\hspace{0.17em}}\left(65\%\right)$, ${}_{24}^{52}\text{Cr\hspace{0.17em}}(81\%)$, and ${}_{26}^{54}\text{Fe\hspace{0.17em}}(60\%)$, and these are just a few examples. At the same time, the typical accuracy of the measured cross sections is claimed to be 3%–5% (labeled B), 5%–8% (C), or 8%–12% (D), which perhaps represent only statistical errors. The true beam energy varies from 496 to 577 MeV nucleon⁻¹, not being 600 MeV nucleon⁻¹ for all beams as claimed. The total error for such measurements used in the fits and in GalProp routines was increased appropriately, reaching up to 50% in some cases. Meanwhile, even such quality measurements are often the only measurement available for a particular reaction, as many astrophysically important reactions were not measured at all.

The isotopic production cross sections were ranked by their contributions to the production of a particular isotope (see, e.g., Moskalenko et al. 2013). The most effort was devoted to the main contributing channels. The approach to the description of each channel depended on the accuracy and availability of experimental data. If the cross-section data were detailed enough, they were approximated with fitted functional dependences or provided as a table for interpolation. If only a few or no data points were available, such cross sections were approximated using the results of the Los Alamos nuclear codes (Moskalenko et al. 2001, 2003, 2005; Moskalenko & Mashnik 2003; Mashnik et al. 2004), such as a version of the Cascade-Exciton Model (CEM2k; Mashnik et al. 2004) and the ALICE code with the Hybrid Monte Carlo Simulation model (HMS-ALICE; Blann 1996; Blann & Chadwick 1998). In general, parameterizations of all isotopic production cross sections are provided from a few MeV nucleon⁻¹ to several GeV nucleon⁻¹, above which they are assumed to be constant.

In the case of a minor contribution channel, the best of the available semiempirical formulae by Webber et al. (WNEWTR code with modifications made in 2003; Webber et al. 2003) or parametric formulae by Silberberg and Tsao (YIELDX code; Silberberg et al. 1998; Tsao et al. 1998) normalized to the data when they exist was used. Each of the thousands of channels was tested to ensure the best description of the available data. A very limited database of the measured cross-section points is supplied with GalProp routines to renormalize the output of WNEWTR and YIELDX codes. The data points to include in this database were selected for the stated validity range of the semiempirical formulae (typically >150 MeV nucleon⁻¹; Webber et al. 2003), while the data points outside of this validity range were excluded from the auxiliary files.

The total (inelastic) fragmentation cross sections for pA- and AA-reactions are calculated using the CRN6 code by Barashenkov & Polanski (1994), or using optional parameterizations by Letaw et al. (1983) or by Wellisch & Axen (1996, with corrections provided by the authors) and A-scaling dependencies.

Though the overall process was very laborious and often impossible to automate, it produced probably the most accurate package (nuc_package.cc and auxiliary files) for massive calculations of the production nuclear cross sections so far. Since it is the core part of GalProp, it was used in numerous studies where the GalProp code was employed. It was also used in many studies of the accuracy of the isotopic production cross sections employed in astrophysical applications (e.g., Tomassetti 2015; Génolini et al. 2018; Evoli et al. 2019) and in other Galactic propagation codes, such as, e.g., Diffusion of cosmic RAys in galaxy modelizatiON code (DRAGON; Evoli et al. 2008, 2016). A more recent attempt to characterize the uncertainties in the calculation of the isotopic production cross sections was made in the framework of the ongoing ISOtopic PROduction Cross Sections (ISOPROCS) project (Moskalenko et al. 2011, 2013).

Production of secondary particles in GalProp is calculated taking into account pp-, pA-, Ap-, and AA-reactions. Calculations of $\overline{p}$ production and propagation are detailed in Moskalenko et al. (2002, 2003), Kachelriess et al. (2015), and Kachelrieß et al. (2019), while inelastically scattered (tertiary) $\overline{p}$ and (secondary) p are treated as separate species owing to the catastrophic energy losses. Production of neutral mesons (π⁰, K⁰, ${\overline{K}}^0$, etc.) and secondary e^± is calculated using the formalism by Dermer (1986a, 1986b) as described in Moskalenko & Strong (1998) or more recent parameterizations (Kamae et al. 2006; Kachelrieß & Ostapchenko 2012; Kachelriess et al. 2014; Kachelrieß et al. 2019).

Production of γ-rays is calculated using the propagated CR distributions, including primary e⁻, secondary e^±, and knock-on e⁻, as well as inelastically scattered (secondary) protons (Strong et al. 2004; Porter et al. 2008). The inverse Compton scattering is treated using the formalism for an anisotropic background photon distribution (Moskalenko & Strong 2000) with full Galactic interstellar radiation field on the 2D or 3D grid (Moskalenko et al. 2006; Porter et al. 2006). Electron bremsstrahlung cross section is calculated as described in Strong et al. (2000). Gas-related γ-ray intensities (π⁰-decay, bremsstrahlung) are computed from the emissivities using the column densities of H₂ + H i (+ H ii, ionized hydrogen) gas for Galactocentric annuli based on 2.6 mm carbon monoxide CO (a tracer of molecular hydrogen H₂) and 21 cm H i (atomic hydrogen) survey data. The synchrotron emission¹⁴ and its polarization are computed (Orlando & Strong 2013) using published models of the Galactic magnetic field for regular, random, and striated components (Sun et al. 2008; Sun & Reich 2010; Pshirkov et al. 2011; Jansson & Farrar 2012). The line-of-sight integration of the corresponding emissivities with the distributions of gas, interstellar radiation, and magnetic fields yields γ-ray and synchrotron sky maps. Spectra of CR species and the γ-ray and synchrotron sky maps are output in standard astronomical formats.

Similarly to ordinary CR species and their diffuse emissions, GalProp has well-developed options to propagate particles produced in exotic sources and processes, such as annihilation or decay of DM particles, and calculate the associated emissions (DM γ-ray and synchrotron sky maps). It can be used alone or run in conjunction with dedicated packages, such as DarkSUSY; the appropriate interface is also provided.

Recent updates and developments of the GalProp code are detailed in Porter et al. (2017, 2019) and Jóhannesson et al. (2018, 2019). All details on GalProp, including the description of all involved processes and reactions, can be found in dedicated publications (Moskalenko & Jourdain 1997; Moskalenko & Strong 1998, 2000; Strong & Moskalenko 1998; Strong et al. 2000, 2004, 2007, 2010, 2011; Moskalenko et al. 2002, 2003, 2017; Ptuskin et al. 2006; Vladimirov et al. 2011, 2012; Orlando & Strong 2013; Génolini et al. 2018).

2.1. HelMod Model for Heliospheric Transport

Before reaching Earth orbit, CR particles pass through the interplanetary medium, called the heliosphere. Though many processes are similar to the Galactic propagation, the heliosphere has its own specifics. Solar activity changes on weekly and monthly scales, and the solar wind and magnetic field vary with time and position in space, and therefore they require a dedicated modeling to understand all factors involved (see discussion in Boschini et al. 2017). The heliospheric propagation of CR species leads to the suppression of the particle flux below ≲50 GV; this phenomenon is called the solar modulation, and the strength of the suppression depends on the solar activity, particle charge sign, polarity of the solar magnetic field, and other conditions. In this work, the particle transport within the heliosphere is treated by means of the HelMod model (Boschini et al. 2019, and references therein). The HelMod model, now version (HelMod-4), numerically solves the Parker (1965) transport equation,¹⁵

$$\frac{\partial U}{\partial t}=\frac{\partial }{\partial x_i}\left(K_{ij}^S\frac{\partial U}{\partial x_j}\right)+\frac{1}{3}\frac{\partial V_{\text{sw},i}}{\partial x_i}\frac{\partial }{\partial T}\left({\alpha }_{\text{rel}}TU\right)-\frac{\partial }{\partial x_i}\left[\left(V_{\text{sw},i}+v_{d,i}\right)U\right],$$ (3)

using a Monte Carlo approach involving stochastic differential equations (see discussion in, e.g., Bobik et al. 2012, 2016, and references therein). Here U is the number density of CR species per unit of kinetic energy T, t is the time, V_sw,i is the solar wind velocity along the axis x_i, $K_{ij}^S$ is the symmetric part of the diffusion tensor, v_d,i is the particle magnetic drift velocity (related to the antisymmetric part of the diffusion tensor), and finally ${\alpha }_{\text{rel}}=\frac{T+2m_r{c}^2}{T+m_r{c}^2}$, with m_r the particle rest mass in units of GeV nucleon⁻¹. Parker’s transport equation describes (i) the diffusion of CR species due to magnetic irregularities, (ii) the so-called adiabatic energy changes associated with expansions and compressions of cosmic radiation, (iii) an effective convection resulting from the convection with solar wind (SW, with velocity V_sw), and (iv) the drift effects related to the drift velocity (v_d).

The particle transport within the heliosphere is computed from the outer boundary (i.e., the heliopause) down to Earth orbit. In the latest version the actual dimensions of the heliosphere and its boundaries were taken into account based on Voyager 1 measurements (Boschini et al. 2019). The heliopause (HP) represents the extreme limit beyond which solar modulation does not affect the CR flux. Thus, the CR spectra measured by Voyager 1 outside the HP are the truly pristine LIS of CR species.¹⁶ Using Parker’s model of the heliosphere (Parker 1961, 1963) in combination with Voyager 1 observations, we were able to estimate the time dependence of the positions of the termination shock (TS, R_TS) and the HP (R_HP) as (Boschini et al. 2019)

$$R_{\text{TS}}=R_{\text{obs}}{\left(\frac{{\rho }_{\text{obs}}{u}_{\text{obs}}^2}{P_{\text{ISM}}}\right)}^{\frac{1}{2}}{\left[\frac{\gamma +3}{2(\gamma +1)}\right]}^{\frac{1}{2}},$$ (4)

$$\frac{R_{\text{HP}}}{R_{\text{TS}}^{\prime }}=1.58\pm 0.05,$$ (5)

where ρ_obs and u_obs are, respectively, plasma density and plasma velocity measured in situ at distance R_obs, P_ISM is the stagnation pressure discussed in Section 4 in Boschini et al. (2019), and γ = 5/3. $R_{\text{TS}}^{\prime }$ is defined as the TS position at the time when it was left by the SW stream that is currently reaching the HP (for more details see Boschini et al. 2019); this typically takes about 4 yr, but it depends on the SW speed. Therefore, the actual dimensions of the heliosphere used in HelMod-4 evolve with time. The predicted TS distances are in good agreement with those observed: for Voyager 1 (Voyager 2) the detected TS position¹⁷ is 93.8 au on 2004 December 14 (83.6 au on 2007 August 30), and the predicted position is 91.8 au (86.3 au), i.e., within 3 au. Regarding the HP, based on the R_HP observed by Voyager 1, the predicted R_HP at the time of the Voyager 2 crossing was 120.7 au on 2018 November 5, while in reality it is 119 au (see also Dialynas et al. 2019; Krimigis et al. 2019).

In the present code, particular attention is paid to the quality of description of the high solar activity periods, which is evaluated though a comparison of HelMod calculations and the CR proton data by AMS-02 (Aguilar et al. 2018a), and to transitions from/to solar minima. This was achieved through introduction of a drift suppression factor and particle diffusion parameters that depend on the level of solar disturbances (see a discussion in Boschini et al. 2019).

3. HEAO-3-C2 Data and CR Transport

Observations of new features in the CR proton and He spectra in the energy range that is deemed well studied by PAMELA (Adriani et al. 2011) and their confirmation by Fermi-LAT (Ackermann et al. 2014) emphasize the importance of high statistics and accuracy in CR studies. Precise measurements by the AMS-02 experiment (Aguilar et al. 2015a, 2015b) provided important details about the observed hardening and extended the accurate measurements of proton and He spectra into the TV rigidity range (see also ATIC-2, Panov et al. 2009; and CREAM, Ahn et al. 2010). Besides the hardening observed at the same rigidity (~370 GV) and the same spectral index change for both species, the He spectrum appears to be flatter than the spectrum of protons in the whole range. Consequently, the observed p/He ratio is smooth and monotonically decreasing with rigidity.

Understanding the nature of these features requires accurate measurements of other CR species, which was accomplished by AMS-02. The detailed spectra of heavier species ₃Li–₈O (Aguilar et al. 2017, 2018b, 2018c) and ₁₀Ne, ₁₂Mg, and ₁₄Si (Aguilar et al. 2020) exhibit hardening (breaks) similar to that observed in the spectra of CR protons and He, where the break rigidity of ~370 GV is about the same for all species. Observations show similarity between the spectra of mostly primary (p, He, C, O, Ne, Mg, Si) and secondary (Li, Be, B) nuclei, while the spectral slopes of these groups of nuclei are different. Nitrogen is about half-primary/half-secondary and behaves as being in between the other two groups.

Meanwhile, getting into the higher Z species is important, as they provide complementary information about properties of CR sources and ISM in our local Galactic environment. Especially important are the spectra of the iron-group nuclei, as they have large fragmentation cross sections, and therefore their fragmentation timescale at relatively low energies is shorter than the timescale of their escape from the Galaxy. Such nuclei can reach us only if accelerated in nearby sources. However, it may take a while to get such data from AMS-02, which is currently collecting statistics. In this energy range data of earlier missions, such as HEAO-3-C2 (Engelmann et al. 1990), ATIC-2 (Panov et al. 2009), CREAM (Ahn et al. 2008, 2009), and NUCLEON (Grebenyuk et al. 2019a, 2019b), are available, while at low energies Voyager 1 (Cummings et al. 2016) and ACE-CRIS can be used. These data do not provide a continuous coverage comparable in quality to the AMS-02 data, but they can be used to deduce the LIS of ₉F–₂₈Ni nuclei—with some caveats discussed below.

A comparison of the available AMS-02 data with HEAO-3-C2 measurements using our derived LIS modulated to the corresponding level of solar activity with the previous version of HelMod (HelMod-3) gives an important insight into the accuracy of the calibration technique used in the 1970s. In particular, the precise measurements of CR nuclei ₄Be–₈O by the AMS-02 experiment (Aguilar et al. 2017, 2018b, 2018c) indicate that there are clear discrepancies with HEAO-3-C2 data at low and high energies (see Figure 7 in Boschini et al. 2018b), while in the middle range between 2.65 and 10.6 GeV nucleon⁻¹ the agreement is fair. Calculations repeated with the GalProp–HelMod-4 framework yield LIS consistent with our previous results within 1%–2% and confirm our previous findings. The likely reasons of these systematic discrepancies in HEAO-3-C2 data at low and high energies are discussed in detail in Appendix B. For details and differences between HelMod-3 and HelMod-4, see a description in Boschini et al. (2019) and at the dedicated website (see footnote 12).

Figure 7.

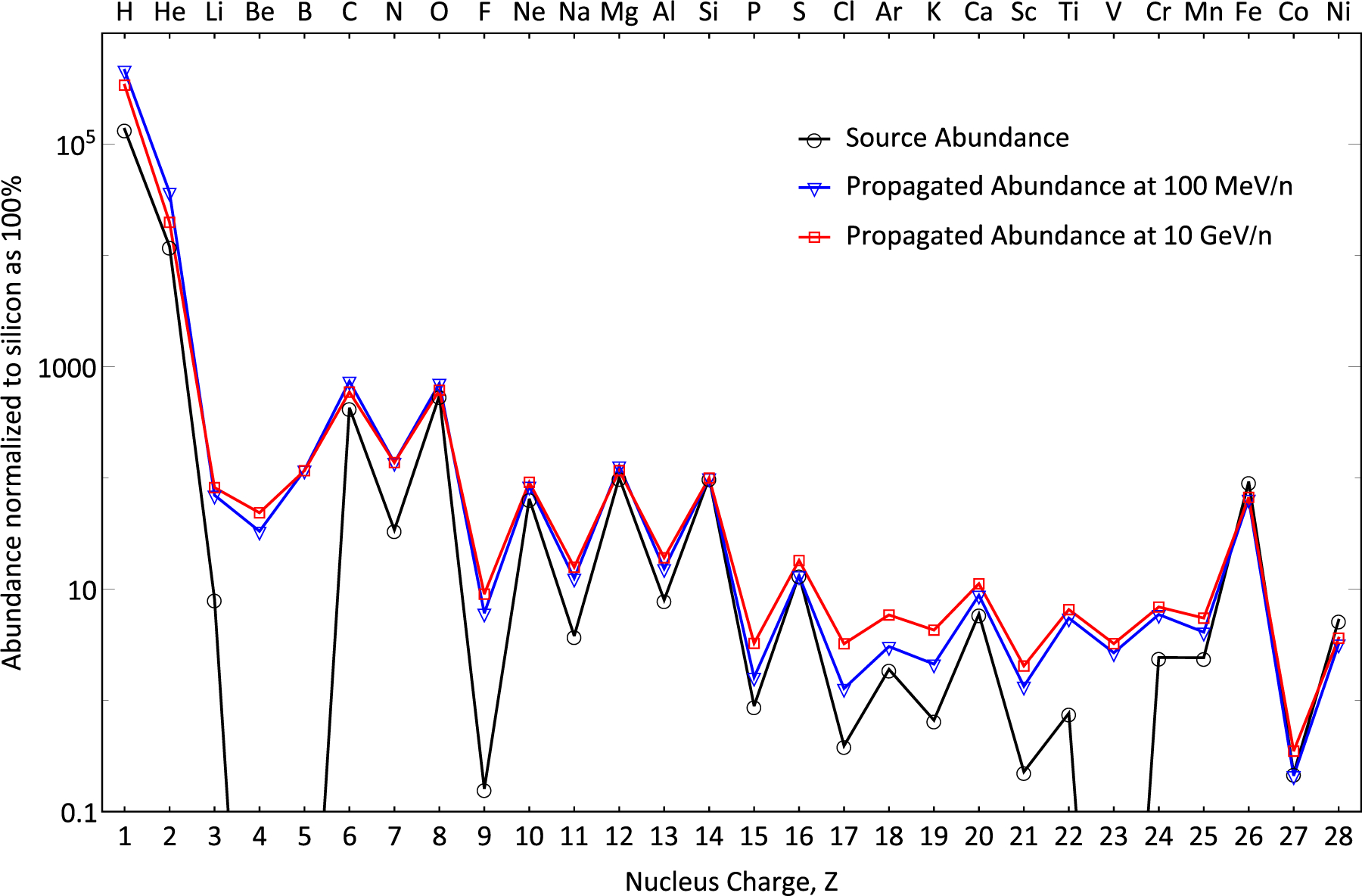
GalProp source and LIS abundances for elements Z = 1–28 at 100 MeV nucleon⁻¹ and 10 GeV nucleon⁻¹ w.r.t. silicon (Si = 100) in our model. The abundances are tuned to Voyager 1 data (Cummings et al. 2016) and the HEAO-3-C2 “plateau” region (Engelmann et al. 1990).

In our following analysis we are using the middle range of HEAO-3-C2 data 2.65–10.6 GeV nucleon⁻¹, which we call the “plateau” because it mimics a plateau in the spectral residual plots, while the data outside this range are discarded. Here we provide the details of the calibration procedure we used for the HEAO-3-C2 (Engelmann et al. 1990) data using AMS-02 measurements of the CR ₄Be–₈O, ₁₀Ne, ₁₂Mg, and ₁₄Si spectra (Section 3.1). Calculations of the interstellar and heliospheric transport are described in Section 3.2.

3.1. Calibration of HEAO-3-C2 Spectra with AMS-02 Data

As already mentioned, the HEAO-3-C2 energy range is significantly affected by the heliospheric modulation. Therefore, a proper evaluation of the systematic errors of the HEAO-3-C2 data can be done through their comparison with LIS, tuned to the AMS-02 data, which are modulated appropriately to the solar activity observed during the HEAO-3-C2 flight as was done in Boschini et al. (2018b, 2020). The LIS spectra tuned to AMS-02 data clearly overlap with the middle part of the HEAO-3-C2 data, exhibiting a flat region at a few GeV nucleon⁻¹ in the relative difference plots. This proper range from 2.65 to 10.6 GeV nucleon⁻¹ is referred to in the present work as the “plateau.” A numerical procedure elaborated with the HEAO-3-C2 data set proves that in the wider energy region outside the “plateau” there is a systematic discrepancy between the data set and calculated spectra that is similar in the spectra of different elements and that is likely a calibration artifact.

The HEAO-3-C2 spectra of ₄Be through ₁₀Ne are shown in Figure 1, where we also show the spectra of ₂He and ₃Li for completeness. The HEAO-3-C2 spectra of ₁₁Na through ₁₉K are shown in Figure 2. Figure 3 shows our LIS and modulated spectra for ₁₀Ne, ₁₂Mg, and ₁₄Si derived using the latest AMS-02 data (Aguilar et al. 2020). Shown are the calculations made in the I-scenario; the P-scenario calculations look similarly.

Figure 1.

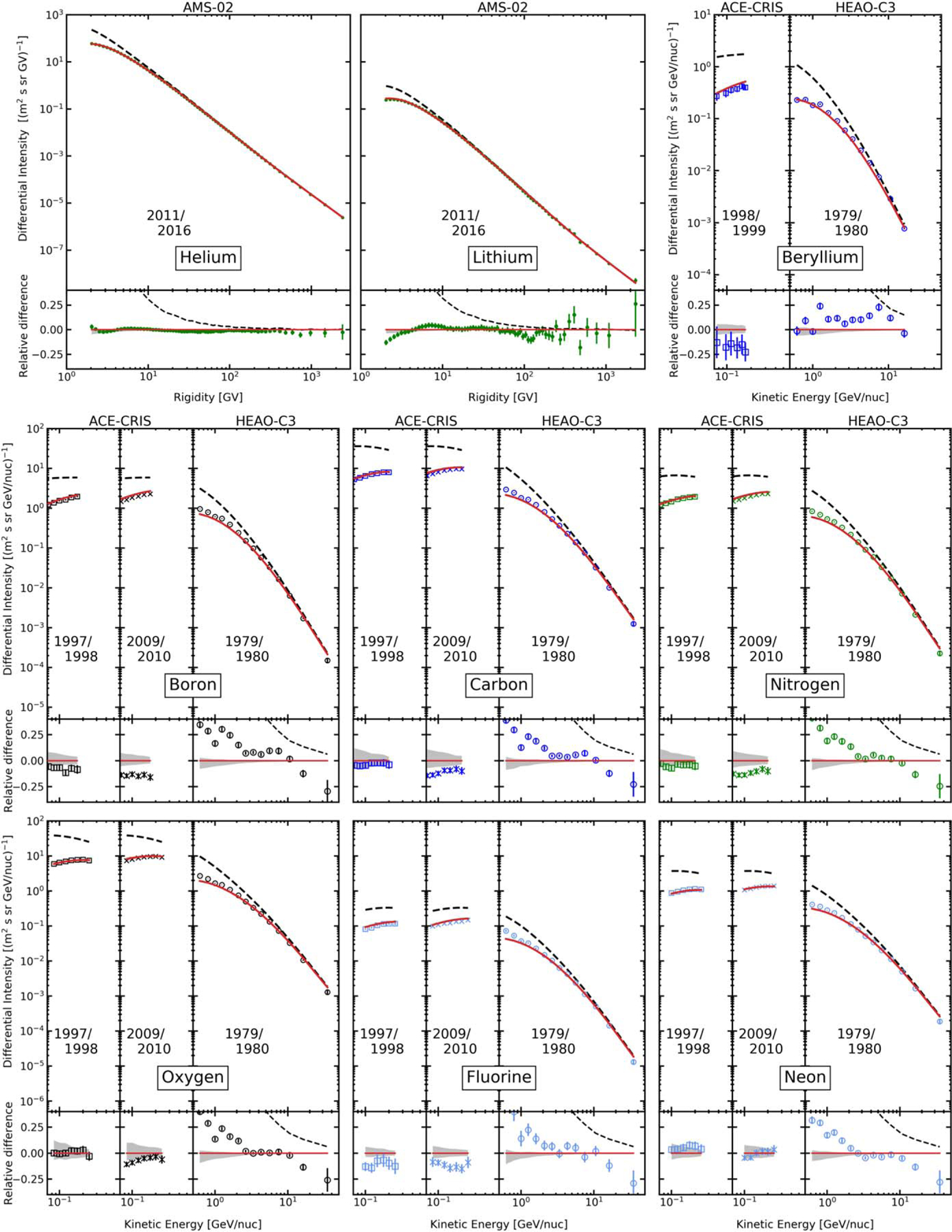
Calculated elemental spectra: ₂He–₁₀Ne. Black dashed lines show the calculated LIS spectra; the red solid lines are modulated to the levels that correspond to the periods of data taking. Data for Z ⩾ 4: ACE-CRIS and HEAO-3-C2 (Engelmann et al. 1990). AMS-02 data for ₂He and ₃Li are compared to the I-scenario calculations; see Section 3.2 for details. Bottom panels in each plot show the relative difference between the calculations and a corresponding data set.

Figure 2.

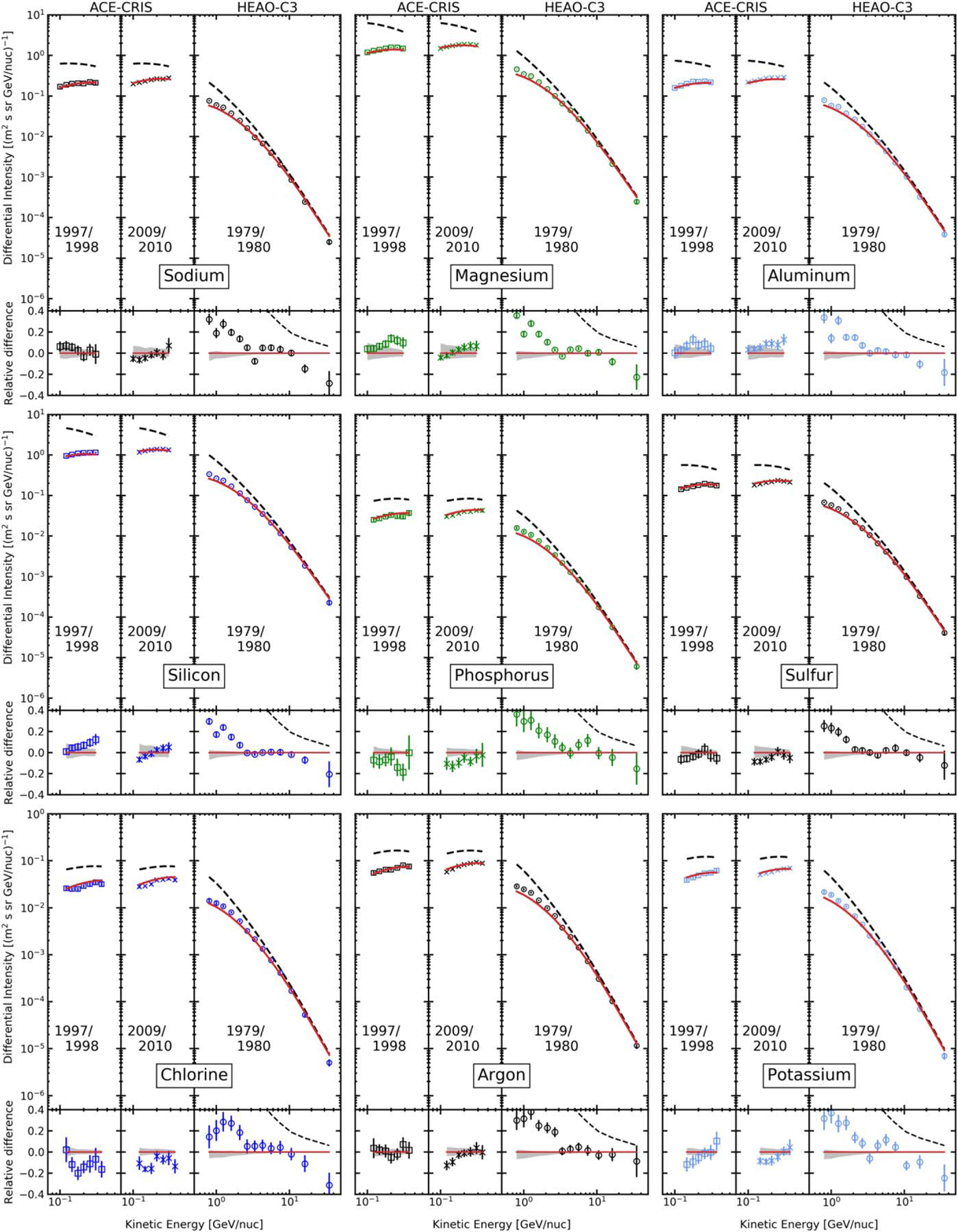
Calculated elemental spectra: ₁₁Na–₁₉K. The line coding and data are the same as in Figure 1.

Figure 3.

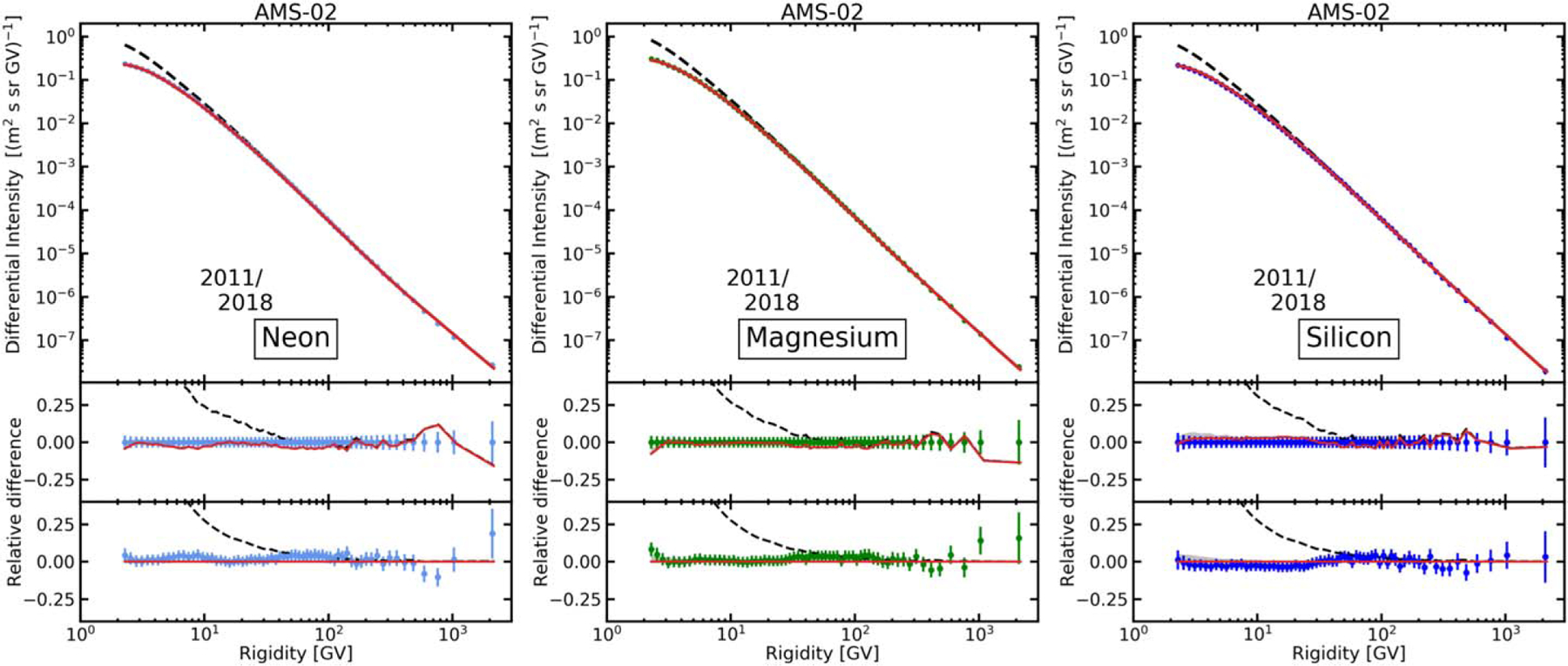
GalProp–HelMod LIS and modulated spectra are compared with AMS-02 data for ₁₀Ne, ₁₂Mg, and ₁₄Si (Aguilar et al. 2020). Shown are the calculations made in the I-scenario. The lower panels show the relative difference in two ways: AMS-02-data-centered as in our previous papers, and in a more traditional model-prediction-centered view. Line coding is the same as in Figure 1.

Only Z ⩾ 4 nuclei (Be and heavier) were measured by HEAO-3-C2, and the time interval corresponds to 1979 October through 1980 June (Engelmann et al. 1990). One can see the flat region from 2.65 through 10.6 GeV nucleon⁻¹ in the relative difference plots of the spectra of B, C, N, O, Ne, Mg, and Si nuclei, which correspond to the aerogel block counter (up to 5.60 GeV nucleon⁻¹) and the first two energy bins of the aerogel sand counter (for a detailed description see Appendix B). In this energy interval the spectra of N, O, Ne, Mg, and Si nuclei measured by HEAO-3-C2 and our modulated LIS agree very well. Meanwhile, the absolute normalizations of the spectra of B and C nuclei are slightly off by ≲5%–8%, while the spectrum of Be demonstrates worst agreement still being within ≲15% of our calculations. The latter is not surprising since Be is the lightest nucleus measured by HEAO-3-C2, and given that “the time-of-flight system is performing well for Z > 6. For lowest charges the resolution is rather poor” (Bouffard et al. 1982; see also discussion in Appendix B.1).

Overall, the differences in normalizations between the appropriately modulated AMS-02 and HEAO-3-C2 “plateau” data are quite small, e.g., the average discrepancy for C, N, O, Ne, Mg, and Si nuclei is below 1%. The reference element used in the HEAO-3-C2 data analysis is O, and the spectra of the other nuclei were derived from their relative abundances with respect to the reference element (Table 2 in Engelmann et al. 1990). One can see that our calculations for O agree well with HEAO-3-C2 data, and therefore in our further analysis we rely on the HEAO-3-C2 data points in the energy range from 2.65 through 10.6 GeV nucleon⁻¹, the “plateau” region, with the data points outside of this range being discarded from further analysis. The HEAO-3-C2 data are used at their nominal values, i.e., no renormalization is applied.

Table 2.

Injection Spectra of CR Species for I- and P-Scenarios

Nucleus	Spectral Parameters
	${\gamma }_0^{R_0(\text{GV})}{s}_0$	${\gamma }_1^{R_1(\text{GV})}{s}_1$	${\gamma }_2^{R_2(\text{GV})}{s}_2$	${\gamma }_3^{R_3(\text{TV})}{s}_3$	γ 4
1H	2.24 0.95 0.29	1.70 6.97 0.22	2.44 400 0.09	2.19 16 0.09	2.37
2He	2.05 1.00 0.26	1.76 7.49 0.33	2.41 340 0.13	2.12 30 0.10	2.37
${}_3^7\text{Li}$ a	… …	1.10 12.0 0.16	2.72 355 0.13	1.90 …	…
6C	1.00 1.10 0.19	1.98 6.54 0.31	2.43 348 0.17	2.12 …	…
${}_7^{14}\text{N}$	1.00 1.30 0.17	1.96 7.00 0.20	2.46 300 0.17	1.90 …	…
8O	0.95 0.90 0.18	1.99 7.50 0.30	2.46 365 0.17	2.13 …	…
9F	0.20 1.50 0.19	1.97 7.00 0.20	2.48 355 0.17	2.14 …	…
10Ne	0.60 1.15 0.17	1.92 9.42 0.26	2.44 355 0.17	1.97 …	…
11Na	0.50 0.75 0.17	1.98 7.00 0.21	2.49 355 0.17	2.14 …	…
12Mg	0.20 0.85 0.12	1.99 7.00 0.23	2.48 355 0.17	2.15 …	…
13Al	0.20 0.60 0.17	2.04 7.00 0.20	2.48 355 0.17	2.14 …	…
14Si	0.20 0.85 0.17	1.97 7.00 0.26	2.47 355 0.17	2.19 …	…
15P	0.25 1.60 0.19	1.95 7.00 0.20	2.48 355 0.17	2.14 …	…
16S	0.80 1.30 0.17	1.96 7.00 0.20	2.49 355 0.17	2.14 …	…
17Cl	1.10 1.50 0.17	1.98 7.20 0.20	2.53 355 0.17	2.14 …	…
18Ar	0.20 1.30 0.17	1.96 7.00 0.20	2.46 355 0.17	2.09 …	…
19K	0.20 1.40 0.15	1.96 7.00 0.20	2.53 355 0.17	2.14 …	…
20Ca	0.30 1.00 0.11	2.07 7.00 0.20	2.48 355 0.17	2.14 …	…
21Sc	0.20 1.40 0.17	1.97 7.00 0.22	2.53 355 0.17	2.14 …	…
22Ti	1.50 0.90 0.17	1.98 7.00 0.22	2.57 355 0.17	2.14 …	…
23V	1.10 0.80 0.17	1.98 7.00 0.22	2.53 355 0.17	2.14 …	…
24Cr	1.70 0.65 0.17	1.99 7.00 0.20	2.48 355 0.17	2.14 …	…
25Mn	0.20 0.85 0.10	2.08 7.00 0.20	2.48 355 0.17	2.14 …	…
26Fe	0.27 1.04 0.18	1.99 7.00 0.20	2.51 355 0.17	2.19 …	…
27Co	0.80 0.70 0.15	1.98 7.00 0.20	2.49 355 0.17	2.14 …	…
28Ni	1.50 0.65 0.17	1.98 7.00 0.20	2.48 355 0.17	2.14 …	…

Notes. For the P-scenario γ₃ = γ₂. For parameter definitions see Equation (2). Fit errors: γ_0,1 ± 0.06, γ_2,3 ± 0.04, R₀ ± 0.5 GV, R₁ ± 1 GV, and R₂ ± 15 GV. For protons and He (I-scenario only): $R_3^p\pm 5\text{\hspace{0.17em}TV}$, ${\gamma }_4^p\pm 0.08$, $R_3^{\text{He}}\pm 15\text{\hspace{0.17em}TV}$, ${\gamma }_4^{\text{He}}\pm 0.1$.

^aPrimary lithium.

(This table is available in machine-readable form.)

3.2. Source Abundances and CR Transport

Diffusion of CRs in the Galaxy is well described by the transport equations (Berezinskii et al. 1990), but the exact values of the propagation parameters depend on the assumed propagation model and selected CR data sets. In this work we are using the same propagation model with distributed reacceleration and convection that was used in our previous analyses (for more details see Boschini et al. 2017, 2018a, 2018b, 2020).

The values of propagation parameters along with their confidence limits are derived from the best available CR data using the Markov Chain Monte Carlo (MCMC) routine. Five main propagation parameters that affect the overall shape of CR spectra were left free in the scan using GalProp running in the 2D mode: the Galactic halo half-width z_h, the normalization of the diffusion coefficient D₀ at the reference rigidity R = 4 GV and the index of its rigidity dependence δ, the Alfvén velocity V_Alf, and the gradient of the convection velocity dV_conv/dz (V_conv = 0 in the plane, z = 0). Their best-fit values tuned to the AMS-02 data are listed in Table 1 and are the same as obtained in Boschini et al. (2020) within the quoted error bars. The radial size of the Galaxy does not significantly affect the values of propagation parameters and was set to 20 kpc. Besides, we introduced a factor β^η in the diffusion coefficient, where β = v/c, and η was left free. The best-fit value of η = 0.70 improves the agreement at low energies and slightly affects the choice of injection indices γ₀ and γ₁ shown in Table 2.

Table 1 shows propagation parameters for two scenarios. The “propagation” P-scenario assumes that the observed break at ~370 GV is the result of a change in the spectrum of interstellar turbulence that translates into a break in the index of the diffusion coefficient. The “injection” I-scenario proposes that the break is due to the presence of populations of CR sources injecting particles with softer and harder spectra. The P-scenario predicts that the break should be observed in spectra of all CR species at about the same rigidity since the interstellar turbulence acts similarly on all particles. The predicted change in the spectral index of secondary species (difference between the spectral indices below and above the break) would then be twice the value of the break observed in the spectra of primary species. The recent AMS-02 measurements of the secondary species Li, Be, and B (Aguilar et al. 2018c) prefer the P-scenario. For more details see Vladimirov et al. (2012), Boschini et al. (2020), and references therein.

The corresponding B/C ratio is shown in Figure 4 for both scenarios, which are identical below the break, with the P-scenario predicting the flatter ratio above the break. Separately shown is a comparison with AMS-02 (Aguilar et al. 2018c) and HEAO-3-C2 (Engelmann et al. 1990), where the left and middle panels are shown for the I-scenario, while the right panel shows a comparison for the P-scenario. The calculated B/C ratio compares well with all available measurements: Voyager 1 (Cummings et al. 2016), ACE-CRIS, AMS-02 (Aguilar et al. 2018c), ATIC-2 (Panov et al. 2009), CREAM (Ahn et al. 2008, 2009), and NUCLEON (Grebenyuk et al. 2019b). For the most part HEAO-3-C2 (Engelmann et al. 1990) data agree well with the modulated LIS ratio, but they show a noticeable discrepancy below 2 GeV nucleon⁻¹. The latter supports our conclusion about the unaccounted-for variations in the rigidity cutoff along the orbit of the instrument that was used for the event selection at low energies (see Appendices B.2, B.3).

Figure 4.

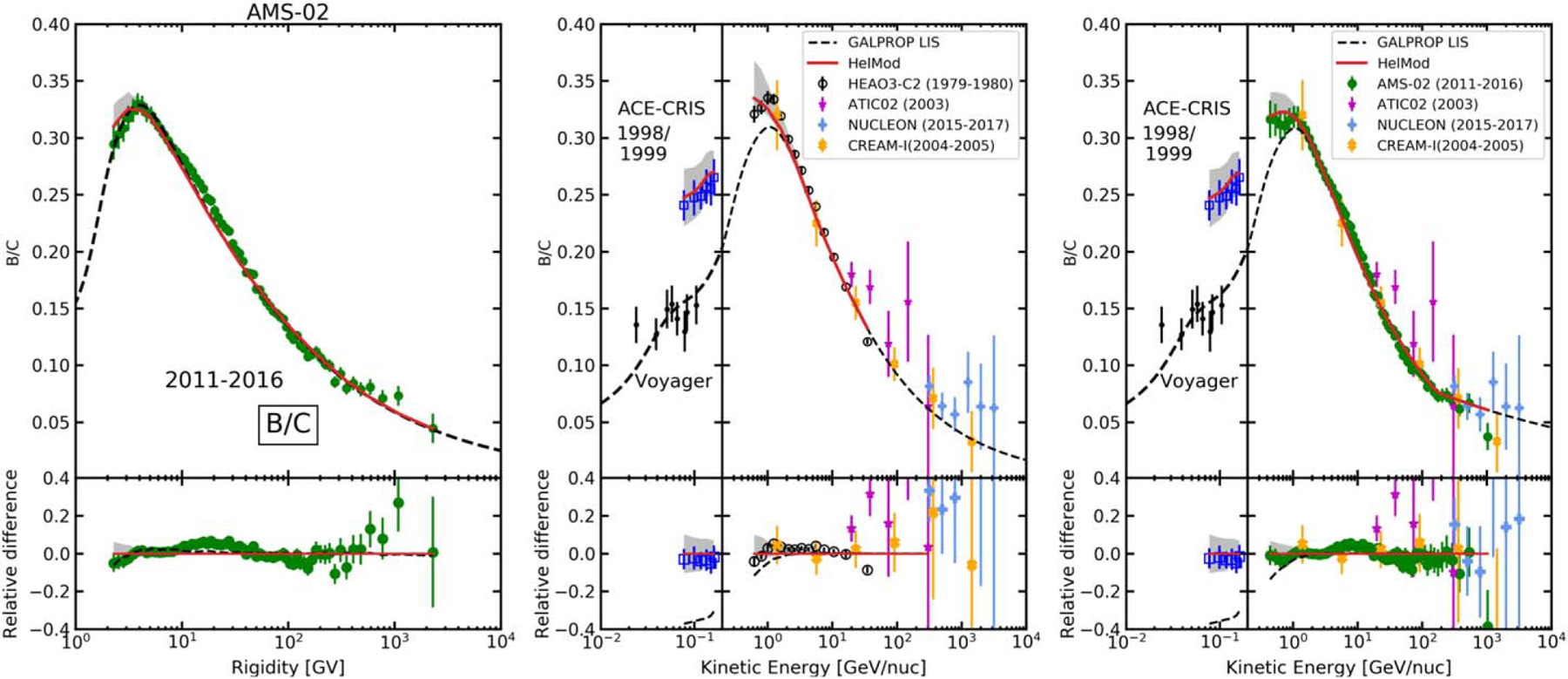
B/C ratio calculated for the I-scenario compared to AMS-02 (left; Aguilar et al. 2018c) and HEAO-3-C2 (middle; Engelmann et al. 1990) data. The right panel shows a comparison of the B/C ratio calculated for the P-scenario with available measurements, where HEAO-3-C2 data are not shown for clarity. In the middle and right panels the measurements by Voyager 1 (Cummings et al. 2016), ACE-CRIS (1998–1999), ATIC-2 (Panov et al. 2009), CREAM (Ahn et al. 2008, 2009), and NUCLEON (Grebenyuk et al. 2019b) are shown. Note that the units in the left panel are rigidity, while the middle and right panels are shown vs. E_kin per nucleon. Line coding is the same as in Figure 1.

To derive the LIS of CR species, we use an optimization procedure that was employed in our previous analyses (Boschini et al. 2017, 2018a, 2018b, 2020), but with some modifications. Abundances and injection parameters for nuclei from ₁H–₈O were fixed along with the parameters of heliospheric transport as detailed in our previous analysis (Boschini et al. 2020). In the current study, these parameters are only slightly changed, while CR source abundances for nuclei ₉F–₂₈Ni are tuned to the data with the MCMC interface to GalProp v.56 (Masi 2016) through sampling their abundance space. The MCMC scan uses new AMS-02 data for ₁₀Ne, ₁₂Mg, and ₁₄Si nuclei (Aguilar et al. 2020) and for the rest uses the subset of HEAO-2-C2 data between 2.65 and 10.6 GeV nucleon⁻¹, the “plateau” region as described in Section 3.1.

At this step, the same parameterization was assigned to the injection spectra of ₉F, ₁₁Na, ₁₃Al, and ₁₅P–₂₈Ni nuclei: three break rigidities R_0,1,2 = 1.0, 7.0, 350 GV, and four spectral indices γ_0,1,2,3 = 1.5, 1.98, 2.48, 2.14. The break rigidities R_0,1,2 and two spectral indices γ_1,2 were chosen to be close to the values found in our recent C, N, O analysis (Boschini et al. 2018b, 2020). Indices γ₀ and γ₃ are used for the energy ranges outside of the HEAO-3-C2 “plateau” region: to describe the spectral bending at Voyager 1 energies (Boschini et al. 2018b, 2020) and the well-known now spectral hardening revealed by AMS-02 (Aguilar et al. 2017, 2018b, 2018c) correspondingly. The fitting procedure is not sensitive to the position of the high rigidity break R₂, so the choice of the I-scenario or the P-scenario with a break in the diffusion coefficient (see Boschini et al. 2020, for details) is a matter of preference, as we restrict our analysis to the region below the break. The P-scenario also implies that γ₃ = γ₂.

Consistency with data is provided through manual fine-tuning of the source abundances and parameters of the injection spectra for each element from ₂₈Ni down to ₆C. The default GalProp abundances that were originally tuned to ACE-CRIS data (Wiedenbeck et al. 2001) are now adjusted to match the HEAO-3-C2 “plateau” data (Engelmann et al. 1990). Meanwhile, relative isotopic abundances for each element are kept consistent with ACE-CRIS.

At the final step, the ACE-CRIS and Voyager 1 (Cummings et al. 2016) data were added to the analysis to refine the LIS at low energies. The spectral indices γ_0,1,2 and the break rigidities R_0,1 were tuned to ACE-CRIS data taken in 1997–1998 (active Sun) and 2009–2010 (quiet Sun) and to Voyager 1 local interstellar data, which resulted only in minor modifications of the default parameterization set at the first step excluding γ₀ that required larger modifications. Our benchmark CR proton spectrum¹⁸ is shown in Figure 5 compared to AMS-02 data (Aguilar et al. 2015a). Here we again went down in Z from ₂₈Ni to ₆C. In particular, adjustment of the break rigidity R₀ improves the agreement with ACE-CRIS data for ₁₀Ne–₁₄Si, ₂₀Ca, and ₂₄Cr–₂₈Ni nuclei. The best-fit values for injection parameters of all species are listed in Table 2; for their definitions see Equation (2).

Figure 5.

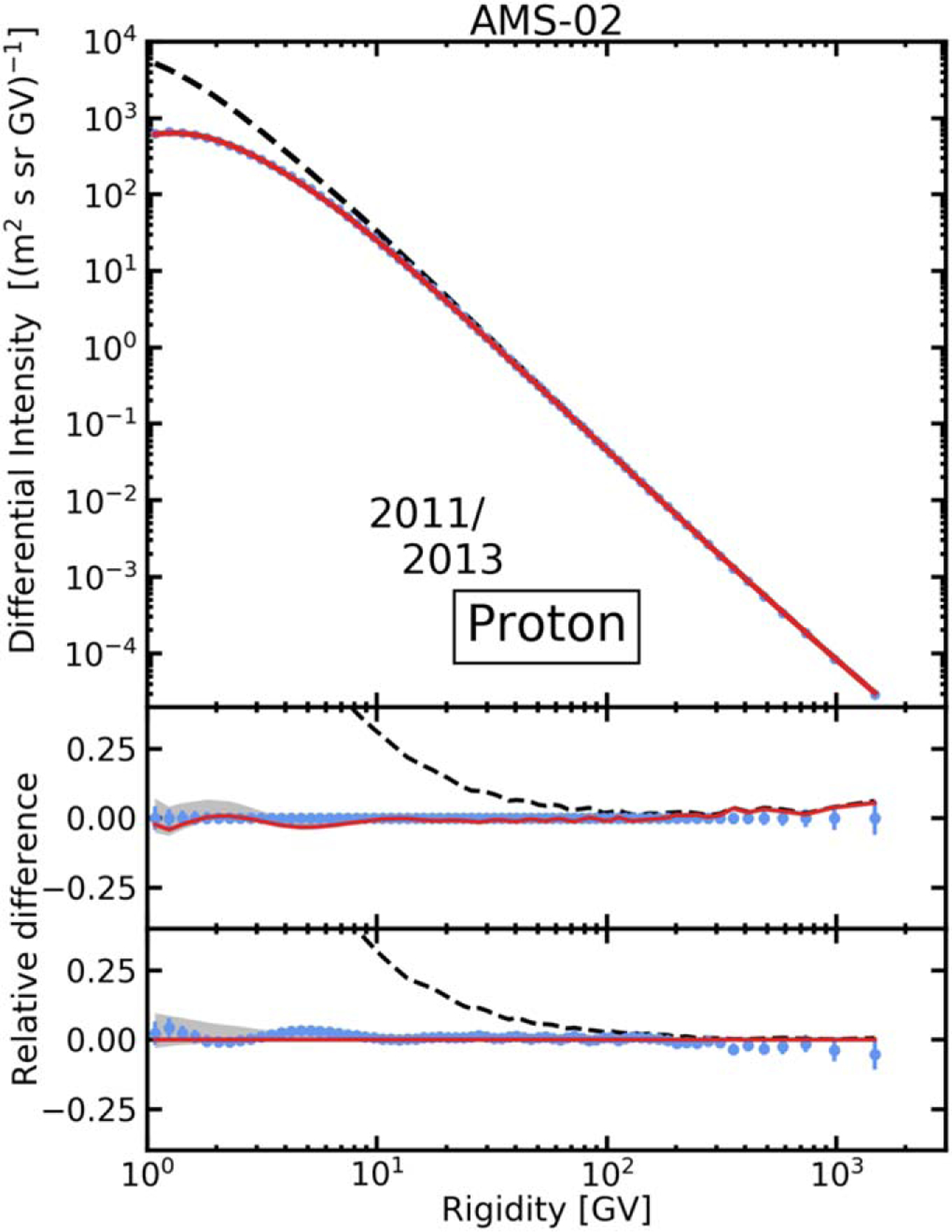
GalProp–HelMod LIS (black dashed line) for CR protons calculated in the I-scenario and modulated spectrum (red solid line) compared to the AMS-02 data (Aguilar et al. 2015a). The lower panels show the relative difference in two ways: AMS-02-data-centered as in our previous papers, and in a more traditional model-prediction-centered view.

The injection spectra of protons and helium are extended up to 200 TV into the region where their CR spectra exhibit another break (softening) at ~10–20 TeV nucleon⁻¹; see Figure 6. It adds another break R₃ and spectral index γ₄ above this break, which are valid only in the I-scenario. CR source abundances are provided in Table 3.

Figure 6.

Our model calculations of the proton and He spectra for the I-scenario and a comparison with available data: HEAO-3-C2 (Engelmann et al. 1990), ATIC-2 (Panov et al. 2009), CREAM (Ahn et al. 2008), NUCLEON (Grebenyuk et al. 2019a, 2019b), AMS-02 (Aguilar et al. 2015a, 2015b), CALET (Adriani et al. 2019), and DAMPE (An et al. 2019). The expanded high-energy parts of the spectra >100 GeV nucleon⁻¹ are shown at the bottom. The line coding is the same as in Figure 1.

Table 3.

Source Abundances of CR Species

Nucleus	Source Abundance	Nucleus	Source Abundance	Nucleus	Source Abundance
${}_1^1\text{H}$	8.77 × 105	${}_{13}^{27}\text{Al}$	51.1	48Ti	<10−4
2H	35	${}_{14}^{28}\text{Si}$	580	49Ti	<10−4
${}_2^3\text{He}$	<10−4	29Si	35	50Ti	<10−4
4He	7.74 × 104	30Si	24.7	${}_{23}^{50}\text{V}$	<10−4
${}_3^6\text{Li}$	<10−4	${}_{15}^{31}\text{P}$	5.7	51V	<10−4
7Li	52	${}_{16}^{32}\text{S}$	82.1	${}_{24}^{50}\text{Cr}$	4
${}_4^7\text{Be}$	0	33S	0.306	51Cr	0
9Be	<10−4	34S	3.42	52Cr	11.1
10Be	<10−4	36S	4.28 × 10−4	53Cr	3.01 × 10−3
${}_5^{10}\text{B}$	1.80 × 10−4	${}_{17}^{35}\text{Cl}$	2.5	54Cr	0.5
11B	7.42 × 10−4	37Cl	1.17 × 10−3	${}_{25}^{53}\text{Mn}$	12.6
${}_6^{12}\text{C}$	2720	${}_{18}^{36}\text{Ar}$	11.4	55Mn	2.9
13C	<10−4	38Ar	0.74	${}_{26}^{54}\text{Fe}$	30.1
${}_7^{14}\text{N}$	207	40Ar	1.74 × 10−3	55Fe	0
15N	<10−4	${}_{19}^{39}\text{K}$	1.39	56Fe	515
${}^{16}\text{O}$	3510	40K	2.80	57Fe	17.7
17O	<10−4	41K	3.34 × 10−4	58Fe	5.34
18O	1.29	${}_{20}^{40}\text{Ca}$	36.1	${}_{27}^{59}\text{Co}$	1.40
${}_9^{19}\text{F}$	0.95	41Ca	1.97	${}_{28}^{58}\text{Ni}$	22.3
${}_{10}^{20}\text{Ne}$	338	42Ca	<10−4	59Ni	0
21Ne	3.56 × 10−3	43Ca	<10−4	60Ni	8.99
22Ne	107	44Ca	<10−4	61Ni	0.599
${}_{11}^{23}\text{Na}$	24.1	48Ca	0.11	62Ni	1.43
${}_{12}^{24}\text{Mg}$	490	${}_{21}^{45}\text{Sc}$	1.46	64Ni	0.304
25Mg	70	${}_{22}^{46}\text{Ti}$	4.9	…	…
26Mg	90	47Ti	<10−4	…	…

Note. For all nonzero relative source abundances below 10⁻⁴ we provide an upper limit. Propagated relative isotopic abundances for each element are tuned to the ACE-CRIS data.

(This table is available in machine-readable form.)

4. Results and Discussion

Figure 7 shows a comparison of the derived elemental abundances in CR sources and propagated abundances at 100 MeV nucleon⁻¹ and 10 GeV nucleon⁻¹ normalized to Si = 100. The source abundances were derived using the AMS-02 data for ₁H–₈O, ₁₀Ne, ₁₂Mg, and ₁₄Si and HEAO-3-C2 data at 10 GeV nucleon⁻¹ for the rest. One can see that the relative source abundances of mostly primary elements, C, O, Ne, Mg, Si, S, Fe, and Ni, remain unchanged after the propagation. The purely secondary elements are Be, B, and V. There are also partially primary/secondary species with a wide range of primary contributions, ranging from about half-and-half for N, Na, Al, Ca, Cr, and Mn nuclei to very low abundant species that are still present in the sources, such as Li, F, P, Cl, Ar, K, Sc, and Ti. One exception is Co, which looks like mostly primary in this figure, but it may be connected with somewhat underestimated contributions from fragmentations of heavier (Z ⩾ 29) nuclei, which were not included in the analysis. One can notice that propagated abundances at 100 MeV nucleon⁻¹ and 10 GeV nucleon⁻¹ do not always match. This is an indication of a difference in the spectral shape between mostly primary elements and those where the secondary contribution is essential, the effect of concurrent fragmentation, production of secondaries, and ionization energy losses as low energies. Our analysis also hints at a presence of primary fluorine ₉F, whose source abundance was set to nonzero; see discussion in Appendix C.1.

Figure 8 shows a comparison of the derived LIS for all elements with Voyager 1 data (Cummings et al. 2016). The open circles show updated Voyager 1 data for H and He taken from 2012 September 1 to 2019 November 13, as posted on the NASA page¹⁹—the remarkable agreement between the two data sets is another evidence that we see the LIS. The elements are sorted into three groups by the approximate amount of primary contribution as discussed in Section 3.2, while within each group they are ordered by Z. One can see a clear difference in the spectral shapes above ~1 GeV nucleon⁻¹ between the groups: the spectra become steeper and steeper as we move from the group of primaries to significantly secondary and to fully secondary groups. Meanwhile, the spectral slopes within each group are pretty similar.

Figure 8.

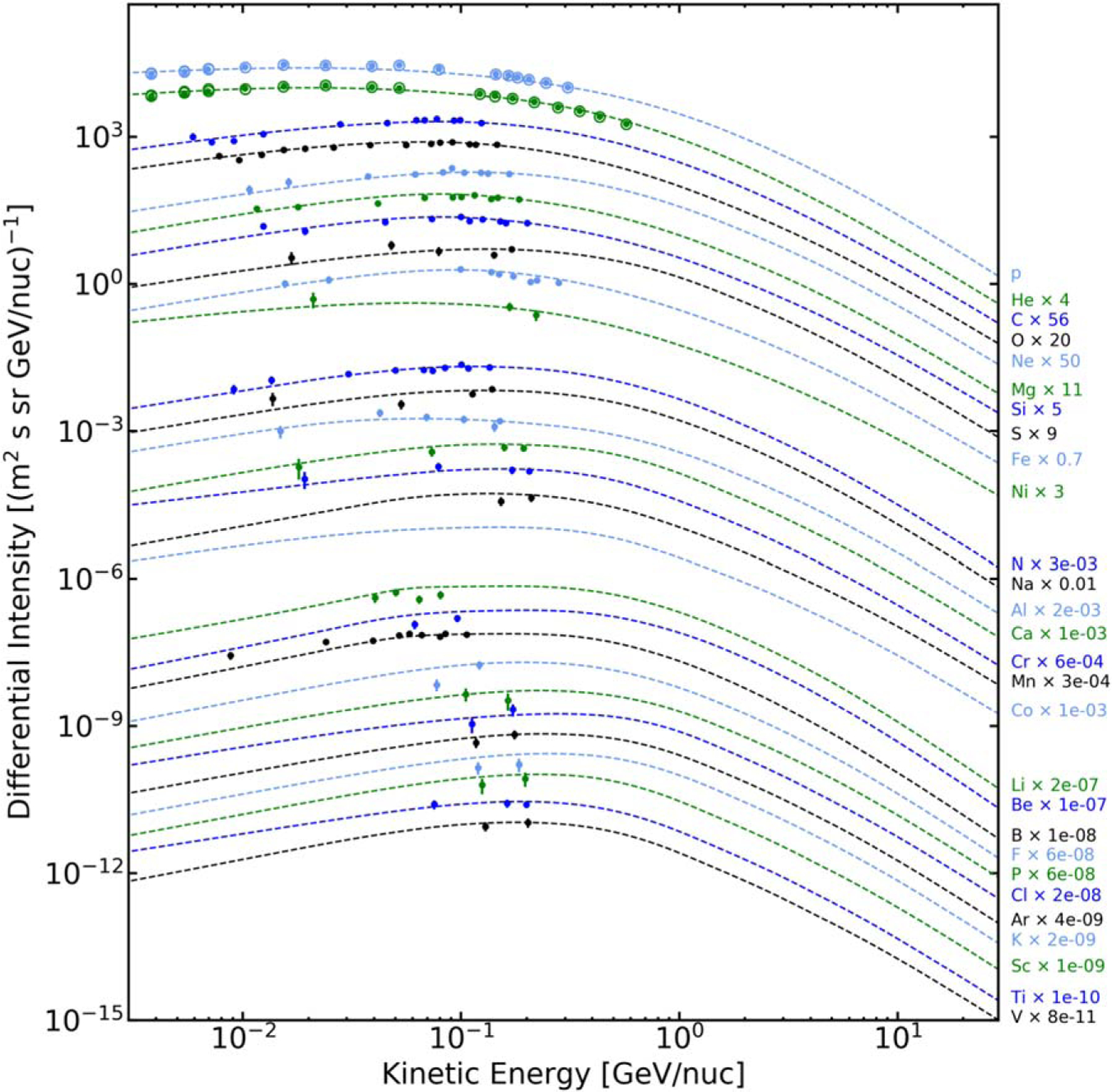
GalProp LIS for all CR species (dashed lines) compared to the Voyager 1 data (filled circles; Cummings et al. 2016). We also show updated Voyager 1 data for H and He (open circles) taken from 2012 September 1 to 2019 November 13, as posted on the NASA page (https://voyager.gsfc.nasa.gov/spectra.html). The elements are sorted by approximate amount of primary contribution: the first group is mostly primary; second, with significant primary contribution; and third, mostly secondary.

A summary plot of all available nuclei species measured by AMS-02, along with our model calculations, is shown in Figure 9. The achieved agreement is impressive and allows a detailed comparison with the HEAO-3-C2 data for those elements where both AMS-02 and HEAO-3-C2 data are available. The extension of our LIS into TeV energies and a comparison with HEAO-3-C2 (Engelmann et al. 1990), TRACER (Gahbauer et al. 2004; Ave et al. 2008; Obermeier et al. 2011), ATIC-2 (Panov et al. 2009), CREAM (Ahn et al. 2008, 2009), and NUCLEON (Grebenyuk et al. 2019a, 2019b) data are illustrated in Figure 10 for the most abundant species for which such data are available: B, C, N, O, Ne, Mg, Si, S, Ar, Ca, and Fe. AMS-02 data are not shown in this plot for clarity. Black dashed lines show the calculated LIS spectra, and the red solid lines are the spectra modulated to the level that corresponds to the period of the HEAO-3-C2 mission. We show calculations for both scenarios: the I-scenario is on the left-hand side, and the P-scenario is on the right-hand side.

Figure 9.

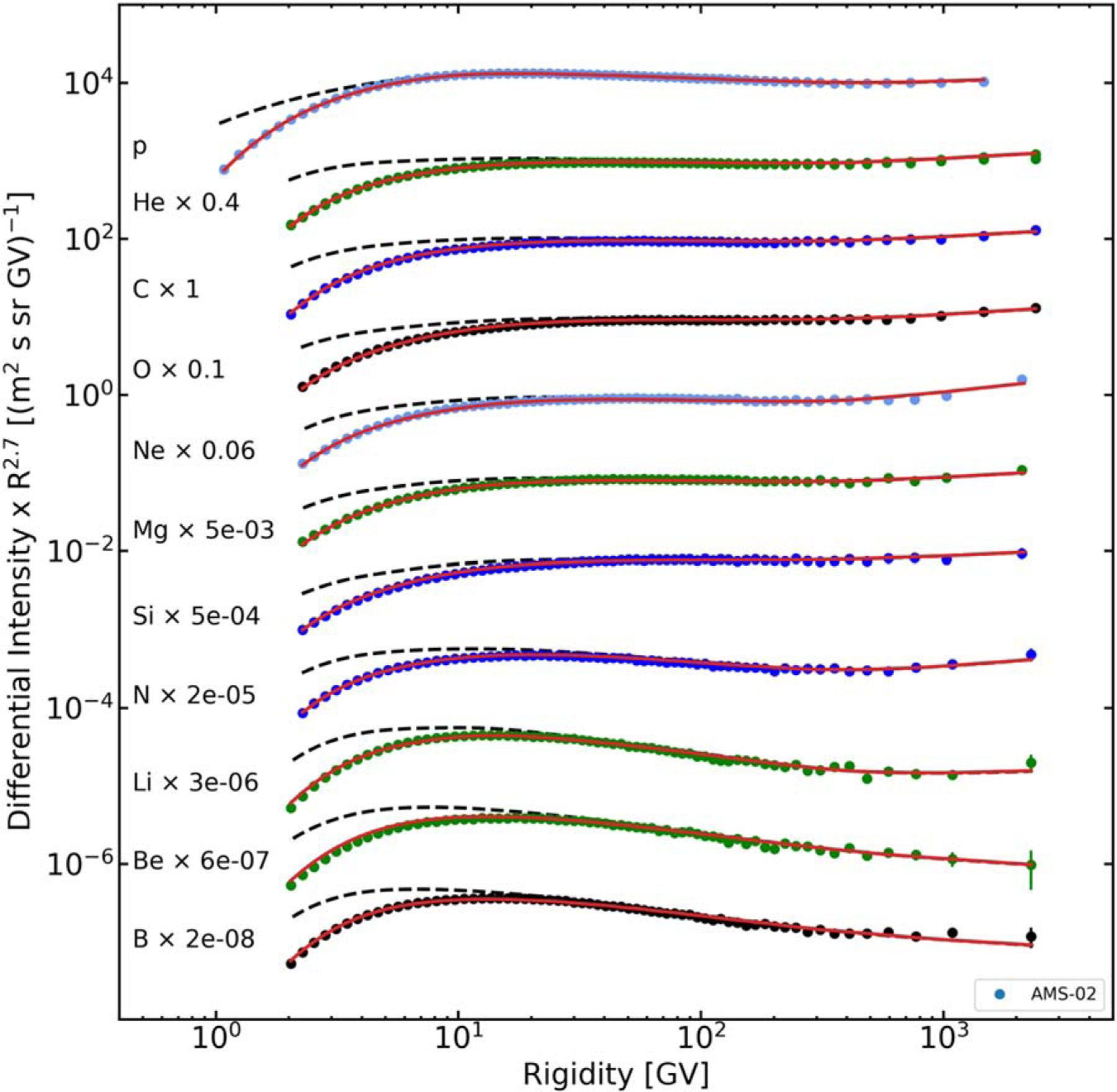
Summary plot of our model calculations for the I-scenario and available AMS-02 data. The color of data points for each element is the same as in Figure 8. Line coding is the same as in Figure 1.

Figure 10.

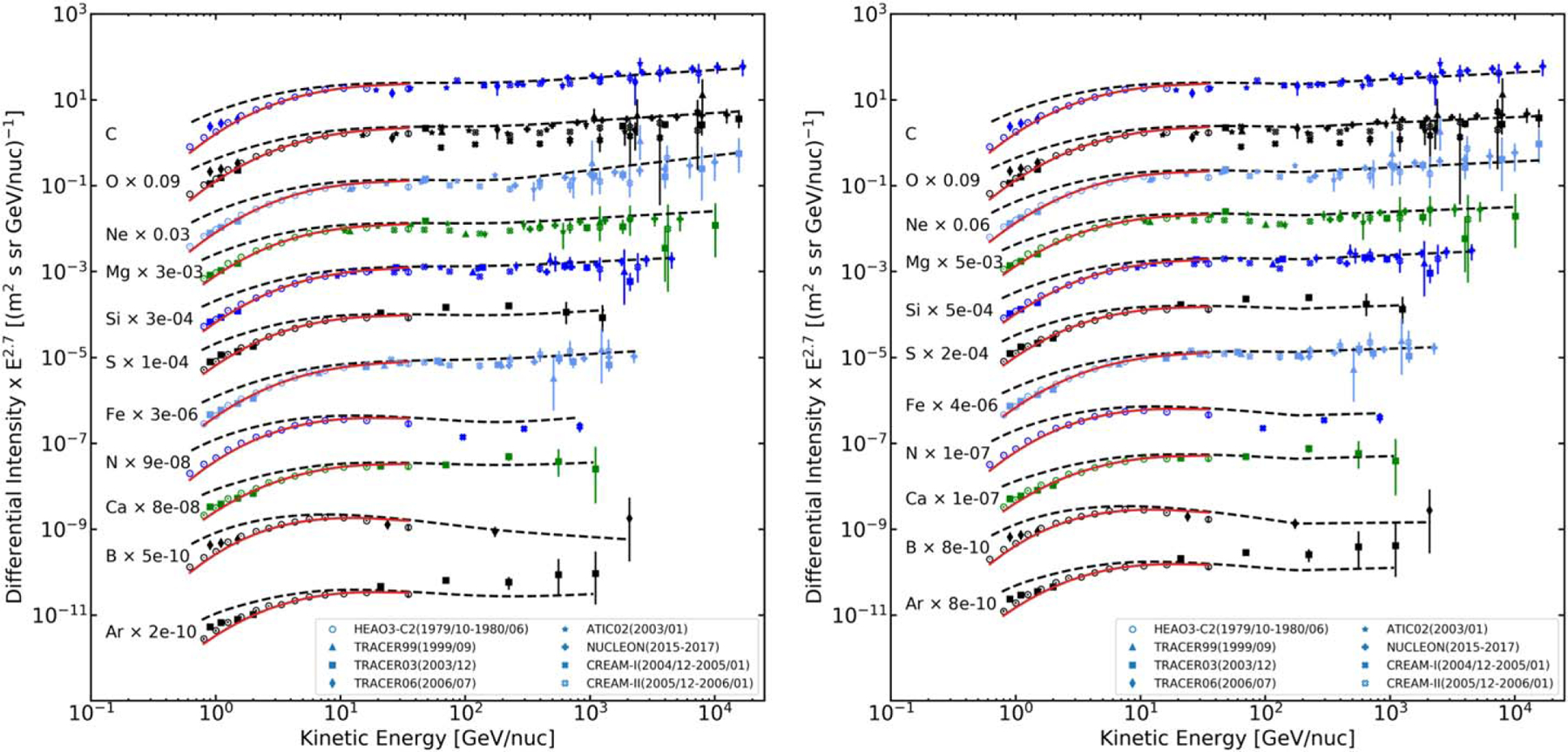
Our model calculations for the I-scenario (left) and P-scenario (right) compared to HEAO-3-C2 (Engelmann et al. 1990), TRACER (Gahbauer et al. 2004; Ave et al. 2008; Obermeier et al. 2011), ATIC-2 (Panov et al. 2009), CREAM (Ahn et al. 2008), and NUCLEON (Grebenyuk et al. 2019a, 2019b) data. AMS-02 data are not shown for clarity. Black dashed lines show the calculated LIS spectra, and the red solid lines are the spectra modulated to the level that corresponds to the period of the HEAO-3-C2 mission. The color of data points for each element is the same as in Figure 8.

As we discussed in Section 3.1, one can see some discrepancies between our modulated spectra (shown with red solid lines) and HEAO-3-C2 data at low and high energies, while the middle range “plateau” was used for the fits. The extension of the “plateau” fits to higher energies agrees well with data taken by other instruments, e.g., for C, O, Ne, Mg, Si, and Fe the agreement is very good, where the highest-energy points reaching ~200 TeV nucleon⁻¹ are coming from CREAM, TRACER, and NUCLEON experiments. This agreement is especially important, as it provides a long lever arm to test our derived LIS in the kinetic energy range from 1 MeV nucleon⁻¹ to ~100–500 TeV nucleon⁻¹, covering 8–9 orders of magnitude in energy.

A detailed comparison of our modulated LIS for elements ₉F to ₂₈Ni with ACE-CRIS and HEAO-3-C2 “plateau” data is illustrated in a series of plots shown in Figures 1, 2, and 11. The modulation is calculated separately for each instrument appropriately to the data-taking periods. The noticeable differences in the HEAO-3-C2 “plateau” region appear only in cases of rare species, such as P and K, where the scatter of the data points and the error bars are large, indicating that the collected statistics is insufficient.

Figure 11.

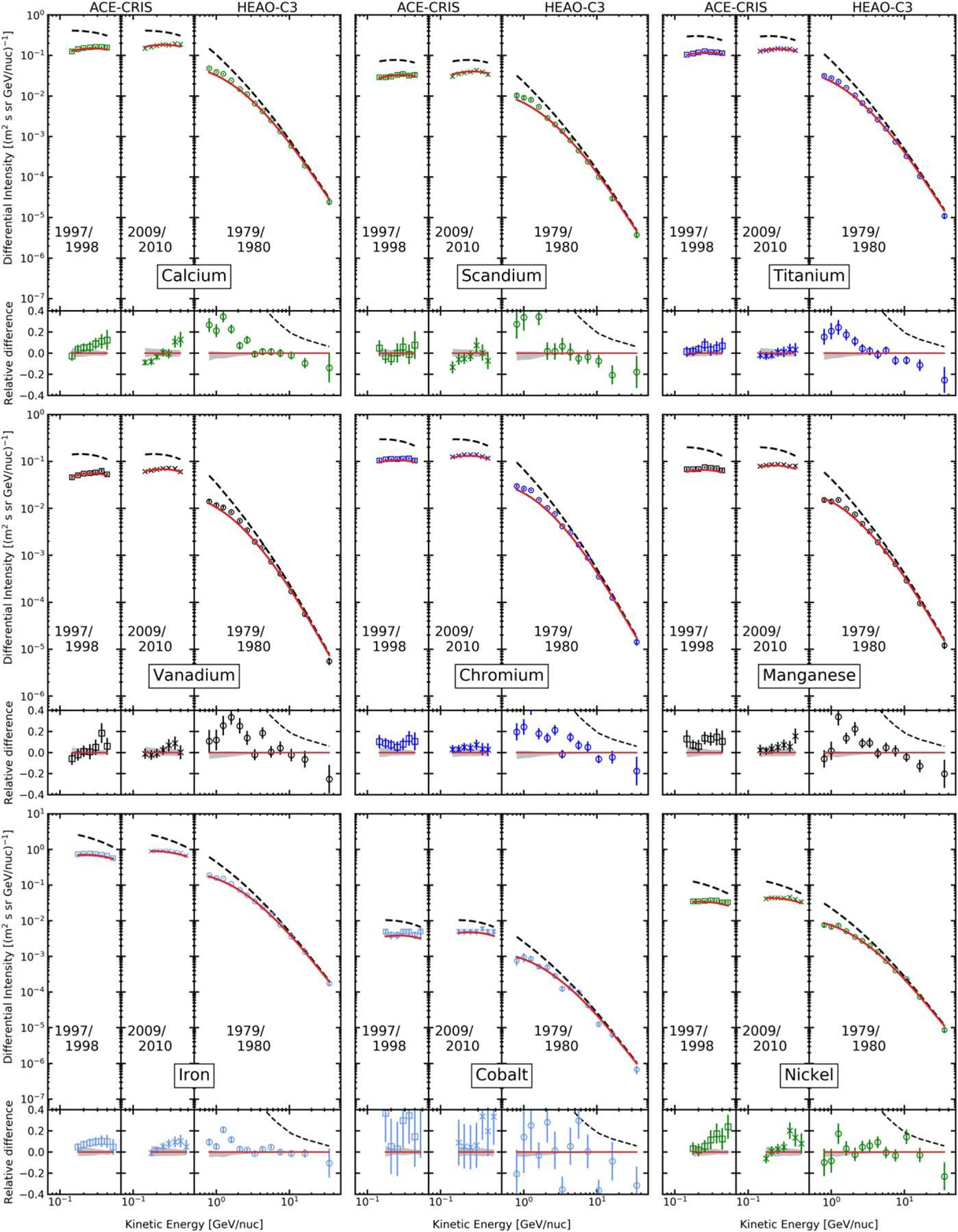
Calculated elemental spectra: ₂₀Ca–₂₈Ni. The line coding and data are the same as in Figure 1.

The ACE-CRIS data are shown for the periods of active (1997–1998) and quiet (2009–2010) Sun. In the case of abundant species, the agreement with ACE-CRIS data is also good within 5%–10% and is consistent with our calculations within the model uncertainties. Again, less abundant species, such as F, P, and Cl, demonstrate worse agreement, but still within 20%. This is mostly related to the period of active Sun when the heliospheric magnetic field is highly turbulent and therefore is not surprising. The significant scattering of the data points in the spectra and residual plots of Na, P, and Cl is hinting at the systematics. One can also see some discrepancies with Ni measurements due to the scattering of the data points, but large error bars make our calculations consistent within 2σ.

Figure 12 shows the ratios of various nuclei species, such as primary/primary, Si/O, Fe/O; secondary/primary, (Sc+Ti+V)/Fe, F/Ne, Al/Si, P/S; and secondary/secondary, Na/Al, F/V, P/Na, as compared to Voyager 1 (Cummings et al. 2016), ACE-CRIS (1997–1998 and 2009–2010), and HEAO-3-C2 (Engelmann et al. 1990) data. The low-energy part of the ratios is formed by the ionization energy losses that increase sharply with particle charge as ∝Z² and by fragmentation that behaves as ∝Z^2/3. This is very clear in the ratios of the primary species, where no secondary component is involved. One can see that both primary LIS ratios, Si/O and Fe/O, go down at low energies, reflecting smaller ionization energy losses of O versus Si or Fe and an increase in the fragmentation cross sections for heavier species.

Figure 12.

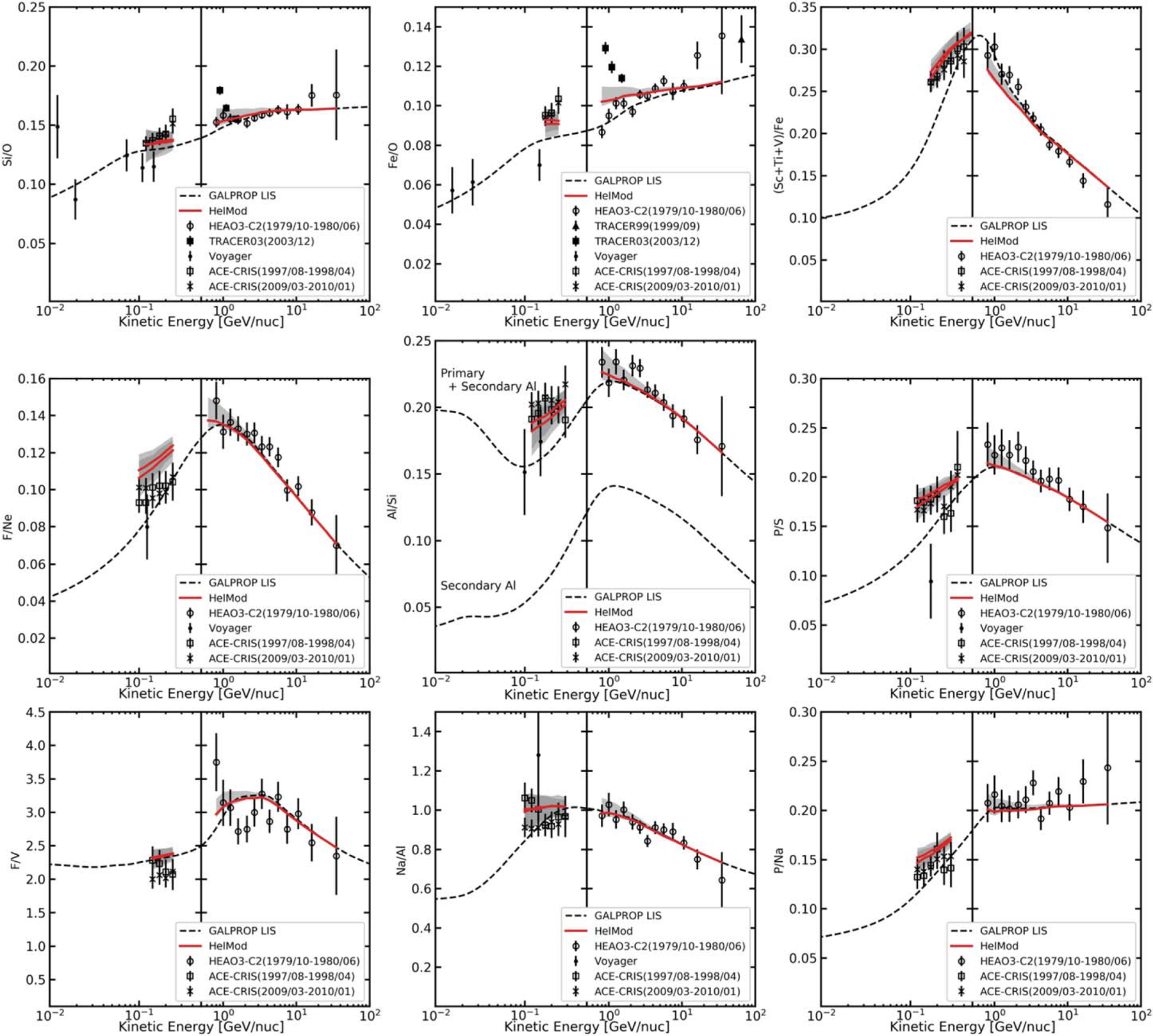
Our model calculations of the ratios of primary/primary species, Si/O, Fe/O; secondary/primary, (Sc+Ti+V)/Fe, F/Ne, Al/Si, P/S; and secondary/secondary: Na/Al, F/V, P/Na, as compared to Voyager 1 (Cummings et al. 2016), ACE-CRIS (1997–1998 and 2009–2010), and HEAO-3-C2 (Engelmann et al. 1990) data. The line coding is the same as in Figure 1.

Apart from the ionization energy losses, the fragmentation cross section plays an important role also in flattening the spectra of heavier species at significantly higher energies, where it competes with the escape rate from the Galaxy. Besides that, the large fragmentation cross section of Fe implies that it comes from sources that are closer than the sources of O. The fragmentation becomes less important with energy, as particles are leaking from the Galaxy faster. It is interesting to see the difference between the ratios for the species that have about the same fragmentation cross section, Si/O, and for the species, Fe/O, whose fragmentation cross sections differ by about a factor of 3. The former is about flat at high energies, while the latter is rising at high energies even though all species are primary and the injection spectrum for Fe is slightly steeper than for O (Table 2). Meanwhile, there are indications that the Fe/O ratio rises even at higher energies, where the leakage from the Galaxy is much faster than the fragmentation timescale.

Comparing with spectra of other species, one may notice that the observed spectrum of He is harder than the spectrum of protons, while the spectra of C and O have about the same spectral index as He (Aguilar et al. 2018b). Given that the most abundant isotopes of C, O, and Si all have A/Z = 2, we see that the increase in A/Z ratio from 1 (protons) to 2 (He, C, O, Si) results in the harder injection spectrum. Heavier elements have even larger A/Z that becomes ≈2.15 in the case of ⁵⁶Fe, the most abundant isotope of Fe, and may result in even flatter injection spectrum if the described tendency holds. However, the injection index of Fe is γ₃ = 2.19 versus 2.15 (He), 2.12 (C), 2.13 (O), and 2.19 (Si) in the I-scenario, and all of them are consistent with each other within the error bars ±0.04. If we look at the injection index γ₂ (the P-scenario, γ₃ = γ₂), the picture is even more confusing: γ₂ = 2.40 (He), 2.43 (C), 2.46 (O), 2.47 (Si), and 2.51 (Fe), i.e., the injection spectrum becomes noticeably steeper with Z, particularly if we compare He and Fe.

It is interesting to compare our results with two hypotheses, initially based on the observed spectra of H and He, proposing that the observed spectral hardening with Z may be the result of the selective acceleration process. Both of them exploit the fact that an SNR shock weakens with time, thus generating progressively softer spectra. However, physically the two proposed mechanisms are quite different.

One mechanism proposed by Ohira & Ioka (2011) and Ohira et al. (2016) assumes that the early strong SNR shock propagates through the inhomogeneous medium enriched with heavy elements from pre-SNR winds while mixing with more regular ISM at later stages. The effect is then due to the radial layering of different elements.

The second mechanism does not require the spatial inhomogeneity of element distribution and relies on an analytical study of the dependence of shock injection efficiency on A/Z ratio (Malkov 1998). It was predicted to grow and saturate with A/Z but is strongly dependent on the current shock Mach number. Young SNR shocks with higher Mach numbers must preferentially inject elements with higher A/Z. After integration over the SNR lifetime, the models by Malkov et al. (2012) and Hanusch et al. (2019) recover the hardening of He and other elements with A/Z ≳ 2. The mechanisms of saturation and ultimate efficiency decline with A/Z that physically should occur in this model are still under investigation. The hybrid simulations (Hanusch et al. 2019) predict the saturation near A/Z = 8–10, with the most rapid growth between A/Z = 1 and 2 (from H to He).

However, these results are not yet confirmed by independent simulations. Some contradictions with simulations that yield unlimited growth with A/Z have been discussed in the abovementioned paper. Our calculations show that the injection spectral indices remain the same or even steepen as we move from He to C, O, Si, and Fe. This pattern could be consistent with the injection saturation and decline with A/Z. Nevertheless, the two mechanisms described above are not mutually exclusive, which may indicate that the origin of the apparent spectral hardening could be more complicated.

The next plot shows the secondary/primary sub-Fe/Fe = (Sc+Ti+V)/Fe ratio, which is the heavy nuclei analogy of the widely used B/C ratio. This ratio includes species with large fragmentation cross sections and therefore is a probe of propagation properties of the local ISM. The agreement is good in the “plateau” energy range given the accuracy of measurements of individual species. Out of three “sub-Fe” elements, Ti and V are contributing most. Meanwhile, V is the least accurately measured, with two points in the “plateau” range being 20% or ~3σ too high relative to the other four (Figure 11). This is an indication of large statistical fluctuations or additional systematics. Consequently, minor deviations can be observed in the (Sc+Ti+V)/Fe ratio at lower and higher energies outside of the “plateau” that are still consistent with predictions within model uncertainties. These deviations are likely experimental artifacts similar to those observed in the B/C ratio rather than the result of the differences in the propagation properties of the local ISM. This is also implied by a good agreement of our model predictions with ACE and Voyager 1 data at low energies. Whether such an interpretation is correct will become clear after AMS-02 releases the elemental spectra of the iron group.

The following three plots show different secondary/primary ratios: F/Ne, Al/Si, and P/S. In many respects these are medium-nuclei versions of the B/C ratio. The data for all ratios agree well with the predictions, indicating that the propagation parameters for the medium nuclei are not changing versus the light species. The upturn in the Al/Si ratio below 100 MeV nucleon⁻¹ is partly due to the sharp peak in the Al production cross section in the reactions $p+{}_{14}^{28}\text{Si}\to {}_{13}^{26,27}\text{Al}$ below 100 MeV nucleon⁻¹. To illustrate the effect of secondary production, we added a plot of the LIS ratio for the case of pure secondary Al (the primary abundance is set to zero), which also shows a distinct flattening at low energies smoothed by the fast ionization energy losses. The second reason for the upturn is the scattering in the Voyager 1 data points for Al and Si (Figure 8). The three data points at 20–80 MeV nucleon⁻¹ in the Si spectrum appear somewhat too low, and so does the model Si spectrum tuned to the data. In the case of Al, it is opposite, and so the Al/Si ratio increases. Higher statistics collected by Voyager 1, 2 spacecraft should resolve this issue.

Finally, we show the mostly secondary/secondary ratios: Na/Al, F/V, and P/Na. They are not exactly flat at high energies. The most interesting is the F/V ratio, which is analogous to the primary/primary Fe/O ratio. The large fragmentation cross section of Fe nuclei and thus its flatter spectrum compared to lighter O species result in the secondary V spectrum also being flatter than the spectrum of F produced from fragmentation of Si-group nuclei. Meanwhile, the low-energy behavior of the F/V ratio is quite different from the ratio of primaries owing to a balance between the competing processes of the ionization energy losses, their fragmentation into the lighter species, and their production from fragmentation of heavier species. In addition, the low-energy parts of the spectra of the Si-group nuclei producing F and of the Fe group fragmenting onto V are also different owing to the differences in fragmentation cross sections and energy losses.

The decreasing Na/Al ratio reflects the difference in the proportion of the primary component, with Na having relatively larger secondary fraction than Al species (Figure 7). The ratio P/Na is almost flat at high energies, which corresponds to about the same proportion of primary component in both species. The slight increase in the ratio reflects the fact that P is produced in fragmentations of heavier species that have a flatter spectrum than the mid-range Si group (see the behavior of the primary/primary Fe/O and secondary/secondary F/V ratios at high energies, where the heavier species exhibit a flatter spectrum).

Finally, we wish to share some thoughts about the new breaks in the TeV range observed in the spectra of H and He; see Figure 6. These breaks make the spectra of CR species softer, in contrast to the break at ~370 GV observed in spectra of H through Si, at least, that makes the spectra harder after the break. The spectral indices of primary and secondary species below and above the 370 GV break are well tuned and are consistent with either the I- or P-scenario, with the preference given to the P-scenario, which requires significantly less free parameters and is consistent with the CR anisotropy measurements. Meanwhile, the breaks in TeV energy range seem to pose a challenge to the P-scenario, which would require the spectrum of interstellar turbulence and thus the diffusion coefficient to experience corresponding twists. More accurate data from CALET, DAMPE, or ISS-CREAM indicating whether the new breaks are observed at the same rigidity or not and whether they are observed in spectra of other species may provide a clue to their origin.

5. Summary

The direct precise measurements of spectra of CR species in the wide energy range are vitally important for CR studies, interpretation of γ-ray and microwave observations, and searches for signatures of new phenomena. The most precise data on CR species that are available in the GV–TV range come from the unique magnetic spectrometer AMS-02 on board the ISS. However, moving from the most abundant and light CR nuclei to rare and heavier species takes time to collect statistics and analyze. So far, spectra of only 11 CR nuclei were published by the AMS-02 collaboration, ₁H–₈O, ₁₀Ne, ₁₂Mg, and ₁₄Si, which show significant deviations from data taken by other instruments in the same energy range. This makes the full-range interpretation of astrophysical measurements difficult, relying on the data from several missions with unknown systematic uncertainties. Folding such uncertainties into the calculations makes the results less reliable and more model dependent. Meanwhile, waiting for AMS-02 to deliver the accurate spectra of all CR species from ₁H–₂₈Ni may take years.

A thorough comparison of the available AMS-02 spectra of CR nuclei and HEAO-3-C2 results reveals a certain energy range, the so-called “plateau” from 2.65 to 10.6 GeV nucleon⁻¹, where the appropriately modulated HEAO-3-C2 measurements agree well with more precise AMS-02 data. The analysis of the description of the HEAO-3-C2 counters made it possible to unveil the systematics associated with HEAO-3-C2 data that support our finding. Therefore, the HEAO-3-C2 data in the “plateau” energy range can be used as a substitute of AMS-02 data for those species for which AMS-02 measurements are not yet available; meanwhile, data outside of this range can be neglected. This is a significant breakthrough that allows reliable CR propagation calculations to be made for all species ₁H–₂₈Ni while AMS-02 data are still being analyzed.

Using the GalProp–HelMod framework and available data from a number of instruments, we derived a self-consistent set of LIS for ₁H–₂₈Ni nuclei and e⁻, $\overline{p}$ for the first time. The LIS energy range covers 8–9 orders of magnitude in energy from 1 MeV nucleon⁻¹ to ~100–500 TeV nucleon⁻¹. We provide the final set of propagation parameters, as well as the injection spectra and relative abundances for each isotope ${}_1^1\text{H}-{}_{28}^{64}\text{Ni}$, while e⁻ and $\overline{p}$ LIS can be found in our previous publications (Boschini et al. 2017, 2018a). For each element we also provide the analytical parameterization of the LIS, as well as their numerical tables that tabulate the LIS in rigidity R and in kinetic energy E_kin per nucleon. This is a significant step forward that allows the propagation in the Galaxy and in the heliosphere to be disentangled, while each future measurement can be analyzed within a self-consistent framework.

We thank the anonymous referee for valuable comments. Special thanks to Pavol Bobik, Giuliano Boella, Karel Kudela, Marian Putis, and Mario Zannoni for their continuous support of the HelMod project and many useful suggestions. This work is supported by ASI (Agenzia Spaziale Italiana) through contract ASI-INFN No. 2019-19-HH.0 and by ESA (European Space Agency) through contract 4000116146/16/NL/HK. I.V.M. and T.A.P. acknowledge support from NASA grant No. NNX17AB48G. We thank the ACE-CRIS instrument team and the ACE Science Center for providing the ACE data. This research has made use of the SSDC Cosmic rays database (Di Felice et al. 2017) and the LPSC Database of Charged Cosmic Rays (Maurin et al. 2014).

Appendix A. Plots of the Spectra of He–O Nuclei

For completeness, Figure A1 shows the spectra of He–O nuclei published by AMS-02 (Aguilar et al. 2015a, 2015b, 2016b, 2017, 2018b, 2018c) compared to the updated spectra calculated with the GalProp–HelMod framework. Spectra of protons, Ne, Mg, and Si are shown in Figures 3 and 5.

Figure A1.

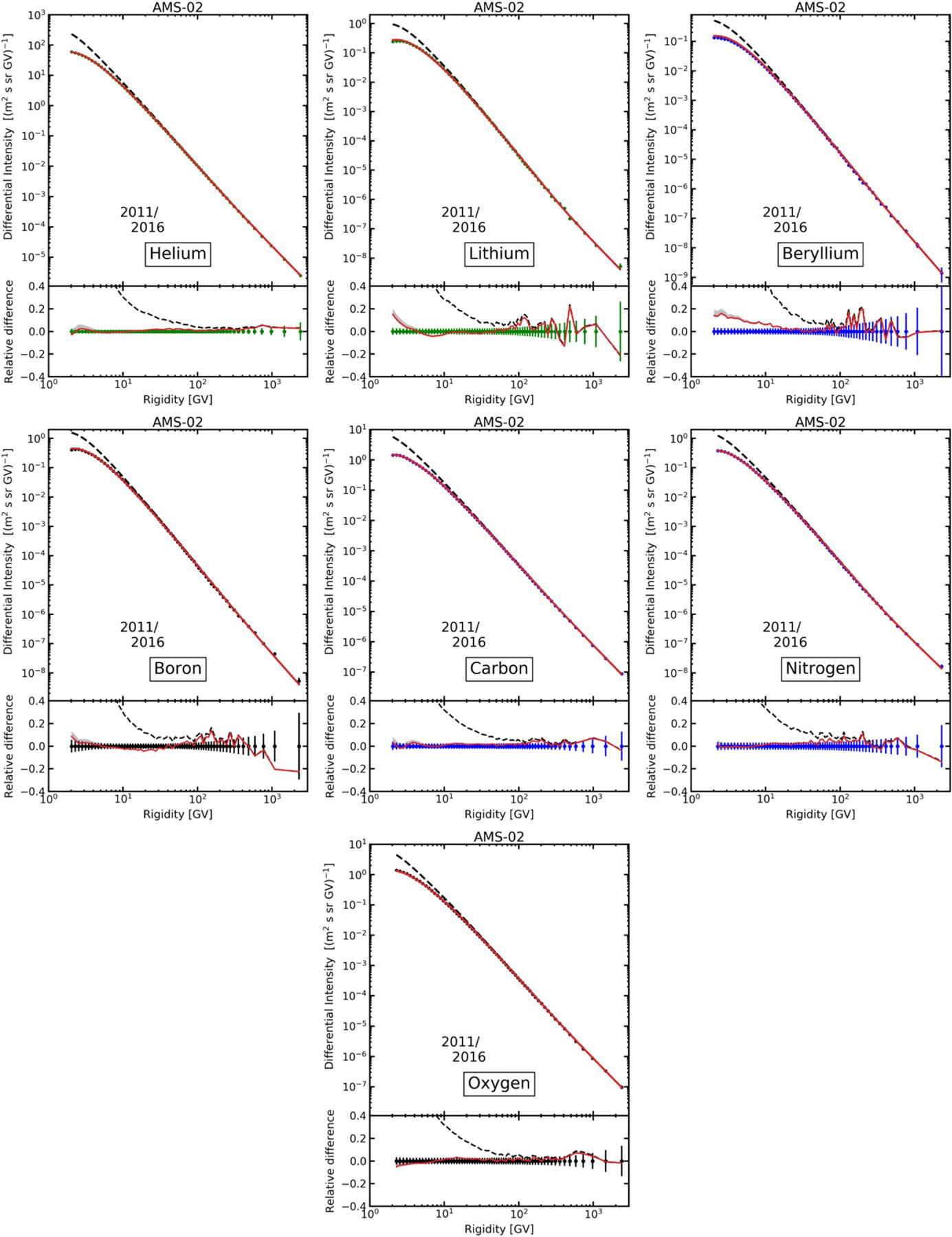
Our updated model calculations compared with AMS-02 data for ₄He–₈O nuclei (Aguilar et al. 2015b, 2015a, 2016b, 2017, 2018b, 2018c), plotted with the same style that was used in our earlier papers. The line coding is the same as in Figure 1. Spectra of protons, Ne, Mg, and Si are shown in Figures 3 and 5.

Appendix B. HEAO-3-C2 Counters and Measurements of the Elemental Spectra of CRs

The French–Danish experiment C2 on board the NASA HEAO-3 satellite has measured the spectra of CR nuclei for 4 ⩽ Z ⩽ 28 in 14 energy windows from 0.62 to 35 GeV nucleon⁻¹ (Engelmann et al. 1990). These spectra were abundantly used in astrophysics to derive parameters of CR propagation and source abundances. Until recently there was no alternative in this energy range, while data at lower (e.g., ACE-CRIS) and at higher energies (e.g., CREAM, Ahn et al. 2008, 2009; ATIC-2, Panov et al. 2009) connect smoothly without visible breaks, thanks to the energy gap between the ACE-CRIS data and HEAO-3-C2 and the large experimental errors at high energies.

New precise measurements of CR nuclei ₄Be–₈O by the AMS-02 experiment (Aguilar et al. 2017, 2018b, 2018c) indicate that there are clear discrepancies with HEAO-3-C2 data at low and high energies (Boschini et al. 2018b, 2020), while in the middle range between 2.65 and 10.6 GeV nucleon⁻¹ the agreement is fair. If there is a particular reason for the whole energy range 0.62–35 GeV nucleon⁻¹ of HEAO-3-C2 to be clearly split into three intervals, with the middle one being the most accurate, it would provide an exciting opportunity to use this limited energy range to build the LIS for all nuclei (Z ⩽ 28), where the AMS-02 data are still unavailable. In this section we look into the published details of the HEAO-3-C2 telescope assembly and discuss possible reasons for the observed split. Because this issue is crucial for future studies, we feel that it is necessary to quote some passages from the original publications.

B.1. The Counters

The HEAO-3-C2 telescope had three Cherenkov counters for measurements of the particle momentum designed to cover the whole energy range. Each counter was made of a different material with a different refractive index to tune it for a particular energy interval (see Table 1 in Engelmann et al. 1990). The materials used for the counters are teflon (refractive index 1.33), aerogel block (1.053), and aerogel “sand” (1.012). Here is an excerpt from the original paper:

“The determination of the charge and momentum of each incoming particle relies upon the double Cherenkov technique (Corydon-Petersen et al. 1970); the three inner detectors are used primarily for velocity determination and the top and bottom counters for charge determination. The main characteristics of the counters are summarized in Table 1.

Each counter is made of one or two discs of radiating material within a light diffusion box of 60 cm in diameter and viewed by twelve 5-inch photomultiplier tubes. Silica aerogel is used as a Cherenkov material in both C2 and C4 counters. This new material with adjustable refractive index was developed by Cantin et al. (1974), in order to match the particle spectrum observable along the HEAO-3 orbit. The C2 radiator is a mosaic of hexagonal blocks of 5.6 cm thick aerogel; its refractive index is 1.052. Silica aerogel is also used for the C4 counter, but with a lower refractive index (1.012). This material being too brittle to be used in the form of blocks was crushed up into an “aerogel sand,” kept in place in the diffusion box by a mylar window. This sand is made of grains about 2 mm in diameter. Two such radiators, each 5.5 cm thick, are placed within the diffusion box (Cantin et al. 1981)…

In the high ‘sand energy’ region, the signal is distorted by the signal broadening due to the finite resolution of the sand counter. To correct for this effect, we simulate how particles with a given energy are redistributed into measured signal bins, according to both the finite resolution of the counters and the spectral index, then we use these simulation results to correct the number of particles in a given energy window, as explained by Juliusson (1974).”

Figure B1.

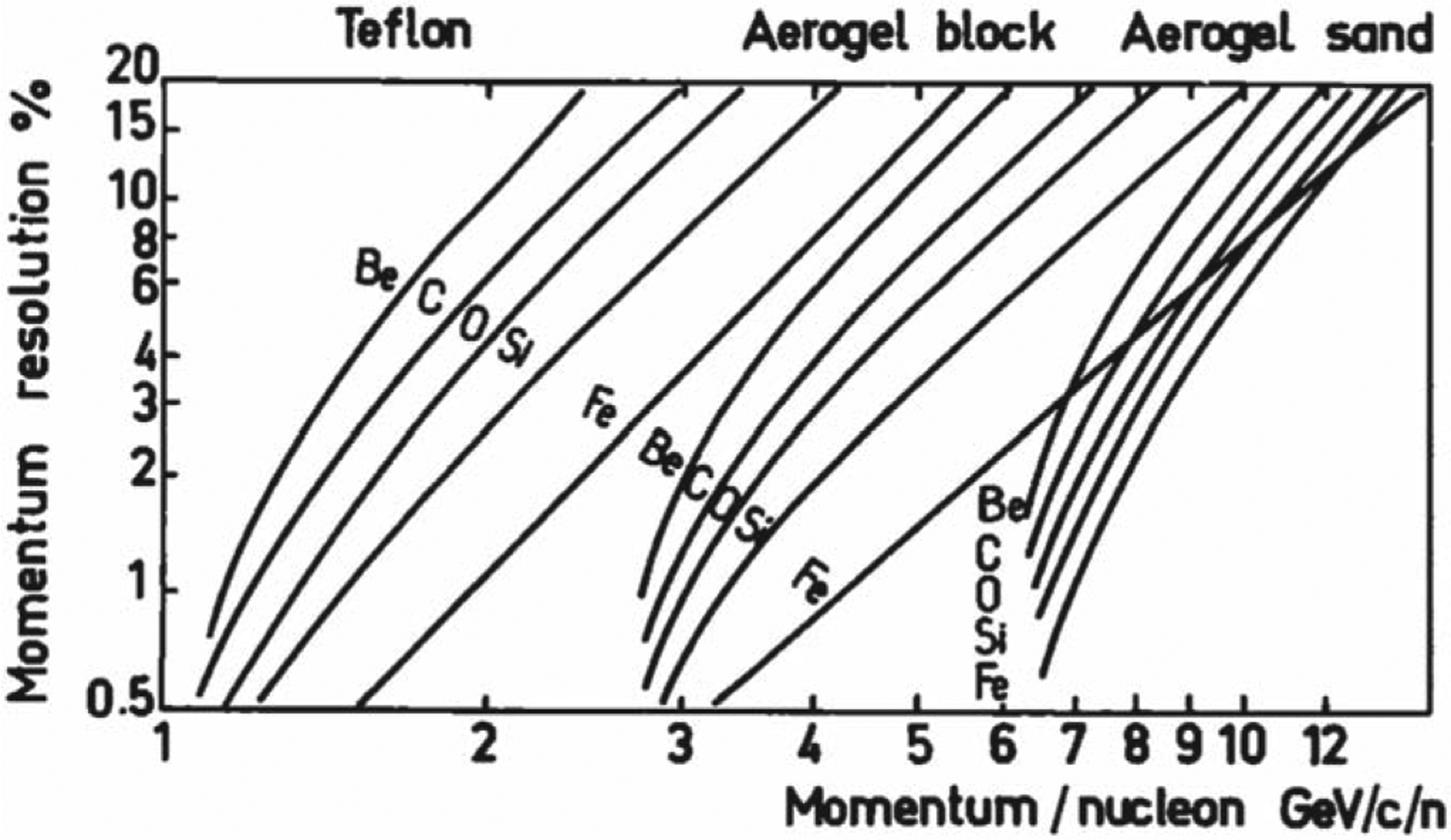
Momentum resolution in the three counters for Be, C, O, Si, and Fe CR nuclei (reproduced from Cantin et al. 1981).

The momentum resolution for each counter is optimal near their thresholds but quickly degrades as the measured momentum increases, as can be seen in Figure B1 (Cantin et al. 1981; see also Figure A1 in Bouffard et al. 1982). However, due to the fluctuations in the background signal, the effective thresholds were set somewhat higher. Here is an excerpt from the original paper (Engelmann et al. 1990):

“…we use teflon spectra up to ~2.4 GeV nucleon⁻¹, then aerogel block spectra from ~2.4 to 6.4 GeV nucleon⁻¹, and sand spectra above ~6.4 GeV nucleon⁻¹. These limits, defining the three energy ranges are chosen slightly higher than the threshold values mentioned in Table 1, as fluctuations in background signal prevent the use of a counter too close to its threshold…

The energy/nucleon limits corresponding to the 14 energy windows are the following:

1. In the teflon range: 0.55, 0.70, 0.91, 1.11, 1.40, 1.82, 2.35 GeV nucleon⁻¹;

2. In the aerogel block range: 2.35, 2.96, 3.79, 4.89, 6.42 GeV nucleon⁻¹;

3. In the aerogel sand range: 6.42, 8.40, 12.0, 17.8 GeV nucleon⁻¹.

The last window is the integral momentum (>17.8 GeV nucleon⁻¹). It is transformed into a differential window, as explained in Appendix 1. The first window can be safely defined only for Z < 10. At higher charges, the range of the particle becomes comparable to the telescope thickness, so that some particles of lower energy and/or larger incidence angle are absorbed in the telescope matter.”

And further (Bouffard et al. 1982): “The time-of-flight system is performing well for Z > 6. For lowest charges the resolution is rather poor.”

The light emission and detection process in the counters was modeled (Lund et al. 1981) considering three sources of the Cherenkov signal: (i) The Cherenkov signal from the primary nucleus is described by the classical expression and is deemed as well defined. (ii) As the primary nucleus traverses the instrument, it ejects numerous knock-on electrons from the material. Such electrons, if sufficiently fast, will emit Cherenkov radiation in the radiators, and this will contribute significantly to the signal and its fluctuations. They are difficult to evaluate because the electrons can have very high energies (~p² MeV), and they are therefore not generally confined to the radiator (or material layer) in which they originate. (iii) According to Lund et al. (1981),

“The light diffusing boxes are lined with white Millipore paper, and the aerogel radiators are held in place by thin mylar foils. Both of these materials emit Cherenkov radiation corresponding to a refractive index n = 1.6, and this contribution is included in our model.”

Lund et al. (1981) show estimates of the Cherenkov signal contributions from different sources (i)–(iii) (see Figure 1 in their paper). While in teflon and aerogel block counters a sum of the secondary (ii) and foil (iii) contribution does not exceed 10%, the aerogel sand has a sum of those contributions very flat and approaching 17% in the whole momentum range.

Figure B2 (reproduced from Lund et al. 1981) shows consistency between the final momentum assignments using all three counters. Teflon counter shows overall consistency with aerogel block counter but exhibits large errors above 4.5 GeV c⁻¹ nucleon⁻¹. The errors become quite large for aerogel block and sand counters above ~10 GeV c⁻¹ nucleon⁻¹, which can be seen from the large scattering of the points and shown with large typical error bars. Here is an excerpt from the original paper (Lund et al. 1981):

“All the parameters entering into the above model have been determined by measurements on the ground with exception of the following: (a) The effective refractive index for Cherenkov emission in the aerogel sand radiator. The value adopted (for consistency reasons) is 1.012 whereas laboratory optical measurements had predicted 1.015 ± 0.002. (b) The rate of occurrence of the ‘faceplate flashes’ (Section 6). To explain the observed fluctuations near threshold we had to assume an occurrence frequency of 5 × 10⁻⁴ per g cm⁻² of overlying material for singly charged particles, the effect being proportional to Z². (c) The signal values in all three counters for particles with β = 1. This critical parameter is difficult to determine precisely from the observed signal distributions as both the CR energy spectrum and the variation of the knock-on contribution to the signal and its fluctuations enter into the calculations in a complex way. Starting from the observed ‘β = 1 points’ for nickel nuclei we have adjusted these for optimum consistency between the three counters. The optimized values, which only differ slightly from the raw ones, are then scaled to other nuclei, assuming Z² proportionality.”

Figure B2.

Consistency of final momentum assignment (reproduced from Lund et al. 1981). Examples of the correlation between the momentum determinations from the three counters are shown for nickel nuclei. The error bars shown are 1σ as predicted by the model.

B.2. Geomagnetic Rigidity Cutoff Selection

The accelerator beam calibration was not possible at that time, so the geomagnetic cutoff rigidity that is varying along the HEAO-3 orbit was used instead. Here is how this procedure is described in Engelmann et al. (1990):

“Now if we want to get the true spectrum of the particles, as they would be observed outside the magnetosphere, we have two possibilities:

1. either to use all particles above the geomagnetic cut off at the point of measurement (here again we must exclude particles of rigidity close to the cut off). In that case, we get a distorted spectrum, which can be corrected by applying an energy dependent correction factor, for the proportion of time spent at various rigidity cut offs during flight.

2. or to select only the particles registered at rigidity cut offs below that corresponding to the velocity threshold of the counter considered (as an example below 2.3 GV for the teflon counter). In this last approach, only a small proportion of particles are selected (about 10% in the case of the teflon counter), and therefore we cannot use directly this method to get the energy spectrum of a rare element like P or Cl. We can use it however to get the spectrum of a reference element like oxygen and derive the spectra of other nuclei by using their relative abundances with respect to the reference element, as given in Table 2. In that case of course, the accuracy of every point in each spectrum is limited by the statistical accuracy of the corresponding point of the oxygen spectrum…

In the present paper, we preferred to use a modified version of the second method: by a proper selection of data, we are able to determine absolute flux values for each type of nucleus, in units of particles m⁻² sr⁻¹ s⁻¹ (GeV/n)⁻¹. More precisely, to determine the spectrum above a threshold rigidity R₀, we have selected the data in such a way that:

1. The geometry of the instrument is accurately known;

2. The geomagnetic cut off corresponding to all viewing directions of the telescope is lower than R₀;

3. The time during which these conditions are met is accurately measured.

All these conditions are fulfilled by selecting data when the telescope axis lies near the local vertical and when the vertical rigidity cut off is lower than 0.8 R₀. The instrument is then single-ended, since it is protected by the solid earth from particles propagating in the reverse direction. The acceptance geometry is known and we have verified that condition (ii) is fulfilled.

Practically, we first select periods of time when the angle between the telescope axis and the local vertical is lower than 25°. In order to have a well defined restricted geometry, we require in addition that the impact points of the particle in the top and bottom counters lie within a circle of 52 cm in diameter, i.e., well inside the radiators of the charge counters, which are 60 cm in diameter. In these conditions, the maximum acceptance angle of the telescope is 28° and the geometrical factor: F = 413 cm² sr. We then derive the oxygen spectrum between 0.55 and 2.4 GeV nucleon⁻¹ from data registered at rigidity cut off values smaller than 1.85 GV and that above 2.4 GeV nucleon⁻¹ from data registered at cut off values smaller than 5.0 GV, so as to improve statistics.”

B.3. Summary of the HEAO-3-C2 Telescope Performance

Above we described main reasons that, in our view, are most likely responsible for the observed discrepancies, but many other issues that may affect calibration of the instrument exist.

It is clear that the whole rigidity range of the instrument is divided between three different counters, which have different responses. The teflon and aerogel block counters are well studied, while a newly introduced aerogel sand counter is not. Besides small momentum range and large errors in the momentum resolution, its refractive index has to be adjusted after the launch to make it consistent with other counters’ response. Therefore, it is likely that the discrepancy between AMS-02 and HEAO-3-C2 data observed at high energies is partly due to the momentum and mass resolutions in the aerogel block and sand counters above ~9 GeV nucleon⁻¹, where the resolution of the block counter degrades being far from the threshold, while the sand counter has large intrinsic errors.

Additionally, the CR spectrum becomes steep at high energies, approaching a power-law index about −2.7. Therefore, the worsening energy resolution of the sand counter has a greater impact on the quality of measurements than that for the other two counters. Interestingly enough, the authors note that

“in comparison with other published data, HEAO-3 data above 10 GeV/n are on the lower side of the distribution, but the spread of the points is relatively large”

(Engelmann et al. 1990, p. 104). This further supports our conclusion since in this energy range the solar modulation is moderate.

The discrepancy at low energies is likely due to the variations in the rigidity cutoff along the orbit of the instrument that was used for the event selection. The HEAO-3 instrument was flown from 1979 September 20 to 1981 May 29, i.e., during the solar maximum conditions (Cycle 21). Meanwhile, during the disturbed periods when the solar wind pressure exceeds ~4 nP, and which occur more often when the solar activity is high, the magnetic field carried by the solar wind affects the geomagnetic field, leading to incorrect estimate of the geomagnetic cutoff. In turn, it can result in incorrect estimates of the particle rigidities during a significant fraction of the mission. The effect could be quite large and is more important for lower rigidities. The influence of such disturbances on AMS-02 was investigated, and the appropriate code was developed.²⁰

In our analysis, we rely on the midrange results of the HEAO-3-C2 telescope as measured by the aerogel block counter and the first two energy bins of the sand counter. The same energy range is used for all species.

Appendix C. Supplementary Material

C.1. Primary Fluorine

Among the elements A ⩾ 5 produced in stars, the abundance of fluorine is anomalously low. This is mainly due to the fact that fluorine is easily destroyed in stars through either p- or α-captures. The solar system abundances of fluorine relative to oxygen range from F/O = 7.4 × 10⁻⁵ in the photosphere to 10.5 × 10⁻⁵ in meteorites (Asplund et al. 2009). This can be compared with the CR sources (Table 3), F/O = 29.1 × 10⁻⁵ or [F/O]_srs = 0.44–0.60 dex depending on the (F/O)_⊙ used, where [X/Y] = log₁₀(X/Y)−log₁₀(X/Y)_⊙, which are apparently 3–4 times more abundant with fluorine.

The main astrophysical sources of fluorine are thought to be Type II supernovae (SNe II), Wolf–Rayet (W-R) stars, and the asymptotic giant branch (AGB) of intermediate-mass stars (e.g., Meynet & Arnould 2000; Renda et al. 2004; Olive & Vangioni 2019). These sources become important at different stages of chemical evolution of the Galaxy, with the ν-spallation of ₁₀Ne in SNe II dominating at early times in low-metallicity environments, while W-R and AGB stars dominate at the later stages at solar and supersolar metallicities. The calculations show that reaching the solar level of [F/O] = 0 at the present epoch requires all three types of sources to contribute (Renda et al. 2004), while exceeding it is problematic. Therefore, the excess fluorine in the CR sources [F/O]_srs = 0.44–0.60 dex may provide important constraints on the origin of CRs.

For quite a long time people noticed that some isotopic ratios in CRs, such as ¹²C/¹⁶O, ²²Ne/²⁰Ne, and ⁵⁸Fe/⁵⁶Fe, significantly exceed values observed in the solar system. This was interpreted as evidence that some fraction of CRs are produced from material of the winds of the W-R stars (Binns et al. 2007). The proportion of ~20% of W-R material mixed with 80% material with solar system composition reproduces the derived CR source abundances quite well. Since W-R stars are evolutionary products of OB stars, and OB stars are formed in associations, the material of such winds can be accelerated by a following SN shock passing through the ISM. A recent observation of the radioactive ⁶⁰Fe by ACE-CRIS (Binns et al. 2016) supports the hypothesis of the SN explosion in the solar neighborhood 2–3Myr ago. This estimate is consistent with other observations, such as the change of the isotopic composition of the deep-sea manganese crust (Knie et al. 2004) and elevated ratio ⁶⁰Fe/Fe in debris on the lunar surface (Fimiani et al. 2016).

Observation of the excess fluorine in the CR source composition seems to agree well with these observations. A study of the rotating and nonrotating W-R stars with the initial composition corresponding to the solar system shows an enrichment of the W-R winds with fluorine relative to oxygen by a factor of ~2 (Meynet et al. 2001). The calculation was made for a star of 60M_⊙ during itsWN and WC stages, and in all cases the wind was enriched with fluorine by about the same factor.

However, the current estimate of the ₉F abundance in CR sources is not very reliable given the accuracy of the available cross sections. The calculated abundance ratio at the CR sources is (F/Ne)_srs ≈ 2.5 × 10⁻³, while in CRs it is (F/Ne)_CR ≈ 0.1 at 10 GeV nucleon⁻¹. Therefore, the relative fraction of primary fluorine in CRs is (F/Ne)_srs/(F/Ne)_CR ≈ 0.025. The fractional contribution of fragmentation of different CR species into the secondary isotopic production was evaluated by Moskalenko et al. (2013) for all isotopes from ${}_3^6\text{Li}$ to ${}_{28}^{62}\text{Ni}$, with ${}_{28}^{64}\text{Ni}$ being the heaviest contributor. The main production channels for ${}_9^{19}\text{F}$ are fragmentations of ${}_{10}^{20}\text{Ne}$, ${}_{10}^{22}\text{Ne}$, ${}_{12}^{24}\text{Mg}$, and ${}_{14}^{28}\text{Si}$ isotopes with less important contributions from fragmentation of ${}_{10}^{21}\text{Ne}$, ${}_{11}^{23}\text{Na}$, ${}_{12}^{25}\text{Mg}$, ${}_{12}^{26}\text{Mg}$, and ${}_{13}^{27}\text{Al}$. Also contributing are decays of intermediate nuclides ${}_{10}^{19}\text{Ne}\left[{\beta }^{+}\right]$ and ${}_8^{19}\text{O}\left[{\beta }^{-}\right]$.

Taking into account only the main channels for production of ${}_9^{19}\text{F}$ and assuming that the propagated abundances of ₁₀Ne, ₁₂Mg, and ₁₄Si are about the same and these elements consist of only one main isotope, we can simply add their contributions: ${\sigma }_{\text{F}}\approx 26\text{\hspace{0.17em}mb\hspace{0.17em}}\left({}_{10}\text{Ne}\right)+10\text{\hspace{0.17em}mb\hspace{0.17em}}\left({}_{12}\text{Mg}\right)+9\text{\hspace{0.17em}mb\hspace{0.17em}}\left({}_{14}\text{Si}\right)+28\text{\hspace{0.17em}mb\hspace{0.17em}}\left({}_{10}^{20}\text{Ne}\to {}_{10}^{19}\text{Ne}\left[{\beta }^{+}\right]\right)+4\text{\hspace{0.17em}mb\hspace{0.17em}}\left({}_{12}^{24}\text{Mg}\to {}_{10}^{19}\text{Ne}\left[{\beta }^{+}\right]\right)\approx 80\text{\hspace{0.17em}mb\hspace{0.17em}}$. Here we used accelerator data at ~600 Mev nucleon⁻¹ and assumed the same values at higher energies. The effective total production cross section of ${}_9^{19}\text{F}$ weighted with the propagated abundances of other contributing isotopes at 10 GeV nucleon⁻¹ would then be of the order of 100 mb. The ratio (F/Ne)_srs/(F/Ne)_CR ≈ 0.025 implies that a 2.5% increase in the effective production cross section, i.e., ≈2.5 mb, would be enough to compensate for the whole primary abundance of ${}_9^{19}\text{F}$. The value 2.5 mb is comparable to the typical 10% cross section error for the main production channels, such as the fragmentation ${}_{10}^{20}\text{Ne}\to {}_9^{19}\text{F}$ and ${}_{10}^{20}\text{Ne}\to {}_{10}^{19}\text{Ne}\left[{\beta }^{+}\right]\to {}_9^{19}\text{F}$, and thus the primary abundance of fluorine is within the cross-section uncertainty and consistent with zero.

Though this exercise does not allow us to make a reliable conclusion about the primary fluorine, it shows how important the accuracy of the production cross sections is for interpretation of CR measurements.

C.2. LIS for Elements from H to Ni

Here we provide analytical parameterizations of the LIS for each species, Equations (C1)–(C27), with parameters summarized in Table C1. They are complemented by numerical tables calculated for the I-scenario for all elements from ₁H to ₂₈Ni; see Tables C2 and C3. The I-scenario has more free parameters than the P-scenario and therefore gives more accurate representation of the data. For each element, we provide two numerical tables that tabulate the LIS in kinetic energy E_kin per nucleon and in rigidity R.

C.2.1. Analytical Parameterizations of the LIS

$$F_{\text{H}}(R)=\{\begin{array}{ll}a{R}^2+bL{(R)}^2+(c+d\tilde{R})G\left[\frac{R}{L(R)}\right]-f-g\tilde{R}-hL(R)i^{G\left[\frac{R}{L(R)}\right]},\hfill & R⩽2.5\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[-l-mR+nL(R)+oG(pR)+\left(q\tilde{R}-s^{L(R)}r\right)\text{cos}(t+u\tilde{R})\right],\hfill & R>2.5\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C1)

$$F_{\text{He}}(R)=\{\begin{array}{ll}a-bR+c\sqrt{\text{sin}(R)}+\left[dRG{(fR)}^2-gR\right]\text{sin}(R)-(h+iR)G(fR),\hfill & R⩽2.5\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[l+\frac{m}{R}-\frac{n}{R^2}+\frac{o}{p+qR}+r\text{\hspace{0.17em}tanh}\left(\frac{s}{t+uR}\right)-z^{\frac{3}{R}}v\right],\hfill & R>2.5\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C2)

$$F_{\text{Li}}(R)=\{\begin{array}{ll}{R}^{1.5}\left\{-a+bR+c{R}^2-d{R}^{1.5}+T(R)\left[f+gG\left(G{(R)}^{rR}T(R)\right)\right]\right\},\hfill & R⩽2.6\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left\{h+i\sqrt{R}-lR+mR\tilde{R}+n\text{\hspace{0.17em}sin\hspace{0.17em}}\tilde{R}+\frac{1}{R}\left[o{\tilde{R}}^{1.5}+p\sqrt{\tilde{R}}G(\sqrt{\tilde{R}})\right]-qG(\sqrt{\tilde{R}})\right\},\hfill & R>2.6\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C3)

$$F_{\text{Be}}(R)=\{\begin{array}{ll}aR-b{R}^2+c{R}^4+RG(R)\left[-d-fR-gG(R)+hL\left(i{R}^2\right)\sqrt{R}\right],\hfill & R⩽2.6\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left\{l+mG\left(n+oR+p{R}^{-1}\right)+q{\left[r+R+\frac{s}{R-t}\right]}^{-0.5}-uR\right\},\hfill & R>2.6\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C4)

$$F_{\text{B}}(R)=\{\begin{array}{ll}a+\text{cos\hspace{0.17em}}R\left[-b+cR+dG(fR)R^3\right]-gR-hG\left(i{R}^2\right),\hfill & R⩽2.7\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[l-\frac{m}{R}+\frac{n}{\sqrt{R}}-\frac{o}{p+qR}+\frac{r}{s+tR\sqrt{R}}-u\text{log}\tilde{R}-v{R}^2\sqrt{R}\right],\hfill & R>2.7\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C5)

$$F_{\text{C}}(R)=\{\begin{array}{ll}a+R\left(-b+c{R}^2\right)+G(R)\left\{-d+R[f+gRG(R)]\right\}-hRG(iR),\hfill & R⩽2.55\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[l+mR-n{R}^2-\frac{o}{R}+\frac{p}{q+R}+r{\tilde{R}}^2+s\text{log}\left(tR+\frac{u}{v+R}\right)\right],\hfill & R>2.55\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C6)

$$F_{\text{N}}(R)=\{\begin{array}{ll}-a-b\tilde{R}+cR\tilde{R}-d\text{\hspace{0.17em}sin}(R)\tilde{R}+f\text{\hspace{0.17em}sin}(R)-g\text{\hspace{0.17em}tanh}(hR)+iG\left(l{\text{sin}}^{2}R\right),\hfill & R⩽3.0\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[m-\frac{n}{R}+\frac{o}{p+qR}-rR-s\tilde{R}+t\text{\hspace{0.17em}log}(p+qR)+\frac{uR}{\text{log}(p+qR)}\right],\hfill & R>3.0\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C7)

$$F_{\text{O}}(R)=\{\begin{array}{ll}a-bR-c\tilde{R}+d\text{\hspace{0.17em}tanh}(R)+f\tilde{R}\text{\hspace{0.17em}tanh}(R)\text{tanh}(\tilde{R})+g\text{\hspace{0.17em}tanh}(\tilde{R})+h{\text{tanh}}^4(\tilde{R})-i{\text{tanh}}^2(\tilde{R}),\hfill & R⩽2.65\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[lR+m\text{log}(R+\tilde{R})+\frac{n}{\sqrt{o+pR}}-\frac{q}{{(o+pR)}^{0.25}}-r-s\sqrt{o+pR}-tR{(o+pR)}^{0.25}\right],\hfill & R>2.65\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C8)

$$F_{\text{F}}(R)=\{\begin{array}{ll}a-bR+\sqrt{cR}(d-fR)-G(R)\left\{g+R^2\left[h+iG{(R)}^2\right]\right\},\hfill & R⩽2.5\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[-l-m\tilde{R}+nR-\frac{o}{R}+\frac{pR-q\tilde{R}}{r+R}+\frac{s\tilde{R}}{t+u\tilde{R}+R\tilde{R}}\right],\hfill & R>2.5\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C9)

$$F_{\text{Ne}}(R)=\{\begin{array}{ll}a-bRH(R)+cH(R)+dH{(R)}^2+G[f-H(R)-gRH(R)]\left[hH{(R)}^2-i\right],\hfill & R⩽2.4\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[l-\frac{m}{\sqrt{R}}+n{R}^{1.5}-o{R}^2+(r\sqrt{R}-s-tR)\text{tanh}\left(pR-\frac{q}{\sqrt{R}}\right)\right],\hfill & R>2.4\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C10)

$$F_{\text{Na}}(R)=\{\begin{array}{ll}a-bR-\frac{c}{G(R)}+(dR-f)G(R)-[g+hG(R)]\text{sin}\left[2G{(R)}^3\right],\hfill & R⩽2.4\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[i-lR-n^{R}m+o\sqrt{R}+p\left(q^R\text{log}(\tilde{R})+r^R{\text{\hspace{0.17em}tanh}}^5(R)\right)\right],\hfill & R>2.4\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C11)

$$F_{\text{Mg}}(R)=\{\begin{array}{ll}-a-bR-c{R}^2\tilde{R}+L\left(d{R}^2\right)[f-gG(R)]+hG\left(i{R}^2\right),\hfill & R⩽2.5\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[-l-m{R}^2-\frac{n}{R}+o\tilde{R}+pR{\tilde{R}}^2+\frac{q}{r+R}+\frac{s}{t+uR}\right],\hfill & R>2.5\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C12)

$$F_{\text{Al}}(R)=\{\begin{array}{ll}a+b\text{\hspace{0.17em}tanh}(\tilde{R})+c\text{\hspace{0.17em}tanh}[\text{log}G(\tilde{R})]-\tilde{R}(d+fR)+G(\tilde{R})[g-h\text{log}G(\tilde{R})],\hfill & R⩽2.7\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left\{-i+R(l-m\sqrt{R})-n\sqrt{R}+\tilde{R}\left[-o+\frac{p}{\sqrt{q\tilde{R}+R\text{log}(r+R)}}\right]+s\text{log}(r+R)\right\},\hfill & R>2.7\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C13)

$$F_{\text{Si}}(R)=\{\begin{array}{ll}-a-b{R}^3+c{R}^4-d{R}^5+f{R}^{-3}+g{\text{tanh}}^2\left(R+R^2\right),\hfill & R⩽2.8\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[\left(h-i{R}^{-1}\right)\tilde{R}+l\sqrt{R}-\frac{m}{\sqrt{R}}+n{R}^{-0.25}-\frac{o\sqrt{R}}{p+qR}-r\right],\hfill & R>2.8\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C14)

Table C1.

Parameters of the Analytical Fits to the LIS

Param	1H	2He	3Li	4Be	5B	6C	7N	8O	9F	10Ne
a	3.2181e+2	2.5869e+2	5.7479e−1	8.0273e−1	2.5879e+0	2.5619e+1	2.5500e+0	8.4830e+0	1.5000e−1	1.7870e−1
b	1.1729e+4	8.8956e+1	2.9099e+0	2.9420e−1	2.0789e+0	9.9880e+0	2.1800e−1	1.5990e+0	1.6240e−2	3.2716e−1
c	2.9232e+3	3.6399e+2	1.0510e+0	6.0570e−3	4.9610e−1	2.7833e−1	1.3780e+0	1.5200e−1	3.3000e−2	1.1690e−1
d	1.0621e+4	1.6337e+3	3.5180e+0	6.4707e−1	2.7110e−1	2.5530e+1	3.3950e+0	1.8090e+0	3.9750e−2	1.0612e+0
f	1.3867e+3	1.9527e+0	4.3210e−1	5.0133e−1	5.5680e−1	1.6329e+1	6.4660e+0	1.9910e−1	6.2900e−2	5.6280e−1
g	1.0399e+4	1.0469e+2	4.0360e−1	2.3520e−1	5.9700e−1	4.0345e+0	2.9065e+0	2.1320e+0	1.5090e−1	4.9458e−1
h	6.7166e−1	3.1229e+2	1.5845e+0	1.0306e+0	5.0461e−1	8.4840e+0	2.3890e+0	1.7750e+0	1.2330e−2	1.0275e+0
i	1.0528e+4	4.4168e+2	5.4231e−2	7.3387e+0	2.5469e+0	7.2138e−1	1.6350e+0	8.6098e+0	5.6880e−2	2.4220e−1
l	2.8240e+3	1.6856e+2	2.6498e−4	7.4500e−1	1.0080e+1	2.4849e+1	4.7350e−1	1.2100e−3	7.8470e−2	1.6120e+1
m	1.7430e−3	4.4660e+3	1.7502e−5	2.6529e−1	1.7032e+2	1.3876e−4	8.1600e+0	4.2350e+1	4.3562e−2	2.7350e+1
n	1.4742e+4	5.9618e+3	2.8438e−1	2.9160e−1	1.2190e+2	3.7283e−10	5.3950e+1	3.9310e+3	1.5406e−7	1.6550e−6
o	2.6617e+3	3.1158e+9	8.0716e+1	3.4785e−5	7.7340e+3	1.2580e+2	8.0730e+1	2.5800e+2	1.5797e+0	1.4017e−9
p	5.2830e−2	2.0719e+8	3.1891e+2	5.6295e+2	1.3010e+3	3.7630e+3	4.0000e+0	5.9100e+0	9.449e−1	2.5368e−3
q	1.7160e+2	8.5045e+4	1.7438e+2	3.5980e+1	3.2100e+0	6.7980e+1	4.4760e−2	1.0744e+2	3.3698e+1	4.8380e+0
r	1.5000e−1	2.9055e+0	3.7640e+0	5.0144e+0	1.1900e+4	1.0795e+0	9.4830e−4	2.1500e+2	3.8300e+1	0.3905e+0
s	1.9222e+4	2.7152e+9	…	3.3384e+1	8.5290e+3	4.8708e+0	3.7827e+0	1.1100e−1	2.6019e+2	8.5850e+0
t	9.4790e−1	6.5850e+8	…	2.0520e+0	3.2100e+0	2.3180e−2	7.3650e+0	2.2500e−5	6.4977e+1	8.4427e−4
u	8.4900e−1	8.5045e+4	…	9.6598e−7	3.3420e+0	5.3880e+3	1.0850e−2	…	3.7667e+1	…
v	…	1.6836e+2	…	…	6.249e−15	6.7980e+1	…	…	…	…
z	…	5.5377e−5	…	…	…	…	…	…	…	…

(This table is available in its entirety in machine-readable form.)

$$F_{\text{P}}(R)=\{\begin{array}{ll}-a+\text{tanh}(R)\left[bR+\text{sin}(R)\left(cR-d{R}^2\right)\right]+f{R}^3\text{\hspace{0.17em}sin}(R)-g\text{\hspace{0.17em}tanh}\left(\text{sin}\left[R^2\text{\hspace{0.17em}tanh}(R)\right]\right),\hfill & R⩽2.4\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[-h-\frac{i}{\tilde{R}}-l{\tilde{R}}^2+m{\tilde{R}}^4+\text{log}(n+R)(o\tilde{R}+p)\right],\hfill & R>2.4\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C15)

$$F_{\text{S}}(R)=\{\begin{array}{ll}{R}^{-2.7}\left[aR{\text{tanh}}^3(R)+\left(b{R}^2{\text{tanh}}^2(R)-c{R}^3\right)\text{tanh}(d+R)\right],\hfill & R⩽3.2\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[f-gR-h\tilde{R}+i\sqrt{R}-\frac{l}{1+\sqrt{R}}-\frac{m{R}^{0.25}}{n+\sqrt{R}}\right],\hfill & R>3.2\text{GV},\hfill \end{array}$$ (C16)

$$F_{\text{Cl}}(R)=\{\begin{array}{ll}a+bR+\text{\hspace{0.17em}sin}\left(R+\frac{c}{R}\right)\left(-d+\frac{f}{R}+gR-h{R}^2+i\text{\hspace{0.17em}tanh\hspace{0.17em}}R\right),\hfill & R⩽2.7\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[l+mR-n{R}^2+\frac{1}{R}\left(o-\frac{p}{\tilde{R}}\right)-q\tilde{R}-r\text{\hspace{0.17em}tanh}\left(\frac{-s\tilde{R}}{R+\tilde{R}}\right)\right],\hfill & R>2.7\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C17)

$$F_{\text{Ar}}(R)=\{\begin{array}{ll}a+R[b+G(R)(c+dR)]+\text{sin\hspace{0.17em}}R(f+g\text{\hspace{0.17em}sin\hspace{0.17em}}R-hG(R)),\hfill & R⩽2.7\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[i+l\text{\hspace{0.17em}tanh\hspace{0.17em}}(-m\sqrt{R})+\sqrt{R}(n-o\tilde{R})+G(\tilde{R})\left(p+q{\tilde{R}}^2-rR\right)\right],\hfill & R>2.7\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C18)

$$F_{\text{K}}(R)=\{\begin{array}{ll}{R}^2\left\{-a+bR+cL(R)-d{\text{tanh}}^2(R)-fR{\text{tanh}}^3(R)-gR\text{log}[\text{tanh}(R)]\right\},\hfill & R⩽2.4\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[-h+iR-\frac{l}{R}-m{R}^2+nG\left(-\frac{o}{R^2}+\frac{pR+R^2}{q+rR+R^2}\right)\right],\hfill & R>2.4\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C19)

$$F_{\text{Ca}}(R)=\{\begin{array}{ll}a+b\text{\hspace{0.17em}tanh\hspace{0.17em}}\left[RG{(R)}^2\right]-cR+G(R)\left\{-d-f{R}^2-G(R)\left[g+h{R}^{2}G{(R)}^2\right]\right\},\hfill & R⩽2.9\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left\{-i+\tilde{R}(l-m\tilde{R})+\text{log}(n+oR)(p+\tilde{R}[q\text{log}(n+oR)-rR\tilde{R}])\right\},\hfill & R>2.9\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C20)

$$F_{\text{Sc}}(R)=\{\begin{array}{ll}R\left[a+bR-c{R}^3+\left(d{R}^2+f{R}^6-g\right)G(R)+hG{(R)}^2\right],\hfill & R⩽2.65\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[-i+lR-m\tilde{R}+n{\tilde{R}}^2+o\text{log}(\tilde{R})+\frac{p-q\tilde{R}}{\sqrt{R}}+\frac{r\tilde{R}}{s+tR}\right],\hfill & R>2.65\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C21)

$$F_{\text{Ti}}(R)=\{\begin{array}{ll}a-bR-c{R}^2-dG(R)+fG{(R)}^3+g\text{\hspace{0.17em}tanh\hspace{0.17em}}\left(hG(R)-\frac{i}{R-l}-m\right),\hfill & R⩽2.8\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[n-\frac{o}{R}-\frac{p}{\sqrt{R}}+\left(q+r\sqrt{R}+\frac{s}{t\sqrt{R}+R^{1.5}}\right)\sqrt{\frac{\sqrt{R}}{u+R}}\right],\hfill & R>2.8\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C22)

$$F_{\text{V}}(R)=\{\begin{array}{ll}a-bR-c{R}^2-dG(R)+fRG(R)+gG{(R)}^4\sqrt{G(R)}+\text{\hspace{0.17em}tanh\hspace{0.17em}}\left\{\text{tanh\hspace{0.17em}}\left(\text{tanh\hspace{0.17em}}\left[hG{(R)}^2\right]\right)\right\},\hfill & R⩽2.1\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[i+lR-m{R}^2-\frac{n}{R^2}-\frac{o}{p+R}+\frac{q}{r+R}+\frac{s-tR}{\sqrt{R}}\right],\hfill & R>2.1\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C23)

$$F_{\text{Cr}}(R)=\{\begin{array}{ll}a-bR-c{R}^2+G(R)[-d+G(R)(fR-g)]+hG(2R),\hfill & R⩽2.65\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[i+lR-\frac{m}{R}+n\tilde{R}+\frac{o}{p+R}+\sqrt{R}\left(-q+r{R}^2-sR\right)\right],\hfill & R>2.65\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C24)

$$F_{\text{Mn}}(R)=\{\begin{array}{ll}a-bR+cRG(R)-dG(R)-fG{(R)}^2+g\text{\hspace{0.17em}tanh\hspace{0.17em}}\left[G{(R)}^2\right]+h{\text{tanh}}^2\left(G{(R)}^3\text{\hspace{0.17em}tanh\hspace{0.17em}}\left[G{(R)}^2\right]\right),\hfill & R⩽2.6\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[-i+lR-\frac{m}{R}+\frac{n}{o+p{R}^2}+q\tilde{R}+\frac{r}{\tilde{R}}-\frac{s}{R\tilde{R}}+\frac{t\tilde{R}}{R^2}\right],\hfill & R>2.6\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C25)

$$F_{\text{Fe}}(R)=\{\begin{array}{ll}a-bR-\frac{c}{\sqrt{R}}+d\text{\hspace{0.17em}tanh\hspace{0.17em}}R+\text{\hspace{0.17em}tanh\hspace{0.17em}}\left(\text{tanh\hspace{0.17em}}{R}^2\right)\left(f-gR+h{R}^2\text{\hspace{0.17em}tanh\hspace{0.17em}}{R}^2\right),\hfill & R⩽2.8\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[i+lR+m{R}^{\frac{1}{4}}-n\sqrt{R}-o{R}^{\frac{5}{4}}-p{\left(\frac{q}{r+R}+\sqrt{R}\right)}^{\frac{1}{4}}\right],\hfill & R>2.8\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C26)

$$F_{\text{Co}}(R)=\{\begin{array}{ll}a+b\tilde{R}-cR+d{R}^{2}G{(R)}^3-G(R)(f+g\tilde{R})-h\text{\hspace{0.17em}sin}\left(i{R}^2\tilde{R}\right),\hfill & R⩽2.8\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[l+m\tilde{R}+n\sqrt{R}-\frac{o}{\tilde{R}}-\frac{p\tilde{R}}{R}-q\sqrt{\tilde{R}}-r\sqrt{s+R}\right],\hfill & R>2.8\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C27)

$$F_{\text{Ni}}(R)=\{\begin{array}{ll}a-bR-cG(R)-dG{(R)}^2+fRG{(R)}^3-gG[G(R)]-h\text{\hspace{0.17em}sin}\left(i{R}^2\right),\hfill & R⩽2.5\text{\hspace{0.17em}GV},\hfill \\ R^{-2.7}\left[-l+mR+n\tilde{R}+\frac{o}{p+q\tilde{R}\sqrt{R}}+\frac{r-sR-t{R}^2}{\sqrt{R}}\right],\hfill & R>2.5\text{\hspace{0.17em}GV},\hfill \end{array}$$ (C28)

where R is the particle rigidity in GV, the values of the fitting parameters from a to z are given in Table C1, and the $\tilde{R}$, G(x), L(x), T(x) and H(x) functions are defined as

$$\tilde{R}=\text{log\hspace{0.17em}}R$$ (C29)

$$G(x)=e^{-x^2}$$ (C30)

$$L(x)=\frac{1}{1+e^{-x}}$$ (C31)

$$T(x)={\left(3.764x^2\right)}^{RG{(x)}^{3.764x}}$$ (C32)

$$H(x)=\text{tanh}(0.9341x).$$ (C33)

C.2.2. Numerical Tables

Numerical tables of the LIS for all elements from ₁H to ₂₈Ni are calculated for the I-scenario. For each element we provide two tables, Tables C2 and C3, tabulated in kinetic energy E_kin per nucleon and in rigidity R. The complete sequences are available in a machine-readable format in the online Journal.

Table C2.

Z = 1—Proton LIS

Ekin (GeV/n)	Differential Intensity	Ekin (GeV/n)	Differential Intensity	Ekin (GeV/n)	Differential Intensity	Ekin (GeV/n)	Differential Intensity	Ekin (GeV/n)	Differential intensity
1.000e−03	1.538e+04	6.309e−02	2.173e+04	3.981e+00	2.253e+02	2.512e+02	3.377e−03	1.585e+04	5.986e−08
1.101e−03	1.652e+04	6.948e−02	2.116e+04	4.384e+00	1.823e+02	2.766e+02	2.585e−03	1.745e+04	4.617e−08
1.213e−03	1.688e+04	7.651e−02	2.057e+04	4.827e+00	1.470e+02	3.046e+02	1.980e−03	1.922e+04	3.559e−08
1.335e−03	1.720e+04	8.425e−02	1.995e+04	5.315e+00	1.182e+02	3.354e+02	1.519e−03	2.116e+04	2.740e−08
1.470e−03	1.752e+04	9.277e−02	1.930e+04	5.853e+00	9.467e+01	3.693e+02	1.167e−03	2.330e+04	2.109e−08
1.619e−03	1.785e+04	1.022e−01	1.863e+04	6.446e+00	7.553e+01	4.067e+02	8.981e−04	2.566e+04	1.621e−08
1.783e−03	1.818e+04	1.125e−01	1.795e+04	7.098e+00	6.001e+01	4.478e+02	6.922e−04	2.825e+04	1.246e−08
1.963e−03	1.852e+04	1.239e−01	1.724e+04	7.816e+00	4.747e+01	4.931e+02	5.343e−04	3.111e+04	9.565e−09
2.162e−03	1.887e+04	1.364e−01	1.653e+04	8.607e+00	3.740e+01	5.430e+02	4.131e−04	3.426e+04	7.340e−09
2.381e−03	1.922e+04	1.502e−01	1.580e+04	9.478e+00	2.933e+01	5.980e+02	3.198e−04	3.773e+04	5.630e−09
2.622e−03	1.958e+04	1.654e−01	1.507e+04	1.044e+01	2.292e+01	6.585e+02	2.479e−04	4.155e+04	4.316e−09
2.887e−03	1.995e+04	1.822e−01	1.433e+04	1.149e+01	1.784e+01	7.251e+02	1.924e−04	4.575e+04	3.308e−09
3.179e−03	2.031e+04	2.006e−01	1.359e+04	1.266e+01	1.384e+01	7.985e+02	1.494e−04	5.038e+04	2.534e−09
3.501e−03	2.068e+04	2.209e−01	1.286e+04	1.394e+01	1.070e+01	8.793e+02	1.161e−04	5.548e+04	1.941e−09
3.855e−03	2.105e+04	2.432e−01	1.212e+04	1.535e+01	8.258e+00	9.682e+02	9.027e−05	6.109e+04	1.486e−09
4.245e−03	2.142e+04	2.678e−01	1.138e+04	1.690e+01	6.358e+00	1.066e+03	7.022e−05	6.727e+04	1.138e−09
4.675e−03	2.178e+04	2.949e−01	1.065e+04	1.861e+01	4.887e+00	1.174e+03	5.464e−05	7.408e+04	8.708e−10
5.148e−03	2.215e+04	3.248e−01	9.925e+03	2.049e+01	3.751e+00	1.293e+03	4.253e−05	8.157e+04	6.664e−10
5.669e−03	2.250e+04	3.577e−01	9.208e+03	2.257e+01	2.875e+00	1.424e+03	3.311e−05	8.983e+04	5.099e−10
6.242e−03	2.285e+04	3.938e−01	8.504e+03	2.485e+01	2.202e+00	1.568e+03	2.577e−05	9.892e+04	3.901e−10
6.874e−03	2.318e+04	4.337e−01	7.815e+03	2.736e+01	1.686e+00	1.726e+03	2.007e−05	1.089e+05	2.985e−10
7.569e−03	2.351e+04	4.776e−01	7.143e+03	3.013e+01	1.289e+00	1.901e+03	1.562e−05	1.199e+05	2.283e−10
8.335e−03	2.381e+04	5.259e−01	6.490e+03	3.318e+01	9.857e−01	2.093e+03	1.216e−05	1.321e+05	1.746e−10
9.179e−03	2.410e+04	5.791e−01	5.860e+03	3.654e+01	7.533e−01	2.305e+03	9.471e−06	1.454e+05	1.336e−10
1.011e−02	2.436e+04	6.377e−01	5.255e+03	4.023e+01	5.755e−01	2.539e+03	7.373e−06	1.602e+05	1.022e−10
1.113e−02	2.459e+04	7.022e−01	4.683e+03	4.431e+01	4.395e−01	2.795e+03	5.739e−06	1.764e+05	7.814e−11
1.226e−02	2.480e+04	7.733e−01	4.149e+03	4.879e+01	3.356e−01	3.078e+03	4.467e−06	1.942e+05	5.976e−11
1.350e−02	2.497e+04	8.515e−01	3.655e+03	5.373e+01	2.561e−01	3.390e+03	3.477e−06	2.139e+05	4.570e−11
1.486e−02	2.511e+04	9.377e−01	3.202e+03	5.916e+01	1.955e−01	3.733e+03	2.705e−06	2.355e+05	3.495e−11
1.637e−02	2.520e+04	1.033e+00	2.789e+03	6.515e+01	1.491e−01	4.110e+03	2.105e−06	2.593e+05	2.673e−11
1.802e−02	2.526e+04	1.137e+00	2.415e+03	7.174e+01	1.138e−01	4.526e+03	1.637e−06	2.856e+05	2.044e−11
1.985e−02	2.527e+04	1.252e+00	2.078e+03	7.900e+01	8.677e−02	4.984e+03	1.273e−06	3.145e+05	1.563e−11
2.185e−02	2.523e+04	1.379e+00	1.777e+03	8.699e+01	6.618e−02	5.489e+03	9.896e−07	3.463e+05	1.195e−11
2.406e−02	2.515e+04	1.518e+00	1.511e+03	9.580e+01	5.047e−02	6.044e+03	7.690e−07	3.813e+05	9.139e−12
2.650e−02	2.501e+04	1.672e+00	1.277e+03	1.055e+02	3.848e−02	6.656e+03	5.974e−07	4.199e+05	6.988e−12
2.918e−02	2.483e+04	1.841e+00	1.073e+03	1.162e+02	2.934e−02	7.329e+03	4.638e−07	4.624e+05	5.343e−12
3.213e−02	2.460e+04	2.027e+00	8.965e+02	1.279e+02	2.237e−02	8.071e+03	3.600e−07	…	…
3.539e−02	2.432e+04	2.233e+00	7.453e+02	1.409e+02	1.706e−02	8.887e+03	2.792e−07	…	…
3.897e−02	2.399e+04	2.458e+00	6.166e+02	1.551e+02	1.301e−02	9.786e+03	2.164e−07	…	…
4.291e−02	2.362e+04	2.707e+00	5.080e+02	1.708e+02	9.925e−03	1.078e+04	1.676e−07	…	…
4.725e−02	2.321e+04	2.981e+00	4.167e+02	1.881e+02	7.574e−03	1.187e+04	1.297e−07	…	…

Note. Differential intensity units: (m² s sr GeV/n)⁻¹.

(This table is available in its entirety in machine-readable form.)

Table C3.

Z = 1—Proton LIS

Rigidity (GV)	Differential Intensity	Rigidity (GV)	Differential Intensity	Rigidity (GV)	Differential Intensity	Rigidity (GV)	Differential Intensity	Rigidity (GV)	Differential Intensity
4.333e−02	7.087e+02	3.498e−01	7.584e+03	4.829e+00	2.250e+02	2.521e+02	3.394e−03	1.585e+04	5.994e−08
4.547e−02	7.989e+02	3.677e−01	7.715e+03	5.238e+00	1.825e+02	2.775e+02	2.597e−03	1.745e+04	4.624e−08
4.772e−02	8.566e+02	3.866e−01	7.827e+03	5.688e+00	1.474e+02	3.055e+02	1.989e−03	1.922e+04	3.564e−08
5.008e−02	9.158e+02	4.064e−01	7.920e+03	6.183e+00	1.187e+02	3.363e+02	1.526e−03	2.116e+04	2.744e−08
5.255e−02	9.790e+02	4.274e−01	7.991e+03	6.726e+00	9.514e+01	3.702e+02	1.172e−03	2.330e+04	2.111e−08
5.515e−02	1.047e+03	4.496e−01	8.039e+03	7.324e+00	7.596e+01	4.076e+02	9.019e−04	2.566e+04	1.623e−08
5.787e−02	1.119e+03	4.730e−01	8.064e+03	7.981e+00	6.040e+01	4.488e+02	6.950e−04	2.826e+04	1.247e−08
6.073e−02	1.196e+03	4.978e−01	8.065e+03	8.704e+00	4.781e+01	4.941e+02	5.365e−04	3.111e+04	9.576e−09
6.373e−02	1.279e+03	5.240e−01	8.040e+03	9.499e+00	3.768e+01	5.440e+02	4.147e−04	3.426e+04	7.349e−09
6.688e−02	1.367e+03	5.518e−01	7.989e+03	1.037e+01	2.956e+01	5.989e+02	3.210e−04	3.773e+04	5.636e−09
7.019e−02	1.461e+03	5.812e−01	7.911e+03	1.134e+01	2.310e+01	6.594e+02	2.488e−04	4.155e+04	4.321e−09
7.366e−02	1.561e+03	6.124e−01	7.806e+03	1.240e+01	1.799e+01	7.260e+02	1.930e−04	4.575e+04	3.311e−09
7.730e−02	1.668e+03	6.455e−01	7.673e+03	1.356e+01	1.396e+01	7.994e+02	1.499e−04	5.038e+04	2.537e−09
8.113e−02	1.781e+03	6.807e−01	7.512e+03	1.484e+01	1.080e+01	8.802e+02	1.165e−04	5.548e+04	1.943e−09
8.514e−02	1.902e+03	7.181e−01	7.324e+03	1.626e+01	8.332e+00	9.692e+02	9.056e−05	6.109e+04	1.488e−09
8.936e−02	2.030e+03	7.579e−01	7.108e+03	1.781e+01	6.415e+00	1.067e+03	7.044e−05	6.727e+04	1.139e−09
9.378e−02	2.166e+03	8.003e−01	6.865e+03	1.952e+01	4.931e+00	1.175e+03	5.481e−05	7.408e+04	8.716e−10
9.842e−02	2.310e+03	8.456e−01	6.597e+03	2.141e+01	3.784e+00	1.294e+03	4.265e−05	8.157e+04	6.670e−10
1.033e−01	2.462e+03	8.939e−01	6.305e+03	2.348e+01	2.901e+00	1.425e+03	3.320e−05	8.983e+04	5.104e−10
1.084e−01	2.622e+03	9.456e−01	5.992e+03	2.577e+01	2.222e+00	1.569e+03	2.584e−05	9.892e+04	3.905e−10
1.138e−01	2.791e+03	1.001e+00	5.659e+03	2.829e+01	1.700e+00	1.727e+03	2.012e−05	1.089e+05	2.987e−10
1.194e−01	2.967e+03	1.060e+00	5.310e+03	3.106e+01	1.300e+00	1.902e+03	1.566e−05	1.199e+05	2.285e−10
1.253e−01	3.152e+03	1.124e+00	4.947e+03	3.411e+01	9.941e−01	2.094e+03	1.220e−05	1.321e+05	1.748e−10
1.316e−01	3.345e+03	1.193e+00	4.574e+03	3.746e+01	7.596e−01	2.306e+03	9.494e−06	1.454e+05	1.337e−10
1.381e−01	3.546e+03	1.266e+00	4.197e+03	4.116e+01	5.802e−01	2.539e+03	7.391e−06	1.602e+05	1.022e−10
1.449e−01	3.754e+03	1.346e+00	3.823e+03	4.523e+01	4.430e−01	2.796e+03	5.753e−06	1.764e+05	7.820e−11
1.522e−01	3.969e+03	1.431e+00	3.458e+03	4.972e+01	3.382e−01	3.079e+03	4.477e−06	1.942e+05	5.980e−11
1.597e−01	4.190e+03	1.524e+00	3.106e+03	5.466e+01	2.581e−01	3.391e+03	3.484e−06	2.139e+05	4.573e−11
1.677e−01	4.416e+03	1.624e+00	2.772e+03	6.009e+01	1.969e−01	3.734e+03	2.711e−06	2.355e+05	3.497e−11
1.760e−01	4.646e+03	1.733e+00	2.456e+03	6.608e+01	1.502e−01	4.111e+03	2.109e−06	2.593e+05	2.674e−11
1.848e−01	4.879e+03	1.851e+00	2.160e+03	7.267e+01	1.146e−01	4.527e+03	1.640e−06	2.856e+05	2.045e−11
1.940e−01	5.115e+03	1.979e+00	1.886e+03	7.993e+01	8.737e−02	4.985e+03	1.275e−06	3.145e+05	1.564e−11
2.037e−01	5.351e+03	2.119e+00	1.636e+03	8.793e+01	6.662e−02	5.490e+03	9.914e−07	3.463e+05	1.196e−11
2.139e−01	5.587e+03	2.270e+00	1.408e+03	9.673e+01	5.079e−02	6.045e+03	7.704e−07	3.813e+05	9.144e−12
2.246e−01	5.821e+03	2.436e+00	1.204e+03	1.064e+02	3.872e−02	6.657e+03	5.984e−07	4.199e+05	6.992e−12
2.358e−01	6.051e+03	2.616e+00	1.022e+03	1.171e+02	2.952e−02	7.330e+03	4.646e−07	4.624e+05	5.346e−12
2.477e−01	6.276e+03	2.813e+00	8.619e+02	1.289e+02	2.250e−02	8.072e+03	3.606e−07	…	…
2.601e−01	6.494e+03	3.029e+00	7.226e+02	1.418e+02	1.716e−02	8.888e+03	2.796e−07	…	…
2.732e−01	6.705e+03	3.265e+00	6.023e+02	1.560e+02	1.308e−02	9.787e+03	2.167e−07	…	…
2.870e−01	6.906e+03	3.523e+00	4.993e+02	1.717e+02	9.979e−03	1.078e+04	1.679e−07	…	…
3.015e−01	7.095e+03	3.805e+00	4.118e+02	1.890e+02	7.614e−03	1.187e+04	1.299e−07	…	…

Note. Differential intensity units: (m² s sr GV)⁻¹.

(This table is available in its entirety in machine-readable form.)