Abstract
The recent advances in relative protein–ligand binding free energy calculations have shown the value of alchemical methods in drug discovery. Accurately assessing absolute binding free energies, although highly desired, remains a challenging endeavour, mostly limited to small model cases. Here, we demonstrate accurate first principles based absolute binding free energy estimates for 128 pharmaceutically relevant targets. We use a novel rigorous method to generate protein–ligand ensembles for the ligand in its decoupled state. Not only do the calculations deliver accurate protein–ligand binding affinity estimates, but they also provide detailed physical insight into the structural determinants of binding. We identify subtle rotamer rearrangements between apo and holo states of a protein that are crucial for binding. When compared to relative binding free energy calculations, obtaining absolute binding free energies is considerably more challenging in large part due to the need to explicitly account for the protein in its apo state. In this work we present several approaches to obtain apo state ensembles for accurate absolute ΔG calculations, thus outlining protocols for prospective application of the methods for drug discovery.
Molecular dynamics based absolute protein–ligand binding free energies can be calculated accurately and at large scale to facilitate drug discovery.
1. Introduction
Computational techniques for estimating relative differences in protein–ligand binding free energy have now reached remarkable accuracy. Relative binding free energy calculations over a large range of protein–ligand complexes have shown average agreement with experiment to be within 1 kcal mol−1 (4.184 kJ mol−1).16,28,52 These methods have become mature and reliable enough to be included in industrial drug discovery and lead optimization pipelines.10,26,35,40 A substantial limitation of this approach, however, is the requirement for the ligands to be structurally similar to each other: the predictive power decreases for ligands with different scaffolds or binding poses. Evaluation of novel ligand classes, therefore, requires a prior experimental absolute binding free energy as a reference for each new class of mutually similar ligands. Thus, the next qualitative leap for the field of first principles based protein–ligand affinity estimation encompasses the reliable and accurate prediction of absolute binding free energies.
The calculation of relative binding free energies is relatively easy in comparison. The bound ligands are confined to the binding site and only the small subset of atoms that differ between two ligands needs to be perturbed. In contrast, absolute binding free energy calculations decouple the entire ligand, meaning it is in principle free to explore the whole simulation box volume. Early work on the topic explored various ways of restraining the decoupled ligand and taking into account the resulting contribution to the free energy.7,18,20,54 The approach introduced by Boresch et al.7 has emerged as a rigorous way to resolve this issue via orthonormal relative restraints between the ligand and the protein.2,3
Another challenge for the absolute binding free energy calculations is posed by the need to explicitly sample the apo state of the protein, i.e. the protein without the bound ligand. As this state may substantially differ from the ligand bound (holo) state, the simulation method needs to be capable of capturing the free energy differences between the protein conformers. Non-equilibrium (NEQ) free energy calculations present an elegant solution to this challenge. Such calculations determine the free energy difference by performing rapid out-of-equilibrium ligand coupling/decoupling transitions initialized from the equilibrium protein apo and holo ensembles (Fig. S1†). This allows one to explicitly include the different apo and holo end-states into the same calculation.17 Several recent applications of the NEQ approach on model host–guest systems showed promising results for the calculation of absolute binding free energies.5,27,37
The NEQ approach does not offer a free lunch in the sense that the relevant conformations still need to be sampled in the end-state ensembles.17 Compared to the more popular free energy perturbation (FEP) series of methods,24,51,56 though, it does offer several advantages in terms of computational efficiency. Namely, such sampling needs to be performed only for physical end-states and can be done with plain molecular dynamics or, if desired, it can also be augmented with enhanced sampling methodologies in a straightforward manner.36 Secondly, the out-of-equilibrium portion of the approach, which accounts for the majority of the compute time, is highly parallelizable, requiring no information exchange between individual simulations, unlike modern FEP approaches with replica exchange.24,51 Furthermore, the NEQ approach allows for initialization of the two end-states with the distinct apo and holo protein structures, which facilitates obtaining reliable equilibrium ensembles for the cases where experimental structures are available. For an equilibrium FEP approach, incorporation of different conformers in a single ΔG estimation would require decision on the mixing rule for seeding the starting structures19 and potentially Hamiltonian replica exchanges would be needed to achieve convergence. Finally, when comparing different ligands, protein mutations, or conformational states NEQ allows for reuse of existing equilibrium sampling of end-states, e.g. the same apo state can be used for assessing affinities of different ligands.
In the current work we use the NEQ approach to demonstrate the feasibility of accurate absolute binding free energy calculations for a large number of protein–ligand systems, showing accuracy on par with the relative binding free energy estimates. To achieve this, we introduce methodological advancements that allow for an efficient treatment of the ligand in its decoupled state and careful considerations of the protein in its apo state. This allows for identification of protein states that have a drastic effect on ligand binding affinity, such as e.g. a flip of a single amino acid rotamer. Our calculation strategy also allows identifying the most representative structure for a protein's apo state for the cases where multiple likely candidates (structures in their local free energy minima, X-ray structures) are available.
2. Results
In this study, we have used an alchemical non-equilibrium free energy calculation approach to calculate absolute protein–ligand binding free energies for 128 complexes. We have developed a novel way of treating the decoupled state of the ligand (see Methods section for details). The large set of investigated systems allows us to have an extensive evaluation of the accuracy that can be achieved with the first principles based calculations. Fig. 1 shows the calculated values for the binding free energy plotted against the experimental measurements. When compared to the experimental values, the absolute unsigned error (AUE) of 4.9 ± 0.5 kJ mol−1 (1.2 ± 0.1 kcal mol−1) only marginally exceeds the state-of-the-art accuracy threshold of 1 kcal mol−1 achievable for relative binding free energy calculations. Accuracies for jnk1 and p38α are exceptionally good with AUEs of 3.0 ± 0.8 and 3.1 ± 0.7 kJ mol−1 (0.7 ± 0.2 kcal mol−1 for both), respectively.
Fig. 1. Overview of the accuracy of calculated absolute binding free energies ΔGCalc.. Error bars represent standard errors for free energies, absolute unsigned errors (AUE, units of kJ mol−1), and the Pearson correlation coefficients (Cor). Apo states were initialized with X-ray crystal structures for all systems except pde2 and tyk2 where holo X-ray structures with the ligand removed were used. Dark and light shaded areas represent regions deviating from experiment by at most 1 and 2 kcal mol−1.
Some systems, however, have a considerably lower accuracy (AUE of 10.8 ± 1.5 kJ mol−1 for tyk2, 5.5 ± 1.4 kJ mol−1 for pde2), revealing a particular challenge for affinity estimation in these systems. An accurate evaluation of the offset in the ΔG is critical for obtaining reliable absolute ΔG values: inaccuracies in this case manifest as large shifts of the calculated values with respect to the experimental measurements, e.g. tyk2 in Fig. 1. Interestingly, even such offsets do not significantly deteriorate the relative free energy difference estimates (Fig. S2†).
We have identified this effect to be a consequence of the inadequate representation of the protein in its apo state. While the apo state is not considered in relative free energy calculations, assessment of absolute free energies needs to explicitly account for it. In the following analysis we demonstrate how failure to capture the free energy differences between the apo and holo protein states affects the absolute binding free energy calculation accuracy.
2.1. Apo and holo states
For the situations where protein rearrangements are required upon ligand binding, sufficient sampling of the two end states may present a considerable challenge. An accurate quantification of the process of ligand binding to an apo protein and forming a stable holo state requires correctly estimating not only the component of the free energy originating from the ligand interaction with the protein, but also the difference between the apo and holo protein states.
Non-equilibrium free energy calculations offer a particularly convenient approach for the computation of binding affinities, as both states, apo and holo, can be explicitly considered in a single simulation.17 The alchemical ligand decoupling transitions can be started from a holo conformer ensemble, while ligand coupling transitions can start from an apo ensemble.
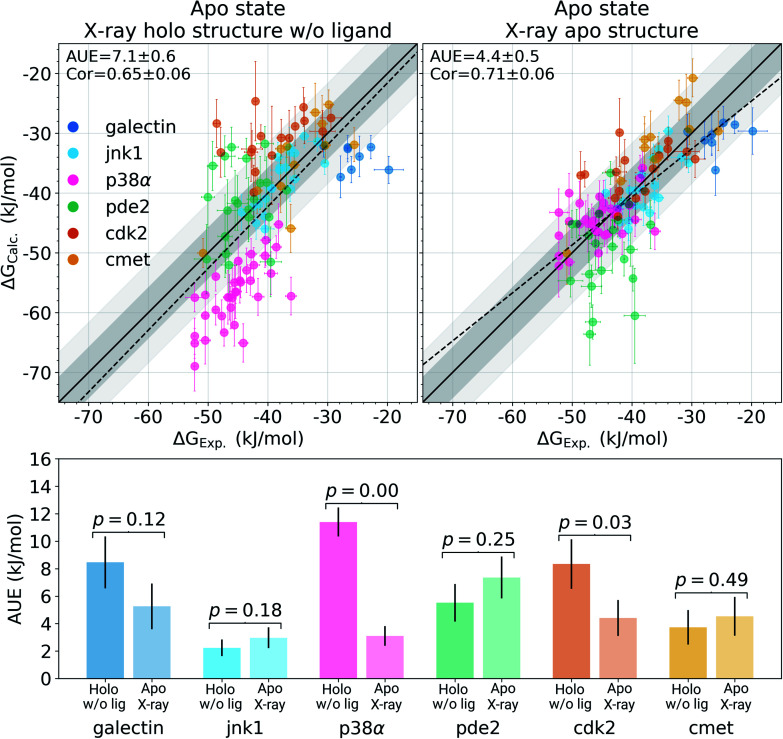
Among the protein–ligand complexes investigated in this work, 6 out of 7 systems have both their apo and holo structures resolved by means of X-ray crystallography. We have probed two methods of calculating the binding ΔG value: firstly, removing the ligand from the holo state and treating the obtained structure as an apo state. For the second approach we used the crystallographically resolved apo structure directly. Overall, there is a large and significant improvement in the calculated binding ΔG accuracy when an experimentally defined apo state is considered explicitly (Fig. 2 and S3†). A substantial improvement in the AUE (from 7.1 ± 0.6 to 4.4 ± 0.5 kJ mol−1) shows that starting the simulations with a corresponding apo structure largely removes an offset which is otherwise present for the calculations initialized with the holo structures only. This indicates that substantial rearrangements occur in the studied proteins upon ligand binding that do not equilibrate at the nanosecond timescale covered in the simulations.
Fig. 2. Experimental binding ΔG values plotted against the calculated estimates. In the panel on the left, the simulations in the apo state were started from the experimental holo structure after removing the ligand. In the panel on the right, the alchemical simulations of the protein in its apo state were initialized with the experimentally resolved apo structure. The starting structure has a marked effect on the calculated ΔG accuracy. The bottom panel shows a break up of the accuracies by protein system. Probability values measure the significance of the difference between apo and holo absolute unsigned errors via a Welch's t-test. Dark and light shaded areas represent regions deviating from experiment by at most 1 and 2 kcal mol−1.
The largest effect from using an experimentally resolved apo structure is observed in the galectin, p38α and cdk2 protein–ligand complexes, while for the other cases the differences in accuracy are less affected. To understand what structural features are responsible for such pronounced effects, we have further explored the p38α system for which ΔG had the largest difference among the systems depicted in Fig. 2.
2.2. Large effect of a single rotamer
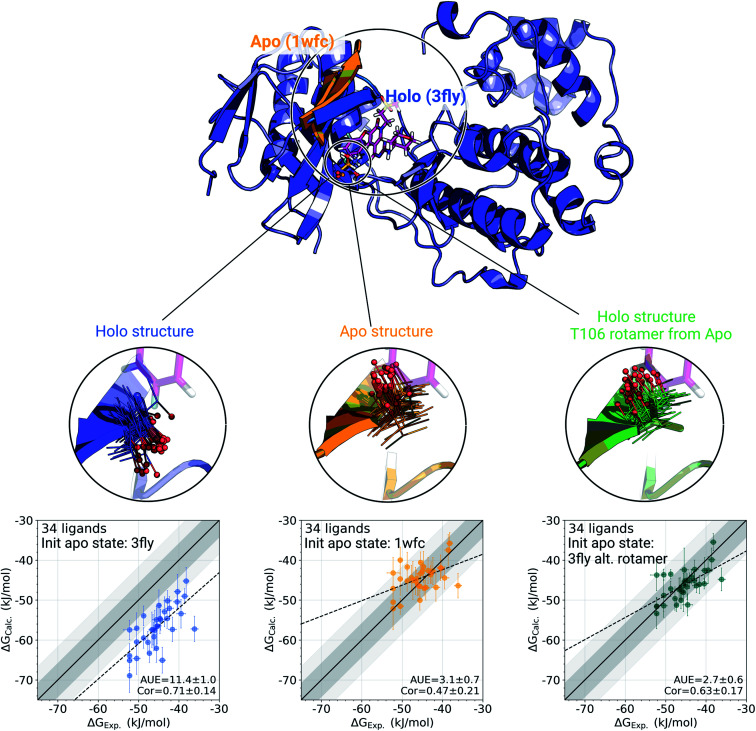
The p38α protein–ligand complex shows a particularly strong dependence of the calculated ΔG on the starting structure. For this case, we were able to identify the particular structural details that are responsible for more than 9 kJ mol−1 offset in the calculated ΔG values (Fig. 3).
Fig. 3. A detailed investigation of the p38α protein–ligand complexes. The apo (1wfc,53 orange) and holo (3fly, blue) structures have several structural differences close to the ligand binding site: a substantial loop motion and a different T106 rotamer state. In the simulations, the rotamer T106 retains its initial state: shown in lines, with a sphere marking threonine's oxygen. The calculated ΔG values depend strongly on the starting structure (holo or apo) that is used to initialize protein simulations in its apo state: scatterplots at the bottom. The green structure in the sub-panel and corresponding ΔG scatterplot depict a case, where apo simulations were initialized with a holo structure (ligand removed), but with the T106 rotamer set into its apo state. Dark and light shaded areas represent regions deviating from experiment by at most 1 and 2 kcal mol−1.
One of the main differences between the apo (pdb id 1wfc53) and holo (3fly) structures occurring close to the binding site is a major loop motion: colored in orange and blue in Fig. 3. However, it appears that even the short (10 ns) equilibrium simulations that we employed in the current protocol are sufficient to sample this loop transition (Fig. S4†). We have also explicitly probed whether this structural feature may modulate the accuracy of the calculated ΔG values. We have filtered the starting structure ensemble for the ligand coupling transitions, retaining only those conformers with a loop position similar to the one from the crystallographic apo structure. This, however, had no effect on the calculated binding ΔG values (Fig. S5†).
While the large loop motion has no substantial effect on the ΔG accuracy, a single rotamer flip appears to be responsible for the larger than 9 kJ mol−1 shift in calculated ΔG. The crystallographic structures 3fly (holo) and 1wfc (apo) have different threonine 106 (T106) rotameric states. Initializing apo simulations with either the experimentally resolved apo structure or a holo structure with the ligand removed yields ensembles where the rotamer never crosses the barrier and remains in its starting state (Fig. 3). The barrier crossing for the T106 sidechain rotamer appears to be too high to be sampled in the short (10 ns) equilibrium simulations used in the free energy calculation protocol.
To verify that T106 is truly the cause for this marked difference, we have initialized ligand coupling simulations from the holo structure (with the ligand removed), but setting the T106 rotamer into its apo state (green structures in Fig. 3). This single change in the holo structure was sufficient to bring the calculated ΔG to the same accuracy as obtained from simulations started with the true apo structure.
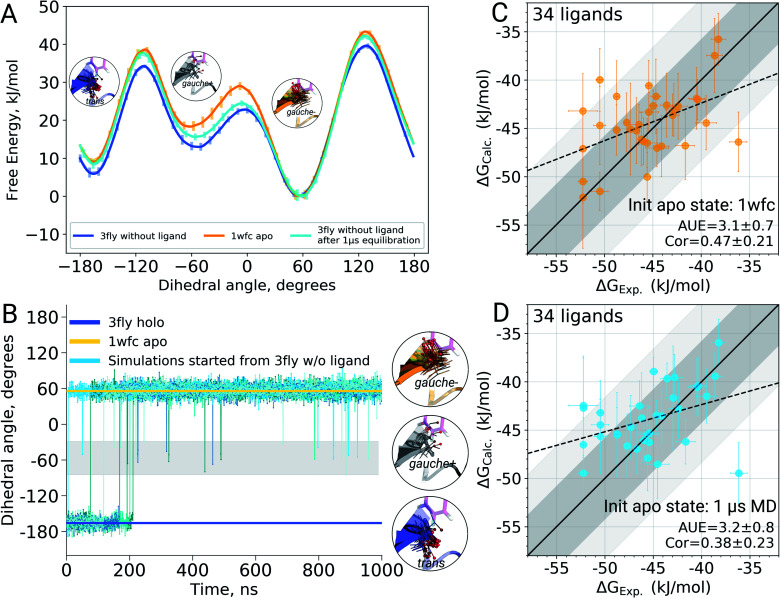
It appears that initializing ligand coupling simulations from holo structures leaves the binding site – in particular the T106 rotamer – pre-arranged to accommodate the ligand. This, in turn, leads to an overly stabilized protein–ligand complex as quantified by the binding ΔG. The missing term in ΔG, in this case, is the free energy required to switch T106 rotamer from its apo to holo state. To demonstrate this, we also computed free energy surfaces for the residue's χ1 dihedral with well-tempered metadynamics4,29 simulations biasing the potential of the dihedral. The free energy surfaces (Fig. 4A) reveal the average free energy difference between the minima of gauche- and trans conformations (present in the 1wfc and 3fly structures, respectively) of the apo state to be ∼8 ± 1 kJ mol−1. This matches well the observed shift in the binding free energies calculated using 1wfc and 3fly starting structures for the apo state. Due to insufficient end-state sampling and high free energy barriers, we do not observe a transition in this rotamer during short 10 ns equilibrium simulations, yet simulations started from the true apo state allowed taking the missing ΔG contribution into account.
Fig. 4. The effect of T106 rotamer states of the p38α kinase on the calculated ligand binding ΔG. Free energy surfaces (A) of the χ1 dihedral angle for the T106 residue obtained from well tempered metadynamics simulations starting from 3fly and 1wfc structures as well as from the output of 1 μs equilibrations started from 3fly. χ1 dihedral angle for the T106 residue in the crystallographic apo (1wfc) and holo (3fly) states, as well as in 5 independent simulations of 1 μs each (B). Binding ΔG calculated by initializing apo state simulations with the 1wfc structure (C) and the end-states from 1 μs simulations (D). Dark and light shaded areas represent regions deviating from experiment by at most 1 and 2 kcal mol−1.
2.3. Can longer simulations reveal true apo states?
Undersampling is a frequently encountered shortcoming of simulation-based phase space exploration, e.g. numerous examples are provided in ref. 14. Naturally, one of the underlying reasons for the inadequate representation of the apo state in the case of p38α protein could be insufficient equilibration of the system. Therefore, we probed whether longer simulations would be able to cross the energy barrier and arrive in the true apo state when starting from a holo crystallographic structure with the ligand removed. To explore this, we have extended the p38α apo state simulations started from 3fly by performing 5 independent runs of 1 μs each.
The longer simulations indeed showed a transition of the T106 rotamer from its trans state (3fly holo conformer) to the gauche− state observed in the apo 1wfc structure (Fig. 4B). In all 5 independent replicas, the transition occurred within the first 200 ns. After this, no recrossings back to the trans rotameric state were observed, only short lived transitions from the gauche− to the gauche+ state occurred.
Binding ΔG calculations where sampling of the decoupled ligand state is initialized with the final structures from 1 μs simulations show this shift and have the same accuracy as those started with the crystallographic apo state 1wfc (Fig. 4C and D). This confirms our previous observation that the rotameric state of T106 plays a crucial role in the ligand binding to p38α. All in all, the observations from the long simulations suggest that, at least in some cases, we can rely on longer (or enhanced) sampling to recover a protein's apo state for the subsequent ΔG calculations.
It is important to note, however, that the increased sampling does not automatically translate into a better agreement of the simulated trajectory with the experimentally measured observables. For example, longer simulations of the tyk2 kinase in its apo state (4gih30 with the ligand removed; Fig. S6†) explore a broader range of conformations. However, as simulations progress, they deviate substantially from the starting crystallographic structure. The substantial drift of simulated trajectories, in turn, results in large uncertainties of the calculated binding affinites and deteriorates the ΔG prediction accuracy. This observation indicates that either the longer sampling reaching 1 μs for each of the 5 repeats is still not sufficient, or the new free energy minima identified by the force field are not representative of the true free energy landscape.
2.4. Using binding ΔG to identify apo states
For the cases where multiple experimentally resolved structures are available, it may not be evident which structure would be best suited for initializing simulations to obtain a representative apo state ensemble. It is, however, possible to exploit binding free energy calculations to identify the structure yielding the most probable conformational ensemble. This analysis does not require any knowledge of the actual (experimentally measured) set of binding affinities. It rather relies on multiple calculations of the binding affinities connecting one holo structure with multiple possible apo states (Fig. 5).
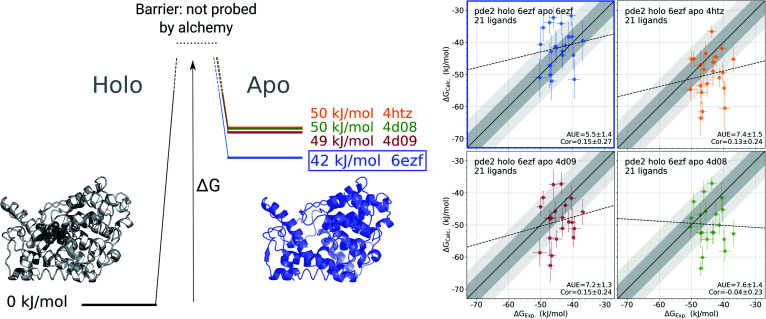
Fig. 5. Identification of the most likely apo state for pde2 system based on binding affinities of 21 inhibitors. The absolute binding free energies were calculated using 6ezf holo state and 4 structures without the ligand to represent the apo state (4htz,55 6ezf,35 4d08 and 4d09 8). The common holo state allows comparing the apo states one to another in terms of ΔG (the uncertainty of each estimate is below 1 kJ mol−1). 6ezf structure is identified as the most likely apo structure based on the binding free energies for the considered ligand set. The panels on the right compare the experimental binding affinities to those calculated with each of the apo structures. Dark and light shaded areas represent regions deviating from experiment by at most 1 and 2 kcal mol−1.
We use phosphodiesterase 2 (pde2) complexed with 21 inhibitors35 to illustrate this approach. Numerous experimentally resolved monomeric pde2 structures are available, where the protein is crystallized in its apo state (e.g. 4htz55) or in a complex with a ligand (e.g. 6ezf,35 4d08, 4d09 8). Availability of these structures allows constructing a set of apo states by using either an actual apo conformer from the crystallographic structure or by removing a ligand from a holo structure. In principle, the most likely apo state is at its free energy minimum, i.e. of the multiple candidate conformers, the one with the lowest free energy would be the most populated in the ensemble. However, calculating free energy differences between the apo conformers directly is a computationally highly demanding challenge.
Instead, we can evaluate relative free energies of these conformers by connecting them via a common holo state. We calculate binding affinities for a set of 21 pde2 inhibitors using the structure 6ezf representing the protein–ligand complex and each of the 6ezf, 4htz, 4d08 and 4d09 structures independently representing the apo state. In this way we relate each apo state to one another via a common reference 6ezf holo state. Setting the free energy of the reference to 0 kJ mol−1 for convenience allows us to directly compare the apo states (Fig. 5): the ΔG for an apo state is represented by averaged binding free energies calculated over the whole ligand set. The barrier (denoted with the dashed lines in Fig. 5) is not attainable with this approach, as alchemical calculations do not explicitly probe the binding-unbinding pathway.
It is, however, important to understand the limitations of the ΔG values obtained this way. The calculated values should not be interpreted as reporting on the actual free energy differences between the apo conformers, but only on a component of ΔG corresponding to the change in the degrees of freedom relevant for ligand binding. It is likely that the binding site rearrangements are experienced by the ligands and have a strong effect on the ΔG calculated based on this approach. At the same time, substantial conformational rearrangements further from the binding site may not have a contribution to ΔG if they do not affect the ligand binding affinity. Therefore, the conclusions about the most likely apo state identified with this approach should be limited to the interpretations of the binding affinities for a specific set of ligands.
In the current analysis, the 6ezf holo structure without the ligand was identified as the most likely representation of the apo structure for the set of 21 pde2 inhibitors. Interestingly, this structure is predicted to have a lower free energy than the crystallographically resolved apo state. One reason for that might be particular structural details that could have been resolved in a higher resolution structure 6ezf (1.5 Å)35 as compared to 4htz (2.0 Å),55 or larger conformational changes that may be more comparable with the full length apo protein.35 Comparison of the experimental binding affinities to the values calculated with the 6ezf structure as a template for the apo state provide further support for this methodology (Fig. 5). The estimated ΔG values for this case have the best agreement to experiment (AUE of 5.5 ± 1.4 kJ mol−1) in comparison to the calculations using the other structures. The similar correlations between experiment and calculation for all examples in Fig. 5 again confirm the effect of the apo state to modify the offset of the calculated binding affinities.
3. Discussion
3.1. Relative free energies
It appears that the calculation of the overall offset is one of the major challenges in the absolute binding free energy estimation. Interestingly, given the equivalent simulation conditions for a set of ligands, even such large overall shifts in the calculated absolute ΔG values may have no effect on the relative free energies between the ligands (e.g. the case of tyk2 in Fig. 1 and S2†). This suggests that the cause of the offset could be largely the same for all the considered ligands and cancels out in calculating the free energy differences. The protein–ligand complexes investigated in this study present a convenient set of systems for testing this hypothesis: the relative free energies for these systems have been previously calculated directly by alchemical transformations between ligand pairs with a non-equilibrium approach and the same force field.16
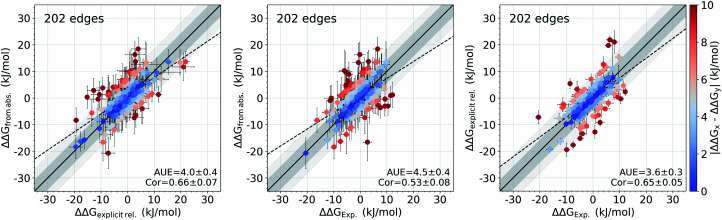
In Fig. 6 we compare the relative binding free energies constructed from the absolute ΔG calculations to the values from Gapsys et al.16 obtained by an explicit relative ΔΔG calculation protocol. The absolute ΔG protocol indeed yields relative free energies comparable to those calculated via direct alchemical transformation of the ligands (AUE of 4.0 ± 0.4 kJ mol−1) (Fig. 6 left), indicating that the relative binding free energies are captured properly even when considering additional challenges of the absolute ΔG estimation. Furthermore, the accuracy of relative free energies obtained from the absolute ΔG protocol is also in good agreement with experimental results (Fig. 6 middle) yielding an AUE of 4.5 ± 0.4 kJ mol−1 (correlation of 0.54 ± 0.08) in comparison to AUE of 3.6 ± 0.3 kJ mol−1 (correlation of 0.65 ± 0.05) for explicit relative calculations (Fig. 6 right) for the same systems.
Fig. 6. Accuracy of the relative ΔΔG values. Comparison of the relative binding free energies calculated from absolute ΔG values to the ΔΔG values calculated by explicit alchemical ligand modifications16 (left). ΔΔG values from absolute ΔG compared to experiment (middle). ΔΔG values from explicit alchemical ligand modifications compared to experiment (right). Dark and light shaded areas represent regions deviating from experiment by at most 1 and 2 kcal mol−1.
This observation is encouraging for the prospective drug design studies. Absolute ΔG calculations can be reliably used for the cases where the main assumptions for estimating relative free energy differences do not hold, e.g. where binding pose changes occur or investigated ligand structures differ substantially. It is, however, important to take into account the computational time required by these methods: absolute ΔG estimates in this work required 10 times longer sampling in comparison to the ΔΔG calculations in ref. 16. The difference in computational cost between these approaches suggests a natural delineation in their application. When exploring large chemical libraries by means of free energy calculations, it would be most efficient to evaluate structurally similar compounds by computing ΔΔG values, while absolute ΔG calculations could be performed less frequently for the cases that are not tractable by the relative free energy estimation.
It is important to mention that there also exist specialized approaches based on the relative ΔΔG calculations to evaluate free energy differences for structurally highly distinct ligands and different binding poses, e.g. separated topology method.39 Using the relative free energy calculations has the advantage of avoiding the requirement to properly represent protein's apo state, as this state is not explicitly considered. Yet, the absolute binding free energy protocol offers a number of additional possibilities. For example, estimation of the absolute ΔG makes it possible to evaluate ligand selectivity against different protein targets, evaluate affinity for various protein conformers, and calculate binding affinities for individual molecules without the need to consider them in a relation to other ligands.
3.2. Sources of statistical uncertainty
Calculations of the absolute binding free energies show larger statistical uncertainties when compared to the relative free energy calculations (Fig. S10†). The increase in statistical errors arises due to larger perturbations to the system required by an alchemical absolute ΔG calculation. Coupling/decoupling of the whole ligand involves introducing/removing more interactions in comparison to the alchemical transformations of a small number of atoms when morphing ligands to one another for relative free energy estimations. Convergence of the absolute ΔG estimates in pharmaceutically relevant systems can be achieved, yet it requires extending the alchemical transitions to nanoseconds.17 Such slower transitions retain the system closer to equilibrium, dissipating less work along the alchemical path, thus facilitating convergence.
Although lower uncertainties of the estimated ΔG are desired, the long alchemical transition times quickly become intractable for large scale ligand binding affinity scans. Therefore, it is necessary to balance the trade-off between the available simulation time and the attainable precision. This, naturally, requires a robust uncertainty estimation for the ΔG estimates. It has been observed that relying on the statistical uncertainties from the ΔG estimators, either analytical expressions, or bootstrapped values, may not be reliable.5,38 Therefore, in this work we rely on independent repeats of the whole free energy calculation procedure to gain access to the variation of the ΔG estimates.14,46 Subsequently, we incorporate both, uncertainties from the independent replicas and statistical uncertainty from the estimator by means of bootstrap into a single uncertainty estimate.16
3.3. Apo protein state in absolute ΔG calculations
The major conceptual difference between the absolute and relative binding free energy calculations stems from the need to explicitly consider the apo protein state when computing absolute ΔG. This poses a challenge for a theoretically rigorous treatment of the decoupled ligand that subsequently needs to be coupled to the system in a well-defined binding site of the protein. In the current work we present a novel approach for the construction of the decoupled ligand state ensembles (see Methods) which, in combination with the ligand restraining protocol,7 provides an efficient solution to the problem. In brief, our method positions and restrains the decoupled ligand in the binding pocket of the apo protein creating a decoupled state ensemble without the need to explicitly simulate it.
Furthermore, explicit consideration of the protein's apo state also requires accurate quantification of a transition between the protein's conformational states sampled upon ligand binding. The non-equilibrium free energy calculation approach presents a convenient setting, where the simulations for holo and apo states can be initialized with different starting structures.17 In such a way, the apo and holo state ensembles can be generated by simulations started with the corresponding experimentally resolved structures whenever they are available. The initialization of the simulations with a proper starting structure has a profound effect on the accuracy of estimated ΔG (Fig. 2).
This observation, however, could be interpreted merely as a sampling issue: routine free energy calculation protocols use short (5–20 ns) equilibrium simulations16,43,52 that may not be sufficient for generating a representative apo state ensemble. Inaccuracies in the estimated free energies due to undersampling have been previously reported for both relative31 and absolute5 protein–ligand binding free energy calculations. The issue can be alleviated with longer simulations or enhanced sampling. This appears to be feasible in the case of p38α kinase, where longer simulation of the protein's apo state was able to recover the experimentally resolved rotamer T106 which proved essential for accurate ΔG calculations (Fig. 4). Yet, the case of tyk2 kinase, for which long (1 μs) simulations were used for the apo state, demonstrates that the extended sampling does not necessarily lead to higher accuracy in ΔG estimation (Fig. S6†). This is in line with several previous observations where enhanced sampling showed no improvement in the accuracy of the free energy estimates.27,48 In fact, a deterioration in prediction accuracy can be observed in longer or enhanced-sampling simulations, when the ligand explores poses that are less relevant for binding.48 In turn, this manifests in an underestimation of the relative binding free energy differences,48 which we have also observed in our study (Fig. 6).
Another approach that we introduced in this study allows to circumvent the need of an exhaustive apo state sampling by probing multiple initial apo states (when they are available) with the absolute ΔG calculation protocol (Fig. 5). This method does not require any prior knowledge of the experimentally measured binding affinities and it allows estimating relative free energies for the apo states by relating them one to another via a common holo reference state. The ΔG value for apo state structures calculated this way represents only one component of the overall free energy of the conformers, as only a contribution that is experienced by the ligand binding is considered. Nevertheless, this method allows identifying the most likely apo state for the use in the absolute binding free energy calculations.
In this study we used datasets that have previously been used for relative binding free energy calculations. We observed how the absolute calculations could yield good correlations with experiment, with the apo state affecting the overall offset seen in terms of the larger AUE. In other words, the difference between apo and holo state conformations had a similar effect on the binding free energies of all the ligands for the same target. It remains to be seen if that will hold true as the diversity of the ligands increases, even if they are binding in the same site. We anticipate that future studies on an even larger scale will be required to examine these effects.
While in this work we have highlighted the importance of the proper apo state ensemble for the accurate absolute binding free energy predictions, it is essential to reliably represent the holo state as well. Here, we relied on the crystallographic protein holo states and carefully modeled ligand binding poses from previous investigation.16 Naturally, the ligand modelling step introduces additional uncertainty in defining the starting structure for initializing the simulations. Accurate binding ΔG estimates suggest that the holo state representation was proper for most of the investigated cases. The tyk2 kinase, however, is an exception, as the calculated ΔG values significantly underestimate the experimentally measured binding affinities (Fig. 1). The apo state representation is unlikely to be solely responsible, as identification of any deeper free energy minima for the apo state would only impose an additional penalty on the ΔG of binding, thus reducing the predicted affinity even further, as illustrated in Fig. S6.† A deeper free energy minimum for the holo state can lead to the prediction of a lower binding ΔG. This prompts us to assume that the holo state representation for the tyk2 kinase could be improved by exploring additional ligand poses, protein conformations, internal water placement or a combination of these components. This way, tyk2 could serve as an interesting candidate for future investigations possibly presenting a challenging case for the holo state description.
4. Conclusions
In this work we propose methodological advances that enable efficient absolute binding free energy calculations with an accuracy on par with relative free energy calculations. We demonstrate the generality of the protocol across multiple pharmaceutically relevant targets in a large scale study. Our approach enables the incorporation of both holo and apo structural information for reliable affinity predictions. The key structural determinants of binding can be as small as a single rotamer change between the apo and holo states and appropriate sampling of such determinants can be computationally demanding. When multiple alternative apo structures exist, absolute binding free energy calculations can be used to identify the most likely candidate for a prospective study.
5. Methods
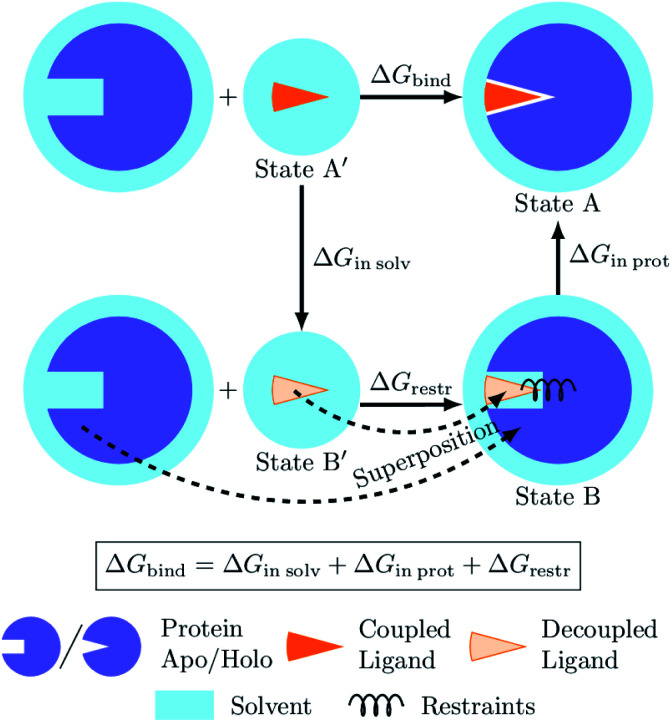
The process of a ligand binding to a protein requires considering two end-states: solvated ligand and ligand bound to the protein. Computationally, these two states can be connected via alchemical paths arranged in a thermodynamic cycle depicted in Fig. 7.2,18
Fig. 7. Diagram of the thermodynamic cycle for absolute binding free energy calculations. As the direct simulation of the protein–ligand binding is computationally expensive, the binding free energy ΔGbind is calculated by traversing across the thermodynamic cycle: first decoupling the ligand from the surrounding solvent, applying the analytical correction for the effect of protein–ligand restraints,7 and then coupling the ligand back in the protein's active cite. The equilibrium structures for the decoupled ligand in the active site (state B) can be generated by aligning its structures in solvent (state B′) into equilibrium frames of the apo protein.
Following this thermodynamic cycle, firstly, the ligand located in solvent (state A′) is decoupled from its environment (state B′). The decoupled ligand (state B′) is allowed to freely sample the whole simulation box. To be able to proceed with the second leg of the cycle, i.e. coupling the ligand to the system in the protein's binding site, the ligand needs to be restrained to the protein (state B). The contribution of the added restraints is taken into account analytically.7 Finally, the ligand in the protein's binding site is coupled to the system and the restraints are removed (state A). The free energies for the two legs of the thermodynamic cycle are obtained separately by performing multiple non-equilibrium transitions in the ligand coupling and decoupling directions, recording the work distributions and using the Crooks Fluctuation Theorem11 to evaluate the free energy differences.
The absolute ΔG calculations are particularly sensitive to the decoupled ligand restraining method. In our setup we employ a rigorous restraining approach7 acting between the protein and the decoupled ligand to anchor it in a narrow range of orientations within the binding pocket (ESI Section 1†). This restraint scheme uses six orthogonal relative restraints with harmonic potentials (a distance, two angles, and three dihedrals) acting on three anchor atoms in the ligand and three in the protein. The orthogonality of the potentials restraining the decoupled ligand allows for an analytical expression of the free energy contribution ΔGrestr.
5.1. Novel approach for treating the ligand's decoupled state
The alchemical approaches for absolute ligand binding free energies require explicit sampling of the ligand-protein complex with the ligand in its decoupled state (state B in Fig. 7). For that, a definition of restraints prior to starting the simulations is needed. The partition function of the decoupled state, however, can be separated into the independent contributions from the apo protein, the restraints, and the internal degrees of freedom of the decoupled ligand.7 The simulation trajectories of the decoupled ligand (state B′) are readily generated for every considered ligand in the ligand-solvation leg of the thermodynamic cycle. The simulation of an apo protein does not contain the ligand, thus a single trajectory of such a protein can be generated and later used in combination with any ligand of interest.
In the novel proposed approach we suggest generating an equilibrium ensemble of the decoupled ligand in the protein's binding site without the explicit simulation of this state. For that purpose we use the readily available trajectories of the decoupled ligand in water and protein in its apo state. Firstly, each frame of the protein–ligand trajectory (state A in Fig. 7) is superimposed onto the corresponding frame of the apo protein trajectory (state B in Fig. 7) by aligning their α-carbons. The corresponding frame of the decoupled ligand in solvent (state B′ in Fig. 7) is then aligned onto the new coordinates of the ligand from the protein–ligand complex using all heavy atoms as a reference. The now appropriately positioned decoupled ligand atoms are added to the apo protein trajectory. Finally, the six orthogonal restraints are constructed to match the potentials that would have generated equivalent distributions for each restrained degree of freedom in an explicit simulation (ESI Section 1†).
An ensemble created this way, however, may contain correlations between the restrained degrees of freedom (Fig. S11 and S12†), therefore, to acquire a well defined ensemble of ligand poses we implemented several correction schemes. For the a priori correction, we sample from the harmonic protein–ligand restraint potentials at the simulation temperature, thus creating a proper ensemble of ligand orientations. This ensemble can be used for calculating the ligand-protein coupling free energy. The post hoc correction allows performing the calculations starting directly with the superpositioned ensemble which still contains the correlations between the restrained degrees of freedom. In this case, the work values obtained from the ligand coupling simulations are adjusted with the contribution from the correlations as illustrated in the scheme in Fig. S13.†
We verified the validity of the superpositioning approach and the performance of the proposed decorrelation techniques, by comparing their predictions for a subset of the studied proteins (tyk2, jnk1, and p38α) to those of a standard protocol where the restrained state was simulated explicitly (Fig. S14 and S15†). For the main results reported in this work we used the post hoc decorrelation method.
5.2. Simulation details
All simulations were carried out with the GROMACS 2019.4 molecular dynamics engine1 modified to correctly handle pair interactions within a decoupled molecule larger than the electrostatic cutoff (bug 3403). The Amber99sb*ILDN6,22,32 force field was used for the proteins throughout this work together with the TIP3P25 water model. Ligand parameters were taken from the previous relative free energy study16 parameterized with the General Amber Force Field (GAFF v2.1)49 using AM1-BCC charges23 assigned with ACPYPE45 and AnteChamber.50 Initial ligand binding poses were reused from the previous relative binding free energy study,16 where the ligands were modeled based on similar compounds in existing holo crystal structures (Table S2†). Initial protein structures were stripped of surrounding water (if present) and resolvated in dodecahedral simulation boxes with 1.5 nm of padding between solute and box edges. For apo simulations started from holo structures the ligands were removed before adding water, so that the binding cavities could also be filled with water. Effects of retaining crystallographic water before filling the remaining cavities were also examined (Fig. S7†). Ions were added to neutralize the system and reach a salt concentration of 150 mM.
Van der Waals interactions were calculated with a 1.1 nm cutoff and a switching function starting at 1.0 nm. Coulomb interactions were computed with Smooth Particle Mesh Ewald12,13 and a real space cutoff of 1.1 nm. For temperature regulation a system-wide stochastic velocity rescale thermostat9 was used with a time constant of 0.1 ps and a target temperature of 298 K. The pressure was kept at 1 bar with the aid of the isotropic Parrinello–Rahman barostat34 with a time constant of 5 ps and a compressibility of 4.6 × 10−5 bar−1. Throughout this work a 2 fs time step was used with all bond lengths constrained via the LINCS21 algorithm.
Initial holo structures for ligands coupled to proteins as well as the solo ligands (used for the ligand in water leg of the thermodynamic cycle) were reused from the relative binding free energy study.16 Initial structures for protein apo simulations were constructed from apo crystal structures (PDB IDs 3o17 (jnk1), 1wfc53 (p38α), 4htz55 (pde2), 1h27 33 (cdk2), 1r1w42 (cmet), 3zsl41 (galectin)), where available. For these structures missing residues were modeled in and the amino acid protonation states were adjusted to match those of the holo structures. Energy minimization and equilibration with NVT and NPT simulations in the presence of solvent and ions were also carried out (in the same manner as in the core part of the protocol below) to relax the reconstructed residues. Finally, the apo protein structures were extracted from the last frame of the NPT simulations (or, in cases where no residue reconstruction was necessary, from the protonation adjustment stage) and were used to initialize the protein-only systems. As no apo crystal structure was available for tyk2, a holo structure with the ligand removed was used instead.
To obtain equilibrium distributions of the coupled protein–ligand and protein-only systems at 298 K, harmonic position restraints with a force constant of 9000 kJ mol−1 nm−2 were applied to all protein and ligand atoms of the initial structures described above and the energy was minimized followed by a 300 ps simulation in the NVT ensemble, where the first 5 ps were used to bring the temperature of the system from 0 to 298 K with simulated annealing. Position restraints were then relaxed to 500 kJ mol−1 nm−2 for a 50 ps NVT simulation followed by a 10 ns production NPT simulation without any position restraints. For the leg of the thermodynamic cycle of ligands in water, the simulations used no position restraints. Firstly, energy minimization was performed followed by the 10 ps NVT and 10 ns production NPT simulations.
To initialize the non-equilibrium alchemical transitions, the first 2.256 ns of all production simulations were discarded and the equilibrium conformations were sampled every 67 ps yielding 165 conformations for each system. The extracted conformers were used to construct an equilibrium ensemble of the decoupled ligand in the protein's binding site and generate protein–ligand restraints as described in Section 1.
The non-equilibrium simulations, each 500 ps long, were run from each conformation to the opposite coupling state of the ligand by linearly interpolating the Hamiltonian between the two end-states. The gradients ∂H(λ, x)/∂λ were integrated over the course of each non-equilibrium simulation to obtain the amount of work performed. Free energies were computed from the work distributions in both directions using a maximum likelihood estimator44 based on the Crooks Fluctuation Theorem11 by means of pmx.15 Finally, free energy estimates from different legs of the thermodynamic cycle were combined and the contribution of restraining the decoupled ligand to the protein was added7 incorporating the correction for the correlations in the restrained degrees of freedom (Section 2).
Well-tempered metadynamics4,29 calculations were carried out with GROMACS 2016.3 1 in combination with plumed 2.3.1.47 A bias factor of (T + ΔT)/T = 11 with a time constant of τ = 10 ps, a time step of 0.002 ps, and a temperature T = 298 K were used for 100 ns simulations started from apo structures previously equilibrated as described above. Every τpace = 2 ps Gaussian biases of 5° width and an initial height of kbΔTτpace/τ = 2kbT ≈ 4.955 kJ mol−1, where kb is the Boltzmann constant, were deposited onto a periodic grid consisting of 360 points equally distributed along the χ1 dihedral. Resulting free energy surfaces and uncertainties are reported as averages and standard errors across 5 repeats.
Throughout this work uncertainties were computed via bootstrap, unless explicitly specified otherwise, and represent standard errors when taking into account all available calculations. Bootstrapping was performed for the individual repeats of free energy predictions for each ligand based on the work values, the final free energy prediction for each ligand across multiple repeats, as well as for AUE and Pearson correlation coefficient across multiple ligands. Actual values around which these uncertainties are reported are the means of the underlying data or estimates of the AUE and correlation coefficient considering all the available data.
Data availability
The calculated free energies and simulation input files are available at https://github.com/deGrootLab/abs_dG_paper_ChemScience2021.
Author contributions
All authors contributed to the manuscript and gave approval to its final version.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
YK was supported by the Vlaams Agentschap Innoveren & Ondernemen (VLAIO) project number HBC.2018.2295, “Dynamics for Molecular Design (DynaMoDe)”. VG was supported by the BioExcel CoE (http://www.bioexcel.eu), a project funded by the European Union (Contract H2020-INFRAEDI-02-2018-823830).
Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc03472c
References
- Abraham M. J. Murtola T. Schulz R. Páll S. Smith J. C. Hess B. Lindahl E. GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1–2:19–25. doi: 10.1016/j.softx.2015.06.001. doi: 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Aldeghi M. Alexander H. Bodkin M. J. Knapp S. Biggin P. C. Accurate calculation of the absolute free energy of binding for drug molecules. Chem. Sci. 2016;7(1):207–218. doi: 10.1039/C5SC02678D. doi: 10.1039/C5SC02678D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aldeghi M. Alexander H. Bodkin M. J. Knapp S. Biggin P. C. Predictions of Ligand Selectivity from Absolute Binding Free Energy Calculations. J. Am. Chem. Soc. 2017;139(2):946–957. doi: 10.1021/jacs.6b11467. doi: 10.1021/jacs.6b11467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barducci A. Bussi G. Parrinello M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008;100(2):020603. doi: 10.1103/PhysRevLett.100.020603. doi: 10.1103/PhysRevLett.100.020603. [DOI] [PubMed] [Google Scholar]
- Baumann H. M. Gapsys V. de Groot B. L. Mobley D. L. Challenges Encountered Applying Equilibrium and Nonequilibrium Binding Free Energy Calculations. J. Phys. Chem. B. 2021;125(17):4241–4261. doi: 10.1021/acs.jpcb.0c10263. doi: 10.1021/acs.jpcb.0c10263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best R. B. Hummer G. Optimized Molecular Dynamics Force Fields Applied to the Helix-Coil Transition of Polypeptides. J. Phys. Chem. B. 2009;113(26):9004–9015. doi: 10.1021/jp901540t. doi: 10.1021/jp901540t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boresch S. Tettinger F. Leitgeb M. Karplus M. Absolute Binding Free Energies: A Quantitative Approach for Their Calculation. J. Phys. Chem. B. 2003;107(35):9535–9551. doi: 10.1021/jp0217839. doi: 10.1021/jp0217839. [DOI] [Google Scholar]
- Buijnsters P. De Angelis M. Langlois X. Rombouts F. J. R. Sanderson W. Gary T. Ritchie A. Trabanco A. A. VanHoof G. Van Roosbroeck Y. Andrés J.-I. Structure-Based Design of a Potent, Selective, and Brain Penetrating PDE2 Inhibitor with Demonstrated Target Engagement. ACS Med. Chem. Lett. 2014;5(9):1049–1053. doi: 10.1021/ml500262u. doi: 10.1021/ml500262u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bussi G. Donadio D. Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007;126(1):014101. doi: 10.1063/1.2408420. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Ciordia M. Pérez-Benito L. Delgado F. Trabanco A. A. Gary T. Application of Free Energy Perturbation for the Design of BACE1 Inhibitors. J. Chem. Inf. Model. 2016;56(9):1856–1871. doi: 10.1021/acs.jcim.6b00220. doi: 10.1021/acs.jcim.6b00220. [DOI] [PubMed] [Google Scholar]
- Crooks G. E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1999;60(3):2721–2726. doi: 10.1103/PhysRevE.60.2721. doi: 10.1103/PhysRevE.60.2721. [DOI] [PubMed] [Google Scholar]
- Darden T. York D. Lee P. Particle mesh Ewald: an Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98(12):10089–10092. doi: 10.1063/1.464397. doi: 10.1063/1.464397. [DOI] [Google Scholar]
- Ulrich E. Perera L. Berkowitz M. L. Darden T. Lee H. Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103(19):8577–8593. doi: 10.1063/1.470117. doi: 10.1063/1.470117. [DOI] [Google Scholar]
- Gapsys V. de Groot B. L. On the importance of statistics in molecular simulations for thermodynamics, kinetics and simulation box size. eLife. 2020;9:e57589. doi: 10.7554/eLife.57589. doi: 10.7554/eLife.57589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gapsys V. Michielssens S. Seeliger D. de Groot B. L. Pmx: Automated protein structure and topology generation for alchemical perturbations. J. Comput. Chem. 2015;36(5):348–354. doi: 10.1002/jcc.23804. doi: 10.1002/jcc.23804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gapsys V. Pérez-Benito L. Aldeghi M. Seeliger D. van Vlijmen H. Gary T. de Groot B. L. Large scale relative protein ligand binding affinities using non-equilibrium alchemy. Chem. Sci. 2020;11(4):1140–1152. doi: 10.1039/C9SC03754C. doi: 10.1039/C9SC03754C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gapsys V. Yildirim A. Aldeghi M. Khalak Y. van der Spoel D. de Groot B. L. Accurate absolute free energies for ligand–protein binding based on non-equilibrium approaches. Commun. Chem. 2021;4(1):1–13. doi: 10.1038/s42004-021-00498-y. doi: 10.1038/s42004-021-00498-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilson M. K. Given J. A. Bush B. L. McCammon J. A. The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys. J. 1997;72(3):1047–1069. doi: 10.1016/S0006-3495(97)78756-3. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahn D. F. König G. Hünenberger P. H. Overcoming Orthogonal Barriers in Alchemical Free Energy Calculations: On the Relative Merits of λ-Variations, λ-Extrapolations, and Biasing. J. Chem. Theory Comput. 2020;16(3):1630–1645. doi: 10.1021/acs.jctc.9b00853. doi: 10.1021/acs.jctc.9b00853. [DOI] [PubMed] [Google Scholar]
- Hermans J. Shankar S. The Free Energy of Xenon Binding to Myoglobin from Molecular Dynamics Simulation. Isr. J. Chem. 1986;27(2):225–227. doi: 10.1002/ijch.198600032. doi: 10.1002/ijch.198600032. [DOI] [Google Scholar]
- Hess B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2008;4(1):116–122. doi: 10.1021/ct700200b. doi: 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
- Hornak V. Abel R. Okur A. Bentley S. Roitberg A. Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins. 2006;65(3):712–725. doi: 10.1002/prot.21123. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jakalian A. Bush B. L. Jack D. B. Bayly C. I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. Method. J. Comput. Chem. 2000;21(2):132–146. doi: 10.1002/(SICI)1096-987X(20000130)21:2<132::AID-JCC5>3.0.CO;2-P. doi: 10.1002/(SICI)1096-987X(20000130)21:2<132::AID-JCC5>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- Jiang W. Roux B. Free Energy Perturbation Hamiltonian Replica-Exchange Molecular Dynamics (FEP/H-REMD) for Absolute Ligand Binding Free Energy Calculations. J. Chem. Theory Comput. 2010;6(9):2559–2565. doi: 10.1021/ct1001768. doi: 10.1021/ct1001768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L. Chandrasekhar J. Madura J. D. Impey R. W. Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79(2):926–935. doi: 10.1063/1.445869. doi: 10.1063/1.445869. [DOI] [Google Scholar]
- Keränen H. Pérez-Benito L. Ciordia M. Delgado F. Steinbrecher T. B. Oehlrich D. Herman W. van Vlijmen T. Trabanco A. A. Gary T. Acylguanidine Beta Secretase 1 Inhibitors: A Combined Experimental and Free Energy Perturbation Study. J. Chem. Theory Comput. 2017;13(3):1439–1453. doi: 10.1021/acs.jctc.6b01141. doi: 10.1021/acs.jctc.6b01141. [DOI] [PubMed] [Google Scholar]
- Khalak Y. Gary T. de Groot B. L. Gapsys V. Non-equilibrium approach for binding free energies in cyclodextrins in SAMPL7: force fields and software. J. Comput. Aided Mol. Des. 2021;35(1):49–61. doi: 10.1007/s10822-020-00359-1. doi: 10.1007/s10822-020-00359-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn M. Firth-Clark S. Tosco P. Antonia S. Mey J. S. Mackey M. Michel J. Assessment of Binding Affinity via Alchemical Free-Energy Calculations. J. Chem. Inf. Model. 2020;60(6):3120–3130. doi: 10.1021/acs.jcim.0c00165. doi: 10.1021/acs.jcim.0c00165. [DOI] [PubMed] [Google Scholar]
- Laio A. Parrinello M. Escaping free-energy minima. Proc. Natl. Acad. Sci. U.S.A. 2002;99(20):12562–12566. doi: 10.1073/pnas.202427399. doi: 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang J. van Abbema A. Balazs M. Barrett K. Leo B. Wade B. Chang C. Delarosa D. DeVoss J. Driscoll J. Eigenbrot C. Ghilardi N. Gibbons P. Halladay J. Johnson A. Kohli P. B. Lai Y. Liu Y. Joseph L. Mantik P. Menghrajani K. Murray J. Peng I. Amy S. Shia S. Young S. Smith J. Sohn S. Tsui V. Ultsch M. Wu L. C. Xiao Y. Yang W. Young J. Zhang B. Zhu B.-y. Magnuson S. Lead Optimization of a 4-Aminopyridine Benzamide Scaffold To Identify Potent, Selective, and Orally Bioavailable TYK2 Inhibitors. J. Med. Chem. 2013;56(11):4521–4536. doi: 10.1021/jm400266t. doi: 10.1021/jm400266t. [DOI] [PubMed] [Google Scholar]
- Lim N. M. Wang L. Abel R. Mobley D. L. Sensitivity in Binding Free Energies Due to Protein Reorganization. J. Chem. Theory Comput. 2016;12(9):4620–4631. doi: 10.1021/acs.jctc.6b00532. doi: 10.1021/acs.jctc.6b00532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindorff-Larsen K. Piana S. Kim P. Paul M. Klepeis J. L. Dror R. O. Shaw D. E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins. 2010;78(8):1950–1958. doi: 10.1002/prot.22711. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowe E. D. Tews I. Cheng K. Y. Brown N. R. Gul S. Martin E. Noble M. Gamblin S. J. Johnson L. N. Specificity Determinants of Recruitment Peptides Bound to Phospho-CDK2/Cyclin A. Biochemistry. 2002;41(52):15625–15634. doi: 10.1021/bi0268910. doi: 10.1021/bi0268910. [DOI] [PubMed] [Google Scholar]
- Parrinello M. Rahman A. Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys. 1981;52(12):7182–7190. doi: 10.1063/1.328693. doi: 10.1063/1.328693. [DOI] [Google Scholar]
- Pérez-Benito L. Keränen H. van Vlijmen H. Gary T. Predicting Binding Free Energies of PDE2 Inhibitors. The Difficulties of Protein Conformation. Sci. Rep. 2018;8(1):4883. doi: 10.1038/s41598-018-23039-5. doi: 10.1038/s41598-018-23039-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Procacci P. Methodological uncertainties in drug-receptor binding free energy predictions based on classical molecular dynamics. Curr. Opin. Struct. Biol. 2021;67:127–134. doi: 10.1016/j.sbi.2020.08.001. doi: 10.1016/j.sbi.2020.08.001. [DOI] [PubMed] [Google Scholar]
- Procacci P. Guido G. SAMPL7 blind predictions using nonequilibrium alchemical approaches. J. Comput. Aided Mol. Des. 2021:1573–4951. doi: 10.1007/s10822-020-00365-3. [DOI] [PubMed] [Google Scholar]
- Rizzi A. Jensen T. Slochower D. R. Aldeghi M. Gapsys V. Ntekoumes D. Bosisio S. Papadourakis M. Henriksen N. M. de Groot B. L. Cournia Z. Dickson A. Michel J. Gilson M. K. Shirts M. R. Mobley D. L. Chodera J. D. The SAMPL6 SAMPLing challenge: assessing the reliability and efficiency of binding free energy calculations. J. Comput. Aided Mol. Des. 2020;34(5):601–633. doi: 10.1007/s10822-020-00290-5. doi: 10.1007/s10822-020-00290-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocklin G. J. Mobley D. L. Dill K. A. Separated topologies—a method for relative binding free energy calculations using orientational restraints. J. Chem. Phys. 2013;138(8):085104. doi: 10.1063/1.4792251. doi: 10.1063/1.4792251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rombouts F. J. R. Gary T. Buijnsters P. Langlois X. Tovar F. Steinbrecher T. B. Vanhoof G. Somers M. Andrés J.-I. Trabanco A. A. Pyrido[4,3-e][1,2,4]triazolo[4,3-a]pyrazines as Selective, Brain Penetrant Phosphodiesterase 2 (PDE2) Inhibitors. ACS Med. Chem. Lett. 2015;6(3):282–286. doi: 10.1021/ml500463t. doi: 10.1021/ml500463t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saraboji K. Håkansson M. Genheden S. Diehl C. Qvist J. Ulrich W. Nilsson U. J. Leffler H. Ryde U. Mikael A. Logan D. T. The Carbohydrate-Binding Site in Galectin-3 Is Preorganized To Recognize a Sugarlike Framework of Oxygens: Ultra-High-Resolution Structures and Water Dynamics. Biochemistry. 2012;51(1):296–306. doi: 10.1021/bi201459p. doi: 10.1021/bi201459p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schiering N. Knapp S. Marconi M. Flocco M. M. Cui J. Perego R. Rusconi L. Cristiani C. Crystal structure of the tyrosine kinase domain of the hepatocyte growth factor receptor c-Met and its complex with the microbial alkaloid K-252a. Proc. Natl. Acad. Sci. U.S.A. 2003;100(22):12654–12659. doi: 10.1073/pnas.1734128100. doi: 10.1073/pnas.1734128100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schindler C. E. M. Baumann H. Blum A. Böse D. Buchstaller H.-P. Burgdorf L. Cappel D. Chekler E. Czodrowski P. Dorsch D. Eguida M. K. I. Follows B. Fuchß T. Grädler U. Gunera J. Johnson T. Lebrun C. J. Karra S. Klein M. Knehans T. Koetzner L. Krier M. Leiendecker M. Leuthner B. Li L. Mochalkin I. Musil D. Neagu C. Rippmann F. Schiemann K. Schulz R. Steinbrecher T. Tanzer E.-M. Lopez A. U. Follis A. V. Wegener A. Kuhn D. Large-Scale Assessment of Binding Free Energy Calculations in Active Drug Discovery Projects. J. Chem. Inf. Model. 2020;60(11):5457–5474. doi: 10.1021/acs.jcim.0c00900. doi: 10.1021/acs.jcim.0c00900. [DOI] [PubMed] [Google Scholar]
- Shirts M. R. Bair E. Giles H. Pande V. S. Equilibrium Free Energies from Nonequilibrium Measurements Using Maximum-Likelihood Methods. Phys. Rev. Lett. 2003;91(14):140601. doi: 10.1103/PhysRevLett.91.140601. doi: 10.1103/PhysRevLett.91.140601. [DOI] [PubMed] [Google Scholar]
- Sousa da Silva A. W. Vranken W. F. ACPYPE - AnteChamber PYthon Parser interfacE. BMC Res. Notes. 2012;5(1):367. doi: 10.1186/1756-0500-5-367. doi: 10.1186/1756-0500-5-367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suruzhon M. Bodnarchuk M. S. Ciancetta A. Russell V. Wall I. D. Essex J. W. Sensitivity of Binding Free Energy Calculations to Initial Protein Crystal Structure. J. Chem. Theory Comput. 2021:1549–9626. doi: 10.1021/acs.jctc.0c00972. [DOI] [PubMed] [Google Scholar]
- Tribello G. A. Bonomi M. Branduardi D. Camilloni C. Bussi G. PLUMED 2: new feathers for an old bird. Comput. Phys. Commun. 2014;185(2):604–613. doi: 10.1016/j.cpc.2013.09.018. doi: 10.1016/j.cpc.2013.09.018. [DOI] [Google Scholar]
- Wan S. Gary T. Pérez-Benito L. Herman V. Coveney P. V. Accuracy and Precision of Alchemical Relative Free Energy Predictions with and without Replica-Exchange. Adv. Theory Simul. 2020;3(1):1900195. doi: 10.1002/adts.201900195. doi: 10.1002/adts.201900195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J. Wolf R. M. Caldwell J. W. Kollman P. A. Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004;25(9):1157–1174. doi: 10.1002/jcc.20035. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Wang J. Wang W. Kollman P. A. Case D. A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006;25(2):247–260. doi: 10.1016/j.jmgm.2005.12.005. doi: 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
- Wang L. Berne B. J. Friesner R. A. On achieving high accuracy and reliability in the calculation of relative protein–ligand binding affinities. Proc. Natl. Acad. Sci. U.S.A. 2012;109(6):1937–1942. doi: 10.1073/pnas.1114017109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L. Wu Y. Deng Y. Kim B. Pierce L. Krilov G. Lupyan D. Robinson S. Dahlgren M. K. Greenwood J. Romero D. L. Craig M. Knight J. L. Steinbrecher T. Beuming T. Damm W. Harder E. Sherman W. Brewer M. Wester R. Murcko M. Frye L. Farid R. Lin T. Mobley D. L. Jorgensen W. L. Berne B. J. Friesner R. A. Abel R. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. J. Am. Chem. Soc. 2015;137(7):2695–2703. doi: 10.1021/ja512751q. doi: 10.1021/ja512751q. [DOI] [PubMed] [Google Scholar]
- Wilson K. P. Fitzgibbon M. J. Caron P. R. Griffith J. P. Chen W. McCaffrey P. G. Chambers S. P. Su M. S.-S. Crystal Structure of p38 Mitogen-activated Protein Kinase. J. Biol. Chem. 1996;271(44):27696–27700. doi: 10.1074/jbc.271.44.27696. doi: 10.1074/jbc.271.44.27696. [DOI] [PubMed] [Google Scholar]
- Woo H.-J. Roux B. Calculation of absolute protein-ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. U.S.A. 2005;102(19):6825–6830. doi: 10.1073/pnas.0409005102. doi: 10.1073/pnas.0409005102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J. Yang Q. Dai D. Huang Q. X-ray Crystal Structure of Phosphodiesterase 2 in Complex with a Highly Selective, Nanomolar Inhibitor Reveals a Binding-Induced Pocket Important for Selectivity. J. Am. Chem. Soc. 2013;135(32):11708–11711. doi: 10.1021/ja404449g. doi: 10.1021/ja404449g. [DOI] [PubMed] [Google Scholar]
- Zwanzig R. W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954;22(8):1420–1426. doi: 10.1063/1.1740409. doi: 10.1063/1.1740409. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The calculated free energies and simulation input files are available at https://github.com/deGrootLab/abs_dG_paper_ChemScience2021.