Revealing the Brønsted-Evans-Polanyi relation in halide-activated fast MoS₂ growth toward millimeter-sized 2D crystals

Ex-situ Arrhenius analyses and calculations reveal the activation mechanism of halide salts for molybdenum disulfide growth.

Abstract

Achieving large-size two-dimensional (2D) crystals is key to fully exploiting their remarkable functionalities and application potentials. Chemical vapor deposition growth of 2D semiconductors such as monolayer MoS₂ has been reported to be activated by halide salts, for which various investigations have been conducted to understand the underlying mechanism from different aspects. Here, we provide experimental evidence showing that the MoS₂ growth dynamics are halogen dependent through the Brønsted-Evans-Polanyi relation, based on which we build a growth model by considering MoS₂ edge passivation by halogens, and theoretically reproduce the trend of our experimental observations. These mechanistic understandings enable us to further optimize the fast growth of MoS₂ and reach record-large domain sizes that should facilitate practical applications.

INTRODUCTION

Two-dimensional (2D) semiconductors such as monolayer MoS₂ are essential building blocks for next-generation ultrathin flexible and low-power electronics (1, 2). A recent study using semimetal Bi as the electrical contact to monolayer MoS₂ has improved the on-current and contact resistance of the monolayer transistor to be on par with traditional Si-based transistors (3). As a premise for large-scale electronics, batch production of the 2D semiconductors requires large domain size (4, 5), large-area continuity, and thickness uniformity (6, 7). These are difficult tasks in particular for synthetic MoS₂ and other transition metal dichalcogenides (TMDs), considering the less controllable mass flux from solid metal precursors (8) in chemical vapor deposition (CVD), as compared to the case of graphene growth with gaseous hydrocarbons (9). One recent advance to mitigate this is the use of alkali metal halide salts [e.g., NaCl, KI, and NaBr (10–12)], which, in conjunction with transition metal or metal oxide powders, could increase the mass flux of metal precursors and accelerate the 2D growth of TMDs. Various research efforts have been made to explain the mechanism, in terms of these metal halides as a molten salt to facilitate the evaporation of the metal oxide precursor (11) or as a surfactant to modify the substrate surface and the MoS₂ edge (12). Both the alkali metal ions (13) and the halogens (11, 14) have been proposed to play an important role in the promoted growth. Continued endeavors are being devoted to shedding further light on understanding the detailed mechanism.

In this work, we provide unambiguous experimental evidence that halogens are closely related to MoS₂ growth dynamics. To achieve this, we implement postgrowth Arrhenius analysis without any involvement of in situ characterizations. We find that within the same reaction family, the halide-assisted growths conform to Brønsted-Evans-Polanyi (BEP) relation, where their reaction barriers are linearly correlated to the Mo─X (X = I, Br, Cl, F, and O) bond dissociation energies (E_b), suggesting the substitution of Mo─X bonds by the Mo─S bonds to be the rate-limiting step for the CVD growth. On the basis of this, we propose a theoretical growth model that not only reproduces the BEP relation but also explains the sulfur concentration–dependent growth dynamics observed in our experiments. By harnessing the synergistic effect of the KI promoter and the sulfur supply, we can reproducibly and rapidly synthesize near millimeter-sized 2D MoS₂ crystals dispersed over the entire SiO₂/Si substrates. These results not only shed light on the detailed mechanism of TMD growth activated by the halide salts but also guide the designer growth toward larger domain sizes that should enable practical applications.

RESULTS

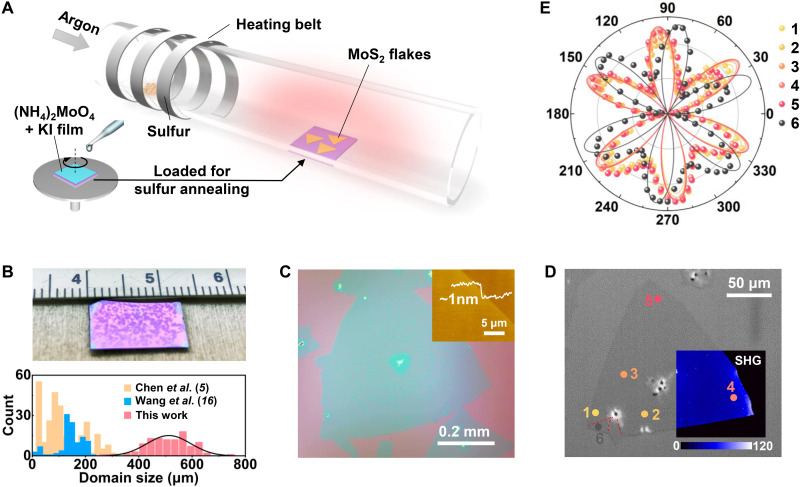
Figure 1A schematically illustrates our method to produce large-size atomically thin MoS₂ crystals. Briefly, MoO₃ dissolved in ammonia is spin-coated on the SiO₂/Si substrates (15) and loaded subsequently into a tube furnace for high-temperature annealing under a sulfur atmosphere (see Materials and Methods for more experimental details). The MoO₃/ammonia solution provides an advantage that soluble salts such as KI can be incorporated into the solution and mix uniformly with the Mo source in the spin-coated film. Moreover, the heating of the sulfur powder is controlled individually in terms of the start time and the target temperature to enable steady sulfur supply during the growth period (fig. S1). Under optimized sulfur heating temperature (T_S = 165°C), large-size 2D MoS₂ crystals are synthesized and distributed over the entire substrate, directly visualizable even with the naked eye (Fig. 1B). The flake sizes follow a Gaussian distribution centered at ~0.5 mm, which is among the largest synthetic 2D MoS₂ domains reported (5, 16).

Fig. 1. Halide-enabled growth of large 2D MoS₂ crystals.

(A) Schematic illustration of the growth process. (B) Photograph of near millimeter-sized 2D MoS₂ crystals over the entire SiO₂/Si substrate (top; photo credit: Qingqing Ji, Massachusetts Institute of Technology) and the corresponding domain size distribution (bottom). The domain size statistics are compared with state-of-the-art achievements on large-domain MoS₂ growth (5, 16). (C) Optical image of a typical 2D MoS₂ crystal with inset atomic force microscopy height image on the flake edge showing the monolayer thickness. (D) SHG mapping of a 2D MoS₂ crystal overlaid on the optical image. Dashed red lines mark the grain boundaries. (E) Plot of the SHG patterns under parallel configuration on the six locations marked in (D). Solid lines are fitted curves.

Figure 1C is an optical image of a typical MoS₂ crystal produced using the above method. The bulged triangle has a domain size of ~0.62 mm measured vertex to vertex, with atomic force microscopy confirming its monolayer thickness of ~1 nm (inset of Fig. 1C). Corresponding Raman and photoluminescence mapping images of this 2D crystal are provided in fig. S2, demonstrating its microscopic uniformity as a monolayer semiconductor. These flakes are proven to be mostly single crystals through second-harmonic generation (SHG) imaging. As shown in Fig. 1D, SHG mapping suggests the absence of any grain boundaries with uniform intensity over one-third of the flake region (17). Polarized SHG patterns under parallel configuration (Fig. 1E) are subsequently used to further verify the identical crystal orientation (18) for the remaining flake area (locations 1 to 5). The single crystallinity is found to extend over the entire flake until another small domain is encountered in the lower left part (location 6). In addition, SHG imaging of another 2D MoS₂ flake (~0.4 mm in size) by stitching several mapping images is presented in fig. S3 and directly verifies its single crystallinity. We note that the scanning step of 0.8 μm used here is sufficient to visualize any embedded grain boundaries, as indicated by the arrows in fig. S3.

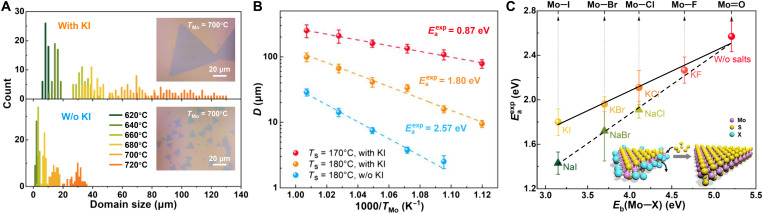
We further demonstrate experimentally that the domain size enhancement achieved here is due to the lowering of the reaction barrier in the presence of KI promoter, by comparing the MoS₂ growth results with and without KI in the spin-coated films. Figure 2A presents domain size statistics for the two cases under varied growth temperature (T_Mo). Detailed growth results can be found in figs. S4 and S5. The effect of KI incorporation is evident, with consistently much larger crystal size than for specimens grown without KI (insets of Fig. 2A). Because all the other growth parameters in these experiments are kept identical except T_Mo, the average domain size D, being T_Mo-dependent and proportional to the crystal growth rate, can be plotted versus 1000/T_Mo for direct Arrhenius fitting (Fig. 2B)

$$\text{log}(D/D_0)=C-(E_{\mathrm{a}}^{\text{exp}}/1000 k_{\mathrm{B}} \text{ln}10)(1000/T_{\text{Mo}})$$ (1)

where D₀ = 1 μm is for normalization, C is a constant, $E_{\mathrm{a}}^{\text{exp}}$ is the experimentally derived reaction barrier, and k_B is the Boltzmann’s constant. We find that the $E_{\mathrm{a}}^{\text{exp}}$ at T_S = 180°C decreases substantially from 2.57 to 1.80 eV after KI incorporation. This indicates that the iodide salt modifies the detailed reaction pathway of the CVD process, in addition to increasing the vapor pressure of the Mo-containing species. With the presence of KI and T_S lowering from 180° to 170°C, the $E_{\mathrm{a}}^{\text{exp}}$ further reduces to 0.87 eV along with the domain sizes increasing to more than 0.2 mm (Fig. 2B; see fig. S6 for the domain size statistics at T_S = 170°C). Optimizing T_S at 165°C results in even larger 2D MoS₂ crystals (Fig. 1C), but the sulfurization reaction cuts off at T_S ≤ 160°C, producing only unsulfurized species (fig. S7) (19). We hence conclude that the MoS₂ growth dynamics are sensitive to the presence of KI and the sulfur concentration at T_S > 160°C.

Fig. 2. Halide-dependent reaction barriers.

(A) Statistics of MoS₂ domain size under varied growth temperature (T_Mo), for the growth with and without KI promoters (top and bottom, respectively). Insets are the corresponding optical images of MoS₂ crystals grown at T_Mo = 700°C for direct comparison. Sulfur heating temperature (T_S) was kept at 180°C. (B) Arrhenius plots of average domain size (D) versus 1000/T_Mo under varied growth conditions. (C) Plot of the experimentally extracted reaction barriers ($E_{\mathrm{a}}^{\text{exp}}$) versus Mo─X bond dissociation energies, E_b(Mo─X) (X = I, Br, Cl, F, and O), for the MoS₂ growth assisted by various potassium and sodium halides. Inset: Schematic model of the bond substitution process that dominates MoS₂ growth.

Following the strategy presented above, we have also been able to extract the CVD reaction barriers incorporating KBr, KCl, and KF promoters (fig. S8). All of these $E_{\mathrm{a}}^{\text{exp}}$ values are found to correlate linearly with the Mo─X bonding energies, E_b(Mo─X) (solid line in Fig. 2C) (20), which indicates that halogens play a vital role in tuning the MoS₂ growth dynamics. The linear correlation can be understood in the context of the BEP principle (21) that predicts, for chemical reactions of the same class, E_a = E₀ + αΔH, where ΔH is the enthalpy of reaction and E₀ and α are linear fitting parameters. In our case, the replacement of ΔH with E_b(Mo─X) holds only if we consider MoX_y + 2S → MoS₂ + yX, where ΔH = yE_b(Mo─X) − 2E_b(Mo─S), as the relevant reaction. Such a BEP relation is frequently observed in surface-catalyzed chemical processes (22, 23) and radical reactions dominated by bond substitution (24), in analog to which the above CVD reaction can also be inferred as bond substitution dominated. The process concerning this analysis is shown in the inset of Fig. 2C, schematically illustrating the substitution of Mo─X bonds by Mo─S bonds during MoS₂ growth.

Furthermore, the above analysis framework has also been applied for sodium halide–assisted MoS₂ growths, revealing and validating a BEP relation as well (dashed line in Fig. 2C). The difference of the two BEP lines suggest that alkali metal ions also play a role in tuning MoS₂ growth dynamics, the details of which have been explored in a previous work that considers MoS₂ lattice strain relaxation by sodium attachment on the edge (12). Our analysis method can thus provide a route to experimentally differentiate the roles of metal and halogen ions on promoting MoS₂ growth.

DISCUSSION

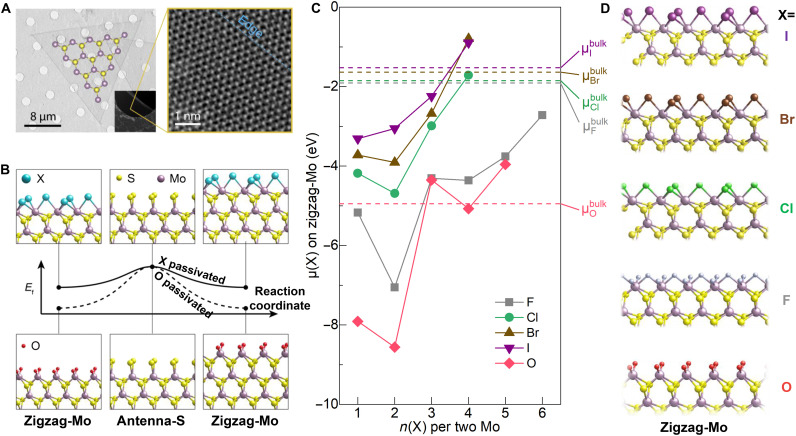
On the basis of the above understandings from experiments, we build a theoretical growth model termed edge passivation-substitution (EPS) to further rationalize the reaction barrier tuning by halide salts. From both selected-area electron diffraction (fig. S9) (25) and atomic-resolution scanning transmission electron microscopy (STEM) (Fig. 3A), the edge of the MoS₂ crystals produced by halide-assisted growth has been identified to be along the crystallographic zigzag-Mo orientation, instead of the zigzag-S orientation. Knowing the edge type is useful to narrow down the possible range of the chemical potential of sulfur (μ_S): Lower (higher) μ_S favors zigzag-Mo (zigzag-S) edge type formation. We note that the edge type here indicates the crystal orientation rather than the detailed atomic structure of the edge (e.g., “zigzag-Mo orientation” corresponds to both zigzag-Mo and antenna-S structures at the edge, the latter being the sulfur-passivated zigzag-Mo edge).

Fig. 3. EPS model of the halide-assisted MoS₂ growth.

(A) TEM and STEM images of the grown MoS₂ flakes. The STEM image is taken close to an edge with the dashed blue line marking the edge orientation. (B) Energy landscapes and intermediate edge structures of MoS₂ growth with (top) and without (bottom) halide promoters. (C) Plot of the calculated incremental chemical potentials of halogens and oxygen versus their coordination numbers on the edge. n(X) per two Mo is used to accommodate bridge bonding structures. Dashed lines mark the corresponding chemical potentials in the bulk phases. (D) Thermodynamically allowed zigzag-Mo edge structures passivated by maximum halogen and oxygen atoms.

Figure 3B is an illustration of the EPS model that exhibits the alternate attachment of S and MoX_y clusters on a zigzag-Mo edge to imitate the MoS₂ growth process (26). The involvement of MoX_y is based on previous observation that molybdenum halides/oxyhalides are generated spontaneously and related to the salt-assisted MoS₂ growth (11). The growth without halide promoters is plotted as a reference, where the zigzag-Mo edges are passivated by oxygen atoms (lower part of Fig. 3B), as confirmed in the BEP relation (Fig. 2C) that the reaction barrier in this case correlates with E_b(Mo═O). The thermodynamically allowed edge configurations passivated by halogens and oxygen are determined by comparing their incremental chemical potentials on the zigzag-Mo edge to that in the bulk phases, μ^bulk, which represent the upper limit of the chemical potentials of corresponding elements (Fig. 3C). If the energy gain of attaching an atom to the MoS₂ edge is lower than its |μ^bulk|, then the edge structure with that additional atom is thermodynamically forbidden. Because the halogen/oxygen atoms are not consumed by the growth reaction, they can be rationally assumed to saturate the edge to its maximum extent, ignoring the kinetic effects. Coordination numbers can thus be derived with the detailed edge structures shown in Fig. 3D.

In our EPS model, the reaction barrier ($E_{\mathrm{a}}^{\text{cal}}$) of zigzag-Mo edge growth is approximated as the formation energy (E_f) difference between the sulfur-bonded intermediate state (antenna-S edge) and the halogen/oxygen-passivated zigzag-Mo edge. Likewise, in the case of zigzag-S edge growth, is the difference of E_f between the halogen/oxygen-passivated Mo-bonded intermediate state (antenna-Mo edge) and zigzag-S edge. More rigorously, we define

$$E_{\mathrm{a}}^{\text{cal}}=\text{max}\{\mid E_{\mathrm{f},\text{zigzag-Mo}}-E_{\mathrm{f},\text{antenna-S}}\mid ,\mid E_{\mathrm{f},\text{zigzag-S}}-E_{\mathrm{f},\text{antenna-Mo}}\mid \}$$ (2)

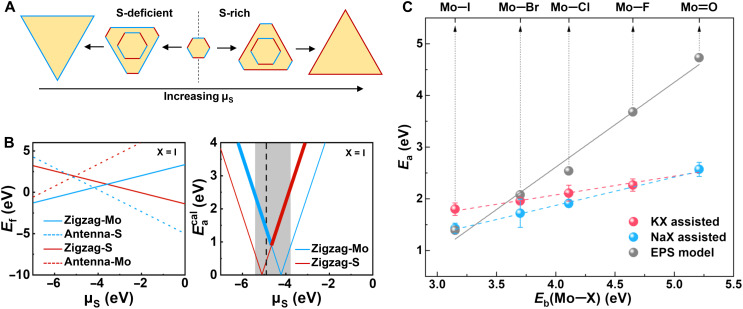
which takes into account the competitive formation of zigzag-Mo and zigzag-S edges governed by Wulff construction theory (27), because the edge growth with smaller activation energy diminishes quickly and the final growth is determined by the slower edge formation process (Fig. 4A). Detailed discussion of the growth model and the density functional theory calculations can be found in Materials and Methods, fig. S10, and tables S1 to S3.

Fig. 4. Theoretically derived reaction barrier and BEP relation using the EPS model.

(A) Schematic shape evolution of MoS₂ crystals under S-deficient (Mo-rich) and S-rich conditions. Blue and red lines represent zigzag-Mo and zigzag-S terminated edges, respectively. (B) Edge formation energy (E_f) and derived reaction barrier ($E_{\mathrm{a}}^{\text{cal}}$) as a function of the chemical potential of sulfur (μ_S) in the case of iodine passivation. In the right panel, the shaded region indicates accessible μ_S, and the vertical dashed line marks where μ_S = −4.9 eV. (C) Halide-dependent $E_{\mathrm{a}}^{\text{cal}}$ (in red) versus E_b(Mo─X) calculated with the above growth model (in gray). μ_S = −4.9 eV is adopted to derive the $E_{\mathrm{a}}^{\text{cal}}$. The experimental data (in red and blue) from Fig. 2C are also provided here for direct comparison.

Figure 4B exemplifies the calculated results for the growth with iodide promoter (calculations of the growth with passivation of oxygen and other halogens are presented in fig. S11). The overall μ_S-dependent $E_{\mathrm{a}}^{\text{cal}}(\mathrm{X}=\mathrm{I})$ according to Eq. 2 is highlighted in bold in the right panel, exhibiting a V-shape curve minimized at μ_S = −4.6 eV. Adopting μ_S = −4.9 eV, which is on the left branches of all the five $E_{\mathrm{a}}^{\text{cal}}(\mathrm{X})-{\mathrm{\mu }}_{\mathrm{S}}$ curves that associates with zigzag-Mo edge formation, as confirmed by the STEM image above, we theoretically reproduce the BEP relation (Fig. 4C) and verify the halogen-dependent MoS₂ growth dynamics. Notably, the calculated BEP slope is higher than the experimental counterparts, which possibly associates with the fact that we do not consider the synergistic Mo─X and Mo─S bond dissociation/formation process in the EPS model for simplicity (see Materials and Methods for more detailed discussion). Regarding the linearly correlated E_a and E_b(Mo─X), the qualitative consistency between experimental and theoretical results justifies our hypothetical EPS model, hence providing useful insights on further engineering the growth of MoS₂ and other TMDs.

Our results suggest that edge passivation by oxygen or other additives, being overlooked in most previous studies, should be considered to better understand the MoS₂ growth dynamics. In addition, while the role of alkali metal ions in the salts is not the primary focus of this work, we anticipate that our growth model could be further extended to incorporate these metal ions by, for example, placing them on the zigzag-S and antenna-S edges to modify the corresponding formation energies and the overall reaction barriers.

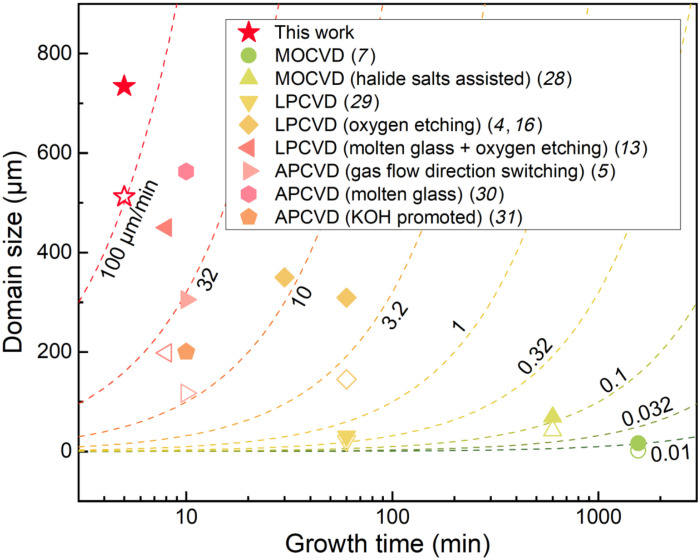
Comparing with previous efforts on large-domain MoS₂ growth (4, 5, 7, 13, 16, 28–31), our method markedly improves the achievable domain size and shortens the required growth time (Fig. 5). It is worth noting that, while crystal growth does not precisely start (end) at the beginning (ending) of max{T_Mo}, the time span of max{T_Mo} is a good approximation of the growth time and a fair gauge for comparison across different methods. As a result, we enhance the growth velocity of MoS₂ by three- to fivefold from the previous record (30). Reaction dynamics engineering mediated by the halide salts has been proven to be the key to achieve this, which differs from other works that focus on improving the nucleation dynamics [e.g., introducing oxygen for nuclei etching (4, 13)] or diffusion dynamics [e.g., using molten glass substrates to facilitate precursor diffusion (13, 30)]. Using a combination of these growth techniques, further improvement of the MoS₂ domain size up to millimeter or even larger scales can be rationally anticipated, which represents a long-term pursuit among the 2D semiconductor community.

Fig. 5. Benchmark of the optimized halide-assisted MoS₂ growth method.

The filled symbols describe the largest achievable domain sizes in these reports, while the corresponding hollow symbols mark the average domain sizes achieved. The “growth time” on the x axis indicates the time span of T_Mo. The dashed contour lines mark various growth velocities estimated by the domain size over the growth time. MOCVD, metal-organic CVD; LPCVD, low-pressure CVD; APCVD, ambient-pressure CVD.

In summary, we have explored large-domain MoS₂ growth activated by halide salts and provided direct evidence that halogens associate closely with the reaction dynamics through the BEP relation. This mechanistic understanding has enabled us to establish a theoretical growth model that rationalizes all the experimental observations, as well as to guide the designer CVD growth toward millimeter-sized 2D MoS₂ crystals with shortened growth time. We postulate that the uncovered activation mechanism is broadly applicable to the growth of diverse 2D metal chalcogenides and will be of great utility to further integrated functionalities.

MATERIALS AND METHODS

Halide-assisted growth of 2D MoS₂ crystals

We take the KI-assisted MoS₂ growth as an example to describe the experimental details. MoO₃ (100 mg; ≥99.9%; Alfa Aesar) and KI (100 mg; ≥99%; Alfa Aesar) were dissolved in 20 ml of ammonia (weight, ~30%; Alfa Aesar) by 5-min sonication. The precursor solution was diluted four times and then spin-coated onto SiO₂/Si at 2500 rpm for 1 min. The obtained precursor film was loaded into a single-zone tube furnace (Thermo Fisher Scientific–Lindberg) for high-temperature annealing under a sulfur atmosphere conveyed downstream by Ar gas flow. A detailed growth program is shown in fig. S1. The first 3 min under 1000-sccm (standard cubic centimeter per minute) Ar gas flow was for purging the tube system (2.54 cm in diameter) and assuring a favorable atmosphere for MoS₂ growth. Under 30-sccm Ar, the furnace was heated to T_Mo = 600° to 720°C within 15 min and held at that temperature for 3 to 5 min to allow the growth of 2D MoS₂ crystals. Sulfur powder of ~30 mg in a quartz boat was placed 6 cm away from the furnace edge and evaporated by a heating belt at T_S = 165° to 180°C. The separate control of T_Mo and T_S allows for more elaborate tuning of the growth process.

We note that the start time of sulfur heating plays an important role in realizing the desirable 2D growth. Too early introduction of sulfur vapor would lead to the sulfurization reaction occurring at low temperature (<550°C) and result in nanoparticulate products, while delayed sulfur introduction would yield unsulfurized species. In our case, the start point was optimized at t = 12.5 min so that T_S was reached at ~3 min before T_Mo was reached, allowing for a nearly constant-rate supply of sulfur vapor during the growth period. Such growth program enabled us to achieve reliable Arrhenius fitting results and to better investigate the T_Mo- and T_S-dependent MoS₂ growth processes.

The synthesis of near millimeter-sized 2D MoS₂ crystals (Fig. 1, B and C) can be achieved at high T_Mo (720°C) and low T_S (165°C) with prolonged growth time (5 min). Small bilayer islands are found to be inevitable for large-domain MoS₂ growth. If we reduce the amount of spin-coated Mo precursors using a lower-concentration solution, then multilayer nucleation can be greatly suppressed yet at the expense of lower MoS₂ coverage and smaller domain size. To study the halide-dependent MoS₂ growth dynamics, solutions containing 100 mg of MoO₃ in mixture with 100 mg of KI, 72 mg of KBr, 45 mg of KCl, and 35 mg of KF, respectively, were prepared and spin-coated for the high-temperature annealing with sulfur vapors. The Mo/X molar ratio (X = I, Br, Cl, and F) was kept almost identical in these solutions for more rational comparison.

Details of the growth model and theoretical calculation of the reaction barriers

The first-principles calculations for geometric optimization and the electronic properties of crystal structure are carried out using density functional theory using projector augmented wave (PAW) method implemented in the Vienna Ab-initio Simulation Package (32, 33). The semilocal generalized gradient approximation in the form of Perdew-Burke-Ernzerhof and the PAW pseudopotentials are adopted. During the ionic optimization steps, the Hellman-Feynman forces of single atoms are optimized to be less than 0.01 eV/Å, where the energy cutoff is set to be 400 eV and only gamma point is used for k-space sampling. The k points are set to be 19 × 1 × 1 for calculating the formation energies.

The energy barrier of the edge growth is deduced from the formation energy of different edges. For example, in zigzag-Mo edge growth, the energy barrier during the growth procedure is the difference of E_f between zigzag-Mo and antenna-S edges (26). The same rule applies to the growth procedure of zigzag-S edge growth, where the barrier is the difference between the E_f of zigzag-S edge and antenna-Mo edge. The role of halogen atoms is to adjust the formation energies of zigzag-Mo and antenna-Mo edges and therefore tune the energy barriers of edge growth.

We begin by considering the energetically possible configurations of the halogen/oxygen-passivated zigzag-Mo and antenna-Mo edges, under the assumption that there are plenty of atomic sources for such edge passivation. Detailed edge structures are listed in tables S1 and S2. We note that according to our calculations, F atoms could passivate both Mo-terminated (zigzag-Mo and antenna-Mo) and S-terminated (zigzag-S and antenna-S) edges because of its distinct electronegativity, while I, Br, Cl, and O can only passivate Mo-terminated edges. Moreover, our calculation results indicate that it is energetically unfavorable to connect Na or K to antenna-S edge of MoS₂ in an open system (grand canonical ensemble): The maximum ratio between K and S atoms on the edge is only 1:2, while no Na can connect to the antenna-S edge. On the other hand, our calculations indeed show that the preferred configuration for zigzag-S edge is to passivate 3 K or 3 Na for every 2 S atoms. Therefore, it is possible to incorporate the alkali metal ions in our EPS model to understand their roles in promoting MoS₂ growth. Nevertheless, we note that the alkali metals can also affect the MoS₂ growth dynamics though other mechanisms. For example, potassium molybdate salts derived from the MoO₃/KI mixture as the liquid Mo source can have completely different surface transport and reaction kinetics (34) from that of gaseous molybdenum oxyhalides.

Given these edge passivation structures, their formation energies can be calculated by considering four types of nanostructures (35) in fig. S10. We denote the formation energies per unit length (the defined unit lengths are marked in fig. S10 by black rectangles) of zigzag-Mo, zigzag-S, antenna-S, and antenna-Mo edges as γ_I, γ_II, γ_III, and γ_IV, respectively. The calculated energies of the three nanobelts and the nano-island are listed as E₁, E₂, E₃, and E₄. The chemical potentials of Mo, S, O, and the halogen atom X (X = F, Cl, Br, and I) are denoted as μ_Mo, μ_S, μ_O, and μ_X, and the chemical potential of the unit cell of MoS₂ is μ_MoS2. At the final equilibrium state, μ_MoS2 = μ_Mo + 2μ_S.

As an example, for F-assisted growth process, the expressions connecting the above calculated energies are

$$\begin{array}{c}{\mathrm{\gamma }}_{\mathrm{I}}+{\mathrm{\gamma }}_{\text{II}}=E_1-7{\mathrm{\mu }}_{\text{Mo}}-14{\mathrm{\mu }}_{\mathrm{S}}-N_1{\mathrm{\mu }}_{\mathrm{X}},\\ {\mathrm{\gamma }}_{\text{II}}+{\mathrm{\gamma }}_{\text{III}}=E_2-6{\mathrm{\mu }}_{\text{Mo}}-14{\mathrm{\mu }}_{\mathrm{S}}-N_2{\mathrm{\mu }}_{\mathrm{X}},\\ {\mathrm{\gamma }}_{\mathrm{I}}+{\mathrm{\gamma }}_{\text{IV}}=E_3-8{\mathrm{\mu }}_{\text{Mo}}-14{\mathrm{\mu }}_{\mathrm{S}}-N_3{\mathrm{\mu }}_{\mathrm{X}},\\ 9{\mathrm{\gamma }}_{\mathrm{I}}+6{\mathrm{\gamma }}_{\text{II}}=E_4-18{\mathrm{\mu }}_{\text{Mo}}-50{\mathrm{\mu }}_{\mathrm{S}}-N_4{\mathrm{\mu }}_{\mathrm{X}}\end{array}$$ (3)

where N₁, N₂, N₃, and N₄ are the total number of halogen atoms in the corresponding nanobelts and nano-islands in unit length. In the case of F-assisted growth process, N₁ = 6, N₂ = 6, N₃ = 6, and N₄ = 45. Solving the above equation set for formation energies of different edges, we have

$$\begin{array}{c}{\mathrm{\gamma }}_{\mathrm{I}}=E_1+2E_2-\frac{1}{3}{E}_4-13{\mathrm{\mu }}_{{\text{MoS}}_2}+\frac{2}{3}{\mathrm{\mu }}_{\mathrm{S}}-3{\mathrm{\mu }}_{\mathrm{F}},(\text{zigzag} \text{Mo})\\ {\mathrm{\gamma }}_{\text{II}}=-2E_2+\frac{1}{3}{E}_4+6{\mathrm{\mu }}_{{\text{MoS}}_2}-\frac{2}{3}{\mathrm{\mu }}_{\mathrm{S}}-3{\mathrm{\mu }}_{\mathrm{F}},(\text{zigzag} \mathrm{S})\\ {\mathrm{\gamma }}_{\text{III}}=3E_2-\frac{1}{3}{E}_4-12{\mathrm{\mu }}_{{\text{MoS}}_2}-\frac{4}{3}{\mathrm{\mu }}_{\mathrm{S}}-3{\mathrm{\mu }}_{\mathrm{F}},(\text{antenna} \mathrm{S})\\ {\mathrm{\gamma }}_{\text{IV}}=-E_1-2E_2+E_3+\frac{1}{3}{E}_4+5{\mathrm{\mu }}_{{\text{MoS}}_2}+\frac{4}{3}{\mathrm{\mu }}_{\mathrm{S}}-3{\mathrm{\mu }}_{\mathrm{F}} (\text{antenna} \text{Mo})\end{array}$$ (4)

From here, we can plot four lines indicating the formation energies of the four edges with respect to the change of sulfur chemical potential. Note that the growth process of MoS₂ edge has merely two edge growth sequences: (i) zigzag-Mo → antenna-S → zigzag-Mo → antenna-S → … and (ii) zigzag-S → antenna-Mo → zigzag-S → antenna-Mo → ….

The formation energies of these edges are different, making one of the edges in the thread have higher energy than the other, therefore creating an energy barrier to cross over. Here, we assume that only these four edge states are related to the energy barriers. The four states are local minimums in the energy landscape, which are connected by many saddle points in between that truly accounts for the reaction barrier. Nevertheless, we are focusing on the qualitative trend instead of a quantitative description of the reaction path, and our simulation results have shown that this assumption is a good approximation for reproducing the trend with respect to different halogen atoms. Therefore, the energy barriers of the two edges under F passivation are

$$E_{\mathrm{a}}(\text{zigzag}-\text{Mo})=\mid {\mathrm{\gamma }}_{\mathrm{I}}-{\mathrm{\gamma }}_{\text{III}}\mid =\mid E_1-E_2-{\mathrm{\mu }}_{\text{Mo}{\mathrm{S}}_2}+2{\mathrm{\mu }}_{\mathrm{S}}\mid$$ (5)

$$E_{\mathrm{a}}(\text{zigzag}-\mathrm{S})=\mid {\mathrm{\gamma }}_{\text{II}}-{\mathrm{\gamma }}_{\text{IV}}\mid =\mid E_1-E_3+{\mathrm{\mu }}_{\text{Mo}{\mathrm{S}}_2}-2{\mathrm{\mu }}_{\mathrm{S}}\mid$$ (6)

Calculating the formation energies of the edges with Cl, Br, I, and O passivation follows the same procedure as that of F except that we use different groups of N₁, N₂, N₃, and N₄ numbers listed in table S3. The calculated reaction barriers are all plotted along with the formation energies in fig. S11. Note that when X = Cl, Br, I, and O, there is also chemical potential of X, μ_X, in the final expression of formation energies and energy barriers.

In our experiment, we have calibrated the amount of sulfur needed for minimizing the growth barrier when using KI. Therefore, a good estimated value of sulfur chemical potential, μ_S, should be close to the minimum of the energy barrier, where we estimate to be −4.9 eV on the basis of three facts: (i) The sulfur concentration is kept at a lowest possible level where the growth speed is optimized. (ii) TEM characterization proves that the edge of MoS₂ is Mo-zigzag type, so μ_S falls into the left side (blue color) of the “V” shape in Fig. 4B. (iii) The value of μ_S is sampled between −5.4 and −4.6 eV to best fit the trend of experiment results in Fig. 4C. Therefore, μ_S = −4.9 eV matches well with all the above criteria. Because the sulfur is kept in the same condition for different halogen-assisted growth, the μ_S of these growth processes should be very close to each other. By taking μ_S = − 4.9 eV shown as the vertical dashed line in fig. S11, we can estimate the energy barrier for each specific halogen-assisted process and use them for the BEP plot.

The EPS model considers thermodynamic properties of the edge structures to approximate the reaction dynamics, which, by nature, is less effective to account for a growth process involving notable kinetic effects. Regarding the nonconcave shape of the monolayer crystals (Fig. 1C) and the fact that MoS₂ growth accelerates with reduced sulfur supply (Fig. 2B), both Mo and S sources are deduced to be sufficient for the reaction and contribute to negligible kinetic effects (36). This explains the validity of the thermodynamic EPS model for our growth results. Nevertheless, to include kinetic effects, a growth model that has inputs of empirical parameters should be developed, for which the vapor-liquid-solid model (34) and the phase-field model (37) are the most promising ones.

Our EPS model can, in principle, be applied for MoS₂ growth with externally supplied Mo sources, on condition of inappreciable kinetic effects. This is however hardly achieved for volatile and reactive molybdenum halides (38), although the EPS model predicts them to be good precursors for fast and large-domain MoS₂ growth. A local feeding strategy reported for graphene growth (39) could possibly avoid premixing and reaction of MoX_y with sulfur in the gas phase and overcome the Mo-associated kinetic effects, lastly enabling the fast growth of ultralarge 2D MoS₂ crystals.

Last, we explain the slope discrepancy for the BEP relationships obtained from both experiments and theoretical calculations (Fig. 4C). The BEP relationship in our case has the form of E_a = E₀ + αE_b(Mo─X), where E_a is the reaction barrier, E_b(Mo─X) is the Mo─X bond energy, and E₀ and α are the fitting parameters. The slope α characterizes how strongly the reaction rate is limited by the dissociation of the Mo─X bonds (sufficiently large α indicates that Mo─X bond dissociation is a prerequisite to proceed the reaction). In the practical growth process, the Mo─X bond dissociation is more likely accompanied by the Mo─S bond formation in a synergistic way, which leads to the E_a having mitigated dependence on E_b(Mo─X) and hence a smaller α value. Our model, to provide a more concise picture, has simplified the growth process without considering the synergistic bond dissociation/formation states and thus overestimated the dependence on E_b(Mo─X). Nevertheless, the essential chemistry conveyed in this model is still valid that the reaction is dominated by the substitution of Mo─X bonds by the Mo─S bonds.

Supplementary Materials

This PDF file includes:

Figs. S1 to S11

Tables S1 to S3