SUMMARY
Memory enables access to past experiences to guide future behavior. Humans can determine which memories to trust (high confidence) and which to doubt (low confidence). How memory retrieval, memory confidence, and memory-guided decisions are related, however, is not understood. In particular, how confidence in memories is used in decision making is unknown. We developed a spatial memory task in which rats were incentivized to gamble their time: betting more following a correct choice yielded greater reward. Rat behavior reflected memory confidence, with higher temporal bets following correct choices. We applied machine learning to identify a memory decision variable and built a generative model of memories evolving over time that accurately predicted both choices and confidence reports. Our results reveal in rats an ability thought to exist exclusively in primates and introduce a unified model of memory dynamics, retrieval, choice, and confidence.
In brief
Joo et al. demonstrate rats use confidence in memories to guide behavior. A novel memory task and a quantitative confidence-reporting method allowed animals to express memory confidence on each trial, and a simple generative model of memories evolving over time accurately predicted both choices and confidence reports.
Graphical Abstract

INTRODUCTION
Animals rely on two sources of information to guide behavior: current sensory information from the external world and memories of the past from internal storage. Because sensory perception and memory are both imperfect, metacognitive monitoring of their possible errors can valuably inform future action, for instance, by motivating information seeking prior to decisions or decreased resource investment afterward.1–6
Studies of this metacognitive monitoring have focused primarily on confidence in information perceived externally (e.g., motion detection and odor discrimination), reporting confidence-related behaviors across multiple species, including dolphins,7 non-human primates,8–12 honeybees,13 and rats.14,15 A statistical framework that formally defines confidence and its signatures14,16,17 has helped establish a correspondence between statistical confidence in perceptions and the subjective sense of human confidence18 and enabled the identification of behavioral and neural confidence markers in species including macaques,10,19 pre-verbal infants,20 and rats.21,22
By comparison, understanding of confidence in information retrieved from memory is limited.23,24 Human and primate studies have focused exclusively on confidence in visual recognition memories,25–30 and whether these findings generalize to other forms of memory is unclear. Progress at a neural circuit level has also been hindered by the lack of a rodent model. Rodents can access various forms of memory,31,32 but whether rodents can use memory confidence as primates do, to weigh evidence from a series of past experiences, remains unclear.33 Specifically, one set of previous studies yielded equivocal results,34,35 while another provided evidence for metacognition, broadly defined, with a binary decision related to an odor memory.36 Moreover, we lack a quantitative account of how memories evolve over time, and we do not understand how this evolution could lead to behavioral expressions of confidence.
Here, we developed a behavioral task in rats that enabled quantitative assessment of memory accuracy and confidence for personally experienced events in their temporal and spatial contexts. On each trial, rats first made a choice based on information retrieved from memory and were incentivized to then place a bet on whether the choice was correct by waiting for a period of self-determined length. Temporal betting provided a graded confidence report on every trial, improving on task designs that assess only a binary confidence,14,27,36 do not allow confidence and choice to be collected in the same trials,8,10,25 or can only assess confidence on a subset of trials.6,21,22 Our task design also enabled collection of thousands of trials from each rat, comprising spatial memory decisions spanning a range of difficulties, each associated with a behavioral confidence report. We found that rats consistently bet more time on correct trials, suggestive of a memory confidence computation. To evaluate this possibility, we constructed a computational model that intuitively unifies memory retrieval, choice, and confidence and found that it accurately predicts choices and temporal bets.
RESULTS
Memory choice and confidence task
We designed a memory decision task augmented with a post-decision wager to assess confidence. Toward the eventual aim of understanding the behavior and neural computation of confidence together, the task was designed to be performed even by rats implanted with neural recording hardware and wired to a recording rig. Rats included here (n = 4) were selected from an original large cohort (n = 30; STAR Methods) based on linear-track pre-screening, pre-trained over a 2- to 3-month period on the basic task logic, and implanted with neural recording hardware prior to the collection of behavioral data (Figures S1A and S1B–S1E). Each animal performed thousands of trials (see below), and we analyzed each animal separately to provide independent replicates of the effects.
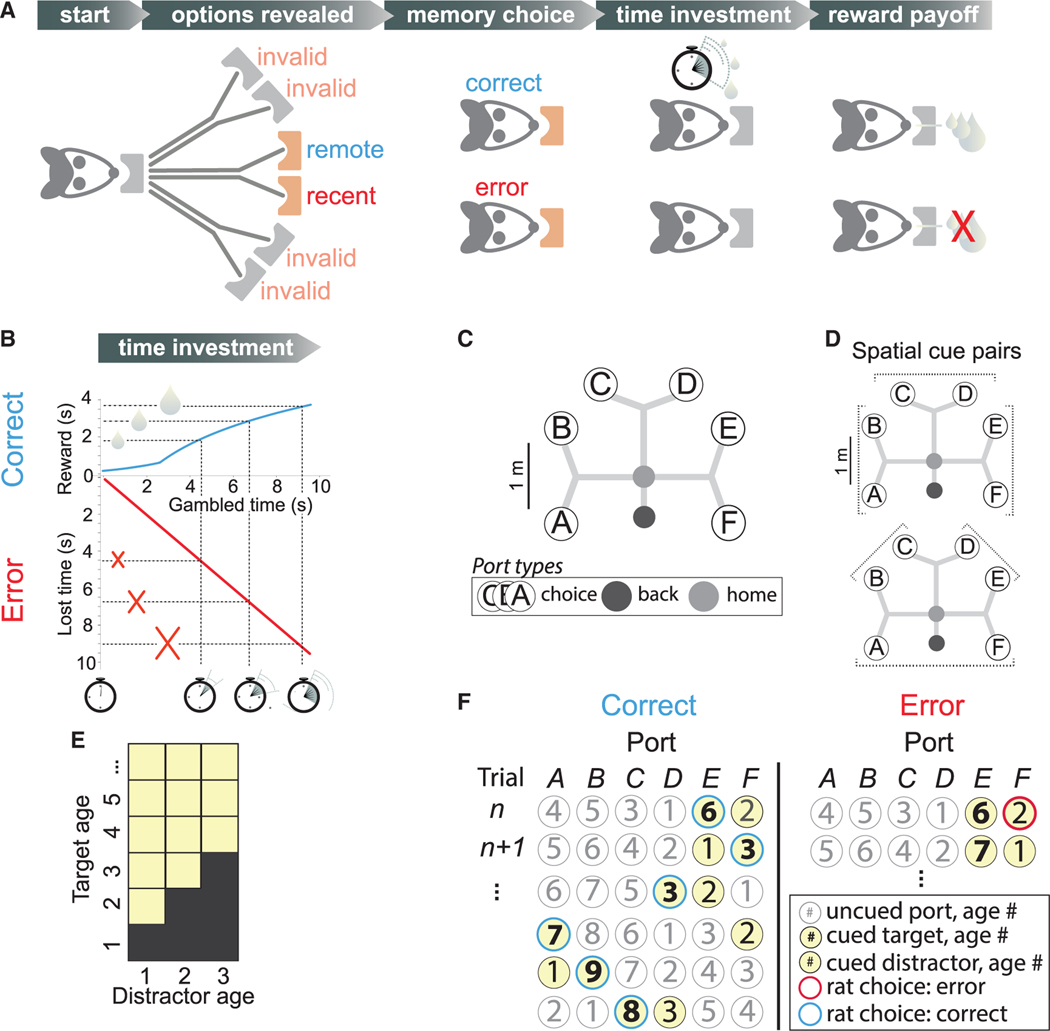
Each trial requires a binary, memory-guided choice, followed by a confidence report (Figures 1A, 1B, and S1F). A randomly selected two of six spatially remote choice ports are cued by a light at the (physically distant) port, and a valid choice is made by entering one of the lit choice ports. The correct choice, or target, is the more temporally remote in the ongoing sequence of visits in the epoch, while the other, more recently visited port is the distractor. Next, rats have an option to bet on their choice by remaining at the choice port for a self-determined duration, with the total time spent serving as a bet (Figure 1B). For correct choices only, longer bets will yield more reward. Importantly, the task takes place in fixed, approximately hour-long epochs, with self-paced trials. Longer temporal bets thus have a higher possible reward payout in the case of a correct choice but also a higher penalty in the case of an incorrect choice, in the form of the opportunity cost of not initiating a next trial. If rats compute confidence in their memories, they should bet more time on choices based on memories they are more confident in, as this will maximize reward over the epoch.
Figure 1. Memory task with time gambling.
(A) Self-paced trials are initiated by nose poke at a home port. Two choice port options are cued with a light; four are uncued, invalid options that are not correct. One cued port was visited longer ago in the ongoing visit sequence (remote, the target) than the other (recent, the distractor), and is correct. Memory choice is indicated by nose poke at a port. Time investment, rats gamble on the choice outcome by maintaining the nose-poke position for a self-determined interval. Reward payoff depends, for correct trials only, on gambled time.
(B) Reward amount (blue) is a function of gambled time and is received at the choice port. On error trials (red), no reward is received.
(C) Track geometry showing back (black), home (gray), and choice ports A–F. After leaving choice port, rats receive at back port the same, gamble-dependent reward, completing the trial. Scale bar, 1 m.
(D) Cued ports are always adjacent, producing three pairs on the same branch that differ by a stem (top, stem trials: AB; CD; and EF) and three that differ by both branch and stem (bottom, branch trials: BC; DE; and FA) trials. Scale bar, 1 m.
(E) Distractor ages 1, 2, and 3, with targets older than given distractor, are allowed (yellow).
(F) Example sequence (top to bottom) of cued ports (yellow) and correct (left, blue outlines) or error (right, red outlines) choices for a range of target (bold number) and distractor (number) ages. After each trial, unvisited port ages increment; last-visited port is set to age 1. Note that trials following error could, but did not usually, present again the same ports.
The reward payoff function was designed to incentivize rats to meaningfully gamble time by countering the possible effects of temporal discounting. Like humans, rats show hyperbolic discounting, preferring smaller rewards sooner to larger rewards later,37,38 which could counteract the incentive to bet high. Therefore, we chose a convex reward payoff function, producing super-linearly increasing reward returns for bets up to 2.2 s (R(t) = 0:27e0.34(t+0.8); Figure 1B). To discourage excessively long gambled times, we chose a concave payoff function beyond 2.2 s, producing sub-linearly increasing reward returns R(t)= 2.6×log(0.44 ×(t + 0.8)) that delivered 300 μL of reward for the longest typically observed gambled time of 10 s. The briefest gamble delivers an approximately 60-μL drop (one minim) of reward, ensuring that rats received an appreciable reward for all correct choices.
The task takes place on a large, branched track to test memory for experiences occurring at distinct times and distinct locations (Figures 1C and S1K). To restrict the number of spatial trial types, target and distractor are always adjacent, resulting in six possible spatial pairs (Figure 1D). To probe a range of memory difficulties, distractor-target pairs were randomly selected spanning a range of ages (trials since last visit; Figure 1E). This enabled study of choice accuracy and confidence as a function of how long ago the queried episodes occurred. The distractor age was restricted to 1, 2, or 3 to limit the total number of trial types for sufficiently powered analysis over a range of difficulties. The target age was strictly higher than the distractor age (e.g., for distractor age 1, allowable target ages are 2, 3, 4, etc.). For each rat, the proportion of trials with distractor ages 1, 2, and 3 was approximately one-third each, across and within epochs (Figures S1G–S1J). Importantly, because distractor-target pairs 1–2, 1–3, and 2–3 are allowable, the task cannot be solved by simply remembering and universally avoiding ports aged 1, 2, and 3. After each trial, the choice is appended to the ongoing sequence of port visits within the epoch (Figure 1F). The correct choice on any given trial therefore depends on the history of actual visits, even if they were errors. This prevents high performance accuracy based exclusively on visual memory for the sequence of lit cues.
Rats learn and apply the memory rule with high choice accuracy
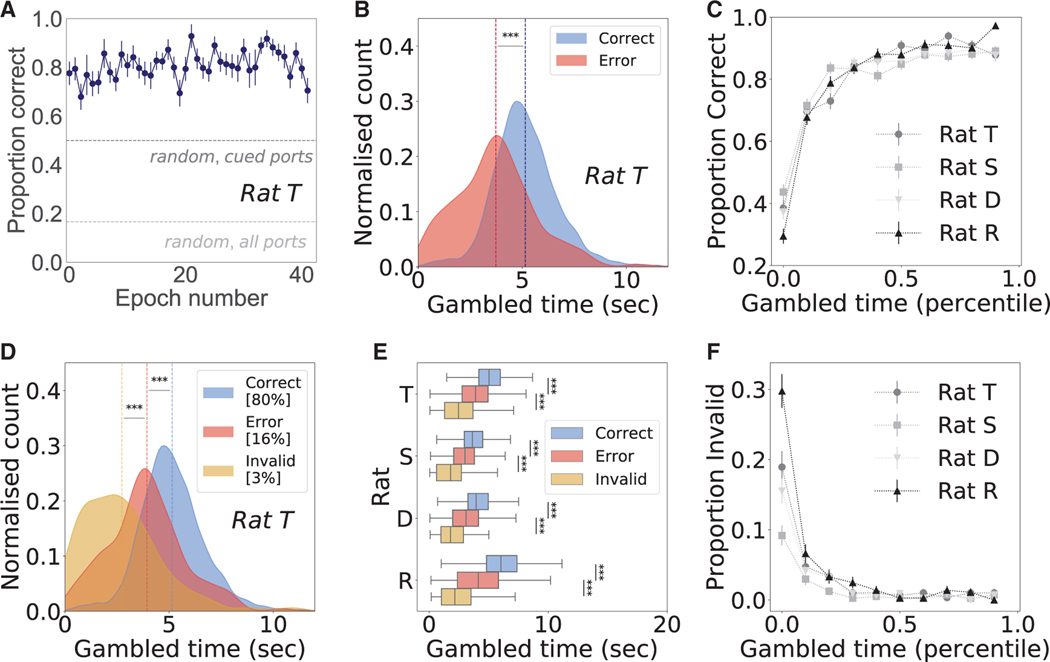
Correct performance across distractor-target pairs requires a comparison of when each location was last visited. This involved a temporal judgement reflecting memory on the timescale of minutes: rats took an average of approximately 45 s to perform a trial, and the previous visits to the target and distractor were often three or more trials in the past. The rats performed 50–100 trials per epoch and approximately 3,000 total trials each, maintaining stable performance accuracy across epochs (STAR Methods). Choice accuracy was 80.2% ± 0.04% (mean ± SEM; n = 192 epochs pooled across 4 rats), substantially higher than what could be achieved by a random decision strategy, either across all six choice ports or between the two cued ports (Figures 2A and S2A–S2C).
Figure 2. Gambled time predicts choice accuracy.
(A) Choice accuracy is stable per epoch, as shown for representative rat T at 80.9% ± 0.9%, significantly above random choice between all six ports (light gray line, 17%) or the two cued ports (dark gray line, 50%).
(B) For representative rat T, average gambled times (dashed vertical lines) were significantly higher for correct (blue) than error choices (red), inclusive over all trials in all epochs (p = 4.8 × 10−69).
(C) For each rat, gambled time (10 percentile bins) predicts choice accuracy, measured as proportion correct. For rats T, S, D, R, n trials = 2,978, 4,111, 4,369, and 3,660.
(D) For representative rat T, average gambled times (dashed vertical lines) were significantly shorter for invalid choices (yellow) than for errors to the cued port (red; p = 2.5 × 10−10). Invalid choices represented the following percentages of total trials: rat T, 3.3%; rat S, 1.7%; rat D, 2.7%; and rat R, 4.6%. Excluding invalid choices, average gambled time on correct trials (blue dashed line) is still significantly longer than for errors (red dashed line; p = 6.6 × 10−48).
(E) For all four rats, gambled times for correct trials were significantly higher than error trials (rat S, p = 4.9 × 10−60; rat D, p = 5.0 × 10−81; rat R, p = 6.5 × 10−118), which were significantly higher than invalid error trials (rat S, p = 2.2 × 10−9; rat D, p = 5.6 × 10−14; rat R, p = 2.2 × 10−17).
(F) Low gambled times (10 percentile bins) predict a higher proportion of invalid trials for all four rats. All error bars represent SEM, and all statistical tests were one-sided rank sum.
See also Figures S2–S4.
Critically, choice accuracy could not be explained by a preference for individual ports or learned port sequences or by any of a variety of alternative strategies (e.g., select the leftmost of the two cued ports; STAR Methods; Figure S3). Nor could accuracy be explained by novelty judgements (i.e., have I been here before?): all arms were familiar to the animals based on extensive prior experience. High performance also required memories for visits to locations, not just memories for when lights at those locations had been lit on previous trials. Specifically, a given port could first be lit as a distractor and then shortly thereafter be lit as a target, and animals’ high performance accuracy reflected their memory of visiting the location, not their memory of when the light at that location was last lit: memory of lit portwould yield 68% correct, significantly lower than the ∼80% correct performance for each (p = 3.1 × 10−23, p = 3.0 × 10−24, p = 7.8 × 10−32, and p = 1.5 × 10−29 for rats T, S, D, and R). High performance further required memory for at least the last three visit locations, because distractor age was restricted to 1, 2, or 3. Additionally, the high levels of correct performance on target-distractor pairs aged 1–2 (correct = 2) and 2–3 (correct = 3) (Figure 2A) demonstrates that animals remembered the actual sequence order of at least the last three visits. Finally, we note that the stable performance accuracy indicates that temporal bets reflect uncertainty regarding the specific choice rather than uncertainty in the rule itself.
Temporal bets reflect decision confidence
Rats consistently gambled more time on choices that turned out to be correct (Figures 2B and S2D–S2F; average area under the curve [AUC] 0.74 ± 0.03 SEM, n = 4 rats; for each rat, one-sided rank-sum test p << 1 × 10−5), pointing to a representation of memory confidence. Similarly, temporal bets predicted overall choice accuracy in a graded manner (Figure 2C). The difference was striking and consistent across rats: on average, temporal bets were 1.45 ± 0.33 s higher for correct than error trials (average ± SEM; n = 4 rats). Temporal bets were also longer for correct trials considering each port pair separately (Figures S2G–S2I; for each rat p << 1 × 10−5, one-sided rank-sum test).
The rats’ behavior on the occasional visits to one of the four uncued, invalid ports (4.6% ± 0.2% of trials; n = 4 rats) also provided evidence for the knowledge of the rule and a metacognitive assessment of memory choice. The low fraction of these choices indicates that the rats had learned that only cued ports yield reward. If rats understood this task contingency, their confidence in receiving reward following an invalid choice should be low; hence, little or no time investment in these choices is optimal. Consistent with this prediction, the time gambled on invalid choices was significantly lower than for error trials (Figures 2D, 2E, and S2J–S2L; average AUC 0.74 ± 0.01 SEM, n = 4 rats; each rat, one-sided rank-sum test p < 1 × 10−5). In addition, the fraction of trials that were invalid was highest for the shortest temporal bets, consistent with the possibility that rats understood these trials as exploratory trials with low expected reward (Figure 2F). Also consistent with this possibility, errors to invalid ports were most common (69.1% ± 3.2%; n = 4 rats) on distractor age 1 trials (Figure S4), which had the highest proportion correct (Figures 3A–3D), indicating a strategy of selective exploration on easy trials. Hence, time bet in invalid trials can be viewed as another form of appropriate metacognitive assessment of memory choice, albeit one that is not formally considered to be decision confidence.39 Excluding invalid errors, temporal bets were still significantly higher for correct than error trials (Figures 2D, 2E, and S2J–S2L; average AUC 0.71 ± 0.02 SEM, n = 4 rats; each rat, one-sided rank-sum test p < 1 × 10−5).
Figure 3. Defining a memory decision variable.
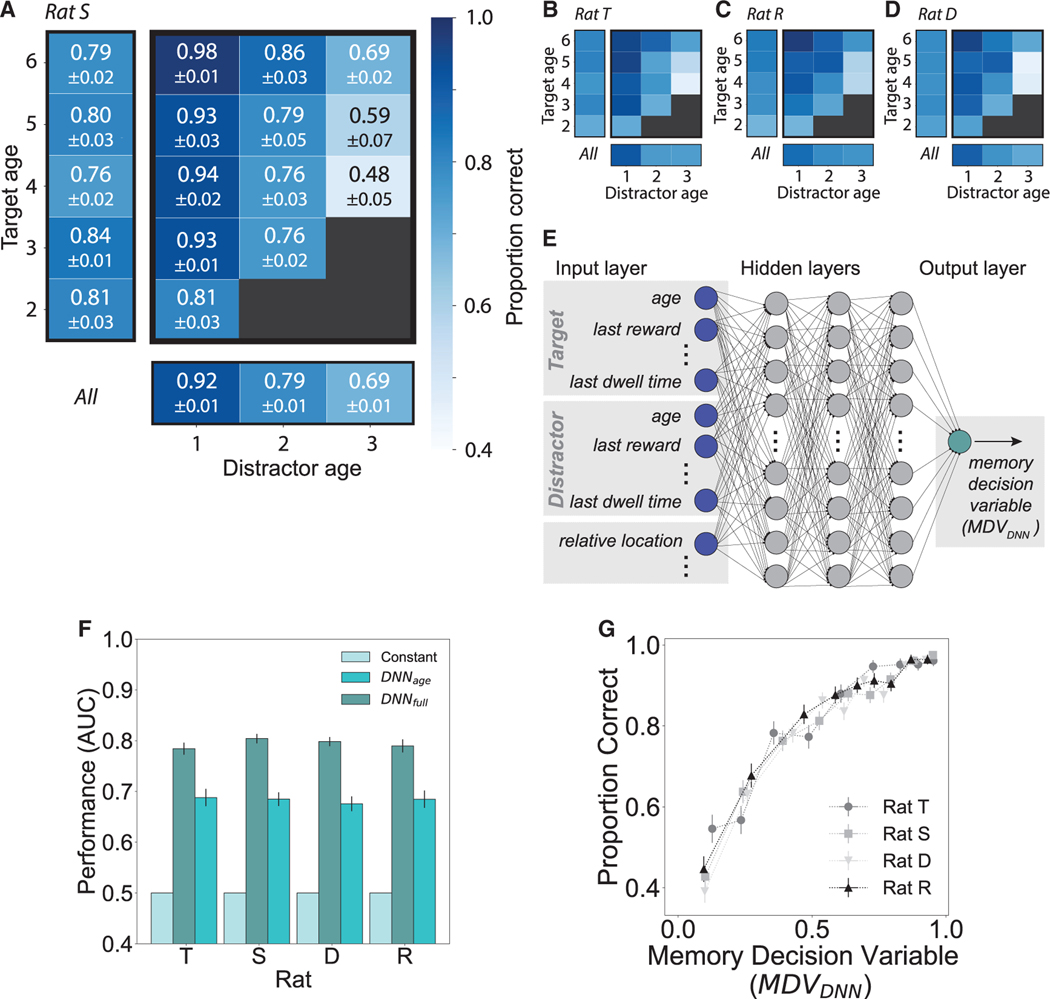
(A–D) Choice accuracy depends on target and distractor ages. For rats S, T, R, and D, the proportion of correct trials decreases with distractor age (columns) and, for a given distractor, increases with target age (rows); marginal performance at left and bottom, respectively. Black boxes indicate trial types not permitted by task logic.
(A) For rat S, proportion correct and SEM are annotated. Target ages below 6 are shown, with n trials: rat S, 2,720; rat T, 2,008; rat R, 2,499; and rat D, 2,881. Color bar (A) applies to all four rats.
(E) A DNN trained by 5-fold cross-validation for each rat takes as input 20 features, a subset of which are depicted in the input layer (left, dark blue). The DNN hasthree hidden layers, each with 32 nodes (gray), and outputs a detection statistic related to the probability a trial will be correct, defined as a memory decision variable (MDVDNN) (green).
(F) Performance (receiver operating characteristic, area under the curve [ROC AUC]) of the DNN trained on the full feature set far exceeded that of a constant model using only the overall proportion correct (constant, cyan), as well as that of a model trained on target and distractor ages only (teal). Error bars = SEM.
(G) For all four rats, a higher MDVDNN predicts a higher proportion of correct choices. Horizontal and vertical error bars = SEM.
As expected from studies in humans and non-human primates,25,40 decision time (here, the elapsed time from nose poke at home to nose poke at choice port) was shorter for correct than error trials for all rats (one-sided rank-sum test p < 1 × 10−5, 0.95, 5.8 × 10−5, and 1.4 × 10−14 for rats T, S, D, and R, respectively). In theory, both confidence and decision time are functions of discriminability, and experimentally, they are both reliably correlated with accuracy.40,41 This raises the question whether reported confidence should be interpreted as a sign of cognitive appraisal of a memory or, alternatively, a “lower level” measurement of choice latency itself, which is a public, external observable.42 We thus asked how well gambled times can be predicted from choice latency. Less than 10% of the variance in gambled time could be explained by choice latency alone (linear regression R2 for rats T, S, D, and R for error trials = 6%, 0.4%, 8%, and 7%; for correct trials = 0.4%, 0.1%, 0.4%, and 0.2%). By contrast, distractor age alone explains approximately three times more of the variance (linear regression R2 for rats T, S, D, and R of 20%, 10%, 20%, and 30%). Moreover, when we considered choices and gambles for specific choice latencies, long gambled times were predictive of high accuracy across a wide range of choice latencies (for each rat, gambles were longer on correct trials than error trials, with p < 1 × 10−5 for below-median latency and p = 1 × 10−30 for above-median latency; one-sided rank sum tests). Together, these results demonstrate that rats can predict choice outcome, consistent with a computation of confidence in memories.
Choice accuracy depends on memory age and discriminability
What information do rats use to predict choice outcome? By design, trials spanned a range of difficulties determined by distractor and target ages. If choices are based on memory, they should be progressively harder for older targets and distractors.43 Choices should also be harder for lesser age differences between target and distractor, as episodes that occur closer together in time are more likely to be confused.44
Both of these predictions proved to be correct. The average choice accuracies for distractor ages 1, 2, and 3, respectively, were 89.5% ± 0.5%, 77.7% ± 0.7%, and 72.7% ± 0.7% (n = 192 epochs pooled from 4 rats; Figures 3A–3D). In addition, choice accuracy increased with the age difference between distractor and target when controlling for distractor age (Figures 3A–3D).
Constructing a synthetic decision variable
Together, these results suggest a memory confidence computation. To evaluate this possibility, we aimed to construct a model of memory confidence that would accurately predict confidence and temporal bets as a function of memory discriminability. We therefore had two goals: first, to characterize the memory discriminability axis for these memory confidence signatures and, second, to build a model of memory dynamics as a function of discriminability.
The first step, corresponding to a long-standing challenge in the study of memory confidence, was to identify an appropriate memory discriminability axis, or decision confidence variable (P. Masset and A. Kepecs, 2017, Conf. Cogn. Comput. Neurosci., conference). In studies of perceptual confidence, the relevant decision variable is typically defined by external task parameters (e.g., motion coherence), where a simple monotonic relationship between the task parameter and task difficulty can be demonstrated.17 Alternatively, in the context of value-based decisions, the decision variable is often inferred using a model-based approach that posits a concrete computational model to explain choice behavior.45 Here, however, multiple task parameters could potentially influence the rats’ choices, and we are not aware of an existing computational model that could be used to fit the choice behavior.
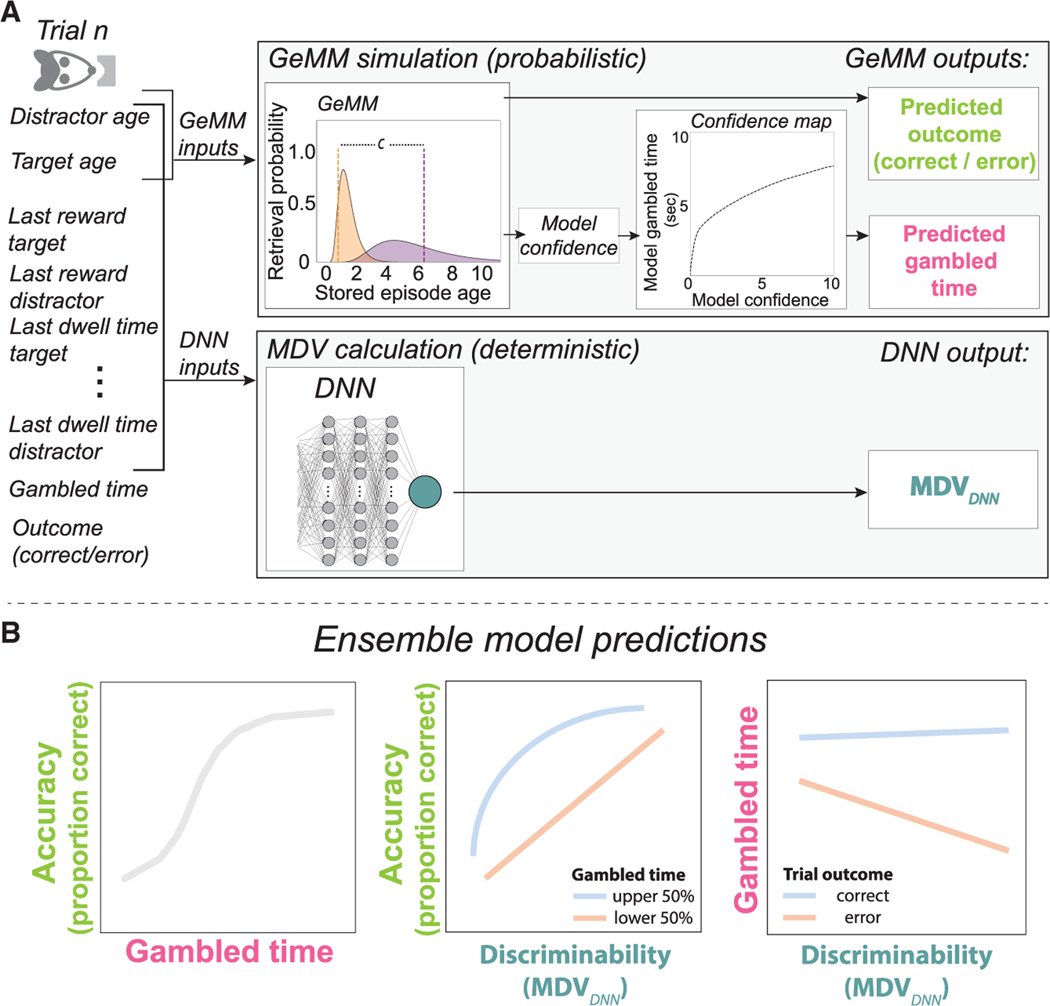
We therefore sought a model-agnostic approach to derive a synthetic memory decision variable (MDV) that is a scalar summary of the available information that rats could potentially access from memory, where higher values of the MDV predict higher accuracy. We trained a deep neural network (DNN) to predict rat choice per trial based on an exhaustive 20-feature set (Figure 3E; STAR Methods). We included only those features accessible in memory, not directly observable on the given trial (e.g., previous reward amounts, but not current port identities); hence, a memory decision variable. A DNN in particular enabled the agnostic approach we sought: because it is robust to inclusion of redundant and correlated features, an intuitive or model-based feature selection step was not necessary; likewise, selection of interaction terms was not required.
Eighteen of the 20 features were, for each of target and distractor, age in units of trials and time; their last, maximum, and cumulative delivered reward amounts; time since last reward; last and cumulative dwell times; and number of trials since any part of its trajectory was last traversed. The final two features were, for the target and distractor, their spatial and temporal (target age – distractor age) trial types. The DNN, trained by 5-fold cross-validation for each rat, output a single value, a detection statistic between 0 and 1 that corresponds to a predicted probability that the trial will be correct. As expected, this model outperformed both a model that learned only the overall proportion of correct trials and a model trained on memory age alone (Figure 3F). We reasoned that a higher DNN-predicted probability of correct output corresponded to lower trial difficulty, equivalent—because the input features were those available in memory—to memory discriminability. Thus, we defined the output of the DNN trained on the full feature set as the MDVDNN, with higher values corresponding to memory discriminability and predicting more accurate recall (Figure 3G). We note that any monotonic function of the inferred MDV will also have the same properties; hence, it is not unique.
A generative memory model (GeMM)
Identifying a memory discriminability axis enabled us to move to the second step of building a model of episode memory dynamics. Our goal was to build a model of memory retrieval, decision, and confidence, based on the MDV as an index of trial difficulty, with parameters fit to decision data, that would generate testable predictions for confidence and its underlying mechanisms. We focused on a subset of parameters and leveraged an understanding of memory phenomena to develop a GeMM that could predict choice and confidence (gambled time) given an underlying representation of memory.
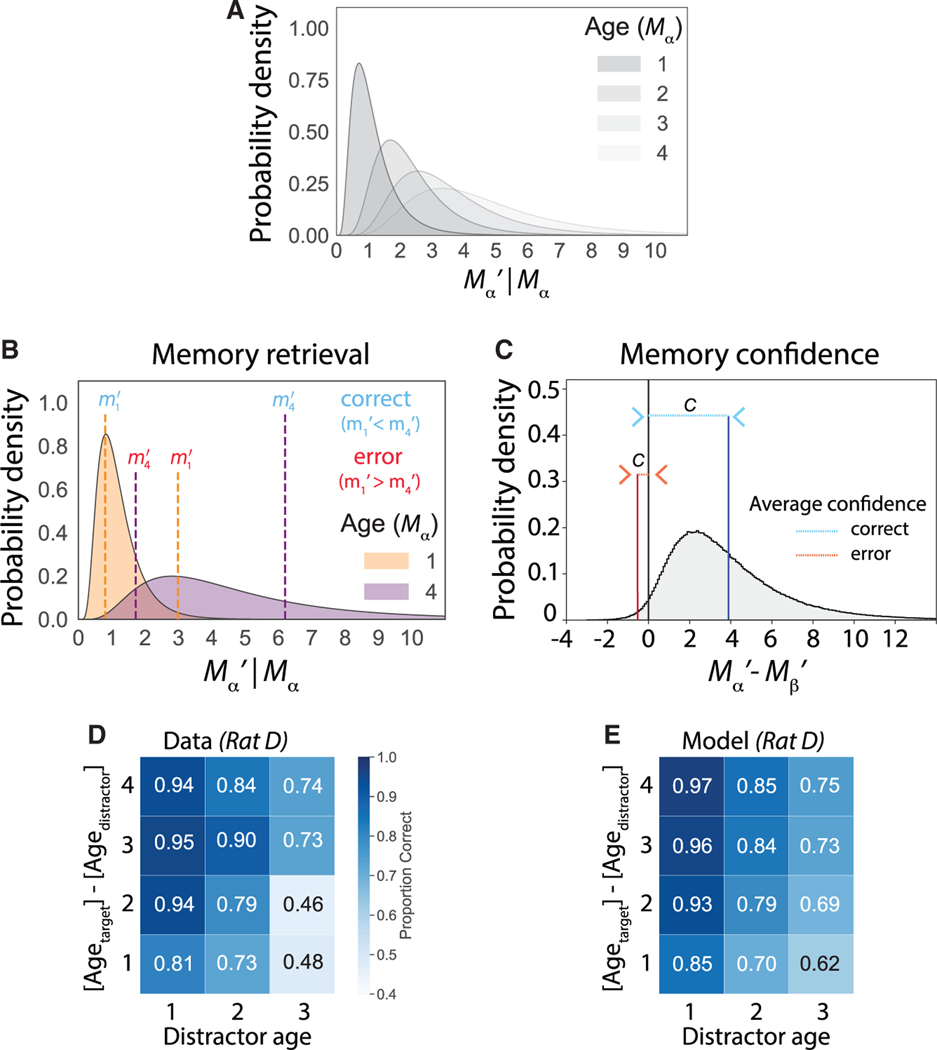
We focused on memory age, an interpretable and established determinant of memorability that, in our task, independently influenced choice accuracy. We represented memory age as a random variable with probability distribution centered on a mental timeline at its time of occurrence. Realizations of this random variable represent specific memory retrievals, corresponding to estimates of how long ago the experience occurred. The distribution’s variance represents mnemonic noise from errors in encoding, consolidation, and/or retrieval. We postulated that (1) these errors accumulate over time such that the memory is less precise, reflected in an increasing variance over time; (2) the distribution should always take on positive values, as it is not possible to mistakenly retrieve an episode from memory as having occurred in the future; and (3) an episode should never be completely forgotten.
Given those constraints, we developed a mathematical formulation of the model. We define Mα as the actual number of trials since the last visit to port α (i.e., the age of that port). We define Mα’ as the subject’s recollection of the port age. Requirements (2) and (3) together specify an asymmetric noise profile with greater spread into preceding than subsequent times. We therefore model Mα’|Mα = mα as a lognormal random variable (uppercase symbols denote random variables, while lowercase symbols represent realizations of those random variables). To satisfy requirement (1), the family of lognormal distributions defined by mα = 1,2,...... nelapsed trials represents the memory’s evolution over time (Figure 4A). This family of lognormal distributions has a time-dependent mean a0mα and a time-dependent standard deviation σ0(1 + a1mα + a2mα2). We parametrized memory age by elapsed trials and not elapsed clock time, as the number of elapsed trials was a better predictor of choice outcome (Figure S5; STAR Methods). The separation parameter a0 sets the unit increment on the mental timeline that corresponds to one real-life trial, the standard deviation σ0 sets the baseline precision of each memory distribution, and the coefficients a1 and a2 set the rate of change for the standard deviation as a second-order polynomial function of its age mα, giving it flexibility to increase or decrease as a function of time, though our hypothesis was that it should strictly increase. For a given trial, two ports α and β are cued, with Mα > Mβ corresponding to target and distractor, respectively. Choice (Figure 4B) is determined by the sign of the difference mα’ – mβ’ and confidence by its magnitude |mα’ – mβ’| (Figure 4C).
Figure 4. The generative memory model (GeMM).
(A) Family of lognormal distributions representing the probability density of recalled episode ages Mα’|Mα = mα as the true age mα increments from 1 to 4 for port α. Uppercase symbols denote random variables (e.g., Mα’ and Mα) while lowercase symbols represent realizations of those random variables (e.g., mα’ and mα).
(B) Example trial has target port with age mα = 4 and distractor port with age mβ = 1. A correct (blue) and error (red) realization of the recalled ages for the two ports is shown as vertical dashed lines for the target (purple) and distractor (orange) at values mα’ and mβ’, respectively.
(C) The probability density of Mα’ – Mβ’ given Mα and Mβ; the area to the right of 0 is the proportion correct for this target-distractor age pair. Confidence (c) is computed as | mα’ – mβ’ |, and the average confidence is indicated for correct (blue) and error (red) trials.
(D) Observed choice accuracy across 12 specifiedtrial types, excluding invalid choices.
(E) Model-predicted choice accuracy across 12 specified trial types, excluding invalid choices. Representative rat D is used for all plots. For rat D, the GeMM uses fitted parameters a0 = 1.20, a1 = 0.32, a2 = 0.38, and σ0 = 0.38 for a lognormal distribution with mean a0mα and standard deviation σ0(1 + a1mα + a2mα2):Positive a1 and a2 define distributions with increasing variance with elapsed trials; σ0 << 1 sets a low overlap between neighboring densities, consistent with high observed choice accuracy.
See also Figures S5 and S6.
Given that model, we iteratively fit the GeMM parameters for each rat to choice accuracy (Figure 4D) across trial types based on a χ2 metric (STAR Methods). Based on that fit to memory accuracy (Figures 4E, S6A–S6C, S6E–S6G, S6I–S6K, and S6M–S6O), we then generated predictions for memory confidence.
Embedding the GeMM in data enables prediction of choice and confidence as a function of the MDV
Finally, we combined the MDV and the GeMM to produce a series of confidence tuning curves22 to which we could compare behavioral data (Figure 5). Generating GeMM predictions as a function of the MDVDNN enabled the best possible estimates and ensured our predictions spanned the full range of per-trial memory discriminability. First, for each trial, we input target and distractor age to the previously fitted GeMM to generate a distribution of simulated trial outcomes (correct versus error) and confidence values (Figure 5A; GeMM simulation). Next, we converted these GeMM-predicted confidence values to gambled times by mapping, for each rat, the inverse cumulative distribution function (CDF) of the observed gambled time distribution (Figures S6D, S6H, S6L, and S6P; STAR Methods). Note that this mapping has no free parameters. Further, it only considers the full gambled time distribution, not individual trials; it does not separately map correct versus error trials or any other subset of the data; and it does not make assumptions about the match between the mappings of trial outcome to confidence for the model and data. Conceptually, this procedure captures the economic aspect of waiting based on the model, that is, how long the animal is willing to wait given a specific degree of confidence.
Figure 5. Ensemble model.
(A) For each trial in data, task features (left) include the 20 features used to calculate the MDVDNN, gambled time, and trial outcome. A subset of these, the distractor age and target age, are input to the fitted GeMM (top panel) to simulate two GeMM outputs: a predicted trial outcome (correct or error; lime) and a predicted confidence value, which is converted by a monotonic mapping function, shown for representative rat T, to predicted gambled time (pink). The process is repeated n = 10 times per trial in data to produce a distribution of model-simulated gambled times per observed gambled time, all with the same MDVDNN (bottom panel). The MDVDNN is calculated from the 20 input features to the trained DNN (green).
(B) The ensemble model makes three signature predictions of memory confidence based on accuracy (lime), gambled time (pink), and the MDVDNN (green), as a memory discriminability axis, to which trends in data can be compared (here, representative schematics). Middle: blue represents upper half of gambled times, and red represents lower half of gambled times. Right: blue represents correct trials, and red represents error trials.
Every one of these simulated trials has the same MDVDNN, directly computed as the DNN output from the 20 input features of the data trial (Figure 5A; MDV calculation). Together, this procedure generated for each trial, (1) a predicted outcome (correct versus error), (2) a predicted gambled time, and (3) a calculated MDVDNN, which we used to generate three nominal tuning curves for memory confidence based on memory discriminability, temporal bets, and choice accuracy (Figure 5B). In effect, this procedure generates GeMM-predicted trends for gambled time that are based on all 20 features of the MDVDNN: although the GeMM only explicitly takes as input distractor and target ages, the GeMM-simulated trials inherit the 20 MDVDNN inputs from the data trial they are based on, thereby preserving the covariance structure of the data (i.e., they are embedded in the data, as for hybrid data-simulation models in collider physics).46
The GeMM accurately predicts memory confidence behavior
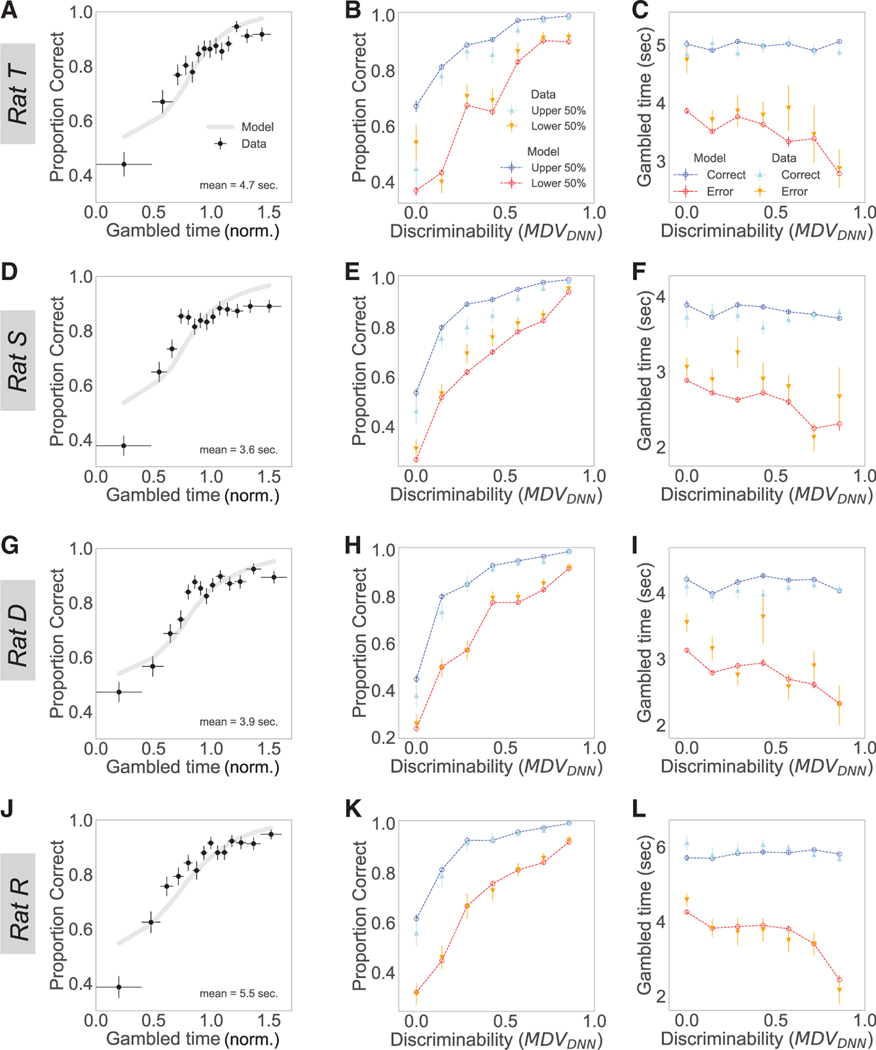
We observed a striking match between GeMM predictions and observed behavior. Because all the assumptions of statistical decision confidence also apply to our memory confidence task, we could quantitatively assess the relationship of behavioral confidence reports and GeMM-derived confidence levels by focusing on the established set of comparisons to evaluate confidence as a decision variable.16 First, a calibration curve makes the intuitive prediction that trials with longer gambled times should have higher choice accuracy (Figures 6A, 6D, 6G, and 6J). Consistent with this prediction, accuracy as a function of gambled time rises for both the model and the data. Second, for any given choice difficulty level (memory discriminability), accuracy should be higher on trials with higher confidence, where more time was gambled. We tested this prediction using a conditioned psychometric curve that divides the data into high and low predicted (GeMM) or actual (data) gambled times. We found that longer gambled times predict higher choice accuracy over a range of memorability for both data and the model (Figures 6B, 6E, 6H, and 6K). Third, for any given trial difficulty level, gambled times should be higher for correct as compared to error trials. Constructing this “vevaiometric” curve revealed consistently higher gambles for correct than error trials over a range of memory discriminabilities in both the model and data (Figures 6C, 6F, 6I, and 6L). For all three signatures and all four rats, the majority of the data points are within two standard deviations of the model, indicating surprisingly accurate predictions given the small number of model parameters and the fact that the model was fit only to choice behavior, not to gambled times. This analysis also revealed evidence of an intuitive signature of confidence consistent with the standard model of perceptual decision confidence: the difference in gambled time between correct and error trials is greater for more memorable trials.
Figure 6. The GeMM predicts trends in memory discriminability, choice, and gambled times in data.
Each plot shows GeMM predictions (lines) with data (points) overlaid.
(A, D, G, and J) GeMM-predicted calibration curves (gray lines) for accuracy as a function of mean-normalized gambled time compared to data (black points), for the lowest 14 of n = 15 percentile bins. Horizontal bars represent bin widths.
(B, E, H, and K) Conditioned psychometric curve predicted by the GeMM shows proportion correct for upper half (dark blue) versus lower half (red) of gambled times compared to proportion correct in upper half (light blue) versus lower half (orange) in data, each in n = 7 percentile bins.
(C, F, I, and L) Vevaiometric curve depicts gambled times predicted by the GeMM for correct (dark blue) and error (red) trials compared to correct (light blue) and error (orange) in data, each in n = 7 percentile bins. Vertical error bars represent SEM for all plots.
DISCUSSION
We studied memory-based choice and confidence together, using a novel form of confidence report, time gambling, which was available on every trial. Critically, we found that temporal bets predicted choice accuracy in a graded manner. The task also allowed us to address the long-standing challenge of defining a MDV: we trained a DNN on an exhaustive list of task observables to predict choice accuracy and interpreted its output detection statistic as defining a synthetic memory difficulty axis or decision variable, the MDVDNN. Next, we developed a GeMM that posited the age of memories is represented as a lognormal distribution that evolves with experiences. We integrated the GeMM and MDVDNN in a final model that used the MDVDNN to assign a difficulty to each trial and found that, across the range of difficulties, GeMM predictions recapitulated choice and confidence behaviors. These findings are consistent with memory confidence in rats and introduce a simple, interpretable model of the underlying computation.
Studies of learning and memory in animals have typically focused on measures of memory accuracy (e.g., time spent freezing in a conditioned context).47 Our results indicate that rats can not only execute behaviors based on representations of multiple past experiences but also evaluate confidence in the content, storage, retrieval, and use of those memories. Rats gambled more time on trials when they had made a correct decision, even though the outcome of the trial was not revealed until after the gambling period ended. That is, when the rats were more confident in a decision, they waited longer in the port, forgoing a smaller, earlier reward in favor of a larger, later reward (correct trials average ∼1.5 s longer than error trials or 0.8 standard deviations of the gambled time distribution).
Rarely, rats selected uncued ports, which were never rewarded (invalid choices), and when they did so, they gambled even less than on errors to cued ports, also consistent with an internal representation of confidence. Invalid choices most often occurred on easy trials (distractor age = 1), and overall, the lowest gambled times correspond to below-chance accuracy, attributable to a high proportion of invalid trials. This is suggestive of an exploration strategy where the true answer is known and “throwing” a trial can therefore ascertain that the optimal strategy is unchanged. Together, these results provide strong evidence of an ability to compute and act on confidence in a memory-guided decision in a non-primate animal. The present study extends the one previous study reporting a form of metacognition in the rat,36 with a novel, graded confidence report; collection of thousands of trials in neural-recording-enabled rats; and a quantitative model of memory confidence.
Evidence for memory confidence and metacognition in rats
Our findings specifically indicate this ability for memories related to where the subject was on the previous three or more trials and at what relative order in time. This memory requirement is similar to that of N-back tasks, used in humans to study “working” memory,48 typically defined as memory on seconds to minutes timescale.49 Although our task does not distinguish a relative familiarity mechanism from a recollective one,50 the recency judgments made by rats cannot be explained by access merely to whether a specific experience is novel or not. As such, its memory requirement differs from the visual recognition memory tasks that have established memory confidence in human and non-human primates,25–28 which require such an old or new judgment but do not require that the subject remember where or specifically when the item was seen. Finally, animals were required to recall an element of “what” had occurred and distinguish whether they had previously seen a visual cue (port light) versus visited its location.
Tasks that require elements of “what, where, and when” are often referred to as episodic or episodic-like.51 Here, we avoid those terms for lack of a precise definition that would allow determination of whether “episodic” is appropriate for any given non-human task. We note that, in general, it is not clear specifically which mechanism(s) rats use for temporal context or whether they qualify as episodic (when).52,53 Regardless, the GeMM operates on a memory decision variable that defines memories for episodes on a timeline and how they evolve over time and thus has the potential to describe memory dynamics in humans and non-human animals alike. As is the case for all tasks, multiple memory systems (procedural and semantic) are also required.
Our task uses a graded confidence report, where previous studies of memory confidence, in monkeys12 and rats,36 used decline option tasks. This class of task poses delayed match-to-sample decisions between target, distractor, and an additional option to decline the decision and earn a lesser reward. The claim that these tasks probe memory confidence rests on two response patterns: (1) the rate of decline choices increases with difficulty and (2) choice accuracy is lower on forced choice trials compared with freely chosen memory tests. However, these choice patterns can be explained by more elementary processes than a confidence computation.6,42,54 Simple reinforcement learning mechanisms can explain why decline choices track difficulty, for example.55 Similarly, accuracy difference between forced and free choices can arise when animals have access to their own motivation or engagement levels, with high motivation and engagement predicting lower declines and higher accuracy.42,56
These interpretational challenges, and similar challenges associated with other tasks,35,57,58 highlight the importance of specifying an explicit computational model, determining whether that model can accurately describe the data, and testing other possible explanations. Thus, an important contribution of our study is providing a new behavioral task design and a model of memory determining choice and confidence. The same framework is also applicable to human behavior and may therefore allow us to place memory confidence on the same footing across species.
A model of memory-guided choice and confidence
To build the model, we first used the behavioral data to infer a decision variable and then devised a generative model, fit its parameters to choice behavior, and generated confidence predictions to test against data. To deduce the memory decision variable, we used a model-agnostic, data-driven approach based on all variables potentially available to the rats in memory. Crucially, in contrast to perceptual59 or value-based60 tasks where the experimenter controls the difficulty of each trial, here, it was unknown how the various elements of each memory trial would interact to define the difficulty. Our DNN reached a high degree of prediction accuracy (∼80%), outperforming a network based on port age alone. Such an approach may be broadly useful when trial difficulty cannot be established a priori.
The nature of the DNN precluded an immediate understanding of how memory confidence might be computed. We thus focused, in the second, modeling step, on a subset of parameters, specifically target and distractor ages, to design a model to predict choice and memory confidence. Under the GeMM, a few parameters govern the evolution of the underlying lognormal distributions based on known features of memory processes. Each memory is represented at the time of encoding as a delta function and therefore does not include perceptual noise. At later time points, its variance represents mnemonic noise from processes including encoding. The GeMM parameters were fit to choice data for each rat and used to predict memory confidence. They define an increasing standard deviation with age, consistent with the understanding that memories become less precise over time and that memory retrieval for consolidation or use precipitates lability.61
Although the GeMM describes memory dynamics as a function of age only, the other MDVDNN features are accounted for by its embedding in the data in the full ensemble model. An alternative approach to generating confidence predictions from the GeMM would be to use the MDVDNN as a decision axis, assume that on each trial the memory decision and memory confidence are both determined based on a simple noise profile (e.g., Gaussian noise with fixed variance),50,62 and from this predict gambled time.18,22 Such a model would predict that confidence increases for correct trials and decreases for error trials as a function of discriminability.16 However, in our data, gambled times do not increase with the ease of the decision; our model captures that feature with an asymmetric noise profile.
The GeMM builds on previous models related to signal detection and memory,63–67 including strength theory63 and episodic trace models.65 It defines confidence as the absolute difference between two samples, or a balance of evidence,68 a model that has been successfully applied to confidence in perception14 and memory.25 This memory decision variable could be interpreted as the strength of association between memory items in a list, a key variable in the influential temporal context model of memory.66,67 As in models of decision making based on diffusion to a bound,40 the GeMM could support sequential sampling from memory distributions when multiple internal retrieval events are used to estimate memory age. Indeed, it has been proposed that decision time in memory-based decisions, as in perceptual discrimination, may also be the result of sequential sampling, potentially in the form of multiple memory retrievals.69–71 Recent reinforcement-learning (RL) models incorporate sampling from memory to explain choice,72–74 using a recency weighting coefficient that down weights older experiences to reflect possible environmental change. Our results suggest that incorporating a factor reflective of the perceived reliability of retrieved memories (i.e., memory confidence) into models of value-based decision making might increase their accuracy.
The importance of understanding memory confidence
Finally, we highlight that aberrant confidence in perceptions has been proposed to account for a variety of psychiatric symptoms.75–77 Distortions in memory confidence could account for additional dimensions of psychiatric pathology. Although psychological studies indicate memory confidence deficits as driving checking behaviors in obsessive compulsive disorder and a risk factor for developing schizophrenia,78 the study of memory confidence has lagged behind perceptual confidence in terms of behavioral tasks for animals and theoretical frameworks for quantifying memory-guided confidence reports. A deeper understanding of memory confidence has potentially broad applications, from judging the credibility of eyewitness testimony (e.g., in the 2018 Kavanaugh hearings)24 to quantifying distorted beliefs in mental illness.
STAR⋆METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Loren Frank (loren@phy.ucsf.edu).
Materials availability
This study did not generate new unique reagents.
Data and code availability
All original code has been deposited at GitHub: https://github.com/hrjoo/TotalRecall and is publicly available as of the date of publication. All original data have been deposited at Zenodo: https://doi.org/10.5281/zenodo.5123545 and are publicly available as of the date of publication. DOIs are listed in the Key resources table. DOIs are listed in the key resources table. Any additional information required to reanalyze the data reported in this paper will be made available upon reasonable request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental models: organisms/strains | ||
| Rattus norvegicus: Crl:LE strain code 006: Long Evans rats | Charles River Laboratories | RRID: RGD_2308852 |
| Deposited data | ||
| Raw data | This paper | https://doi.org/10.5281/zenodo.5123545 |
| Software and algorithms | ||
| Code repository for this paper | This paper | https://github.com/hrjoo/TotalRecall |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
All procedures followed the guidelines from the University of California San Francisco Institutional Animal Care and Use Committee and US National Institutes of Health. Male Long-Evans hooded rats, age 1–2 years at the time of data collection, were trained to perform a memory task with time gambling for liquid reward. Rats were housed in pairs during training (stages I – III, see below) and singly housed during data collection (stage IV).
METHOD DETAILS
Behavioral training and task
Behavioral testing was controlled by custom software written in Python using data acquisition hardware (Trodes ECU, SpikeGadgets LLC) to record rat nose-pokes and un-pokes at the ports and to control reward delivery.
Habituation
Four cohorts of experimental behavior-naive Long Evans male rats (3–4 months old, 450–600 g; n = 8 rats in cohorts 1, 3, and 4; n = 6 rats in cohort 2) were habituated to daily handling for a week and to hand-delivered liquid food reward (evaporated milk plus 5 percent sucrose) from a syringe in the home cage for three days.
Stage I: Raised linear track plus delayed reward
Animals were then food deprived to 85–90 percent of their baseline weight and pre-trained on a raised linear track for 3–4 days, 2–3 epochs/day, 10 mins/epoch (Figure S1A). A port was located at each end of the track, equipped with an LED light and an IR beam, to detect entry and exit from the port. Each port could automatically deliver reward, which was available for only a specified length of time as it flowed through the port at a rate of 0.17mL/sec to a drainage outlet and did not remain in the port. A variable delay τ between nose-poke and reward delivery was drawn from an exponential distribution, which was gradually incremented from τ = 0.2 – 0.5 seconds to τ = 1 – 8 seconds. Only one port was cued by a light on each trial. After nose-poke detection, the light went out and reward was delivered. The two ports were lit alternatingly over the course of the epoch. Rats learned to run back and forth on the track to visit the currently lit port and to wait for the delayed reward. From each cohort, rats with the highest accuracy and speed were selected for training on the memory confidence task (from cohort 1, n = 2 rats; from cohort 2, n = 3 rats; from cohort 3, n = 2 rats, from cohort 4, n = 5 rats).
Stage II: Full memory confidence task sequence with single light cue and experimenter-delayed reward
In Stage II, rats learned the basic task structure (Figures S1B–S1E), but with only one cue lit per trial and a pseudo-gambled time determined by the experimenter. The track has eight ports in total: one home port at the center, one back port, six choice ports at each end of six branches. As in Stage I, each port could be cued with a light and deliver liquid milk reward. On each day, data was collected over 1–3 periods, called epochs, between which the animal was returned to a sleep box or home cage. Each epoch was of a fixed length per animal, during which trials were self-paced. The lit cue corresponded to the target selected by the same code as in the final task logic; lighting of the distractor port was suppressed. The sequence of visits within a trial was: home port light on; rat pokes at home port for a small fixed reward (350 ms); home port light off; after a variable cue delay, one choice port light on; rat pokes lit choice port; choice port light off and port delivers initial reward (350 ms) and, after a variable, experimenter-controlled reward delay, a wait-dependent reward; back port light on; rat pokes back port; back port light off and port delivers back reward. Choice accuracy was measured as the percentage of trials for which the rat visited the lit choice well.
The cue delay was introduced to jitter the events of each trial relative to every other trial, to control for across-trial temporal correlations between behavioral and neural events. To train rats to wait for the cue lights to come on, the cue delay was gradually increased from range [0.2, 0.5] to [0.5, 2.0] seconds. Initially, the back port delivered the same reward amount as the wait-dependent reward regardless of trial outcome, which encouraged the animals to solidify knowledge of the port visit sequence (i.e., to not skip the back port). After three epochs, back port reward was only delivered on correct trials. The reward delay was determined by sampling from an exponential distribution with rate parameter λ = 1/2, accepting only samples that were between 1–3 at the start of this training phase and 2–10 by the end, with a wait-dependent reward amount that increased accordingly, to allow rats to learn that a longer period spent nose-poked in the port would result in a larger reward. At this stage, three rats were excluded from cohort 4 for relatively low accuracy and trial counts.
For rats that were consistently performing at above 80 percent choice accuracy and waiting for the full reward delay, the initial reward was omitted. Once rats were able to wait for the majority of the reward delays (6–10 s), the switch was made to gambling logic. In the gambling logic of the final task, rats voluntarily reported the time they were willing to wait for a potential reward. The gambled time began at the time of nose-poke in the choice port and ended when rats withdrew from the port. Nose-poke withdrawal was detected with a ‘grace period’ (800 ms for rats T, S, D; 700ms for rat R in final behavior, calibrated based on how quickly each rat moved) to allow for small head movements during the gambling period: rats were only declared to have ended the gambling period after a grace period had passed between the port’s IR beam re-forming (un-poke) and being broken again (re-poke).
Stage III: Binary choice
After gambled times were observed to be stable across at least three epochs, the distractor cue was introduced alongside the target cue, starting with distractor age 1 (Figure S1F). Distractors age 2 and 3 were introduced when choice accuracy was approximately 80 percent and stable. At this training stage, two rats were excluded from cohort 2 for relatively low accuracy or insufficient body weight (Figure S1A).
Neurosurgical device implantation and recovery
Rats (n = 7) with satisfactory performance, trial count, and body weight were implanted with neural recording devices. Intraoperative and post-operative mortalities (n = 3) resulted in a final cohort (n = 4) for behavioral data collection (Figure S1A).
Stage IV: Data collection
Approximately 3000 – 4000 trials were collected from each of four rats following neural recording device implantation. Each rat had a typical length of time for which he would continuously perform the task, after which he would occasionally perform trials but otherwise sleep or lean off the edge of the track and attempt to eat the milk tubes or cables, and this determined the epoch length. Epochs shorter than 20 minutes (Rat T, n = 5 excluded epochs), 40 minutes (Rat S, n = 0 excluded epochs, and Rat D, n = 2 excluded epochs) or 45 minutes (Rat R, n = 2 excluded epochs) were excluded from final analyses. This resulted in the following epoch and trial counts: From rat T, 2978 trials over 42 epochs; from rat S, 4111 trials over 40 epochs; from rat D, 4369 trials over 61 epochs; from rat R, 3660 trials over 49 epochs. Typically rats ran an average of 350–400 m per day (the human equivalent of approximately five miles) and consumed 50 mL of sweetened evaporated milk.
Parameter setting: distractor and target selection
The selection of distractor and target was random with temporal weighting, to guarantee that trials with distractor ages 1, 2, and 3 were evenly distributed throughout the epoch. This also prevented success of the alternative strategy to choose the least recently lit port, rather than the true rule, to choose the least recently visited, by increasing the number of trials for which a port was lit but not visited. During an initialization period, the rat was cued to visit each of the six choice ports in a randomly generated order, establishing a history of visits. After every port was visited at least once, the logic used for selection of the two cued ports on each trial was: from the list of possible port pairs with their ages, for example, the top row of Figure 1F, [AB(4,5), BC(5,3), CD(3,1), DE(1,6), EF(6,2), FA(2,4)], select candidate pairs for which at least one of the ports has an allowable distractor age (1, 2, or 3), which are [BC(5,3), CD(3,1), DE(1,6), EF(6,2), FA(2,4)] here. If there is more than one candidate pair in this list, remove from it the candidate pairs with distractor ages equal to those presented on the last trial, the penultimate trial, and the trial before that, in that order, until candidate pairs with only one distractor age remain. If there is only one candidate pair in this set, select it as the presented pair. If there is more than one candidate pair in this set, randomly select between them with equal probability. For example, if the last three trials were distractor ages 1, 2, 3 (N.B.: regardless of which ports these distractor ages corresponded to), then on the upcoming trial, the candidate pair(s) with distractor age 3, [BC(5,3)], would be removed first, then the candidate pair(s) with distractor age 2, [EF(6,2), FA(2,4)]. The candidate pair(s) with distractor age 1, [CD(3,1), DE(1,6)], would be selected; if there were more than one candidate pair with distractor age 1 remaining, the cued pair would be selected randomly from this set. On every trial, there will necessarily be a candidate pair with distractor age 1. There will not, however, be candidate pairs with distractor ages 2 and 3 on every trial; this can occur in the case of revisits, where the port with distractor age 3 is the same as the port with distractor age 1 (or the age 2 port = the age 1 port, or the age 3 port = the age 2 port = the age 1 port). This selection algorithm has the effect of sampling evenly across distractor types, resulting in approximately 1/3 each per epoch and preventing an alternation sequence from developing.
We verified by simulation (for each rat, n = 100 synthetic experiments, where each experiment matched the number of epochs and trials per epoch in experimental data) that with this port selection rule, an alternative strategy using memory of when the ports were last lit would yield a maximum average performance accuracy of 68%. Rats that achieved stable performance accuracy higher than this could not be relying on a visual working memory of the light cues alone (see Evaluation of alternative strategies below).
Parameter setting: reward function
The reward function was designed to counter the potential effects of temporal discounting on gambled times. The expected effect of such temporal discounting is that rats would reduce their gambled times to receive a smaller reward sooner rather than waiting for a larger one. This effect may be greater on trials where they are highly confident in their memories and choice, as the option of a smaller reward sooner is more certain. This effect could obscure the difference between gambled times on correct and error trials by inducing a left shift of gambled times on correct trials. To counter this possible effect, the reward amount delivered was a piecewise function of gambled time with a relatively low derivative for the first 2.2 s and a relatively high derivative after 2.2 s (Figure 1B). On correct trials, for investments less than 2.2 s, the length of time for which a sweetened evaporated milk reward was delivered at a constant rate of 0.17 mL/sec was given by R = 0:27e0.34(t+0.8); for investments greater than 2.2 s, R = 2.6×log(0:44 ×(t + 0.8)). A ten-second wait, for example, will yield a four-second reward. The desired effect was to bias the rat toward longer gambled times on trials for which he would already have waited at least 2.2 s, as he could double the reward amount by waiting just one second longer. If rats were able to access memory confidence, these longer waits should be more common for correct trials, and the reward function could help resolve them from error trials. The non-zero intercept ensured that the rat received an appreciable reward amount (350 ms, 60 mL, equal to approximately one drop, or minim) even for very short waits on correct trials, preventing the development of uncertainty in the memory rule itself following correct trials that resulted in zero reward due to short gambled times. To ensure a high enough number of trials per epoch to sample trial types evenly, we discouraged extremely long gambled times greater than 9.5 s by choosing a reward function with a derivative that fell by 9.5 s to the level it was prior to 2.2 s. Rats took an average of 15 s to perform a trial excluding gambled time. With a 9.5 s gambled time and the resulting 4 s reward delivered at both choice and back ports, this yields approximately 30 s trials and our aim of at least 80 trials per epoch.
Rats that performed many trials per epoch with a large spread in gambled times were implanted with hardware for recording neural data. Following a week or more of recovery, behavioral data in the final task were acquired from implanted rats.
QUANTIFICATION AND STATISTICAL ANALYSIS
Correlation of choice latency and gambled time
For analysis of correlation between gambled times and latency to choice, outliers with gambled times greater than 10 s or latency to choice greater than 20 s were excluded, leaving over ninety percent of the data per rat. Linear regression was implemented in SciPy.
To test whether choice latency alone could account for the difference in gambled time for correct versus error trials, we excluded outliers as above, split each rat’s data by the median choice latency and performed a one-sided rank-sum test for a difference in the distribution of gambled times for correct versus error in the low and high latency subsets: for rat T, n trials = 2770, median gambled time = 3.8 s, low p = 8.0 × 10−19, high p = 1.2 × 10−46; for rat S, n trials = 3930, median gambled time = 3.3 s, low p = 4.8 × 10−22, high p = 7.8 × 10−33; for rat D, n trials = 4026, median gambled time = 4.2 s, low p = 1.4 × 10−9, high p = 2.0 × 10−65; for rat R, n trials = 3247, median gambled time = 3.3 s, low p = 1.4 × 10−20, high p = 2.8 × 10−73. These highly significant differences indicate that there was a difference in gambled times even when selecting trials to match latencies.
Evaluation of alternative strategies
For each rat, the proportion of times that each port was presented as target versus distractor were compared. Per epoch, these values were rarely above or below 50 percent by greater than 3 percent, and the majority of differences were not statistically significant at p = 0.05 by a t test for independent samples.
We tested whether there existed an alternative strategy that could better explain the rat’s choices than the true rule, which is to select the least recently visited of the two cued ports. For every trial in every epoch, for each rat, we determined whether the alternative rule would have resulted in the same choice as the one the rat made, or the same choice dictated by the true rule. This resulted in two proportions per epoch for each rat.
To compare each rat’s performance accuracy to that which could be achieved by relying on a visual working memory of the light cues alone, we simulated 100 experiments for each rat, matching the number of epochs and trials per epoch to experimental data. The simulated rat made visits to the least recently cued port, and made no errors aside from those introduced by this logic. A one-sided rank-sum test compared the overall distribution of per-epoch accuracies in data to those in simulation for each rat.
Evaluation of logistic regression and neural network models of choice accuracy
We used a DNN model to predict choice outcome (correct or error) as a function of an exhaustive feature set, or a feature set comprised of target age and distractor age alone. The exhaustive feature set included for each of target and distractor: age in trials and time; their last, maximum, and cumulative delivered reward amounts; time since last reward; last and cumulative dwell times; number of trials since any parts of its trajectory was last traversed. The feature set also included, for the target and distractor, their spatial trial type (branch/stem) and temporal (target age – distractor age) relationships. The features were each standardized to have zero mean and unit variance. The DNNs were feedforward, fully connected networks implemented in KERAS using the TENSORFLOW backend and optimized using ADAM. Each network had three hidden layers with 32 nodes each and the rectified linear unit activation. The output of the last layer was a sigmoid and the binary cross-entropy was the loss function. Networks were trained with 200 epochs with early stopping using a patience of 5 epochs. A k = 5-fold training procedure was used whereby 1/kth of the data were withheld for testing, 1/kth were withheld for validation and the rest were used for training. Datasets used for training were subsets of the full dataset for each of rats T, S, D, R (N = 2857, 4031, 4246, 3452, respectively) due to the requirement that training trials have data for every feature in the exhaustive set. The trials that comprise each fold were uniformly selected at random. A total of 10 networks were trained for this configuration and the network with the best validation loss was used to evaluate on the test set. The test set was then rotated k times until all data are used for testing. The loss was weighted during training so that the weighted number of instances from the two trial outcomes (i.e., correct or error) are the same.
Logistic regression was implemented in KERAS, where it is simply a neural network without any hidden layers.
Fitting the generative memory model (GeMM) parameters
The GeMM was fit on a subset of distractor-target trial types for which there was enough data, excluding invalid errors. The reduced datasets were 1877, 2593, 2722, and 2284 trials for rats T, S, D, R, respectively. Model parameters a0, a1, a2 and σ0 were fit for each rat based on its performance across trial types defined by distractor and target - distractor ages (excluding invalid error trials and target - distractor ages > 4). The probability density of the difference between two lognormal distributions (whose negative density is the error rate) does not have a closed-form analytic solution, so we simulated 104 trials for each trial type within the fit. Each simulated trial generated an m1′and m0′, from which we computed an outcome (correct or error). Across many simulated trials, this returned a predicted error rate pattern across trial types for the current set of parameters.
A χ2 metric was used to evaluate model performance and find the best fit parameters:
where ε is the error rate and σε is the uncertainty in the error rate. The uncertainty σε is determined via bootstrapping, accounting for correlations between the number of trials that were incorrect (Ni) and the total number of trials (NT) by modeling each as an independent Poisson random variable and taking the standard deviation of Ni/(Ni + Nc) over 100,000 simulated trials. We use the Nelder-Mead method with 200 maximum iterations as implemented in SCIPY, minimizing the χ2 fit to error rates across trial types. Then, using these parameters, we generated the distributions corresponding to each episode memory and sampled from each 100,000 times to generate target memories, distractor memories, the outcome of the trial (correct/error) and a confidence (absolute value of the difference between target and distractor).
Mapping GeMM-predicted confidence to gambled time
To convert the simulated confidence values to invested times, we mapped the confidence (C) probability density onto the probability density of the rat’s invested times (T). Let F(x)= Pr(C ≤x) be the cumulative distribution function (CDF) for C and G(x)= Pr(T < x) be the CDF of the invested times. Then, the mapping procedure proceeds as follows:
Compute the empirical CDF of the confidence values from the model using ECDF from STATSMODELS. Trials are generated from the model such that the number of trials from each trial type follows the relative rates in data which are not uniform. The minimum number of trials generated is 104.
Compute the empirical CDF of the wait times from data using ECDF from STATSMODELS. This is inclusive over trial types.
For each confidence value c, evaluate. The inverse is computed via linear interpolation (using NUMPY’s interp function) inverting the x and y coordinates.
Supplementary Material
Highlights.
A novel rodent task combines a memory-guided choice and confidence report
Rats demonstrate the ability to compute memory confidence
A deep-neural-network-derived memory decision variable tracks trial difficulty
A generative model of evolving memory distributions predicts choice and confidence
ACKNOWLEDGMENTS
We thank J. Kuhl for design contributions to Figures 1A and 1B and the graphical abstract. We thank the Frank and Kepecs labs, particularly D. Liu, G. Rothschild, and T. Davidson for advice on early versions of this task; A. Comrie for discussion and assistance; T. Ott for modeling advice; and P. Masset for the idea of temporal betting and comments on the manuscript. We are grateful to J. Berke, M. Brainard, A. Nelson, and V. Sohal for advice on task design and analysis and to U. Rutishauser for comments on the manuscript. We are thankful for the catalytic advice to focus on behavior and build a model, the GeMM being a product of those conversations. This work was funded by NIMH F30MH115582 (H.R.J.), F30MH109292 (J.E.C.), and R01MH097061 (A.K.); NINDS U01 NS107667 (L.M.F.) and U01 NS094288 (L.M.F. and A.K.); NIGMS MSTP grant T32GM007618 (J.E.C. and H.R.J.); Howard Hughes Medical Institute (L.M.F.); and DOE DE-AC02-05CH11231 (B.P.N.). We thank NVIDIA for providing Volta GPUs for the neural network training.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
INCLUSION AND DIVERSITY
While citing references scientifically relevant for this work, we actively worked to promote gender balance in our reference list.
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.cub.2021.08.013.
REFERENCES
- 1.Grimaldi P, Lau H, and Basso MA (2015). There are things that we know that we know, and there are things that we do not know we do not know: confidence in decision-making. Neurosci. Biobehav. Rev 55, 88–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pouget A, Drugowitsch J, and Kepecs A. (2016). Confidence and certainty: distinct probabilistic quantities for different goals. Nat. Neurosci 19, 366–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bach DR, and Dolan RJ (2012). Knowing how much you don’t know: a neural organization of uncertainty estimates. Nat. Rev. Neurosci 13, 572–586. [DOI] [PubMed] [Google Scholar]
- 4.Meyniel F, Sigman M, and Mainen ZF (2015). Confidence as Bayesian probability: from neural origins to behavior. Neuron 88, 78–92. [DOI] [PubMed] [Google Scholar]
- 5.Pouget A, Beck JM, Ma WJ, and Latham PE (2013). Probabilistic brains: knowns and unknowns. Nat. Neurosci 16, 1170–1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kepecs A, and Mainen ZF (2012). A computational framework for the study of confidence in humans and animals. Philos. Trans. R. Soc. Lond. B Biol. Sci 367, 1322–1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Smith JD, Schull J, Strote J, McGee K, Egnor R, and Erb L. (1995). The uncertain response in the bottlenosed dolphin (Tursiops truncatus). J. Exp. Psychol. Gen 124, 391–408. [DOI] [PubMed] [Google Scholar]
- 8.Kiani R, and Shadlen MN (2009). Representation of confidence associated with a decision by neurons in the parietal cortex. Science 324, 759–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Middlebrooks PG, and Sommer MA (2012). Neuronal correlates of metacognition in primate frontal cortex. Neuron 75, 517–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Komura Y, Nikkuni A, Hirashima N, Uetake T, and Miyamoto A. (2013). Responses of pulvinar neurons reflect a subject’s confidence in visual categorization. Nat. Neurosci 16, 749–755. [DOI] [PubMed] [Google Scholar]
- 11.Vining AQ, and Marsh HL (2015). Information seeking in capuchins (Cebus apella): a rudimentary form of metacognition? Anim. Cogn 18, 667–681. [DOI] [PubMed] [Google Scholar]
- 12.Hampton RR (2001). Rhesus monkeys know when they remember. Proc. Natl. Acad. Sci. USA 98, 5359–5362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Perry CJ, and Barron AB (2013). Honey bees selectively avoid difficult choices. Proc. Natl. Acad. Sci. USA 110, 19155–19159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kepecs A, Uchida N, Zariwala HA, and Mainen ZF (2008). Neural correlates, computation and behavioural impact of decision confidence. Nature 455, 227–231. [DOI] [PubMed] [Google Scholar]
- 15.Stolyarova A, Rakhshan M, Hart EE, O’Dell TJ, Peters MAK, Lau H, Soltani A, and Izquierdo A. (2019). Contributions of anterior cingulate cortex and basolateral amygdala to decision confidence and learning under uncertainty. Nat. Commun 10, 4704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hangya B, Sanders JI, and Kepecs A. (2016). A mathematical framework for statistical decision confidence. Neural Comput. 28, 1840–1858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ott T, Masset P, and Kepecs A. (2018). The neurobiology of confidence: from beliefs to neurons. Cold Spring Harb. Symp. Quant. Biol 83, 9–16. [DOI] [PubMed] [Google Scholar]
- 18.Sanders JI, Hangya B, and Kepecs A. (2016). Signatures of a statistical computation in the human sense of confidence. Neuron 90, 499–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lak A, Nomoto K, Keramati M, Sakagami M, and Kepecs A. (2017). Midbrain dopamine neurons signal belief in choice accuracy during a perceptual decision. Curr. Biol 27, 821–832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Goupil L, and Kouider S. (2016). Behavioral and neural indices of metacognitive sensitivity in preverbal infants. Curr. Biol 26, 3038–3045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lak A, Costa GM, Romberg E, Koulakov AA, Mainen ZF, and Kepecs A. (2014). Orbitofrontal cortex is required for optimal waiting based on decision confidence. Neuron 84, 190–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Masset P, Ott T, Lak A, Hirokawa J, and Kepecs A. (2020). Behavior- and modality-general representation of confidence in orbitofrontal cortex. Cell 182, 112–126.e18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Roediger HL 3rd, and DeSoto KA (2014). Confidence and memory: assessing positive and negative correlations. Memory 22, 76–91. [DOI] [PubMed] [Google Scholar]
- 24.Wixted JT, and Wells GL (2017). The relationship between eyewitness confidence and identification accuracy: a new synthesis. Psychol. Sci. Public Interest 18, 10–65. [DOI] [PubMed] [Google Scholar]
- 25.Rutishauser U, Ye S, Koroma M, Tudusciuc O, Ross IB, Chung JM, and Mamelak AN (2015). Representation of retrieval confidence by single neurons in the human medial temporal lobe. Nat. Neurosci 18, 1041–1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Miyamoto K, Osada T, Setsuie R, Takeda M, Tamura K, Adachi Y, and Miyashita Y. (2017). Causal neural network of metamemory for retrospection in primates. Science 355, 188–193. [DOI] [PubMed] [Google Scholar]
- 27.Miyamoto K, Setsuie R, Osada T, and Miyashita Y. (2018). Reversible silencing of the frontopolar cortex selectively impairs metacognitive judgment on non-experience in primates. Neuron 97, 980–989.e6. [DOI] [PubMed] [Google Scholar]
- 28.Kwok SC, Cai Y, and Buckley MJ (2019). Mnemonic introspection in macaques is dependent on superior dorsolateral prefrontal cortex but not orbitofrontal cortex. J. Neurosci 39, 5922–5934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kornell N, Son LK, and Terrace HS (2007). Transfer of metacognitive skills and hint seeking in monkeys. Psychol. Sci 18, 64–71. [DOI] [PubMed] [Google Scholar]
- 30.Rutishauser U, Aflalo T, Rosario ER, Pouratian N, and Andersen RA (2018). Single-neuron representation of memory strength and recognition confidence in left human posterior parietal cortex. Neuron 97, 209–220.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Eichenbaum H, and Cohen NJ (2001). From Conditioning to Conscious Recollection (Oxford University; ). [Google Scholar]
- 32.Babb SJ, and Crystal JD (2006). Episodic-like memory in the rat. Curr. Biol 16, 1317–1321. [DOI] [PubMed] [Google Scholar]
- 33.Smith JD, Couchman JJ, and Beran MJ (2014). Animal metacognition: a tale of two comparative psychologies. J. Comp. Psychol 128, 115–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kirk CR, McMillan N, and Roberts WA (2014). Rats respond for information: metacognition in a rodent? J. Exp. Psychol. Anim. Learn. Cogn 40, 249–259. [DOI] [PubMed] [Google Scholar]
- 35.Yuki S, and Okanoya K. (2017). Rats show adaptive choice in a metacognitive task with high uncertainty. J. Exp. Psychol. Anim. Learn. Cogn 43, 109–118. [DOI] [PubMed] [Google Scholar]
- 36.Templer VL, Lee KA, and Preston AJ (2017). Rats know when they remember: transfer of metacognitive responding across odor-based delayed match-to-sample tests. Anim. Cogn 20, 891–906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Richards JB, Mitchell SH, de Wit H, and Seiden LS (1997). Determination of discount functions in rats with an adjusting-amount procedure. J. Exp. Anal. Behav 67, 353–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mazur JE (1987). An adjusting procedure for studying delayed reinforcement. In The Effect of Delay and of Intervening Events on Reinforcement Value, , Commons ML, Mazur JE, Nevin JA, and Rachlin H, eds. (Lawrence Erlbaum Associates; ), pp. 55–73. [Google Scholar]
- 39.Yeung N, and Summerfield C. (2012). Metacognition in human decision-making: confidence and error monitoring. Philos. Trans. R. Soc. Lond. B Biol. Sci 367, 1310–1321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fetsch CR, Kiani R, and Shadlen MN (2014). Predicting the accuracy of a decision: a neural mechanism of confidence. Cold Spring Harb. Symp. Quant. Biol 79, 185–197. [DOI] [PubMed] [Google Scholar]
- 41.Sauerland M, Sagana A, Sporer SL, and Wixted JT (2018). Decision time and confidence predict choosers’ identification performance in photographic showups. PLoS ONE 13, e0190416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hampton RR (2009). Multiple demonstrations of metacognition in non-humans: converging evidence or multiple mechanisms? Comp. Cogn. Behav. Rev 4, 17–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kesner RP, and Novak JM (1982). Serial position curve in rats: role of the dorsal hippocampus. Science 218, 173–175. [DOI] [PubMed] [Google Scholar]
- 44.Chiba AA, Kesner RP, and Gibson CJ (1997). Memory for temporal order of new and familiar spatial location sequences: role of the medial prefrontal cortex. Learn. Mem 4, 311–317. [DOI] [PubMed] [Google Scholar]
- 45.Corrado GS, Sugrue LP, Brown JR, and Newsome WT (2009). The trouble with choice: studying decision variables in the brain. In Neuroeconomics: Decision Making and the Brain, , Glimcher PW, Camerer CF, Fehr E, and Poldrack RA, eds. (Academic; ), pp. 463–480. [Google Scholar]
- 46.Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, Brandstetter J, Dragicevic M, Erö J, Valle AED, et al. (2019). An embedding technique to determine ττ backgrounds in proton-proton collision data. J. Instrum 14, P06032. [Google Scholar]
- 47.Shettleworth SJ (2010). Cognition, Evolution, and Behavior (Oxford University; ). [Google Scholar]
- 48.Kirchner WK (1958). Age differences in short-term retention of rapidly changing information. J. Exp. Psychol 55, 352–358. [DOI] [PubMed] [Google Scholar]
- 49.Chaudhuri R, and Fiete I. (2016). Computational principles of memory. Nat. Neurosci 19, 394–403. [DOI] [PubMed] [Google Scholar]
- 50.Yonelinas AP, Aly M, Wang WC, and Koen JD (2010). Recollection and familiarity: examining controversial assumptions and new directions. Hippocampus 20, 1178–1194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Clayton NS, Bussey TJ, and Dickinson A. (2003). Can animals recall the past and plan for the future? Nat. Rev. Neurosci 4, 685–691. [DOI] [PubMed] [Google Scholar]
- 52.Roberts WA, Feeney MC, Macpherson K, Petter M, McMillan N, and Musolino E. (2008). Episodic-like memory in rats: is it based on when or how long ago? Science 320, 113–115. [DOI] [PubMed] [Google Scholar]
- 53.Zhou W, and Crystal JD (2009). Evidence for remembering when events occurred in a rodent model of episodic memory. Proc. Natl. Acad. Sci. USA 106, 9525–9529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jozefowiez J, Staddon JER, and Cerutti DT (2009). Metacognition in animals: how do we know that they know? Comp. Cogn. Behav. Rev 4, 29–39. [Google Scholar]
- 55.Le Pelley ME (2012). Metacognitive monkeys or associative animals? Simple reinforcement learning explains uncertainty in nonhuman animals. J. Exp. Psychol. Learn. Mem. Cogn 38, 686–708. [DOI] [PubMed] [Google Scholar]
- 56.Sanders J. (2014). A computational framework for understanding decision confidence (Cold Spring Harbor Laboratory), PhD thesis. [Google Scholar]
- 57.Foote AL, and Crystal JD (2007). Metacognition in the rat. Curr. Biol 17, 551–555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Foote AL, and Crystal JD (2012). “Play it again”: a new method for testing metacognition in animals. Anim. Cogn 15, 187–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Fetsch CR, Kiani R, Newsome WT, and Shadlen MN (2014). Effects of cortical microstimulation on confidence in a perceptual decision. Neuron 83, 797–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Sugrue LP, Corrado GS, and Newsome WT (2004). Matching behavior and the representation of value in the parietal cortex. Science 304, 1782–1787. [DOI] [PubMed] [Google Scholar]
- 61.Dudai Y, Karni A, and Born J. (2015). The consolidation and transformation of memory. Neuron 88, 20–32. [DOI] [PubMed] [Google Scholar]
- 62.Wixted JT, and Mickes L. (2010). A continuous dual-process model of remember/know judgments. Psychol. Rev 117, 1025–1054. [DOI] [PubMed] [Google Scholar]
- 63.Kahana MJ (2012). Foundations of Human Memory (Oxford University; ). [Google Scholar]
- 64.Raaijmakers JGW, and Shiffrin RM (1980). SAM: a theory of probabilistic search of associative memory. In Psychology of Learning and Motivation, , Bower GH, ed. (Academic; ), pp. 207–262. [Google Scholar]
- 65.Raaijmakers JG, and Shiffrin RM (1992). Models for recall and recognition. Annu. Rev. Psychol 43, 205–234. [DOI] [PubMed] [Google Scholar]
- 66.Howard MW, and Kahana MJ (2002). A distributed representation of temporal context. J. Math. Psychol 46, 269–299. [Google Scholar]
- 67.Howard MW, Fotedar MS, Datey AV, and Hasselmo ME (2005). The temporal context model in spatial navigation and relational learning: toward a common explanation of medial temporal lobe function across domains. Psychol. Rev 112, 75–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Vickers D. (1979). 6 - Confidence. In Decision Processes in Visual Perception, , Vickers D, ed. (Academic; ), pp. 171–200. [Google Scholar]
- 69.Shadlen MN, and Shohamy D. (2016). Decision making and sequential sampling from memory. Neuron 90, 927–939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Bakkour A, Palombo DJ, Zylberberg A, Kang YH, Reid A, Verfaellie M, Shadlen MN, and Shohamy D. (2019). The hippocampus supports deliberation during value-based decisions. eLife 8, e46080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Joo HR, and Frank LM (2018). The hippocampal sharp wave-ripple in memory retrieval for immediate use and consolidation. Nat. Rev. Neurosci 19, 744–757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Gershman SJ, and Daw ND (2017). Reinforcement learning and episodic memory in humans and animals: an integrative framework. Annu. Rev. Psychol 68, 101–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Bornstein AM, Khaw MW, Shohamy D, and Daw ND (2017). Reminders of past choices bias decisions for reward in humans. Nat. Commun 8, 15958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Bornstein AM, and Norman KA (2017). Reinstated episodic context guides sampling-based decisions for reward. Nat. Neurosci 20, 997–1003. [DOI] [PubMed] [Google Scholar]
- 75.Rouault M, Seow T, Gillan CM, and Fleming SM (2018). Psychiatric symptom dimensions are associated with dissociable shifts in metacognition but not task performance. Biol. Psychiatry 84, 443–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Sterzer P, Adams RA, Fletcher P, Frith C, Lawrie SM, Muckli L, Petrovic P, Uhlhaas P, Voss M, and Corlett PR (2018). The predictive coding account of psychosis. Biol. Psychiatry 84, 634–643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Kepecs A, and Mensh BD (2015). Emotor control: computations underlying bodily resource allocation, emotions, and confidence. Dialogues Clin. Neurosci 17, 391–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Hoven M, Lebreton M, Engelmann JB, Denys D, Luigjes J, and van Holst RJ (2019). Abnormalities of confidence in psychiatry: an overview and future perspectives. Transl. Psychiatry 9, 268. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All original code has been deposited at GitHub: https://github.com/hrjoo/TotalRecall and is publicly available as of the date of publication. All original data have been deposited at Zenodo: https://doi.org/10.5281/zenodo.5123545 and are publicly available as of the date of publication. DOIs are listed in the Key resources table. DOIs are listed in the key resources table. Any additional information required to reanalyze the data reported in this paper will be made available upon reasonable request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental models: organisms/strains | ||
| Rattus norvegicus: Crl:LE strain code 006: Long Evans rats | Charles River Laboratories | RRID: RGD_2308852 |
| Deposited data | ||
| Raw data | This paper | https://doi.org/10.5281/zenodo.5123545 |
| Software and algorithms | ||
| Code repository for this paper | This paper | https://github.com/hrjoo/TotalRecall |