Abstract
A largely unexplored question in neuronal plasticity is whether synapses are capable of encoding and learning the timing of synaptic inputs. We address this question in a computational model of synaptic input time difference learning (SITDL), where N‐methyl‐d‐aspartate receptor (NMDAR) isoform expression in silent synapses is affected by time differences between glutamate and voltage signals. We suggest that differences between NMDARs’ glutamate and voltage gate conductances induce modifications of the synapse’s NMDAR isoform population, consequently changing the timing of synaptic response. NMDAR expression at individual synapses can encode the precise time difference between signals. Thus, SITDL enables the learning and reconstruction of signals across multiple synapses of a single neuron. In addition to plausibly predicting the roles of NMDARs in synaptic plasticity, SITDL can be usefully applied in artificial neural network models.
Subject terms: Computational models, Computational neuroscience, Learning algorithms, Synaptic plasticity, Learning and memory
Introduction
Synaptic plasticity is a process in which synaptic properties are often modified, through activity-dependent changes in expression of post-synaptic receptors or in pre-synaptic neurotransmitter release. Most studies of synaptic plasticity in both physiological systems and artificial neural networks (ANNs) focus on the strengthening or weakening of synapses. Many of the studies emphasize NMDARs’ role in changing synaptic strengths and their importance in memory. However, only a few1,2 have examined another possible role where synaptic timing is changed, in terms of the actual speed of postsynaptic receptor activation. Here we propose that NMDARs are potentially important for changing synaptic timing in an activity-dependent manner, given that NMDAR dynamics can be regulated in many different ways, and NMDAR composition can change over time, with different subunits conferring distinct activation rates to NMDARs.
NMDAR dynamics and expression
NMDARs are heteromeric cation channels whose activation requires binding of glycine or D-serine, and glutamate, as well as local depolarization3–6. Essentially, the NMDAR acts as a coincidence detector, as it has both a glutamate gate and a voltage gate that require near-coincident activation for the NMDAR channel to fully open (Fig. 1). Note that throughout this paper, mentions of glutamate binding and activation of NMDAR’s glutamate gate imply coincident binding of the co-agonists glycine and D-serine. Once NMDARs are activated, they permit cation flow, including significant Ca2+ influx, to cause slow depolarization.
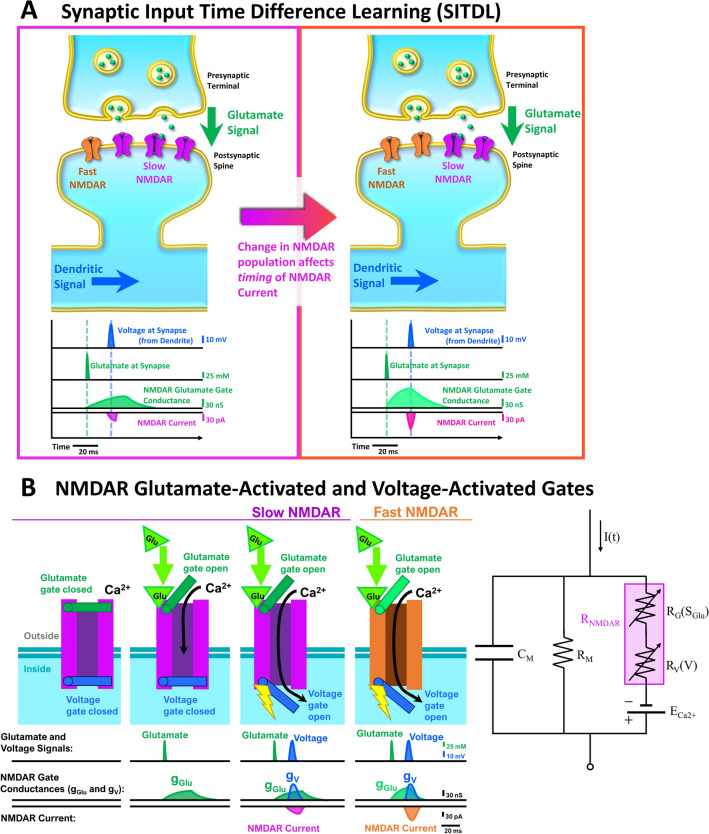
Figure 1.
The SITDL hypothesis: An example of how activity-dependent changes in NMDAR population can affect synaptic current timing. (A) Left: A developing silent synapse starts with a majority of slow NMDARs with slower glutamate gate activation than fast NMDARs. The synapse receives a glutamate signal followed later by a dendritic voltage signal, causing a difference in activation of NMDARs’ voltage and glutamate gates. Right: As the synapse develops and experiences the same timing between voltage and glutamate signals, its NMDAR population may change, caused by the difference in glutamate and voltage gate activation. In this case, fast NMDARs replace slow NMDARs until the gate conductance difference is minimized, thus aligning the overall NMDAR current peak with the peak of the voltage signal. This allows the developing synapse to learn the timing difference between the voltage and glutamate signals by encoding it in the NMDAR population’s glutamate gate activation time. (B) Left: Each NMDAR has a glutamate gate and a voltage gate that can be activated independently, with corresponding gate conductances shown. Coincident activation of both gates allows influx of Ca2+ (NMDAR Current). A slow NMDAR has a slower glutamate gate activation, therefore experiencing slower change in glutamate gate conductance than a fast NMDAR. Right: Circuit diagram of a post-synaptic spine containing only NMDARs. An NMDAR (RNMDAR) is shown as variable serial resistances of its glutamate gate (RG) and voltage gate (RV) that depend on the glutamate signal (SGlu) and dendritic spine’s voltage (V), respectively. CM denotes the membrane capacitance, RM the membrane resistance, ECa2+ the cell’s Nernst potential for Ca2+, and I(t) the external input.
The dynamics of an NMDAR for glutamate binding and channel opening rates depend on its subunits. Each NMDAR is made of two obligatory GluN1 subunits, and two additional subunits of GluN2 or GluN3. Distinct GluN2 and GluN3 isoforms can determine NMDAR gating properties7. We focus on the GluN2 isoforms, GluN2A and GluN2B, as they predominate in many brain structures associated with memory and precise timing. GluN2A-containing NMDARs typically have faster activation, faster deactivation, and higher affinity for glutamate than GluN2B-containing NMDARs7. Notably, computational modeling of NMDAR subtype activation suggests that diheteromeric GluN1/GluN2A NMDARs have a rise time to peak activation of about 7 ms, while diheteromeric GluN1/GluN2B NMDARs have a markedly longer rise time of approximately 50 ms8. This suggests that changes in NMDAR subunit composition at a synapse effectively change how quickly glutamate activates the NMDAR glutamate gate, thus changing the timing of NMDAR-mediated Ca2+ influx.
There is significant regulation of NMDAR dynamics through ligand binding and post-translational modifications4,9,10. This includes a minimum of six distinct ligand binding sites on the NMDAR that can affect the probability of NMDAR channel opening, such as a polyamine regulatory site, and recognition sites for agonists and different ions. NMDARs also interact with proteins in the post-synaptic density. The anchoring of NMDARs to the post-synaptic density protein, PSD-95, through their GluN2 subunits, stabilizes their expression in the post-synaptic membrane and also couples them to intracellular signaling systems involving calmodulin4. The binding of the Ca2+-calmodulin complex to an NMDAR results in a Ca2+-dependent reduction of the NMDAR’s channel opening frequency and channel open time. Furthermore, NMDAR activity regulates casein kinase 2 phosphorylation of GluN2B subunits, which disrupts the subunits’ interactions with PSD-95 and decreases the GluN2B surface expression in neurons9–11. The wide diversity of ways in which NMDAR expression and dynamics can be modulated, through binding, post-translational modifications, and changing subunit composition, provides a wealth of opportunity for activity-dependent changes in synaptic current timing through NMDARs.
While NMDARs are present even at “silent” synapses, which do not generate detectable excitatory post-synaptic potentials (EPSPs) in response to neurotransmitter release12, specific NMDAR subunit expression varies over time and across brain regions7. For instance, GluN2B expression tends to be highest in early development, while GluN2A subunits are more widely expressed in adulthood. Notably, there is evidence of rapid activity-dependent bidirectional switching between GluN2A and GluN2B containing NMDARs, on the order of seconds in neonatal synapses13, and even in adult hippocampal synapses14. Distinct NMDAR expression is implicated not only in brain structures important for memory, but in other systems that rely on precise timing, such as in mammalian Calyx of Held and avian auditory brainstem15–17, important for inter-aural time and intensity difference calculations in sound localization, as well as in weakly electric fish relay cells, which are important for precise temporal regulation of the jamming avoidance response18,19. Notably, these delay line systems can resolve temporal disparities in the microsecond range, which may arise at the level of individual neurons. For instance, single neurons of the pre-pacemaker nucleus in a weakly electric fish are sensitive to temporal disparities as small as 1 µs, and their signaling and precision may involve NMDARs20,21. In one of the few studies on changes in NMDAR subunit composition during the development of a delay line system, it has been shown that GluN2A replace GluN2B subunits in chicken cochlear nuclei, after onset of hearing17.
SITDL hypothesis
Much is still unknown about NMDARs for the intricacies of their dynamics and regulation, the roles of different subunits, and their specific roles in memory formation. Here, we propose a hypothetical model, Synaptic Input Time Difference Learning (SITDL), of how activity-dependent changes in fast and slow NMDAR expression could affect synaptic current timing. In particular, we assume that synaptic NMDAR expression depends on differences in voltage and glutamate gate conductances, and that matching of these conductances provides optimal Ca2+ influx through NMDAR gates. This process is driven by changes in subunit composition of the NMDARs, which determine glutamate gate characteristic activation time.
For example, the left panel of Fig. 1A shows a silent synapse having a majority of slow NMDARs, with slower activation times in response to glutamate than fast NMDARs. The slow NMDARs can resemble NMDARs containing GluN2B subunits, while fast NMDARs resemble those with GluN2A subunits. The silent synapse receives a synaptic glutamate signal followed by a voltage signal carried by the dendrite from a non-silent synapse, whose peaks occur several milliseconds apart. This difference in timing accompanies a difference in NMDAR voltage and glutamate gate conductance. We propose that as the synapse develops and experiences the same timing difference between voltage and glutamate signals, the difference in glutamate and voltage gate conductances causes its NMDAR population to change.
In the right panel of Fig. 1A, fast NMDARs replace slow NMDARs until there is a minimization of the difference in glutamate and voltage gate conductance, thus aligning the NMDAR glutamate gate conductance peak with the peak of the voltage signal. In effect, the synapse learns the timing difference between the voltage and glutamate signals, encoding it in the NMDAR population’s glutamate gate activation time, which is a function of the numbers of fast and slow NMDARs. Then, stabilization of a synaptic NMDAR population, such that there are no more removals and insertions of fast or slow NMDARs, possibly due to PSD-95 anchoring, would mean a stable memory of the timing difference. Note that silent synapses are particularly useful substrate for this SITDL mechanism, as glutamate signals alone do not cause depolarization of the synapse, thus providing a greater degree of independence between NMDAR glutamate gate and voltage gate activation.
Furthermore, maturation, which involves the insertion of α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic receptors (AMPARs), may provide the synapse with a way of “recalling” the memorized timing difference. In this case, the NMDAR population no longer must rely on passing dendritic voltage signals for activation of their voltage gates, as AMPARs can provide depolarization in response to the glutamate signal. Thus, in theory, a glutamate signal alone could provide activation of NMDARs’ glutamate gates, and also indirectly provide depolarization to activate NMDARs’ voltage gates through the AMPARs. The resulting overall NMDAR current depends on the glutamate gate activation time of the stabilized NMDAR population, which encodes the previously memorized timing difference, in effect, recalling it.
In particular, SITDL and recall mechanisms may be useful for signal reconstruction when there are many silent redundant synapses and few non-silent synapses, as there often are in developing neurons22. Notably, networks of developing neurons have been shown to exhibit coordinated activity and rhythmic firing patterns23,24, essential to normal development of networks and synaptic connections. These developmental activity patterns are significantly different from those in mature circuits25. Thus, if a developing neuron receives rhythmic glutamate signals from presynaptic neurons, activation of a non-silent synapse would produce a rhythmic dendritic voltage signal in the neuron. Each of its silent synapses could therefore potentially receive both rhythmic voltage and glutamate signals, which would produce consistent overlap between signals. If these synapses could learn and encode the timing differences of these rhythmic signals during development, then once they mature, they would be able to recall and reproduce certain parts or patterns from the original developmental signals.
We explore the hypothesis of SITDL further and provide a computational single-compartment model (Methods). We also show that with many redundant silent synapses, as in a developing neuron, SITDL mechanisms, along with activity-dependent synaptic elimination and maturation, can enable reconstruction and recall of original developmental signals. Supplemental Slides S1 provide an overview and visualization of the SITDL mechanism and multi-synaptic signal reconstruction.
Methods
Input signals
To construct dendritic and glutamate signals to test the plasticity model, periodic input signals, SN and SGlu (Figure S2), were generated using a gaussian-like shape for the spikes in voltage, and a right-skewed shape for synaptic glutamate concentration26–28:
| 1 |
| 2 |
| 3 |
where SN = SN(t) determines the shape of the voltage input spike with parameters tN0 and σN. Glutamate signal, SGlu = SGlu(t) has characteristic right-skewed shape, with constant αL that determines the width and decay of the spike, and tL0 is simply shifted relative to tN0 , with tL0 = tN0 − 1/αL, to ensure that the spike peaks of both SN(t) and SGlu(t) occur at the same exact time (Figure S2). The input signals, SN and SGlu were normalized by their respective maximums, SNMax and SGluMax such that and . The dendritic signal, ID = ID (t), depends on I0, a constant current, and the signal SN. Values for all constants are given in Table 1.
Table 1.
SITDL model constants.
| Symbol | Description | Values (no units, unless indicated) |
|---|---|---|
| σN | Dispersion constant for SN | |
| αL | Exponential constant for SGlu | 10.0 |
| I0 | Constant current for ID | 0.01 |
| aV | Exponential constant for gV(t) | – 8.0 |
| bV | Exponential constant for gV(t) | 5.0 |
| aL | Decay factor constant for gL(t) | 0.999 |
| bL | Signal input factor for gL(t) | 0.065 |
| Δt | Simulation time step constant | 0.01 ms |
| τFast | Time constant for glutamate gate activation of fast NMDARs | 7.0 ms |
| τSlow | Time constant for glutamate gate activation of slow NMDARs | 50.0 ms |
| nTotal | Total number of NMDAR receptors | 50 receptors |
| γ | Constant for scaling the time step Δτ | 1.0 |
| Δτ | Time step for changing τGlu | 0.05 ms |
| VRest | Normalized resting potential | 0.0 |
| τR | Time constant for V(t) | 1.0 ms |
| kD | Constant for dendritic current contribution | 3.9 |
| kS | Constant for synaptic current contribution | 0.40 |
| τP | Time constant for determining how slowly σ(t) changes | 20.0 ms |
| ΔτMax | Maximum of ΔτGlu, used for modulating changes in σ(t) | 0.0125 ms |
| aP | Exponential constant for logistic function of σ(t) in P(t) | 0.30 |
| bP | Exponential constant for logistic function of σ(t) in P(t) | – 70.0 |
| δ | Threshold factor for synaptic elimination (for τD step = 8 ms and 2 ms, respectively) | 1.002, and 1.0215 |
NMDAR voltage and glutamate gate dynamics of a single synapse
NMDARs play important role in learning, memory, and development by regulating synaptic properties at the post-synaptic membrane. Each NMDAR is a heteromeric cation channel with a glutamate-activated gate and voltage-activated gate. Activations of the glutamate and voltage gates are largely independent, and either alone does not open the NMDAR channel completely. However, the activation of either gate will cause specific changes in conformation or channel structure and may potentially affect the NMDAR’s binding and phosphorylation sites. With near-coincident activation of both gates, the NMDAR channel opens, permitting Ca2+ influx.
We consider the glutamate and voltage gates as separate variable resistors, with each NMDAR composed of the glutamate gate resistor in series with the voltage gate resistor (Fig. 1B, Right). Therefore, in a single synapse, the overall post-synaptic NMDAR conductance, g = g(t), can be expressed as follows:
| 4 |
where gGlu = gGlu(t) represents the conductance of the NMDAR population’s glutamate gates, and gV = gV(t) represents the conductance of its voltage gates. g determines the level of permeability and Ca2+ influx through channels of the NMDAR population (Fig. 1B, Left). The product of gGlu and gV in Eq. 4 also implies necessity of coincidence of glutamate and voltage gate activation.
The voltage dependence of an NMDAR has been previously modeled with experimental data as a logistic function of synaptic Mg2+ concentration and the post-synaptic voltage29,30. We can similarly describe the conductance of a population of NMDARs’ voltage gates, gV, as a simplified logistic function of the normalized voltage along the dendrite, VD = VD (t):
| 5 |
with constants av and bv provided in Table 1. In Eq. 5, we assume that Mg2+ concentration stays relatively constant in the synapse, as expected for physiological conditions.
The evolution of gGlu can be written as:
| 6 |
with approximate solution in the form of a single-time-step mapping:
| 7 |
where
| 8 |
τGlu is glutamate gate conductance characteristic time, Δt is a single time step, and aL and bL are constants between 0 and 1, the values for which are provided in Table 1. Here, we assume that glutamate gate conductance limit, gL, acts as an eligibility trace of glutamate signal SGlu (Eq. 8), since NMDAR conductance depends on synaptic glutamate concentration and prior activations.
On a sub-second time scale, local changes in τGlu represent modification of receptors that transiently affect their dynamics and membrane stability, such as phosphorylation of NMDARs9. On a longer scale of seconds or more, overall changes in τGlu define the changes in numbers of slow and fast NMDARs, which significantly affect the dynamics of NMDAR glutamate gate conductance, gGlu. A key point and assumption of the SITDL hypothesis is that NMDAR subunit composition, and consequent value of τGlu, depend on the difference between the NMDAR gate conductances, gGlu and gV. So, the optimal Ca2+ influx occurs when the value of gGlu matches that of gV. Following the assumption, temporal evolution of τGlu can be written as:
| 9 |
where Δτ is time step for τGlu, γ is a scaling constant. The primary goal of the SITDL model is to find value of τGlu that minimizes the gate conductance mismatch, (gGlu − gV), which would effectively represent the estimated time difference between the synaptic glutamate signal and the dendritic voltage signal.
Equation 9 results from gradient descent minimization of the function F(τGlu) = (gGlu − gV)2, with dF/dτGlu =− 2t(gGlu − gV)(gL − gGlu)/ τGlu2. Equation 9 has two fixed points, at gGlu = gV and gL = gGlu. Figure S4 shows evolution of (gL − gGlu) and (gGlu − gV) toward stable solution, where the peaks of gGlu and gV are aligned. Optimal solution is reached when gGlu → gV and gL ≈ gV.
There are few studies modeling the dynamics of the NMDAR glutamate gate and how they change with different NMDAR subunit compositions. For instance, they primarily involve kinetic modeling of NMDARs with different subunit compositions31–33, but provide little suggestion for modeling the synaptic population of NMDARs, its overall dynamics, and how the NMDAR population may change over time in an activity-dependent manner. While τGlu describes the dynamics of NMDAR glutamate gate conductance, it depends on the glutamate signal and is difficult to compare to the experimentally known characteristics of slow and fast NMDARs. Therefore, it is useful to look at the NMDAR dynamics in response to a fixed signal: a single glutamate spike. For each synapse, we are particularly interested in the gGlu rise-to-peak time, τSyn, in response to a single glutamate spike, which is defined through the numbers of slow and fast NMDARs (nSlow and nFast)34:
| 10 |
where nTotal is the total number of NMDAR receptors, τFast and τSlow are known time constants of fast and slow NMDARs, respectively.
Using Eq. 14, and the assumption that nTotal stays constant, numbers of slow and fast NMDARs can be calculated from τSyn as follows:
| 11 |
| 12 |
τSyn is calculated as the rise-to-peak time of NMDAR glutamate gate conductance, gGlu, for a single glutamate spike as signal SGlu, similarly to previous studies34. τSyn dependence of τGlu is shown in Figure S3. τSyn values were calculated from gGlu response to a single glutamate spike, at fixed τGlu vaues (ranging from τGlu = 1 ms to 2000 ms).
Synaptic current and dendritic voltage
We can calculate the synaptic current, ISyn = ISyn (t), that results from NMDAR activation and consequent Ca2+ influx, using overall NMDAR conductance, g, and dendritic voltage, VD:
| 13 |
Changes in dendritic voltage are described via a single-compartment conductance-based model:
| 14 |
where VRest is resting membrane potential, τR = CR is a time constant, kD and kS are current contribution constants, τD is the dendritic delay time constant, indicating the time difference between synaptic and dendritic signal, ID(t − τD) is delayed dendritic signal, and ISyn is synaptic current resulting from NMDAR activation.
Stabilization of glutamate gate conductance characteristic time τGlu
The change in τGlu described by Eq. 9 is always dominated by the gate conductance mismatch. Therefore, unless there is a consistent and perfect match of the gate conductances, gGlu and gV, τGlu will constantly change. We propose the existence of a stabilization mechanism that depends on the overall NMDAR conductance, g, such that when g is consistently large, τGlu will eventually stabilize. We modify Eq. 9 to include a stabilization variable, P, with the following set of equations:
| 15 |
where
| 16 |
| 17 |
| 18 |
P and σ define the stabilization mechanism: when g is consistently greater than zero (Eqs. 17, 18), and concurrently the change in τGlu, ΔτGlu, is close to zero, τGlu stops changing. ΔτMax is the maximum possible value for ΔτGlu. Its value and the values for constants aP, bP, and τP are provided in Table 1.
SITDL multi-synaptic memory and recall
To test whether SITDL mechanisms could be used to memorize peak times of a glutamate signal and reconstruct it, several alterations are made. Multiple synapses are used, with each synapse represented as a single-compartment SITDL model with stabilization mechanisms (Eqs. 1–18), with its own dendritic delay time constant, τD, and initial glutamate gate characteristic time, τGlu. A set of “Learning Phase” simulations starts with a full set of synapses (i = 1, …,N), with 49 τD values uniformly distributed between 4 and 100 ms, and initial τGlu = 20 ms. In these simulations, each synapse receives a periodic glutamate signal as described before, and a sparse voltage signal with one spike repeating over the same period as the glutamate signal (Figs. 5, S2 bottom). For each synapse i, gAvg, the overall NMDA conductance averaged over the last 0.1% of the simulation time (last 150,000 points), is calculated. If a synapse’s gAvg is lower than a threshold factor, δ, times the value of gAvg averaged across the entire set of synapses, such that , then it is eliminated. This is similar to the performance-based synaptic elimination rule used in the Clusteron model35, and to minimal-value deletion algorithms36. All synapses that have not been eliminated are considered stabilized, with τGlu permanently fixed. We assume that stabilized synapses express AMPARs, which depolarize the synapse upon binding glutamate. Therefore, for “Recall Phase” simulations, each stabilized synapse receives a single glutamate spike coincident with a single voltage spike (Fig. 5C). Note that kD and kS, the constants for dendritic and synaptic current contribution to voltage, respectively, are set to 2.0 and 3.0 for these simulations. The resulting synaptic voltage traces are shifted by their corresponding τD and summed over all stabilized synapses to give a “recall signal”, which is compared against the original glutamate signal used during Learning Phase simulations. A smaller set of 12 synapses was also used for SITDL learning and recall simulations, with τD values uniformly distributed between 8 and 96 ms, and initial τGlu = 20 ms. “No-SITDL” simulations use the same Learning Phase and Recall Phase simulations, except there are no SITDL mechanisms during the Learning Phase, such that there are no changes in τGlu for any synapse.
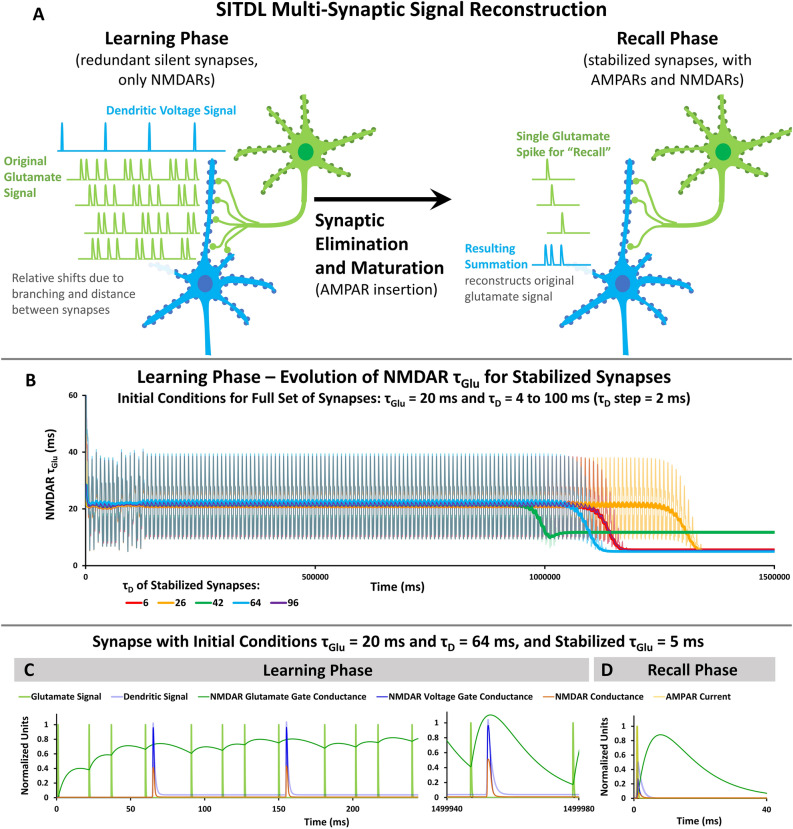
Figure 5.
Multi-synaptic SITDL simulations of learning. (A) The Learning Phase starts with a large number of redundant synapses, each receiving the same periodic glutamate signal, delayed relative to a similarly periodic but sparse voltage signal by dendritic time constant τD. After learning, synapses are eliminated or stabilized based on overall NMDAR conductance. During the Recall Phase each mature stabilized synapse receives a single glutamate spike. The summation of resulting voltages across all stabilized mature synapses with the appropriate dendritic delays, produces a reconstruction of the original glutamate signal received during the learning phase. (B) Evolution of τGlu for synapses that were stabilized at the end of Learning Phase simulations. The full set of synapses started with initial conditions τGlu = 20 ms and τD values uniformly distributed from 4 to 100 ms, with a step of 2 ms. Synapses with insufficient average overall NMDAR conductance were eliminated, leaving only stabilized synapses, whose corresponding τD are shown. (C) An example of a Learning Phase simulation, showing how NMDAR conductances change over time for a synapse with initial τGlu = 20 ms and τD = 64 ms. The synapse receives a periodic glutamate signal and a sparse voltage signal with the same period. The first voltage spike occurs close to the fourth spike of the glutamate signal. At the end of the simulation the average overall NMDAR conductance is sufficient for this synapse to be stabilized. (D) Recall Phase simulation of stabilized synapse from (C) with final values τGlu = 5.0 ms and τD = 64 ms. Since stabilized synapses are assumed to express AMPARS, in this case the synapse receives a single glutamate spike coincident with a single voltage spike.
Mutual information (MI) analysis
A mutual information (MI) estimator (Adaptive partition using Interspike intervals MI Estimator (AIMIE)), was used to compare recall signal and original glutamate signal37. Short signals were repeated with proper periodicity, such that each signal had at least 4000 spikes for more accurate MI estimation. A higher MI estimate for the two signals suggests that they have a greater dependency and higher degree of similarity. AIMIE has been shown to work well with spike time series with disparate firing rates and may provide more accurate estimates of MI than several other commonly used MI estimators. Details on AIMIE’s calculations and its use in information flow analysis of a spiking network are provided in previous work37.
All simulations of the SITDL model were programmed and run in Spyder 3.0.0, a Python 3.5 environment. SITDL data were analyzed using MATLAB R2016b and Excel 2016.
Code availability
The Python code for SITDL is available at https://github.com/KatyaGribkova/SITDL.
Results
The SITDL mechanism increases overlap of NMDAR gate conductances
The core mechanism of the SITDL model is learning the timing difference between synaptic glutamate and dendritic voltage signals. This involves changes in numbers of fast and slow NMDARs, and consequent changes in NMDAR glutamate gate characteristic time, τGlu, and τSyn, the corresponding rise-to-peak time of the glutamate gate conductance in response to a single glutamate spike. Using periodic glutamate and voltage signals and computational single-compartment model described in Methods (Eqs. 1–14), we ran multiple simulations for a range of initial values of dendritic delay, τD, and τGlu. It may be noted that the relative timing delay between signals, τD, can result from travelling along post-synaptic dendrites, as well as from travelling along the pre-synaptic axon. Conduction delays in certain systems, such as corticothalamic projections and some unmyelinated axons, can range from less than 2 ms to as long as 100 ms38–40, and in development the regulation of myelination can also significantly affect conduction delays41.
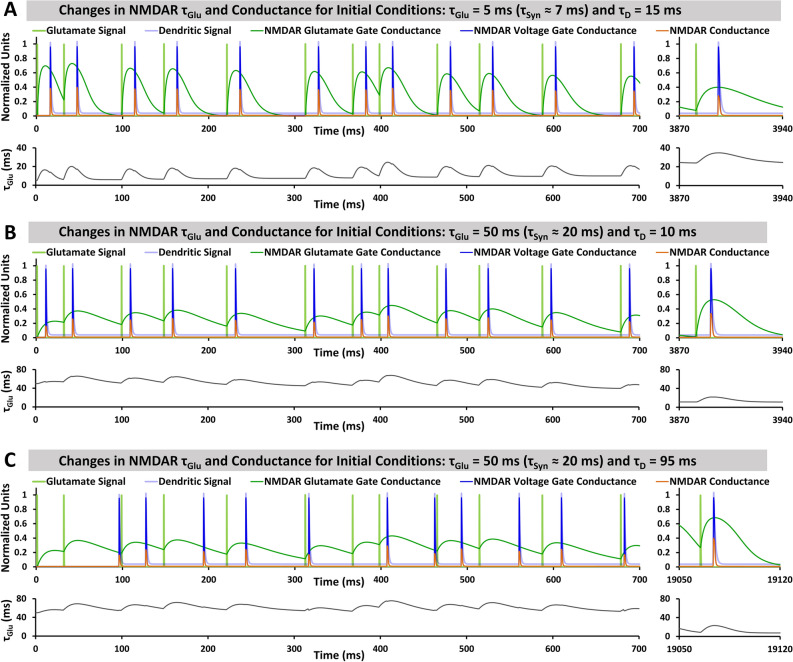
Figure 2 shows the evolution of τGlu and NMDAR conductances for a single synapse receiving the glutamate signal, SGlu, followed by the dendritic voltage signal, VD. Both are copies of a similar periodic signal, with dendritic signal delayed by time τD. The timing difference between signals produces a gate conductance mismatch, (gGlu − gV) (Eq. 9), changing τGlu and shifting gGlu peaks. This leads to greater overlap of the gate conductances. With initial values τGlu = 5 ms (corresponds to τSyn ≈ 7 ms) and τD = 15 ms (Fig. 2A), glutamate gate conductance, gGlu, initially peaks before voltage gate conductance, gV. This results in overall increase of τGlu over time. Coincidence appears to have been achieved at the end of the 4000 ms simulation. In Fig. 2B, gV initially peaks before gGlu, and τGlu decreases over time, resulting in greater overlap of gate conductances. Figure 2C shows that SITDL mechanisms can still work to achieve greater gate conductance coincidence even when dendritic delay, τD, is significant (τD = 95 ms) and there is much less overlap in signals.
Figure 2.
SITDL simulations of a single synapse receiving periodic inputs and showing evolution of τGlu and conductances for different initial conditions of τGlu and τD. In each case, the synapse receives a synaptic glutamate signal (light green) followed by a dendritic voltage signal (light blue) delayed by time τD. τGlu changes over time due to the NMDAR gate conductance mismatch. (A) Simulation with initial values τGlu = 5 ms and τD = 15 ms. Initially, glutamate gate conductance, gGlu, peaks before voltage gate conductance, gV. Over time, τGlu grows, delaying the gGlu peak and achieving greater coincidence. (B) Simulation with initial values τGlu = 50 ms and τD = 10 ms. In this case, gV initially peaks before gGlu. τGlu decreases over time, resulting in greater coincidence of the gate conductances. (C) Simulation with initial values τGlu = 50 ms and τD = 95 ms. Though there is much less overlap between glutamate and voltage signals, due to periodicity of the signal, the SITDL mechanism still appears to achieve greater coincidence over time.
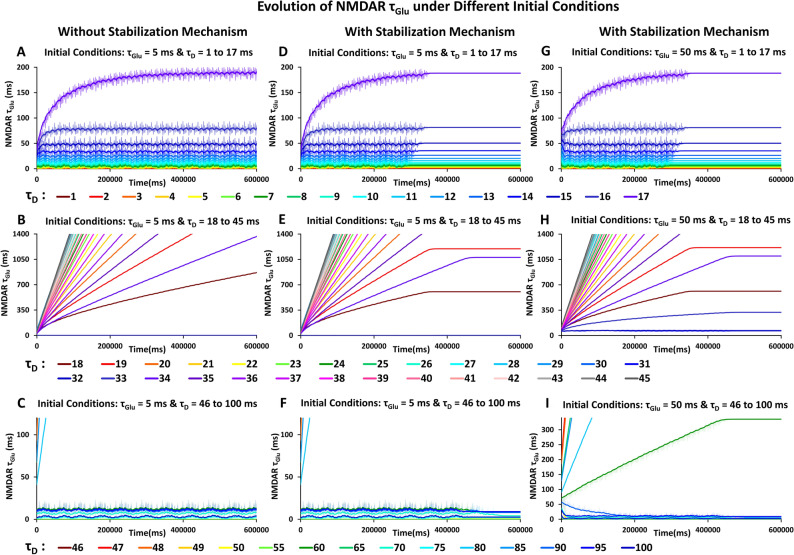
Figure 3A–C shows simulations of the SITDL model with a greater range of initial delays and longer simulation time of 600,000 ms to explore the evolution of τGlu. For initial τGlu = 5 ms, and τD = 1 ms to 17 ms, τGlu seems to quickly attain relatively stable values, with little change towards the end of the simulation. The smaller the τD, the more quickly τGlu stabilizes. This can be explained by smaller gate conductance mismatch and greater overlap between glutamate and voltage signals. For τD = 18 to 45 ms (Fig. 3B), τGlu grows but does not stabilize as much as for smaller τD. For some τD, τGlu keeps growing past 1000 ms without achieving greater stability, suggesting an insufficient overlap of signals. Likewise, for τD = 46 to 100 ms (Fig. 3C), only certain τD values, such as τD = 49 to 60 ms, 70 to 75 ms, and 90 to 100 ms, seem to provide sufficient overlap for τGlu to approach small stable values at the end of the 600,000 ms simulation time. Different initial τGlu and longer simulation times may allow τGlu to stabilize, paticularly for τD values larger than 17 ms, and to potentially achieve coincidence of glutamate and voltage gate conductances.
Figure 3.
SITDL simulations with and without stabilization mechanisms, under different sets of initial conditions. Each curve shows the changes in τGlu over time, for a single simulation with the specific initial τD value indicated by the color of the curve. (A) Changes in τGlu when starting with τGlu = 5 ms and different initial τD value for each curve, ranging from 1 to 17 ms. By 600,000 ms simulation time, each curve appears to reach more stable values. (B) Changes in τGlu with initial conditions τGlu = 5 ms and τD value ranging from 18 to 45 ms. In most cases, τGlu increases, but there does not appear to be sufficient simulation time for it to reach more stable values as in (A). (C) Changes in τGlu with initial conditions τGlu = 5 ms and τD value ranging from 46 to 100 ms, which provide much less overlap of glutamate and voltage signals. Certain τD values, such as 49 to 60 ms, 70 to 75 ms, and 90 to 100 ms, seem to provide sufficient overlap for τGlu to change significantly and potentially achieve coincidence of gate conductances with enough simulation time. (D–F) Same simulations and initial conditions as in Fig. 4A–C, but with stabilization mechanisms, which cause τGlu to stop changing when there is sufficient overall NMDAR conductance. Note, τGlu stabilization generally occurs more quickly for smaller τD, and even at high τD (18 to 100 ms), τGlu still stabilizes for certain values at the end of the simulation, despite limited overlap of the periodic signals. (G–I) Same simulations with stability mechanisms as in Figure (D–F), except with initial τGlu = 50 ms.
It may be noted that while τGlu approaches a more stable range of values in most cases, τGlu does not fully stabilize in Fig. 3A–C. Thus, we made key alterations to the SITDL model, using Eqs. 15–18 for implementing τGlu stabilization mechanisms, which are important for demonstrating stable memory formation and recall. Figure 3D–F demonstrates simulations of this variation of SITDL model for τD ranging from 1 to 100 ms, similar to Fig. 3A–C, with initial τGlu of 5 ms. Likewise, Fig. 3G–I shows that τGlu can decrease from a higher initial value (τGlu = 50 ms), and fully stabilize at values similar to those in Fig. 3D–F, due to SITDL stabilization mechanism. In some cases, the higher initial τGlu allows for stabilization at additional τD values (Fig. 3H). While we showed that τGlu is able to stabilize at values lower than 5 ms (Fig. 3A,D,G) to demonstrate the range of capabilities of the SITDL algorithm, for all subsequent simulations we limited τGlu to values between 5 and 1410 ms to correspond to the more biologically relevant NMDAR conductance rise-to-peak time limits of around 7 ms and 50 ms, respectively.
NMDAR τGlu corresponds to fractions of slow and fast NMDARs
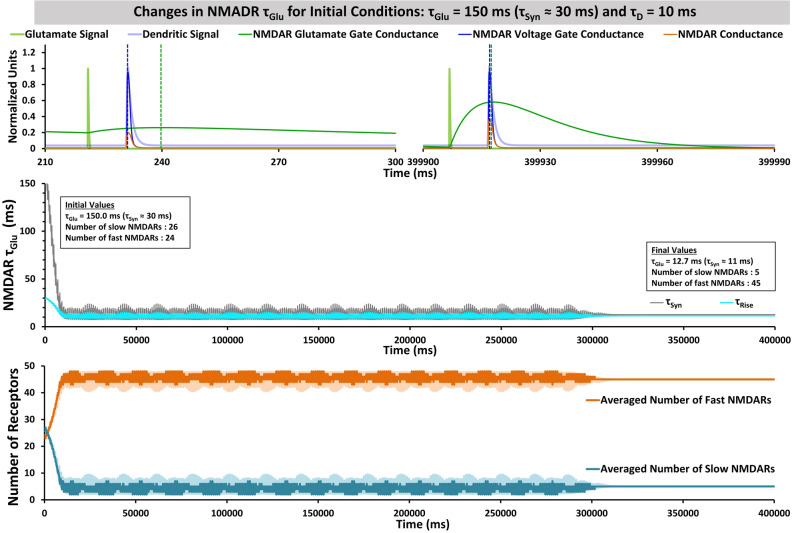
We assumed that τGlu is determined by the numbers of fast and slow NMDARs. Fast NMDARs can be considered those with GluN1/GluN2A subunit composition, with estimated rise-to-peak time, τSyn, of 7 ms, and slow NMDARs as those with GluN1/GluN2B subunit composition, with estimated rise-to-peak time τSyn of 50 ms8. Over the course of development, slow NMDARs are typically replaced with fast NMDARs7. As a test, we ran a SITDL model simulation with initial values τGlu = 150 ms and τD = 10 ms, and calculated numbers of fast and slow NMDARs using estimated τSyn and Eqs. 10–12 with nTotal = 50, τFast = 7 ms, and τSlow = 50 ms. τSyn was estimated from τGlu values, using linear interpolation of data points from the τSyn vs. τGlu plot of Figure S3.
Because τGlu decreases, the gGlu maximum shifts significantly closer to gV maximum (Fig. 4A). Initially, τGlu = 150 ms (τSyn ≈ 30 ms), with 26 slow NMDARs and 24 fast NMDARs. As τGlu decreases and stabilizes at its final value of ~ 12.7 ms (τSyn ≈ 11 ms), there are 5 slow NMDARs and 45 fast NMDARs (Fig. 4B,C). Reduction of τGlu can therefore represent a replacement of slow NMDARs with fast NMDARs, and τGlu convergence can be considered as stabilization in expression of fast and slow NMDARs.
Figure 4.
Simulation of the SITDL synapse model, showing changes in τGlu, and corresponding changes in numbers of slow and fast NMDARs. This simulation was run with plasticity and stabilization mechanisms for τGlu, with initial conditions τGlu = 150 ms and τD = 10 ms, and with constants for calculating the numbers of slow and fast NMDARs nTotal = 50, τFast = 7 ms, and τSlow = 50 ms. (A) Segments of 90 ms close to the start and end of the simulation are shown at the left and right, respectively, with gGlu and gV peaks (green and blue dashed lines) noticeably becoming more coincident. (B) shows the time course of τGlu, with an initial value of 150 ms (τSyn ≈ 30 ms), which corresponds to the synapse having 26 slow NMDARs and 24 fast NMDARs. τGlu decreases overall, with some oscillation, until it stabilizes at 12.7 ms (τSyn ≈ 11 ms), which corresponds to 5 slow NMDARs and 45 fast NMDARs in the synapse, indicating a replacement of slow NMDARs with fast NMDARs. (C) shows the corresponding numbers of slow and fast NDMARs over time, each averaged over a 800 ms time window (darker traces).
SITDL mechanisms across multiple synapses enable reconstruction of synaptic signal
The potential for SITDL mechanisms to achieve greater coincidence between NMDAR glutamate and voltage gate conductances, even with very limited overlap of signals, suggests that they could be used to memorize peak times of a glutamate signal and reconstruct it. To explore this, large numbers of SITDL synapses, with stabilization mechanisms and τD values uniformly distributed between 4 and 100 ms, were run through Learning Phase simulations like the previous simulations in Fig. 3, with ranges of different initial conditions. During the Learning Phase simulation, each synapse receives a periodic glutamate signal, and a sparse rhythmic voltage signal of the same period, delayed relative to the glutamate signal by time constant, τD (Fig. 5A,C). We can consider this initial set of synapses to be located along a neuron’s dendrite, receiving the same glutamate signal from the branched axon of a single pre-synaptic neuron (Fig. 5A). These types of redundant multi-synaptic connections are seen in neocortex, striatum and hippocampus42–45, and they may also arise as a result of long-term potentiation (LTP)46. Notably, this synaptic multiplicity appears to increase during development in hippocampal CA3-CA1 synapses47,48.
As before, τGlu and conductance values change over the course of the Learning Phase simulations (Fig. 5B,C). After simulations end, synapses with insufficient overall NMDAR conductance are eliminated, similar to NMDAR-dependent and Ca2+-based synaptic elimination in biological neurons49,50, and to synaptic elimination mechanisms in computational models such as the Clusteron35, and minimal-value deletion algorithms36. Figure 5B shows the changes in τGlu for synapses that were stabilized, with an initial set of synapses having initial conditions τGlu = 20 ms, and τD uniformly distributed from 4 to 100 ms, with a step size of 2 ms. The τD step can represent how far apart the initial synapses are on the dendrite (Fig. 5A). The leftover stabilized synapses are assumed to express AMPARs. These were run through Recall Phase simulations, where each stabilized synapse received a single glutamate spike and a single voltage spike that coincided due to AMPAR expression (Fig. 5D).
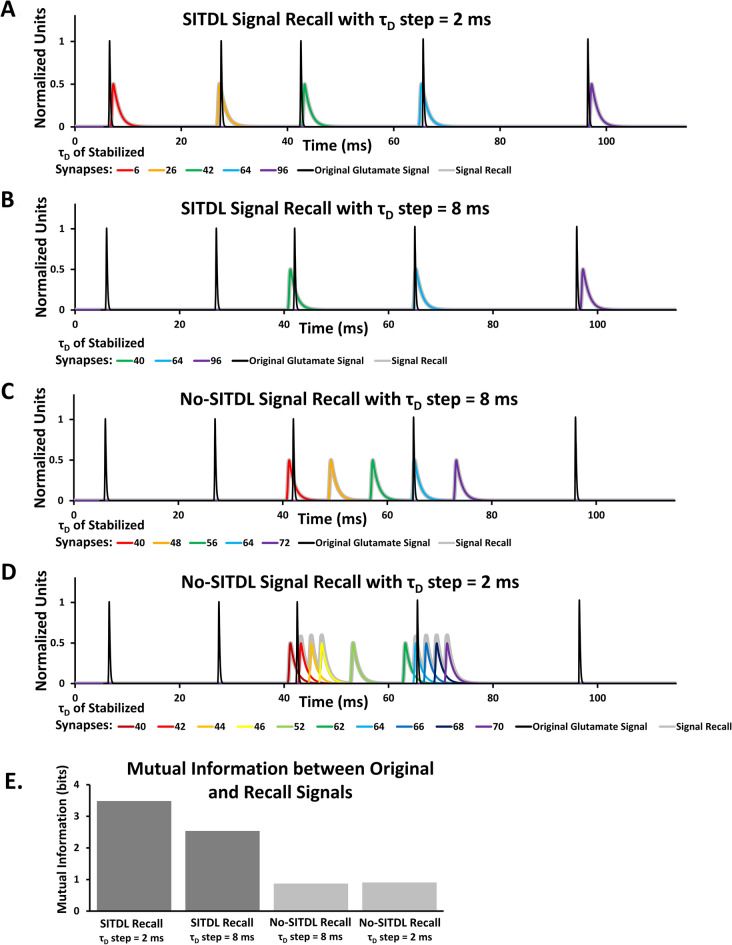
The summation of resulting Recall Phase voltage signals across the stabilized synapses (Fig. 6, traces in color), shifted by the corresponding τD value, provides a “recall signal” that very closely resembles the original glutamate signal from the Learning Phase (Fig. 6A). For recall signals constructed from SITDL simulations with much larger τD step, there are less spikes and peak times are slightly less similar to those of the glutamate signal (Fig. 6B). Furthermore, recall signals constructed from simulation sets (Learning Phase, elimination, Recall Phase) without SITDL mechanisms such that τGlu cannot change, appear to be even less similar to the original glutamate signal, as they are missing the first, second, and fifth glutamate spikes, and have additional spikes in the vicinity of the third and fourth glutamate spikes (Fig. 6C,D). Using the MI estimator AIMIE37, we show that there is a greater degree of similarity between the original signal and recall signal reconstructed from SITDL simulations (Fig. 6E). SITDL mechanisms across a set of synapses, particularly when they are distributed closely enough, can therefore be used to effectively memorize and recall synaptic signals.
Figure 6.
Results of Recall Phase simulations for synapses with and without SITDL mechanisms. There are 4 different sets of synaptic simulations, each with their own starting conditions: 2 sets of SITDL simulations with τD step = 2 ms and 8 ms, and 2 sets of simulations without SITDL mechanisms with τD step = 2 ms and 8 ms. For all simulation sets, τD values are initially distributed uniformly with the corresponding τD step, and all initial τGlu = 20 ms. For each simulation set, following Learning Phase simulations, synaptic elimination, and Recall Phase simulations, a recall signal is obtained by summating the resulting Recall Phase voltage signals (Fig. 5C), shifted by corresponding τD (A–D traces in color), over all stabilized synapses. Note, to provide better visual comparison of original and recall signals, the original signal was slightly shifted relative to the recall signal, with a delay of 5.5 ms for (A,D), and 5 ms for (B,C). (A) The recall signal for SITDL simulation set with τD step = 2 ms very closely resembles the original glutamate signal that was used during Learning Phase. (B) Recall signal for SITDL simulation set with τD step = 8 ms is less similar to the original glutamate signal, because of the much larger τD step used during Learning Phase. (C,D) Recall signals for no-SITDL simulation sets with τD step = 8 ms and 2 ms, respectively. There are no changes in τGlu in these simulations, thus synapses are unable to achieve greater overlap of glutamate and voltage gate conductances. Even with synapses that were stabilized, the peaks of the recall signal are significantly shifted from the peaks of the original glutamate signal. (E) Estimates of MI between original glutamate signal and recall signal for each simulation set, using MI estimator AIMIE37. SITDL simulation sets, particularly the one with smaller τD step (2 ms), provide greater MI estimates than no-SITDL simulation sets, suggesting greater degree of similarity between their reconstructed recall signal and the original glutamate signal.
Discussion
SITDL explores the potential for a single synapse to learn the timing of input signals through changes of its receptor dynamics. In the computationally simple SITDL model we show that single synapse can “learn” the timing difference between glutamate and dendritic voltage signals. The functioning principle of single-compartment SITDL model is to reach optimal combination of fast and slow NMDAR subunits and corresponding glutamate gate conductance characteristic time, τGlu, through minimization of NMDAR gate conductance mismatch, (gGlu − gV). τGlu stabilizes when optimal Ca2+ influx is achieved. Decreases in τGlu correspond to a replacement of slow NMDARs by fast NMDARs (Fig. 4), as is typical during neural development. However, depending on initial conditions, such as initial τGlu value and dendritic delay τD, τGlu can also increase over time (Fig. 3), relating to the observed bidirectional switching of fast and slow NMDARs in hippocampus13,51.
NMDARs are particularly suited to mediate relations of the SITDL hypothesis because of their largely independent glutamate and voltage gates. SITDL mechanisms would likewise function under the assumption of NMDAR’s slow Mg2+ unblock52. Furthermore, it is possible that other receptors with coincidence detector properties, such as the inositol 1,4,5-trisphosphate receptor (IP3R)53,54, could be involved in SITDL-like mechanisms. Additionally, a variety of ligand-gated ion channels also have active voltage-sensitive conductances that could dispose them toward various ways of regulation in sensitive ranges of voltage. While the assumptions of the SITDL model have not yet been tested in physiological experiments, the functional principles may significantly expand synaptic capabilities in both biological and artificial systems.
Much is still unknown about NMDAR properties, and their activity-dependent modifications. It is possible that specific changes in NMDAR conformation, occurring independently for glutamate and voltage gate activation, can convey the mismatch between gate conductances through interfacing with cellular signaling pathways. For instance, if τGlu is too large, with too many slow NMDARs at a synapse, then glutamate gate activation peaks after the voltage gate activation, producing a specific combined conformational state in NMDARs, particularly slow ones, that indicates the NMDAR gate conductance mismatch. This specific conformational state could affect the NMDAR’s anchoring with post-synaptic density proteins, such as PSD-95. Therefore, NMDARs with the highest mismatch, as indicated by their specific combined conformational state, can be removed from the membrane, and replaced with other NMDARs. This NMDAR cycling process can continue until the balance of slow and fast receptors is found, where glutamate and voltage gate conductances peak at the same time, for an optimal τGlu. The different nanodomain organization of slow and fast NMDARs in the postsynaptic density could also provide more dynamic cycling and replacement of NMDARs55,56, such that unstable slow NMDARs with high mismatch would be more likely replaced with fast NMDARs, and vice versa. Moreover, SITDL provides potential mechanisms for new learning rules in ANNs, which currently employ primarily synaptic weight changes.
The SITDL model can increase overlap of gGlu and gV in a synapse that receives very similar periodic signals with small relative time shifts (Fig. 2). This may be particularly useful for developing synapses in delay line systems like those of mammalian and avian auditory brainstem and sensory circuits of weakly electric fish57,58, all of which rely on very precise timing of signals. Some delay line systems resolve temporal disparities in the microsecond range even with just a single neuron21, and some depend on NMDARs in development17. Notably, there have been few computational models for achieving precise timing in delay line systems. One such model explores temporal precision in the barn owl auditory system59, using unsupervised Hebbian learning rules and a broad random distribution of transmission delays. While this may show how delay line systems with large numbers of neurons are able to achieve such temporal precision, it does not explain how it can be achieved with much more limited numbers of neurons and transmission delays, such as in pre-pacemaker nucleus neurons of weakly electric fish21. Furthermore, the vast diversity of neuronal morphology and circuit organization, as found in cerebral cortex and cerebellum60,61, may require fine-tuning of synaptic input timing. Even without τGlu stabilization mechanisms, the SITDL model can still increase overlap of NMDAR gate conductances with larger dendritic delays, such as for some τD greater than 45 ms, which provide very little overlap of glutamate and voltage signals (Figs. 2C and 3). Due to periodicity of the signals, less frequent but repeated overlap can cause significant changes in τGlu. With τGlu stabilization mechanisms depending on overall changes in τGlu, and overall NMDAR conductance, the SITDL model stabilizes τGlu even with quite small overlap between glutamate and voltage signals. Changes in τGlu are bidirectional (Fig. 3), and represent replacement of fast and slow NMDARs (Fig. 4). This relates to mechanisms of rapid bidirectional switching in NMDAR subunit compositions of developing hippocampus13.
Achieving greater gate conductance overlap with very limited overlap of signals may be quite useful, especially in memory formation. For instance, in a neuron that receives highly delayed copies of the same or similarly periodic signal, any memorized timing differences may represent the commonly occurring inter-spike intervals of the signal. We show in SITDL simulations that it is possible to memorize and reconstruct the original synaptic glutamate signal (Figs. 5, 6). Notably, synapses which stabilized at the smallest τGlu values provided the largest NMDAR conductances, saving them from synaptic elimination.
Potential tests of SITDL in biological systems
SITDL mechanisms would be particularly valuable in systems that rely on precise timing and sequence memorization, such as the neural circuits involved in avian song and human speech learning40,62, as well as spatial map formation63. If we consider the auto-associative networks of the CA3 region of the hippocampus, where synapses can exhibit bidirectional changes in NMDAR subunit compositions51, then the SITDL mechanism could potentially be used for sequence memorization in single neurons. Figure S5 shows one potential mechanism of sequence learning in CA3, with each synapse learning the timing between two distinct inputs. Notably, in hippocampal neurons, the distribution and nanoscale organization of GluN2B subunits vary significantly between proximal and distal synapses64. Likewise, spike timing dependent plasticity (STDP) rules of synapses also vary in a location-dependent manner65. SITDL mechanisms could potentially be used to establish specific NMDAR expression, and consequently the synaptic timing required for the distinct location-dependent STDP rules, along the dendritic arbor.
To test for the existence of SITDL mechanisms in real neurons, in vitro studies of neuronal cultures and brain slices, such as those of hippocampus and developing neocortex could be useful. In particular, it would be interesting to observe axonal and synaptic activity across multiple points in developing multi-synaptically connected neurons, through multi-electrode recordings or with calcium and voltage indicators. Furthermore, neuronal activity might be manipulated, pharmacologically or with stimulating electrodes, alongside single particle tracking of different NMDAR subunits in post-synaptic membranes66, to provide more insight into possible existence of neuronal SITDL mechanisms. Molecular analyses of NMDARs in these cases, including conformational changes and phosphorylation site alterations under different stimulation protocols, might provide a deeper understanding of the potential mechanisms involved. For instance, it is possible that NMDAR gate conductance mismatch could be due to the different conformational changes caused by glutamate binding and depolarization of an NMDAR. These specific conformational changes could alter the NMDAR’s phosphorylation sites, modifying its dynamics and anchoring stability in the post-synaptic membrane, and leading to potential subunit switching.
Supplementary Information
Acknowledgements
This study was supported by Navy N00014-19-1-2373. Author E.D.G. thanks for inspiration the directors of the 2017 Methods in Computational Neuroscience course at the Marine Biological Laboratory, Professors Mark Goldman and Michale Fee, and the many other instructors and participants of the course.
Author contributions
Conceptualization, Methodology, Software, Formal Analysis, Investigation, Original Draft, and Concepts—E.D.G.; Writing—Review & Editing, E.D.G. and R.G.; Supervision, R.G.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-021-00516-y.
References
- 1.Sabatini B, Regehr W. Timing of synaptic transmission. Annu. Rev. Physiol. 1999;61:521–542. doi: 10.1146/annurev.physiol.61.1.521. [DOI] [PubMed] [Google Scholar]
- 2.Evans RC, et al. The effects of NMDA subunit composition on calcium influx and spike timing-dependent plasticity in striatal medium spiny neurons. PLoS Comp. Biol. 2012;8:e1002493. doi: 10.1371/journal.pcbi.1002493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lüscher C, Malenka RC. NMDA receptor-dependent long-term potentiation and long-term depression (LTP/LTD) Cold Spring Harb. Perspect. Biol. 2012;4:a005710. doi: 10.1101/cshperspect.a005710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hassel, B. & Dingledine, R. Glutamate and glutamate receptors in Basic Neurochemistry 342–366 (Elsevier, 2012).
- 5.Lester RA, Clements JD, Westbrook GL, Jahr CE. Channel kinetics determine the time course of NMDA receptor-mediated synaptic currents. Nature. 1990;346:565–567. doi: 10.1038/346565a0. [DOI] [PubMed] [Google Scholar]
- 6.Neame S, et al. The NMDA receptor activation by d-serine and glycine is controlled by an astrocytic Phgdh-dependent serine shuttle. Proc. Nat. Acad. Sci. USA. 2019;116:20736–20742. doi: 10.1073/pnas.1909458116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Paoletti P, Bellone C, Zhou Q. NMDA receptor subunit diversity: Impact on receptor properties, synaptic plasticity and disease. Nat. Rev. Neurosci. 2013;14:383–400. doi: 10.1038/nrn3504. [DOI] [PubMed] [Google Scholar]
- 8.Singh P, Hockenberry AJ, Tiruvadi VR, Meaney DF. Computational investigation of the changing patterns of subtype specific NMDA receptor activation during physiological glutamatergic neurotransmission. PLoS Comp. Biol. 2011;7:e1002106. doi: 10.1371/journal.pcbi.1002106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen B-S, Roche KW. Regulation of NMDA receptors by phosphorylation. Neuropharmacology. 2007;53:362–368. doi: 10.1016/j.neuropharm.2007.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Qiu, S., Li, X.-Y. & Zhuo, M. Post-translational modification of NMDA receptor GluN2B subunit and its roles in chronic pain and memory. Semin. Cell Dev. Biol.22, 521–529 (Elsevier, 2011). [DOI] [PubMed]
- 11.Chung HJ, Huang YH, Lau L-F, Huganir RL. Regulation of the NMDA receptor complex and trafficking by activity-dependent phosphorylation of the NR2B subunit PDZ ligand. J. Neurosci. 2004;24:10248–10259. doi: 10.1523/JNEUROSCI.0546-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kullmann D. Silent synapse. Scholarpedia. 2011;6:10705. doi: 10.4249/scholarpedia.10705. [DOI] [Google Scholar]
- 13.Bellone C, Nicoll RA. Rapid bidirectional switching of synaptic NMDA receptors. Neuron. 2007;55:779–785. doi: 10.1016/j.neuron.2007.07.035. [DOI] [PubMed] [Google Scholar]
- 14.Jung S-C, Kim J, Hoffman DA. Rapid, bidirectional remodeling of synaptic NMDA receptor subunit composition by A-type K+ channel activity in hippocampal CA1 pyramidal neurons. Neuron. 2008;60:657–671. doi: 10.1016/j.neuron.2008.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Joshi I, Yang Y-M, Wang L-Y. Coincident activation of metabotropic glutamate receptors and NMDA receptors (NMDARs) downregulates perisynaptic/extrasynaptic NMDARs and enhances high-fidelity neurotransmission at the developing calyx of Held synapse. J. Neurosci. 2007;27:9989–9999. doi: 10.1523/JNEUROSCI.2506-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Futai K, Okada M, Matsuyama K, Takahashi T. High-fidelity transmission acquired via a developmental decrease in NMDA receptor expression at an auditory synapse. J. Neurosci. 2001;21:3342–3349. doi: 10.1523/JNEUROSCI.21-10-03342.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tang YZ, Carr CE. Development of N-methyl-D-aspartate receptor subunits in avian auditory brainstem. J. Comp. Neurol. 2007;502:400–413. doi: 10.1002/cne.21303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zakon H, Oestreich J, Tallarovic S, Triefenbach F. EOD modulations of brown ghost electric fish: JARs, chirps, rises, and dips. J. Physiol.-Paris. 2002;96:451–458. doi: 10.1016/S0928-4257(03)00012-3. [DOI] [PubMed] [Google Scholar]
- 19.Bekkers, J. & Stevens, C. Computational implications of NMDA receptor channels in Cold Spring Harbor Symp. Quant. Biol.55, 131–135 (Cold Spring Harbor Laboratory Press, 1990). [DOI] [PubMed]
- 20.Spiro JE, Brose N, Heinemann SF, Heiligenberg W. Immunolocalization of NMDA receptors in the central nervous system of weakly electric fish: Functional implications for the modulation of a neuronal oscillator. J. Neurosci. 1994;14:6289–6299. doi: 10.1523/JNEUROSCI.14-10-06289.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kawasaki M, Rose G, Heiligenberg W. Temporal hyperacuity in single neurons of electric fish. Nature. 1988;336:173–176. doi: 10.1038/336173a0. [DOI] [PubMed] [Google Scholar]
- 22.Liao D, Zhang X, O'Brien R, Ehlers MD, Huganir RL. Regulation of morphological postsynaptic silent synapses in developing hippocampal neurons. Nat. Neurosci. 1999;2:37–43. doi: 10.1038/4540. [DOI] [PubMed] [Google Scholar]
- 23.Lippe W. Rhythmic spontaneous activity in the developing avian auditory system. J. Neurosci. 1994;14:1486–1495. doi: 10.1523/JNEUROSCI.14-03-01486.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kamioka H, Maeda E, Jimbo Y, Robinson HP, Kawana A. Spontaneous periodic synchronized bursting during formation of mature patterns of connections in cortical cultures. Neurosci. Lett. 1996;206:109–112. doi: 10.1016/S0304-3940(96)12448-4. [DOI] [PubMed] [Google Scholar]
- 25.Blankenship AG, Feller MB. Mechanisms underlying spontaneous patterned activity in developing neural circuits. Nat. Rev. Neurosci. 2010;11:18–29. doi: 10.1038/nrn2759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sargent PB, Saviane C, Nielsen TA, DiGregorio DA, Silver RA. Rapid vesicular release, quantal variability, and spillover contribute to the precision and reliability of transmission at a glomerular synapse. J. Neurosci. 2005;25:8173–8187. doi: 10.1523/JNEUROSCI.2051-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ventriglia F, Di Maio V. A Brownian simulation model of glutamate synaptic diffusion in the femtosecond time scale. Biol. Cybern. 2000;83:93–109. doi: 10.1007/s004220000150. [DOI] [PubMed] [Google Scholar]
- 28.Einolghozati, A., Sardari, M., Beirami, A. & Fekri, F. Capacity of discrete molecular diffusion channels. 2011 IEEE International Symposium on Information Theory Proceedings, 723–727 (2011).
- 29.Jahr CE, Stevens CF. A quantitative description of NMDA receptor-channel kinetic behavior. J. Neurosci. 1990;10:1830–1837. doi: 10.1523/JNEUROSCI.10-06-01830.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dayan, P. & Abbott, L. F. Theoretical neuroscience: Computational and mathematical modeling of neural systems. (2001).
- 31.Vargas-Caballero M, Robinson HP. Fast and slow voltage-dependent dynamics of magnesium block in the NMDA receptor: The asymmetric trapping block model. J. Neurosci. 2004;24:6171–6180. doi: 10.1523/JNEUROSCI.1380-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zheng W, Wen H, Iacobucci GJ, Popescu GK. Probing the structural dynamics of the NMDA receptor activation by coarse-grained modeling. Biophys. J. 2017;112:2589–2601. doi: 10.1016/j.bpj.2017.04.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gibb AJ, et al. A structurally derived model of subunit-dependent NMDA receptor function. J. Physiol. 2018;596:4057–4089. doi: 10.1113/JP276093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shouval HZ, Bear MF, Cooper LN. A unified model of NMDA receptor-dependent bidirectional synaptic plasticity. Proc. Nat. Acad. Sci. USA. 2002;99:10831–10836. doi: 10.1073/pnas.152343099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mel BW. The clusteron: Toward a simple abstraction for a complex neuron. Adv. Neural Inf. Process. Syst. 1992;4:35–42. [Google Scholar]
- 36.Chechik G, Meilijson I, Ruppin E. Synaptic pruning in development: A computational account. Neural Comput. 1998;10:1759–1777. doi: 10.1162/089976698300017124. [DOI] [PubMed] [Google Scholar]
- 37.Gribkova ED, Ibrahim BAE, Llano DA. A novel mutual information estimator to measure spike train correlations in a model thalamocortical network. J. Neurophysiol. 2018;120:2730–2744. doi: 10.1152/jn.00012.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Stoelzel CR, Bereshpolova Y, Alonso J-M, Swadlow HA. Axonal conduction delays, brain state, and corticogeniculate communication. J. Neurosci. 2017;37:6342–6358. doi: 10.1523/JNEUROSCI.0444-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Swadlow HA, Waxman SG. Axonal conduction delays. Scholarpedia. 2012;7:1451. doi: 10.4249/scholarpedia.1451. [DOI] [Google Scholar]
- 40.Egger R, et al. Local axonal conduction shapes the spatiotemporal properties of neural sequences. Cell. 2020;183:537–548. doi: 10.1016/j.cell.2020.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Pajevic S, Basser PJ, Fields RD. Role of myelin plasticity in oscillations and synchrony of neuronal activity. Neuroscience. 2014;276:135–147. doi: 10.1016/j.neuroscience.2013.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kasthuri N, et al. Saturated reconstruction of a volume of neocortex. Cell. 2015;162:648–661. doi: 10.1016/j.cell.2015.06.054. [DOI] [PubMed] [Google Scholar]
- 43.Hiratani N, Fukai T. Redundancy in synaptic connections enables neurons to learn optimally. Proc. Nat. Acad. Sci. USA. 2018;115:E6871–E6879. doi: 10.1073/pnas.1803274115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bartol TM, Jr, et al. Nanoconnectomic upper bound on the variability of synaptic plasticity. Elife. 2015;4:e10778. doi: 10.7554/eLife.10778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sorra K, Harris KM. Occurrence and three-dimensional structure of multiple synapses between individual radiatum axons and their target pyramidal cells in hippocampal area CA1. J. Neurosci. 1993;13:3736–3748. doi: 10.1523/JNEUROSCI.13-09-03736.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Toni N, Buchs P-A, Nikonenko I, Bron C, Muller D. LTP promotes formation of multiple spine synapses between a single axon terminal and a dendrite. Nature. 1999;402:421–425. doi: 10.1038/46574. [DOI] [PubMed] [Google Scholar]
- 47.Hsia AY, Malenka RC, Nicoll RA. Development of excitatory circuitry in the hippocampus. J. Neurophysiol. 1998;79:2013–2024. doi: 10.1152/jn.1998.79.4.2013. [DOI] [PubMed] [Google Scholar]
- 48.Fuenzalida M, Aliaga E, Olivares V, Roncagliolo M, Bonansco C. Developmental increase of asynchronic glutamate release from hippocampal synapses in mutant taiep rat. Synapse. 2009;63:502–509. doi: 10.1002/syn.20622. [DOI] [PubMed] [Google Scholar]
- 49.Riccomagno MM, Kolodkin AL. Sculpting neural circuits by axon and dendrite pruning. Annu. Rev. Cell. Dev. Biol. 2015;31:779–805. doi: 10.1146/annurev-cellbio-100913-013038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Colonnese MT, Constantine-Paton M. Developmental period for N-methyl-D-aspartate (NMDA) receptor-dependent synapse elimination correlated with visuotopic map refinement. J. Comp. Neurol. 2006;494:738–751. doi: 10.1002/cne.20841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hunt DL, Puente N, Grandes P, Castillo PE. Bidirectional NMDA receptor plasticity controls CA3 output and heterosynaptic metaplasticity. Nat. Neurosci. 2013;16:1049. doi: 10.1038/nn.3461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kampa BM, Clements J, Jonas P, Stuart GJ. Kinetics of Mg2+ unblock of NMDA receptors: Implications for spike-timing dependent synaptic plasticity. J. Physiol. 2004;556:337–345. doi: 10.1113/jphysiol.2003.058842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kelly PT, MacKinnon RL, II, Dietz RV, Maher BJ, Wang J. Postsynaptic IP3 receptor-mediated Ca2+ release modulates synaptic transmission in hippocampal neurons. Mol. Brain Res. 2005;135:232–248. doi: 10.1016/j.molbrainres.2004.12.018. [DOI] [PubMed] [Google Scholar]
- 54.Bender VA, Bender KJ, Brasier DJ, Feldman DE. Two coincidence detectors for spike timing-dependent plasticity in somatosensory cortex. J. Neurosci. 2006;26:4166–4177. doi: 10.1523/JNEUROSCI.0176-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kellermayer B, et al. Differential nanoscale topography and functional role of GluN2-NMDA receptor subtypes at glutamatergic synapses. Neuron. 2018;100:106–119. doi: 10.1016/j.neuron.2018.09.012. [DOI] [PubMed] [Google Scholar]
- 56.Liu P-W, Hosokawa T, Hayashi Y. Regulation of synaptic nanodomain by liquid–liquid phase separation: A novel mechanism of synaptic plasticity. Curr. Opin. Neurobiol. 2021;69:84–92. doi: 10.1016/j.conb.2021.02.004. [DOI] [PubMed] [Google Scholar]
- 57.Carr CE. Time coding in electric fish and barn owls. Brain Behav. Evol. 1986;28:122–133. doi: 10.1159/000118697. [DOI] [PubMed] [Google Scholar]
- 58.Ashida G, Carr CE. Sound localization: Jeffress and beyond. Curr. Opin. Neurobiol. 2011;21:745–751. doi: 10.1016/j.conb.2011.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Gerstner W, Kempter R, Van Hemmen JL, Wagner H. A neuronal learning rule for sub-millisecond temporal coding. Nature. 1996;383:76–78. doi: 10.1038/383076a0. [DOI] [PubMed] [Google Scholar]
- 60.Lodato S, Arlotta P. Generating neuronal diversity in the mammalian cerebral cortex. Annu. Rev. Cell. Dev. Biol. 2015;31:699–720. doi: 10.1146/annurev-cellbio-100814-125353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hibi M, Matsuda K, Takeuchi M, Shimizu T, Murakami Y. Evolutionary mechanisms that generate morphology and neural-circuit diversity of the cerebellum. Dev. Growth Differ. 2017;59:228–243. doi: 10.1111/dgd.12349. [DOI] [PubMed] [Google Scholar]
- 62.Bolhuis JJ, Okanoya K, Scharff C. Twitter evolution: Converging mechanisms in birdsong and human speech. Nat. Rev. Neurosci. 2010;11:747–759. doi: 10.1038/nrn2931. [DOI] [PubMed] [Google Scholar]
- 63.Mehta MR. From synaptic plasticity to spatial maps and sequence learning. Hippocampus. 2015;25:756–762. doi: 10.1002/hipo.22472. [DOI] [PubMed] [Google Scholar]
- 64.Ferreira JS, et al. Distance-dependent regulation of NMDAR nanoscale organization along hippocampal neuron dendrites. Proc. Nat. Acad. Sci. USA. 2020;117:24526–24533. doi: 10.1073/pnas.1922477117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Froemke RC, Letzkus JJ, Kampa B, Hang GB, Stuart G. Dendritic synapse location and neocortical spike-timing-dependent plasticity. Front. Synaptic Neurosci. 2010;2:29. doi: 10.3389/fnsyn.2010.00029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Dupuis JP, Groc L. Surface trafficking of neurotransmitter receptors: From cultured neurons to intact brain preparations. Neuropharmacol. 2020;169:107642. doi: 10.1016/j.neuropharm.2019.05.019. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.