Fast two-stage phasing of large-scale sequence data

Summary

Haplotype phasing is the estimation of haplotypes from genotype data. We present a fast, accurate, and memory-efficient haplotype phasing method that scales to large-scale SNP array and sequence data. The method uses marker windowing and composite reference haplotypes to reduce memory usage and computation time. It incorporates a progressive phasing algorithm that identifies confidently phased heterozygotes in each iteration and fixes the phase of these heterozygotes in subsequent iterations. For data with many low-frequency variants, such as whole-genome sequence data, the method employs a two-stage phasing algorithm that phases high-frequency markers via progressive phasing in the first stage and phases low-frequency markers via genotype imputation in the second stage. This haplotype phasing method is implemented in the open-source Beagle 5.2 software package. We compare Beagle 5.2 and SHAPEIT 4.2.1 by using expanding subsets of 485,301 UK Biobank samples and 38,387 TOPMed samples. Both methods have very similar accuracy and computation time for UK Biobank SNP array data. However, for TOPMed sequence data, Beagle is more than 20 times faster than SHAPEIT, achieves similar accuracy, and scales to larger sample sizes.

Introduction

Haplotype phasing is the estimation of the haplotypes that are inherited from each parent. Genotypes obtained from a SNP array or from sequencing are typically unphased, and statistical methods must be used for inferring the sequence of alleles on each inherited chromosome.

Haplotype phasing is a common analysis because phased haplotypes are required or desirable for many downstream analyses, including genotype imputation,^{1, 2, 3, 4} detection of deleterious compound heterozygotes,⁵ genetic association testing,^6,7 detection of identity-by-descent segments,^{8, 9, 10} inference of population ancestry at a locus,^{11, 12, 13} and testing for natural selection.^{10,14, 15, 16}

The accuracy of haplotype phasing increases with sample size, and this has motivated the development of increasingly powerful phasing methods. The fastPHASE,¹⁷ Beagle,¹⁸ long-range phasing,¹⁹ and Mach²⁰ methods were among the first methods designed for genome-wide data. The next major advance came from methods such as HAPI-UR,²¹ SHAPEIT,²² and EAGLE²³ that could analyze much larger datasets and whose computation time and memory scaled linearly or nearly linearly with sample size.

Further improvements in computation time came from incorporating methodological ideas from genotype imputation and from data compression, such as the use of a small, custom reference panel for each individual,^24,25 and from the use of the positional Burrows-Wheeler transform²⁶ for efficiently identifying long shared allele sequences.^27,28

Large sequence datasets with hundreds of millions of markers pose new challenges for phasing methods. In this paper, we present a haplotype phasing method, implemented in Beagle 5.2, that is designed for these data. The method uses built-in marker windowing to limit the data that must be stored in memory. It employs a Li and Stephens hidden Markov model (HMM)²⁹ with a parsimonious state space of composite reference haplotypes³ to achieve linear scaling with sample size, and it uses a computationally efficient two-stage phasing algorithm. The two-stage algorithm first phases high-frequency markers by using a progressive phasing methodology that incrementally expands the set of phased heterozygotes. The second stage uses the phased high-frequency markers as a haplotype scaffold for allele imputation and infers phase at low-frequency markers from imputed allele probabilities.^1,30

The resulting method is computationally fast, multi-threaded, and memory efficient. We compare Beagle 5.2 and SHAPEIT 4.2.1 by using default parameters for phasing UK Biobank SNP array data³¹ and TOPMed sequence data.³² We find that the two methods have similar accuracy and computation time on UK Biobank SNP array data. However, Beagle is more than 20 times faster than SHAPEIT on TOPMed sequence data, achieves similar accuracy, and scales to larger sample sizes.

Subjects and methods

The Beagle 5.2 phasing method uses an iterative algorithm. The estimated haplotypes at the beginning of each iteration determine an HMM,³³ which is used for updating the estimated haplotypes. Beagle 5.2 uses the Li and Stephens HMM,^3,20,29,34 which is described in Appendix A.

The HMM state transition probabilities depend on a user-specified effective population size parameter. Because an appropriate value for this parameter may be unknown for some species, Beagle uses the HMM determined by the initial effective population size parameter to estimate and update this parameter via the algorithm described in Appendix B. In the results, we show that this parameter estimation produces good phase accuracy even if the initial parameter value is several orders of magnitude too small or too large.

Marker windows

Beagle uses a sliding marker window. The default window length is 40 cM with 2 cM overlap between adjacent windows. Beagle processes windows in chromosome order and phases the genotypes in each window. If the window is not the first window on the chromosome, Beagle uses the estimated haplotypes from the previous window in the first half of the overlap region.

Beagle’s memory requirements can be controlled by adjusting the length of the sliding marker window. We investigate the relationship between window size, computation time, and memory use in the results.

Progressive phasing

Beagle 5.2 employs a progressive phasing algorithm. Each heterozygous genotype is either “in progress” or “finished.” Initially, all heterozygotes are in progress. In each iteration, we estimate and update the phase of each in-progress heterozygote with respect to the preceding heterozygote. At the end of each phasing iteration, the most confidently phased in-progress heterozygotes are marked as finished. Once a heterozygote is finished, its phase with respect to the previous heterozygote is fixed and cannot be changed in later iterations. At the end of the final iteration, any remaining in-progress heterozygotes are marked as finished.

Our method for estimating the phase of an in-progress heterozygote produces a ratio that measures the confidence in the estimated phase (see updating phase). In each phasing iteration, we rank the remaining in-progress heterozygotes by this ratio and mark a proportion $p$ of these heterozygotes that are the most confidently phased as finished. The proportion $p$ depends on the individual and the number of heterozygous genotypes the individual has in the marker window. We use the same proportion $p$ in each of the individual’s phasing iterations. If there are $I$ phasing iterations ($I=12$ by default), and if an individual has $L$ in-progress heterozygotes at the start of the phasing iterations, we choose $p$ to solve $L{\left(1-p\right)}^I=1,$ so that $p=1-\sqrt[I]{1/L}$. With this choice of $p$, the individual will have approximately one in-progress heterozygote remaining at the end of the final phasing iteration.

Updating phase

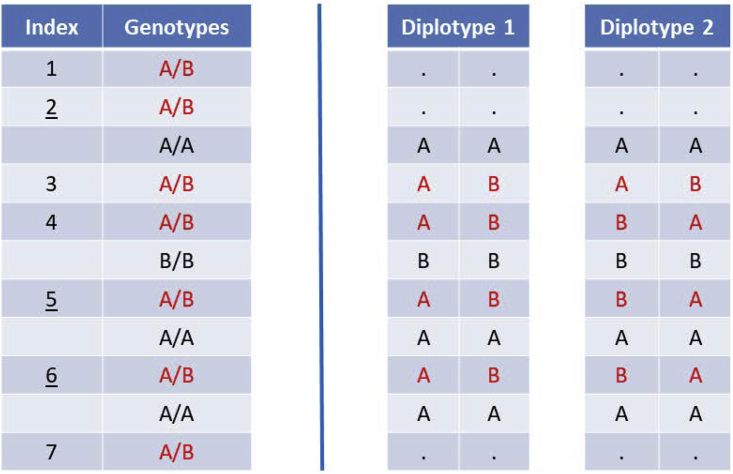
In each iteration, we update the phase of each in-progress heterozygote with respect to the preceding heterozygote. When more than one computing thread is used, phase updating is parallelized by individual. When phasing a target in-progress heterozygote, we mask (i.e., set to missing) all heterozygous genotypes for the individual except the target heterozygote, the preceding heterozygote, and heterozygotes whose phase is known with respect to the target heterozygote or with respect to the preceding heterozygote. For example, if the heterozygote following the target heterozygote is finished, the target heterozygote will have known phase with respect to the following heterozygote. Figure 1 provides an example of this heterozygote masking. After heterozygote masking, there are only two diplotypes consistent with the non-masked genotypes, and these two diplotypes correspond to the two possibilities for the phase of the target heterozygote with respect to the preceding heterozygote.

Figure 1.

Two possible diplotypes after heterozygote masking

The left side lists eleven genotypes in chromosome order whose alleles are labeled A and B. The seven heterozygous genotypes are in red font and are indexed in the left column. Indices of three heterozygous genotypes are underlined (2, 5, and 6). Each of these three heterozygous genotypes is “finished,” which means that the heterozygote has known phase with respect to the preceding heterozygote. Alleles are labeled so that each heterozygote with known phase has the A allele on the same haplotype as the preceding heterozygote. The right side shows the two possible diplotypes after heterozygote masking when phasing the 4^th heterozygote with respect to the 3^rd heterozygote. The 2^nd heterozygote, which has known phase with respect to the 1^st heterozygote, is masked because the 3^rd heterozygote has unknown phase with respect to the 2^nd heterozygote.

We calculate the probability of each haplotype in each of the two diplotypes by using the HMM forward-backward algorithm³³ and Equation A4 in Appendix A evaluated at the marker preceding the target heterozygote. We assume Hardy-Weinberg equilibrium and multiply the probabilities of the two haplotypes in a diplotype to obtain the diplotype probability. The diplotype with larger probability determines the updated phase of the target heterozygote with respect to the previous heterozygote. The ratio of the larger diplotype probability to the smaller diplotype probability is a measure of confidence in the inferred phase.

We avoid duplicate calculations when calculating haplotype probabilities by computing, storing, and reusing HMM forward and backward algorithm results when all heterozygotes are masked. When we estimate the probability of a haplotype by using Equation A4 of Appendix A, the HMM forward calculations are identical to HMM forward calculations with all heterozygotes masked until the first non-masked heterozygote is encountered. Similarly, the HMM backward calculations are identical to HMM backward calculations with all heterozygotes masked until the last non-masked heterozygote is encountered.

The HMM model state space for each individual is constructed from a fixed number of composite reference haplotypes (see composite reference haplotypes below). Consequently, the computational complexity of the HMM calculations for each individual is fixed, and the computation time for updating the phase of all individuals scales linearly with the number of individuals.

In each iteration, after a sample’s haplotype phase is updated, missing alleles are imputed with haploid imputation. For each possible allele, we sum the HMM state probabilities for states (i.e., reference haplotypes) that carry that allele and then impute the missing allele to be the allele with maximal probability.^{1, 2, 3, 4,30,35}

Burn-in iterations

We obtain an initial phasing by using the SHAPEIT 4.0 initialization algorithm that is based on the positional Burrows-Wheeler transform (PBWT).^26,27 This initialization algorithm phases one marker at a time in chromosome order. When phasing marker $m$, the reversed haplotypes for the preceding phased markers (from marker $m-1$ to marker $1$) are sorted in lexicographic order with the PBWT. Homozygous genotypes at marker $m$ determine the alleles carried on that individual’s haplotypes, and these alleles are assigned to haplotypes that are nearby in the PBWT sorting via an algorithm that ensures the assignment is consistent with the genotype data.²⁷ Once alleles are assigned to all haplotypes at marker $m$, the marker is phased, and the algorithm proceeds to the next marker.

After obtaining an initial phasing, Beagle 5.2 performs three burn-in iterations. During each burn-in iteration, Beagle updates the phase of each heterozygous genotype (see updating phase) but does not mark any heterozygotes as finished (see progressive phasing). If fewer than 1% of heterozygotes have their phase changed in a burn-in iteration, the remaining burn-in iterations are skipped.

Composite reference haplotypes

In each iteration, we construct a set of composite reference haplotypes³ for each individual. These composite reference haplotypes are the reference haplotypes in the HMM that is used for updating the individual’s haplotypes. Each composite reference haplotype is a mosaic of haplotype segments from the estimated haplotypes in other individuals at the start of the iteration. Each of these haplotype segments contains an allele sequence that the target individual shares identical by state with another individual.

The algorithm for constructing a set of composite reference haplotypes has been described previously in the context of genotype imputation.³ In the remainder of this section, we summarize the construction algorithm and describe the modifications that we make to the algorithm parameters when constructing composite reference haplotypes for genotype phasing.

The algorithm parameters are as follows:

• (1)the number, $J$, of composite reference haplotypes to be constructed;
• (2)non-overlapping intervals, $I_1,I_2,\dots ,I_K$, that partition the marker window;
• (3)sets $S_1,S_2,\dots ,S_K$ of haplotypes such that haplotypes in $S_k$ are identical by state with the target haplotype in interval $I_k$.

For application to genotype phasing, we make the following changes to the values of these parameters. We construct $J=140$ composite reference haplotypes for each haplotype in the target individual. We combine the composite reference haplotypes for each haplotype in the target individual to obtain an HMM state space of 280 composite reference haplotypes.

We define the intervals $I_1,I_2,\dots ,I_K$ by partitioning the marker window into non-overlapping intervals such that each interval includes all markers whose cM distance from the first marker in the interval is less than three times the median inter-marker cM distance in the marker window.

We define the set $S_k$ to be a singleton set with one haplotype from another individual that has the same allele sequence as the target haplotype in interval $I_k$. If there are no other haplotypes with the same allele sequence in interval $I_k$, $S_k$ is the empty set. We use the PBWT²⁶ to identify a set of $T$ haplotypes from other individuals that have the longest allele sharing with the target haplotype, where length is measured in number of intervals, starting from $I_k$ and working backward toward the first interval. We select a random haplotype that is identical by state with the target haplotype in interval $I_k$ from these $T$ haplotypes, and this random haplotype is the singleton element of the set $S_k$. The value of $T$ is 100 in the burning iterations and decreases linearly with each phasing iteration, starting with $T=90$ in the first phasing iteration and ending with $T=5$ in the final phasing iteration.

Once the sets $S_k$ are determined, we construct the set of $J$ composite reference haplotypes. Each composite reference haplotype is a sequence of haplotype segments. The sequence of haplotype segments is represented by a list of the first markers and a list of the haplotypes in the sequence of segments. The last marker in a segment is the marker preceding the first marker in the following segment or the last marker in the window if there is no following segment. We add a new haplotype segment to a composite reference haplotype by adding the first marker in the segment to the list of first markers and the haplotype to the list of haplotypes.

We process the $S_k$ in order of increasing $k$. Each non-empty, singleton set $S_k=\left\{h\right\}$ generates a haplotype segment that is added to a composite reference haplotype. The copied haplotype is $h$. The starting marker is midway between the first marker in the interval $I_k$ for the current $S_k$ and the first marker in the most recent interval $I_{k^{\prime }}$ $(k^{\prime }<k)$ whose singleton set $S_{k^{\prime }}$contains the haplotype in the preceding segment of the composite reference haplotype.³

Computation time for construction of composite reference haplotypes scales linearly with sample size because the PBWT scales linearly with sample size, and the $S_k$ sets are obtained for all target haplotypes via a single run of the PBWT algorithm.

Two-stage phasing

Sequence data from large samples of individuals contain many markers with very low minor allele frequency. Beagle divides markers into low- and high-frequency markers depending on whether all non-major alleles have frequency $<0.002$ or $\ge 0.002$ (markers may be multi-allelic). If less than 25% of the markers in a window have low frequency, Beagle phases all variants via the progressive phasing algorithm described above. If more than 25% of the markers in a window have low frequency, Beagle employs a two-stage phasing algorithm that substantially reduces the computational effort required to phase the low-frequency markers.

In the first stage, Beagle ignores low-frequency markers and phases the high-frequency markers via the progressive phasing algorithm described above. In the second stage, Beagle uses the phased high-frequency markers and Beagle’s genotype imputation methodology^3,30 to phase the remaining low-frequency heterozygotes. The second stage performs the HMM forward-backward algorithm once per sample and does not use an iterative algorithm. There are two important differences between our use of imputation for phasing and the imputation of ungenotyped markers: our method does not require an external reference panel, and we use imputation to infer the phase of heterozygous genotypes rather than the alleles in missing genotypes.

Because Beagle’s genotype imputation method has been described previously,³ we outline the parts of the second stage algorithm that are borrowed without change, and focus on describing how Beagle’s genotype imputation method is modified to phase low-frequency heterozygous genotypes.

For each target haplotype, we construct a reference panel of composite reference haplotypes at high-frequency markers from the estimated haplotypes in the other individuals. We estimate the HMM haplotype state probabilities by using the HMM forward-backward algorithm at the high-frequency markers.³³ We then use linear interpolation on genetic distance to estimate HMM state probabilities (probabilities of which composite reference haplotype is being copied) at each low-frequency marker for which the target sample has a heterozygous or missing genotype.³⁰

For each composite reference haplotype, we must assign an allele to the haplotype at each low-frequency marker because low-frequency markers were not phased in the first stage. If the reference individual contributing the haplotype segment to the composite reference haplotype is homozygous for an allele at the low-frequency marker, the composite reference haplotype carries that allele. If the reference individual is heterozygous, we assign the lower-frequency allele if the target individual carries that allele and the higher-frequency allele otherwise.

For each haplotype in a target individual, we obtain posterior allele probabilities at a missing or heterozygous low-frequency marker by summing the state probabilities for all reference haplotypes that have been assigned the same allele.^3,30 If the genotype is missing, we choose the allele with highest probability for each target haplotype. If the genotype is heterozygous, we assume Hardy-Weinberg equilibrium and multiply posterior allele probabilities to calculate the posterior probability of the two possible phased heterozygous genotypes. We then choose the phased heterozygous genotype with higher posterior probability.

A phased haplotype scaffold was also used in the 1000 Genomes Project³⁶ for estimating phased haplotypes from genotype likelihoods.³⁷ In the 1000 Genomes Project, external SNP array data for samples were phased separately for production of a haplotype scaffold. During phasing of the 1000 Genomes Project sequence data, estimated haplotypes in each iteration were required to be consistent with this scaffold. In our two-stage method, the input data are genotypes instead of genotype likelihoods, the haplotype scaffold is generated from internal data instead of external data, non-scaffold markers are phased with genotype imputation instead of an iterative phasing algorithm and the two-stage algorithm is used for decreasing computation time rather than improving haplotype accuracy.

Phasing of IBD2 regions

Special care must be taken when phasing a pair of individuals in regions where the two individuals share both haplotypes identically by descent. Such regions are called IBD2 regions, and they commonly occur in full siblings. Two individuals have identical genotypes in an IBD2 region except at sites where an allele is miscalled or a mutation has arisen since the common ancestor. Consequently, both individuals can have identical estimated haplotypes in an IBD2 region. If the estimated haplotypes in the two individuals are identical, they can contain many phase errors and yet still be the most probable haplotypes determined by the HMM.

To protect against elevated phase error rates in IBD2 regions, Beagle 5.2 does not allow either related individual to contribute a haplotype segment to a composite reference haplotype for the other related individual in an IBD2 region.

Beagle detects IBD2 regions by using markers with minor allele frequency $\ge 0.05$. These markers are thinned to ensure a minimum 0.002 cM inter-marker spacing and divided into disjoint intervals that are 1 cM in length, unless there are less than 50 markers in an interval, in which case, the interval is extended to include 50 markers.

For each pair of individuals, we select all intervals that have concordant genotypes at all markers (i.e., the same genotype in both individuals or a missing genotype in at least one individual). We merge any of these intervals separated by a gap of less than 4 cM into a single interval that contains the intervening gap. We then extend the boundaries of the intervals to include any adjacent markers with concordant genotypes. If any interval is longer than 2 cM after this extension, the interval is recorded as an IBD2 segment for the pair of individuals.

The computation time for IBD2 segment detection scales linearly with increasing sample size if the number of pairs of individuals with concordant genotypes in the 1 cM intervals scales linearly with the number of individuals. IBD2 segment detection scales linearly with sample size for the UK Biobank SNP array data and TOPMed sequence data analyzed in this study.

UK Biobank data

We downloaded the UK Biobank autosomal genotype data. After we removed withdrawn individuals, there were 488,332 individuals and 784,256 autosomal diallelic markers before quality control filtering. We excluded markers with more than 5% missing genotypes (n = 70,247), markers that had only one individual carrying a minor allele (n = 5,126), and markers that failed one or more of the UK Biobank’s batch quality control tests (n = 1,527).³¹ There were 711,651 autosomal markers after excluding markers that failed one or more of these filters.

We then excluded 968 individuals that were identified by the UK Biobank as outliers with respect to their proportion of missing genotypes or proportion of heterozygous genotypes, and we excluded nine individuals that were identified by the UK Biobank as showing third degree or closer relationships with more than 200 individuals, which indicates possible sample contamination. There were 487,355 individuals remaining after these exclusions.

We identified parent-offspring trios by using the kinship coefficients and the proportion of markers that share no alleles (IBS0) that are reported by the UK Biobank.^31,38 Pairs of individuals with kinship coefficient between $2^{-2.5}$ and $2^{-1.5}$ were considered to be first-degree relatives. First-degree relatives with IBS0 $<0.0012$ were considered to have a parent-offspring relationship. These are the same kinship coefficient and IBS0 thresholds used by the UK Biobank.³¹ We considered an individual to be the offspring in a parent-offspring trio if the individual has a parent-offspring relationship with exactly one male and exactly one female (the putative parents) and the kinship coefficient for the male and female is less than $2^{-4.5}$. Using this procedure, we identified 1,064 parent-offspring trios having 2,054 distinct parents.

We phased heterozygous genotypes in trio offspring by using Mendelian inheritance constraints when both parent genotypes are non-missing and at least one parent genotype is homozygous. We used these phased genotypes in the trio offspring as the truth when estimating the phase error rate.

We then excluded the 2,054 trio parents, leaving 485,301 individuals. We listed the 1,064 trio offspring followed by the remaining 484,237 individuals in random order. We created five datasets by restricting the UK Biobank data to the first 5,000, 15,000, 50,000, 150,000, and 485,301 individuals in this list.

TOPMed project data

We downloaded Freeze 8 data from the Trans-Omics for Precision Medicine (TOPMed) Program³² for the following studies and dbGaP³⁹ accession numbers: Barbados Asthma Genetics Study (dbGaP: phs001143), Mount Sinai BioMe Biobank (dbGaP: phs001644), Cleveland Clinic Atrial Fibrillation Study (dbGaP: phs001189), Framingham Heart Study (dbGaP: phs000974), Hypertension Genetic Epidemiology Network (dbGaP: phs001293), Jackson Heart Study (dbGaP: phs000964), My Life Our Future (dbGaP: phs001515), Severe Asthma Research Program (dbGaP: phs001446), Venous Thromboembolism Project (dbGaP: phs001402), Vanderbilt Genetic Basis of Atrial Fibrillation (dbGaP: phs001032), and Women’s Health Initiative (dbGaP: phs001237).

We merged and filtered the TOPMed data by using bcftools.⁴⁰ The merged data contain 39,961 sequenced individuals. We restricted the data to polymorphic SNVs with “PASS” in the VCF filter field, leaving 318,858,817 autosomal markers, which include 7,209,890 chromosome 20 markers.

We used the pedigree data for the 1,022 sequenced Barbados Asthma Genetics Study (BAGS) individuals and for the 4,166 sequenced Framingham Heart Study (FHS) individuals to identify 217 BAGS and 669 FHS parent-offspring trios for which the offspring was not a parent in another parent-offspring trio. We phased heterozygous genotypes in trio offspring by using Mendelian inheritance constraints when both parent genotypes are non-missing and at least one parent genotype is homozygous. We used these phased genotypes in the trio offspring as the truth when estimating the phase error rate.

We then excluded the 1,574 parents of the trio offspring, leaving 38,387 individuals. We listed the 886 trio offspring followed by the remaining 37,501 individuals in a random order. We created four datasets by restricting the TOPMed data to the first 5,000, 10,000, 20,000, and 38,387 individuals in this list.

Results

We phased UK Biobank SNP array data and TOPMed sequence data by using Beagle 5.2 (28Jun21.202 release) and SHAPEIT 4.2.1. We ran each method with default parameters. SHAPEIT’s default parameters for sequence data were applied by including its “--sequencing” argument when phasing TOPMed sequence data.

All analyses were run on a 20-core 2.4 GHz computer with Intel Xeon E5-2640 processors and 256 GB of memory. Beagle and SHAPEIT were each run with 20 computational threads. Wall clock computation time was measured with the Linux time command.

We measured phase error by using switch error rate, which is the proportion of heterozygous genotypes that are phased incorrectly with respect to the preceding heterozygous genotype.

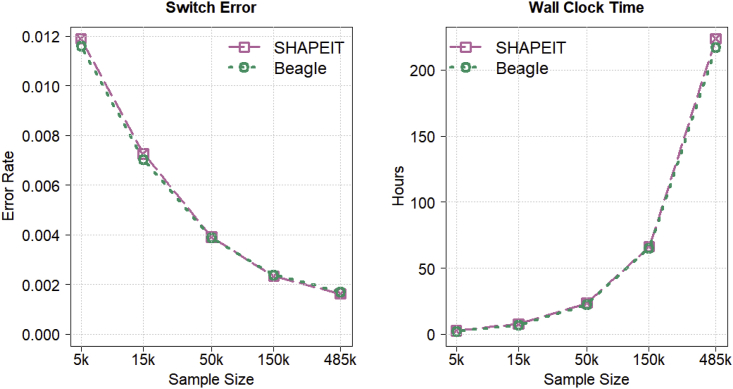
Figure 2 shows autosomal switch error rate and wall clock computation time when phasing expanding subsets of 485,301 UK Biobank individuals. Beagle 5.2 and SHAPEIT 4.2.1 have very similar phase error and computation time for all sample sizes. Beagle’s computation time for phasing the UK Biobank SNP array data scales linearly with sample size, and Beagle’s phase error decreases with increasing sample size.

Figure 2.

Phase accuracy and computation time for autosomal UK Biobank SNP array data

Switch error rate and wall clock computation time for Beagle 5.2 and SHAPEIT 4.2.1 when phasing 5,000, 15,000, 50,000, 150,000, and 485,301 UK Biobank individuals genotyped for 711,651 autosomal markers with default parameter values. Sample size is plotted on the log scale. Switch error rate is calculated with heterozygous genotypes in 1,064 offspring whose phase is determined from parental data that were excluded from the phasing analysis. All analyses were run with 20 threads on a computer server with 20 CPU cores and 256 GB memory.

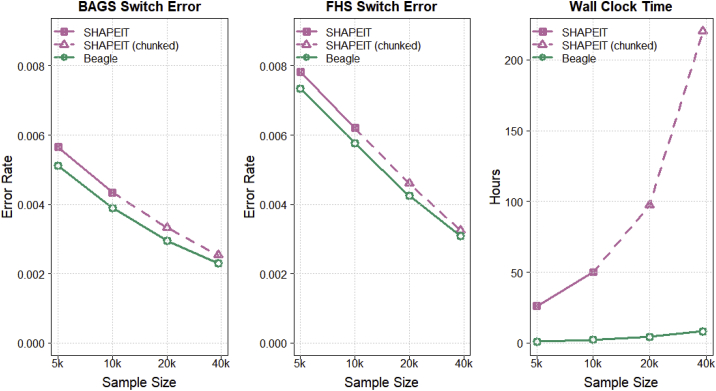
Figure 3 shows switch error rate and computation time for chromosome 20 when phasing expanding subsets of 38,387 sequenced TOPMed individuals. The left panel shows switch error rate in the BAGS trio offspring, the middle panel shows switch error rate in the FHS trio offspring, and the right panel shows wall clock computation time. As with the UK Biobank data, the switch error rate decreases with increasing sample size. SHAPEIT results for phasing chromosome 20 in its entirety are available only for the 5,000 and 10,000 sequenced individuals because SHAPEIT could not phase the 20,000 and 38,387 sequenced individuals within the 256 GB of available computer memory when default parameters were used. Consequently, we ran a chunked SHAPEIT phasing analysis by dividing the chromosome into two segments for the 20,000 samples and dividing the chromosome into three segments for the 38,387 samples. We included 500 kb of overlap between adjacent segments. After the chunked phasing analysis, we created a single phased VCF output file by aligning the haplotypes in adjacent chunks by using the phase of a heterozygote in the middle of the overlap and then splicing haplotypes in adjacent chunks with a splice point in the middle of the overlap.

Figure 3.

Phase accuracy and computation time for phasing TOPMed chromosome 20 sequence data

Switch error rate and wall clock computation time for Beagle 5.2 and SHAPEIT 4.2.1 when phasing 5,000, 10,000, 20,000, and 38,387 sequenced TOPMed individuals genotyped for 7,209,890 chromosome 20 markers with default parameter values. Sample size is plotted on the log scale. Switch error rate is computed with heterozygous genotypes in 217 BAGS and 669 FHS offspring whose phase is determined from parental data that were excluded from the phasing analysis. All analyses were run with 20 threads on a computer server with 20 CPU cores and 256 GB of memory. The SHAPEIT whole-chromosome phasing of the 20,000 and 38,387 individuals did not complete because of insufficient memory. SHAPEIT results for the 20,000 and 38,387 individuals were obtained by dividing the chromosome into two and three chunks, respectively, and phasing each chunk separately. Adjacent chunks had 500 kb overlap. The SHAPEIT wall clock for each sample size is the sum of the wall clock times for the individual chunks. The procedure for merging the individual chunks for each sample size is described in the subjects and methods.

Beagle’s computation time for phasing the TOPMed sequence data scales linearly with sample size, and Beagle’s phase error decreases with increasing in sample size. Beagle 5.2 and SHAPEIT 4.2.1 have similar error rates on the TOPMed sequence data, but Beagle’s computation time ranged from 23.0 times faster (for 20,000 samples) to 26.7 times faster (for 38,387 samples). For each sample size, the phase error rate is lower in the BAGS trio offspring than in the FHS trio offspring, which could be due to differences in population demographic history.

The computational efficiency of two-stage phasing in the sequence data can be seen by comparing the wall clock time for phasing 5,000 sequenced TOPMed samples and 5,000 UK Biobank samples. The TOPMed chromosome 20 data have 7,209,890 markers and the UK Biobank chromosome 20 data have 18,424 markers. Although the TOPMed sequence data have 391-fold more markers than the UK Biobank SNP array data, there is only a 17-fold difference in wall clock time (62.4 versus 3.6 min). For the TOPMed sequence data, Beagle’s wall clock time for the second stage of phasing is approximately one-third of the wall clock time for the first stage of phasing.

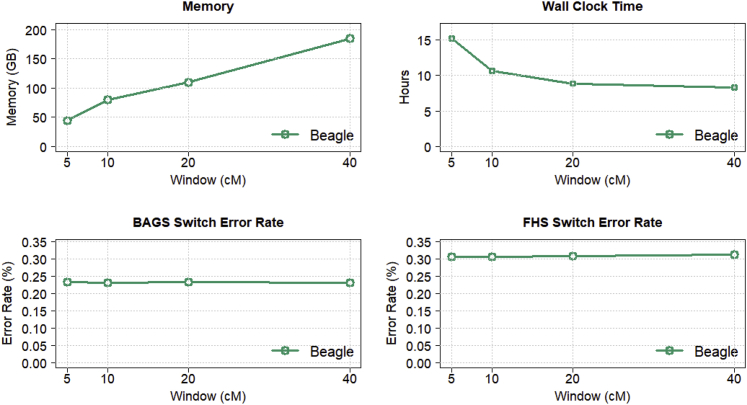
One can reduce Beagle’s memory requirements to permit analysis of larger datasets by shortening the marker window. The default window length is 40 cM. We repeated the Beagle phasing of the 38,387 TOPMed individuals with 5, 10, 20, and 40 cM window lengths and default values for all other parameters. For each window length, we ran phasing analyses with different limits on the amount of memory available to the Java virtual machine in order to determine the minimum amount of memory (in units of 5 GB) required to successfully complete the analysis.

Figure 4 shows results for 5, 10, 20, and 40 cM marker windows. Accuracy is similar for all window lengths. Reducing the window length from the default 40 cM to 10 cM reduces memory use by 57% (from 185 GB to 80 GB) at the cost of a 28% increase in running time. Further reducing the window length from 10 cM to 5 cM gives an additional 44% reduction in memory use (from 80 GB to 45 GB) and an additional 43% increase in running time. Computational efficiency decreases as the window length decreases because the 2 cM overlap between windows occupies an increasing proportion of each window.

Figure 4.

Memory and computation time as a function of window length

Beagle 5.2 memory use, wall clock time, and switch error rate when phasing 38,387 sequenced TOPMed individuals genotyped for 7,209,890 chromosome 20 markers when using 5, 10, 20, and 40 cM marker windows. The default window length is 40 cM. All other parameters were set to default values. Switch error rate is computed with heterozygous genotypes in 217 BAGS and 669 FHS offspring whose phase is determined from parental data that were excluded from the phasing analysis. All analyses were run with 20 threads on a computer server with 20 CPU cores and 256 GB of memory.

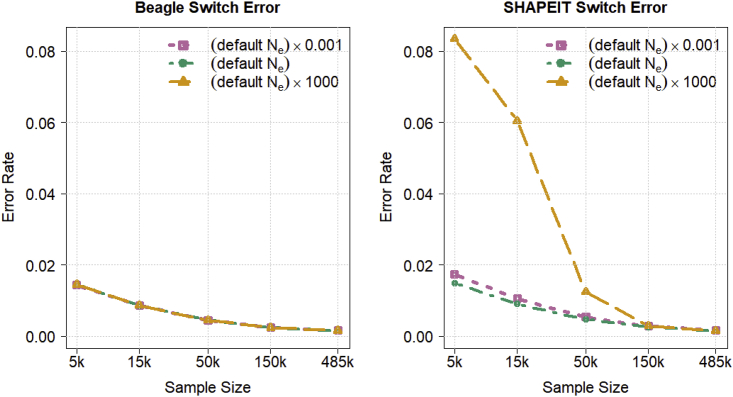
We tested Beagle’s methods for estimating the effective population size parameter used in the HMM transition probabilities by using Beagle and SHAPEIT to phase expanding samples of the chromosome 20 UK Biobank data. For each program, we varied the user-specified effective population size parameter to range from three orders of magnitude smaller than the default value to three orders of magnitude larger than the default value. All other parameters were set to their default values. Figure 5 shows that Beagle’s parameter estimation results in phase accuracy that is independent of the user-specified effective population size. The SHAPEIT results in Figure 5 illustrate that without such estimation the switch error rate can be inflated when the user-specified effective population size is too large unless the sample size is very large.

Figure 5.

Phase accuracy as a function of user-specified effective population size

Switch error rate for Beagle 5.2 and SHAPEIT 4.2.1 when phasing 5,000, 15,000, 50,000, 150,000, and 485,301 UK Biobank individuals genotyped for 18,424 chromosome 20 markers for three different user-specified values of the effective population size parameter: the program’s default parameter value, a value 1,000 times smaller than the default value, and a value 1,000 times larger than the default value. All other analysis parameters are set to their default values. Switch error rate is calculated with heterozygous genotypes in 1,064 offspring whose phase is determined from parental data that were excluded from the phasing analysis. Beagle’s switch error rate does not depend on the user-specified effective population size parameter because Beagle estimates and updates this parameter.

Discussion

We have introduced a haplotype phasing method that is implemented in Beagle 5.2. The computation time for this phasing method scales linearly with sample size, and it can phase hundreds of thousands of array-genotyped samples and tens of thousands of sequenced samples.

We compared phase accuracy by using default settings for Beagle 5.2 with SHAPEIT 4.2.1 when phasing UK Biobank autosomal SNP array data³¹ and TOPMed chromosome 20 sequence data.³² Both methods had similar accuracy on both types of data and similar computation time when phasing SNP array data. However, when phasing sequence data, Beagle was more than 20 times faster and was able to analyze larger samples within the available computer memory.

Beagle uses a sliding marker window that limits memory use and enables whole-chromosome phasing of large sequence datasets in a single analysis. Memory use can be decreased without loss of accuracy by decreasing the window length. For the TopMed data, a reduction of window length from 40 cM to 5 cM reduced memory use by 76% at the cost of an 82% increase in computation time.

Beagle version 5.2 introduces a two-stage, progressive phasing methodology, and it incorporates methodological ideas that were originally developed for genotype imputation, such as composite reference haplotypes³ and linear interpolation of HMM state probabilities.³⁰

Progressive phasing identifies confidently phased heterozygotes and fixes the phase of these heterozygotes in subsequent iterations. As a result, the information available to phase the heterozygotes with more ambiguous phasing increases with each phasing iteration.

Two-stage phasing gives a large reduction in computation time when a high proportion of variants have low frequency, as is generally the case with sequence data. The first stage phases the limited number of high-frequency variants and these variants become a haplotype scaffold for imputing alleles at low-frequency variants in the second stage. The two-stage approach reduces computation time because the low-frequency markers are excluded from the time-consuming iterative phasing algorithm.

For non-human species, the effective population size may be unknown. Beagle 5.2 protects against a misspecified effective population size by estimating and updating the effective population size parameter during its burn-in iterations. The Mach phasing method also estimates and updates this parameter.²⁰ Beagle calculates its estimate from HMM state probabilities as described in Appendix B, while Mach calculates its estimate by using data obtained from sampled haplotypes.²⁰

Memory continues to be a constraint when phasing large sequence datasets, and reducing memory requirements is an area for future work. Improved memory efficiency would enable larger datasets to be analyzed on computers that have less memory. Beagle 5.2 is implemented in Java, and memory deallocation is under the control of the Java virtual machine. Implementing Beagle in a systems programming language that gives fast execution times and fine-grained control of memory has the potential to significantly reduce memory use and computation time. Another important area for future work will be adding the capability to incorporate existing phase information, such as phase information extracted from sequence reads.²⁷ Extraction of phase information from sequence reads is feasible for smaller sample sizes that have a manageable amount of sequence read data.

As genotype datasets have grown, phasing methodology has responded. The release of the UK Biobank SNP array data³¹ motivated the development of a series of statistical phasing methods that advanced the state of the art, including Eagle1,²³ SHAPEIT3,⁴¹ Eagle2,²⁸ Beagle 5.1, and SHAPEIT4.²⁷ The advent of whole-genome sequence datasets has provided a new impetus for further development of phasing methodology. We show that Beagle 5.2 scales to tens of thousands of sequenced individuals. Further advances in phasing methodology will be needed to address the challenge of future datasets with hundreds of thousands or millions of sequenced individuals.

Published: September 2, 2021

Appendix A: Hidden Markov model

We use the Li and Stephens HMM to calculate the probability of a haplotype of alleles from $M$ markers.^3,20,29,34 The model states are a set of $H$ reference haplotypes. Let ${\mathcal{S}}_m\in \left\{1,2,\dots ,H\right\}$denote the unobserved HMM state at marker $m\in \left\{1,2,\dots ,M\right\}$. In the Li and Stephens HMM, a target haplotype is modeled as a mosaic of reference haplotype segments, and the state ${\mathcal{S}}_m$ represents the reference haplotype being copied at marker $m$. The initial HMM probabilities are $P\left({\mathcal{S}}_1=h\right)=1/H$ for each reference haplotype $h$. The emission probabilities are determined by the reference haplotype alleles. A state ${\mathcal{S}}_m=h$ emits the allele carried by reference haplotype $h$ at marker $m$ with probability $\left(1-\epsilon \right)$ and emits a different allele with probability $\epsilon$, where $\epsilon =\theta /\left(2\theta +2H\right)$ and $\theta =1/\left(\log H+0.5\right)$.³⁴

Transition probabilities depend on the genetic distance, effective population size $N_e$, and number of reference haplotypes $H$.³⁴ If markers $m-1$ and $m$ are separated by $d_m$ Morgans and if

$${\tau }_m=1-e^{-4N_e{d}_m/H},$$ (Equation A1)

then the state transition probabilities are defined as³⁴

$$P\left({\mathcal{S}}_m=h^{\text{′}}|{\mathcal{S}}_{m-1}=h\right)=\{\begin{array}{l}{\tau }_m/H,h\ne h^{\prime }\hfill \\ \left(1-{\tau }_m\right)+{\tau }_m/H,h=h^{\prime }\hfill \end{array}.$$ (Equation A2)

An observed haplotype $O$ is a sequence of alleles $O_1,O_2,\dots ,O_M$ where $O_m$ denotes the allele at the $m$-th marker. Because the observed haplotype is assumed to correspond to an unobserved sequence of HMM states ${\mathcal{S}}_1,{\mathcal{S}}_2,\dots ,{\mathcal{S}}_M$, we can use the HMM forward-backward algorithm³³ to calculate the haplotype probability $P\left(O\right)$. The forward probabilities ${\alpha }_m\left(h\right)$ and backward probability ${\beta }_m\left(h\right)$ for reference haplotype $h$ at marker $m$ for the observed haplotype $O$ are defined as

$${\alpha }_m\left(h\right)=P\left({\mathcal{S}}_m=h,O_1,O_1,\dots ,O_m\right){\beta }_m\left(h\right)=P\left(O_{m+1},O_{m+2},\dots ,O_M|{\mathcal{S}}_m=h\right).$$ (Equation A3)

These probabilities are calculated via a dynamic programming algorithm.³³ For any marker $m$, the probability of the observed allele sequence is

$$P\left(O\right)=\sum _{h=1}^{H}P\left(O_1,O_2,\dots ,O_M,{\mathcal{S}}_m=h\right)=\sum _{h=1}^H{\alpha }_m\left(h\right){\beta }_m\left(h\right).$$ (Equation A4)

The probability of an individual state, conditional on the observed data, is

$$P\left({\mathcal{S}}_m=h|O\right)=\frac{{\alpha }_m\left(h\right){\beta }_m\left(h\right)}{{\sum }_{h^{\text{′}}=1}^H{\alpha }_m\left(h^{\text{′}}\right){\beta }_m\left(h^{\text{′}}\right)}.$$ (Equation A5)

We use Equation A5 to impute missing alleles on a haplotype. We obtain posterior allele probabilities by summing the state probabilities for all reference haplotypes that carry the same allele and choosing the allele with highest posterior probability.^1,30

Appendix B: Estimating effective population size

The HMM transition probabilities in Equation A2 of Appendix A depend on the effective population size, which may be unknown for non-human populations. Consequently, after the initial haplotypes are determined and after each burn-in iteration, Beagle 5.2 estimates and updates the effective population size via an iterative expectation-maximization-type procedure.^33,42

At each marker $m$, Beagle estimates ${\tau }_m$ by setting $h=h’$ in Equation A2, conditioning on an observed haplotype $O$, and then summing the conditional transition probabilities for the haplotypes weighted by the state probabilities $P\left({\mathcal{S}}_{m-1}=h|O\right)$:

$$\left(1-{\tau }_m\right)+\frac{{\tau }_m}{H}=\sum _{h=1}^{H}P\left({\mathcal{S}}_m=h|{\mathcal{S}}_{m-1}=h,O\right)P\left({\mathcal{S}}_{m-1}=h|O\right)=\sum _{h=1}^{H}P\left({\mathcal{S}}_m=h,{\mathcal{S}}_{m-1}=h|O\right)=\frac{1}{P\left(O\right)}\sum _{h=1}^{H}P\left({\mathcal{S}}_m=h,{\mathcal{S}}_{m-1}=h,O\right).$$

Solving the preceding equation for ${\tau }_m$ gives the estimate

$${\hat{\tau }}_m=\frac{H}{H-1}\left(1-\frac{1}{P\left(O\right)}\sum _{h=1}^{H}P\left({\mathcal{S}}_m=h,{\mathcal{S}}_{m-1}=h,O\right)\right).$$

We calculate $P\left(O\right)$ by using Equation A4. We calculate $P\left({\mathcal{S}}_m=h,{\mathcal{S}}_{m-1}=h,O\right)$ by using the forward and backward probabilities defined in Equation A3 and the transition probability defined by Equations A1 and A2 and the current value of the $N_e$ parameter:

$$P\left({\mathcal{S}}_m=h,{\mathcal{S}}_{m-1}=h,O\right)={\beta }_m\left(h\right)P\left(O_m|{\mathcal{S}}_m=h\right)P\left({\mathcal{S}}_m=h|{\mathcal{S}}_{m-1}=h\right){\alpha }_{m-1}\left(h\right)={\beta }_m\left(h\right)P\left(O_m|{\mathcal{S}}_m=h\right)\left(\left(1-{\tau }_m\right)+\frac{{\tau }_m}{H}\right){\alpha }_{m-1}\left(h\right).$$

For small genetic distances, ${\tau }_m$ $\approx \left(\frac{4N_e}{H}\right)d_m$ by Equation A1. We select a random set of 500 samples or all samples if there are fewer than 500 samples. After we estimate the ${\hat{\tau }}_{m,h}$ for each marker $m$ and each haplotype $h$ in these samples, we estimate the effective population size $N_e$ as

$${\hat{N}}_e=\frac{H{\sum }_{m,h}{\hat{\tau }}_{m,h}}{4{\sum }_{m,h}{d}_m}.$$

We update the effective population size parameter $N_e$ to be the estimated value. This procedure for updating the $N_e$ parameter is repeated until a stopping condition is met. The iterative procure stops when the updated value of $N_e$ results in less than a 10% change in the value of $\left(\frac{4N_e}{H}\right)$.

Data and code availability

Beagle is licensed under the GNU General Public License (version 3) and is freely available for academic and commercial use. The Beagle 5.2 source code is written in Java and can be downloaded from https://faculty.washington.edu/browning/beagle/beagle.html.

Web resources

Beagle 5.2, https://faculty.washington.edu/browning/beagle/beagle.html