Unconventional Disorder by Femtosecond Laser Irradiation in Fe₂O₃

Abstract

This paper demonstrates that femtosecond laser-irradiated Fe₂O₃ materials containing a mixture of α-Fe₂O₃ and ε-Fe₂O₃ phases showed significant improvement in their photoelectrochemical performance and magnetic and optical properties. The absence of Raman-active vibrational modes in the irradiated samples and the changes in charge carrier emission observed in the photocurrent density results indicate an increase in the density of defects and distortions in the crystalline lattice when compared to the nonirradiated ones. The magnetization measurements at room temperature for the nonirradiated samples revealed a weak ferromagnetic behavior, whereas the irradiated samples exhibited a strong one. The optical properties showed a reduction in the band gap energy and a higher conductivity for the irradiated materials, causing a higher current density. Due to the high performance observed, it can be applied in dye-sensitized solar cells and water splitting processes. Quantum mechanical calculations based on density functional theory are in accordance with the experimental results, contributing to the elucidation of the changes caused by femtosecond laser irradiation at the molecular level, evaluating structural, energetic, and vibrational frequency parameters. The surface simulations enable the construction of a diagram that elucidates the changes in nanoparticle morphologies.

1. Introduction

The abundance of iron compounds in nature has attracted much interest in fundamental research due to their technological applications, mainly in the nanoscale, and the presence of polymorphs.¹ However, at atmospheric pressure and room temperature, Fe₂O₃ polymorphs have the same chemical composition for the five different structural phases: α-Fe₂O₃, β-Fe₂O₃, γ-Fe₂O₃ (maghemite), ε-Fe₂O₃, and ζ-Fe₂O₃. α-Fe₂O₃ is the most abundant and the most thermodynamically stable phase form.^1,2 The ε-Fe₂O₃ phase is commonly detected along with other polymorphs (γ-Fe₂O₃ and/or α-Fe₂O₃), being considered a metastable product between these two Fe₂O₃ phases.³ Additionally, despite having low abundance in nature, it can be found in clays and as biogenic nanoparticles mixed with magnetite.^4,5 The formation and existence of this phase are dependent on low surface energy of the particles.⁶ The physicochemical properties of the Fe₂O₃ compounds are strategic for the development of information storage devices in the digital world because these chemical compounds have different crystal structures and therefore distinct magnetic properties.^1,7−10

Additionally, water splitting is a successful technology that uses solar energy for photoelectrochemical processes^2,11,12 to generate clean, renewable, and sustainable energy as electricity or green fuel such as hydrogen.^13,14 α-Fe₂O₃ is a potential sunlight converter, as it is an n-type semiconductor with a band gap from 1.9 to 2.2 eV. Other interesting applications include lithium batteries,¹⁵ pigments,¹⁶ gas sensors,¹⁷ electroanalysis for lead detection,¹⁸ and even carriers of drugs to treat cancer cells.^19,20 One way to connect the properties to the crystalline structure of the materials is to understand the order–disorder effects on their structures, providing several technological applications that allow the control of physicochemical properties.²¹

Among the conventional disorders of Fe₂O₃ materials are those caused by heat treatments that enable the phase transformation of their metastable polymorphs to the α-Fe₂O₃ phase, associated with the growth of the surfaces of metastable polymorphs that contribute as a substrate for the conversion of the α-Fe₂O₃ phase. However, an unconventional disorder caused by femtosecond laser irradiation in Fe₂O₃ materials occurs by changing the chemical energy, which leads to an increase in the density of defects on the surfaces of metastable polymorphs, preventing phase transition and optimizing photoelectrochemical, magnetic, and optical properties of these irradiated materials. The femtosecond laser irradiation treatment enables the synthesis of materials with new features, changing the structure of the surface and improving the material properties, such as the structure and ablation.^22,23 The strong modification produced by the femtosecond laser irradiation creates oxygen and cation vacancies, modulating the electronic states (orbitals) on the valence band (VB) of the material.²⁴

This study aimed to evaluate the surface effects of the Fe₂O₃ particles heat-treated at 860 °C for 30 min, at 900 °C for 10 min, and at 900 °C for 30 min, before and after femtosecond laser irradiation. Experimental measurements and computational simulations via the density functional theory (DFT) method to explain the singular properties and the interface associated with the ε-Fe₂O₃ → α-Fe₂O₃ phase transformation were carried out.

2. Results and Discussion

The thermogravimetric analysis (TGA)/differential thermal analysis (DTA) curves illustrated in Figure 1 show four thermal events of the Fe₂O₃ sample obtained by the hydrothermal process; two endothermic processes at 110 and 650 °C, attributed to the loss of water of hydration of the sample and to the Néel temperature of the hematite, respectively;⁵² and two exothermic processes, the first one being at 243 °C, corresponding to the release of CO₂ and/or CO gases due to the presence of organic impurities resulting from the synthesis process, while the second and the most important thermal event, at 860 °C, exhibited no mass loss in the TGA curve.

Figure 1.

TGA (red line) and DTA (blue line) in the curves of Fe₂O₃ samples.

Besides, the exothermic peak seen in the figure can be attributed to the ε-Fe₂O₃ → α-Fe₂O₃ phase transformation.⁵³ Based on the thermal behavior, it was possible to evaluate the surface effects of the Fe₂O₃ particles that were submitted to heat treatments at 860 °C for 30 min and at 900 °C for 10 and 30 min, hereafter referred to as 860-30, 900-10, and 900-30 samples, respectively.

The X-ray diffraction (XRD) patterns for the nonirradiated and femtosecond laser-irradiated materials are shown in Figure 2. The 900-10 and 860-30 (nonirradiated and irradiated samples) are identified as a multiphase, and the peaks are indexed to the Inorganic Crystal Structure Database (ICSD) number 15840⁵⁴ and 415250,^55,56 corresponding to the α-Fe₂O₃ and ε-Fe₂O₃ phases, respectively. These phases have rhombohedral (R3̅cH) and orthorhombic (Pna2₁) structures with six and eight molecular formulas per unit cell (Z = 6 and 8), respectively. On the other hand, the 900-30 nonirradiated and irradiated samples are a single phase, formed by α-Fe₂O₃.

Figure 2.

XRD patterns for the α-Fe₂O₃ and ε-Fe₂O₃ materials heat-treated at 860 °C for 30 min (860-30), at 900 °C for 10 min (900-10), and at 900 °C for 30 min (900-30). In (a) nonirradiated materials and in (b) femtosecond laser-irradiated materials.

To better understand the long-range properties of the α-Fe₂O₃ and ε-Fe₂O₃ particles, the Rietveld refinement²⁶ method was applied. Table 1 and Figure SI-1 (Supporting Information) display the results. The sharp and well-defined diffraction peaks indicate a high-crystalline structural order at a long range. The lattice parameter and unit cell volume data in accordance with those reported in the previous work⁵⁴⁻⁵⁶ and with our computational simulations are reported in Table 1. The fitting parameters (Rw %) show a good agreement between the calculated XRD patterns and those observed for all samples. However, a nonlinear variation in the Rw % is connected to the crystallization solubilization and recrystallization processes promoted by heat treatment on the α-Fe₂O₃ and ε-Fe₂O₃ particles.

Table 1. Lattice Parameters (Å), Unit Cell Volume (V in ų), Crystallite Size (Å), Microstrain, and Rietveld Refinement Quality Factors (% wt and Rw %) for Both α-Fe₂O₃ and ε-Fe₂O₃ Phases.

	α-Fe2O3						ε-Fe2O3
	lattice parameters (Å)						lattice parameters (Å)
sample	a = b	c	V (Å3)	crystallite size (Å)	microstrain	% wt fraction	a	b	c	V (Å3)	crystallite size (Å)	microstrain	% wt fraction	Rw %
900-30	5.0403	13.7583	302.699	0.84	921.9	1.000
900-30 irradiated	5.0354	13.7481	301.886	0.73	1390.9	1.000
900-10	5.0231	13.7097	299.573	0.96	1290.4	0.681	5.0735	8.7681	9.4428	420.073	0.29	7347.5	0.319	12.615
900-10 irradiated	5.0331	13.7359	301.350	0.80	1267.7	0.565	5.0869	8.7999	9.3856	420.147	0.26	142396.6	0.435	12.315
860-30	5.0350	13.7329	301.505	0.45	1282.7	0.376	5.0907	8.7808	9.4649	423.088	0.25	–599.4	0.624	9.414
860-30 irradiated	5.0375	13.7385	301.930	0.40	2215.5	0.379	5.0912	8.7894	9.4696	423.739	0.25	–1741.8	0.621	8.943
DFT	5.107 (this work)	13.779	311.27				5.183 (this work)	8.911	9.616	444.12
	5.06758	13.882					5.12542	8.854	9.563	433.94
α-Fe2O354	5.038	13.772	302.72
ε-Fe2O355, 56							5.0715	8.7359	9.4178	417.25

Another point to consider is that the Rietveld refinement method identified the percentage of the α-Fe₂O₃ and ε-Fe₂O₃ phases present under each different heat treatment condition, after and before femtosecond laser irradiation. Table 1 shows that the preferential formation of the α-Fe₂O₃ phase (900-30 nonirradiated samples) is attributed to the increase in temperature and time during the heat treatment when compared to the 860-30 nonirradiated samples.

Local distortion of the crystalline planes gives rise to nonuniform variations in the interplanar spacings called microstains.⁵⁷ The femtosecond laser irradiation contributed to an increase in the microstrain value through an increase in the density of defects and stress in the crystalline lattice, leading to structural deformations. This phenomenon affects many material properties, creating corrosion, fatigue strength, hardness, and cracking.

From an inspection of Tables 1 and SI-1 (Supporting Information), the α-Fe₂O₃ crystalline structure is composed of regular prismatic [FeO₆] clusters, while the ε-Fe₂O₃ phase exhibits a distorted crystalline arrangement constituted by three highly distorted [FeO₆] clusters and one [FeO₄] unit, as shown in Figure 3.

Figure 3.

Conventional unit cell representation for both (a) α-Fe₂O₃ and (b) ε-Fe₂O₃ phases, highlighting the cluster units. The brown and red balls correspond to iron and oxygen atoms, respectively.

Theoretical results for lattice parameters of both phases (Table 1) indicate an overestimated value in comparison with the experimental values, the relative percentage errors being 1.37 (a) and 0.05% (c) for α-Fe₂O₃ and 2.20 (a), 2.00 (b), and 2.10% (c) for ε-Fe₂O₃. From a theoretical point of view, these crystalline arrangements are important to elucidate the intriguing properties associated with the ε → α-Fe₂O₃ phase transition. Indeed, such distortions contribute to creating intermediary energy levels in the band gap region and inducing very singular magnetic orderings connected to the interface between the phases.

The calculated energy difference between antiferromagnetic (AFM) and ferromagnetic (FEM) models indicates the AFM state as the magnetic ground state for both α-Fe₂O₃ and ε-Fe₂O₃ phases, being the greatest difference associated with the spin distribution along the different axis. For instance, a G-type arrangement described the AFM ground state for the α-Fe₂O₃, where each Fe²⁺ (4.297 μ_B) was ordered antiparallel to each neighbor. On the other hand, the ε-Fe₂O₃ showed a spin arrangement as a function of different Fe-centered clusters (↓↑↑↓); the local magnetic moments were calculated as −4.257, 4.276, 4.242, and −4.204 μ_B for Fe(I), Fe(II), Fe(III), and Fe(IV), respectively.

The 860-30 nonirradiated sample was mainly composed of ε-Fe₂O₃, although a small amount of α-Fe₂O₃ was also present. With the temperature increase to 900 °C, the amount of α-Fe₂O₃ increases (sample 900-10, nonirradiated). When increasing the time for the 900-30 nonirradiated sample, only the phase α-Fe₂O₃ was detected, as observed in the Rietveld refinement results. To complement the experimental analysis, Raman modes were calculated for the α-Fe₂O₃ and ε-Fe₂O₃ phases and were compared to the nonirradiated sample Raman vibrational modes, as shown in Figure 4a.

Figure 4.

Raman spectra for (a) nonirradiated samples and theoretical spectra simulated for both α-Fe₂O₃ and ε-Fe₂O₃ phases. In (b) irradiated samples.

Raman modes of the irradiated samples are shown in Figure 4b. The vibrational modes obtained in this work are shown in Tables SI-2 and SI-3. For α-Fe₂O₃, the results indicated seven Raman-active modes described as 2A_1g + 5E_g. On the other hand, the calculated Raman-active modes for the ε-Fe₂O₃ indicated the presence of 117 modes without any degeneracy, following group theory, 29A₁ + 30A₂ + 29B₁ + 29B₂; while experimentally, only the 860-30 nonirradiated samples had the vibrational modes of ε-Fe₂O₃, these samples showed seven vibrational modes in Raman.

Figure SI-2 helps to identify the atomic displacement for each Raman-active mode to α-Fe₂O₃, shown in Figure 4. The 218.90 and 229.37 cm^–1 modes are attributed to the stretching of Fe–O bonds in symmetric and asymmetric directions, respectively. The intense ones at 307.89 and 415.03 cm^–1 are related to the bending of Fe–O–Fe bond paths, while those at 511.92 and 585.92 cm^–1 are assigned to the bending and stretching movements of the [FeO₆] units, respectively.

The appearance of two other modes, one at 1320 cm^–1, referring to the transition of collective rotation derived from a typical dispersion of two magnets,⁵⁹ and another one at 1313 cm^–1, related to 2-magnon scattering bands of α-Fe₂O₃,⁶⁰ was seen in the Raman spectrum of the 900-10 nonirradiated and 900-30 nonirradiated samples.

The simulation of Raman spectra was fundamental to effectively assign the experimental peaks. Indeed, the calculated Raman spectra for the ε-Fe₂O₃ (Figure 4a) evidenced the complex nature of the spectroscopic properties of this phase, as shown in Figure SI-2. In particular, theoretical Raman spectra agree with the experimental data reported by López-Sánchez et al.⁶¹ The bending movements of the O–Fe–O bonds for all [FeO₆] and [FeO₄] clusters are attributed to low-energy bands located up to approximately 300 cm^–1. In the medium-energy range (300–450 cm^–1), the band corresponds to the symmetric and asymmetric stretching of the Fe–O bonds in the Fe(III), [FeO₆] cluster. The 450–610 cm^–1 range is assigned to the stretching of Fe(I)–O/Fe(II)–O, Fe(I)–O/Fe(IV)–O, Fe(I)–O, and Fe(I)–O/Fe(IV)–O bonds, which are connections between [FeO₆] and [FeO₄] clusters. The symmetrical stretching of Fe(I)–O bonds is associated with the high-energy peak located at 753.90 cm^–1. Here, it is important to highlight that the high structural distortion on the [FeO₆] and [FeO₄] clusters justifies the complexity of Raman analysis for the ε-Fe₂O₃ phase.

As far as we know, Raman vibrational modes of the ε-Fe₂O₃ phase have not been identified in the literature yet, since no spectrum from an isolated phase has ever been measured. Therefore, the theoretical studies were essential; the high-level theoretical approach to simulate the ε-Fe₂O₃-phase Raman vibrational modes is a strong indication of the structural properties of this material. One of the advantages of the DFT approach was the ability to simulate every single phase apart from fomenting an analysis more accurately and without the interference of the other phases.

According to Figure 4b, it is possible to observe that the effect of femtosecond laser irradiation on the sample order is very pronounced. The results of full width at half maximum (fwhm) of the Raman bands of the nonirradiated and irradiated samples (Tables SI-4 and SI-5, respectively) show that the irradiated particles presented higher values than the other samples, which may be an indication of the increase in the crystalline lattice disorder in these samples. Such results demonstrate that femtosecond laser irradiation causes a break in the Fe–O bonds, a distortion in the crystalline lattice of the samples, and an increase in the defect density, which can result in changes in the sample properties.

Figure SI-3 illustrates the UV–vis diffuse reflectance spectra in the range of 250–800 nm of nonirradiated and irradiated samples. The optical band gap energy (E_gap) values of the Fe₂O₃ samples were calculated according to Wood and Tauc⁶² and Chen et al.⁶³ All samples showed absorbance in the region close to 570 nm, indicating that in this wavelength range, these samples have potential for application as absorbent materials.⁶⁴

Concerning the DFT-based electronic structure analysis, the band structure profiles for α-Fe₂O₃ (Figure SI-4a) indicated an indirect band gap energy value of 2.77 eV, starting from an intermediary point between Γ and T called as Y to Γ in the CB (conduction band). For ε-Fe₂O₃ (Figure SI-4b), the band gap was determined as 3.08 eV, being an indirect band gap transition between the symmetry points (U–Γ). Herein, it is important to note that theoretical values agree with previous investigations considering a hybrid exchange–correlation functional.⁶⁵

Considering the indirect transition, the results show that the nonirradiated samples presented an E_gap value of approximately 2 eV, which agrees with the literature.⁶⁶ A slope responsible for decreasing the E_gap value can be seen in the optical absorption curves for all samples. However, with the increase in the heat-treatment time and temperature, the samples become more ordered, thus reducing the slope. The major sources of the difference between theoretical and experimental data are represented by the surface exposure that can generate undercoordinated sites with a reduced band gap energy as discussed later.

Defects produced in Fe₂O₃ by femtosecond laser irradiation induce changes in bonds and bond angles of clusters on different surfaces. This disorder influences the different electronic densities of the surfaces, changing the semiconductor band gap and consequently its properties. In this way, different semiconductors can be obtained depending on the desired property, characterizing a more conductive behavior of the irradiated samples in the medium-range order.⁶⁷ These findings also point to the existence of electronic levels located within the prohibited band, which are associated with the presence of defects, such as distortions and vacancies, responsible for causing a structural lattice disorder, previously observed in XRD and Raman analyses.

The analysis of density of states (DOS) projections, as depicted in Figure SI-4, indicates that for the α-Fe₂O₃ phase (Figure SI-4a), the VB is mainly composed of oxygen (2p) states, while the CB is predominantly constituted by empty Fe 3d states. On the other hand, the DOS profiles for ε-Fe₂O₃ (Figure SI-4b) revealed that the major composition of the VB and CB remained similar to that in the previous phase but with a singular distribution for the CB based on the different Fe environments.

Figure SI-5 shows the photoelectrochemical measurements for the nonirradiated and femtosecond laser-irradiated samples. The current density versus potential curves in Figure SI-5a,b, both under illumination and dark conditions, reveal that the irradiated samples presented a higher photocurrent density than the nonirradiated ones, demonstrating that the conductivity through the electrode/electrolyte interface increased due to femtosecond laser irradiation. The results show that the photocurrent density of the nonirradiated samples increased when the films were illuminated with a 100 W Xe light source. The order of the photocurrent density improvement was 860-30 > 900-30 > 900-10 (Figure SI-5a). The 860-30 nonirradiated sample exhibited the highest photocurrent density (0.60 mA cm^–2) at 1.23 V versus reversible hydrogen electrode (RHE). When these samples were exposed to femtosecond laser irradiation, Figure SI-5b, the 860-30 irradiated sample still showed the best performance, even though the 900-30 irradiated sample exhibited a very similar performance.

The photocurrent density increased from 1.06 to 1.35 mA cm^–2 for the 860-30 irradiated sample and from 0.61 to 1.30 mA cm^–2 for the 900-30 irradiated sample at 1.23 V versus RHE. To measure the photoresponse property, chronoamperometry analyses were performed to characterize the photogenerated current density under a potential of 0.9 V and periodic illumination of a 100 W Xe light source (Figure SI-5c,d). As indicated, the femtosecond laser-irradiated samples exhibited a higher photocurrent density than the nonirradiated ones. In particular, from Figure SI-5c, it is possible to note that the 900-30 nonirradiated sample exhibited a higher photocurrent density than the 860-30 and 900-10 nonirradiated ones. However, the shape of the chronoamperometry curve of the 900-30 and 860-30 nonirradiated samples was not maintained after eight cycles of light illumination. The photocurrent density of these samples did not remain constant, thus implying low stability. The exception is the 900-10 nonirradiated sample, which maintained the photocurrent density, however, with a very low value, 0.15 mA cm^–2. In Figure SI-5d, the 900-30 irradiated sample presented the highest photocurrent density (ca. 1.10 mA cm^–2), while the 860-30 irradiated and 900-10 irradiated ones exhibited a photocurrent density of ca. 1.00 and ca. 0.46 mA cm^–2, respectively. The photocurrent density results show a change in the emission of the charge carrier caused by association of heat treatment and followed by an irradiation increase in the defect density of the irradiated samples.

In addition, the shape of the chronoamperometric curve of the 900-30 irradiated sample stabilized after three cycles of light illumination, thus implying that this electrode is stable in an electrochemical environment. In contrast, the 860-30 irradiated sample did not stabilize after eight cycles of light illumination, indicating that this material does not have good stability in an electrochemical environment, whereas the 900-10 irradiated sample maintained the photocurrent after eight cycles, however, with a low photocurrent density, 0.47 mA cm^–2. The photoelectrochemical measurements indicated that femtosecond laser irradiation made 900-30 a promising material for applications in dye-sensitized solar cells and water splitting.

Figure 5 shows that the morphology of the nonirradiated samples was characterized by field emission scanning electron microscopy (FESEM). SEM images of the 860-30 nonirradiated samples are shown, which presented the richest ε-Fe₂O₃ phase. It can be observed that the particles form agglomerates assembled by nanoplates with nonuniform size and irregular surfaces with equiaxial formats. As the heat treatment temperature increases, 900-10 nonirradiated samples are obtained. These samples also present agglomerates composed of irregular nanoplates; however, the plates now have a smooth surface with microparticles scattered over them.

Figure 5.

FESEM micrographs of the nonirradiated and irradiated samples.

Figure 6 shows the high-resolution transmission electron microscopy (HRTEM) of the nonirradiated and irradiated samples, while the inset displays the interplanar distances that enabled the indexing of the Fe₂O₃ phases. The results from the HRTEM images corroborate those from the XRD standards (Figure 2), indicating that the irradiated particles coalesced and remained with the ε-Fe₂O₃ phase. It can be observed that the femtosecond laser irradiation treatment of the ε-Fe₂O₃ particles increased the defect density, which may have contributed to the maintenance of the metastable phase.

Figure 6.

HRTEM images of the nonirradiated and irradiated samples.

Table 2 presents the comparison of the theoretical and experimental values for interplanar distances, obtained by pelos DFT-based results and by confirming the (hkl) indexing of the HRTEM images. An excellent agreement between theoretical and experimental values was found, confirming the (hkl) indexing for the obtained nanoparticles.

Table 2. Comparison of the Theoretical and Experimental Values for Interplanar Distance Surfaces of ε-Fe₂O₃ and α-Fe₂O₃ Phases.

interplanar distances (hkl)	theoretical values (nm)	experimental values (nm)
ε-Fe2O3 (122)	0.276	0.271
ε-Fe2O3 (013)	0.302	0.295
α-Fe2O3 (110)	0.255	0.255

From now on, our major interest is devoted to rationalize the energetics and structural, electronic, and morphological properties of the investigated surface models for both α-Fe₂O₃ and ε-Fe₂O₃ phases. Table 3 summarizes the calculated E_surf values for each Fe₂O₃ surface, the spin density, and its band gap energy. In addition, Figures SI-6 and SI-7 (Supporting Information) show the optimized geometries for all investigated surfaces, highlighting the undercoordinated Fe site.

Table 3. Calculated E_surf, Surface Area, Spin Density, E_gap, and Fe Coordination Site (c) for the α-Fe₂O₃ and ε-Fe₂O₃ Surfaces.

	surface	area (nm2)	Dμ (μB nm–2)	Esurf (J m–2)	Egap (eV)	Fe site
α-Fe2O3	(012)	0.279	30.04	1.27	2.83	Fe5c
	(110)	0.406	0.00	1.58	2.40	Fe5c
	(001)	0.226	18.00	1.60	2.80	Fe3c
	(101)	0.246	16.83	1.79	2.62	Fe5c and Fe4c
	(100)	0.704	5.82	1.99	2.84	Fe4c
	(104)	0.382	22.03	2.11	2.56	Fe4c
	(116)	0.608	0.00	2.35	2.17	Fe5c and Fe3c
ε-Fe2O3	(100)	0.857	0.00	1.80	2.85	Fe4c and Fe5c
	(110)	0.991	0.00	1.81	2.69	Fe4c
	(111)	1.094	8.04	2.06	2.28	Fe3c, Fe4c and Fe5c
	(012)	1.050	3.88	2.20	2.23	Fe3c, Fe4c and Fe5c
	(013)	1.473	6.21	2.37	1.65	Fe3c and Fe4c
	(122)	1.792	2.31	2.33	1.03	Fe3c, Fe4c and Fe5c

For α-Fe₂O₃, the stability order of investigated surfaces was (012) > (110) > (001) > (101) > (100) > (104) > (116), which is in agreement with the broken bonds reported in Table 3, implying that the higher number of broken bonds along the exposed surface induces higher E_surf values. Similar findings and discussion on Ag₂O,⁶⁸ MnTiO₃,⁴⁸ CaMoO₄/Tb,⁶⁹ and FeCrO₃⁶⁹ are reported in previous studies. Then, a strong connection between the energy surface and degree of defects was found, shedding light on the rationalization and surface selection for particular phenomena, such as photocatalysis,⁷⁰ magnetism,⁷¹ antimicrobial activity,⁷² and charge separation in heterostructures,⁷³ among others. Femtosecond laser irradiation is a promise to control or to promote the superficial defects on individual surfaces, reaching intended properties that are sometimes hard to synthesize due to the potential to generate intrinsic defects that govern the electronic structure and surface properties.^24,74

Regarding the calculated band gap energy, the (100), (001), and (012) surfaces showed values similar to those of the bulk, while the other surfaces exhibited reduced values that can be associated with the singular chemical environment of each exposed surface, perturbing the distribution of energy levels in the vicinity of the band gap region.

On the other hand, for ε-Fe₂O₃, the stability order of the investigated surfaces was found to be (100) > (110) > (111) > (012) > (013) > (112). In this case, the nonregular relation with the degree of undercoordination observed was due to different Fe-centered clusters that could have contributed to the balance of the surface energy redistribution. As to the calculated band gap energy, the (013) and (122) surfaces exhibited a narrowed band gap compared to the bulk (860-30 nonirradiated samples), Figure SI-3, suggesting that the increased degree of undercoordination induced a perturbation of energy levels near the Fermi level.

By comparing the theoretical band gap energy values for the α-Fe₂O₃ (2.17–2.84 eV) and ε-Fe₂O₃ (1.03–2.85 eV) surfaces with the experimental results, in Figure SI-3, for iron oxide particles (1.78–2.05 eV), the reduced experimental band gap values can be interpreted following the major contributions of the (110) plane for α-Fe₂O₃ and the (013)/(122) surfaces for ε-Fe₂O₃, along with the obtained HRTEM micrographs (Figure 6).

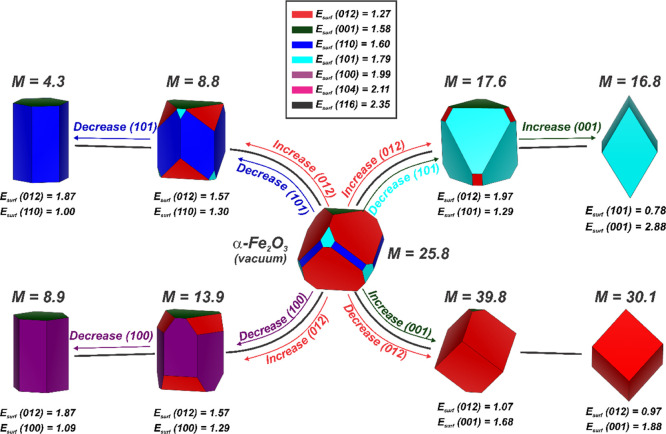
Aiming to investigate the role of exposed surfaces in the crystal morphology of both Fe₂O₃ phases, the Wulff construction was applied considering the optimized E_surf values.^44,49,75,76Figure 7 presents the Wulff shapes predicted for α-Fe₂O₃, where it can be observed that the vacuum ideal morphology (T = 0 K and P = 0 bar) for α-Fe₂O₃ is a corner- and side-truncated cubic shape, enclosing the (012), (001), (110), and (101) surfaces.

Figure 7.

Representation of different morphologies obtained for α-Fe₂O₃. The E_surf values are reported in J m^–2. The M values correspond to the magnetization index calculated by eq 3.

By controlling the E_surf values for different α-Fe₂O₃ surfaces, two main types of morphological paths can be observed. In the left side of Figure 7, it is possible to see that the control of the E_surf values for the (012), (101), and (100) planes resulted in a hexagonal cylindrical shape containing the (110) and (001) surfaces in one path and the (100) and (001) surfaces in the other.

On the other hand, according to the right side of Figure 7, two cubic shapes (regular and nonregular) appeared due to the control of the exposure of (012) and (101). In the first case, the cubic shape enclosing the (012) surface plane is regular, whereas the second case involves a triclinic-like shape (nonregular) containing the (101) surface.

Figure 8 displays the Wulff shapes predicted for ε-Fe₂O₃ in vacuum ideal morphology; here, it is possible to observe the existence of highly truncated rhombic shapes enclosing the (100), (110), (111), (012), and (112) surfaces. It is important to note that the (012) surface is more unstable in the α-Fe₂O₃ phase; however, it plays an essential role in determination of the ideal morphology for the ε-Fe₂O₃, reaffirming the importance of such exposed surfaces on Fe₂O₃ nanoparticles for photoelectrochemical, optical, and magnetic properties.

Figure 8.

Representation of different morphologies obtained for ε-Fe₂O₃. The E_surf values are reported in J m^–2. The M values correspond to the magnetization index calculated by eq 3.

By controlling the E_surf values for different ε-Fe₂O₃ surfaces, several types of morphological paths are described. The lower part of Figure 8 shows that two distinct shapes control the E_surf for the (100), (110), and (111) surfaces: a prismatic shape enclosing the (110) and (012) planes and a hexagonal truncated shape containing the (111) and (012) surfaces. In contrast, in the upper part of Figure 8, it can be seen that the control of the exposure of (112), (013), and (100) resulted in corner-truncated octahedral (left panel), corner- and side-truncated octahedral (center panel), and triclinic-like (right panel) shapes.

The uncompensated spin density along the α-Fe₂O₃ surfaces (Table 3) indicates that the exposed (012) surface shows the highest spin density, followed by the (104), (001), (101), and (100) planes. This fact is interesting in the theoretical point of view, as the most stable Fe₂O₃ surface presented an increased magnetization density along the exposed surface, reaffirming the intriguing magnetic properties of the α-Fe₂O₃ nanoparticles. For the ε-Fe₂O₃ surfaces, the spin density values obtained reinforced the role of uncompensated spins along the (111), (013), (012), and (122) exposed surfaces.

By comparing the results, two main points could be observed. First, the (012) surface stability for α-Fe₂O₃ was modified when ε-Fe₂O₃ became stable, suggesting that the disordered arrangement of the Fe center along the last structure generated a singular electron density distribution that led to a new surface energy stability order. Second, regarding the uncompensated spins along the exposed surfaces, the change in the stability order was followed by a reduced role of the uncompensated spins for the ε-Fe₂O₃ in comparison with the α-Fe₂O₃, which could be attributed to the highest values of D_μ found for the most unstable surfaces.

For α-Fe₂O₃, the morphological paths reported in the left panel of Figure 7 lead to a decreased value of uncompensated spin density, consequently reducing the role of surface effects in the global magnetism of such particles. In contrast, the right panel of Figure 7 shows that the cubic shape enclosing the (012) surface exhibits an increased magnetization density in comparison with the ideal morphology, whereas the triclinic-like shape containing the (101) surface shows a reduced uncompensated spin density. In this case, it can be noted that surface exposure has an important role in shape-oriented magnetic properties since the control of the exposure of (012) induces the highest values for M, evidencing the contribution of surface states to the global magnetism of cubic α-Fe₂O₃ particles.

In Figure 8, the calculated ideal shape for ε-Fe₂O₃ nanoparticles exhibits a smaller magnetization index than that for α-Fe₂O₃, since the surfaces with the highest magnetization density (D_μ) have a low contribution to the ideal polyhedral. In order to increase the magnetization density, two main morphological modulations were found. The first refers to the shapes in the upper panel of Figure 8, which showed an increased magnetization density due to the control of the exposure of (112) and (013) surfaces, according to the experimental results, while the second refers to the truncated hexagonal shape enclosing the (111) and (012) surfaces (right lower panel of Figure 8), which exhibited an increased superficial magnetism because of the major exposure of the (111) surface.

Analyzing both phases, the overall morphologies for the α-Fe₂O₃ phase exhibited an increased superficial magnetism compared to the ε-Fe₂O₃ phase. Despite the very distinct polyhedral arrangements, such analysis reveals that the crystal growth associated with the ε → α phase transition clearly shows the change in the magnetic character of the surfaces once the uncompensated spins became more important as there is an increase in the α phase.

According to the HRTEM images (Figure 6), the obtained nanoparticles show the interaction between the (110) plane of the α-Fe₂O₃ phase and the (013) and (112) surfaces of the ε-Fe₂O₃ phase. From the theoretical point of view, the chemical environment of such surfaces is depicted in Figures SI-6 and SI-7.

Now, the growth process involving the α-Fe₂O₃ and ε-Fe₂O₃ particles can be investigated by combining surface analysis, Wulff construction, and HRTEM.

Similar to a previous study reported by Lee and Xu,⁷⁷ the (013) and (112) surfaces of ε-Fe₂O₃ act as a substrate for the growth mechanism, converting ε-Fe₂O₃ → α-Fe₂O₃ phases. In this case, laser irradiation can act on the crystalline structure of ε-Fe₂O_3, generating the required oxygen vacancies responsible for exposing both (112) and (013) surfaces. However, such surfaces are excessively unstable in comparison with the (110) plane of the α-Fe₂O₃ phase, inducing the phase conversion. In particular, the increased surface energy for the (112) and (013) planes induces a major reactivity against oxygen to restore the cluster unit. Therefore, the chemical energy involved in the laser irradiation acting on the crystalline structure of the exposed surfaces promotes a reconstruction mechanism, guiding the phase transition of the (112)/(013) surface templates of the ε-Fe₂O₃ arrangement to the (110) surface of the α-Fe₂O₃.

Figure 9 presents magnetization measurements as a function of the applied magnetic field applied at room temperature for nonirradiated and irradiated samples (Figure 9a,b, respectively). As proposed by Dzyaloshinsky⁷⁸ and Moriya,⁷⁹ the magnetic behavior of ferrite samples is explained by the mechanism of “weak ferromagnetism” as observed in α-Fe₂O₃,⁸⁰ which was also found to be weak for the ε-Fe₂O₃ phase.⁸¹ In Figure 9a, this behavior is exhibited by the approximately linear dependence of the magnetization on the applied magnetic field, as expected for ferrite samples, for the α-Fe₂O₃ and ε-Fe₂O₃ phases, with high-saturation fields around 12 kOe.^82,83

Figure 9.

Magnetization curves. In (a) nonirradiated samples and in (b) femtosecond laser-irradiated samples.

However, we observed that the irradiated samples showed different behaviors in relation to the nonirradiated samples, as shown in Table 4. First, we identified the difference between the coercive fields (Hc) from Hc ∼ 270–280 Oe to Hc ∼ 1400–1800 Oe for irradiated and nonirradiated samples. This behavior is consistent with the size of the particles and the size of the crystallite (Table 1) presented by the samples. In Figure 5, it is clear that the particle size of nonirradiated samples is larger than that of irradiated samples. Coercive fields are associated with the magnetic domain wall, which in turn is related to particle size.

Table 4. Magnetic Parameters Obtained by the Hysteresis Loops of the Nonirradiated and Irradiated Samples.

samples	900-30	900-30 irradiated	900-10	900-10 irradiated	860-30	860-30 irradiated
M (10 kOe) (emu/g)	1.04	2.67	0.81	3.16	1.54	3.82
χ	1.17127 × 10–4		6.431845 × 10–5		1.403085 × 10–4
Mr (emu/g)	0.18	0.63	0.17	0.61	0.17	0.77
Hc (Oe)	1460	270	1800	278	1020	282
Mr/Ms	0.17	0.24	0.21	0.19	0.11	0.21

Another important point is the dependence of magnetization on the applied magnetic field in irradiated samples compared to nonirradiated samples. The shape of the values of magnetization in the high field is very different.

In Table 4, where there is magnetization at high field, remanent magnetization parameters and coercive field, average particle size, and hysteresis loss are displayed. The coercive field (Hc) for the 900-10, 900-30, and 860-30 nonirradiated samples exhibited values higher than those for irradiated samples and an increase of six, five, and three times, respectively. This is an indication that an increase in the density of defects observed from the absence of vibrational modes active in Raman measurements of the 900-10 and 860-30 irradiated samples (Tables SI-4 and SI-5) induced an additional increase in magnetic moments.⁸⁴

To better understand the effect of femtosecond laser irradiation on magnetic moments in the α-Fe₂O₃ and ε-Fe₂O₃ phases of the samples, we performed a linear fitting in the positive quadrant of magnetization of nonirradiated samples to calculate the dependence of magnetization as a function of the applied magnetic field, M = χH, where χ is the magnetic susceptibility. The values of χ are present in Table 4. From these data, the contribution of magnetization of the nonirradiated part was subtracted from the irradiated samples, as shown in Figure 10.

Figure 10.

Magnetization as a function of the applied magnetic field performed at room temperature of irradiated samples, with the nonirradiated sample contribution subtracted.

In Figure 10, we observed that the effects of femtosecond laser irradiation on samples induce a FEM behavior, as by subtracting the magnetization values associated with nonirradiated samples, we can only observe the contribution to magnetization due to defects produced by the irradiation process. As a result, it is shown that the defects induced the formation of magnetic moments, without leading to the formation of new phases or introducing significant stresses in the crystalline lattice.

Interestingly, the magnetic behavior of the samples before and after femtosecond laser irradiation was dependent on the crystallinity, defects, size, and morphology of the particles due to the presence or absence of the ε-Fe₂O₃ phase.⁸⁵⁻⁸⁸ These results corroborate the micrographs obtained in this work (Figure 5).

3. Conclusions

This study evidenced that the heat- treatment allowed the phase change (ε-Fe₂O₃ → α-Fe₂O₃) due to the growth of the (112) and (013) surfaces. Such surfaces act as a substrate to convert the ε-Fe₂O₃ into the α-Fe₂O₃ phases. The instability of the (112) and (013) surfaces in relation to the (100) plane in α-Fe₂O₃ enabled the phase transition. However, the femtosecond laser irradiation changes the chemical energy of the (112) and (013) surfaces, increasing the defects density and consequently causing the blockade of the phase transition, as shown by the experimental Raman spectra.

The magnetic properties of the irradiated samples showed more promising results than the nonirradiated ones. Therefore, the defects generated in the particles by femtosecond laser irradiation contributed to the increase in magnetization. These defects did not allow the formation of new phases or the introduction of significant tensions in the crystal lattice. Even so, these defects led to the formation of magnetic moments. The theoretical studies on the α-Fe₂O₃ connected the reported magnetic properties to a higher spin density exhibited by the (012) exposed surface, followed by the (104), (001), (101), and (100) planes. In addition, the (100) surface was found to be the most stable, showing increased magnetization density along the exposed surface.

The calculated band gap energy and experimental investigations on the optical properties are in accordance. The reduction of the band gap obtained experimentally and evidenced theoretically indicates the higher conductance of the irradiated samples than that of the nonirradiated ones. Besides, the decrease in the band gap occurred because of the existence of electronic levels within the prohibited range associated with the presence of defects. The HRTEM micrographs presented contributions of the (013) and (122) surfaces to the ε-Fe₂O₃ phase and (110) surface to the α-Fe₂O₃ phase, evidencing that the properties of the Fe₂O₃ particles were controlled by the exposure of these surfaces.

The photoelectrochemical measurements revealed that irradiation using a femtosecond laser improved the photocurrent density, reaching a maximum of 1.30 mA cm^–2 for the 900-30 irradiated sample. The chronoamperometric analyses showed that this sample stabilized and maintained the photocurrent during the three cycles of light illumination, demonstrating a potential application in dye-sensitized solar cells and water splitting. Furthermore, it was found that the synergistic effect of heat- treatment and subsequent irradiation in the samples irradiated allowed an increase in the defect density, due to the change in charge carrier emission, as demonstrated by the photocurrent results.

4. Experimental Section

4.1. Synthesis and Characterization

Fe₂O₃ particles were obtained by the synthesis route described by Gou et al.¹⁷ Initially, 2 mmol Fe(NO₃)₃·9H₂O, 4 mmol sodium citrate dihydrate, and 5 mmol CO(NH₂)₂ were simultaneously dissolved in 30 ml of deionized water under constant stirring. Then, the solution underwent a conventional hydrothermal treatment at 160 °C for 10 h. Sequentially, the Fe₂O₃ particles were collected at room temperature, washed first with distilled water three times and after with isopropyl alcohol, and dried in a conventional furnace at 110 °C for 4 h. Lastly, the material was heat-treated at 860 °C for 30 min and 900 °C for 10 and 30 min.

The study regarding laser irradiation used a procedure similar to the one described in Assis et al.²⁴ However, the Fe₂O₃ particles were irradiated for a continuum period of 100 min using a Ti/sapphire laser (CPA-2001 system from Clark-MXR Inc.), delivering 150 fs (fwhm) at 775 nm, with a repetition rate of 1 kHz. An average power of 300 mW was used for sample irradiation. At the experimental setup, the laser beam was focused using a convergent lens with a focal distance of 8 cm, giving a beam waist of approximately 70 μm. The samples were positioned at 1 mm from the focal point, which is inside the Rayleigh range.

TGA and DTA were performed to evaluate the thermal behavior of the Fe₂O₃ samples obtained by the hydrothermal process (NETZSCH—409 Cell). The samples were placed inside aluminum oxide crucibles in an oxidizing atmosphere with a 50 mL min^–1 flux and heated to 1000 °C.

The femtosecond laser-irradiated and nonirradiated samples were structurally characterized by XRD using a diffractometer (Shimadzu) with Cu Kα radiation (λ = 1.5406 Å). XRD patterns were acquired with a sweeping angular range between 10 and 110° and steps of 0.02°. The General Structure Analysis System²⁵ (GSAS) program was used to analyze the data obtained by the Rietveld refinement method.²⁶

All Raman spectra were collected in the range of 100–1400 cm^–1 using a SENTERRA (Bruker) spectrometer coupled to a microscope with a 20× objective and a 785 nm He–Ne laser excitation source with the laser power of 1 mW. UV–vis measurements were carried out on a Varian Cary 5G spectrometer at room temperature in the diffuse reflectance mode.

For the photoelectrochemical procedure, all electrodes were prepared using 4 mg of the material together with 10 μL of Nafion (5 wt) and 1 mL of a solution of deionized water/isopropyl alcohol (in the proportion of 3:1). This mixture was processed with ultrasound for 1 h. The obtained suspensions (100 μL) were applied onto fluorine-doped tin oxide substrates using a micropipette in an area of 1 cm². The films were then allowed to dry at the greenhouse at 60 °C for 1 h. The photoelectrochemical measurements were carried out in a conventional three-electrode cell with a quartz glass window using 1 M Na₂SO₄ solution as the electrolyte. The prepared electrode samples, Pt wire and Ag/AgCl, were used as working, counter, and reference electrodes. The photocurrent–potential (J–V) curves of the samples were swept at 10 mV s^–1 from −0.2 to 1.2 V versus Ag/AgCl. These curves were analyzed using an Autolab PGSTAT302 N potentiostat and evaluated under both illuminated and dark conditions using a Newport Sol3A Class AAA solar simulator with a 100 W xenon lamp.

The morphological aspect of the femtosecond laser-irradiated and nonirradiated Fe₂O₃ particles was analyzed through images obtained with a Zeiss Supra 35 scanning electron microscope; using a secondary electron detector (Everhart–Thornley detector) and with a FEI Tecnai G2 F20 transmission electron microscope in a bright field and HRTEM. Besides, measurements of energy dispersive spectroscopy coupled with TEM were performed.

Magnetization measurements as a function of the applied magnetic field were performed using a vibrating sample magnetometer at room temperature up to 12 kOe.

4.2. Computational Details

To simulate the crystalline structures from experimental results for the α-Fe₂O₃ and ε-Fe₂O₃ particles, quantum mechanical calculations in the framework of DFT were carried out using the B3LYP^27,28 exchange correlation functional implemented in the CRYSTAL17 code.²⁹ The atom-centered all-electron basis sets used for Fe and O atoms were 86-411d41G and 8-411G*, respectively.³⁰ The crystalline structure reached a full optimization regarding atomic positions and lattice parameters as a function of the total energy. The electronic integration over the Brillouin zone was performed using a 6 × 6 × 6 Monkhorst–Pack k-mesh.³¹ Five thresholds (ITOL) set to 8, 8, 8, 8, and 14 control the accuracy of the Coulomb and exchange integral calculations according to overlap-like criteria, that is, when the overlap between two atomic orbitals is smaller than 10^–ITOL. The self-consistent field convergence threshold on total energy was set to 10^–8 hartree, while the root-mean-square (rms) gradient, rms displacement, maximum gradient, and maximum displacement were set to 3 × 10^–4, 1.2 × 10^–3, 4.5 × 10^–4, and 1.8 × 10^–3 a.u., respectively.

Regarding the magnetic ground state, we considered two collinear magnetic configurations as FEM and AFM orders using the primitive and conventional unit cell for both α-Fe₂O₃ and ε-Fe₂O₃ materials, following other theoretical studies,^32,33 which report that the FM and AFM states are associated with each α-Fe₂O₃ and ε-Fe₂O₃ material. The magnetic ground state was defined according to the energy difference between the models (ΔE = E_AFM–E_FEM), where a positive (negative) value indicates the AFM (FM) states. All magnetic calculations were carried out at T = 0 K within collinear magnetic configurations to describe the major differences between the spin density distributions for both Fe₂O₃ phases without considering spin dynamics effects.

The Γ-point vibrational frequencies were computed for the optimized geometry solving the mass-weighted Hessian matrix.³⁴ The relative Raman intensities were computed exploiting the orbital energy-weighted density matrix based on the self-consistent solution of first- and second-order coupled perturbed Hartree–Fock/Kohn–Sham (CPHF/KS) equations for the electronic response to external electric fields at the equilibrium geometry.^35,36

Also, the electronic properties were evaluated through the DOS and band structure profiles implemented in the CRYSTAL17 code.²⁹

To get deep insights into the structural, electronic, and magnetic properties of Fe₂O₃ surfaces, symmetrical slab models of both α-Fe₂O₃ and ε-Fe₂O₃ phases were considered. Herein, the (001), (100), (101), (110), (012), (104), and (116) surfaces were considered for the α-Fe₂O₃ phase with (100), (110), (111), (012), (112), and (013) considered for ε-Fe₂O₃.³⁷⁻⁴²

The surface energy (E_surf) was calculated following the equation

1

Here, E_slab and E_bulk correspond to the total energies for the surface model and the relaxed bulk unit cell, whereas n and A represent the number of bulk units used in the model construction and the surface area, respectively.

The equilibrium shape of a crystal and its modulations were calculated from the Wulff construction, minimizing the total surface free energy at a fixed volume and providing a simple relationship between the (hkl) surface energy (E_surf) and its distance from the crystallite center in the normal direction.^43,44

The advance of the simulation of the magnetic properties in surfaces progressed in the last years.⁴⁵⁻⁴⁷ Thus, to deeply investigate the magnetic properties of the α-Fe₂O₃ and ε-Fe₂O₃ morphologies, it is essential to know the magnetization index (M) in each (hkl) Miller index. To reach this goal, we applied a recent and innovative method.⁴⁸⁻⁵¹ In the first stage, the magnetization index (D_μ) of a given (hkl) surface (eq 2) is calculated, where D_μ is connected to the magnetic moment (μ_B) in a particular (hkl) surface per unit cell area (A). Posteriorly, M is calculated from eq 3, where the M value represents the combination of all contributions of each surface plane to the morphology, c_(hkl), and the corresponding D_μ.

2

3

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c04079.

• Auxiliary graphs to understand the differences between α-Fe₂O₃ and α,ε-Fe₂O₃ nonirradiated and irradiated samples, Rietveld refinement, atomic displacement of Raman-active modes for α- and ε-Fe₂O₃ phases, UV–vis spectra and Tauc function, band structures and atom-resolved DOS profiles, linear sweep voltammetry and chronoamperometric analysis, schematic representation of the surfaces for α-Fe₂O₃ and ε-Fe₂O₃, tables of theoretical values for Fe–O bond distances (Å) in the α- and ε-Fe₂O₃ phases, experimental Raman and wavenumbers (cm^–1), and fwhm (PDF)

The authors declare no competing financial interest.