Abstract
This paper reviews the hypothesis of harmonic cancellation according to which an interfering sound is suppressed or canceled on the basis of its harmonicity (or periodicity in the time domain) for the purpose of Auditory Scene Analysis. It defines the concept, discusses theoretical arguments in its favor, and reviews experimental results that support it, or not. If correct, the hypothesis may draw on time-domain processing of temporally accurate neural representations within the brainstem, as required also by the classic equalization-cancellation model of binaural unmasking. The hypothesis predicts that a target sound corrupted by interference will be easier to hear if the interference is harmonic than inharmonic, all else being equal. This prediction is borne out in a number of behavioral studies, but not all. The paper reviews those results, with the aim to understand the inconsistencies and come up with a reliable conclusion for, or against, the hypothesis of harmonic cancellation within the auditory system.
Keywords: pitch perception, auditory scene analysis, segregation, harmonicity, harmonic cancellation
Introduction
Our environment is cluttered with sound sources, but to act effectively we must focus on one or a few and ignore the others. This is hard because the mixing process, by which sounds from the various sources add up before entering the ears, cannot be undone. We usually do not know the mixing matrix (i.e., the delays and gains applied to each source before adding) and, even if we did, that matrix is generally not invertible. Recovering individual sources is thus impossible except in very simple cases. Nonetheless, we sometimes feel that we can follow an individual source, for example, a voice within a conversation, or an instrument within an ensemble, as if it were alone. The ability to make sense of a complex acoustic scene in terms of individual sources is known as Auditory Scene Analysis (Bregman, 1990).
Auditory Scene Analysis is sometimes discussed as a process of “grouping” elements (e.g., partials) to form sources or objects (Bregman, 1990), for example, according to Gestalt principles. However, such “elements” are conceptual rather than operational. While sinusoids and clicks serve well as synthesis parameters, it may not be possible to extract them from the sound due to theoretical limits (e.g., time–frequency uncertainty tradeoff, Gábor, 1947) and physiological limits (e.g., temporal and frequency resolution of cochlear analysis, Moore & Glasberg, 1983; Plack & Moore, 1990). If they cannot be accessed, postulating that they can be grouped is perhaps misleading.
Fortunately, perfect isolation of each source is usually not necessary. According to the principle of unconscious inference (Helmholtz, 1867; Kersten et al., 2004), we need only to recover enough information to infer the presence or nature of a target. Regularities within the world, internalized as models within the perceptual system, allow us to fill in missing parts. This process, which manipulates incomplete information “under the hood,” provides us with the illusion of perceiving each object just as if true unmixing had taken place. Information about the source is partial but, thanks to inference, it appears to us that it is complete (al Haytham, 1030; Hatfield, 2002; Imbert, 2020).
For this to work, it is essential that the sensory representation be stripped of the influence of background objects. If not, a different background might lead to a different percept, defeating the goal of perceiving the target as if it were in isolation. In other words, the sensory representation should be made invariant to the presence of interfering sources. This is analogous to invariance with respect to intra-class variability in pattern classification (Duda et al., 2012).
Several aspects of auditory processing might contribute to this goal. If target and background differ by their spectral content, cochlear filtering can be used to split sensory input into channels dominated by the target, distinct from those that reflect the background. Discarding the latter then yields a representation that is invariant to the presence of the background—albeit incomplete because of the missing channels. Likewise, if target and background occur at different points in time, temporal resolution properties of the auditory system (Moore et al., 1988; Plack & Moore, 1990) can be used to discard time intervals contaminated by the background.
Putting both elements together, the target can be “glimpsed” within spectro-temporal gaps of the background (Cooke, 2006). The glimpsed “pixels” of the time-frequency representation are handed over to subsequent processing together with a mask to indicate their position. Discarded pixels are not merely set to zero: they are given zero weight (Cooke et al., 1997). Spectro-temporal glimpsing has been proposed in speech processing applications (Wang & Brown, 2006; Wang, 2008), and to account for human perceptual abilities and derive predictive measures of intelligibility (e.g., Best et al., 2019; Josupeit et al., 2020).
Binaural disparity is another potentially useful cue. In addition to head shadow effects that produce favorable target-to-masker ratios within certain frequency channels at either ear (Grange & Culling, 2016), perception benefits from binaural interaction, which is commonly understood to follow the well-known equalization cancellation (EC) model (Durlach, 1963), and its extensions (e.g. Culling & Summerfield, 1994; Breebaart et al., 2001; Akeroyd, 2004). Signals at each ear are differentially time-shifted and scaled (“equalization”), and then subtracted one from the other (“cancellation”) to suppress interaurally coherent sound from a competing source. The internal time shift and scale factor are tuned to match the interfering source. The EC model is assumed to involve temporally accurate neural patterns processed by specialized neural circuitry within the auditory brainstem (Tollin & Yin, 2005; Joris & van der Heijden, 2019).
To summarize this viewpoint, Auditory Scene Analysis entails canceling and/or ignoring irrelevant features of the sensory input, and matching the remainder to an internal model to produce a reliable percept. The process draws on spectro-temporal analysis within the cochlea, complemented by neural time-domain signal processing within the brain, to provide the brain with a rich—albeit incomplete—representation within which a target can be “glimpsed.” The glimpses are then interpreted according to a Helmholtzian inference process.
The remainder of this paper asks whether this process can be extended to include, as a cue, the harmonic (periodic) structure of interference such as a competing talker. So-called “double-vowel” experiments found that vowels mixed in pairs are easier to identify if their fundamental frequencies (F0s) differ (Brokx & Nooteboom, 1982; McKeown, 1992; Culling & Darwin, 1993; Assmann & Summerfield, 1994), suggesting that harmonic structure somehow assists segregation. Furthermore, it appears that this effect is driven mainly by the harmonicity of the background, for example, the competing vowel (Lea, 1992; Summerfield & Culling, 1992; de Cheveigné et al., 1997). This is the harmonic cancellation hypothesis.
To set the stage, I assume a “segregation module” that works hand in hand with a “pattern-matching” module (Figure 1). The segregated sensory pattern (dark red arrow) is accompanied by a “reliability mask” (gray arrow) to assist matching of a pattern that is incomplete or distorted by the segregation process. Sensory representations might consist of a spectral profile (e.g., place-rate representation), or a temporal, or place-time pattern. Examples of the latter are a matrix of autocorrelation functions (ACFs), one per channel (autocorrelogram), or the sum over channels of these ACFs (summary ACF, SACF) (Licklider, 1959; Lyon, 1984; Meddis & Hewitt, 1992). The flow of sensory information in this figure is purely bottom-up: the only top-down influence is attentional control (dotted arrow). Top-down transfer of a sensory-like pattern is also conceivable (“schema-driven” segregation), but not considered here.
Figure 1.
Segregation and matching. Sensory input is stripped of correlates of interfering sources, and the selected pattern, possibly incomplete, is passed on for pattern-matching (or model-fitting), together with a mask that indicates which parts are missing or unreliable. Initial stages are under attentional control.
We want to know whether harmonic cancellation is instantiated in the auditory system, but it is often easier to reason in terms of the acoustic waveform, for clarity and to distinguish theoretical from implementation limits: if a principle fails in abstract terms, consideration of biological constraints is premature. That said, references to “cochlear filtering” or “neural processing” will sometimes creep into the discussion without warning. I beg your patience when this occurs.
Harmonic Cancellation—Possible Mechanisms
How might harmonic cancellation be implemented? This section investigates several hypotheses, including frequency-domain, time-domain, and hybrid models. A later section will ask which—if any—is used by the auditory system. The busy reader might want to read about frequency domain and time domain models, then skip to the Psychophysics section and come back for details as needed. There are also interesting things to be found in the Appendix.
Frequency Domain
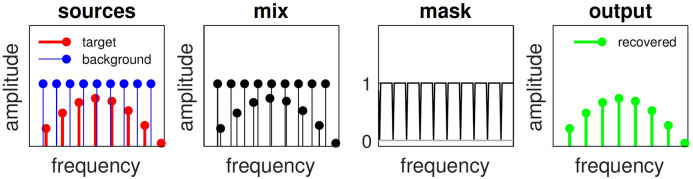
Conceptually, harmonic cancellation is straightforward: just zero all spectral components at multiples of , where is the period of the background, as shown in Figure 2 (Parsons, 1976; Stubbs & Summerfield, 1988). Target components emerge intact (right panel), except in the event, vanishingly unlikely in this idealized world, that a target component falls on the harmonic series of the background.
Figure 2.
Harmonic cancellation in the idealized frequency domain. Left: line spectra of a “target” sound (red) and a “background” (blue). Next to left: mixture. Next to right: harmonic mask with zeros at all harmonics of background. Right: recovered target.
A practical implementation, however, needs to deal with two issues: one is limited frequency resolution of the spectral representation, the other is the spectral widening expected when analyzing a time-limited or otherwise non-stationary signal. Figure 3(a) shows short-term amplitude spectra of two harmonic sounds, a 200 Hz “background” with a flat spectral envelope (blue), and a weaker 238 Hz “target” with a broad peak centered at 1 kHz (red).
Figure 3.
Harmonic cancellation in the frequency domain using a short-term Fourier representation, or a filter bank. (a) 238 Hz target (red) and 200 Hz background (blue) analysed by a filter bank with 100 Hz resolution, (b) mixture, (c) harmonic mask, (d) target recovered from mixture (green), and same in the absence of the background (thin red), (e) same analysis but using a filter bank with non-uniform frequency resolution. Filter bandwidth depends on center frequency (CF) according to estimates of cochlear frequency resolution from Moore and Glasberg 1983 as implemented by Slaney (1993).
This spectral transform has limited frequency resolution (or, equivalently, infinite resolution but the signals are time-limited, in this case eight cycles of a 200 Hz fundamental, shaped with a Hanning window). When target and masker are mixed, here with a target-to-masker ratio (TMR) of 12 dB, the spectrum of the mix (Figure 3(b), black) is almost entirely dominated by the background (Figure 3(a), blue). This differs radically from the idealized picture of Figure 2.
If we multiply the spectrum of the mix with a harmonic mask with zeros at the harmonics of the background (Figure 3(c)), we obtain a “recovered” spectral pattern (d, green) very different from the true target (a, red). Two terms contribute to this difference. One is multiplicative distortion from the masking procedure (compare d, red to a, red), the other is additive distortion due to the incompletely canceled background (compare d, green to d, red). The former can, in principle, be taken into account by a pattern-matching stage if it has access to the nature of that distortion, for example, via the gray arrow in Figure 1. The latter is more serious because it is unknown and cannot be compensated for, and because it implies that we miss our goal of invariance with respect to the background. The shape of the harmonic mask (Figure 3(c)) affects the balance between error terms but a different mask would not yield a radically different result. The contrast between Figure 2 (conceptual model) and Figure 3 (feasible implementation) is sobering.
Spectral resolution is critical. Cochlear filters are narrower, on a linear frequency scale, at low than at high CFs (Figure 3(e)). From this figure, it would seem that low-frequency target features might be recovered, but perhaps not high-frequency (compare green and thin red). This illustration used a bank of gammatone filters (Slaney, 1993) with equivalent rectangular bandwidths (ERBs) from psychophysical estimates (Moore & Glasberg, 1983). If cochlear filters were narrower (e.g., Shera et al., 2002; Sumner et al., 2018) a wider frequency range might be recoverable (not shown), but resolution would still be limited if the stimulus were short or non-stationary.
In summary, frequency-domain cancellation requires (a) a spectral representation with resolution sufficient to cancel background partials while retaining enough of the target to support pattern matching, (b) an estimate of the background period , and (c) a pattern-matching process that tolerates distortion of target spectral patterns. How to estimate the background period is discussed in the Appendix (Period Estimation).
Time Domain
Harmonic cancellation can also be implemented in the time domain by a simple filter with impulse response
| (1) |
where is the period of the interfering sound and is the Kronecker delta function translated to (Figure 4(a), left). The filtered version of a signal is simply . The magnitude transfer function of this filter has deep dips at all harmonics of 1/ (Figure 4(a), right).
Figure 4.
Harmonic cancellation in the time domain. (a) Impulse response of the cancellation filter (left) and corresponding magnitude transfer function (right). (b) Input (left) and output (right) of the cancellation filter for the background 100 Hz vowel /a/ (top), target 132 Hz vowel /e/ (middle), and mixture at TMR= 12 dB (bottom). (c) Schematic diagram of a circuit implementing the cancellation filter (Equation (1)) (left) and neural circuit with similar function (right). A spike on the direct pathway (black) is transmitted unless it coincides with a spike on the delayed pathway (red). The delay can be applied to the positive/excitatory input, instead of negative/inhibitory, with equivalent results.
Figure 4(b) shows a background vowel stimulus /a/ with fundamental 100 Hz (top), a weaker target vowel /i/ with fundamental 132 Hz (middle), and their mixture (bottom), before (left) and after (right) filtering with a cancellation filter with lag equal to the period of the background vowel. The response consists of initial and final one-period glitches, separated by a short steady-state portion, in red. The steady-state portion is zero for the background (top). For the target, it is a distorted version of the target waveform (compare middle right, red, to middle left). For the mixture, it is the same as for the target alone (compare middle right, red, to bottom right, red). In other words, this part of the pattern is invariant with respect to the presence of a background of period , which is what we need. This contrasts with frequency-domain cancellation for which none of the recovered pattern was background-invariant.
In summary, time-domain cancellation requires (a) a time-domain signal representation such that Equation (1) can be implemented, (b) an estimate of the background period (see Appendix, Period Estimation), (c) a pattern matching process capable of selecting the intervals of perfect cancellation, and compensating for distortion of the target within these intervals.
Hybrid Models
A hybrid model combines spectral and temporal processing, for example, cochlear filter bank analysis followed by time-domain harmonic cancellation within the brainstem. There is a rich literature based on this idea for the purpose of auditory modeling and sound processing applications (e.g., Lyon, 1983, 1988; Weintraub, 1985; Meddis & Hewitt, 1992; Assmann & Summerfield, 1990). A benefit of the filter bank is that TMR varies across channels, some favoring the target and others the background (Figure 5(a)), which may be useful if the dynamic range of temporal processing is limited.
Figure 5.
(a) TMR within each channel of a model cochlear filter bank for an input consisting of a 124 Hz harmonic target mixed with a 100 Hz harmonic background with overall TMR=0 dB (black), 12 dB (dotted blue), or +12 dB (dotted red). Thanks to the filter bank, the TMR is enhanced in certain channels within which the target can be “glimpsed.”(b) Linear operations can be swapped. Filtering the signal before the filter bank is equivalent to applying the same filter to each channel after the filter bank.
It is worth remembering that linear, time-invariant operators can be swapped: a time-domain cancellation filter applied to the acoustic waveform can instead be applied to each channel after filtering: the result is the same (Figure 5(b)). Cochlear filtering and transduction are both non-linear and non-stationary (e.g., adaptation), but the “equivalence” of Figure 5(b) may nonetheless be useful conceptually. I review briefly here a selection of hybrid schemes for harmonic cancellation, described in detail in the Appendix (Hybrid Models). In brief:
Hybrid Model 1: Cancellation-enhanced spectral patterns. A time-domain cancellation filter is applied to each channel of the cochlear filter bank, resulting in are cleaner spectral patterns for pattern matching.
Hybrid Model 2: Channel rejection on the basis of periodicity. Channels dominated by the background periodicity are discarded, and the remaining channels are used to form a time-domain pattern for pattern matching, as in the concurrent vowel identification model of Meddis and Hewitt (1992).
Hybrid Model 3: Cancellation filtering of selected channels. As in Hybrid Model 2, channels dominated by the background are discarded, and channels dominated by the target are left intact. In contrast to Hybrid Model 2, channels with intermediate TMR are processed by a cancellation filter. The result is used for time-domain pattern matching.
Hybrid Model 4: Channel-specific cancellation filter. The parameter of the cancellation filter can differ between channels, in contrast to other models that use the same for all channels. The result is used for time-domain pattern matching.
Hybrid Model 5: Synthetic delays. The “synthetic delay” mechanism of de Cheveigné and Pressnitzer (2006) is used to implement the relatively long delays required by the temporal model of harmonic cancellation. The result is used for time-domain pattern matching.
Hybrid Model 6: Logan’s theorem. This is not a specific model but a processing principle. A narrowband signal can be reconstructed perfectly from its zero crossings (and hence also from its half-wave rectified version) (Logan, 1977). This implies that, despite the non-linearities, the temporal model can be implemented after transduction as if it were applied to the acoustic waveform (the theorem does not say how).
These examples illustrate how peripheral filtering and temporal processing might work hand-in-hand to enhance a spectral model (Hybrid Model 1) or a temporal model (Hybrid Models 2–6) of harmonic cancellation. To summarize, a wide variety of mechanisms can implement harmonic cancellation: spectral, temporal, and hybrid.
Alternatives to Harmonic Cancellation
It is important to consider alternatives: to the extent that they are viable, the case for harmonic cancellation is weaker. Other aspects of the spectral structure of the target or background might support segregation, even in situations that seem to implicate harmonic cancellation.
Harmonic Enhancement
According to this hypothesis, the harmonic structure of a target sound allows its extraction from a background. The idea is attractive: it fits with the Auditory Scene Analysis credo that components of a sound are “grouped” together, here on the basis of harmonicity, to form a coherent “object” that can be distinguished from other parts of the scene (Bregman, 1990). It is satisfying to hypothesize that voiced speech might be “engineered” for this purpose through evolution (e.g., Popham et al., 2018).
The mechanisms just reviewed can be re-purposed for enhancement. For example, the mask in Figure 2 can be made to select target harmonics rather than reject background harmonics. Likewise, replacing the minus by a plus in Equation (1), and setting to the period of the target, yields a harmonic enhancement filter:
| (2) |
Enhancement and cancellation seem symmetric one of the other, but they have rather different properties. Enhancement requires the period of the target, but this is hard to estimate when TMR is small, which is unfortunately when segregation is most necessary. Cancellation works well in that situation. An enhancement filter provides only a limited boost in TMR (6 dB for the simple filter of Equation (2)) in contrast to cancellation that can reject the masker perfectly, at least in principle. A larger boost would require a longer impulse response (as explained in Appendix A of de Cheveigné, 1993, courtesy of Jean Laroche), but this might not be practical for a non-stationary signal such as speech. Anticipating, behavioral results also don’t favor the enhancement hypothesis.
Incidentally, the term “harmonic enhancement” appears in other contexts with a different meaning: perceptual enhancement of one harmonic of a complex when it is turned on or off (e.g., Hartmann & Goupell, 2006). Hopefully no confusion will result from this overloading of the terminology.
Spectral Glimpsing
Between the lines of a harmonic spectrum are gaps where target components might be glimpsed (Deroche et al., 2013; Guest & Oxenham, 2019), and this might conceivably account for the benefit observed when a background is harmonic rather than inharmonic. Figure 5(a) shows how individual channels in the low-frequency region can preferentially reflect one source or the other, as long as partials are not too close. The spectral-glimpsing hypothesis glosses over the question of how target channels are distinguished from background channels. In that, it differs from Hybrid Model 2 above.
Waveform Interactions
The sinusoidal waveforms of two or more partials can interact within a channel of a filter bank to produce a complex “beat” pattern. This can occur between partials of the same sound (with a rate equal to the fundamental if the sound is harmonic) or partials of different sounds. The patterns that result are quite diverse (static summation, slow fluctuations, rapid beats, etc.), and they depend in a complex way on several parameters (frequencies, levels, filter shapes). The “waveform interactions” hypothesis is thus ill-defined unless further specified.
From slow to fast: phase-dependent summation of same-frequency partials constitutes a potential confound in experiments that include a “zero F ” condition (de Cheveigné, 1999c). Slow beats between closely-spaced partials from different sounds cause the short-term spectrum to cycle between shapes that might favor perception of one or the other sound, either because it momentarily resembles that of one of the sounds in isolation, or because temporal contrast effects enhance important spectral features (Summerfield et al., 1981; Assmann & Summerfield, 1994; Culling & Darwin, 1994). Faster beats might evoke a sensation of roughness signaling the presence of a target (Treurniet & Boucher, 2001), or the spectral location of such beats might provide cues to its spectral features (e.g., the location of a formant peak, or the boundary between formants of different sounds). Conversely, the lack of beats at a rate slower than F (or the perceptual correlate of this lack, “smoothness”) could signal the absence of a target, or the spectral location of channels dominated by harmonics of a single sound. Finally, the absence of any modulation at F implies that the channel is dominated by a single partial, as in the phenomenon of “synchrony capture” which might signal the position of a formant peak of a successfully isolated sound (Carney et al., 2015; Maxwell et al., 2020).
Interaction of more than two harmonics produces a phase-dependent beat pattern that is more deeply sculpted for certain phase relations, such as cosine, or “Klatt” phase that approximates natural phonation with a glottal pulse within each period. Valleys between pulses might then allow a target to be glimpsed for a favorable alignment, as might occur if sounds of different F are mixed (the pitch period asynchrony hypothesis, PPA, Summerfield & Assmann, 1991).
Beat patterns might be exploited to group channels by correlation (Hall et al., 1984; Sinex et al., 2002; Sinex & Li, 2007; Fishman & Steinschneider, 2010; Shamma et al., 2011) or, alternatively, beat rates in the F range might be compared across channels (Roberts & Bregman, 1991; Treurniet & Boucher, 2001; Roberts & Brunstrom, 2003). This requires the existence of some mechanism to analyze beat patterns and quantify their rates (see Modulation Filter Bank below).
Beat amplitude depends non-monotonically on the amplitude of sources within the stimulus, and the shape of the beat pattern is phase-dependent (for three or more partials). Beat rate affects perceptual salience (e.g., roughness) non-monotonically, and the rate itself may depend non-monotonically on F difference, depending on which partials happen to be close. Finally, each channel has its own pattern of beats. For these reasons, a “waveform interaction hypothesis” is hard to delineate and test (which does not imply that it is incorrect).
Modulation Filter Bank
An influential idea is that cochlear filtering and transduction are followed by analysis by a modulation filter bank within the auditory system (Kay & Matthews, 1972; Viemeister, 1979; Dau et al., 1997; Joris et al., 2004; Stein et al., 2005; Jepsen et al., 2008). Conceptually, this seems rather like reproducing internally an operation (spectral analysis) that is already carried out in the cochlea. A major difference, however, is that it occurs after demodulation of each output of the peripheral filter bank (non-linearity followed by smoothing), which makes it primarily sensitive to features of the waveform envelope, and less sensitive to carrier phase. The concept makes most sense when applied to slow fluctuations (e.g., below 30 Hz), but models have been proposed with channels up to 500 Hz, capitalizing on the smooth transition between neural coding of fine structure at low frequencies and of envelope at higher frequencies (Joris et al., 2004). A modulation filter bank applied to each peripheral channel results in a center frequency best modulation frequency pattern that can be collapsed across channels to obtain a “summary modulation spectrum.” One could imagine a frequency-domain harmonic cancellation model applied to this “internal spectrum.” However, most estimates of modulation filter width are rather wide (quality factor 1), which makes this idea unlikely to work given the issues mentioned earlier.
Alternatively, the 2D pattern could be used to tag channels for the purpose of segregation (Ewert & Dau, 2000; Meyer et al., 1997). One might consider implementing this modulation filter bank using cancellation filters, which would result in a model similar to the hybrid models reviewed previously, a major difference being the demodulation step which renders the model sensitive to envelope periodicity rather than (or in addition to) waveform periodicity.
In Summary
Multiple models have been put forward to explain how the harmonic structure of sounds within an acoustic scene can be used to analyze the scene and attend to particular sources. Some fit the definition of harmonic cancellation, others do not. The next section reviews psychophysical evidence in favor—or against—this hypothesis and its alternatives.
Psychophysics
Detection Benefits from ΔF0
When presented with a mixture of two vowels, subjects more often report that they hear two vowels if the F0s differ (de Cheveigné et al., 1997; Arehart et al., 2005, 2011; McPherson et al., 2020). Likewise, when presented with a harmonic tone with one partial mistuned, they may detect the partial as “standing out” as a separate sound (Moore et al., 1985, 1986). Such a mistuned target tone can be detected at 15 dB relative to a harmonic masker, whereas against a noise background the threshold is 15 dB higher (Micheyl et al., 2006). In each of these examples, background harmonicity seems to affect how many sources are heard. An interpretation, in the context of harmonic cancellation, is that a single entity is perceived if cancellation is perfect, and multiple entities if it leaves a residual.
Discrimination and Identification Benefit from F
Mistuning one partial of a harmonic complex allows it to be matched to a pure tone (Hartmann et al., 1990), implying not only that this “second sound” is detectable, but also that its frequency can be accessed. Subjects are more likely to identify both vowels of a concurrent pair if their s differ (Brokx & Nooteboom, 1982; Scheffers, 1983; Zwicker, 1984; Summerfield & Assmann, 1991; McKeown, 1992; Chalikia & Bregman, 1993; Culling & Darwin, 1993; Assmann & Summerfield, 1994; Shackleton et al., 1994; Arehart et al., 2011). The pattern of results is similar across studies: poor performance (albeit well above chance) for F =0, rapid improvement up to about one semitone, followed by a plateau and possibly a dip at the octave. To create the F =0 condition with continuous speech, the voices must be re-synthesized on a monotone, or one voice given the same F track as the other, so that F s remain the same throughout the presentation. With that manipulation, a similar benefit of non-zero F is obtained (Brokx & Nooteboom, 1982; Leclère et al., 2017).
Improved performance with F 0 is taken to reflect a harmonicity-based segregation mechanism that fails when F0s are the same, and indeed, identification is less good if both voices are whispered (Lea, 1992), or inharmonic (de Cheveigné et al., 1997). This brings up the question as to whether each voice benefits from its harmonic structure, that of its competitor, or both. To answer that question, voices must be parametrized individually, and responses tallied separately. It cannot be answered if the performance metric is “both correct” (Brokx & Nooteboom, 1982; Scheffers, 1983; Summerfield & Assmann, 1991), or if both voices are made inharmonic at the same time (Popham et al., 2018).
Background Harmonicity is Important
In “double vowel experiments,” listeners give two answers on each trial, but it has been noted that one constituent (the “dominant” vowel) is usually identified regardless of F , whereas identification of the other depends on F (Zwicker, 1984; McKeown, 1992; McKeown & Patterson, 1995). “Dominance” is phoneme- and subject-dependent, but this can be overridden by changing the relative level of the vowels, in which case the F effects are mainly observed for the weaker (smaller amplitude) vowel (McKeown, 1992; de Cheveigné et al., 1997; Arehart et al., 2005). This is congruent with the harmonic cancellation hypothesis, in that estimation of the harmonic structure of the background should be easy when the target is weak. However, it could also simply result from a reduced ceiling effect for the more challenging, weaker vowel.
With the F 0 condition as a starting point, performance degrades if the competing vowel is whispered (Lea, 1992) or made inharmonic (de Cheveigné et al., 1997), regardless of whether the target is harmonic or not. This too is consistent with the harmonic cancellation hypothesis. Similar results are reported for connected speech: Steinmetzger and Rosen (2015) found that speech reception thresholds (SRTs) were up to 11 dB lower for periodic than aperiodic maskers, while Deroche et al. (2014b) reported a 4 dB elevation in SRT for inharmonic versus harmonic maskers. Incorporating harmonic cancellation within a predictive model of speech intelligibility improved its fit to experimental data (Prud’homme et al., 2020).
Gockel et al. (2002) found that the threshold for detecting noise in a harmonic masker was 11–14 dB lower than the converse, and Gockel et al. (2003) found a similar result for loudness. This suggests that a harmonic masker might be less potent than a noise masker, as expected from harmonic cancellation. As mentioned earlier, Micheyl et al. (2006) found that a harmonic complex tone (HCT) was easier to detect within a background consisting of another HCT than within noise, and Klinge et al. (2011) found a lower threshold for detection of a tone embedded in (but mistuned from) a harmonic rather than inharmonic or noise background (see also Oh & Lutfi, 2000).
All these results are consistent with harmonic cancellation. However, harmonic cancellation is not exclusive of other mechanisms, and one might expect the auditory system to use several or all if they are effective. The next section reviews evidence for harmonic enhancement.
Target Harmonicity is Less Important
The idea that harmonicity ensures that a sound does not “fall apart into a sea of individual harmonics” is seducing (Popham et al., 2018), but studies that tried to demonstrate an advantage of target harmonicity for segregation have met with mixed results. As noted earlier, in double-vowel experiments the benefit of a F is greatest for weak targets, and measurable for TMR as low as 25 dB (McKeown, 1992; de Cheveigné et al., 1997; Arehart et al., 2005). Estimating the F of a target that weak would be challenging. Replacing a voiced target by a whispered target does not impair intelligibility, regardless of whether the competitor is voiced or whispered (Lea, 1992), nor does randomly perturbing its harmonics to make it inharmonic (de Cheveigné et al., 1997). Modulating the F of target speech in the presence of reverberation disrupts its periodicity, but Culling et al. (1994) found no effect on SRTs (see also Deroche & Culling, 2011b).
For continuous speech, it has been hypothesized that target harmonicity (one aspect of “temporal fine structure,” TFS) could aid glimpsing within a spectro-temporally modulated noise, by tagging time–frequency regions that are voiced. However, a direct test of this hypothesis gave negative results (Shen & Pearson, 2019). There is however some evidence that continuity of target F helps to connect information over time, or reduce informational masking if target and masker F ranges are non-overlapping (Darwin & Bethell-Fox, 1977).
A difficulty in testing the enhancement hypothesis is that manipulation of the target might affect its intelligibility independently of any segregation effect. Whispered speech is reportedly less intelligible than voiced speech (Ruggles et al., 2014), and reverberation, which disrupts harmonicity of an intonated target, also degrades intelligibility (Deroche & Culling, 2011b). Manipulating F (monotonizing, transposing, or inverting the F track) may also affect intrinsic intelligibility (Binns & Culling, 2007; Deroche et al., 2014a; Guest & Oxenham, 2019). Such effects might conceivably offset the benefits of harmonic enhancement, making them unmeasurable, so the best we can say is that we lack strong evidence in favor of harmonic enhancement.
An Intriguing Exception: Target Pitch
In contrast to results just reviewed, a target within a noise background is easier to detect if it is harmonic than inharmonic (McPherson et al., 2020). This inconsistency is resolved if we reflect that a harmonic target is likely detected in noise on the basis of its pitch (Scheffers, 1984; Hafter & Saberi, 2001; Gockel et al., 2006), which is probably more salient if the sound is harmonic. If frequency discrimination in noise relies on a pitch percept, it too should benefit from target harmonicity, as found by McPherson et al. (2020). Thus, we cannot with confidence attribute such benefits to enhanced segregation as opposed to an enhanced pitch percept.
It is also intriguing that the pitch of a target is easier to discriminate if mixed with a noise background rather than a harmonic background (Micheyl et al., 2006), opposite to what we expect of harmonic cancellation (indeed, in that study the same sounds were easier to detect within a harmonic background than a noise background). It would seem that background harmonicity interferes with target pitch, possibly in a way similar to the phenomenon of pitch discrimination interference (PDI) (Gockel et al., 2009; Micheyl et al., 2010). That interference is not absolute: the pitch of a mistuned partial may be heard within a harmonic background (Hartmann et al., 1990; Hartmann & Doty, 1996), and individual tones may be heard within a chord (Graves & Oxenham, 2019), consistent with skills found in competent musicians.
Is the Benefit Explained by Spectral Glimpsing?
Several results seem consistent with this hypothesis. The benefit of F to vowel identification is mainly limited to the region of resolved partials (Culling & Darwin, 1993), and it improves with a higher background F at which partials are more widely spaced (Deroche et al., 2013, 2014a). Guest and Oxenham (2019) found that removing the even harmonics of a masker reduced masking of a target placed one octave above, also consistent with glimpsing within the large gaps between background partials of odd rank.
However, Deroche et al. (2013, 2014a, 2014b) argued that the larger gaps that arise when a masker is made inharmonic should reduce masking, contrary to their results. A possible explanation is that cancellation and glimpsing are both involved (Deroche et al., 2014b), consistent with Hybrid Models 2 or 3.
Is the Benefit Explained by Waveform Interactions?
As pointed out earlier, waveform interaction comes in multiple forms, and it is not always clear which version of the hypothesis is implied when it is invoked. One difficulty, common to many versions, is that the non-monotonic dependency of beat amplitude on component amplitudes implies that the magnitude (and spectral locus) of beat-dependent cues should show non-monotonic variations with level, whereas identification usually varies monotonically with TMR. Another challenge is that F -based segregation seems to benefit mostly partials of low rank, for which, thanks to resolvability, the distribution over channels of high-amplitude beats is likely sparse (Deroche et al., 2014).
Phase effects attributable to PPA were found at 50 Hz, but not at 100 Hz or higher (Summerfield & Assmann, 1991; de Cheveigné et al., 1997; Deroche et al., 2013, 2014; Green & Rosen, 2013, but see Summers & Leek 1998). Furthermore, reverberation should scramble the phase relations required by PPA, whereas it does not affect segregation unless F is modulated (Culling et al., 1994, 2003; Deroche & Culling, 2011b).
Culling and Darwin (1994) attributed effects of small F to the ability to shop for favorable spectral patterns among those offered by slow beats. Random starting phase should reduce this benefit due to the haphazard temporal alignment of beat patterns, but, de Cheveigné et al. (1997) found that the F benefit did not depend on the phase pattern (random vs sine) of either target or background. The slow-beat hypothesis was further tested by de Cheveigné (1999c), again with limited support. The reader should refer to those two papers for a detailed discussion of several forms of the waveform interactions hypothesis. Given the diversity, it is hard to rule out that some form of waveform interaction contributes to segregation. Indeed, harmonic cancellation itself could be construed as a mechanism to exploit a particular form of waveform interaction specific to harmonically-related partials.
The Special Case of Maskers With Frequency-Shifted or Odd-Order Harmonics
In experiments that require detecting (or matching the pitch of) a mistuned partial of rank within a harmonic complex of fundamental F , the subject likely attends to channels with a center frequency close to . The task might then be hampered by the presence, within those channels, of neighboring harmonics, in particular harmonics of rank and . A cancellation filter tuned to F would suppress those unwanted harmonics, but it would also suppress the target unless it is mistuned. We would thus expect performance to improve with mistuning, as indeed is observed (Moore et al., 1986; Hartmann et al., 1990).
However, Roberts and Brunstrom (1998) found a similar result when the background series had been made inharmonic by shifting all partials by the same amount , in which case partials are regularly spaced but harmonicity is disrupted. This suggests that spectral regularity, rather than harmonicity, might be the driving factor, which would put in doubt the harmonic cancellation account. However, that proposal hinges on the existence of a mechanism to detect spectral regularity: Roberts and Brunstrom (2001) doubted the existence of a dictionary of shifted-harmonic templates.
An alternative is that harmonic cancellation is applied locally within peripheral channels, for example based on Hybrid Model 4 (analogous to what has been proposed for the binaural EC model, Culling & Summerfield, 1994; Akeroyd, 2004; Breebaart et al., 2001). Specifically: the shifted partials and can be approximated with harmonics of rank and of a harmonic series of fundamental . A cancellation filter tuned to that series would approximately cancel the closest offending background partials (more distant ones are attenuated by cochlear filtering). The th zero of that filter falls at , that is, it fits the “spectral regularity” template invoked by Roberts and Brunstrom (1998), which would explain why they found that “mistuning” a partial from that position makes it easier to detect or match. An array of such CF-dependent cancellation filters, each tuned to an “equivalent F ” equal to would attenuate a shifted-harmonic complex across all channels, allowing “mistuning” relative to that spectrally regular (but inharmonic) pattern to be detected.
This reasoning can be extended to the case of a background harmonic complex with only odd harmonics of F , as it is equivalent to a series of harmonics of 2F each shifted by . This series can be canceled perfectly by a cancellation filter tuned to F , or approximately, within each peripheral channel, by a cancellation filter tuned near 2F as just described. The reason for considering the latter is that it requires a shorter delay, which is relevant if there is a penalty on longer delays as has been suggested in the context of pitch perception (Moore, 2003; de Cheveigné & Pressnitzer, 2006; Bernstein & Oxenham, 2008). An array of cancellation filters, each tuned to , would spare anything that does not fit the series of odd harmonics, in particular an even-numbered harmonic. If so, it might explain why a single even-numbered harmonic embedded among odd-numbered harmonics is “heard out” more easily than any of the odd-numbered partials (Roberts & Bregman, 1991), and similar explanation might underlie the benefit for identification of a speech target of removing even harmonics of the masker (Guest & Oxenham, 2019) mentioned earlier. This question is revisited in the Discussion.
In Summary
A body of evidence agrees with the hypothesis that harmonic cancellation assists auditory scene analysis, complementing the well-known benefits of peripheral frequency analysis. Dissenting results are sparse. The alternative hypothesis of harmonic enhancement, while attractive, garners little experimental support. Harmonic cancellation raises a number of issues that are discussed further in the Appendix. These include period estimation (necessary to apply cancellation), the relations between correlation and cancellation, analogies with the well-known EC model of Durlach, pattern matching with missing data, potential anatomical and physiological substrates, and the possible synergy between cochlear filtering and neural filtering.
Discussion
Periodicity (or harmonicity)—and its perceptual correlate, pitch—have long captured the attention and imagination of thinkers and scientists (Micheyl & Oxenham, 2010). A periodic sound within the right parameter range evokes a salient percept that is long-lasting in memory (McPherson et al., 2020), is robust to masking by noise (Hafter & Saberi, 2001; McPherson et al., 2020), and supports fine discrimination (e.g., Micheyl & Oxenham, 2010). However, the idea that a sound “falls apart” unless it is harmonic does not withstand a bit of reflection. A one-period tone pulse seems unitary without the aid of harmonicity, meaningless at that duration. A harmonic tone of longer duration may sound unitary, but so does noise which lacks harmonicity. An alternative proposition is that the percept evoked by a sound is unitary by default, and that “multiplicity” is inferred from the accumulation of evidence in favor of additional sources. A complex with a mistuned harmonic initially sounds like a single object but, given time and encouragement, a subject might detect something amiss and interpret it as an additional source. The process requires time (Moore et al., 1985; Hartmann et al., 1990; McKeown & Patterson, 1995), and is harder if the background is made inharmonic (Roberts & Brunstrom, 2003; Roberts & Holmes, 2006). Thus, one could argue, the harmonic nature of one part of the stimulus makes it easier to detect the presence of other parts. From this perspective, harmonicity of a source may contribute to a percept of multiplicity for mixtures in which it participates, rather than to its own unity.
That background harmonicity is crucial comes as a surprise, as it suggests that segregation must rely on an adventitious quality of the environment. Also surprising is that target harmonicity has only a minor role, as it goes against the attractive idea that communication sounds are “engineered” through evolution to be harmonic for resilience. It does make sense, however, when one realizes that cancellation works well (and enhancement poorly) at low TMR, which is when segregation is most needed. Infinite TMR improvement can be achieved, in principle, for very short stimuli for which enhancement offers more limited benefit. Cancellation meshes well with the concept that perception involves a quest for invariance to irrelevant dimensions.
Cancellation as a Model of Sound
The ability to cancel unwanted sounds is clearly useful for perception, but one might take a step further and argue that it is, in part, constitutive of perception. As a predictive model, a harmonic cancellation filter characterizes the part of input that it can cancel, just as an autoregressive model characterizes its spectral envelope, or a binaural EC model its spatial position. The residual, which by definition does not fit that model, informs us about “what else is out there.” It too can be characterized by recursively applying the same model or, alternatively, a compound model can be applied to the original sound to estimate parameters jointly (as in the multiple F model described in the Appendix, Period Estimation). This is related to concepts of predictive coding (Friston, 2018) and compression (Schmidhuber, 2009).
Like pattern classification (Duda et al., 2012), cancellation seeks invariance with respect to irrelevant dimensions of the input, specifically those that reflect the background. In contrast to classifiers that involve non-linear transforms, cancellation as described here is purely linear, which makes sense given that the acoustic mixing process itself is linear.
How Useful is it in Practice?
Auditory Scene Analysis benefits from multiple cues and regularities, of which harmonicity is but one. Harmonic cancellation is likely to be useful in situations where neither temporal separation, nor spectral separation, nor binaural disparities are effective to suppress interfering sources, and then only if the interference is harmonic. Thus, at best, it is one tool among many, beneficial in a restricted set of circumstances.
Measured in terms of TMR at threshold performance, the harmonicity benefit can reach 17 dB for identifying synthetic vowels, although most studies report smaller effects (Summerfield et al., 1992; Culling et al., 1994; de Cheveigné et al., 1997). This is of the same order of magnitude as reported for binaural unmasking (Colburn & Durlach, 1965; Jelfs et al., 2011). In terms of proportion of tokens recognized, the benefit appears maximal for TMR around 15 dB and vanishes below 30 dB or above +15 dB (McKeown, 1992; de Cheveigné et al., 1997; de Cheveigné, 1999b). Thanks in part to harmonicity-based segregation, a target (wide-band harmonic or noise) mixed with a harmonic background can be detected at TMRs down to 20 dB (Gockel et al., 2002; Micheyl et al., 2006), or 32 dB for a narrowband noise target (Deroche & Culling, 2011a). The benefit relative to a noise or inharmonic masker is on the order of 5–15 dB (Micheyl et al., 2006; Deroche & Culling, 2011a; Deroche et al., 2014). Overall, harmonic cancellation mainly benefits weak targets.
For vowel identification, the benefit is measurable for F s as small as 0.4% but not less (de Cheveigné, 1997b), and plateaus for F s beyond 6%. It is greater for longer stimuli (200 ms) than shorter stimuli (50 ms) (Assmann & Summerfield, 1994), but measurable for stimuli as short as four cycles of the lower F (23 ms at 175 Hz, McKeown & Patterson, 1995). It is reduced but not abolished if the masker’s F is modulated at rates as fast as 5 Hz (200 ms period) (Summerfield et al., 1992; de Cheveigné, 1997b; Deroche & Culling, 2011b), suggesting a remarkable ability to track F variations. However, this breaks down in the presence of reverberation, whereas a similar degradation is not observed if the masker F is steady-state (Culling et al., 1994; Sayles et al., 2015). Data from mistuned harmonic experiments suggest that the benefit might be limited to the spectral region below 2–3 kHz (Hartmann et al., 1990). Indeed, in concurrent vowel experiments the benefit appears to stem mainly from the region below 1 kHz that includes a vowel’s first formant (Culling & Darwin, 1993).
Real speech maskers differ from ideal harmonic maskers in that periodic portions are sparsely distributed over time (Hu & Wang, 2008), the F varies due to intonation, and periodicity is further degraded by articulation, irregularities in voice excitation, and added noise including reverberation. The benefit of a F between a monotonized speech target and monotonized masker (two concurrent voices with the same F , or harmonic complex with spectral envelope similar to speech) ranges from 3 to 8 dB (Deroche & Culling, 2013; Deroche et al., 2014a, 2017), which is also on the same order as binaural effects for similar stimuli (Deroche et al., 2017).
Learning?
Pattern-matching models of pitch perception (de Boer, 1976) postulate some form of harmonic template, or “sieve” (Schroeder, 1968; Duifhuis et al., 1982), and the same template is also required for a spectral domain model of segregation. This is non-trivial: the dictionary of templates must cover the full range of F0s, there must be some mechanism to align the templates accurately with the substrate of frequency analysis (e.g., cochlea), and each template itself is a complex affair involving multiple slots with accurate tuning. It has been proposed that templates are learned from exposure to harmonic sounds such as speech (Terhardt, 1974; Divenyi, 1979; Bowling & Purves, 2015; Saddler et al., 2020) possibly modulated by cultural preferences (McDermott & Hauser, 2004; McDermott et al., 2010, 2016; McPherson et al., 2020). The demonstration that templates can be learned from noise (Shamma & Klein, 2000; Shamma & Dutta, 2019) makes that argument more tenuous, and highlights the question of what, exactly, is being learned. Perhaps that algorithm discovers, rather than learns, the mathematical property that is exploited more directly by the cancellation filter.
The template-like properties of a time-domain cancellation filter (Equation (1), Figure 4) stem from mathematics, rather than learning. This is a big appeal: why jump through hoops when a simple solution is at hand? The organism may still need to discover that this regularity exists and is worth attending to, and the mechanism may need tuning, particularly if it involves combining frequency channels. This leaves ample room for learning, and possibly even cultural influences.
Is There Time?
In a classic chapter, de Boer (1976) likened auditory theory to a pendulum moving between “time” and “place” (spectrum). The pendulum is still swinging, and several recent papers have strengthened the case for spectral and place-rate accounts (e.g., Shera et al., 2002; Sumner et al., 2018; Verschooten et al., 2018; Whiteford et al., 2020; Su & Delgutte, 2020). Arguments for time remain (a) evidence for temporal mechanisms of binaural processing (see section Analogy with Binaural EC of the Appendix), (b) existence of specialized neural circuitry within the brain (see section Anatomy and Physiology of the Appendix), and (c) the simplicity, effectiveness and ease of implementation of a time-domain harmonic filter, in contrast to a harmonic template or sieve in the frequency domain.
Hybrid models offer the best of both worlds, but they may worry scholars who care about parsimony or falsifiability. As a case in point, if we admit that delay might arise by cross-channel interaction (de Cheveigné & Pressnitzer, 2006), it is hard to say anything for, or against, the hypothesis that processing involves neural delays. On the other hand, it would be unwise to let this blind us to the possibility that auditory system does rely on a combination of spectral and time-domain analysis.
My personal inclination is that auditory perception involves time-domain processing within the brain, but the effectiveness of that processing is enhanced by the peripheral bandpass filter bank that helps overcome the effects of non-linear transduction and noise (based on principles related to Logan’s theorem). High-resolution mechanical filtering serves to “pre-calculate” a set of useful basis functions upon which the brain then operates in the time-domain (see sections Transforms in Filter Space and Non-Linearity of the Appendix). In this perspective, cochlear mechanics are the “last chance” to process acoustical signals with good resolution, linearity, and low noise, before handing transduced patterns over to more flexible but less accurate neural processing.
Carving Sound at its Joints
Auditory Scene Analysis is often described as a process of assembling elements across the spectrum (simultaneous grouping) or across time (sequential grouping) (Bregman, 1990), mirroring the common process of additive or concatenative synthesis by which stimuli are created in the lab. It glosses over the issue of whether these ingredients are recoverable from the mix, upon which this assumption depends. Once the coins are thrown into the melting pot, can we pull them out intact? According to classic Auditory Scene Analysis, we can: spectral analysis reveals “natural kinds” (partials), between which are found the “joints” at which sounds may be carved (Campbell et al., 2011). Indeed, according to this view, a grouping mechanism is required for any complex sound to form a coherent whole, otherwise it might shatter into as many percepts as partials (although few of us would claim to ever have heard more than a couple of such percepts within a sound). The wisdom of invoking sinusoidal partials as “natural kinds” on which Auditory Scene Analysis processes operate is rarely questioned.
In contrast, harmonic cancellation requires no analysis-into-parts or grouping. Whereas a bandpass filter is defined by what it selects (a frequency band), a cancellation filter is defined by what it removes (periodic power at period ). This is an example, like a shadow, of what Sorensen (2011) calls a “para-natural kind.” The process is effective both to characterize a periodic sound by its parameter , and to get rid of that sound and search for more. It is an alternative way to “carve sound at its joints.”
Conclusion
The harmonic cancellation hypothesis states that the harmonic (or periodic) structure of interfering sounds can be exploited to suppress or ignore them. A large body of experimental results are consistent with this hypothesis, whereas alternative hypotheses for F -based segregation are less well supported. In particular, harmonic enhancement, according to which harmonicity of a target makes it resilient to masking, receives little support, which is surprising because counter to our intuition and inconsistent with textbook explanations of scene analysis involving a harmonicity-based “grouping” operation. Harmonic cancellation fits well with an account of perception as seeking invariance with respect to irrelevant dimensions of the sensory pattern, and with the concept of “unconscious inference” promoted by Helmholtz. Harmonic cancellation can be implemented in the frequency domain (based on cochlear analysis) or time domain (based on the temporal processing of neural discharge patterns). Support for the latter comes from the success of the related EC model of binaural interactions, from the presence of neural structures apparently specialized for processing of temporal information, and from theoretical considerations that suggest that a time-domain implementation might be more straightforward and effective.
Appendix: Deeper Issues
The harmonic cancellation hypothesis is straightforward and well supported experimentally, but it raises a number of interesting questions that are worth considering.
Hybrid models
The hybrid harmonic cancellation models enumerated in the main text are described here in greater detail.
Hybrid Model 1: Cancellation-enhanced spectral patterns. Each channel of a filter bank is convolved with a cancellation filter tuned to . This has the effect of sharpening spectral analysis so that the outcome is closer to the ideal (Figure 2 right). The pattern of power over channels is then handed over to a frequency-domain pattern-matching stage. This is illustrated in Figure 6(a). Two vowels, /a/ and /e/ with fundamentals 100 and 106 Hz, respectively (left), are mixed. Cues to /e/ are indistinct within the spectrum of the mix (right, black), but can be enhanced by applying to each channel a cancellation filter tuned to suppress /a/ (right, red). This model is reminiscent of periodicity tagging of tonotopic patterns (Keilson et al., 1997), or of the place-time model of Assmann and Summerfield (1990) in which a spectral profile for the target vowel was taken by sampling the ACF at the target’s period. If the spectral profile were derived from a limited window of cancellation-filtered signal, placing that window within the background-invariant part (red in Figure 4(b), right) would make the profile invariant with respect to backgrounds of period . The pattern would still be distorted by the cancellation filtering, and spectral pattern-matching would need to take this into account.
Hybrid Model 2: Channel rejection on the basis of periodicity. Filter bank channels are divided into two groups based on TMR (estimated based on residual power at the output of a cancellation filter tuned to ). The first group consists of channels dominated by the background; these are rejected. The remaining channels are handed over to the pattern-matching stage to be matched based on their temporal pattern. This principle was employed in the concurrent vowel identification model of Meddis and Hewitt (1992), itself inspired from earlier ideas for binaural or periodicity-based segregation (Lyon, 1983, 1988; Weintraub, 1985). Spectral resolution must be sufficient so that enough channels are spared to represent the target.
-
Hybrid Model 3: Cancellation filtering of selected channels. Filter bank channels are divided into three groups based on TMR. Channels with large TMR are left untouched, channels with small TMR are discarded, and intermediate channels are processed by the cancellation filter. Keeping the first group intact reduces target distortion, and discarding the second group avoids contamination from noise if the cancellation filter is imperfect (as it might be due to non-linearity or noise). Cancellation filtering is reserved for channels with intermediate TMR, for which it can be effective. This model differs from Hybrid Model 2 by the presence of this third group. A similar suggestion was made by Guest and Oxenham (2019).
Hybrid Model 3 is illustrated in Figure 6(b). The black line shows the TMR per channel at the output of a filter bank in response to the mix /a/+/e/ with overall TMR = 0 dB. Channels for which TMR exceeds some threshold (+12 dB in this example) are left intact (green), channels for which TMR is below a second threshold ( 12 dB in this example) are discarded (black). Channels with intermediate TMR are processed with a cancellation filter (red).
Hybrid Model 4: Channel-specific cancellation filter. In contrast to previous models, for which the parameter is the same for all channels, here it is allowed to vary across channels. This is analogous to the channel-dependent versions of the EC model of binaural unmasking (Culling & Summerfield, 1994; Akeroyd, 2004; Breebaart et al., 2001). This hypothesis may be useful to explain results found with inharmonic stimuli (e.g., Roberts & Brunstrom, 1998) as discussed in the main text.
Hybrid Model 5: Synthetic delays. The cancellation filter of Equation (1) requires a delay equal to the background period (e.g., 20 ms for a 50 Hz fundamental). The existence of delays of this size in the auditory system has been questioned (e.g., Laudanski et al., 2014), and to address this issue it has been suggested that long delays might arise from cross-channel interaction (de Cheveigné & Pressnitzer, 2006). According to this model, the filter bank serves mainly that purpose: to help synthesize the delay required by Equation (1).
Hybrid Model 6: Logan’s theorem. Rather than a specific model, this is a processing principle that addresses the issue of the non-linear transduction that follows cochlear filtering. Due to half-wave rectification, each transduced signal is “blind” to one-half of every cycle, and thus one might worry that some information was lost. Logan’s theorem states instead that a narrowband signal can be reconstructed perfectly from its zero crossings, and hence also from its half-wave rectified version (Logan, 1977; Shamma & Lorenzi, 2013). To the extent that it is applicable here, the benefit of cochlear filtering would be to linearize transduction, so that neural signal processing has, in effect, full access to the acoustic waveform (see the section “Non-Linearity” below).
Figure 6.
Two hybrid models of harmonic cancellation. (a) Hybrid Model 1. Left: power as a function of CF for synthetic vowels /a/, F =100 Hz (blue) and /e/, F =106 Hz (red). Short lines above the plot indicate the first two formant frequencies of each vowel. Right: power as a function of CF for the mix before (black) and after (red) applying a cancellation filter tuned to suppress the period of /a/. (b) Hybrid Model 3. Black: per-channel TMR of vowel /e/ as a function of CF for a mixture of /a/+/e/ at overall TMR=0 dB. Channels are divided into three groups: TMR>12 dB (green, to be left intact), (black, to be discarded), and 12 dB TMR 12 dB (red, to be filtered by a cancellation filter).
Period Estimation
Harmonic cancellation requires an estimate of the interferer period . Harmonic cancellation itself can be used for that purpose: an array of cancellation filters, each tuned to a different delay (lag) covering the range of expected periods, shows a minimum in output power at a lag equal to the period. This is equivalent to searching for a peak in the ACF (Licklider, 1951; Meddis & Hewitt, 1991; de Cheveigné, 1998). The relation between cancellation and correlation is detailed in the next section.
From this perspective, cancellation is both an analysis tool (it cancels part of a signal to reveal the remainder), and an estimation tool (it estimates the period of the part it cancels). Applied recursively to a mixture of two sounds, it can reveal two periods: we first estimate the period of the dominant sound and cancel it, and then recurse on the remainder. These steps can be performed in parallel by searching the two-dimensional parameter space of a cascade of cancellation filters defined as and for a minimum in output power. This output is zero when for integers , (de Cheveigné, 1993; de Cheveigné & Kawahara, 1999). Interestingly, a neural version of this model designed to estimate the pitch of a mistuned partial (de Cheveigné, 1999a) accurately accounted for the subtle shifts observed by Hartmann and Doty (1990), Hartmann et al. (1996), see also Holmes and Roberts (2012).
Associated with the period is an estimate of the degree to which the sound is, in fact, periodic. A straightforward measure is output power of a cancellation filter tuned to the period , normalized by power at the input (or by output averaged over other lags, e.g., 1,…, T). A value of zero indicates that the sound is perfectly periodic, and a small value indicates that it is “approximately periodic.” This same measure can be used as a criterion to detect a target in the presence of a harmonic background.
The threshold beyond which a sound should be declared “aperiodic” depends on the application, and more specifically on the distributions of “periodic” and “aperiodic” sounds as defined by the application’s needs. It is worth noting that residual aperiodic power at the output of a narrowband filter (e.g., filter bank channel) takes on relatively low values even if the stimulus is aperiodic. The threshold needs adjusting accordingly.
Correlation and Cancellation
We can define the running autocorrelation function (ACF) at time as
| (3) |
(dropping the scaling factor 1/W for simplicity), where is the duration of a sliding integration window that serves to smooth the time course of . Power at time can then be defined as . Likewise, we can define a squared difference function (SDF) as power at time of the cancellation filter output
| (4) |
ACF and SDF are then related by
| (5) |
A peak in correlation, cue to the period, maps to a trough in difference function. It is convenient to normalize ACF and SDF
| (6) |
| (7) |
in which case the normalized functions are related more simply by
| (8) |
For a periodic sound with period , , and
Equation (5) is useful to derive the ACF from the SDF or vice-versa. It can also be extended to more terms, for example to implement a cascade of cancellation filters in terms of correlation. This allows different modeling strands to be unified, and justifies some flexibility when speculating about hypothetical neural implementations (see below).
Analogy with Binaural EC
Durlach’s EC model has been successful in accounting for binaural unmasking (Durlach, 1963; Culling & Summerfield, 1994; Culling, 2007) and binaural pitch phenomena (Culling, Summerfield, & Marshall, 1998), and in predictive models of speech intelligibility (Beutelmann & Brand, 2006; Lavandier et al., 2012; Cosentino et al., 2014; Schoenmaker et al., 2016). Binaural interaction has also been couched in terms of inter-aural correlation rather than cancellation (Jeffress, 1948) but, as pointed out by Green (1992), an EC model can be implemented on the basis of inter-aural correlation, and vice versa, as the two are related: , where and are sounds at left and right ears, respectively. A cancellation residue in one model maps to decorrelation in the other.
An interesting suggestion is that EC might operate independently within frequency channels (Culling & Summerfield, 1994; Akeroyd, 2004; Breebaart et al., 2001), rather than with parameters common to all channels as in the original EC model (Durlach, 1963). It has been further suggested that EC parameters can be estimated and applied within short-time windows (Wan et al., 2014; Hauth & Brand, 2018), which paves the way for a spectro-temporal form of the EC model that supports “glimpsing” (Beutelmann et al., 2010).
A monaural version of the EC model has been invoked to explain comodulation masking release (CMR) (Piechowiak et al., 2007).
Anatomy and Physiology
Time-domain and hybrid models entail time-domain signal processing within the brain. Anatomical and physiological specializations to support such processing include transduction and coding of acoustic temporal structure in the auditory nerve (up to 4–5 kHz or possibly higher, Heinz et al., 2001; Hartmann et al., 2019; Carcagno et al., 2019; Verschooten et al., 2019), specialized synapses in the cochlear nucleus and subsequent relays, and fast excitatory and inhibitory interaction in the medial and lateral superior olives (MSO and LSO) (Grothe, 2000; Zheng & Escabí, 2013; Keine et al., 2016; Beiderbeck et al., 2018; Stasiak et al., 2018) and other nuclei (Albrecht et al., 2014; Caspari et al., 2015; Felix et al., 2017). Some of these circuits are interpreted as serving binaural interaction, but presumably could be borrowed for other needs (see Joris & van der Heijden, 2019; Kandler et al., 2020, for recent reviews).
The time-domain cancellation filter of Figure 4(c, left), Equation (1), can be approximated by the “neural cancellation filter” of Figure 4(c, right). Spikes arriving via the direct pathway are suppressed by the coincident arrival of spikes delayed by . Applied to data recorded from the auditory nerve in response to a mixture of two vowels with different F s (Palmer, 1990), that simple circuit was effective in estimating both their periods and suppressing correlates of one or the other vowel (de Cheveigné, 1993, 1997a; Guest & Oxenham, 2019). Such a mechanism would require temporally accurate neural representations (excitatory and inhibitory), delays, and an inhibitory gating or “anticoincidence” mechanism.
Temporally accurate inhibitory transforms of sensory input are created in several nuclei, including cochlear nucleus (CN) (stellate-D cells), medial and lateral nuclei of trapezoid body (MNTB and LNTB), and ventral nucleus of the lateral lemniscus (VNLL) (Arnott et al., 2004; Caspari et al., 2015; Joris & Trussell, 2018). Fast interaction between direct and delayed neural patterns could in principle occur as early as the dendritic fields of cells in CN (Shore et al., 1991; Schofield, 1994; Davis & Voigt, 1997; Needham & Paolini, 2006; Xie & Manis, 2013), or as late as dendritic fields of the inferior colliculus (IC) (Caspari et al., 2015; Chen et al., 2019). A recent study reported evidence for an inhibitory “veto” mechanism at the axon initial segment of LSO principal neurons, with very narrow tuning to inter-aural time differences (Franken et al., 2021). Transmission failure at reputed “secure” synapses in CN and MNTB might conceivably reflect a similar veto mechanism (Mc Laughlin et al., 2008; Englitz et al., 2009; Stasiak et al., 2018).
The cancellation-correlation equivalence discussed earlier implies that fast interaction might also be excitatory-excitatory, the correlation pattern being later converted to a cancellation-like statistic by slower inhibitory interaction along the lines of Equations (5) and (8). Note, however, that finding a minimum of cancellation would then require subtraction of two large correlation values, which may be a problem if those values are coded by a representation (like rate of a Poisson-like process) for which the noise variance of the value increases with its mean. One might speculate that the cost of specialized fast inhibitory circuitry is recouped by the benefit of performing cancellation directly.
There is also evidence in favor of accurate rate-place spectral representations (Larsen et al., 2008; Fishman et al., 2013, 2014; Su & Delgutte, 2020) that might support a spectral version of the harmonic cancellation hypothesis, particularly as it has been argued that tuning might be narrower in humans than in most model animals (Shera et al., 2002; Verschooten et al., 2018; Sumner et al., 2018; Walker et al., 2019). Narrow tuning might also benefit a spectro-temporal mechanism, with the caveat that narrower filters are temporally more sluggish.
Sinex et al. (2002), Sinex and Li (2005), Sinex et al. (2007) report stronger responses in IC neurons for mistuned partials, consistent with the output of a cancellation filter, but they explain it by a different model based on cross-channel interaction of between-partial beat patterns, analogous to the waveform interaction models described earlier. Their model also accounts for the particular temporal structure of the response; whether that structure too could be explained by cancellation remains to be determined.
In summary, known neural circuitry might support both temporal and spectral mechanisms of harmonic cancellation, however I am not aware of evidence as strong as that reported in favor of the EC model. A rate-frequency response such as Figure 4(a) might evade notice if attention is devoted to peaks of activity rather than dips. It could also elude discovery if the output pattern follows a latency code rather than rate code (Chase & Young, 2007). The filter output in Figure 4(b) is evocative of ON–OFF patterns observed in the superior paraolivary nucleus (SPON) (Kandler et al., 2020) but this similarity could be fortuitous, indeed those patterns have been attributed to gap detection or duration encoding (Kadner & Berrebi, 2008).
Smart Pattern Matching
As discussed in the main text (Harmonic Cancellation—Possible Mechanisms), each recovered target pattern is affected by two error terms: imperfect cancellation of the background, and distortion undergone by the target. In the time-domain model, the first term can be reduced to zero over part of the pattern (red segment in Figure 4(b), right). This assumes the ability to locate and isolate reliable intervals, which is commonly granted for auditory perception (Viemeister & Wakefield, 1991; Moore et al., 1988).
There remains the second error term due to filter-induced target distortion. This can be mitigated if it is known to the pattern matching stage, for example, by applying the same distortion to each pattern in the dictionary. Distortion consists of an attenuation factor applied to each target component depending on how close it falls to the harmonic series of the background, as quantified by the filter transfer function (Figure 4(a), right). This produces a “moiré effect” that can be quantified (and thus taken into account) if F s of both background and target are known.
Target patterns can be further refined if the background is stationary over more than two periods, as illustrated in Figure 7. Specifically, if the stimulus is long enough to define distinct observation intervals temporally separated by , these intervals can form distinct pairs from which to infer the target. These observations are not all strictly independent, but the distortion (Figure 7, right) and noise patterns differ between pairs and this may assist inference. A perceptual mechanism operating in this fashion might seem implausibly complex. On the other hand, we cannot rule out that the trick is discovered by a learning process. The point made here is that the opportunity exists.
Figure 7.
Left: waveform of the mix of target vowel /e/ (132 Hz) with background vowel /a/ (100 Hz) at TMR= 12 dB. Given four background cycles, intervals can be paired over spans of , 2 , and 3 , with three, two and one repeats, respectively (blue arrows). Right: spectrum of target vowel /e/ (black line) and cancellation-filtered estimates obtained for spans , 2 , and 3 (symbols). Averaging over estimates (or better: taking their maximum) would yield a more accurate estimate of the target, and averaging over repeats might further attenuate uncorrelated noise (not shown).
Transforms in Filter Space
The idea that cochlear filtering works hand in hand with neural filtering is intriguing. What are the possibilities, what are the limits? As an example, the bandwidth of cochlear filters is usually seen as a hard limit on spectral resolution, but it appears that with neural filtering that limit can be overcome, as exploited by past schemes such as the “second filter” (Huggins & Licklider, 1951), stereausis (Shamma et al., 1989), lateral inhibitory network (LIN) (Shamma, 1985), phase opponency (Carney et al., 2002), synthetic delays (de Cheveigné & Pressnitzer, 2006), EC (Durlach, 1963), selectivity focusing in inferior colliculus (IC) (Chen et al., 2019), and here harmonic cancellation.
This section attempts to make sense of this situation by casting both filtering stages into a common framework. Any filter can be approximated as a finite impulse response (FIR) filter of order , defined by the column vector of impulse response coefficients. A signal is filtered by convolving it with this impulse response. Alternatively, using matrix notation, if is the matrix of time-lagged signals, the filtered signal is obtained as the product . A useful way to think of it is that the lags [ ] create a memory of the past signal, within which the filter can “shop” for useful information to characterize variations over time.
Extending to a -channel filter bank, the filters can be defined by a matrix of impulse responses of size , where each column of represents the impulse response of one channel. The matrix of filtered signals is then obtained as the product . To relate this to the context of this paper, picture as an acoustic signal, as a bank of “cochlear” filters, and as a matrix of vibration waveforms at different points along the basilar membrane.
If the matrix is of rank , it has a right inverse such that , the identity matrix. Why might this be useful? Suppose that we wish to speculate that the auditory brain implements a particular filter (defined by its impulse response applicable to the acoustic waveform). It does not have access to time-lagged acoustic signals , so it cannot implement that filter directly, but it does have access to peripheral filter outputs . We want to know if our speculation is realistic.
We can write
| (9) |
where is a vector of weights. Applying weights to yields the desired filtered signal, exactly as if we had applied the filter directly to the acoustic waveform. Whereas the filter was originally defined by its coordinates on a basis of time shifts applicable to the acoustic signal, it is now defined using coordinates on a basis of filter bank channels. The outcome is the same.
Why is this relevant here? It means that essentially any filter can be implemented (or its implementation can be complemented) by forming a weighted sum of cochlear filter outputs, as long as their impulse responses are long enough to reach the required order . This is the gist of the “synthetic delay” model of de Cheveigné and Pressnitzer (2006). According to this view, peripheral filtering and neural time-domain interaction work hand in hand to perform acoustic signal processing (subject to limits imposed by noise and non-linearity discussed in the next section).
A matrix of cancellation filters with lag parameters ranging from 0 to -1 is also invertible (if one replaces the degenerate =0 filter by ), and thus one can treat it as a “basis” similar to the filter bank basis just described. A filter defined by its coefficients on a lags basis, or on a filter bank basis, can therefore also be defined by a set of coefficients on this new basis. One can, at least conceptually, transform the sensory representation back and forth between these three representations: lagged waveforms, band-pass filter bank channels, and cancellation-filtered channels, with no loss of information. The cancellation-filtered representation is reminiscent of the pitch-like “level of representation” invoked by Hafter and Saberi (2001).
There remains one difficult issue: given a periodic sound with period , how do we find the coefficients of a cancellation filter (defined over a basis of peripheral filter outputs) that can cancel it? In the standard formulation (Equation (1)) based on a basis of lags, the filter consists of all zeros except =1 and , so the parameter can easily be found by scanning a linear array for a minimum. For , the situation is more complex because we must find a set of parameters, rather than one, to obtain the same result. This is a serious obstacle unless a “smart” way of finding is found. A full discussion of the problem is beyond the scope of this paper, but it is worth taking note of three points.
The first is that, if principal component analysis (PCA) is applied to the matrix for a periodic input with period , at least one column of the PCA transform matrix defines a FIR filter that cancels that input. This is because the th column of is identical to the 0th column (periodicity), hence is not of full rank.
The second point follows from the first: if PCA is applied to the matrix of filter bank outputs, at least one column of the PCA transform matrix defines a set of coefficients that also cancels its input. This is because rank deficiency of implies rank-deficiency of . Thus, the appropriate coefficients can be also be found by applying PCA to filter bank outputs for a periodic input. This data-dependent process can be seen as a form of data-driven learning, analogous to what we discussed earlier.
The third point is that PCA is widely considered as a plausible neural operation (Oja, 1982; Qiu et al., 2012; Minden et al., 2018). Putting these pieces together, we can speculate that the hypothesis that Equation (1) is implemented in the brain as a weighted sum of filter bank outputs, rather than a simple delay , is not completely unrealistic. This rough sketch needs fleshing out, but it suggests a possible direction to model how the auditory brain might implement complex signal processing tasks, cancellation being one particular example.
Again, such operations might seem implausibly complex for a biological implementation, but knowing that the option exists, in principle, and understanding how it works, can guide speculation that something similar is discoverable by a learning process.
Non-Linearity
Previous sections mostly glossed over the issue of non-linear transduction. The suggestion that linear operations can be swapped, as shown in Figure 5(b), or linear transforms inverted as in the previous paragraph, is moot if the systems are not linear. What can be salvaged from those simple ideas?
First, note that any time-invariant transform of a periodic signal is periodic with the same period (or submultiple of that period), so a canceation filter tuned to the period would produce zero output as in the linear case. Thus, for example, Hybrid Model 1 would work as advertized. Second, pattern distortions due to non-linearity may be compensated for in the pattern-matching stage. Thus, Hybrid Model 2 might also work. Third, more generally, we can invoke Logan’s theorem and assume that the deleterious effects of non-linearity, whatever they are, can be redressed by subsequent processing. The theorem doesn’t say how, but it is easy to imagine simple situations in which this might pan out. For example, sampling the steep phase characteristic of the cochlear filter bank at two points differing by might give access to both polarities of the signal at that point, reversing effects of half-wave rectification. Fourth, non-linearity demodulates the band-pass filtered signal, thus abstracting an informative temporal envelope from less robust fine structure (Dau et al., 1997). In this respect, non-linearity is a feature, rather than a bug.
In summary, non-linearity does not prevent harmonic cancellation, although it does make it harder to understand the limits of what can be achieved, and how.
Acknowledgements
Mickael Deroche, John Culling and Josh McDermott made useful comments on a previous version, and Maria Chait and Israel Nelken offered useful advice. The manuscript also benefitted greatly from comments of two anonymous reviewers and the Editor, Chris Plack.
Footnotes
Declaration of Conflicting Interests: The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: This work was supported by grants ANR-10-LABX-0087 IEC, ANR-10-IDEX-0001-02 PSL, and ANR-17-EURE-0017.
ORCID iD: Alain de Cheveigné https://orcid.org/0000-0002-7305-1891
References
- Akeroyd M. A. (2004). The across frequency independence of equalization of interaural time delay in the equalization-cancellation model of binaural unmasking. Journal of the Acoustical Society of America, 116, 1135–1148. 10.1121/1.1768959 [DOI] [PubMed] [Google Scholar]
- Albrecht O., Dondzillo A., Mayer F., Thompson J. A., Klug A. (2014). Inhibitory projections from the ventral nucleus of the trapezoid body to the medial nucleus of the trapezoid body in the mouse. Frontiers in Neural Circuits, 8, 83. 10.3389/fncir.2014.00083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- al Haytham I. 1030. (2002) Book of optics (in Hatfield).
- Arehart K. H., Rossi-Katz J., Swensson-Prutsman J. (2005). Double-vowel perception in listeners with Cochlear hearing loss: differences in fundamental frequency, ear of presentation, and relative amplitude. Journal of Speech, Language, and Hearing Research, 48, 236–252. 10.1044/1092-4388(2005/017) [DOI] [PubMed] [Google Scholar]
- Arehart K. H., Souza P. E., Muralimanohar R. K., Miller C. W. (2011). Effects of age on concurrent vowel perception in acoustic and simulated electroacoustic hearing. Journal of Speech, Language, and Hearing Research, 54, 190–210. 10.1044/1092-4388(2010/09-0145) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnott R., Wallace M., Shackleton T., Palmer A. (2004). Onset neurones in the anteroventral cochlear nucleus project to the dorsal cochlear nucleus. Journal of the Association for Research in Otolaryngology, 5, 153–170. 10.1007/s10162-003-4036-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assmann P. F., Summerfield Q. (1990). Modeling the perception of concurrent vowels: Vowels with different fundamental frequencies. Journal of the Acoustical Society of America, 88, 680–697. 10.1121/1.399772 [DOI] [PubMed] [Google Scholar]
- Assmann P. F., Summerfield Q. (1994). The contribution of waveform interactions to the perception of concurrent vowels. Journal of the Acoustical Society of America, 95, 471–484. 10.1121/1.408342 [DOI] [PubMed] [Google Scholar]
- Beiderbeck B., Myoga M. H., Müller N. I. C., Callan A. R., Friauf E., Grothe B., Pecka M. (2018). Precisely timed inhibition facilitates action potential firing for spatial coding in the auditory brainstem. Nature Communications, 9, 1771. 10.1038/s41467-018-04210-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein J. G. W., Oxenham A. J. (2008). Harmonic segregation through mistuning can improve fundamental frequency discrimination. Journal of the Acoustical Society of America, 124, 1653–1667. 10.1121/1.2956484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best V., Roverud E., Baltzell L., Rennies J., Lavandier M. (2019). The importance of a broad bandwidth for understanding “glimpsed” speech. Journal of the Acoustical Society of America, 146, 3215–3221. 10.1121/1.5131651 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beutelmann R., Brand T. (2006). Prediction of speech intelligibility in spatial noise and reverberation for normal-hearing and hearing-impaired listeners. Journal of the Acoustical Society of America, 120, 331–342. 10.1121/1.2202888 [DOI] [PubMed] [Google Scholar]
- Beutelmann R., Brand T., Kollmeier B. (2010). Revision, extension, and evaluation of a binaural speech intelligibility model. Journal of the Acoustical Society of America, 127, 2479–2497. 10.1121/1.3295575 [DOI] [PubMed] [Google Scholar]
- Binns C., Culling J. F. (2007). The role of fundamental frequency contours in the perception of speech against interfering speech. Journal of the Acoustical Society of America, 122, 1765–1776. 10.1121/1.2751394 [DOI] [PubMed] [Google Scholar]
- Bowling D. L., Purves D. (2015). A biological rationale for musical consonance. Proceedings of the National Academy of Sciences, 112, 11155–11160. 10.1073/pnas.1505768112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breebaart J., van de Par S., Kohlrausch A. (2001). Binaural processing model based on contralateral inhibition. I. Model structure. Journal of the Acoustical Society of America, 110, 1074–1088. 10.1121/1.1383297 [DOI] [PubMed] [Google Scholar]
- Bregman A. S. (1990). Auditory scene analysis. MIT Press. [Google Scholar]
- Brokx J., Nooteboom S. (1982). Intonation and the perceptual separation of simultaneous voices. Journal of Phonetics, 10, 23–36. 10.1016/S0095-4470(19)30909-X [DOI] [Google Scholar]
- Campbell J. K., O’Rourke M., Slater M. H. (eds) (2011). Carving nature at its joints: Natural kinds in metaphysics and science. MIT Press. [Google Scholar]
- Carcagno S., Lakhani S., Plack C. J. (2019). Consonance perception beyond the traditional existence region of pitch. Journal of the Acoustical Society of America, 146, 2279–2290. 10.1121/1.5127845 [DOI] [PubMed] [Google Scholar]
- Carney L. H., Heinz M. G., Evilsizer M. E., Gilkey R. H., Colburn H. S. (2002). Auditory phase opponency: A temporal model for masked detection at low frequencies. Acta Acust. Acust., 88, 15. [Google Scholar]
- Carney L. H., Li T., McDonough J. M. (2015). Speech coding in the brain: Representation of vowel formants by midbrain neurons tuned to sound fluctuations 1,2,3. eNeuro, 2(4). e0004-15.2015 1X12. 10.1523/ENEURO.0004-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caspari F., Baumann V. J., Garcia-Pino E., Koch U. (2015). Heterogeneity of intrinsic and synaptic properties of neurons in the ventral and dorsal parts of the ventral nucleus of the lateral lemniscus. Frontiers in Neural Circuits, 9, 74. 10.3389/fncir.2015.00074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chalikia M. H., Bregman A. S. (1993). The perceptual segregation of simultaneous vowels with harmonic, shifted, or random components. Perception & Psychophysics, 53(2), 125–133. 10.3758/BF03211722 [DOI] [PubMed] [Google Scholar]
- Chase S. M., Young E. D. (2007). First-spike latency information in single neurons increases when referenced to population onset. Proceedings of the National Academy of Sciences, 104(12), 5175–5180. 10.1073/pnas.0610368104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C., Read H. L., Escabí M. A. (2019). A temporal integration mechanism enhances frequency selectivity of broadband inputs to inferior colliculus. PLOS Biology, 17(6), e2005861. 10.1371/journal.pbio.2005861 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colburn H. S., Durlach N. I. (1965). Time-intensity relations in binaural unmasking. Journal of the Acoustical Society of America, 38(1), 93–103. 10.1121/1.1909625 [DOI] [PubMed] [Google Scholar]
- Cooke M. (2006). A glimpsing model of speech perception in noise. Journal of the Acoustical Society of America, 119(3), 1562–1573. 10.1121/1.2166600 [DOI] [PubMed] [Google Scholar]
- Cooke M., Morris A., Green P. (1997). Missing data techniques for robust speech recognition. In IEEE International Conference on Acoustics, Speech, and Signal Processing, Munich, Germany (Vol. II) (pp. 863–866).
- Cosentino S., Marquardt T., McAlpine D., Culling J. F., Falk T. H. (2014). A model that predicts the binaural advantage to speech intelligibility from the mixed target and interferer signals. Journal of the Acoustical Society of America, 135(2), 796–807. 10.1121/1.4861239 [DOI] [PubMed] [Google Scholar]
- Culling J. F. (2007). Evidence specifically favoring the equalization-cancellation theory of binaural unmasking. The Journal of the Acoustical Society of America, 122(5), 2803–2813. 10.1121/1.2785035 [DOI] [PubMed] [Google Scholar]
- Culling J. F., Darwin C. J. (1993). Perceptual separation of simultaneous vowels: Within and across-formant grouping by F . Journal of the Acoustical Society of America, 93(6), 3454–3467. 10.1121/1.405675 [DOI] [PubMed] [Google Scholar]
- Culling J. F., Darwin C. J. (1994). Perceptual and computational separation of simultaneous vowels: Cues arising from low-frequency beating. Journal of the Acoustical Society of America, 95(3), 1559–1569. 10.1121/1.408543 [DOI] [PubMed] [Google Scholar]
- Culling J. F., Hodder K. I., Toh C. Y. (2003). Effects of reverberation on perceptual segregation of competing voices. Journal of the Acoustical Society of America, 114(5), 2871. 10.1121/1.1616922 [DOI] [PubMed] [Google Scholar]
- Culling J. F., Summerfield A. Q., Marshall D. H. (1998). Dichotic pitches as illusions of binaural unmasking I. Huggins’ pitch and the ”binaural edge pitch”. Journal of the Acoustical Society of America, 103(6), 3509–3526. http://asa.scitation.org/doi/10.1121/1.423059 https://doi.org/10.1121/1.423059 [DOI] [PubMed] [Google Scholar]
- Culling J. F., Summerfield Q. (1994). Binaural segregation of concurrent sounds involves within-channel rather than across-channel processes. Journal of the Acoustical Society of America, 95(5), 2915–2915. http://asa.scitation.org/doi/10.1121/1.409275 https://doi.org/10.1121/1.409275 [Google Scholar]
- Culling J. F., Summerfield Q., Marshall D. H. (1994). Effects of simulated reverberation on the use of binaural cues and fundamental-frequency differences for separating concurrent vowels. Speech Communication, 14, 71–95. https://linkinghub.elsevier.com/retrieve/pii/0167639394900582 10.1016/0167-6393(94)90058-2 [DOI] [Google Scholar]
- Darwin C. J., Bethell-Fox C. E. (1977). Pitch continuity and speech source attribution. Journal of Experimental Psychology: Human Perception and Performance, 3, 665–672. 10.1037/0096-1523.3.4.665 [DOI] [Google Scholar]
- Dau T., Kollmeier B., Kohlrausch A. (1997). Modeling auditory processing of amplitude modulation. I.Detection and masking with narrow-band carriersa. J. Acoust. Soc. Am., 102, 2892–2905. 10.1121/1.420344 [DOI] [PubMed] [Google Scholar]
- Davis K. A., Voigt H. F. (1997). Evidence of stimulus-dependent correlated activity in the dorsal cochlear nucleus of decerebrate gerbils. Journal of Neurophysiology, 78(1), 229–247. https://www.physiology.org/doi/10.1152/jn.1997.78.1.229 [DOI] [PubMed] [Google Scholar]
- de Boer E. (1976) On the “residue” and auditory pitch perception. In Keidel W., Neff W. (Eds) Handbook of sensory physiology, Vol. v-3 (pp. 479– 583). Springer-Verlag. [Google Scholar]
- de Cheveigné A. (1993). Separation of concurrent harmonic sounds: Fundamental frequency estimation and a time-domain cancellation model of auditory processing. Journal of the Acoustical Society of America, 93, 3271–3290. 10.1121/1.405712 [DOI] [Google Scholar]
- de Cheveigné A. (1997a). Concurrent vowel identification III: A neural model of harmonic interference cancellation. Journal of the Acoustical Society of America, 101, 2857–2865. 10.1121/1.419480 [DOI] [Google Scholar]
- de Cheveigné A. (1997b). Ten experiments on vowel segregation. (Tech. Rep.) ATR Human Information Processing Research Labs technical report TR-H-217. https://hal.archives-ouvertes.fr/hal-03090891.
- de Cheveigné A. (1998). Cancellation model of pitch perception. Journal of the Acoustical Society of America, 103, 1261–1271. http://audition.ens.fr/adc/pdf/1998_JASA_pitch.pdf https://doi.org/10.1121/1.423232 [DOI] [PubMed] [Google Scholar]
- de Cheveigné A. (1999a). Pitch shifts of mistuned partials: A time-domain model. Journal of the Acoustical Society of America, 106(2), 887–897. http://asa.scitation.org/doi/10.1121/1.427104 https://doi.org/10.1121/1.427104 [DOI] [PubMed] [Google Scholar]
- de Cheveigné A. (1999b). Vowel-specific effects in concurrent vowel identification. Journal of the Acoustical Society of America, 106, 327–340. [DOI] [PubMed] [Google Scholar]
- de Cheveigné A. (1999c). Waveform interactions and the segregation of concurrent vowels. Journal of the Acoustical Society of America, 106, 2959–2972. 10.1121/1.428115 [DOI] [PubMed] [Google Scholar]
- de Cheveigné A., Kawahara H. (1999). Multiple period estimation and pitch perception model. Speech Communication, 27, 175–185. 10.1016/S0167-6393(98)00074-0 [DOI] [Google Scholar]
- de Cheveigné A., Kawahara H., Tsuzaki M., Aikawa K. (1997). Concurrent vowel identification I: Effects of relative level and F0 difference. Journal of the Acoustical Society of America, 101, 2839–2847. 10.1121/1.418517 [DOI] [Google Scholar]
- de Cheveigné A., McAdams S., Marin C. (1997). Concurrent vowel identification II: Effects of phase, harmonicity and task. Journal of the Acoustical Society of America, 101, 2848–2856. 10.1121/1.419476 [DOI] [Google Scholar]
- de Cheveigné A., Pressnitzer D. (2006). The case of the missing delay lines: Synthetic delays obtained by cross-channel phase interaction. Journal of the Acoustical Society of America, 119(6), 3908–3911. http://audition.ens.fr/adc/pdf/2006_JASA_delay.pdf 10.1121/1.2195291 [DOI] [PubMed] [Google Scholar]
- Deroche M. L., Culling J. F. (2011a). Narrow noise band detection in a complex masker: Masking level difference due to harmonicity. Hearing Research, 282(1-2), 225–235. https://linkinghub.elsevier.com/retrieve/pii/S0378595511001961 https://doi.org/10.1016/j.heares.2011.07.005 [DOI] [PubMed] [Google Scholar]
- Deroche M. L., Culling J. F. (2011b). Voice segregation by difference in fundamental frequency: Evidence for harmonic cancellation. Journal of the Acoustical Society of America, 130(5), 2855–2865. http://asa.scitation.org/doi/10.1121/1.3643812 https://doi.org/10.1121/1.3643812 [DOI] [PubMed] [Google Scholar]
- Deroche M. L., Culling J. F. (2013). Voice segregation by difference in fundamental frequency: Effect of masker type. Journal of the Acoustical Society of America, 134(5), EL465–EL470. http://asa.scitation.org/doi/10.1121/1.4826152 https://doi.org/10.1121/1.4826152 [DOI] [PubMed] [Google Scholar]
- Deroche M. L., Culling J. F., Chatterjee M. (2013). Phase effects in masking by harmonic complexes: Speech recognition. Hearing Research, 306, 54–62. https://linkinghub.elsevier.com/retrieve/pii/S0378595513002311 https://doi.org/10.1016/j.heares.2013.09.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deroche M. L., Culling J. F., Chatterjee M. (2014). Phase effects in masking by harmonic complexes: Detection of bands of speech-shaped noise. Journal of the Acoustical Society of America, 136(5), 2726–2736. http://asa.scitation.org/doi/10.1121/1.4896457 https://doi.org/10.1121/1.4896457 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deroche M. L., Culling J. F., Chatterjee M., Limb C. J. (2014a). Roles of the target and masker fundamental frequencies in voice segregation. Journal of the Acoustical Society of America, 136(3), 1225–1236. http://asa.scitation.org/doi/10.1121/1.4890649 https://doi.org/10.1121/1.4890649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deroche M. L., Culling J. F., Chatterjee M., Limb C. J. (2014b). Speech recognition against harmonic and inharmonic complexes: Spectral dips and periodicity. Journal of the Acoustical Society of America, 135(5), 2873–2884. http://asa.scitation.org/doi/10.1121/1.4870056 https://doi.org/10.1121/1.4870056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deroche M. L., Culling J. F., Lavandier M., Gracco V. L. (2017). Reverberation limits the release from informational masking obtained in the harmonic and binaural domains. Attention, Perception, & Psychophysics, 79(1), 363–379. http://link.springer.com/10.3758/s13414-016-1207-3 https://doi.org/10.3758/s13414-016-1207-3 [DOI] [PubMed] [Google Scholar]
- Divenyi P. L. (1979). Is pitch a learned attribute of sounds? Two points in support of Terhardt’s pitch theory. Journal of the Acoustical Society of America, 66(4), 1210–1213. http://asa.scitation.org/doi/10.1121/1.383317 https://doi.org/10.1121/1.383317 [DOI] [PubMed] [Google Scholar]
- Duda R. O., Hart P. E., Stork D. G. (2012). Pattern classification. John Wiley & Sons. [Google Scholar]
- Duifhuis H., Willems L., Sluyter R. (1982). Measurement of pitch in speech: An implementation of Goldstein’s theory of pitch perception. Journal of the Acoustical Society of America, 71, 1568–1580. 10.1121/1.387811 [DOI] [PubMed] [Google Scholar]
- Durlach N. (1963). Equalization and cancellation theory of binaural masking-level differences. The Journal of the Acoustical Society of America, 35, 1206–1218. 10.1121/1.1918675 [DOI] [Google Scholar]
- Englitz B., Tolnai S., Typlt M., Jost J., Rübsamen R. (2009). Reliability of synaptic transmission at the synapses of held in vivo under acoustic stimulation. PloS One, 4(10), e7014. https://dx.plos.org/10.1371/journal.pone.0007014 https://doi.org/10.1371/journal.pone.0007014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewert S. D., Dau T. (2000). Characterizing frequency selectivity for envelope fluctuations. Journal of the Acoustical Society of America, 108(3), 1181–1196. http://scitation.aip.org/content/asa/journal/jasa/108/3/10.1121/1.1288665 https://doi.org/10.1121/1.1288665 [DOI] [PubMed] [Google Scholar]
- Felix R. A. I., Gourévitch B., Gòmez-Àlvarez M., Leijon S. C. M., Saldaña E., Magnusson A. K. (2017). Octopus cells in the posteroventral cochlear nucleus provide the main excitatory input to the superior paraolivary nucleus. Frontiers in Neural Circuits, 11, 37. http://journal.frontiersin.org/article/10.3389/fncir.2017.00037/full https://doi.org/10.3389/fncir.2017.00037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishman Y. I., Micheyl C., Steinschneider M. (2013). Neural representation of harmonic complex tones in primary auditory cortex of the awake monkey. Journal of Neuroscience, 33(25), 10312–10323. https://www.jneurosci.org/lookup/doi/10.1523/JNEUROSCI.0020-13.2013 https://doi.org/10.1523/JNEUROSCI.0020-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishman Y. I., Steinschneider M. (2010). Neural correlates of auditory scene analysis based on inharmonicity in monkey primary auditory cortex. Journal of Neuroscience, 30(37), 12480–12494. https://www.jneurosci.org/lookup/doi/10.1523/JNEUROSCI.1780-10.2010 https://doi.org/10.1523/JNEUROSCI.1780-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishman Y. I., Steinschneider M., Micheyl C. (2014). Neural representation of concurrent harmonic sounds in monkey primary auditory cortex: Implications for models of auditory scene analysis. Journal of Neuroscience, 34(37), 12425–12443. https://www.jneurosci.org/lookup/doi/10.1523/JNEUROSCI.0025-14.2014 https://doi.org/10.1523/JNEUROSCI.0025-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franken T. P., Bondy B. J., Haimes D. B., Goldwyn J. H., Golding N. L., Smith P. H., Joris P. X. (2021). Glycinergic axonal inhibition subserves acute spatial sensitivity to sudden increases in sound intensity. eLife, 10, e62183. https://elifesciences.org/articles/62183 https://doi.org/10.7554/eLife.62183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K. (2018). Does predictive coding have a future? Nature Neuroscience, 21(8), 1019–1021. http://www.nature.com/articles/s41593-018-0200-7 https://doi.org/10.1038/s41593-018-0200-7 [DOI] [PubMed] [Google Scholar]
- Gábor D. (1947). Acoustical quanta and the theory of hearing. Nature, 159, 591–594. 10.1038/159591a0 [DOI] [PubMed] [Google Scholar]
- Gockel H., Carlyon R. P., Plack C. J. (2009). Further examination of pitch discrimination interference between complex tones containing resolved harmonics. Journal of the Acoustical Society of America, 125(2), 1059–1066. http://asa.scitation.org/doi/10.1121/1.3056568 https://doi.org/10.1121/1.3056568 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gockel H., Moore B. C. J., Patterson R. D. (2002). Asymmetry of masking between complex tones and noise: The role of temporal structure and peripheral compression. Journal of the Acoustical Society of America, 111(6), 2759–2770. http://asa.scitation.org/doi/10.1121/1.1480422 https://doi.org/10.1121/1.1480422 [DOI] [PubMed] [Google Scholar]
- Gockel H., Moore B. C. J., Patterson R. D. (2003). Asymmetry of masking between complex tones and noise: Partial loudness. Journal of the Acoustical Society of America, 114(1), 12. 10.1121/1.1582447 [DOI] [PubMed] [Google Scholar]
- Gockel H., Moore B. C. J., Plack C. J., Carlyon R. P. (2006). Effect of noise on the detectability and fundamental frequency discrimination of complex tones. Journal of the Acoustical Society of America, 120(2), 957–965. http://asa.scitation.org/doi/10.1121/1.2211408 https://doi.org/10.1121/1.2211408 [DOI] [PubMed] [Google Scholar]
- Grange J. A., Culling J. F. (2016). The benefit of head orientation to speech intelligibility in noise. Journal of the Acoustical Society of America, 139(2), 703–712. http://asa.scitation.org/doi/10.1121/1.4941655 https://doi.org/10.1121/1.4941655 [DOI] [PubMed] [Google Scholar]
- Graves J. E., Oxenham A. J. (2019). Pitch discrimination with mixtures of three concurrent harmonic complexes. Journal of the Acoustical Society of America, 145(4), 2072–2083. http://asa.scitation.org/doi/10.1121/1.5096639 https://doi.org/10.1121/1.5096639 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green D. M. (1992). On the similarity of two theories of comodulation masking release. Journal of the Acoustical Society of America, 91(3), 1769–1769. http://asa.scitation.org/doi/10.1121/1.402457 https://doi.org/10.1121/1.402457 [DOI] [PubMed] [Google Scholar]
- Green T., Rosen S. (2013). Phase effects on the masking of speech by harmonic complexes: Variations with level. Journal of the Acoustical Society of America, 134(4), 2876–2883. http://asa.scitation.org/doi/10.1121/1.4820899 https://doi.org/10.1121/1.4820899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grothe B. (2000). The function of the medial superior olive in small mammals: temporal receptive fields in auditory analysis. Journal of Comparative Physiology A, 186, 413–423. 10.1007/s003590050441 [DOI] [PubMed] [Google Scholar]
- Guest D. R., Oxenham A. J. (2019). The role of pitch and harmonic cancellation when listening to speech in harmonic background sounds. Journal of the Acoustical Society of America, 145(5), 3011–3023. http://asa.scitation.org/doi/10.1121/1.5102169 https://doi.org/10.1121/1.5102169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hafter E. R., Saberi K. (2001). A level of stimulus representation model for auditory detection and attention. Journal of the Acoustical Society of America, 110(3), 1489–1497. http://asa.scitation.org/doi/10.1121/1.1394220 https://doi.org/10.1121/1.1394220 [DOI] [PubMed] [Google Scholar]
- Hall J. W., Haggard M. P., Fernandes M. A. (1984). Detection in noise by spectro-temporal pattern analysis. Journal of the Acoustical Society of America, 76(1), 50–56. http://asa.scitation.org/doi/10.1121/1.391005 https://doi.org/10.1121/1.391005 [DOI] [PubMed] [Google Scholar]
- Hartmann W. M., Cariani P. A., Colburn H. S. (2019). Noise edge pitch and models of pitch perception. Journal of the Acoustical Society of America, 145(4), 1993–2008. http://asa.scitation.org/doi/10.1121/1.5093546 https://doi.org/10.1121/1.5093546 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartmann W. M., Doty S. (1996). On the pitches of the components of a complex tone. The Journal of the Acoustical Society of America, 99, 567–578. 10.1121/1.414514 [DOI] [PubMed] [Google Scholar]
- Hartmann W. M., Goupell M. J. (2006). Enhancing and unmasking the harmonics of a complex tone. The Journal of the Acoustical Society of America, 120(4), 2142–2157. 10.1121/1.2228476 [DOI] [PubMed] [Google Scholar]
- Hartmann W. M., McAdams S., Smith B. K. (1990). Hearing a mistuned harmonic in an otherwise periodic complex tone. The Journal of the Acoustical Society of America, 88(4), 1712–1724. 10.1121/1.400246 [DOI] [PubMed] [Google Scholar]
- Hatfield G. (2002) Perception as unconscious inference. In Heyer D., Mausfeld R. (Eds) Perception and the physical world: Psychological and philosophical issues in perception (pp. 113– 143). John Wiley and Sons. [Google Scholar]
- Hauth C. F., Brand T. (2018). Modeling sluggishness in binaural unmasking of speech for maskers with time-varying interaural phase differences. Trends in Hearing, 22, 233121651775354. http://journals.sagepub.com/doi/10.1177/2331216517753547 https://doi.org/10.1177/2331216517753547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinz M. G., Colburn H. S., Carney L. H. (2001). Evaluating auditory performance limits: I. one-parameter discrimination using a computational model for the auditory nerve. Neural Computation, 13(10), 2273–2316. https://www.mitpressjournals.org/doi/abs/10.1162/089976601750541804 https://doi.org/10.1162/089976601750541804 [DOI] [PubMed] [Google Scholar]
- Helmholtz H. (1867). Handbuch der Physiologischen Optik (English tranl.: 1924 JPC Southall as Treatise on Physiological Optics) . Voss. [Google Scholar]
- Holmes S. D., Roberts B. (2012). Pitch shifts on mistuned harmonics in the presence and absence of corresponding in-tune components. Journal of the Acoustical Society of America, 132(3), 1548–1560. http://asa.scitation.org/doi/10.1121/1.4740487 https://doi.org/10.1121/1.4740487 [DOI] [PubMed] [Google Scholar]
- Hu G., Wang D. (2008). Segregation of unvoiced speech from nonspeech interference. Journal of the Acoustical Society of America, 124(2), 1306–1319. http://asa.scitation.org/doi/10.1121/1.2939132 https://doi.org/10.1121/1.2939132 [DOI] [PubMed] [Google Scholar]
- Huggins W., Licklider J. (1951). Place mechanisms of auditory frequency analysis. Journal of the Acoustical Society of America, 23, 290–299. 10.1121/1.1906760 [DOI] [Google Scholar]
- Imbert M. (2020). La fin du regard éclairant. Une révolution dans les sciences de la vision au XIe siècle. Ibn al-Haytham. [Google Scholar]
- Jeffress L. A. (1948). A place theory of sound localization. Journal of comparative and physiological psychology, 41, 35–39. 10.1037/h0061495 [DOI] [PubMed] [Google Scholar]
- Jelfs S., Culling J. F., Lavandier M. (2011). Revision and validation of a binaural model for speech intelligibility in noise. Hearing Research, 275(1-2), 96–104. https://linkinghub.elsevier.com/retrieve/pii/S0378595510004387 https://doi.org/10.1016/j.heares.2010.12.005 [DOI] [PubMed] [Google Scholar]
- Jepsen M. L., Ewert S. D., Dau T. (2008). A computational model of human auditory signal processing and perception. Journal of the Acoustical Society of America, 124(1), 422–438. 10.1121/1.2924135 [DOI] [PubMed] [Google Scholar]
- Joris P. X., Schreiner C. E., Rees A. (2004). Neural processing of amplitude-modulated sounds. Physiological Reviews, 84(2), 541–577. https://www.physiology.org/doi/10.1152/physrev.00029.2003 https://doi.org/10.1152/physrev.00029.2003 [DOI] [PubMed] [Google Scholar]
- Joris P. X., Trussell L. O. (2018). The Calyx of held: A hypothesis on the need for reliable timing in an intensity-difference encoder. Neuron, 100, 534–549. 10.1016/j.neuron.2018.10.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joris P. X., der van Heijden M., (2019). Early binaural hearing: The comparison of temporal differences at the two ears. Annual Review of Neuroscience, 42(1), 433–457. https://www.annualreviews.org/doi/10.1146/annurev-neuro-080317-061925 https://doi.org/10.1146/annurev-neuro-080317-061925 [DOI] [PubMed] [Google Scholar]
- Josupeit A., Schoenmaker E., Par S., Hohmann V. (2020). Sparse periodicity-based auditory features explain human performance in a spatial multitalker auditory scene analysis task. European Journal of Neuroscience, 51(5), 1353–1363. https://onlinelibrary.wiley.com/doi/abs/10.1111/ejn.13981 https://doi.org/10.1111/ejn.13981 [DOI] [PubMed] [Google Scholar]
- Kadner A., Berrebi A. (2008). Encoding of temporal features of auditory stimuli in the medial nucleus of the trapezoid body and superior paraolivary nucleus of the rat. Neuroscience, 151(3), 868–887. https://linkinghub.elsevier.com/retrieve/pii/S030645220701408X https://doi.org/10.1016/j.neuroscience.2007.11.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandler K., Lee J., Pecka M. (2020). The superior olivary complex. In the senses: A comprehensive reference. (pp.533–555). Elsevier.https://linkinghub.elsevier.com/retrieve/pii/B978012805408600021X https://doi.org/10.1016/B978-0-12-805408-6.00021-X. [Google Scholar]
- Kay R. H., Matthews D. R. (1972). On the existence in human auditory pathways of channels selectively tuned to the modulation present in frequency-modulated tones. The Journal of Physiology, 225(3), 657–677. http://doi.wiley.com/10.1113/jphysiol.1972.sp009962 https://doi.org/10.1113/jphysiol.1972.sp009962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keilson S. E., Richards V. M., Wyman B. T., Young E. D. (1997). The representation of concurrent vowels in the cat anesthetized ventral cochlear nucleus: Evidence for a periodicity-tagged spectral representation. Journal of the Acoustical Society of America, 102(2), 1056–1071. http://asa.scitation.org/doi/10.1121/1.419859 https://doi.org/10.1121/1.419859 [DOI] [PubMed] [Google Scholar]
- Keine C., Rübsamen R., Englitz B. (2016). Inhibition in the auditory brainstem enhances signal representation and regulates gain in complex acoustic environments. eLife, 5, e19295. https://elifesciences.org/articles/19295 https://doi.org/10.7554/eLife.19295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kersten D., Mamassian P., Yuille A. (2004). Object Perception as Bayesian Inference. Annual Review of Psychology, 55(1), 271–304. http://www.annualreviews.org/doi/10.1146/annurev.psych.55.090902.142005 https://doi.org/10.1146/annurev.psych.55.090902.142005 [DOI] [PubMed] [Google Scholar]
- Klinge A., Beutelmann R., Klump G. M. (2011). Effect of harmonicity on the detection of a signal in a complex masker and on spatial release from masking. PLoS ONE, 6(10), e26124. https://dx.plos.org/10.1371/journal.pone.0026124 https://doi.org/10.1371/journal.pone.0026124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsen E., Cedolin L., Delgutte B. (2008). Pitch Representations in the Auditory Nerve: Two Concurrent Complex Tones. Journal of Neurophysiology, 100(3), 1301–1319. https://www.physiology.org/doi/10.1152/jn.01361.2007 https://doi.org/10.1152/jn.01361.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laudanski J., Zheng Y., Brette R. (2014). A structural theory of pitch. eneuro, 1(1), 1–13.ENEURO.0033–14.2014. http://eneuro.org/lookup/doi/10.1523/ENEURO.0033-14.2014 https://doi.org/10.1523/ENEURO.0033-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavandier M., Jelfs S., Culling J. F., Watkins A. J., Raimond A. P., Makin S. J. (2012). Binaural prediction of speech intelligibility in reverberant rooms with multiple noise sources. Journal of the Acoustical Society of America, 131(1), 218–231. http://asa.scitation.org/doi/10.1121/1.3662075 https://doi.org/10.1121/1.3662075 [DOI] [PubMed] [Google Scholar]
- Lea A. (1992). Auditory Models of Vowel Perception [Unpublished doctoral thesis]. University of Nottingham.
- Leclère T., Lavandier M., Deroche M. L. (2017). The intelligibility of speech in a harmonic masker varying in fundamental frequency contour, broadband temporal envelope, and spatial location. Hearing Research, 350, 1–10. https://linkinghub.elsevier.com/retrieve/pii/S0378595516304191 https://doi.org/10.1016/j.heares.2017.03.012 [DOI] [PubMed] [Google Scholar]
- Licklider J. C. R. (1951). A duplex theory of pitch perception. Experientia, 7, 128–134. 10.1007/BF02156143 [DOI] [PubMed] [Google Scholar]
- Licklider J. C. R. (1959) Three auditory theories. In Koch S. (Ed.) Psychology: A study of a science (pp.41–144). Mcgraw-Hill. [Google Scholar]
- Logan B. F. J. (1977). Information in the Zero Crossings of Bandpass Signals. Bell System Technical Journal, 56(4), 487–510. https://onlinelibrary.wiley.com/doi/abs/10.1002/j.1538-7305.1977.tb00522.x https://doi.org/10.1002/j.1538-7305.1977.tb00522.x [Google Scholar]
- Lyon R. (1983, 1988) A computational model of binaural localization and separation. In Richards W. (Ed.) Natural computation (pp.319–327). MIT Press, (reprinted from Proc. ICASSP 83: 1148–1151.). [Google Scholar]
- Lyon R. (1984) Computational models of neural auditory processing. In IEEE ICASSP, San Diego, USA (pp. 41-44).
- McDermott J., Hauser M. (2004). Are consonant intervals music to their ears? Spontaneous acoustic preferences in a nonhuman primate. Cognition, 94(2), B11–B21. https://linkinghub.elsevier.com/retrieve/pii/S0010027704001337 https://doi.org/10.1016/j.cognition.2004.04.004 [DOI] [PubMed] [Google Scholar]
- McDermott J. H., Lehr A. J., Oxenham A. J. (2010). Individual differences reveal the basis of consonance. Current Biology, 20(11), 1035–1041. 10.1016/j.cub.2010.04.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDermott J. H., Schultz A. F., Undurraga E. A., Godoy R. A. (2016). Indifference to dissonance in native Amazonians reveals cultural variation in music perception. Nature, 535(7613), 547–550. http://www.nature.com/articles/nature18635 https://doi.org/10.1038/nature18635 [DOI] [PubMed] [Google Scholar]
- McKeown D. J. (1992). Perception of concurrent vowels: The effect of varying their relative level. Speech Communication, 11(1), 1–13. https://linkinghub.elsevier.com/retrieve/pii/016763939290059G https://doi.org/10.1016/0167-6393(92)90059-G [Google Scholar]
- McKeown D. J., Patterson R. D. (1995). The time course of auditory segregation: Concurrent vowels that vary in duration. Journal of the Acoustical Society of America, 98(4), 1866–1877. http://asa.scitation.org/doi/10.1121/1.413373 https://doi.org/10.1121/1.413373 [DOI] [PubMed] [Google Scholar]
- Mc Laughlin M., van der Heijden M., Joris P. X. (2008). How secure is in vivo synaptic transmission at the calyx of held? Journal of Neuroscience, 28(41), 10206–10219. http://www.jneurosci.org/cgi/doi/10.1523/JNEUROSCI.2735-08.2008 https://doi.org/10.1523/JNEUROSCI.2735-08.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPherson M. J., Dolan S. E., Durango A., Ossandon T., Valdès J., Undurraga E. A., Jacoby N., Godoy R. A., McDermott J. H. (2020). Perceptual fusion of musical notes by native Amazonians suggests universal representations of musical intervals. Nature Communications, 11(1), 2786. http://www.nature.com/articles/s41467-020-16448-6 https://doi.org/10.1038/s41467-020-16448-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPherson M. J., Grace R. C., McDermott J. H. (2020). Harmonicity aids hearing in noise. bioRxiv. http://biorxiv.org/lookup/doi/10.1101/2020.09.30.321000 https://doi.org/10.1101/2020.05.07.082511
- Maxwell B. N., Richards V. M., Carney L. H. (2020). Neural fluctuation cues for simultaneous notched-noise masking and profile-analysis tasks: Insights from model midbrain responses. Journal of the Acoustical Society of America, 147(5), 3523–3537. http://asa.scitation.org/doi/10.1121/10.0001226 https://doi.org/10.1121/10.0001226 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meddis R., Hewitt M. (1992). Modeling the identification of concurrent vowels with different fundamental frequencies. Journal of the Acoustical Society of America, 91, 233–245. 10.1121/1.402767 [DOI] [PubMed] [Google Scholar]
- Meddis R., Hewitt M. J. (1991). Virtual pitch and phase sensitivity of a computer model of the auditory periphery I: Pitch identification. Journal of the Acoustical Society of America, 89(6), 2866–2882. http://asa.scitation.org/doi/10.1121/1.400725 https://doi.org/10.1121/1.400725 [Google Scholar]
- Meyer G. F., Plante F. (Berthommier F. (1997) Segregation of concurrent speech with the reassigned spectrum. In: IEEE international conference on acoustics, speech, and signal processing, Vol. 2 (pp.1203–1206: 10.1109/ICASSP.1997.596160: [DOI]
- Micheyl C., Bernstein J. G. W., Oxenham A. J. (2006). Detection and F0 discrimination of harmonic complex tones in the presence of competing tones or noise. Journal of the Acoustical Society of America, 120(3), 1493–1505. http://asa.scitation.org/doi/10.1121/1.2221396 https://doi.org/10.1121/1.2221396 [DOI] [PubMed] [Google Scholar]
- Micheyl C., Keebler M. V., Oxenham A. J. (2010). Pitch perception for mixtures of spectrally overlapping harmonic complex tones. Journal of the Acoustical Society of America, 128(1), 257–269. 10.1121/1.3372751 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheyl C., Oxenham A. J. (2010). Pitch, harmonicity and concurrent sound segregation: Psychoacoustical and neurophysiological findings. Hearing Research, 266(1-2), 36–51. https://linkinghub.elsevier.com/retrieve/pii/S0378595509002366 https://doi.org/10.1016/j.heares.2009.09.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minden, V. , Pehlevan, C. , Chklovskii, D. B. (2018) Biologically plausible online principal component analysis without recurrent neural dynamics. In: IEEE 52nd Asilomar conference on signals systems and computers 8, 10.1109/ACSSC.2018.8645109 [DOI]
- Moore B. C. J. (2003). An introduction to the psychology of hearing. Academic Press. [Google Scholar]
- Moore B. C. J., Glasberg B. (1983). Suggested formulae for calculating auditory-filter bandwidths and excitation patterns. Journal of the Acoustical Society of America, 74, 750–753. 10.1121/1.389861 [DOI] [PubMed] [Google Scholar]
- Moore B. C. J., Glasberg B. R., Peters R. W. (1986). Thresholds for hearing mistuned partials as separate tones in harmonic complexes. Journal of the Acoustical Society of America, 80(2), 479–483. http://asa.scitation.org/doi/10.1121/1.394043 https://doi.org/10.1121/1.394043 [DOI] [PubMed] [Google Scholar]
- Moore B. C. J., Glasberg B. R., Plack C. J., Biswas A. K. (1988). The shape of the ear’s temporal window. Journal of the Acoustical Society of America, 83(3), 1102–1116. http://asa.scitation.org/doi/10.1121/1.396055 https://doi.org/10.1121/1.396055 [DOI] [PubMed] [Google Scholar]
- Moore B. C. J., Peters R. W., Glasberg B. R. (1985). Thresholds for the detection of inharmonicity in complex tones. Journal of the Acoustical Society of America, 77(5), 1861–1867. http://asa.scitation.org/doi/10.1121/1.391937 https://doi.org/10.1121/1.391937 [DOI] [PubMed] [Google Scholar]
- Needham K., Paolini A. G. (2006). Neural timing, inhibition and the nature of stellate cell interaction in the ventral cochlear nucleus. Hearing Research, 216–217, 31–42. https://linkinghub.elsevier.com/retrieve/pii/S0378595506000396 https://doi.org/10.1016/j.heares.2006.01.016 [DOI] [PubMed] [Google Scholar]
- Oh E. L., Lutfi R. A. (2000). Effect of masker harmonicity on informational masking. Journal of the Acoustical Society of America, 108(2), 706–709. http://asa.scitation.org/doi/10.1121/1.429603 https://doi.org/10.1121/1.429603 [DOI] [PubMed] [Google Scholar]
- Oja E. (1982). Simplified neuron model as a principal component analyzer. Journal of Mathematical Biology, 15, 267–273. 10.1007/BF00275687 [DOI] [PubMed] [Google Scholar]
- Palmer A. R. (1990). The representation of the spectra and fundamental frequencies of steady-state single- and double-vowel sounds in the temporal discharge patterns of guinea pig cochlear-nerve fibers. Journal of the Acoustical Society of America, 88(3), 1412–1426. http://asa.scitation.org/doi/10.1121/1.400329 https://doi.org/10.1121/1.400329 [DOI] [PubMed] [Google Scholar]
- Parsons T. (1976). Separation of speech from interfering speech by means of harmonic selection. Journal of the Acoustical Society of America, 60(4), 911–918. 10.1121/1.381172 [DOI] [Google Scholar]
- Piechowiak T., Ewert S. D., Dau T. (2007). Modeling comodulation masking release using an equalization-cancellation mechanism. Journal of the Acoustical Society of America, 121(4), 2111–2126. 10.1121/1.2534227 [DOI] [PubMed] [Google Scholar]
- Plack C. J., Moore B. C. J. (1990). Temporal window shape as a function of frequency and level. Journal of the Acoustical Society of America, 87, 2178–2187. 10.1121/1.399185 [DOI] [PubMed] [Google Scholar]
- Popham S., Boebinger D., Ellis D. P. W., Kawahara H., McDermott J. H. (2018). Inharmonic speech reveals the role of harmonicity in the cocktail party problem. Nature Communications, 9(1), 21–22. http://www.nature.com/articles/s41467-018-04551-8 https://doi.org/10.1038/s41467-018-04551-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prud’homme L., Lavandier M., Best V. (2020). A harmonic-cancellation-based model to predict speech intelligibility against a harmonic masker. Journal of the Acoustical Society of America, 145(3), 3246–3254. http://asa.scitation.org/doi/10.1121/1.5101323 https://doi.org/10.1121/1.5101323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu J., Wang H., Lu J., Zhang B., Du K.-L. (2012). Neural network implementations for PCA and its extensions. ISRN Artificial Intelligence, 2012, 1–19. https://www.hindawi.com/journals/isrn/2012/847305/ https://doi.org/10.5402/2012/847305 [Google Scholar]
- Roberts B., Bregman A. S. (1991). Effects of the pattern of spectral spacing on the perceptual fusion of harmonics. Journal of the Acoustical Society of America, 90(6), 3050–3060. 10.1121/1.401779 [DOI] [Google Scholar]
- Roberts B., Brunstrom J. M. (1998). Perceptual segregation and pitch shifts of mistuned components in harmonic complexes and in regular inharmonic complexes. Journal of the Acoustical Society of America, 104, 2326–2338. 10.1121/1.423771 [DOI] [PubMed] [Google Scholar]
- Roberts B., Brunstrom J. M. (2001). Perceptual fusion and fragmentation of complex tones made inharmonic by applying different degrees of frequency shift and spectral stretch. Journal of the Acoustical Society of America, 110(5), 2479–2490. http://asa.scitation.org/doi/10.1121/1.1410965 https://doi.org/10.1121/1.1410965 [DOI] [PubMed] [Google Scholar]
- Roberts B., Brunstrom J. M. (2003). Spectral pattern, harmonic relations, and the perceptual grouping of low-numbered components. Journal of the Acoustical Society of America, 114(4), 17. 10.1121/1.1605411 [DOI] [PubMed] [Google Scholar]
- Roberts B., Holmes S. D. (2006). Grouping and the pitch of a mistuned fundamental component: Effects of applying simultaneous multiple mistunings to the other harmonics. Hearing Research, 222(1-2), 79–88. https://linkinghub.elsevier.com/retrieve/pii/S0378595506002498 https://doi.org/10.1016/j.heares.2006.08.013 [DOI] [PubMed] [Google Scholar]
- Ruggles D. R., Freyman R. L., Oxenham A. J. (2014). Influence of musical training on understanding voiced and whispered speech in noise. PLOS ONE, 9(1), 8. 10.1371/journal.pone [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saddler M. R., Gonzalez R., McDermott J. H. (2020). Deep neural network models reveal interplay of peripheral coding and stimulus statistics in pitch perception. biorRxiv, 57. 10.1101/2020.11.19.389999. [DOI]
- Sayles M., Stasiak A., Winter I. M. (2015). Reverberation impairs brainstem temporal representations of voiced vowel sounds: challenging “periodicity-tagged” segregation of competing speech in rooms. Frontiers in Systems Neuroscience, 8(248), 19. 10.3389/fnsys.2014.00248 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheffers M. T. M. (1983). Sifting vowels. Unpublished doctoral dissertation, Gröningen.
- Scheffers M. T. M. (1984). Discrimination of fundamental frequency of synthesized vowel sounds in a noise background. Journal of the Acoustical Society of America, 76(2), 428–434. http://asa.scitation.org/doi/10.1121/1.391134 https://doi.org/10.1121/1.391134 [DOI] [PubMed] [Google Scholar]
- Schmidhuber J. (2009). Driven by Compression Progress: A Simple Principle Explains Essential Aspects of Subjective Beauty: Novelty: Surprise, Interestingness: Attention: Curiosity: Creativity: Art: Science, Music: Jokes. arXiv:0812.4360 [cs]. arXiv: 0812.4360.
- Schoenmaker E., Brand T., van de Par S. (2016). The multiple contributions of interaural differences to improved speech intelligibility in multitalker scenarios. Journal of the Acoustical Society of America, 139(5), 2589–2603. http://asa.scitation.org/doi/10.1121/1.4948568 https://doi.org/10.1121/1.4948568 [DOI] [PubMed] [Google Scholar]
- Schofield B. R. (1994). Projections to the cochlear nuclei from principal cells in the medial nucleus of the trapezoid body in guinea pigs. The Journal of Comparative Neurology, 344(1), 83–100. http://doi.wiley.com/10.1002/cne.903440107 https://doi.org/10.1002/cne.903440107 [DOI] [PubMed] [Google Scholar]
- Schroeder M. (1968). Period histogram and product spectrum: New methods for fundamental-frequency measurement. Journal of the Acoustical Society of America, 43, 829–834. 10.1121/1.1910902 [DOI] [PubMed] [Google Scholar]
- Shackleton T. M., Meddis R., Hewitt M. J. (1994). The role of binaural and fundamental frequency difference cues in the identification of concurrently presented vowels. The Quarterly Journal of Experimental Psychology Section A, 47(3), 545–563. http://journals.sagepub.com/doi/10.1080/14640749408401127 https://doi.org/10.1080/14640749408401127 [Google Scholar]
- Shamma S. A. (1985). Speech processing in the auditory system II: Lateral inhibition and the central processing of speech evoked activity in the auditory nerve. Journal of the Acoustical Society of America, 78(5), 1622–1632. http://asa.scitation.org/doi/10.1121/1.392800 https://doi.org/10.1121/1.392800 [DOI] [PubMed] [Google Scholar]
- Shamma S. A., Dutta K. (2019). Spectro-temporal templates unify the pitch percepts of resolved and unresolved harmonics. Journal of the Acoustical Society of America, 15, 515-628. 10.1121/1.5088504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shamma S. A., Elhilali M., Micheyl C. (2011). Temporal coherence and attention in auditory scene analysis. Trends in Neurosciences, 34(3), 114–123. https://linkinghub.elsevier.com/retrieve/pii/S0166223610001670 https://doi.org/10.1016/j.tins.2010.11.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shamma S. A., Klein D. (2000). The case of the missing pitch templates: How harmonic templates emerge in the early auditory system. Journal of the Acoustical Society of America, 107(5), 2631–2644. http://asa.scitation.org/doi/10.1121/1.428649 https://doi.org/10.1121/1.428649 [DOI] [PubMed] [Google Scholar]
- Shamma S. A., Lorenzi C. (2013). On the balance of envelope and temporal fine structure in the encoding of speech in the early auditory system. Journal of the Acoustical Society of America, 133(5), 2818–2833. http://asa.scitation.org/doi/10.1121/1.4795783 https://doi.org/10.1121/1.4795783 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shamma S. A., Shen N. M., Gopalaswamy P. (1989). Stereausis: Binaural processing without neural delays. Journal of the Acoustical Society of America, 86(3), 989–1006. 10.1121/1.398734 [DOI] [PubMed] [Google Scholar]
- Shen Y., Pearson D. V. (2019). Efficiency in glimpsing vowel sequences in fluctuating makers: Effects of temporal fine structure and temporal regularity. Journal of the Acoustical Society of America, 145(4), 2518–2529. http://asa.scitation.org/doi/10.1121/1.5098949 https://doi.org/10.1121/1.5098949 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera C. A., Guinan J. J., Oxenham A. J. (2002). Revised estimates of human cochlear tuning from otoacoustic and behavioral measurements. Proceedings of the National Academy of Sciences, 99(5), 3318–3323. http://www.pnas.org/cgi/doi/10.1073/pnas.032675099 https://doi.org/10.1073/pnas.032675099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shore S. E., Helfert R. H., Bledsoe S. C., Altschuler R. A., Godfrey D. A. (1991). Descending projections to the dorsal and ventral divisions of the cochlear nucleus in guinea pig. Hearing Research, 52(1), 255–268. https://linkinghub.elsevier.com/retrieve/pii/037859559190205N https://doi.org/10.1016/0378-5955(91)90205-N [DOI] [PubMed] [Google Scholar]
- Sinex D. G., Henderson Sabes J., Li H. (2002). Responses of inferior colliculus neurons to harmonic and mistuned complex tones. Hearing Research, 168(1-2), 150–162. https://linkinghub.elsevier.com/retrieve/pii/S0378595502003660 https://doi.org/10.1016/S0378-5955(02)00366-0 [DOI] [PubMed] [Google Scholar]
- Sinex D. G., Li H. (2007). Responses of inferior colliculus neurons to double harmonic tones. Journal of Neurophysiology, 98(6), 3171–3184. https://www.physiology.org/doi/10.1152/jn.00516.2007 https://doi.org/10.1152/jn.00516.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinex D. G., Li H., Velenovsky D. S. (2005). Prevalence of stereotypical responses to mistuned complex tones in the inferior colliculus. Journal of Neurophysiology, 94(5), 3523–3537. https://www.physiology.org/doi/10.1152/jn.01194.2004 https://doi.org/10.1152/jn.01194.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slaney M. (1993). An efficient implementation of the Patterson-Holdsworth auditory filter bank (technical report No. 35). Apple Computer.
- Sorensen R. (2011) Para-natural kinds. In Campbell J. K., O’Rourke M., Slater M. H. (Eds.) Carving nature at its joints: Natural kinds in metaphysics and science (pp.113–127). MIT Press. [Google Scholar]
- Stasiak A., Sayles M., Winter I. M. (2018). Perfidious synaptic transmission in the guinea-pig auditory brainstem. PloS one, 13(10), e0203712. https://dx.plos.org/10.1371/journal.pone.0203712 https://doi.org/10.1371/journal.pone.0203712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein A., Ewert S. D., Wiegrebe L. (2005). Perceptual interaction between carrier periodicity and amplitude modulation in broadband stimuli: A comparison of the autocorrelation and modulation-filterbank model. Journal of the Acoustical Society of America, 118(4), 2470–2481. http://asa.scitation.org/doi/10.1121/1.2011427 https://doi.org/10.1121/1.2011427 [DOI] [PubMed] [Google Scholar]
- Steinmetzger K., Rosen S. (2015). The role of periodicity in perceiving speech in quiet and in background noise. Journal of the Acoustical Society of America, 138(6), 3586–3599. http://asa.scitation.org/doi/10.1121/1.4936945 https://doi.org/10.1121/1.4936945 [DOI] [PubMed] [Google Scholar]
- Stubbs R. J., Summerfield Q. (1988). Evaluation of two voice-separation algorithms using normal-hearing and hearing-impaired listeners. Journal of the Acoustical Society of America, 84(4), 1236–1249. http://asa.scitation.org/doi/10.1121/1.396624 https://doi.org/10.1121/1.396624 [DOI] [PubMed] [Google Scholar]
- Su Y., Delgutte B. (2020). Robust rate-place coding of resolved components in harmonic and inharmonic complex tones in auditory midbrain. The Journal of Neuroscience, 40(10), 2080–2093. http://www.jneurosci.org/lookup/doi/10.1523/JNEUROSCI.2337-19.2020 https://doi.org/10.1523/JNEUROSCI.2337-19.2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Summerfield Q., Assmann P. F. (1991). Perception of concurrent vowels: Effects of harmonic misalignment and pitch-period asynchrony. Journal of the Acoustical Society of America, 89(3), 1364–1377. http://asa.scitation.org/doi/10.1121/1.400659 https://doi.org/10.1121/1.400659 [DOI] [PubMed] [Google Scholar]
- Summerfield Q., Culling J. (1992). Periodicity of maskers not targets determines ease of perceptual segregation using differences in fundamental frequency (abstract). Journal of the Acoustical Society of America, 92, 2317. 10.1121/1.405031 [DOI] [Google Scholar]
- Summerfield Q., Culling J. F., Fourcin A. (1992). Auditory segregation of competing voices: Absence of effects of FM or AM coherence. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences, 336(1278), 357–366. https://royalsocietypublishing.org/doi/10.1098/rstb.1992.0069 https://doi.org/10.1098/rstb.1992.0069 [DOI] [PubMed] [Google Scholar]
- Summerfield Q., Foster J., Gray S., Haggard M. (1981). Perceiving vowels from ’flat spectra’. Journal of the Acoustical Society of America, S69(1), S116–S116. http://asa.scitation.org/doi/10.1121/1.386490 https://doi.org/10.1121/1.386490 [Google Scholar]
- Summers V., Leek M. R. (1998). Masking of tones and speech by Schroeder-phase harmonic complexes in normally hearing and hearing-impaired listeners. Hearing Research, 118(1-2), 139–150. https://linkinghub.elsevier.com/retrieve/pii/S0378595598000306 https://doi.org/10.1016/S0378-5955(98)00030-6 [DOI] [PubMed] [Google Scholar]
- Sumner C. J., Wells T. T., Bergevin C., Sollini J., Kreft H. A., Palmer A. R., Oxenham A. J., Shera C. A. (2018). Mammalian behavior and physiology converge to confirm sharper cochlear tuning in humans. Proceedings of the National Academy of Sciences, 115(44), 11322–11326. http://www.pnas.org/lookup/doi/10.1073/pnas.1810766115 https://doi.org/10.1073/pnas.1810766115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terhardt E. (1974). Pitch, consonance, and harmony. Journal of the Acoustical Society of America, 55(5), 1061–1069. http://asa.scitation.org/doi/10.1121/1.1914648 https://doi.org/10.1121/1.1914648 [DOI] [PubMed] [Google Scholar]
- Tollin D. J., Yin T. C. T. (2005). Interaural phase and level difference sensitivity in low-frequency neurons in the lateral superior olive. The Journal of Neuroscience, 25, 10648–10657. 10.1523/JNEUROSCI.1609-05.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treurniet W. C., Boucher D. R. (2001). A masking level difference due to harmonicity. Journal of the Acoustical Society of America, 109(1), 306–320. http://scitation.aip.org/content/asa/journal/jasa/109/1/10.1121/1.1328791 https://doi.org/10.1121/1.1328791 [DOI] [PubMed] [Google Scholar]
- Verschooten E., Desloovere C., Joris P. X. (2018). High-resolution frequency tuning but not temporal coding in the human cochlea. PLOS Biology, 16(10), e2005164. https://dx.plos.org/10.1371/journal.pbio.2005164 https://doi.org/10.1371/journal.pbio.2005164 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verschooten E., Shamma S., Oxenham A. J., Moore B. C., Joris P. X., Heinz M. G., Plack C. J. (2019). The upper frequency limit for the use of phase locking to code temporal fine structure in humans: A compilation of viewpoints. Hearing Research, 377, 109–121. https://linkinghub.elsevier.com/retrieve/pii/S0378595518305604 https://doi.org/10.1016/j.heares.2019.03.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viemeister N. F. (1979). Temporal modulation transfer functions based upon modulation thresholds. Journal of the Acoustical Society of America, 66(5), 1364–1380. http://asa.scitation.org/doi/10.1121/1.383531 https://doi.org/10.1121/1.383531 [DOI] [PubMed] [Google Scholar]
- Viemeister N. F., Wakefield G. H. (1991). Temporal integration and multiple looks. Journal of the Acoustical Society of America, 90(2), 858–865. http://asa.scitation.org/doi/10.1121/1.401953 https://doi.org/10.1121/1.401953 [DOI] [PubMed] [Google Scholar]
- Walker K. M., Gonzalez R., Kang J. Z., McDermott J. H., King A. J. (2019). Across-species differences in pitch perception are consistent with differences in cochlear filtering. eLife, 8, e41626. https://elifesciences.org/articles/41626 https://doi.org/10.7554/eLife.41626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan R., Durlach N. I., Colburn H. S. (2014). Application of a short-time version of the Equalization-Cancellation model to speech intelligibility experiments with speech maskers. Journal of the Acoustical Society of America, 136(2), 768–776. http://asa.scitaion.org/doi/10.1121/1.4884767 https://doi.org/10.1121/1.4884767 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang D. (2008). Time-frequency masking for speech separation and its potential for hearing aid design. Trends in Amplification, 12(4), 332–353. http://journals.sagepub.com/doi/10.1177/1084713808326455 https://doi.org/10.1177/1084713808326455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang D.-L., Brown G. (2006). Computational auditory scene analysis: Principles Algorithms and Applications Computational auditory scene analysis: Principles, algorithms and applications. IEEE Press/Wiley. [Google Scholar]
- Weintraub M. (1985). A theory and computational model of auditory monaural sound separation. Unpublished doctoral dissertation, Stanford.
- Whiteford K. L., Kreft H. A., Oxenham A. J. (2020). The role of cochlear place coding in the perception of frequency modulation. eLife, 9, e58468. https://elifesciences.org/articles/58468 https://doi.org/10.7554/eLife.58468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie R., Manis P. B. (2013). Target-specific IPSC kinetics promote temporal processing in auditory parallel pathways. Journal of Neuroscience, 33(4), 1598–1614. https://www.jneurosci.org/lookup/doi/10.1523/JNEUROSCI.2541-12.2013 https://doi.org/10.1523/JNEUROSCI.2541-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y., Escabí M. A. (2013). Proportional spike-timing precision and firing reliability underlie efficient temporal processing of periodicity and envelope shape cues. Journal of Neurophysiology, 110(3), 587–606. https://www.physiology.org/doi/10.1152/jn.01080.2010 https://doi.org/10.1152/jn.01080.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwicker U. (1984). Auditory recognition of diotic and dichotic vowel pairs. Speech Communication, 3(4), 265–277. https://linkinghub.elsevier.com/retrieve/pii/0167639384900232 https://doi.org/10.1016/0167-6393(84)90023-2 [Google Scholar]