Abstract
Temporal complexity refers to qualities of a time series that are emergent, erratic, or not easily described by linear processes. Quantifying temporal complexity within a system is key to understanding the time based dynamics of said system. However, many current methods of complexity quantification are not widely used in psychological research due to their technical difficulty, computational intensity, or large number of required data samples. These requirements impede the study of complexity in many areas of psychological science. A method is presented, tangle, which overcomes these difficulties and allows for complexity quantification in relatively short time series, such as those typically obtained from psychological studies. Tangle is a measure of how dissimilar a given process is from simple periodic motion. Tangle relies on the use of a 3-dimensional time delay embedding of a 1-dimensional time series. This embedding is then iteratively scaled and premultiplied by a modified upshift matrix until a convergence criterion is reached. The efficacy of tangle is shown on five mathematical time series and using emotional stability, anxiety time series data obtained from 65 socially anxious participants over a five-week period, and positive affect time series derived from a single participant who experienced a major depression episode during measurement. Simulation results show tangle is able to distinguish between different complex temporal systems in time series with as few as 50 samples. Tangle shows promise as a reliable quantification of irregular behavior of a time series. Unlike many other complexity quantification metrics, tangle is technically simple to implement and is able to uncover meaningful information about time series derived from psychological research studies.
Keywords: Complexity, Time Series, Mental Health, Tangle, Dynamical Systems
Many natural systems exhibit dynamic change over time. From physical phenomena such as the formation of stars, to biological and behavioral phenomena impacting the day-to-day lives of individuals, things change. In order to fully understand such phenomena, it is not only imperative to understand that these systems change over time, but to also understand how these systems change over time (Brown et al., 2002; Z. Liu, 2010). While some systems change over time in relatively simplistic and predictable ways, other systems exhibit more complicated time dependent behaviors (Bak & Paczuski, 1995; Lorenz, 1963). That is to say, different natural processes exhibit different amounts of complexity in the ways in which such processes change over time. Understanding complexity of change is therefore crucial to understanding and making valid inferences regarding a given system (Abarbanel, 2013).
Researchers across multiple disciplines have attempted to understand temporal complexity in different ways (e.g., W. Chen, Zhuang, Yu, & Wang, 2009; Efatmaneshnik & Ryan, 2016; Flood, 1987; Peitgen, Jürgens, & Saupe, 1992). Although there are many definitions of complexity, what appears to be common across these definitions is an overarching relationship between complexity and self-organization, dimensional scaling, non-linearity, and determinism within a system. Self-organization refers to the behavior of some systems to organize into larger, sustainable groups that in themselves act as a singular unit (e.g., flocks of birds, schools of fish, or neurons in a brain), or for systems to structure themselves in such ways as to reach meaningful and sustainable equilibria (Odum, 1988). Dimensional scaling or fractal-like behavior refers to changing qualities of a system when observing that system on different scales, and how changing the dimensional scale of a system may also change the behavior of said system (e.g., the length of coastlines, political leanings of countries versus. cities versus people, or daily fluctuations in temperature versus yearly weather patterns) (West, 1999). Nonlinear and chaotic behavior characterizes qualities of a system that do not grow or change in linear increments, or that show sensitive dependence on initial condition (Theiler, Eubank, Longtin, Galdrikian, & Farmer, 1992). Examples of nonlinear and chaotic behavior include bifurcations, non-stationary behavior, and systems showing other multiplicative or exponential components (e.g., changes in the physical states of matter, the growth rates of humans over their lifespans, or attempting to balance a sharpened pencil on its tip). Determinism versus randomness within a system can be thought of as the interplay between components of a system that do not deviate from underlying rules governing said system, and components of a system that are noise or are purely probabilistic in nature (e.g.,all humans need water [determinism], although the quantity and quality of water that an individual drinks on a given day can be described by a probability distribution [randomness]) (Bassingthwaighte, 1988). Though not necessarily an umbrella term for these qualities, complexity as a concept is deeply linked to the interplay between these (and assuredly more) dynamic and universal qualities of nature. As such, complexity theory has been applied to aid in understanding the behavior of systems studied in many scientific disciplines.
Applications of Complexity Theory
Recent methodological and technological advances in data collection have allowed researchers in many scientific disciplines to begin collecting the necessary time series data needed in order to understand complexity within the time-based dynamics of their respective systems. For example, biological systems such as the human heart have been shown to display fractal-like behavior in time. Iyengar, Peng, Morin, Goldberger, and Lipsitz (1996) have shown that fractal scaling behavior is consistent in the interbeat intervals of hearts in healthy young individuals, but this consistency was not displayed in older individuals. This can be thought of as a decrease in the underlying complexity of interbeat intervals of heart rates as individuals age. Furthering this point, Mäkikallio et al. (2001) found that individuals with smaller short-term fractal exponents of heart rate variability (HRV), and thus less complexity in HRV, had a significantly lower 10-year survival rate compared to those individuals with larger short-term fractal exponents of HRV. These findings are unsurprising as the human heart is a system regulated by many different components. Each regulatory component can be thought of as adding a little more complexity to the behavior of human hearts. A decline in this complexity may then be indicative of a decline in the effectiveness of these regulatory components (Iyengar et al., 1996).
Complexity is also studied in fields such as ecology and economics. Garcia Martin and Goldenfeld (2006) showed how a power-law describes the self-organization of a species within a given area. Such power-law distributions have also been shown to describe economic phenomena. Gabaix, Gopikrishnan, Plerou, and Stanley (2003) ran a large analysis of more than 30-million stock transactions and found that an inverse-cube power-law, known to adequately model U.S. markets, was able to model market transactions in other markets as well. Similar self-organization behavior has also been observed in chemistry (e.g., the Belousov—Zhabotinsky reaction) and in electrical blackout propagation in major cities (Dobson, Carreras, Lynch, & Newman, 2007; Petrov, Gáspár, Masere, & Showalter, 1993). In neuroscience research, complexity manifesting as non-linearity and chaotic behavior is central to many models of neuron spiking such as the FitzHugh–Nagumo model, the Hodgkin-Huxley model, and the Hindmarsh–Rose model (FitzHugh, 1961; Hindmarsh & Rose, 1984; Hodgkin & Huxley, 1952). Given complexity’s breadth of impact across many fields of study, complexity is unlikely to be rare, but is likely to be central to many common phenomena in nature.
Complexity in Behavioral Science and Mental Health Research
Concepts from complexity theory have also influenced behavioral science and mental health research. It may be difficult to characterize humans as anything other than complex systems. Human social groups from friendship circles to large societies show self-organization patterns, the behaviors of individual humans may show nonlinear/chaotic properties, and human communication patterns show fractal-like behavior (Ashenfelter, Boker, Waddell, & Vitanov, 2009; Barton, 1994; Lanham et al., 2013).
In modeling these complexities, researchers are able to gain insight into human systems in ways not admissible by more common mathematical and statistical methodologies. For example, D. Chen, Lin, Chen, Tang, and Kitzman (2014) found a relationship between an individual’s cognitive ability and grip strength to follow the behavior of a cusp catastrophe, a type of bifurcation occurring in more than 1 dimension. Galea, Hall, and Kaplan (2009) found that a simple complex adaptive system model could replicate human drug purchasing behaviors. More recently, multiple researchers have begun modeling mental disorders as complex networks of associations with relatively high rates of comorbidity between disorders (Borsboom, 2017; Fried et al., 2017; Wigman et al., 2015). These findings are due to an increase in technical and computational methodologies allowing researchers to easily quantify complexity within human systems over time.
Quantifying Time Series Complexity
Researchers seeking to quantify complexity within their respective areas of study have relied on many mathematical, computational, and statistical techniques to model complexity over time. As complexity is a diverse and broad concept, so are the means of quantifying complexity. Researchers have attempted to quantify complexity using methods from information theory (e.g., approximate entropy), network modeling, and attractor reconstruction through dimensional embedding to name a few. Each of these methods quantify complexity in different ways, which may lead to different results.
Information theory.
Perhaps the most widely used method for quantifying complexity is through information theory. Metrics of time series complexity arising from information theory center around calculations of entropy within a system H (X),
| (1) |
and mutual information between systems I (X; Y),
| (2) |
Here, p(xi) is the probability of observing a given event or discrete value in from a given signal X. H(X) is maximized when the distribution of pi is uniform, representing a system in its most entropic state. H(X) is minimized when pi tends to 1 or 0, representing certainty in the existence (or nonexistence) of a discrete value. When H(X) is conditional on additional information from an additional signal Y, represented as H(X |Y), this parabolic relationship also holds. I(X; Y) then represents the amount of entropy accounted for in signal X by knowing signal Y. Entropy may be conceptualized as the amount of disorder or randomness within a system, while mutual information can be thought of as the reduction of disorder in a system once new information, Y, is taken into account. Information metrics seeking to quantify complexity tend to rely on comparisons of entropy between two or more systems, information gain/loss between systems, or disorder within a system (X. Liu, Jiang, Xu, & Xue, 2016; Pincus, Gladstone, & Ehrenkranz, 1991). Time series complexity quantification methods arising from information theory then define complexity as either entropy or changes in entropy over time.
Network analysis.
Due to increases in computational power, network analysis is becoming a popular method for quantifying time series complexity (Epskamp, Waldorp, Mõttus, & Borsboom, 2018; Marwan, Donges, Zou, Donner, & Kurths, 2009). Researchers using network analysis seek to model systems as individual units (nodes) that have some connection (edges) to other units. Network modeling can be generally divided into two distinct areas: social network analysis, modeling connections between discrete units such as people, and networks that estimate the connections between sets of variables. In either area, the structures formed once these connections are estimated/defined may then be used to quantify complexity and dynamics between units and over the entire network (Watts & Strogatz, 1998). Complexity quantification in the network analysis framework then focuses on complexity of structure and relationships between units. It should be noted that network analysis is not mutually exclusive to information theory as a means for quantifying complexity and information theory metrics may be used to define the connections in a network.
Dynamic metrics and dimensional embedding.
Another means of complexity quantification is the use of dynamic and nonlinear metrics derived from dimensional embedding of a time series (e.g., fractal dimension estimates, maximum Lyapunov exponents, and recurrence quantification analysis) (Theiler, 1990; Trulla, Giuliani, Zbilut, & Webber, 1996; Wolf, Swift, Swinney, & Vastano, 1985). Dimensional embedding is a method for mapping a set from one dimensional area to another. A given set existing in some dimension, D, can be mapped/projected to a lower dimension for the purposes of increasing ease of understanding, data aggregation, or latent variable construction (Golino & Epskamp, 2017; Kambhatla & Leen, 1997). A set can also be mapped/projected into higher dimensions in order to reconstruct phase space dynamics, and under certain conditions, the attractor of a system (Takens, 1981). Temporal complexity metrics, such as those obtained through recurrence quantification analysis, rely on embedding a 1D time series into a >1D space in order to understand patterns in the dynamics of said time series. Temporal complexity metrics derived from high dimensional embedding can be interpreted as measuring complexity in the underlying dynamics of a system. That is, complexity quantification from dimensional embedding gives information dealing with how the trajectory of a time series changes over time.
Challenges in Complexity Quantification in Applied Research
While temporal complexity quantification methods may give researchers unique insight into their respective areas of study, technical difficulties in implementing and understanding temporal complexity quantification methods reduce the widespread use of these methods by researchers in behavioral science and mental health research. For instance, perhaps the two most studied metrics for describing a given continuous distribution of data are sample mean and sample variance. These metrics are taught in elementary statistics courses and are the basis for most linear analyses (e.g., analysis of variance and linear regression). Metrics derived from complexity theory however tend to be more mathematically complicated and do not lend themselves to being as intuitively understood. While simplistic, means and standard deviations alone may be sufficient to gain some meaningful insight into the underlying dynamics of a given system (Dejonckheere et al., 2019).
However, this is not true for all cases. In fact, it may not be true for most. For example, consider a time series, Xsine, which is 10,000 equally spaced samples of a sine wave with a frequency high enough to show between 5 and 10 peaks and troughs. Let mean(Xsine) = 0 and sd(Xsine) = 1. Now consider a second time series, Xrand, which is 10,000 samples of random Gaussian noise with mean(Xrand) = 0 and sd(Xrand) = 1. Any method using means and standard deviations of each series alone would be unable to distinguish between these two series, even though a simple visual inspection would show obvious differences. Unlike means and standard deviations, complexity metrics such as fractal dimension would be able to distinguish between these series (Gneiting, Ševčíková, & Percival, 2012). Although useful, calculating fractal dimension of a time series (like many other complexity metrics) is generally more difficult compared to the calculation of a mean or standard deviation.
Further, it may be difficult to obtain data of sufficient quality as is needed by most current complexity metrics. Sources of error and noise are quite common in data obtained from research on human participants and error may impact the estimation of a given complexity metric. For instance, metrics of structure obtained from social network analysis may be biased when derived from data with poor signal:noise ratios (Thomason, Coffman, & Marcus, 2004). Even methods that can accurately calculate complexity metrics in the presence of signal:noise ratios like those observed in behavioral science and mental health data require a large number of data points (H.-F. Liu, Dai, Li, Gong, & Yu, 2005; Rosenstein, Collins, & De Luca, 1993; Wornell & Oppenheim, 1992). Time series data seen in behavioral science and mental health data, aside from physiological measurements, tend to be relatively short and quite noisy. That is, time series common in psychological and behavioral studies tend the be less than 100 total observations and have relatively small ratios of true variation to variation due to measurement error (< 5:1 signal to noise ratios). Much of the data obtained from ecological momentary assessment (EMA) and ambulatory assessment studies have substantial noise components, have missing data, and only tend to be a few hundred observations at best, to less than 10 at worst (Haedt-Matt & Keel, 2011a, 2011b; Versluis, Verkuil, Spinhoven, van der Ploeg, & Brosschot, 2016; Wen, Schneider, Stone, & Spruijt-Metz, 2017). Researchers interested in modeling complexity of these data require a complexity metric that gives valid inference on some aspect of complexity even in relatively short time series data with noise components.
With this in mind, we present a new method for quantifying complexity based on a 3D embedding of a 1D time series. This new method, tangle, relies on a 3D embedding of a time series and is a quantification of how erratically a short time series moves throughout this space. Tangle is a measure of how difficult it is to transform some reconstructed shape in a space into an ellipse, or equivalently, how difficult it is to turn a time series into a simple periodic function. Of note, we show that tangle may be appropriate for short time series such as those obtained in behavioral science and mental health research. The remainder of this article focuses on the mathematical derivation of tangle as a complexity quantification and provides examples of tangle on both simulated mathematical time series and on real-world mental health data. We then discuss limitations of tangle and conclude with closing remarks.
Method
One possible way of studying a time series is through studying its attractor. An attractor of a time series can be thought of as a manifold/shape in some dimension that represents the long-term behavior of that time series. This shape, if traced and then moved over time, would reconstruct the original time series. For example, an ellipse is the attractor of a sine wave. If one were to begin drawing the shape of an ellipse on a sheet of paper and then move that paper in one direction, the resulting tracing would be a sine wave. All of the dynamics of the sine wave are captured in the shape of the ellipse. This property of attractors generalizes to any bounded time series (Takens, 1981).
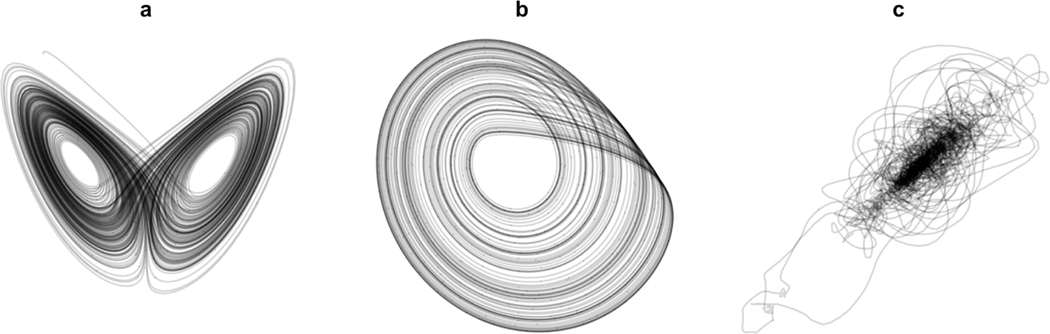
Unlike sine waves, many dynamical systems have more complicated attractor structures. These more complicated attractors may still show regular patterns such as the Lorenz attractor or Rössler attractor, Figure 1a - 1b. However, other attractors including those obtained from behavioral data do not show such visual consistency, Figure 1c. This is due to the complex and often erratic nature of behavioral time series as time series move through phase space. While this erratic behavior may seem in stark contrast to the regularity and beauty seen in attractors from purely theoretical mathematical systems, it is this very behavior that is the basis for the new complexity metric proposed in the current article. We will refer to this metric as tangle, referencing the tendency of attractors reconstructed from behavioral time series to appear as tangled webs or strings. Tangle is a measure of how erratically a time series traces its phase space relative to simple periodic motion, quantifying complexity of phase space trajectories across a measured length of time. Tangle accomplishes this by an iterative “untangling” process. This process iteratively forces any low dimensional phase space reconstruction into an ellipse, thereby untangling the phase space reconstruction into an ordered system. Complexity is then defined by tangle as the difficulty in forcing a phase space reconstruction into an ellipse. Similar to the behavior of a physical string that has become tangled in itself, the difficulty of untangling an attractor is indicative of the original complexity of the tangled system.
Figure 1.
Three examples of attractors of nonlinear systems. (a) a Lorenz attractor, (b) a Rössler attractor, and (c) a reconstructed attractor from human head motion data. Mathematical attractors (a) and (b) are more well-behaved than (c), however attractors like (c) are more common in behavioral data sets.
Mathematical Background
Dimensional embedding.
Given a time series , of sufficient length and sampled at equal intervals from some continuous process, an attractor may be reconstructed based on a D dimensional time delay embedding of this time series at some constant time lag, τ (Takens, 1981). We will denote this embedding matrix as,
| (3) |
This reconstructed attractor from discrete samples is a topologically consistent diffeomorphism of the associated attractor of a sampled continuous system. That is, an attractor can be reconstructed from discrete samples of a continuous process such that the reconstructed attractor is a smooth functional transformation of the attractor underlying the associated continuous process. This smooth transform preserves many qualities of the continuous attractor and it is generally accepted that many qualitative inferences obtained from a reconstructed attractor also hold true for its associated continuous time attractor, even in the presence of noise (Yap, Eftekhari, Wakin, & Rozell, 2014). In practice, D may be estimated by methods such as those proposed by Cao (1997) and Kennel, Brown,and Abarbanel (1992), and τ may be estimated through minimization of average mutual information or autocorrelation between Xi and Xi+τ or through the C-C method (Cao, 1997; Kennel, Brown, & Abarbanel, 1992; Kim, Eykholt, & Salas, 1999). Though many methods of estimating an optimal D may give vastly different values, the value of D generally does not influence qualitative inferences derived from attractor reconstruction and dimensional embedding as long as D is sufficently large. (Aleksić, 1991; Kantz, 1994; Small & Tse, 2004).
Iterative untangling and scaling.
Matrix now represents a reconstructed attractor in some D dimensional space, preserving qualities up to homeomorphisms of the underlying continuous time attractor. That is, behaves qualitatively similar to the underlying continuous time attractor, but guarantees conservation of only topological structure and not geometric structure (Yap et al., 2014). Thus, metrics relying on topological structures (i.e., global structure of an attractor), or change in topological structure, remain unaffected by attractor reconstruction.
One way of changing the topological structure of a given manifold is through use of a shift matrix. A shift matrix, S, is a singular matrix used to shift the position of elements of another matrix into new rows and columns. For example given S and an arbitrary matrix A
| (4) |
S can be used to modify the position of elements within A:
| (5) |
Of note is that once S multiplied by any A, SA or AS can not be mathematically converted back into A due to information loss. For example, there are infinitely many matrices that A in the example above could be before being transformed into AS, as any other matrix sharing rows 2, 3, and 4 of A would also yield AS.
Elmachtoub and Van Loan (2010) showed how a modified shift matrix, known as an upshift matrix, Su, can be used to create an averaging matrix M : M = (Su +1)/2. This averaging matrix can be used to average successive elements of columns of another matrix.
For example:
| (6) |
Premultiplication of matrix M averages successive column values of arbitrary matrix A. If A is an m × 2 matrix, then the columns of A represent coordinates of vectors representing a polygon, P, in some 2D space. Iterative premultiplication of M will result in P converging to a point in that space (Elmachtoub & Van Loan, 2010). By scaling A at each iteration (e.g., dividing each column of A by its euclidean norm) and also centering each column of A at 0, P will not converge to a point, but will unfold into an ellipse, no matter the initial shape (or indeed the dimension) of P (Elmachtoub & Van Loan, 2010).
Quantifying tangle
Tangle relies on the fact that is essentially a D dimensional polygonal representation of the smooth manifold of an underlying continuous attractor. Thus, by iterative premultiplication of with M, will tend to an ellipse in phase space. An ellipse in phase space is identical to a regular periodic function across time. By counting the number of iterations required to transform into an ellipse, a quantification of complexity of can be derived. In this way tangle is a direct measure of how much more erratic and complex a system is relative to simple periodic behavior.
Let S(·) be a centering and scaling function on , centering each column at 0 and dividing each column by its euclidean norm. Let be defined as:
| (7) |
and
| (8) |
Here K is a count of the number of times has been premultiplied by M. K is finalized when forms an ellipse in phase space. There exists a number of principled ways of determining when transformation into an ellipse occurs. We consider the convex hull as a proper stopping rule, though a difference in distance (e.g., the normalized -norm) between all elements of and of a downshifted less than some small threshold value may also be used.
Stopping rule.
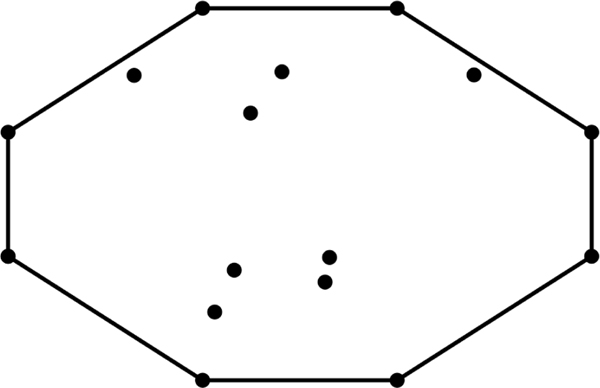
The convex hull, Conv(·), of an arbitrary matrix A, is the set of all points in A such that all other points in A are contained within Conv(A). See Figure 2 for an example. As convex hull calculations are common in computer generated imaging, there exists many computationally simple convex hull calculation algorithms (e.g., Avis, Bremner, & Seidel, 1997; Barber, Dobkin, & Huhdanpaa, 1996; Eddy, 1977; Graham & Frances Yao, 1983; Kirkpatrick & Seidel, 1986). For to form an ellipse, each point in must be on the convex hull. Thus the choice of convex hull algorithm is arbitrary so long as the algorithm is able to establish when each point in A is on the convex hull and the same algorithm is used when comparing tangle values obtained from different systems. Indeed this computation becomes easier as forms an ellipse (2D), and not an ellipsoid (>2D). Thus, all points of only a single projection of into 2D space need to exist on the convex hull for to form an ellipse. K is then set as the point in which forms an ellipse in any 2D projection of after iterative premultiplication of M on.
Figure 2.
All points in this image can be represented by a 16×2 coordinate matrix. The black line represents the convex hull of this coordinate matrix. The concept extrapolates to 3-dimensional sets, where the convex hull is a shell around all points, as well as to higher dimensions.
Tangle equation.
As the number of points T of a time series increases, K will also generally increase at an exponential rate given that the trajectory of a discrete time series X is not already simple periodic motion. Thus, the derivative of K with respect to T for K > 0 and T > 0 may the be approximately modeled as
| (9) |
yielding the analytical solution
| (10) |
This gives:
| (11) |
The tangle of a given is then calculated by dividing ln(K) by T:
| (12) |
Thus, tangle is the time series length normalized log number of iterations it takes to untangle a system by forcing said system into an ellipse in a 3D space through premultiplication by a modified upshift matrix. Systems that show more erratic temporal behavior (i.e., behavior less like simple periodic motion), and thus more complexity, will take more iterations to converge to an ellipse. Tangle can be shown to asymptotically converge to α as . Thus, assuming an adequate sampling rate, for longer time series the influence of C will be minimized and the tangle of a given system will tend to α. See Figure 3 for an example of this method untangling a system and quantifying tangle.
Figure 3.
Tangle algorithm in action on a down-sampled reconstructed attractor. First, an attractor is reconstructed for a given system (a). This system is then iteratively untangled through the use of a modified upshift matrix. (b) shows the system after 100 iterations. (c) shows the “untangled” system at algorithm termination.
Results
Simulated Time Series
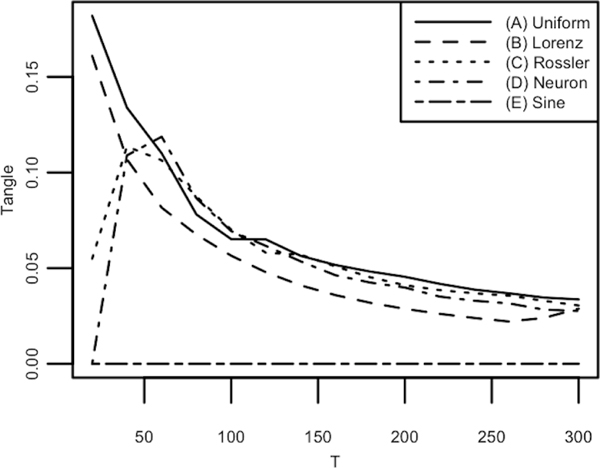
For tangle to be a valid measure of deviation from simple periodic motion across a time series, and thus a valid measure of temporal complexity, it should be able to distinguish between systems known to be simple periodic functions and systems that are known to show more complicated and erratic behaviors. In order to verify the efficacy of tangle as a complexity quantification metric, tangle was calculated for 5 mathematical systems known to display differing amounts of complexity: (A) random uniform noise, (B) a Lorenz attractor, (C) a Rössler attractor, (D) a Hindmarsh-Rose neuron model, and (E) a sine wave with added noise. (A) represents a highly erratic system and (D) represents a highly regular system with measurement error. By other extant complexity metrics, systems (B), (C), and (D) represent systems somewhere in between. For (E) random normal noise was added to a sine wave such that variance of (E) would be composed of a signal:noise ratio of 5:1. Tangle was assessed on each system from 20 – 300 samples. Figure 4 shows the results.
Figure 4.
Each line in the figure represents the tangle value of a different mathematical system, for longer time series derived from those systems. Line (A) represents the tangle computed for uniform noise. This would in theory be a highly complex system and it indeed has the highest line. Lines (B) - (D) represent the tangle computed for 3 known chaotic time series. These series should be complex, but not as complex as (A). The lines (B) - (D) do indeed stay below uniform noise as the length of each time series increases. Finally, (E) represents a simple periodic system with a small amount of random noise. This series shows a tangle estimate of 0 across all time points as it is already simple periodic motion. The tangle calculation for these systems show a stabilizing behavior at 50 time points, indicating 50 time points to be a minimum for valid tangle estimation of a time series. Longer time series give more stable tangle estimates.
As expected, the most erratic time series (A) shows the highest tangle values and smoothly converges to a constant as T increases. The most regular system (E), although sampled with a relatively high amount of noise, was shown to have a tangle value of 0 across all T. This is due to being fairly robust to noise. (B) shows a similar pattern to (A), although (B) has noticeably lower tangle values. This makes sense as (B), though being known to show chaotic behavior, is still a deterministic system and thus has some regularity compared to noise. (C) and (D) are systems known to show regular behavior in short bursts, thus tangle first increases as T increases due to each system showing more irregular behavior (folding in [C] and spiking/resting in [D]) as T increases. (C) and (D) then begin to converge after these irregular behaviors becomes better assessed through larger T. The results of this analysis show that tangle is able to determine differences in complexity between these systems in as few as 50 samples, as this is where Figure 4 begins to stabilize. More samples however increase the stability of tangle estimation and allow for more valid inferences in magnitude and direction of complexity between different time series.
To verify that tangle estimates would remain stable regardless of embedding dimension D, we repeated the above analysis with D = [2, 3, 4] for time series derived from (A) - (D). Values were then correlated between each time series across embedding dimensions. All correlations were between .94 and .99. Assuming this extrapolates to other time series, this gives evidence that D may play little role in tangle estimation. This is perhaps due to the fact that W will force into a 2D ellipse with a 45-degree tilt defined by the eigenvalues of W (Elmachtoub & Van Loan, 2010). In experimentation, was quickly “flattened” towards a 2D form after a relatively small number of iterations, quickly mirroring a projection of the attractor into 2D space. Consider that a D − 1 dimensional embedding may be considered a projection of a D dimensional embedding (Takens, 1981). The eigenvalues of W are pushing toward a 2D space rapidly though W’s largest eigenvalues. It appears then that higher dimensions are quickly forced into a 2D space, only adding a relatively small number of iterations to the tangle calculation procedure. However, future research is needed to verify this possibility.
Effects of Measurement Error.
Measurement error is inherent in data collected from human systems commonly studied in psychological and behavioral science. Measurement error may also produce bias in parameter estimation and may increase variability of measured complexity values as measurement error is difficult to separate from genuine complexity (Yu, Ott, & Chen, 1990). That is, measurement error can bias complexity metrics as the measurement error is adding complexity to the observed time series values. In order to study the behavior of tangle under different error conditions, we conducted another simulation study. In each iteration, a time series of 75 observations was generated from either a Lorenz system, a Rössler system, or a neuron model. Then an amount of Gaussian noise was added to each time series such that each time series had specific a signal:noise ratio. Signal:noise ratios used this simulation are 100:1, 20:1, 10:1, 5:1, and 2:1. Here, 100:1 represents an ideal case with little measurement error (e.g., from a bio-metric device such as a heart rate monitor) and the 5:1 and 2:1 conditions represent signal:noise ratios more common in behavioral data. Tangle was then assessed for each time series at each signal:noise ratio. This process was then repeated 1000 times for a total of 15,000 simulations. Table 1 shows the means and standard deviations of 1000 tangle estimates for each time series at each signal:noise ratio. All distributions were approximately normal.
Table 1.
Means and (standard deviation) of tangle estimates at different signal:noise ratios over 1000 simulations
| Simulated Time Series | |||
|---|---|---|---|
|
| |||
| Signal:Noise | Lorenz | Rössler | Neuron |
|
| |||
| 100:1 | 0.0803 (0.0030) | 0.0884 (0.0003) | 0.0913 (0.0003) |
| 20:1 | 0.0826 (0.0037) | 0.0883 (0.0005) | 0.0913 (0.0007) |
| 10:1 | 0.0836 (0.0039) | 0.0882 (0.0008) | 0.0914 (0.0009) |
| 5:1 | 0.0845 (0.0047) | 0.0882 (0.0011) | 0.0915 (0.0012) |
| 2:1 | 0.0856 (0.0048) | 0.0878 (0.0017) | 0.0917 (0.0017) |
For the Lorenz system, increased measurement error lead to higher tangle estimates. The same effect was found for the neuron model, but to a lesser degree. The Rössler system showed an overall decrease in tangle estimates. As expected, across all systems the standard deviation of the simulated sampling distributions increased, but all values from within a given signal have good coverage across all signal:noise rations. That is, the estimates generally fall within 2 standard deviation units of the noiseless tangle estimate for each system. These findings imply that the point estimate of tangle remain stable even at relatively large signal:noise ratios.
However, the increased variation in the simulated distributions may make distinguishing time series from one another difficult. While tangle estimates from the Lorenz system, Rössler system, and neuron model are able to distinguish these three systems from one another when there is no measurement error, this may not be true in the presence of measurement error. Thus we compared the simulated distributions of tangle values from each time series across each signal:noise level using simple t-tests, table 2.
Table 2.
t-tests comparing simulated distributions of three time series across multiple signal:noise ratios
| t-test Comparisons | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| Lorenz vs. Rossler | Lorenz vs. Neuron | Neuron vs. Rossler | |||||||
|
|
|
|
|||||||
| Signal:Noise | t | p | cohen’s d | t | p | cohen’s d | t | p | cohen’s d |
|
| |||||||||
| 100:1 | −59.03 | < .001 | 3.73 | −80.30 | < .001 | 5.08 | 154.38 | < .001 | 9.76 |
| 20:1 | −34.62 | < .001 | 2.19 | −52.21 | < .001 | 3.30 | 73.67 | < .001 | 4.66 |
| 10:1 | −25.72 | < .001 | 1.63 | −43.16 | < .001 | 2.73 | 59.57 | < .001 | 3.77 |
| 5:1 | −17.05 | < .001 | 1.08 | −32.58 | < .001 | 2.06 | 46.63 | < .001 | 2.95 |
| 2:1 | −9.41 | < .001 | 0.60 | −26.63 | < .001 | 1.68 | 36.85 | < .001 | 2.33 |
Results of this analysis show an expected decrease in t values and effect size (cohen’s d) as measurement error increases. At high signal:noise ratios we see large t values and large effect size estimates. At low signal:noise ratios we still see large t values and effect size estimates, but these values are lower. However, even the lowest cohen’s d value (Lorenz vs. Rössler at 2:1 signal:noise ratio) is still a moderate/strong effect. This gives evidence that tangle is able to distinguish between complexity of deterministic systems even with relatively large amounts of measurement error, assuming measurement error distributions are iid across comparison groups.
Comparison to Other Complexity Metrics
In order to determine the behavior of tangle relative to other measures of complexity commonly used when quantifying complexity in short time series, we conducted a simulation study comparing tangle estimates to both approximate entropy (ApEn) and fractal dimension. Both ApEn and fractal dimension are common complexity metrics for short time series (Sase, Ramírez, Kitajo, Aihara, & Hirata, 2016; Yentes et al., 2013). The ApEn of a time series is defined as:
| (13) |
| (14) |
where N is time series length, m is embedding dimension, r is a positive real number generally set to be 20% of the standard deviation of the time series under study, and is the correlation sum of the time series under study. ApEn is a measure of how patterns of behaviors in a time series remain similar as embedding dimension is increased (Pincus, 1991).
Fractal dimension, on the other hand, is a measure of the “roughness” of a time series. There are numerous ways to approximate the fractal dimension of a time series. Perhaps the most popular of which is the box-counting dimension (Gneiting, Ševčíková, & Percival, 2012). In its simplest form, calculate the box-counting dimension of a time series is done by using boxes of a known size to tile a graph of a time series. The number of boxes containing values of the time series is then compared to the total number of boxes used to tile the graph. Then this process repeats with increasingly smaller boxes. The ratio of number of boxes used to the number of boxes containing part of the time series at each repetition is then used to calculate the box-counting dimension. This can also be achieved by measuring the area of the boxes. The box-counting dimension D of a time series is defined as:
| (15) |
where is the width of boxes used to tile a time series, is the total area of the boxes defined by and is a function time time series length.
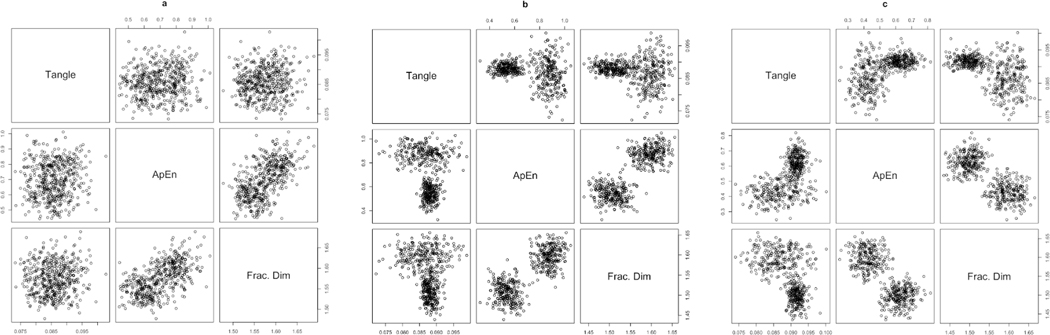
In each iteration of this simulation, a Lorenz system, a Rössler system, and a Neuron model were created, each consisting of 75 observations. Gaussian noise was then added to each time series such that each system would have a signal:noise ratio of 3:1. Values of tangle, ApEn, and fractal dimension were then recorded. This process was repeated 500 times for a total of 1500 simulated time series. Figure 5 displays the bivariate joint distributions of tangle, ApEn, and fractal dimension for each time series studied.
Figure 5.
Pairs plots displaying joint distributions of tangle with approximate entropy (ApEn) and fractal dimension for (a) a Lorenz system, (b) a Rössler system, and (c) a neuron model. Each simulated time series consists of 75 observations with added Gaussian noise (Signal:Noise ratio = 3:1).
Tangle shows little relation to both ApEn and fractal dimension for the Lorenz system. However, tangle shows clustering behavior with both ApEn and fractal dimension for the Rössler system and neuron model. Although within each cluster there appears to be little relation between tangle and either complexity metric, across these clusters there is a slight curvilinear relationship. Additionally, both ApEn and fractal dimension show little relationship to one another, but still show a clustering behavior with one another across the Rössler system and neuron model. This is unsurprising as both ApEn and fractal dimension conceptualize time series complexity in different ways and researchers have found both to be useful when discussing specific aspects of temporal complexity of real-world systems (e.g. Yeragani et al., 1998). This lack of systematic relation between tangle, ApEn, and fractal dimension give evidence that these metrics are indeed measuring different aspects of temporal complexity. Any relationship between these metrics would then indicate a relationship between these distinct complexities within a given time series.
Real Data Example - Anxiety
We now present the results of an application of tangle to a real-world data set from an emotion regulation study of highly anxious individuals. The purpose of this example is to (a) demonstrate how tangle may be used to compare complexity values of time series across a number of covariates, (b) show a proposed way of discussing tangle as complexity, and (c) to give researchers interested in using tangle in their own research a scaffolding to build upon. Additionally, we believe the results of this study add to existing literature on changes in behavioral complexity with regard to mental health issues.
Difficulty regulating emotions is considered to be a hallmark of mood and anxiety-related psychopathology (e.g., Sloan et al., 2017). Specifically, many mental illnesses are characterized by numerous difficulties in emotional reactivity (hypo- or hyperreactivity), response duration (too short or too long; see Gross and Jazaieri (2014)), and (in)stability (Association, 2013). Although the vast majority of research investigating emotion dysregulation has been conducted cross-sectionally or in lab-based experiments, experience sampling studies have begun to link trait emotion dysregulation to state emotional experiences in daily life to reflect complex, more externally valid emotional processes (e.g., complex processes that are making it difficult for individuals to identify and regulate their emotions in real time). For example, individuals with higher (vs. lower) trait emotion dysregulation report more labile negative affect and less ability to identify their emotions over the course of the day (Daros et al., 2019; MacIntyre, Ruscio, Brede, & Waters, 2018).
However, the field has lacked good methods to simply and directly assess emotional complexity in daily life. We know, for instance, that socially anxious individuals frequently experience distress in the face of perceived social threat, but what does this experience actually look like in terms of complex emotional processes? Is it a case of more intense, sustained negative affect throughout the day (e.g., low complexity), or many erratic oscillations in affective states, making one’s emotional world feel unpredictable and overwhelming (e.g., high complexity)? To help address this gap in understanding, the tangle complexity quantification method was applied to time series data that were collected in a sample of socially anxious individuals to investigate whether differences in trait emotion dysregulation predict different levels of complexity in naturally occurring state anxiety and state affect (positive vs. negative valence) ratings over time.
Hypotheses.
We pre-registered (https://osf.io/53b2g/) competing hypotheses. On the one hand, it is possible that higher (vs. lower) trait emotion dysregulation is associated with a more complex profile of emotional experiences in daily life, given that emotion dysregulation is associated with greater emotional reactivity, lack of clarity, and affect instability (e.g., Gross & Jazaieri, 2014). Conversely, it is also possible that higher (vs. lower) trait emotion dysregulation is associated with a less complex profile of emotional experiences in daily life, given that dysregulated individuals rate themselves as more negative throughout daily life than better regulated individuals (e.g., MacIntyre et al., 2018) and experience more blunted positive affect (e.g., Lasa-Aristu, Delgado-Egido, Holgado-Tello, Amor, & Domínguez-Sánchez, 2019), potentially resulting in a more consistently negative (i.e., less complex) emotional presentation. Our predictions did not differ between state affect and state anxiety ratings.
Methods.
One-hundred and thirteen individuals scoring relatively high on a measure of trait social anxiety severity were recruited to complete a five-week ecological momentary assessment (EMA) study consisting of up to six randomly timed surveys sent to their mobile phone each day. (This study was part of a larger intervention trial: see https://osf.io/eprwt/). Prior to starting the EMA protocol, all participants completed a measure of trait emotion dysregulation. At each random time point, participants rated their in-the-moment level of anxiety and in-the-moment affect (general positive/negative valence). According to the pre-registered plan for analysis, observations were binned into “half-day” (e.g., before 3pm or after 3pm) time windows to create approximately equal time spacing between observations. Within each time window, we averaged together multiple responses per participant and marked data as missing if no survey was submitted. We decided a priori that participants with greater than 20% missingness would be removed from analyses to ensure a sufficient sample of assessment points for this proof-of-principle application of the tangle method, leaving 65 participants (self-reported as 69.2% female; 64.6% Non-Hispanic White, 20% Asian, 6.2% Black/African American, 3.1% Hispanic White, 4.6% Multiracial, 1.5% prefer not to answer; Mage = 20.25 years old, SDage = 3.27). Missing data for the remaining participants were imputed according to linear interpolation using the na_interpolation() function from the imputeTS package within the R programming language for statistical computing (Moritz & Bartz-Beielstein, 2017; R Core Team, 2018). All analyses were run using robust linear models in R. All analyses were run using robust linear models using the rlm() function from the MASS package.
Measures.
Trait emotion dysregulation was assessed using the 18-item Difficulties in Emotion Regulation Scale (DERS) (Gratz & Roemer, 2004). Participants rated their agreement with 18 statements on a 1 (“almost never, 0–10%”) to 5 (“almost always, 90–100%”) scale, with higher scores indicating greater emotion regulation difficulties. Internal consistency for the overall score was acceptable (Cronbach’s α = .78). In addition to an overall composite score, six subscale scores were computed: non-acceptance of negative emotions (α = .76), difficulties engaging in goal-directed behaviors (α = .95), difficulties refraining from impulsive behaviors (α = .84), lack of awareness of emotional experiences (α = .74), lack of emotional clarity about the emotions one is experiencing (α = .76), and beliefs that one has limited access to emotion regulation strategies (α = .74).
In order to assess state anxiety and affect at each random time prompt, participants rated the degree to which they were feeling calm relative to anxious and positive relative to negative, using a 1 (“Very calm”/ “Very negative”) to 10 (“Very anxious” / “Very positive”) sliding scale. For further details on response rates and additional measures included in the larger study, please see (Daniel et al., 2020).
Results.
Analyses predicting the complexity of state anxiety and state affect from the overall DERS score were not significant. However, exploratory analyses predicting the complexity of these emotional experiences from the DERS subscales (where all six subscales were entered as simultaneous predictors) each found one significant predictor, table 3.
Table 3.
Robust linear model of DERS subscales predicting affect and anxiety complexity
| Outcome | Predictor | robust β | robust t | robust p |
|---|---|---|---|---|
|
| ||||
| Tangle(Affect) | nonacceptance | 0.08 | 0.43 | 0.670 |
| goal directed | −0.41 | −2.62 | 0.011** | |
| impulse | 0.05 | 0.31 | 0.761 | |
| access | 0.17 | 1.03 | 0.306 | |
| awareness | 0.02 | 0.15 | 0.884 | |
| clarity | −0.01 | −0.07 | 0.940 | |
| Tangle(Anxious) | nonacceptance | −0.24 | −1.23 | 0.222 |
| goal directed | −0.02 | −0.10 | 0.924 | |
| impulse | −0.08 | −0.47 | 0.635 | |
| access | 0.27 | 1.48 | 0.138 | |
| awareness | −0.03 | −0.22 | 0.827 | |
| clarity | 0.28 | 1.67 | 0.097* | |
p < .1
p < .05
We found that endorsing lower trait difficulties with engaging in goal-directed behaviors when upset was associated with greater complexity in daily life affect ratings (feeling positive relative to negative, B = −.41, t = −2.62, p < .011), suggesting that people who feel that their ability to concentrate and work is not as hindered when they are upset tend to display a more erratic pattern of state affect ratings than people who report themselves to be more disrupted when upset. It is possible that people who believe they can handle negative emotions and still function will be more tolerant of experiencing a full range of emotions and therefore demonstrate greater complexity in their daily affect ratings (vs. being consistently negative or consistently positive). Alternatively, it could be that people who have lots of complex, emotional ups-and-downs have to learn how to still function and meet their goals even in the face of emotional instability. Notably, the current sample was socially anxious but generally high functioning (e.g., many were undergraduate and graduate students at a prestigious university); thus, it would be interesting in future work to determine if this same finding would hold for a more disabled, anxious sample.1
Discussion.
Difficulty regulating emotions is associated with psychopathology (Sloan et al., 2017). The current study shows that individual differences in facets of trait emotion dysregulation (namely, less difficulty engaging in goal directed behavior when upset) are associated with emotional complexity in daily life, though not in consistent ways. This points to the importance of investigating multiple facets of emotion dysregulation and multiple affective states to comprehensively evaluate the complexities of emotional functioning in daily life. Tangle appears to be a useful metric to apply to EMA studies focused on emotional processes and may help uncover important indicators of emotion dysregulation and psychopathology in daily life. Differences in tangle were found even though data were from a more homogeneous sample (i.e., individuals high in trait social anxiety severity) than the general population, and thus had less possible variation in complexity than would have been observed otherwise.
Real Data Example - Depression
To further demonstrate the applicability of tangle on real-world data known to show complex behavior, we applied tangle to openly available time series data from an experience sampling method (ESM) study of a single participant measured up to 10 times daily over a period of 239 days (Kossakowski, Groot, Haslbeck, Borsboom, & Wichers, 2017; Wichers et al., 2016). The participant, a 57-year old male with a history of major depression, agreed to be part of a multi-phase double-blind study in which his depression medication (the antidepressant venlafaxine) was systematically reduced from a full dose (150gm) to a placebo (0mg) over an 8-week period. At each measurement occasion, the participant answered items relating to his positive affect, negative affect, and mental unrest. This data is available from http://osf.io/j4fg8.
In their original study, Wichers et al. (2016) found that a complex phenomenon known as critical slowing down was apparent in the participant’s time series data prior to an unexpected major depressive episode. Critical slowing down is a process in which a system becomes unusually sensitive to perturbations before a major qualitative change occurs in that system (e.g., a bifurcation). Scheffer et al. (2009) note that a consequence of critical slowing down is that a system will show stronger auto-correlation across time (i.e. less erratic behavior) as it approaches a qualitative change point. This is because the system is no longer able to adapt as easily to external influences as it would otherwise, causing the system to show more regular and less adaptive patterns. Thus the system undergoes a change in order to gain back some level of adaptive resilience and again display variation and adaptive patterns (Ives, 1995). While Wichers et al. (2016) used network based metrics and change point analysis to determine the existence of critical slowing down, we show that tangle is also able to model critical slowing down as a change in complexity in the participant’s positive affect. Specifically, we show that immediately prior to his major depressive episode, the participant’s positive affect showed significantly less complexity than during his major depressive episode.
Measures.
Each day of measurement, the participant was asked at random times to rate how much a statement reflected his positive affect. These questions include “I feel relaxed”, “I feel satisfied”, “I feel enthusiastic”, “I feel cheerful”, “I feel strong”, “I like myself”, and “I can handle anything”. Responses were rated on a scale of 1 (Not) to 7 (Very). For the current analysis, a time series consisting of 75 measurements immediately preceding the participant’s major depressive episode and 75 measurements from the start of the depressive episode for each positive affect question, yielding 7 total time series of 150 measurements each.
Results.
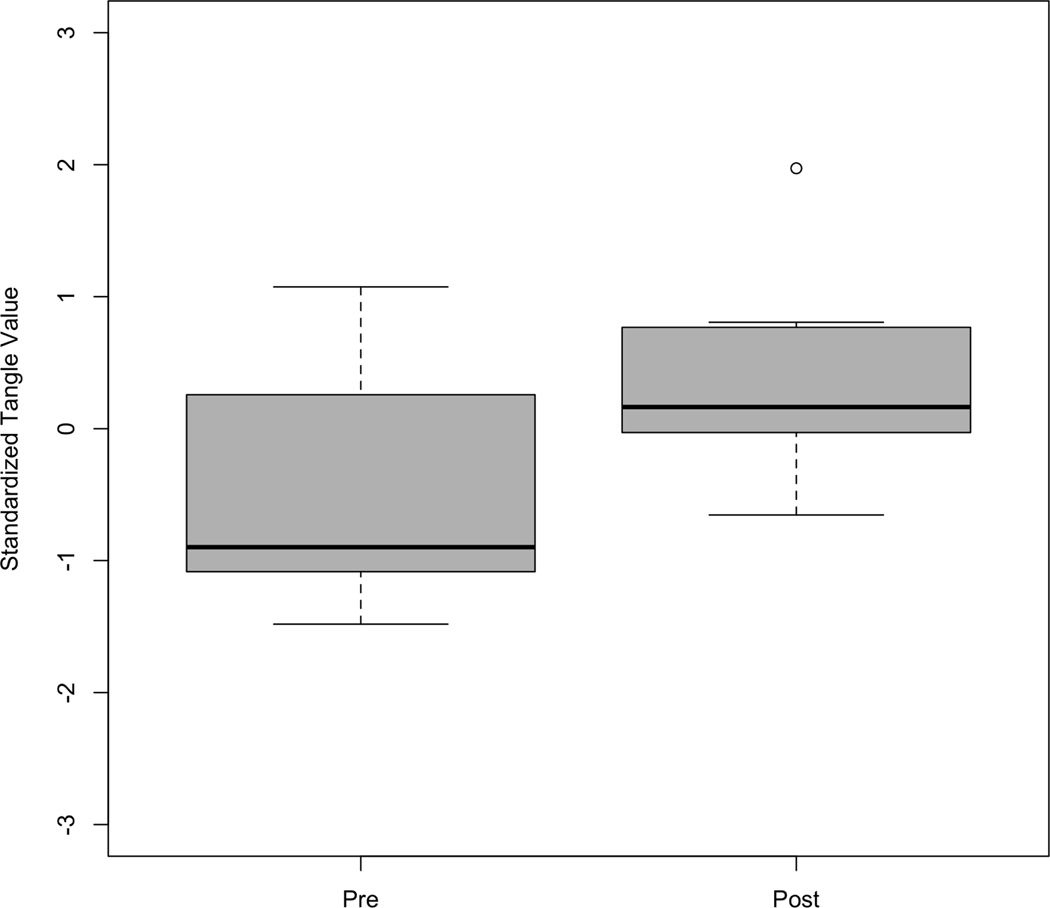
The tangle algorithm was performed on each of the participant’s positive affect time series. These values were then converted to z-scores for ease of interpretation. A robust mixed-effects model (quantile regression on the median) was conducted to test for significant change in complexity of these 7 time series before and after the participant’s depressive episode (Geraci, 2014). A significant positive increase in the median standardized tangle values of these time series was found (β = 1.10, t = 2.46, p = 0.013). The average complexity of each time series was significantly lower before the participant’s major depressive episode than after the episode’s start, Figure 6.
Figure 6.
Box-plot of tangle values of 7 positive affect time series 75 measurements prior to when a participant experienced a major depressive episode (Pre) versus after the episode’s start (Post).
Discussion.
Critical slowing down is characterized by a reduction in complexity and increased auto-correlation of a system. Critical slowing down is a symptom of a system becoming not as adaptive to outside influences immediately prior to a major qualitative change or transition. After transition, the system regains some level of adaptive behavior and complexity. Wichers et al. (2016) demonstrated critical slowing down was present in a participant’s positive affect time series immediately prior to a major depressive episode using network metrics of complexity. We have successfully replicated this finding by modeling time series complexity directly through tangle analysis. This gives further evidence of the validity of tangle as a measure of time series complexity.
Discussion
We have presented tangle as a metric for quantifying temporal complexity as deviation of a time series from simple periodic motion. Temporal complexity analysis using tangle was able to show theoretical rank-order differences in complexity between known chaotic time series. Additionally, given that complex signals are made of multiple simple signals interacting with one another (i.e., Fourier series), tangle may be used as a quantifier for deregulation as lower values of tangle may indicate less regulatory processes making up an observed time series compared to time series with higher values of tangle. That is, higher tangle values may imply there are more underlying processes involved within a given time series.
Understanding the temporal dynamics and complexity of a system is a critical part of understanding and making valid inferences about that system. While many metrics exist for understanding temporal complexity in large data sets with thousands of samples, fewer methods exist for data with < 100 samples. By allowing researchers with access to relatively few data points (as is often the case for behavioral science and mental health researchers) to investigate claims about the complexity of their data, tangle makes an important contribution to the emerging study of complex processes and has many benefits. First, tangle is a computationally simple alternative for studying temporal complexity as it is quantified by erratic temporal behavior. Next, tangle only estimates one hyper-parameter (τ), which lessens the impact of individual researcher decisions on the tangle value of a given system, thereby increasing confidence in derived values. Notably, tangle accurately differentiates between systems with as few as 50 time samples, far fewer than the requisite 1000+ samples needed for many established complexity methods.
Limitations
While a promising metric for understanding erratic behavior within a given time series, researchers attempting to use tangle should be aware of the following limitations. Although embedding dimension D did not appear to effect tangle estimates from the systems studied in this article, it is possible that some systems may be highly sensitive to estimates of D, especially those with theoretically infinite dimensions (Doyne Farmer, 1982). Further, although tangle appears to measure the degree of erratic temporal behavior versus simple periodic behavior within a time series, not all researchers view erratic behavior as synonymous with complexity. However, this is a limitation with all complexity metrics. It is of note that misunderstandings of complexity and chaos can be detrimental to scientific research (Kincanon & Powel, 1995). Thus it is imperative to discuss tangle in as direct terms as possible, i.e., a quantification of complexity as erratic behavior of a system across time compared to simple periodic motion. Established temporal complexity metrics such as the maximal Lyapunov exponent, fractal dimension, average mutual information, and correlation dimension each measure different distinct qualities of a time series that may not necessarily be related to one another (Chlouverakis & Sprott, 2005; Rosenstein et al., 1993). The distinct quality of complexity that tangle measures is how difficult it is to transform a time series into a simple periodic function (e.g., a sine wave).
Another consideration is that tangle, like other complexity metrics for short time series, is dependant on time series length. That is, tangle is a relative measure of time series complexity that may differ quite substantially if time series have different lengths. This means that time series compared with tangle should have the same length. This problem of time series length confounded with complexity estimation is a well-known problem in the complexity literature with no current solution (Montesinos, Castaldo, & Pecchia, 2018; Nagaraj & Balasubramanian, 2017; Zhou et al., 2017). We have shown that time series length becomes less of an influence on tangle as time series length tends to infinity, however this influence may still be relevant for short time series as those seen in the social and behavioral sciences. Thus, while 50 observations may be a hard cutoff for stabilization of tangle estimation in purely deterministic systems with no measurement error, we suggest researchers use a minimum of 75 observations when calculating tangle (as we have in our simulations) so as to further reduce the influence of time series length for systems with measurement error.
A current limitation of tangle, and other complexity metrics, related to the issue of time series length is that tangle requires complete data sets of equal length for direct comparison. While current methods exist for up-sampling, down-sampling, and imputation for handling missing data in time series analysis, these methods may not be applicable for many of the time series collected in the social and behavioral sciences. Additionally, imputation may indeed reduce the complexity of a time series as underlying imputation models are generally less complex than the theoretical generating processes for a given set s of psychological or behavioral data. In the real world data example, we employed imputation to account for missing data as this is perhaps the most common and easy to j implement method for handling missing data from EMA studies (see supplemental material for an analysis of tangle values compared to the number of imputed time points in the j applied data example). However, the effects of missing data handling procedure on tangle estimates is an open question in need of further research. Indeed, because tangle relies on dimensional embedding (a method known to be robust to deletion of missing data by treating missing data as sampling misspecification) missing data handling procedures may not be necessary at all (Boker, Tiberio, & Moulder, 2018).
Future Directions
Future work regarding the advancement of tangle as a complexity quantification should focus on testing the stability, sensitivity, and accuracy of tangle across more systems and more embedding dimensions. We have studied tangle across multiple time series and multiple embedding dimensions, however there are many more of each to study. Tangle’s sensitivity to the τ hyper-parameter is also an important question for future work, as well as stability of tangle estimation across a number of methods available for estimating τ. Recent research in attractor reconstruction methods suggest that a universal τ of 1 may be sufficient for most cases (Brunton, Brunton, Proctor, Kaiser, & Kutz, 2017).
Additionally, the time to calculate tangle increases exponentially with time series length and thus could make tangle difficult to calculate for longer time series. There may be ways to estimate tangle at convergence of the convex hull without needing to reach the convex hull stopping point, based on modeling change in distance between points in the time-delay embedding matrix as K increases.
Missing data/attrition is perhaps the most common data problem in time series derived from longitudinal behavioral and mental health studies, as well as those in many other fields measuring human traits (Eysenbach, 2005). In this article, we dealt with these issues by assuming missing data were missing completely at random (MCAR) and employing a linear interpolation method. It is probable that different missing data methods will give different tangle estimates, however the amount to which missing data effects tangle estimates is an open question. There is some evidence that imputation may indeed be a poor method for missing data handling when using time-delay embedding and that simply ignoring missing values when constructing a time-delay embedding matrix (i.e., allowing for time misspecification) yields robust estimates (Boker et al., 2018).
Future work should also assess tangle on systems outside of the ones assessed in this article. Although tangle was able to accurately distinguish theoretical rank-order differences in temporal complexity between the studied time series, testing on a wider variety of known complex systems is needed to fully establish whether what is being measured by tangle (i.e., difficulty in transforming a time series into simple periodic motion) continues to correlate with theoretical differences in complexity, thus better establishing tangle as a general measure of complexity. Additionally, although the systems assessed in this article are well-known representative models of highly complex systems, all systems studied (besides uniform random noise) are purely deterministic, albeit with added measurement error. However, many systems may not be purely deterministic. That is, systems may be considered to have deterministic and stochastic components, as well as measurement error (Tschacher & Haken, 2019). The behavior of tangle on mixed deterministic/stochastic processes (e.g., a Fokker-Planck system), or on purely stochastic systems (e.g., random walks and moving average models) is yet to be assessed. Indeed, the applicability of many complexity metrics have not yet been tested for mixed deterministic/stochastic processes or for a wide range of purely stochastic processes.
It is also possible that tangle is applicable to data outside of time series data. For instance, network models estimate structure based on qualities of data. It is possible that this structure may be untangled to determine network complexity. In this way, it may be possible to generalize tangle to cross-sectional data as well as time series data.
In the current article, we have defined and demonstrated tangle as a new method for assessing temporal complexity as erratic behavior within a time series. We have shown that tangle gives valid inferences of differences in complexity between two systems even with as few as 50 data points. For individuals interested in using tangle in their own research, we have a number of recommendations.
Although tangle may be valid in short time series, longer time series are encouraged. We believe 50 observations may be enough to give valid inference in direction, however researchers should aim for ideally 75+ observations given the results of our simulation study.
Complexity is an ill-defined term across multiple disciplines. We have chosen to discuss tangle estimates as quantifying erratic behavior in a time series, an important facet of temporal complexity. We suggest that other researchers use this language with discussing tangle estimates until further research better refines a colloquial definition.
Our stopping rule, all points existing on the convex hull, is only one possible stopping rule. Other rules may give other estimates. Due to this and other differences between computational implementations, tangle should only be used as a relative measure of complexity between time series of equal length sampled at the same rate, and should not be interpreted between studies using different time series lengths, sampling rates, or stopping rules.
Following these recommendations, we believe tangle will allow researchers in many fields to begin asking questions regarding time series complexity, where such questions were unable to be answered before. To further this goal, R code for calculating tangle of a time series can be found at https://github.com/RobertGM111/Tangle.
Supplementary Material
Acknowledgments
This work was supported in part by a grant from the National Institute on Drug Abuse (NIH DA-018673), a grant from the National Institute of Mental Health (R01MH11375), the Jefferson Scholars Foundation of Charlottesville, VA, and A University of Virginia Hobby Postdoctoral and Predoctoral Fellowship Grant. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of any supporting agency. The dataset and code supporting the conclusions of this article are available in the Open Science Framework (OSF) repository, https://osf.io/53b2g/ (Moulder, Daniel, Teachman, & Boker, 2019).
A portion of the material in this article has been presented at the 2019 International Meeting of the Psychometric Society in Santiago, Chile, and at the 2019 annual meeting of the Society for Multivariate Experimental Psychology (SMEP) in Baltimore, Maryland.
Footnotes
A preprint of this article was posted on October 06, 2019 at https://psyarxiv.com/23csa/
We would like to acknowledge Laura Barnes and her lab for their role in collecting and processing the data used for the real world example.
A Type-I error rate of .1 was also considered for exploratory purposes (Venables & Ripley, 2013). Endorsing lower trait clarity about the emotions one experiences was associated with higher complexity in daily life anxiety ratings (feeling calm relative to anxious, B = .28, t = 1.67,p = .096). This finding may indicate that volatile feelings of anxiety throughout daily life make it more difficult for individuals to identify their emotions, or that a lower ability to differentiate between one’s emotions contributes to volatile momentary anxiety. This is consistent with recent findings that greater trait difficulties in emotional clarity are associated with corresponding regulation difficulties in daily life (Daros et al., 2019).However, given the small sample size and exploratory nature of the test, the result should be interpreted with considerable caution.
Contributor Information
Robert G. Moulder, Department of Psychology, University of Virginia .
Katharine E. Daniel, Department of Psychology, University of Virginia .
Bethany A. Teachman, Department of Psychology, University of Virginia .
Steven M. Boker, Department of Psychology, University of Virginia .
References
- Abarbanel H. (2013). Predicting the future: completing models of observed complex systems. New York: NY: Springer. [Google Scholar]
- Aleksić Z. (1991). Estimating the embedding dimension. Physica D: Nonlinear Phenomena, 52(2–3), 362–368. doi: 10.1016/0167-2789(91)90132-S [DOI] [Google Scholar]
- Ashenfelter KT, Boker SM, Waddell JR, & Vitanov N. (2009). Spatiotemporal symmetry and multifractal structure of head movements during dyadic conversation. Journal of experimental psychology. Human perception and performance, 35(4), 1072–1091. doi: 10.1037/a0015017 [DOI] [PubMed] [Google Scholar]
- Association, A. P. (2013). Diagnostic and statistical manual of mental disorders (dsm-5@). American Psychiatric Pub. [Google Scholar]
- Avis D, Bremner D, & Seidel R. (1997). How good are convex hull algorithms? Computational Geometry, 7(5–6), 265–301. doi: 10.1016/S0925-7721(96)00023-5 [DOI] [Google Scholar]
- Bak P, & Paczuski M. (1995). Complexity, contingency, and criticality. Proceedings of the National Academy of Sciences, 92(15), 6689–6696. doi: 10.1073/pnas.92.15.6689 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barber CB, Dobkin DP, & Huhdanpaa H. (1996). The quickhull algorithm for convex hulls. ACM Transactions on Mathematical Software, 22(4), 469–483. doi: 10.1145/235815.235821 [DOI] [Google Scholar]
- Barton S. (1994). Chaos, self-organization, and psychology. American Psychologist, 49(1), 5–14. doi: 10.1037/0003-066X.49.1.5 [DOI] [PubMed] [Google Scholar]
- Bassingthwaighte J. (1988). Physiological Heterogeneity: Fractals Link Determinism and Randomness in Structures and Functions. Physiology, 3(1), 5–10. doi: 10.1152/physiologyonline.1988.3.1.5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boker SM, Tiberio SS, & Moulder RG (2018). Robustness of time delay embedding to sampling interval misspecification. In Continuous time modeling in the behavioral and related sciences (pp. 239–258). Basel: Switzerland: Springer. doi: 10.1007/978-3-319-77219-6_10 [DOI] [Google Scholar]
- Borsboom D. (2017). A network theory of mental disorders. World Psychiatry, 16(1), 5–13. doi: 10.1002/wps.20375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JH, Gupta VK, Li BL, Milne BT, Restrepo C, & West GB (2002). The fractal nature of nature: Power laws, ecological complexity and biodiversity. Philosophical Transactions of the Royal Society B: Biological Sciences, 357(1421), 619–626. doi: 10.1098/rstb.2001.0993 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunton SL, Brunton BW, Proctor JL, Kaiser E, & Kutz JN (2017). Chaos as an intermittently forced linear system. Nature Communications, 8(1), 19. doi: 10.1038/s41467-017-00030-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao L. (1997). Practical method for determining the minimum embedding dimension of a scalar time series. Physica D: Nonlinear Phenomena, 110(1–2), 43–50. doi: 10.1016/S0167-2789(97)00118-8 [DOI] [Google Scholar]
- Chen D, Lin F, Chen X, Tang W, & Kitzman H. (2014). Cusp Catastrophe Model: A Nonlinear Model for HealthOutcomes in Nursing Research. Nursing Research, 63(3), 211–220. doi: 10.1097/NNR.0000000000000034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W, Zhuang J, Yu W, & Wang Z. (2009). Measuring complexity using FuzzyEn, ApEn, and SampEn. Medical Engineering & Physics, 31 (1), 61–68. doi: 10.1016/j.medengphy.2008.04.005 [DOI] [PubMed] [Google Scholar]
- Chlouverakis KE, & Sprott J. (2005). A comparison of correlation and Lyapunov dimensions. Physica D: Nonlinear Phenomena, 200(1–2), 156–164. doi: 10.1016/j.physd.2004.10.006 [DOI] [Google Scholar]
- Daniel KE, Daros AR, Beltzer ML, Boukhechba M, Barnes LE, & Teachman BA (2020). How anxious are you right now? using ecological momentary assessment to evaluate the effects of cognitive bias modification for social threat interpretations. Cognitive Therapy and Research, 1–19. doi: 10.1007/s10608-020-10088-2 [DOI] [Google Scholar]
- Daros AR, Daniel KE, Boukhechba M, Chow PI, Barnes LE, & Teachman BA (2019). Relationships between trait emotion dysregulation and emotional experiences in daily life: an experience sampling study. Cognition and Emotion, 1–13. doi: 10.1080/02699931.2019.1681364 [DOI] [PubMed] [Google Scholar]
- Dejonckheere E, Mestdagh M, Houben M, Rutten I, Sels L, Kuppens P, & Tuerlinckx F. (2019). Complex affect dynamics add limited information to the prediction of psychological well-being. Nature Human Behaviour, 3(5), 478–491. doi: 10.1038/s41562-019-0555-0 [DOI] [PubMed] [Google Scholar]
- Dobson I, Carreras BA, Lynch VE, & Newman DE (2007). Complex systems analysis of series of blackouts: Cascading failure, critical points, and self-organization. Chaos: An Interdisciplinary Journal of Nonlinear Science, 17(2), 026103. doi: 10.1063/1.2737822 [DOI] [PubMed] [Google Scholar]
- Doyne Farmer J. (1982). Chaotic attractors of an infinite-dimensional dynamical system. Physica D: Nonlinear Phenomena, 4 (3), 366–393. doi: 10.1016/0167-2789(82)90042-2 [DOI] [Google Scholar]
- Eddy WF (1977). A New Convex Hull Algorithm for Planar Sets. ACM Transactions on Mathematical Software, 3(4), 398–403. doi: 10.1145/355759.355766 [DOI] [Google Scholar]
- Efatmaneshnik M, & Ryan MJ (2016). A general framework for measuring system complexity. Complexity, 21 (S1), 533–546. doi: 10.1002/cplx.21767 [DOI] [Google Scholar]
- Elmachtoub AN, & Van Loan CF (2010). From Random Polygon to Ellipse: An Eigenanalysis. SIAM Review, 52(1), 151–170. doi: 10.1137/090746707 [DOI] [Google Scholar]
- Epskamp S, Waldorp LJ, Mõttus R, & Borsboom D. (2018). The Gaussian Graphical Model in Cross-Sectional and Time-Series Data. Multivariate Behavioral Research, 53(4), 453–480. doi: 10.1080/00273171.2018.1454823 [DOI] [PubMed] [Google Scholar]
- Eysenbach G. (2005). The Law of Attrition. Journal of Medical Internet Research, 7(1), e11. doi: 10.2196/jmir.7.1.e11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- FitzHugh R. (1961). Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophysical Journal, 1 (6), 445–466. doi: 10.1016/S0006-3495(61)86902-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flood RL (1987). Complexity: A definition by construction of a conceptual framework. Systems Research, 4 (3), 177–185. doi: 10.1002/sres.3850040304 [DOI] [Google Scholar]
- Fried EI, van Borkulo CD, Cramer AOJ, Boschloo L, Schoevers RA, & Borsboom D. (2017). Mental disorders as networks of problems: a review of recent insights. Social Psychiatry and Psychiatric Epidemiology, 52(1), 1–10. doi: 10.1007/s00127-016-1319-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabaix X, Gopikrishnan P, Plerou V, & Stanley HE (2003). A theory of power-law distributions in financial market fluctuations. Nature, 423 (6937), 267–270. doi: 10.1038/nature01624 [DOI] [PubMed] [Google Scholar]
- Galea S, Hall C, & Kaplan GA (2009). Social epidemiology and complex system dynamic modelling as applied to health behaviour and drug use research. International Journal of Drug Policy, 20(3), 209–216. doi: 10.1016/j.drugpo.2008.08.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia Martin H, & Goldenfeld N. (2006). On the origin and robustness of power-law species-area relationships in ecology. Proceedings of the National Academy of Sciences, 103(27), 10310–10315. doi: 10.1073/pnas.0510605103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geraci M. (2014). Linear quantile mixed models: the lqmm package for laplace quantile regression. Journal of Statistical Software, 57(13), 1–29. doi: 10.18637/jss.v057.i1325400517 [DOI] [Google Scholar]
- Gneiting T, Sevcíková H, & Percival DB (2012). Estimators of Fractal Dimension: Assessing the Roughness of Time Series and Spatial Data. Statistical Science, 27(2), 247–277. doi: 10.1214/11-STS370 [DOI] [Google Scholar]
- Gneiting T, Sevcíková H, & Percival DB (2012). Estimators of fractal dimension: Assessing the roughness of time series and spatial data. Statistical Science, 247–277. doi: 10.1214/11-STS370 [DOI] [Google Scholar]
- Golino HF, & Epskamp S. (2017). Exploratory graph analysis: A new approach for estimating the number of dimensions in psychological research. PLoS ONE, 12(6), 1–26. doi: 10.1371/journal.pone.0174035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graham RL, & Frances Yao F. (1983). Finding the convex hull of a simple polygon. Journal of Algorithms, 4 (4), 324–331. doi: 10.1016/0196-6774(83)90013-5 [DOI] [Google Scholar]
- Gratz KL, & Roemer L. (2004). Multidimensional assessment of emotion regulation and dysregulation: Development, factor structure, and initial validation of the difficulties in emotion regulation scale. Journal of psychopathology and behavioral assessment, 26(1), 41–54. doi: 10.1108/wjstsd-08-2017-0022 [DOI] [Google Scholar]
- Gross JJ, & Jazaieri H. (2014). Emotion, emotion regulation, and psychopathology: An affective science perspective. Clinical Psychological Science, 2(4), 387–401. doi: 10.1177/2167702614536164 [DOI] [Google Scholar]
- Haedt-Matt AA, & Keel PK (2011a). Hunger and binge eating: A meta-analysis of studies using ecological momentary assessment. International Journal of Eating Disorders, 44 (7), 573–578. doi: 10.1002/eat.20868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haedt-Matt AA, & Keel PK (2011b). Revisiting the affect regulation model of binge eating: A meta-analysis of studies using ecological momentary assessment. Psychological Bulletin, 137(4), 660–681. doi: 10.1037/a0023660 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hindmarsh JL, & Rose RM (1984). A model of neuronal bursting using three coupled first order differential equations. Proceedings of the Royal Society of London. Series B. Biological Sciences, 221 (1222), 87–102. doi: 10.1098/rspb.1984.0024 [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, & Huxley AF (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology, 117(4), 500–544. doi: 10.1113/jphysiol.1952.sp004764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ives AR (1995). Measuring resilience in stochastic systems. Ecological Monographs, 65(2), 217–233. doi: 10.2307/2937138 [DOI] [Google Scholar]
- Iyengar N, Peng CK, Morin R, Goldberger AL, & Lipsitz LA (1996). Age-related alterations in the fractal scaling of cardiac interbeat interval dynamics. The American journal of physiology, 271 (4 Pt 2), R1078–84. doi: 10.1152/ajpregu.1996.271.4.R1078 [DOI] [PubMed] [Google Scholar]
- Kambhatla N, & Leen T. (1997). Dimension Reduction by Local {PCA}. Neural Computation, 9, 1493. [Google Scholar]
- Kantz H. (1994). A robust method to estimate the maximal lyapunov exponent of a time series. Physics letters A, 185(1), 77–87. doi: 10.1016/0375-9601(94)90991-1 [DOI] [Google Scholar]
- Kennel MB, Brown R, & Abarbanel HD (1992). Determining embedding dimension for phase-space reconstruction using a geometrical construction. Physical review A, 45(6), 3403. [DOI] [PubMed] [Google Scholar]
- Kim H, Eykholt R, & Salas J. (1999). Nonlinear dynamics, delay times, and embedding windows. Physica D: Nonlinear Phenomena, 127(1–2), 48–60. doi: 10.1016/S0167-2789(98)00240-1 [DOI] [Google Scholar]
- Kincanon E, & Powel W. (1995). Chaotic analysis in psychology and psychoanalysis. Journal of Psychology: Interdisciplinary and Applied, 129(5), 495–505. doi: 10.1080/00223980.1995.9914922 [DOI] [PubMed] [Google Scholar]
- Kirkpatrick DG, & Seidel R. (1986). The Ultimate Planar Convex Hull Algorithm? SIAM Journal on Computing, 15(1), 287–299. doi: 10.1137/0215021 [DOI] [Google Scholar]
- Kossakowski J, Groot P, Haslbeck J, Borsboom D, & Wichers M. (2017). Data from ‘critical slowing down as a personalized early warning signal for depression’. Journal of Open Psychology Data, 5(1). doi: 10.5334/jopd.29 [DOI] [Google Scholar]
- Lanham HJ, Leykum LK, Taylor BS, McCannon CJ, Lindberg C, & Lester RT (2013). How complexity science can inform scale-up and spread in health care: Understanding the role of self-organization in variation across local contexts. Social Science and Medicine, 93, 194–202. doi: 10.1016/j.socscimed.2012.05.040 [DOI] [PubMed] [Google Scholar]
- Lasa-Aristu A, Delgado-Egido B, Holgado-Tello FP, Amor PJ, & Domínguez-Sánchez FJ (2019). Profiles of cognitive emotion regulation and their association with emotional traits. Clinical and Health, 30(1), 33–39. doi: 10.5093/clysa2019a6 [DOI] [Google Scholar]
- Liu H-F, Dai Z-H, Li W-F, Gong X, & Yu Z-H (2005). Noise robust estimates of the largest lyapunov exponent. Physics Letters A, 341 (1–4), 119–127. doi: 10.1016/j.physleta.2005.04.048 [DOI] [Google Scholar]
- Liu X, Jiang A, Xu N, & Xue J. (2016). Increment Entropy as a Measure of Complexity for Time Series. Entropy, 18(1), 22. doi: 10.3390/e18010022 [DOI] [Google Scholar]
- Liu Z. (2010). Chaotic Time Series Analysis. Mathematical Problems in Engineering, 2010, 1–31. doi: 10.1155/2010/720190 [DOI] [Google Scholar]
- Lorenz EN (1963). Deterministic Nonperiodic Flow. Journal of the Atmospheric Sciences, 20(2), 130–141. doi: [DOI] [Google Scholar]
- MacIntyre JM, Ruscio AC, Brede E, & Waters AJ (2018). Emotion dysregulation and negative affect: Laboratory and ema investigations in smokers. Addictive behaviors reports, 7, 65–70. doi: 10.1016/j.abrep.2018.01.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mäkikallio TH, Huikuri HV, Mäkikallio A, Sourander LB, Mitrani RD, Castellanos A, & Myerburg RJ (2001). Prediction of sudden cardiac death by fractal analysis of heart rate variability in elderly subjects. Journal of the American College of Cardiology, 37(5), 1395–1402. doi: 10.1016/S0735-1097(01)01171-8 [DOI] [PubMed] [Google Scholar]
- Marwan N, Donges JF, Zou Y, Donner RV, & Kurths J. (2009). Complex network approach for recurrence analysis of time series. Physics Letters A, 373(46), 4246–4254. doi: 10.1016/j.physleta.2009.09.042 [DOI] [Google Scholar]
- Montesinos L, Castaldo R, & Pecchia L. (2018). On the use of approximate entropy and sample entropy with centre of pressure time-series. Journal of neuroengineering and rehabilitation, 15(1), 116. doi: 10.1186/s12984-018-0465-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moritz S, & Bartz-Beielstein T. (2017). imputeTS: Time Series Missing Value Imputation in R. The R Journal, 9 (1), 207. doi: 10.32614/RJ-2017-009 [DOI] [Google Scholar]
- Moulder RG, Daniel KE, Teachman B, & Boker SM (2019). Tangle: A metric for quantifying complexity and erratic behavior in short time series. PsyArXiv. Retrieved from psyarxiv.com/23csa doi: 10.31234/osf.io/23csa [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagaraj N, & Balasubramanian K. (2017). Dynamical complexity of short and noisy time series. The European Physical Journal Special Topics, 226(10), 2191–2204. doi: 10.1140/epjst/e2016-60397-x [DOI] [Google Scholar]
- Odum HT (1988). Self-Organization, Transformity, and Information. Science, 242(4882), 1132–1139. doi: 10.1126/science.242.4882.1132 [DOI] [PubMed] [Google Scholar]
- Peitgen H-O, Jürgens H, & Saupe D. (1992). Length, area and dimension: measuring complexity and scaling properties. In Chaos and fractals (pp. 183–228). New York: NY: Springer. [Google Scholar]
- Petrov V, Gáspár V, Masere J, & Showalter K. (1993). Controlling chaos in the Belousov—Zhabotinsky reaction. Nature, 361 (6409), 240–243. doi: 10.1038/361240a0 [DOI] [Google Scholar]
- Pincus SM (1991). Approximate entropy as a measure of system complexity. Proceedings of the National Academy of Sciences, 88(6), 2297–2301. doi: 10.1073/pnas.88.6.2297 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pincus SM, Gladstone IM, & Ehrenkranz RA (1991). A regularity statistic for medical data analysis. Journal of Clinical Monitoring, 7(4), 335–345. doi: 10.1007/BF01619355 [DOI] [PubMed] [Google Scholar]
- R Core Team. (2018). R: A language and environment for statistical computing [Computer software manual]. Vienna, Austria. [Google Scholar]
- Rosenstein MT, Collins JJ, & De Luca CJ (1993). A practical method for calculating largest Lyapunov exponents from small data sets. Physica D, 65, 117–134. doi: 10.1016/0167-2789(93)90009-P [DOI] [Google Scholar]
- Sase T, Ramírez JP, Kitajo K, Aihara K, & Hirata Y. (2016). Estimating the level of dynamical noise in time series by using fractal dimensions. Physics Letters A, 380(11–12), 1151–1163. doi: 10.1016/j.physleta.2016.01.014 [DOI] [Google Scholar]
- Scheffer M, Bascompte J, Brock WA, Brovkin V, Carpenter SR, Dakos V, ... Sugihara G. (2009). Early-warning signals for critical transitions. Nature, 461 (7260), 53–59. doi: 10.1038/nature08227 [DOI] [PubMed] [Google Scholar]
- Sloan E, Hall K, Moulding R, Bryce S, Mildred H, & Staiger PK (2017). Emotion regulation as a transdiagnostic treatment construct across anxiety, depression, substance, eating and borderline personality disorders: A systematic review. Clinical psychology review, 57, 141–163. doi: 10.1016/j.cpr.2017.09.002. [DOI] [PubMed] [Google Scholar]
- Small M, & Tse C. (2004). Optimal embedding parameters: a modelling paradigm. Physica D: Nonlinear Phenomena, 194 (3–4), 283–296. doi: 10.1016/j.physd.2004.03.006 [DOI] [Google Scholar]
- Takens F. (1981). Detecting strange attractors in turbulence. In Lecture notes in mathematics (Vol. 898, pp. 366–381). doi: 10.1007/BFb0091924 [DOI] [Google Scholar]
- Theiler J. (1990). Estimating fractal dimension. Journal of the Optical Society of America A, 7(6), 1055. doi: 10.1364/J0SAA.7.001055 [DOI] [Google Scholar]
- Theiler J, Eubank S, Longtin A, Galdrikian B, & Farmer JD (1992). Testing for nonlinarity in time series: the method of surrogate data. Physica D, 58(1–4), 77–94. [Google Scholar]
- Thomason B, Coffman T, & Marcus S. (2004). Sensitivity of social network analysis metrics to observation noise. In 2004 ieee aerospace conference proceedings (ieee cat. no.04th8720) (pp. 3206–3216). IEEE. doi: 10.1109/AER0.2004.1368126 [DOI] [Google Scholar]
- Trulla L, Giuliani A, Zbilut J, & Webber C. (1996). Recurrence quantification analysis of the logistic equation with transients. Physics Letters A, 223(4), 255–260. doi: 10.1016/S0375-9601(96)00741-4 [DOI] [Google Scholar]
- Tschacher W, & Haken H. (2019). Causation and chance: Detection of deterministic and stochastic ingredients in psychotherapy processes. Psychotherapy research, 1–13. doi: 10.1080/10503307.2019.1685139 [DOI] [PubMed] [Google Scholar]
- Venables WN, & Ripley BD (2013). Modern applied statistics with s-plus. Springer Science & Business Media. [Google Scholar]
- Versluis A, Verkuil B, Spinhoven P, van der Ploeg MM, & Brosschot JF (2016). Changing Mental Health and Positive Psychological Well-Being Using Ecological Momentary Interventions: A Systematic Review and Meta-analysis. Journal of Medical Internet Research, 18(6), e152. doi: 10.2196/jmir.5642 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts DJ, & Strogatz SH (1998). Collective dynamics of ‘small-world’ networks. Nature, 393(6684), 440–442. doi: 10.1038/30918 [DOI] [PubMed] [Google Scholar]
- Wen CKF, Schneider S, Stone AA, & Spruijt-Metz D. (2017). Compliance With Mobile Ecological Momentary Assessment Protocols in Children and Adolescents: A Systematic Review and Meta-Analysis. Journal of Medical Internet Research, 19 (4), e132. doi: 10.2196/jmir.6641 [DOI] [PMC free article] [PubMed] [Google Scholar]
- West GB (1999). The Fourth Dimension of Life: Fractal Geometry and Allometric Scaling of Organisms. Science, 284 (5420), 1677–1679. doi: 10.1126/science.284.5420.1677 [DOI] [PubMed] [Google Scholar]
- Wichers M, Groot PC, Borsboom D, Cramer A, Epskamp S, Kendler K, ... Scheffer M. (2016). Critical slowing down as a personalized early warning signal for depression. Psychotherapy and psychosomatics, 85(2), 114–116. doi: 10.1159/000441458 [DOI] [PubMed] [Google Scholar]
- Wigman JTW, van Os J, Borsboom D, Wardenaar KJ, Epskamp S, Klippel A, ... Wichers M. (2015). Exploring the underlying structure of mental disorders: cross-diagnostic differences and similarities from a network perspective using both a top-down and a bottom-up approach. Psychological Medicine, 45(11), 2375–2387. doi: 10.1017/S0033291715000331 [DOI] [PubMed] [Google Scholar]
- Wolf A, Swift JB, Swinney HL, & Vastano JA (1985). Determining Lyapunov exponents from a time series. Physica D: Nonlinear Phenomena, 16(3), 285–317. doi: 10.1016/0167-2789(85)90011-9 [DOI] [Google Scholar]
- Wornell G, & Oppenheim A. (1992). Estimation of fractal signals from noisy measurements using wavelets. IEEE Transactions on Signal Processing, 40(3), 611–623. doi: 10.1109/78.120804 [DOI] [Google Scholar]
- Yap HL, Eftekhari A, Wakin MB, & Rozell CJ (2014). A first analysis of the stability of Takens’ embedding. In 2014 ieee global conference on signal and information processing (globalsip) (pp. 404–408). IEEE. doi: 10.1109/GlobalSIP.2014.7032148 [DOI] [Google Scholar]
- Yentes JM, Hunt N, Schmid KK, Kaipust JP, McGrath D, & Stergiou N. (2013). The appropriate use of approximate entropy and sample entropy with short data sets. Annals of biomedical engineering, 41 (2), 349–365. doi: 0.1007/s10439–012-0668–3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeragani VK, Sobolewski E, Jampala V, KAY J, YERAGANI S, & IGEL G. (1998). Fractal dimension and approximate entropy of heart period and heart rate: awake versus sleep differences and methodological issues. Clinical Science, 95(3), 295–301. doi: 10.1042/cs0950295 [DOI] [PubMed] [Google Scholar]
- Yu L, Ott E, & Chen Q. (1990). Transition to chaos for random dynamical systems. Physical review letters, 65(24), 2935. doi: 10.1103/PhysRevLett.65.2935 [DOI] [PubMed] [Google Scholar]
- Zhou R, Yang C, Wan J, Zhang W, Guan B, & Xiong N. (2017). Measuring complexity and predictability of time series with flexible multiscale entropy for sensor networks. Sensors, 17(4), 787. doi: 10.3390/s17040787 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.