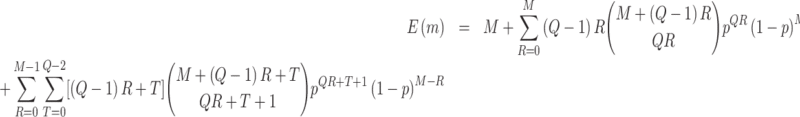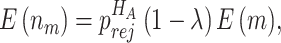Summary
Candidate biomarkers discovered in the laboratory need to be rigorously validated before advancing to clinical application. However, it is often expensive and time-consuming to collect the high quality specimens needed for validation; moreover, such specimens are often limited in volume. The Early Detection Research Network has developed valuable specimen reference sets that can be used by multiple labs for biomarker validation. To optimize the chance of successful validation, it is critical to efficiently utilize the limited specimens in these reference sets on promising candidate biomarkers. Towards this end, we propose a novel two-stage validation strategy that partitions the samples in the reference set into two groups for sequential validation. The proposed strategy adopts the group sequential testing method to control for the type I error rate and rotates group membership to maximize the usage of available samples. We develop analytical formulas for performance parameters of this strategy in terms of the expected numbers of biomarkers that can be evaluated and the truly useful biomarkers that can be successfully validated, which can provide valuable guidance for future study design. The performance of our proposed strategy for validating biomarkers with respect to the points on the receiver operating characteristic curve are evaluated via extensive simulation studies and compared with the default strategy of validating each biomarker using all samples in the reference set. Different types of early stopping rules and boundary shapes in the group sequential testing method are considered. Compared with the default strategy, our proposed strategy makes more efficient use of the limited resources in the reference set by allowing more candidate biomarkers to be evaluated, giving a better chance of having truly useful biomarkers successfully validated.
Keywords: Biomarker validation, Group sequential testing, Reference set, Rotation, Two-stage
1. Introduction
The process of biomarker development has been categorized into five consecutive phases (Pepe and others, 2001). In particular, pre-clinical exploratory studies are conducted in phase 1 to identify potentially useful biomarkers based on tumor and control tissues; retrospective biomarker validation is performed in phase 2 using specimens from individuals with and individuals without disease; phase 3 involves retrospective longitudinal studies to evaluate the capacity of biomarkers for detecting disease; phase 4 involves prospective screening studies for assessing performance; and phase 5 studies aim to estimate mortality reduction due to screening.
Usually, phase 1 studies identify a large number of candidate biomarkers from various laboratories and their performance is validated in later phases. The validation of biomarkers in phase 2 studies is typically based on biobanks of stored specimens. In our motivating application, the National Cancer Institute’s Early Detection and Research Network (EDRN) has developed highly valuable reference sets of specimens collected under rigorous standards from multiple institutions for the validation of biomarkers (Feng and others, 2013; Haab and others, 2015). Using such high quality specimens has been recommended as a way to increase the chance of successful validation. Moreover, specimens such as blood or urine samples in a reference set can allow the validation of multiple candidate biomarkers from various laboratories. Since obtaining high quality specimens is an expensive and time-consuming process and these specimens are often limited in volume, it is important to utilize these valuable specimens in a reference set wisely and efficiently, in order to optimize the chance of successful validation.
In this article, we focus on biomarker validation study designs using samples from a reference set, assuming equal volumes of specimens are available from each participant. Motivated by the need to more efficiently utilize the specimens, instead of using the common strategy of measuring each biomarker using specimens from all participants, here, we consider a two-stage validation process: for validation of each biomarker, participants in the reference set are partitioned into two groups. Each biomarker is first evaluated using group 1 samples; only those biomarkers satisfying a predefined performance criterion are then tested using group 2 samples. If the split of participants into group 1 and group 2 is the same across biomarkers, samples from group 1 will be quickly exhausted, such that only the group 2 samples will be available for evaluating biomarkers that come in later. To deal with this problem, we also propose a strategy that rotates group membership in order to maximize the usage of all available samples.
To control the error rate in the two-stage validation procedure, we adopt the group sequential testing strategy (Emerson and Fleming, 1989; O’Brien and Fleming, 1979). Group sequential designs allow early termination when the candidate biomarker is evidently superior or inferior, so that the remaining specimens can be conserved for validation of other candidate biomarkers. Previously in the field of biomarker evaluation, Pepe and others (2009) considered conditional estimators of sensitivity and specificity for a dichotomous diagnostic biomarker under a two-stage study that allows early termination for futility. This method was extended in Koopmeiners and others (2012) for the evaluation of continuous biomarkers.
In our research, for validating multiple biomarkers using the limited resources in the reference set, we consider two important criteria to characterize the performance of a validation design. The first is the expected number of biomarkers that can be studied using the available specimens from the reference set; the second is the expected number of truly useful biomarkers that can be successfully validated. We develop analytical formulas for both criteria, which can provide useful guidance for validation study designs in practice.
This article is organized as follows: In Section 2, we propose a new strategy for validating biomarkers in reference sets that combines a two-stage validation process with rotation of participant sets. We also develop analytical formulas for important performance criteria in the proposed validation strategy. In Section 3, we conduct extensive simulation studies to evaluate the performance of our proposed strategy under different types of early stopping rules and stopping boundaries of the group sequential testing, and compare the performance with the alternative one-stage strategy of testing each biomarker in all samples. We also demonstrate the use of analytical formulas for the design of validation studies. In Section 4, the performance of the proposed strategy is further demonstrated using a numerical setting constructed based on the data from the EDRN pancreatic cancer reference set study. Finally, we end the article with concluding remarks in Section 5.
2. Methodology
2.1. Group sequential tests of biomarker performance
Suppose we have a reference set that consists of specimens of equal volumes from  participants. The specimen volume (e.g., volume of blood or urine) from each individual is typically determined by the study budget and by practical considerations. Our goal is to have multiple laboratories assess their candidate biomarkers using specimens from this reference set and to validate the classification performance of individual biomarkers.
participants. The specimen volume (e.g., volume of blood or urine) from each individual is typically determined by the study budget and by practical considerations. Our goal is to have multiple laboratories assess their candidate biomarkers using specimens from this reference set and to validate the classification performance of individual biomarkers.
For the validation of each individual biomarker, we consider a hypothesis test for its classification accuracy to measure whether  passes a predefined performance threshold. That is, for each biomarker we want to use a one-sided test for the null hypothesis
passes a predefined performance threshold. That is, for each biomarker we want to use a one-sided test for the null hypothesis  against the alternative hypothesis
against the alternative hypothesis  , with type I error controlled at a level
, with type I error controlled at a level 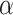 , where
, where  is a pre-specified threshold for classification performance. In this article, we consider
is a pre-specified threshold for classification performance. In this article, we consider  to be the points on the receiver operating characteristic (ROC) curve, although the methods apply in general to other classification measures such as the area under the ROC curve (AUC) or partial AUC (Pepe, 2003; Zhou and others, 2009).
to be the points on the receiver operating characteristic (ROC) curve, although the methods apply in general to other classification measures such as the area under the ROC curve (AUC) or partial AUC (Pepe, 2003; Zhou and others, 2009).
In a study utilizing a reference set to validate biomarkers, all labs with biomarkers of interest can request specimens from the reference set to analyze their biomarkers. Statisticians from the Data Management and Coordinating Center (DMCC) of EDRN are responsible for distributing the appropriate specimens to each lab and later analyzing the biomarker data measured from those specimens to validate their classification performance. For validating individual biomarkers using the reference set, the default strategy is to provide the needed volumes of specimens from all participants in the reference set to each individual lab, and repeat this process until all specimens have been consumed. While this strategy is simple and easy to implement, it almost certainly does not make the most efficient use of the reference set samples. For instance, a number of factors during the biomarker discovery process could lead to over-estimation of a biomarker’s performance, meaning that resources could be inefficiently directed towards validating candidate biomarkers with inferior performance. If, however, candidate biomarkers with inferior performance can be identified earlier during the validation process using a small set of samples, the rest of the samples can be spared and used to validate other biomarkers with greater potential. On the other hand, biomarkers with superior performance could potentially also be validated using a smaller number of samples.
We propose a two-stage validation process with rotation of participants into each stage, geared specifically for the reference set study. First, for evaluation of each individual marker, we break the individuals in the reference set into two groups, group 1 and group 2. The biomarker is measured in samples from group 1 to test its classification performance; only the biomarkers that satisfy some predefined performance criteria in group 1 are subsequently measured in group 2 samples, such that their performance is ultimately tested on the whole sample set. To control for type I error rate in this two-stage testing, we adopt the sequential testing strategy used in group sequential designs (Jennison and Turnbull, 1999).
Recall that in a typical group sequential design in which test statistics  are observed at analyses
are observed at analyses  , the one-sided group sequential test that controls the overall type I error at a significance level
, the one-sided group sequential test that controls the overall type I error at a significance level 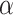 has the following form:
has the following form:
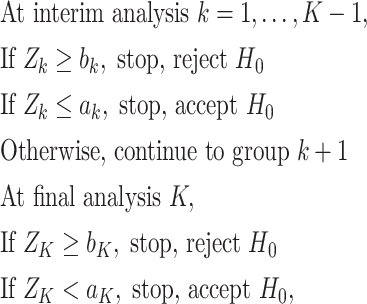 |
where constants  for
for 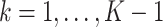 correspond to the threshold of early termination for futility and efficacy, respectively;
correspond to the threshold of early termination for futility and efficacy, respectively;  ensures that the test terminates at the last analysis; and
ensures that the test terminates at the last analysis; and  or
or  for
for 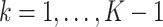 corresponds to early termination for futility or efficacy only, respectively. For the design allowing early stopping for both futility and efficacy, we adopt the one-sided symmetric sequential test designs proposed in Emerson and Fleming (1989), which treat the null and alternative hypotheses symmetrically with respect to early termination, i.e., the interchange of null and alternative hypotheses would lead to identical boundaries for stopping. Let
corresponds to early termination for futility or efficacy only, respectively. For the design allowing early stopping for both futility and efficacy, we adopt the one-sided symmetric sequential test designs proposed in Emerson and Fleming (1989), which treat the null and alternative hypotheses symmetrically with respect to early termination, i.e., the interchange of null and alternative hypotheses would lead to identical boundaries for stopping. Let  be the proportion of sample size enrolled at analysis
be the proportion of sample size enrolled at analysis  relative to the total sample size, for
relative to the total sample size, for  . The boundaries for one-sided symmetric tests are defined as
. The boundaries for one-sided symmetric tests are defined as
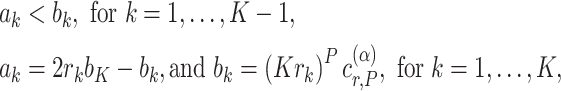 |
(2.1) |
where 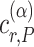 is a critical value such that setting
is a critical value such that setting  will result in a test with size
will result in a test with size 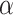 . The parameter
. The parameter 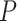 corresponds to the boundary shape; lower values of
corresponds to the boundary shape; lower values of  lead to more conservative testing at earlier analyses. We consider two different types of boundary:
lead to more conservative testing at earlier analyses. We consider two different types of boundary:  or 0.5, corresponding to the O’Brien–Fleming boundary (O’Brien and Fleming, 1979) and the Pocock boundary (Pocock, 1977), respectively. Note that while the boundary given by (2.1) defines the test in terms of the partial sum statistic, we can always transform the boundary on a different scale according to a different choice of test statistic.
or 0.5, corresponding to the O’Brien–Fleming boundary (O’Brien and Fleming, 1979) and the Pocock boundary (Pocock, 1977), respectively. Note that while the boundary given by (2.1) defines the test in terms of the partial sum statistic, we can always transform the boundary on a different scale according to a different choice of test statistic.
In this article, we adopt the sequential design with 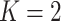 . We consider the construction of a standardized test statistic with respect to the points on the ROC curve. Let
. We consider the construction of a standardized test statistic with respect to the points on the ROC curve. Let 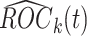 be the sequential empirical estimator of
be the sequential empirical estimator of  at analysis
at analysis 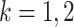 based on all observed data at that analysis point. According to Corollary 3.3 from Koopmeiners and Feng (2011),
based on all observed data at that analysis point. According to Corollary 3.3 from Koopmeiners and Feng (2011), 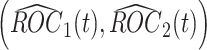 is approximately multivariate normal with
is approximately multivariate normal with
 |
and
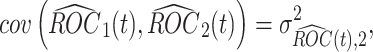 |
where
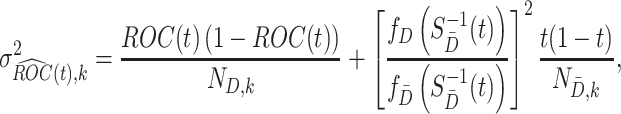 |
(2.2) |
in which 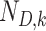 and
and 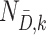 denote the sample sizes for cases and controls at analysis
denote the sample sizes for cases and controls at analysis  ,
, 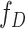 and
and 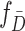 are the probability density functions of the biomarker among cases and controls, respectively, and
are the probability density functions of the biomarker among cases and controls, respectively, and 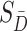 is the survival function of the biomarker among controls. To perform a one-sided
is the survival function of the biomarker among controls. To perform a one-sided 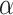 -level hypothesis test
-level hypothesis test  against
against  , we use the following standardized test statistics:
, we use the following standardized test statistics:
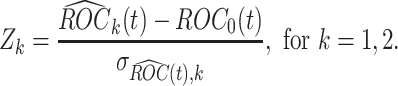 |
(2.3) |
It is immediate from Corollary 3.3 in Koopmeiners and Feng (2011) that 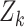 follows a standard normal distribution under the null hypothesis. Under the alternative hypothesis, i.e.,
follows a standard normal distribution under the null hypothesis. Under the alternative hypothesis, i.e., 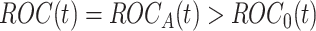 holds, the test statistic
holds, the test statistic 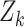 is normally distributed with mean
is normally distributed with mean  and variance 1, where
and variance 1, where 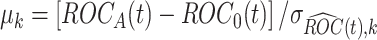 . Usually the variance
. Usually the variance 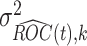 is unknown. In practice, the unknown components in the expression of
is unknown. In practice, the unknown components in the expression of  need to be estimated. The components
need to be estimated. The components  and
and 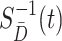 in (2.2) can be substituted by their corresponding sequential empirical estimators. As for the ratio of density function
in (2.2) can be substituted by their corresponding sequential empirical estimators. As for the ratio of density function 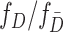 , by Bayes’ rule, we have
, by Bayes’ rule, we have
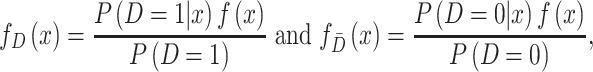 |
where 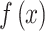 is the density function of biomarker. Therefore,
is the density function of biomarker. Therefore,
 |
Note that  can be estimated by fitting a logistic regression model of disease status
can be estimated by fitting a logistic regression model of disease status  on biomarker
on biomarker 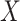 . Then, the estimate for the ratio of density functions can be obtained.
. Then, the estimate for the ratio of density functions can be obtained.
2.2. Rotation of group membership
Consider the two-stage testing strategy described in Section 2.1 and let  denote the proportion of samples in group 1 relative to the total sample size in the reference set. If
denote the proportion of samples in group 1 relative to the total sample size in the reference set. If  or
or 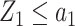 , then the validation of a biomarker stops at the first stage and only
, then the validation of a biomarker stops at the first stage and only  samples are used for measuring this marker. Thus, the remaining
samples are used for measuring this marker. Thus, the remaining 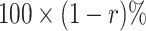 samples are spared and can be used to validate other biomarkers. If instead we have
samples are spared and can be used to validate other biomarkers. If instead we have 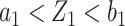 , the biomarker passes the first stage of testing and samples from all individuals in the reference set would be used for validating this biomarker. Note that if the split of individuals into group 1 and group 2 is the same across biomarkers, then specimens from the individuals in group 1 will be quickly exhausted and only specimens from individuals in group 2 will be left for evaluation of biomarkers that are evaluated later in the queue. We thus propose a procedure that rotates group membership.
, the biomarker passes the first stage of testing and samples from all individuals in the reference set would be used for validating this biomarker. Note that if the split of individuals into group 1 and group 2 is the same across biomarkers, then specimens from the individuals in group 1 will be quickly exhausted and only specimens from individuals in group 2 will be left for evaluation of biomarkers that are evaluated later in the queue. We thus propose a procedure that rotates group membership.
We consider a design where the total number of participants in the reference set is 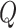 -fold of the number included in the first stage, for some positive number
-fold of the number included in the first stage, for some positive number  . That is, the biomarker is first assessed in specimens from
. That is, the biomarker is first assessed in specimens from 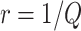 participants. To begin with, for the first biomarker entering the validation process, we randomly partition the participants in the reference set into
participants. To begin with, for the first biomarker entering the validation process, we randomly partition the participants in the reference set into  blocks. One block is randomly selected to be group 1 and the rest of the blocks are treated as group 2. A one-sided group sequential test with
blocks. One block is randomly selected to be group 1 and the rest of the blocks are treated as group 2. A one-sided group sequential test with  is then performed. Next, each time a new biomarker enters the validation process, we first check how many specimen volumes remain within each block. Among the blocks with the maximum remaining amount of specimens, we randomly draw one block as group 1 and then perform this sequential test again. This procedure is repeated for evaluating incoming biomarkers until the specimens have been fully consumed in at least one of the blocks. Note that at this point it is possible that specimens could remain in other blocks. One could potentially use those remaining available specimens to validate another biomarker with a fix-sample test. We explored adding this extra step in our numerical studies. The difference with respect to the performance criteria is negligible when the number of biomarkers that can be evaluated in a reference set is not small. Therefore, we present results without this extra step.
is then performed. Next, each time a new biomarker enters the validation process, we first check how many specimen volumes remain within each block. Among the blocks with the maximum remaining amount of specimens, we randomly draw one block as group 1 and then perform this sequential test again. This procedure is repeated for evaluating incoming biomarkers until the specimens have been fully consumed in at least one of the blocks. Note that at this point it is possible that specimens could remain in other blocks. One could potentially use those remaining available specimens to validate another biomarker with a fix-sample test. We explored adding this extra step in our numerical studies. The difference with respect to the performance criteria is negligible when the number of biomarkers that can be evaluated in a reference set is not small. Therefore, we present results without this extra step.
2.3. Theoretical results
In this section, we develop theoretical results for several performance criteria of the proposed validation design. These results will be useful in guiding the choice of validation design in practice.
2.3.1. Performance criteria under the proposed design
Without loss of generality, here, we consider a simple setting where measurement of each biomarker requires equal specimen volume (denoted as one unit). We also set the total volume of specimens from each participant in the reference set as 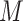 units. The validation strategy described in Section 2.2, however, is applicable to general settings where biomarkers may require different specimen volumes for measurement.
units. The validation strategy described in Section 2.2, however, is applicable to general settings where biomarkers may require different specimen volumes for measurement.
We consider the following two performance criteria, which are important for biomarker validation using a reference set. The first is the expected number of biomarkers that can be evaluated using the available specimens from the reference set. The second is the expected number of truly useful biomarkers that can be successfully validated. The analytical formulas of the two criteria for the proposed design are presented in Results 1 and 3, respectively.
Result 1
Let
be the number of biomarkers evaluated using the proposed two-stage validation design. For any integer
and
, the expected number of biomarkers evaluated equals
where
.
Proof.
For a group sequential design with
, the proportion of samples used for evaluating one biomarker equals
Obviously,
, and we further notice that
for
,
and
. Consequently, the expected value of
equals
□
Result 1 provides a general analytical formula for the expected number of biomarkers evaluated using our proposed two-stage validation design. In our numerical studies, we adopt the validation design with 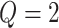 or 3, i.e.,
or 3, i.e., 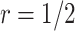 or
or 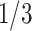 .
.
The second performance criterion, we are interested in is the expected number of truly useful biomarkers that are successfully validated. Before presenting the corresponding analytical formula, we first present the following result regarding the expected number of tested biomarkers found to be useful using the proposed design.
Result 2
Let
denote the number of biomarkers evaluated with the null hypothesis rejected, the expected number of biomarkers declared to have adequate performance equals
where
is the rejection rate, and
is the expected number of biomarkers evaluated which is given in Result 1.
Proof.
We observe that
, thus one has
□
To study the second performance criterion of the proposal design, we make the assumption that the true performance of the biomarkers to be validated in the reference set follows a mixture distribution, i.e., 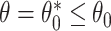 with probability
with probability 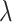 and
and 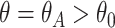 with probability
with probability 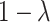 , where
, where 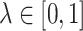 . Notice that when
. Notice that when  , all
, all  biomarkers testing positive using the reference set samples are truly useful. When
biomarkers testing positive using the reference set samples are truly useful. When  , some biomarkers with null performance can incorrectly test as positive. We are interested in finding out how many truly useful biomarkers are successfully validated as positive. Let
, some biomarkers with null performance can incorrectly test as positive. We are interested in finding out how many truly useful biomarkers are successfully validated as positive. Let 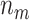 denote the number of truly useful biomarkers that are successfully validated. We then have the following result about its expected value.
denote the number of truly useful biomarkers that are successfully validated. We then have the following result about its expected value.
Result 3
Let
denote the number of truly useful biomarkers that are successfully validated, the expected number of truly useful biomarkers that are successfully validated equals
where
is the value of
under the alternative hypothesis,
,
is the expected number of biomarkers evaluated which is given in Result 1.
Proof.
Let
denote the number of truly useful biomarkers evaluated among the
evaluated biomarkers. Since
, we have
□
Suppose the standardized test statistic used in the sequential testing method follows the standard normal distribution under the null hypothesis and is normally distributed with mean  and variance
and variance 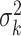 at analysis
at analysis  . Under the assumption that the true performance of the biomarkers to be validated in the reference set follows a mixture distribution, the probability
. Under the assumption that the true performance of the biomarkers to be validated in the reference set follows a mixture distribution, the probability  defined in Result 1 has the form
defined in Result 1 has the form
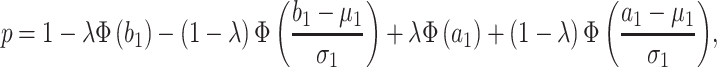 |
where  denotes the cumulative distribution function of a standard normal distribution. The corresponding value of
denotes the cumulative distribution function of a standard normal distribution. The corresponding value of 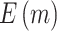 can then be computed based on Result 1. Furthermore, the rejection rate
can then be computed based on Result 1. Furthermore, the rejection rate 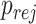 defined in Result 2 can be written as
defined in Result 2 can be written as
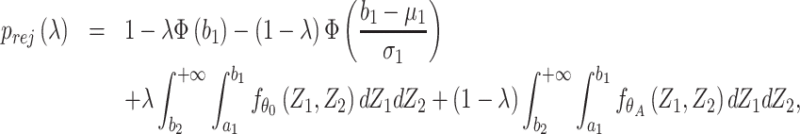 |
where 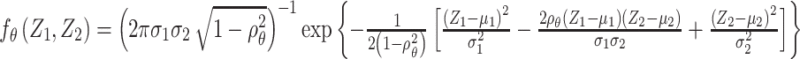 is the joint probability density function of
is the joint probability density function of 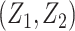 , in which
, in which 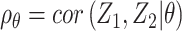 ,
,  and
and 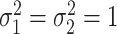 when the null hypothesis holds. In addition,
when the null hypothesis holds. In addition, 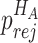 defined in Result 3 equals
defined in Result 3 equals 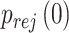 . We can then compute
. We can then compute  and
and  based on Results 2 and 3.
based on Results 2 and 3.
3. Simulation study
In this section, we conduct simulation studies to evaluate the performance of the proposed validation design as described in Section 2 for validating candidate biomarkers using samples from a reference set.
We consider a reference set that includes specimens with 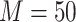 volume units from each participant. We further assume that there are many candidate biomarkers waiting to be evaluated using the specimens in the reference set, and that the validation of a single biomarker requires one unit volume of specimen. Let
volume units from each participant. We further assume that there are many candidate biomarkers waiting to be evaluated using the specimens in the reference set, and that the validation of a single biomarker requires one unit volume of specimen. Let 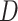 be a binary disease outcome. Biomarker
be a binary disease outcome. Biomarker  for the controls is generated from a standard normal distribution, and for the cases
for the controls is generated from a standard normal distribution, and for the cases 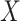 follows a normal distribution with mean
follows a normal distribution with mean 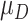 and variance 1. We consider case/control samples with 1:1 ratio and total sample size
and variance 1. We consider case/control samples with 1:1 ratio and total sample size 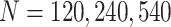 , or 1200. Suppose the performance of interest is
, or 1200. Suppose the performance of interest is  . For the validation of each individual biomarker, we conduct a one-sided test of the null hypothesis
. For the validation of each individual biomarker, we conduct a one-sided test of the null hypothesis  with type I error probability controlled at
with type I error probability controlled at 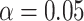 , where the threshold for the null hypothesis is set at
, where the threshold for the null hypothesis is set at  . Suppose the biomarkers to be validated comprise a mixture of null biomarkers and useful biomarkers, such that the true
. Suppose the biomarkers to be validated comprise a mixture of null biomarkers and useful biomarkers, such that the true 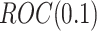 follows a mixture distribution:
follows a mixture distribution:  with probability
with probability  , and
, and 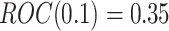 with probability
with probability  . In our simulations, we achieve this by simulating
. In our simulations, we achieve this by simulating  of biomarkers with
of biomarkers with 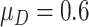 such that those biomarkers have null performance with
such that those biomarkers have null performance with 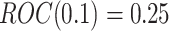 , and for the other
, and for the other 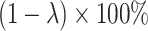 of biomarkers, we set
of biomarkers, we set 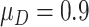 such that
such that  . A series of
. A series of 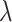 varying within
varying within 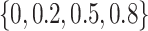 is considered in the simulation studies.
is considered in the simulation studies.
For validating the performance of individual biomarkers, we apply our proposed two-stage testing strategy with rotation of group membership. To complete the test procedure, we use the standardized test statistic defined in (2.3). We consider the design for which a biomarker is first validated using specimens from half or one-third of the participants, i.e., 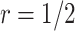 or
or 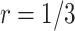 . With respect to the group sequential designs, two different types of stopping rule and boundary shape are considered. Specifically, the designs allowing early stopping for both futility and efficacy, i.e.,
. With respect to the group sequential designs, two different types of stopping rule and boundary shape are considered. Specifically, the designs allowing early stopping for both futility and efficacy, i.e.,  and
and 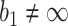 , or allowing early stopping for futility only, i.e.,
, or allowing early stopping for futility only, i.e.,  and
and 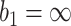 , are considered. We hereafter refer to these two types of stopping rules as Stop
, are considered. We hereafter refer to these two types of stopping rules as Stop  “Both” and Stop
“Both” and Stop  “Null”, respectively, where the one-sided symmetric boundaries proposed in Emerson and Fleming (1989) are used for the design with Stop
“Null”, respectively, where the one-sided symmetric boundaries proposed in Emerson and Fleming (1989) are used for the design with Stop  “Both”. Also, two different types of boundary shape, the O’Brien–Fleming boundary (
“Both”. Also, two different types of boundary shape, the O’Brien–Fleming boundary ( ) and the Pocock boundary (
) and the Pocock boundary (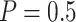 ), are considered. In our simulations, the boundaries are calculated using the RCTdesign package in R (http://www.rctdesign.org/Welcome.html). For comparison purposes, we also consider the default design (
), are considered. In our simulations, the boundaries are calculated using the RCTdesign package in R (http://www.rctdesign.org/Welcome.html). For comparison purposes, we also consider the default design ( ) in which the test statistic
) in which the test statistic  is compared with a standard normal distribution. To evaluate the performance of different designs, we examine the number of biomarkers evaluated,
is compared with a standard normal distribution. To evaluate the performance of different designs, we examine the number of biomarkers evaluated, 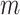 , and the number of truly useful biomarkers that are successfully validated,
, and the number of truly useful biomarkers that are successfully validated, 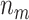 . Average values of
. Average values of 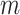 and
and 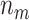 based on 5000 Monte Carlo simulations are calculated, denoted by
based on 5000 Monte Carlo simulations are calculated, denoted by 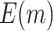 and
and 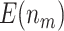 , respectively.
, respectively.
3.1. Results comparing the proposed design with the default design
Table 1 compares the simulation results for testing 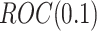 using the proposed validation strategy with
using the proposed validation strategy with 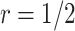 to those obtained using the default strategy. The results clearly show that, compared with the default strategy, our proposed validation strategy can evaluate more candidate biomarkers. Moreover, our proposed validation strategy can correctly validate more biomarkers that are truly useful. Among the different types of stopping rules and boundary shapes used for the proposed strategy, the design that allows early stopping under both null and alternative hypotheses with the Pocock boundary (Stop
to those obtained using the default strategy. The results clearly show that, compared with the default strategy, our proposed validation strategy can evaluate more candidate biomarkers. Moreover, our proposed validation strategy can correctly validate more biomarkers that are truly useful. Among the different types of stopping rules and boundary shapes used for the proposed strategy, the design that allows early stopping under both null and alternative hypotheses with the Pocock boundary (Stop  “Both”,
“Both”, 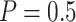 ) generally has the best performance in terms of largest
) generally has the best performance in terms of largest  and
and 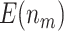 . The design that allows early stopping under the null hypothesis alone using the O’Brien–Fleming boundary (Stop
. The design that allows early stopping under the null hypothesis alone using the O’Brien–Fleming boundary (Stop  “Null”,
“Null”,  ) has smaller
) has smaller  and
and 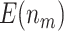 , but still yields improved results compared with the default strategy. Among both designs with Stop
, but still yields improved results compared with the default strategy. Among both designs with Stop  “Both” and designs with Stop
“Both” and designs with Stop  “Null”, using the Pocock boundary (
“Null”, using the Pocock boundary (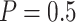 ) leads to better performance compared with the O’Brien–Fleming boundary, in terms of both
) leads to better performance compared with the O’Brien–Fleming boundary, in terms of both  and
and 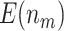 . This is due to the fact that using the O’Brien–Fleming boundary leads to more conservative testing in the first stage compared with the Pocock boundary. Thus, more candidate biomarkers would enter the second stage of testing, fewer biomarkers would be evaluated, and consequently fewer truly useful biomarkers would be successfully validated. Table 1 shows that for a moderate sample size of
. This is due to the fact that using the O’Brien–Fleming boundary leads to more conservative testing in the first stage compared with the Pocock boundary. Thus, more candidate biomarkers would enter the second stage of testing, fewer biomarkers would be evaluated, and consequently fewer truly useful biomarkers would be successfully validated. Table 1 shows that for a moderate sample size of 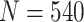 , compared with the default design, the relative increases of
, compared with the default design, the relative increases of  and
and  using the proposed design range from 42.4% to 61.7% and from 25.2% to 44.9%, respectively, with Stop
using the proposed design range from 42.4% to 61.7% and from 25.2% to 44.9%, respectively, with Stop  “Both” and
“Both” and  , and from 2.4% to 25.0% and from 1.2% to 27.3%, respectively, with Stop
, and from 2.4% to 25.0% and from 1.2% to 27.3%, respectively, with Stop  “Null” and
“Null” and  , for
, for 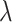 varying from 0 to 0.8. In reality, the candidate biomarkers are not truly useful in most cases. Therefore,
varying from 0 to 0.8. In reality, the candidate biomarkers are not truly useful in most cases. Therefore, 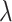 is typically large, with its value close to 1.
is typically large, with its value close to 1.
Table 1.
Comparison of the performance of the default design ( ) and the proposed two-stage validation design with rotation of group membership (
) and the proposed two-stage validation design with rotation of group membership (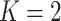 ,
, 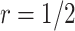 ) using different types of stopping rules (Stop
) using different types of stopping rules (Stop  “Both” or “Null”) and boundary shapes (
“Both” or “Null”) and boundary shapes ( or 0.5). The table shows the average number of biomarkers evaluated
or 0.5). The table shows the average number of biomarkers evaluated  , the average number of truly useful biomarkers that are successfully validated
, the average number of truly useful biomarkers that are successfully validated  , and the corresponding standard error of
, and the corresponding standard error of 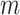 and
and 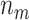 (in parentheses) for testing
(in parentheses) for testing  . Simulations were performed using case/control samples with a 1:1 ratio and total sample size
. Simulations were performed using case/control samples with a 1:1 ratio and total sample size  , 240, 540, or 1200.
, 240, 540, or 1200. 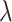 is the proportion of null markers in the population
is the proportion of null markers in the population
 ,
, 
|

|
||||||
|---|---|---|---|---|---|---|---|

|

|
Performance | Stop  “Both” “Both” |
Stop  “Null” “Null” |
|||

|
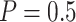
|

|
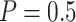
|
||||
| 0 | 120 |

|
57.84 (0.03) | 73.06 (0.04) | 53.94 (0.02) | 59.42 (0.03) | 50 |
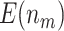
|
20.99 (0.05) | 25.01 (0.06) | 18.25 (0.05) | 19.85 (0.05) | 17.16 (0.05) | ||
| 240 |
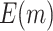
|
56.61 (0.03) | 71.58 (0.04) | 52.19 (0.02) | 57.15 (0.03) | 50 | |
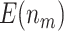
|
27.46 (0.06) | 31.56 (0.06) | 24.67 (0.05) | 26.36 (0.05) | 23.79 (0.05) | ||
| 540 |
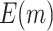
|
57.50 (0.03) | 71.20 (0.04) | 51.20 (0.01) | 54.14 (0.02) | 50 | |

|
41.32 (0.05) | 45.53 (0.06) | 36.82 (0.04) | 37.58 (0.04) | 36.37 (0.04) | ||
| 1200 |

|
66.93 (0.04) | 80.02 (0.04) | 50.04 (0.003) | 50.59 (0.01) | 50 | |
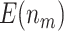
|
63.44 (0.05) | 73.04 (0.06) | 47.49 (0.02) | 47.40 (0.02) | 47.52 (0.02) | ||
| 0.2 | 120 |

|
58.86 (0.03) | 74.40 (0.04) | 55.41 (0.02) | 61.47 (0.03) | 50 |
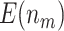
|
17.28 (0.05) | 20.55 (0.05) | 15.22 (0.04) | 16.66 (0.04) | 13.85 (0.04) | ||
| 240 |

|
57.78 (0.03) | 73.24 (0.04) | 53.85 (0.02) | 59.71 (0.03) | 50 | |

|
22.62 (0.05) | 26.11 (0.06) | 20.51 (0.05) | 22.13 (0.05) | 18.99 (0.05) | ||
| 540 |
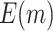
|
59.11 (0.03) | 73.40 (0.04) | 53.57 (0.02) | 57.48 (0.02) | 50 | |
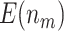
|
34.20 (0.05) | 37.72 (0.06) | 31.15 (0.04) | 32.16 (0.04) | 29.11 (0.04) | ||
| 1200 |

|
66.67 (0.04) | 80.54 (0.04) | 52.08 (0.01) | 54.12 (0.02) | 50 | |
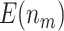
|
50.93 (0.04) | 59.15 (0.05) | 39.94 (0.02) | 40.96 (0.02) | 38.02 (0.02) | ||
| 0.5 | 120 |
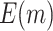
|
60.61 (0.03) | 76.78 (0.04) | 57.91 (0.03) | 65.04 (0.04) | 50 |
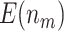
|
11.12 (0.04) | 13.24 (0.04) | 9.89 (0.04) | 11.00 (0.04) | 8.58 (0.03) | ||
| 240 |
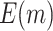
|
59.67 (0.03) | 75.96 (0.04) | 56.76 (0.02) | 64.18 (0.03) | 50 | |
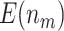
|
14.58 (0.04) | 16.89 (0.05) | 13.51 (0.04) | 14.91 (0.04) | 11.87 (0.04) | ||
| 540 |
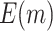
|
61.79 (0.03) | 76.97 (0.04) | 57.72 (0.02) | 63.67 (0.03) | 50 | |

|
22.42 (0.04) | 24.73 (0.04) | 20.97 (0.03) | 22.24 (0.03) | 18.22 (0.03) | ||
| 1200 |
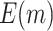
|
66.40 (0.04) | 81.35 (0.04) | 55.97 (0.02) | 60.70 (0.02) | 50 | |

|
31.70 (0.03) | 37.35 (0.03) | 26.77 (0.02) | 28.62 (0.02) | 23.76 (0.02) | ||
| 0.8 | 120 |
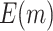
|
62.28 (0.03) | 79.09 (0.04) | 60.47 (0.03) | 69.04 (0.04) | 50 |
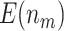
|
4.65 (0.02) | 5.53 (0.03) | 4.21 (0.02) | 4.71 (0.02) | 3.43 (0.02) | ||
| 240 |

|
61.60 (0.03) | 78.97 (0.04) | 59.94 (0.03) | 69.53 (0.04) | 50 | |

|
6.18 (0.03) | 7.14 (0.03) | 5.84 (0.02) | 6.58 (0.03) | 4.77 (0.02) | ||
| 540 |

|
64.62 (0.04) | 80.83 (0.04) | 62.51 (0.03) | 71.11 (0.04) | 50 | |
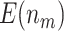
|
9.57 (0.02) | 10.55 (0.03) | 9.27 (0.02) | 10.15 (0.02) | 7.28 (0.02) | ||
| 1200 |
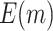
|
66.02 (0.04) | 82.10 (0.04) | 60.39 (0.03) | 68.92 (0.03) | 50 | |

|
12.92 (0.01) | 15.36 (0.02) | 11.83 (0.01) | 13.28 (0.01) | 9.52 (0.01) | ||
In addition, when examining the absolute change of  , we notice that for the proposed design with Stop
, we notice that for the proposed design with Stop  “Both”,
“Both”, 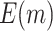 tends to increase as sample size increases. It also increases as the value of
tends to increase as sample size increases. It also increases as the value of 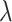 increases for small or moderate sample size, while the magnitude of its change as
increases for small or moderate sample size, while the magnitude of its change as 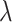 varies is small for large sample size. As for the proposed design with Stop
varies is small for large sample size. As for the proposed design with Stop  “Null”,
“Null”, 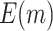 decreases slightly as sample size increases when
decreases slightly as sample size increases when 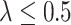 , and increases as
, and increases as  increases. This is because early termination is more likely when there are more biomarkers with null performance. Although the pattern of the change in
increases. This is because early termination is more likely when there are more biomarkers with null performance. Although the pattern of the change in  as sample size or
as sample size or 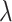 varies between designs with different types of stopping rules, the pattern of the change in
varies between designs with different types of stopping rules, the pattern of the change in 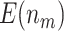 is consistent across different types of designs. We observe that
is consistent across different types of designs. We observe that 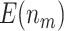 increases as sample size increases, and decreases as the value of
increases as sample size increases, and decreases as the value of  increases. For example, for the proposed design with Stop
increases. For example, for the proposed design with Stop  “Both” and
“Both” and 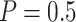 , when
, when 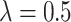 ,
,  increases from 13.24 to 37.35 as the sample size increases from 120 to 1200 and
increases from 13.24 to 37.35 as the sample size increases from 120 to 1200 and 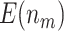 decreases from 73.04 to 15.36 as
decreases from 73.04 to 15.36 as  increases from 0 to 0.8 for sample size
increases from 0 to 0.8 for sample size  . This finding is expected, since a larger sample size provides greater power, while a larger value of
. This finding is expected, since a larger sample size provides greater power, while a larger value of 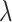 indicates fewer truly useful biomarkers to be validated. In fact, it is more relevant to see if
indicates fewer truly useful biomarkers to be validated. In fact, it is more relevant to see if  increases relative to the default study design. Let
increases relative to the default study design. Let 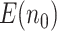 indicate the average number of truly useful biomarkers validated in the default design. When compared with the default design, we observed that for the proposed design with Stop
indicate the average number of truly useful biomarkers validated in the default design. When compared with the default design, we observed that for the proposed design with Stop  “Both”, the increase in truly useful biomarkers identified (i.e.,
“Both”, the increase in truly useful biomarkers identified (i.e., 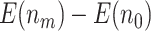 ) decreases as
) decreases as 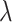 increases; for the proposed design with Stop
increases; for the proposed design with Stop  “Null”,
“Null”, 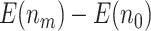 increases as
increases as 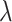 increases from 0 to 0.5 and then falls back when
increases from 0 to 0.5 and then falls back when 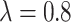 . The relative improvement in truly useful biomarkers identified, i.e.,
. The relative improvement in truly useful biomarkers identified, i.e., 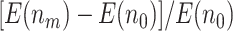 , clearly increases as
, clearly increases as 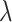 increases. For example, for the proposed design with Stop
increases. For example, for the proposed design with Stop  “Both” and
“Both” and 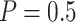 , for sample size
, for sample size 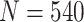 ,
, 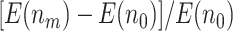 increases from 25.2% to 44.9% when
increases from 25.2% to 44.9% when  increases from 0 to 0.8. To summarize, our proposed design can have appreciable practical advantage compared with the default design, especially when the proportion of null markers is large in the population (
increases from 0 to 0.8. To summarize, our proposed design can have appreciable practical advantage compared with the default design, especially when the proportion of null markers is large in the population (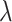 is large). For example, when
is large). For example, when 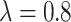 and
and 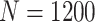 , the relative improvements of our design compared with the default design with respect to
, the relative improvements of our design compared with the default design with respect to 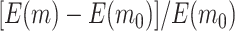 and
and  are 64.2% and 61.3%, respectively, using the Pocock boundary with Stop = “Both”; corresponding relative improvements are 37.8% and 39.4% with Stop = “Null”.
are 64.2% and 61.3%, respectively, using the Pocock boundary with Stop = “Both”; corresponding relative improvements are 37.8% and 39.4% with Stop = “Null”.
For the proposed strategy with 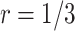 , simulation results are presented in Table 1 in Appendix A of the supplementary material available at Biostatistics online. As in the case of
, simulation results are presented in Table 1 in Appendix A of the supplementary material available at Biostatistics online. As in the case of 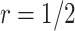 , in both designs with Stop
, in both designs with Stop  “Both” and Stop
“Both” and Stop  “Null”, using the Pocock boundary (
“Null”, using the Pocock boundary ( ) has better performance with respect to
) has better performance with respect to  and
and 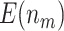 compared with using the O’Brien–Fleming boundary (
compared with using the O’Brien–Fleming boundary ( ). The performance of the proposed design is similar between
). The performance of the proposed design is similar between  and
and 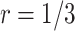 with the Pocock boundary and better in
with the Pocock boundary and better in 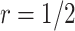 compared with
compared with  with the O’Brien–Fleming boundary. The pattern of the change in
with the O’Brien–Fleming boundary. The pattern of the change in  ,
,  ,
, 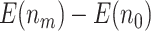 , and
, and 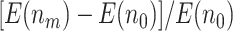 as
as  and sample size vary is similar between the designs using
and sample size vary is similar between the designs using 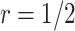 and
and 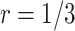 . In practice, if a more conservative test (corresponding to the lower value of the shape parameter,
. In practice, if a more conservative test (corresponding to the lower value of the shape parameter, 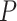 ) is preferred in the first stage, then using a larger value of
) is preferred in the first stage, then using a larger value of 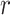 , i.e.,
, i.e.,  , is recommended. As the shape parameter increases to 0.5, the results suggest that the performance of designs using smaller values of
, is recommended. As the shape parameter increases to 0.5, the results suggest that the performance of designs using smaller values of  (such as
(such as 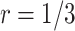 ) would be greatly improved and approach that of a design using
) would be greatly improved and approach that of a design using 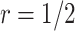 . When
. When  , designs using
, designs using 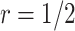 and
and  have comparable performance.
have comparable performance.
Table 2 in Appendix B of the supplementary material available at Biostatistics online presents the power of the group sequential strategy and the default strategy (i.e., for scenarios with  ). A small loss of power can be observed using the group sequential design compared with the default strategy when sample size is large. However, such minor loss of power is negligible, especially considering its great advantage in allowing the evaluation of more candidate biomarkers and the successful validation of more truly useful biomarkers.
). A small loss of power can be observed using the group sequential design compared with the default strategy when sample size is large. However, such minor loss of power is negligible, especially considering its great advantage in allowing the evaluation of more candidate biomarkers and the successful validation of more truly useful biomarkers.
3.2. Use of analytical formulas for design recommendation
In section 2.3, we developed analytical formulas for the expected number of biomarkers that can be evaluated and the expected number of truly useful biomarkers that are successfully validated, using a given amount of specimens from a reference set. These analytical results can provide valuable guidance for the choices of validation design in practice.
As an example, we compute the expected numbers of 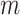 and
and 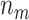 given
given 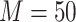 using the analytical formulas presented in Results 1 and 3, and plot in Figure 1 the values of
using the analytical formulas presented in Results 1 and 3, and plot in Figure 1 the values of  ,
,  ,
,  and
and  against
against 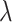 using the proposed designs and the default design. The plots show that the proposed two-stage strategy can evaluate more candidate biomarkers and successfully validate more truly useful markers than the default design. The proposed design with Stop
using the proposed designs and the default design. The plots show that the proposed two-stage strategy can evaluate more candidate biomarkers and successfully validate more truly useful markers than the default design. The proposed design with Stop  “Both” and the shape parameter
“Both” and the shape parameter 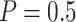 gives the maximum values of
gives the maximum values of  and
and  among all designs considered. Its advantage is apparent especially for small
among all designs considered. Its advantage is apparent especially for small 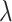 . For both designs with stopping rule Stop
. For both designs with stopping rule Stop  “Both” and Stop
“Both” and Stop  “Null”, the designs using the Pocock boundary have the best performance in terms of
“Null”, the designs using the Pocock boundary have the best performance in terms of  and
and 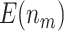 . These findings are consistent with what we observed in our simulation results. Furthermore, we notice that as
. These findings are consistent with what we observed in our simulation results. Furthermore, we notice that as  increases,
increases,  decreases because the total number of truly useful biomarkers decreases, but its relative improvement over the default design
decreases because the total number of truly useful biomarkers decreases, but its relative improvement over the default design  increases as
increases as 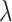 increases to approach 1. Note that
increases to approach 1. Note that  is undefined when
is undefined when 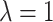 , since
, since  when there are no truly useful biomarkers.
when there are no truly useful biomarkers.
Fig. 1.
Comparison of the expected numbers of biomarkers evaluated (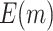 ) and truly useful biomarkers that are successfully validated (
) and truly useful biomarkers that are successfully validated (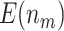 ) using the two-stage validation strategy with rotation of group membership and the default strategy. Results were calculated using case/control samples with a 1:1 ratio and total sample size
) using the two-stage validation strategy with rotation of group membership and the default strategy. Results were calculated using case/control samples with a 1:1 ratio and total sample size 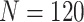 , 240, 540, or 1200. Different types of stopping rule (Stop
, 240, 540, or 1200. Different types of stopping rule (Stop  “Both” or “Null”) and boundary shape (
“Both” or “Null”) and boundary shape ( or 0.5) of group sequential testing are represented by the dashed (Stop
or 0.5) of group sequential testing are represented by the dashed (Stop  “Both”,
“Both”, 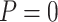 ), dotted (Stop
), dotted (Stop  “Both”,
“Both”,  ), dot-dash (Stop
), dot-dash (Stop  “Null”,
“Null”, 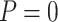 ), and long-dash (Stop
), and long-dash (Stop  “Null”,
“Null”, 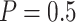 ) lines. Solid lines represent the results from the default design.
) lines. Solid lines represent the results from the default design.  denotes the expected number of truly useful biomarkers successfully validated based on the default design.
denotes the expected number of truly useful biomarkers successfully validated based on the default design.
To further compare the theoretical results with the numerical results, we next plot the values of 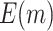 and
and 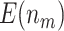 using the analytical formulas along with the corresponding values based on Monte-Carlo studies. Figure 2 shows that as the sample size increases, the numerical results based on Monte-Carlo simulations are closer to the corresponding theoretical values. For smaller sample sizes (
using the analytical formulas along with the corresponding values based on Monte-Carlo studies. Figure 2 shows that as the sample size increases, the numerical results based on Monte-Carlo simulations are closer to the corresponding theoretical values. For smaller sample sizes (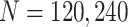 ), the finite sample performances of
), the finite sample performances of  (
(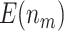 ) tend to be slightly smaller (larger) than the corresponding theoretical results. However, the pattern is similar for both the proposed design and the default design, so the relative order in performance of the two designs is preserved. When sample size increases to
) tend to be slightly smaller (larger) than the corresponding theoretical results. However, the pattern is similar for both the proposed design and the default design, so the relative order in performance of the two designs is preserved. When sample size increases to 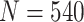 , the finite sample performance of each design is very close to the corresponding theoretical result. Therefore, with moderate or large sample size (
, the finite sample performance of each design is very close to the corresponding theoretical result. Therefore, with moderate or large sample size (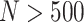 ), the developed analytical formula can provide an accurate estimation of the design performance. When sample size is small, the analytical formula can again be used to provide preliminary results for investigating performance of the proposed designs under various parameters, such as percent of truly useful markers and sample size, followed by Monte Carlo studies for more precise evaluation under a few scenarios of particular interest.
), the developed analytical formula can provide an accurate estimation of the design performance. When sample size is small, the analytical formula can again be used to provide preliminary results for investigating performance of the proposed designs under various parameters, such as percent of truly useful markers and sample size, followed by Monte Carlo studies for more precise evaluation under a few scenarios of particular interest.
Fig. 2.
Comparison of the expected numbers of biomarkers evaluated and truly useful biomarkers that are successfully validated, as obtained from analytical formulas, with those obtained from the simulation results, for case/control samples with a 1:1 ratio and a total sample size of 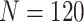 , 240, or 540. Results are shown for the default design and proposed two-stage validation design using different types of stopping rule (Stop
, 240, or 540. Results are shown for the default design and proposed two-stage validation design using different types of stopping rule (Stop  “Both” or “Null”) and shape parameter (
“Both” or “Null”) and shape parameter ( or 1). Solid black and dashed gray lines represent the corresponding values of
or 1). Solid black and dashed gray lines represent the corresponding values of 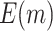 or
or  using the proposed and default strategies, respectively. Black circles and gray rectangles represent the corresponding values of
using the proposed and default strategies, respectively. Black circles and gray rectangles represent the corresponding values of 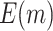 or
or  using the proposed and default strategies, respectively, based on 5000 Monte Carlo simulations.
using the proposed and default strategies, respectively, based on 5000 Monte Carlo simulations.
4. Pancreatic cancer reference set study
In this section, we demonstrate the application of the proposed two-stage validation strategy using a numerical setting constructed based on data from a multicenter EDRN pancreatic cancer reference study (Haab and others, 2015). This pancreatic cancer reference set study was developed to facilitate the validation of biomarkers for pancreatic cancer early detection. Blood samples were collected at five different institutions under a standard operating procedure, from 98 patients with pancreatic cancer, 62 patients with chronic pancreatitis, 31 patients with benign biliary obstruction, and 61 healthy individuals. For this analysis, we consider validation of biomarkers for separating patients with pancreatic cancer from healthy controls, i.e., 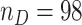 and
and  .
.
The reference set dataset includes measurements of a set of biomarkers from every study participant, including ATQ, TNC.FIII.C, AT, TFPI, CA199:CSLEX1, CSLEX1:CSLEX1, GDF15, MUC5AC, and ATATQ. We create a numerical setting that mimics the biomarker performance observed in this dataset by bootstrapping participant data with replacement stratified on case/control status and then randomly selecting one marker among the set as the incoming biomarker for validation each time. We assume there are  volume units of specimen from each participant, and the evaluation of a single biomarker requires one unit volume of specimen. For validation of each single biomarker, we perform a one-sided test for specificity at sensitivity
volume units of specimen from each participant, and the evaluation of a single biomarker requires one unit volume of specimen. For validation of each single biomarker, we perform a one-sided test for specificity at sensitivity  0.9. That is, we consider the null hypothesis
0.9. That is, we consider the null hypothesis 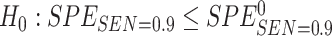 with type I error rate controlled at
with type I error rate controlled at  . Note that the methodology we developed for testing
. Note that the methodology we developed for testing  can be simply applied here by reversing case/control status and reverting the sign of the biomarker. The value of
can be simply applied here by reversing case/control status and reverting the sign of the biomarker. The value of  for the set of markers varies within
for the set of markers varies within 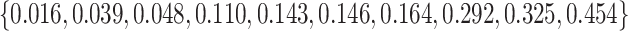 . We set the value of
. We set the value of 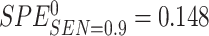 based on the performance of a standard CA19-9 assay. We consider the proposed design where a biomarker is first evaluated using specimens from half or one-third of participants, i.e.,
based on the performance of a standard CA19-9 assay. We consider the proposed design where a biomarker is first evaluated using specimens from half or one-third of participants, i.e., 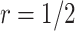 or
or 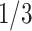 . Again, two different types of stopping rule (Stop
. Again, two different types of stopping rule (Stop  “Both” and Stop
“Both” and Stop  “Null”) and boundary shape (O’Brien–Fleming boundary and Pocock boundary) are adopted. Performance of designs is evaluated by examining the average number of biomarkers evaluated,
“Null”) and boundary shape (O’Brien–Fleming boundary and Pocock boundary) are adopted. Performance of designs is evaluated by examining the average number of biomarkers evaluated, 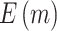 , and average number of truly useful biomarkers that are successfully validated,
, and average number of truly useful biomarkers that are successfully validated, 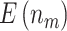 .
.
Table 2 shows the results for the validation of biomarkers using the proposed two-stage strategy and the default strategy. Obviously, adopting the proposed validation strategy allows us to evaluate more candidate biomarkers and eventually be able to successfully validate more truly useful biomarkers. Furthermore, it can be seen that using the Pocock boundary gives the best performance for either the design allowing early stopping for both futility and efficacy or the design allowing early stopping for futility only. These findings are consistent with that from the simulation studies.
Table 2.
Performance of the default design (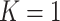 ) and the proposed two-stage validation design with rotation of group membership (
) and the proposed two-stage validation design with rotation of group membership (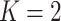 ) using different types of stopping rules (Stop
) using different types of stopping rules (Stop  “Both” or “Null”) and boundary shapes (
“Both” or “Null”) and boundary shapes (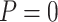 or 0.5), for the numerical setting constructed based on data from the pancreatic cancer reference set study. The table shows the average number of biomarkers evaluated
or 0.5), for the numerical setting constructed based on data from the pancreatic cancer reference set study. The table shows the average number of biomarkers evaluated  , the average number of truly useful biomarkers that are successfully validated
, the average number of truly useful biomarkers that are successfully validated  , and the corresponding standard error of
, and the corresponding standard error of 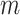 and
and 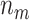 (in parentheses)
(in parentheses)

|

|
|||||
|---|---|---|---|---|---|---|

|
Performance | Stop  “Both” “Both” |
Stop  “Null” “Null” |
|||

|
|

|
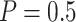
|
|||

|

|
77.77 (0.04) | 89.17 (0.04) | 73.61 (0.03) | 77.69 (0.04) | 50 |
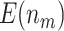
|
7.19 (0.02) | 7.38 (0.03) | 6.40 (0.02) | 6.67 (0.02) | 5.04 (0.02) | |
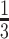
|

|
74.92 (0.05) | 100.71 (0.07) | 71.33 (0.04) | 86.69 (0.06) | 50 |
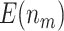
|
7.42 (0.02) | 9.76 (0.03) | 6.66 (0.02) | 7.60 (0.02) | 5.04 (0.02) | |
5. Concluding remarks
In this article, we considered design strategies for validating multiple candidate biomarkers using a reference set with limited specimen volume. In order to efficiently utilize the valuable specimens from the reference set, we proposed a new strategy for validating candidate biomarkers that incorporates a two-stage validation process with rotation of group membership, which allows the validation of some biomarkers using samples from only a subset of the study participants. Compared with the default strategy that validates every biomarker using samples from all study participants, the advantage of the proposed validation strategy is clearly demonstrated in our numerical studies. In particular, it allows the evaluation of more candidate biomarkers with the reference set samples, and eventually allows more truly useful biomarkers to be successfully validated. We adopted the sequential testing technique in the two-stage design and recommend the use of the Pocock boundary, which appears to perform best for either the design allowing early termination for futility and efficacy or the design allowing early termination for futility only. Moreover, we developed analytical formulas for calculating the expected numbers of candidate biomarkers that can be evaluated and the truly useful biomarkers that can be successfully validated. These analytical results can provide valuable guidance to researchers in practice for selecting validation strategies.
We, here, assume a simple setting where equal volumes of specimens are available from each participant. When this assumption does not hold, i.e., when volume of specimens varies among participants, the basic idea of our proposed design is the same while some technical details need to be modified. Instead of randomly partitioning the participants in the reference set into Q blocks, the participants should be grouped according to the available specimen volume. To begin with, we list the participants in descending order by the volume of specimens, and then partition the ordered participants into Q blocks to ensure rough balance in specimen volumes across blocks. One of blocks with the maximum average amount of specimens is randomly selected and treated as group 1, then the rest of blocks are treated as group 2. The sequential testing procedure is the same as that for the simple setting. Each time when a new biomarker enters the validation process, we randomly draw one block with the maximum average amount of specimens as group 1 and then perform the test again. This procedure can be repeated until the number of participants who have adequate specimen remaining is low.
For the validation of biomarker, in this article, we considered a hypothesis test with respect to the points on the ROC curve. However, the proposed method is generally applicable to other classification measures, such as the AUC or partial AUC. Moreover, while we here focused on the group sequential design with two analyses for ease of implementation and given the popularity of two-stage designs in sequential trials, our proposed strategy can be extended to designs with multiple interim analyses.
In this article, our main interest is to provide a sample source (a common reference set) to allow different labs to have an early phase validation of their candidate biomarker performance. Multiplicity adjustment is not deemed essential here and is not always feasible: candidate biomarkers are coming in one by one and validation results are usually reported to individual labs during the process before all samples are used up. There are scenarios however when multiplicity adjustment could be of interest. For example, at the end of the study when all samples have been used up, there might be plans for follow-up studies and interests to have a simultaneous review of all biomarkers, in order to identify a small subset to be validated in the next step. Multiplicity adjustment can be easily accommodated in our proposed design to control for criteria such as the false discovery rate or family-wise error rate. Instead of declaring significance of individual biomarkers based on their nominal p-values, one can apply p-value adjustment methods to control for the desired error rate among all biomarkers that have been evaluated and make decisions based on the adjusted p-value. To illustrate how this works, we have applied the false discovery rate adjustment method proposed by Benjamini and Hochberg (1995) to adjust the nominal p-value of individual tests to control the false discovery rate at 0.05 level. The results are reported in Table 3 in Appendix C of the supplementary material available at Biostatistics online. The proposed two-stage strategy still performs better than the default design; it successfully validated more truly useful biomarkers, especially under the scenario where majority of biomarkers are not actually useful.
Finally, in practice one might have some established biomarker(s) for detecting a certain disease, and the goal is to evaluate individual markers for combining with the established biomarker(s) to develop a new classification panel. For this problem, one can first measure the established biomarkers from samples in all participants in the reference set and then apply the proposed design to the rest of the specimens. This is a topic for future research.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
6. Software
The R code is available at https://github.com/WangLu88/ValidationDesign.git.
Funding
This work was supported by the U.S. National Institutes of Health under awards R01GM106177 and U24CA086368.
References
- Benjamini, Y. and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society: Series B (Methodological) 57, 289–300. [Google Scholar]
- Emerson, S. S. and Fleming, T. R. (1989). Symmetric group sequential test designs. Biometrics 45, 905–923. [PubMed] [Google Scholar]
- Feng, Z., Kagan, J., Pepe, M., Thornquist, M., Rinaudo, J. A., Dahlgren, J., Krueger, K., Zheng, Y., Patriotis, C., Huang, Y. and others. (2013). The early detection research network’s specimen reference sets: paving the way for rapid evaluation of potential biomarkers. Clinical Chemistry 59, 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haab, B. B., Huang, Y., Balasenthil, S., Partyka, K., Tang, H., Anderson, M., Allen, P., Sasson, A., Zeh, H., Kaul, K. and others. (2015). Definitive characterization of ca 19-9 in resectable pancreatic cancer using a reference set of serum and plasma specimens. PLoS One 10, e0139049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jennison, C. and Turnbull, B. W. (1999). Group Sequential Methods with Applications to Clinical Trials. Boca Raton, FL: Chapman and Hall/CRC. [Google Scholar]
- Koopmeiners, J. S. and Feng, Z. (2011). Asymptotic properties of the sequential empirical roc, ppv and npv curves under case-control sampling. Annals of Statistics 39, 3234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koopmeiners, J. S., Feng, Z. and Pepe, M. S. (2012). Conditional estimation after a two-stage diagnostic biomarker study that allows early termination for futility. Statistics in Medicine 31, 420–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Brien, P. C. and Fleming, T. R. (1979). A multiple testing procedure for clinical trials. Biometrics 35, 549–556. [PubMed] [Google Scholar]
- Pepe, M. S. (2003). The Statistical Evaluation of Medical Tests for Classification and Prediction. Oxford, UK: Oxford University Press. [Google Scholar]
- Pepe, M. S., Etzioni, R., Feng, Z., Potter, J. D., Thompson, M. L., Thornquist, M., Winget, M. and Yasui, Y. (2001). Phases of biomarker development for early detection of cancer. Journal of the National Cancer Institute 93, 1054–1061. [DOI] [PubMed] [Google Scholar]
- Pepe, M. S., Feng, Z., Longton, G. and Koopmeiners, J. (2009). Conditional estimation of sensitivity and specificity from a phase 2 biomarker study allowing early termination for futility. Statistics in Medicine 28, 762–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pocock, S. J. (1977). Group sequential methods in the design and analysis of clinical trials. Biometrika 64, 191–199. [Google Scholar]
- Zhou, X. H., McClish, D. K. and Obuchowski, N. A. (2009). Statistical Methods in Diagnostic Medicine, Volume 569. John Wiley & Sons. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.