Different computations underlie overt presaccadic and covert spatial attention

Abstract

Perception and action are tightly coupled: visual responses at the saccade target are enhanced right before saccade onset. This phenomenon, presaccadic attention, is a form of overt attention—deployment of visual attention with concurrent eye movements. Presaccadic attention is well-documented, but its underlying computational process remains unknown. This is in stark contrast to covert attention—deployment of visual attention without concurrent eye movements—for which the computational processes are well characterized by a normalization model. Here, a series of psychophysical experiments reveal that presaccadic attention modulates visual performance only via response gain changes. A response gain change was observed even when attention field size increased, violating the predictions of a normalization model of attention. Our empirical results and model comparisons reveal that the perceptual modulations by overt presaccadic and covert spatial attention are mediated through different computations.

Humans and primates make large and rapid eye movements, saccades, multiple times per second to explore visual scenes. Already before saccade onset, visual performance is improved (for example, d′ in discrimination tasks)^1–8 and featural representations are modulated^9–11 at the saccade target location. These effects, due to presaccadic attention, reveal a strong coupling between perception and action.

Presaccadic attention can be considered a type of overt attention—deployment of visual attention with concurrent eye movements. Even though behavioural (e.g., refs.^2,5,6,9) and neural correlates^12–16 of presaccadic attention have been widely studied, their underlying computational processes remain unknown. This is in stark contrast with the research of covert attention—deployment of attention without concurrent eye movements—for which not only the behavioural^17,18 and neural correlates^15,19,20, but also the underlying computations have been extensively investigated^21–25. To address this knowledge gap, here we ask: can a unified computational framework account for the perceptual modulations by both overt presaccadic and covert spatial attention?

Characterizing how attention modulates the visual system’s input-and-output functions—here specifically defined as visual performance as a function of stimulus contrast—is an essential step towards understanding the computations underlying attentional modulations. Contrast response functions have often been used to investigate attentional modulations. Several neurophysiological^26–30, psychophysical^31–42 and human neuroimaging^43–47 studies have investigated how covert spatial attention and feature-based attention affect contrast response functions. Overall, the contrast response functions measured under various forms of covert attention can be explained by the Reynolds–Heeger normalization model of attention (NMA)²¹; for other normalization models of attention, see refs.^22,24,48,49.

In this NMA, the attentional modulation is modelled as attentional gain factors that increase or decrease the input drive of visual neurons. The modulation by the attentional gain factors precedes normalization, and thus this modulation affects both the excitatory inputs and the suppressive inputs (the normalization pool) of visual neurons. This principle explains attentional modulations in many neurophysiological studies (e.g., refs.^21,50–52).

Key predictions of this NMA regarding how covert attention modulates contrast response functions have been confirmed by empirical psychophysical findings: spatial covert attention can modulate neural responses by horizontally shifting the contrast response function (contrast gain, quantified as a change of semisaturation contrast; Fig. 1a). Spatial covert attention can increase neural responses by a multiplicative gain factor, improving behavioural performance by vertically scaling the psychometric function (response gain, quantified by a change of asymptotic response; Fig. 1b). The NMA and empirical studies have shown that spatial covert attention can induce a response gain change, a contrast gain change or a mix of both, depending on the attention field size relative to the stimulus size (Fig. 1)^21,40.

Fig. 1 |. Different forms of attentional modulation on contrast response functions.

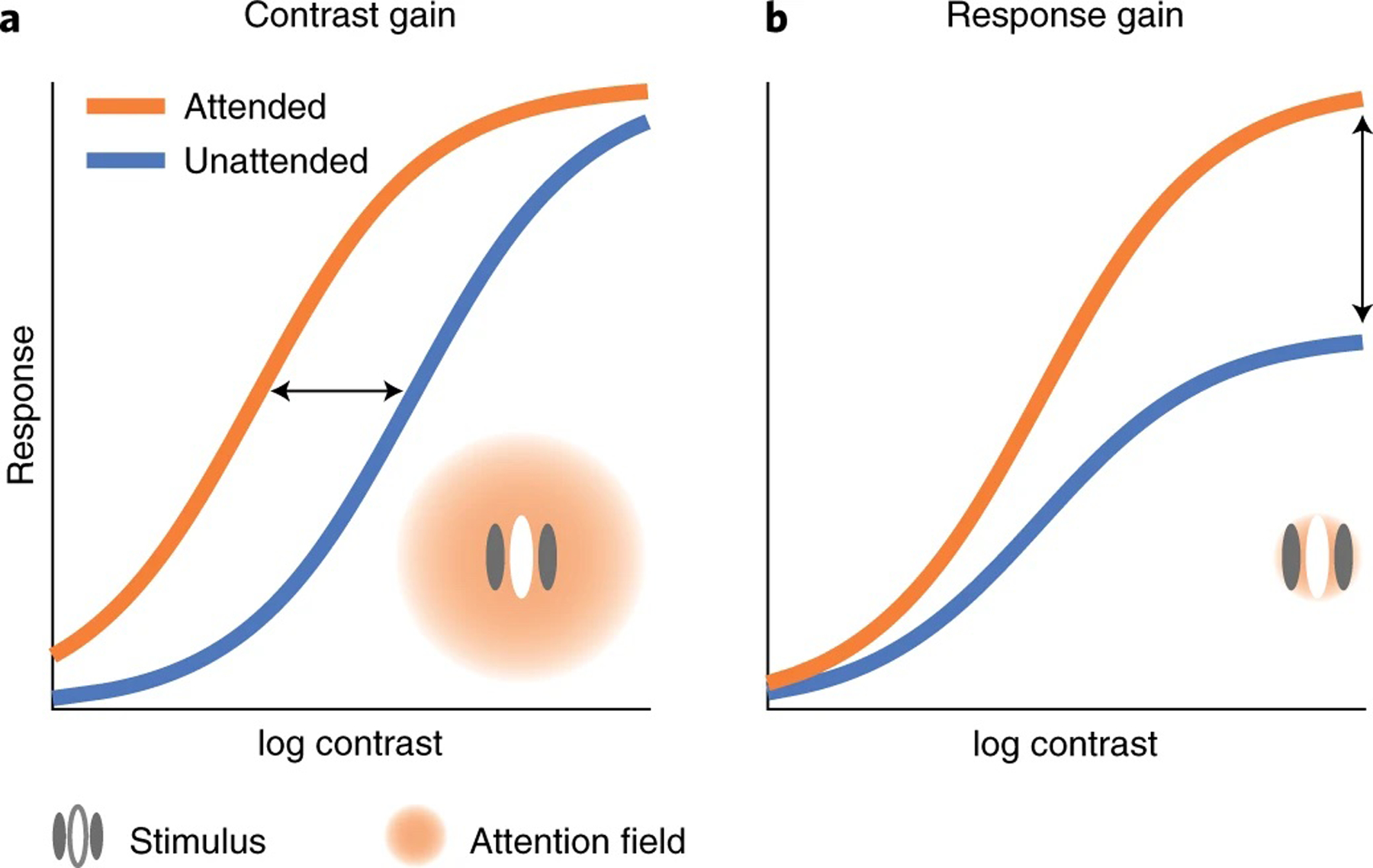
a, Contrast gain change: attention horizontally shifts the response function as if attention scales the input contrast. b, Response gain change: attention scales neural response by a multiplicative gain factor, modulating the asymptotic response of the neuron. The NMA²¹ predicts that attention exhibits different modulations depending on the relative size of the attention field and the stimulus. A large attention field size (relative to the stimulus size) leads to contrast gain changes (a) and a small attention field size leads to response gain changes (b).

To elucidate the computation underlying presaccadic attention, here we characterize its effect on the contrast response function in a series of psychophysical experiments. In experiment 1, we investigated the effect of presaccadic attention when only one stimulus was presented at the saccade target location. In experiment 2, we assessed the effect of presaccadic attention at both the saccade target and its mirrored location in the opposite hemifield, and we compared these effects with those of covert endogenous and covert exogenous attention with the same stimulus parameters and task difficulty. In experiment 3, we investigated whether the effect of presaccadic attention depends on the location uncertainty of the target stimulus. In all cases, the effects of presaccadic attention were compared to a neutral baseline in which no saccadic eye movements were executed.

To preview our results, we found that presaccadic attention only generated a response gain change, whereas covert attention generated a mix of response gain and contrast gain changes. The response gain change generated by presaccadic attention was robust even when we encouraged observers to use a larger attentional field by increasing the location uncertainty of the target stimulus. We found that a model in which attention modulates the neural response by a gain factor multiplicatively after normalization outperformed the NMA. Conversely, the NMA, in which attention modulates the neural response by a gain factor multiplicatively before normalization, best explains the perceptual modulations by covert attention. These results reveal that the gain modulations by presaccadic attention are mediated through neural computations that differ from those proposed²¹ and empirically confirmed^21,40 for covert attention.

Results

Experiment 1.

We characterized the modulation of presaccadic attention on the contrast response functions when a stimulus was presented at the saccade target location. Observers were asked to discriminate the target orientation, presented 8° left or right of the fixation. To map out the psychometric function, the contrast of the target varied on a trial-by-trial basis. In the neutral condition, a neutral precue instructed observers to maintain fixation at the screen centre throughout the trial. In the saccade condition, a saccadic precue instructed observers to saccade to the upcoming target location (Fig. 2a), in which the target was presented shortly after the cue onset. Observers had to report the target orientation, left or right of vertical. Observers’ gaze positions were monitored throughout the trials.

Fig. 2 |. Experiment 1.

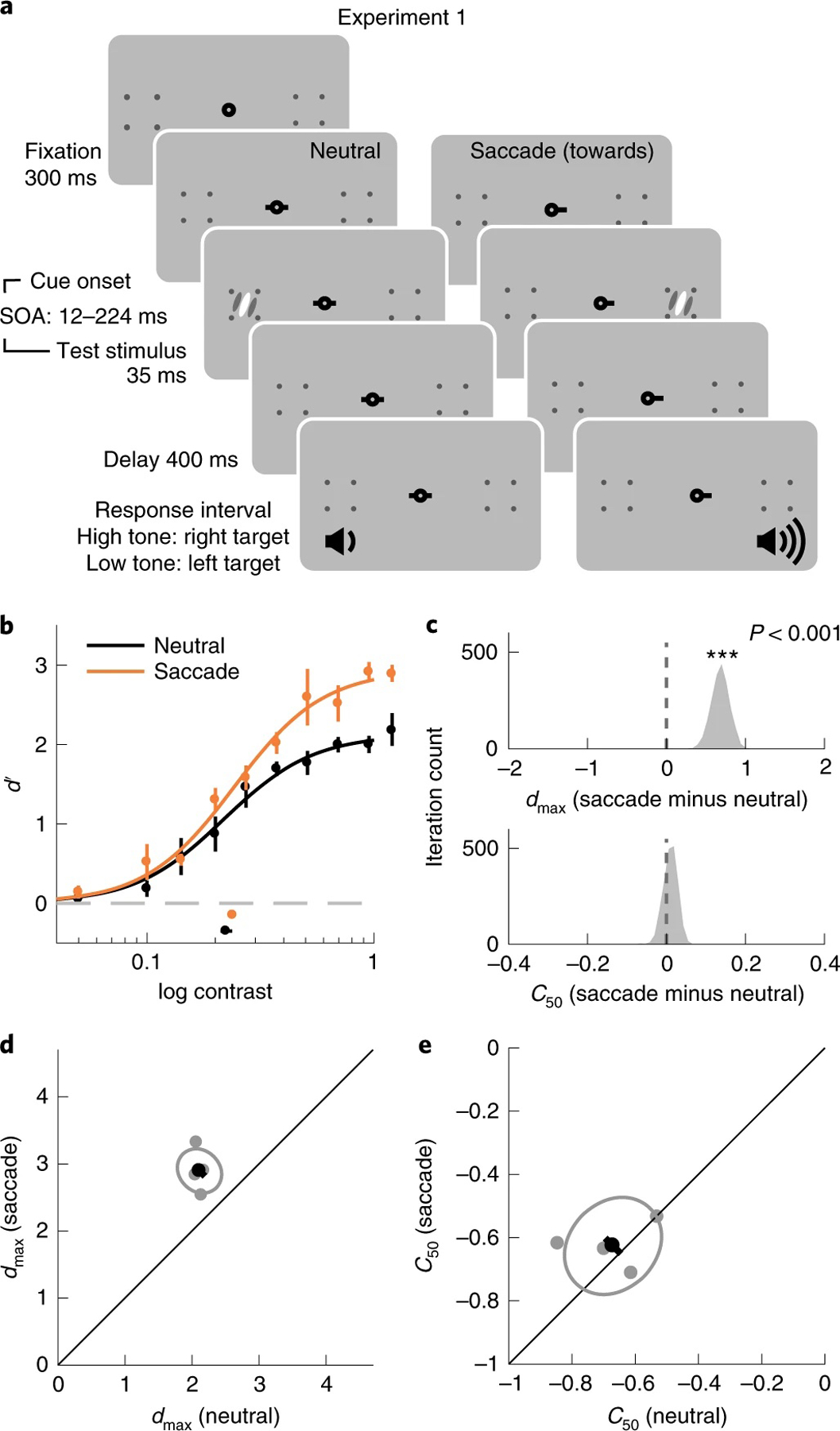
a, Procedure. Each trial started with a fixation period. A neutral precue or a saccadic precue directed observers to either maintain fixation or make a saccade towards the upcoming target location. The target appeared shortly after the cue onset. Observers were asked to report the orientation of the target after hearing an auditory response cue. Two tones in different frequencies were used to inform observers of the target location to eliminate the uncertainty regarding the target location. b, Group-averaged psychometric functions (d′ versus contrast). d_max and C₅₀ of the group-averaged psychometric functions are plotted at the right and the bottom of the figure. The error bars represent 95% bootstrapped confidence interval. c, The bootstrapped distribution of the difference of d_max (top) and the difference of C₅₀ (bottom) between the neutral and saccade conditions. Asterisks denote that the distribution is significantly different from zero. d, Grey dots, best-fitted d_max of individual observers; grey ellipse, the ellipse with the major axes oriented towards the difference and the sum of the d_max across two conditions. The difference (or sum) of d_max is first computed for individual observers, and the major axis of the ellipse represents ±1 s.d. of the difference (or sum); the black dot shows the group-averaged d_max and the error bar represents the standard deviation of the bootstrapped distribution of the difference between neutral and saccade conditions. e, C₅₀ illustrated in the same format as in d.

Trials in the saccade condition were sorted offline on the basis of the relative timing between saccade onset and stimulus offset (Supplementary Fig. 1). We compared the performance in the neutral condition to the performance in a presaccadic time window (75 to 0 ms before saccade onset)^6,9,10,53. We fitted performance (d′) as a function of target contrast with the Naka–Rushton function (Methods). Presaccadic attention enhanced performance at the saccade target through an increment of d_max, the asymptotic performance level (P < 0.001, 95% bootstrapped confidence interval (CI) 0.49, 0.93; d = 6.32; from here on we report P values and 95% confidence interval obtained by bootstrapping). C₅₀, the semisaturation constant, was not significantly different between the two conditions (P = 0.38, CI −0.02, 0.04; d = 0.86) (Fig. 2b–e). These results are consistent with a response gain change.

Experiment 2.

We investigated the effect of presaccadic attention at both the saccade target location and its mirrored location in the opposite hemifield. Moreover, we compared the effects of presaccadic attention and covert spatial attention. Observers performed three different tasks in separate sessions: a presaccadic attention, a covert endogenous (voluntary) attention and a covert exogenous (involuntary) attention task. We compared these three attention types with the same stimulus parameters and task difficulty, and with their optimal cue location and cue timing to maximize their effects (Methods and Fig. 3).

Fig. 3 |. Experiment 2.

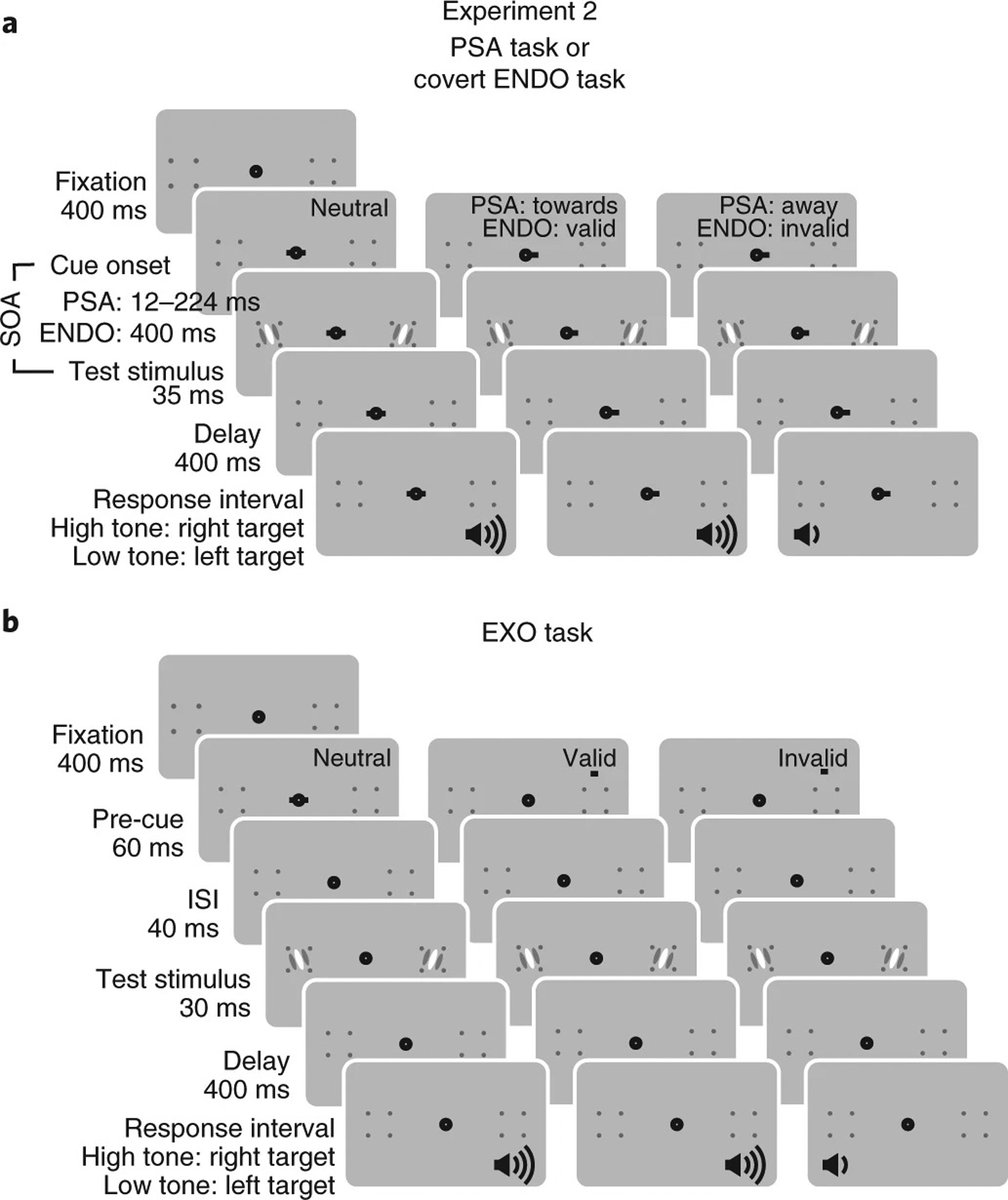
Observers were tested with three tasks in different sessions: the presaccadic attention (PSA) task, covert endogenous attention (ENDO) task and covert exogenous attention (EXO) task. a, Here we illustrate the procedures of the PSA task and the ENDO task together as they shared a similar stimulus sequence. The cue-to-target SOA was shorter in the PSA task than in the ENDO task. Two stimuli, a target and a distractor, were presented simultaneously. In the PSA task, the precue instructed observers to saccade to the cued location. In the saccade towards condition, the precue matched the target location, whereas in the saccade away condition, the precue indicated the distractor. Saccade towards and saccade away conditions were interleaved with equal probability; therefore, the saccade cue was uninformative regarding the target location. In the ENDO task, observers maintained fixation throughout the trials and the precue instructed observers to covertly pay attention to the cued location. The valid and invalid trials were interleaved within the blocks with a 70 and 30% probability, respectively; thus, the precue was informative regarding the target location. At the end of a trial, observers reported the orientation of the target probed by the auditory response cue (high tone, target at the right; low tone, target at the left). b, In the EXO task, the precue was a brief flash. In the neutral condition, the precue was presented at the fixation. In the valid condition, the precue was flashed above the target whereas in the invalid condition, the precue was flashed above the distractor. The valid and the invalid trials were interleaved with equal probability, hence, the precue was uninformative regarding the target location. See details in the Methods.

For the presaccadic attention task, two stimuli (a target and a distractor), one in the left and one in the right visual field, were presented simultaneously in each trial (Fig. 3a). In the saccade condition, a saccadic precue instructed observers to saccade either towards the target (towards condition) or away from the target, to the distractor (away condition) with equal probability. Observers had to report the orientation of the target indicated by an auditory response cue after stimulus offset. This design allowed us to investigate the effects of presaccadic attention without conflating saccade direction with cue validity as the saccadic precue did not convey information regarding the stimulus relevance, that is, which stimulus was the target to be discriminated.

In the endogenous attention task, covert attention was manipulated by an informative (70% validity) central precue. The cue indicated the target location in the valid trials and the distractor in the invalid trials (Fig. 3a), and observers were instructed to pay attention to the cued location. In the exogenous attention task, an uninformative peripheral precue was flashed above the target or the distractor with equal probability, and observers were told the cue was uninformative (Fig. 3b). In both tasks, observers maintained fixation at the screen centre throughout each trial.

We observed both a benefit and a cost of presaccadic attention. Compared to the neutral condition, when averaging d′ across contrast levels, performance (d′) increased in the towards condition (P < 0.001, CI 0.67, 0.97, d = 10.92) and decreased in the away condition (P < 0.001, CI −0.53, −0.25, d = 5.60). Comparing the fit of the Naka–Rushton functions between the towards and the away conditions, we observed a significant change of d_max (P = 0.004, CI 1.31, 2.61, d = 6.34) without a significant change of C₅₀ (P = 0.16, CI −0.38, 0.06, d = 1.12) (Fig. 4a–d).

Fig. 4 |. Experiment 2.

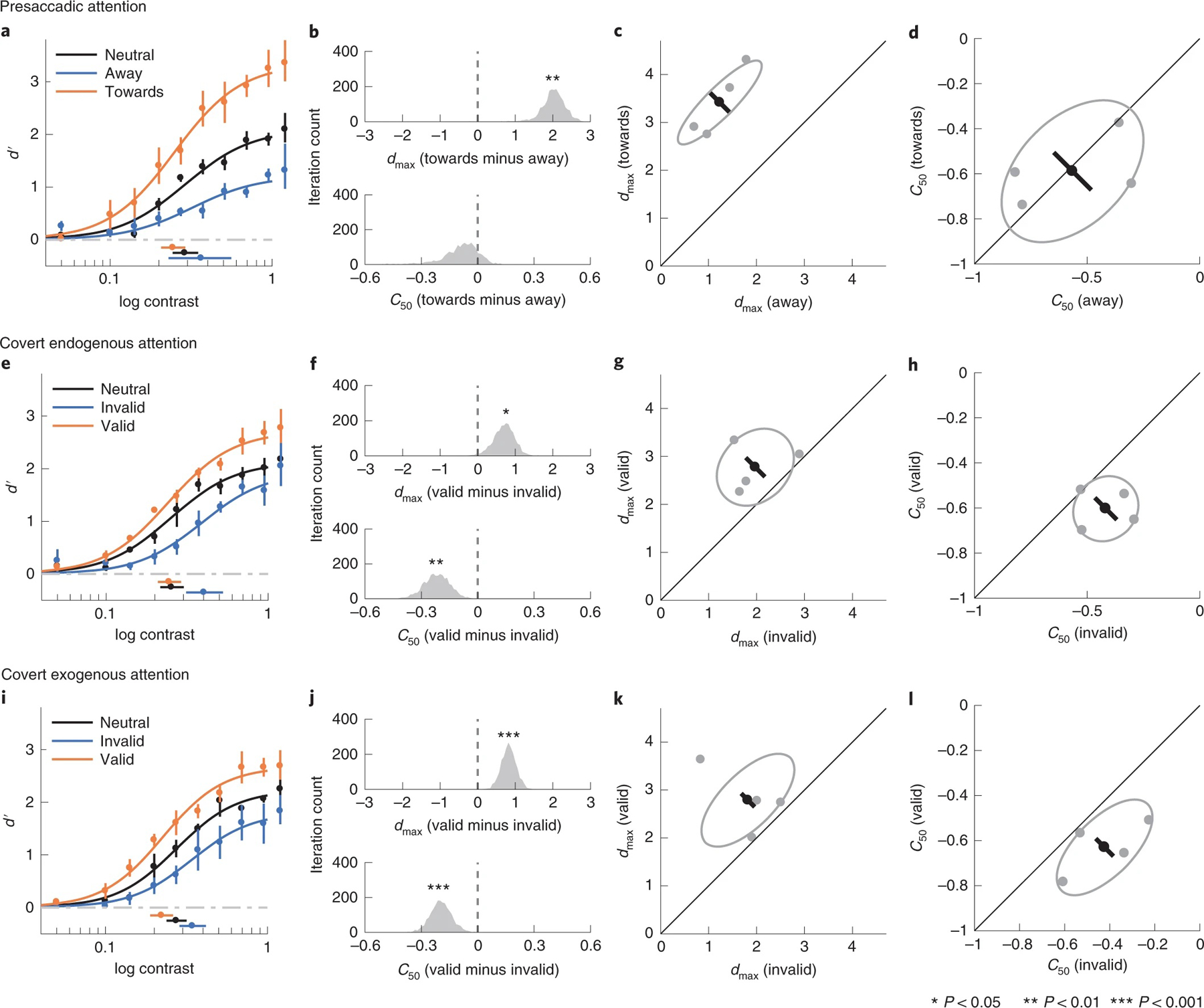
a–d, Presaccadic condition. a, Group-averaged psychometric functions (d′ versus contrast). d_max and C₅₀ of the group-averaged psychometric functions are plotted to the right and bottom of the figure. The error bars represent the 95% bootstrapped confidence interval. b, The bootstrapped distribution of the difference of d_max (top) and the difference of C₅₀ (bottom) between the towards and away conditions. Asterisks denote that the distribution is significantly different from zero. c, Grey dots, best-fitted d_max of individual observers; grey ellipse, the ellipse with the major axes oriented towards the difference and the sum of the d_max across two conditions. The difference (or sum) of d_max is first computed for individual observers; the major axis of the ellipse represents ±1 s.d. of the difference (or sum). The black dot shows the group-averaged d_max and the error bar represents the standard deviation of the bootstrapped distribution of the difference between the towards and away conditions. d, C₅₀ illustrated in the same format as in c. e–h, Covert endogenous attention condition; corresponding to a–d. i–l, Covert exogenous attention condition; corresponding to a–d and e–h.

Pooling across stimulus contrast levels, covert endogenous attention, similar to presaccadic attention, also increased performance in the valid condition (P < 0.001, CI 0.22, 0.48, d = 5.30) and decreased performance in the invalid condition (P < 0.001, CI −0.50, −0.19, d = 4.48). Comparing the fits of the Naka–Rushton function between the valid and the invalid conditions, we observed changes in both d_max (P = 0.02, CI 0.11, 1.24, d = 2.56) and C₅₀ (P = 0.006, CI −0.30, −0.05, d = 2.50; Fig. 4e–h).

The effects of covert exogenous attention and covert endogenous attention were similar. Compared to the neutral condition, performance was higher in the valid condition (P < 0.001, CI 0.30, 0.58, d = 6.08) and lower in the invalid condition (P < 0.001, CI −0.49, −0.21, d = 5.18) than the neutral condition. Both d_max (P < 0.001, CI 0.46, 1.25, d = 4.32) and C₅₀ (P < 0.001, CI −0.21, −0.05, d = 3.09) showed significant changes when the valid and invalid conditions were compared (Fig. 4i–l).

Even when asked to maintain a stable fixation, humans make microsaccades, involuntary small fixational eye movements. To explore if microsaccades contributed to the covert attentional effects, we removed the trials in which microsaccades occurred during the critical interval (from the cue onset to the test stimuli onset): about a quarter of the trials (28%) in the endogenous attention condition and only 3% in the exogenous attention condition. Again, both endogenous attention and exogenous attention exhibited a mixture of a contrast gain change and a response gain change (Supplementary Fig. 2). It is not surprising that we found the same results given that a low percentage of trials contained microsaccades.

Could presaccadic attention’s predominant modulations on d_max be due to a minor difference in its experimental protocol compared to that for covert attention? For the presaccadic attention condition, trials with failed saccades (5.2% for the towards condition and 4.9% for the away condition) were aborted and repeated at the end of each block (Methods). Thus, we may have prevented the inclusion of some lapsed trials in the dataset, in which the participants ‘zoned out’. In contrast, there were no behavioural indices (except blinks; see Methods) that allow us to exclude lapsed trials in the covert attention conditions. To rule out the possibility that the absence of lapse trials in the presaccadic condition contributed to the difference with covert attention, we treated the trials in which the participants failed to saccade correctly as the lapsed trials. For these trials, we simulated lapsed responses by assigning random button presses, instead of using the participants’ responses when these trials were repeated at the end of each block. Because the percentages of these trials were similarly low in both the towards and the away conditions, they had little impact on the psychometric functions, hence leaving d_max and C₅₀ practically unchanged. Again, presaccadic attention only modulated d_max (P = 0.002, CI 1.22, 2.53, d = 5.63), without significantly changing C₅₀ (P = 0.18, CI −0.42 0.06, d = 1.09) (Supplementary Fig. 3).

In sum, we found that presaccadic and covert attention modulated performance through different gain changes. Covert attention generated a mix of response gain and contrast gain changes, regardless of the presence or absence of microsaccades, whereas presaccadic attention only generated a response gain change, with or without simulated lapsed trials.

Experiment 3.

Both the NMA²¹ and empirical results^39,40 have demonstrated that the modulations generated by both exogenous and endogenous covert attention are affected by the attention field size relative to the stimulus size. For spatial covert attention, when the attention field size is large compared to the stimulus, attention generates a contrast gain change, and when the attention field size is small relative to the stimulus, attention generates a response gain change (Fig. 1). Thus, the finding that presaccadic attention generated a pure response gain change in experiment 2 might reflect that attention was deployed locally at the saccade target location. The deployment of covert spatial attention might have been less precise, indicating a larger attention field size than the one during presaccadic attention.

Were the effect of presaccadic attention to follow the predictions of the NMA, contrast gain changes would emerge with an enlarged attentional field size. To test this prediction, following the protocols in covert attention studies^40,54, we increased stimulus location uncertainty. This manipulation encourages observers to pay attention to a larger spatial area, thus increasing the attention field size. Sometimes, while preparing a saccade to a particular location, we may want to monitor a larger area in case the object of interest is nearby, but not certainly at, the saccade location.

We considered the presaccadic attention task in experiment 2 as a low-uncertainty condition. In experiment 3, we measured the effect of presaccadic attention in medium- and high- uncertainty conditions, in which the target and the distractor were each randomly presented in one of several predesignated locations in each trial (Fig. 5a,b). We asked observers to still saccade to the centre of the placeholder. According to the NMA, the effect of presaccadic attention should be transformed from the observed pure response gain change (in experiments 1 and 2) to a contrast gain change (or a mix of both) in the medium- and high- uncertainty conditions.

Fig. 5 |. Experiment 3.

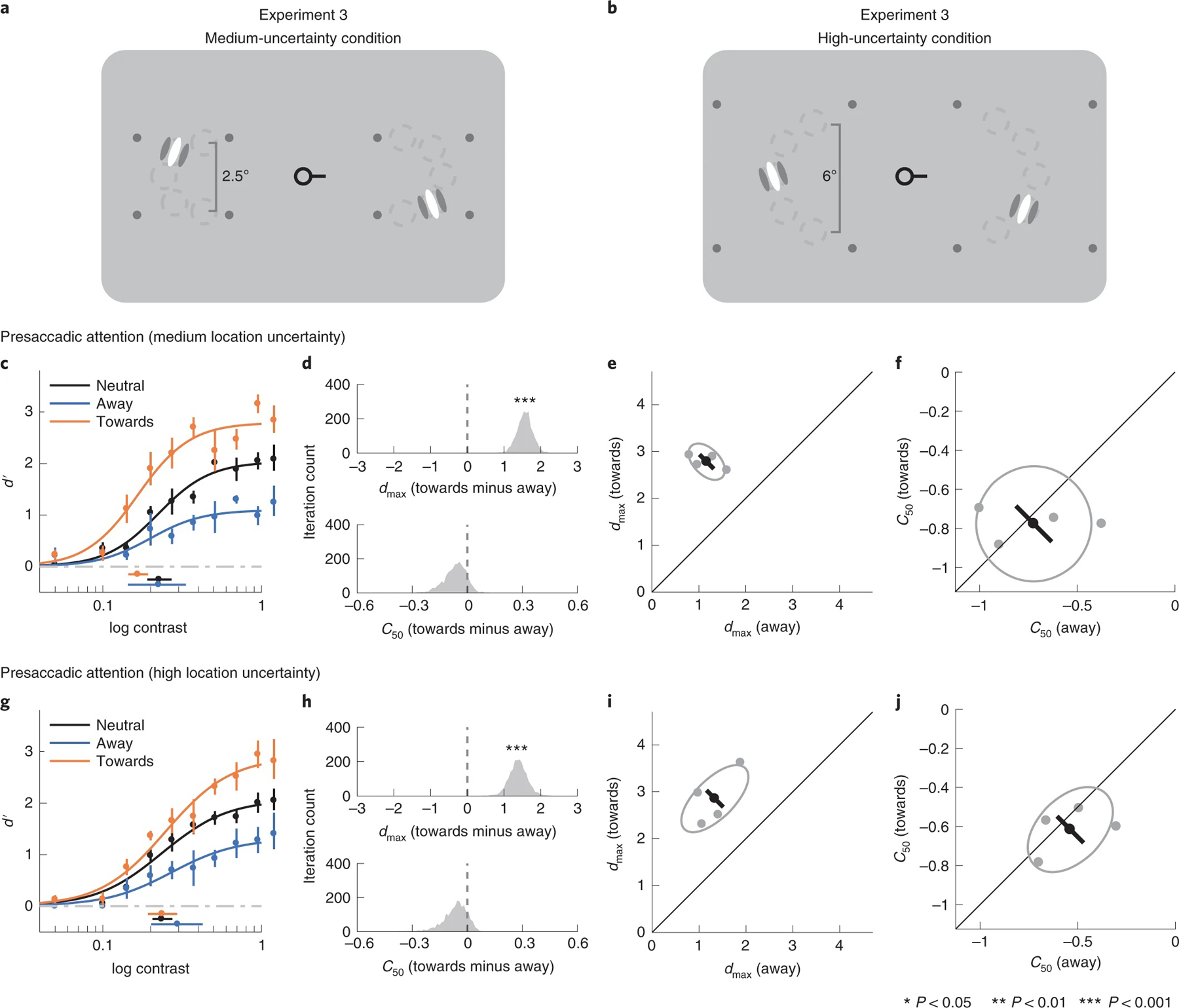
a,b, The procedure of experiment 3 is the same as the presaccadic attention task in experiment 2, except that the test stimuli were presented with location uncertainty. Stimuli appeared at one of five predefined iso-eccentric locations. Stimulus locations were randomly and independently selected in the left and right placeholder. The dashed circles (not displayed during the experiments) indicate the possible stimulus locations (five in each placeholder; the figures here are for the purpose of illustration only. See Methods for the details of the stimulus parameters). c–f, Medium-uncertainty condition. c, Group-averaged psychometric functions (d′ versus contrast). d_max and C₅₀ of the group-averaged psychometric functions are plotted at the right and bottom of the figure. The error bars represent 95% bootstrapped confidence interval. d, The bootstrapped distribution of the difference of d_max (top) and the difference of C₅₀ (bottom) between the towards and away conditions. Distributions significantly different from zero are denoted with asterisks. e, Grey dots, best-fitted d_max of individual observers; grey ellipse, the ellipse with major axes oriented towards the difference and the sum of the d_max across two conditions. The difference (or sum) of d_max is first computed for individual observers, and the major axis of the ellipse represents ±1 s.d. of the difference (or sum). The black dot shows the group-averaged d_max and the error bar represents the standard deviation of the bootstrapped distribution of the difference between the towards and away conditions. f, C₅₀ illustrated in the same format as in e. g–j, High-uncertainty condition, corresponding to c–f.

Presaccadic attention exhibited response gain changes even when location uncertainty increased. In the medium-uncertainty condition, d_max differed significantly between the towards and the away conditions (P < 0.001, CI 1.16, 2.00, d = 7.38) but the corresponding C₅₀ did not (P = 0.29, CI −0.19, 0.04, d = 1.00) (Fig. 5c–f). Likewise, in the high-uncertainty condition, there were significant changes in d_max (P < 0.001, CI 0.91, 1.91, d = 5.57), but not in C₅₀ (P = 0.36, CI −0.23, 0.04, d = 0.86), between the towards and away conditions (Fig. 5g–j).

We conducted simulations to compare the predictions of the NMA with the data in experiments 2 and 3. Simulations are based on Reynolds and Heeger’s NMA²¹ and the stimulus parameters of our experiments. To simulate the effect of location uncertainty, we scaled the width of the attention field size from 0.5, 2.5 to 6° for the low-, medium- and high-uncertainty conditions, respectively (Supplementary Fig. 4). The model predicted that attentional modulations on neural responses shift from a response gain change to a contrast gain change with increasing attention field size (indexed by location uncertainty) (Supplementary Fig. 4). Note that the simulation here is only to ensure that given the assumptions of the NMA, with our stimuli and attention field size, which increases with location uncertainty, we should observe a shift from response gain change to contrast gain change. However, we did not observe such a shift.

Presaccadic attention field size.

Is it possible that observers’ attention field sizes did not increase with location uncertainty as we expected? For example, observers’ attention fields might have remained small and at the centre of the placeholder. Were this the case, the mismatch between the predictions of the NMA and the empirical results would be due to the ineffectiveness of our experimental manipulations.

To investigate this possibility, we binned the trials in the high-uncertainty condition on the basis of the target location: the two outmost locations, two intermediate locations and the central location (Fig. 6a,e,i). We found significant changes in d_max between the towards and the away conditions at all target locations (outmost locations P = 0.03, CI 0.01, 2.19, d = 3.00; intermediate locations P = 0.02, CI 0.25, 1.65, d = 2.97; central location P = 0.004, CI 0.64, 1.82, d = 4.33). We did not observe significant C₅₀ shifts at any of the locations (outmost locations P = 0.78, CI −0.47, 0.17, d = 0.06; intermediate locations P = 0.10, CI −0.37, 0.02, d = 1.40; central location P = 0.45, CI −0.16, 0.05, d = 0.46). In addition, there was no significant difference in the magnitude of response gain changes (quantified as the d_max in the towards condition minus the d_max in the away condition) across the three bins (central versus outmost P = 0.75, CI −1.23, 1.26, d = 0.24; central versus intermediate P = 0.52, CI −0.61, 1.19, d = 0.61; outmost versus intermediate P = 0.40, CI −0.96, 1.46, d = 0.70). We further conducted a Bayesian one-way repeated-measures analysis of variance (ANOVA) using target location (outmost, intermediate and central locations) as the independent variable and the magnitude of response gain changes as the dependent variable. The results show weak support for a null model assuming no effect of target location on response gain change (BF₁₀ = 0.85). Moreover, the distributions of saccade landing points were almost constant regardless of the location at which the target was presented (Supplementary Fig. 5). These results are in line with the assumptions in the simulations that in the high-uncertainty condition, the size of the attention field extends beyond the central target location.

Fig. 6 |. Performance binned by target location in high-uncertainty condition.

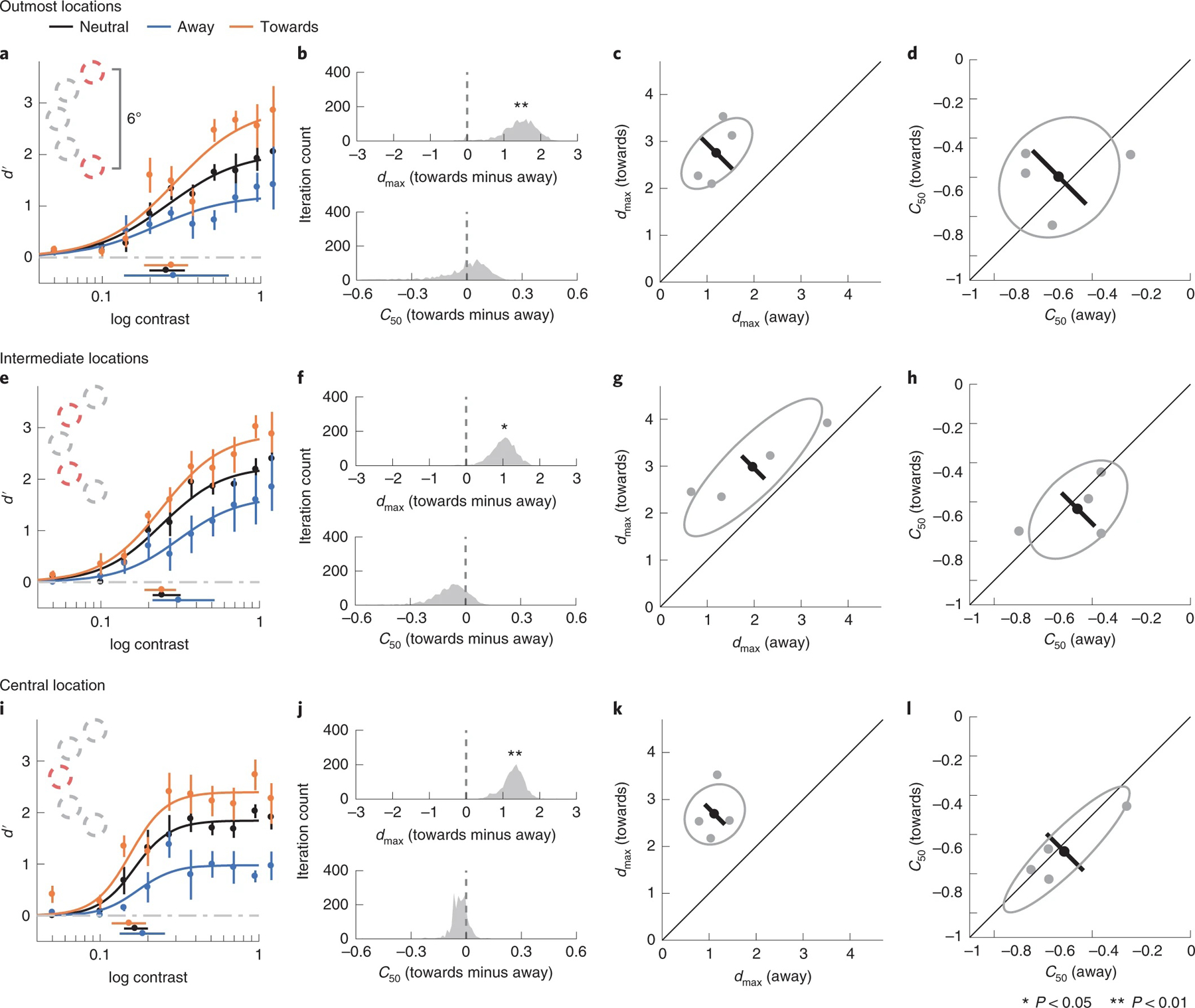
a–d, Outmost locations. a, Group-averaged psychometric functions (d′ versus contrast). d_max and C₅₀ of the group-averaged psychometric functions are plotted at the right and the bottom of the figure. The error bars represent 95% bootstrapped confidence interval. b, The bootstrapped distribution of the difference of d_max (top) and the difference of C₅₀ (bottom) between the towards and away conditions. Distributions significantly different from zero are denoted with asterisks. c, Grey dots, best-fitted d_max of individual observers; grey ellipse, the ellipse with major axes oriented towards the difference and the sum of the d_max across two conditions. The difference (or sum) of d_max is first computed for individual observers, and the major axis of the ellipse represents ±1 s.d. of the difference (or sum). The black dot shows the group-averaged d_max and the error bar represents the standard deviation of the bootstrapped distribution of the difference between towards and away conditions. d, C₅₀ illustrated in the same format as in c. e–h, Intermediate locations, corresponding to a–d. i–l, Central location, corresponding to a–d and e–h.

So far, we found that increasing location uncertainty did not affect the response gain changes generated by presaccadic attention, and that the effect of presaccadic attention was robust and similar across different target locations. We further explored whether and how location uncertainty affected participants’ oculomotor behaviours. Analysing the trials in which the target was presented at the central location (for example, Fig. 6i), we found that both saccade landing points (P < 0.001, CI −1.95, −0.55, d = 3.43) and saccade reaction times (the interval between saccadic cue onset and saccade onset; P < 0.001, CI −41.73, −7.45, d = 2.37) were significantly less variable in the low- than the high-uncertainty condition (Supplementary Fig. 6). These results also confirm that the uncertainty manipulation was successful.

Model comparisons.

The absence of a size-dependent gain change by presaccadic attention in our experiments indicates that the modulations by presaccadic attention deviated from the critical predictions²¹ and empirical tests^39,40 of the NMA. To directly test the NMA against alternative models, we built and compared various computational models. We computed theoretical neural response and used signal detection theory to link population neural response and behavioural reports. This approach has several advantages: (1) we no longer commit to specific parameterizations of the psychometric functions. Instead, the assumptions are made on the computation of the neural responses, as described below. (2) With the goal of understanding the modulations of neural response underlying the behavioural responses, rather than extracting different indices from the psychometric functions, we compared models with different assumptions about how attention affects population neural response. (3) The models made predictions of behavioural choices on a trial-by-trial basis using all the trials in the dataset, without emphasizing particular data points on the psychometric functions (for example, asymptotic performance). (4) By computing the response of the neural population with neurons selective for different locations and by considering the neurons’ excitatory field and suppressive surround, the models account for the effect of stimulus size and attentional field size, which are the critical components of the NMA.

The models are based on the framework that neural response can be estimated by a normalization equation⁵⁵, which effectively estimates neural firing rate in visual cortex. In different models, attention modulates neural response through different stages of normalization: (1) in the response gain model, attention is modelled by response gain factors that multiplicatively modulate the response of the neurons after normalization (Fig. 7a); (2) in the NMA model, attention affects neural responses through attentional gain factors that multiplicatively modulate the excitatory drives of the neurons before normalization (Fig. 7c)²¹; (3) in the contrast gain model, attention divisively modulates the suppression constant in normalization (Supplementary Fig. 7); (4) in the input baseline model⁵⁶, attention modulates the excitatory inputs of the neurons additively before normalization (Supplementary Fig. 8) and (5) in the output baseline model^45,57, attention is modelled as an additive term after normalization (Supplementary Fig. 9) (see Methods for details of all the models).

Fig. 7 |. Models and models’ fits.

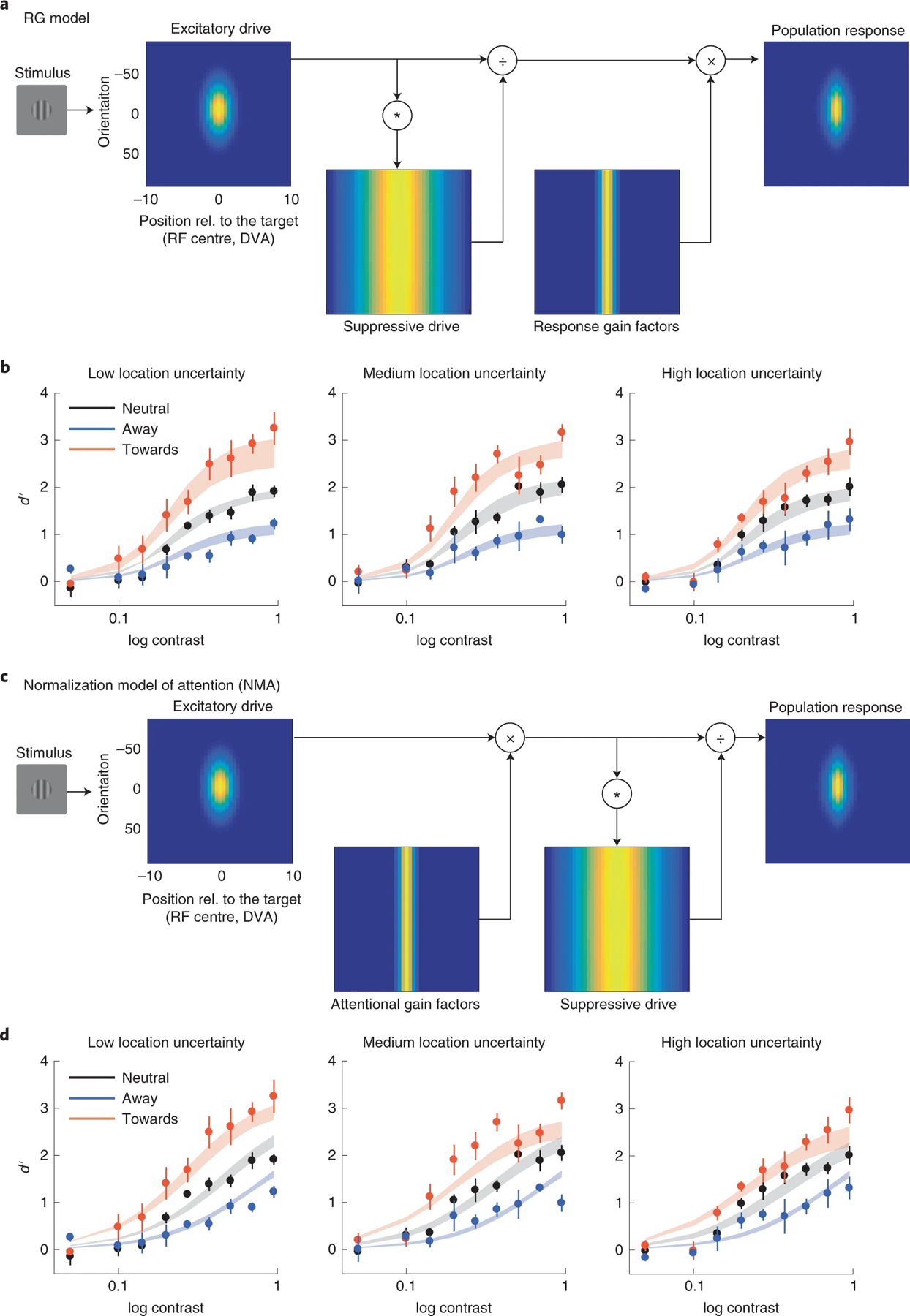
a, Response gain (RG) model: attention multiplicatively modulates neural response after normalization. Simulated neurons are arranged in each panel according to their receptive field centre (x axis; DVA, degree visual angle) and preferred orientation (y axis, where 0 represents vertical orientation). The excitatory drive is determined by the preferred orientation and location of the simulated neurons. Brightness at each location in the image corresponds to the excitatory drive of a single neuron. The suppressive drive is computed by convolving the excitatory drive with the suppression kernel (Supplementary Fig. 14). That is, the suppressive drive is the excitatory drive pooled over space and orientation. In the response gain model, the neural response is computed by dividing the excitatory drive by the suppressive drive, and then multiplied by the response gain factors. b, Model fit of the response gain model. Data points and error bars represent group-averaged data and ±1 s.e.m. The model was fitted to individual observers, and the shaded areas represent the average of the fits across observers (mean ± 1 s.e.m.). c, Attentional modulation based on Reynolds and Heeger’s NMA. Different from the response gain model, attention is modelled by attentional gain factors that are multiplied with the excitatory drive of the neurons before normalization. d, Model fit of the NMA model. Data points and error bars represent group-averaged data and ±1 s.e.m. The model was fitted to individual observers, and the shaded areas represent the average of the fits across observers (mean ± 1 s.e.m.).

We jointly fitted the models to the data of the presaccadic attention condition across three levels of location uncertainty (low, experiment 2, Fig. 4a; medium, experiment 2, Fig. 5c and high, experiment 2, Fig. 5g). We fitted the free parameters to the data from each individual observer using maximum-likelihood estimation, and used the Akaike information criterion (AIC)^58,59 and log-likelihood cross-validation as the indexes for the model comparisons.

The response gain model outperformed the NMA in fitting the data by a group-summed ΔAIC score of 84 (CI 28, 216) (Fig. 8, and Supplementary Tables 2 and 3), whereas the output baseline model performed the worst. With a factorial model comparison, we tested different variations of the models (20 in total, Methods). The ranking of the models was not specific to the setup of the other factors in the model: The response gain model was the best-fit model even when we changed the setup of the response bias or the trade-off between the attentional field size and the magnitude of attentional modulation (Supplementary Fig. 10).

Fig. 8 |. Model comparison using AIC.

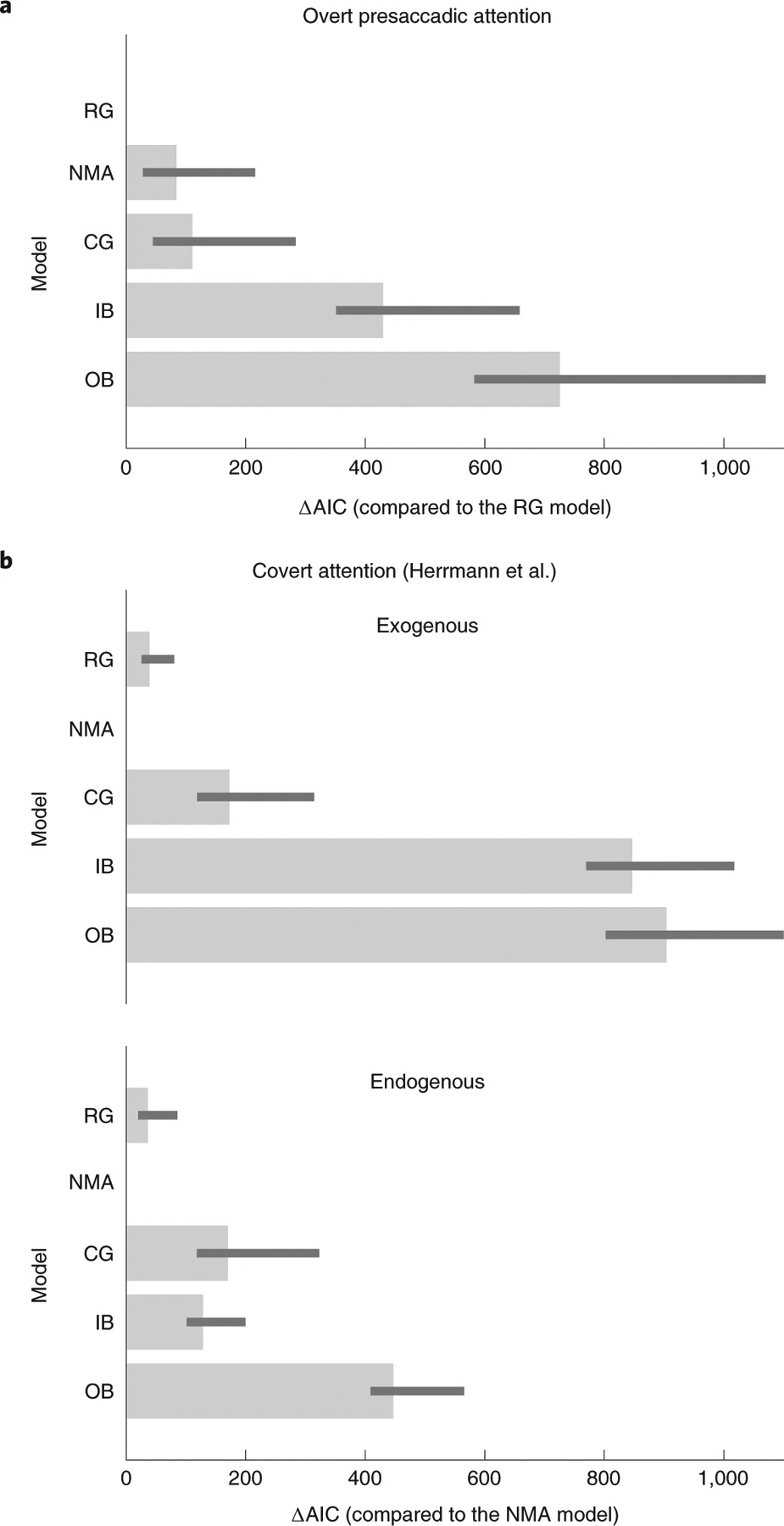
a, Model comparisons for the presaccadic attention experiments. The smaller the AIC, the better the model performed in fitting the data. ΔAIC is the AIC of each model minus the AIC of the best-fit model (response gain, RG, model). The bars represent ΔAIC summed across observers. The error bars represent 95% bootstrapped confidence interval. b, Model comparisons for the data reported in Herrmann et al.⁴⁰. ΔAIC is the AIC of each model minus the AIC of the best-fit model (NMA). CG, contrast gain; IB, input baseline and OB, output baseline. Here, all the models contain a response bias term c as a free parameter, without a trade-off term p (see details in Methods and Supplementary Figs. 10–12 for complete illustrations of the results of model comparisons).

We also fitted the models to the data of a study reporting the size-dependent gain changes induced by covert exogenous and covert endogenous attention⁴⁰. Herrmann et al.⁴⁰ fitted Naka–Rushton functions to the psychometric functions (d′ versus contrast) without fitting process models such as ours that incorporated both population neural response and behavioural reports, and generated predictions at a single-trial level. Critically, we found that different from the results of presaccadic attention, the NMA model is the best model to explain the effect of both exogenous and endogenous covert attention (ΔAIC between the NMA model and the response gain model: endogenous attention, 36 CI 25, 82; exogenous attention, 39 CI 25, 80) (Fig. 8b, Supplementary Figs. 11 and 12).

To check the robustness of our results we also used cross-validated log likelihood as an alternative index for model comparisons. Again, the response gain model outperforms the NMA model for fitting the data of overt presaccadic attention experiment, and the NMA model is the best model for explaining the effect of exogenous and endogenous covert attention (Supplementary Fig. 13).

Discussion

We investigated the perceptual modulations of presaccadic attention, a form of overt attention, by characterizing its effect on performance as a function of stimulus contrast. We found that presaccadic attention exhibited a response gain change, which was robust even when location uncertainty of the stimuli increased.

We compared the effects of presaccadic attention with those of covert endogenous and covert exogenous attention, which exhibited a mixture of response gain and contrast gain changes on the psychometric functions. The effect of covert attention was the same whether we analysed all the trials or excluded the minority of trials containing microsaccades. These results are consistent with previous findings that covert attention affects performance even when only the trials without microsaccades were analysed, or even when the retinal image was stabilized⁶⁰.

By model comparisons, we found that a response gain model, a model that assumes that overt presaccadic attention modulates neural responses after normalization, outperformed the Reynolds and Heeger’s NMA²¹, a computational model that has explained various phenomena of covert attention^{39,40,50–52}. These findings indicate that the computations underlying the modulations of these two types of spatial attention—overt presaccadic and covert—are different.

Previous studies have distinguished presaccadic attention and covert attention by creating experimental conditions that limit the effect of one type of attention but not the other. For example, presaccadic attention can take effect at a shorter latency than covert endogenous attention^6,9,10, covert attention can facilitate performance for stimuli outside of the oculomotor range⁷ and observers can covertly attend to a task-relevant location even when a saccade was made to other locations⁶¹. Here, while keeping experimental designs, stimulus parameters and task difficulty as similar as possible, we optimized cue location and timing to maximize the operation of each attention type (Fig. 3). Our results demonstrate that overt presaccadic and covert spatial attention not only differ in the conditions under which they can take effect, but also in the consequences of their deployment.

Psychophysical experiments of covert attention had found varying gain modulations across studies. For example, covert attention exhibits both contrast and response gain changes in contrast discrimination tasks³⁴, and response gain changes for both luminance-defined and colour-defined stimuli with a dual-task procedure³⁵. Furthermore, studies from our laboratory reported contrast gain for endogenous attention and response gain for exogenous attention^31,37,38. The NMA²¹ and experiments testing its predictions^39,40 pointed out that the degree of response gain and contrast gain changes by covert attention depends on the relation of the attentional field size to the stimulus size (Fig. 1). Thus, to obtain a pure response gain or contrast gain change for covert attention, stimulus size and attentional field size should relate in a specific manner. Our results that both endogenous and exogenous attention exhibited a mix of response gain and contrast gain change resulted from the stimulus parameters we used: the stimuli eccentricity, the size and eccentricity of the placeholders and the size and eccentricity of the peripheral precue for exogenous attention—all parameters that could influence the size of the attentional field, resulting in similar attention field sizes in both the exogenous and endogenous attention tasks.

Albeit the differences in their details^21,50–52, in the NMA, the computations of attention can be conceptualized by a normalization equation: R = E(c_center)/ [S(c_center + c_surround) + σ], in which the visual neuron’s response R is determined by the excitatory drive E, suppressive drive (normalization pool) S and a non-negative suppression constant σ. E is a function of the input contrast c_centre at the location central to the neuron’s receptive field. Visual neurons have an extended suppressive surround and thus S is a function of the input contrast (c_centre and c_surround) at both the centre and the surround. Critically in the NMA, attention is modelled as a gain factor a that concurrently modulates excitatory and suppressive inputs before divisive normalization. When the attention field is large (covering both the centre and the surround), neural response becomes R = E(ac_center)/ [S(ac_center + ac_surround) + σ], leading to a contrast gain change as in Fig. 1a; when attention field is small (without ‘attending to’ the surround), the neural response is R = E(ac_center)/ [S(ac_center + c_surround) + σ], leading to a response gain change as in Fig. 1b (ref.²¹). The absence of size-dependent gain change by presaccadic attention in our experiments indicates that the modulations by presaccadic attention can instead be summarized by a response gain factor γ that scales neural responses after normalization R = γE(c_center)/ [S(c_center + c_surround) + σ].

These concepts are confirmed by model comparisons. The model assuming that attention multiplicatively modulates neural response after normalization is best at explaining the effect of presaccadic attention. In contrast, the NMA is best in explaining the effect of both endogenous and exogenous covert attention. Thus, whereas the NMA can explain many neural and perceptual modulations generated by covert attention, our results indicate that such computation does not apply to presaccadic overt attention. A response gain mechanism seems to be a signature of the perceptual modulations rooted in saccade preparation.

The modelling approach we took is more comprehensive than the approach in the previous studies, in which the data were compared with the predictions of the NMA by fitting Naka–Rushton functions to the psychometric functions^39,40. Instead of describing the data by parameter values d_max and C₅₀, in our models we computed population neural response and made predictions on trial-by-trial behavioural reports. Among a neural population, depending on the neurons’ preferred orientation and location, different neurons could exhibit different magnitudes or forms of attentional modulation⁵⁷. This heterogeneity of the attentional effect was taken into account by the models we used here because the signal available for the observers to make a decision encompasses the entire simulated neural population. In addition, this approach also allowed non-sensory or decision-related factors (for example, response bias) to be fitted in the models (Methods and Supplementary Figs. 10–12).

Our models assumed that the attentional field is maintained at the centre of the placeholder regardless of location uncertainty. This assumption is in line with the findings that presaccadic attention depends on the planned location during oculomotor programming rather than the exact saccade landing point^62–64. Moreover, in our data, the averaged saccade landing points changed very little (<0.13°) when the target was presented away from the central location (Supplementary Fig. 5). Jittering the location of the simulated attention field by this amount led to negligible changes on the simulated neural responses.

It may be surprising that the response gain model outperformed the NMA in fitting the data, as the NMA could mimic either response gain or contrast gain by adjusting the size of the attention field to be either small or large, respectively. Note that our models take into account the stimulus location on a trial-by-trial basis. For the conditions with location uncertainty, if the size of the attention field remains small, there would be no attention effect at the outmost or intermediate locations, or attention could even generate a suppressive effect on the target, which was not observed in the data (Fig. 6). The fits of the NMA to the presaccadic attention condition (Fig. 7d) seem to indicate that the model used shallower (non-saturating) functions in an attempt to generate different maximum responses at the highest contrast level (a response gain-like pattern) across the toward, away and neutral conditions. However, this led to model fits that cannot capture the shape of the psychometric function as well as the response gain model.

For the NMA²¹ to explain our data, the following conditions would have had to be fulfilled: in the high-uncertainty condition, the attention field size would have to remain small, and attention would have to shift to the location wherever the target appeared during the presaccadic interval, as if the target attracted stimulus-driven attention onto itself, while participants were still able to saccade to the centre of the placeholder. This is unlikely for two reasons. First, this stimulus-driven attention would have to be extremely fast and only occur in the presence of presaccadic attention; otherwise, the target in the endogenous and exogenous attention tasks would have had the same effect. Second, if the stimulus generated an attention-capture effect, saccade endpoints would have been affected, resulting in averaged saccades that landed between the planned saccade landing point and the target stimulus^65,66. However, the mean of the saccade endpoints remained practically constant even when location uncertainty was high (Supplementary Fig. 5).

We did not directly measure the change of the attentional field size as a function of location uncertainty with fMRI, as has been done for covert attention⁴⁰. Nevertheless, such limitation is unlikely to invalidate the dissociations between presaccadic and covert attention reported here for the following reasons. (1) Several data analyses indicated that the location uncertainty manipulation was effective. The magnitude of the response gain was similar when we analysed the central or the most peripheral locations, indicating that the size of attention field extends throughout all the possible target locations. Furthermore, oculomotor behaviours showed that when uncertainty was low, both the saccade landing points and the saccade reaction times were less variable, consistent with the findings that overt attention decreases neural variability⁶⁷ and that location uncertainty increases variability in oculomotor behaviour⁶⁸. (2) All the models we compared contained free parameters allowing adjustments for the attentional field sizes under different location uncertainties, and the best-fit attentional field sizes were comparable between the NMA and the response gain model (Supplementary Tables 2 and 3). Thus, more direct estimates of the attentional field size are unlikely to change the results of model comparisons.

The coupling between saccadic eye movements and visual attention are well-documented at both the behavioural^{1–4,8,69–71} and neural^15,72–77 levels. Our results resonate with the notion that even though the neural correlates of saccade and covert attention are shared at a coarse scale, the two phenomena are neurophysiologically dissociable^16,78–81. For example, in the frontal-eye field (FEF), visual and visuomotor cells show enhanced firing rate during a covert attention task, whereas motor and visuomotor cells show enhanced firing rate (time-locked to saccade onset) during a saccade task⁷⁸. In addition, the synchronization between FEF and visual cortex V4 also depends both on cell types and task. These distinct neural substrates underlying saccade execution and covert attention might contribute to the differential perceptual modulations and computations we observed for presaccadic attention and covert attention.

Our results are consistent with the findings that neural responses in sensory visual cortex are enhanced in a retinotopically specific manner^12,14,82,83 before eye movements. This presaccadic enhancement is accompanied by an improvement of orientation decodability of saccade target⁸⁴. The enhancement of neural firing rate can occur at two locations simultaneously, a task-relevant location and a saccade target location, indicating that attentional demand (task relevance) and presaccadic enhancement are dissociable¹⁶. However, in that study the modulations by saccade preparation and attention (relevancy) were very similar in both their form (increased firing rate) and magnitude. This is probably not surprising as they aligned the neural response to cue onset and analysed an epoch long before (>800 ms) saccade execution. Moreover, given our results, to reveal the differences between the modulations by presaccadic attention and covert attention, a finer characterization of the modulations is called for by mapping out the entire contrast response functions just before saccade onset. Future neurophysiological studies can take this approach to investigate whether the neural modulations by overt and covert attention in visual cortex are supported by different computations as our behavioural and computational results indicate.

We have proposed that presaccadic attention facilitates transaccadic integration by making the peripheral saccade target more fovea-like, specifically by sharpening orientation tuning^9,11 and preferentially enhancing high spatial frequencies^9,10. The robust response gain change of presaccadic attention revealed in our study is consistent with this proposal. To achieve transaccadic stability, it would be more useful for the visual system to upscale the contrast of the saccade target regardless of its physical contrast (similar to a response gain change), rather than to preferentially enhance the target whose contrast is at a threshold level (a contrast gain change).

To conclude, our study reveals that presaccadic attention and covert attention are mediated by different computations. Whereas a well-established model of covert attention, the NMA, does not account for the computations underlying the effects of presaccadic attention on contrast sensitivity, a response gain model does.

Methods

Participants.

Four observers (two females and two males, age range 22–33 years) participated in the three experiments (a total of 21 1-h sessions per observer). No statistical methods were used to predetermine sample sizes; our sample sizes are similar to those reported in previous publications^38–40. All observers had normal or corrected-to-normal vision. The experiment was conducted with the written consent of each observer and the University Committee on Activities involving Human Subjects at New York University approved the experimental protocols. Data from all the particpants were analysed. We conducted trial exclusion on the basis of observers’ eye movements described in Eye position below.

Setup.

Observers sat in a dimly lit room with the chin rest positioned 57 cm from the monitor. Presentation of the stimuli was controlled by MATLAB (Mathworks) using the Psychophysics Toolbox extensions⁸⁵. The monitor was gamma-corrected and had a resolution of 1,280 × 960 pixels with a refresh rate of 85 Hz. The gaze position of the right eye was recorded by an EyeLink 1000 with the Desktop Mount (SR Research).

Experiment 1.

Each trial started with a fixation period of 300 ms followed by the onset of a neutral cue in the neutral condition or a saccadic cue in the saccade condition. The saccadic cue was a bar at the fixation pointing towards the upcoming target location (8° left or right from the fixation, Fig. 2a). Two placeholders, marking the two potential target locations, were presented throughout the experiment. Observers were instructed to make a saccadic eye movement to the cued location as fast as possible when they saw the saccadic cue. The neutral cue was composed of two bars pointing to both locations, instructing observers to maintain fixation at the centre throughout the trials. The test stimulus (the target, a Gabor presented for 35 ms) appeared shortly after the cue onset. Eye position was monitored throughout the trials.

The SOA (stimulus onset asynchrony) between the cue and the target was randomly sampled between 12 and 224 ms in each trial. This range of SOA was used because it allowed the test stimulus to be presented before saccade onset in most of the trials in the saccade condition. Moreover, this interval was shorter than the time (roughly 300 ms) required for covert endogenous spatial attention to take full effect¹⁷. After the offset of the test stimulus and a delay of 400 ms, an auditory tone was played as the response cue. Tones in two different frequencies informed the observer at which location (left or right) the target had been presented. After hearing the response cue, the observer reported the orientation of the target (left versus right tilt from vertical) by pressing either the left-arrow or right-arrow key on the keyboard. Observers were given 3 s to respond after the response cue. After the button press, the next trial started after an intertrial-interval ranging from 0.8 to 1.2 s. The neutral condition and the saccade condition were tested in separate blocks, in a randomized order. On average, every observer performed 2,592 trials in three sessions on different days.

Experiment 2.

Three types of attention were manipulated in experiment 2: presaccadic attention, covert endogenous (voluntary) attention and covert exogenous (involuntary) attention. On average, every observer completed 8,892 trials in 11 sessions on different days. The procedures for the presaccadic attention task were identical to the ones used in experiment 1, except for the following modifications: the test stimuli in experiment 2 were composed of two Gabors, a target and a distractor, one presented 8° to the left and one presented 8° to the right of fixation simultaneously (Fig. 3a). The location of the target was determined randomly in each trial. In the saccade condition, the saccadic cue either pointed towards the target (towards condition) or the distractor (away condition) with equal probability. Thus, the observer had to saccade to the distractor (that is, away from the target) in half of the trials. At the end of each trial, an auditory response cue (either in a high or a low tone) informed observers about the location of the target. Observers then reported the orientation of the target using the keyboard. The neutral condition and the saccade condition were tested in separate blocks in a randomized order. In the saccade blocks, equal number of trials of the towards and away conditions were randomly interleaved. Observers were explicitly told that the direction of the saccadic cue was not informative regarding the target location.

There were three conditions to investigate the effect of covert endogenous attention: neutral, valid and invalid (Fig. 3a). The procedures in these conditions were similar to the procedures of the neutral, saccade towards and saccade away conditions described above, except for the following changes. The SOA between the precue and the test stimulus was 400 ms so that the effect of covert endogenous attention could take full effect¹⁷. For all the conditions, observers had to maintain fixation at the screen centre throughout each trial; eye position was monitored throughout the trials. There were two types of block, one containing only the neutral condition and the other containing both the valid and invalid conditions. In the latter, 70% of the trials were valid trials (with the precue pointing towards the target) and the remaining 30% were invalid trials (with the precue pointing towards the distractor). Observers were told that the precue was informative regarding the target location and that they should pay attention to the cued location.

The covert exogenous attention task was similar to the endogenous attention task, except for the following modifications. The precue was presented peripherally and transiently with a duration of 60 ms. The precue was followed by an interstimulus interval (40 ms) before the test stimulus. This led to a 100-ms SOA between the precue and the test stimulus, which yields the greatest effect for exogenous attention¹⁷. In the valid condition, the precue was a black line (0.5° length) presented above the target (1.8° above the centre of the target), whereas in the invalid condition, the precue was presented above the distractor. In the neutral condition, the precues were black bars presented at the fixation, equivalent to the neutral cue in the saccade and the endogenous attention tasks. Similar to the endogenous attention task, there were two types of block, one containing only the neutral condition and the other containing both the valid and invalid condition. In the latter, equal number of valid and the invalid trials were randomly interleaved. Observers were told that the precue was uninformative regarding the target location. Eye position was monitored throughout the trials.

Experiment 3.

We repeated the presaccadic attention task in experiment 2 with increased location uncertainty. Again, we instructed observers to saccade to the centre of the placeholder in the saccade condition. There were still two placeholders on the screen, but now with five potential target locations within each placeholder. We considered the presaccadic attention task in experiment 2 as a low-uncertainty condition and we tested two levels of location uncertainty here, named as medium-uncertainty (Fig. 5a) and high-uncertainty (Fig. 5b) conditions that differed in the area covered by the placeholders. In each trial, the target was presented at any one of the five locations in a placeholder with equal probability. Similarly, the distractor was presented at any one of the five locations in the other placeholder. The location of the test stimuli varied across trials. On average, every observer completed 7,722 trials in ten sessions on different days.

Stimuli.

The test stimuli were Gabor patches generated by a sinusoidal function (four cycles per degree with its phase randomly determined in each trial) weighted by a Gaussian with a standard deviation of 0.5°. Test stimuli in nine contrast levels (5, 10, 14, 20, 27, 37, 51, 70, 95%) were tested. Contrast levels were randomly selected on each trial, and were interleaved in each of the experiments. In experiments 2 and 3, the target and the distractor in a trial were always presented with the same contrast level.

The orientation of the Gabors was titrated for each observer. The titration procedure was conducted using the procedure of the neutral condition of each experiment and task. Three types of task (presaccadic attention, endogenous attention and exogenous attention) in experiment 2 were titrated separately. The medium-uncertainty and high-uncertainty condition in experiment 3 were also titrated separately. Test stimuli were presented at the highest contrast level and an adaptive procedure⁸⁶ was used to determine the amount of tilt (from vertical) at which observers’ performances in discriminating the orientation (left versus right tilt) of the target were at about d′ = 2.

Two placeholders (centred at 8° left and right from the fixation) were presented on the screen throughout all the experiments. The placeholders were composed of four black dots forming a square with a width of 2.3° in experiments 1 and 2. In experiment 3, the placeholders had a width of 3.4° and 6.3° in the medium-uncertainty and large uncertainty conditions, respectively.

In experiments 1 and 2, the test stimuli were presented at 8° left or right from the central fixation. In experiment 3, the test stimuli were also presented 8° from fixation but could occur at any one of the five locations within the placeholder. The five locations were evenly spaced on an imaginary circular arc symmetric around the horizontal meridian. The imaginary arc had a radius of 8° and an angle of 18° and 44° in the medium- and the high-uncertainty conditions, respectively. Thus, the two outmost locations (the top and the bottom) had a distance of 2.5° and 6° in the medium- and the high-uncertainty conditions, respectively (see Fig. 5a,b, in which the locations are marked by dashed lines for illustration purposes). Observers were told to saccade to the centre of the placeholder.

Analysis.

We fitted psychometric functions (d′ as a function stimulus contrast) with Naka–Rushton functions parameterized as d′ = d_maxCⁿ/(Cⁿ + Cⁿ₅₀) where C is the contrast level, d_max is the asymptotic performance, C₅₀ is the contrast level corresponding to half the asymptotic performance and n determines the slope of the function. A change in d_max indicates a response gain change and a change of C₅₀ indicates a contrast gain change.

A bootstrapping procedure was used to test the statistical significance of the change of d_max and C₅₀ across conditions. We first resampled (with replacement) the data to obtain a psychometric function (nine data points) for each observer and condition. We then computed group-averaged psychometric functions by averaging the data points across observers. Naka–Rushton functions were then fitted to the group-averaged psychometric functions. We subtracted the d_max (or C₅₀) between valid and invalid conditions to obtain the difference score. This procedure was repeated 2,000 times to generate the distribution of difference scores. We computed the proportion of the difference scores that fell below (or above) zero and multiplied this proportion by two as the P value for the two-tailed bootstrapping test. Effect size (d) was computed as the mean of the difference score distribution divided by its standard deviation.

For experiment 3, to investigate whether the magnitude of response gain change was constant across different locations in the high-uncertainty condition, we conducted Bayesian one-way repeated-measured ANOVA using JASP⁸⁷. The ANOVA compared the strength of the evidence of a null model against a model assuming response gain change differs across target locations. The prior probabilities of the two models were set equal.

Eye position.

We monitored eye positions online. Trials with blinks or saccades (except for the response saccade required in the saccade condition) detected from the beginning of the trial to 200 ms after the offset of the test stimuli were aborted and repeated at the end of the block. Trials with no response saccade detected online in the presaccadic attention condition were also aborted and repeated. For offline analysis, we smoothed the raw eye data with a Gaussian and computed smoothed eye velocity using the eye positions of five neighbouring time points. Saccades were detected when the eye velocities exceeded the median velocity by five standard deviations for at least 8 ms (ref.⁸⁸). Saccades separated by less than 10 ms were merged as a single saccade. For the saccade condition, we analysed the trials in which observers’ first response saccades occurred between 70–400 ms after the cue onset and landed within the cued location with an error smaller than 2.5° (from the centre of the aperture) in experiment 1 and 2, and smaller than 3.5° in experiment 3.

We also extracted fixational eye movements from the data of both the exogenous and endogenous covert attention conditions (for the analysis presented in Supplementary Fig. 2). Fixational eye movements were extracted using the same velocity-based method described above, except that we defined fixational eye movements as the saccadic eye movements with an amplitude smaller than 1°.

Models.

NMA.

We simulated population neural responses following Reynolds and Heeger’s NMA²¹. We simulated a two-dimensional array of neurons with orientation tiling the orientation space in steps of 1°, and receptive field centres ranging from −10° (degree visual angle) to +10° relative to the target location in steps of 0.5°. The responses of the neurons (R) were computed as

$$\begin{gathered} R(x,\theta )=\frac{A(x,\theta )E\left(x,\theta ;c^n\right)}{S\left(x,\theta ;c^n\right)+{\sigma }^n} \\ S\left(x,\theta ;c^n\right)=K(x,\theta )*\left[A(x,\theta )E\left(x,\theta ;c^n\right)\right] \end{gathered}$$ (1)

where E is the excitatory drive, S is the suppressive drive, A is the attentional gain factor, c is stimulus contrast, n is an exponent term and σ is a non-negative suppression constant (Fig. 7a). The excitatory drive E was determined by each neuron’s receptive field centre x and preferred orientation θ. The spatial excitatory field of each simulated neuron was a Gaussian with 1° standard deviation and the orientation tuning was a circular Gaussian with 48° full-width at half-maximum, approximating the spatial and orientation tunings reported for macaque primary visual cortex^89,90. Suppressive drive S was computed as a suppression kernel K convolved with attentional-modulated excitatory drive. * represents the convolution operator. K is a two-dimensional suppression kernel in which the spatial extent was modelled as a Gaussian with a width four times that of the spatial excitatory field, emulating the broad suppressive surround of visual neurons (Supplementary Fig. 14). For simplicity, we set K to be uniform across orientations, meaning that at the same locations, the normalization pool was summed across all the neurons.

Attentional modulation was modelled by attentional gain factor (A) that multiplicatively modulates the excitatory drive before normalization. Attentional gain factors are uniform across orientation (Fig. 7a), and the spatial extent of the attentional gain factor is modelled as a Gaussian,

$$A(x,\theta )=1+w\frac{1}{{\sigma }_a^p}{\text{e}}^{\frac{-{\left(x-{\mu }_a\right)}^2}{2{\sigma }_a^2}}$$ (2)

where 1 is the baseline of the attention gain factor, μ_a is the attended location (assumed to be centred at the central target location), σ_a determines the size (width) of the spatial extent of the attentional gain factor and p is a parameter controlling the trade-off between the spatial extent and the magnitude of attentional modulation. If p = 1, spatial attention has a fixed volume, decreasing in magnitude when its spatial extent increase. If p = 0, the magnitude of the attentional gain is independent of the spatial extent of attentional modulation. w is a weight that determines the strength of attentional modulation. We fitted this weight with two free parameters w_n, w_t, corresponding to the strength of attention in the neutral and the towards (or the valid) condition. The weight of the away (or the invalid) condition was fixed at zero.

Behavioural performance (d′) in a discrimination task is proportional to the neural responses given the assumption of an additive, independent and identically distributed noise. An alternative model with Poisson noise and a maximum-likelihood decision rule would yield the same linkage between neural response and behavioural performance^37,91. Therefore, we fitted a free parameter, σ_n, representing the magnitude of the noise, to relate the underlying neural responses to behavioural reports.

We computed probabilistic behavioural report using the simulated population neural response and signal detection theory. The available signal s for an observer is computed as the Euclidean norm of the subtraction between two vectors s = ∥r_R − r_L∥, in which the vector r_R represents the population neural response for a right-tilted target and r_L represents the population neural response for a left-tilted target. On the basis of signal detection theory, the observer’s performance is d′ = s/σ_n and the probability for the observer to correctly discriminate a right-tilted target is $p(\widehat{C}=\text{R}\mid C=\text{R})=\Phi \left(\frac{d\prime }{2}-c\right)$, where C is the true category of the target (left-tilted L or right-tilted R), $\widehat{C}$ is the observer’s response, c is a response bias (that is, an idiosyncratic preference for reporting a particular category) and Φ is cumulative distribution function of the standard normal distribution.

The inputs to the model were based on the stimuli in the experiments. We simulated population neural responses (r_R and r_L) for the right- and the left-tilted orientation by setting the orientation of the input stimulus at 4° and −4° relative to vertical respectively. For the medium- and high-location uncertainty conditions, the neural responses for the outmost locations, intermediate locations and the central location were simulated separately by moving the location of the input stimulus based on our stimuli (Fig. 5a).

Below, we consider alternative models. All the models share the same implementations as the NMA described above but differ in how and when attention modulates neural responses.

Response gain model.

The effect of attention is modelled as the response gain factor γ that scales the response of the neurons multiplicatively after normalization. The responses of the neurons (R) are computed as

$$R(x,\theta )=\gamma (x,\theta )\frac{E\left(x,\theta ;c^n\right)}{S\left(x,\theta ;c^n\right)+{\sigma }^n}$$

$$S\left(x,\theta ;c^n\right)=K(x,\theta )*E\left(x,\theta ;c^n\right)$$

Contrast gain model.

The effect of attention is modelled as the contrast gain factor ϕ that divisively modulate the suppression constant of the neuron. ϕ horizontally shifts the response functions of the neurons left (ϕ > 1) or right (ϕ < 1). The responses of the neurons (R) are computed as

$$R(x,\theta )=\frac{E\left(x,\theta ;c^n\right)}{S\left(x,\theta ;c^n\right)+{[\sigma /\varphi (x,\theta )]}^n}$$

$$S\left(x,\theta ;c^n\right)=K(x,\theta )*E\left(x,\theta ;c^n\right)$$

Input baseline model (IB).

Here attention is modelled as a change of baseline input I. The responses of the neurons (R) are computed as

$$R(x,\theta )=\frac{E\left(x,\theta ;{(c+I(x,\theta ))}^n\right)}{S\left(x,\theta ;c^n\right)+{\sigma }^n}$$

$$S\left(x,\theta ;c^n\right)=K(x,\theta )*\left[E\left(x,\theta ;{(c+I(x,\theta ))}^n\right)\right]$$

We found that an input baseline added after the exponent term E(x, θ;cⁿ) + I(x, θ) to fit the data almost equally well as the input baseline added before exponentiation. Thus, we only report one version of this model.

Output baseline model.

Attention is modelled as an additive term O after normalization. This is similar to the ‘increased baseline’ observed in previous human fMRI studies on covert spatial attention⁴⁵.

$$R(x,\theta )=\frac{E\left(x,\theta ;c^n\right)}{S\left(x,\theta ;c^n\right)+{\sigma }^n}+O(x,\theta )$$

$$S\left(x,\theta ;c^n\right)=K(x,\theta )*E\left(x,\theta ;c^n\right)$$

Response gain factor γ, contrast gain factor ϕ are all modelled using equation (2) with the same free parameters p and σ_a. Baseline input I and output baseline O also follow equation (2), except that they have a baseline at 0, instead of 1.

After fitting the output baseline model, we found that the model predicts the same behavioural performance regardless of attention. This makes sense as the signal s for an observer for discriminating between the two orientations is s = ∥r_R − r_L∥ in which r_R and r_L are two vectors representing the population neural response for a right- and left-tilted target. Adding an output baseline O to neural response left s = ∥(r_R + O) − (r_L + O)∥ unchanged. We present the results of the output baseline model for completeness.

Note that all these variables, γ, ϕ, I, O, can be conceptualized as attentional gain factors. Here, we use different names and symbols to distinguish them from the terms used in the NMA.

Model variants.

In addition to different models of attentional modulation (NMA, response gain, contrast gain, input baseline and output baseline), we varied other factors in the model: (1) the response bias c was either fitted as a free parameter or fixed at zero (no bias). (2) The trade-off between the size of attentional field and the magnitude of attention was either allowed to be a free parameter (p in equation (2)) or fixed at 0 (no trade-off).

We conducted factorial model comparison using all the factors above leading to 20 models in total: five types of attentional modulation (NMA, response gain, contrast gain, input baseline, output baseline), X bias or no bias allowed X trade-off or no trade-off allowed (Supplementary Table 1). This procedure ensures that the winning model does not depend on the setting of the models we choose a priori.

Model fitting.

We denote the free parameters collectively by θ (free parameters of each model are listed in Supplementary Table 1). We fit each model to individual data by maximizing the log likelihood of θ, log L(θ) = log p(data|θ). We assume that the trials are conditionally independent. The log likelihood is $\text{log}L(\theta )=\text{log}\prod _{i}p\left({\widehat{C}}_i\mid C_i,l_i,\theta \right)=\sum _i\text{log}p\left({\widehat{C}}_i\mid C_i,l_i,\theta \right)$, where l_i is the location of the target, C_i the true category (right or left tilt) of the target and ${\widehat{C}}_i$ represent observers’ responses on the ith trial, respectively. We optimized the parameters for each observer using Bayesian adaptive direct search⁹². To select the best model, we computed the AIC for each observer and model. The best-fit model is the model with the lowest group-summed AIC. We reported group-summed ΔAIC (the AIC of the models minus the AIC of the best-fit model) and its confidence interval estimated by bootstrapping.

In addition to AIC, we conducted a tenfold cross-validation procedure to fit and compare the models. The cross-validation procedure trains and tests the models using different portions of the data, and thus naturally accounted for the complexity of the model and its goodness-of-fit. Specifically, for each participant, we segmented the data into ten subsets in a pseudo-random fashion (ensuring that the trials from different conditions were evenly distributed across subsets). In each of the ten iterations, we treated one subset as the test set and the other nine subsets as the training sets. The training sets were used to estimate the best-fit parameters. We then used the test sets to compute the log likelihood of the model, which was then summed across the ten test sets. In Supplementary Fig. 13, we report the delta negative log likelihood (negative log likelihood of each model minus the negative log likelihood of the best-fit model) summed across all participants.

Simulation before experiment 3.

Before conducting experiment 3, we ran a simulation to investigate the predictions of the NMA (Supplementary Fig. 4). In this simulation, the model parameters were handpicked. We scaled the size of attention field with the size of the placeholders, and we set the weight of the attentional modulation so that the ratio between the asymptotes of the simulated neural response in the towards and the away condition (under the low location uncertainty) was similar to the ratio of d_max between the towards and away conditions in the data.

Reporting Summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Data availability

The data that support the findings of this paper are available at https://github.com/hsinhungli/overt-covert-attention.