Abstract
Elastin fibers assemble in the extracellular matrix from the precursor protein tropoelastin and provide the flexibility and spontaneous recoil required for arterial function. Unlike many proteins, a structure-function mechanism for elastin has been elusive. We have performed detailed NMR relaxation studies of the dynamics of the minielastins 24x′ and 20x′ using solution NMR, and of purified bovine elastin fibers in the presence and absence of mechanical stress using solid state NMR. The low sequence complexity of the minielastins enables us to determine average dynamical timescales and degrees of local ordering in the cross-link and hydrophobic modules separately using NMR relaxation by taking advantage of their residue-specific resolution. We find an extremely high degree of disorder, with order parameters for the entirety of the hydrophobic domains near zero, resembling that of simple chemical polymers and less than the order parameters that have been observed in other intrinsically disordered proteins. We find that average backbone order parameters in natural, purified elastin fibers are comparable to those found in 24x′ and 20x′ in solution. The difference in dynamics, compared with the minielastins, is that backbone correlation times are significantly slowed in purified elastin. Moreover, when elastin is mechanically stretched, the high chain disorder in purified elastin is retained, showing that any change in local ordering is below that detectable in our experiment. Combined with our previous finding of a 10-fold increase in the ordering of water when fully hydrated elastin fibers are stretched by 50%, these results support the hypothesis that stretch induced solvent ordering, i.e., the hydrophobic effect, is a key player in the elastic recoil of elastin as opposed to configurational entropy loss.
Significance
Elastin is responsible for the spontaneous recoil of arterial walls that is necessary for cardiovascular function. Despite this critical role, the mechanism driving entropic recoil has remained unclear. Elastin is unusual in that it is intrinsically disordered in both soluble and fibrous forms. Using NMR, we have determined the domain average timescales and amplitudes of dynamics in two soluble elastin mimetics and in relaxed and stretched states of purified bovine elastin fibers. Although dynamical timescales are different, both the soluble elastin mimetic and fibrillar elastin display an exceptionally high degree of disorder. No detectable increase in protein ordering was observed upon stretching, suggesting that entropic recoil is primarily driven by the hydrophobic effect and not configurational entropy loss.
Introduction
Elastin, an extracellular matrix protein that is the principal elastic protein in vertebrates, is abundantly expressed in blood vessels, lung tissue, ligaments, and skin (1). The mature elastic matrix is formed when tropoelastin, one of the most hydrophobic proteins found in nature, is exported to the extracellular matrix and consecutively undergoes an oligomerization transition known as coacervation, followed by cross-linking via the enzymatic oxidation of lysyl ε-amino groups (2). The reversible entropic elasticity of fully matured elastin fibers in blood vessel walls is responsible for elastic energy storage during the cardiac cycle and the dampening of pulsatile flow in distal arteries via the Windkessel effect (3). Elastogenesis terminates in adolescence, and in the course of a human lifetime, arterial elastin undergoes in excess of 107 stretching and contracting cycles. Oxidative damage accrued over human elastin’s lifetime reduces blood vessel compliance, resulting in hypertension, vascular calcification, ventricular hypertrophy, renal dysfunction, and stroke (4). It is critical to understand the structural and dynamic origin of elastin’s entropic elasticity to understand how this oxidative structural damage leads to the pathogenesis and progression of these diseases.
Elastin proteins are organized in alternating proline-rich hydrophobic domains and alanine-rich cross-linking domains (5). The hydrophobic domains are quasirepeats of three to seven amino acids rich in hydrophobic residues including proline, whereas the alanine-rich cross-linking domains are weakly helical (6) and present the cross-linking lysine residues in close proximity at i and i + 3 or i + 4 positions (7). The elastic function of elastin proteins primarily arises from the hydrophobic domains. These were, for some time, thought to have a stable repeating type II β-turn secondary structure (8). However, we have shown using NMR analyses of both natural elastin fibers (9) and a series of simplified designed minielastin proteins (6) that these domains are intrinsically disordered in the unstressed relaxed state (9).
The entropically driven recoil of a stretched disordered polymer can have two different origins: configurational entropy gain similar to that of vulcanized rubber (10), or the reduction of hydrophobic side-chain exposure as the domain contracts and becomes more compact (11,12). It is an important open question to what extent each of these mechanisms contribute to elastin function. To answer this question, we have performed detailed NMR studies of the dynamics of two designed minielastin proteins in solution, 24x′ and 20x′, and of purified bovine elastin in the presence and absence of mechanical stress.
Like natural elastin, our designed minielastins have an alternating structure of hydrophobic modules, (APGVGV)7 or (VPGVGG)5, and cross-link modules, (DA5KA2KF). Unlike natural elastin, 24x′ and 20x′ have identical repeats, which has allowed us to completely assign resonances in the proteins (6). In a protein with dynamic motion on these timescales, NMR chemical shifts reflect the time average chemical environment of each atom. In our earlier work, we closely looked for chemical shift variation in the hydrophobic domains and found that chemical shifts for all but the outermost residues are identical and independent of whether the hydrophobic domain is in isolation, internal, or located at either protein terminus. This includes backbone (Ha, Ca, CO, HN, and N) and side-chain atoms. Furthermore, varying the number of modules in the construct or changing the sequence of the cross-link modules does not change the chemical shifts that are (within the uncertainty of 2° chemical shifts) equivalent to random coil values in the hydrophobic modules or somewhat shifted toward α-helical values in the center of the cross-linker (6). Herein, we also show that R1 and R2 relaxation rates, within experimental error, are the same in two proteins that have, respectively, a molecular weight of 138 kDa with two (APGVGV)7 modules (20x′) and a molecular weight of 203 kDa with four (APGVGV)7 modules (24x′). All of these observations are consistent with a high degree of local dynamics that does not vary significantly with the position of the repeat along the length of the protein, protein terminal residues aside. With the reduced range of chemical shifts in intrinsically disordered protein (IDPs), complete residue-specific NMR studies of dynamics in this type of protein are technically unfeasible, and all repeats are approximated as dynamically equivalent in our analysis of the relaxation data which represents an average over all of the hydrophobic repeat domains and all of the cross-link modules. This approximation allows us to determine both the average dynamical timescale(s) and the average degree(s) of local ordering with residue-specific resolution in the cross-link and hydrophobic modules of 24x′ and 20x′ from solution NMR relaxation studies (R1, R2, and nuclear Overhauser effect (NOE)) at three field strengths. We find an extremely high degree of disorder resembling that of some simple chemical polymers and comparable to only the smallest order parameters observed in natural IDPs (13, 14, 15). We also note that hydrophobic modules in natural elastin have an approximate repeat-like sequence.
We then examined the natural, purified elastomer using solid state 13C-NMR without magic angle spinning (MAS). Chain ordering was determined from the residual shielding anisotropy and dynamical timescales from R1 and R2 of the entire backbone carbonyl resonance envelope. We find a similarly high degree of average disorder in the natural protein and, importantly, mechanical stretching does not detectably decrease this disorder. As the polymer disorder we observe in both relaxed and stretched elastin is essentially identical, we infer that elastin’s recoil does not arise from configurational entropy loss at the residue level.
Materials and methods
Protein expression
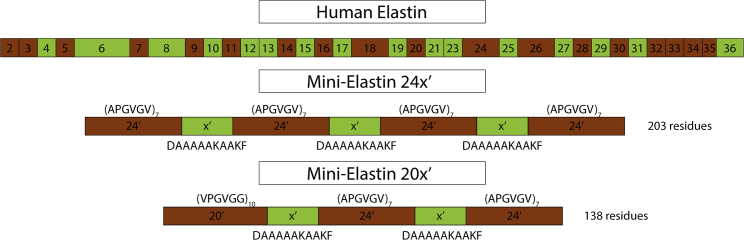
15N-labeled samples of minielastin constructs (Figure 1) with sequence 24′-x′-24′-x′-24′-x′-24′ (24x′) and 20′-x′-24′-x′-24′ (20x′), where 24′ = (APGVGV)7, 20′ = (VPGVGG)5, and x′ = DA5KA2KF, were expressed and prepared as described previously (6). 13C-,15N-labeled 24x′ was expressed using a 1:100 dilution of Bioexpress media (Cambridge Isotope Laboratories, Tewksbury, MA) in labeled M9 media (16). NMR samples were ∼300 μM protein in (pH 6) 50 mM phosphate buffer (90% H2O and 10% D2O).
Figure 1.
Domain structure of human elastin and the domain structure and sequences of minielastin proteins 24x′ and 20x′. Hydrophobic domains are brown and crosslinking domains are green. To see this figure in color, go online.
Purification of elastin fibers
Purification of elastin fibers from fresh bovine neck ligaments was performed using a protocol (17) that yields pure elastin fibers with smooth surface and uniform diameter (Fig. 6 a). Briefly, samples of appropriate size for NMR were initially cut from the large ligament, washed with aqueous sodium chloride to remove water-soluble proteins and then with organic solvents to remove lipids. Other proteins were removed by treatment with cyanogen bromide (elastin has no methionine) followed by a wash with aqueous urea containing β-mercaptoethanol and final purification by limited trypsin digestion for 4 h at 37°C to remove microfibrillar components (in mature elastin, most trypsin cut sites are eliminated because of cross-linking). Purified samples were stored at −80°C.
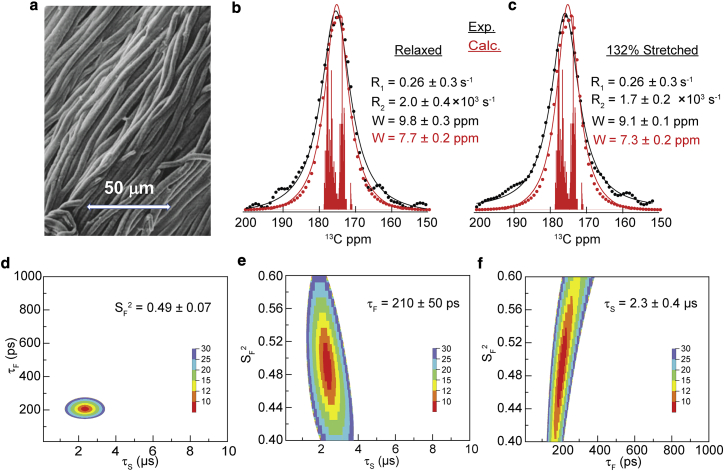
Figure 6.
(a) Mean ± SE of purified bovine elastin fibers. (b and c) 500 MHz 13C-spectra of (black dots) fibers relaxed and 132% stretched. Vertical red lines are the “stick” spectrum indicating the simulated chemical shifts of the bovine elastin sequence. Calculated spectra (red dots) obtained by convoluting the stick spectrum with the indicated R2-values. Continuous curves are Lorentzian fits of the experimental (black lines) and calculated spectra (red lines) with the indicated linewidths, W. (d–f) χ2 surfaces of Eq. 12 fit to the relaxation data (R1 and R2 at 500 and 700 MHz). To see this figure in color, go online.
NMR measurements of backbone amide exchange
Amide 15N-1H-exchange rates in 24x′ were measured on a 700-MHz Varian Inova Instrument (Varian, Inc., Palo Alto, CA) using the CLEANEX-PM pulse sequence during which buildup of NMR signal, I(τ), as a function of the exchange time, τ, is as follows (18):
| (1) |
where I0 is the reference signal intensity obtained from the fast heteronuclear single quantum coherance (HSQC) spectrum and kex is the amide proton exchange rate. RA and RB are NMR relaxation rates of the water and amide protons, respectively. Spectra were accumulated with 1500 and 64 complex points in the direct and indirect dimensions, respectively, 16 scans per t1 increment, a recycle delay of 1.5 s and six exchange times: 5, 50, 100, 200, 350, and 400 ms. Values of kex were extracted from the plots of the signal intensity ratio I(τ)/I0 vs. τ, and reported errors are errors of the fit.
NMR relaxation measurements of minielastins
NMR relaxation measurements of minielastins were collected at 298 K on Bruker (Billerica, MA) Avance 500, 600, 700, and 800 MHz Instruments equipped with cryoprobes. For 15N-HN relaxation, 90° pulse widths on all four instruments varied from 7 to 10 μs (1H) and 25–40 μs (15N). Data were processed using NMRPipe (19) and TopSpin 3.5pI7 software. Relaxation rates were calculated using peak heights and steady-state 1H-15N-NOE values were calculated from the ratio of peak heights in NMR spectra acquired with and without proton saturation. The signal/noise ratio in each spectrum was used to estimate the experimental uncertainty.
15N-R1, R2, and NOE at 600 MHz were measured by chemical exchange saturation transfer (CEST) (20) to probe for the presence of slow exchange processes, which are not present. 15N-CEST spectra were recorded with a B1 field of 87.5 ± 4 Hz calibrated as previously described (21,22), with an 1H-decoupling field strength of 3.5 kHz centered at 8.5 ppm during the mixing time (500 ms) and 70 B1 offsets from 102 to 136.5 ppm. A reference experiment with a null mixing time was also acquired. The spectral parameters were 512 and 64 complex points in the direct and indirect dimensions, respectively, four scans per t1 increment and a recycle delay of 1.5 s. Data were plotted as normalized peak intensity (to the reference intensity) versus offset and errors in the data points were estimated from the deviation of peak intensities in which peak attenuation was not occurring. Extraction of R1 and R2 from the data utilized an in-house python script. R1 spectra were recorded with 10 delay times (10–1200 ms) and 2-s recycle delay and R2 spectra with eight delays (10–350 ms) and 1-s recycle delay. NOE spectra were recorded with a 10-s saturation period and 4-s recycle delay. Acquisition parameters were 1024 and 200 complex points in direct and indirect dimensions, respectively, and 20 scans per t1 increment.
15N-R1, CPMG R2, and NOE at 500 and 800 MHz on 24x′ were determined using the pulse sequences of Farrow et al. (23). R1 spectra were recorded as pseudo-three-dimensional (3D) experiments with nine delay times (10–1200 ms) and 2-s recycle delay; R2 pseudo-3D spectra were acquired with eight CPMG delay times (17–340 ms) and a 1-s recycle delay. NOE spectra were recorded with a 5-s saturation period and no recycle delay.
15N-R1, R2, and NOE at 500 and 700 MHz on 20x′ were determined using the pulse sequences of Farrow et al. (23). R1 spectra were recorded as pseudo-3D experiments with nine delay times (20–1200 ms) and 1.5-s recycle delay; R2 pseudo-3D spectra were acquired with eight CPMG delay times (17–340 ms) and a 1.5-s recycle delay.
HNCO-based 13CO-R1 and R2 at 500 and 700 on 24x′ were determined using the pulse sequences of Chang and Tjandra (24). R1 spectra were recorded with nine delay times (10–1600 ms) and a 1.5-s recycle delay; R1rho spectra were acquired with a B1 field of 2500 Hz, seven τ-values (10–240 ms), and a 1.5-s recycle delay.
Fitting parameters (correlation times and order parameters) to the relaxation data
R1, R2, and NOE were fit with Eqs. S1a–S1c and spectral density functions Eq. 3 or Eq. 10b for minielastin and Eq. 12 for purified natural elastin fibers. To account for the contributions to relaxation from dipolar coupling to protons and chemical-shielding anisotropy, we have used rHN = 1.02 Å, η = 0, and = −114.7 ppm for 15N and rHC′ = 1.69 Å (14), η = 0.81, and = −77 ppm for 13C′ (25). Optimum parameter values were obtained by a Monte Carlo or a grid search for the minimal value of χ2 with χ2 defined (23,26) as follows:
| (2) |
and subscripts “e” and “c” indicate experimental and calculated values, respectively. The sum is over NMR frequencies. Standard errors in the parameters were determined by Monte Carlo simulation as previously described (27, 28, 29). Five hundred normally distributed data sets were generated using the relaxation parameters back calculated from the optimum fit and the experimental uncertainties (Tables S1 and S4) as the Gaussian means and standard deviations, respectively. A distribution for each fit parameter was then obtained by fitting each of the data sets in the same way as the experimental data. The fit parameters, shown in Figs. 4 and 6 and listed in Tables S2, S3, and S5, are the optimum parameters obtained at minimum χ2 with the indicated error limit calculated as the standard deviation of each parameter distribution.
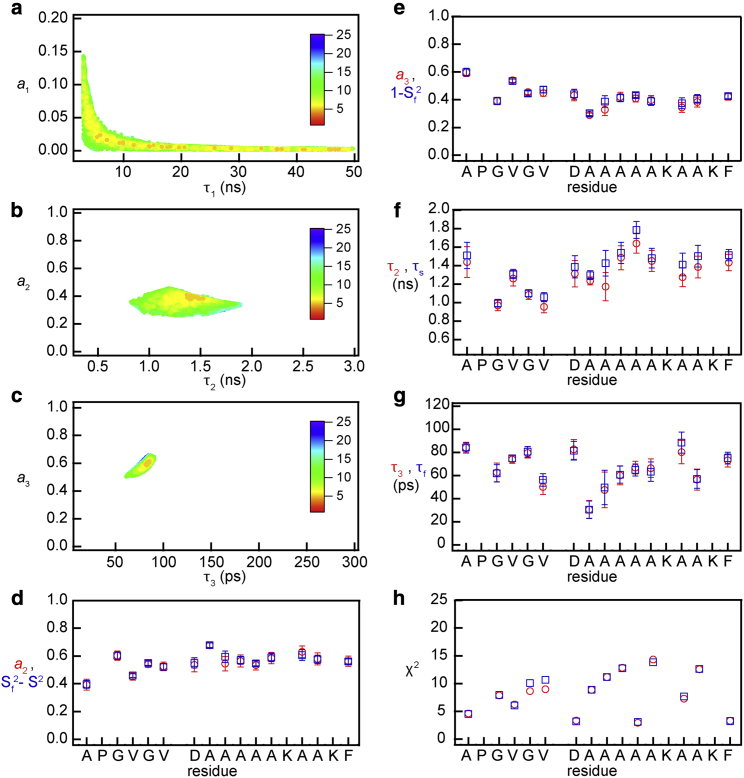
Figure 4.
(a–c) χ2 surfaces for the fit of the Eq. 3 spectral density to the relaxation data from the first residue of the hydrophobic repeat (A1). (d–g, red) Fit parameters obtained using the three-term Lorentzian (five parameters), Eq. 3. (d–g, blue) Fit obtained using Eqs. 10 (four parameters). Errors in both cases are determined as described in the Fitting parameters (correlation times and order parameters) to the relaxation data section of the Materials and methods. (h) Per residue χ2 of the fits using Eq. 3 (red) and Eqs. 10 (blue). To see this figure in color, go online.
Static 13C-NMR spectra of stretched and relaxed elastin
Static 13C-NMR spectra of stretched and relaxed elastin were obtained on a homebuilt 500 MHz spectrometer and a 700-MHz Varian Inova Spectrometer. For the 500 MHz instrument, the ends of a dry elastin sample (∼2 mm × 25 mm) were superglued to ∼2-cm length of a 3.2-mm G10 rod (purchased from McMaster-Carr, Elmhurst, IL) overnight equilibration in 2H2O, the fiber assembly was inserted into a 5-cm length of a 5-mm NMR tube open at both ends. At one end, the rod was sealed to the glass tube with glue. So that the sample could be stretched, the rod protruding at the other end was held in place and sealed with parafilm. This assembly was inserted into the horizontal coil of the homebuilt probe (30). R1 and R2 relaxation times were measured using inversion recovery and Hahn echo pulse sequences with relaxation delays of 4 s. An arrangement similar to the above was adapted for the unmodified cryoprobe of the 700 MHz instrument and a 5-mm sample tube with the closed end removed. G10 rods were cut to protrude from the ends of the NMR tube so that the elastin sample (2 mm × 29 mm) was centered in the sample coil. The lower rod was glued to the NMR tube, and the upper rod was held in place with parafilm. R1 spectra were recorded at nine delays (0.25–12 s) and R2 spectra measured with a Hahn echo at 500 MHz and with CPMG echoes at 700 MHz were recorded at 10 delays (0.2–1.2 ms) with 4-s recycle delays. The 13C-NMR relaxation data of hydrated elastin were processed in a same manner as the 24x′ using χ2 minimization to obtain the best fit parameters, τF, τS, and SF2.
Theory
Dynamic analyses using R1, R2, and NOE data are less well developed for IDPs than for folded proteins. In both cases, the key function in the analysis is J(ω), the Fourier transform of the correlation function c(t) for the dynamics that contribute to spin relaxation. R1, R2, and NOE are related to J(ω) by three standard equations (Eqs. S1a–S1c) (14,31,32). In the widely used Lipari-Szabo (LS) model-free approach, c(t) is factored into independent dynamical modes, each of which is parameterized by an effective correlation time and a corresponding order parameter that are related to the timescale and amplitude of each dynamical mode, respectively (33,34). LS has been used to analyze NMR relaxation in folded proteins and recently to analyze the 30-residue disordered terminus of an otherwise folded protein (14,15). However, the general application of LS to IDPs has been questioned (35) and an alternative procedure, spectral density mapping (SDM), has also been used (36). In this method, the correlation function is not parameterized. Instead, the spectral density at five frequencies (0, ωN, ωH − ωN, ωH, and ωΗ + ωN is determined from R1, R2, and NOE at two or more magnetic field strengths (35,36). Insofar, because Eqs. S1a–S1c are valid, SDM is rigorous. However, SDM does not directly relate to molecular properties such as the timescales and amplitudes of dynamical modes that are discussed next in the context of parameterized spectral densities. A useful test is to compare the parameterized spectral density with the spectral density map.
An adjunct to SDM that potentially provides greater physical insight is the general form of the correlation function, c(t), for dynamical processes like diffusive or jump-like dynamics (37,38):
| (3) |
The spectral density is then the following equation:
| (4) |
and is the Lorentzian function with correlation time,. Khan and co-workers constrained the correlation times to a range from 21 ps to 21 ns and separated by factors of 4, to limit the general correlation function to six terms with five adjustable coefficients, (15). A method for detecting the predominant correlation times in the spectral density has also been recently described (39). Here, we simply limit the number of terms in Eq. 3 so that the minimal number of parameters required to fit the data within experimental errors is not exceeded. In this way, timescales of the dynamical modes present in the system under study can be identified. Note that the coefficients specify the contribution of each dynamical mode to the total spectral density but not a physical property like the amplitude of a motion.
To better understand the coefficients, a master equation for a specific dynamical model can be used (37). However, for even simple models, the number of terms in the spectral density (Eq. 4) typically exceeds what is experimentally accessible. Ways in which this is reduced in structured proteins have been discussed in detail (33,34,40) and those potentially relevant to IDPs are summarized next. Details of individual steps are provided in the theory section of the Supporting materials and methods.
For IDPs in solution, the slowest motion is diffusional reorientation of the aggregate protein. Insofar as the correlation times for overall reorientation are greater by a factor of 10 or more than those for internal dynamics, c(t) can be approximated as a product (34,39,41):
| (5) |
where co(t) and cI(t) are, respectively, the correlation functions for overall and internal motions. For structured proteins that are not spherical, co(t) is well approximated by a correlation function with two terms (34):
| (6) |
With A = 1, Eq. 6 reduces to co(t) for a spherical protein.
IDPs have a flexible backbone and, in turn, a distribution of hydrodynamic radii (42,43). The distribution of overall correlation times is not easily obtained from NMR relaxation of backbone atoms, which is dependent on both overall reorientation and large amplitude internal motions. Norton and co-workers circumvented this problem by assuming that the hydrodynamic radius, , in the Stokes-Einstein equations for translational diffusion, , and rotational diffusion, , are the same (44). Then, the average hydrodynamic radius is independently determined by measuring the translational diffusion constant using pulsed field gradient (PFG) NMR or ultracentrifugation (6,45).
For many polymers and IDPs, the distribution of hydrodynamic radii is approximately Gaussian and for IDPs with molecular weights comparable with 24x′, the average hydrodynamic radius, is fourfold to fivefold greater than the Ggaussian width, σ (42,43,46). With this distribution, and are equivalent within a few percent for n = ±1, ±3 (Supporting materials and methods, Theory), and are used interchangeably. Thus, we calculate the average hydrodynamic radius from the experimentally determined translational diffusion constant, as follows,
| (7a) |
and the average rotational correlation time is then:
| (7b) |
Averaging Eq. 6 with a discrete Gaussian distribution and A = 1, we obtain the following equation:
| (8a) |
with the following equation:
| (8b) |
To account for internal dynamics with more than a single-exponential correlation function, we use the four-parameter from the extended LS method (41):
| (9) |
are the generalized order parameters, and are effective correlation times for fast (F) and slow (S) internal motions. The three order parameters are constrained by the relation, . In the limit of axially symmetric motion, , which is the same as the order parameter S used in solid state NMR (34). When using Eq. 9, it is assumed that the fast and slow modes can be approximated with single-exponential correlation functions and that and differ by an order of magnitude or more (41). With these conditions, the order parameters , are equilibrium properties of the dynamics.
The total correlation function, Eq. 5, is the product of Eqs. 8a and 9:
| (10a) |
Equation 10a has 3L terms and this simplifies to L + 2 terms when overall reorientation is slow compared with internal dynamics, . After Fourier transformation, the result is (Supporting materials and methods, Theory) the following equation:
| (10b) |
Equation 10b is closely related to the general spectral density, Eq. 4, truncated to three terms. In the limit that , where is the lowest NMR frequency, Eq. 10b also reduces to three terms:
| (10c) |
with,
| (10d) |
In this limit, Eq. 4, which was truncated to three terms, and Eq. 10c are formally equivalent with parameters related by the following equation:
| (11) |
The above equation results can also be used to analyze relaxation in fibrous elastin, a material that is extensively cross-linked, and overall reorientation is quenched. In the limit of , Eq. 10c reduces to the following equation:
| (12) |
Results
Backbone amide solvent exchange
To focus on motional dynamics, we first show that proton exchange at solvent exposed amides, known to affect NMR relaxation (47), is negligible in our experiments which were performed at pH 6.0 to slow this exchange. Proton exchange rates were obtained using the CLEANEX-PM method (18) (Fig. 2). Baum and co-workers studied amide proton exchange rates in an IDP displaying exchange rates from 3 to 35 s−1, significantly larger than those observed here (47). They showed that decay of the NMR signal, I(t), as a function of the CPMG echo delay, t, obeys Eq. 13:
| (13) |
where 0.011 is the fractional antiphase magnetization and Q = 0.9 for 10% solvent deuteration as we used here. The term in between brackets in Eq. 13 is the exchange correction to the experimentally observed R2 decay. In the worst case in our data, R2 = 2 s−1and kex = 0.8 s−1, the calculated correction is less than 5% of the R2-value, smaller than the average error of our uncorrected fits (Fig. 2; Tables S1a and S1b) and, therefore, this correction was not made. Additionally, CEST experiments show the absence of other slow exchange processes.
Figure 2.
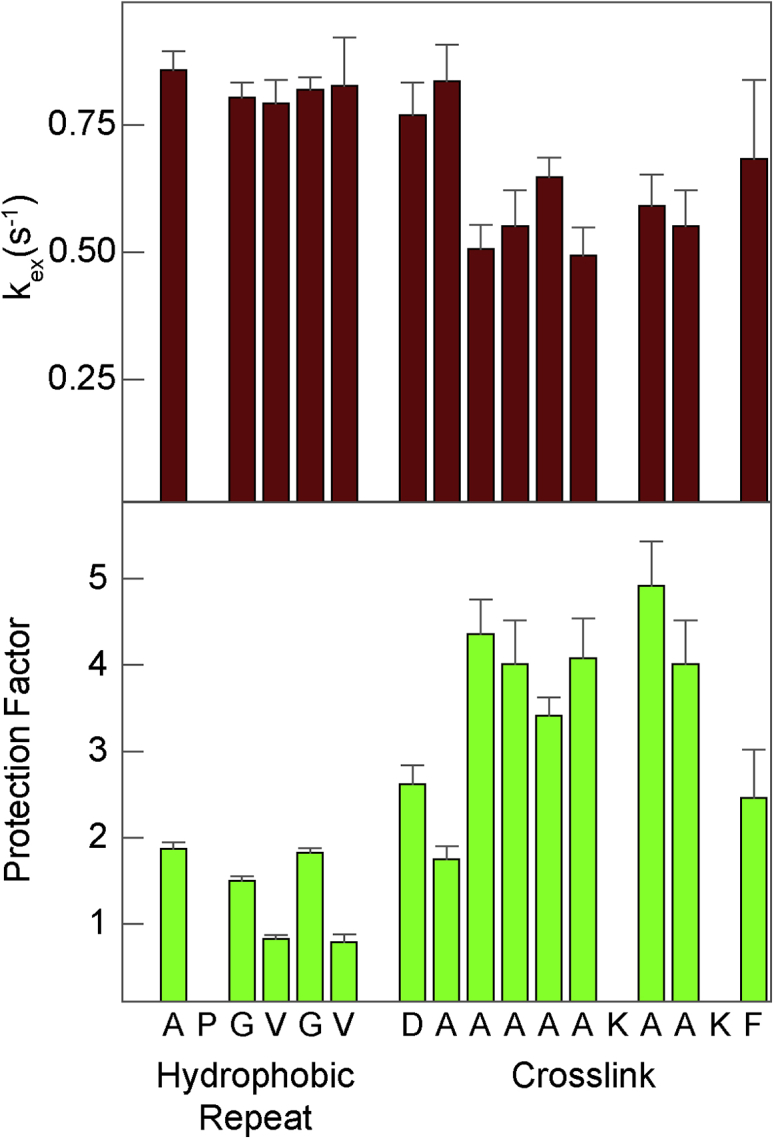
Amide proton exchange rates (top) in the hydrophobic repeat 24′ = (APGVGV)7, and cross-link, x′ = (DA5KA2KF), modules at pH 6 in 24x′. Error bars depict errors of the exponential fits. Protection factors (bottom) are calculated from the exchange rates as described by Englander and co-workers (48). To see this figure in color, go online.
Protection factors calculated from the exchange rates (48,49) are less than two for residues in hydrophobic modules and, systematically, higher than three for residues in the central portion of the cross-link module. Protection factors less than five indicate an absence of secondary structure (50). Thus, these amide protein exchange rates reflect the absence of secondary structure in the hydrophobic modules and weak ordering in the central residues of the cross-link modules confirming our previous conclusion formed on the basis of backbone chemical shifts (6).
Backbone 15N- and 13C-relaxation parameters
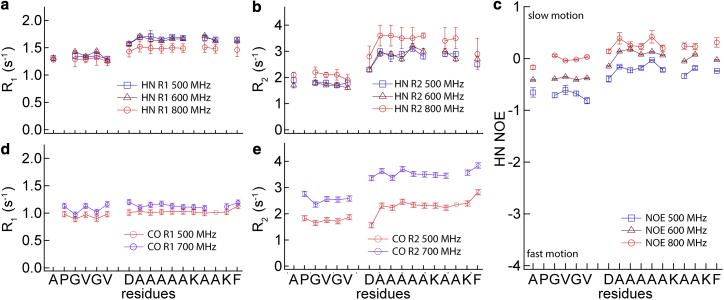
Backbone 15N- and 13C-relaxation parameters obtained from 24x′, a 203-residue minielastin, are shown graphically in Fig. 3. 15N-data were obtained at three NMR frequencies (500, 600, and 800 MHz) and 13C-data were obtained at two frequencies (500 and 700 MHz). The complete data sets are listed in Tables S1a and S1c. 15N-relaxation data from a 138-residue minielastin, 20x′, closely parallels the 15N-data from 24x′ and is listed in Table S1b. There are three key features of the data: First, the faster R1 and R2 relaxation rates and larger 15N-NOEs observed in the cross-link modules indicate slower and/or more restricted motion than in the hydrophobic modules. This is consistent with our earlier chemical shift-based prediction of partial helical conformation in the cross-link modules (6). Second, the small R2/R1 ratios (∼2–∼3) in both hydrophobic repeat and cross-link residues indicate that fast backbone motions with correlation times less than a few nanoseconds affect spin relaxation significantly more than overall reorientation of the protein, which has a substantially longer correlation time (τM > 10 ns) (14). Third, observed NOEs are frequency dependent and approach the slow-motion limit (NOE ≈ 0.85) at 800 MHz. This indicates the presence of motions with correlation time(s) shorter than that for overall reorientation and longer than that for fast backbone motions (41).
Figure 3.
NMR relaxation data for 24x′ at the indicated NMR frequencies. (a–c) [15N]amide R1, R2, and NOE. (d and e) [13C]carbonyl R1 and R2. R1 and R2 error bars reflect errors of exponential fits to the relaxation data. NOE error bars reflect the ratio of the differential NOE signal to the baseline noise. To see this figure in color, go online.
Fits of the 15N-relaxation data
Fits of the 15N-relaxation data using Eq. 3 truncated at three terms and Eq. 10a are summarized in Fig. 4. Although R1- and R2-values could be fit with two terms in Eq. 3, this three-parameter correlation function predicted NOEs that were less than the experimental values. This was resolved by adding a third term with an intermediate correlation time and an additional coefficient (41). χ2 surfaces for this five-parameter fit with Eq. 3 are shown for a representative residue, A1, in the hydrophobic repeat, Fig. 4, a–c. Residue-specific parameters from this fit are shown in Fig. 4, d–g (red marks). Standard errors are typically ±15% except for the slowest motion that is fit with τ1-values from 4 ns to more than 50 ns and a1 from 0 to 0.15. However, within this large range, the best fit values of τ2, τ3, a2, and a3 are essentially unchanged (Fig. 4, b and c). Importantly, there is a timescale separation between τ2 and τ3: in all cases τ2 > 10τ3.
To determine the slowest motion, we have used the hydrodynamic radii previously determined by PFG NMR for 20x′ and 24x′, 29.4 and 35 Å, respectively (6). Other possible slow motions, amide proton exchange and slow conformational change, are shown above to have negligible effect on R2 relaxation rates and we assume that the slowest motion in these soluble minielastins is global reorientation of the disordered protein. Using the Stokes-Einstein relation for rotational diffusion, the average rotational correlation times are 36 ns for 24x′ and 22 ns for 20x′. Combined with the timescale separation between τ1 and τ2, we see that <τM> > 10τ2 > 10τ3 and the modified LS spectral density is fit to the 24x′ relaxation data with <τM> = 36 ns. Fits of the four adjustable parameters to Eq. 10b, Fig. 4, d–g (blue marks) and Table S3, are insensitive to the width of the distribution of hydrodynamic radii and the spectral density Eq. 10b reduces to Eq. 10c. Because the value of <τM> determined from the hydrodynamic radius is within the large range that τ1 is constrained by the relaxation data alone, τS and τF are essentially equivalent to τ2 and τ3 and the minimal χ2-values, Fig. 4 h, for the four-parameter fit are, in most cases, the same as for the five-parameter fits. Values of the correlation times for slow internal motions (chain dynamic) vary from 1.0 ± 0.1 to 1.5 ± 0.2 ns for residues in the hydrophobic repeat and 1.3 ± 0.1 to 1.8 ± 0.1 ns in the cross-link modules. Correlation times for the fast chain motions vary from 56 ± 5 to 84 ± 4 ps in the hydrophobic repeat and from 30 ± 7 to 88 ± 7 ps in the cross-link modules with the longer values grouped in the in the center of the module. Because of the timescale separation between parameters, order parameters indicating the amplitudes of the backbone motions have been determined in addition to the correlation times. A striking result of this analysis is the nearly complete overall dynamic disorder, .
To test these conclusions, we performed the same analysis of 15N-relaxation data from 20x′, a smaller minielastin (Table S1b), and to 13C-relaxation data from the backbone carbonyl atoms in 24x′ (Fig. 3, d and e; Table S1c). Because 20x′ (138 residues) is shorter than 24x′ (203 residues), the correlation time for global reorientation is closer to the backbone correlation times, and this experiment tests the assumption that global reorientation and backbone dynamics in an IDP can be treated as independent dynamical modes because of their different timescales. The modular structure of 20x′ (20′-x′-24′-x′-24′ (20′ = (VPGVGG)5)) has the same cross-linker flanked by the same hydrophobic modules at the C-terminus and the chemical shifts of residues in the 24′ and x′ modules are equivalent to those in 24x′. Fits of the 15N-relaxation using the LS spectral density and the smaller rotational correlation time (<τM> = 24 ns) yields backbone order parameters, S2 and SF2, and correlation times, τS and τF, that are essentially equivalent to those determined for 24x′. We conclude that the assumption of independent global reorientation and internal dynamics is a good approximation for minielastins with molecular weights greater than 13 kDa. The 13C-experiments examine backbone motions at atomic locations between the amide groups and sample the spectral density at different frequencies. From the analysis of the 13C-data, Table S3c, we see that the correlation times and order parameters are in close agreement with those determined using 15N-NMR, Table S3a. Thus, the high backbone disorder found at the backbone amide sites is also observed at the intervening carbonyl sites.
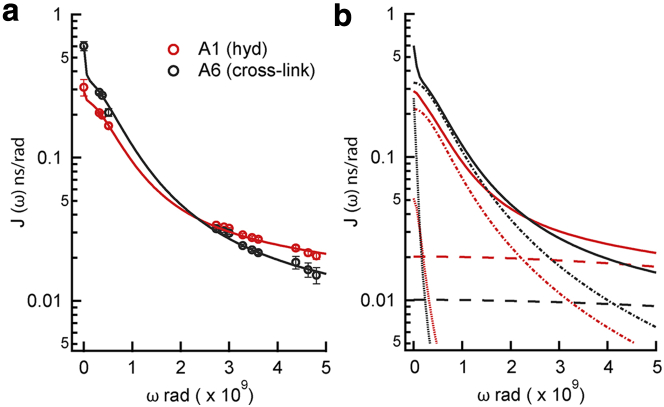
The agreement between the LS spectral density and the spectral density map, Fig. 5, is excellent in frequency ranges in which the two methods overlap and both analyses show that the dynamics of residues in the hydrophobic modules and the cross-link modules are different. Contributions to the parameterized spectral density from the three dynamical modes are shown in Fig. 5 b. At frequencies below 0.5 × 109 s−1, the contribution from slow backbone motions is greater than the contribution from much slower global reorientation due to the high amplitude of the backbone motions (S2 ≈ 0). At frequencies above 6 × 109 s−1, only motions from fast backbone dynamics contribute to the spectral density.
Figure 5.
Logarithmic graphs of the spectral density versus NMR frequency. Red and black indicate A1 in the hydrophobic repeat and A6 in the center of the cross-link module, respectively. (a) The total spectral density obtained from Eq. 10 with Fig. 3 parameters (continuous curve) and SDM (solid circles). (b) Contributions to the total spectral density (continuous curves) from the terms with slow (dotted lines), intermediate (dot-dashed lines),and fast (dashed lines) correlation times. To see this figure in color, go online.
Dynamic analysis of purified bovine elastin
To compare dynamics in fibrous elastin with soluble 24x′, we have studied the backbone carbonyl atoms of purified elastin fibers with 13C-NMR. Carbonyl isotropic shifts are dispersed over a small range that is well separated from other carbon shifts and 98% of carbonyl groups in elastin are from the protein backbone. Because global reorientation of the highly cross-linked protein does not occur, the overall order parameter, S, for backbone motions can be estimated from the line width of spectra obtained without MAS. Linewidths in the spectra of static samples (Fig. 6, b and c) are 9–10 ppm and similar to those previously observed with MAS (9) and small compared with static shielding anisotropy of carbonyl groups, Δσstat ∼116 ppm, indicating that the carbonyl groups in fibrous elastin are highly disordered. The small residual anisotropy and, in turn, the backbone order parameter were estimated from the spectrum line width by accounting for the contributions to the line width from the experimentally determined spin relaxation rate R2/π = 640 Hz (5 ppm) and the dispersion of isotropic chemical shifts. A simulated 13C-spectrum of tropoelastin carbonyl isotropic shifts was convoluted with the experimentally determined R2 and then fit to a Lorentzian (Fig. 6, b and c). Isotropic shifts were simulated for the bovine tropoelastin sequence (51) using the chemical shift protocol that predicted observed 13C′-shifts in 24x′ (6,52). The residual shielding anisotropy, Δσres, is then the difference between the linewidths of Lorentzian fits of the observed and the calculated spectra indicating a residual anisotropy in the range of 1–4 ppm. In turn, the estimated value of S for chain dynamics in purified elastin, Δσres/Δσstat, is in the range of 0.01–0.03 and S2 ≈ 0.001, which is well within the range of S2 determined for the minielastins using 15N- or 13C-NMR relaxation. At the resolution of this experiment, we find no evidence for either stretch induced ordering of the elastin backbone or greater ordering of the protein in cross-linked elastin fibers compared with soluble minielastins.
Combined with the order parameter determined from the residual shielding anisotropy of the backbone carbonyls, the timescales of backbone motions in natural elastin were determined from the 500 and 700 MHz R1 and R2 data (Fig. 6; Table S4). Compared with 13C-relaxation rates of 24x′ in solution, R1 is fourfold lower and R2 is three orders of magnitude greater. Because global reorientation makes only a small contribution to relaxation in 24x′ (S2 ≈ 0), these large differences in the relaxation rates are not because of the loss of global reorientation. Moreover, the observed R1- and R2-values are not consistent with a single-correlation time for backbone dynamics, and we have fit the relaxation data to Eq. 12, the modified LS spectral density that includes backbone motion with two correlation times and no global reorientation. Because sample stretch did not affect R1 or R2 within experimental error, their averages were used and S2 was set at the value estimated from the residual anisotropy. The χ2 surfaces, Fig. 6, d–f, show that the correlation times τS and τF but not SF2 are well constrained by the available data. Limiting the fit range to 0.4 < SF2 < 0.6, we find that τF = 210 ± 50 ps and τS = 2.3 ± 0.4 μs. Compared with the soluble minielastins, elastin has no significant increase in backbone ordering, a large increase (by three orders of magnitude) in the slow correlation time for backbone motions and a small increase (fourfold) of the correlation time for the fast backbone motions. We also find no experimentally significant increase in backbone ordering when the elastin samples were stretched.
Discussion
We have used NMR methods to determine the domain average timescales and amplitudes of dynamics in two soluble minielastins and the protein-average dynamics in purified natural elastin fibers. For the minielastins, 13C- and 15N-relaxation data were combined with PFG data and analyzed using three methods: SDM (36), a general spectral density function (37), and a modified LS spectral density (33). The latter accounts for the distribution of hydrodynamic radii found in IDPs (42,43) and protein backbone motions with well-separated correlation times, τS and τF. If the distribution of hydrodynamic radii is symmetric and the correlation time <τM> for the average hydrodynamic radius is large, the modified LS spectral density is mathematically equivalent to the general spectral density truncated at three Lorentzian terms. Analysis of the relaxation data obtained at three fields was found to be consistent with a general spectral density that has at least three Lorentzian terms and thus, the modified LS spectral density as well. Fits of a two-term spectral density to the R1 and R2 data predicted incorrect NOEs. With three terms, the correlation times τ2 = τS and τ3 = τF were well constrained by the relaxation data. At different residues, 1.0 < τS < 1.6 ns and 30 < τF < 84 ps. However, the longest correlation time, τ1, was not well constrained by the NMR relaxation data alone (Fig. 4 a) indicating the need for additional information to determine the slowest motions. Effects on relaxation rates from slow conformational exchange and amide proton exchange rates were determined to be negligible, indicating that the longest correlation time is due to overall reorientation of the protein, i.e., τ1 = <τM>. Using the average hydrodynamic radius of 35 Å for 24x′, 29.4 Å for 20x′ (6), and the Stokes-Einstein relation, <τM> were determined to be 36 and 22 ns, respectively. The separation of timescales, <τM> > 20τS > 20τF, indicates that an LS type spectral density can be used and that the coefficients of the Lorentzian terms (ai in the general spectral density in Eq. 3) are related to generalized order parameters (and in Eq. 11) that are measures of the amplitudes of the “internal” chain dynamics. Although the number of different dynamical modes in an IDP is likely to be large, the number of terms in the spectral density was not extended beyond three given the available data. Previously, a three-term spectral density was used to analyze NMR relaxation data of an IDP (53). Herein, we have tested this simplification in three ways. First, the spectral density is in excellent agreement with the spectral density map over a wide range of frequencies indicating that it accounts for the available data, Fig. 5. To test the key assumption that global reorientation of an IDP is independent of the large amplitude chain motions, NMR data from a smaller minielastin (138 compared with 203 residues) with a smaller <τM> (22 ns compared with 36 ns) that is closer to the timescale of the internal chain dynamics was also studied. The parameters (τF, τS, , and 2) determined for the backbone motions in 20x′ from the relaxation data are the same as those for 24x′. In other words, changing the length of the protein did not change the description of the chain motions obtained from our analysis. Finally, we used 13C-NMR to study the backbone motions at the carbonyl groups in 24x′. In this experiment, backbone dynamics were studied at positions close to the amide groups and the spectral density was sampled at additional frequencies. The correlation times and order parameters from our analysis of the 13C-data, Table S3c, are in close agreement with those determined using 15N-NMR, Table S3a.
A key result of our analysis is that the overall backbone order parameters, , at amide and carbonyl sites have been determined in addition to the correlation times; both of which can be compared with values found in folded proteins and other IDPs. We find that the backbone correlation times in 20x′ and 24x′ are similar to those reported in both well-structured proteins (54) and in IDPs such as the disordered region of GCN4 (14), residues 146–199 of Engrailed 2 (15) and the disordered C-terminus of a Sendai virus protein (53). As expected, the overall order parameter for backbone motions in 20x′ and 24x′, is significantly smaller than found in well-structured proteins, (32). However, the -values in the minielastins studied here are also less than in the disordered region of GCN4 except for the most disordered residues at the N-terminus (14). Using Eq. 11 to interpret the coefficients of the three-term correlation function used in the analysis of the Sendai virus protein (53), we again find that this protein is also more ordered than 20x′ or 24x′ except for residues at the termini. We note that the disordered region of GCN4 folds upon DNA binding (55), whereas elastin retains high disorder after assembly into the mature elastic matrix. The absence of secondary structure in these minielastins that is indicated by NMR relaxation is in agreement with our previous results based on secondary chemical shifts and NOEs (6). IDPs with high proline content have a propensity for the formation of flexible structures with extended backbone conformations similar to polyproline II helices (45,56,57). For example, this is consistent with the observation of upfield Cα-secondary shifts observed in Pdx1-C (58), an IDP with a proline content of 22%. However, upfield Cα-secondary shifts were not observed in either 20x′ or 24x′, which have a smaller proline percentage in their sequences, at 14% (6).
To compare dynamical amplitudes and timescales in soluble minielastins with those in mature cross-linked elastin fibers, we have refined an earlier study of disorder in bovine elastin (9) and determined the relevant correlation times in purified elastin fibers using natural abundance 13C-NMR without MAS. Although this experiment does not have residue-specific resolution, it provides an overall picture of the timescale and amplitude of carbonyl group dynamics and refines an earlier estimate of backbone disorder obtained from 13C-NMR with MAS (9). Because of extensive cross-linking, global reorientation of the protein is absent and the overall order parameter for chain dynamics is estimated directly from the contribution of residual 13C-shielding anisotropy to the observed line widths. In both stretched and relaxed elastin, the residual anisotropy is small indicating that the average backbone order parameter in cross-linked elastin is essentially the same as found in soluble 20x′ and 24x′. This result fully supports our analysis of the amplitude of backbone dynamics in the minielastins. Thus, elastin-like sequences are highly disordered both in solution and in the natural, cross-linked material (6,9). Results from Reichheld and co-workers (59) indicate that this is also the case in a coacervated minielastin. However, the dramatically different relaxation times in elastin (Fig. 6) indicate that backbone motions are significantly slowed in the cross-linked material: the slow correlation time τS increases by a factor of 103, whereas τF is much less affected and increases by a factor of 4. This suggests that the slow motion corresponds to chain dynamics on the length scale of the spacing between cross-links and the fast motion on a shorter and more local length scale that would be less affected by cross-links. The spacing between cross-links in elastin is the length of the hydrophobic domains that varies from 11 to 55 residues (7). We conclude that structured regions in mature elastin are either absent or constitute a small part of the protein. Thus, a recent study of the naturally occurring cross-links in elastin, which shows that all cross-link domains are connected in multiple ways (60) is in complete agreement with the dynamical properties of elastin and minielastins determined here.
Conclusions
We find that the very high chain disorder observed in solution is retained in mature, cross-linked elastin. Moreover, no evidence for increased local ordering of the protein backbone induced by mechanical stretch is observed. Although the exact quantitative correlation between backbone order parameters and configurational entropy remains a topic of discussion (61,62), it is clear that order parameters as low as we observe in both minielastins and in natural elastin fibers in stretched and relaxed states are indicative of high flexibility and, consequently, high configurational entropy (63,64). Previously, we reported a 10-fold increase of the ordering of water when fully hydrated elastin fibers are stretched by 50% (65). Together, these results support the hypothesis that stretch induced solvent ordering, i.e., the hydrophobic effect, is a key player in the elastic recoil of elastin (11,12).
Author contributions
M.F.C.A.C., J.M.P., R.J.W., and R.L.K. designed research. M.F.C.A.C., J.M.P., N.M.J., T.M.S., S.B., and J.M.A. performed research. M.F.C.A.C., R.J.W., and R.L.K. wrote the manuscript.
Acknowledgments
The authors gratefully acknowledge support from the National Science Foundation (DMR-1410678) to R.J.W. and R.L.K. Program and infrastructure support was from the National Institutes of Health, National Center for Research Resources to the City College of New York (5G12-MD007603-30). Prof. R.L.K. is a member of the New York Structural Biology Center. Some of the work presented here was conducted at the Center on Macromolecular Dynamics by NMR Spectroscopy located at the New York Structural Biology Center, supported by a grant from the National Institutes of Health, National Institute of General Medical Sciences (GM118302). J.M.P. was the recipient of a fellowship award from the U.S. Department of Education Graduate Assistance in Areas of National Need Program in Biochemistry, Biophysics, and Biodesign at The City College of New York (PA200A150068). The authors declare no competing financial interests.
Editor: Elizabeth Rhoades.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.06.043.
Contributor Information
Richard J. Wittebort, Email: dick.wittebort@louisville.edu.
Ronald L. Koder, Email: rkoder@ccny.cuny.edu.
Supporting material
References
- 1.Cocciolone A.J., Hawes J.Z., Wagenseil J.E. Elastin, arterial mechanics, and cardiovascular disease. Am. J. Physiol. Heart Circ. Physiol. 2018;315:H189–H205. doi: 10.1152/ajpheart.00087.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Vrhovski B., Weiss A.S. Biochemistry of tropoelastin. Eur. J. Biochem. 1998;258:1–18. doi: 10.1046/j.1432-1327.1998.2580001.x. [DOI] [PubMed] [Google Scholar]
- 3.Parker K.H. A brief history of arterial wave mechanics. Med. Biol. Eng. Comput. 2009;47:111–118. doi: 10.1007/s11517-009-0440-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wagenseil J.E., Mecham R.P. Elastin in large artery stiffness and hypertension. J. Cardiovasc. Transl. Res. 2012;5:264–273. doi: 10.1007/s12265-012-9349-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.He D., Chung M., Parkinson J. Comparative genomics of elastin: sequence analysis of a highly repetitive protein. Matrix Biol. 2007;26:524–540. doi: 10.1016/j.matbio.2007.05.005. [DOI] [PubMed] [Google Scholar]
- 6.Greenland K.N., Carvajal M.F.C.A., Wittebort R.J. Order, disorder, and temperature-driven compaction in a designed elastin protein. J. Phys. Chem. B. 2018;122:2725–2736. doi: 10.1021/acs.jpcb.7b11596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tamburro A.M., Pepe A., Bochicchio B. Localizing alpha-helices in human tropoelastin: assembly of the elastin “puzzle”. Biochemistry. 2006;45:9518–9530. doi: 10.1021/bi060289i. [DOI] [PubMed] [Google Scholar]
- 8.Urry D.W., Hugel T., Parker T. Elastin: a representative ideal protein elastomer. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2002;357:169–184. doi: 10.1098/rstb.2001.1023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pometun M.S., Chekmenev E.Y., Wittebort R.J. Quantitative observation of backbone disorder in native elastin. J. Biol. Chem. 2004;279:7982–7987. doi: 10.1074/jbc.M310948200. [DOI] [PubMed] [Google Scholar]
- 10.Hoeve C.A., Flory P.J. The elastic properties of elastin. Biopolymers. 1974;13:677–686. doi: 10.1002/bip.1974.360130404. [DOI] [PubMed] [Google Scholar]
- 11.Weis-Fogh T., Anderson S.O. New molecular model for the long-range elasticity of elastin. Nature. 1970;227:718–721. doi: 10.1038/227718a0. [DOI] [PubMed] [Google Scholar]
- 12.Gosline J.M. Hydrophobic interaction and a model for the elasticity of elastin. Biopolymers. 1978;17:677–695. doi: 10.1002/bip.1978.360170311. [DOI] [PubMed] [Google Scholar]
- 13.Salvi N., Abyzov A., Blackledge M. Solvent-dependent segmental dynamics in intrinsically disordered proteins. Sci. Adv. 2019;5:eaax2348. doi: 10.1126/sciadv.aax2348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gill M.L., Byrd R.A., Palmer A.G., III Dynamics of GCN4 facilitate DNA interaction: a model-free analysis of an intrinsically disordered region. Phys. Chem. Chem. Phys. 2016;18:5839–5849. doi: 10.1039/c5cp06197k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Khan S.N., Charlier C., Ferrage F. Distribution of pico- and nanosecond motions in disordered proteins from nuclear spin relaxation. Biophys. J. 2015;109:988–999. doi: 10.1016/j.bpj.2015.06.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang L., Anderson J.L., Koder R.L. Manipulating cofactor binding thermodynamics in an artificial oxygen transport protein. Biochemistry. 2011;50:10254–10261. doi: 10.1021/bi201242a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Daamen W.F., Hafmans T., van Kuppevelt T.H. Isolation of intact elastin fibers devoid of microfibrils. Tissue Eng. 2005;11:1168–1176. doi: 10.1089/ten.2005.11.1168. [DOI] [PubMed] [Google Scholar]
- 18.Hwang T.L., van Zijl P.C., Mori S. Accurate quantitation of water-amide proton exchange rates using the phase-modulated CLEAN chemical EXchange (CLEANEX-PM) approach with a Fast-HSQC (FHSQC) detection scheme. J. Biomol. NMR. 1998;11:221–226. doi: 10.1023/a:1008276004875. [DOI] [PubMed] [Google Scholar]
- 19.Delaglio F., Grzesiek S., Bax A. NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- 20.Gu Y., Hansen A.L., Brüschweiler R. Rapid determination of fast protein dynamics from NMR chemical exchange saturation transfer data. Angew. Chem. Int.Engl. 2016;55:3117–3119. doi: 10.1002/anie.201511711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vallurupalli P., Bouvignies G., Kay L.E. Studying “invisible” excited protein states in slow exchange with a major state conformation. J. Am. Chem. Soc. 2012;134:8148–8161. doi: 10.1021/ja3001419. [DOI] [PubMed] [Google Scholar]
- 22.Guenneugues M., Berthault P., Desvaux H. A method for determining B1 field inhomogeneity. Are the biases assumed in heteronuclear relaxation experiments usually underestimated? J. Magn. Reson. 1999;136:118–126. doi: 10.1006/jmre.1998.1590. [DOI] [PubMed] [Google Scholar]
- 23.Farrow N.A., Muhandiram R., Kay L.E. Backbone dynamics of a free and phosphopeptide-complexed Src homology 2 domain studied by 15N NMR relaxation. Biochemistry. 1994;33:5984–6003. doi: 10.1021/bi00185a040. [DOI] [PubMed] [Google Scholar]
- 24.Chang S.L., Tjandra N. Temperature dependence of protein backbone motion from carbonyl 13C and amide 15N NMR relaxation. J. Magn. Reson. 2005;174:43–53. doi: 10.1016/j.jmr.2005.01.008. [DOI] [PubMed] [Google Scholar]
- 25.Allard P., Hard T. NMR relaxation mechanisms for backbone carbonyl carbons in a 13 C, 15 N-labeled protein. J. Magn. Reson. 1997;126:48–57. doi: 10.1006/jmre.1997.1131. [DOI] [PubMed] [Google Scholar]
- 26.Ochsenbein F., Guerois R., van Heijenoort C. 15N NMR relaxation as a probe for helical intrinsic propensity: the case of the unfolded D2 domain of annexin I. J. Biomol. NMR. 2001;19:3–18. doi: 10.1023/a:1008390606077. [DOI] [PubMed] [Google Scholar]
- 27.Ochsenbein F., Neumann J.M., van Heijenoort C. Dynamical characterization of residual and non-native structures in a partially folded protein by (15)N NMR relaxation using a model based on a distribution of correlation times. Protein Sci. 2002;11:957–964. doi: 10.1110/ps.4000102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Palmer A.G., Rance M., Wright P.E. Intramolecular motions of a zinc finger DNA-binding domain from Xfin characterized by proton-detected natural abundance C-12 heteronuclear nmr-spectroscopy. J. Am. Chem. Soc. 1991;113:4371–4380. [Google Scholar]
- 29.Press W.H., Teukolsky S.A., Vetterling W.T. Second Edition. Cambridge University Press; Cambridge, UK: 1992. Numerical Recipes in Fortran 77: The art of Scientific Computing, Volume 2. [Google Scholar]
- 30.Zhang Q.W., Zhang H.M., Wittebort R.J. Double and triple resonance circuits for high-frequency probes. J. Magn. Reson. 1998;132:167–171. [Google Scholar]
- 31.Cavanagh J., Fairbrother W.J., Skelton N.J. Protein NMR Spectroscopy. Academic Press; 1996. Experimental aspects of NMR spectroscopy; pp. 114–270. [Google Scholar]
- 32.Kay L.E., Torchia D.A., Bax A. Backbone dynamics of proteins as studied by 15N inverse detected heteronuclear NMR spectroscopy: application to staphylococcal nuclease. Biochemistry. 1989;28:8972–8979. doi: 10.1021/bi00449a003. [DOI] [PubMed] [Google Scholar]
- 33.Lipari G., Szabo A. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 2. Analysis of experimental results. J. Am. Chem. Soc. 1982;104:4559–4570. [Google Scholar]
- 34.Lipari G., Szabo A. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982;104:4546–4559. [Google Scholar]
- 35.Kadeřávek P., Zapletal V., Žídek L. Spectral density mapping protocols for analysis of molecular motions in disordered proteins. J. Biomol. NMR. 2014;58:193–207. doi: 10.1007/s10858-014-9816-4. [DOI] [PubMed] [Google Scholar]
- 36.Farrow N.A., Zhang O., Kay L.E. Spectral density function mapping using 15N relaxation data exclusively. J. Biomol. NMR. 1995;6:153–162. doi: 10.1007/BF00211779. [DOI] [PubMed] [Google Scholar]
- 37.Wittebort R.J., Szabo A. Theory of NMR relaxation in macromolecules - restricted diffusion and jump models for multiple internal rotations in amino-acid side-chains. J. Chem. Phys. 1978;69:1722–1736. [Google Scholar]
- 38.King R., Jardetzky O. General formalism for analysis of NMR relaxation measurements on systems with multiple degrees of freedom. Chem. Phys. Lett. 1978;55:15–18. [Google Scholar]
- 39.Smith A.A., Ernst M., Ferrage F. Reducing bias in the analysis of solution-state NMR data with dynamics detectors. J. Chem. Phys. 2019;151:034102. doi: 10.1063/1.5111081. [DOI] [PubMed] [Google Scholar]
- 40.Lipari G., Szabo A., Levy R.M. Protein dynamics and NMR relaxation - comparison of simulations with experiment. Nature. 1982;300:197–198. [Google Scholar]
- 41.Clore G.M., Szabo A., Gronenborn A.M. Deviations from the simple 2-parameter model-free approach to the interpretation of N-15 nuclear magnetic-relaxation of proteins. J. Am. Chem. Soc. 1990;112:4989–4991. [Google Scholar]
- 42.Sterckx Y.G., Volkov A.N., Loris R. Small-angle X-ray scattering- and nuclear magnetic resonance-derived conformational ensemble of the highly flexible antitoxin PaaA2. Structure. 2014;22:854–865. doi: 10.1016/j.str.2014.03.012. [DOI] [PubMed] [Google Scholar]
- 43.Martin E.W., Holehouse A.S., Mittag T. Sequence determinants of the conformational properties of an intrinsically disordered protein prior to and upon multisite phosphorylation. J. Am. Chem. Soc. 2016;138:15323–15335. doi: 10.1021/jacs.6b10272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yao S., Babon J.J., Norton R.S. Protein effective rotational correlation times from translational self-diffusion coefficients measured by PFG-NMR. Biophys. Chem. 2008;136:145–151. doi: 10.1016/j.bpc.2008.06.002. [DOI] [PubMed] [Google Scholar]
- 45.Marsh J.A., Forman-Kay J.D. Sequence determinants of compaction in intrinsically disordered proteins. Biophys. J. 2010;98:2383–2390. doi: 10.1016/j.bpj.2010.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Flory P.J. Oxford University Press; 1969. Statistical Mechanics of Chain Molecules. [Google Scholar]
- 47.Kim S., Wu K.P., Baum J. Fast hydrogen exchange affects 15N relaxation measurements in intrinsically disordered proteins. J. Biomol. NMR. 2013;55:249–256. doi: 10.1007/s10858-013-9706-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Nguyen D., Mayne L., Walter Englander S. Reference parameters for protein hydrogen exchange rates. J. Am. Soc. Mass Spectrom. 2018;29:1936–1939. doi: 10.1007/s13361-018-2021-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bai Y., Milne J.S., Englander S.W. Primary structure effects on peptide group hydrogen exchange. Proteins. 1993;17:75–86. doi: 10.1002/prot.340170110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mori S., van Zijl P.C., Shortle D. Measurement of water-amide proton exchange rates in the denatured state of staphylococcal nuclease by a magnetization transfer technique. Proteins. 1997;28:325–332. [PubMed] [Google Scholar]
- 51.Raju K., Anwar R.A. Primary structures of bovine elastin-a, elastin-B and elastin-C deduced from the sequences of CDNA clones. Fed. Proc. 1987;46:1989. [PubMed] [Google Scholar]
- 52.Kjaergaard M., Poulsen F.M. Sequence correction of random coil chemical shifts: correlation between neighbor correction factors and changes in the Ramachandran distribution. J. Biomol. NMR. 2011;50:157–165. doi: 10.1007/s10858-011-9508-2. [DOI] [PubMed] [Google Scholar]
- 53.Abyzov A., Salvi N., Blackledge M. Identification of dynamic modes in an intrinsically disordered protein using temperature-dependent NMR relaxation. J. Am. Chem. Soc. 2016;138:6240–6251. doi: 10.1021/jacs.6b02424. [DOI] [PubMed] [Google Scholar]
- 54.Grasberger B.L., Gronenborn A.M., Clore G.M. Analysis of the backbone dynamics of interleukin-8 by 15N relaxation measurements. J. Mol. Biol. 1993;230:364–372. doi: 10.1006/jmbi.1993.1152. [DOI] [PubMed] [Google Scholar]
- 55.Weiss M.A., Ellenberger T., Struhl K. Folding transition in the DNA-binding domain of GCN4 on specific binding to DNA. Nature. 1990;347:575–578. doi: 10.1038/347575a0. [DOI] [PubMed] [Google Scholar]
- 56.Adzhubei A.A., Sternberg M.J.E., Makarov A.A. Polyproline-II helix in proteins: structure and function. J. Mol. Biol. 2013;425:2100–2132. doi: 10.1016/j.jmb.2013.03.018. [DOI] [PubMed] [Google Scholar]
- 57.English L.R., Tilton E.C., Whitten S.T. Intrinsic α helix propensities compact hydrodynamic radii in intrinsically disordered proteins. Proteins. 2017;85:296–311. doi: 10.1002/prot.25222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Cook E.C., Sahu D., Showalter S.A. Solution ensemble of the C-terminal domain from the transcription factor Pdx1 resembles an excluded volume polymer. J. Phys. Chem. B. 2019;123:106–116. doi: 10.1021/acs.jpcb.8b10051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Reichheld S.E., Muiznieks L.D., Sharpe S. Direct observation of structure and dynamics during phase separation of an elastomeric protein. Proc. Natl. Acad. Sci. USA. 2017;114:E4408–E4415. doi: 10.1073/pnas.1701877114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Schräder C.U., Heinz A., Schmelzer C.E.H. Elastin is heterogeneously cross-linked. J. Biol. Chem. 2018;293:15107–15119. doi: 10.1074/jbc.RA118.004322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Baxa M.C., Haddadian E.J., Sosnick T.R. Loss of conformational entropy in protein folding calculated using realistic ensembles and its implications for NMR-based calculations. Proc. Natl. Acad. Sci. USA. 2014;111:15396–15401. doi: 10.1073/pnas.1407768111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Genheden S., Akke M., Ryde U. Conformational entropies and order parameters: convergence, reproducibility, and transferability. J. Chem. Theory Comput. 2014;10:432–438. doi: 10.1021/ct400747s. [DOI] [PubMed] [Google Scholar]
- 63.Mendelman N., Zerbetto M., Meirovitch E. Conformational entropy from mobile bond vectors in proteins: a viewpoint that unifies NMR relaxation theory and molecular dynamics simulation approaches. J. Phys. Chem. B. 2020;124:9323–9334. doi: 10.1021/acs.jpcb.0c05846. [DOI] [PubMed] [Google Scholar]
- 64.Yang D., Kay L.E. Contributions to conformational entropy arising from bond vector fluctuations measured from NMR-derived order parameters: application to protein folding. J. Mol. Biol. 1996;263:369–382. doi: 10.1006/jmbi.1996.0581. [DOI] [PubMed] [Google Scholar]
- 65.Krivokhizhina T.V., Wittebort R.J. 2Q NMR of (2)H2O ordering at solid interfaces. J. Magn. Reson. 2014;243:33–39. doi: 10.1016/j.jmr.2014.02.022. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.