Spontaneous transmembrane pore formation by short-chain synthetic peptide

Abstract

Amphiphilic β-peptides, which are synthetically designed short-chain helical foldamers of β-amino acids, are established potent biomimetic alternatives of natural antimicrobial peptides. An intriguing question is how the distinct molecular architecture of these short-chain and rigid synthetic peptides translates to its potent membrane-disruption ability. Here, we address this question via a combination of all-atom and coarse-grained molecular dynamics simulations of the interaction of mixed phospholipid bilayer with an antimicrobial 10-residue globally amphiphilic helical β-peptide at a wide range of concentrations. The simulation demonstrates that multiple copies of this synthetic peptide, initially placed in aqueous solution, readily self-assemble and adsorb at membrane interface. Subsequently, beyond a threshold peptide/lipid ratio, the surface-adsorbed oligomeric aggregate moves inside the membrane and spontaneously forms stable water-filled transmembrane pores via a cooperative mechanism. The defects induced by these pores lead to the dislocation of interfacial lipid headgroups, membrane thinning, and substantial water leakage inside the hydrophobic core of the membrane. A molecular analysis reveals that despite having a short architecture, these synthetic peptides, once inside the membrane, would stretch themselves toward the distal leaflet in favor of potential contact with polar headgroups and interfacial water layer. The pore formed in coarse-grained simulation was found to be resilient upon structural refinement. Interestingly, the pore-inducing ability was found to be elusive in a non-globally amphiphilic sequence isomer of the same β-peptide, indicating strong sequence dependence. Taken together, this work puts forward key perspectives of membrane activity of minimally designed synthetic biomimetic oligomers relative to the natural antimicrobial peptides.

Significance

The development of bacterial resistance to conventional antibiotics is a major concern for public health. Antimicrobial peptides, which provide a natural defense against a large range of pathogens,are emerging as a sustainable substitute of antibiotics. However, serious issues with the naturally occurring antimicrobial peptides that have prevented their widespread appreciation are their susceptibility to degradation and lack of specificity for microbial targets. In this regard, synthetic biomimetic peptides are coming up as a viable alternative. Here, we provide clarity on how these synthetic antimicrobial peptides, which often involves distinctly short architecture, act on the membrane. We show that despite its short architecture, a 10-residue biomimetic peptide can spontaneously form stable membrane-spanning pores and induce water leakage.

Introduction

The development of bacterial resistance to conventional antibiotics is a major concern for public health. Antimicrobial peptides, which provide a natural defense against a large range of pathogens, including bacteria and fungi, are emerging as a sustainable substitute of antibiotics. The peptide-based antimicrobial agents are less prone to bacterial resistance than the natural antimicrobial agents and have got well-deserved prominence (1, 2, 3, 4). However, serious issues with the naturally occurring antimicrobial peptides that have prevented their widespread appreciation are their susceptibility to degradation by cellular proteases and lack of specificity for microbial targets over host cells. In this regard, synthetic oligomers and synthetic peptides that adopt helical conformations are coming up as a viable alternative to overcome these limitations of natural antimicrobial peptides (5, 6, 7, 8). This work focuses on a promising class of potentially novel biomimetic antimicrobial synthetic peptides, referred as β-peptides, and provides key molecular insights into the underlying mechanisms of their membrane-disruption capability.

β-peptides are synthetic oligomers of β-amino acids and are rationally designed to mimic and improve the biological activities of their natural counterparts, namely α-peptides. The backbone of a β-amino acid contains an extra carbon atom compared to that of an α-amino acid, which provides an additional site for introducing the side chain and makes the β-peptides resistant to degradation by natural proteases (9). Synthetic oligomers and random copolymers of β amino acids (10,11) have shown potent antibacterial (12, 13, 14) and antifungal (15,16) activity. The synthetic peptide of our interest is an amphiphilic 10-residue-long β-peptide sequence βY-(ACHC-ACHC-βK)₃ (hereby called “AAK”), in which βY, βK, and ACHC refer to β-tyrosine, β-lysine, and trans-2-amino cyclohexyl carboxylic acid (see Fig. 1). The cyclic constraint of ACHC residues confers a stable 14-helical conformation to this significantly short β-peptide sequence.

Figure 1.

Three-dimensional representation of the β-peptides of our interest (“AAK”). (A) Globally amphiphilic (GA) and (B) non-globally amphiphilic (non-GA) isomers of AAK. The β-peptide is shown in licorice representation with hydrophobic ACHC residues in red, β-lysine groups in green, and β-tyrosine are in blue. To see the figure in color, go online.

The ability to form stable 14-helical amphiphilic conformation with only 10 β-amino acid residues provides the peptide a greater synthetic advantage over relatively long-chain naturally occurring antimicrobial peptides such as magainin, melittin, or LL37. More importantly, Gellman and co-workers (12) have explored the interplay of sequence specificity and antimicrobial activity in AAK. Specifically, the design of a sequence arrangement of AAK in which the hydrophobic ACHC and hydrophilic β-homolysine residues are globally segregated gave rise to a globally amphiphilic (hereby called “GA” isomer) sequence isomer (see Fig. 1 A)). Experimental investigations led by Gellman and co-workers (12) have previously shown that the GA isomer of AAK can impart strong antibacterial activity on both Gram-positive and Gram-negative bacteria at a very low minimal inhibitory concentration (MIC). The GA isomer of AAK was found to retain antifungal activity against Candida albicans (15) with MIC values ranging between 16 and 32 μg/mL. AAK was also found to induce leakage of enzyme β-galactosidase from Bacillus subtilis (13), thereby suggesting membrane permeabilization by β-peptides. In a related study, the Gellman group also had investigated the role of amphiphilicity in the antimicrobial activity of AAK by synthetically designing a non-globally amphiphilic sequence isomer of AAK (hereby called the “non-GA” isomer of AAK) via evenly distributing a single hydrophilic β-homolysine residue on all faces of 14-helical AAK. It was found that the antibacterial potency of the non-GA isomer is significantly low, in contrast to its potent counterpart (12). We also note that these two same sequences had later been investigated by Karlsson and co-workers for their antifungal activity (16). The lack of antifungal activity in the non-GA isomer was evident in that investigation. These observations suggested that the antimicrobial activity of AAK is strongly sequence dependent, with the GA isomer of AAK showing stronger antibacterial and antifungal propensity than its non-GA counterpart. However, in all these experimental investigations, the relative comparison of MIC has remained the key metric of these two peptides’ antimicrobial activities. There is no report of more quantitative investigation of membrane affinity and cell leakage for these two β-peptide sequences. Together, although the precedent experimental investigations provide convincing macroscopic evidence of the antimicrobial activity of AAK and the associated sequence dependence, to the best of our knowledge, a molecule-level insight toward plausible mechanism of the antimicrobial activity of this “short-chain” β-peptide, in comparison to its natural counterpart, has largely remained unexplored.

Because the origin of antimicrobial peptides’ activity is believed to be rooted in their interaction with the membranes of bacteria (17), we wanted to explore how a membrane environment would respond to exposure to an increasingly growing concentration of β-peptides. In this work, we ask a pertinent question: what is the plausible mechanism of membrane-disruption ability by these AAK? Multiple hypotheses exist (1, 2, 3) in general to describe the principal steps leading to membrane disruption by antimicrobial peptides. Central to all prevailing hypotheses is the possibility of transmembrane pore formation by antimicrobial peptides (18,19). Does it form any transmembrane water channels? Or does it disrupt the membrane integrity in the so-called “carpet-like” (3,4) mechanism? In fact, natural antimicrobial peptides, namely magainin-H2 and melittin, are believed to form transmembrane pores across the membrane bilayer (20,21). However, it is also believed that in general, there is no unique mechanism, and it strongly depends on the specific antimicrobial peptides of interest (22,23). The question of the membrane-disruption mechanism is even more relevant for AAK, mainly because of the significantly distinct molecular architecture and short sequence lengths of these rigid β-peptides compared to its flexible and sequentially long large-molecular-weight natural counterparts such as magainin-H2 and melittin.

In this work, we address these questions via coarse-grained molecular dynamics (MD) simulations of interactions of GA and non-GA isomers AAK with a mixed 3:1 bilayer of 1-palmitoyl-3-oleoyl-sn-glycero-2-phosphoethanolamine (POPE) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoglycerol (POPG) lipids, a model bacterial-mimicking membrane (24, 25, 26). We systematically develop a coarse-grained model for both sequence isomers of the β-peptide within the framework of the popular MARTINI model. The developed coarse-grained model, in combination with the MARTINI membrane (27) and MARTINI polarizable coarse-grained water (28), enabled us to investigate longer-timescale events involving membrane and β-peptide interaction. Interestingly, in these ultralong coarse-grained MD simulations involving multiple copies of GA isomers of AAK and membrane, we observed spontaneous formation of peptide-induced transmembrane pores and water leakage inside the hydrophobic core, leading to disruption of membrane integrity. Analysis based on the tilt angle and end-to-end distance of the pore-forming β-peptides suggested that these short-chain biomimetic peptides are able to form transmembrane pores by stretching themselves across the membrane in a tilted manner. The pore predicted by the coarse-grained simulation was found to be resilient even in an atomically refined model. Finally, the pore-forming ability by β-peptides was found to be sequence dependent, with the non-GA isomers at a similar peptide/lipid ratio not being able to disrupt the membrane integrity. Taken together, the investigation elucidated a comprehensive mechanism of membrane disruption by short-chain synthetic biomimetic peptides and identified water-filled pore formation as a key event.

Materials and methods

Benchmark all-atom simulation

All-atom simulations of membrane adsorption of the β-peptide were first carried out as a benchmark for validating the coarse-grained model. Toward this end, a system of single copy of the β-peptide in a mixed 3:1 POPE/POPG lipid bilayer in water was constructed. For this purpose, the mixed lipid bilayers were first assembled by introducing 292 POPE and 96 POPG lipid molecules (and hence a total of 388 lipid molecules) along with 15,722 water molecules using CHARMM-GUI web server (29). The single copy of β-peptide was placed in solvent phase. To account for the residual positive charges introduced by the addition of the β-peptide (having three β-lysine groups) and the charged POPG lipids, in the aqueous media of the membrane, an appropriate number of ions were introduced so that each of the final systems are rendered charge neutral. The all-atom system with the β-peptide and lipid molecules (at a P/L ratio of 1:388) was simulated by 500 ns, the timescale of which was ascertained by visual inspection of the peptide getting attached to the membrane surface. Each simulation was repeated five times by varying the velocity seeds. We also carried out multiple realizations of additional all-atom MD simulations at a higher P/L ratio of 7:128 (seven copies of β-peptides with a 128-lipid bilayer in the presence of 10,755 water molecules in a charge-neutral system) for 1 μs to get firsthand knowledge of peptide-membrane interaction in an all-atom model at a considerably high peptide concentration.

CHARMM36 force field parameters (30) were employed to model the all-atom lipid molecules. The CHARMM force field, specifically parameterized for these β-peptides by Zhu et al. (31,32), and previously used by Mondal et al. (33), was employed here to model the β-peptides. The water molecules are modeled by the CHARMM-TIP3P water model (34). CHARMM (30) parameters were also used for the parameters of ions.

All atomistic simulations were performed using the Gromacs-2018 software package (35). Each of the simulations was first subjected to an energy minimization and subsequently, classical MD was performed at an average pressure of 1 bar and average temperature of 310 K. Each of the components (β-peptides, lipids, and water molecules) were also coupled separately with the thermostat. The temperature was maintained at the desired value employing Nosé-Hoover temperature coupling scheme (36,37) using a coupling constant of 1 ps. A semi-isotropic pressure coupling using the Parrinello-Rahman protocol (38) was implemented to maintain the desired pressure of 1 bar. The pressure coupling constants and compressibilities along the xy and z directions were 5 ps and 4.5 × 10⁵ bar⁻¹, respectively. In all simulations, center-of-mass motions were removed every 100 steps for β-peptides, lipids, and water molecules individually. Verlet cutoff (39) schemes were implemented for the Lennard-Jones interaction extending up to 1.2 nm, and particle mesh Ewald schemes were implemented for treating electrostatic interactions. All bond lengths involving hydrogen atoms of the protein and the ligand benzene were constrained using the LINCS (40) algorithm, and water hydrogen bonds were fixed using the SETTLE approach (41). Simulations were performed using the leapfrog integrator with a time step of 2 fs and initiated by randomly assigning the velocities of all particles from a Maxwell-Boltzman distribution.

Development of coarse-grained model for β-peptide

Because of the difference in the nature of the backbone framework between α- and β-amino acids, the project required us to develop a MARTINI-compatible model of GA and non-GA isomers of AAK. Toward this end, we followed the usual MARTINI protocol for parameterizing a new molecule, in this case a 10-residue β-peptide. Accordingly, as described in the previous section, we first performed a benchmark all-atom simulation of single copy of AAK in bulk water, and the simulation trajectories served as the reference.

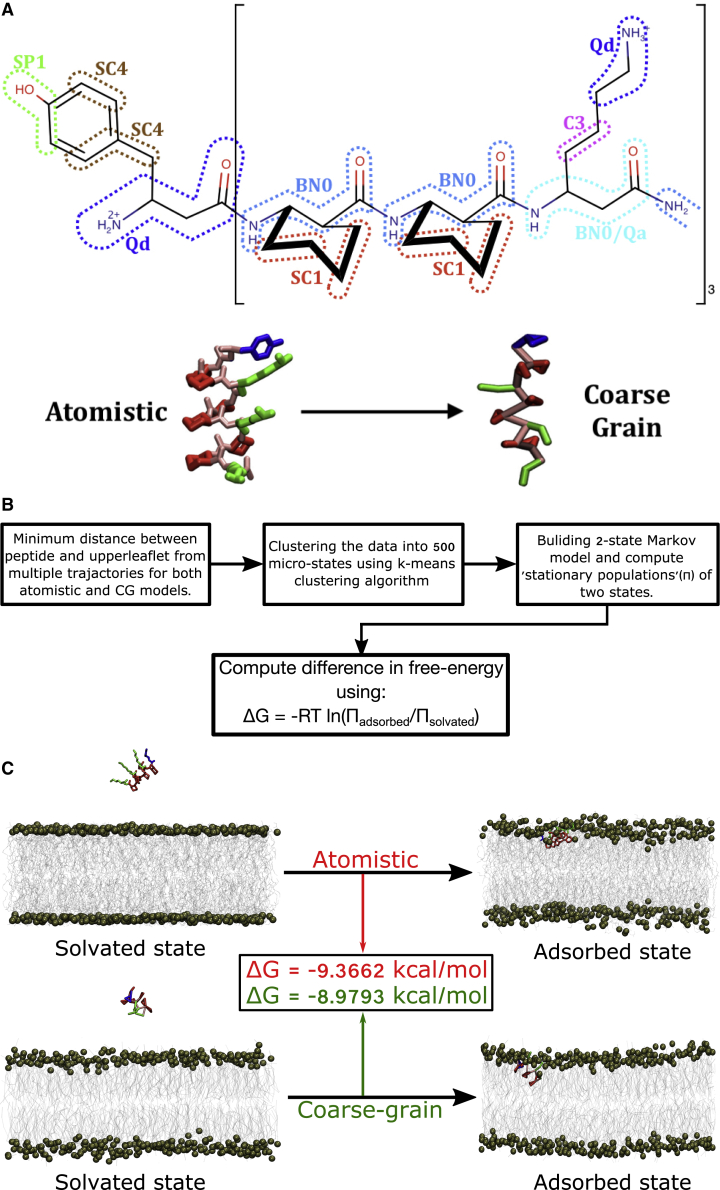
Fig. 2A represents the coarse-grained mapping scheme of the GA isomer of AAK. The backbone of β-amino acid has one more carbon atom than natural α-amino acid. Accordingly, we used 5:1 bead mapping for the backbone of the β-amino acid. To mimic the effective size and hydrophobicity of 5:1 mapping (compared to the usual MARTINI 4:1 mapping (27)), the nonbonding LJ parameters for backbone were increased to σ = 0.50 nm (instead of MARTINI backbone value of 0.47 nm), and backbone ε-values were increased to 125 percent of the MARTINI backbone values. Because both GA and non-GA sequence isomers of AAK are known to retain their rigid 14-helical conformations in membrane as well, similar MARTINI backbone nonbonding parameters for α-helix were introduced as the atom types. The bond, angle, and dihedral parameters of the backbone of AAK were then iteratively parameterized by performing iterative simulation of coarse-grained AAK in MARTINI polarizable water and comparing the distributions against the all-atom trajectories of the single chain of the β-peptide in water, till a best fit was obtained for respective distributions derived from all-atom simulations (see Fig. S1). The side-chain parameters of βY and βK were directly adopted from analogous MARTINI side-chain parameters of their α-amino acid counterparts (42) (compatible with MARTINI polarizable water), as the side chains in both cases are identical. Finally, the cyclic β-amino acid ACHC was coarse grained via 3:1 mapping (the usual MARTINI protocol for modeling the cyclic functional group), and analogous MARTINI parameters of cyclohexane were adopted for the side chain of ACHC. To determine the qualitative accuracy of the coarse-grained model developed for β-peptide, we first investigated whether, at the single-peptide level, the coarse-grained model of GA isomer displays qualitatively similar membrane interaction as its atomistic counterpart. Accordingly, we compared the adsorption ability of a single copy of the GA isomer of AAK on a POPE/POPG mixed bilayer in both the all-atom and coarse-grained models. We found that the coarse-grained model was able to display spontaneous adsorption process of GA isomer of AAK on the membrane interface, consistent with all-atom simulation (Fig. 2 C). For a more quantitative validation, we analyzed the free energetics of adsorption of the single copy of the β-peptide with the membrane interface in both all-atom and coarse-grained simulations. Keeping in the spirit of this investigation’s theme of using unbiased simulation, we employed a robust Markov state modeling (MSM) (43,44) approach for computing the free energy of membrane adsorption of a single peptide in both representations. PyEMMA (45) (http://www.emma-project.org/latest/) was used to construct and analyze the MSM from all the obtained trajectories. The schematic of the MSM protocol is illustrated in Fig. 2 B. For this purpose, we individually initiated multiple sets of all-atom and coarse-grained MD trajectories of a single β-peptide in its course of getting adsorbed on the POPE/POPG mixed bilayer. As per the protocol of MSM, the simulation trajectories in both representations (all atom and coarse grained) were discretized into 500 microstates, using the minimal distance between the membrane surface and the β-peptide as the clustering metric. The discretized MD data were then used to develop a Markov state model. Subsequently, the MSM is lumped into a two-macrostate model by dividing the microstates between “adsorbed” and “solvated” macrostates. Finally, the stationary or equilibrium populations of both macrostates are calculated from the MSM.

Figure 2.

(A) Mapping of β-peptides to MARTINI-based coarse-grained model. Bottom also shows a snapshot of all-atom and coarse-grained counterparts. (B) Illustration of MSM scheme for computing the free energy of membrane adsorption of a single copy of β-peptide in all-atom and coarse-grained models. (C) Comparison of MSM-derived free energy of adsorption at P/L ratio 1:388 between all-atom and coarse-grained simulations. To see the figure in color, go online.

Adsorption free energies (ΔG) of β-peptide to membrane were calculated from the stationary populations of adsorbed and solvated macrostates as obtained from the MSM,

$$\text{Δ}G=-RTlog\left(\frac{{\pi }_{adsorbed}}{{\pi }_{solvated}}\right)$$ (1)

For a systematic comparison, the entire simulation protocol and parameterization were repeated for the non-GA sequence isomer as well. We refer to Table S1 for system details for simulation using the non-GA isomer. See Fig. S2 for the mapping scheme and optimized distributions.

For reference, we have uploaded topology and parameter files of GA and non-GA isomers of AAK, along with an initial configuration of a single AAK in the presence of membrane, to Github. The link for downloading the materials is https://github.com/JMLab-tifrh/coarse-grained-models-of-beta-peptides.

Long-timescale peptide-membrane simulation using coarse-grained model

Table 1 provides a summary of each of the coarse-grained MD simulations carried out with GA isomers of AAK in POPE/POPG lipid bilayers. A total of four separate systems were investigated, using a wide range of P/L ratios that involved 1–15 copies of GA isomer copies. In all CG simulations, we first mapped atomistic protein structure to the coarse-grained model using the martinize.py script, appropriately modified for β-amino acid. Subsequently, we set up the POPE/POPG (3:1) bilayer along with its solvation by MARTINI polarized water by insane.py (http://www.cgmartini.nl/index.php/downloads/tools/239-insane). In all our systems of interest, simulations were initiated by placing all the β-peptide copies in the aqueous phase close to one of the monolayers of the POPE/POPG (3:1) bilayer, with the empty space filled with martini polarized water ionized with a suitable amount of Na⁺ and Cl⁻ martini ions to reach an electro-neutral solution. The overlapping molecular contacts were initially removed by energy minimization using the steepest-descent algorithm. The asymmetric distribution of the peptides mimics the addition of peptide to a solution containing cells or liposomes, in which peptides adsorb to one monolayer only. Sufficient water layer was introduced on the both side of the bilayer to ensure that the β-peptide copies do not artificially reach to the other leaflet via the periodic boundary condition. The production MD simulations were carried out for 20 μs. All production MD simulations were performed at 310.15 K, representing physiological temperature, and 1 atmospheric pressure. The average temperature was maintained by a velocity rescale temperature coupling scheme with membrane, proteins, and water molecules individually coupled to a thermal bath with a coupling constant of 1 ps. A semi-isotropic pressure coupling approach was employed via the Parrinello-Rahman scheme with a pressure coupling constant of 12 ps and isothermal compressibility of 1 bar⁻¹. A Verlet cutoff scheme was employed for nonbonded interaction with a cutoff for the Lennard-Jones potential at 1.1 nm. The real-space cutoff Coulomb potential was 1.1 nm with a relative dielectric constant of 2.5 for polarized water. The long-range electrostatic interaction was handled by reaction field, as per so-called MARTINI new-RF recommendations (46). All MD simulations were performed with the Gromacs 2018 simulation package (35), together with GPU accelerations (46). A time step of 20 fs was used, and the neighbor list was updated every 10 steps. The simulation length for each trajectory at higher P/L ratios of 1:39 and 1:22 was 20 μs, whereas at a P/L ratio of 1:67, the simulations were extended for 40 μs. All simulation times are reported as coarse-grained timescale. For each P/L ratio, four independent simulation trajectories were spawned. A 5-μs-long control simulation with only POPE/POPG lipid bilayers containing 336 lipids (i.e., lacking any peptides) was also performed for comparison purposes.

Table 1.

Details of the systems for simulation using GA isomer of AAK using MARTINI model

System	Number of waters	P/L ratio	Simulation time (μs) × number of replicas
β-peptide-less bilayer	6538	0	5 μs × 2
1 GA in 388 lipids	7761	1:388	20 μs × 2
5 GA in 336 lipids	6461	1:67	40 μs × 4
10 GA in 388 lipids	10,010	1:39	20 μs × 4
15 GA in 336 lipids	8324	1:22	20 μs × 4

All β-peptide copies were initially placed in aqueous phase close to one side of the membrane. Each system was charge neutralized by adding necessary counterions.

The resilience of the β-peptide and membrane complex, as predicted by the coarse-grained model, was further assessed by reconstruction of the all-atom model via the “back mapping” algorithm (47) and subsequently subjecting the refined structure to two independent all-atom 1-μs-long trajectories. The same all-atom simulation protocol as described earlier (for benchmarking simulation) was implemented.

Results

An optimized model for membrane and β-peptide interaction

To access relatively longer-timescale events of interaction between membrane and our biomimetic peptide of interest, β-peptide, we employed a coarse-grained framework based on the MARTINI force field (27,42,48, 49, 50). In this work, a mixed composition of a phospholipid bilayer of POPE and POPG at a 3:1 ratio has been chosen because of its past consideration as a mimic for bacterial membrane (24, 25, 26). Additionally, β-peptides also have been previously investigated for its membrane activity in experimental assays solely involving model phospholipid bilayers or large unilamellar vesicle (51). The lipid bilayer composition was modeled using the MARTINI lipid force field. The choice of coarse-grained model allowed us to use a relatively wider lipid bilayer (see Table 1) than that typically employed in all-atom simulations. We employed a polarizable MARTINI water model (28) for the coarse-grained MARTINI force field for simulating the aqueous phase of the lipid bilayers. The choice was due to its superior ability to reproduce the water dielectric property, orientational polarizabilities, and membrane interfacial electrostatic property more faithfully than the regular MARTINI water model. Accordingly, the Martini lipid and protein force fields compatible with MARTINI polarizable water were chosen in this work. As detailed later, we would find that the usage of polarizable MARTINI water (28) (in contrast to regular MARTINI coarse-grained water (27)) was instrumental in observing the peptide-induced transmembrane pore in long-timescale simulations. Because of the difference in the nature of the backbone framework between naturally occurring α-amino acid and synthetically designed β-amino acid, the project prompted us to design a coarse-grained model of GA and non-GA isomers of AAK. As detailed in the Materials and methods, we developed a MARTINI-compatible coarse-grained model for the 10-residue β-peptide AAK by iterative optimization against an all-atom simulation trajectory. Fig. 2 A provides the coarse-grained mapping scheme employed in this work for the GA isomer of the β-peptide.

Both in vitro and in vivo investigations into the antifungal and antibacterial abilities of the sequence isomers of the β-peptide of our interest, AAK, have shown that it kills pathogen cells at a much lower concentration than many naturally occurring antimicrobial peptides. Toward this end, we first explored how the membrane and β-peptide interaction behavior at the single-peptide level, simulated using a coarse-grained framework, would compare against those performed using an atomically detailed force field. We individually simulated the interaction of a single copy of the GA isomer of AAK, initially present in aqueous media, with a 3:1 POPE/POPG phospholipid bilayer in all-atom and coarse-grained representations. We find that in both all-atom and coarse-grained simulations, a single copy of AAK, starting from aqueous media, gradually approaches the hydrophilic interface of the phospholipid bilayer and eventually gets partitioned in the inner membrane interface. Representative snapshots in Fig. 2 C provide a pictorial view of the solvated and eventual membrane-adsorbed state of the GA isomer of AAK at the single-peptide level, obtained from all-atom and coarse-grained models. The comparison indicates qualitatively a very similar membrane-adsorbed state obtained in both types of simulations at the single-peptide level. For a quantitative comparison of the quality of the coarse-grained model against the atomistic model, we computed the free energy of the β-peptide’s membrane adsorption in both models. As described in the Materials and methods, we adapted a framework of MSM (see Fig. 2 B for details of protocol), based on multiple unbiased simulation trajectories, to compute the relative stationary or equilibrium populations of two macrostates of β-peptides, namely “solvated” and “membrane-adsorbed” states. The stationary populations of the “solvated” (π_solvated) and “adsorbed” (π_adsorbed) states, as derived from MSM underlying the all-atom model, were found to be 0.0142 and 99.9858%, respectively. On the other hand, MSM built using the coarse-grained simulation predicted a value of π_solvated = 0.0273% and π_adsorbed = 99.9727%. Accordingly, the free energy of adsorption, as computed by Eq. 1, turned out to be −9.37 kcal/mol in atomistic simulation, as compared to −8.97 kcal/mol in coarse-grained model, indicating reasonable agreements. Together, these observations validate that the coarse-grained model is able to capture the basic membrane-adsorption feature of the amphiphilic β-peptide very well. Moreover, at high peptide concentrations, we find that on a short timescale, this coarse-grained model reproduces very similar early-stage behavior of membrane and β-peptide interaction as found in 1-μs-long all-atom simulation of membrane interactions with multiple copies of β-peptides; in both cases (see first two rows of Fig. 3 for coarse-grained simulation and Fig. S3 for all-atom simulation), the β-peptides undergo spontaneous self-aggregation and membrane adsorption within a 1-μs-long simulation. These initial benchmark assessments of the coarse-grained model provided early promise for employing them in long-timescale investigations.

Figure 3.

Time profile of the account of β-peptide and membrane interaction at diverse P/L ratios. As a general trend, the β-peptides, after initiating from aqueous media, gradually assemble and partition into the membrane interface. This is followed by transmembrane insertion of a number of β-peptide copies inside the membrane. The β-peptides eventually span across both the bilayer. Color code: tan, phosphate groups of lipids; orange, polarized water; blue, tyrosine; green, lysine; red, ACHC residues. To see the figure in color, go online.

Simulations capture spontaneous transmembrane pore formation by short-chain β-peptides

Encouraged by the observation of an efficient membrane-adsorption GA isomer of AAK toward membrane interaction manifested at the single β-peptide level in a coarse-grained model, we explored the effect of high concentrations of the GA isomer on the membrane. As enumerated in Table 1, in our coarse-grained simulation, we systematically varied the P/L ratios within a wide range of 1:388 to 1:22 to investigate the interaction of increasing concentration of β-peptides with the membrane. At a very low P/L ratio of 1:388, which involved interaction of a single copy of AAK with the membrane as described earlier, the β-peptide approached the membrane interface of the proximal leaflet and remained partitioned across the membrane interface. However, intriguingly, at a threshold P/L ratio of 1:67 (containing 5 peptides and 336 lipid molecules), coarse-grained simulations at a longer coarse-graining timescale up to 40 μs displayed that (see Video S1 and left column of Fig. 3 for a visual account of process) few copies of the GA isomer of AAK, initially mutually well separated in bulk water, get self-assembled and adsorbed on the membrane surface. The aggregates of β-peptides, upon being docked on the surface, act as a cage and displace a number of lipid headgroups (see Fig. S4 A). The lipid displacement provides the required opening for favorable hydrophobic interaction between ACHC residues and the lipid tails, and as a result, the β-peptide copies got past the polar headgroup of the proximal leaflet of the membrane interface. The aggregation and organization process of the β-peptides continues past the event of membrane adsorption. Eventually, the peptide aggregate, upon attachment to membrane interface, snorkeled past the membrane interface of proximal leaflet and got embedded in a transmembrane orientation and spanned across proximal and distal leaflets of the membrane. As seen in Video S1 and in the left column of Fig. 3, the defects created because of peptide insertions across the membrane interface led to a number of water molecules getting leaked inside the membrane interiors, thereby giving rise to a transmembrane-pore-like structure for maximizing favorable contacts between lipid tails and the hydrophobic β-amino acid residues.

Video S1. The trajectory capturing the transmembrane-pore-formation process by GA isomer at a P/L ratio of 1:67 5

copies of peptides. Color code: tan : Phosphate groups of lipids, orange : Plolarized water, blue :: Tyrosin, green : Lysin, red : ACHC residues.

A cooperative pore-formation process

We systematically increased the P/L ratios to 1:39 and 1:22 by introducing additional copies of the GA isomers on the same side of the water phase and performed a series of individual MD simulations using the coarse-grained model. Videos S2 and S3 demonstrate the event of the β-peptide and membrane interaction at P/L ratios of 1:39 and 1:22. Fig. 3 provides a visual account of membrane-peptide interaction at different time points of multi-microsecond-long trajectories at P/L ratios of 1:67, 1:39, and 1:22. In all three P/L ratios, the trend of pore formation is generic, except that the event gets accelerated at higher P/L ratios. At a P/L ratio of 1:22, the formation of two distinct transmembrane pores is also seen at an intermediate time point; these eventually coalesce into a single large pore. The pore formation event was found to be reproducible across multiple trajectories (two out of four trajectories for P/L = 1:67 and three out of four trajectories for P/L = 1:39 and 1:22 displayed stable pore-formation. Each trajectory was 20–40 μs long). As shown in Fig. S5, at less than five peptide copy numbers and at a P/L ratio lower than 1:67, the peptides would only settle below the surface of the bilayer, causing a partial disruption. This indicates that preassociation of the peptides may increase pore propensity, as shown experimentally in the case of tetravalent magainin peptides (52). Once the formation of the transmembrane pore is completed, the pore remains stable for the rest of the period of simulation. On the basis of the observation that pore formation is facilitated by self-aggregation of β-peptides and a threshold P/L ratio is required for transmembrane pore formation, we conclude that this is a cooperative process. This is qualitatively consistent with past free-energy-based simulation results, albeit ones focused on the naturally occurring antimicrobial peptide melittin, that increasing the number of peptide copies reduces the barrier to pore formation (53).

Video S2. The trajectory capturing the transmembrane-pore-formation process by GA isomer at a P/L ratio of 1:38

10 copies of peptides. Color code: tan : Phosphate groups of lipids, orange : Plolarized water, blue :: Tyrosin, green : Lysin, red : ACHC residues.

Video S3. The trajectory capturing the transmembrane-pore-formation process by GA isomer at a P/L ratio of 1:22

15 copies of peptides. Color code: tan : Phosphate groups of lipids, orange : Plolarized water, blue :: Tyrosin, green : Lysin, red : ACHC residues.

Quantifying and characterizing the pore-formation process

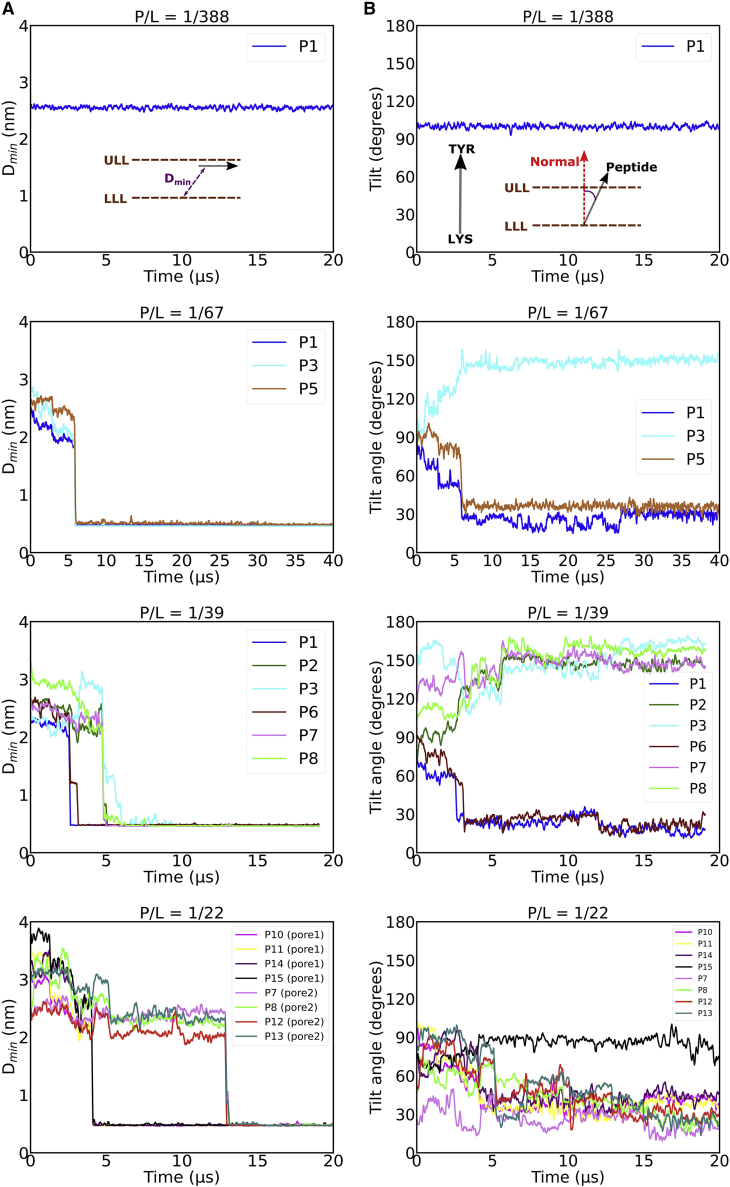
To characterize the extent of β-peptide insertion inside the membrane at a given P/L ratio, we compute the minimal distance (d_min) between individual peptide copies and the phosphate group of the distal leaflet of the membrane (see schematic in Fig. 4 A). As shown in Fig. 4 A, at the single-peptide level, d_min remains stable at a value of 2.5 nm, which corresponds to the peptide remaining adsorbed in the membrane interface of the proximal leaflet at a P/L ratio of 1:388. However, at higher P/L ratios of 1:67, 1:39, and 1:22, we observe a sharp collective drop in the value of d_min from 2.5 to 0.5 nm for a number of peptide copies on a timescale of 5–10 μs in coarse-grained simulations, indicating the onset of translocation of a cluster of peptides inside the membrane interior and initiation of eventual transmembrane pore formation (left column of Fig. 4). Interestingly, for a P/L ratio of 1:22, we observe two such events in which d_min decreased for two independent peptide clusters, indicating the onsets of two distinct pore formations as confirmed by Video S3 and the top panel of Fig. 4 A. Once the transmembrane pore formation is completed, the pore remains stable for the rest of the duration of 20 μs (40 μs for a P/L ratio of 1:67) simulation.

Figure 4.

(A) Comparison of time profile of the extent of peptide insertions. Here, the minimal distance between the phosphate group of the distal leaflet and the peptide (d_min) has been considered as the metric. The sudden drop in the value of d_min signifies the onset of peptide translocation and pore formation. Only the time profile of pore-forming peptide copies (annotated as “P1, P2…”) has been shown. (B) Comparison of time profile of tilt angle of the peptides with the membrane interface at diverse P/L ratios. LLL, Lower Leaf Let; ULL, Upper Leaf Let. To see the figure in color, go online.

Fig. 4B characterizes the tilt angle between the β-peptide copy and the membrane surface normal. Based on this analysis, a tilt angle of 90° would imply that the peptide is horizontally oriented with the membrane interface, which is the case for the single peptide at a P/L ratio of 1:388. However, with increasing P/L ratio, we found that the β-peptides that formed the core of the pore eventually transitioned from a tilt angle of 90° to a tilt angle closer to 30 or 150° (suggestive of a reversal of the peptide’s orientation during membrane translocation), indicating that these pore-forming peptides have attained a transmembrane orientation. However, the tilt angle is not perfectly zero, suggesting a tilted orientation subtended by these pore-forming β-peptides with the membrane interface. Together, the analysis of the time profile of the tilt angle and d_min of the peptides indicate that the formation of the transmembrane pore involves collective translocation of β-peptides at a multi-microsecond-long timescale, in which this peptide eventually makes a tilted orientation with the membrane interface. The timescale required for the formation of pore containing a minimum of five peptides (at a P/L ratio of 1:67) was around 8–9 μs in coarse-grained units. As the P/L ratio and number of β-peptide copies increased to 1:39 and 1:22, the pore-formation process and reorientation to the transmembrane pose get expedited (2.5–5 μs). The reorientation of the peptide from a surface to a transmembrane conformation is generally considered an important step in its pore-forming ability (54,55) and is believed to be associated with a considerable free energy barrier (56). The observation of expedited transmembrane reorientation of β-peptides beyond a threshold P/L ratio qualitatively coincides with the previous report of a reduced free energy barrier of reorientation of melittin with increasing P/L ratio (56). Overall, a similar analysis based on distance and tilt angle also characterizes the transmembrane insertion of peptide clusters across multiple trajectories (see Figs. S6 and S7 for P/L ratios of 1:39 and 1:22).

Fig. 5A compares the peptide density profiles along the surface normal for all P/L ratios investigated here. These density profiles were averaged over the last 3-μs duration of the simulation (see snapshot in Fig. 5 B). Consistent with the previous section’s description, with increasing P/L ratio, we find that the β-peptide density past the phosphate group gradually increases inside the hydrophobic core of the membrane and eventually the tail of the density profile stretches up to the distal leaflet of the membrane at high P/L ratios, implying that the peptides span both the leaflets and form a transmembrane channel. The β-tyrosine residue mostly remains localized close to the membrane interface, whereas the hydrophobic ACHC groups span the core of the transmembrane pore. The density of the phosphate groups (Fig. 5 C) also increases inside the hydrophobic core of the membrane with increasing P/L ratio. The sharp phosphate density profile in neat membrane gets gradually smeared with increasing P/L ratio. Most importantly, as is observed in the water density profile (see Fig. 5 C), the peptide-membrane interaction leads to a considerable increase in water density inside the hydrophobic core of the membrane with increasing P/L ratio. The representative snapshots at high P/L ratios of 1:39 and 1:22 especially depict (Fig. 5 B) the presence of a distinct layer of water near the inner part of both leaflets. This suggests that these transmembrane pores are wet in nature, and we believe that these interfacial waters help maintain the transmembrane pore via favorable interactions with the polar terminal residues of AAK.

Figure 5.

(A) Density profile of GA peptides across membrane interface at multiple P/L ratios. (B) shows representative snapshots of equilibrium conformation in all P/L ratios. (C and D) Density profiles of phosphate and waters at multiple P/L ratios. To see the figure in color, go online.

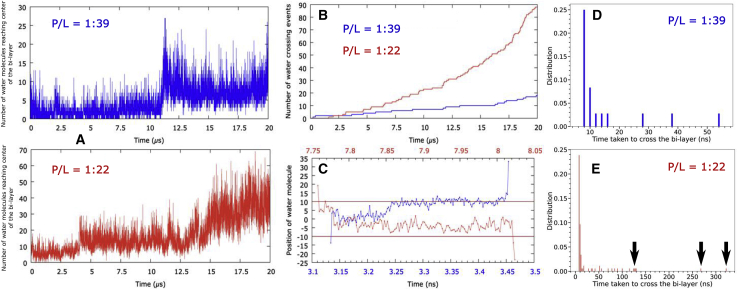
Fig. 6A quantifies the extent of water leakage to the membrane center at two high P/L ratios of 1:39 and 1:22 (at which the pore formation was most prominent). We find that a considerable number of water molecules get past the membrane leaflets and the number of leaked water molecules systematically increases as the event of peptide-induced pore formation proceeds. The trend of water leakage is also higher at larger P/L ratios. The simulation trajectories were quantitatively analyzed for exploring the possibility of occurrences of transmembrane water permeation events, in which a water molecule, after starting from one membrane leaflet, would be tracked for its completing the full passage to the other leaflet. Fig. 6 B compares the cumulative number of such water permeation events though the membrane at two P/L ratios. The trend reveals that there are, in fact, multiple occurrences of water permeation events in which water molecules traverse from one leaflet to other leaflets, and the extent of water permeation increases with increasing P/L ratio. Fig. 6 C illustrates a time profile of two representative water permeation events across the two leaflets. An analysis of the water permeation trajectory indicated that the duration of the water permeation event can be diverse. The distribution of durations of water permeation events at two P/L ratios (Fig. 6, D and E) shows that although the majority of the transmembrane water passages complete in 10 ns, there are numerous occurrences of considerably slow permeation events, as represented by the long tail of the distributions.

Figure 6.

(A) Time profile of number of waters leaked up to the membrane center at two higher P/L ratios (1:39 and 1:22). (B) Cumulative number of water permeation events during the simulation period at two P/L ratios. Only those water molecules that made a full pass from one leaflet to the other leaflet were counted. (C) Trajectory of two representative water permeation events across the leaflet. (D and E) The distribution of permeation time at two P/L ratios. To see the figure in color, go online.

There are diverse proposals of variants of transmembrane pores, including barrel-stave, toroidal, and carpet types (3,4,18,19). The detailed characterization of the pore showed that β-peptides induce local defects in the bilayer, and subsequently, the headgroups of the lipids line the pore together along with the peptides. The visual inspection of the pore also revealed that the peptides are unevenly distributed, i.e., higher concentrations of peptides were present in the upper leaflet in comparison to the ones in the lower leaflet. The tilt-angle analysis of the pore-forming peptides (discussed in the previous paragraph) indicates that the β-peptide aggregate gets inserted almost vertically into the membrane, almost bearing the characteristics of a barrel-stave pore. However, the pore is not perfectly cylindrical; rather, it subtends a nonzero angle with the membrane normal. Additionally, the snapshots of the pore also show minor line up of the displaced lipid headgroups. However, the lining of lipid headgroups is not as prominent as what would be observed in an ideal toroidal pore.

Finally, we stress that the choice of the polarizable MARTINI coarse-grained water (28) for modeling solvent was instrumental in the observation of the pore in these simulations. The usage of the regular Martini coarse-grained LJ water model only resulted in peptide adsorption on the membrane leaflet and did not lead to any pore formation (see Fig. S8). This suggests the importance of appropriate representation of the membrane interfacial electrostatics via choice of better water model.

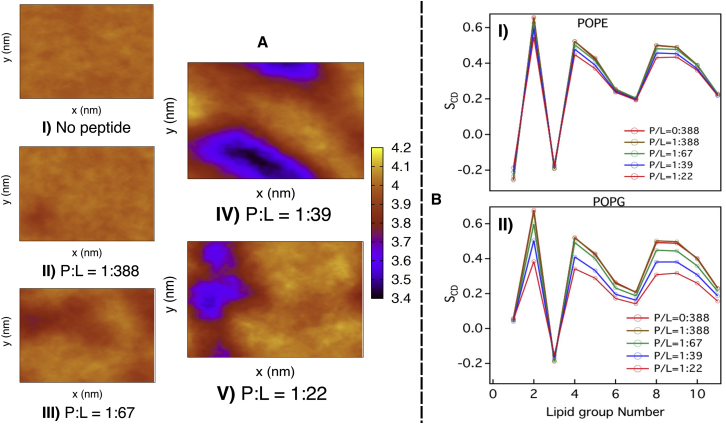
We find that the impact of pore formation and water leakage on the overall membrane integrity is mostly local. This is demonstrated in the two-dimensional bilayer thickness profiles (Fig. 7) at diverse P/L ratios. Within P/L ratios of 1:388 to 1:67, the bilayer thickness profile remains uniform, similar to that in peptide-less membrane. However, at a higher P/L ratio of 1:39, we find localized nonuniformity in the membrane-thickness profile, which eventually grows at a P/L ratio of 1:22. As an indication of disrupted membrane integrity induced by the GA isomer of β-peptide, the deuterium order parameters of the POPG lipid tails systematically decrease with increasing P/L ratio. Interestingly, the order parameter of POPE lipid does not change in the presence of peptides, indicating specific interaction between POPG lipids and β-peptide.

Figure 7.

Comparison of (A) bilayer thickness profile and (B) lipid order parameter of the POPE and POPG lipids across multiple P/L ratios of GA isomer. To see the figure in color, go online.

Reconciling short-chain architecture of β-peptides and its transmembrane-pore-formation ability

A distinct feature of the β-peptide of interest, i.e., the GA isomer of AAK, is its relatively shorter architecture (only 10 residues) than typical natural antimicrobial peptides such as magainin (23 residues), melittin (27 residues), or LL37 (37 residues). A pertinent question is how these short-length β-peptides are able to form membrane-spanning pores in the bilayer. Toward this end, we analyze the end-to-end distance of the β-peptide in different media. Fig. 8 A compares the distribution of end-to-end distances of this specific β-peptide. We find that in bulk water, the average end-to-end distance is ∼1.5 nm, which remains almost similar in the case in which a single peptide remains adsorbed in the membrane-water interface (i.e., at P/L ratio = 1:388). However, at higher P/L ratios, we note that the end-to-end distance of individual transmembrane peptides, which are constituent of the pore, increases to ∼2.5 nm over time (Fig. 8 A). A careful inspection of the time profile of the end-to-end distance in Fig. S9 suggests that the onset of increase in the pore-forming β-peptides’ end-to-end distance coincides with the onset of transmembrane pore formation of the β-peptides inside the membrane. The extended chain length of these peptides inside the membrane interior enables them to span the membrane and form a transmembrane pore.

Figure 8.

(A) Comparison of the probability distribution of GA isomer’s end-to-end distance between that in neat water and that inside membrane at multiple P/L ratio. (B) Representative snapshot of pore showing water layer anchoring the transmembrane pores. To see the figure in color, go online.

A plausible rationale for the observed extension of these pore-forming peptides is that once inside the hydrophobic core of the membrane, the polar N-terminal residue β-tyrosine or hydrophilic C-terminal residue β-lysine residue of these β-peptides aims to reach out to the polar headgroups of the distal leaflet for favorable interaction (see Fig. S4 B), which leads to a possible elongation of these peptides. Although the transmembrane β-peptides are stretched inside the bilayer, it is still shorter than the average membrane thickness of the neat POPE/POPG bilayer. A visual inspection of the transmembrane pore and analysis of bilayer thickness profiles at high P/L ratios of 1:39 and 1:22 (Fig. 8 B) show that the bilayer becomes nonuniform in the presence of these β-peptides and undergoes localized thinning, which helps these extended pore-forming β-peptides to span the leaflet. Finally, as discussed earlier, the presence of layer of interfacial water acts (Fig. 8 B) as an additional cushion to support the transmembrane pore.

A refined model of the pore

This prediction of the formation of a transmembrane pore by these short-chain peptides is, however, made in a coarse-grained model, which might be argued to lack chemical details. To assess the resilience of the predicted pore, we reverse mapped a representative conformation of the coarse-grained morphology of the water-filled pore into its full all-atom representation via the “back-mapping” algorithm (47) and subsequently subjected it to relaxation via MD simulation. Fig. 9 depicts the refined all-atom representation of peptide in complex with membrane, as obtained after equilibration. We find that the structure of the pore is retained in the reconstructed model. An expanded view of the figure of the refined model confirms the presence of a large density of water and displaced phosphate headgroups inside the pore. We find that the extended conformation of the β-peptides retains its stability in the membrane interior when subjected to microsecond-long all-atom MD simulation as well, which further validates that the extended conformations of the β-peptides inside the membrane core, as predicted by coarse-grained simulations, are a realistic possibility.

Figure 9.

All-atom refined model of the peptide-membrane complex formed at P/L of 1:39, as obtained via reverse mapping the coarse-grained structure and subsequent microsecond-long MD simulation. The presence of water and displaced phosphates in the membrane interior is evident in the expanded image (see insets i and ii). Also shown is the expanded image of the eventual conformation of the β-peptides in the all-atom representation. The extended conformation of the peptides is apparent in the all-atom simulation. To see the figure in color, go online.

The pore-formation ability of β-peptide is sequence selective

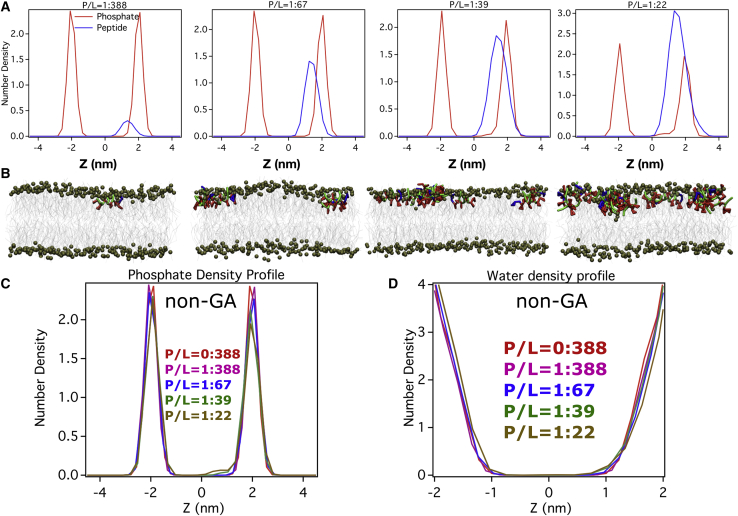
We investigated whether the pore-forming propensity of β-peptides is sequence dependent. Accordingly, we also simulated the interaction of non-GA isomers of AAK with the membrane at a wide range of P/L ratios, similar to GA isomers. The peptide density profiles of non-GA isomers are compared in Fig. 10 A across P/L ratios ranging between 1:388 and 1:22. We find that, unlike the GA isomer, the peptide density profile does not span across both leaflets in the non-GA isomer even at the highest P/L ratio of 1:22. Instead, as shown by the representative snapshot in Fig. 10 B, we see that the β-peptide copies in the non-GA isomer self-assemble into small isolated oligomeric cluster and remain adsorbed on the membrane interface, without showing any tendency of translocation inside the membrane interior. This is also reflected in unchanged phosphate density profiles and water density profiles in the membranes across the entire range of P/L ratios involving non-GA isomers (Fig. 10, C and D). Finally, relatively unchanged bilayer thickness profiles (Video S1. The trajectory capturing the transmembrane-pore-formation process by GA isomer at a P/L ratio of 1:67 5, Video S2. The trajectory capturing the transmembrane-pore-formation process by GA isomer at a P/L ratio of 1:38, Video S3. The trajectory capturing the transmembrane-pore-formation process by GA isomer at a P/L ratio of 1:22, Document S2. Article plus supporting material A) and deuterium order parameters (Fig. S10 B) across P/L ratios in the case of the non-GA isomer relative to the GA isomer clearly suggest that the non-GA isomer of AAK would not be able to disrupt the membrane integrity, unlike the GA isomer at a similar P/L ratio. These results clearly suggest that the presence of global segregation of hydrophilic and hydrophobic residues in a β-peptide, as in the GA isomer, is key to its ability to form a water-lined transmembrane pore and disrupt membrane integrity.

Figure 10.

(A) Density profile of non-GA isomers across membrane interface at multiple P/L ratios. (B) Representative snapshots of non-GA isomers interacting with membrane at all P/L ratios. (C) Comparison of phosphate density profiles in the presence of non-GA isomers at diverse P/L ratios. (D) Comparison of water density profiles in the presence of non-GA isomers at diverse P/L ratios. To see the figure in color, go online.

Discussion

Unraveling the mechanistic action of antimicrobial agents at an atomistic resolution has always been a key desirable from both experimental and computational perspectives. Specifically, it remains more intriguing to decipher the membrane-disrupting mechanism for amphiphilic biomimetic peptides, which manifest strong antimicrobial properties despite being much shorter in chain length and lower molecular weight than their natural counterparts. In this work, via computer simulation using a coarse-grained model, we have elucidated key mechanisms of the membrane-disruption process of a set of isomers of a β-peptide, AAK, that is known for its proven antimicrobial activity.

Our ultralong coarse-grained simulations involving a systematically developed coarse-grained model for AAK, in combination with MARTINI lipid and polarizable water models, were able to capture the spontaneous membrane-disruption processes induced by short-chain β-peptide. As a key observation, beyond a threshold peptide/lipid ratio, these coarse-grained simulations revealed the formation of a spontaneous peptide-induced disordered pore and eventual water leakage inside the membrane interior. These pores remained stable during the period of 20- to 40-μs-long coarse-grained trajectories. The pore-forming peptides are not perfectly vertical with the membrane interface. Rather, these peptides showed a nonzero tilt angle with the membrane interface. Interestingly, the pore-forming peptides were found to be considerably extended inside the membrane interior in a ploy for the polar residues to reach out to the headgroups of the distal leaflet. The pore-formation propensity increased with increasing P/L ratio, with eventual observation of multiple pores at high P/L ratios. The β-peptide-induced pore formation also led to increasing nonuniformity in membrane thickness and disordered lipid tail. Related to this finding, Huang and co-workers (57, 58, 59) had majorly used orientational Circular Dichroism spectroscopy to analyze the P/L ratio dependence and pore formation. Their investigation proposed a two-state model of antimicrobial peptides in membrane-parallel and membrane-normal poses. Their analysis based on experimental spectra showed that with increasing P/L ratio, the membrane perpendicular pose is getting prominent. This model is consistent with our analysis of tilt-angle and water leakage profiles as a function of P/L ratio. In particular, this simulation showed that although at a lower P/L ratio below 1:67, these short-chain β-peptides remained located at membrane interface at a parallel orientation, with increasing P/L ratio, these β-peptides reorient themselves into a perpendicular conformation to get past the membrane and eventually induce pore formation. These results are in line with the Huang group’s proposal. Finally, similar computer simulations using a non-GA isomer of the same β-peptide neither led to any transmembrane pore formation nor induced any water leakage inside the membrane core, which explained its experimentally proven nonpotency in antimicrobial activity.

We note that the coarse-grained model used in this work, i.e., the MARTINI force field together with MARTINI polarizable water, is not devoid of criticism. The model has in the past been found to require more free energy for pore formation that its all-atom counterpart (60) and has recently been reported (61) for a discrepancy in representing the membrane-adsorption process by nanoparticle. However, the employed coarse-grained force field has also been previously successful in the prediction of peptide-induced pores in the membrane (62,63). Additionally, the ability of the currently presented coarse-grained model in recovering all-atom simulation results of the early stages of peptide-membrane interaction and the observed resilience of the predicted pore in a refined all-atom model (see Fig. 9) provide confidence in its prediction of long-timescale behavior. The observation of the extended conformation of the β-peptides inside the membrane interior in all-atom refined simulation also lends credence to the prediction from the coarse-grained simulation. Nonetheless, setting aside the validation of the protein conformational changes by the all-atom simulations, there are also precedent reports of larger conformational changes in coarse-grained models (see (49) and references of examples therein). The observation of pore formation in this coarse-grained simulation is consistent with a previous biochemical investigation of Epand and co-workers (51), in which a pair of different but closely related 14-helical β-peptides were probed for their interaction with model membranes. Using an assay involving large unilamellar vesicles, this work had indicated leakage and possible pore formation and lipid flip-flop by this class of β-peptides. Our work provides convincing evidence in support of pore formation by a related but more potent antimicrobial β-peptide AAK and brings out the associated molecular mechanism of the full process.

As a major advancement, this work highlights key perspectives of the membrane activity of synthetic biomimetic oligomers. Going beyond precedent computer simulation studies, which have explored mainly membrane-attachment of peptides at a low peptide/lipid ratio or have started with manually preformed specific transmembrane pore (22,23,64), our work takes a step forward and captures the complete process of membrane disruption via spontaneous formation of a barrel-stave pore. The thermodynamic feasibility of membrane disruption via spontaneous pore formation by these rigid 10-residue-long β-peptide foldamers was also validated in a wide range of P/L ratios. The superior ability of imparting antimicrobial activity by AAK at a lower MIC than the natural antimicrobial peptides has previously been stressed by Gellman and co-workers (12). In this regard, the observation of transmembrane pore formation via these short-chain peptides and the possibility of chain extension to reach out to the distal leaflet are interesting phenomena. Moreover, the ability to induce a transmembrane pore by AAK at a threshold P/L ratio of 1:67, as found in the current simulation, at considerably lower concentrations also speaks of potent membrane-disrupting ability by these β-peptides. As we have emphasized earlier in the article, the choice of polarizable MARTINI coarse-grained water (28) (in contrast to regular uncharged MARTINI water (27)) was instrumental in capturing the pore-formation process by these β-peptides, which suggests the proper role of the water model in capturing the process. The requirement of the presence of multiple copies of β-peptides for pore formation is suggestive of a cooperative process. In addition, the observation that the reorientation of β-peptides from the surface-bound state to the transmembrane state is facilitated beyond threshold P/L ratios opens up a future direction for systematic quantification via free-energy-based characterization of the pore-formation process (53,55,56) using suitable collective variable (65).

The membrane-disruption process by antimicrobial agent via pore formation is considered to be a slow process (54,55,66), the timescale of which is often prohibitive via all-atom simulation. For example, a 5-μs-long all-atom simulation of 10 copies of the surface-bound antimicrobial peptide alamethicin did not show any spontaneous membrane insertion (22). To accelerate insertion of the peptides, the temperature had to be artificially raised very high, and an external electric field needed to be employed. In this regard, our work’s implementation of the coarse-grained model in combination with Martini polarizable water is a practical way forward, and more insights can potentially be further harnessed via a resolution switch to an all-atom model, as has been shown here by the refinement of the coarse-grained model and also in earlier investigations (67). The investigation reported here opens up multitudes of opportunities toward understanding the mechanistic aspects of the membrane-disruption capability by both natural and biomimetic macromolecules across multiple membrane compositions. Recent works by Gellman and co-workers on exploring random copolymeric biomimetic peptides as cost-effective and efficient antimicrobial agents are being seen as major paradigm shifts (68, 69, 70). These works suggest a departure from the preconceived notion of requirement of secondary structure as a key prerequisite for the manifestation of antimicrobial activity and open up possibilities of venturing into atomistic view of these random copolymeric antimicrobial agents.

Author contributions

J.M., P.G., J.K.K., and N.D. designed the project. J.K.K., D.D.P., N.D., and J.M. developed the model. J.K.K., J.M., and D.D.P. performed the coarse-grained simulations. J.K.K. and D.D.P. performed structural refinement. J.K.K., D.D.P., N.D., P.G., and J.M. analyzed the results. J.K.K. and J.M. wrote the manuscript.

Editor: Charles Deber.