Abstract
Mechanical thrombectomy has become the standard treatment for patients with an acute ischemic stroke. In this approach, to remove blood clots, mechanical force is applied using thrombectomy devices, in which the interaction between the clot and the device could significantly affect the clot retrieval performance. It is expected that the finite element method (FEM) could visualize the mechanical interaction by the visualization of the stress transmission from the device to the clot. This research was aimed at verifying the constitutive theory by implementing FEM based on the visco-hyperelastic theory, using a three-dimensional clot model. We used the visco-hyperelastic FEM to reproduce the mechanical behavior of blood clots, as observed in experiments. This study is focused on the mechanical responses of clots under tensile loading and unloading because in mechanical thrombectomy, elongation is assumed to occur locally on the clots during the retrieval process. Several types of cylindrical clots were created by changing the fibrinogen dose. Tensile testing revealed that the stiffness (E0.45-value) of clots with fibrinogen could be more than three times higher than that of clots without fibrinogen. It was also found that the stiffness was not proportional to the fibrinogen dose. By fitting to the theoretical curve, it was revealed that the Mooney-Rivlin model could reproduce the hyperelastic characteristics of clots well. From the stress-relaxation data, the three-chain Maxwell model could accurately fit the experimental viscoelastic data. FEM, taking the theoretical models into account, was then carried out, and the results matched well with the experimental visco-hyperelastic characteristics of clots under tensile load, reproducing the mechanical hysteresis during unloading, the stress dependence on the strain rate, and the time-dependent stress decrease in the stress-relaxation test.
Significance
In mechanical thrombectomy, a blood clot is retracted by mechanical force using a medical device. It is therefore important to analyze the interactions between clots and the devices to evaluate the device performance. The finite element method (FEM) has great potential for the visualization of mechanical interactions. We studied the validity of FEM by assessing its ability to reproduce the mechanical characteristics of clots under tensile load. It was found that by incorporating viscoelastic theory into the FEM, typical characteristics of clots such as stress relaxation and the strain-rate and hysteresis characteristics could be computationally reproduced, indicating that the viscoelastic law is applicable to predict the mechanical behavior of clots to understand the rather complex mechanism of thrombectomy.
Introduction
Strokes are the second leading cause of death and the third leading cause of disability worldwide (1). An ischemic stroke, which accounts for 87% of all strokes in the United States (2), is caused by sudden neurologic deficits through blockage of blood vessels; blood clots often cause blockages that would lead to ischemic strokes. Recently, mechanical thrombectomy, an effective treatment to restore blood flow by mechanically removing blood clots from the brain, is conducted for patients with an acute ischemic stroke who are ineligible for intravenous tissue plasminogen activator. In fact, the number of cases of mechanical thrombectomy has been increasing as evidence for the efficacy and safety of the procedure increases (3).
However, there still remain critical cases that cannot be treated using existing medical devices. It has been reported that vessel occlusion by hypodense, fibrin-rich thrombi and occlusion of the distal arteries are factors for treatment failure (4,5). Also, some of the mechanical thrombectomies resulted in adverse outcomes such as the embolization of clots to new vascular territories and hemorrhagic events (6,7).
In mechanical thrombectomy, in which a thrombectomy device removes blood clots by mechanical force, the interaction between a blood clot and a device plays a key role in overcoming the above issues, directly affecting clot retrieval performance. However, only a limited number of studies have been reported so far regarding the study of these interactions (8,9). For the understanding of the clot-device interaction from a mechanical perspective, the mechanical properties of blood clots should be examined and analyzed.
The mechanical properties of clots have been studied experimentally and theoretically. Brown et al. evaluated clots made from purified human fibrinogen and concluded that the clots had a nonlinear stress-strain relationship and that the samples could be stretched up to three times their relaxed length before breaking (10). Further imaging has revealed that this nonlinearity is attributable to the structural transitions of fibrin, including protein unfolding and the expulsion of water. Also, blood clots are known to exhibit viscoelastic properties (11). Liu et al. performed stress-relaxation tests on single fibrin fibers and reported that the relaxation time was 2–52 s (12). Moreover, the stress-relaxation behavior (time-dependent weakening) of clots has also been confirmed in several studies (13, 14, 15).
Theoretically, the material parameters of a blood clot have been determined by applying a rheology model, consisting of elastic springs and viscous dashpots, to the clot (16,17). These studies indicated that the strain-energy function can be effectively utilized to explore the hyperelastic property, and a rheology model such as the generalized Maxwell model is applicable to the investigation of the viscoelastic properties of clots (13).
Using the theoretical model, the finite element method (FEM) has great potential for the understanding and analysis of the mechanism of mechanical thrombectomy by enabling visualization of stress transmission from the device to the clot. The efficacy of FEM in this context has been investigated by Luraghi et al. (9). Their study reports that each thrombectomy procedure could be replicated in silico and clot deformation and stress distribution of the clot could be visualized, showing the significance of the development of the numerical approach.
The further development of computational tools requires an accurate underlying constitutive theory and an attendant validated numerical implementation of the theory. As basic research, we have focused on the numerical simulation of the mechanical responses of clots. The aim of this study is to investigate the validity of the viscoelastic theory and the numerical simulation of the mechanical behavior of clots.
In mechanical thrombectomy, clots receive tensile stress during their retrieval. Clots are withdrawn by stent retrievers through patient vessels or receive negative pressure from aspiration catheters. Elongation is assumed to occur locally on the clots during the retrieval process. Thus, this study is focused on the mechanical responses of clots under tensile load.
In addition, it is crucial to incorporate viscoelastic properties into the simulation because the embedding speed of a stent strut into a clot and the clot aspiration speed should differ among medical devices. Sugerman et al. have evaluated in detail the viscoelasticity of clots (15). Their experiments revealed that clots exhibited the Mullins effect, hysteresis, strain-rate dependence, and nonlinear stress relaxation. FEM approaches that incorporated the viscoelastic law have been established. Johnson et al. performed a series of FEMs using the viscoelastic law and showed that the model was capable of reproducing the compressive behavior of clots (18). Rausch et al. presented an FEM that dealt with the Ogden hyperelastic model, a viscoelastic model, and a damage model (19). The experimental and numerical results of the mechanical responses of clots under a load-unload tensile test were compared. The stress relaxation and the hysteresis were successfully captured by the FEM reported in the above studies.
However, to the best of our knowledge, the validity of numerical simulations has not been tested for the tensile loading and unloading of clots with varying contents and at different strain rates. In this study, the tensile properties of different types of clots were examined to evaluate the efficacy of the numerical simulations under various conditions. A procedure flow to determine material parameters by changing test conditions is presented. Also, this would be the first study, to our knowledge, that tested the validity of numerical simulations for the mechanical response using cylindrical clots with dimensions that may reproduce situations similar to human strokes (20, 21, 22), providing us with clinically relevant results. In addition, because all FEM results were conducted using an implicit scheme, the solutions were unconditionally stable, and the method facilitated the use of large time steps. We compared the experimental and numerical results to verify the capability of the theory and the computational method for the prediction of the actual visco-hyperelastic characteristics of clots.
Materials and methods
Constitutive equation
In this study, in the aim of capturing the visco-hyperelastic behavior of clots, a constitutive model with the strain-energy function and a viscoelastic rheology model were employed.
Hyperelastic law
When the strain-energy density function per unit undeformed volume is defined, one may determine the stress-strain from
| (1) |
where ψe is the strain-energy function and Sije and Cij are the elastic second Piola-Kirchhoff stress tensor and the right Cauchy deformation tensor, respectively (i, j = 1, 2, 3). The use of the strain-energy function makes it possible to compute the stress of hyperelastic materials efficiently.
The strain-energy function ψe can be additively decomposed into two parts as follows:
| (2) |
where ψiso represents the isochoric (deviatoric) strain-energy function that accompanies shape changes at constant volume and ψvol represents the volumetric strain-energy function that accompanies volumetric changes.
Several types of strain-energy functions have been proposed to simulate incompressible hyperelastic materials. Among them are the Arruda-Boyce, the Mooney-Rivlin, the Yeoh, and the Ogden models. As described in Hyperelastic model determination, the Mooney-Rivlin strain-energy function was selected as a result of experimental curve fitting. The Mooney-Rivlin model was shown to be the best model to describe the hyperelastic behavior of materials with two material parameters.
The Mooney-Rivlin strain-energy function, ψiso, is given as
| (3) |
where c10 and c01 are material parameters and Ī1 and Ī2 are the first and the second invariants of the tensor
| (4) |
| (5) |
and
| (6) |
where J is the determinant of the deformation gradient tensor.
The volumetric strain-energy function is assumed to take the form
| (7) |
where the constant D is the double reciprocal of the bulk modulus (23), which can be determined from the experimental tests.
Viscoelastic law
In the nonlinear visco-hyperelasticity, the stress of visco-hyperelastic materials is expressed in the form of the convolution of a strain-dependent function Se(λ) and a time-dependent function g(t):
| (8) |
where S is the second Piola-Kirchhoff stress, λ is the stretch ratio along the loading direction, and t is the time.
g(t) is represented by the Prony series:
| (9) |
| (10) |
where g∞ is the equilibrium modulus and gi and τi are the characteristic amplitude and the relaxation time associated with the i-th (1 < i < N) Maxwell model component (Fig. 1 a). The number N is generally selected to increase the accuracy of the fitting model.
Figure 1.
Rheology model and flow chart of material parameter identification. (a) Rheology model (the generalized Maxwell model). The model consists of N Maxwell elements connected in parallel. In each Maxwell element, a spring (moduli Gi) and a dashpot (viscosity ηi) are connected in series. An extra isolated spring is added in parallel to represent the equilibrium modulus (moduli G∞). (b) Flow chart of material parameter identification. Each procedure was done for clots without fibrinogen (BC-0) and clots with 100 mg of fibrinogen (BC-100).
From Eqs. 8, 9, and 10, S becomes
| (11) |
where s is the historical time variable. Se, the elastic second Piola-Kirchhoff stress tensor, is computed by differentiation of the strain-energy function ψe, as described in Hyperelastic law.
The hereditary integral in Eq. 11 can be computed using an algorithm presented by Goh et al., which is based on a finite time increment formulation of the convolution integral (24):
| (12) |
where Δt is the time increment and hi(t) is the stress at the previous time step.
Implementation to FEM
Implicit time integration schemes in FEM require the computation of the tangent stiffness matrix at each time step. Thus, the tangent stiffness matrix in the material description is installed. is additively decomposed into an isochoric part and a volumetric part. Each part involves elasticity tensors computed as the derivative of Se with respect to C:
| (13) |
Se and are derived from the standard rules of tensor algebra and tensor calculus (25) as follows:
| (14) |
and
| (15) |
where the sign “:” denotes the double contraction of two tensors.
From Eqs. 14 and 15, is computed as the derivative of Se with respect to C.
The isochoric part is computed as follows:
| (16) |
where the sign “” denotes the dyadic product of two tensors. and are the projection tensor and the transpose of , respectively (25), expressed as
| (17) |
and
| (18) |
where denotes the fourth-order unit tensor.
The volumetric part becomes
| (19) |
where in the last term is expressed as follows:
| (20) |
From the above formulation, the stress tensor and the tangent stiffness matrix of a visco-hyperelastic material are expressed in discrete form as follows:
| (21) |
| (22) |
and
| (23) |
where gvis is the viscous constituent.
Determination of material parameters
Material parameters were determined from tensile tests on clot analogs. The diagram in Fig. 1 b shows the procedures of the experimental tests and the parameter determination. First, clots were stretched at a constant strain rate of 10 per min until fragmentation. The stress-strain characteristics were recorded. Curve fitting to the theoretical stress curve of each type of strain-energy function was then performed with optimization algorithm using the leastsq function in Python 3.8.5. In this procedure, an incompressible model was applied, and the viscoelastic relaxation was not included in the model. The relative errors of the theoretical-to-experimental curve fittings were calculated. Considering the aspects of errors and the number of parameters needed, the strain-energy function for the FEM was selected. The hyperelastic material parameters were also identified. Next, the viscoelastic material parameters were identified from stress-relaxation tests. The stress-relaxation tests were performed by applying and holding 100% tensile strain for 10 min while measuring the corresponding decrease in tensile load over time. After obtaining the time-stress characteristics, curve fitting to the theoretical curve presented by Goh et al. (24) was applied. Constants were identified referring to the algorithm presented by Pawlikoski (26). The number of Maxwell elements was increased starting from 1, and τi and gi were identified at each step. The rate of change in error was computed by comparing the errors in N- and N-1-chain Maxwell element models. The increase in the number of Maxwell elements was stopped when the rate of change in error became smaller than 1%. Finally, loading and unloading tensile tests were performed at the two strain rates of 10 per min and 1 per min. The final material constants were identified from the curve fitting using the two experimental curves at the same time.
Experimental setup
Clot formation
Fresh blood was collected from swine arteries. Clots were made by adding thrombin and fibrinogen to the obtained blood. Clots 4 mm in diameter were formed in polyvinyl chloride (PVC) tubes. We referred to the Gralla technique (20), which has been the most commonly used technique for the preclinical evaluation of mechanical thrombectomy device performance (20,27,28). Chueh et al. have shown that the mechanical characteristics of clot analogs created by the Gralla technique are similar to those of thromboemboli retrieved from the cerebral arteries of patients with acute ischemic stroke (28).
For the purpose of verifying numerical simulation under various conditions, clots with different compositions were created. Luo et al. found that the addition of fibrinogen to the Gralla clot model changed the mechanical properties in proportion to the fibrinogen dose (29). Thus, three types of clot analog were created by changing the amount of fibrinogen to 0, 100, and 200 mg.
Clots without adding fibrinogen (BC-0) were made by adding 25 International Units (IU) thrombin to 10 mL of blood. The mixture was carefully blended and injected into PVC tubes. To create clots with fibrinogen, doses of 100 mg (BC-100) and 200 mg (BC-200) of bovine fibrinogen were used. Blood was collected into receiving vessels that were preloaded with specific amounts of fibrinogen. Then, 25 IU thrombin was added and mixed carefully, followed by injection into PVC tubes.
To reduce variation in the data caused by differences in individual animals, the three types of clots were created from blood obtained from the same animal on the same day. This procedure was conducted for four animals.
Tensile test setup
Tensile tests were performed using Autograph, a universal material testing machine (Shimadzu, Kyoto, Japan). All tests were carried out in an air environment at 24–26°C. Clots were cut into 25-mm-long pieces and subjected to tensile tests until breakage, stress-relaxation tests, and loading and unloading tensile tests. All tests were performed for three clots of each type.
To test clot specimens in a shape similar to that of the actual clot in the blood vessel, and thus to make experimental setups more clinically relevant, tests were conducted using cylindrical clot samples without postprocessing (Fig. 2 a). The clots were gripped with especially developed grips, roundly cut to prevent the sample from breaking at the grip faces (Fig. 2, b and c). Besides, because the grip was made in an L-shape, there was enough space to insert tweezers to grasp the clot, enhancing the workability of the sample setting.
Figure 2.
Experimental setups. (a) Actual created clots. (b) A schematic illustration of a custom-made grip used in the tensile test. (c) Tensile test. (d) Numerical model adapted to FEM.
The tensile tests until sample breakage were conducted to select the best hyperelastic model with which to describe the mechanical behavior of the clot. The samples were gripped at 15 mm gauge length and elongated at a strain rate of 10 per min until failure. In the stress-relaxation test, clots were elongated at a strain rate of 10 per min to the nominal strain of 100%, followed by a recovery period of 10 min. In the loading and unloading tensile tests, clots were elongated to a nominal strain of 50% at a constant strain rate and unloaded to their initial configuration at the same strain rate. The test was performed at the strain rates of 10 per min and 1 per min to analyze the strain-rate dependence. A nominal strain of 50% was chosen to obtain a sufficient amount of data without clot fragmentation.
The tensile force on a clot specimen was normalized by the cross-sectional area of the specimen to calculate the stress. The clot diameters were measured at three separate positions using a caliper. The average diameter was used to calculate the cross-sectional area. To evaluate the stiffness of the clot, the stiffness E0.45 (N/mm2) was calculated as E0.45 = σ0.45/0.45, where σ0.45 is the tensile stress on the specimen at a nominal strain of 45%, referring to the literature (30).
Finite element simulation
A cylindrical model of a clot with an outer diameter of 4 mm and a length of 15 mm was generated using the Computer-Aided Design (CAD) program Solid Edge ST10 (Siemens PLM Software, Dallas, TX). The clot model geometry was discretized into 1440 hexahedral elements using Salome (Open Cascade EDF CEA, Guyancourt, France). The mesh convergence was evaluated by examining the changes in the key output variables in response to the mesh density. The finite element simulations were performed on 16 CPUs of an Intel Xeon Gold 6234 with 96 GB of RAM memory, using the open-source FEM solver FrontISTR Release 5.0b (University of Tokyo, Tokyo, Japan). All simulations were implemented within an implicit time integration scheme, the total Lagrangian method. The constitutive model formulated as Eqs. 21, 22, and 23 was introduced to the software as a user subroutine. The model, with the boundary conditions and the kinematical load, is shown in Fig. 2 d. The FEM was employed with the same elongation and strain rate as those of the experimental conditions. The elongations at the strain rates of 10 per min and 1 per min were computed with time steps of 0.01 and 0.1 s, respectively. Stress-strain curves were obtained from the FEM results. The computed data were visualized using Paraview 5.6.0. The deformations and the stress distributions of the clot models were also visualized.
Results
Stress-strain characteristics of clots
The stress-strain curves until fracture are presented in Fig. 3 a. Representative clot data from one animal are shown. The clot exhibited nearly linear stress-strain behavior. The strains at fracture were between 110 and 160%. The observed characteristics showing that the samples could be stretched to more than double their original length before breaking matched well with the results represented in the literature (10,29).
Figure 3.
Results of tensile tests. (a) Representative experimental data of tensile tests up to fracture. Green line: clot with 200 mg fibrinogen. Red line: clot with 100 mg fibrinogen. Blue line: clot without fibrinogen. (b) E0.45 of each clot with different compositions (n = 12 each). (c–i) Stress-strain properties of the hyperelastic models considered. The dots represent the experimental data, and the lines show the theoretical curves (red: BC-100, blue: BC-0). The λ in the equation in the legends represents the stretch rate. c1–3, c10, c01, μ, Jm, β, α1–3, and μ1–3 are material parameters. For the Arruda-Boyce model, α1 = 1/2, α2 = 0.05, α3 = 0.0105, α4 = 0.00271, and α5 = 7.703 × 10−4. I1 is an invariant which is calculated by I1 = λ2 + : (c) neo-Hookean model, (d) Mooney-Rivlin model, (e) Gent model, (f) Fung model, (g) Arruda-Boyce model, (h) Yeoh model, and (i) Ogden model.
The stiffness of each clot type, as indicated by E0.45, is shown in Fig. 3 b. The E0.45 of clots with fibrinogen were more than three times higher than those of clots without fibrinogen (p = 0.0002). However, the stiffness was not proportional to the fibrinogen dose. Thus, two types of clots with different compositions, BC-0 and BC-100, were chosen for the determination of material parameters.
Hyperelastic model determination
The stress-strain curves of the two types of clots were fitted to those of the seven standard hyperelastic models: neo-Hookean, Mooney-Rivlin, Gent, Fung, Arruda-Boyce, Yeoh, and Ogden with N = 3 (Fig. 3, c–i). The determined parameters and relative errors are listed in Table 1. The Ogden model with N = 3, the Yeoh model, and the Mooney-Rivlin model exhibited the smallest, the second smallest, and the third smallest error, respectively. In this study, the Mooney-Rivlin model was selected because the model may have adequate accuracy with only two material parameters.
Table 1.
Material parameters and relative errors of each hyperelastic model
| Hyperelastic model | Clot | Material parameters | Relative error | Relative error (average) |
|---|---|---|---|---|
| Ogden | BC-0 | μ1 = 1.42 × 10−8, μ2 = 1.97 × 10−3, μ3 = 1.38 × 10−8, a1 = 1.10, a2 = 1.66, a3 = 9.33 × 10−1 | 3.62 × 10−8 | 1.33 × 10−7 |
| BC-100 | μ1 = −3.88 × 10−2, μ2 = 3.47 × 10−2, μ3 = 7.21 × 10−3, a1 = −1.64 × 10−1, a2 = 8.09 × 10−6, a3 = 1.06 | 2.30 × 10−7 | ||
| Yeoh | BC-0 | c1 = 9.65 × 10−4, c2 = −2.94 × 10−5, c3 = 2.67 × 10−6 | 3.57 × 10−8 | 1.79 × 10−7 |
| BC-100 | c1 = 1.79 × 10−3, c2 = 1.58 × 10−5, c3 = −4.13 × 10−6 | 3.22 × 10−7 | ||
| Mooney-Rivlin | BC-0 | c10 = 7.37 × 10−4, c01 = 2.91 × 10−4 | 4.16 × 10−8 | 1.88 × 10−7 |
| BC-100 | c10 = 1.80 × 10−3, c01 = 8.38 × 10−6 | 3.35 × 10−7 | ||
| Neo-Hookean | BC-0 | c1 = 8.99 × 10−4 | 2.03 × 10−7 | 2.68 × 10−7 |
| BC-100 | c1 = 1.80 × 10−3 | 3.34 × 10−7 | ||
| Gent | BC-0 | μ = 1.80 × 10−3, Jm = 9.97 × 104 | 2.03 × 10−7 | 2.68 × 10−7 |
| BC-100 | μ = 3.60 × 10−3, Jm = 7.32 × 104 | 3.34 × 10−7 | ||
| Arruda-Boyce | BC-0 | C1 = 1.80 × 10−3, β = 4.88 × 10−22 | 2.03 × 10−7 | 2.69 × 10−7 |
| BC-100 | C1 = 3.60 × 10−3, β = 2.28 × 10−3 | 3.35 × 10−7 | ||
| Fung | BC-0 | c1 = 1.80 × 10−3, c2 = 7.20 × 10−21 | 2.03 × 10−7 | 5.73 × 10−7 |
| BC-100 | c1 = 3.60 × 10−3, c2 = 1.15 × 10−17 | 3.34 × 10−7 |
Identification of viscoelastic material parameters
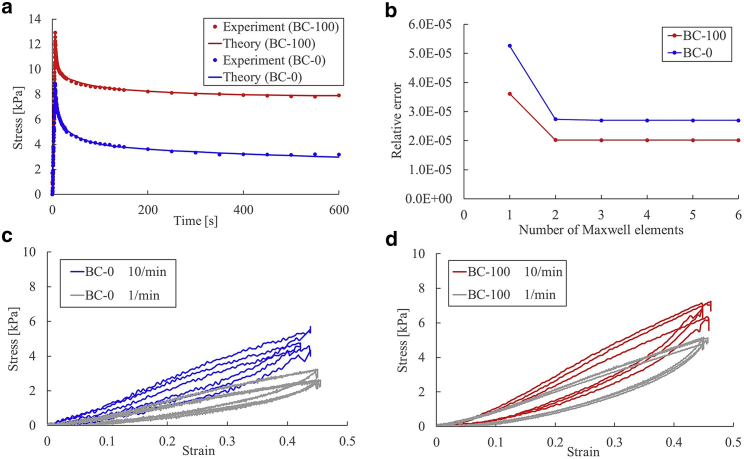
In Fig. 4 a, the experimental relaxation curves and the fitted theoretical curves are depicted. The data show a time-dependent decrease in stress, which is indicative of a viscous process. The material parameters τi and gi determined in the course of curve fitting are presented in Table 2.
Figure 4.
Relaxation and loading-unloading tests. (a) Stress-time data obtained from relaxation tests. The dots show experimental data, and the lines show the theoretical curves (red: BC-100, blue: BC-0). (b) Relative errors between experimental and theoretical data in relation to the number of Maxwell elements. (c and d) Representative results of the loading-unloading test (n = 3). Red line: BC-100; blue line: BC-0, both tested at the strain rate of 10 per min. Gray line: strain rate of 1 per min.
Table 2.
Viscoelastic material constants identified
| Clots without fibrinogen | Clots with 100 mg fibrinogen | |
|---|---|---|
| c10 | 1.16 × 10−3 | 2.97 × 10−3 |
| c01 | 1.18 × 10−3 | 1.59 × 10−5 |
| g1 | 0.149 | 0.058 |
| g2 | 0.192 | 0.062 |
| g3 | 0.455 | 0.431 |
| τ1 | 3.17 | 2.14 |
| τ2 | 40.65 | 45.73 |
| τ3 | 600.00 | 205.77 |
| D | 0.124 | 0.077 |
The decrease in relative error related to an increase in the number of Maxwell elements is shown in Fig. 4 b. N = 3 was determined because the rate of change in the error became smaller than 1% for N ≥ 4.
When the relaxation time was calculated as the time required for an exponentially decreasing variable to drop from an initial value to 1/e, all the clots with fibrinogen (BC-100 and BC-200) had relaxation times over 600 s (n = 24). In regard to the clots without fibrinogen (BC-0), 8 of 12 samples had a relaxation time over 600 s. This observation indicates that clots without fibrinogen had low durability and fragmentation of the internal structure occurred because of strain, which led to stress reduction.
Strain-rate dependence
Representative stress-strain curves obtained from loading-unloading tensile tests are presented in Fig. 4, c and d, demonstrating loading-unloading hysteresis again with material viscoelasticity. When clots were stretched and unloaded, nonlinear behavior could be clearly observed only in the unloading phase. Regarding the influence of the strain rate, the stress decreased when the strain rate was reduced, especially for clots without fibrinogen. However, because of variance in the animals, there were no significant differences in both clot types (p = 0.127 and p = 0.679 for BC-0 and BC-100, respectively).
FEM
The visco-hyperelastic FEM was implemented using the parameters determined by experiments. The maximum principal stress distributions before and after loading (clot: BC-0, strain rate: 10 per min) are presented in Fig. 5 a. Stress relaxation is presented in Fig. 5 b. It can be noted from the reported curves that the numerical model results matched well with those of the experiments. The stress-strain responses to loading and unloading are shown in Fig. 5, c–f. The FEM results satisfactorily matched those of the experiments. The hysteresis during unloading, which was a typical viscoelastic characteristic of the clot, was computationally reproduced. However, some particular parts of the stress-strain curve could not be well reproduced, especially at the parts when the unloading process started and ended.
Figure 5.
FEM results: (a) maximum principal stress distributions (in MPa) on the clot before and after loading (clot: BC-0, strain rate: 10 per min). (b) Stress relaxations obtained from experiments and FEM. (c–f) Stress-strain curves obtained from experiments and FEM. Red, blue, and black lines are experimental data of the clots with 100 mg fibrinogen, without fibrinogen, and FEM data, respectively. (c and e) Test results of the strain rate of 10 per min. (d and f) Test results of the strain rate of 1 per min.
The model also reproduced the stress dependence on the strain rate (Fig. 5, c–f). The results from the FEM indicated that the presented theory was capable of reproducing the visco-hyperelastic characteristics of clots accurately.
Discussion
Mechanical properties of clots under several conditions
The tensile tests of clots with different compositions were performed with varying strain rates to verify the numerical simulations under various conditions. It was found that the addition of fibrinogen increased the clot stiffness more than threefold, which was consistent with the results of Luo et al. (29), in which the addition of fibrinogen to a Gralla experimental blood clot model changed the mechanical properties. However, it was also found that the stiffness was not proportional to the fibrinogen dose.
Blood clots are generally formed as a result of a highly complex cascade with multiple coagulation factors (31). The experimental results indicated that fibrinogen alone could not increase fibrin networks to the extent that the stiffness increased unless other coagulation factors such as thrombin increased simultaneously.
From the loading and unloading tests at different strain rates, the stress tended to be dependent on the strain rate, although statistical differences could not be confirmed. Sugerman et al. also reported similar strain-rate dependence of clots (15), consistent with our experimental and FEM results.
Stress-strain curves from experiments
In the tensile test, the stress was nearly linear to the strain in the loading phase, whereas it was nonlinear in the unloading phase. Some studies have shown that fibrin fibers exhibited nonlinear responses in tensile testing (10,12,32). However, other studies have reported that their clot materials exhibited nearly linear responses (33,34). The reason for such behavioral difference between fibrins and clots has not yet been explored to the best of our knowledge. The mechanical characteristics of clots are known to be largely determined by fibrin networks (35). However, this behavioral discrepancy indicates that other blood components such as red blood cells or platelets could largely contribute to the stress-strain response of clots.
The hysteresis during the unloading process was observed in this study, which had also been reported in the studies of single fibrin fibers (12) and blood clots (15,18). This hysteresis represented the energy loss in the stretching process typical of viscoelastic materials and that is also known to be typical in filled rubbers. Several physical interpretations have been proposed to describe such hysteresis loss (the Mullins effect) (36), such as a change in the entanglement density of polymer chains. Sugerman et al. demonstrated that blood clots exhibited Mullins-like effects (15). The experimental results in our work supported the contention that this phenomenon in rubber materials also occurs in blood clots consisting of fibrin fibers.
Comparison of experimental and FEM data
Using the viscoelastic FEM, the hysteresis in loading and unloading, the strain-rate dependence, and the stress relaxation experimentally observed in blood clots were closely reproduced, indicating a strong correlation of the mechanical behavior of clots under tensile load with the viscoelastic theory. The validity of the FEM for clots under compressive load and unloading has been confirmed by a similar approach (18). This work may have first verified, to our knowledge, that the theory and the viscoelastic FEM were also applicable to cylindrical clots under tensile loading and unloading. However, some particular parts of the stress-strain curve could not be well reproduced, especially the parts at which the unloading process started and ended (Fig. 5, c–f). This discrepancy resulted from the unique characteristics of blood clots exhibiting linear responses only when they were stretched. The half-moon-like shape observed in the stress-strain curves made it difficult to compute and analyze using a standard viscoelastic law. Besides, the difference of the data strain range for hyperelastic model selection (∼1–1.05 in Fig. 3) and FEM (0.5 in Fig. 5) was assumed to be the cause of the discrepancy. The physical phenomena occurring in these ranges may not be the same. There is a difference between the experimental and theoretical curves in Fig. 3 when the strain is less than 0.2. This observation indicates that for a strain range lower than 0.5, other hyperelastic models would have better accuracy.
Regarding the end of unloading, a residual strain of 4.9% occurred in the experiments on average (n = 12). Few studies have focused on the residual strain (15). Liu et al. reported that fibrin fibers exhibited permanent deformation at a strain as low as 10% (12). In our work, as a consequence of the deformation delay characterized by the parameters gi and τi, the strain remained at the zero-stress state. To consider the plastic deformation correctly, the theory of elastic-plastic deformation should be incorporated.
We also acknowledge that there are some limitations to this study that need additional future work. First, FEM was implemented by assuming clots to be incompressible, whereas previous works in the literature have shown that clots exhibited an anomalously large Poisson effect compared with the rubber and traditional models (10). The presented model should be further modified to capture this typical characteristic for the accurate simulation of mechanical thrombectomy, especially when we want to assess how clots deform and roll inside a stent retriever.
Second, mechanical loading was limited to extension. The mechanical behavior of blood clots should be significantly different in compressive and tensile loadings because of the structural mechanisms of fibrin networks. Fiber alignment is a key characteristic observed in clot elongation (10,37,38). In compression, clots exhibit a nonlinear mechanical response because of the densification of the compressed network and reorientation of the whole fibrillar network (39). Thus, the presented model cannot reproduce the mechanical responses of both loading types with the same material parameter sets. Future research is required to verify whether the constitutive theory presented in this study has the capability of reproducing clot behavior under compressive load.
It is therefore necessary that the constitutive theory and the parameter determination procedure should be further modified to incorporate the overall picture of the phenomena unique to blood clots, which are interesting but challenging studies we intend to pursue in the future.
In mechanical thrombectomy, clots receive tensile stress during their retrieval. Elongation is assumed to occur locally on the clots during the retrieval process. This technically demands an effective numerical simulation of such hyperelastic materials. Besides, because the embedding speed of a stent strut in clots or the clot aspiration speed differs among medical devices, it is crucial to incorporate details of the viscoelastic property of the clots in the simulation. By incorporating these properties into the FEM, we may understand how the time factors, such as the time after deploying a stent retriever to integrate clots into the device and the withdrawal speed of a thrombectomy device, could affect thrombectomy performance. The theory and methodology developed in this study may highly offer potential for the computational visualization of the mechanical interactions between clots and devices, promoting understanding of the underlying mechanism of mechanical thrombectomy.
Conclusions
Tensile testing of blood clots was experimentally carried out to identify the material parameters. The results of curve fitting indicated that the Mooney-Rivlin model could accurately reproduce the hyperelastic characteristics of clots using only a few material parameters. In regard to the viscoelasticity of clots, the three-chain Maxwell model was found to fit the experimental data well. The stiffness (E0.45-value) of clots with fibrinogen was more than three times higher than that of clots without fibrinogen, and the stiffness was not proportional to the fibrinogen dose. A visco-hyperelastic FEM was implemented, and the results satisfactorily matched the experimental data. The model could reproduce the viscoelastic behavior of clots under tensile load, including the hysteresis during unloading, the stress dependence on the strain rate, and the time-dependent stress decrease in the stress-relaxation test. The results from FEM indicated that the theory presented is capable of reproducing the actual visco-hyperelastic characteristics of clots.
Author contributions
K.T. conducted experiments, developed the computational model, carried out FEM, analyzed the results, and wrote the manuscript (original draft). Y.S. planned the research, wrote the manuscript (review and editing), and coordinated the project. I.O. recorded experimental results. A.H. was the research supervisor, wrote the manuscript (reviewing and editing), and coordinated the project.
Acknowledgments
We thank Kazuya Shobayashi for dedicated assistance with this study. We also thank Hiroki Ishida, Mai Mikata, Yuta Doi, Megumi Hinomoto, Atsunori Yoshida, Taisa Ogasawara, Takanobu Kidokoro, and Mami Uehara for preparing clot samples.
Editor: Guy Genin.
References
- 1.Johnson W., Onuma O., Sachdev S. Stroke: a global response is needed. Bull. World Health Organ. 2016;94 doi: 10.2471/BLT.16.181636. 634–634A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Virani S.S., Alonso A., Tsao C.W., American Heart Association Council on Epidemiology and Prevention Statistics Committee and Stroke Statistics Subcommittee Heart disease and stroke statistics-2020 update: a report from the American Heart Association. Circulation. 2020;141:e139–e596. doi: 10.1161/CIR.0000000000000757. [DOI] [PubMed] [Google Scholar]
- 3.Yarbrough C.K., Ong C.J., Derdeyn C.P. Endovascular thrombectomy for anterior circulation stroke: systematic review and meta-analysis. Stroke. 2015;46:3177–3183. doi: 10.1161/STROKEAHA.115.009847. [DOI] [PubMed] [Google Scholar]
- 4.Yeo L.L.L., Bhogal P., Andersson T. Why does mechanical thrombectomy in large vessel occlusion sometimes fail?: a review of the literature. Clin. Neuroradiol. 2019;29:401–414. doi: 10.1007/s00062-019-00777-1. [DOI] [PubMed] [Google Scholar]
- 5.Kim B.M. Causes and solutions of endovascular treatment failure. J. Stroke. 2017;19:131–142. doi: 10.5853/jos.2017.00283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gascou G., Lobotesis K., Costalat V. Stent retrievers in acute ischemic stroke: complications and failures during the perioperative period. AJNR Am. J. Neuroradiol. 2014;35:734–740. doi: 10.3174/ajnr.A3746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Leishangthem L., Satti S.R. Vessel perforation during withdrawal of Trevo ProVue stent retriever during mechanical thrombectomy for acute ischemic stroke. J. Neurosurg. 2014;121:995–998. doi: 10.3171/2014.4.JNS132187. [DOI] [PubMed] [Google Scholar]
- 8.Weafer F.M., Duffy S., Gilvarry M. Characterization of strut indentation during mechanical thrombectomy in acute ischemic stroke clot analogs. J. Neurointerv. Surg. 2019;11:891–897. doi: 10.1136/neurintsurg-2018-014601. [DOI] [PubMed] [Google Scholar]
- 9.Luraghi G., Rodriguez Matas J.F., Migliavacca F., INSIST investigators Applicability assessment of a stent-retriever thrombectomy finite-element model. Interface Focus. 2021;11:20190123. doi: 10.1098/rsfs.2019.0123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Brown A.E., Litvinov R.I., Weisel J.W. Multiscale mechanics of fibrin polymer: gel stretching with protein unfolding and loss of water. Science. 2009;325:741–744. doi: 10.1126/science.1172484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ryan E.A., Mockros L.F., Lorand L. Structural origins of fibrin clot rheology. Biophys. J. 1999;77:2813–2826. doi: 10.1016/S0006-3495(99)77113-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liu W., Carlisle C.R., Guthold M. The mechanical properties of single fibrin fibers. J. Thromb. Haemost. 2010;8:1030–1036. doi: 10.1111/j.1538-7836.2010.03745.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.van Dam E.A., Dams S.D., van de Vosse F.N. Non-linear viscoelastic behavior of abdominal aortic aneurysm thrombus. Biomech. Model. Mechanobiol. 2008;7:127–137. doi: 10.1007/s10237-007-0080-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ashton J.H., Vande Geest J.P., Haskett D.G. Compressive mechanical properties of the intraluminal thrombus in abdominal aortic aneurysms and fibrin-based thrombus mimics. J. Biomech. 2009;42:197–201. doi: 10.1016/j.jbiomech.2008.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sugerman G.P., Parekh S.H., Rausch M.K. Nonlinear, dissipative phenomena in whole blood clot mechanics. Soft Matter. 2020;16:9908–9916. doi: 10.1039/d0sm01317j. [DOI] [PubMed] [Google Scholar]
- 16.Schmitt C., Hadj Henni A., Cloutier G. Characterization of blood clot viscoelasticity by dynamic ultrasound elastography and modeling of the rheological behavior. J. Biomech. 2011;44:622–629. doi: 10.1016/j.jbiomech.2010.11.015. [DOI] [PubMed] [Google Scholar]
- 17.van Kempen T.H., Donders W.P., Peters G.W. A constitutive model for developing blood clots with various compositions and their nonlinear viscoelastic behavior. Biomech. Model. Mechanobiol. 2016;15:279–291. doi: 10.1007/s10237-015-0686-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Johnson S., McCarthy R., McGarry J.P. Investigating the mechanical behavior of clot analogues through experimental and computational analysis. Ann. Biomed. Eng. 2021;49:420–431. doi: 10.1007/s10439-020-02570-5. [DOI] [PubMed] [Google Scholar]
- 19.Rausch M.K., Sugerman G.P., Dortdivanlioglu B. Hyper-viscoelastic damage modeling of whole blood clot under large deformation. Biomech. Model. Mechanobiol. 2021 doi: 10.1007/s10237-021-01467-z. Published online June 2, 2021. [DOI] [PubMed] [Google Scholar]
- 20.Gralla J., Schroth G., Brekenfeld C. A dedicated animal model for mechanical thrombectomy in acute stroke. AJNR Am. J. Neuroradiol. 2006;27:1357–1361. [PMC free article] [PubMed] [Google Scholar]
- 21.Gralla J., Schroth G., Brekenfeld C. Mechanical thrombectomy for acute ischemic stroke: thrombus-device interaction, efficiency, and complications in vivo. Stroke. 2006;37:3019–3024. doi: 10.1161/01.STR.0000248457.55493.85. [DOI] [PubMed] [Google Scholar]
- 22.Luo Z.H., Chung A., Rösch J. Iodine based radiopacity of experimental blood clots for testing of mechanical thrombectomy devices. Radiol. Oncol. 2013;47:14–18. doi: 10.2478/raon-2013-0001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Doll S., Schweizerhof K. On the development of volumetric strain energy functions. J. Appl. Mech. 2000;67:17–21. [Google Scholar]
- 24.Goh S.M., Charalambides M.N., Williams J.G. Determination of the constitutive constants of non-linear viscoelastic materials. Mech. Time-Depend. Mater. 2004;8:255–268. [Google Scholar]
- 25.Holzapfel G.A. Wiley; Chichester, UK: 2000. Nonlinear Solid Mechanics. A Continuum Approach for Engineering. [Google Scholar]
- 26.Pawlikowski M. Non-linear approach in visco-hyperelastic constitutive modelling of polyurethane nanocomposite. Mech. Time-Depend. Mater. 2013;18:1–20. [Google Scholar]
- 27.Jahan R. Solitaire flow-restoration device for treatment of acute ischemic stroke: safety and recanalization efficacy study in a swine vessel occlusion model. AJNR Am. J. Neuroradiol. 2010;31:1938–1943. doi: 10.3174/ajnr.A2169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chueh J.Y., Wakhloo A.K., Gounis M.J. Mechanical characterization of thromboemboli in acute ischemic stroke and laboratory embolus analogs. AJNR Am. J. Neuroradiol. 2011;32:1237–1244. doi: 10.3174/ajnr.A2485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Luo Z.H., Chung A., Rösch J. Creation of fibrinogen-enhanced experimental blood clots to evaluate mechanical thrombectomy devices for treatment of acute stroke: an in vitro study. J. Vasc. Interv. Radiol. 2012;23:1077–1083. doi: 10.1016/j.jvir.2012.04.031. [DOI] [PubMed] [Google Scholar]
- 30.Liu Y., Reddy A.S., Savastano L.E. Standardized fabrication method of human-derived emboli with histologic and mechanical quantification for stroke research. J. Stroke Cerebrovasc. Dis. 2020;29:105205. doi: 10.1016/j.jstrokecerebrovasdis.2020.105205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Furie B., Furie B.C. Mechanisms of thrombus formation. N. Engl. J. Med. 2008;359:938–949. doi: 10.1056/NEJMra0801082. [DOI] [PubMed] [Google Scholar]
- 32.Averett R.D., Menn B., Guthold M. A modular fibrinogen model that captures the stress-strain behavior of fibrin fibers. Biophys. J. 2012;103:1537–1544. doi: 10.1016/j.bpj.2012.08.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Di Martino E., Mantero S., Fumero R. Biomechanics of abdominal aortic aneurysm in the presence of endoluminal thrombus: experimental characterisation and structural static computational analysis. Eur. J. Vasc. Endovasc. Surg. 1998;15:290–299. doi: 10.1016/s1078-5884(98)80031-2. [DOI] [PubMed] [Google Scholar]
- 34.Gasser T.C., Görgülü G., Swedenborg J. Failure properties of intraluminal thrombus in abdominal aortic aneurysm under static and pulsating mechanical loads. J. Vasc. Surg. 2008;48:179–188. doi: 10.1016/j.jvs.2008.01.036. [DOI] [PubMed] [Google Scholar]
- 35.Weisel J.W. The mechanical properties of fibrin for basic scientists and clinicians. Biophys. Chem. 2004;112:267–276. doi: 10.1016/j.bpc.2004.07.029. [DOI] [PubMed] [Google Scholar]
- 36.Diani J., Fayolle B., Gilormini P. A review on the Mullins effect. Eur. Polym. J. 2009;45:601–612. [Google Scholar]
- 37.Tutwiler V., Singh J., Weisel J.W. Rupture of blood clots: mechanics and pathophysiology. Sci. Adv. 2020;6:eabc0496. doi: 10.1126/sciadv.abc0496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Fereidoonnezhad B., Dwivedi A., McGarry P. Blood clot fracture properties are dependent on red blood cell and fibrin content. Acta Biomater. 2021;127:213–228. doi: 10.1016/j.actbio.2021.03.052. [DOI] [PubMed] [Google Scholar]
- 39.Kim O.V., Litvinov R.I., Alber M.S. Structural basis for the nonlinear mechanics of fibrin networks under compression. Biomaterials. 2014;35:6739–6749. doi: 10.1016/j.biomaterials.2014.04.056. [DOI] [PMC free article] [PubMed] [Google Scholar]