Abstract
We used computational methods to analyze the mechanism of actin filament nucleation. We assumed a pathway where monomers form dimers, trimers, and tetramers that then elongate to form filaments but also considered other pathways. We aimed to identify the rate constants for these reactions that best fit experimental measurements of polymerization time courses. The analysis showed that the formation of dimers and trimers is unfavorable because the association reactions are orders of magnitude slower than estimated in previous work rather than because of rapid dissociation of dimers and trimers. The 95% confidence intervals calculated for the four rate constants spanned no more than one order of magnitude. Slow nucleation reactions are consistent with published high-resolution structures of actin filaments and molecular dynamics simulations of filament ends. One explanation for slow dimer formation, which we support with computational analysis, is that actin monomers are in a conformational equilibrium with a dominant conformation that cannot participate in the nucleation steps.
Significance
More than half a century has passed since the first proposal of a mathematical description of actin filament nucleation and elongation. The kinetics of elongation have been described both mathematically and experimentally, but the kinetics of nucleation remain in question. This study demonstrates that actin filament nucleation is not only thermodynamically unfavorable but also kinetically unfavorable.
Introduction
Pioneering experiments by Oosawa et al. (1) provided the first clues about the nucleation reactions at the outset of the spontaneous polymerization of purified monomeric actin isolated from skeletal muscle. They used flow birefringence and capillary viscometry to measure the polymer concentration over time. Observing a lag at the outset of the reaction, they proposed that actin polymerization begins with unfavorable nucleation reactions. In a seminal article (2), they applied gas condensation theory to biopolymers to derive equations that describe the time course of the polymerization of actin. To simplify solving their derived equations, they assumed they could neglect the dissociation of subunits from the oligomers.
Wegner and Engel (3) further developed the mathematical description of actin nucleation by including subunit dissociation. However, they simplified the model by assuming that the multistep nucleation proceeds via a single, dimerization reaction that quickly attains a steady state. They used light scattering to follow the time course of actin polymerization and fitted two equations to characterize the nucleation reactions.
Further progress depended on the discovery by Kouyama and Mihashi (4) that incorporation of pyrene-labeled monomeric actin into filaments increases the fluorescence 20–25-fold. Thus, the fluorescence of pyrene-labeled actin can produce a signal proportional to the polymer concentration without disturbing the sample by the mechanical flow. Two groups (4,5) showed that the critical concentration of pyrenyl-actin is similar to that of unlabeled actin. This suggested that labeling with pyrene does not change the elongation rate constants, a conclusion confirmed by electron microscopy measurements of actin filament length over time (5). However, little is known about the effect of pyrenyl-actin on nucleation.
Three groups (6, 7, 8) used the time course of pyrenyl-actin polymerization to estimate equilibrium or rate constants for the unknown nucleation parameters. They all used computer simulations to fit their experimental data, but each group used different assumptions. Tobacman and Korn (6) analyzed the time course of pyrenyl-actin monomer assembly over a range of ionic conditions by fitting the equations derived by Wegner and Engel. This model did not allow for a direct determination of the nucleation rate constants. Instead, it produced a parameter related to all steps leading to nucleation. Cooper et al. (7) separated each nucleation step by using a model that built the filament nucleus by sequential addition of monomers with equivalent association and dissociation rate constants. Given very limited computing power at the time, Cooper et al. (7) made the same steady-state assumption as Wegner and Engel (3). They assumed a dissociation rate constant of 500 s−1 for each nucleation step, a value that produced a rapid equilibrium. Simulations with dimers and trimers forming with a slow association rate constant of 6.7 × 10−3 μM−1 s−1 (an average of two data sets) fit the experimental data. However, because of their assumption of a fixed dissociation rate constant, this result did not represent the true kinetic value. Frieden (8) used numerical integration of kinetic equations that did not rely on the assumption of any rapid equilibria. He did not report rate constants but obtained good fits to polymerization data with dissociation equilibrium constants of 800,000 μM for dimers and 5 μM for trimers. All three studies agreed that dimers and trimers are energetically unstable (Table 1), whereas longer oligomers elongate like the ends of filaments.
Table 1.
Nucleation rate and equilibrium constants from previous studies
| Cooper et al. (7) | Frieden (8) | Sept and McCammon (9) | Oda et al. (10) | This study | |
|---|---|---|---|---|---|
| k+1 (μM−1 s−1) | 6.7 × 10−3 | — | 35.7 | — | 3.5 (1.2–11) × 10−6 |
| k−1 (s−1) | 500 | — | 1.63 × 108 | — | 0.041 (0.036–0.047) |
| Kd of dimer (μM) | 75,000 | 800,000 | 4.6 × 106 | 1700 | 12,000 (3300–39,000) |
| k+2 (μM−1 s−1) | 6.7 × 10−3 | — | 2.18 | — | 13 (4.0–40) × 10−5 |
| k−2 (s−1) | 500 | — | 1300 | — | 22 (19–25) |
| Kd of trimer (μM) | 75,000 | 5 | 600 | 5.5 × 105 | 1.7 (0.48–6.3) × 105 |
Two monomers associate reversibly to form a dimer with rate constants of k+1 and k−1. A monomer binds reversibly to a dimer to form a trimer with rate constants of k+2 and k−2. The ratios of the rate constants give the dissociation equilibrium constants, Kd. Bold numbers are assumed values. We report the average of the association rate constants of two data sets reported in Cooper et al. (7) and calculated the dissociation equilibrium constants accordingly. The Sept and McCammon (9) values are also reported in Table 2, column 2. Our values (final column) are the values also reported in Table 2, column 5. Our values are best-fit values followed by 95% confidence intervals in parentheses.
Sept and McCammon (9) carried out the most ambitious analysis of nucleation and were the first to calculate actual kinetic constants. They relied on the best available information at the time about the structure of the filament, the 1990 Holmes et al. (11) model. This model used subunits in the twisted, monomeric conformation observed by x-ray crystallography (12) to build a helical structure constrained by x-ray fiber diffraction data. Using Brownian dynamics simulations of rigid actin molecules in the twisted monomeric conformation, Sept and McCammon (9) estimated binding free energies and association rate constants for monomer addition to form dimers, trimers, tetramers, and pentamers. They assumed a monomer adds to a tetramer with the known rate constant for monomers adding to the barbed end of filaments (13) and scaled their calculated values to match this constant. They used this ratio to scale their calculated nucleation association rate constants, which were large owing to Brownian dynamic simulations inherently leading to diffusion-limited reactions. Curve fitting to polymerization time courses provided the best value for an unknown energy term in their equations. Combining this value with terms derived from Brownian dynamics simulations, they used the known free energy of binding of a monomer to a tetramer to obtain the Gibbs free energy changes of the nucleation reactions. They obtained the dissociation rate constants from the association rate constants and the Gibbs free energy changes. Their simulations favored a model in which two monomers form a longitudinal dimer that subsequently interacts laterally with a monomer to form a trimeric nucleus. Simulating the reactions with their large association and dissociation rate constants (Table 1) gave good fits to experimental measurements of the time courses of polymerization over a range of actin monomer concentrations.
Oda et al. (10) used small-angle x-ray scattering (SAXS) to study nucleation. Addition of salt to very high concentrations (30.9–49.9 μM) of actin monomers resulted in the formation of actin dimers (including what they interpreted as nonpolymerizable dimers), oligomers, and filaments, with filaments replacing monomers and oligomers at later time points. They modeled the x-ray scattering data with a monomer addition model in which the formation of dimers, trimers, and tetramers are unfavorable, and larger oligomers elongate at the same rate as long filaments. This approach provided a thermodynamic parameter for dimer and trimer formation but not rate constants.
Because much more is now known about the structure of actin filaments and much more powerful computational methods are available, we took a fresh look at the four-decade old search for the nucleation rate constants. We revisited the mechanism of nucleation without making assumptions about the rate or equilibrium constants of the reactions. We used powerful computational methods to search for values of the unknown nucleation rate constants that best fit the experimental time courses of spontaneous polymerization over a range of actin monomer concentrations. In agreement with previous work, we found that the formation of dimers and trimers is unfavorable. In contrast to previous work, our simulations revealed that nucleation reactions are unfavorable because of the very slow association reactions rather than rapid dissociation rates. One plausible explanation for the slow nucleation rate constants is that the dominant monomer conformation in solution is not favorable for dimer formation.
Materials and methods
Polymerization time courses
Ca-ATP-actin monomers purified from chicken muscle (14) were exchanged for Mg2+ by adding 0.1 volume of 2 mM EGTA and 0.5 mM MgCl2 for 2 min at 25°C. Mg-ATP-actin (with a fraction of pyrene-labeled monomers (15)) with Antifoam 204 (0.00005%; Sigma-Aldrich, Waltham, MA) was placed in an upper row of a 96-well nonbinding black plate (Corning, Corning, NY). Buffer 10× KMEI (500 mM KCl, 10 mM MgCl2, 10 mM EGTA, and 100 mM imidazole (pH 7.0)) and Mg-buffer G (2 mM Tris (pH 8.0), 0.2 mM ATP, 0.1 mM MgCl2, and 0.5 mM dithiothreitol) were placed in a lower row of the plate. Reactions were initiated by mixing contents of the lower wells and the actin monomers in the upper wells with a 12-channel pipettor (Eppendorf, Hamburg, Germany). The fluorescence change during the assembly of pyrenyl-actin was measured by excitation at 364 nm and emission at 407 nm with a SpectraMax Gemini XPS Microplate Reader (Molecular Devices, San Jose, CA). Final actin concentrations as well as the molar fraction of pyrene-labeled actin are indicated in the figures and their legends.
Data analysis
To analyze the data, the dead time was added to the first time points, and the other time points were shifted accordingly. We first made a preliminary normalization of the fluorescence data by subtracting the lowest fluorescence point from each fluorescence data point. We divided all points by the average of the highest fluorescence points. The normalized data were then converted to polymerized actin concentrations using a method similar to Doolittle et al. (16) with some modifications. The time at which the plateau of the normalized data occurred (tmax) was determined by taking the average of the time that the 10 highest points appear. To correct for photobleaching, all the points after tmax were fitted to an exponential, and all the points of the curve were divided by the exponential component of the fit to give the corrected intensity (Icorrected). The exponential for each of the different percentages of pyrene was averaged together for a given monomer concentration, and the average was used to correct for photobleaching for that monomer concentration. Since the 1-μM samples did not have an adequate plateau to measure photobleaching, the values from the 2.5-μM samples were used because their acquisition times were equivalent. The five points above and below tmax were averaged to give the maximal intensity (Imax). If on the rare occurrence of the tmax being the point, then that point and the four below it and the five above it were averaged. The minimal intensity (Imin) of the corrected data was determined by producing multiple linear fits starting with the first three points and continually adding one point to the fit. An F-test testing the null hypothesis that the slope of the line was 0 was used to determine at which point the slope was significantly different from 0. The average of all the points before the first group of points passing the F-test served as the minimal intensity. The corrected intensity was then converted to polymerized actin (P) concentration according to Eq. 1. This equation subtracts the background intensity from each measurement and multiplies it by the ratio of the final polymer concentration divided by the range of intensity. To determine the final polymer concentration, we subtracted the critical concentration of actin from the initial monomer concentration (M0). We calculated the critical concentration from the sum of the barbed and pointed ends dissociation rate constants divided by the sum of the barbed and pointed ends association rate constants ( μM, using values from Pollard (13)). All values occurring more than five points after tmax were not used in the fits.
| (1) |
To calculate the monomer concentration over time, we assume (based upon decades of kinetic analysis and the results of SAXS (10)) that during spontaneous assembly of low concentrations of actin monomers the concentrations of five of the seven species (dimer, trimer, tetramer, barbed end, and pointed end) are very small compared with the concentrations of monomers or polymerized actin. Thus, we approximate the monomer concentration at each point in time as the difference between the initial monomer concentration and the polymer concentration.
We calculated the concentration of barbed ends (EB) at points along the polymerization curve from the rate of polymerization , monomer (M) concentration, and rate constants for association and dissociation from the barbed ends (k+B = 11.6 μM−1 s−1 and k−B = 1.4 s−1 (13)) and pointed ends (k+P = 1.3 μM−1 s−1, and k−P = 0.8 s−1 (13)) according to Eq. 2.
| (2) |
After ∼75% of the monomers were consumed, calculations of filament end concentration were noisy, so we only used filament end concentrations before this time to constrain the search for parameters. The Supporting materials and methods contains a more detailed analysis of the calculation of the barbed ends.
Model design
We used the standard, nucleation-elongation model (7, 8, 9,17) with monomer association and dissociation to the polymeric species. Like Sept and McCammon (9), we assumed that only monomers add to and dissociate from the oligomeric nucleation species and polymers. This assumption stems from the fact that the monomer concentration is much higher than any other species during nucleation (9). Our simulations with 7.5% pyrenyl-Mg-ATP-actin confirmed that the concentration of monomers is always more than two orders of magnitude higher than the sum of all the oligomeric species (Fig. S1).
The model has the nucleation process start with two actin monomers (M) reversibly forming a dimer (D) with association and dissociation rate constants of k+1 and k−1 (Eq. 3).
| (3) |
A dimer reversibly forms a trimer (T) by addition of a monomer with association and dissociation rate constants of k+2 and k−2 (Eq. 4).
| (4) |
Next, addition of a monomer to the barbed end (Eq. 5) or pointed end (Eq. 6) of the trimer produces a tetramer (Tet). We assumed that these rate constants are the same as those for elongating filaments, k+B = 11.6 μM−1 s−1, k−B = 1.4 s−1, k+P = 1.3 μM−1 s−1, and k−P = 0.8 s−1 (13).
| (5) |
| (6) |
Monomer addition to a barbed end (Eq. 7) or pointed end (Eq. 8) of the tetramer produces a barbed end (EB) or a pointed end (EP). We assumed that these association rate constants are the same as those for elongating filaments, k+B and k+P.
| (7) |
| (8) |
Under the conditions of our experiments, short filaments elongate rapidly and have a negligible probability of dissociating into monomers. Therefore, for computational purposes, we assumed that the reactions forming barbed and pointed ends are irreversible as in previous models (9,17).
Filaments elongate or shorten by adding or dissociating a monomer from either the barbed (Eq. 9) or pointed (Eq. 10) end of the filament. In these equations, the ends are treated as a catalyst (see (18) for a similar treatment) that forms a new species that we call polymer or polymerized actin (P), which tracks monomers incorporated into filaments, not filament ends (which is equal to EB or EP).
| (9) |
| (10) |
Because of the use of this tracking species, the differential equation describing the change in the concentration of P (Eq. 11) is independent of the actual concentration of P.
| (11) |
Therefore, below the critical concentration when (EBk−B + EPk−P) > M(EBk+B + EPk+P), the polymer concentration decreases over time.
Simplifying the model by either combining the barbed and pointed end contributions (Fig. S2; Table S1) or by completely ignoring the pointed end contribution (Fig. S3; Table S1) had little impact on the estimation of unknown parameters. We chose to use the full model because it depicts the whole spontaneous polymerization process.
Model calibration
We formulated the model in Virtual Cell 7.2 (19,20) (available in the VCell database, https://vcell.org/, as the public BioModel “NucleationMechanism” under username “AaronRosenbloom”); we then exported the model as Systems Biology Markup Language (SBML) code (21) for import into COmplex PAthway SImulator (COPASI) software (22), which was used to fit simulations simultaneously to experimental time courses of the concentrations of polymer, monomer, and barbed ends versus time for all starting actin monomer concentrations. We used a multistart fitting approach by optimizing the fit using the Levenberg-Marquardt algorithm (23, 24, 25) on 2000 random initial values for each of the four unknown parameters, k+1, k−1, k+2, and k−2. The lower and upper limits were set at 10−15 and 1015 s−1 for the dissociation rate constants and to 10−7 and 103 μM−1 s−1 for the association rate constants. This process produced multiple minima. We then used the values of the four parameters that gave the lowest objective values to further refine the fit. The fit was refined by continually using COPASI’s implementation of the Hooke and Jeeves algorithm (26, 27, 28, 29) until no change in the parameter values occurred. These values were then used as the initial values with COPASI’s implementation of the Particle Swarm algorithm (30). The resulting values were continually refined using the Hooke and Jeeves algorithm (26) until no change in the parameter values occurred. This process was repeated until no change in five significant figures of the objective value occurred. Although the fit could be further refined, it would have little impact on the final result because the 95% confidence interval (CI) objective value at the most differed in the third significant digit. On occasion, it was noticed that some fits determined from the profile likelihood estimation (PLE) were better than the original best fit, so we used those parameters in further refining the fits as described. For all fitting procedures, the objective value to be fitted was a weighted residual sum of squares (RSS). COPASI calculated this weight by the mean square of the experimental data.
Fit using local algorithm only
The four unknown rate constant parameters were assigned the initial values estimated by Sept and McCammon (9). Using COPASI, the model was fitted using the Levenberg-Marquardt local algorithm. The fit was further refined by using the resulting values as the initial values for an additional fit using the Levenberg-Marquardt local algorithm. This process was continued until there were no further changes. Additional refinement using the Hooke and Jeeves algorithm (26) did not change the values.
Identifiability analysis
We used Differential Algebra for Identifiability of SYstems (DAISY) (31), STRuctural Identifiability taKen as Extended-Generalized Observability with Lie Derivatives and Decomposition 2 (STRIKE-GOLDD2) (32), and Generating Series for testing Structural Identifiability 2.0 (GenSSI 2.0) (33) to check for structural identifiability of the unknown parameters in our model, which is the theoretical ability to determine the values of unknown parameters based on the inputs, outputs, unknowns, and observables of a given model. The Supporting materials and methods has a more thorough description of the equations.
We also report the practical identifiability, which tells if the available experimental data allow for a finite determination of the unknown parameters of the model. To determine the practical identifiability, we used the PLE method (34) as implemented with COPASI (35). In this estimation, one unknown rate constant is fixed, whereas the remaining unknown parameters are fitted to the experimental data. We used the Hooke and Jeeves direct search algorithm with the determined best fits as starting values for this analysis. Plots of the residual sum of the squares of each fit over the range of fixed parameters give one-dimensional contours of the parameter landscape.
We obtained the 95% CI for parameter values according to the likelihood-based confidence region (35) using Eq. 12 described by Schaber (35).
| (12) |
where RSS is the residual sum of squares of each fit, m is the number of parameters, and n is the number of data points. F is the F-value using m and n − m as the degrees of freedom. In our model, without an activation step, m = 4, for our model contains four unknown parameters that are fitted. For the models with an activation step, m = 6. The value of n differed for each mole fraction of pyrene (Table S2) and was 517 for the activation step models and for the standard model only fitting the polymerization time courses. Sometimes the bounds of the 95% CI were noisy with some values falling inside and other values falling outside the CI. Additionally, the values would sometimes depend on the incremental change of the fixed value of the PLE. To deal with this issue, we calculated the PLE boundaries (the values in parentheses in the tables) in the same manner for all simulations: the fixed values were incrementally changed by increasing its third significant digit by one. The boundary was determined based upon the last value that fell into the 95% CI. We made sure that all values at least an order of magnitude above the PLE boundaries were not within the 95% CI. The lower and upper limits of the CI for the equilibrium constants were calculated directly from the rate constants. The lower limit was calculated by dividing the lower limit of the dissociation rate constant by the upper limit of the association rate constant. The upper limit was calculated by dividing the upper limit of the dissociation rate constant by the lower limit of the association rate constant. The best-fit values were calculated by dividing the best fit of the dissociation rate constant by the best-fit value of the association rate constant.
Results
There is currently no experimental way to measure accurately, and with enough time resolution, the concentrations of the small oligomeric species that initiate spontaneous actin polymerization. Because of this limitation, we sought to estimate the rate constants for the nucleation reactions by fitting a model to the full time course of spontaneous polymerization for a range of actin monomer concentrations. Because the filament elongation rate constants are known, simulations that simultaneously fit all time courses provide estimated values for the unknown rate constants for nucleus formation. To constrain these simulations, we measured the time course of polymerization of Mg-ATP-actin monomers (the physiologically relevant species) over a range of concentrations and mole fractions of pyrene-labeled subunits.
We used the accepted nucleation-elongation model of actin polymerization (7, 8, 9,17), wherein unfavorable nucleation of a trimer occurs before addition of actin monomers. Specifically, two actin monomers associate to form a dimer. A third monomer adds to form a trimer. Thereafter, monomers add to the barbed and pointed ends of the trimer at favorable rates similar to the elongation of a filament. This model requires only eight rate constants to fully describe the kinetics. We treated four of these rate constants as unknown parameters: association rate constants of the dimer (k+1) and trimer (k+2) and dissociation rate constants of the dimer (k−1) and trimer (k−2). The other four of the rate constants are known: the association of monomers with the barbed and pointed ends of filaments and the dissociation of subunits from both ends (13).
Sept and McCammon (9) obtained the most advanced estimates of the nucleation rate constants using Brownian dynamics simulations of rigid actin molecules to estimate binding free energies and association rate constants for monomer addition to forming dimers, trimers, tetramers, and pentamers. However, simulations using their rate constants (Table 1, column 4 and Table 2, column 2) did not fit our experimental data well (Fig. 1 A). Hypothesizing that the values of Sept and McCammon (9) are order of magnitude approximations, we set out to refine the fit by using a derivative-based optimization algorithm. This local algorithm determined the minima in the vicinity of the Sept and McCammon (9) estimated rate constants that we used as starting values. After several iterations, the local optimization algorithm gave much better fits to the assembly time courses over a range of actin concentrations (Fig. 1 B) with rate constants within one to two orders of magnitudes of the starting values (Table 2, column 3).
Table 2.
Comparison of rate and equilibrium constants for nucleation reactions
| Sept and McCammon (9) | Local algorithm; defined start value | Multistart fit to polymer only | Multistart fit to polymer and filament ends | Multistart fit to polymer, filament ends, and monomer | |
|---|---|---|---|---|---|
| k+1 (μM−1 s−1) | 35.7 | 9.6 (0.0039–6600) | 4.7 (1.3–32) × 10−6 | 15 (0.96–170) × 10−6 | 3.5 (1.2–11) × 10−6 |
| k−1 (s−1) | 1.63 × 108 | 9.1 (0.016–170,000) × 108 | 0.040 (0.034–0.049) | 0.047 (0.038–0.058) | 0.041 (0.036–0.047) |
| Kd of dimer (μM) | 4.6 × 106 | 9.5 (0.000024–440,000,000) × 107 | 8500 (1100–38,000) | 3100 (220–60,000) | 12,000 (3300–39,000) |
| k+2 (μM−1 s−1) | 2.18 | 0.78 (0.0000015–450) | 9.6 (1.5–35) × 10−5 | 3.4 (0.38–56) × 10−5 | 13 (4.0–40) × 10−5 |
| k−2 (s−1) | 1300 | 15 (12–19) | 27 (23–33) | 21 (18–27) | 22 (19–25) |
| Kd of trimer (μM) | 600 | 19 (0.027–13,000,000) | 2.8 (0.66–22) × 105 | 6.2 (0.32–71) × 105 | 1.7 (0.48–6.3) × 105 |
Best-fit values are followed by 95% CIs in parentheses. The Sept and McCammon (9) values are also reported in Table 1, column 4. The data in column 3 come from fits to the experiments in Fig. 1B. The data in column 4 come from fits to the experiments in Fig. 1E. The data in column 5 come from the fits to experiments in Fig. 2. All fitted parameters in columns 3–6 are practically identifiable.
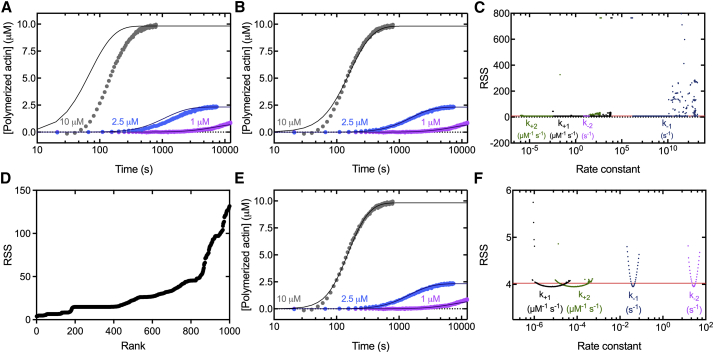
Figure 1.
Time courses of spontaneous polymerization of 7.5% pyrenyl-Mg-ATP-actin monomers and fits of different optimized simulations of the nucleation model to the data constrained by the concentrations of polymer over time. Symbols are the experimental measurements. Smooth curves are numerical simulations of the model. (A) Simulations of polymer concentration versus time using the nucleation rate constants of Sept and McCammon (9) compared with experimental data. (B) Fits of simulations of polymer concentration versus time to experimental data starting with the values of Sept and McCammon (9) as initial values and refining the fit locally. (C) PLEs of the nucleation rate constants derived from calibrating our model in (B). At each fixed value of a rate constant on the x axis, the model was fitted to the polymer concentration versus time to estimate the three unknown rate constants. The residual sum of squares (RSS) from the fit is plotted on the y axis. These plots give one-dimensional contours of the parameter landscape with the best-fit value having the lowest RSS. The red line indicates the 95% CI. The two intersections of the curves give the range in which each parameter is identifiable. (D) A plot showing the objective value (RSS) of the top 1000 fits from a multistart fitting workflow using multiple, random initial values plotted against the rank of best to worst fit. (E) Fits of simulations of polymer concentration versus time to experimental data using a multistart fitting workflow and multiple, random initial values. (F) PLEs of the nucleation rate constants (as in C) derived from calibrating our model in (E). The CIs for the four unknown rate constants are narrower than in (C), as reported in Table 2, columns 3 and 4. To see the figure in color, go online.
Despite this improved fit, we discovered that the fit depended heavily on the values used to start the fitting process. Different initial values would give equally good fits with drastically different rate constants. This result led us to question the identifiability of the parameters. If a given set of observed values can produce a finite number of possible solutions to an unknown parameter of a given model, the parameter is said to be practically identifiable. We determined the validity of our fits by testing the practical identifiability of each parameter by calculating the PLE of each parameter (34). This is done by fixing the value of a parameter while optimizing the remaining unknown parameters to best fit the experimental data. This optimization process is repeated for a range of values of the fixed parameter, yielding a one-dimensional contour of the parameter landscape (Fig. 1, C and F). We repeated this procedure for each of the unknown parameters. Intersection of the PLE curve with a calculated 95% CI was used to determine the practical identifiability of each parameter.
This analysis revealed the practical identifiability of the four nucleation rate constants (Fig. 1 C; Table 2, column 3). However, the 95% CIs for k+1, k−1, and k+2 spanned six to eight orders of magnitude; only k−2 had a 95% CI within an order of magnitude. Thus, the values determined by Sept and McCammon (9) are one of many other sets of values that produce equally good fits.
Fitting the model using a multistart fitting workflow
Seeing that the fits to our data are heavily dependent upon starting values, we sought to determine the rate constants without bias from initial values. We circumvented the problem of bias in the initial values with a multistart fitting workflow. We used 2000 random initial values for each data set as starting points for running the algorithm. Importantly, we set wide ranges within which these initial values could be chosen randomly. We set the upper limit for the association rate constants to 103 μM−1 s−1 based upon the fastest rate constant possible via a diffusion-controlled reaction. Using the observed experimental data as a guide, along with trial-and-error from optimizations, we determined the association reactions cannot be slower than 10−7 μM−1 s−1, so we used that as the lower limit. We did not have a good way to guess the limits for the dissociation rate constants, so we set a high upper limit of 1015 s−1 and a small lower limit of 10−15 s−1. This set of constraints allowed the model freedom to proceed via diffusion-limited reactions or not.
We used this workflow to calibrate our model to experimental time courses of spontaneous polymerization of three concentrations of 7.5% pyrenyl-Mg-ATP-actin. A graph ranking the best 1000 fits by lowest objective value (RSS) shows multiple plateaus (Fig. 1 D), which are local minima in the fitting landscape. The existence of many local minima above our best-fit values increases the likelihood that we indeed found the global minima of the fitting landscape indicating that our workflow avoided biases from initial values.
Fits of the model to the polymer concentration time courses using the multistart workflow (Fig. 1 E) were better than the fits in Fig. 1, A and B, and the 95% CIs (Fig. 1 F; Table 2, column 4) were relatively narrow compared with Fig. 1 C.
Analysis of identifiability
To determine if our model, experimental data, and fitting procedures can produce a single, global minimum in the fitting landscape, we used software designed to determine mathematically if unique solutions exist for the unknown parameters of a given model by determining their structural identifiability. If an unknown parameter has a unique solution based upon the inputs, outputs, unknowns, and observables of the model, the parameter is said to be structurally identifiable. If a parameter is structurally identifiable locally, then in a given region of parameter space, only one unique solution exists. If it is structurally identifiable globally, then only one unique solution exists. If the parameter is not identifiable, then an infinite number of different solutions can exist, making the determination of an unknown parameter impossible.
Analysis of the structural identifiability of our unknown parameters showed that if the polymer concentration is the only observable, then our parameters are structurally identifiable only locally. The same is true if we use polymer and filament end concentrations over time. However, if we constrain the fitting with the polymer and monomer concentrations or the polymer, filament end, and monomer concentrations, then all the unknown parameters are structurally identifiable globally. Therefore, the model can produce a single unique solution for the values of all the unknown parameters.
Constraining fits of the model with additional observables
Our identifiability analysis indicated that using more observables can produce solutions for our unknown parameters that are globally unique. Furthermore, using more observables has additional benefits. The model includes seven species: monomer, dimer, trimer, tetramer, barbed end, pointed end, and polymer. Using only the polymer concentration time course constrains the model to fit the known concentrations of polymer over time. However, the fits of the other species concentrations over time are not constrained unless they are included as observables. Therefore, using the concentrations of filament ends (by which we mean either the barbed or pointed end) and monomers over time as observables further constrains fitting of the model.
We calculated the monomer concentration at each time point as the difference between the starting monomer concentration and the polymer concentration for use in constraining the fitting of our model (see Data analysis). The assumption behind this calculation is justified by prior studies of actin polymerization, including small-angle x-ray diffraction data (10), showing that the concentrations of monomers and polymers are much higher than dimers, trimers, and other small oligomers during polymerization. This assumption makes the calculated monomer concentration distinct from the measured polymer concentration and adds a strong constraint during fitting of the model to the experimental data. Calculating the concentration of filament ends at each time point from the rate of polymerization and the monomer concentration did not require additional assumptions.
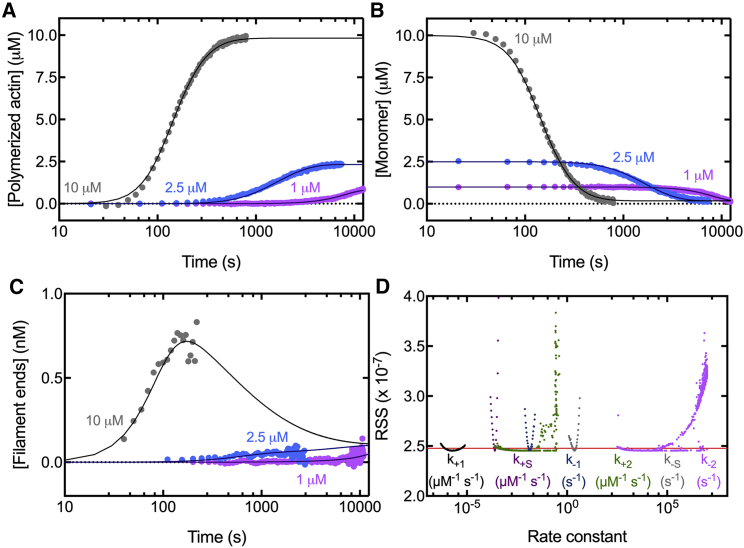
Compared with fitting the polymer concentration alone, fitting the model constrained by the filament end concentrations in addition to the polymer concentrations gave roughly the same best-fit values for the rate constants with similar CIs, except for k+1 (Fig. 2, column 2; Table 2, column 5). Including the monomer concentration further constrained the fit with additional data but also added to the model the assumption that the monomer concentration is much higher than the concentrations of dimers and trimers. Fits constrained by the concentrations of polymer, filament end, and monomer produced values of the unknown rate constants for the polymerization of 7.5% pyrenyl-Mg-ATP-actin (Fig. 2, column 3) with only small differences in the best-fit values and a modestly reduced CI for k+1 (Table 2) compared with fits with fewer constraints. The fits of the simulations of filament ends versus time were good given the noisy experimental calculations of the concentration of ends from the rate of polymerization, particularly as the polymerization rate approached zero.
Figure 2.
Three methods of fitting simulations of the nucleation model to the time courses of spontaneous polymerization of three concentrations of 7.5% pyrenyl-Mg-ATP-actin monomers. Symbols are the experimental measurements of the polymer concentration or calculated concentrations of monomers and filament ends. Smooth curves are numerical simulations of the model constrained by time courses of (column 1) the concentration of polymerized actin measured from the pyrene fluorescence for polymer, (column 2) polymer and filament end concentration calculated at each time point from the rate of polymerization and the actin monomer concentration, and (column 3) polymer, monomer (calculated at each time point from the concentration of total actin minus the polymer concentration), and filament end concentrations. Shown are (row 1) concentration of polymer versus time, (row 2) concentration of actin monomer versus time, and (row 3) concentration of filament ends versus time. Concentration of actin monomer was only used to constrain column 3. Concentration of filament ends versus time was only used to constrain columns 2 and 3. Shown in row 4, PLEs of the actin nucleation parameters for the three methods to constrain the fits. Symbols correspond to the RSS from best-fit values for each fixed value of the rate constant plotted on the x axis. The red line indicates the 95% CI. The two intersections of the curves give the range in which each parameter is identifiable. To see the figure in color, go online.
All four rate constants differed by orders of magnitude from the estimates of Sept and McCammon (9) (Table 2). The rate constant for the association of two monomers to form a dimer was on the order of 10−6 μM−1 s−1, and the addition of a third subunit to form a trimer was 10−4 μM−1 s−1. Thus, these nucleation reactions are not diffusion limited, a conclusion previously assumed untenable. Given these slow association reactions, our dissociation rate constants (10−2 s−1 for dimers and 10 s−1 for trimers) are much smaller than prior estimates (9), so dimers and trimers are orders of magnitude more stable than previously thought.
A model with a monomer conformational change
Because the rate constants for dimer and trimer formation are much smaller than expected for diffusion-limited reactions, we considered how factors other than diffusion could affect the reaction. We hypothesized that a minor fraction of actin monomers in solution is in a high-energy conformation (M∗) that is essential for dimer formation. The discussion explains why we think these active monomers have a flattened-open conformation with a higher energy and lower abundance than twisted-closed monomers. Requiring at least one monomer in the M∗ conformation would severely limit the rates of the nucleation reactions.
To address this hypothesis, we added an equilibrium between two monomer conformations (Eq. 15): a twisted-closed conformation captured in crystal structures (12) and a flattened-open conformation (M∗) found in the core of filaments (36).
| (15) |
We can imagine dimers forming in two ways. One possibility requires only one flattened-open monomer to form a dimer (Eq. 16a).
| (16a) |
Alternatively, two flattened-open monomers are required to form a dimer (Eq. 16b).
| (16b) |
In addition to the two mechanisms of dimerization, we considered two fashions in which initial conditions affect the conformational equilibrium. First, all monomers are in the twisted-closed state until salt is added, so the conformational equilibrium can occur solely under polymerizing conditions. A second explanation assumes that the two conformations are at equilibrium before the introduction of polymerizing conditions (i.e., in low-salt buffer).
Considering all combinations of these mechanisms, we tested four models. Two models assume that only one flattened-open monomer (M∗) is required to form a dimer, but they differ in assuming that salt does (1M∗: Salt) or does not (1M∗: Eq.) influence the conformational equilibrium. The other two models assume that two flattened-open monomers (M∗) are required to form a dimer, and they, too, differ in assuming that salt does (2M∗: Salt) or does not (2M∗: Eq.) influence the conformational equilibrium. To simplify the models, we assumed that the involvement of the M∗ state in reactions other than dimer formation is negligible because of the low abundance resulting from the high energy required to occupy this state. The low abundance of the flattened-open monomeric M∗ state was confirmed after fitting all the models to the experimental data (Fig. S4).
In the two models in which salt initiates the conformational change, all of the monomers are assumed to be in the twisted-closed (M) conformation before adding salt; however, we did not know the concentrations of M and M∗ when the conformational equilibrium is established before the introduction of polymerizing conditions. Therefore, instead of setting the initial values of the monomeric species, we made the initial concentrations of the two monomer conformations a function of the unknown conformational change rate constants and the total initial monomer concentration. This dependency determined the two monomeric conformation initial concentrations while simultaneously fitting the conformational change rate constants to the polymerization time courses.
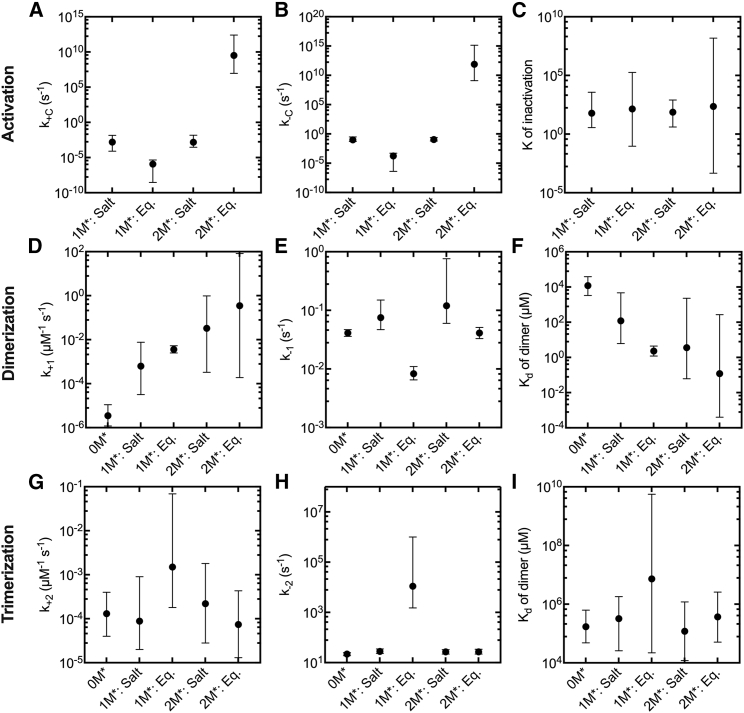
Each of these four models fits the time courses of polymerization of 7.5% pyrenyl-Mg-ATP-actin well (Fig. 3, A, C, E, and G). Indeed, the RSS values (Table S3) were as good or better than for the model without the monomer conformational change (compared using polymer only as in Fig. 1 E). We cannot specify precise rate constants for most steps during nucleus formation owing to the wide CIs (Fig. 3, B, D, F, and H; Fig. 4; Table S4). However, the lower ranges of k1 in the fits for all four conformational change models were larger than the upper range determined for k1 of the model fitting polymer, monomer, and barbed ends (Fig. 4 D). Therefore, all four models suggest an unfavorable monomer equilibrium is a plausible mechanism to explain the very slow dimer formation; however, it cannot fully explain the slow apparent association rate constants, for it does not raise the rate constants to the diffusion limit.
Figure 3.
Simulations of four models with a monomer conformation change as a requirement for dimer formation. Searches for the six unknown rate constants gave good fits to the experimental data. Symbols are the experimental measurements. Smooth curves are numerical simulations of the model. (A, C, E, and G) Time courses of the concentration of polymerized actin measured from 7.5% pyrenyl-Mg-ATP-actin fluorescence for four models: (A) one monomer salt-induced conformational change model, (C) one monomer equilibrated conformational change model, (E) two monomer salt-induced conformational change model, and (G) two monomer equilibrated conformational change model. (B, D, F, and H) PLEs of the actin nucleation parameters for (B) the one monomer salt-induced conformational change model, (D) one monomer equilibrated conformational change model, (F) two monomer salt-induced conformational change model, and (H) two monomer equilibrated conformational change model. Symbols correspond to the RSS from best-fit values for each fixed value of the rate constant plotted on the x axis. The red line indicates the 95% CI. The two intersections of the curves give the range in which each parameter is identifiable. To see the figure in color, go online.
Figure 4.
Rate and equilibrium constants for the nucleation reactions for no monomer activation required to form a dimer (0M∗) and four models with a monomer conformation change required to form dimers: salt and activation of one monomer is required (1M∗: Salt); activation of one monomer already equilibrated in low salt is required (1M∗: Eq.); salt and activation of two monomers is required (2M∗: Salt); activation of two monomers already equilibrated in low salt is required (2M∗: Eq.). The values for 0M∗ appear in the final columns of Tables 1 and 2. Symbols correspond to best-fit values. The bars are 95% CIs from the PLEs. (A) Rate constants for the conformational change from the twisted-closed state to the flattened-open state, k+C. (B) Rate constants for conformational change from the flattened-open state to the twisted-closed state, k−C. (C) Equilibrium constants for the change between the twisted-closed and flattened-opened conformations, K of inactivation. (D) Rate constants for dimer formation, k+1. (E) Rate constants for dimer dissociation, k−1. (F) Dissociation equilibrium constants of dimer formation, Kd of dimer. (G) Rate constants for trimer formation, k+2. (H) Rate constants for trimer dissociation, k-2. (I) Dissociation equilibrium constants of trimer formation, Kd of trimer.
Alternative nucleation pathways: contribution of severing to spontaneous polymerization
To test whether including severing and annealing of filaments in the model changes rate constants or improves fits to the polymerization data, we simplified our model slightly and added the severing and annealing reaction. Instead of forming a barbed end (EB) and a pointed end (EP) as two distinct species, we simplified this reaction to make a filament (F). Thus Eq. 7 and Eq. 8 become
| (7′) |
| (8′) |
We added to the model a reaction for the reversible severing of a filament into two filaments.
| (17) |
Simulations of the model modified with severing and annealing with best-fit rate constant values fit the experimental data well for 7.5% pyrenyl-Mg-ATP-actin (Fig. 5, A–C). Calculations of the PLE of each parameter indicated that all six of the unknown parameters are identifiable (Fig. 5 D; Table 3). The ranges within the 95% CIs for k+1, k−1, and k+2 are the same or differ only slightly from our original model. In fact, the RSS was slightly lower (2.45 × 10−7) for the model with severing than the standard model (RSS of 4.73 × 10−7).
Figure 5.
Time courses of spontaneous polymerization of 7.5% pyrenyl-Mg-ATP-actin monomers and fits of simulations of the nucleation model with the addition of a reversible severing reaction to the data constrained by the concentrations of polymer, monomer, and ends versus time. Symbols are the experimental measurements. Smooth curves are numerical simulations of the model. (A) Time courses of the concentration of polymerized actin measured from the pyrene fluorescence. (B) Time courses of the concentration of actin monomers calculated from the total actin minus the concentration of polymerized actin. (C) Time courses of the concentration of filament ends calculated from the rate of polymerization and the actin monomer concentration. (D) PLEs of the actin nucleation parameters. Symbols correspond to the RSS from best-fit values for each fixed value of the rate constant plotted on the x axis. The red line indicates the 95% CI. The two intersections of the curves give the range in which each parameter is identifiable. To see the figure in color, go online.
Table 3.
Comparison of rate and equilibrium constants for nucleation reactions from the standard model with and without reversible severing and with modeling the elongation reactions in two different ways
| Standard | Annealing and severing | Tetramer from two dimers | |
|---|---|---|---|
| k+1 (μM−1 s−1) | 3.5 (1.2–11) × 10−6 | 1.9 (0.79–5.2) × 10−6 | 2.8 (1.4–16) × 10−6 |
| k−1 (s−1) | 0.041 (0.036–0.047) | 0.014 (0.012–0.016) | 0.050 (0.045–0.056) |
| Kd of dimer (μM) | 12,000 (3300–39,000) | 7400 (2300–20,000) | 18,000 (2800–40,000) |
| k+2 (μM−1 s−1) | 1.3 (0.40–4.0) × 10−4 | 55 (3.7–2900) × 10−4 | 0.51 (0.094–0.99) × 10−4 |
| k−2 (s−1) | 22 (19–25) | 5100 (440–9,500,000) | (<0.64) |
| Kd of trimer (μM) | 1.7 (0.48–6.3) × 105 | 930,000 (1500–26,000,000,000) | (<68,000) |
| k+S (s−1) | — | 2.5 (2.3–2.7) × 10−4 | — |
| k−S (μM−1 s−1) | — | 2.4 (2.0–2.8) | — |
| K of annealing (μM) | — | 9600 (7400–12,000) | — |
| k+3 (μM−1 s−1) | — | — | 0.23 (0.0071–1.2) |
| k−3 (s−1) | — | — | (<5.0) |
| Kd of tetramer to dimer (μM) | — | — | (<700) |
Best-fit values are followed by 95% CIs in parentheses. For parameters that are not identifiable, we did not include the best-fit value for they were unrealistically small (1.1 × 1015 for k−2, 2.2 × 10−11 for Kd of trimer, 4.7 × 10−17 for k−3, and 4.7 × 10−17 for Kd of tetramer to dimer) but do include their upper boundary in parentheses.
However, this outcome is unrealistic: 1) simulations starting with 10-μM actin monomers gave a peak filament end concentration of 0.75 nM corresponding to 13,000 subunits per filament, a length of 35 μm, longer than observed (37). 2) After the peak, the number concentration of filament ends declined to 0.11 nM because of rapid annealing of these long filaments, which does not actually happen (37), but occurs during this simulation with the same rate constant appropriate for short filaments.
The likely explanation is that the model does not take into account the size of the filaments, which strongly influences both severing and annealing. We can calculate the average length of the filaments from the polymer concentration and the number concentration of filament ends. However, this approximation would not adequately reproduce the annealing and severing that take place. Although the results in this simulation are unrealistic, inclusion of a reversible severing reaction does not dramatically alter the slow association rate constants to make dimers and trimers.
Alternative nucleation pathways: contribution of two dimers forming tetramers
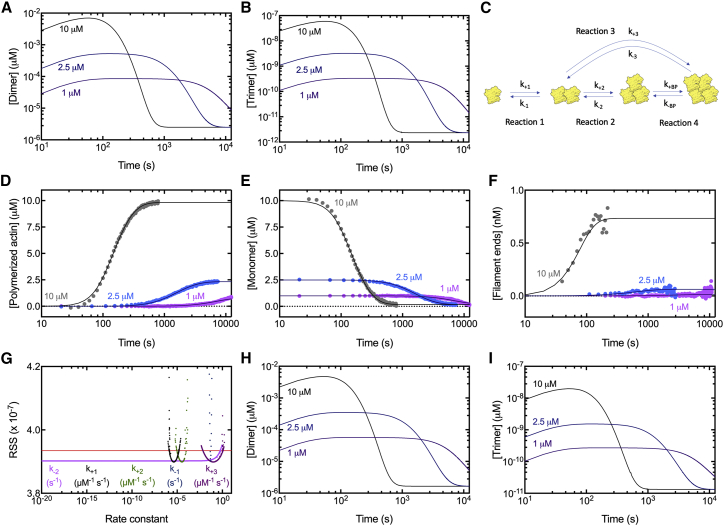
Our simulations using monomer addition reactions produce concentrations of dimers several orders of magnitude higher than the femtomolar concentration of trimers (Fig. 6, A and B). The rate of formation of a tetramer from a trimer and a monomer depends on the product of the monomer and trimer concentrations. Alternatively, tetramers may form from two dimers at a rate proportional to the square of the dimer concentration. Because the dimer concentration is high relative to the trimer concentration, the square of the dimer concentration is larger than the product of the trimer and monomer concentrations. This suggests that tetramers may form from two dimers.
Figure 6.
Time courses of spontaneous polymerization of 7.5% pyrenyl-Mg-ATP-actin monomers and fits of simulations to the data of the modified nucleation model with tetramer formation by two parallel pathways constrained by the concentrations of polymer, monomer, and ends versus time. Shown are simulations of the time courses of the concentrations of (A) dimers and (B) trimers during the polymerization of 7.5% pyrenyl-Mg-ATP-actin using our estimated nucleation rate constants from the model that does not include a tetramer from two dimers. (C) Two pathways to form tetramers. (D) Time courses of the concentration of polymerized actin measured from the pyrene fluorescence. (E) Time courses of the concentration of actin monomers calculated from the total actin minus the concentration of polymerized actin. (F) Time courses of the concentration of filament ends calculated from the rate of polymerization and the actin monomer concentration. (G) PLEs of the actin nucleation parameters. Symbols correspond to the RSS from best-fit values for each fixed value of the rate constant plotted on the x axis. The red line indicates the 95% CI. The two intersections of the curves give the range in which each parameter is identifiable. (H and I) Simulations of the time courses of the concentrations of (H) dimers and (I) trimers during the polymerization of 7.5% pyrenyl-Mg-ATP-actin using our estimated nucleation rate constants from the model that includes a tetramer from two dimers. Symbols in (D–F) are the experimental measurements. Smooth curves are numerical simulations of the model. To see the figure in color, go online.
To test this idea, we modified our model to allow two dimers to form a tetramer. First, we combined monomer addition to the pointed and barbed ends into a single reaction. We found that this simplification has little impact on the rate constants derived from the simulations (Fig. S2; Table S1), which makes sense because the equations do not change. We then allowed the tetramer to form in one of two ways: 1) a monomer adds to a trimer with rate constants k+BP and k−BP. 2) Two dimers come together via rate constants k+3 and k−3 to make a tetramer (Fig. 6 C).
To constrain the fits of this more complicated model to the data, we note that both pathways start with a monomer and end with a tetramer but differ in the intermediate reactions. This means that the starting and ending energies are equivalent in the two pathways. One pathway is reaction 1 + reaction 2 + reaction 4 with an overall Kd of K1K2KBP, where , , and . The other pathway is reaction 1 + reaction 1 + reaction 3 with an overall Kd of K1K1K3, where . Therefore, K1K3 = K2KBP. Thus, one can obtain the equation
| (18) |
This allows us to reduce the number of unknown parameters in the system from six to five by making one unknown parameter a function of the other known and unknown parameters. We chose to use the equivalency
| (19) |
Therefore, the rate equation for forming tetramers from two dimers becomes
| (20) |
In this way, we no longer have to fit for k−3, for it is a function of other parameters. Furthermore, this constrains all the other parameters because they are now forced to conform to the conservation of energy. For the fits to work without being cut off by the boundary conditions, we set the limits for the association rate constants to between 10−15 and 103 μM−1 s−1 and the limits for the dissociation rate constants to between 10−15 and 1015 s−1. For the parameters that were not identifiable, the best-fit values were unrealistically small. This just means that our model and data cannot constrain the lower limit of the CI.
Simulations of the model with best-fit rate constant values constrained by the thermodynamic relationship fit the experimental data well for 7.5% pyrenyl-Mg-ATP-actin (Fig. 6, D–F). Calculations of the PLE of each parameter indicated that four of the five fitted parameters are identifiable (Fig. 6 G; Table 3) except for k−2. However, we were able to determine an upper boundary for k−2. The ranges within the 95% CIs for k+1, k−1, and k+2 are the same or slightly higher than our original model (Table 3). Although k+3 is identifiable, its range spans more than three orders of magnitude, larger than the approximate order of magnitude intervals for k+1, k−1, and k+2, which overlap the values obtained in our original model. However, k−2 is reduced from 19–25 to <0.64 s−1. This means that trimers are at least two orders of magnitude more stable in this model than in our original model. The range of rate constants to form tetramers from two dimers (k+3) is 0.0071–1.2 μM−1 s−1, at least one order of magnitude higher than the rate constant of 9.4–99 × 10−6 to form a trimer from a monomer and a dimer (k+2). Therefore, forming tetramers from two dimers is complementary with forming tetramers by the successive addition of two monomers to a dimer. Importantly, including the parallel pathway of tetramer formation from dimers does not change the values of the association rate constants for monomer addition to form dimers and trimers. Thus, the alternate pathway of tetramer formation cannot explain the slow association rate constants for the reactions observed in our simulations.
Effect of pyrene on the nucleation rate
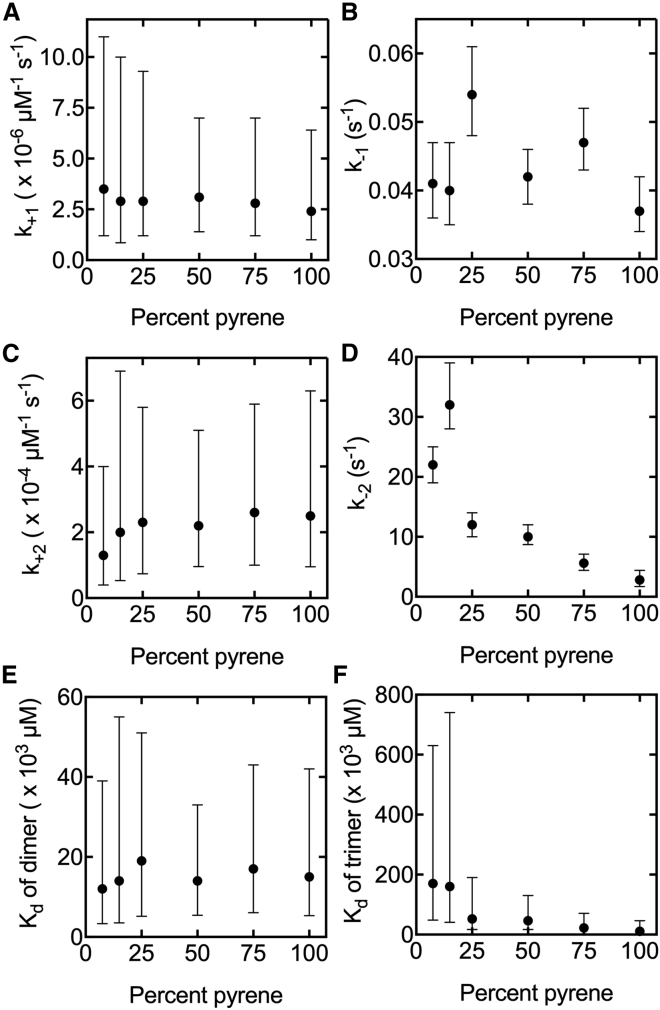
We applied our robust workflow to determine the effect of pyrene labeling on actin nucleation. Because the elongation rate constants for pyrenyl-actin are identical to native actin (5), we used the elongation rate constants for unlabeled filaments. We analyzed the time courses of spontaneous polymerization of six different molar fractions of pyrenyl-actin to estimate the nucleation rate constants (Figs. 2 and 7; Figs. S5–S9; Table S5). The fraction of pyrene-labeled actin monomers did not affect the rate constants for the association and dissociation of dimers (Fig. 7, A and B) because all were the same within error. The same holds for the association of a monomer with a dimer to make a trimer (Fig. 7 C). However, the dissociation rate constant for trimers declined by an order of magnitude between 7.5 and 100% labeled monomers (Fig. 7 D), thereby reducing the Kd of trimers (Fig. 7 F) but not the Kd of dimers (Fig. 7 E). Thus, pyrenyl-actin stabilizes trimers.
Figure 7.
Rate and equilibrium constants for the nucleation reactions (dimer and trimer formation) for a range of mole fractions of pyrenyl-Mg-ATP-actin. Symbols correspond to the starting values used for the PLEs (best-fit value). The bars give the 95% CIs from the PLEs. The 7.5% values appear in the final columns of Tables 1 and 2. (A) Values of rate constants for dimer formation, k+1. (B) Values of rate constants for dimer dissociation, k−1. (C) Dissociation equilibrium constants of dimer formation, Kd of dimer. (D) Values of rate constants for trimer formation, k+2. (E) Values of rate constants for trimer dissociation, k−2. (F) Dissociation equilibrium constants of trimer formation, Kd of trimer.
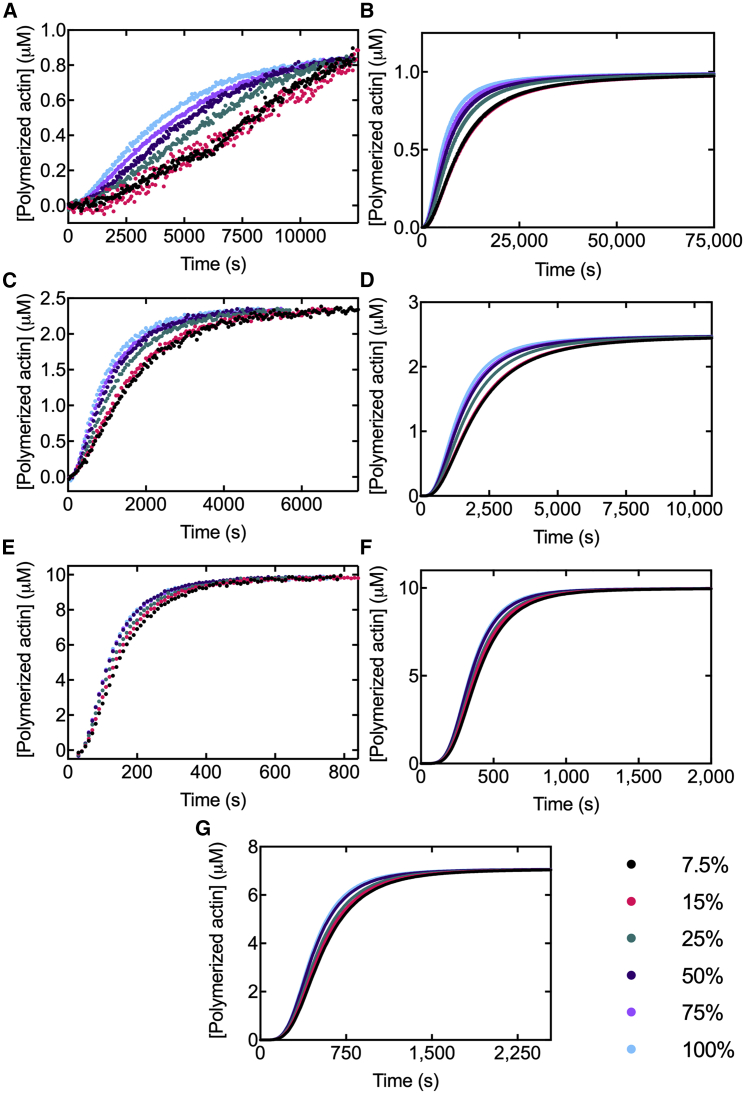
Prior work showed that the pyrene label does not alter actin filament elongation (4,5) or affect the overall time course of spontaneous polymerization (5,38). However, our experiments show clear differences in the time course of spontaneous polymerization over a range of mole fractions of pyrenyl-actin (Fig. 8, A, C, and E). This observation led us to consider differences between the studies that may explain the opposing results.
Figure 8.
Time courses of spontaneous polymerization of actin monomers with a range of mole fractions of pyrenyl-ATP-actin monomers. Shown are (A) 1-μM, (C) 2.5-μM, and (E) 10-μM monomers with a range of mole fractions of pyrenyl-Mg-ATP-actin monomers. The change in fluorescence over time was converted to concentration of polymer by normalizing the curves based upon the critical concentration of actin. (B, D, F, and G) Simulated time courses of spontaneous polymerization of (B) 1-μM, (D) 2.5-μM, and (F) 10-μM Ca-ATP-actin monomers with a range of mole fractions of pyrene-labeled actin monomers in a buffer with 2 mM Mg2+. Each simulation used the best-fit rates determined from the fits of experimental data for each molar fraction of pyrenyl-actin. (G) Simulated time courses of spontaneous polymerization of 7.1 μM Ca-ATP-actin monomers with a range of mole fractions of pyrene-labeled actin monomers in a buffer with 2 mM Mg2+. This simulation matched the monomer concentration from Cooper et al. (5). To see the figure in color, go online.
One difference in our work from earlier work comes from the cationic species of actin used. Previous studies polymerized Ca-ATP-actin in buffer with MgCl2 rather than starting with Mg-ATP-actin monomers as we did. This raised the possibility that divalent cation exchange might have obscured effects of the pyrene label. To address this difference, we used a model including Ca2+ exchange (see Supporting materials and methods, Cation exchange model and Differential equations describing our models) to simulate the polymerization time course of an actin with a range of mole fractions labeled with pyrene. The simulated data matches the trend of our findings (Fig. 6, B, D, F, and G). Thus, this rate-limiting reaction does not mask the effect of pyrene on nucleation.
Two other differences, a higher concentration of actin monomers and a lower mole fraction of pyrenyl-actin, may have obscured the detection of effects. Tellam and Frieden tested mole fractions up to 0.05 at a monomer concentration of 24 μM (38). Cooper et al. tested mole fractions of pyrenyl-actin up to 1.0; however, they used a monomer concentration of 7.1 μM (5). Our results indicate the effect on the course of polymerization only becomes obvious at high mole fractions of pyrenyl-actin and low concentrations of actin monomers (Fig. 8, A, C, and E). Therefore, the results of our experiments that included both variation in monomer concentration and pyrenyl-actin mole fraction reveal a change to the overall time course of actin polymerization.
Discussion
Our simulations of actin filament nucleation reactions agree with previous work that the formation of dimers and trimers is unfavorable; however, the reasons differ from the most advanced previous work of Sept and McCammon (9). They used Brownian dynamics simulations with rigid actin monomers forming dimers, trimers, and longer filaments to map the pathway from monomers to longitudinal dimers to trimers with the third subunit making lateral bonds with the dimer (Fig. 9 A). They concluded that the reactions are fast and limited by diffusion like the elongation of the barbed end of actin filaments (Fig. 9 A). Their assumption of diffusion-limited association reactions required large dissociation rate constants for dimers and trimers to make those reactions unfavorable (Table 1, column 4; Table 2, column 2).
Figure 9.
Comparison of the nucleation pathways. (A) Nucleation pathway and rate constants determined by Sept and McCammon (9). (B) Our measurements of rate constants from fitting the model to the concentrations of polymer, monomer, and ends versus time (Fig. 2) using the same pathway as in (A). (C) Our hypothesized nucleation pathway with a monomer equilibrium between twisted-closed (orange) and flattened-opened (yellow) conformations. The pathway and rate constants indicated reflect those from a model assuming dimer formation requires one salt-induced flattened-open monomer; however, only twisted-closed monomer conformations participate in the other reactions (Fig. 3, 1M∗: Salt). To see the figure in color, go online.
We used new computational methods free of assumptions about the values of the rate constants to estimate nucleation rate constants from time courses of spontaneous polymerization of Mg-ATP-actin. We assumed, as others have done (6, 7, 8), that the process uses monomer addition reactions to form dimers, trimers, and then tetramers, which elongate like the ends of actin filaments. Our analysis indicates that dimers form very slowly and are relatively stable (Fig. 7 B; Table 1, column 5; Table 2, column 5; Table 3, column 2). Remarkably, dimers dissociate slower than ATP-actin subunits from actin filament barbed ends (1.4 s−1 (13)). Trimers also form slowly. Simulations of models with severing and annealing or a parallel pathway of tetramer formation from two dimers also produced slow rates of dimer and trimer formation.
The only previous report of slow association rate constants for productive dimers and trimers by Cooper et al. (7) focused on the thermodynamics of the nucleation reactions. They fixed the dissociation rate constants of all nucleation steps at 500 s−1 because larger values did not improve their fits to the polymerization time courses. Had they chosen a different fixed value for the dissociation rate constants, their association rate constants would have changed accordingly.
Conformations of intermediates along the nucleation pathway
Interpretation of our simulations depends on the structures of the intermediates along the nucleation pathway. We use a wide range of evidence to discuss what is known about these structures.
Monomer conformations
Actin monomers in a large number of crystal structures adopt a twisted conformation with the hydrophobic pocket above the W-loop (residues 167-171) closed (12,39), whereas interactions between subunits in filaments depend on two differences. First, the dihedral angle between the two halves of the molecule must flatten to optimize both longitudinal and lateral interactions (36). Second, and more subtly, a pocket above the W-loop in the barbed end groove must open up to accommodate the side chain of residue M44 from the D-loop (residues 40-50) of the adjacent subunit (36). This interaction, which accounts for 10% of the surface area buried between subunits along the long-pitch helix (36), is crucial for polymer stability, as indicated by the oxidation of M44 depolymerizing filaments (40). The distance between the alpha carbons of Y143 and Y169 (at the end of the W-loop) is a measure of the openness of the pocket. Indeed, in the twisted ATP-actin crystal structure (PDB: 1NWK), the distance measures 11.8 Å, whereas this distance opens up to 13.4 Å in flattened subunits in filaments (36). Thus, it is plausible that the flattening and an open W-loop pocket are both required to form dimers.
Actin monomers had a high tendency to flatten spontaneously in molecular dynamics simulations of Jepsen and Sept (41), but flattening did not open the hydrophobic pocket above the D-loop. We measured an average distance of 11.0 ± 1.0 Å between the alpha carbons of Y143 and Y169 across the opening of the pocket in the MD simulation of ATP-actin (41). Thus, the unfavorable opening of the W-loop pocket is independent of the flattening of the monomer. Thus, we expect that most monomers in solution are in a rapid equilibrium between twisted-closed and flattened-closed states, whereas a minority is in the higher energy flattened-open state, which may correspond to the M∗ state, which limits the rate of dimer formation in our simulations.
Dimer conformations
Much less is known about the structure of actin dimers in solution, but evidence favors dimers associated by longitudinal interactions related to the long-pitch helix in filaments for multiple reasons. First, the longitudinal interactions between subunits in filaments bury 1200 Å2 of surface area, 1.35 times the surface area of 890 Å2 buried by lateral interactions (see Supporting materials and methods, Buried surface area calculation). Second, Brownian dynamics simulations led Sept and McCammon (9) to conclude that longitudinal dimers dominate the pathway despite using rigid actin monomers and an actin filament model (11) with twisted subunits and lateral interactions that buried more surface area than the longitudinal interactions. Third, electron microscopy of actin filaments showed that lateral interactions are less stable than longitudinal interactions (42). Fourth, all-atom MD simulations of Zsolnay et al. (43) revealed that the terminal subunit at the barbed end of a filament interacts much more stably with the next subunit along the long-pitch helix than the lateral interaction with the penultimate subunit along the short-pitch helix. The lateral interaction is weak, in part, because neither the terminal subunit nor the penultimate subunit is flattened, which occurs in a gradient away from the end. The same simulations showed that the D-loop alone can tether the terminal subunit to its longitudinal neighbor, a situation we expect to exist in a longitudinal dimer in solution, making these two subunits a plausible model for dimers in solution.
On the other hand, the coarse-grained simulations of Horan et al. (44) produced lateral dimers rather than longitudinal dimers. Coarse-grained simulations out of necessity ignore the contributions of side chains such as M44 in the D-loop. Without this strong D-loop interaction, the simulations of Horan et al. (44) emphasized lateral and antiparallel interactions. Although chemical cross-linking (45), neutron scattering (46), and SAXS (10) also detected antiparallel actin dimers, these are likely to be off the main nucleation pathway.
Trimer conformations
Even less is known about the structure(s) of actin trimers in solution. One option is a purely longitudinal trimer, but Brownian dynamics simulations (9) favored trimer formation from a longitudinal dimer by the lateral addition of a third subunit that interacts with both subunits of the dimer. Flattening of all three subunits is likely to strengthen their interactions, whereas opening the W-loop of the middle subunit would favor adding a subunit to the barbed end of the trimer. All-atom MD simulations of the barbed end of filaments (43) emphasized that such a lateral interaction is weak because the penultimate subunit dissociated from the terminal subunit. A contributing factor is none of the three subunits in those simulations were completely flattened.
Tetramer conformations
Essentially nothing is known about the structures of actin tetramers. However, it may be similar to the two ends of long filaments, with one subunit tethered at the barbed end and a distorted pointed end unfavorable for subunit addition (43).
Nucleation pathways
Ideally, one would include all possible intermediates in models of the nucleation pathway; however, considering just pathways using stepwise monomer addition and dissociation reactions, the number of plausible dimeric, trimeric, and tetrameric species exceeds the capacity of the fitting software (Fig. S10). Simulations of our models with six unknown parameters produced estimates of the parameter values with large CIs, adding many more parameters would only further obfuscate the true values. Therefore, one must make simplifying assumptions, which we have done based on structural and biochemical data.
Dimer formation
Collision complexes between actin monomers should form rapidly by a diffusion-limited reaction, as reflected in the values of the rate constants reported by Sept and McCammon (9), but our kinetic analysis shows that the formation of productive dimers is unfavorable with a slow association rate constant and a modest dissociation rate constant.
Why might most collision complexes fail to form a stable intermediate? We suggest that slow dimer association is due to the unfavorable conformational equilibrium that results in a very low concentration of high-energy, flattened monomers with open W-loops, which are capable of forming a longitudinal bond with the flexible D-loop of another monomer (Fig. 9 C). Indeed, four different models requiring a monomer conformational change all led to faster association rate constants for dimers when compared with the model with no conformational equilibrium (Fig. 4 D). Our analysis could not pinpoint an exact value for the rate constants, but it does support our hypothesis of an unfavorable conformational equilibrium.
Our proposal is consistent with the analysis of nucleation by SAXS by Oda et al. (10). They also concluded that dimers (Kd = 1700 μM) are more stable than trimers (Kd = 550,000 μM). This differs from previous studies, which concluded that trimers (Kd = 5 μM (8) or 600 μM (9)) are more stable than dimers (Kd = 800,000 μM (8) or 4,600,000 μM (9)).
Trimer formation
We suggest that the two subunits in a longitudinal dimer are twisted and loosely tethered together, so they do not provide a favorable binding site for the lateral association of an incoming monomer. Therefore, conformational changes of one or both subunits of the dimer and the incoming monomer are likely to be required to form a stable trimer. Consequently, the lateral subunit in a trimer dissociates >500 times faster than dissociation of a dimer because the unfavorable twisted conformations in oligomers are not as stable as those between subunits in the core of filaments or even between longitudinal dimers. Including these and other conformational changes in the pathway would create far too many variables to constrain the model when fitting the experimental data.
Tetramer formation
We find that tetramers can be formed by two parallel pathways: monomer addition to a trimer and reaction of two dimers. Adding a monomer to a trimer to form a tetramer is likely to be more favorable than the formation of both dimers and trimers. The new subunit makes one strong longitudinal interaction and one weaker lateral interaction. We used the actin filament elongation rate constants for this reaction, although the subunits in the trimer are unlikely to be fully flattened, similar to the subunits near the barbed end of the simulated filament (43). Thus, given more of the relatively stronger longitudinal interactions, tetramers and dimers are more stable than trimers as seen in the results of our simulations. Combining two dimers to form tetramers can also contribute to tetramer formation because the concentration of dimers is much higher than the concentration of trimers (Fig. 6, A and B). We note that inclusion of tetramer formation from dimers does not change the values of the association rate constants for monomer addition to form dimers and trimers. Thus, the alternate pathway of tetramer formation cannot explain the slow association rate constants for the reactions observed in our simulations.
Oda et al. (10) also noted that the time course of changes in SAXS are consistent with two dimers forming tetramers. They suggest that a flattened monomer may interact with a twisted monomer to form a longitudinal dimer.
Nucleation of pyrenyl-actin
Pyrene conjugated to C374 of actin has remarkably little effect on the rate constants for actin filament nucleation. However, the rate constant for trimer dissociation declines 10-fold with the mole fraction of pyrene-labeled subunits (Fig. 7 D). When bonded to C374, the flat hydrophobic pyrene molecule of four conjugated aromatic rings fits almost perfectly in a hydrophobic pocket between subunits along the long-pitch helix of the filament (47). This interaction may stabilize the loosely tethered dimer in a conformation favorable for lateral binding of the third subunit. In fact, although pyrene does not contact the laterally bonded subunit, the surface area buried by lateral interactions is 60 Å2 greater in the presence of pyrene. This larger binding area may stabilize lateral interactions.
Conclusions
We hope that our study will inspire additional work to gain the full picture of actin nucleation. Molecular dynamics simulations will be required to explore the conformational changes at each step in the pathway because the concentrations of these intermediates are too low to explore with these biophysical methods. If nucleation of actin with a nonhydrolyzable ATP analog differs from ATP-actin, ATP hydrolysis, and phosphate dissociation should be considered as part of the mechanism. A fundamental understanding of spontaneous nucleation will open up investigations of proteins that promote nucleation.
Author contributions
A.D.R. built the models and analyzed the data. A.D.R. and T.D.P. wrote the bulk of the manuscript. E.W.K. and D.R.K. collected the polymerization data and contributed to Materials and methods. L.M.L. provided advice about computational methods. All authors read and edited the manuscript.
Acknowledgments
We thank Steven Chou for his advice in calculating buried surface area. We thank Vilmos Zsolnay for helpful discussions about monomer flattening and Dr. Edwin Taylor for valuable discussions about kinetics and his critical reading of the manuscript. We owe special thanks to the reviewers for their thoughtful comments, questions, and criticisms, which contributed to major revisions of the article. The authors thank Dr. Rachel Mahaffy for helping collect some of the polymerization data and Dr. Pedro Mendes for his guidance in the use of COPASI and his advice on modeling. The authors would also like to thank Dr. Maria P. Saccomani for discussions about structural identifiability.
Research reported in this publication was supported by National Institute of General Medical Sciences of the National Institutes of Health under award number R01GM026338. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Additionally, the authors thank the creators of Virtual Cell and COPASI, software resources both supported by National Institutes of Health Grant R24-GM137787 from the National Institute of General Medical Sciences. We thank the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco for the use of their program University of California, San Francisco, Chimera, supported by National Institutes of Health P41-GM103311, which we used in calculating the added buried surface area of pyrene in the actin filament.
Editor: Dimitrios Vavylonis.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.09.006.
Supporting citations
References (48, 49, 50, 51) appear in the Supporting material.
Supporting material
References
- 1.Oosawa F., Asakura S., Ooi T. G-F transformation of actin as a fibrous condensation. J. Polym. Sci. 1959;37:323–336. [Google Scholar]
- 2.Oosawa F., Kasai M. A theory of linear and helical aggregations of macromolecules. J. Mol. Biol. 1962;4:10–21. doi: 10.1016/s0022-2836(62)80112-0. [DOI] [PubMed] [Google Scholar]
- 3.Wegner A., Engel J. Kinetics of the cooperative association of actin to actin filaments. Biophys. Chem. 1975;3:215–225. doi: 10.1016/0301-4622(75)80013-5. [DOI] [PubMed] [Google Scholar]
- 4.Kouyama T., Mihashi K. Fluorimetry study of N-(1-pyrenyl)iodoacetamide-labelled F-actin. Local structural change of actin protomer both on polymerization and on binding of heavy meromyosin. Eur. J. Biochem. 1981;114:33–38. [PubMed] [Google Scholar]
- 5.Cooper J.A., Walker S.B., Pollard T.D. Pyrene actin: documentation of the validity of a sensitive assay for actin polymerization. J. Muscle Res. Cell Motil. 1983;4:253–262. doi: 10.1007/BF00712034. [DOI] [PubMed] [Google Scholar]
- 6.Tobacman L.S., Korn E.D. The kinetics of actin nucleation and polymerization. J. Biol. Chem. 1983;258:3207–3214. [PubMed] [Google Scholar]
- 7.Cooper J.A., Buhle E.L., Jr., Pollard T.D. Kinetic evidence for a monomer activation step in actin polymerization. Biochemistry. 1983;22:2193–2202. doi: 10.1021/bi00278a021. [DOI] [PubMed] [Google Scholar]
- 8.Frieden C. Polymerization of actin: mechanism of the Mg2+-induced process at pH 8 and 20 degrees C. Proc. Natl. Acad. Sci. USA. 1983;80:6513–6517. doi: 10.1073/pnas.80.21.6513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sept D., McCammon J.A. Thermodynamics and kinetics of actin filament nucleation. Biophys. J. 2001;81:667–674. doi: 10.1016/S0006-3495(01)75731-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Oda T., Aihara T., Wakabayashi K. Early nucleation events in the polymerization of actin, probed by time-resolved small-angle x-ray scattering. Sci. Rep. 2016;6:34539. doi: 10.1038/srep34539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Holmes K.C., Popp D., Kabsch W. Atomic model of the actin filament. Nature. 1990;347:44–49. doi: 10.1038/347044a0. [DOI] [PubMed] [Google Scholar]
- 12.Kabsch W., Mannherz H.G., Holmes K.C. Atomic structure of the actin:DNase I complex. Nature. 1990;347:37–44. doi: 10.1038/347037a0. [DOI] [PubMed] [Google Scholar]
- 13.Pollard T.D. Rate constants for the reactions of ATP- and ADP-actin with the ends of actin filaments. J. Cell Biol. 1986;103:2747–2754. doi: 10.1083/jcb.103.6.2747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.MacLean-Fletcher S., Pollard T.D. Identification of a factor in conventional muscle actin preparations which inhibits actin filament self-association. Biochem. Biophys. Res. Commun. 1980;96:18–27. doi: 10.1016/0006-291x(80)91175-4. [DOI] [PubMed] [Google Scholar]
- 15.Pollard T.D. Polymerization of ADP-actin. J. Cell Biol. 1984;99:769–777. doi: 10.1083/jcb.99.3.769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Doolittle L.K., Rosen M.K., Padrick S.B. Measurement and analysis of in vitro actin polymerization. Methods Mol. Biol. 2013;1046:273–293. doi: 10.1007/978-1-62703-538-5_16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Frieden C., Goddette D.W. Polymerization of actin and actin-like systems: evaluation of the time course of polymerization in relation to the mechanism. Biochemistry. 1983;22:5836–5843. doi: 10.1021/bi00294a023. [DOI] [PubMed] [Google Scholar]
- 18.Ditlev J.A., Vacanti N.M., Loew L.M. An open model of actin dendritic nucleation. Biophys. J. 2009;96:3529–3542. doi: 10.1016/j.bpj.2009.01.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schaff J., Fink C.C., Loew L.M. A general computational framework for modeling cellular structure and function. Biophys. J. 1997;73:1135–1146. doi: 10.1016/S0006-3495(97)78146-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cowan A.E., Moraru I.I., Loew L.M. Spatial modeling of cell signaling networks. Methods Cell Biol. 2012;110:195–221. doi: 10.1016/B978-0-12-388403-9.00008-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hucka M., Finney A., Wang J., SBML Forum The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics. 2003;19:524–531. doi: 10.1093/bioinformatics/btg015. [DOI] [PubMed] [Google Scholar]
- 22.Hoops S., Sahle S., Kummer U. COPASI--a COmplex PAthway SImulator. Bioinformatics. 2006;22:3067–3074. doi: 10.1093/bioinformatics/btl485. [DOI] [PubMed] [Google Scholar]
- 23.Levenberg K. A method for the solution of certain non linear problems in least squares. Q. Appl. Math. 1944;2:164–168. [Google Scholar]
- 24.Marquardt D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963;11:431–441. [Google Scholar]
- 25.Goldfeld S.M., Quandt R.E., Trotter H.F. Maximization by quadratic hill-climbing. Econometrica. 1966;34:541–551. [Google Scholar]
- 26.Hooke R., Jeeves T.A. “Direct search” solution of numerical and statistical problems. J. Assoc. Comput. Mach. 1961;8:212–229. [Google Scholar]
- 27.Kaupe A.F. Algorithm 178: direct search. Commun. ACM. 1963;6:313–314. [Google Scholar]
- 28.Bell M., Pike M.C. Remark on algorithm 178 [E4] direct search. Commun. ACM. 1966;9:684–685. [Google Scholar]
- 29.Swann W. In: Numerical Methods for Unconstrained Optimization. Murray W., editor. Academic Press; 1972. Direct search methods; pp. 13–28. [Google Scholar]
- 30.Kennedy J., Eberhart R. Proceedings of ICNN’95 - International Conference on Neural Networks. Vol. 4. 1995. Particle swarm optimization; pp. 1942–1948. [Google Scholar]
- 31.Bellu G., Saccomani M.P., D’Angiò L. DAISY: a new software tool to test global identifiability of biological and physiological systems. Comput. Methods Programs Biomed. 2007;88:52–61. doi: 10.1016/j.cmpb.2007.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Villaverde A.F., Evans N.D., Banga J.R. Input-dependent structural identifiability of nonlinear systems. IEEE Control Syst. Lett. 2018;3:272–277. [Google Scholar]
- 33.Ligon T.S., Fröhlich F., Hasenauer J. GenSSI 2.0: multi-experiment structural identifiability analysis of SBML models. Bioinformatics. 2018;34:1421–1423. doi: 10.1093/bioinformatics/btx735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Raue A., Kreutz C., Timmer J. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics. 2009;25:1923–1929. doi: 10.1093/bioinformatics/btp358. [DOI] [PubMed] [Google Scholar]
- 35.Schaber J. Easy parameter identifiability analysis with COPASI. Biosystems. 2012;110:183–185. doi: 10.1016/j.biosystems.2012.09.003. [DOI] [PubMed] [Google Scholar]
- 36.Chou S.Z., Pollard T.D. Mechanism of actin polymerization revealed by cryo-EM structures of actin filaments with three different bound nucleotides. Proc. Natl. Acad. Sci. USA. 2019;116:4265–4274. doi: 10.1073/pnas.1807028115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sept D., Xu J., McCammon J.A. Annealing accounts for the length of actin filaments formed by spontaneous polymerization. Biophys. J. 1999;77:2911–2919. doi: 10.1016/s0006-3495(99)77124-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tellam R., Frieden C. Cytochalasin D and platelet gelsolin accelerate actin polymer formation. A model for regulation of the extent of actin polymer formation in vivo. Biochemistry. 1982;21:3207–3214. doi: 10.1021/bi00256a027. [DOI] [PubMed] [Google Scholar]
- 39.Dominguez R., Holmes K.C. Actin structure and function. Annu. Rev. Biophys. 2011;40:169–186. doi: 10.1146/annurev-biophys-042910-155359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hung R.-J., Pak C.W., Terman J.R. Direct redox regulation of F-actin assembly and disassembly by Mical. Science. 2011;334:1710–1713. doi: 10.1126/science.1211956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Jepsen L., Sept D. Effects of nucleotide and end-dependent actin conformations on polymerization. Biophys. J. 2020;119:1800–1810. doi: 10.1016/j.bpj.2020.09.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bremer A., Millonig R.C., Aebi U. The structural basis for the intrinsic disorder of the actin filament: the “lateral slipping” model. J. Cell Biol. 1991;115:689–703. doi: 10.1083/jcb.115.3.689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zsolnay V., Katkar H.H., Voth G.A. Structural basis for polarized elongation of actin filaments. Proc. Natl. Acad. Sci. USA. 2020;117:30458–30464. doi: 10.1073/pnas.2011128117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Horan B.G., Hall A.R., Vavylonis D. Insights into actin polymerization and nucleation using a coarse-grained model. Biophys. J. 2020;119:553–566. doi: 10.1016/j.bpj.2020.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Millonig R., Salvo H., Aebi U. Probing actin polymerization by intermolecular cross-linking. J. Cell Biol. 1988;106:785–796. doi: 10.1083/jcb.106.3.785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Goddette D.W., Uberbacher E.C., Frieden C. Formation of actin dimers as studied by small angle neutron scattering. J. Biol. Chem. 1986;261:2605–2609. [PubMed] [Google Scholar]
- 47.Chou S.Z., Pollard T.D. Cryo-electron microscopy structures of pyrene-labeled ADP-Pi- and ADP-actin filaments. Nat. Commun. 2020;11:5897. doi: 10.1038/s41467-020-19762-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Estes J.E., Selden L.A., Gershman L.C. Tight binding of divalent cations to monomeric actin. Binding kinetics support a simplified model. J. Biol. Chem. 1987;262:4952–4957. [PubMed] [Google Scholar]
- 49.Gershman L.C., Selden L.A., Estes J.E. High affinity divalent cation exchange on actin. Association rate measurements support the simple competitive model. J. Biol. Chem. 1991;266:76–82. [PubMed] [Google Scholar]
- 50.Estes J.E., Selden L.A., Gershman L.C. Tightly-bound divalent cation of actin. J. Muscle Res. Cell Motil. 1992;13:272–284. doi: 10.1007/BF01766455. [DOI] [PubMed] [Google Scholar]
- 51.Pettersen E.F., Goddard T.D., Ferrin T.E. UCSF Chimera--a visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.