Integrin-based mechanosensing through conformational deformation

Abstract

Conversion of integrins from low to high affinity states, termed activation, is important in biological processes, including immunity, hemostasis, angiogenesis, and embryonic development. Integrin activation is regulated by large-scale conformational transitions from closed, low affinity states to open, high affinity states. Although it has been suggested that substrate stiffness shifts the conformational equilibrium of integrin and governs its unbinding, here, we address the role of integrin conformational activation in cellular mechanosensing. Comparison of wild-type versus activating mutants of integrin αVβ3 show that activating mutants shift cell spreading, focal adhesion kinase activation, traction stress, and force on talin toward high stiffness values at lower stiffness. Although all activated integrin mutants showed equivalent binding affinity for soluble ligands, the β3 S243E mutant showed the strongest shift in mechanical responses. To understand this behavior, we used coarse-grained computational models derived from molecular level information. The models predicted that wild-type integrin αVβ3 displaces under force and that activating mutations shift the required force toward lower values, with S243E showing the strongest effect. Cellular stiffness sensing thus correlates with computed effects of force on integrin conformation. Together, these data identify a role for force-induced integrin conformational deformation in cellular mechanosensing.

Significance

Cells sense extracellular matrix stiffness through integrins to regulate many functions. Despite extensive study, major questions about molecular mechanisms remain unanswered. Here, we report evidence that direct effects of force on integrin conformation determine cellular stiffness sensing. These results are conceptually important because they identify integrins as true mechanosensors that determine signaling outputs.

Introduction

Integrin-based adhesions are the primary structures through which cells sense and respond to the physicochemical properties of the extracellular matrix, including variations in stiffness, composition, topology, and spatial distribution (1). The ability of integrin-based adhesions to respond to matrix stiffness is critical for many cellular processes, including cell division (2), migration (3,4), embryogenesis (5), and wound healing (6), among others. Variations in the stiffness of the extracellular matrix affect the assembly, binding properties, clustering, and stability of integrins and integrin-based adhesions and govern cell spreading and traction force (1,7). Dysregulation of mechanosensing from integrin-based adhesions is associated with a wide variety of disorders, including cardiovascular disease (8,9), musculoskeletal dysfunction (10), fibrosis (11), and cancer (3).

Integrins are heterodimeric transmembrane receptors that bidirectionally transmit mechanical and biochemical signals. They specifically bind components of the extracellular matrix, with each integrin dimer exhibiting a specific repertoire of ligands. Integrins exist in a range of affinity states whose interconversion from inactive to active involves long-range transitions from bent to extended conformations (12). Conformational activation can be regulated through both intracellular activators (i.e., Rap1, talin, and kindlin) and through extracellular matrix ligands (i.e., fibronectin and collagen), thus providing tight control of integrin engagement with the extracellular matrix.

Force applied to integrins facilitates a transition from bent to extended conformation and contributes to the maintenance of the active conformation (13). Application of force to already activated, ligand-bound integrins induces additional recruitment of intracellular adaptor molecules, adhesion reinforcement, and growth (1,7,14,15). Force on active, ligand-bound integrins also stabilizes the bound state, increases cellular traction force and spreading on surfaces, and activates downstream signaling pathways (16, 17, 18). These effects are generally attributed to transmission of force to talin, which then undergoes conformational transitions in which unfolding of helix bundle domains under tension triggers changes in binding partners, which both reinforces adhesions and regulates signaling (19). Other focal adhesion proteins such as p130Cas have also been proposed to function as direct mechanotransducers (20).

However, activating exogenous integrins with manganese ions increases cell spreading on soft surfaces that normally do not allow spreading (21). Integrin αVβ3 is especially critical in cellular stiffness sensing (22). This integrin shows catch and then slip bond behavior as a function of force, in which ligand-bond lifetimes for integrin increase with moderate force and then decrease at higher forces (23,24). The idea that force either drives the conversion from inactive to active conformations or stabilizes the high affinity state, or both, suggests that integrin activation itself might play a role in mechanotransduction.

We therefore investigated the role of integrin conformation in stiffness sensing. Analysis of a collection of equivalently activated αVβ3 mutants on elastic substrates of varying stiffness showed that these mutants shift cell spreading, activation of mechanosensitive signaling pathways (YAP and pFAK), traction forces, and force on the central adhesion adaptor protein talin toward lower stiffness but to varying degrees. We then developed computational simulations based on coarse-grained (CG) modeling that utilize data from μs-long all-atom (AA) molecular dynamics (MD) simulations. The calculations predict that the different mutants respond differently to force. Importantly, force-dependent transition to more extended conformations correlates closely with cellular stiffness sensing. These results identify a key role for force-induced integrin conformational deformation in cellular stiffness sensing.

Materials and methods

Cell culture and transfection

Mouse lung endothelial cells (MLECs) isolated from β3 integrin-null mice were generously provided by Mark Ginsberg and Brian Petrich (University of California at San Diego, La Jolla, CA) (25). β3 integrin single point mutants were generously provided by Timothy Springer (Harvard University, Boston, MA) (26). These sequences were subcloned into pBOB vector and virus prepared in HEK 293Tx cells by co-transfecting with pCMV-VSV-G and psPAX2 using Lipofectamine 2000 (Invitrogen, Waltham, MA). The temperature-sensitive mutant of the SV40 virus large T antigen was employed for conditional immortalization of these cells. Immortalized β3^−/− MLECs were infected with wild-type (WT) or mutant β3 integrin viruses and subsequently sorted to obtain homogenous populations with equal expression levels (24). For expansion, MLECs were cultured in 1:1 Hams F-12 and high-glucose Dulbecco’s Modified Eagle Medium (DMEM) with 20% fetal bovine serum, 1% penicillin-streptomycin, 2.5 mM glutamine, and endothelial cell growth supplement (50 mg/L) at the permissive temperature of 30°C. For experiments, cells were switched to 37°C to inactivate large T 1 day prior.

Polyacrylamide substrate preparation

Small polyacrylamide gels for imaging experiments were prepared as described (27). Briefly, 20 mm coverslip bottom dishes (MatTek, Ashland, MA) were silanized with a 2% solution of 3-aminopropyltrimethoxysilane in isopropanol for 10 min at room temperature. After washing with ddH₂O and drying, coverslips were incubated with 1% glutaraldehyde solution in ddH₂O for 30 min and then washed three times. Polyacrylamide gels were cast onto the silanized surface by preparing acrylamide/bis-acrylamide solutions (Bio-Rad Laboratories, Hercules, CA) of various ratios (Table S1) and polymerizing with ammonium persulfate (AmericanBio, Canton, MA) and N,N,N',N'-tetramethylethylenediamine (Sigma, St. Louis, MO). Gels were cast between the silanized surface and 12 mm uncoated glass coverslips with a volume of 8 μL. After casting, gels were treated with fresh sulfosuccinimidyl 6-(4'-azido-2'-nitrophynlamino)hexanoate (Sigma) in ddH₂O (2 mg/mL) and exposed to ultraviolet light for 3 min (8 W, 254 nm wavelength at a distance of 2–3 inches). After ultraviolet light treatment, gels were washed with ddH₂O and then covered with fibrinogen (200 μg/mL in phosphate-buffered saline (PBS) at pH 7.4) overnight at 4°C. Before seeding, gels were washed three times with PBS and preincubated with medium for 1 h. Cell spreading experiments were performed in serum-free conditions to prevent fibronectin deposition (high-glucose DMEM (Gibco, Waltham, MA) with 0.5% w/v bovine serum albumin (BSA) (Sigma) and 1× Insulin-Transferrin-Selenium (ITS premix; Gibco)).

Larger polyacrylamide gels for Western blot experiments were prepared using a modified version of the protocol from A. Elosegui et al. (28). Briefly, 35-mm glass-bottom dishes were activated with glacial acetic acid, 3-(trimethoxysilyl) propyl methacrylate, and 96% ethanol solution (1:1:14 ratio, respectively) for 10 min in room temperature. For fibrinogen-conjugated gels, acrylamide was partially replaced with acrylic acid N-hydroxysuccinimide ester, according to Table S2, as derived from (28). Cast gels were coated with fibrinogen (200 μg/mL in PBS (pH 7.4)) overnight at 4°C. Cells were plated in serum-free medium (high-glucose DMEM (Gibco) with 0.5% w/v BSA (Sigma), 1× ITS premix (Gibco)) to prevent fibrinogen deposition.

Cell immunostaining and quantification

Cells seeded on fibrinogen-coated glass or polyacrylamide were fixed with 4% paraformaldehyde (Electron Microscopy Sciences, Hatfield, PA) in PBS. Cells were washed and permeabilized with 0.05% Triton X-100 in PBS supplemented with 320 mM sucrose and 6 mM MgCl₂ and then washed three times with PBS and blocked for 30 min with 1% BSA in PBS. Cells were incubated overnight at 4°C with anti-YAP antibody (1:200, catalog number sc-101199; Santa Cruz Biotechnology, Dallas, TX) diluted in 1% BSA in PBS. Cells were washed three times with PBS and incubated at room temperature for 1 h with secondary antibody (Alexa Fluor 647 anti-mouse, 1:1000; Molecular Probes, Eugene, OR) and Alexa Fluor 565-conjugated phalloidin (1:1000; Molecular Probes). They were washed again three times with PBS and mounted with 4′,6-diamidino-2-phenylindole (DAPI) in Fluoromount-G (SouthernBiotech, Birmingham, AL). Cell areas were quantified using ImageJ by background subtracting, thresholding to generate cell masks, and using the analyze particles function. YAP nuclear/cytosolic ratios were quantified by masking nuclear areas (DAPI) and cell areas (phalloidin) of interest in ImageJ and then dividing the background-subtracted average signal in the nucleus by the average signal in the cytoplasm using MATLAB (The MathWorks, Natick, MA).

Quantitative polymerase chain reaction

Relative expression of CTGF versus β-actin was determined by reverse transcription polymerase chain reaction with primers for mouse actin (forward: 5′-cgagcgtggctacagcttc-3′; reverse: 5′-gccatctcctgctcgaagtc-3′) and mouse CTGF (forward: 5′-ctgcagactggagaagcaga-3′; reverse: 5′-gatgcactttttgcccttctt-3′). Cells were cultured on soft (3 kPa) or stiff (30 kPa) fibrinogen-coated silicone gels for 24 h in serum-free media with fibronectin-blocking antibody (16G3, 25 μg/mL) with fresh antibody added at 0 and 12 h to prevent cell-deposited fibronectin from interfering. Messenger RNA was isolated at 24 h by directly lysing cells on the gel surface using the mRNeasy kit (QIAGEN, Hilden, Germany), and complementary DNA was synthesized using iScript complementary DNA synthesis kit (Bio-Rad Laboratories). Polymerase chain reaction was run for 40 cycles on a Bio-Rad CFX96 reverse transcription polymerase chain reaction machine using SsoAdvanced universal SYBR green supermix (Bio-Rad Laboratories).

Western blot

MLECs seeded on polyacrylamide gels were lysed directly in sodium dodecyl sulfate (SDS) sample buffer (100 mM Tris-Cl (pH 6.8), 4% SDS, 0.2% Bromophenol blue, and 20% glycerol) with protease and phosphatase inhibitors (Halt protease inhibitor cocktail 100×; Thermo Fisher Scientific, Waltham, MA) and 2.5% β-mercaptoethanol. Lysates were sonicated for 30 s and boiled at 95°C for 5 min. Samples were loaded onto 8 or 10% SDS-polyacrylamide gels and run for 90 min at 120 V in Tris-glycine buffer with SDS. Transfer was performed using Tris-glycine 20% Methanol buffer onto nitrocellulose membranes (Bio-Rad Laboratories) with a Transblot Turbo (Bio-Rad Laboratories). Membranes were blocked with 5% BSA in Tris-buffered saline with 0.1% Tween 20 in 150 mM NaCl and 50 mM Tris-HCl (pH 7.6) (TBS-T) for 1 h. Membranes were incubated overnight at 4°C with primary antibodies directed at total focal adhesion kinase (FAK) (1:1000; Cell Signaling Technology, Danvers, MA) or phosphorylated FAK (Y397, 1:1000; Cell Signaling Technology) in TBS-T. Membranes were washed three times for 5 min with TBS-T and incubated for 1 h at room temperature with peroxidase-conjugated anti-mouse or anti-rabbit secondary antibodies (1:4000 in TBS-T; Vector Laboratories, Burlingame, CA). Membranes were washed three times for 5 min, and bands were detected using Supersignal West Pico PLUS or Fempto detection reagents (Thermo Fisher Scientific) and imaged on a G:BOX gel imager (Syngene, Bangalore, India).

Traction force microscopy

Silicone traction force microscopy (TFM) substrates were fabricated as described (29). Briefly, cover glass-bottom 96-well plates were spin coated with a ∼40 μm-thick layer of a silicone gel prepolymer polydimethylsiloxane (CY 52–276 by Dow, Midland, MI, mixed at various A:B ratios, 1.4 kPa = 0.8:1; 3.1 kPa = 0.9:1; 11 kPa = 1.2:1; and 1.6:1 30 kPa). Gel prepolymer is cured by baking at 70°C overnight and then treated with 3-aminopropyl trimethoxysilane for 5 min and incubated for 10 min at room temperature under a suspension of 40 nm Alexa Fluor 647 beads (Molecular Probes) in a 100 μg/mL solution of 1-ethyl-3-(3-dimethylaminopropyl) carbodiimide (Sigma) in water to covalently link beads to the gel surface. Gel modulus for each batch was measured using a microfluidic device (29) and is reported as Young’s elastic modulus.

TFM gels were coated with fibrinogen (10 μg/mL) in PBS overnight at 4°C. Before seeding, gels were washed three times with PBS. Traction force experiments were performed in serum-free conditions to limit fibronectin deposition (Phenol-Free high-glucose DMEM (Gibco) with 0.5% w/v BSA (Sigma), 1× ITS premix (Gibco), and 1 μM lysophosphatidic acid (Sigma)). The day of the experiment, cells were trypsinized and seeded on TFM substrates at low density (∼3000 cells per cm²) for 2 h. Cells and florescent beads were imaged on a spinning disk confocal microscope (UltraVIEW VoX; PerkinElmer, Waltham, MA) attached to a Nikon A-1 microscope equipped with a temperature and CO₂-controlled incubation chamber and 60× 1.4 NA lens. Fluorescent images of Alexa Fluor 647 beads and differential interference contrast images of cells were acquired before and after cell lysis with 0.05% SDS. Images were drift corrected, and bead displacements were quantified using a previously developed open source TFM software in MATLAB 2015a (26). Force fields and traction stresses were calculated using Fourier transform traction cytometry force reconstruction with regularization parameter set at 1 kPa = 0.01, 3.1 kPa = 0.001, 11 kPa = 0.0001, and 31 kPa = 0.00005. Regularization parameter was chosen to give smooth traction maps, and a single parameter was used for all groups at a given stiffness. Average stress per cell was calculated as the total force for a cell divided by its spread area.

Fluorescence resonance energy transfer imaging and quantification

Quantification of fluorescence resonance energy transfer (FRET) data was performed using the custom software in MATLAB we developed previously (30). All three FRET images (eGFP, tagRFP, and FRET) were corrected for illumination gradient, pixel shift, and background subtraction, followed by three-point smoothening. Bleed through and cross-excitation co-efficients were calculated by imaging cells transfected with eGFP-talin or tagRFP-talin. The slope of the pixel-wise donor or acceptor channel intensity versus FRET channel intensity gives bleed through (x) or cross-excitation (y) fraction, respectively. Heat maps of FRET and pixel-wise FRET index were calculated using the following equation:

$$FRETIndex=\frac{FRET-x\left(GFP\right)-y\left(RFP\right)}{RFP},$$

where FRET, GFP, and RFP are the shade, shift, and background-corrected pixel intensities for each of the respective channels. Average FRET index was calculated for masked focal adhesions in each cell. Focal adhesion sizes for talin tension sensor images were quantified using the Focal Adhesion Analysis Server (31) with default settings for static properties only and for adhesions greater than 0.2 μm².

Computational models of active αVβ3 integrin under force

We used a CG computational model to study the effect of force on WT αVβ3 integrin and the L138I, K417E, and S243E mutants. Starting from μs-long equilibrium all-atom MD simulations, we decreased the representation of each integrin from 1780 Cα atoms to 300 CG beads (average resolution 8 ± 4 Cα atoms per CG bead), using the Essential Dynamics Coarse Graining approach (32). Each CG bead of bent αVβ3 was placed at the center of geometry of the corresponding Cα atoms of open αIIbβ3 integrin (33). Then, CG beads were connected using effective harmonic and Morse interaction potentials by applying our recent hetero-elastic network models (hENM)-based approach (for details, see (34) and Supporting materials and methods). Last, we ran Langevin Dynamics using the MD software LAMMPS (35), with the temperature set at 310 K, with a constant number of particles, volume, and temperature ensemble. To mimic the effect of the cell membrane, transmembrane helices were spatially restrained; to mimic the effect of substrate rigidity, a pulling force was applied on the ligand binding site. For outputs, we analyzed structural parameters representative of conformational stability of integrin, including overall integrin length and separation between the two integrin legs.

Backmapping of CG to all-atom models

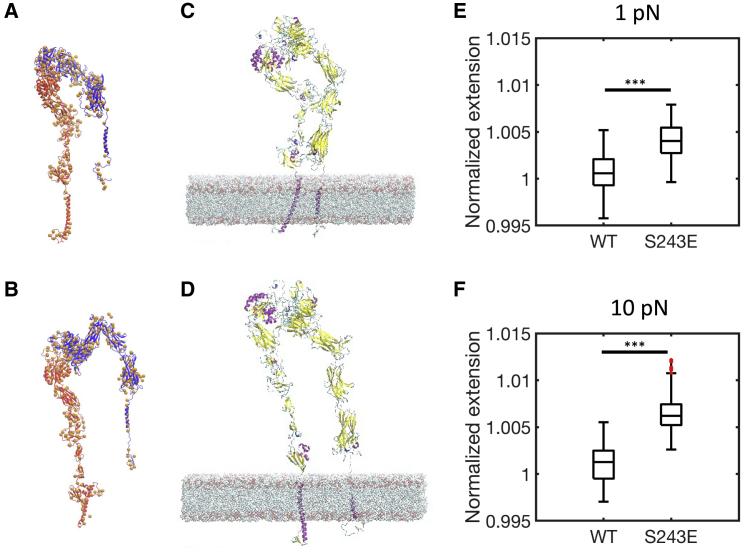
The initial atomic model for WT integrin was constructed from structures obtained via x-ray crystallography and solution NMR (3IJE.pdb (36) and 2KNC.pdb (37)). Missing amino acid backbones were built using MODELER (38), and missing side chains were optimized using SCWRL4 (39). In the all-atom model of integrin, center-of-mass (COM) positions of atoms belonging to each CG particle were computed of the unloaded CG system. The COM positions were grouped on the basis of distinct secondary structural elements of the protein. For each secondary structural element, rotation and translation matrices were computed by minimizing the root mean-square displacement (RMSD) in a rigid-body fit of the COM positions to the CG conformation of WT integrin derived from the CG MD simulations without force. These transformation matrices were then applied to the corresponding all-atom model for each secondary structural element to generate an initial backmapped model (Fig. 5 A and B). The backmapped all-atom structures were subsequently refined using steepest descent and adopted basis Newton Raphson energy minimization algorithms in the CHARMM36 force field (40,41). The same backmapping procedure was repeated for the S243E integrin mutant and the corresponding CG conformation derived from the CG MD simulations. The backmapped all-atom structures were inserted into a lipid bilayer with 80% 1,2-dioleoyl-sn-glycero-3-phosphocholine and 20% 1,2-dioleoyl-sn-glycero-3-phosphoserine lipids (960 lipids in each leaflet and total 1920 lipids in membrane) using CHARMM-GUI membrane builder (33). Similar to the initial AA MD simulations, the lipid-membrane/integrin systems were hydrated with TIP3P water molecules and 150 mM NaCl, for a total of ∼1.9 million atoms for WT integrin and 2.2 million atoms for S243 mutant. The sizes of these systems were significantly larger than the initial AA systems, owing to the more extended and open configurations of stretched integrin, which occupy a larger volume in the computational domain. Energy minimization was run for 5000 steps of steepest descent algorithm, and then equilibration was performed to relax the system. We used a six-step protocol in which decreasing restraints were applied to the protein, lipids, and water molecules; constant volume and temperature dynamics was used for the first two steps, followed by constant pressure, area, and temperature dynamics for the rest at 310 K. At the end of equilibration, we analyzed structural properties of AA wild-type and S243 mutant integrins. Consistent with the structural properties of the stretched CG structures, comparison of stretched WT integrin to the S243E mutant showed a more bent headpiece (122 ± 7.8° for WT genu angle vs. 166° ± 18.3 for S243E) and closer chains (genu separation 7.6 ± 0.4 nm for WT vs. 4.7 ± 1.1 nm for S243E) (see Fig. 5, C and D). Constant force steered MD was done on the backmapped all-atom systems and revealed that the S243E mutant extended more than WT under force (Fig. 5, E and F). These results indicate that the structural properties of the CG systems are maintained at the molecular levels in stretched integrins and provide further evidence that force stabilizes extended integrin conformations.

Figure 5.

All-atom backmapped structures of WT and S243E under force. All-atom backmapped configurations for (A) WT and (B) S243E integrins after energy minimization. CG beads (in orange) and secondary structure elements (in blue and red to distinguish between the two chains) are superimposed. AA backmapped configurations for integrins in the absence of force, embedded in multicomponent lipid bilayer, after energy minimization and equilibration. (C) WT and (D) S243E mutant are shown in ribbon representation; lipids are shown in van der Waals representation. Boxplots of extension under constant force for WT and mutant integrins (computed between 100 and 200 ps of constant force steered MD simulations), normalized by the average extension of integrin without force (computed between 1 and 20 ns of equilibrium simulations). These values are extracted from backmapped all-atom models of WT and mutant integrins at 1 pN (E) and 10 pN (F) force. Box plots indicate median, 25th and 75th percentile, and minimum and maximum; ^∗∗∗p < 0.001, unpaired t-test. To see this figure in color, go online.

Steered MD of backmapped all-atom integrin models

To evaluate the effect of an external force on the extension of all-atom integrin, we performed steered MD simulations on the backmapped and energy-minimized AA WT and S243 mutants. A constant vertical force of 1 or 10 pN was applied to the center of mass of the ligand binding site, whereas the β-chain transmembrane helix was held fixed within the lipid bilayer. The simulations were performed using Gromacs 5.0.4 (42) for 500 ps in the fixed number of particles N, pressure P, and temperature T ensemble using Berendsen barostat (43), keeping the temperature at 310 K and pressure at 1 atm with semi-isotropic pressure coupling with a compressibility of 4.5 × 10⁻⁵ bar⁻¹. Long-range electrostatic interactions were incorporated through the Particle Mesh Ewald method with a cutoff of 1 nm (44). Analysis of extension at 1 pN or 10 pN constant force was performed.

Statistics

All of the statistical analysis was performed using Prism version 7.01 (GraphPad Software). Details regarding the specific statistical tests used, the sample size, p-values, and number of independent experiments are provided in the figure legends. All experimental data are included in the Supporting materials and methods. Modeling results are available at https://github.com/tamarabidone/integrins_AA_CG.

Results

Activating mutants drive cell spreading on soft substrates

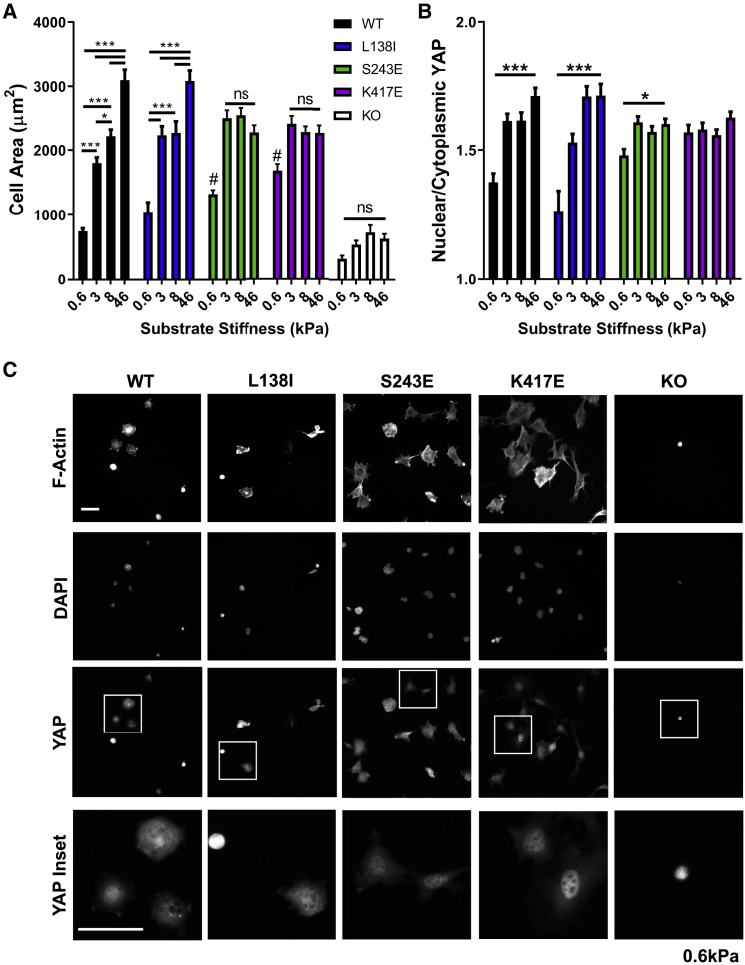
To assess the effects of activating mutations on stiffness sensing, we expressed WT β3 integrin or activated mutants (L138I, S243E, and K417E) (45) in immortalized β3 integrin knockout MLECs. Previous studies used binding to the monomeric high affinity soluble ligand WOW-1 as the optimal assay for integrin affinity without interference from clustering and in the absence of force (46). These results showed that the mutations resulted in increased affinity that was indistinguishable between the mutants (34). To assess spreading and YAP nuclear localization as typical stiffness-dependent functions, polyacrylamide gels of varying stiffnesses were coated with the β3 ligand fibrinogen. β3^−/− cells show minimal adhesion to these surfaces, demonstrating specificity. Cells expressing equivalent levels of WT or mutant β3 were plated and assayed at 3 h to minimize fibrinogen proteolysis or other modifications of the substrates. WT β3 cells adhered well and showed the expected stiffness-dependent increase in spread area and YAP nuclear localization (Fig. 1, A and B; Fig. S1). Activating mutations shifted the ability of cells to spread and induce YAP nuclear localization toward lower stiffnesses (Fig. 1, A–C). Interestingly, L138I had only a weak effect, whereas S243E and K417E strongly shifted the behavior toward softer substrates without increasing maximal cell spreading or YAP nuclear localization on stiff substrate. These results were confirmed by quantification of the YAP target gene CTGF (Fig. S2 A), which showed increased expression for all mutants on soft (3 kPa) gels. Integrin activation thus promotes spreading on soft substrates, confirming the results with Mn2 + activation of integrin (21). Additionally, our results show that the mechanosensitive YAP pathway is similarly regulated.

Figure 1.

Integrin-activating mutants increase spreading and YAP nuclear localization at low stiffness. (A) Cell spread area 3 h after seeding on fibrinogen-coated polyacrylamide of the indicated Young’s modulus. Area was quantified from area of phalloidin-stained β3 knockout (KO) MLECs reconstituted with the indicated β3 integrin. Values are means ± SEM. n = 25–123 cells per group from two independent experiments; ^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001, and ^#p < 0.05 versus WT at same stiffness, two-way ANOVA with Tukey’s post hoc (KO cells n = 10–25 because of limited adhesion). (B) Quantification of the ratio of nuclear to cytoplasmic YAP signal at each stiffness. Values are means ± SEM. n = 25–123 cells per group from two independent experiments; ^∗p < 0.05 and ^∗∗∗p < 0.001, two-way ANOVA with Tukey’s post hoc. (C) Representative images of F-actin (Phalloidin), YAP, and DAPI staining for MLECs on 0.6 kPa gels. Scale bars, 50 μm. To see this figure in color, go online.

Activating mutants and tyrosine phosphorylation

We next assessed phosphorylation of FAK on tyrosine 397, a well-established mechanosensitive event, in cells plated on gels of different stiffness. As expected (47,48), cells expressing WT β3 showed increasing pFAK (Fig. 2, A and B) with increasing stiffness. All of the activating β3 mutations showed nonsignificant trends toward higher phosphorylation of FAK (Fig. 2 B) in suspension, which we take as the baseline levels. Importantly, the S243E mutant showed a large and significant increase in pFAK/tFAK at low stiffness (0.5 kPa) (Fig. 2 B). We also analyzed these curves by calculating the effective stiffness required for 50% maximal FAK activation, YAP nuclear translocation, and cell spreading (ES50 for these variables). This metric revealed downward shifts in the threshold for stiffness-dependent activation for all mutants, with S243E having the most consistent and largest effect for all three outputs (Fig. S2 B). Although this approach provides a simple, convenient way to quantify the shift in stiffness sensitivity, it may underestimate the actual difference because of the fact that the WT group did not reach saturation at the highest stiffness values.

Figure 2.

FAK phosphorylation. (A) Western blots for phosphorylated FAK (Y397) normalized to total FAK on fibrinogen-coated polyacrylamide gels of the indicated stiffness (S = suspension) for β3 KO MLECs reconstituted with WT or mutant β3 integrin (L138I, S243E, and K417E activating mutations). (B) Densitometry of phosphorylated FAK normalized for total FAK. Values are means ± SEM. n = 4 independent experiments; ^#p < 0.05, one-way nonparametric ANOVA with Dunn’s multiple comparison. To see this figure in color, go online.

Activating mutants and traction force

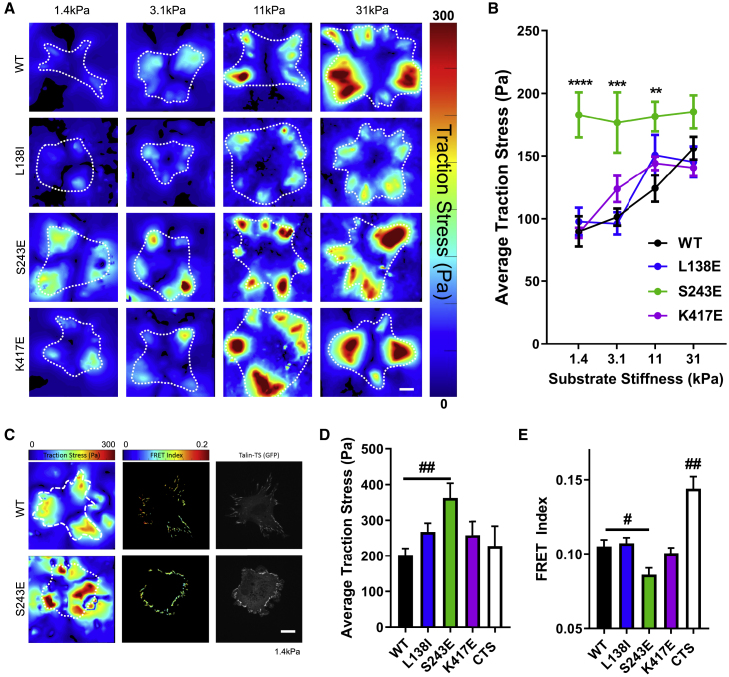
To assay the mechanical forces at the cellular length scale, we measured traction stresses as a function of substrate stiffness (1.4, 3.1, 11, and 31 kPa). Cells plated on fibrinogen-coated silicone gels containing fluorescent beads were imaged before and after cell lysis. Cell-induced bead deformations were analyzed to generate heat maps of traction stress (Fig. 3 A; Fig. S3, A–D), which were cropped for the area occupied by the cell to calculate average traction stress per cell (Fig. 3 B). Measurements were performed 2 h after seeding when traction forces stabilize but are specific to β3 integrin (Fig. S2 C). Cells expressing WT β3 showed increasing traction stress with increasing stiffness, as expected (28). The L138I and K417E mutants showed only slightly elevated stresses at the intermediate stiffnesses (Fig. 3 B). By contrast, the S243E mutant showed maximal traction stress at low stiffness with no further increase (Fig. 3 B). Traction forces are well known to increase as a function of cell spreading (49). Reporting these values as stress, which is force per unit area, partly accounts for this effect. That traction stresses for the L138E and K417E mutants are not significantly different from WT β3 indicates that their increased cell spreading on soft substrates largely accounts for the resultant increase in traction force. By contrast, S243E significantly increased traction stress, especially at low stiffness, meaning that the increase in force is greater than what would be expected for the increased spreading.

Figure 3.

Traction stresses and force on talin. (A) Heat maps of traction stress for MLECs with WT or mutant β3 integrin on fibrinogen-coated silicone surfaces of the indicated stiffness. Surfaces were coated with fluorescent beads (Alexa Fluor 647), and bead displacements were tracked before and after cell lysis for calculation of stresses, which were cropped for the area of the cell (outlined in yellow; scale bars, 10 μm). (B) Quantification of average traction stress per cell for WT and mutant reconstituted cells. Values are means ± SEM. n = 33–41 cells per group from three independent experiments; ^∗∗p < 0.01, ^∗∗∗p < 0.001, and ^∗∗∗∗p < 0.0001, two-way ANOVA with Dunnett’s multiple comparison. (C) Heat maps of traction stress (left) and FRET index of talin tension sensor (middle) with images of GFP-talin focal adhesions (right) for experiments with simultaneous measurement of traction force and force on talin on soft fibrinogen-coated silicone surfaces (1.4 kPa). Scale bars, 10 μm. (D) Quantification of average traction stress per cell. Values are means ± SEM. n = 7–10 cells per group from two independent experiments; ^##p = 0.0119, one-way ANOVA with Dunnett’s multiple comparison. (E) Quantification of average FRET index per cell. Values are means ± SEM. n = 7–10 cells per group from two independent experiments; ^#p = 0.0286 and ^##p < 0.001, one-way ANOVA with Dunnett’s multiple comparison. CTS indicates talin C-terminal control sensor expressed in WT cells. To see this figure in color, go online.

With accumulating evidence that the S243E mutation uniquely influences forces at the cellular scale, these effects might conceivably be due to recruitment of a greater number of activated integrins to the adhesions. To exclude such effects, we used a previously developed FRET-based tension sensor, which uses a FRET pair (eGFP and mRFP) separated by an elastic peptide linker that reports force/molecule (50). To assay force on talin, the central focal adhesion protein that links integrins to F-actin, we used the previously characterized tension sensor in which the module was inserted between the head domain that binds the integrin β tail and the rod domain that binds F-actin (30). Force on talin results in separation of the FRET pair and decreased FRET efficiency. These results were compared with the control FRET sensor in which the module is fused to the C-terminus; this construct localizes similarly but is not exposed to force. A previous study (30) validated the force sensitivity of the probe and showed that force on talin is diminished on soft substrates. We simultaneously measured force on talin (FRET index) and average traction stress (Fig. 3 C) on soft (1.4 kPa) silicone gels in the same cells. The S243E mutant showed the highest traction stress (Fig. 3 D) and the lowest FRET index (Fig. 3 E; Fig. S2 G), indicating the highest force on talin. On glass, which is very stiff, there was a trend toward higher talin tension in S243E cells, but it did not reach significance (Fig. S2, D and E). Measurement of focal adhesion size showed that the S243E displayed larger talin adhesions on soft gels but similar focal adhesion sizes on glass (Fig. S2, D and F). Together, multiple assays indicate that the S243E-activating mutation induces high stiffness responses on soft gels, thus appearing to sensitize cells to low forces.

Computational analysis of integrin mechanical properties

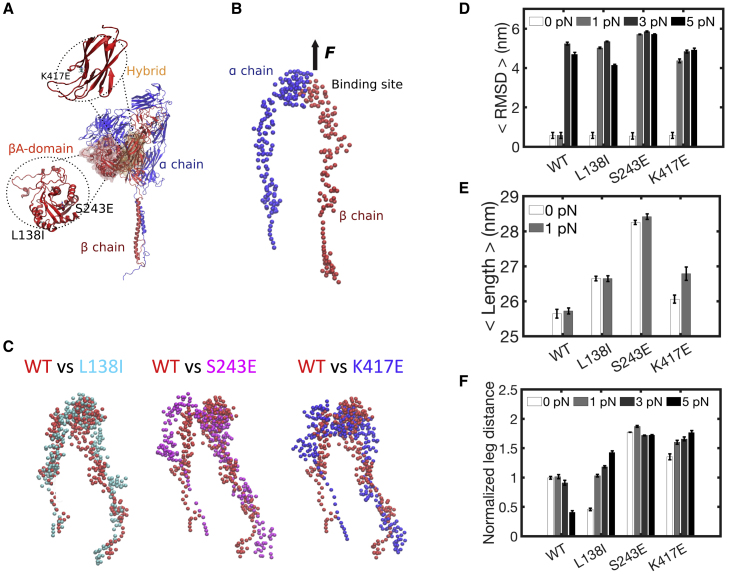
To investigate how integrin-activating mutations alter stiffness sensing at the length scale of individual integrins, we built computational simulations using a CG modeling approach built “bottom-up” from all-atom MD data converted into hENM (Fig. 4, A and B) (51). Integrins were represented by CG “beads” representing groupings of amino acids interconnected by effective harmonic and anharmonic potentials (Fig. 4 B), according to our recently developed method (34). Force, F, was applied to the ligand binding site in the β-headpiece (Fig. 4 B), and the subsequent changes for each mutant were evaluated (Fig. 4 C). We first used F = 0 pN as the starting point and F = 1 pN to mimic soft substrates/low force. Although catch bond behavior has not been analyzed for integrin avb3, studies of LFA1 (aLb2) detected catch bond in the low pN range (52), similar to the values used here. Simulations were then run for 1 μs. The RMSD of the integrin, computed as the averaged displacement of all the beads, was then evaluated for each mutant. All of the activating mutants exhibited increased displacement (movement away from the starting positions during the simulation) under this low force compared with WT, with the difference being somewhat higher for S243E relative to the other mutants (Fig. 4 D). S243E also presented significantly lower elastic constants and equilibrium separations between CG beads (Fig. S4, A–C), resulting in higher conformational flexibility (Fig. S4 D) and headpiece fluctuations (Fig. S4 E). Under 0 or low (1 pN) force, the mutant integrins were more extended than WT, with the mutant S243E showing the largest effect (Fig. 4 E). At higher forces (3 and 5 pN), all constructs showed significant increases in RMSD (Fig. 4 D).

Figure 4.

Computational analysis of integrin conformation. (A) Ribbon representation of bent integrin, with point mutations in the hybrid or βA domain highlighted. (B) hENM-extended integrin, with CG beads of α- and β-chain in red and blue, respectively. (C) Snapshots from timestep 10 of the simulations under 1 pN force, in which the mutants (cyan, magenta, and blue) are overlaid to WT (in red). (D) Average RMSDs for WT and mutant integrins at F = 0–5 pN with respect to WT integrin at F = 0 pN. (E) Average length of WT and mutant integrins at F = 0 and 1 pN. (F) Leg distance at F = 0–5 pN, normalized by WT integrin at F = 0 pN, computed as average of the COM distance between the two transmembrane helices. All mean values are computed between 30 and 300 timesteps of simulations. Values are means ± SEM; p < 0.0001. To see this figure in color, go online.

Integrin activation at the ligand binding site is communicated to the cytoplasmic domains via a long-range conformation change that separates the legs of the α and β subunits, leading to intracellular signaling (53). Separation of the legs is thus linked to activation. This distance, measured at the genu region, was highest for S243E under 0 pN force and did not increase further (Fig. 4 F; Fig. S4 D), consistent with the increased signaling under conditions of low force. S243E also showed increased force-extension relations (Fig. S4, F and G). To assess the validity of the tension-dependent CG configurations, we backmapped wild-type and S243E into atomistic models, which were energy minimized and equilibrated with all-atom MD in lipid membranes and then subjected to constant force steered MD simulations. These structures exhibited no steric clashes between lateral chains (Fig. 5, A–D), and S243E integrin extended more than WT under force (Fig. 5, E and F). Together, these results show that the activating integrin mutant S243E is uniquely responsive to soft substrates because of its enhanced protein extension and flexibility under low forces.

Discussion

The ability of cells to sense the mechanical properties of their extracellular matrix through integrins is critical for cell differentiation, migration, tissue mechanical homeostasis, and other functions (1, 2, 3, 4, 5, 6). Because of their critical role in creating the physical link between cells and extracellular matrix, integrins are a key component of matrix mechanosensing (1,15). But whether integrins are true mechanotransducers, that is, proteins whose conformational transitions under force are critical to signaling, is unknown. Published work has focused on talin (28), vinculin (16), FAK (47), YAP (54), or integrin type (17) as the main determinant of stiffness sensing and mechanotransduction. However, it is known that integrin-ligand bonds stabilize under moderate forces, exhibiting so-called catch bond behavior (23). A previous study using manganese to activate integrins suggested a role for integrin activation in stiffness sensing (21). We therefore investigated the role of integrin conformation in mechanosensing in greater detail.

Here, we report a correlation between integrin conformational flexibility at the single molecule level and cellular stiffness sensing. For the endothelial cells used in this study, the transition in spreading, traction force, and signaling is centered around 3–5 kPa, with those functions reaching a plateau above ∼10 kPa, similar to published data for other adherent, well-spread cell types (28,47,48). We also show that downstream mechanosensory pathways are impacted by this activation on soft gels, directly implicating integrin activation as a “mechanosensor.” However, examination of several β3 mutants revealed distinct effects on cellular mechanosensing that cannot be explained by differences in simple binding affinity, i.e., in the absence of force. Instead, the S243E mutant had strong effects in multiple assays despite an equivalent increase in the binding of soluble ligand (34).

Understanding these results requires analysis of effects of force on integrin conformation. However, this goal is not experimentally accessible. We therefore used our recently developed CG simulation approach to address how integrin conformation changes under tension. The benefit of the CG model is its ability to sample large conformational changes by explicitly incorporating breakage of effective bonds between CG beads from atomistic fluctuations. By taking interaction parameters directly from all-atom MD simulations, our hENM-based CG model implicitly incorporates the effects of single point mutations on residue motions into the strength and functional forms of the interactions between beads in the CG systems. Consequently, when force is applied between the ligand binding site and the cytoplasmic domain, all CG integrins examined here extend and rearrange their beads on the headpiece chains relative to lower legs. In particular, WT αVβ3 extended, consistent with increased activation of integrins under tension. By contrast, all of the activating mutations increased length in the absence of tension (“resting” length) with further increases upon application of tension, with the S243E mutant showing the largest effect. It is noteworthy that both experimental and simulation data show that the mutations induce a leftward shift in the force dependence, which is greatest for S243E.

Together, these results provide evidence that integrin conformational activation is not only force dependent but imparts mechanosensitivity that determines multiple signaling outputs, including cell spreading, YAP and FAK activation, and exertion of traction force. These effects fit well with the widely accepted model in which early integrin outside-in signaling promotes adhesion reinforcement to amplify subsequent events such as activation of tyrosine kinases, RhoA, and cell contractility, which increase additional downstream signals such as Yap/Taz (55,56). These findings thus indicate that integrin αVβ3 is a true mechanosensor. Many studies have implicated integrins in mechanosensory processes, and previous modeling work has identified that force accelerates hinge-angle opening from inactive to active states (57). However, the importance of force-induced deformation of the active and ligand-bound integrin in mechanosensing, meaning regulation of signaling pathways, has not, to our knowledge, been previously demonstrated.

Although not accessible by the methods used here, it seems likely that integrin catch bond behavior plays a significant role in these processes. Thus, the S243E mutant may convert to high affinity or long-lived states at lower force thresholds. In any case, bond lifetime information must be relayed to the cell interior to regulate signaling pathways. Integrins are well suited for this function as conformational effects are transmitted over long distances to the cytoplasmic domain. Leg separation distance may also be an important regulator of intracellular binding, and our modeling results indicate that the S243E mutant has the largest leg separation distance at 0 and 1 pN applied force. The interaction with talin is an obvious candidate, but contributions from other proteins that interact with integrin cytoplasmic domains are also likely. The ILK-PINCH-parvin complex and kindlins are also implicated in mechanosensing and could thus mediate effects. Understanding how alterations in integrin conformation affect both extracellular and intracellular binding interactions is the major direction for future work.

Author contributions

M.A.S., G.A.V., T.P.D., and T.C.B. designed the research. T.P.D., T.C.B., and S.J.A. performed the research. T.P.D., T.C.B., A.G., and G.A.V. contributed new regents/analytic tools. T.P.D. and T.C.B. analyzed the data. A.Y. and T.C.B. performed the backmapping. T.P.D., T.C.B., and M.A.S. wrote the article.

Editor: Philip LeDuc.