Optometry for a short-sighted microscope

Abstract

Evanescent-wave scattering is a topic in classical electrodynamics and in the study of colloidal particles near a boundary. However, how such near-surface scattering at subcellular refractive-index heterogeneities degrades the excitation confinement in biological total internal reflection fluorescence microscopy has not been well studied. An elegant theoretical work by Axelrod and Axelrod now addresses this very relevant question and reveals that—even when scattered—evanescent light preserves some of its surprising optical properties.

Evanescent-wave scattering is a topic in classical electrodynamics and in the study of colloidal particles near a boundary. However, how such near-surface scattering at subcellular refractive-index heterogeneities degrades the excitation confinement in biological total internal reflection fluorescence microscopy has not been well studied. An elegant theoretical work by Axelrod and Axelrod now addresses this very relevant question and reveals that—even when scattered—evanescent light preserves some of its surprising optical properties.

Main text

Total internal reflection fluorescence (TIRF) microscopy is a technique for imaging dynamic processes at or close to the basal plasma membrane of cells cultured on a glass substrate (1,2). The distinctive feature of TIRF is the confinement of fluorescence excitation to the cell-substrate boundary. Total reflection of an oblique, collimated laser beam sets up an inhomogeneous electromagnetic “evanescent” wave (EW), propagating along the interface and decaying rapidly in z. When scatterers are present above the interface, part of the energy of the EW is spatially redistributed. This is readily observed as far-field light detectable when looking from above at the objective lens (Fig. 1 A). In the absence of EW scattering, theory predicts a single exponential decay, $I\left(z;\vartheta \right)=I_{\circ }\left(\vartheta \right)\exp \left[-\text{z}/\delta \left(\vartheta \right)\right]$ with a penetration depth, $\delta \left(\vartheta \right)$ = [4(n₂² sin²$\vartheta$ − n₁²⁾]^−1/2 that depends on the wavelength λ, the refractive indices of the substrate and sample (n₁ < n_2), respectively, and on the polar beam angle $\vartheta$. $\left(\vartheta \right)$ is a figure of merit of how tight the light confinement near the reflecting interface is (3). It is also used in single-molecule (or single-organelle) studies to convert measured fluorescence intensities to axial fluorophores distance, either by taking epifluorescence/TIRF image pairs and rearranging the exponential scaling law to yield z = $\delta$ ln(I₀/I) or else by acquiring multiangle image stacks and making assumptions on the axial fluorophore distribution for the pixel- or object-wise localization of fluorescent objects (4, 5, 6).

Figure 1.

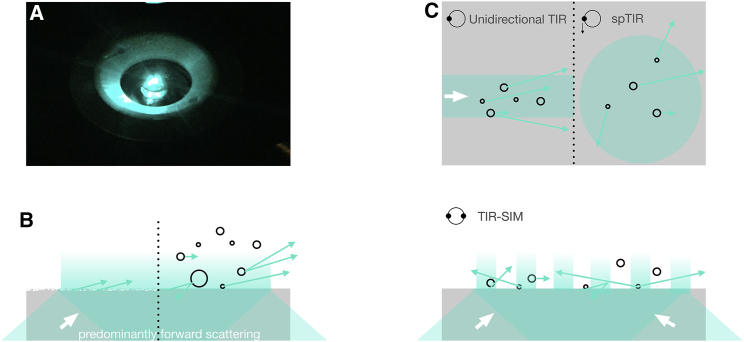
Evanescent-wave excitation and scattering. (A) Far-field excitation light is readily observed even with a clean coverslip in objective-type TIRF. Intensity enhanced for better visibility. (B) Surface and volume scattering are in forward direction. (C) Beam-spinning spinning total internal refection fluorescence, (top) or structured-illumination in a TIR geometry (bottom) allow for estimating the contribution of EW scattering to the image. To see this figure in color, go online.

EW scattering is one contributor to imperfect TIRF images

Calculated values of $\delta$ are often taken for granted and reported in the literature with astounding precision. Approaches and limitations for estimating the true value of $\delta$ at a given angle have been reviewed in this journal (3). In objective-type TIRF, in addition to a typically larger than calculated $\delta$, an additional far-field excitation component of 10–15% relative intensity is consistently being observed. Such long-range illumination can result from a number of factors, as follows: 1) $\vartheta$ is neither accurately nor precisely known (see (3,7) for angle calibration), and even perfect Gaussian laser beams have an intrinsic angular spread that translates into a continuous range of penetration depths ($\vartheta$±Δ$\vartheta$). Imperfect alignment, the limited repeatability of the beam scanner(s), and the imprecise placement of the sample with respect to the optical axis (a 0.5–1° tip-tilt angle is common) all introduce some percentage of error. More difficult to quantify, 2) stray light is generated along the excitation optical path. Glare from surfaces located in intermediate conjugate object planes (like the scanning mirrors in some arrangements) is imaged into the sample plane (8). Nonevanescent light also comes from the multiple optical interfaces inside the objective lens, and this contribution is increasingly relevant at small penetration depths (high $\vartheta$) when the excitation beam propagates very close to the objective’s boundary at ${\vartheta }_{\text{NA}}$; 3) a final source of unwanted excitation light is EW scattering from roughness and nonhomogeneities at the reflecting interface as well as from volume scattering within the sample (Fig. 1 B). The highly directional EW scattering at intracellular refractive-index boundaries is the topic of a theoretical study in this issue of the Biophysical Journal.

EW scattering in biological samples

Along with absorption, EW scattering is the mechanism that attenuates the reflected intensity in a technique called “frustrated” total internal reflection, which compares the incident and reflected intensities. EW scattering is being used for studying the size, shape, and density of colloidal (nano) particles (see e.g., (9, 10, 11) for recent work). It is also a known nuisance for adding unknowns in biological TIRF microscopy (8). Scattered excitation is abolished with nonlinear TIRF (12). But even with that, the field decay would not be monoexponential. The smooth decay of the EW intensity assumes a well-defined, flat, and homogenous rarer medium. Biological cells, cultured on a glass-bottomed dish, instead display shape and refractive-index heterogeneity (see (13,14) and references therein). Local adhesion sites, lipid rafts, membrane ruffles, and intracellular organelles result in refractive-index boundaries that produce a locally varying EW penetration depth and also result in predominantly forward scattering. In extreme cases, sites of locally high index can even disrupt total internal reflection (TIR) and generate intense beamlets of light. Considerable effort has been made to reduce the effects of directional EW scattering, but a detailed theoretical treatment relevant for biological TIRF microscopy has been missing.

In the current issue of the Biophysical Journal, Axelrod, father and son, investigate the very relevant question of the degradation of excitation confinement in several model situations approaching a biological “real-life” experiment (15). Their theory, based on a first-order perturbation approximation, is held against the exact result obtained from Mie theory for the well-known (but biologically irrelevant) case of a single scattering sphere. They then extend their treatment to scattering cylinders (assuming an object that varies little in z over the distance illuminated by the EW), and they ingeniously use a previously experimentally generated refractive-index map of an adherent cell (14) to evaluate how bad things can get in a “true” biological experiment. Making several assumptions and simplifications, their theory predicts a number of interesting and sometimes surprising features of scattered evanescent light, as follows: 1) in a typical adherent cell experiment, scattering is expected to not even double the effective penetration depth, i.e., despite the scattering, the overall excitation confinement will be maintained; 2) this feature is in part due to the observation that scattered light itself can be evanescent and nonpropagating, thus only adding a local intensity modulation but not extra far-field excitation components; and 3) as expected, EW scattering scales with the illuminated volume, and thus, it is reduced for illumination at very high polar angles (i.e., for shallow penetration depths $\delta$), but—of course—their theoretical treatment neglects objective-boundary effects and high-NA aberrations observed in a practical experiment.

The current work by Axelrod and Axelrod provides the theoretical framework for why biological TIRF microscopy still permits the selective observation of near-membrane processes even in scattering specimens like chromaffin cells. At the same time, the authors emit clear doubt as to the direct translation of EW-excited fluorescence intensities into axial fluorophore distances, which has important consequences not only for axial single-particle tracking, for measuring cell adhesion or membrane dynamics, and quantitation from multiangle TIRF data sets but also for phase imaging using tomographic approaches (16). Beyond classical axial localization studies, many applications in the TIRF field require a quantitative interpretation of data, e.g., multiangle (aka: multidepth) excitation TIRF, selective bleaching, or read out of fluorescence fluctuations in controlled volumes (see (3) for details). Variants of frustrated TIR make use of the spatial intensity distribution in the reflected beam. Here, EW scattering will result in depth heterogeneity and intensity gradients across the field of view that will invalidate the exponential power law underlying intensity quantifications. Adhesion sites, protein-rich lipid rafts, and interorganelle interfaces like endoplasmic reticulum-plasma membrane junctions in the near-membrane space will produce a heterogeneous, complicated, and space-dependent “local” penetration depth—thus, the concept of a uniform well-defined excitation volume needs to be revised and replaced by an effective and typically larger penetration depth with both intensity and depth “noise” superimposed.

Apart from a proper error propagation and extreme prudence when reporting absolute z-distances, we can draw five lessons from this new work of Axelrod and Axelrod:

• 1)It is better to spin around. Although not abolishing EW scattering, part of the excitation heterogeneity within the sampled volume is abolished by beam-scanning strategies that temporally average over scattering directions and “dilute” the effect of directional EW scattering.
• 2)Even in the near field, two photons are better than one. Albeit rarely used, nonlinear evanescent-field excitation abolishes fluorescence excitation by scattered light and reliably confines surface excitation.
• 3)Prism-type TIRF is not dead. An experimental validation of the effects predicted by the Axelrod and Axelrod article would require prism TIRF (17,18), in which the excitation and emission optical paths are separated, and high-NA effects inside the objective lens are absent, which will allow for studying EW scattering in isolation.
• 4)Use incoherent illumination. Part of the predicted fringes and intensity modulations come from interference. The use of incoherent light, e.g., from a light-emitting diode source (19) or by scrambling the laser beam (20), will provide a more uniform and homogenous EW illumination.
• 5)Better safe than sorry. Combining the optical sectioning of TIR excitation and large-field supercritical angle fluorescence detection (21) eliminates fluorescence from distant fluorophores incapable of emitting into “forbidden angles.” The use of evanescence both in excitation and emission better controls the probed volume (22,23). A direct comparison of images acquired with classical unidirectional TIRF and azimuthal beam-spinning TIRF will provide an effective means of estimating the build-up of scattered exaction across the field of view (Fig. 1 C, top). Likewise, as Axelrod and Axelrod point out in their discussion, the fringe pattern characteristic for structured-illumination TIRF can be used to tell apart confined and scattered excitation (Fig. 1 C, bottom).

Taken together, the article by Axelrod and Axelrod advances the field by going beyond earlier treatments of EW scattering in idealized geometries and providing a theoretical framework for predicting the impact on microscopic images of biological specimen. By generating testable predictions, their work will inspire future studies that link theory and experiments.

Editor: Gerhard Schutz.