Making sense of some odd ratios: A tutorial and improvements to present practices in reporting and visualizing quantities of interest for binary and count outcome models

Abstract

Objective:

Generalized linear models (GLMs) such as logistic and Poisson regression are among the most common statistical methods for modeling binary and count outcomes. Though single-coefficient tests (odds ratios, incidence rate ratios) are the most common way to test predictor-outcome relations in these models, they provide limited information on the magnitude and nature of relations with outcomes. We assert that this is largely because they do not describe direct relations with quantities of interest (QoIs) such as probabilities and counts. Shifting focus to QoIs makes several nuances of GLMs more apparent.

Method:

To bolster interpretability of these models, we provide a tutorial on logistic and Poisson regression and suggestions for enhancements to current reporting practices for predictor-outcome relations in GLMs.

Results:

We first highlight differences in interpretation between traditional linear models and GLMs, and describe common misconceptions of GLMs. In particular, we highlight that link functions A) introduce non-constant relations between predictors and outcomes and B) make predictor-QoI relations dependent on other covariates. Each of these properties causes interpretation of GLM coefficients to diverge from interpretations of linear models. Next, we argue for a more central focus on QoIs (probabilities and counts). Finally, we propose and provide graphics and tables, with sample R code, for enhancing presentation and interpretation of QoIs.

Conclusions:

By improving present practices in the reporting of predictor-outcome relations in GLMs, we hope to maximize the amount of actionable information generated by statistical analyses and provide a tool for building a cumulative science of substance use disorders.

Public Health Significance:

We propose several enhancements to current reporting practices for statistical analyses of binary outcomes (e.g., psychiatric diagnoses) and count outcomes (e.g., number of alcoholic drinks consumed). We encourage researchers to interpret results in terms of quantities of interest (probabilities for binary models, counts for count models) and provide a tutorial and R code for implementing these analyses. Doing so can provide richer information about a statistical analysis, make study results easier for research consumers to understand, and facilitate comparison of results across studies.

Many outcomes in addictions research have a discrete set of possible values; these outcomes might be either present or absent (e.g., a psychiatric diagnosis, a behavior) or they might be a count of discrete events (e.g., recent stressful life events, alcoholic drinks consumed). There is growing recognition that these outcomes are not accurately modeled by traditional linear regression, which has led to increased use of generalized linear models (GLMs) to accommodate the distributions characteristic of binary and count outcomes (Atkins, Baldwin, Zheng, Gallop, & Neighbors, 2013; Coxe, West, & Aiken, 2009; Neal & Simons, 2007). The most well-known GLMs in addictions research are logistic regression for binary data and Poisson regression for count data. Despite the broad accessibility of GLM methods via widespread software packages to model nonlinear data, software packages and online resources provide only basic guidance on reporting and interpreting parameter estimates from these models. In the current work, we aimed to highlight shortcomings of current practices for interpreting results of GLMs and to propose improvements to these practices.

The most commonly-reported quantity from a GLM is a transformed coefficient such as an odds ratio (OR) or an incidence rate ratio (IRR). The magnitude of the OR or IRR is often presented as representing the strength of association between a predictor and an outcome. However, commonly-taught heuristics for understanding these values are imprecise and can be misleading even in very common scenarios (Cummings, 2016; Schwartz, 2003; Persoskie & Ferrer, 2017; Andrade, 2015). The potential for misinterpretation stems largely from the fact that transformed coefficients in GLMs cannot be interpreted in the same manner as coefficients in traditional linear models.

Generalized Linear Models vs. Traditional Linear Regression

The central reason that current reporting practices for GLMs fall short is that when modeling binary or count outcomes, interpretation of individual model parameters is not analogous to the interpretation of traditional linear regression models. For the sake of clarity, we define traditional linear regression as a regression model that fits the expected value of an outcome to a linear function of substantive predictors, with no product or polynomial terms, assuming constant error variance. In traditional linear regression, model coefficients have a straightforward interpretation: for a 1-unit increase in a given predictor x, the conditional expectation of Y increases by β units, regardless of the levels of other covariates.

To highlight the differences between traditional linear regression and GLMs, we contrast the presentation of traditional linear model results with GLM results. A published study of adolescent drug use by the senior author (K. M. King & Chassin, 2008) reported both a traditional linear regression result and a GLM result. The authors reported a linear relation: …stressful life events at Time 2 predicted increases in...Time 3 externalizing (B = .10, p < .01). Whereas B represents a standardized coefficient in this paper, in the table beside it, an unstandardized coefficient of b = .02 is reported. A plain-language interpretation of this finding is that for each additional stressful life event, an individual’s externalizing score is estimated to increase by .02 points on average. Along with the intercept of the externalizing score, this interpretation is sufficient to characterize the relation between stressful life events and externalizing symptoms. This interpretation holds at any level along the continuum of stressful life events, and at all levels of other covariates.

Drawing from traditional linear regression practices, researchers tend to interpret a single regression coefficient in a GLM as a test of their research hypothesis: that is, the relation between a predictor and an outcome, controlling for all other covariates in the model. Take the following example of a typical interpretation of a GLM coefficient from the aforementioned study by the senior author: Along with family history of alcohol use disorder (OR = 2.07), the direct effects of Time 3 externalizing symptoms on drug dependence were significant and positive (B = 0.88, p < .001; OR = 3.55). A standard interpretation of the effect of externalizing symptoms might be that for a one-unit increase in externalizing symptoms, we expect the odds of drug dependence to be 3.55 times higher. Given the above information, the investigators state correctly that there is a positive relation between externalizing symptoms and drug dependence; but how should one contextualize and interpret this relation? What is the probability of a particular adolescent being diagnosed with drug dependence at follow-up? How much higher is that probability for an adolescent who has a family history of alcohol use disorder? Although the GLM fit by the authors can provide answers to these questions, they remain unanswerable for readers when provided only with the information above.

This is because there are several fundamental difficulties with converting an odds ratio of 3.55 into a plain-language interpretation in the same fashion as linear models. The clearest difficulty is that an odds ratio of 3.55 does not imply that the predicted probability of a drug use disorder increases by a factor of 3.55 for a change in externalizing symptoms. For GLMs, single coefficients do not directly describe relations with probabilities (note the introduction of the term odds), and heuristic understandings of single coefficients such as odds ratios can be misleading, as mentioned above. As an added complexity (which we explore in-depth in a later section), the impact of any one predictor in a GLM on an outcome A) is not constant and B) depends on the levels of all other predictors in the model. Given these properties, binary and count models require additional steps to draw out interpretable findings.

The Case for Presenting Quantities of Interest

One method for drawing out interpretable findings in spite of these complexities is to focus on Quantities of Interest (QoIs) in reporting GLM findings. As introduced by G. King, Tomz, and Wittenberg (2000), QoIs are broadly defined as the empirical quantities that research questions concern, which researchers choose based on substantive knowledge and prior research. On a broad level, transformed coefficients represent relations between predictors and mathematically convenient quantities that are not QoIs. While it is sometimes of interest to understand the relation between a predictor and, for example, the log-odds of an outcome, our work defines QoIs as those quantities which map onto colloquial understandings of alcohol and drug use outcomes. We specifically define probabilities (e.g., the probability of having a drug use disorder) as the relevant QoI for binary outcome models, and expected counts (e.g., the number of drug-using days in the past week) as the relevant QoI for count outcome models. In traditional linear models, interpretation of predictor-QoI relations is straightforward because there is a linear relation between the model coefficients and the QoI; coefficients from traditional linear models represent constant increases or decreases in the QoI. When models include a link function to address probability or count QoIs, there is no longer a direct linear relation between model coefficients and the QoI. Instead, model coefficients represent the relation between a predictor and a transformed version of the QoI. Even when we account for this transformation by exponentiating model coefficients, these quantities still do not represent changes in QoIs for changes in predictors. Shifting focus to QoIs has the potential to minimize the burden on readers who are currently forced to calculate their way through models in order to understand relations between predictors and QoIs. Moreover, established methods exist for converting results to the scale of the QoI, which can render results interpretable even to non-experts, and can be made available to substantive researchers without additional intensive statistical training.

Current Generalized Linear Model Reporting Practices

We reviewed the current state of GLM reporting practices to understand the extent to which researchers report QoIs vs. transformed coefficients. Though we derive these transformed coefficients in more depth later, we briefly describe the OR and IRR here. For binary outcome models, the most commonly reported metric of the predictor-QoI association is an OR. The odds of an event is the ratio of the probability of an event occurring to the probability of the event not occurring $\left(\frac{\pi }{1-\pi }\right)$, and the OR describes the change in odds for a change in a predictor; it is a ratio of ratios. For count models, the most commonly-reported statistic is the IRR, which involves the number of events predicted to occur per unit time, referred to as the incidence rate (λ). The IRR represents a multiplicative increase or decrease in the incidence rate based on a change in the predictor. Practically, both of these metrics are calculated by exponentiating the coefficient for the predictor in question, exp(β). As we will discuss in detail below, neither of these metrics is related to a constant change in the QoI. However, it is exceedingly rare that addiction researchers transform model results back into the QoI they set out to understand.

In a literature search of 52 articles selected randomly from five highly-cited journals from the addiction and psychology fields from 2007 to 2017, only 5% of articles interpreted results in terms of a QoI.¹ Most articles (69%) only described the GLM coefficient in terms of significance and direction, with no interpretation of the strength of the relation (e.g., x was positively related to Y, p < .05). About a quarter (27%) of coded articles interpreted the coefficient in question as a percentage increase in either the odds or the incidence rate (e.g., the odds of Y was 25% higher for those with risk factor x). Though there are many reasons for including or omitting model information in an empirical article, there is clearly room for including more information that might help readers contextualize findings from parameter estimates.

The Current Study

In order for results to be compared with one another across studies and eventually integrated into a cumulative science, we propose several attainable improvements to current practices in reporting and interpretation of GLMs for binary and count outcomes. In the current article, we aimed to 1) present a brief tutorial on common GLM methods in addiction research, and in doing so highlight common misconceptions about predictor-QoI relations in binary and count models, 2) provide guidelines for effective communication of binary and count model findings, and 3) present examples using real and simulated data along with sample R code.

A Brief Tutorial on Generalized Linear Models

The Case for using Generalized Linear Models

GLMs were developed primarily because imposing a direct linear relation between a predictor x and the expectation of an outcome Y in a statistical model is not always appropriate. When traditional linear models are used to fit outcome data generated by a nonlinear process, traditional regression assumptions of linearity and homoscedasticity can be violated. Fitting a traditional linear regression model to binary outcome data, for example, introduces dependence between the variance of the residuals and the expected value, violating the assumption of homoscedasticity (Cohen, Cohen, West, & Aiken, 2013). Violating these assumptions can lead to bias in standard errors (and therefore p values), as well as loss of statistical power (Atkins & Gallop, 2007; G. King, 1988). Recent work has called for more widespread use of the GLM to address these violations by formalizing implicit assumptions about the data generation process (Hilbe, 2011; G. King et al., 2000; Atkins & Gallop, 2007).

The defining feature of GLMs is the presence of a link function which can specify a nonlinear relation between a set of predictors and the conditional expectation of the outcome. The shape of the nonlinear relation depends on the link function chosen. By specifying a link function between the outcome and the model parameters, model assumptions may be made to fit the data much more closely, allowing for more accurate estimation of predictor-QoI relations (Aiken, Mistler, Coxe, & West, 2015). To facilitate the use of GLMs, resources such as tutorials (Atkins & Gallop, 2007; Atkins et al., 2013) and software packages have become widely accessible (R Core Team, 2013; Muthén & Muthén, 2016; StataCorp, 2019; IBM Corp, 2017). Though conducting GLMs for binary and count data has become a common practice, statistical methods training in graduate programs is limited, and innovations in statistical methods are often not widely disseminated to current practitioners (Aiken, West, Sechrest, & Reno, 1990; Aiken, West, & Millsap, 2008; K. M. King, Pullmann, Lyon, Dorsey, & Lewis, 2019). We provide a brief tutorial here, primarily in order to emphasize issues in interpreting GLMs that are not present for traditional linear models. We limit our focus to the three most widespread models, logistic regression for binary outcomes and Poisson and negative binomial for count outcomes, though several others are sometimes used in the empirical literature as well (probit for binary outcomes, beta-binomial, quasi-Poisson, zero-inflated, and hurdle models for counts). We do so to introduce these concepts for models most relevant in addictions research, though we note that many of the concerns we describe here apply similarly to these other GLM approaches.

The Logic of Generalized Linear Models

To explain the logic of GLMs, we begin by recalling the equation for traditional linear regression using a single predictor:

$$\mathbb{E}[Y\mid x]={\beta }_0+{\beta }_{1}x,$$ (1)

Here, β₀ is the intercept, β₁ is the coefficient on x, and $\mathbb{E}[Y\mid x]$ is the expected value of an outcome Y given the predictor x. Compare the equation above with the following mathematical formulation for a one-predictor GLM:

$$g(\mathbb{E}[Y\mid x])={\beta }_0+{\beta }_{1}x.$$ (2)

Above, g(·) is the link function (any invertible function) that relates predictors linearly to a transformed version of our QoI. In this sense, g(·) allows the predictors to relate to this quantity in a linear fashion similar to Equation 1. However, this similarity to Equation 1 can cause confusion when understanding results of GLMs. In Equation 2, it is easy to lose sight of the idea that the quantity $g(\mathbb{E}[Y\mid x])$ is not typically our QoI (i.e. $\mathbb{E}[Y\mid x]$), but rather a transformation of this quantity that permits the model to be estimated conveniently using a linear framework. For example, $\mathbb{E}[Y\mid x]$ might be a probability, while $g(\mathbb{E}[Y\mid x])$ would represent a logit value. Although we can state that each one unit increase in x corresponds with a β₁ unit increase in $g(\mathbb{E}[Y\mid x])$, additional steps must be taken to recover the direct relation between x and the QoI (i.e. $\mathbb{E}[Y\mid x]$).

To do so, one must “back-transform” the model using an inverse link function, which typically reflects some nonlinear transformation of the coefficients produced by the model. We can express this inverse link function as:

$$\mathbb{E}[Y\mid x]=g^{-1}\left({\beta }_0+{\beta }_{1}x\right).$$ (3)

This flexible approach enables analysts to describe relations with a broad range of outcome variables. In all but the identity link case², this involves applying a nonlinear transformation to the regression coefficients to obtain estimates in the scale of QoIs.

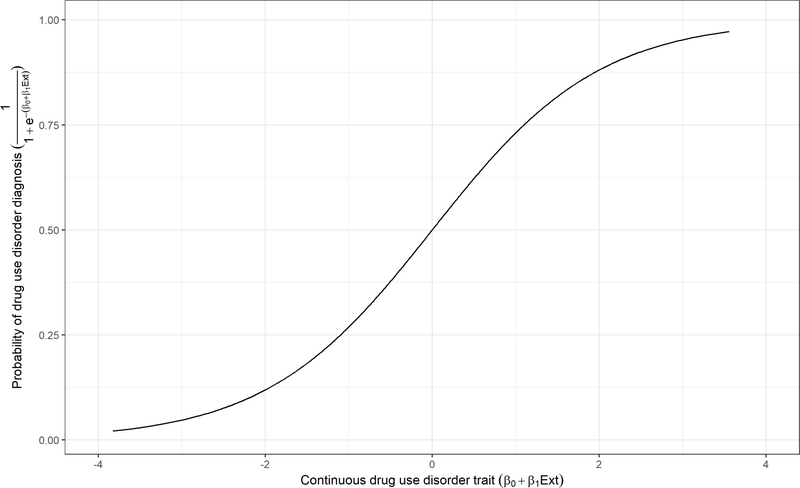
One way to conceptualize this distinction is that the estimated model describes how the predictors relate linearly to a continuous tendency or quantity, whereas the inverse link function maps this continuous tendency onto possible values in the space of QoIs. Thus, the link function formalizes our assumptions about the process that generates our data. For the sake of explanation, we take our running example of logistic regression. In logistic regression, we assume that whether an event occurs or not is in fact due to a continuous quantity representing levels of a continuous trait, and that values above a certain threshold result in an event occurring. Figure 1 demonstrates this relation graphically. In the aforementioned example, an individual’s tendency toward drug use disorder (a theoretical continuous quantity) due to greater externalizing symptoms might determine whether he/she receives a diagnosis of drug use disorder (a binary outcome). In observing whether an individual has received a diagnosis, we do not observe the “true” continuous level of disorder. However, we can assume that what we have measured about this individual (e.g., level of externalizing problems) would relate to his/her underlying level of drug use disorder, and thus to whether he/she meets criteria for the disorder. Finally, we can use the logit function to transform the expected level of the “level of disorder” into a probability of drug use disorder diagnosis. Thus, in a sense, GLM coefficients can be thought of as representing a nonlinear relation between a predictor and an expected outcome via a continuous variable.

Figure 1.

Demonstration of logistic link function mapping a continuous trait into probability space (0 to 1).

Note: Ext = externalizing problems. Figure 1 depicts the relation between a continuous trait representing drug use disorder symptoms and the probability of drug use disorder from a logistic regression model. The continuous trait is a linear function of externalizing problems in this example. The value of this continuous trait is entered into the logistic function $\left(\frac{1}{1+\exp (-x)}\right)$, which maps these x values to y values between 0 and 1. Although these data are simulated, hypothetical labels are provided to match the running example.

In the sections that follow, we explore the two GLMs most commonly used in research on substance use disorders, explaining the logic of each model and highlighting two properties of these models that make interpretation of these models diverge from interpretation of traditional linear models. The formal reasons for this divergence are that typically-reported transformed versions of parameters, such as ORs and IRRs, A) do not represent constant changes in QoIs, and B) do not take into account that any particular predictor-QoI relation in a GLM is conditional on the levels of other covariates. By conditional, we mean that predictors in the same model are functionally dependent on one another in the context of their relation with an outcome: that is, the relation between any predictor x_j and the outcome depends on the level of any other predictor x_k (and vice versa). Referring back to our previous example, property A indicates that one’s probability of drug use diagnosis does not change by a constant value across the range of externalizing problems, whereas property B means that the strength of the externalizing-drug use disorder relation differs based on whether a person has a parent with an alcohol use disorder. Though predictor-QoI relations in a traditional linear regression context are described as the independent contribution of a single variable in a multivariate equation, these relations in GLMs are not conditionally independent from one another as they are in traditional linear regression. Thus, the impact of a predictor x_j on the expected value of the outcome varies based on the level of any other predictor x_k in the same model (Tsai & Gill, 2013; McCabe, Halvorson, King, Cao, & Kim, under review). In the sections that follow, we work through the most common GLMs in the study of drug and alcohol use disorders with two goals: to review and build intuition on the models themselves and to explicate properties A and B for each class of models.

Binary Outcome Models

Binary outcome models are used to predict whether an outcome is likely to occur based on a set of predictors. The QoI researchers tend to be most interested in is the predicted probability of an occurrence (e.g., of a disease) for individuals with a set of characteristics. More specifically, many research questions focus on how strongly the change in a predictor affects the probability of an outcome occurring. For the sake of explanation, we will consider a hypothetical study with the same variables as the K. M. King and Chassin (2008) example in the second paragraph of the Introduction.

The Logistic Model

The logistic regression model relates predictors to the probability of an event occurring, and is formulated with a logit-link. Logistic regression is the most commonly used model of binary outcomes in the social sciences.³ Our hypothetical study aims to predict the probability of a drug use disorder diagnosis from an individual’s level of externalizing problems. As the target QoI is a probability, we give $\mathbb{E}[Y\mid x]$ the label π: The function ln $\left(\frac{\pi }{1-\pi }\right)$ is referred to as the logit function.

$$\mathrm{logit}(\pi )=\ln \left(\frac{\pi }{1-\pi }\right)={\beta }_0+{\beta }_{1}x.$$ (4)

To obtain π, we apply the inverse of the logit function (also known as the logistic function, $\frac{1}{1+\exp (-x)}$) to each side of the equation:

$$\pi ={\mathrm{logit}}^{-1}\left({\beta }_0+{\beta }_{1}x\right)=\frac{1}{1+\exp \left(-\left({\beta }_0+{\beta }_{1}x\right)\right)}.$$ (5)

To describe the simplest mathematical relation between a one-unit change in x (externalizing problems) and a corresponding change in the probability of drug use disorder, we expand the logit function for ease of derivation. Suppose we wish to write Equation 5 for a specific value of x we will call a. We can express ${\pi }_a=\mathbb{E}[Y\mid x=a]$ and $\mathrm{odds}(a)=\frac{{\pi }_a}{1-{\pi }_a}$. Notice that β₁ is equivalent to taking the difference in log-odds for a 1-unit change in x.

$$\begin{gathered} \ln \left(\frac{{\pi }_{a+1}}{1-{\pi }_{a+1}}\right)-\ln \left(\frac{{\pi }_a}{1-{\pi }_a}\right)=\left({\beta }_0+{\beta }_1(a+1)\right)-\left({\beta }_0+{\beta }_{1}a\right) \\ ={\beta }_0+{\beta }_{1}a+{\beta }_1-{\beta }_0-{\beta }_{1}a \\ ={\beta }_1. \end{gathered}$$ (6)

Using this finding, we can see how a 1-unit change in x affects the odds of an event occurring:

$$\begin{gathered} {\beta }_1=\ln \left(\frac{{\pi }_{a+1}}{1-{\pi }_{a+1}}\right)-\ln \left(\frac{{\pi }_a}{1-{\pi }_a}\right) \\ =\ln (\mathrm{odds}(a+1))-\ln (\mathrm{odds}(a)) \\ =\ln \left(\frac{\mathrm{odds}(a+1)}{\mathrm{odds}(a)}\right) \\ \exp \left({\beta }_1\right)=\frac{\mathrm{odds}(a+1)}{\mathrm{odds}(a)}=\text{odds}\text{ratio}(\text{OR}). \end{gathered}$$ (7)

In the context of logistic regression, the odds ratio describes the relation between the odds of an outcome for a given predictor value versus the odds of the outcome when incrementing the predictor by one.⁴ In contrast, another metric of the strength of a predictor-QoI relation might be the ratio of the probability of an outcome for one predictor value to the corresponding probability for incrementing the predictor; this value is called the rate ratio. An odds ratio is said to be a close approximation for the rate ratio when probabilities are very small (Hosmer & Lemeshow, 2000). By this heuristic, an odds ratio of 2.0 for a base rate of 1% would mean that for each increase in x, the probability of Y doubles from 1% to 2% to 4%, and so on. In some research domains, this is a tenable assumption: in the study of rare medical conditions, base rates are small and thus odds ratios approximate a percentage increase in probability well. In research on alcohol and drug use, this is often an unreasonable assumption: an adult who drinks socially might have a 60% chance of drinking on a given Friday. As base rates increase, the odds ratio increasingly overestimates the percentage increase in probability (Zhang & Yu, 1998). Even in low-base-rate situations, it is difficult to argue that reporting the odds ratio is preferable if the rate ratio is calculable. Thus, presented in isolation (i.e., without the magnitude of probabilities), an odds ratio provides minimal information regarding change in the magnitude of a predicted probability.

The nonlinearity introduced by the logit function has two consequences: A) increases in the QoI of probability are not constant, and B) predictor-QoI relations in a multivariate model are conditional on the levels of all other predictors. Since the logit-link function is nonlinear – predictors relate to probabilities through a logarithmic function - the increase in the probability of an event for a 1-unit increase in x_j is not constant across the range of x_j. Therefore no single number directly describes the change in probability for a change in x_j for all x_j. The logit-link function used in logistic regression also introduces conditionality of predictor-QoI relations to the model.

Until now, we have considered only one-predictor models; however, it is rare in empirical research to examine single-predictor models. Most often, researchers are interested in the simultaneous relations of several predictors to an outcome, or at the very least, controlling for some covariates in quantifying a single predictor-QoI relationship. Including multiple predictors introduces complexity even in the traditional linear model: each relation is now interpreted in the context of controlling for the levels of all other predictors. Moreover, product terms or nonlinear relations can quickly complicate model interpretation. GLMs add another layer of complexity to multivariate research in that property B (conditionality of predictor-QoI relations) applies as well. Even so, we argue that a focus on QoIs can lend rich information both on the general utility of a model and on the relative impacts of predictors in complex models.

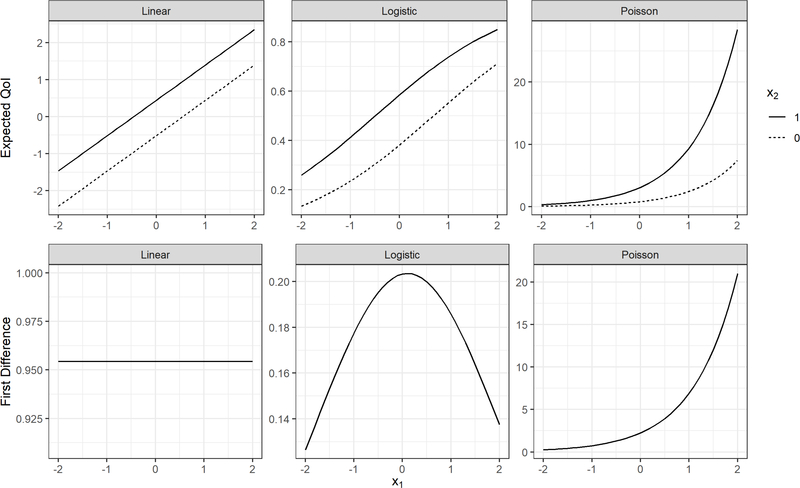
This conditional nature is depicted in Figure 2, for which the top panel shows the expected value for several types of models across levels of a continuous predictor x₁ and a categorical predictor x₂. x₁ consists of draws from a standard normal distribution and x₂ is a dichotomous dummy variable with a 50% chance of being a 1. Graphically, if the relation of x₁ on Y is independent of x₂, then the slope of x₁ when x₂ = 0 should be parallel to the slope of x₁ when x₂ = 1. In the left-hand linear graph, for example, we see that these two relations are indeed independent, as demonstrated by the lines being parallel. However, for the logistic and Poisson examples, the curve of each line makes it visually clear that a one-unit increase in x₁ does not lead to a constant increase in Y. The bottom panel of Figure 2 illustrates this even more directly by displaying the differences in expected value between x₂ = 1 and x₂ = 0, across the range of x₁. For traditional linear regression, whether x₁ is large or small, the difference between the expected values when x₂ = 0 and x₂ = 1 is the same value (0.95). By contrast, first difference values varied markedly in the logistic and Poisson cases. For logistic regression, the first difference is smallest when x₁ approaches its maximum or minimum value, and is largest when x₁ is close to its own mean. In the Poisson example, the first difference across values of x₂ grows increasingly larger as x₁ increases due to the exponential nature of the model.⁵ Thus, even though product terms are not specified, predictor-QoI relations in logistic regression (and Poisson regression) are conditional on levels of other predictors.

Figure 2.

Expected values and first differences for linear, logistic, and Poisson regression models with two predictors.

Note: Y-axis units in all graphs represent QoIs. x₁ was simulated as a standardized continuous predictor and x₂ as a dummy-coded predictor with P(x₂)=0.50. In traditional linear regression, QoI is the expected level of Y. In logistic regression, QoI is the probability of Y occurring. In Poisson regresion, QoI is the count of events. The top panel shows expected QoI values plotted across x₁ and x₂, while the bottom panel shows the differences in expected value between x₂ = 1 and x₂ = 0 (the difference between categories given x₂ is a dummy variable).

Count Models

The Poisson Model

Poisson models are the basic model used to characterize count distributions, and are based on the idea that the likelihood of any single event occurring is constant per unit time. Modifying our hypothetical study slightly, let’s say we are now interested in predicting the number of drug using days in the past week from externalizing problems. The Poisson model for count outcomes is formulated as follows. The link function for Poisson regression is a logarithm function:

$$\ln (\mathbb{E}[Y\mid x])={\beta }_0+{\beta }_{1}x,$$ (8)

and the expected count from the model is commonly given the label λ:

$$\ln (\lambda )={\beta }_0+{\beta }_{1}x.$$ (9)

To obtain estimated counts, we use the inverse of the logarithm function (the exponential function) to connect β values to the expected count:

$$\lambda ={\ln }^{-1}\left({\beta }_0+{\beta }_{1}x\right)=\exp \left({\beta }_0+{\beta }_{1}x\right).$$ (10)

The strength of a predictor’s impact on model-expected counts is typically described via an incidence rate ratio. Let ${\lambda }_a=\mathbb{E}[Y\mid x=a]$ and a be a value of x. Similar to logistic models, β₁ is equivalent to taking the difference in the log of expected counts for a 1-unit change in x.

$$\begin{gathered} \ln \left({\lambda }_{a+1}\right)-\ln \left({\lambda }_a\right)=\left({\beta }_0+{\beta }_1(a+1)\right)-\left({\beta }_0+{\beta }_{1}a\right) \\ ={\beta }_0+{\beta }_{1}a+{\beta }_1-{\beta }_0-{\beta }_{1}a \\ ={\beta }_1. \end{gathered}$$ (11)

From here we can see how a 1-unit change in x affects the ratio of expected counts:

$$\begin{gathered} {\beta }_1=\ln \left({\lambda }_{a+1}\right)-\ln \left({\lambda }_a\right) \\ =\ln \left(\frac{{\lambda }_{a+1}}{{\lambda }_a}\right) \\ \exp \left({\beta }_1\right)=\frac{{\lambda }_{a+1}}{{\lambda }_a}=\text{incidence}\text{rate}\text{ratio}(\mathrm{IRR}). \end{gathered}$$ (12)

The IRR thus describes the proportional change in incidence rate when increasing x by one unit (e.g., the multiplicative change in number of days of drug use predicted for an increase in externalizing).

Similar to the logit-link function, since the log-link function is not linear, the increase in expected count for a 1-unit increase in x is also not linear (see Figure 2). In the case of multiple predictors, Figure 2 shows as well that the effect of a predictor x₂ on the expected count is conditional on x₁, noting that across the range of x₁, the effect of x₂ becomes larger in this case. The non-parallelism of the lines representing x₂ = 1 and x₂ = 0, as well as the non-constant differences in the bottom panels, show this conditional nature.

Poisson models assume that for a given time period, there is a given expected count of events λ such that we expect λ events to occur during that time period, with a variance of λ:

$$\mathrm{Var}(Y\mid x)=\lambda .$$ (13)

Though the use of a single parameter (λ) makes Poisson models straightforward to estimate, the assumption that the mean number of events is identical to the variance of the number of events is in practice often untenable. To address this shortcoming of Poisson models, negative binomial models were developed to allow for the variance of the expected count to exceed the mean.

The Negative Binomial Model

The negative binomial model is a generalization of the Poisson model, in which an extra parameter is added to account for a variance that exceeds the mean (often referred to as overdispersion). Poisson models fit to count data very often output a variance estimate that is much lower than the conditional variance of the outcome. Though several parameterizations of this model exist, one such formulation (NB2) is used in most software GLM implementations and is a mixture of Poisson distributions where λ is drawn from a gamma distribution (Hilbe, 2011).

In spite of the underlying gamma distribution, the mean model of the negative binomial distribution is identical to that of a Poisson distribution: a single parameter, λ, describes the expected count. The variance of the distribution, however, is allowed to vary as a function of the mean:

$$\mathrm{Var}(Y\mid x)=\lambda +\frac{1}{r}{\lambda }^2,$$ (14)

where r is an overdispersion parameter. As r approaches infinity, the negative binomial model reduces to the Poisson model.

Because the negative binomial model is a generalization of the Poisson model, the properties of non-constant first differences and conditionality of predictor-QoI relations continue to apply to negative binomial regression.

Recommendations for Reporting Generalized Linear Model Results

In light of the shortcomings of single coefficients, and the properties of A) non-constant first differences and B) conditionality of predictor-QoI relations, there is room for improvement in the presentation of GLM results. In the following section, we propose several improvements upon current best practices for presenting predictor-QoI relations in binary and count models.

To illustrate suggested reporting for models, we simulated 500 observations with a binary response variable (Y) and two weakly correlated (r = −.10) continuous linear predictors of Y, x₁ and x₂. Both x₁ and x₂ are normally distributed with a mean of 0 and a variance of 1. Observed values of Y are generated from a binomial distribution, where $\mathrm{logit}\left(\mathbb{E}\left[Y\mid x_1,x_2\right]\right)$ is a linear combination of predictor values, in this case,

$$\mathrm{logit}\left(\mathbb{E}\left[Y\mid x_1,x_2\right]\right)={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2,$$ (15)

where β₀ = 0, β₁ = −2, and β₂ = 1. Running a logistic regression, we estimate the parameters (see Table 1). We use this model and these data as a running example through the remainder of this section. Data and code to generate examples below are publicly available at https://github.com/mhalvo/glm_interpret.

Table 1.

Logistic regression model for simulated binary outcome data with two continuous predictors.

	Coefficient	Std. Error	OR [95% CI]
intercept	−0.01	0.12
x 1	−.1.65	0.16	0.19 [0.14, 0.26]
x 2	0.96	0.14	2.61 [2.02, 3.44]
Observations	500

Note: OR = odds ratio.

Graphical Presentation of Results

Presenting results graphically allows readers to quickly grasp and develop intuition about a scientific finding, and can display many dimensions of information simultaneously (Tufte, 2001). This may be especially helpful in the case of GLMs, as effects cannot be informatively boiled down to a single parameter, as in traditional linear regression. An odds ratio of 2.0, for example, could have infinite two-dimensional graphical representations depending on base rates and other covariates, whereas a traditional linear regression coefficient of 2.0 will always define a line with a certain slope. However, graphics of GLM effects are rarely found in the literature. Few articles (12%) from the surveyed literature mentioned earlier included any graphical representation of findings, and even fewer (10%) included any graphic on the scale of QoIs.

To make results easier to understand, we recommend 1) that results of GLM models should be presented graphically in terms of QoIs, and 2) that covariate values should be chosen thoughtfully and reported clearly. Requiring readers to perform mental algebra or other mathematical transformations places unnecessary burden on readers and distracts from interpretation of substantive findings (G. King et al., 2000; Tufte, 2001). Presenting model results graphically can obviate the need for research consumers to have a deep understanding of particular statistical methods in order to understand answers to research questions. Thus, plotting model-expected outcome values across different levels of predictors may help facilitate intuition and represent complex nonlinear relations in an intuitive manner that scientists and practitioners alike can understand.

Creating these graphics can be accomplished by 1) fitting models as usual, 2) choosing covariate values at which to probe the model and plugging these values into models to generate point estimates, and 3) creating confidence intervals around these expected values. The first two steps are readily accomplished using available software functions, and we accomplish the third step using a bootstrapping approach. Although many readers may be familiar with bootstrapping approaches to testing mediation (MacKinnon, Fairchild, & Fritz, 2007), bootstrapping represents a broad range of resampling methods that have many applications. Here, we used a non-parametric bootstrap approach (Raykov, 1998; Preacher & Selig, 2012) to generate a sampling distribution of model parameters, from which we generated confidence intervals for expected values. In brief, the non-parametric bootstrap resamples the data with replacement to generate a distribution of plausible alternate datasets. The same model is fit for each dataset, resulting in slightly different coefficients for each. Hypothetical predictor values are then entered into these plausible models, and QoIs are estimated. The 2.5th and 97.5th percentiles of these QoI estimates create a confidence interval around the point estimate. For example, if 10,000 models were estimated, and estimates of the outcome were rank-ordered, the 250th and the 9,750th estimates would define the lower and upper bound of a 95% confidence interval. Although other methods exist for incorporating uncertainty into model estimates (e.g., the delta method, using the asymptotic covariance matrix to generate estimates), the bootstrap approach is consistent with the work of G. King et al. (2000) and has the advantage of being generalizable to a wide range of models, including those with link functions that are not monotonic. We provide example R code for generating estimates and graphics online on the aforementioned GitHub site.

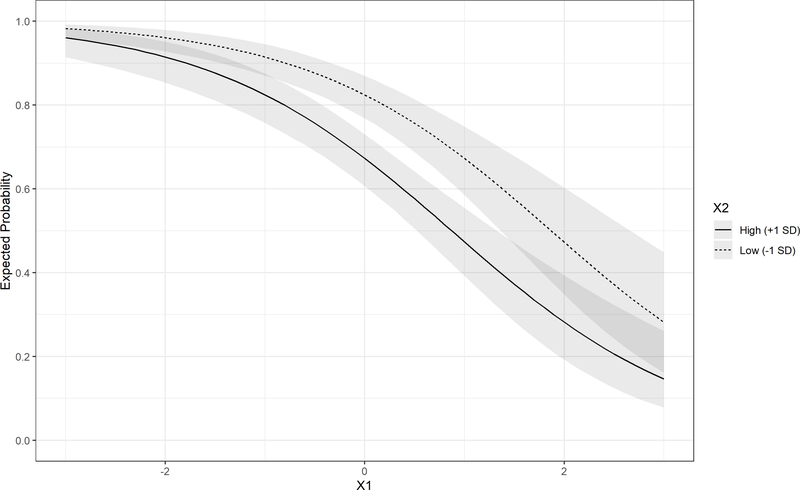
For our simulated example, the relation between x₁ and the probability of Y, controlling for x₂, is depicted in Figure 3. Inspection of Figure 3 immediately makes clear that as x₁ increases, the probability of Y decreases. Moreover, Figure 3 shows that the effect of x₂ on the probability of Y is smaller for high and low values of x₁ and larger at intermediate values of x₁. Figure 3 also allows readers to obtain a rough estimate of the probability of Y at any value of x₁ for either low or high x₂. Though graphics can be very informative, they can only contain so much information before they begin to appear overly busy. Thus, we propose supplementing graphics with tables that highlight expected QoIs at various covariate values.

Figure 3.

Probability of Y by x₁ and x₂ for simulated data example.

Note: Shaded regions represent 95% bootstrapped confidence intervals for expected values.

Tables that Highlight Covariates and Quantities of Interest

Another solution to the paucity of information communicated by transformed coefficients is to present tables of QoI values at combinations of covariates and focal predictors that are substantively interesting (see Table 2 for an example). Fitted models are readily able to output direct model-based predictions of these QoIs, and bootstrapping confidence intervals around these predictions is straightforward to implement. Presenting these tables in terms of QoIs can enable readers to compare changes in a focal predictor at multiple levels of other covariates. We propose that researchers should choose their covariate values thoughtfully and describe QoIs at several levels of covariates of interest.

Table 2.

The probability of Y across levels of x₁ and x₂.

	x 2
x 1	Low (−1)	Mean	High (+1)
Low (−1)	.66 [.57, .75]	.84 [.78, .89]	.93 [.89, .96]
Mean	.27 [.21, .33]	.50 [.44, .56]	.72 [.65, .79]
High (+1)	.07 [.04, .10]	.16 [.11, .21]	.33 [.24, .43]

Note: Values in square brackets are bootstrapped 95% confidence intervals.

Even given a focus on QoIs, currently-used tables can provide a broad estimate of magnitude and direction of an effect, and can be useful to reference when building successive models. We do not believe these tables should be discarded; however, in addition to these broad estimates of strength of effect, presenting several model-based estimates allows other researchers to understand effect sizes in terms of QoIs and to compare results across studies with similar outcome measures. Despite the advantages of graphical approaches, they can be difficult to glean individual estimates from; thus, tables and graphics can complement each other and allow the researcher to effectively communicate a scientific story.

Returning to our simulated-data example, we report the probability of Y at low, mean, and high levels of both x₁ and x₂ in Table 2. The information in Table 2 supplements the graphical information from Figure 3 by probing at an additional level of x₂. Even in our simple model, this additional information allows Figure 3 to remain clean and interpretable. These probed values can also allow researchers to highlight salient or substantively-important contrasts, or to probe at covariate values which aren’t represented in a graphic.

Informative in-Text Reporting

Given the enhanced granularity of information available from the graphics and tables described above, additional in-text explanation can allow researchers to make the results of their models clear and concrete to readers. In particular, reporting QoIs at specific covariate levels can give enough information for readers with substantive knowledge to contextualize results.

For our running example, we might describe the model results as follows: The probability of Y decreased across the range of x₁ (from .84 at 1 SD below x₁’s mean to .16 at 1 SD above x₁’s mean), holding x₂ at its mean. While the probability of Y was generally higher for higher values of x₂, changes in the probability of Y for a given change in x₂ differed across levels of x₁ (see Table 2). For observations low on x₁, the change in the probability of Y for a change in x₂ from mean to high was 9 percentage points (84. to .93). For observations high on x₁, the change in the probability of Y for a change in x₂ from mean to high was 17 percentage points (.16 to .33).

Results of a Count Model: An Empirical Example from a Published Study

Next, we turn to an empirical example using data from an unpublished study of alcohol and impulsive personality traits. We fit a Poisson model predicting the number of negative alcohol-related consequences in the past year. Data were collected from 491 college students (mean age 19.3; 56.4% female; 55.0% Caucasian; 33.2% Asian/Pacific Islander) enrolled in lower-level courses at a university in the Pacific Northwest. Participants completed a computerized survey and received course extra credit. The study was reviewed and approved by the university’s Institutional Review Board, and permission to share de-identified data was obtained from the university human subjects division. Our hypothetical research question concerns the impact of positive urgency (the tendency to act on impulse when experiencing positive emotion) on consequences resulting from alcohol use, controlling for gender.

Positive urgency, premeditation, and sensation seeking are each impulsive personality traits from the UPPS-P measure of impulsive personality traits (Lynam, Smith, Whiteside, & Cyders, 2006). Each scale was a mean score of 12 items, with item anchors of 1=Disagree Strongly to 4=Agree Strongly. Individuals high on positive urgency report acting rashly when experiencing extreme positive emotion; those high on premeditation report planning ahead more often; and those high on sensation seeking report seeking out risky or intensely pleasurable experiences more often. Negative alcohol consequences included self-reported past-year behavioral consequences of alcohol use such as hangovers, blackouts, missed classes, or interpersonal conflict, and higher numbers represent a greater count of consequences (Hurlburt & Sher, 1992; Mallett, Bachrach, & Turrisi, 2008). Gender was self-reported by participants. A sample results section, following our own recommendations, might read as follows:

Results.

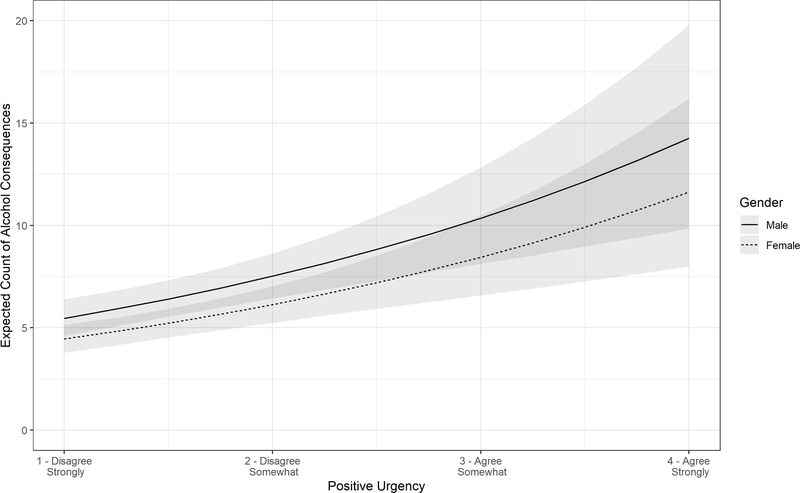
Positive urgency was positively related to the count of alcohol consequences experienced in the past year, such that each one-unit increase in positive urgency was associated with a 38% increase in the rate of alcohol consequences (IRR = 1.38, 95% CI = [1.31, 1.45]) controlling for planning and gender (see Table 3). As seen in Figure 4, the predicted count of consequences increased more rapidly on the high end of the positive urgency scale than it does at the low end of the scale. Whereas an increase in positive urgency from 1 to 2 was associated with an increase of 2.1 consequences for men (1.7 for women), an increase in positive urgency from 3 to 4 was associated with an increase of 3.9 consequences for men (3.2 for women). Overall, women experienced 18% fewer alcohol consequences than men (IRR = 0.82, 95% CI = [0.75, 0.88]). Table 4 shows the expected level of alcohol consequences across levels of gender and positive urgency; the reader is encouraged to examine the table to understand the effect of positive urgency on alcohol consequences, accounting for gender.

Table 3:

Poisson regression model of negative alcohol consequences.

	Coefficient	Std. Error	IRR [95% CI]
intercept	2.10	0.16
Gender (1=female)	−0.20	0.04	0.82 [0.75, 0.88]
Positive Urgency	0.32	0.03	1.38 [1.31, 1.45]
Planning	−0.27	0.03	0.76 [0.72, 0.81]
Sensation Seeking	0.15	0.03	1.17 [1.11, 1.22]
Observations	423

Note: IRR = incidence rate ratio.

Figure 4.

Expected count of alcohol consequences by positive urgency and gender.

Note: Shaded regions represent 95% bootstrapped confidence intervals for expected values.

Table 4:

Expected count of alcohol consequences across levels of gender and positive urgency.

	Gender
Positive Urgency	Female	Male
1 - Disagree Strongly	4.45 [3.78, 5.16]	5.45 [4.62, 6.36]
2 - Disagree Somewhat	6.12 [5.25, 7.04]	7.51 [6.44, 8.63]
3 - Agree Somewhat	8.43 [6.58, 10.56]	10.33 [8.07, 12.84]
4 - Agree Strongly	11.60 [7.98, 16.20]	14.23 [9.77, 19.80]

Note: values in square brackets are bootstrapped 95% confidence intervals.

Despite no product term being specified, the difference between the estimated number of alcohol consequences for men and women was greater at higher values of positive urgency. At the lowest level of positive urgency, men reported approximately 5.5 alcohol consequences (4.5 for women) in the past year, whereas at the highest level of positive urgency, men reported approximately 14.2 alcohol consequences (11.6 for women). Despite a greater estimated difference at the high end of positive urgency, estimates were more uncertain at higher levels of positive urgency than they were at low levels of positive urgency, as indicated by the widening of confidence intervals of estimates at the high end of positive urgency. Although the IRR for gender was significantly different from 1, Figure 4 indicates that the difference in alcohol consequences based on gender was relatively small compared to uncertainty in these estimates.

Discussion

Current practices in reporting results of GLM models leave room for improvement. To address this issue, we proposed methods (with R code) for presenting findings in terms of QoIs, using graphics and tables that are straightforward to interpret. Given the volume of scientific papers that researchers and practitioners of addiction science consume, any efforts that authors can put towards presenting results clearly and in terms of a straightforward research question are likely to be well-received. G. King et al. (2000) advocated for the use of QoIs, emphasizing that the findings of our statistical models can and should be understandable by non-experts. We further expect that if a research study can provide straightforward, actionable information, its likelihood of influencing policy and practice should increase. We acknowledge that getting to plain-language interpretations for GLMs does requires additional analytical work; as such, we aimed in this paper to facilitate this additional lift by bolstering understanding of GLMs and presenting software tools for reporting results.

Reporting results in terms of QoIs not only lessens the mental burden on readers, but it also uncovers some of the nuances of GLMs that are not captured by exponentiated coefficients. Viewing a figure makes immediately clear the impact of non-constant predictor-QoI relations and conditionality of predictor-QoI relations, but does not impose them as a barrier to interpretation. Rather, doing so allows readers to extract information on QoIs without additional calculation. Although we recognize the additional burden that generating new graphics and tables may place on researchers, we believe that doing so will enhance the range and number of readers who might grasp and implement findings. In addition to the simulated and empirical examples presented in this manuscript, we have applied our approach in recent empirical work (K. M. King et al., 2020), and hope that our general approach might be adopted, scrutinized, and refined by other scholars.

Though we believe our approach has potential for improving present practices in reporting GLM results, it also comes with some limitations. We narrowed our focus in the current work to the most common GLM types, which led us to exclude several classes of models, including hybrid count models that account for excess zeroes such as zero-inflated and hurdle models. Certain GLM model complexities were deemed beyond the scope of this paper, but are addressed elsewhere, such as addressing nonlinear predictors (Kim & McCabe, under review) and interaction effects in GLMs (McCabe et al., under review). As we propose displaying bootstrapped confidence intervals rather than displaying raw data, researchers should be careful when using this approach not to extrapolate beyond the range of observed data or interpolate at predictor values that are not observed. The current methods are only implemented in R at present. Future work might make these types of methods available to a broader range of data analysts by implementing them in graphical user interface-based applications.

Models of count and binary data can be a source of rich interpretation; however, current approaches to reporting limit the ability of readers to interpret available results. We aimed to highlight shortcomings of current approaches to GLMs, to build intuition on GLMs and their results, and to recommend thoughtful tabular and graphical presentation of results. In doing so, we aimed to present tools for creating results sections in the style that we propose. By focusing on QoIs, research practictioners can present scientific findings with greater clarity and precision without increasing burden on readers. Moreover, extracting concrete predictions from models in terms of QoIs allows for a common quantitative language which is critical for cumulative psychological science. With QoIs as a common metric, efforts can be made to compare results from disparate studies. Our hope is that by enhancing current reporting standards for GLM models, the findings of complex analyses might be made more understandable, more generalizable, and more impactful.