Tobin’s $q$ and corporate investment with a pandemic shock

Abstract

We analyze the impact of COVID-19 on investment by incorporating a stochastic transmission shock into the standard $q$ theoretical framework. Our model suggests that the adjustment cost amplifies the negative pandemic shock to investment and decreases firm value. In particular, when the infection rate is low, the reduction in investment is higher for firms with low adjustment costs in that they are more sensitive to the infection rate. An optimistic expectation of the arrival rate of a vaccine reduces the probability of executing mitigation policy. Moreover, the uncertainty of the pandemic increases investment and enhances firm value during the pandemic regime.

1. Introduction

COVID-19 has damaged the economy and reduced firm value. Recent literature studies the effects of the pandemic on macroeconomic dynamics (Guerrieri et al., 2020) and the financial market shocks. The spread of the pandemic threatens the survival of firms, which thus have to take action to mitigate the impact of the pandemic and pay the costs. Numerous studies focus on the impact of pandemic shocks and policy reaction(see, e.g., Wang et al., 2021). The existing literature provides some tractable epidemic frameworks (see, e.g., Acemoglu et al., 2020, Hong et al., 2021 henceforth HWY).1 These models focus on reducing the expected number of secondary infections in a susceptible population. However, the discussion of the pandemic shock’s impact on investment has not been addressed, especially in the costly capital adjustment costs case. Thus, this paper contributes by emphasizing the investment shock due to a pandemic. Based on generalized $q$ theory, our analysis applies the $SIS$ model of HWY in which COVID-19 infection cannot lead to long-lasting immunity. We investigate how investment and mitigation policy vary with different adjustment costs by incorporating the spirit of Lin et al. (2018) and the COVID-19 shock.

The main results are as follows. First, the pandemic shock reduces investment, and adjustment costs are a factor that multiplies the negative shock. Adjustment costs impede firms’ attempts to adjust investment to adapt to the pandemic shock. This is because the adjustment cost makes updating equipment technology difficult. Second, with regard to asset pricing, the mitigation policy creates an option that will affect investment and asset values. Firms trade off the benefit and cost of mitigation according to different adjustment cost parameters. Firms with lower adjustment costs can benefit from slowing the transmission rate of COVID-19 and realize a higher firm value. Third, a higher arrival rate of a vaccine leads to a more aggressive corporate investment strategy. More importantly, our model indicates that higher pandemic risk uncertainty can result in higher investment and average $q$ value. This is because people will imagine that COVID-19 will end abruptly even under a high infection rate.

2. Model setup

2.1. Production with a COVID-19 shock

Technology and profit. Following Hayashi (1982), we assume that capital evolves according to:

$$d{K}_t=\left(I_t-\delta K_t\right)dt,$$ (1)

where $\delta$ is the depreciation rate of the capital stock, $I$ is gross investment, and $K$ is the capital stock.

Under a risk-neutral measure, we assume that aggregate output $Y$ has an “AK” type production technology. After the unanticipated pandemic arrives, the utilization of capacity in the economy will be affected because COVID-19 reduces the labor force participation rate. The formula for productivity is $A\left(N_t\right)$:

$$A\left(N_t\right)=A_0(1-{\xi }_1{N}_t^{{\xi }_2}).$$ (2)

Productivity $A\left(N_t\right)$ is a function of the infection rate of COVID-19, and $A_0$ is the productivity level under the normal regime. In addition, ${\xi }_1>0$ and $0<{\xi }_2<1$ capture the shrinking impact of infection rates on productivity.

Under the pandemic regime, the firm’s operating profits over $(t,t+dt)$ are given by:

$$d{P}_t=A\left(N_t\right)d{K}_t-I_{t}dt-G\left(I_t,K_t\right)dt.$$ (3)

Following the Hayashi (1982), we assume that adjustment cost $G(I,K)$ is homogeneous with degree one in $I$ and $K$. Thus, $G(I,K)=g\left(i\right)K$, where $i$ is the firm’s investment-to-capital ratio, $i=I/K$. $g\left(i\right)=\frac{\theta i^2}{2}$ is increasing and convex in $i$, where $\theta >0$ is the capital adjustment cost parameter.

2.2. Stochastic SIS model

Following HWY, let $N_t$ denote the infected group and the gross number of people be defined as 1. Suppose that the probability that an infectious individual meets a susceptible is proportional to the product of their population mass, $N_t(1-N_t)$. $\beta$ denotes the expected transmission rate. Let $\gamma >0$ denote the rate at which an infected person recovers. Thus, the duration that an infected person is infective is $1/\gamma$. Therefore, we obtain the net change in $N_t$, $d{N}_t=\beta N_t(1-N_t)dt-\gamma N_{t}dt$. The transmission rate $\tilde{\beta }$ is a stochastic rate: $\tilde{\beta }=\beta dt+\sigma d{\mathcal{Z}}_t$, where $\sigma$ is a constant parameter and ${\mathcal{Z}}_t$ is a standard brownian motion. If a vaccine is successfully released, the pandemic will end. Thus we set a jump Poisson process, ${\mathcal{J}}_t$ with a constant arrival rate, $\lambda$, to capture the arrival of vaccines. Therefore, combining the stochastic transmission and the effect of vaccines, the dynamics of $N_t$ without mitigation obey the following rule:

$$d{N}_t=\left(\beta (1-N_{t-})-\gamma \right)N_{t-}dt+\sigma N_{t-}(1-N_{t-})d{\mathcal{Z}}_t-N_{t-}d{\mathcal{J}}_t,$$ (4)

The formula captures the epidemiological evolution process.2 We can analyze the steady state of $N_t$ as follows. Let $f(N_t,t;N_0)$ denote the time-0 conditional density function for $N_t$. The density function $f(N_t,t)$ satisfies Kolmogorov equation:

$$0=\frac{\partial f(N,t)}{\partial t}+\frac{\partial \left[(\beta (1-N)-\gamma )Nf(N,t)\right]}{\partial N}-\frac{1}{2}\frac{{\partial }^2\left[{\left(\sigma N(1-N)\right)}^{2}f(N,t)\right]}{\partial N^2}.$$ (5)

When $t\to \infty$, the conditional distribution converges to the steady state, and the first term of Eq. (5) is zero. The long-run distribution of the infection rate $N$ depends on three parameters in a nonlinear way. Simply relying on ${\mathcal{R}}_0=\beta /\gamma$, which is the ratio between the expected transmission rate $\beta$ and exit rate $\gamma$, the variance-adjusted basic reproduction number is given by: ${\overline{\mathcal{R}}}_0=\left(\beta -{\sigma }^2/2\right)/\gamma$. Gray et al. (2011) show that whether ${\overline{\mathcal{R}}}_0$ exceeds one dictates the long-run convergence property of the model. When ${\overline{\mathcal{R}}}_0<1$, COVID-19 disappears in the long run. When ${\overline{\mathcal{R}}}_0>1$, COVID-19 persists in the long run.

Before the vaccine arrives, firms will choose whether to mitigate the transmission of the disease according to the principle of profit maximization. The realized expected transmission rate will be reduced to ${\beta }_{t0}-h\left(x_t\right)$ and $h\left(x_t\right)\ge 0$. The evolution of $N_t$ under the optimal mitigation policy satisfies the following equation:

$$d{N}_t=\left(\left({\beta }_{t0}-h\left(x_{t-}\right)\right)(1-N_{t-})-\gamma \right)N_{t-}dt+\sigma N_{t-}(1-N_{t-})d{\mathcal{Z}}_t-N_{t-}d{\mathcal{J}}_t.$$ (6)

There is a process driving the mitigation cost $\{X_t;t_0<t<\tau \}$, where $\tau$ is the arrival time of the vaccine. By homogeneity, at $t>t_0$, the scaled mitigation cost is $x_t=X_t/K_t$. A firm’s mitigation efficacy takes the following form:

$$h_t=h\left(x_t\right)={\kappa }_1{x_t}^{{\kappa }_2},$$ (7)

where $h\left(x\right)$ is increasing and concave in $x$.

2.3. The firm’s maximization problem

Under the pandemic regime, let $V(K,N)$ denote the firm value:

$$V(K,N)=\tilde{\mathbb{E}}\left[{\int }_0^{\tau }{e}^{-rs}(P_s-\pi P_s{\mathbf{1}}_{X_s>0})ds+{\int }_{\tau }^{\infty }{e}^{-rs}\widehat{P_s}ds\right].$$ (8)

The indicator function ${\mathbf{1}}_{X_t>0}$ is equal to one when the mitigation cost is positive ($X_t>0$) and zero otherwise. $\pi P$ is the proportional fixed cost of mitigation, where $\pi >0$ is a constant.

3. Model solution

By using dynamic programming, the value function $V(K,N)$ satisfies the following Hamilton–Jacobi–Bellman (HJB) equation:

$$rV(K,N)=\underset{I,x}{max}{A}_0(1-{\xi }_1{N}^{{\xi }_2})K-\left(\pi A_0(1-{\xi }_1{N}^{{\xi }_2})+x\right)K{\mathbf{1}}_{x>0}-I-G(I,K)+(I-\delta K)V_K+\left((\beta -h\left(x\right))(1-N)-\gamma \right)N{V}_N+\frac{{\sigma }^2}{2}{N}^2{(1-N)}^2{V}_{NN}+\lambda \left(V(K,0)-V(K,N)\right).$$ (9)

The first-order condition (FOC) with respect to $I$ is given by:

$$G_I(I,K)+1=V_K.$$ (10)

Under the pandemic regime, based on the principle in Lin et al. (2018) and HWY, we conjecture the value function by using $V(K,N)=q\left(N\right)K$. $q\left(N\right)$ denotes the average value of capital, and thus $q\left(N\right)=V_K$, which indicates that the marginal $q$ equals the average $q$. In the case of $X>0$, the FOC with respect to mitigation policy $x$ is given by:

$$1=-h^{\prime }\left(x\right)q_N\left(N\right)N(1-N).$$ (11)

Combining these two FOCs (10), (11), we simplify the HJB equation and obtain the ordinary differential equation (ODE) for $q\left(N\right)$:

$$(r+\lambda +\delta -i^{\ast })q\left(N\right)=\left(\left(\beta -h\left(x^{\ast }\right)\right)N(1-N)-\gamma N\right)q^{\prime }\left(N\right)+\frac{1}{2}{N}^2{(1-N)}^2{\sigma }^2{q}^{″}\left(N\right)+\lambda q\left(0\right)+(1-\pi {\mathbf{1}}_{x>0})A_0(1-{\xi }_1{N}^{{\xi }_2})-x^{\ast }-i^{\ast }-g\left(i^{\ast }\right).$$ (12)

The above ODE is subject to two boundary conditions. For $N=0$, the firm recovers to the normal regime,

$$q\left(0\right)=\theta i^{FB}+1,$$ (13)

where $i^{FB}=r+\delta -\sqrt{{(r+\delta )}^2-2(A_0-(r+\delta ))/\theta }$ is the first-best investment under the normal regime. When $N=1$, the right boundary is:

$$0=\left(\lambda q\left(0\right)+\frac{1}{2\theta }+A_0(1-{\xi }_1)\right)+\frac{1}{2\theta }{q}^2\left(1\right)-(r+\lambda +\frac{1}{\theta }+\delta )q\left(1\right)-\gamma q^{\prime }\left(1\right).$$ (14)

In fact, there are two endogenously determined cutoff levels $\underset{\_}{N}$ and $\overline{N}$ of the infected population mass for the mitigation policy and value function. In the region $\underset{\_}{N}<N\le \overline{N}$, $x>0$, and the ODE for $q\left(N\right)$ is given by Eq. (12). In the two inaction regions $0\le N<\underset{\_}{N}$ and $\underset{\_}{N}<N\le 1$, firms choose not to mitigate, $x=0$. Therefore, $q\left(N\right)$ satisfies:

$$0=\left(\frac{1}{2\theta }+\lambda q\left(0\right)+A_0(1-{\xi }_1{N}^{{\xi }_2})\right)+\frac{1}{2\theta }{q}^2\left(N\right)-\left(r+\lambda +\delta +\frac{1}{\theta }\right)q\left(N\right)+\left(\beta (1-N)-\gamma \right)N{q}^{\prime }\left(N\right)+\frac{1}{2}{N}^2{(1-N)}^2{\sigma }^2{q}^{″}\left(N\right).$$ (15)

Naturally, there are two value-matching conditions and four smooth-pasting conditions:

$$q\left({\underset{\_}{N}}_{-}\right)=q\left({\underset{\_}{N}}_{+}\right),q\left({\overline{N}}_{-}\right)=q\left({\overline{N}}_{+}\right),$$ (16)

$$q^{\prime }\left({\underset{\_}{N}}_{-}\right)=q^{\prime }\left({\underset{\_}{N}}_{+}\right),q^{\prime }\left({\overline{N}}_{-}\right)=q^{\prime }\left({\overline{N}}_{+}\right),q^{″}\left({\underset{\_}{N}}_{-}\right)=q^{″}\left({\underset{\_}{N}}_{+}\right),q^{″}\left({\overline{N}}_{-}\right)=q^{″}\left({\overline{N}}_{+}\right).$$ (17)

4. Model implications

4.1. Parameter choices

Referring to Eberly et al. (2012), we set $A=18\text{\%}$, $\theta =3$, 5, and $\theta \to \infty$. We adopt a capital depreciation rate $\delta =0.11$ according to Riddick and Whited (2009). We pin down the productivity reduction parameters ${\xi }_1=0.3$ and ${\xi }_2=0.6$. These values imply moderate long-run declines absent mitigation. For comparison, the risk-free rate $r=4\text{\%}$ and pandemic-related parameter $\beta =6.616\times 12$, $\sigma =1.689\times \sqrt{12}$, $\gamma =2.173\times 12$, $\lambda =1.1$, ${\kappa }_1=20$, ${\kappa }_2=0.032$, $\pi =0.05$ and $N_{t0}=2\times 10^{-7}$ are in line with HWY.

4.2. Investment, Tobin’s average $q$ and mitigation

The optimal investment and$q$value. The optimal investment is given by:

$$i\left(N\right)=\frac{q\left(N\right)-1}{\theta }.$$ (18)

Panel A of Fig. 1 depicts the optimal investment $i\left(N\right)$ with respect to the infection rate $N$ for different values of $\theta$. Evidently, the investment level is decreasing with $N$. Moreover, a higher adjustment cost (larger $\theta$) results in lower investment $i\left(N\right)$. Fixing $\theta =3$, when infection $N$ approaches 1 from $N_{t0}=2\times 10^{-7}$, the investment level declines from 0.1 to 0.088, the reduction is approximately 11 percent. Setting $\theta \to \infty$,3 when the infection rate $N$ increases from $N_{t0}=2\times 10^{-7}$ to 1, investment declines from 0.002 to 0.0017, a 15% reduction. Under the COVID-19 regime, a firm with a higher adjustment cost firm has a lower initial investment and a larger investment reduction.

Fig. 1.

Investment $i\left(N\right)$, Tobin’s average $q\left(N\right)$, mitigation cost $x\left(N\right)$ and reproduction number ${\mathcal{R}}_0$. .

Panel B of Fig. 1 shows that $q\left(N\right)$ monotonically decreases with the infection rate $N$. Moreover, as we increase $\theta$, firm value will be reduced by considerably more. The average $q$ value $q\left(N\right)$ is reduced substantially more by a larger adjustment cost (larger $\theta$). For example, as infection $N$ approaches 1 from $N_{t0}=2\times 10^{-7}$, the average $q$ value $q\left(N\right)$ drops 2% from 1.3 to 1.27 for the value of $\theta =3$. When $\theta \to \infty$, $q\left(N\right)$ decreases from 1.2 to 1.169 for a reduction of 3%. The Panels A and B of Fig. 1 show the negative effect of adjustment costs on firm value, but the extent of the decrease is smaller than for investment. A larger adjustment cost $\theta$ implies that a larger investment adjustment friction distorts investment and reduces firm value (Lorenzoni and Walentin, 2007). Under the COVID-19 regime, if companies renew assets more quickly, they have more opportunities for future growth and are expected to recover more quickly.

The implications of mitigation. According to Panel C of Fig. 1, the mitigation cost $x\left(N\right)$ exhibits a hump-shaped relation with the infection rate $N$. At low levels of the infection rate $N$, although the smaller $\theta$ slightly flattens the mitigation cost-infection curve, the adjustment cost does not affect the stopping point of mitigation policy. Unless infection is high enough ln$\left(N\right)=-0.803,N=0.448$, the mitigation cost $x\left(N\right)$ drops to zero with $\theta =3$. This indicates that a firm chooses to stop mitigating ($x\left(N\right)=0$). With lower adjustment costs, firms face a slightly higher mitigation cost in the region of $N\in (0,0.015)$ or ln$\left(N\right)\in (-15,-4.22)$, whereas for high values of $N$, the parameter $\theta$ does not affect the mitigation cost when $\theta =3$ or $\theta =5$. Thus, a firm’s adjustment cost is not fundamentally related to mitigation cost. However, a firm with a very high adjustment cost never chooses not to mitigate the transmission of the pandemic.

${\mathcal{R}}_0=({\beta }_{t_0}-h\left(x\right))/\gamma$ is the reproduction number of infected people. Panel D of Fig. 1 shows that ${\mathcal{R}}_0$ will be reduced by the same level regardless of the value of the adjustment parameter $\theta$ (e.g., $\theta =3$ or $\theta =5$). From Panels C and D of Fig. 1, we find that a firm with a low adjustment cost actively takes on social responsibility because doing so benefits the firm more. The intuition is that mitigation decision creates an option that depends on the benefit from the investment. The investment benefit being negative relates to the adjustment cost parameter $\theta$. For extremely high values of $\theta$, an option with a mitigation benefit is out of the money.

Dynamics of investment$i\left(N\right)$with optimal mitigation. We define the expected growth rate and volatility of investment as ${\mu }_i\left(N\right)$ and ${\sigma }_i\left(N\right)$ respectively:

$${\mu }_i\left(N\right)=\frac{q^{\prime }\left(N\right)}{q\left(N\right)-1}N\left(\left((\beta -h\left(x\right))(1-N)-\gamma \right)\right)+\frac{1}{2}\frac{q^{\prime \prime }\left(N\right)}{q\left(N\right)-1}{\sigma }^2{(1-N)}^2{N}^2,$$ (19)

$${\sigma }_i\left(N\right)=\frac{q^{\prime }\left(N\right)}{q\left(N\right)-1}\sigma (N-1)N.$$ (20)

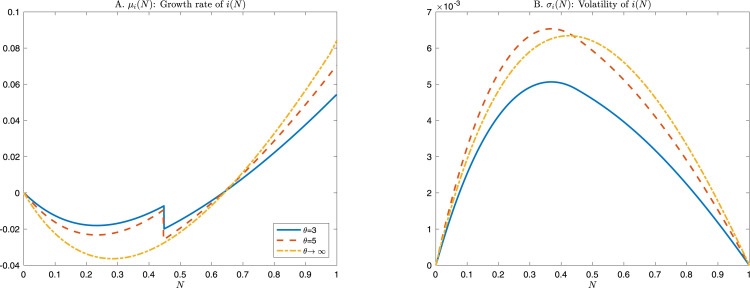
First, according to Panel A of Fig. 2 for values of $N$ (e.g., $N\in (0,0.43)$ ), a higher adjustment cost parameter $\theta$ implies a lower growth rate of investment ${\mu }_i$. In contrast, in the region of $N\in (0.43,1)$, a higher adjustment cost parameter $\theta$ implies a higher growth rate of investment. This is because when infection rate is low, firms with lower adjustment costs have a higher marginal $q$ value, which makes the corporate investment strategy more sensitive to the infection rate. Nevertheless, when the infection rate is high enough, all firms choose not to mitigate the transmission of the pandemic. Reducing the divestiture of assets or investment are easier for firms with lower adjustment costs, which leads to a lower expected growth rate of capital investment.

Fig. 2.

Dynamics of $i\left(N\right)$.

Second, the curve’s downward jump in the expected growth rate ${\mu }_i$ with regard to $\theta =3$ and $\theta =5$ (in Panel A in Fig. 2) is induced by the stopping point of mitigation policy $x\left(N\right)$ (according to Panel C of Fig. 1, we find that all firms choose to stop mitigating when $N>0.448$). Without mitigation, the pandemic transmission rate returns to a higher state (i.e., $\beta$), and thus the marginal $q$ value declines, which results in lower expected investment growth.

Regarding volatility, in Panel B of Fig. 2, we find that the curves with respect to $\theta =3$ and $\theta =5$ are steeper than the curve with respect to $\theta \to \infty$ in the region of $N\in (0,0.43)$. Recall that from Panel B of Fig. 2, we understand that this feature is induced by mitigation policy. This is because the volatility of investment is affected by the superposition of two forces. On the one hand, adjustment costs will amplify investment fluctuation. On the other hand, mitigation can increase the marginal $q$ value and thus increase investment volatility.4

4.3. Implications of vaccine and pandemic uncertainty

Effect of vaccine arrival rate$\lambda$. As panel A of Fig. 3 shows, if the vaccine is expected to arrive much earlier, a higher arrival rate $\lambda$ leads to higher investment $i\left(N\right)$. For $\lambda =2$ and $\lambda =0.5$, there is a large gap between the different investment curves. Investment is approximately 15% higher than in the case of $\lambda =0.5$ if the arrival time of the vaccine is expected to be six months $\lambda =2$. Panel B of Fig. 3 shows a similar but weaker impact of the vaccine. When the infection rate $N$ is too high for investors, the marginal return on investment becomes very low even if a faster end of COVID-19 is expected.

Fig. 3.

The effects of the vaccine arrival rate $\lambda$ and transmission volatility $\sigma$.

Effect of transmission volatility$\sigma$. In Panels C and D of Fig. 3, we plot how investment $i\left(N\right)$ and the average $q$ value $q\left(N\right)$ vary with transmission volatility $\sigma$. A high $\sigma$ implies a high uncertain pandemic risk and results in a more aggressive investment policy and a higher average $q$ value. This arises because the high uncertainty means that the firm expects herd immunity. The greater fluctuation in the infection rate $N$ results in the economy being more likely return to normal in a short time. Therefore, in this case, a firm with more optimistic expectations will gamble to increase production and restore the economy through more radical investment. Hence, there is a different prediction from the standard $q$ framework that the high uncertainty risk $\sigma$ stimulates investment and increases firm value.

5. Conclusion

This paper investigates the impact of a pandemic and adjustment costs on investment. After providing an analysis of the investment dynamics in an SIS setting, we proceed to a qualitative investigation of the average $q$ value under the optimal mitigation policy. We recognize the importance of adjustment costs for investment during the period of the COVID-19 shock. Mitigation creates an option that varies with adjustment costs. The vaccine has a more significant effect on firm value when the infection rate is relatively low. This explains why the government supports vaccine development. Moreover, greater transmission volatility leads to a greater incentive for firms to invest.