MR Denoising Increases Radiomic Biomarker Precision and Reproducibility in Oncologic Imaging

Abstract

Several noise sources, such as the Johnson–Nyquist noise, affect MR images disturbing the visualization of structures and affecting the subsequent extraction of radiomic data. We evaluate the performance of 5 denoising filters (anisotropic diffusion filter (ADF), curvature flow filter (CFF), Gaussian filter (GF), non-local means filter (NLMF), and unbiased non-local means (UNLMF)), with 33 different settings, in T2-weighted MR images of phantoms (N = 112) and neuroblastoma patients (N = 25). Filters were discarded until the most optimal solutions were obtained according to 3 image quality metrics: peak signal-to-noise ratio (PSNR), edge-strength similarity–based image quality metric (ESSIM), and noise (standard deviation of the signal intensity of a region in the background area). The selected filters were ADFs and UNLMs. From them, 107 radiomics features preservation at 4 progressively added noise levels were studied. The ADF with a conductance of 1 and 2 iterations standardized the radiomic features, improving reproducibility and quality metrics.

Introduction

Magnetic resonance (MR)–reconstructed images from different scanners, series, and patients have different noise levels that reduce the quality of the images, affect the signal-to-noise ratio (SNR), and decrease reproducibility of imaging biomarkers. The noise reduces the visibility in low-contrast structures and blurs the edges, having an impact on both the qualitative radiological reporting and the quantitative measurements extracted from either feature extraction or dynamic signal fitting [1].

Reducing noise and increasing SNR and final image quality are common goals in precision imaging. At the acquisition level, MR parameters are adjusted to improve the SNR. Unfortunately, this usually results in increased acquisition time and in sensitivity to motion artifacts. New MR developments reconstructing the k-space with artificial intelligence methods have been proposed as an efficient way to acquire faster and almost noise-free images. In daily practice, MR images need to improve their quality by removing noise applying computer vision techniques known as denoising [2]. Denoising filters face the challenges of maximizing noise removal, smoothing homogenous regions, and preserving morphological detail [3].

The Johnson–Nyquist noise is one of the common source of noise, being induced by thermal fluctuations and modelled as a Rician distribution in the magnitude images [4, 5]. This noise can be approximated as Gaussian spreading in areas with high SNR. Noise is responsible of the low reproducibility of imaging biomarkers in the phenotyping, treatment prediction, and patient’s prognostication in oncology, as image quality variability affects the related radiomics features and dynamic parameters.

We hypothesize that the use of MR denoising filters will increase the precision and reproducibility of extracted computational metrics, lowering biases when obtaining radiomic biomarkers. Our primary objective was to measure the impact of different denoising filters on the final image quality and on the stability of radiomic metrics to finally select the optimal filter parameters in both physical phantoms and real-world data from patients with neuroblastic tumors. Secondary objectives were to evaluate the MR image quality by different signals (PSNR, peak signal-to-noise ratio), border (ESSIM, edge-strength similarity–based image quality metric), and noise (SD, standard deviation of the signal intensity of the background area) metrics, and to assess the impact of the filters on the radiomics characteristics [6].

Material and Methods

Image Database

Phantom

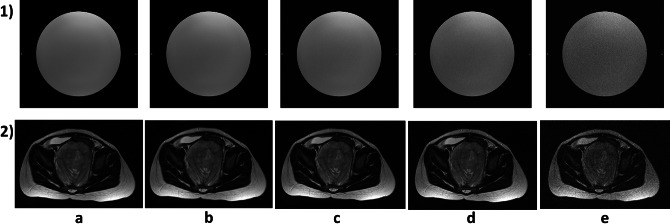
A 200-mm MR head phantom (Philips Healthcare, The Netherlands) was used. The phantom was composed of 4 different modules: the geometric module, consisting of a cube; a homogeneous cylinder having a central hole with a ramp, referred to as the slice thickness module; a homogeneous cylinder, referred to as the SNR module; and the spatial resolution module consisting of a set of rods (Fig. 1) [7].

Fig. 1.

MR Phantom distribution: 1) Image of the Phantom; 2) Sagittal MR survey; and the 4 modules: a geometry, b slice thickness, c SNR, and d spatial resolution

MR images were obtained on a 3-T magnet (Philips Achieva, Philips Healthcare, The Netherlands) with a head coil using a T2-weighted turbo spin echo sequence with the following parameters: TR = 3000 ms, TE = 120 ms, flip angle = 90°, anteroposterior axis encoding, field of view = 270 mm, acquisition matrix = 630 × 630, interslice gap = 2.75 mm, and voxel size = 0.421 × 0.421 × 2.5 mm. A total of 7 MR acquisitions were performed, split in two different days, 1 week apart. To avoid partial volume effects, only the 4 central slides were analyzed from each module.

Patients

Patients were stratified into two groups: discovery and validation databases. The MR discovery database consisted of 15 children, 12 females and 3 males, having a neuroblastic tumor: neuroblastoma (8 patients) and ganglioneuroma (7 patients). The mean age was 4.5 ± 3.1 years old (range, 1 month to 10 years old). The validation database consisted of 10 children, 7 females and 3 males, with a diagnosis of neuroblastoma (8 patients) and ganglioneuroma (2 patients). The mean age was 3.4 ± 5.3 years old (range, 1 month to 15 years old).

All childhood cancer patients had an MR study of the primary tumor before treatment from different MR machines. Images were centralized at the PRIMAGE platform repository [8]. This repository includes clinical, molecular, genetic, and imaging data of children with neuroblastic tumors, having been developed in the context of the Horizon 2020 PRIMAGE Project. All MR images from different vendors (General Electric (GE), Siemens, and Philips) and field strengths (1.5-T and 3-T magnets) were acquired with a surface coil. The turbo/fast spin echo T2-weighted images were used for this study.

MR Image Preparation

In order to measure the performance of the filter at different noise levels, artificial Rician noise was added to the phantom and patient’s databases at four different noise levels (σ = 0.005, σ = 0.01, σ = 0.02, and σ = 0.05) (Fig. 2) [5, 9]. The noise is added to the original images, which were visually classified by an experienced radiologist as noise-free or very low-noise images. From now on, the original databases are referred to as Original Phantom database, Original Patients Discovery database, and Original Patients Validation database. The databases to which noise has been added are referred to as Noised Phantom database, Noised Patients Discovery database, and Noised Patients Validation database.

Fig. 2.

Original and Noised databases examples: 1) Physical Phantoms; 2) Patient Discovery; Noise level: a original, b σ = 0.005, c σ = 0.01, d σ = 0.02, and e σ = 0.05

Denoising Filters

Five of the main denoising filters were used: Gaussian filter (GF) [10], curvature flow filter (CFF) [11], anisotropic diffusion filter (ADF) [12], non-local means filter (NLMF) [13], and unbiased-non-local means filter (UNLMF) [14]. All these filters belong to the group of “edge-preserving” filters, with the exception of the Gaussian filter which attempts to remove noise while preserving morphological structures.

The low-pass GF removes speckle noise. The filtered image was the result of applying three Gaussian distribution kernels with standard deviations of σ_x, σ_y, and σ_z at the frontal, sagittal, and longitudinal axes, respectively. The main disadvantage of this kind of filter is that it tends to blur the edges while it removes the noise. Despite this, it is widely used as a preprocessing before the extraction of imaging biomarkers or segmentation due to its simplicity [15–17]. Four different GFs were applied by varying the sigma value [σ_x, σ_y, σ_z] to [0.4, 0.4,0.2], [0.5, 0.5,0.2], [0.6, 0.6,0.2], and [0.7, 0.7,0.2].

The CFF is characterized by preserving the edge definition smoothing perpendicular to the isointensity contours [11]. CFF preserves sharp edges while regions between edges are smoothed. However, these edges can be removed with the repetition of the process, shrinking the information until its disappearance. Original voxels with low signal intensity may be transformed to negative values when the filter is applied. Different CFFs were applied by modifying the number of iterations (1 to 5) with a step of one iteration.

The ADF associates images with the thermodynamic behavior of fluids. Noise voxels act as small volumes of fluid which need less time to homogenize their temperature while edges act as big containers which need more time [12]. Thus, ADF acts as a high-pass filter, removing high-frequency noise while edges are preserved. Two parameters were tuned for the optimization of this filter: the number of iterations, which took a value from 1 to 3, and the diffusion rate or conductance, which took values of 0.5, 1, 1.5, and 2. This last parameter tends to preserve features of the image as high gradients or curvature when its value its low.

The NLMF calculates a weighted image average. The weighted function measures the similarities between the neighborhood of filtered voxel and each neighborhood of voxels inside a window centered in filtered voxel, no matter the distance to it [13]. Two ways of implementing this filter were carried out: a three-dimensional approach in which the entire volume was processed, and a two-dimensional approach in which the filter was applied slide-by-slide in the transversal plane. The window size was set to 3 voxels and the strength of the filter took values of 0.001, 0.0025, 0.005, and 0.01 in the three-dimensional approach, and 1.2 and 2.4 times the standard deviation of the image background in the two-dimensional approach.

The UNLMF is an evolution of the NLMF that manages effectively the effect of Rician noise [14]. This filter takes advantage of the fact that Rician noise becomes independent of the signal by using the square of the signal, so it can be removed by subtracting twice the standard deviation of the background volume. The same fitting parameters and approaches used in NLMF were used in this filter.

Noise Filters’ Performance Metrics

To evaluate the performance of the filters, three different metrics were selected and measured: PSNR, ESSIM, and the standard deviation of a background area representing noise (R_SD). Background noise was defined by the standard deviation of the signal intensity of a ROI located in the background outside the patient or phantom area. ROIs were located in two different places depending on the database. In the Phantom database, two ROIs of 60 × 630 voxels were delimited at the right and left sides of the image outside the phantom. The ROI in the Patient databases was delimited at the right posterior corner of the field of view (FOV) with an area of 30 × 30 voxels along the longitudinal axis. In order to compare the differences between the SD of the original image and the denoised images, the R_SD ratio was calculated as follows, where the lower the ratio, the more noise is removed:

$$R_{\mathit{SD}}=\frac{{\mathit{SD}}_{\mathit{denoised}}-{\mathit{SD}}_{\mathit{original}}}{{\mathit{SD}}_{\mathit{original}}}$$

The PSNR is a metric commonly used to estimate image quality based on the mean squared error (MSE) [9]. The PSNR is expressed in decibels and it is defined as:

$$PSNR=10{\mathit{log}}_{10}\left(\frac{L^2}{\mathit{MSE}}\right),$$

where L is the dynamic range of the voxel intensity of the original image. The MSE was calculated between the original image and the filtered one. Large values of the PSNR are associated with a better quality image or image recovery. This metric is one of the most common to measure the performance of denoising filters [3, 9, 18–22].

The ESSIM uses the edge strength of each pixel of an image to represent its semantic information in order to measure the edge preservation between two images (original vs. filtered) [3, 23]. ESSIM is defined as:

$$ESSIM\left(f,,,g\right)=\frac{1}{N}\sum _{i=1}^N\frac{2E\left(f,,,i\right)E\left(g,,,i\right)+C}{({E(f,i))}^2+({E(g,i))}^2+C},$$

where E is the edge strength and is calculated as the average of a Prewitt kernel applied in two perpendicular orientations, f and g are the two images to be compared, i is the i^th voxel, and C is a parameter introduced to avoid 0 in the denominator. In the patient’s database, the ESSIM was calculated as the average of the ESSIM in each slide. The closer the ESSIM to 1, the better edge preservation.

Two combined metrics were used, defined as follows: $R_{\mathit{SD}}$ × ESSIM and PSNR × ESSIM. These two metrics weighted the $R_{\mathit{SD}}$ and the PSNR with the ESSIM level ([0–1]), calculated as their corresponding product for each patient by averaging over all slices. The higher these metrics are, the better the performance of the filter.

The concordance correlation coefficient (CCC) was used to investigate the recovery of the radiomics features calculated on the tumors. The CCC was calculated between Original and Noised Patients database radiomics features (original-noise features) and between Original and Noised filtered Patients database radiomics features (original-filtered features) and was calculated as:

$$CCC=\frac{2s_{\mathit{xy}}}{{\sigma }_x^2+{\sigma }_y^2+{({\mu }_x-{\mu }_y)}^2}$$

where s is the covariance, σ is the standard deviation, and $\mu$ corresponds to the mean value of the features. The extracted features were normalized using the natural logarithm due to the huge variability in the images’ dynamic range. Values of CCC above 0.8 indicated a strong correlation, implying the stability of the radiomic features [24]. Furthermore, the CCC of original-noise features was compared to the CCC of original-filtered features. If the CCC of the original-filtered features are higher than the CCC of the original-noise features, it can be assumed that the application of the corresponding filter has managed to recover the value of the original features.

Finally, 107 radiomics features were analyzed: 14 shape features, 18 first-order features, 24 Gy-level co-occurrence matrix (GLCM) features, 14 Gy-level dependence matrix (GLDM) features, 16 Gy-level run length matrix (GLRLM) features, 16 Gy-level size zone matrix (GLSZM) features, and 5 neighboring gray-tone difference matrix (NGTDM) features.

The effects of the filtering process on image quality (signal, edges, and noise) were evaluated with a Friedman test, firstly, and with a Tukey–Kramer test for post hoc analysis. CCC was calculated to compare the effect of the different types of filters between original-noise features and original-filtered features. Comparisons between the effect of MR acquisition (e.g., different vendors) on image quality (ESSIM × PSNR) were performed with a Kruskal–Wallis test, and with a Tukey–Kramer test for post hoc analysis. Statistical significance was established at p < 0.05.

Evaluation Stages

The study considered different stages:

• Selection of the most optimal filters using Original Phantom database was performed by discarding one-third of the filters, focusing on the $R_{\mathit{SD}}$ × ESSIM metric;

• PSNR and ESSIM analyses in the Noised Phantom database discarding filters that had lower values than the unfiltered noise cases;

• Mean PSNR × ESSIM metric analysis of the different noise levels, resulting in the selection of two filters of each type;

• Visual inspection of the Original Patients Discovery database by a radiologist to exclude filters with over-smoothing;

• Evaluation of the Original and Noised Patients Discovery database to select the best filter performance, focusing on the $R_{\mathit{SD}}$ × ESSIM and the PSNR × ESSIM metrics and the recovery of original radiomics features value; and

• Validation of the results with the Original and Noised Patients Validation database.

Results

Original Phantom Database Results

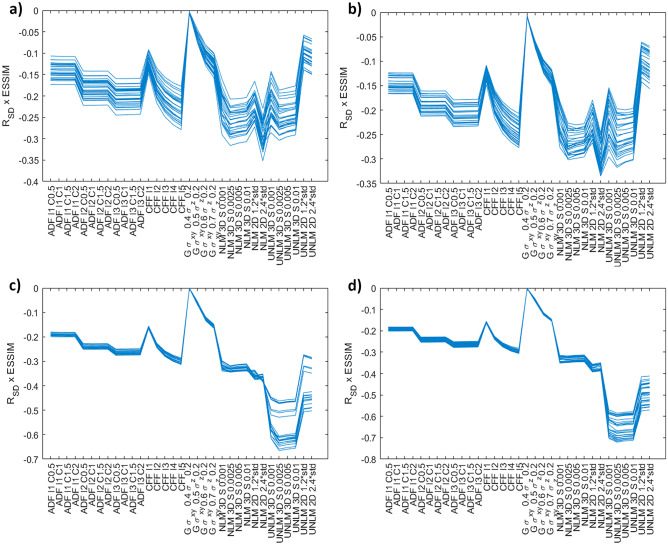
Initial experiments performed with the Original Phantom database constituted a controlled study scenario (same object, equipment, and acquisition conditions). The filters that removed less background noise and did not preserve the edges were discarded, regarding a combination of the R_SD and the ESSIM. One-third of the filters were discarded, including the GF filter and a few iterations of the CFF and ADF filters. It should be mentioned that the variability of the evaluated metrics was very small (σ < 7.61), with the exception of the UNLMF filter where the R_SD increased considerably (σ > 18.32) due to the differences between each phantom module and the sensitivity of the UNLMF to the background signal (Fig. 3).

Fig. 3.

Phantom database R_SD × ESSIM results where each line represents R_SD × ESSIM value for each image; a) slice thickness module; b) SNR module; c) geometric module; d) spatial resolution. I is the number of iterations for ADF and CFF, DF is C is the conductance for ADF, σ is σx, σy, σz for GF and S is the strength of the NLMF or UNLMFF, and std is the standard deviation of the background

Noised Phantom Database Results

The Noised Phantom database allowed a second filter discard. The PSNR and ESSIM metrics were calculated between the Original and Noise Phantom database (original-noise metric) and between the Original Phantom database and the result of filtering this database (original-filtered metric). The performance of the filters selected in the previous stage is shown in Fig. 4. All cases with lower original-filtered metrics than original-noise metric were discarded. At low noise levels (σ ≤ 0.01) the more aggressive ADF and CFF filters resulted in a worsening of both metrics. As the noise level increased, the NLMF and UNLMF filters showed a loss in effectiveness, obtaining values similar to the noise, thus discarding the NLMF and UNLMF filters with low strength. The case of higher noise (σ = 0.05) has not been taken into account when discarding filters since this level of noise does not normally occur in clinical practice. Therefore, a total of 11 filters were discarded.

Fig. 4.

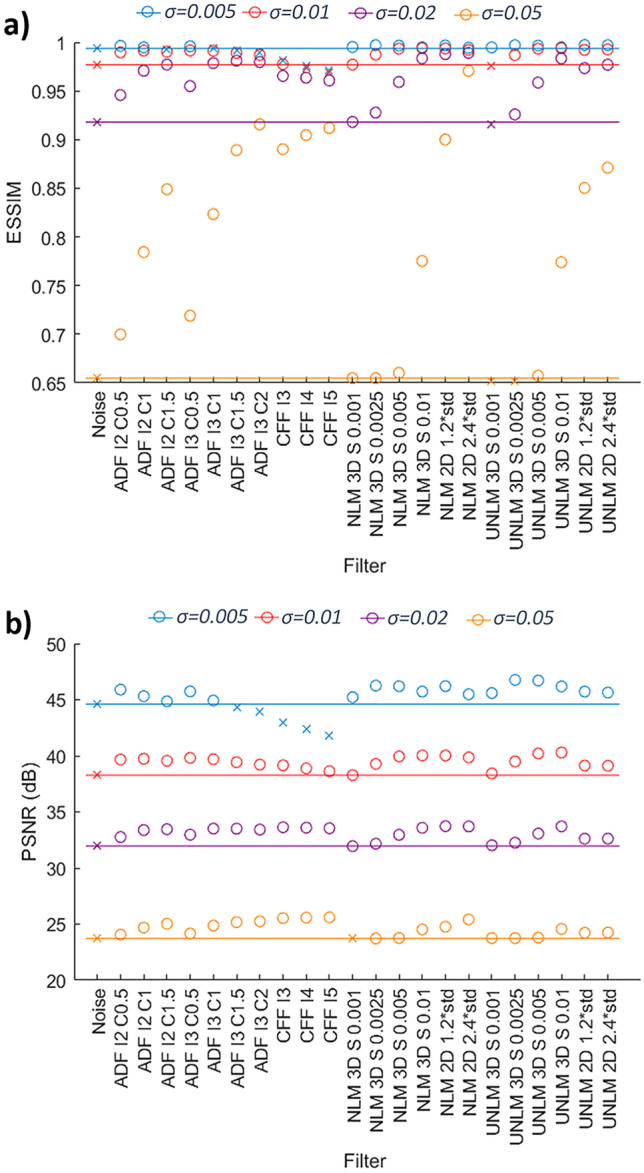
a) Noised Phantom database PSNR results, b) Noised Phantom database ESSIM results. Crosses correspond to values equal to or inferior to noise level and circles to higher values. Each line represents a noise level. I is the number of iterations for ADF and CFF, C is the conductance for ADF; S is the strength of the NLMF or UNLMFF; and std is the standard deviation of the background

From those 5 filters and 33 final settings, only two filters of each type with the best performance at different noise levels were selected to finally select the best ones. For this purpose, the average of the combination of the PSNR and ESSIM metrics of low and medium noise levels was calculated as well as for all levels. The selection was made based on the average of medium and low noise metrics and, in case of doubt, the average of the metrics for all levels (including high noise levels) was analyzed (Table 1). Thus, the filters finally selected were the ADF filter with 2 and 3 iterations and a conductance of 1 and 0.5, respectively, the 2D NLMF and the 3D UNLMF filters.

Table 1.

Noised Phantom dataset PSNR × ESSIM mean results. Selected filters are shown in bold. I is the number of iterations for ADF, C is the conductance for ADF, S is the strength of the NLMF or UNLMFF, and std is the standard deviation of the background

	PSNR × ESSIM mean for noise σ ≤ 0.02	PSNR × ESSIM mean for noise σ ≤ 0.05
ADF I 2 C 0.5	40.8 ± 0.6	34.8 ± 0.9
ADF I 2 C 1	40.8 ± 0.5	35.5 ± 0.7
ADF I 3 C 0.5	40.9 ± 0.5	35.0 ± 0.9
NLMF 3D S 0005	41.2 ± 0.5	34.8 ± 0.9
NLMF 3D S 001	41.3 ± 0.4	35.8 ± 0.6
NLMF 2D S 1.2 std	41.8 ± 0.6	36.9 ± 0.7
NLMF 2D S 2.4 std	41.3 ± 0.6	37.1 ± 0.7
UNLMF 3D S 0.005	41.6 ± 0.4	35.1 ± 0.9
UNLMF 3D S 0.01	41.7 ± 0.3	36.0 ± 0.6
UNLMF 2D S 1.2 std	41.0 ± 0.5	35.9 ± 0.6
UNLMF 2D S 2.4 std	41.0 ± 0.6	36.0 ± 0.6

Patient Discovery Database Results

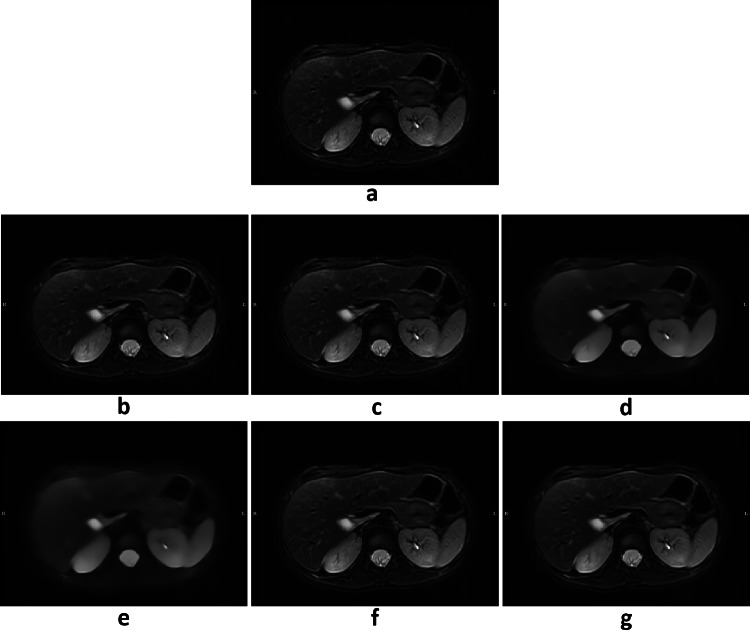
Before studying the behavior of the metrics in the Patients Discovery database, a visual inspection was carried out to check the effect of the filters on the images of Original Patients Discovery database. In this analysis, the NLMF filters were discarded due to excessive smoothing of some cases, as shown in Fig. 5.

Fig. 5.

Denoising example from Original Patients Discovery database: a original, b ADF I2 C1, c ADF I3 C0.5, d NLMF 2D S 1.2 std, e NLMF 2D S 2.4 std, f UNLMF 3D S 0.005, g UNLMF 3D S 0.01. I is the number of iterations for ADF; C is the conductance for ADF; S is the strength of the NLMF or UNLMFF; and std is the standard deviation of the background

For each of the four remaining filters, R_SD × ESSIM as well as PSNR × ESSIM was calculated between Original and Noised Patients Discovery database and between Original Patients Discovery database and the result of filtering Noised Patients Discovery database. These results are shown in Table 2 and Fig. 6. The UNLMF filters provided the best results in terms of the R_SD × ESSIM metric, achieving the best performance with the one with a strength of 0.005. This confirms the results obtained from the Phantom database. Figure 6 shows that for low noise levels, the UNLMF filter with a strength of 0.005 has the best PSNR × ESSIM metric performance, and this effect is attenuated as the noise level increases. It is observed that the ADF filter with 3 iterations and a conductance of 0.5 has a similar pattern and behavior. On the opposite side, the UNLMF filter with a strength of 0.01 and the ADF filter with 2 iterations and a conductance of 1.0 improve their performance by increasing the noise level.

Table 2.

Original Patient Discovery dataset RSD × ESSIM results. I is the number of iterations for ADF; C is the conductance for ADF; S is the strength of the NLMF or UNLMFF; and std is the standard deviation of the background

ADF I 2 C 1	ADF I 3 C 0.5	UNLMF 3D S 0.005	UNLMF 3D S 0.01
−15.05 ± 12.15	−17.02 ± 13.77	−47.55 ± 45.30	−48.25 ± 44.78

Fig. 6.

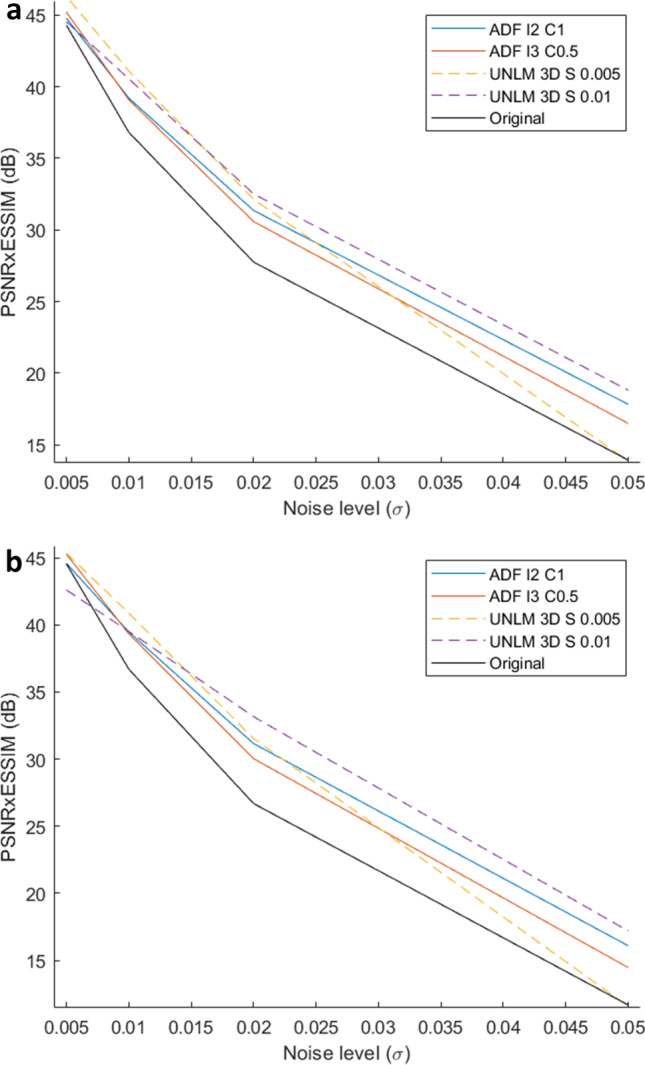
a Noised Patient Discovery database PSNR × ESSIM results; b Noised Patient Validation database PSNR × ESSIM results. I is the number of iterations for ADF; C is the conductance for ADF; S is the strength of the UNLMF

The percentage of invariable characteristics (CCC ≥ 0.8) per type of radiomics features is shown in Table 3. The results obtained show that the four selected filters restore some of the modified values of radiomics features after adding artificial noise. The filter’s behavior was similar within the same group of filters, but the ADF filters presented a better general preservation of the characteristics, especially the ADF filter of 2 iterations and a conductance of 1.0, which showed the best results.

Table 3.

Radiomics features preservation Patient Discovery dataset. In each cell of the table is shown the number of invariant characteristics and in brackets the percentage of invariant characteristics within each group. I is the number of iterations for ADF, C

	Ruido 0.005				ADF I2 C1				ADF I3 C0.5
	σ = 0.005	σ = 0.01	σ = 0.02	σ = 0.05	σ = 0.005	σ = 0.01	σ = 0.02	σ = 0.05	σ = 0.005	σ = 0.01	σ = 0.02	σ = 0.05
SHAPE	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)
FIRST ORDER	17 (94.4%)	17 (94.4%)	17 (94.4%)	15 (83.3%)	17 (94.4%)	17 (94.4%)	17 (94.4%)	16 (88.9%)	17 (94.4%)	17 (94.4%)	17 (94.4%)	15 (83.3%)
GLCM	24 (100%)	24 (100%)	23 (95.8%)	13 (54.2%)	24 (100%)	24 (100%)	24 (100%)	19 (79.2%)	24 (100%)	24 (100%)	24 (100%)	18 (75%)
GLDM	14 (100%)	14 (100%)	12 (85.7%)	10 (71.4%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	11 (78.6%)
GLRLM	16 (100%)	16 (100%)	12 (75%)	11 (68.8%)	16 (100%)	16 (100%)	16 (100%)	13 (81.3%)	16 (100%)	16 (100%)	16 (100%)	12 (75%)
GLSZM	16 (100%)	15 (93.8%)	12 (75%)	9 (56.3%)	15 (93.8%)	15 (93.8%)	16 (100%)	12 (75%)	15 (93.8%)	16 (100%)	15 (93.8%)	12 (75%)
NGTDM	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)
Mean	106 (99.1%)	105 (98.1%)	95 (88.8%)	77 (72%)	105 (98.1%)	105 (98.1%)	106 (99.1%)	93 (86.9%)	105 (98.1%)	106 (99.1%)	105 (98.1%)	87 (81.3%)
Total mean	95.75 (89.4%)				102.25 (95.5%)				100.75 (94.2%)

	UNLM 0.005				UNLM 0.01
	σ = 0.005	σ = 0.01	σ = 0.02	σ = 0.05	σ = 0.005	σ = 0.01	σ = 0.02	σ = 0.05
SHAPE	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)
FIRST ORDER	17 (94.4%)	17 (94.4%)	17 (94.4%)	15 (83.3%)	17 (94.4%)	17 (94.4%)	17 (94.4%)	15 (83.3%)
GLCM	24 (100%)	24 (100%)	23 (95.8%)	13 (54.2%)	24 (100%)	24 (100%)	24 (100%)	14 (58.3%)
GLDM	14 (100%)	14 (100%)	14 (100%)	10 (71.4%)	14 (100%)	14 (100%)	14 (100%)	10 (71.4%)
GLRLM	16 (100%)	16 (100%)	15 (93.8%)	11 (68.8%)	16 (100%)	16 (100%)	16 (100%)	11 (68.8%)
GLSZM	16 (100%)	16 (100%)	15 (93.8%)	9 (56.3%)	15 (93.8%)	15 (93.8%)	16 (100%)	9 (56.3%)
NGTDM	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)
Mean	106 (99.1%)	106 (99.1%)	103 (96.3%)	77 (72%)	105 (98.1%)	105 (98.1%)	106 (99.1%)	78 (72.9%)
Total mean	98 (91.6%)				98.5(92%)

Shape characteristics remained constant as expected due to the fact that the tumor delimitation is not affected by the application of filters. The GLCM, GLDM, GLRLM, and GLSZM were the groups of radiomics features mostly affected by the presence of high noise levels, but seem to stay invariant at low noise levels. These alterations were corrected by both types of filters at medium noise levels and by the ADF filters for high noise levels.

Patient Validation Database Results

The results from the patient validation database are shown in Table 4 and Fig. 6 supports the results obtained from the Original Patient database (2.19 maximum difference of PSNR × ESSIM metric and 1.87% maximum features recovery difference between Discovery and Validation databases).

Table 4.

Radiomic features preservation Patient Validation dataset. In each cell of the table is shown the number of invariant characteristics and in brackets the percentage of invariant characteristics within each group. I is the number of iterations for ADF, C

	Ruido 0.005				ADF I2 C1				ADF I3 C0.5
	σ = 0.005	σ = 0.01	σ = 0.02	σ = 0.05	σ = 0.005	σ = 0.01	σ = 0.02	σ = 0.05	σ = 0.005	σ = 0.01	σ = 0.02	σ = 0.05
SHAPE	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)
FIRST ORDER	17 (94.4%)	17 (94.4%)	17 (94.4%)	15 (83.3%)	17 (94.4%)	17 (94.4%)	17 (94.4%)	16 (88.9%)	17 (94.4%)	17 (94.4%)	17 (94.4%)	15 (83.3%)
GLCM	24 (100%)	24 (100%)	23 (95.8%)	13 (54.2%)	23 (95.8%)	24 (100%)	24 (100%)	19 (79.2%)	24 (100%)	24 (100%)	23 (95.8%)	18 (75%)
GLDM	14 (100%)	14 (100%)	11 (78.6%)	10 (71.4%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	12 (85.7%)	14 (100%)	14 (100%)	11 (78.6%)
GLRLM	16 (100%)	16 (100%)	13 (81.3%)	11 (68.8%)	16 (100%)	16 (100%)	16 (100%)	13 (81.3%)	16 (100%)	16 (100%)	16 (100%)	12 (75%)
GLSZM	16 (100%)	16 (100%)	14 (87.5%)	9 (56.3%)	16 (100%)	16 (100%)	16 (100%)	12 (75%)	16 (100%)	16 (100%)	16 (100%)	12 (75%)
NGTDM	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)
Mean	106 (99.1%)	106 (99.1%)	97 (90.7%)	77 (72%)	105 (98.1%)	106 (99.1%)	106 (99.1%)	93 (86.9%)	104 (97.2%)	106 (99.1%)	105 (98.1%)	87 (81.3%)
Total mean	96.5 (90.2%)				102.5 (95.8%)				100.5 (93.9%)

	UNLM 0.005				UNLM 0.01
	σ = 0.005	σ = 0.01	σ = 0.02	σ = 0.05	σ = 0.005	σ = 0.01	σ = 0.02	σ = 0.05
SHAPE	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)	14 (100%)
FIRST ORDER	17 (94.4%)	17 (94.4%)	17 (94.4%)	15 (83.3%)	17 (94.4%)	17 (94.4%)	18 (100%)	15 (83.3%)
GLCM	24 (100%)	24 (100%)	23 (95.8%)	13 (54.2%)	24 (100%)	24 (100%)	24 (100%)	14 (58.3%)
GLDM	14 (100%)	14 (100%)	14 (100%)	10 (71.4%)	14 (100%)	14 (100%)	14 (100%)	10 (71.4%)
GLRLM	16 (100%)	16 (100%)	16 (100%)	11 (68.8%)	16 (100%)	16 (100%)	16 (100%)	11 (68.8%)
GLSZM	16 (100%)	16 (100%)	16 (100%)	9 (56.3%)	16 (100%)	16 (100%)	16 (100%)	9 (56.3%)
NGTDM	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)	5 (100%)
Mean	106 (99.1%)	106 (99.1%)	105 (98.1%)	77 (72%)	106 (99.1%)	106 (99.1%)	107 (100%)	78 (72.9%)
Total mean	98.5 (92.1%)				99.25 (92.8%)

MR Vendors Influence Results

The influence of the MR vendor company on the filter performance was analyzed using the neuroblastoma databases with a Kruskal–Wallis test and the Tukey–Kramer test as a post hoc analysis. The results showed that there were no significant differences for any filter at any noise level except for the 0.005 and 0.01 UNLMF strengths at a noise level of σ = 0.01 between Philips and GE (p = 0.046 and p = 0.023, respectively). GE images showed the best performance.

Discussion and Conclusion

This study proposes a novel methodology for the selection of the optimal denoising filter based on two new approaches: the use of real phantoms instead of digital phantoms and the analysis of radiomics recovery.

The phantom acquisition sequence simulates as closely as possible the MR sequences used in the evaluation of neuroblastoma patients, allowing to simulate real scenarios (noise, bias field inhomogeneities) under similar conditions, obtaining a homogeneous database on which to perform the first approximations in a controlled context. For a clinically applicable solution, the selected filters were finally tuned in the neuroblastoma database of patients to bring the results closer to clinical reality. Many reported studies used digital phantoms or simulated MR for this type of analysis [3, 14, 18, 25]. In [3], it is reported that the results obtained in digital phantoms do not necessarily support those obtained in real cases of RM. Considering the similarities between phantoms’ and patients’ MR acquisitions, we assumed that the filters that work best for one database will work for the other unlike what may happen with digital phantom.

Quality metrics analysis showed, both in the phantom and patient databases, a strong dependence between the noise level and the used filter. More aggressive filters worsen the behavior of quality metrics for low noise levels and improve it at high levels, unlike those that produce less aggressive smoothing. This occurs for both the UNLMF and the ADF filters, although with some important differences. While UNLMF filters delivered a general better performance in the case of quality metrics, the ADF filters showed better results in the preservation of radiomics.

A closer analysis shows that at low noise levels the quality metrics with the UNLMF filter are higher than those obtained with the ADF, but this difference decreases as the noise level increases. In the case of radiomics, the results are good and similar for both filters at low noise levels, but at high noise levels the UNLMF filter no longer recovers them. This is because the amount of noise that the UNLMF is able to remove is directly related to the strength value of the filter, not being able to perform effectively when noise levels exceed the filter’s capacity. While the ADF is able to better adapt to the level of noise in the image, the UNLMF fails to perform this task successfully.

The study of the preservation of radiomics features for the evaluation of different filters is novel. Several articles assessed the reproducibility and robustness of radiomics after applying different preprocessing techniques, such as denoising or normalization, on the original source images [24, 26–28], although there are no references evaluating the impact of denoising filters on radiomics after adding artificial noise. We directly evaluated the impact of denoising on the posterior extraction of image biomarkers. Our results showed that the application of some denoising filters, such as ADF, improved the recovery of radiomics features. This improvement is mainly observed on second-order radiomics features, which are based on the computation of gray matrices (GLCM, GLDM, GLRLM, and GLSZM features). These matrices measure the relationship between a voxel and its neighboring voxels; therefore, changes in voxel intensity due to an increase of noise modify the value of these features. ADF filters are particularly efficient at removing these changes, restoring the original intensity values by smoothing slightly the image while preserving its structural information.

It is important to note that a small distortion of the radiomics characteristics was observed at low noise levels. In this case, filters may remove not only the artificially added noise, but also some intrinsic noise of the image as the Johnson–Nyquist noise [4, 5], by modifying the original radiomics of the image, which does not imply a necessarily worse result. Similarly, quality metrics could be affected by this fact because images are not noise-insulated.

Considering the large variance between cases and there are no significant differences between filters, we used an external validation database to support the selected filter reproducibility (extrapolation to independent cases and overfitting avoidance). The additional Patient Validation database supported our results by showing the independence and robustness of the selected filter, ADF with a conductance of 1 and 2 iterations, against the database used. In addition, the performance of the filters is practically unaffected by the type of vendor.

The study has some limitations. Original clinical images have different noise levels. We do believe that noise distribution was small and similar between groups. Also, the proportion of cases from the different vendors was unbalanced (18 GE, 4 Philips, 3 Siemens), although we do not see this might affect our results.

In conclusion, the comparison of 5 different filter families (ADF, CFF, GF, NLMF, and UNLMF) in T2-weighted MR images from both phantoms and pediatric patients with neuroblastoma showed that the ADF, with a conductance of 1 and 2 iterations, should be used for a more reproducible extraction of radiomics features and determination of imaging biomarkers in oncology.

Funding

This work was supported by Horizon 2020 project (RIA, topic SC1-DTH-07–2018).

Availability of Data and Material

Images were centralized at the PRIMAGE platform repository.

Declarations

Conflict of Interest

The authors declare no competing interests.