Abstract
Objective:
Study the impact of local policies on near-future hospitalization and mortality rates.
Materials and Methods:
We introduce a novel risk-stratified SIR-HCD model that introduces new variables to model the dynamics of low-contact (e.g., work from home) and high-contact (e.g., work on-site) subpopulations while sharing parameters to control their respective R0(t) over time. We test our model on data of daily reported hospitalizations and cumulative mortality of COVID-19 in Harris County, Texas, from May 1, 2020, until October 4, 2020, collected from multiple sources (USA FACTS, U.S. Bureau of Labor Statistics, Southeast Texas Regional Advisory Council COVID-19 report, TMC daily news, and Johns Hopkins University county-level mortality reporting).
Results:
We evaluated our model’s forecasting accuracy in Harris County, TX (the most populated county in the Greater Houston area) during Phase-I and Phase-II reopening. Not only does our model outperform other competing models, but it also supports counterfactual analysis to simulate the impact of future policies in a local setting, which is unique among existing approaches.
Discussion:
Mortality and hospitalization rates are significantly impacted by local quarantine and reopening policies. Existing models do not directly account for the effect of these policies on infection, hospitalization, and death rates in an explicit and explainable manner. Our work is an attempt to improve prediction of these trends by incorporating this information into the model, thus supporting decision-making.
Conclusion:
Our work is a timely effort to attempt to model the dynamics of pandemics under the influence of local policies.
Keywords: COVID-19, SIR-HCD, SIR, Epidemic forecasting model, Reopening policy, Risk stratification
1. Introduction
COVID-19 has taken the international community by surprise [1]. At the time of writing this paper, the COVID-19 pandemic has reached almost 100 million confirmed cases and surpassed two million deaths worldwide [2]. COVID-19 has had a dramatic impact on health care systems in even the most developed countries [3]. Without effective vaccines and treatments in sight, the only effective actions include containment, mitigation, and suppression [4].
The infection, hospitalization, and mortality trends of COVID-19 across different countries vary considerably and are affected mainly by policy-making and resource mobilization [5]. A recent study, which spatiotemporally analyzed COVID-19 related tweets, found that the evolution of social distancing facets significantly affects potential pandemic hotpots [6]. Predicting local trends of the epidemic is critical for the timely allocation of medical resources and for evaluating policy changes to curtail economic impact [7]. In the United States, policies vary by state and city, and therefore, robust local models are essential for learning fine-grained changes that meet the needs of local communities and policymakers.
Under appropriate intervention, early studies observed a downward trend on COVID-19 epidemic curves near the end of the eight-week post-outbreak period (following classical epidemiology models) [8]. However, traditional models do not account for the impact of local policies, such as a multi-phase reopening. Due to varying restrictions, the local hospitalization and mortality trends in Texas have experienced multiple upward and downward trends. The large variations between different counties in Texas during the months from May to October motivated the need to study the underlying impact of policy on local mortality and hospitalization trends. In this paper, we present the design of our regional model and demonstrate its use by applying them to the Harris County, TX area marking their difference from global trend estimation models.
According to the 2019 census, Harris County is the most populous county in Texas and the third most populous county in the United States. The hospitalization and mortality rate in Harris County is large enough to support model optimization during the training process, and avoid excessive overfitting issues. In order to evaluate the model ability of fitting the trends followed by changing policies, we assembled COVID-19 epidemic data in Harris County from the beginning of the reopening phase (May 1, 2020) to October 4, 2020.
Owing to the lack of accepted estimations of infection rates in asymptomatic individuals (using, e.g., random serological testing [9]), we focused on the more reliable mortality and hospitalization rates. We developed a forecasting model using local fine-grained hospital-level data to track the changes in hospitalization and mortality rates owing to reopening orders in the greater Houston area encompassing nine counties in the state of Texas, USA. The modeled area consists of 4,600 km2, incorporating a population of 4,713,325 people (by the 2019 census) and includes over 100 hospitals with a total bed capacity of 23,940 [10,11]. Our methodological contribution is by incorporating the impact of phased reopening into the model. We achieve it by splitting the targeted population into low-contact and high-contact groups (determined by job category and the subpopulations from that job category that return to work at different phases of the reopening, e.g. health-care provider or public transportation workers). The mechanism adjusts the proportion of infectious subpopulations (determined by their job category) to quantitatively represent the policy impact on the epidemiological dynamical system (refer to Fig. 1 for a high-level overview). We demonstrate our new approach using a policy-aware risk-Stratified Susceptible-Infectious-Recovered Hospitalization-Critical-Dead (SSIR-HCD) model, which compares favorably to existing models.
Fig. 1.
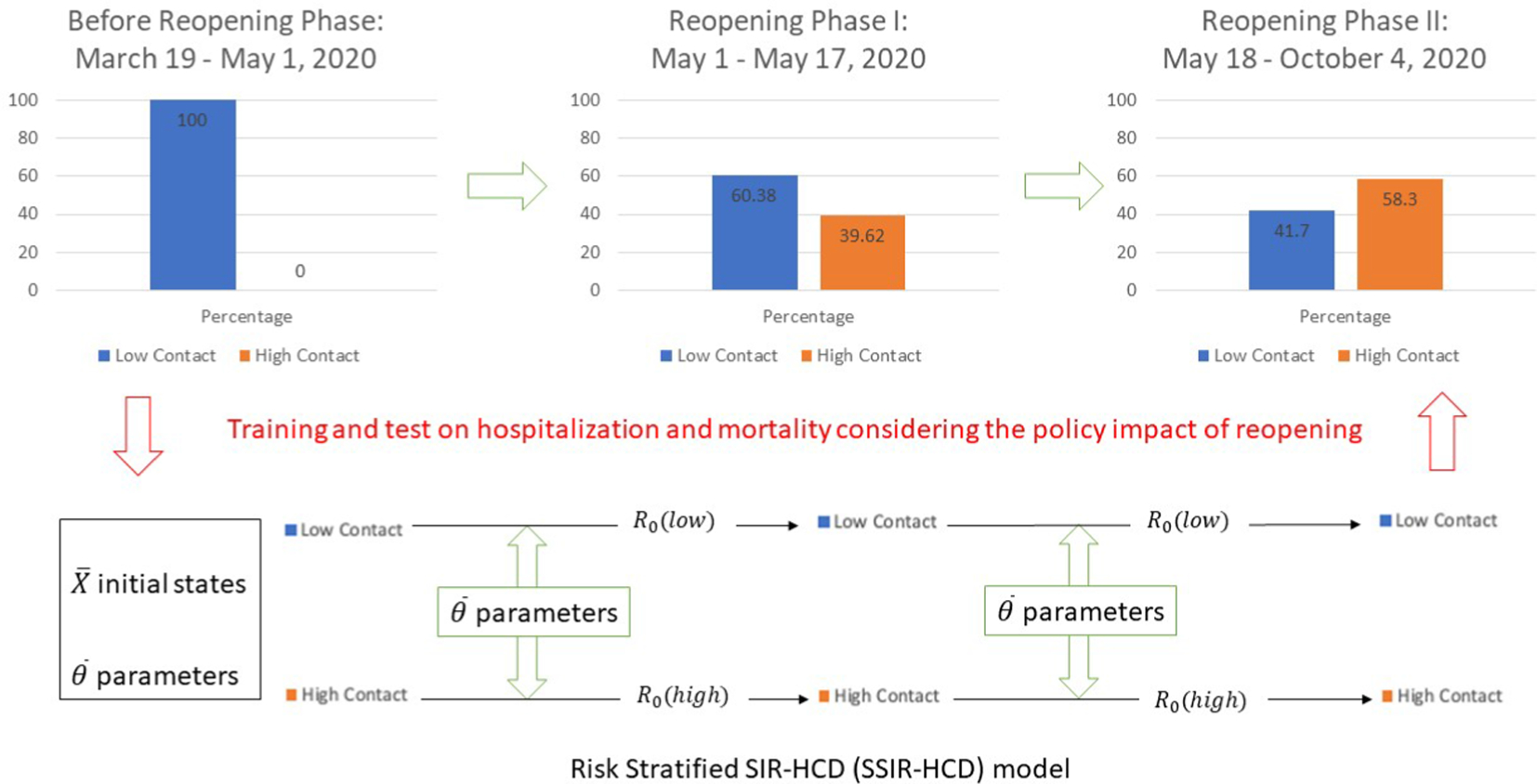
A high-level illustration of our new model SSIR-HCD to accommodate the subpopulation changes during the implementation of the phased reopening policy.
2. Background and related work
There are many predictive models for COVID-19 trend prediction. The Center for Disease Control (CDC) already hosts 37 different trend predictors [14] to forecast total death, and 13 different forecasting models for total hospitalization [15]. They belong to four l categories:
Data-driven models (with no modeling of dynamic population compartments s), which includes regression-based parametric and non-parametric models (Auto-Regressive Integrated Moving Average or ARIMA, Support Vector Regression, Random Forest), Double Exponential Model built by Sampaio [16], neural network (deep learning) based trend prediction (e.g., GT-DeepCOVID [17]), VDM-based machine learning model [18], among others.
Epidemiology based dynamic models based on grouping populations into a discrete set of compartments (i.e., states), and defining ordinary differential equations (ODE) rate equations describing the movement of people between compartments: SEIR (Susceptible, Exposed, Infected, Recovered) models and their myriad variants are examples in this category.
Individual-level network-based models: fine-grain modeling of a population through agent simulation, including NetLogo by Marathe et al. [19] and NotreDame-FRED [20].
Ensemble and hybrid models: including the Imperial College London short-term ensemble forecaster [14] and the IHME model [21] that combines a mechanistic disease transmission model and a curve-fitting approach.
Among existing models, the ODE compartment-based models occupy a middle ground between network models at the individual-level and count-driven statistical analyses that are disease-dynamics-agnostic. ODE compartment-based models will thus be our main focus in this paper. Compartment models, which originated in the early 20th century [22], still represent the mainstream in epidemiological studies of infectious disease. They make a critical mathematical simplification by decomposing the entire population into compartments (i.e., states), e.g., susceptible, infectious, recovered, and use ODEs to model the transitions between the compartments (Table 1). These compartment models make assumptions that the observation counts in the various compartments naturally reflect the reproduction number R0 that changes over time. The recent COVID-19 pandemic, however, has introduced the need to incorporate knowledge about lockdown policy interventions (i.e., how long the population will remain at home), which existing compartment models do not take into account. We observe different patterns of hospitalization and mortality even within a single metropolitan area such as Harris County in the greater Houston area, TX, which poses challenges to traditional epidemiological models. While it is expected that local policies (shutdown and reopening) introduce perturbations to the disease dynamics, it is not clear how to quantify these impacts and provide counterfactual reasoning to support future policy decisions. One model that attempts to address this gap is using reduced-form econometric methods to model anti-contagion policies [23] but does not consider stratifying the population into risk groups based on potential exposure. Cartocci’s work [24] proposes a prediction model compartalized by sex and age groups using a time-varying susceptible-infected-recovered-deceased (SIRD) model, but does not account for social reflections towards pandemic evolution and spread. Another study by Rubin et al. [25] developed a model using replication factors for infection and social distancing, humidity levels and population density in counties across the United States. However, it does not model disease dynamics, focusing instead on building a hierarchical linear mixed-effects model with random intercepts for each county to demonstrate that distancing has the most significant association with a reduction in SARS-CoV-2 transmission. The article written by Nikolopoulos et al. [26] reports on the county-level performance of 52 methods involving time series, machine learning, deep learning, non-parametric (e.g., nearest neighbors), one epidemiological model – SIR model. It does consider lockdowns but only from the point of view of projecting various things like groceries, and none of these 52 approaches model the spread of COVID-19 disease because of lockdown policies. Some prior works utilize deep learning approaches to forecast the trend. Aljaaf [27] introduced a feed forward neural network to forecast COVID-19 confirmed cases in Iraq, but the model optimization process does not involve lockdown policy interventions and stratified population to adjust parameters.
Table 1.
ODE compartment models used by epidemiologists to study infectious diseases.
| Model | Infection | Hospitalization | Mortality | Exposure Period | Policy | Employment |
|---|---|---|---|---|---|---|
|
| ||||||
| SIR [19] | x | |||||
| SIRD [20] | x | |||||
| SEIRD [21] | x | x | x | |||
| SIR-HCD (simplified from [46]) | x | x | x | x | ||
| SEIR-HCD [46] | x | x | x | x | ||
| Anti-contagion policy integrated SIR [18] | x | x | ||||
| YYG [28] | x | x | x | |||
| NN-SIR-HCD | x | x | x | x | x | |
| Stratified SIR-HCD | x | x | x | x | x | |
S: susceptible population, E: exposed population, I: infectious population, R: recovered population, H: hospitalized population, C: critical population, and D: dead population.
Note that NN-SIR-HCD and Stratified SIR-HCD are developed in this paper, the former serves as a baseline model.
Our SSIR-HCD is a unique effort to close the modeling gap by using appropriate data to enrich the established compartment models. It stratifies the population into high-contact and low-contact groups reflecting the causal relationship between social distancing and disease transmission. Our approach is different from another SEIR-based model, YYG, that works with a discretized version of the standard continuous ODE SEIR model and focus on predicting deaths with a simple data-driven mechanism to account for reproduction number R0 that reflect reopening policies [28]. Unlike our model, they do not stratify population groups in the SEIR model to account for differences in exposure risk.
3. Method
3.1. Data and materials
We collected experimental datasets of the daily reported hospitalization and cumulative morality of COVID-19 that occurred in Harris, Texas, from May 1, 2020 (the start date of Phase 1 reopening in Houston, TX) until October 4, 2020. Population data was retrieved from by USA FACTS [29], industry employment data was gathered from the U.S. Bureau of Labor Statistics BUREAU OF LABOR STATISTICS [30], and the hospitalization data sources originate from Southeast Texas Regional Advisory Council (SETRAC) COVID-19 report [31]. We retrieved used the length of hospitalization and critical cases from the TMC daily news [32] (length of hospitalization and critical cases) to set the initial length of hospitalization for our model and. We also downloaded used mortality data from the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University county-level report [33]). Note that New York Times data combine confirmed and suspected cases in their reporting of mortality. To be consistent, we used SETRAC hospitalization reporting that contains both confirmed and suspected cases. In this study, we focused on Harris County data, one of the nine counties in Houston, TX, with the largest population.
3.2. SIR-HCD overview
We propose a forecast model based on SIR-HCD with a novel variant on compartments to address differences in local policy. In SIR-HCD, the entire population is divided into six sub-groups: susceptible population S, exposed population E, infectious population I, recovered population R, hospitalized population H, critical population C, and dead population D. The transitions between sub-groups are governed by nonlinear ordinary differential equations. Please refer to Table 2 for our nomenclature. We use the SIR-HCD to model the state transitions. The model is a simplification of SEIR-HCD.
Table 2.
Nomenclature for variables, parameters and their roles in the ODE system.
| Symbol | Meaning | Roles in the ODE system |
|---|---|---|
|
| ||
| S(t) | Susceptible population at a timet | Fitted variable |
| I(t) | Infectious population at a timet | Fitted variable |
| R(t) | Recovered population at a timet | Fitted variable |
| H(t) | Hospitalized population at a timet | Fitted variable |
| C(t) | Critical population at a timet | Fitted variable |
| D(t) | Dead population at a timet | Fitted variable |
| R0, aka,R0 (t) | Reproduction number of coronavirus at a time t, which differs from changing quarantine protocols | Fitted parameter |
| Tinc | COVID-19 incubation period | Fixed parameter |
| Thosp | Average time a patient is in the hospital before either recovering or becoming critical | Fitted parameter |
| Tcrit | Average time a patient is in critical state before either recovering or dead | Fitted parameter |
| ra | Asymptomatic rate in the infected population | Fitted parameter |
| rc | Critical rate in the hospitalized population | Fitted parameter |
| rf | Deceased rate in the critical population | Fitted parameter |
Variables are the targets of modeling in the ODE system while parameters influence the optimization.
We decided to drop exposed state (E), which cannot be reliably modeled in COVID-19 because the CDC guideline for exposure, determined as staying within less than six feet for more than fifteen minutes from a person with known or suspected COVID-19 [13], is too short a time period to be modeled adequately. Thus, a simpler SIR-HCD model, which assumes the possibility of direct transitions between the susceptible state and the infectious state, is more suitable for COVID-19.
In the SIR-HCD model, some susceptible people may enter the infectious state after the incubation period. Infectious people may either get hospitalized or recover after a certain period of time. A proportion of the hospitalized people might be admitted to the Intensive Care Unit (ICU), while the rest of them will recover in the hospital. Similarly, among the critical cases (i.e., ICU patients), some people might die, and others will recover. Thus, the SIR-HCD model follows a series of nonlinear ODEs to model the state transitions:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
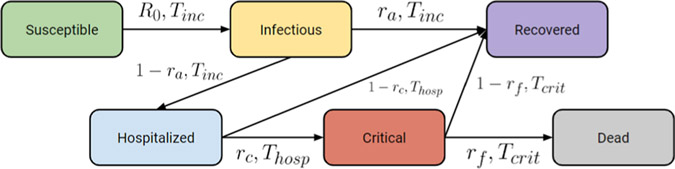
Note that R0(t), which is shorted as R0 and used interchangeably in our paper, denotes a dynamically changing reproduction number (the changes are due to dynamic quarantine policies in Houston). The symbol Tinc denotes the average incubation period of COVID-19. In the equations that model H, C, R, D, the term Thosp, represents the average time that a patient is in a hospital before either recovering or becoming critical, and Tcrit denotes the average time that a patient is in a critical state before either recovering or dying. In addition, ra refers to the asymptomatic rate in infected populations I, rc refers to the critical rate in hospitalized population H, and rf refers to the deceased rate in critical population C. This model is more robust than SIR, as the introduction of more reliable observations of H, C, D provides extra stabilization to the dynamic system. Fig. 2 illustrates the SIR-HCD model with its primary states and transitions implied by the ODE function.
Fig. 2.
SIR-HCD model at a high level with different compartments and transitions.
With reopening policies in place, there are more interactions between people and so the likelihood of spread increases. Our expectation is either that R0 remains constant (because people maintain safe distances and follow CDC protocols), or (more likely) that it increases/decreases periodically with spotty compliance with pandemic protocols. To make the computation tractable, we used a step function to fix R0 at different time stages following the policy status. As expected, the value of R0(t) varied over time following changes in the strictness of the quarantine protocols in Texas, which may impacted social distancing behaviors. Specifically, R0(t) initially reached a higher value following the start date of Reopening Phase II (May 18, 2020) when the Texas government eased the quarantine level to restore the economy, and then dropped to a lower point when a face-covering order was issued on July 2, 2020 [34]. Based on the observation in early August that the prevalence curve went through a plateau and then climbed again, which slightly slowed down the hospitalization downward curve, here we set August 1, 2020, as the turning point of the prevalence increases.
We set the starting point t = 0 as the reopening date, May 1, 2020. The initial states H(t = 0) and D(t = 0) are the numbers of reported hospitalized cases and cumulative mortality in Harris County on that date. We decided not to rely on confirmed cases, assuming that the actual number for the infected population is larger than the reported number (such an effect has been reported in California [35] and New York [36]). Since a fraction of the actual infected patients were hospitalized on the first day, the initial infectious population I(t = 0) is therefore estimated to be m times the initially hospitalized number H(t = 0), where m is a positive constant coefficient. Some studies suggested that true positive infectious cases should be 50–90 times more than the reported positives [37,38]. In the Harris County projection, we set m to be 60, assuming that H(t = 0) is approximately equal to “known positives” on the first day. To estimate the recovery rate, we divided the case mortality rate in Harris County (the number of confirmed deaths on the current day) by the number of confirmed cases 14 days before that, as reported by Johns Hopkins University. The average mortality rate during the first month of training data was 2%. Therefore, we have an estimated recovery rate of 98%. In this case, the initially recovered individuals R(t = 0) = 0.98·H(t = −14) = 0.98m∙H(t = −14), where t = −14 refers to 14 days earlier than the starting date (i.e., April 17, 2020). The number of critical individuals C(t = 0) is set to be 50% of hospitalized individuals H(t = 0) based on the average proportion of ICU usages among COVID-19 hospitalization in Texas [13,31]. The initial number of the susceptible population S(t = 0) is
| (7) |
where N is the total population in the county.
Following a previous SIR-HCD optimization method [39], we used the limited memory Broyden–Fletcher–Goldfarb–Shanno algorithm (L-BFGS-B) [40] to optimize the ODE system. According to previous COVID-19 studies [41], the constant parameter Tinc is set to 11.5 days. The optimal values of parameters Thosp, Tcrit, ra, rc, and rf in the model were obtained by minimizing the weighted average mean squared log error (MSLE) loss function L(MSLE). To make the prediction more focused on the recent trajectory, we used the squared log error at each time point with a weight parameter satisfying the condition Wt > Wt−1. Finally, we used a time inverse function Wt = 1/(tmax − t + 1) in our model, where tmax is the maximum time.
| (8) |
3.3. SSIR-HCD model to explicitly account for local policy’s impact
In this section, we introduce the unique aspect of our model that differentiates it from existing ones. Our intuition here is that people get infected either through family transmission or through social (including job) activities. In the transition from a strict stay-at-home to reopening, the population is subject to changes in their social activities, which impact their probability of infection as well as their risk of transmission to their family members. Therefore, we can divide the total population in Harris County into two groups; a low-contact group, which includes people in industries that were still closed (e.g., working from home subpopulation and their families, including those who are unemployed but not homeless), and a high-contact group includes people in industries that were reopened due to economic restart (e.g., working on-site subpopulation and their families). Intuitively, the subpopulation of people who work from home is those who continue to stay at home and have limited chances of contacting the working subpopulation.
The two groups share the same fitted parameters Thosp, Tcrit, rm, rc, rf, as well as the same constant incubation period Tinc, but they are associated with different R0. To differentiate two subpopulations, we set parameter bounds so that R0(t) for the low-contact group is proportionally lower than that of the high-contact group over time. The unique coupling strategy makes it possible to directly reflect the impact of policy on SSIR-HCD.
According to reopening announcements released on the Texas government website [42] and the Houston employment rates by industry (reported by the Greater Houston Partnership Research [43]), necessary industries such as transportation, utilities, government, and a subset of the health services kept running before and during the reopening of the economy, accounting for 32.3% of the population in Houston. After releasing Reopening Phase I policies (May 1, 2020), 100% of the essential industries reopened, in addition to 15% health services, 25% professional and business service, and 25% leisure and hospitality, constituting a working on-site (high-contact) subpopulation proportion of 39.62% after subtracting the unemployment rate of 0.4% [44]. The proportion of the high-contact population after Reopening Phase II (May 18, 2020) was a combination of 100% of the essential industries, 100% health services, 50% of professional and business service, and 50% of leisure and hospitality industries. Hence, the high-contact proportion among Reopening Phase II was 58.3% after subtracting the unemployment rate. Our model accounts for the change of low-contact and high-contact subpopulations between Reopening Phase I and Reopening Phase II, therefore directly modeling the policy’s impact on epidemiological data over time.
3.4. Experimental setting
Our training process uses MSLE to minimize the errors in curve-fitting. Additionally, we evaluated the performance using mean absolute error (MAE), which was not used for the curve-fitting process.
Fig. 3 shows the reported hospitalization and cumulative mortality from March 19, 2020, to October 4, 2020. The Texas government started phased-in reopening of the state on May 1, 2020 (the stay-at-home order was issued on March 31, 2020), then continued to expand reopening industries on May 18, 2020. The reopening strategies continued in steps until, faced with a serious COVID-19 transmissibility rebound, the government issued the face-covering order on July 2, 2020, to urge all residents to protect themselves from possible infections. Following these reopening phases in Texas, the daily hospitalization curve in Harris County was divided into three phases, where Reopening Phase II involved two subphases:
Fig. 3.
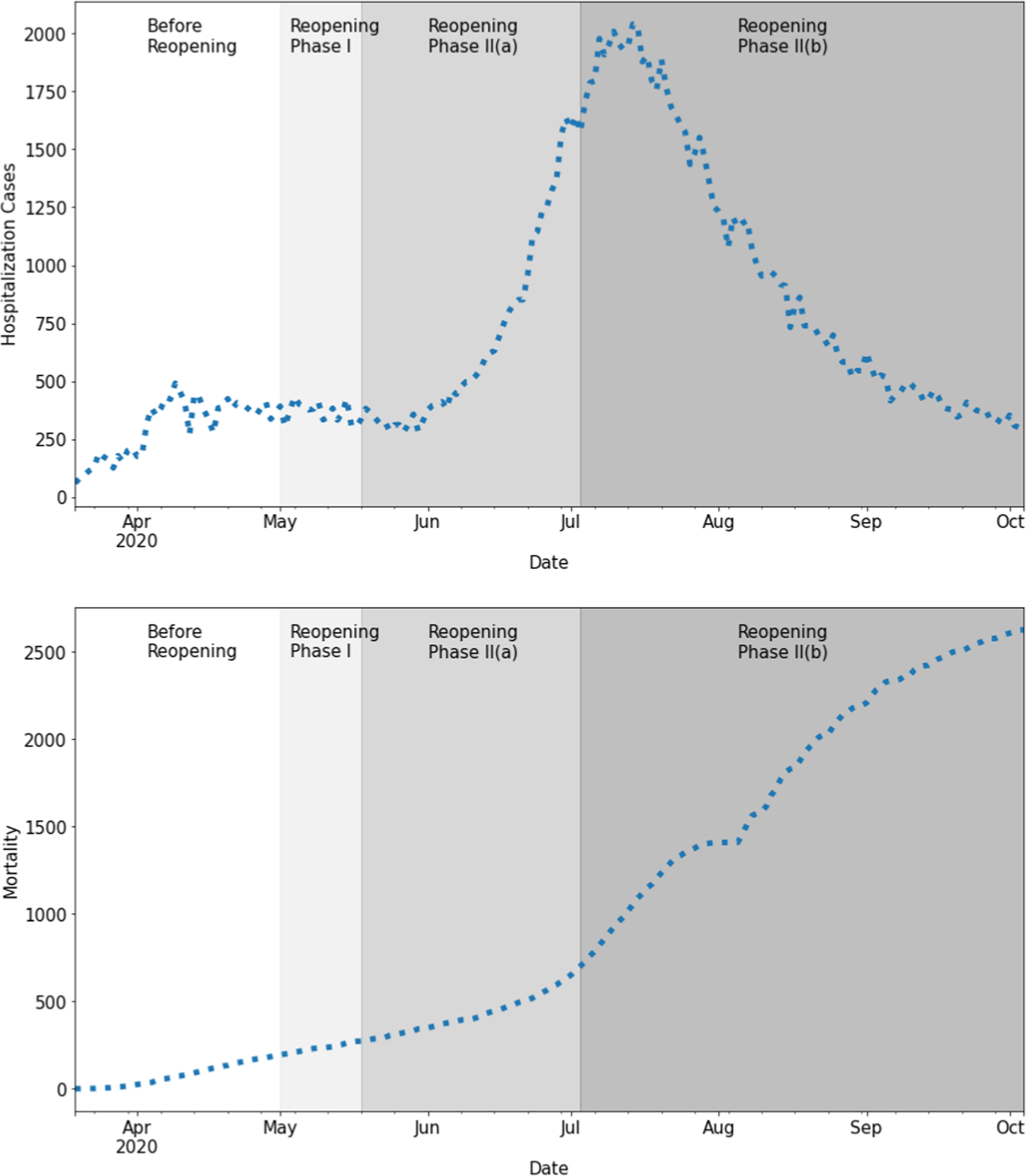
Daily hospitalization (left) and cumulative mortality (right) during the time period from March 19, 2020, to October 4, 2020.
Before Reopening Phase: March 19 - May 1, 2020
Reopening Phase I: May 1 - May 17, 2020
- Reopening Phase II: May 18 - October 4, 2020
- Reopening Phase II(a): May 18 - July 1, 2020
- Reopening Phase II(b): July 2 - October 4, 2020
The hospitalization curve represents a delayed epidemic effect since the publication of the strict stay-at-home order on March 30, 2020. After reopening policies were issued in Texas (May 1, 2020), it influenced the disease dynamics during Reopening Phase I and Reopening Phase II.
Our local hospitalization and mortality modeling aim to fit the most recent phases (i.e., Reopening Phase I and Reopening Phase II) starting from May 1, 2020, to October 4, 2020. We validated the 7-day accuracy with data between September 13 and September 19, 14-day accuracy with data between September 13 and September 26, and 21-day accuracy between September 13 and October 4. For comparison, our baselines were time-series regression models (exponential smoothing, autoregression, and ARIMA), Double Exponential Model, YYG model [28], and vanilla SIR-HCD. Note that the baseline comparison models predict hospitalization and mortality time series separately, while ours make joint predictions. We also included our own Neural Network SIR-HCD model, which is equally flexible as SSIR-HCD. Interested readers can find the details in the Appendix.
Our experiments were conducted using Python 3.8, with parallel GPUs running on CUDA version 11.0. The associated Jupyter notebook code is available on Github (see the link in Abstract).
4. Results
Trained with Harris County cumulative hospitalization and mortality data in Reopening Phase I and Reopening Phase II, our SSIR-HCD model fits the trends in the training data well: Reopening Phase I (MAE = 98.40 for hospitalization, MAE = 13.10 for mortality), Reopening Phase II(a) (MAE = 72.24 for hospitalization, MAE = 12.70 for mortality), and Reopening Phase II(b) (MAE = 55.43 for hospitalization, MAE = 69.47 for mortality). As Fig. 4 shows, the local hospitalization and mortality training curves are very close to the reported data, and the test curves also follow the data trends closely, which indicates our model is not overfitting to the training period.
Fig. 4.
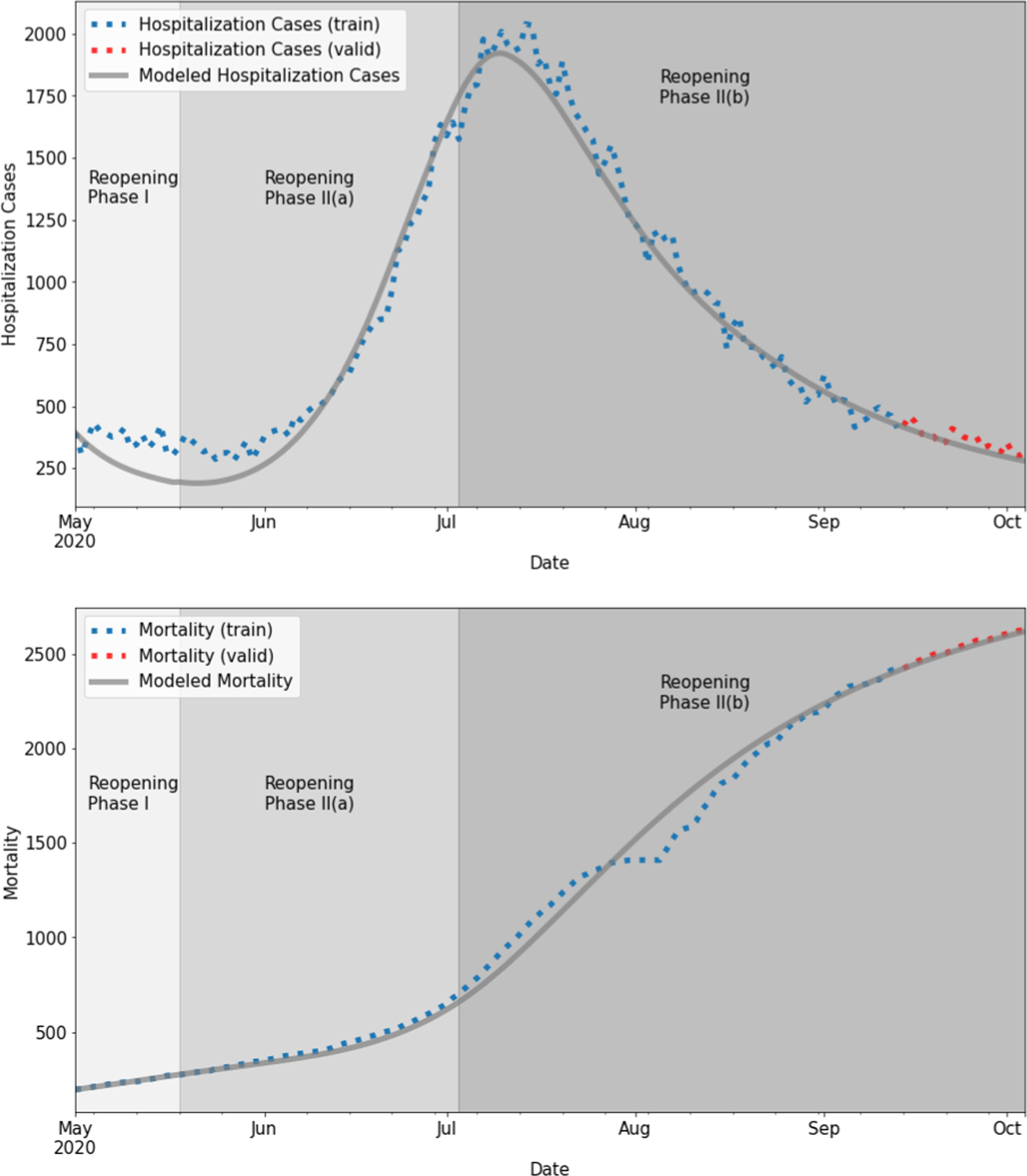
Fitted daily hospitalization cases and cumulative mortality (training: blue + test: red) using SSIR-HCD with step function. For hospitalization training, reopening phase I, II(a), and II(b) had MAE = 98.40, MAE = 72.24, and MAE = 55.43, respectively. For mortality training, reopening phase I, II(a), and II(b) had training MAE = 13.10, MAE = 12.70, and MAE = 69.47, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Table 3(a), (b), (c) summarizes the prediction accuracies of the baseline models and the risk-stratified SIR-HCD model (SSIR-HCD) in three different timeframes. Since the Double Exponential Model and YYG model do not make hospitalization projections, their comparison results are only based on mortality. As expected, 7-day evaluations performed better than 21-day evaluations in most cases. While the performance of the baseline models decreases for longer evaluation periods, the performance of our proposed model still obtained high accuracy. For the hospitalization prediction in all evaluation timeframes, the proposed SSIR-HCD model with R0(t) step function had significantly higher accuracies (7-day MAE = 22.89, 14-day MAE = 36.35, 21-day MAE = 54.14) compared to the baseline time-series regressions involving Simple Exponential Smoothing (7-day MAE = 33.57, 14-day MAE = 44.99, 21-day MAE = 79.30), Autoregression (7-day MAE = 32.31, 14-day MAE = 55.74, 21-day MAE = 86.53), and ARIMA (7-day MAE = 48.94, 14-day MAE = 89.50, 21-day MAE = 124.15). For mortality prediction, we found that the time-series regression models generally predict well, and our proposed model had comparable accuracy. This high accuracy in mortality prediction of the general time-series regression models is mainly because the mortality rates were more stable than the hospitalization curve over time. For SIR-HCD model family comparison, the hospitalization and mortality prediction in our proposed SSIR-HCD model with R0(t) step function performs slightly better than the vanilla SIR-HCD model, and SSIR-HCD model with R0(t) exponential function using hill decay operation to smooth between different R0(t) values. Another advantage of the SSIR-HCD model with R0(t) step function over the vanilla SIR-HCD model and SSIR-HCD model with R0(t) exponential function resides in the ability to conduct counterfactual analysis and parameter simplicity, respectively. The YYG model had the lowest error in mortality prediction out of the SEIR models family as it utilized daily mortality data as the training set, which may lead to a good prediction when daily data do not vary substantially. Moreover, the performances with the auto-regressive model and the SSIR-HCD model with exponential function are very close to our proposed model. The family auto-regressive model has the capability to achieve good fitting results accounting for historical patterns of the curve, and our prediction period has a relatively stable trending, which is discernible for auto-regressive modeling. The only difference with the SSIR-HCD model with exponential function is the way to control transmission rates. The hill-decay exponential function may have more significant performance with pandemic curves in state or country level supported by the more smoothing trend.
Table 3a.
7-day forecast using time-series regression baselines, SSIR-HCD, and Neural Network SIR-HCD model. The 7-day forecast period was from September 13 to September 19, 2020.
| Method | Training period | Hospitalization MSLE | Mortality MSLE | Hospitalization MAE | Mortality MAE | |
|---|---|---|---|---|---|---|
|
| ||||||
| Baselines | Simple Exponential Smoothing | Phase 1 and Phase 2 | 0.00914 | 0.00050 | 33.57 | 48.00 |
| Auto Regression | Phase 1 and Phase 2 | 0.00876 | 0.00001 | 32.31 | 6.70 | |
| ARIMA | Phase 1 and Phase 2 | 0.01853 | 0.00030 | 48.94 | 7.06 | |
| Double Exponential Model | Phase 1 and Phase 2 | N/A | 0.41438 | N/A | 1166.43 | |
| YYG | Phase 1 and Phase 2 | N/A | 0.00005 | N/A | 17.04 | |
| Vanilla SIR-HCD | Phase 1 and Phase 2 | 0.01233 | 0.00033 | 39.29 | 43.91 | |
| Proposed models | SSIR-HCD with step function | Phase 1 and Phase 2 | 0.00525 | 0.00008 | 22.89 | 20.86 |
| SSIR-HCD with exponential function | Phase 1 and Phase 2 | 0.01063 | 0.00011 | 36.23 | 25.04 | |
| Nonlinear extension of SIR-HCD* with neural networks | Phase 1 and Phase 2 | 0.63089 | 0.03723 | 432.99 | 219.74 | |
See Appendix for more details.
Table 4 displays the fitted values of five training parameters in SSIR-HCD equations for the low-contact group and the high-contact group. These fitted parameter values correspond well to the values obtained in previous studies of COVID-19 [45,46,13]. The ratio of hospitalizations turning into critical is close to the average ICU proportion among hospitalizations in Harris County, which was 30% in our initial state settings [31,13]. The constant parameter Tinc is set at 11.5 in both groups based on the values suggested by the World Health Organization (WHO) [47] and the CDC [13]. As a sanity check, the R0 values in the low-contact group are indeed lower than those values in the high-contact group, indicating a lower expected number of cases directly infected by individuals in the low-contact group.
Table 4.
Fitted values of parameters learned from the training data in SSIR-HCD model.
| Low-contact group | High-contact group | |
|---|---|---|
|
| ||
| Proportion of population in Reopening Phase I | 60.38% | 39.62% |
| Proportion of population in Reopening Phase II | 41.70% | 58.30% |
| Hospitalization period Thosp | 10.00 days | |
| Critical period Tcrit | 14.00 days | |
| Asymptomatic rate among infectious people ra | 0.996 | |
| Ratio of hospitalizations turning into critical rc | 0.45 | |
| Ratio of critical patients turning into death rf | 0.44 | |
Fig. 5 displays the SSIR-HCD model’s counterfactual analysis results (of our model) on what would have happened in the absence of reopening policies after 236 days on May 1, 2020. In the x-axis, day 0 refers to May 1, 2020, day 17 refers to May 18, 2020, and day 135 refers to September 13, 2020. We restored the proportion of low-contact people and high-contact people to the no-reopening status (corresponding to 31.90% high-contact proportion of the population) while keeping all the trained parameters the same. Upon excluding all changes resulting from the reopening policies, it is noted that both modeled hospitalization and mortality curves become dramatically flat. The hospitalization curve with intervention reaches its peak on day 70, reducing nearly 800 existing cases. This demonstrates that quarantine policies are effective in controlling the spread of coronavirus as well as reducing the number of hospitalizations and mortality rates. Similarly, Fig. 6 displays the counterfactual estimations on what would have happened if the Texas government did not continue to reduce limitations in Reopening Phase II. In Fig. 6, the presumed reopening policies in Reopening Phase I represent moderate control to the hospitalization and mortality curves, reducing nearly 500 existing cases. Since a long stay-at-home order is not economically practical, our counterfactual analysis demonstrates that moderate reopening policies, keeping essential quarantine measures (such as mask order adoption), and opening several industries to lower capacity, may offer a reasonable middle ground between the strict quarantine and fully open economy. The chart of dynamic R0 values show how dynamic R0 differentiates the low-contact group and high-contact group such that modeled hospitalization and mortality curves would be flattened by increasing the proportion of the low-contact population. The model does not use one single reproduction number value to measure the integral transmission rate as the two subgroups have different levels of risks for getting infected.
Fig. 5.
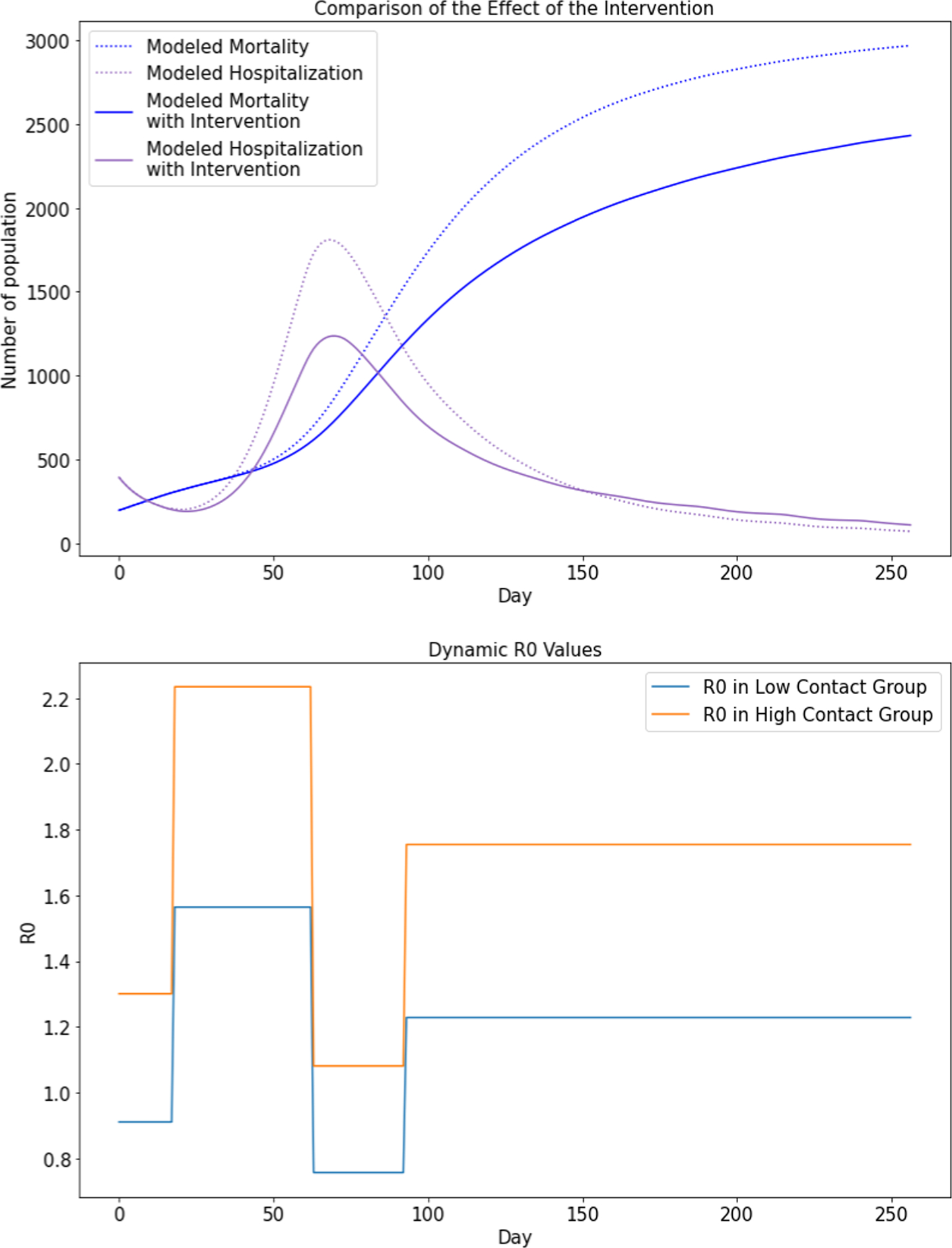
Counterfactual analysis plots assuming Reopening Phase I was not implemented (i.e., no reopening policies were issued).
Fig. 6.
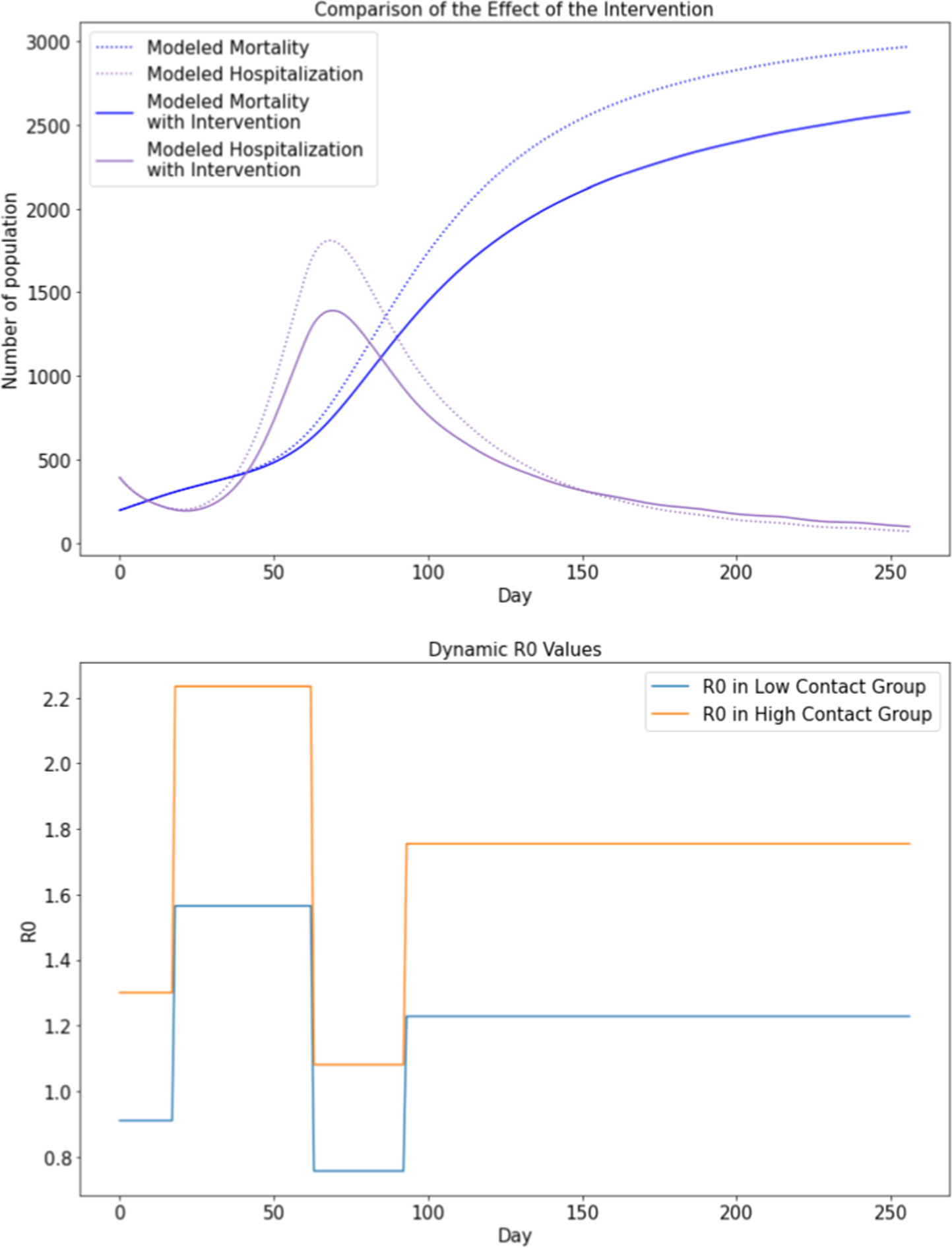
Counterfactual analysis plots assuming Reopening Phase II was not implemented (i.e., only Reopening Phase I policies were issued, but not include Reopening Phase II policies).
5. Discussion
Our SSIR-HCD model forecasts fine-grained COVID-19 hospitalization and mortality by accounting for the impact of local policies. One challenge is that the SSIR-HCD model is very sensitive to the initial values of S, I, R, H, C and D as the number of infectious agents is non-zero at the initial time point. We have managed to avoid overfitting the local time-series curve by deploying values based on the accumulated knowledge of these initial variables. After variable adjustment, the predictive results obtained a low error rate, while also obtaining parameters that are close to real-world values, such as the hospitalization period Thosp and critical period Tcrit that are close to the suggested value in the COVID-19 Scenarios outcome summary [45].
In publicly reported data, the cumulative mortality data in Reopening Phase II does not perfectly follow the hospitalization trends. Our expectation was that it would lag hospitalization cases by approximately 14 days. The actual mortality rate fluctuated in the middle of Reopening Phase II when the number of hospitalization cases started to increase rapidly. Nonetheless, our SSIR-HCD model still approximates the hospitalization and mortality trends better than competing models. Thus, our model is advantageous over baseline regressions. It can fit epidemiological data with complicated shapes, such as Harris hospitalization data, based on the proportion of low-contact and high-contact groups and can consider several epidemiological states together into one model that can make predictions for one or more sub-populations simultaneously. In addition to forecasting, our model offers another unique functionality to support counterfactual analysis, which can be useful in supporting critical decision-making.
The SSIR-HCD model suffers from three major limitations. In particular, our SSIR-HCD model inherits the limitation of the base SIR-HCD model in assuming idealized R0 time-variable function that follows the strength of issued quarantine protocols. This assumption does not hold in future scenarios when economic reopening might change the scope. One possible strategy is to introduce an adjustable R0 control to the model, such as our extended model called Neural Network SIR-HCD (See Appendix), which learns the quarantine strength over time to determine non-monotonic changes in R0. Additionally, our model interprets the recovered population as those who can no longer infect other individuals so that the number of susceptible individuals keeps decreasing over time. We did not consider the possibility that some COVID-19 survivors may be reinfected after they have recovered, which could influence the modeling of the coronavirus transmission rate. Several of these aspects involve controversial discussions in the scientific community, but a powerful model should be able to accommodate different assumptions.
A second limitation is that our model is not taking into consideration certain constraints that are governed from limited resources. For example, the number of daily hospitalizations and critical patients cannot increase without limit due to total bed capacity in hospitals. In fact, Texas Medical Center reported they reached 100% of ICU basis capacity on June 25, 2020 [48]. Our model did not consider hospitalization and ICU delays when some hospitals are fully loaded, which needs more model parameters.
Finally, another limitation of our model is the lack of full consideration for population density, demographics composition, daily in-bound/out-bound traffic flows, and medical resource disparities. For example, many patients in Harris County might come from other counties, but they are treated in the Texas Medical Center (in Harris County), so the total hospitalization and mortality might not completely match the local infection rates. Joint consideration of multiple counties and decomposition of hospitalized patients in terms of their residency would produce more accurate predictions. Moreover, our future improvement may also account for incorporating demographics compositions into the epidemiological ODE sytem in terms of patient sex and age, with stratified parameters indicating different transition rates between clinical states.
6. Conclusion
We have presented a proof-of-concept of a policy-aware compartmental dynamical epidemiological model by stratifying populations into low-contact and high-contact groups based on people’s affiliated industries during the reopening phases at a county level using limited data. We believe it is an important effort to better understand the dynamic feedback of this stratification through an ODE control system. We listed some limitations and future directions to address some of them. We will further explore these challenges with more data and better assumptions to improve existing models.
Supplementary Material
Table 3b.
14-day forecast using time-series regression baselines, SSIR-HCD, and Neural Network SIR-HCD model. The 14-day forecast period was from September 13 to September 26, 2020.
| Method | Training period | Hospitalization MSLE | Mortality MSLE | Hospitalization MAE | Mortality MAE | |
|---|---|---|---|---|---|---|
|
| ||||||
| Baselines | Simple Exponential Smoothing | Phase 1 and Phase 2 | 0.01169 | 0.00155 | 36.35 | 86.07 |
| Auto Regression | Phase 1 and Phase 2 | 0.01807 | 0.00001 | 44.99 | 5.05 | |
| ARIMA | Phase 1 and Phase 2 | 0.10973 | 0.00007 | 89.50 | 18.38 | |
| Double Exponential Model | Phase 1 and Phase 2 | N/A | 0.58694 | N/A | 1320.90 | |
| YYG | Phase 1 and Phase 2 | N/A | 0.00003 | N/A | 11.04 | |
| Vanilla SIR-HCD | Phase 1 and Phase 2 | 0.03671 | 0.00037 | 59.49 | 47.17 | |
| Proposed models | SSIR-HCD with step function | Phase 1 and Phase 2 | 0.01444 | 0.00009 | 36.53 | 22.79 |
| SSIR-HCD with exponential function | Phase 1 and Phase 2 | 0.00012 | 0.00180 | 58.25 | 26.44 | |
| Nonlinear extension of SIR-HCD* with neural networks | Phase 1 and Phase 2 | 0.03984 | 0.77674 | 453.30 | 224.77 | |
See Appendix for more details.
Table 3c.
21-day forecast using time-series regression baselines, SSIR-HCD, and Neural Network SIR-HCD model. The 21-day forecast period was from September 13 to October 4, 2020.
| Method | Training period | Hospitalization MSLE | Mortality MSLE | Hospitalization MAE | Mortality MAE | |
|---|---|---|---|---|---|---|
|
| ||||||
| Baselines | Simple Exponential Smoothing | Phase 1 and Phase 2 | 0.02895 | 0.00285 | 54.14 | 119.05 |
| Auto Regression | Phase 1 and Phase 2 | 0.06123 | 0.00003 | 79.30 | 11.06 | |
| ARIMA | Phase 1 and Phase 2 | 0.39133 | 0.00030 | 124.15 | 35.94 | |
| Double Exponential Model | Phase 1 and Phase 2 | N/A | 0.00063 | N/A | 167.75 | |
| YYG | Phase 1 and Phase 2 | N/A | 0.00008 | N/A | 19.03 | |
| Vanilla SIR-HCD | Phase 1 and Phase 2 | 0.00575 | 0.00039 | 68.32 | 49.53 | |
| Proposed models | SSIR-HCD with step function | Phase 1 and Phase 2 | 0.01816 | 0.00009 | 39.70 | 23.20 |
| SSIR-HCD with exponential function | Phase 1 and Phase 2 | 0.05769 | 0.00012 | 67.65 | 26.93 | |
| Nonlinear extension of SIR-HCD* with neural networks | Phase 1 and Phase 2 | 0.88530 | 0.04211 | 470.87 | 219.59 | |
See Appendix for more details.
Footnotes
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A. Supplementary material
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jbi.2021.103818.
References
- [1].Khatib A, International trends of combating COVID-19: present and future perspectives:, Technium Conference. 4 (2020) 30.05.2020–13:20 GMT. [Google Scholar]
- [2].Puci MV, Loi F, Ferraro OE, Cappai S, Rolesu S, Montomoli C, COVID-19 Trend Estimation in the Elderly Italian Region of Sardinia, Front Public Health. 8 (2020) 153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Leung CC, Cheng KK, Lam TH, Migliori GB, Mask wearing to complement social distancing and save lives during COVID-19, Int. J. Tuberc. Lung Dis. 24 (6) (2020) 556–558. [DOI] [PubMed] [Google Scholar]
- [4].Shah K, Awasthi A, Modi B, Unfolding trends of COVID-19 transmission in India: Critical review of available Mathematical models, Indian Journal of. (2020). http://search.ebscohost.com/login.aspx?direct=true&profile=ehost&scope=site&authtype=crawler&jrnl=22489509&AN=143065544&h=Jw1sIMzKzTXmFnwHLblzxxhD7k4hPhTaNjjnpMgonadPztLGOA%2BamPXlAEbHPhS5LCFLvH1OfLUgpnWaL3vQgw%3D%3D&crl=c. [Google Scholar]
- [5].Xu C, Dong Y, Yu X, Wang H, Tsamlag L, Zhang S, Chang R, Wang Z, Yu Y, Long R, Wang Y, Xu G, Shen T, Wang S, Zhang X, Wang H, Cai Y, Estimation of reproduction numbers of COVID-19 in typical countries and epidemic trends under different prevention and control scenarios, Front. Med. 14 (5) (2020) 613–622, 10.1007/s11684-020-0787-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Kwon J, Grady C, Feliciano JT, Fodeh SJ, Defining facets of social distancing during the COVID-19 pandemic: Twitter analysis, J. Biomed. Inform. 111 (2020) 103601, 10.1016/j.jbi.2020.103601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Liu Q, Liu Z, Li D, Gao Z, Zhu J, Yang J, Wang Q, Assessing the Tendency of 2019-nCoV (COVID-19) Outbreak in China, Epidemiology. (2020). 10.37473/fic/10.1101/2020.02.09.20021444. [DOI] [Google Scholar]
- [8].Chen H, Qian W, Wen Q, The Impact of the COVID-19 Pandemic on Consumption: Learning from High Frequency Transaction Data, (2020). 10.2139/ssrn.3568574. [DOI]
- [9].Brunori P, Resce G, Searching for the Peak Google Trends and the COVID-19 Outbreak in Italy, (2020). 10.2139/ssrn.3569909. [DOI]
- [10].Harris County Community Services Department, (n.d.). https://csd.harriscountytx.gov/ (accessed July 13, 2020).
- [11].Health, (n.d.). https://www.houstontx.gov/abouthouston/health.html (accessed July 13, 2020).
- [13].CDC, Coronavirus Disease 2019 (COVID-19), Centers for Disease Control and Prevention. (2020). https://www.cdc.gov/coronavirus/2019-ncov/hcp/clinical-guidance-management-patients.html#:~:text=The%20incubation%20period%20for%20COVID,CoV%2D2%20infection. (accessed July 8, 2020). [Google Scholar]
- [14].Home - COVID 19 forecast hub, (n.d.). https://covid19forecasthub.org/ (accessed July 13, 2020).
- [15].CDC, COVID-19 Forecasts: Hospitalizations, (2021). https://www.cdc.gov/coronavirus/2019-ncov/cases-updates/hospitalizations-forecasts.html (accessed January 25, 2021).
- [16].Sampaio MOP, Covid-19: A surprisingly effective data driven model, Medium. (2020). https://medium.com/@marcoopsampaio/covid-19-a-surprisingly-effective-data-driven-model-1a3bb0361d7a (accessed August 26, 2020). [Google Scholar]
- [17].COVID-19 Response, AdityaLab, Georgia Tech, (n.d.). https://www.cc.gatech.edu/~badityap/covid.html (accessed July 10, 2020). [Google Scholar]
- [18].da Silva RG, Ribeiro MHDM, Mariani VC, Coelho LDS, Forecasting Brazilian and American COVID-19 cases based on artificial intelligence coupled with climatic exogenous variables, Chaos Solitons Fractals. 139 (2020), 110027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].A Simulation Study of Coronavirus as an Epidemic Disease Using Agent-Based Modeling | Journal Of AHIMA, Journal Of AHIMA. (2020). https://journal.ahima.org/a-simulation-study-of-coronavirus-as-an-epidemic-disease-using-agent-based-modeling/ (accessed July 10, 2020).
- [20].GuidoEspana, covid19_ND_forecasting, Github, n.d. https://github.com/confunguido/covid19_ND_forecasting (accessed July 10, 2020). [Google Scholar]
- [21].IHME | COVID-19 Projections, Institute for Health Metrics and Evaluation. (n.d.). https://covid19.healthdata.org/united-states-of-america (accessed July 10, 2020). [Google Scholar]
- [22].Kermack WO, McKendrick AG, Walker GT, A contribution to the mathematical theory of epidemics, Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. 115 (1927) 700–721. [Google Scholar]
- [23].Hsiang S, Allen D, Annan-Phan S, Bell K, Bolliger I, Chong T, Druckenmiller H, Huang LY, Hultgren A, Krasovich E, Lau P, Lee J, Rolf E, Tseng J, Wu T, The effect of large-scale anti-contagion policies on the COVID-19 pandemic, Nature 584 (7820) (2020) 262–267, 10.1038/s41586-020-2404-8. [DOI] [PubMed] [Google Scholar]
- [24].A compartment modelling approach to reconstruct and analyze gender and age-grouped CoViD-19 Italian data for decision-making strategies, J. Biomed. Inform. (2021) 103793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Rubin D, Huang J, Fisher BT, Gasparrini A, Tam V, Song L, Wang X.i., Kaufman J, Fitzpatrick K, Jain A, Griffis H, Crammer K, Morris J, Tasian G, Association of Social Distancing, Population Density, and Temperature With the Instantaneous Reproduction Number of SARS-CoV-2 in Counties Across the United States, JAMA Netw Open. 3 (7) (2020) e2016099, 10.1001/jamanetworkopen.2020.16099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Nikolopoulos K, Punia S, Schäfers A, Tsinopoulos C, Vasilakis C, Forecasting and planning during a pandemic: COVID-19 growth rates, supply chain disruptions, and governmental decisions, Eur. J. Oper. Res. 290 (2021) 99–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].A fusion of data science and feed-forward neural network-based modelling of COVID-19 outbreak forecasting in IRAQ, J. Biomed. Inform. (2021) 103766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].About covid19-projections.com, (n.d.). https://covid19-projections.com/about/ (accessed August 26, 2020).
- [29].Covid-19 in the United States, USAFACTS. (n.d.). https://usafacts.org/visualizations/coronavirus-covid-19-spread-map (accessed 2020). [Google Scholar]
- [30].Houston Area Employment — April 2020 : Southwest Information Office : U.S. Bureau of Labor Statistics, (2020). https://www.bls.gov/regions/southwest/news-release/areaemployment_houston.htm (accessed July 12, 2020). [Google Scholar]
- [31].COVID-19 Data Report, SETRAC. (n.d.). https://www.setrac.org/ (accessed 2020). [Google Scholar]
- [32].TMC Daily New Covid-19 Hospitalizations - Texas Medical Center, Texas Medical Center. (n.d.). https://www.tmc.edu/coronavirus-updates/tmc-daily-new-covid-19-hospitalizations/ (accessed July 6, 2020). [Google Scholar]
- [33].COVID-19, Github, n.d. https://github.com/CSSEGISandData/COVID-19 (accessed August 26, 2020). [Google Scholar]
- [34].Texas Department of State Health Services, Opening the State of Texas, (n.d.). https://www.dshs.state.tx.us/coronavirus/opentexas.aspx (accessed September 17, 2020).
- [35].Bendavid E, Mulaney B, Sood N, Shah S, Ling E, Bromley-Dulfano R, Lai C, Weissberg Z, Saavedra-Walker R, Tedrow J, Tversky D, Bogan A, Kupiec T, Eichner D, Gupta R, Ioannidis J, Bhattacharya J, COVID-19 Antibody Seroprevalence in Santa Clara County, California, Epidemiology. (2020), 10.1101/2020.04.14.20062463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Mandavilli A, Actual Coronavirus Infections Vastly Undercounted, C.D.C. Data Shows, The New York Times. (2020). https://www.nytimes.com/2020/06/27/health/coronavirus-antibodies-asymptomatic.html (accessed July 10, 2020). [Google Scholar]
- [37].Bennett ST, Steyvers M, Estimating COVID-19 Antibody Seroprevalence in Santa Clara County, California. A re-analysis of Bendavid et al, (n.d.). 10.1101/2020.04.24.20078824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Hôpitaux Universitaires de Genève, (n.d.). https://www.hug-ge.ch/ (accessed July 2, 2020). [Google Scholar]
- [39].anjum, SEIR-HCD Model, Kaggle. (2020). https://www.kaggle.com/anjum48/seir-hcd-model/ (accessed June 26, 2020). [Google Scholar]
- [40].Zhu C, Byrd RH, Lu P, Nocedal J, Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization, ACM Trans. Math. Softw. 23 (1997) 550–560. [Google Scholar]
- [41].COVID-19 Kaggle community contributions, (n.d.). https://www.kaggle.com/covid-19-contributions (accessed June 26, 2020).
- [42].Home, (n.d.). https://gov.texas.gov (accessed July 8, 2020). [Google Scholar]
- [43].Houston Data, Insight and Analysis, (n.d.). https://www.houston.org/houston-data.
- [44].Houston-Sugar Land-Baytown, TX Economy at a Glance, (n.d.). https://www.bls.gov/eag/eag.tx_houston_msa.htm (accessed July 8, 2020).
- [45].COVID-19 Scenarios, (n.d.). https://covid19-scenarios.org/.
- [46].Unlu E, Leger H, Motornyi O, Rukubayihunga A, Ishacian T, Chouiten M, Epidemic analysis of COVID-19 Outbreak and Counter-Measures in France, Epidemiology. (2020), 10.1101/2020.04.27.20079962. [DOI] [Google Scholar]
- [47].Coronavirus disease 2019 (COVID-19) Situation Report – 73, WHO Website. (n.d.). https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200402-sitrep-73-covid-19.pdf?sfvrsn=5ae25bc7_6#:~:text=The%20incubation%20period%20for%20COVID,persons%20can%20be%20contagious. [Google Scholar]
- [48].Champagne SR, Texas won’t specify where hospital beds are available as coronavirus cases hit record highs, The Texas Tribune. (2020). https://www.texastribune.org/2020/07/02/texas-hospital-capacity-coronavirus/ (accessed July 12, 2020). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.