Abstract
The outbreak of the COVID-19 pandemic caused some of the largest – and fastest – market dislocations in modern history. During the outbreak, liquidity quickly evaporated in a coordinated fashion across global markets. We show that a sudden increase in margin requirements during the pandemic is correlated with the withdrawal of global liquidity providers. These effects are concentrated in securities most exposed to high-frequency market makers, consistent with the binding nature of increased capital constraints.
Keywords: COVID-19; Margin requirements; Stock market liquidity, liquidity spiral
1. Introduction
“We can’t bid on anything that adds to the balance sheet right now”.1
This quote from Vikram Rao — head bond trader of Capital Group — with respect to the purchase of U.S. Treasury bonds during the height of the COVID-19 pandemic exposes one of the major issues faced by global equity market makers — a downward liquidity spiral exacerbated by the significant increase in margin requirements the world over. A press release from the only listed global equity market makers, Virtu Financial, echoed a similar sentiment2 : “Given the sustained levels of extraordinary volatility in the current macro environment …we consider it prudent to opportunistically supplement our borrowing capacity”. Indeed, Virtu required a temporary addition of US $450 million in “additional broker dealer capital” to continue their global market making operations. Their announcement came nine days after the World Health Organization (WHO) declared COVID-19 to be a global pandemic: A procyclical period of increasing margin requirements across global equities and futures markets.
According to recent theory models, there is potential for a negative liquidity spiral when there is a sharp drop in traders’ funding liquidity. Brunnermeier and Pedersen (2009) document that the increased trading margins required by exchanges to minimize counterparty default risk between participants increases funding liquidity. These rising margin requirements cause reductions in market liquidity, resulting in a procyclical negative liquidity spiral. However, there are few empirical tests of these predictions, as large changes to margin requirements occur infrequently.
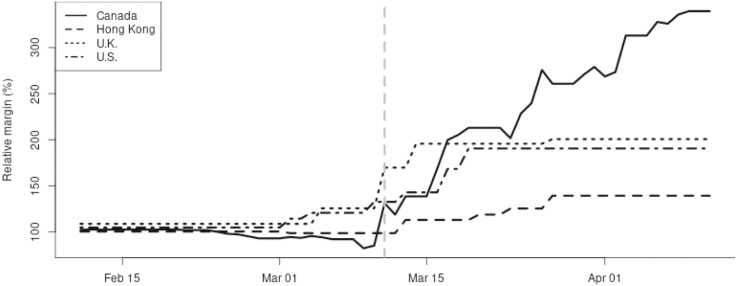
The WHO’s declaration of the COVID-19 pandemic in March 2020 is associated with some of the largest dislocations in market history. Equity market values fell by 30%–40% globally, and the withdrawal of liquidity supply was correlated with a sharp increase in margin requirements for exchange-traded equity products, in some instances by more than 300% (Fig. 2). Moreover, some markets (such as the United Kingdom) experienced much larger increases in margins relative to other markets (such as the United States), resulting in a margin differential across exchanges.
Fig. 2.
The evolution of global margin requirements. The figure shows the evolution in margin requirements for global markets. At each date, the margin requirement is presented as a percentage of the margin requirement in January 2020. Canada refers to the TSX 60 Index futures, which trade on the Montreal Exchange. Hong Kong refers to the Hang Seng Index futures, which trade on the Hong Kong Futures Exchange. U.K. refers to the margin for the FTSE 100 Index futures, which trade on the Intercontinental Exchange. U.S. refers to the margin for the S&P 500 Index futures, which trade on the Chicago Mercantile Exchange. Our data spans February 11 to April 11, 2020. The broken vertical line represents March 11, 2020, when the World Health Organization declared the COVID-19 outbreak a pandemic.
In this study, we test theory predicting that an increase in capital requirements results in a reduction in market liquidity. Using a difference-in-differences framework, we exploit the change in margin differential between the U.K. and U.S. markets and examine the liquidity of exchange-traded funds (ETFs) that both track the S&P 500 Index, but trade in the U.K. and U.S., respectively. Because both the U.K.- and U.S.-traded ETFs track the same underlying index, we effectively control for any common changes to liquidity in these ETFs due to changes in the fundamental value of the S&P 500. Thus, the U.K.- and U.S.-traded ETFs primarily differ only by the margin required to trade them on their respective exchange.
Next, we extend our analysis to a global setting and investigate changes in the liquidity of index and non-index stocks following the margin spike in March 2020 for a large cross-section of global equity markets. We argue that high-frequency market makers (HFMMs), who are heavily reliant on leverage for liquidity provision, are more sensitive to margin requirements than traditional investors, and thus, more likely to withdraw from the market following large increases in margin requirements. Further, HFMMs are more likely to be present in index stocks, relative to non-index stocks, which have lower HFMM participation (Brogaard et al., 2014, Shkilko and Sokolov, 2020). Because of these factors, as margin requirements increase, we expect a larger decline in the liquidity of index stocks in which HFMM are more active, relative to non-index stocks. Last, using the order to trade ratio to proxy for HFMM activity in global equities, we test whether HFMMs withdraw their activity more from index stocks than non-index stocks, following an increase in margin requirements.
Our results strongly support the theoretical model of Brunnermeier and Pedersen (2009), which predicts that an increase in capital requirements leads to a decline in equity market liquidity. Our research provides three main findings. First, for our analysis on the ETFs tracking the S&P 500 Index, we show that market liquidity deteriorates more for the U.K.-traded ETF, which experienced a larger increase in margin, relative to the U.S.-traded ETF, for which margins remained relatively static. Further, we find the reverse effect when the margin differential narrows. Specifically, while U.K. margins increased precipitously when U.S. margins remained relatively stable, the U.S. subsequently experienced a large jump in margin requirements, thereby narrowing the margin differential. Corresponding to this subsequent jump in U.S. margins, we show that the market liquidity of the U.S.-traded ETF deteriorates relative to that of the U.K.-traded ETF.
Second, generalizing our findings to a global setting, we report a larger deterioration in liquidity for index stocks when compared to non-index stocks. This result is consistent with the notion that increases in margin requirements have a larger impact on stocks that are more reliant on margin-sensitive HFMM for liquidity provision. This result is also consistent with the theoretical model developed by Cespa and Foucalt (2014), which shows that liquidity contagion from the index derivatives has a muted impact on non-index stocks.
Finally, using the order to trade ratio as a proxy for HFMM activity, we show that HFMMs withdrew more from index stocks than non-index stocks when margin requirements suddenly increased.
Our results are robust to a plethora of robustness and falsification tests. The sudden increase in exchange margin requirements in March 2020 also corresponded to large declines in stock prices, which could also be correlated with declining stock liquidity. To control for a falling stock price, we identify a period in 2015 when stock prices declined significantly without a corresponding change to exchange margin requirements. Importantly, for this falsification test, we do not find differential changes in stock liquidity following large stock declines. Our results are also robust to different sample windows and alternate regression frameworks.
Overall, our results show that an increase in funding costs due to higher margin requirements is correlated with a sharp reduction in equity market liquidity. This margin-induced shock to funding liquidity impacted the available market liquidity exactly at the time equity market price levels were falling, due to the unprecedented global risk COVID-19 posed to company cash flows. Our findings suggest that traders must de-leverage their positions precisely at the point in time when prices are declining, thereby potentially further depressing prices and increasing margin, consistent with the theoretical findings of Morris and Shin (2004). This process can create a margin loss-spiral, consistent with the rapid reduction in both market liquidity and prices observed in March 2020.
We contribute to the extant literature in two key ways. First, we empirically test theories documenting the procyclical nature of margin requirements and the negative spirals they could generate for market participants (Brunnermeier and Pedersen, 2009, Repullo and Suarez, 2013, Hugonnier and Morellec, 2017). While Behn et al. (2016) and Berger et al. (2016) study the impacts of margin requirements during the 2008 Global Financial Crisis in a banking context, we are the first to test these theories in equity markets.
Second, we contribute to a growing literature seeking to understand and explain why the effects of the COVID-19 pandemic are so significant and swift for asset valuations and the overall trading environment. Market participants have come to expect the underlying market architecture, or “plumbing”, to facilitate smooth and orderly trading of vast proportions within our financial institutions. Any failure of such systems, no matter how brief, must be examined and understood. For example, there are studies seeking to understand dislocations in U.S. Treasury assets (Cheng et al., 2020, Duffie, 2020), dislocations from the NYSE trading floor (Brogaard et al., 2020), and the magnitude of asset price responses and dislocations (Baker et al., 2020, Ramelli and Wagner, 2020). Our work provides a channel by which such dislocations can occur — namely changes in the margin required for liquidity suppliers.
The significance of the capital constraints faced by high-frequency market makers has become particularly important in a world where the majority of liquidity is provided by only a handful of firms, such as Citadel and Virtu. When these firms represent the majority of liquidity provision not only within a market, but also across markets, the procyclicality of their available committed capital represents a systemic risk that should no longer be ignored.
The remainder of the paper is organized as follows. In Section 2, we discuss the relevant literature on margin requirements and market liquidity. In Section 3, we describe the data used in the study. Sections 4, 5 report on the evolution of margin requirements and liquidity over the pandemic period, respectively. In Section 6, we present the results of our study and Section 7 concludes.
2. Related literature
Theoretical models identify shocks to market liquidity following price declines in a variety of ways. Collateral-based models rely on market makers to absorb these temporary buy–sell imbalances. However, market makers with finite funding levels obtain financing by posting margins, utilizing the underlying securities they hold as collateral. When stock prices fall rapidly, intermediaries hit their funding limits and are forced to liquidate. This “liquidity spiral” is documented by Brunnermeier and Pedersen (2009), and supported by the work of Weill (2007). Procyclical increases in margins in response to volatility limit the ability of participants to provide liquidity, particularly when such constraints become binding. Similar models are proposed with funding constrained arbitrageurs as liquidity providers (Gromb and Vayanos, 2002) or with short-term traders unable to take on inventory due to funding constraints (Morris and Shin, 2004). In a model proposed by Gârleanu and Pedersen (2011), the impact of binding margin requirements becomes “priced”, resulting in discounts on high-margin assets.
This procyclicality has been studied extensively in previous banking studies in response to the 2007–2009 Global Financial Crisis (GFC), both theoretically (Repullo and Suarez, 2013, Hugonnier and Morellec, 2017) and empirically (Behn et al., 2016, Berger et al., 2016). Empirically, studies of the margin requirements for equity market makers have been hindered by the availability of such data. In some markets, the link between liquidity provision and margin constraints have been explicitly documented. For example, in bond markets, Adrian et al. (2017) document larger reductions in liquidity after the GFC in bonds traded by firms with more leverage, indicating the binding nature of their margin requirements. Aramonte and Szerszeń (2020) use a supervisory dataset to examine U.S. corporate bonds and credit default swaps and show that dealer profitability plays a significant role in secondary market liquidity. Daskalaki and Skiadopoulos (2016) examine the commodity futures markets and show that an increase in margins following the Dodd-Frank Act increases transactions costs and reduces depth. Finally, Dudley and Nimalendran (2011) show that increases in the funding margins for futures markets increase the illiquidity and contagion risk of mutual hedge funds.
Empirical studies of equity trading have alluded to the role binding margin constraints play in harming overall market liquidity, but have not been able to directly demonstrate this relation. For example, Hameed et al. (2010) document reductions in liquidity around market declines, particularly when the funding markets are tight, which are likely to arise from capital constraints on market makers. Similarly, Comerton-Forde et al. (2010) show that the inventory levels and trading revenues of NYSE market makers are correlated with their propensity to supply liquidity. In a global study, Karolyi et al. (2012) find that commonality in liquidity is greater in countries with higher market volatility, and is also higher at points in time when volatility is greatest, consistent with the impact of binding funding liquidity constraints. Despite this consistent evidence from equity markets of the potential role margin plays in equity market liquidity provision, to date, no study has been able to clearly identify this mechanism.
Our global findings for the equity markets align well with evidence from Duffie (2020), who investigates U.S. Treasury markets and shows that the inventory risk faced by dealers results in bid–ask spreads that increase to over 10 times their (relatively stable) pre-pandemic levels. The larger magnitudes observed in these markets likely reflects the greater leverage (and lower historic volatility) utilized in these settings. Similarly, other recent papers, including Bent et al., 2019, Cheng et al., 2020 and Fleming and Ruela (2020), show that increased margin requirements during the COVID-19 pandemic caused significant deterioration in overall measures of market liquidity in Treasury bond markets.
Our paper further complements studies examining the effects of COVID-19 on equity markets. While the majority of these papers aim to understand the asset pricing implications of the pandemic,3 studies focusing on the working of financial equity markets during the COVID-19 crisis is more limited. For example, Brogaard et al. (2020) show that the suspension of trading by physical market makers on the trading floor at the NYSE deteriorates overall market quality.
3. Data and sample selection
In this section, we provide details on the markets investigated and describe the data sources. We also provide descriptive statistics on the main variables analyzed in the study.
3.1. Sample selection
Our analysis considers equity markets across a broad range of developed countries. Table 1 outlines the markets and index stocks in our sample. This set of markets yields not only a broad cross-section of the developed world, but also provides variation in the societal response to the COVID-19 crisis, as well as variation in the absolute scale of the outbreak. Fig. 1 illustrates the disruption to global stock markets, showing how our sample markets fell from their price levels on February 1, 2020 (normalized to 100).
Table 1.
Markets and exchanges.
| Market | Index | No. constituents |
|---|---|---|
| Canada | TSX 60 | 60 |
| Hong Kong | Hang Seng Index | 58 |
| Norway | OBX | 25 |
| Sweden | OMX Stockholm | 30 |
| U.K. | FTSE 100 | 100 |
The table lists the sample markets considered in the study, the main index for the market, and the number of constituents in the market’s main index.
Fig. 1.
The evolution of stock market prices. This figure illustrates the movement in stock market prices for the indices listed in Table 1. The plots show the change in index price levels, relative to the index level on February 1, 2020, which takes a value of 100. The broken vertical line represents March 11, 2020, when the World Health Organization declared the COVID-19 outbreak a pandemic.
3.2. Market data
In Section 6.2, we investigate liquidity metrics for stocks that are index constituents of the market’s main index, relative to stocks outside of the main index. For Hong Kong, we use stocks in the Hang Seng LargeCap and MidCap indices that are outside of the main Hang Seng Index as the sample of non-index stocks. For the U.K., we use data for the firms in the FTSE 250, but not within the FTSE 100, to represent our non-index stocks. For the remaining markets, we use data for all reasonably liquid non-index stocks listed on these exchanges, which we define as stocks above the median market capitalization among the non-index stocks, conditional on having more than 100 trades per day.
We source the data for this study from the Refinitiv database.4 The data contain millisecond timestamped records of quotes and trades. For each stock, we calculate intraday quoted spread, effective spread, realized spread, and price impact. For the latter two, we use a 10-second delay in the calculations to capture the returns to HFMMs, consistent with the work of Conrad and Wahal (2020).5 We consider only the trading activity during the continuous trading session at the main (listing) exchange.6
In Section 6.1, we investigate the liquidity of an U.S.-traded ETF tracking the S&P 500 relative to a U.K.-traded ETF that also tracks the S&P 500.7 We also collect data on the trades and quotes for these ETFs from Refinitiv. Similarly, we calculate the same liquidity measures outlined above, but we compute them as averages every trading hour, rather than as daily averages.
Table 2 provides descriptive statistics for the stocks in our sample. To illustrate a representative non-pandemic period, these tables provide averages for the liquidity measures over the period January 1 to February 15, 2020. Panel A presents statistics for the stocks that are constituents of the market’s main index, as listed in Table 1, while Panel B provides descriptive statistics for the sample of relatively liquid stocks outside of the main index. We observe a high similarity in quoted spreads across markets, and as expected, the transaction costs for non-index stocks are substantially higher than those of their index-constituent counterparts.
Table 2.
Descriptive statistics.
| Quoted spread (bps) | Effective spread (bps) | Realized spread (bps) | Price impact (bps) | |
|---|---|---|---|---|
| Panel A: Index stocks | ||||
| Canada | 5.2 | 2.3 | −0.2 | 2.5 |
| Hong Kong | 14.1 | 6.8 | 3.9 | 4.5 |
| Norway | 9.9 | 4.4 | 7.0 | 0.7 |
| Sweden | 6.7 | 3.3 | 0.4 | 3.2 |
| U.K. | 6.2 | 2.5 | −0.3 | 2.8 |
| Panel B: Non-index stocks | ||||
| Canada | 21.9 | 9.9 | 0.7 | 9.2 |
| Hong Kong | 25.1 | 12.1 | 3.9 | 8.2 |
| Norway | 36.2 | 13.1 | 9.7 | 3.5 |
| Sweden | 26.1 | 12.4 | 3.8 | 8.8 |
| U.K. | 19.0 | 7.1 | 0.4 | 6.8 |
| Panel C: ETFs | ||||
| U.K. | 4.0 | 0.9 | 0.4 | 0.6 |
| U.S. | 0.8 | 0.3 | 0.2 | 0.2 |
The table provides descriptive statistics for our liquidity variables for January 1 to February 15, 2020. Quoted spread is the difference between the best bid and ask, divided by the current midpoint. Effective spread is the difference between the traded price and the current midpoint, relative to the current midpoint. Realized spread and Price impact are calculated using a 10-second delay. The statistics in Panel A are for stocks in the main indices, as listed in Table 1. In Panel B, we describe the stocks we use outside of the main indices. For Hong Kong, we use the constituents of the Hang Seng LargeCap and MidCap indices that are not in the main Hang Seng Index. For the U.K., we use the constituents of the FTSE 250 that are not in the FTSE 100. For the other markets (Canada, Norway, and Sweden), we only include stocks with market capitalization higher than the median company outside of the main index, and with more than 100 daily trades. In Panel C, we provide liquidity measures for the U.S. ETF (SPY), which trades at the NYSE, and the U.K. ETF (CSPX.L), which trades at the LSE. Both ETFs track the S&P 500 Index. We provide the average liquidity variables based on hourly estimates.
3.3. Margin data
Margins refer to the minimum amount of money a trader must deposit in their margin trading account to fund the notional exposure of their portfolio. These margins serve as a collateral deposit and minimize credit risk. Specifically, exchanges typically define both an initial margin (IM) and maintenance margin (MM). The IM is the collateral required as a proportion of the total traded value to open a new leveraged position. The MM is the minimum collateral a trader must retain to maintain their open position. For example, a $100 buy order may require an IM of 5% (or $5). Appreciation in the bought asset, say to $110, results in the value of the margin account increasing by $10. However, reductions in price will be deducted from the margin account. For a MM of 2.5%, the trader’s position is automatically closed if the price falls below $97.5 (leaving only the minimum 2.5% margin).
We collect the daily IM requirements for equity index futures contracts for multiple indices. We obtain these data directly from regulatory information available on each exchange’s webpage.8 Typically, exchanges report margin as the dollar amount required to trade a contract.9 For example, the margin to buy one S&P 500 futures contract that has a notional exposure of approximately $840,000 is reported as $31,500 at the start of our sample period. Table 3, Panel A, contains descriptive statistics for the dollar margin for each contract for a pre-pandemic and a post-pandemic period around the WHO’s declaration of a pandemic on March 11, 2020. The pre-pandemic period spans from February 11 to March 10, 2020 and the post-pandemic period spans from March 11 to April 11, 2020.
Table 3.
Margin summary statistics.
| Pre-period |
Post-period |
|||||
|---|---|---|---|---|---|---|
| Min. | Mean | Max. | Min. | Mean | Max. | |
| Panel A: Margin per contract | ||||||
| Canada (CAD) | 5,988 | 7,089 | 7,480 | 8,653 | 18,161 | 24,739 |
| Hong Kong (HKD) | 82,300 | 83,300 | 83,750 | 82,300 | 106,987 | 116,200 |
| U.K. (£) | 3,629 | 3,745 | 4,191 | 5,667 | 6,563 | 6,699 |
| U.S. (USD) | 33,000 | 34,543 | 41,750 | 41,750 | 57,024 | 60,000 |
| Panel B: Margin as percentage of exposure | ||||||
| Canada | 3.10 | 3.42 | 3.52 | 5.79 | 11.43 | 14.45 |
| Hong Kong | 5.99 | 6.20 | 6.57 | 6.77 | 9.16 | 10.07 |
| U.K. | 4.82 | 5.40 | 7.03 | 10.56 | 12.06 | 13.08 |
| U.S. | 3.90 | 4.39 | 5.79 | 6.64 | 9.01 | 10.73 |
The table provides the summary statistics for the margin (Panel A) and percentage margin (Panel B) for the equity index futures contract of selected markets. Canada refers to the TSX 60 Index futures, which trade on the Montreal Exchange (expressed in CAD). Hong Kong refers to the Hang Seng Index futures, which trade on the Hong Kong Futures Exchange (expressed in HKD). U.K. refers to the margin for the FTSE 100 Index futures, which trade on the Intercontinental Exchange (expressed in pounds). U.S. refers to the margin for the S&P 500 Index futures, which trade on the Chicago Mercantile Exchange (expressed in USD). In Panel B, we express the margin as a percentage of the notional exposure of the contract. The pre-period is from February 11 to March 11, 2020 and the post-period is from March 12 to April 12, 2020.
Because the notional value for equity index futures contracts differs significantly across markets, the reported dollar margin can be hard to interpret. Accordingly, Table 3, Panel B, reports the margin required as a percentage of the notional exposure. For example, if a margin of $35,000 is required to purchase one contract with a notional exposure of $840,000, then the percentage margin is 4.167%. This percentage margin allows a more intuitive comparison across our global futures contracts.
While the figures reported in Panel B allow for an intuitive comparison across exchanges, a change in percentage margin can occur due to a change in the notional exposure (caused by a change in price), rather than a change in the dollar margin. Thus, to avoid any potential contamination of margin changes due to changes in the underlying price (or notional exposure), we use the dollar margin per contract, rather than the percentage margin, for our analysis in the following sections.10 However, to allow for a comparison across each contract, we present the summary statistics for the dollar margin requirement on each day, relative to the average daily margin requirement in January, 2020.
Because we are unable to obtain margin data for the Nordic markets, for reasons outlined in Sections 4, 6.2, we rely on the systemic increase in global margins to proxy for the margin requirements in these markets.
4. Margin during the COVID-19 pandemic
To understand the impact of the pandemic on margin levels, in Fig. 2 we plot the margin requirements for equity index futures in markets for which we are able to obtain margin data: Canada, Hong Kong, U.K., and U.S. The figure shows that the margin requirements remain reasonably constant throughout January and February, 2020, but rapidly increase around the WHO’s announcement of a pandemic on March 11, 2020, reaching over 300% of pre-pandemic levels in the case of Canada. Because of the systemic increase in global margin requirements in March, 2020, it is reasonable to assume that other markets for which we do not have margin data (i.e., Norway and Sweden), also experienced similar jumps in margin requirements, which we discuss further in Section 6.2.
The sudden dramatic jump in margin for equity index futures is likely to affect stock liquidity in several ways. First, while we are unable to obtain data on individual stock margins, it is reasonable to assume that stock margins experienced similar jumps,11 thereby directly imposing binding constraints on leveraged traders, who subsequently withdraw from the market. Second, a jump in the margin requirements for equity index futures is likely to affect leveraged sophisticated investors and cross-market arbitrageurs, who typically hedge their underlying equity positions via equity derivative products, such as index futures. Thus, these sophisticated investors could also withdraw from equity markets if they are unable to effectively manage their risk via the futures markets.
We argue that HFMMs are more sensitive to margin requirements than traditional traders due to their unique trading style. HFMMs operate over short time horizons, and typically carry no overnight inventory risk (Hasbrouck and Saar, 2013, Bartlett and McCrary, 2019, Shkilko and Sokolov, 2020). Accordingly, their positions are unlikely to precipitate a margin call, as large adverse price moves are unlikely to occur during their short holding periods. For this reason, HFMMs require less “buffer” in their margin accounts and can effectively trade on higher leverage ratios closer to the binding margin limits than other market participants. Moreover, HFMMs are often propriety trading firms, with smaller balance sheets than large institutional investors that use leveraged derivative positions to hedge price risk.
5. Liquidity during the COVID-19 pandemic
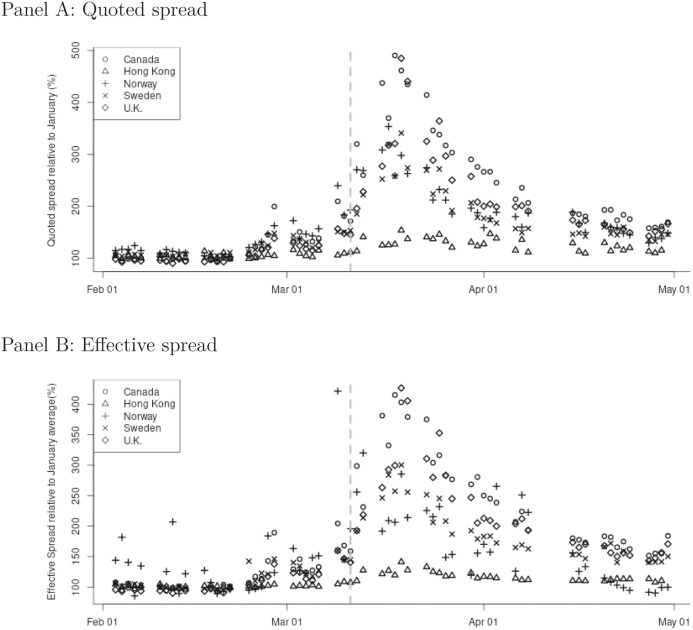
A key component of the health of any market is liquidity. Fig. 3 illustrates the evolution of liquidity during the pandemic. We document the changes across two key metrics: quoted spread (the anticipated cost of liquidity provision) and effective spread (the cost of traded liquidity).
Fig. 3.
Liquidity evolution during the COVID-19 crisis. The figures illustrate the changes in liquidity during the COVID-19 crisis, starting in February 1, 2020 and ending on June 19, 2020. At each date, the liquidity measures are presented as a percentage of their average in January 2020. Quoted spread is the difference between the best bid and ask, divided by the current midpoint. Effective spread is the difference between the traded price and the current midpoint, relative to the current midpoint. The gray vertical line represents March 11, 2020, when the World Health Organization declared the COVID-19 outbreak a pandemic.
Panel A shows the quoted spread relative to the average daily levels during January, 2020. We observe that quoted spreads, which measure the marginal cost charged by a liquidity provider for an additional unit of liquidity, begin rising around the beginning of March. However, after the WHO’s declaration of a pandemic on March 11, 2020, we observe a significant increase in this measure of transaction costs.12 For Canada and the U.K., the quoted spread increases from around 200% of January levels in the beginning of March to upwards of 500% by the end of March. All other markets show a similar response, with significant increases from pre-pandemic levels. This sharp increase in quoted spreads supports the notion that liquidity providers became more cautious in their liquidity provision once it became clear that COVID-19 would become a global issue. By early May 2020, these costs had fallen to a more typical level, but still remain between 125% and 200% of their pre-pandemic levels.
Panel B documents the evolution of effective spreads, representing the transaction cost of liquidity demanders when liquidity is consumed. Unlike the quoted spread, which measures the cost of trading an additional share, the effective spread measures the cost of liquidity in the size demanded—large market orders are likely to walk the book, increasing their actual cost. Rapid, correlated “fire sales” by market participants are likely to exhaust available market liquidity, increasing the transaction costs borne by market participants. Panel B shows that effective spreads follow a similar evolution to quoted spreads, with the cost of demanding liquidity in the U.K. increasing the most, peaking at 450% of January levels during March 2020.
One feature of the models proposed by Morris and Shin (2004) and Brunnermeier and Pedersen (2009) is that volatile markets may result in increased capital margin requirements. These increased margins may constrain the ability of market makers, arbitrageurs, and speculators to provide liquidity exactly when it is needed. This constraint can result in reduced liquidity, further increasing volatility, resulting in a negative “liquidity spiral” or “liquidity black hole”. The COVID-19 pandemic provides a fertile field to test these theoretical arguments in an equity market setting.
6. Results
This section presents our main results. In Section 6.1, we examine a unique case of two ETFs tracking the S&P 500 Index. While these ETFs track the same underlying asset, the ETFs trade on different markets, which experience different changes in their margin requirements during March 2020. We exploit this unique setting to test the relation between margin requirements and market liquidity. In Section 6.2, we extend the analysis to the world’s major equity markets. We argue that changes to margin requirements affect stocks that are index constituents more than stocks that are outside the index due to a higher concentration of margin sensitive high-frequency market makers (HFMM) in index constituents. Using a difference-in-differences analysis, we find a larger fall in liquidity for stocks that are index constituents than non-index constituents, following a margin increase. Last, in Section 6.3, using the order to trade ratio as a proxy for HFMM activity, we test whether HFMMs withdraw more from index stocks, relative to non-index stocks, when margin requirements increase.
6.1. Liquidity of two ETFs tracking the S&P 500 Index
We investigate liquidity differentials between two ETFs that track the same underlying index and test if these differentials are correlated to changes in margin requirements. Specifically, we investigate SPY, an ETF tracking the S&P 500 that trades on the NYSE (the U.S. ETF), and CPSX.L, an ETF that also tracks the S&P 500, but trades on the London Stock Exchange (the U.K. ETF). Accordingly, these two ETFs trade on different exchanges and are subject to their respective exchange margins, but track the same underlying asset. Thus, while not fungible, the ETFs are synthetically identical and primarily differ only by the margin required to trade them. Because the ETFs are synthetically identical, any shock to the fundamental value of the S&P 500 should equally affect both ETFs. For this reason, we can control for any common changes to liquidity in these ETFs due to falling prices or increased volatility of the S&P 500 using a difference-in-differences framework.
While all exchange margins increased around the time of the WHO’s declaration of a pandemic (Fig. 2), some markets experienced larger increases in margins, relative to other exchanges. Exploiting this phenomenon, we use a difference-in-differences framework to isolate the effect of an idiosyncratic margin increase on market liquidity. We note, however, due to data limitations, we are unable to obtain the exact margin for the two ETFs. Thus, we proxy the respective ETF margin by using the margin corresponding to the main equity index future for each market. We proxy the margin requirement for the U.K. ETF using the margin for the FTSE 100 Index futures, which are traded on the Intercontinental Exchange (ICE). Similarly, we proxy the margin requirement for the U.S. ETF margin using the margin for the S&P 500 Index futures, which are traded on the Chicago Mercantile Exchange (CME).13
Fig. 4 illustrates the differential increase in U.K. and U.S. ETF margin proxies. Panel A shows a large jump in the U.K. margin proxy (dotted line), relative to the U.S. margin proxy (solid line) on March 11 (indicated with a vertical line). To illustrate the difference in margin changes more distinctly, Panel B shows the margin differential, which is the difference between the U.K. and U.S. margin proxies. Panel B shows a clear increase in the margin differential for the period March 11 to March 16: over this period, the U.K. margin proxy increases more substantially, relative to the U.S. margin proxy. For this reason, we select the March 11 to March 16 period as the post-period for the difference-in-differences estimation, to test the prediction from Brunnermeier and Pedersen (2009) that binding margin constraints lead to deterioration in market liquidity.
Fig. 4.
Relative margins for U.S. and U.K. exchanges. In Panel A, we plot the time series evolution of margins in the U.S. (solid line) and U.K. (dotted line). The margin is presented as a percentage of the margin requirement on February 1, 2020. U.K. refers to the margin for the FTSE 100 futures, which trade on the Intercontinental Exchange. U.S. refers to the margin for the S&P 500 futures, which trade on the Chicago Mercantile Exchange. In Panel B, we plot the margin differential, which is the difference between the U.K. and U.S. relative margins. The vertical lines indicate the pre- (February 5 to February 10, 2020) and post- (March 11 to March 16, 2020) periods for our difference-in-differences analysis.
Because the U.K. margin proxy increased earlier, and by more than the U.S. margin proxy, we expect market liquidity to deteriorate more in the U.K. market than in the U.S. market. Turning to the two ETF contracts, Fig. 5 shows the evolution of the effective spread in the U.K. ETF (gray markers) and the U.S. ETF (black markers). We see a much larger increase in the effective spread for the U.K. ETF, relative to the U.S. ETF, which is consistent with the theoretical prediction from Brunnermeier and Pedersen (2009) and Morris and Shin (2004).
Fig. 5.
Effective spreads for U.S. and U.K. ETFs tracking the S&P 500 Index. This figure shows the evolution of effective spreads for the U.S. (SPY traded on the New York Stock Exchange) and U.K. (CSPX.L traded on the London Stock Exchange) ETFs. The effective spread is the time-weighted average effective spread (in basis points) over an hour. We only consider spreads for times of the day when both markets are open. On the right axis, we show the margin differential (in percent), which is the difference between the U.K. and U.S. margins. The U.K. margin refers to the margin for the FTSE 100 futures, which trade on the Intercontinental Exchange. The U.S. margin refers to the margin for the S&P 500 futures, which trade on the Chicago Mercantile Exchange. The gray vertical lines indicate the pre- (February 5 to February 10, 2020) and post- (March 11 to March 16, 2020) periods for our difference-in-differences analysis.
To formalize these observations, we perform a difference-in-differences estimation using the pre- and post-periods indicated in Fig. 4. The pre-period covers the February 5 to February 10, 2020 period, and Fig. 4 shows there is no material deviation in the margin differential over this period. Our post-period covers the March 11 to March 16, 2020 period, which corresponds to the jump in margin differential described earlier. Importantly, we observe a 43% margin differential in the post-period while the margin differential is only 1% in the pre-period.14 We run the following difference-in-differences regression model:
| (1) |
where is one of the following liquidity variables: quoted spread, effective spread, realized spread or price impact. Each liquidity variable is averaged over hourly intervals. is an indicator variable equal to 1 if the ETF trades in the U.K., and 0 otherwise. is an indicator variable equal to 1 for the post-period from March 11 to March 16, 2020 and 0 for the pre-period from February 5 to February 10, 2020. The interaction term U.K. Margin increase isolates the effect of the margin increase on stock liquidity. To control for differences between trading conditions in the U.K. and U.S., we include and , where is computed as and is computed as over one-hour intervals. For Return and Volatility, we use index levels for the FTSE 100 and S&P 500 for the U.K. and U.S. markets, respectively.15
Table 4 reports the results from the difference-in-differences regression models. Consistent with the theoretical predictions of Morris and Shin (2004) and Brunnermeier and Pedersen (2009), our results show a decrease in liquidity for the U.K. ETF after the jump in the U.K. margin proxy, relative to the U.S. margin proxy. Across all model specifications, U.K. Margin increase is positive and significant, indicating that transaction costs (i.e., quoted, effective, and realized spreads) increase for the U.K ETF after the margin differential widens between the U.K. and U.S. markets. Further, the price impact of trades for the U.K. ETF increases after the margin differential widens. Prior empirical studies show that increases in margin correspond to a deterioration in market quality for commodity futures markets (Daskalaki and Skiadopoulos, 2016) and CDS and bond markets (Aramonte and Szerszeń, 2020). Our results complement these studies by showing that the relation between increasing margins and deterioration in market quality extends to equity markets.
Table 4.
Difference-in-differences regression for U.K. and U.S. ETFs (widening on March 11, 2020) .
| Quoted spread | Effective spread | Realized spread | Price impact | |
|---|---|---|---|---|
| U.K. | 4.47 | 1.09 | 0.84 | 0.24 |
| (4.52) | (1.38) | (1.14) | (0.42) | |
| Margin increase | −5.14 | −3.45 | −2.07 | −1.46 |
| (6.47) | (1.98) | (1.63) | (0.60) | |
| U.K. × Margin increase | 18.21 | 7.32 | 3.04 | 4.20 |
| (6.20) | (1.90) | (1.57) | (0.57) | |
| Volatility | 247.90 | 154.02 | 87.07 | 71.33 |
| (199.41) | (61.05) | (50.35) | (18.43) | |
| Return | 51.92 | 6.84 | 30.15 | −30.15 |
| (147.30) | (45.09) | (37.20) | (13.62) | |
| Constant | −0.37 | −0.32 | −0.25 | −0.07 |
| (3.25) | (1.00) | (0.82) | (0.30) | |
| Observations | 56 | 56 | 56 | 56 |
| 0.38 | 0.47 | 0.16 | 0.78 |
The table reports the changes to liquidity measures around the widening of the margin differential for the CSPX.L (U.K.) and SPY (U.S.), which are ETFs that track the performance of the S&P 500, traded on the LSE and NYSE, respectively. Specifically, we report the results for the following difference-in-differences regression:
where is one of the following liquidity variables: Quoted spread, Effective spread, Realized spread or Price impact for the U.S. or U.K. ETF, . The dependent variables are calculated over one-hour intervals, and are expressed in basis points. is an indicator variable equal to 1 if the ETF trades in the U.K., and 0 otherwise. is an indicator variable equal to 1 for the post-period from March 11 to March 16, 2020 and 0 for the pre-period from February 5 to February 10, 2020. and are based on the FTSE 100 and S&P 500 Index levels for the U.K. and U.S. markets, respectively. and are calculated over one-hour intervals as and , respectively. , , and denote statistical significance at the 1%, 5%, and 10% levels, respectively.
6.1.1. Reduction in the margin differential
While the U.K. initially experiences a larger jump in margins relative to the U.S., shortly after, on March 17, 2020, the U.S. margin also jumps, and the difference between the U.K. and U.S. margins narrows (see Fig. 4). Our second test exploits this narrowing in the margin differential. Because there is a narrowing in the margin differential between the U.K. and U.S. markets, there should be a reduction in the market quality differences between the markets. That is, we expect spreads on the U.K. market to decrease, relative to spreads on the U.S. market.
For this experiment, we use a similar difference-in-differences framework to Eq. (1):
| (2) |
where is an indicator variable equal to 1 for the post-period from March 17 to March 21, 2020 and 0 for the pre-period from March 12 to March 16, 2020. The remaining variables are defined in the same way as for Eq. (1). In Appendix E, we show that the average margin differential is 43% for the pre-period, which declines to 14% for the post-period.16 Based on the predictions of Gârleanu and Pedersen (2011), we expect to see a negative and significant coefficient on U.K. Margin narrowing.
Table 5 shows the results for the difference-in-differences regression around the March 17, 2020 margin narrowing event. Consistent with our expectations, we find that the interaction term U.K. Margin narrowing is negative and significant across all model specifications. Complementing the results of Eq. (1) for the widening of the margin differential in Section 6.1, Table 5 shows that the narrowing of the margin differential is associated with an improvement in the market quality for the U.K. ETF, relative to the U.S. ETF, evidenced through tighter quoted, effective and realized spreads, and lower price impacts.
Table 5.
Difference-in-differences regression for U.K. and U.S. ETFs (narrowing on March 17, 2020).
| Quoted spread | Effective spread | Realized spread | Price impact | |
|---|---|---|---|---|
| U.K. | 25.80 | 9.70 | 4.66 | 5.07 |
| (4.81) | (1.46) | (1.35) | (0.66) | |
| Margin narrowing | −0.11 | 0.40 | 0.25 | 0.18 |
| (4.20) | (1.27) | (1.18) | (0.58) | |
| U.K. × Margin narrowing | −11.57 | −4.43 | −2.98 | −1.38 |
| (5.73) | (1.74) | (1.60) | (0.79) | |
| Volatility | 21.56 | 83.20 | 23.17 | 70.11 |
| (208.64) | (63.24) | (58.43) | (28.75) | |
| Return | 40.31 | 5.33 | 9.37 | −8.26 |
| (102.83) | (31.17) | (28.80) | (14.17) | |
| Constant | 0.77 | −2.14 | −0.77 | −1.64 |
| (7.41) | (2.24) | (2.07) | (1.02) | |
| Observations | 56 | 56 | 56 | 56 |
| 0.47 | 0.54 | 0.20 | 0.63 |
The table reports the changes to liquidity measures around the narrowing of the margin differential for the CSPX.L (U.K.) and SPY (U.S.), which are ETFs that track the performance of the S&P 500, traded on the LSE and NYSE, respectively. Specifically, we report the results for the following difference-in-differences regression:
,
where is one of the following liquidity variables: Quoted spread, Effective spread, Realized spread or Price impact for the U.S. or U.K. ETF, . The dependent variables are calculated over one hour intervals, and are expressed in basis points. is an indicator variable equal to 1 if the ETF trades in the U.K., and 0 otherwise. Margin narrowing is an indicator variable equal to 1 for the period March 17 to March 21, 2020 and 0 for the period March 12 to March 16, 2020. and are based on the FTSE 100 and S&P 500 index levels for the U.K. and U.S. markets, respectively. and are calculated over one-hour intervals as and , respectively. ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
6.1.2. Robustness: Alternative specification
Above, we use a difference-in-differences approach, which relies on an indicator variable to define the post-period, when the margin differential between the U.K. and U.S. markets increased (Section 6.1) or reduced (Section 6.1.1). Based on the difference-in-differences approach, we are unable to capture the actual daily margin differences between the two ETFs. To provide additional robustness, we repeat the prior experiment using an alternative approach, which captures the granularity of the daily differences in the margin proxies. For the daily analysis, we estimate the following regression:
| (3) |
where is defined as , or the difference between the U.K. and U.S. variable on day . represents one of the variables defined in Eq. (1) (i.e., quoted spread, effective spread, realized spread, price impact, volatility, and return) for market . We estimate equation (3) over the February 11 to April 11, 2020 period, which covers the one-month period before and after the WHO’s declaration of a pandemic on March 11, 2020.17
The results in Table 6 show that is positive and significant for all but one model specification. Importantly, consistent with our findings in Section 6.1, we show that when the margin on the U.K. ETF increases (decreases) more than the margin on the U.S. ETF, we observe a relative deterioration (improvement) in the liquidity measures for the U.K. ETF.
Table 6.
Alternate test for U.K. and U.S. ETFs.
| Quoted spread | Effective spread | Realized spread | Price impact | |
|---|---|---|---|---|
| Margin | 17.61 | 7.21 | 1.41 | 5.00 |
| (4.71) | (1.96) | (1.42) | (1.32) | |
| Volatility | −2.85 | −2.68 | 32.36 | −34.85 |
| (51.31) | (21.38) | (15.47) | (14.40) | |
| Return | −5.31 | −4.72 | 9.85 | −13.49 |
| (31.75) | (13.23) | (9.57) | (8.91) | |
| Constant | 3.70 | 1.48 | 0.07 | 0.99 |
| (0.88) | (0.37) | (0.27) | (0.25) | |
| Observations | 34 | 34 | 34 | 34 |
| 0.27 | 0.27 | 0.08 | 0.38 |
The table reports the relation between the margin differential and the liquidity differential for the CSPX.L (U.K.) and SPY (U.S.), which are ETFs that track the performance of the S&P 500, traded on the LSE and NYSE, respectively. Specifically, we report the results for the following equation:
,
where is computed as or the difference between the U.K. and U.S. ETF variables on day . represents one of the variables defined in Eq. (1) (Quoted spread, Effective spread, Realized spread, Price impact, Volatility and Return) for the U.S. or U.K. ETF, , for day, . represents the difference between the U.K. and U.S. margin proxies. The U.K. margin is proxied using the margin for the FTSE 100 futures trading on the Intercontinental Exchange. The U.S. margin is proxied using the margin for the S&P 500 futures trading on the Chicago Mercantile Exchange. Variables are calculated daily for the period February 11, 2020 to April 11, 2020. ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
6.1.3. Robustness: Falsification tests
In Section 6.1, we exploit a period when the U.K. margin proxy increases by more than the U.S. margin proxy. However, during this interval, there were also significant falls in the underlying S&P 500. To provide further confidence that our results are driven by the widening of the margin differential, rather than the fall in the S&P 500, we conduct a similar analysis over an interval when the market fell without a change in margins. Because there is no change in the margin differential, we do not expect to observe changes to market quality between the two markets.
For this investigation, we identify the period with the largest fall in stock price, without a corresponding change in the margin differential.18 Specifically, we identify the August 19 to August 25, 2015 period, when the S&P 500 Index fell by more than 10%. Importantly, the margins for both the U.K. and U.S. markets remained stable during the interval. We re-estimate equation (1), where is equal to 1 for the post-period from August 19 to August 25, 2015 and 0 for the pre-period from August 12 to August 18, 2015. Because the stock price fall is not associated with a corresponding change in margin, we expect the interaction term U.K. Margin increase to be insignificant in our model specifications.
Table 7 reports the results for the falsification test. Importantly, we find that U.K. Margin increase is insignificant for all but one of the model specifications.19 These findings show that market quality between the U.K. and U.S. markets does not change when there is no change to the margin differential. Based on these findings, the change in market quality reported in Section 6.1 is likely due to the change in the margin differential, rather than the fall in stock prices.
Table 7.
Difference-in-differences regression for U.K. and U.S. ETFs: Falsification test .
| Quoted spread | Effective spread | Realized spread | Price impact | |
|---|---|---|---|---|
| U.K. | 21.65 | 1.07 | 0.31 | 0.77 |
| (14.36) | (2.79) | (1.76) | (2.56) | |
| Margin increase | −6.48 | −1.68 | −0.30 | −1.64 |
| (11.16) | (2.17) | (1.37) | (1.99) | |
| U.K. × Margin increase | 2.73 | 5.75 | 1.11 | 4.10 |
| (17.01) | (3.31) | (2.09) | (3.03) | |
| Volatility | 1,353.01 | 361.58 | 36.67 | 380.69 |
| (581.08) | (112.98) | (71.24) | (103.58) | |
| Return | −722.45 | −174.68 | −176.56 | −10.41 |
| (609.68) | (118.54) | (74.75) | (108.68) | |
| Constant | −4.98 | −1.20 | −0.14 | −1.29 |
| (9.37) | (1.82) | (1.15) | (1.67) | |
| Observations | 69 | 69 | 69 | 69 |
| 0.14 | 0.26 | 0.04 | 0.20 |
The table reports the results to a falsification test in August 2015, when the S&P 500 fell over 10% with no corresponding change to exchange margin requirements. The CSPX.L (U.K.) and SPY (U.S.) are ETFs that track the performance of the S&P 500, traded on the LSE and NYSE, respectively. Specifically, we report the results for the following difference-in-differences regression:
,
where is one of the following liquidity variables: Quoted spread, Effective spread, Realized spread or Price impact for the U.S. or U.K. ETF, . The dependent variables are calculated over one hour intervals, and are expressed in basis points. is an indicator variable equal to 1 if the ETF trades in the U.K., and 0 otherwise. Margin increase is an indicator variable equal to 1 for the period August 19 to August 25, 2015 and 0 for the period August 12 to 18, 2015. and are based on the FTSE 100 and S&P 500 index levels for the U.K. and U.S. markets, respectively. and are calculated over one-hour intervals as and , respectively. ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
In Appendix F, we report the results of additional falsification tests, in which we repeat the difference-in-differences analyses from Sections 6.1, 6.1.1 using data from March 2019, the year before the COVID-19 shock. Again, based on these falsification tests, we do not detect significant changes in market quality between the U.K. and U.S. ETFs when there is no change in the margin differential in 2019.
Taken together, our evidence provides strong empirical support for the prediction that an exogenous increase in margins leads to a decrease in market liquidity as proposed by Brunnermeier and Pedersen (2009) and Gârleanu and Pedersen (2011). This result is further supported by a reduction in the margin differential on March 17, 2020. Our main result is also robust to several falsification tests over periods when there are no changes to the differential between the U.K. and U.S. margin proxies.
6.2. Global analysis
In the previous subsection, we investigate two ETFs tracking the same underlying index, but trading on separate exchanges, where the exchanges implemented differential changes to their margin requirements during the COVID-19 pandemic. Exploiting this unique scenario, we find strong evidence that market quality declines more for the U.K. ETF, which experienced larger increases in margin requirements, relative to the U.S. ETF. In this subsection, to generalize our main findings and to provide additional robustness for our results, we extend our analysis to a larger cross-section of listed equities. However, due to the difficulty in identifying additional ETFs that track the same underlying index while trading on different exchanges with varying margins, we use an alternate experimental design focusing on factors that are likely to affect some stocks more than others.
Specifically, we argue that an increase in a market’s margin requirements is likely to affect stocks that are index constituents (index stocks) more than stocks that are not index constituents (non-index stocks). This argument is based on the assertion that HFMMs are 1) more margin sensitive than traditional investors and 2) are more likely to be present in index stocks than non-index stocks. For reasons outlined in Section 4, HFMMs are likely to be more margin sensitive due to their unique trading style, which focuses on trading across short time horizons and using leveraged derivatives to hedge price risk. Similarly, Brogaard et al., 2014, Shkilko and Sokolov, 2020 show that high-frequency traders are more prevalent in index stocks, which is also supported by our empirical tests in Section 6.3. Thus, because HFMMs are more likely to withdraw their liquidity from stocks in which they are most active, we expect larger liquidity declines for index stocks, relative to non-index stocks, when margin increases.
For this investigation, we conduct a difference-in-differences test using the systemic increase in global margin requirements after the WHO’s declaration of COVID-19 as a pandemic on March 11, 2020 for identification. Our treatment group contains stocks with a higher level of HFMM participation (i.e., stocks within the market’s primary index as outlined in Table 1). Our control group contains stocks with a lower HFMM participation. To control for stock liquidity, we select the most liquid stocks outside the primary index for the sample of low HFMM stocks. Specifically, to be included in the sample of low HFMM stocks, we require the stock to have at least 100 daily trades and to be above the median market capitalization of non-index stocks.
For this difference-in-differences test, we use the systemic increase in global margin requirements after the WHO’s declaration of a pandemic on March 11, 2020 to define our post-period. While there exists some variation in the margin evolution across different equity index futures (which we exploit in Section 6.1), Fig. 2 shows striking similarities in both the level and timing of the sudden jump in margin requirements for all equity index futures after March 11, 2020. Given we use a difference-in-differences framework, we need only the average margin in the post-period to be different to the average margin in the pre-period and do not need the exact daily movements of margin. Accordingly, because of the sharp systemic jump in margin across all equity index futures, we believe the treatment period identified should capture the required increase in margin differential for the difference-in-differences analysis. Further, while we are unable to obtain margin data for the Nordic markets, given the sudden increase in global margins observed in Fig. 2, it is reasonable to assume that these markets also experienced significant increases in margin requirements.20
We also note that due to data limitations, we are unable to observe margin requirements on individual stocks and can only observe a systemic increase in equity index futures after March 11, 2020. The observed systemic jump in margin requirement for equity index futures appropriately captures a jump in stock margins for three reasons. First, given that Fig. 2 shows a sudden jump in margin requirements for equity index futures across all the major exchanges after March 11, 2020, it is reasonable to assume that individual stocks also experience a similar jump in margin requirements. Second, in Appendix C, we provide two empirical tests showing that the margin requirements for equity index futures closely approximate the margin requirements for individual equities using data from the Hong Kong Exchange (HKEX).21 Specifically, we create a “synthetic” index margin from the individual stocks and show that the margin for the synthetic index closely tracks the margin for the equity index futures and that the margin for all individual stocks have systemic, highly correlated changes. Finally, even if individual stock margins did not increase, and the increase in margin only applies to equity index futures, the liquidity of individual stocks is still likely to be affected. This is because HFMMs, who provide liquidity to these stocks, typically hedge price risk for underlying equity positions in the futures market.
Using this design, we estimate the following difference-in-differences regression:
| (4) |
where is one of the following liquidity variables (quoted spread, effective spread, realized spread, price impact) in stock i on day t as described previously. High margin is an indicator variable equal to 1 for the one-month period after the WHO declares the COVID-19 outbreak a pandemic (i.e., March 11–April 11, 2020), and 0 for the one-month period prior (i.e., February 11–March 10, 2020). Index constituent is an indicator variable equal to 1 if the stock belongs to a major stock market index as listed in Table 1.
The results in Table 8 support our main result that increased margin requirements contribute to the reduction in stock liquidity. Specifically, we find that the interaction term High margin Index constituent is positive and significant for quoted, effective, and realized spreads, indicating that the increase in spreads for index stocks is larger than the increase for non-index stocks after margin requirements increased. These results confirm the conjecture of Hameed et al. (2010) that the reduction in liquidity around market declines is driven by margin constraints imposed on market makers. Our evidence for the market quality impacts of margin on equity markets is complementary to the emerging results on COVID-19’s impact on corporate bonds (O’Hara and Zhou, 2021) and government bonds (Duffie, 2020), where inventory risk generated significant increases in transaction costs.
Table 8.
Difference-in-differences analysis for index and non-index stocks around the COVID-19 pandemic.
| Quoted spread | Effective spread | Realized spread | Price impact | |
|---|---|---|---|---|
| High margin | 109.9 | 99.1 | −66.9 | 114.8 |
| (1.0) | (0.9) | (38.7) | (1.5) | |
| Index constituent | −10.7 | −12.9 | 81.0 | −7.5 |
| (1.8) | (1.6) | (81.1) | (2.6) | |
| High margin × Index constituent | 36.2 | 32.6 | 227.7 | 10.4 |
| (2.1) | (1.9) | (100.5) | (3.1) | |
| Volume | 3.9 | 3.8 | 0.1 | −1.5 |
| (0.4) | (0.3) | (14.5) | (0.5) | |
| Return | −1.3 | −0.9 | −7.8 | −1.1 |
| (0.1) | (0.1) | (5.7) | (0.2) | |
| Constant | 107.4 | 100.0 | −300.6 | 183.6 |
| (5.6) | (5.0) | (209.3) | (8.1) | |
| Observations | 47,805 | 47,805 | 26,239 | 47,805 |
| 0.3 | 0.4 | 0.003 | 0.2 |
The table reports the changes to liquidity measures around the COVID-19 pandemic for index and non-index stocks in global markets. Specifically, we report the results for the following difference-in-differences regression:
where is one of the following liquidity variables: Quoted spread, Effective spread, Realized spread or Price impact for stock i on day t. The dependent variables are calculated daily, and are expressed in basis points. For each stock, the liquidity measure is normalized based on the average of January liquidity measures. High margin is an indicator variable equal to 1 for the period after the World Health Organization declares the COVID-19 outbreak a pandemic (March 11–April 11, 2020), and 0 for the pre-pandemic period (February 11–March 10, 2020). Index constituent is an indicator variable equal to 1 if the stock belongs in the main market index for the stock’s listing market as outlined in Table 1. Volume is the natural logarithm of the daily number of shares traded in the stock. Return is the percentage return for the main stock market index for the stock’s listing market as outlined in Table 1. The estimation uses data for Canada, Hong Kong, Norway, Sweden and U.K. , , and denote statistical significance at the 1%, 5%, and 10% levels, respectively.
6.3. HFMM behavior
In the previous subsections, we show that market liquidity declines when stock exchange margins increase. Here, we analyze a potential channel contributing to the reduction in market liquidity. In Section 6.2, we assert that margin sensitive HFMM withdraw more liquidity from index stocks than non-index stocks and thus, we expect to see a larger reduction (or withdrawal) of their activity from index stocks after the increase in margin requirements.
Due to the large number of markets investigated and the lack of available trader identifiers, following Hendershott et al., 2011, Hagströmer and Nordén, 2013, and Jørgensen et al. (2018), we use the order-to-trade ratio (OTR) as a proxy for the overall level of HFMM activity. As HFMMs withdraw from the market, we expect to see a decline in the OTR as high-frequency quote updates become less necessary. Further, this decline in the OTR is likely to be more pronounced for index stocks, which have a higher concentration of HFMM activity, relative to non-index stocks.
Following the empirical design from Section 6.2, we use a difference-in-differences regression framework to test whether HFMM activity falls more for index stocks, which are likely to have higher HFMM participation, versus non-index stocks. For this analysis, we replace the dependent variable in Eq. (4) with OTR:
| (5) |
where is the sum of the number of asks and bid updates at the top of the book, divided by the number of trades for stock i on day t. All other variables are defined as for Eq. (4).
The results in Table 9 support the assertion that index stocks, which have higher HFMM participation, experience a larger fall in HFMM activity, relative to non-index stocks with lower HFMM participation, after the increase in margin requirements. We find that the interaction term High margin Index constituent is negative and significant, indicating that OTR falls more for index stocks, relative to non-index stocks, following the significant increase in exchange margin requirements.
Table 9.
Changes in the order to trade ratio around the COVID-19 pandemic .
| Canada | Hong Kong | Norway | Sweden | U.K. | |
|---|---|---|---|---|---|
| High margin | −134.6 | 1.8 | 16.2 | 11.2 | 24.4 |
| (56.2) | (0.4) | (3.1) | (1.4) | (1.6) | |
| Index constituent | 39.4 | 4.8 | 22.2 | 30.4 | 30.2 |
| (102.9) | (0.8) | (4.8) | (2.3) | (2.6) | |
| High margin × Index constituent | 118.1 | −1.9 | −11.1 | −20.6 | −38.0 |
| (123.3) | (1.1) | (5.2) | (2.6) | (2.9) | |
| Volume | −57.4 | −3.6 | −14.2 | −12.0 | −11.1 |
| (18.0) | (0.1) | (1.2) | (0.5) | (0.6) | |
| Return | 0.2 | −0.01 | −2.1 | 0.01 | 0.3 |
| (5.4) | (0.1) | (0.4) | (0.2) | (0.2) | |
| Constant | 1,102.9 | 159.4 | 318.1 | 279.6 | 268.5 |
| (271.2) | (2.4) | (16.8) | (7.1) | (8.9) | |
| Observations | 11,908 | 11,200 | 2,933 | 8,133 | 13,631 |
| 0.001 | 0.1 | 0.1 | 0.1 | 0.1 |
The table reports changes to order to trade ratio (OTR) around the COVID-19 pandemic for index and non-index stocks in global markets. Specifically, we report the results for the following difference-in-differences regression:
where is the sum of the number of asks and bid updates at the top of book, divided by the number of trades for stock i on day t, normalized based on the average of January OTRs. High margin is an indicator variable equal to 1 for the period after the World Health Organization declares the COVID-19 outbreak a pandemic (March 11–April 11, 2020), and 0 for the pre-pandemic period (February 11–March 10, 2020). Index constituent is an indicator variable equal to 1 if the stock belongs in the main market index for the stock’s listing market as outlined in Table 1. Volume is the natural logarithm of the daily number of shares traded in the stock. Return is the percentage return for the main stock market index for the stock’s listing market as outlined in Table 1. The estimation uses data for Canada, Hong Kong, Norway, Sweden and U.K. ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
To provide additional robustness to these results, we perform a falsification test to show that our results are due to increasing margins, rather than the falling stock price. For this test, we estimate equation (5) for a period in 2015. During August 2015, the S&P 500 fell by more than 10% with no corresponding changes to margin requirements, as discussed in Section 6.1.3. Importantly, our results for the falsification test in Appendix F show no differential changes in OTR for index stocks, relative to non-index stocks, for this period when margins did not increase.
Together, our findings from Table 8, Table 9 are consistent with the hypothesis that escalating margins during times of crises negatively impacts market liquidity via the withdrawal of margin sensitive HFMMs.
7. Conclusion
We show that the WHO’s declaration of the COVID-19 pandemic in 2020 is associated with a sharp and sudden increase in margin requirements for exchanges worldwide. Using this change in margin requirements across a variety of developed equity markets globally, we test the theoretical predictions of Brunnermeier and Pedersen (2009) and document three main findings.
First, we show that an increase in capital requirements correlates with a decline in market liquidity. Using ETFs tracking the S&P 500 Index listed in the U.K. and U.S. markets, we find a larger deterioration in market liquidity for the U.K. ETF, which experienced a larger increase in margin, relative to the U.S. ETF.
Second, we demonstrate that stock liquidity decreases more for index stocks, which tend to have a higher proportion of liquidity provided by high-frequency market makers (HFMMs), than for non-index stocks. Due to their higher portfolio turnovers and shorter holding periods, HFMMs are more reliant on margin as they hold leveraged portfolios. This finding is consistent with the notion that increases in margin requirements have a larger impact on the liquidity of stocks in which HFMMs are more active.
Third, our findings suggest that HFMMs withdrew more from index stocks in which they are typically more prevalent. Specifically, we document that the order to trade ratio (OTR) declined more for index stocks, relative to non-index stocks, when exchange margin requirements increased.
Our findings contribute to ongoing policy debates around systemic risk and the regulation of markets and their participants. The systemic risks of concentrating the liquidity provision functions, particularly in a global setting, among a handful of high-frequency firms is becoming more apparent. The increases in equity market margins observed during 2020 are some of the largest and fastest on record. The associated withdrawal of HFMMs has the potential to reignite the debates surrounding positive obligations for market makers. It is possible that market structure changes, such as imposing positive obligations on appointed designated market makers, or regulatory capital reserves to act as a “countercyclical buffer” in times of stress, could potentially mitigate the liquidity crisis observed during such turbulent times.
Footnotes
We are grateful to an anonymous referee, as well as Angelo Aspris, Jonathan Goldberg, Ron Masulis, Peter O’Neill, Talis Putnins, Andriy Shkilko, Bart Yueshen and audience members at the SFM 2020 conference in Taiwan and the FIRS 2021 conference. We are particularly thankful to Marius Zoican for early discussion and assistance with data collection.
“The Day Coronavirus Nearly Broke the Financial Markets”, by Justin Baer, The Wall Street Journal, May 20, 2020.
See, for example, Ashraf, 2020, Baker et al., 2020, Ellul et al., 2020, Gormsen and Koijen, 2020, Hansen, 2020, and Ramelli and Wagner (2020).
Previously called Thomson Reuters Tick History (TRTH).
Detailed definitions of our liquidity measures are in Appendix A.
We remove the first and last fifteen minutes of trading when calculating our liquidity measures to exclude the impact of the opening and closing auctions.
The U.S. ETF trades on the New York Stock Exchange with Reuters instrument code (RIC) SPY, and the U.K. ETF trades on the London Stock Exchange with RIC CSPX.L.
See Table B.1 in Appendix B for a list of webpages.
See Appendix B for further details on the dollar margin reported across exchanges.
Our results are robust to either the dollar or percentage measure of margin.
In Appendix C, we confirm that margins for equity index futures are likely to be highly correlated with the margin requirements for their underlying stocks.
Consistent with the work of Donadelli et al. (2017), we use the WHO’s announcement of a pandemic as a significant event, which has been shown to impact stock returns.
In Appendix C, we provide evidence that a market’s equity index futures margin is a suitable proxy for both ETF and individual stock margins traded in the market’s primary exchange.
In Appendix D, we report similar results using a smaller two-day window around the March 11 event.
Our regressions contain 56 observations. We have 24 observations for the pre-period, which consists of 4 trading days, each with 3 × 1 h observations when both the U.K. and U.S. markets are open. In the post-period, because of daylight saving, there is a 4 h overlap when both markets are open. Thus, our post-period contains 32 observations, which consists of 4 trading days, each with 4 × 1 h observations when both markets are open.
We use a five-day pre- and post- window to maintain consistency with the results in Section 6.1. In Appendix D, we show that our results are robust to a shorter two-day window around the margin narrowing event.
In unreported results, our findings are robust to alternate sample windows.
We have data on margin requirements for both the U.K. and U.S. markets from January 2015.
For the Effective spread regression, U.K.Margin increase is weakly significant at the 10% level.
Our results are robust to removing the Nordic markets from the analysis.
While we can only obtain margin requirements for equity index futures for the majority of markets, we are able to obtain margin requirements for both the equity index futures and individual stock futures for the Hong Kong Exchange.
The underlying instrument for the ETF future and Index future are not identical, but both reflect trading on the Hong Kong Exchange.
While we cannot obtain the margin requirements for the ETF trading on the Stock Exchange of Hong Kong, it is reasonable to assume that the margin requirements for the ETF future trading on the Hong Kong Futures Exchange are highly correlated as both exchanges are owned by the same parent company.
The Hang Seng Index is the most widely quoted index for the Hong Kong equities market and contains approximately 60 constituents.
Appendix A. Data definitions
A.1. The liquidity variables for individual stocks
We use trade-and-quote data from Refinitiv to construct standard measures of market quality. We calculate our market quality metrics using data from continuous trading sessions. Accordingly, we exclude trades that occur during the first and last 15 min of each trading day.
-
•
The Quoted Spread is the difference between the current best bid and ask in that venue’s order book divided by the midpoint, . The quoted spread is recalculated whenever the limit order book is updated. The daily for stock on day is the daily time-weighted average.
-
•The Effective Spread is defined as:
where is an indicator variable that equals for buyer-initiated trades and for seller-initiated trades; is the trade price; and is the quote midpoint prevailing at the time of the trade. To determine whether an order is buyer or seller initiated, the transaction price is compared to the previous quote midpoint — if the price is above (below) the midpoint, we classify the order as buyer (seller) initiated. is the volume-weighted average of all trades for stock on day .(A.1) -
•The Price Impact is defined as:
where is the quote midpoint ten seconds after the th trade for stock and has the same definition used for Effective Spread. is the volume-weighted average of all trades for stock on day .(A.2) -
•The Realized Spread is defined as:
where is the quote midpoint ten seconds after the th trade for stock and has the same definition used for Effective Spread. is the volume-weighted average of all trades for stock on day .(A.3)
A.2. The liquidity variables for the U.K. and U.S. etfs
For the ETFs traded in the U.S. and the U.K., we calculate the same market quality metrics defined above at an hourly, rather than daily, frequency. Thus, rather than taking averages across all trade observations in the day, we compute hourly averages using only trades contained within each respective hour. We use hourly intervals for two reasons: (1) to compare market quality across the U.S. and U.K. during the interval when both markets are open; and (2) to ensure a large enough sample size to conduct meaningful analyses.
Appendix B. Margins
Margins are collected from exchange homepages, and are specific to an underlying contract. We choose the contract whose underlying best reflects the market’s equity index. For the U.S., we consider the margin requirement on S&P 500 Index futures traded on the Chicago Mercantile Exchange. For the U.K., we consider the margin requirements for the FTSE 100 Index futures traded on the Intercontinental Exchange (ICE). Similarly, for Hong Kong and Canada, we choose the Hang Seng Index futures and TSX 60 Index Futures traded on the Hong Kong Futures Exchange (HKX) and the Montreal Exchange, respectively. Table B.1 illustrates the monthly evolution of selected margins and provides the links to the data sources.
Table B.1.
Selected margins.
| Canada | Hong Kong | U.K. | U.S. | |
|---|---|---|---|---|
| (CAD) | (HKD) | (£) | (USD) | |
| Panel A: Margin requirements | ||||
| Jan 2, 2020 | 7,288 | 83,450 | 3,339 | 31,500 |
| Feb 3, 2020 | 4,725 | 83,750 | 3,339 | 33,000 |
| Mar 2, 2020 | 6,883 | 82,300 | 3,629 | 36,000 |
| Apr 1, 2020 | 19,579 | 116,200 | 6,699 | 60,000 |
| May 1, 2020 | 24,556 | 116,200 | 6,699 | 60,000 |
| Panel B: Data sources | ||||
| Canada | reg.m-x.ca | |||
| Hong Kong | www.hkex.com.hk | |||
| U.K. | www.theice.com | |||
| U.S. | www.cmegroup.com | |||
The table shows the currency margin requirements for selected markets and the links to the data sources. Panel A shows the average currency margin required to trade one futures contract for each market. We average the daily observations and provide the monthly average. Canada refers to the TSX 60 Index futures, which trade on the Montreal Exchange (expressed in CAD). Hong Kong refers to the Hang Seng Index futures, which trade on the Hong Kong Futures Exchange (expressed in HKD). U.K. refers to the margin for the FTSE 100 Index futures, which trade on the Intercontinental Exchange (expressed in pounds). U.S. refers to the margin for the S&P 500 Index futures, which trade on the Chicago Mercantile Exchange (expressed in USD). Panel B provides the links to the data sources.
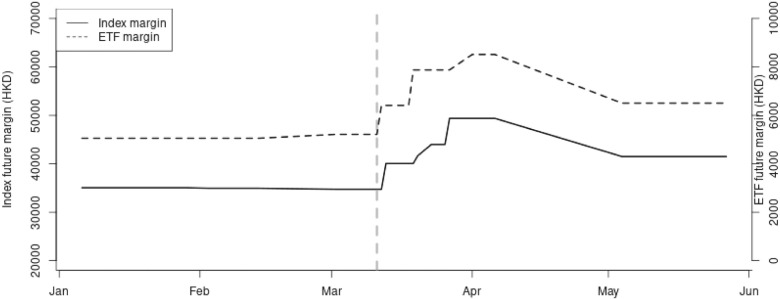
Appendix C. Margin proxy
C.1. Margin for index futures as proxy for ETF margins
Due to data limitations, we are unable to obtain margin requirements for ETFs in the U.S. and U.K markets. For this reason, in Section 6.1, we use the margin for the S&P 500 Index futures to proxy the margin for the SPY ETF, which trades on the New York Stock Exchange, and the margin for the FTSE 100 Index futures to proxy the margin for the CSPX.L ETF, which trades on the London Stock Exchange. In this Appendix, we show that the margin of a market’s equity index futures is a reasonable proxy for the margin of the ETFs trading in that market. For this analysis, we use data from the Hong Kong Exchange, which provides margins for selected index futures and ETF futures. Specifically, the Hong Kong Exchange data contains margin requirements for futures on the iShares FTSE China A50 ETF (ETF future) and margin for futures on the Hang Seng China Enterprises Index (Index future).22 In Fig. C.1, we plot the margin for the ETF future and Index future over the sample period. The plots show a remarkable similarity between the margins of the ETF future and the Index future (), which provides confidence that the margin of the index future is a reasonable proxy for the margin of the ETF future.23
Fig. C.1.
Margin requirements for an Index future and an ETF future. In the figure, we plot the margin requirements for the Hang Seng China Enterprises Index Futures (left axis) and I-Shares FTSE China A50 ETF (broken line, right axis) over the period January 6 to May 27, 2020.
C.2. Margin for index futures as proxy for equity margins
Next, we conduct two tests to provide assurance that the margin for the index future is an appropriate proxy for the margin on individual equities trading in the market. First, we compare the margin of an equity index futures with the margin of a “synthetic” equity index, which we construct from the margin of individual stock futures. Second, we test that changes in margin are systematic across all stocks.
To conduct these tests, we use Hong Kong Exchange margin data, which contains margins for both index futures and individual stock futures. Our aim is to create the margin for a “synthetic” Hang Seng Index using the margins for the individual stock futures of the index constituents.24 To create the synthetic Hang Seng Index margin, we weight the percentage margin of each index constituent by market capitalization. On the days the margin changes, we observe a correlation of 0.956 between the synthetic index percentage margin and the percentage margin requirements for the Hang Seng Index futures, as reported by the Hong Kong Exchange. This finding provides confidence that changes in margin on index futures is a reasonable proxy for changes in the margin on individual stocks.
Next, we show that the correlation of 0.956 is driven by a systematic margin change for all stock futures in the index, rather than by a change in margin for a small number of stock futures. Specifically, on the days margin changes for the future consist of at least one index constituent, we calculate the correlation between the margins of all stock futures for the constituents of the Hang Seng Index. During our sample period, we find that the margin of all stocks move in unison with a mean correlation of 0.93. Fig. C.2 provides a histogram of all correlations between the index constituents. The figure shows high correlations between all constituents, with only 0.6% of the sample reporting a correlation below 0.8.
Fig. C.2.
Histogram of correlations. This figure shows a histogram of the correlation in margins for stocks in the Hang Seng Index. We analyze data for the period January 1 to May 27, 2020. During this period, there are 33 days that the dollar margin changed for at least one index constituent. On these days, we calculate the correlation between the margin for all constituents in the index.
Appendix D. Window robustness
In this Appendix, we conduct robustness tests to ensure our results in Table 4, Table 5 are insensitive to sample windows of different lengths. Specifically, we use a shorter two-day window for our pre- and post-periods to provide robustness for our primary findings around the widening and narrowing of the margin differential between the U.K. and U.S. markets.
Table D.1 reports the results for the widening of the margin differential using a pre-period from February 5 to February 6, 2020 and a post-period from March 11 to March 12, 2020. Consistent with our primary findings, we find the interaction term (U.K. Margin increase) is generally positive and significant, which confirms the correlation between higher margins and lower market quality.
Table D.2 reports the results for the narrowing of the margin differential using a pre-period from March 15 to March 16, 2020 and a post-period from March 17 to March 18, 2020. Again, consistent with our primary findings, we find the interaction term (U.K. Margin narrowing) is generally negative and significant. This finding confirms that market quality improves for the U.K. market (i.e., there is a decline in spreads), relative to the U.S. market, when the margin differential narrows.
Table D.1.
Difference-in-differences regression for ETFs tracking the S&P 500 Index .
| Quoted spread | Effective spread | Realized spread | Price impact | |
|---|---|---|---|---|
| U.K. | 5.61 | 1.31 | 0.92 | 0.40 |
| (3.66) | (1.84) | (1.54) | (0.58) | |
| Margin increase | −8.25 | −4.24 | −3.36 | −1.22 |
| (4.66) | (2.34) | (1.96) | (0.74) | |
| U.K. × Margin increase | 9.93 | 5.32 | 2.08 | 3.47 |
| (5.02) | (2.52) | (2.11) | (0.79) | |
| Volatility | 369.30 | 193.03 | 139.92 | 68.36 |
| (147.68) | (74.17) | (62.05) | (23.34) | |
| Return | −224.91 | −101.50 | −91.55 | −23.62 |
| (144.75) | (72.70) | (60.83) | (22.88) | |
| Constant | −0.79 | −0.46 | −0.43 | −0.08 |
| (2.63) | (1.32) | (1.11) | (0.42) | |
| Observations | 28 | 28 | 28 | 28 |
| 0.48 | 0.39 | 0.16 | 0.72 |
The table reports the changes to liquidity measures around the widening of the margin differential for the CSPX.L (U.K.) and SPY (U.S.), which are ETFs that track the performance of the S&P 500, traded on the LSE and NYSE, respectively. Specifically, we report the results for the following difference-in-differences regression:
,
where is one of the following liquidity variables: Quoted spread, Effective spread, Realized spread or Price impact for the U.S. or U.K. ETF, . The dependent variables are calculated over one hour intervals, and are expressed in basis points. is an indicator variable equal to 1 if the ETF trades in the U.K., and 0 otherwise. is an indicator variable equal to 1 for the post-period from March 11 to March 12, 2020 and 0 for the pre-period from February 5 to February 6, 2020. and are based on the FTSE 100 and S&P 500 index levels for the U.K. and U.S. markets, respectively. and are calculated over one-hour intervals as and , respectively. ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
Table D.2.
Difference-in-differences regression for U.K. and U.S. ETFs (narrowing on March 17, 2020) .
| Quoted spread | Effective spread | Realized spread | Price impact | |
|---|---|---|---|---|
| U.K. | 40.82 | 12.98 | 8.24 | 4.30 |
| (9.67) | (2.67) | (1.94) | (1.09) | |
| Margin narrowing | −2.08 | 0.03 | 0.18 | −0.13 |
| (7.34) | (2.03) | (1.47) | (0.83) | |
| U.K. × Margin narrowing | −27.66 | −7.54 | −5.67 | −1.48 |
| (9.72) | (2.69) | (1.95) | (1.09) | |
| Volatility | −251.67 | 22.29 | −26.64 | 51.31 |
| (377.95) | (104.51) | (75.69) | (42.53) | |
| Return | −122.17 | −21.80 | −12.09 | −7.71 |
| (161.29) | (44.60) | (32.30) | (18.15) | |
| Constant | 9.95 | −0.20 | 0.59 | −0.79 |
| (14.11) | (3.90) | (2.83) | (1.59) | |
| Observations | 24 | 24 | 24 | 24 |
| 0.65 | 0.67 | 0.62 | 0.56 |
The table reports the changes to liquidity measures around the narrowing of the margin differential for the CSPX.L (U.K.) and SPY (U.S.), which are ETFs that track the performance of the S&P 500, traded on the LSE and NYSE, respectively. Specifically, we report the results for the following difference-in-differences regression:
,
where is one of the following liquidity variables: Quoted spread, Effective spread, Realized spread or Price impact for the U.S. or U.K. ETF, . The dependent variables are calculated over one hour intervals, and are expressed in basis points. is an indicator variable equal to 1 if the ETF trades in the U.K., and 0 otherwise. Margin narrowing is an indicator variable equal to 1 for the period March 17 to March 18, 2020 and 0 for the period March 15 to March 16, 2020. and are based on the FTSE 100 and S&P 500 index levels for the U.K. and U.S. markets, respectively. and are calculated over one-hour intervals as and , respectively. ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
Appendix E. Margin narrowing illustration
Fig. E.1 illustrates the evolution of the differential between the U.K. and U.S. ETF margin proxies. We observe a sharp narrowing in the margin differential on March 17, 2020. Accordingly, we use the period just prior to this narrowing as our pre-period and the interval directly after the narrowing as our post-period, as indicated in the figure.
Fig. E.1.
Margin differential for U.S. and U.K. exchanges. The figure shows the time series evolution of the margin differential between the U.K. and U.S. margin proxies. The vertical lines indicate the pre (March 12 to March 16, 2020) and post (March 17 to March 21, 2020) periods for our difference-in-differences analysis.
Appendix F. Additional falsification tests for the U.K. and U.S. ETFs
In this Appendix, we conduct falsification placebo tests over the same time intervals in the previous year to provide robustness to our main results. In our primary analysis, we investigate changes to market liquidity around the margin increase in March 2020. Accordingly, for our placebo margin increase test, we repeat the difference-in-differences using the full second and fourth trading weeks in March 2019 for our pre- and post-periods, respectively. In contrast to our main results, we observe that U.K. Margin increase is insignificant across all model specifications for the placebo tests in 2019, when there is no change in the margin differential between the U.K. and U.S. markets (see Table F.1).
Next, we extend our falsification placebo tests to our analysis of the narrowing of the margin differential. Specifically, in our main results, we use a pre-period from March 12 to March 16, 2020 and a post-period from March 17 to March 21, 2020 to investigate the narrowing of the margin differential. For our falsification placebo tests, we use these same intervals during the previous year. In contrast to our main results, the placebo results in Table F.2 show that U.K. Margin narrowing is insignificant across all model specifications.
Table F.1.
Difference-in-differences regression for U.K. and U.S. ETFs (placebo widening in March, 2019) .
| Quoted spread | Effective spread | Realized spread | Price impact | |
|---|---|---|---|---|
| U.K. | 7.00 | 0.77 | 0.08 | 0.68 |
| (4.34) | (0.05) | (0.40) | (0.41) | |
| Margin increase | 3.93 | −0.01 | −0.10 | 0.09 |
| (5.09) | (0.06) | (0.47) | (0.48) | |
| U.K. × Margin increase | 0.31 | 0.04 | 0.42 | −0.37 |
| (6.19) | (0.07) | (0.57) | (0.58) | |
| Volatility | −1,770.74 | 9.69 | 31.62 | −23.00 |
| (1,403.45) | (15.24) | (130.36) | (131.66) | |
| Return | 454.92 | 2.55 | −4.16 | 7.31 |
| (757.73) | (8.23) | (70.38) | (71.09) | |
| Constant | 4.42 | 0.14 | −0.04 | 0.19 |
| (4.69) | (0.05) | (0.44) | (0.44) | |
| Observations | 80 | 80 | 80 | 80 |
| 0.07 | 0.88 | −0.04 | −0.01 |
The table reports the changes to liquidity measures around the placebo widening of the margin differential for the CSPX.L (U.K.) and SPY (U.S.), which are ETFs that track the performance of the S&P 500, traded on the LSE and NYSE, respectively. Specifically, we report the results for the following difference-in-differences regression:
,
where is one of the following liquidity variables: Quoted spread, Effective spread, Realized spread or Price impact for the U.S. or U.K. ETF, . The dependent variables are calculated over one hour intervals, and are expressed in basis points. is an indicator variable equal to 1 if the ETF trades in the U.K., and 0 otherwise. Margin increase is an indicator variable equal to 1 for the period March 25 to March 29, 2020 and 0 for the period March 11 to March 15, 2020. and are based on the FTSE 100 and S&P 500 index levels for the U.K. and U.S. markets, respectively. and are calculated over one-hour intervals as and , respectively. ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
Table F.2.
Difference-in-differences regression for U.K. and U.S. ETFs (placebo narrowing in March, 2019) .
| Quoted spread | Effective spread | Realized spread | Price impact | |
|---|---|---|---|---|
| U.K. | 4.70 | 0.72 | 0.02 | 0.70 |
| (1.80) | (0.06) | (0.24) | (0.25) | |
| Margin narrowing | −0.31 | −0.0002 | −0.08 | 0.07 |
| (1.94) | (0.06) | (0.26) | (0.27) | |
| U.K. × Margin narrowing | −1.27 | −0.02 | 0.29 | −0.30 |
| (2.52) | (0.08) | (0.33) | (0.35) | |
| Volatility | 207.20 | 2.98 | −30.60 | 23.66 |
| (772.92) | (24.62) | (102.20) | (108.17) | |
| Return | −196.68 | 4.69 | −92.63 | 101.36 |
| (348.46) | (11.10) | (46.08) | (48.77) | |
| Constant | 0.09 | 0.16 | 0.20 | −0.02 |
| (2.24) | (0.07) | (0.30) | (0.31) | |
| Observations | 64 | 64 | 64 | 64 |
| 0.10 | 0.83 | 0.04 | 0.11 |
The table reports the changes to liquidity measures around the placebo narrowing of the margin differential for the CSPX.L (U.K.) and SPY (U.S.), which are ETFs that track the performance of the S&P 500, traded on the LSE and NYSE, respectively. Specifically, we report the results for the following difference-in-differences regression:
,
where is one of the following liquidity variables: Quoted spread, Effective spread, Realized spread or Price impact for the U.S. or U.K. ETF, . The dependent variables are calculated over one hour intervals, and are expressed in basis points. is an indicator variable equal to 1 if the ETF trades in the U.K., and 0 otherwise. Margin narrowing is an indicator variable equal to 1 for the period March 17 to March 21, 2019 and 0 for the period March 12 to March 16, 2019. and are based on the FTSE 100 and S&P 500 index levels for the U.K. and U.S. markets, respectively. and are calculated over one-hour intervals as and , respectively. ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
Appendix G. Falsification test for the order to trade ratio
In Section 6.1.3, we perform a falsification test to provide further confidence that our results are driven by the widening of the margin differential during the pandemic period, rather than a sudden fall in stock price. Specifically, we use a period in August 2015 when the S&P 500 fell by over 10% with no corresponding change to exchange margin requirements.
In this Appendix, we conduct a similar falsification test during August 2015 to show that the reported change in OTR in Section 6.3 is associated with the change in margin, rather than a fall in stock price. Fig. G.1 shows that the fall in stock prices is not limited to the U.S. market: we observe similar falls in global stock values during August 2015. Using the same length of sample window in Section 6.3, for our falsification test, we use a pre-period from August 1 to August 24, 2015 and a post-period from August 25 to September 30, 2015.
Fig. G.1.
The evolution of stock market prices, July–October 2015. The figure illustrates the movement in stock market prices for the indices listed in Table 1. The plots show the change in index price levels, relative to the index level on July 1, 2015, which takes a value of 100. The broken vertical line marks August 25, 2015.
The results reported in Table G.1 show that OTR did not decline more for index stocks, relative to non-index stocks, as a result of the price decline in August 2015 (High margin Index constituent is not negative and significant for any of the markets). This result provides support for the hypothesis that high-frequency market makers withdrew more liquidity from index stocks, relative to non-index stocks, as a result of rising margins, rather than the sharp fall in prices, during the 2020 pandemic period.
Table G.1.
Changes in the order to trade ratio during August–September 2015 .
| Canada | Hong Kong | Norway | Sweden | U.K. | |
|---|---|---|---|---|---|
| High Margin | −6.6 | −2.3 | −30.1 | 5.2 | 10.1 |
| (1.0) | (0.7) | (13.3) | (1.5) | (0.8) | |
| Index Constituent | 5.8 | 10.4 | 45.3 | 6.3 | 1.3 |
| (2.2) | (1.5) | (28.5) | (2.4) | (1.2) | |
| High margin × Index constituent | −2.4 | 8.6 | 40.9 | −1.5 | 0.2 |
| (2.7) | (1.7) | (31.7) | (2.8) | (1.5) | |
| Volume | −5.6 | −4.6 | −13.7 | −2.7 | −1.8 |
| (0.3) | (0.2) | (2.8) | (0.4) | (0.2) | |
| Return | −0.6 | 0.8 | 2.9 | −0.8 | −1.7 |
| (0.3) | (0.2) | (3.8) | (0.4) | (0.2) | |
| Constant | 189.4 | 176.1 | 318.4 | 145.4 | 133.0 |
| (4.8) | (3.8) | (39.6) | (6.3) | (3.2) | |
| Observations | 17,491 | 8,443 | 7,024 | 7,283 | 13,223 |
| 0.02 | 0.1 | 0.003 | 0.01 | 0.02 |
The table reports changes to the order to trade ratio (OTR) for a period during August to September 2015, when global stock markets declined, with no corresponding change to exchange margin requirements. Specifically, we report the results for the following difference-in-differences regression:
where is the sum of the number of asks and bid updates at the top of book, divided by the number of trades for stock i on day t, normalized based on the average of January OTRs. High margin is an indicator variable equal to 1 for the period after the market decline (August 25–September 30, 2015), and 0 for the period immediately before the market decline (August 1–August 24, 2015). Index constituent is an indicator variable equal to 1 if the stock belongs in the main market index for the stock’s listing market as outlined in Table 1. Volume is the natural logarithm of the daily number of shares traded in the stock. Return is the percentage return for the main stock market index for the stock’s listing market as outlined in Table 1. The estimation uses data for Canada, Hong Kong, Norway, Sweden, and U.K. ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
References
- Adrian T., Boyarchenko N., Shachar O. Dealer balance sheets and bond liquidity provision. J. Monetary Econ. 2017;89:92–109. doi: 10.1016/j.jmoneco.2017.03.011. [DOI] [Google Scholar]
- Aramonte S., Szerszeń P.J. Cross-market liquidity and dealer profitability: Evidence from the bond and CDS markets. J. Financial Mark. 2020;51 doi: 10.1016/j.finmar.2020.100559. [DOI] [Google Scholar]
- Ashraf B.N. Stock markets’ reaction to COVID-19: Cases or fatalities? Res. Int. Bus. Finance. 2020;54 doi: 10.1016/j.ribaf.2020.101249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker S.R., Bloom N., Davis S.J., Kost K., Sammon M., Viratyosin T. The unprecedented stock market reaction to COVID-19. Rev. Asset Pricing Stud. 2020;10(4):742–758. doi: 10.1093/rapstu/raaa008. [DOI] [Google Scholar]
- Bartlett R.P., McCrary J. How rigged are stock markets? Evidence from microsecond timestamps. J. Financial Mark. 2019;45:37–60. doi: 10.1016/j.finmar.2019.06.003. [DOI] [Google Scholar]
- Behn M., Haselmann R., Wachtel P. Procyclical capital regulation and lending. J. Finance. 2016;71(2):919–956. doi: 10.1111/jofi.12368. [DOI] [Google Scholar]
- Bent, A., Duffie, D., Zhu, Y., 2019. The decline of too big to fail. In: Working Paper, Australia National University.
- Berger A.N., Bouwman C.H.S., Kick T., Schaeck K. Bank liquidity creation following regulatory interventions and capital support. J. Financ. Intermediation. 2016;26:115–141. doi: 10.1016/j.jfi.2016.01.001. [DOI] [Google Scholar]
- Brogaard J., Hendershott T., Riordan R. High-frequency trading and price discovery. Rev. Financ. Stud. 2014;27(8):2267–2306. doi: 10.1093/rfs/hhu032. [DOI] [Google Scholar]
- Brogaard, J., Ringgenberg, M.C., Roesch, D., 2020. Does floor trading matter?. In: Working Paper, SSRN.
- Brunnermeier M.K., Pedersen L.H. Market liquidity and funding liquidity. Rev. Financ. Stud. 2009;22(6):2201–2238. [Google Scholar]
- Cespa G., Foucalt T. Illiquidity contagion and liquidity crashes. Rev. Financ. Stud. 2014;27(6):1615–1660. [Google Scholar]
- Cheng, J., Wessel, D., Younger, J., 2020. How did COVID-19 discrupt the market for U.S. treasury debt?. In: Working paper, Hutchins Center, Brookings Institution.
- Comerton-Forde C., Hendershott T., Jones C.M., Moulton P.C., Seasholes M.S. Time variation in liquidity: The role of market-maker inventories and revenues. J. Finance. 2010;65(1):295–331. doi: 10.1111/j.1540-6261.2009.01530.x. [DOI] [Google Scholar]
- Conrad J., Wahal S. The term structure of liquidity provision. J. Financ. Econ. 2020;136(1):239–259. doi: 10.1016/j.jfineco.2019.09.008. [DOI] [Google Scholar]
- Daskalaki C., Skiadopoulos G. The effects of margin changes on commodity futures markets. J. Financ. Stab. 2016;22:129–152. doi: 10.1016/j.jfs.2016.01.002. [DOI] [Google Scholar]
- Donadelli M., Kizys R., Riedel M. Dangerous infectious diseases: Bad news for main street, good news for wall street? J. Financial Mark. 2017;35:84–103. doi: 10.1016/j.finmar.2016.12.003. [DOI] [Google Scholar]
- Dudley E., Nimalendran M. Margins and hedge fund contagion. J. Financ. Quant. Anal. 2011;46(5):1227–1257. [Google Scholar]
- Duffie, D., 2020. Still the world’s safe haven? Redesigning the U.S. Treasury Market after the COVID-19 Crisis. In: Working paper, Stanford University.
- Ellul A., Erel I., Rajan U. The COVID-19 pandemic crisis and corporate finance. Rev. Corp. Financ. Stud. 2020;9(3):421–429. doi: 10.1093/rcfs/cfaa016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming M., Ruela F. Liberty Street Economics. Federal Reserve Bank of New York; 2020. Treasury market liquidity during the COVID-19 crisis. [Google Scholar]
- Gârleanu N., Pedersen L.H. Margin-based asset pricing and deviations from the law of one price. Rev. Financ. Stud. 2011;24(6):1980–2022. doi: 10.1093/rfs/hhr027. [DOI] [Google Scholar]
- Gormsen N.J., Koijen R.S. Coronavirus: Impact on stock prices and growth expectations. Rev. Asset Pricing Stud. 2020;10(4):574–597. doi: 10.1093/rapstu/raaa013. [DOI] [Google Scholar]
- Gromb D., Vayanos D. Equilibrium and welfare in markets with financially constrained arbitrageurs. J. Financ. Econ. 2002;66(2):361–407. doi: 10.1016/S0304-405X(02)00228-3. [DOI] [Google Scholar]
- Hagströmer B., Nordén L. The diversity of high-frequency traders. J. Financial Mark. 2013;16(4):741–770. doi: 10.1016/j.finmar.2013.05.009. [DOI] [Google Scholar]
- Hameed A., Kang W., Viswanathan S. Stock market declines and liquidity. J. Finance. 2010;65(1):257–293. doi: 10.1111/j.1540-6261.2009.01529.x. [DOI] [Google Scholar]
- Hansen L.P. Repercussions of pandemics on markets and policy. Rev. Asset Pricing Stud. 2020;10(4):569–573. doi: 10.1093/rapstu/raaa020. [DOI] [Google Scholar]
- Hasbrouck J., Saar G. Low-latency trading. J. Financial Mark. 2013;16(4):646–679. [Google Scholar]
- Hendershott T., Jones C.M., Menkveld A.J. Does algorithmic trading improve liquidity? J. Finance. 2011;66(1):1–33. [Google Scholar]
- Hugonnier J., Morellec E. Bank capital, liquid reserves, and insolvency risk. J. Financ. Econ. 2017;125(2):266–285. doi: 10.1016/j.jfineco.2017.05.006. [DOI] [Google Scholar]
- Jørgensen K., Skjeltorp J.A., Ødegaard B.A. Throttling hyperactive robots - order to trade ratios at the oslo stock exchange. J. Financial Mark. 2018;37(1):1–16. [Google Scholar]
- Karolyi G.A., Lee K.-H., van Dijk M.A. Understanding commonality in liquidity around the world. J. Financ. Econ. 2012;105(1):82–112. doi: 10.1016/j.jfineco.2011.12.008. [DOI] [Google Scholar]
- Morris S., Shin H.S. Liquidity black holes. Rev. Financ. 2004;8(1):1–18. doi: 10.1023/B:EUFI.0000022155.98681.25. [DOI] [Google Scholar]
- O’Hara M., Zhou X.A. Anatomy of a liquidity crisis: corporate bonds in the covid-19 crisis. J. Financ. Econ. 2021;142(1):46–68. doi: 10.1016/j.jfineco.2021.05.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramelli S., Wagner A.F. Feverish stock price reactions to COVID-19. Rev. Corp. Financ. Stud. 2020;9(3):622–655. doi: 10.1093/rcfs/cfaa012. [DOI] [Google Scholar]
- Repullo R., Suarez J. The procyclical effects of bank capital regulation. Rev. Financ. Stud. 2013;26(2):452–490. doi: 10.1093/rfs/hhs118. [DOI] [Google Scholar]
- Shkilko A., Sokolov K. Every cloud has a silver lining: Fast trading, microwave connectivity, and trading costs. J. Finance. 2020;75(6):2899–2927. doi: 10.1111/jofi.12969. [DOI] [Google Scholar]
- Weill P.-O. Leaning against the wind. Rev. Econom. Stud. 2007;74(4):1329–1354. doi: 10.1111/j.1467-937X.2007.00451.x. [DOI] [Google Scholar]