Cooperation among cancer cells: applying game theory to cancer

Abstract

Cell cooperation promotes many of the hallmarks of cancer via the secretion of diffusible factors that can affect cancer cells or stromal cells in the tumour microenvironment. This cooperation cannot be explained simply as the collective action of cells for the benefit of the tumour because non-cooperative subclones can constantly invade and free-ride on the diffusible factors produced by the cooperative cells. A full understanding of cooperation among the cells of a tumour requires methods and concepts from evolutionary game theory, which has been used successfully in other areas of biology to understand similar problems but has been underutilized in cancer research. Game theory can provide insights into the stability of cooperation among cells in a tumour and into the design of potentially evolution-proof therapies that disrupt this cooperation.

Cells within a tumour compete for space and resources but also cooperate with one another by secreting diffusible factors that promote tumour growth and invasion^1–5. Interactions between cancer cells and with their microenvironment are essential for cancer progression^6–8 and are also a form of cooperation². Many of the molecules responsible for these interactions, their genes and their downstream signalling pathways, are known, but why cells within a tumour cooperate remains unexplained. The ‘why’ here relates to the adaptive advantage^9–11 of cooperation: what selective advantage does a cell gain by cooperating (for example, by producing a beneficial diffusible factor)?

The idea that cells within a tumour cooperate for the benefit of the tumour — an appealing and apparently reasonable explanation — is a logical fallacy that has a parallel in the history of evolutionary ecology, where it is known as the ‘group selection’ argument¹². This idea states that the behaviour of individuals is driven by the success of their group or species; it was popular until the 1960s, but evolutionary biologists now agree that the logic behind it is flawed^12–14. A mutation making an individual cheat, for instance, by free-riding on shared resources produced by other cooperative individuals, would confer a reproductive advantage to the cheating individual and its descendants. Thus, its type would increase in frequency in the population over time irrespective of the consequences for the population in the long term — leading to what is generally referred to as ‘tragedy of the commons’¹⁵. In the original example, a group of herders whose cows graze a common land have a selfish short-term interest in putting as many cows as possible onto the land, even if the land is damaged as a result, because the benefit is private while the damage to the common land is shared with the entire group; if all herders make this selfish decision, however, the land will be degraded. Evolution is short-sighted, and nothing evolves for the benefit of the group, or the species, even if that may lead to inefficiencies and extinctions¹⁴.

In the case of cooperation among cancer cells, a mutant cell that stopped producing growth factors would still benefit from the growth factors secreted by its neighbouring cells without paying the cost of producing these factors; hence, that mutant subclone would have a higher fitness and spread within the tumour. Over time, the subclones originating from this non-producer cell should drive the original producer subclone to extinction — a tragedy of the commons at the cellular level. Clonal selection^16–18, like natural selection in the wild, promotes only phenotypes that increase an individual cell’s fitness and not the long-term benefit of the group it happens to belong to (the tumour). Nothing evolves for the benefit of the group — in this case, of the tumour.

How is cooperation maintained then? This question is the source of complex analysis and never-ending debates in other fields, ranging from evolutionary biology^14,19–22 to economics^23–25, but is generally glossed over in cancer biology. In this Opinion article, we argue that a full understanding of cooperation between cancer cells requires the application of methods and concepts from game theory.

Game theory of cancer

Evolutionary game theory.

Game theory is the study of strategic interactions, that is, situations in which an individual’s payoff depends on not only its own behaviour but also the behaviour of other individuals^26–29. In other words, game theory is the study of optimization problems in which payoff functions are frequency-dependent, that is, when fitness depends on not only the environment but also the changing frequencies of the other phenotypes in the population, which includes competitors and cooperators. Such problems are called ‘games’, the individuals are called ‘players’, and the behaviour each player adopts is a ‘strategy’.

In game theory applied to human behaviour, it is assumed that decisions are taken through rational decision-making and that payoffs correspond to profit. In evolutionary game theory^30–33, payoff corresponds to Darwinian fitness, and there is no need to assume rationality or intention: the players are replicating individuals (in this case, cancer cells or stromal cells), and strategies are phenotypes produced by mutations that differentiate one type (in this case, a subclone) from another within the population (in this case, the tumour). Optimization is achieved at the population level via natural selection (in this case, clonal selection), which changes the frequencies of the strategies over time in a manner proportional to their fitness.

While for an ecologist, it is clear that natural selection in the wild is often frequency-dependent, in cancer research, the traditional view of tumorigenesis as a clonal population of cells developing all of the necessary genetic traits independently to form a tumour might suggest that the fitness of a genotype is independent of its relative abundance. Game theory does not offer new insight into hallmarks of cancer that are not frequency-dependent, such as genome instability and the limitless replicative potential of cancer cells. Most of the hallmarks of cancer, however, such as self-sufficiency in growth signals, evading apoptosis and the immune system, neoangiogenesis and metastasis, depend on interactions between cancer cells or between cancer cells and stromal cells^6–8, which are frequency-dependent. Evolutionary game theory can help understand these interactions.

The simplest game describing the problem of cooperation is the Prisoner’s Dilemma³⁴ (PD) (BOX 1). There is a vast literature in evolutionary biology^14,19–22 and economics^23–25 about the PD and on how, in spite of its predictions, cooperation can evolve because of genetic relatedness^14,22 or repeated interactions over time^19,21. In cancer research, game theory was introduced^35,36 using a version of the game of Chicken^37–39 (BOX 2). Subsequent papers using game theory in cancer research^40–49 were extensions of this pairwise game, and analogous games with pairwise interactions continue to be used. These, however, are simple models that do not capture fundamental features of cancer: most cases of cooperation in cancer are examples of multiplayer games, where payoffs are calculated from the effect of the collective interactions of many cells, rather than from the pairwise interactions of cells. This is because in most cases, cooperation in cancer depends on the effect of diffusible factors.

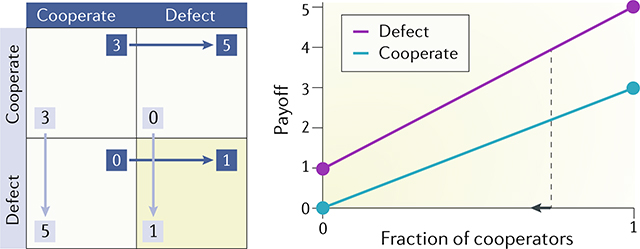
Box 1 |. The Prisoner’s Dilemma.

Pairwise games can be described by payoff matrices that list the payoffs of all the possible interactions between the two players. In the figure, two players (dark blue and grey) must decide, simultaneously, to either cooperate or defect: mutual cooperation rewards both with 3 points, whereas mutual defection leads to only 1 point each; if only one player cooperates, he or she gets 0 points and the defector gets 5 points. The actual entries of the matrix do not matter as long as the ranking of the payoffs is conserved — this type of payoff matrix defines what is generally called the Prisoner’s Dilemma (PD)³⁴.

Mutual cooperation is better (payoffs are higher for both players) than mutual defection; hence, one might think that the players should cooperate (this is the traditional — but erroneous — explanation of cooperation among cancer cells). If the first player cooperates, however, the second player is better off defecting (getting 5 points instead of 3); and if the first player defects, the second player is better off defecting too (getting 1 point instead of 0). So, no matter what the other player does, the only rational strategy is to defect (the stable outcome of the game can be found simply by identifying the cell where the arrows, which describe an increase in payoff for each player, converge). However, both players would be better off by choosing mutual cooperation, hence the dilemma.

In terms of evolutionary game theory, the plot in the right panel of the figure shows the dynamics of the process in a population: the two coloured lines show the fitness of the two strategies (cooperation and defection) as a function of the fraction f of cooperators in the population. At the extremes, interactions are always either with a cooperator (at f = 1) or with a defector (at f = 0); hence, the value of the two functions at those values of f can be taken from the matrix in the left panel. The intermediate values show the frequency-dependent fitness of the two types. Because the fitness of a defector is always higher than the fitness of a cooperator, at the next generation, there will be fewer cooperators in the population; hence the fraction of cooperators in the population will always decline irrespective of the current fraction (the arrow shows the direction of the dynamics), and the final outcome will be the extinction of cooperation: all players will defect and have fitness equal to 1.

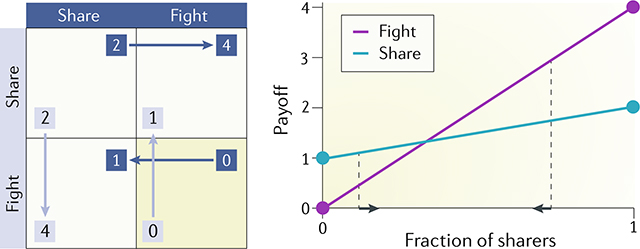
Box 2 |. The game of Chicken.

In the game of Chicken³⁷, also called Snowdrift³⁸ or Hawk–Dove game³⁹, two players must decide to either share a resource or fight to have exclusive control over it. Sharing confers 2 points to each player (see the figure, left panel), whereas if both fight, they both get 0 points (for instance, because the benefit of the resource is offset by the cost of fighting — note that the zero here does not mean that the costs and benefits exactly cancel each other; the actual values matter only in relation to each other’s rank). However, if one player fights and the other does not, the fighter gets most of the resource and neither player has a cost (the fighter gets 4, and the other player gets 1). Therefore, here it is better to fight if the other player does not and vice versa, and this is the equilibrium of the game.

An equilibrium occurs when the frequencies of the two types (here, fighters and sharers) do not change. Hence, one can find the equilibrium by equating the payoff of the two strategies: if s is the fraction of sharers in the population, the fitness of a sharer is given by s times 2 and (1 − s) times 1 because a sharer has payoff 2 when interacting with another sharer and 1 when interacting with a fighter. Hence, s(2) + (1 − s)(1) = 1 + s. Similarly, the fitness of a fighter is s(4) + (1 − s)(0) = 4 s. At equilibrium, the fitness of a fighter equals that of a sharer (1 + s = 4 s), and therefore, s = 1/3. As we can see in the plot on the right in the figure, this is where the fraction of sharers converges in the population dynamics of the game: at high frequencies of sharers, the fitness of a fighter is higher, and hence, fighters will increase in frequency; at low frequencies of sharers, however, fighters have lower fitness, and hence, the sharers will not be eliminated from the population.

A similar logic applies to public goods games that describe the production of beneficial diffusible factors in multiplayer interactions with nonlinear benefit effects.

Cooperation via diffusible factors.

Game theory has been applied to cancer to explain a variety of situations in which cancer cells cooperate with each other (FIG. 1). The production of diffusible growth factors is the most straightforward example^3,50–53, and the first empirical test³ of game theory in cancer was performed on insulin-like growth factor II (IGF2), which promotes proliferation and evasion of apoptosis in neuroendocrine pancreatic cancer cells. Similar dynamics arguably apply to other diffusible factors in other types of cancer. Other examples include the role of isocitrate dehydrogenase 1 (IDH1)-mutated tumour cells in secondary glioblastomas⁴⁴, prostate tumour growth under intermittent androgen suppression therapy⁵⁴, metabolic mutualism between hypoxic and oxygenated cancer cells⁵⁵, interactions mediated by lactic acid production and angiogenesis⁵⁶ and the Warburg effect^43,57,58.

Fig. 1 |. Cooperative interactions within the tumour and with the stroma.

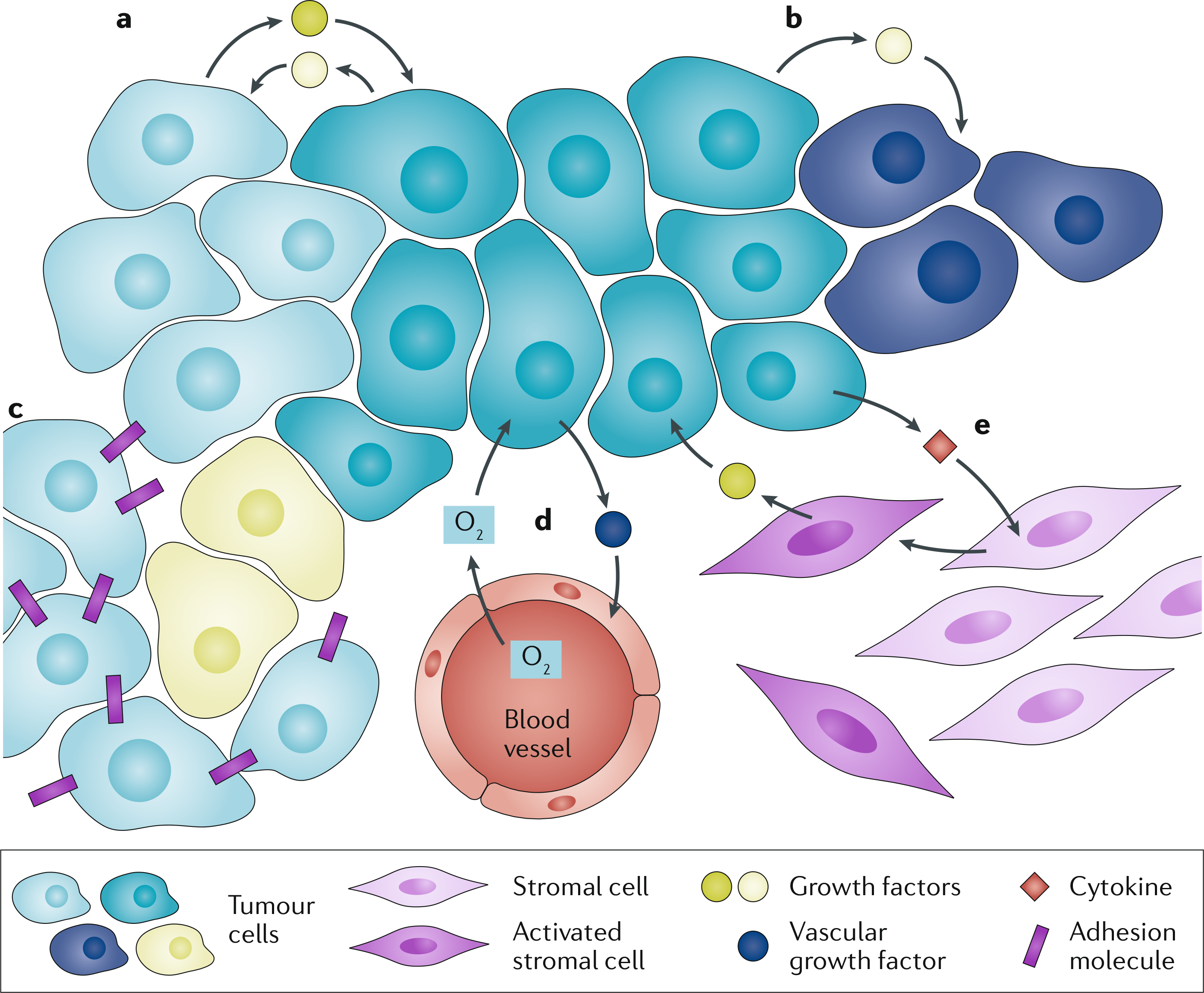
a | Two cancer subclones exchange mutually beneficial growth factors. b | One cancer subclone provides a growth factor to itself and to another, non-producer subclone. c | Cancer cells producing adhesion molecules provide a benefit to those nearby that do not produce adhesion molecules. d | Cancer cells producing growth factors trigger the formation of new blood vessels, which provide oxygen to the tumour. e | Cancer cells produce cytokines that activate stromal cells, which in turn provide growth factors to the cancer cells.

Cooperation can also be mediated by the stroma. Normal fibroblasts, for example, are recruited and activated by the tumour, becoming cancer-associated fibroblasts (CAFs) and acquiring pro-tumorigenic functions, secreting growth factors and cytokines that promote tumour progression⁵⁹. This is a form of coercion, not cooperation, given that the stromal cells are recruited and activated by the cancer cells for their own advantage. Cancer cells, however, do cooperate with each other by secreting the diffusible factors that recruit and activate the fibroblasts. In other cases, the benefit for the tumour arises from growth factors, produced by the cancer cells, that promote neoangiogenesis or disable the immune system by activating or inhibiting a variety of immune cells⁶. In all these cases, cancer cells cooperate with each other by producing diffusible factors that induce the stroma to provide a benefit to the tumour. Game theory has been used to describe tumour–stroma interactions in the production of matrix metalloproteinases and tissue inhibitors of metalloproteinases⁶⁰, in the dynamics of prostate cancer progression and treatments⁴¹ and in the dynamics of multiple myeloma^46,61,62.

The Warburg effect⁶³ is another example of intratumour cooperation that depends on diffusible factors. In some cases, a glycolytic subpopulation of cancer cells under hypoxia will release lactate as a by-product, thus providing new fuel for adjacent cancer cells⁶⁴. The Warburg effect, however, is not merely an adaptation to hypoxia and can occur even under normal oxygen concentrations⁶⁵. In fact, its main function may be the acidification of the microenvironment through its diffusible by-products⁶⁶, which promotes the death of normal cells, facilitates tumour invasiveness, has immunosuppressive effects and stimulates release of growth factors. The cooperative nature of the Warburg effect is clear: energy production through glycolysis is less efficient for a cell than through oxidative phosphorylation (when oxygen is not limited) but induces a beneficial effect for the tumour as a whole: the acidification of the microenvironment brought about by the diffusible metabolites produced by cooperative (glycolytic) cells^43,44,57,58. Cancer cells can even promote the Warburg effect in neighbouring CAFs, a process referred to as the ‘reverse Warburg effect’⁶⁷; these CAFs then secrete metabolites that can be used by cancer cells and oxidized for energy production⁶⁸, promoting tumour growth and metastasis⁶⁹.

Cooperation among cancer cells, therefore, occurs whenever diffusible molecules, with autocrine and/or paracrine effects, affect the survival and proliferation of the tumour. The production of growth factors that promote proliferation or angiogenesis or that help cancer cells evade apoptosis or the immune system are examples of cooperation among the cancer cells or between tumour cells and stroma. Cooperation can also be brought about by diffusible factors other than growth factors, such as the metabolites produced by the Warburg effect (discussed above) or small molecules. For example, cancer cells secrete diffusible factors that induce adipocytes to release free fatty acids through lipolysis, which can be directly taken up by cancer cells to sustain tumour growth⁷⁰. Cancer cells can also secrete molecules that modify metabolites present in the microenvironment during seeding and colonization of a metastatic site. Disseminated colorectal cancer cells, for example, release creatine kinase B-type that reacts with hepatocyte-derived creatine to produce phosphocreatine, which is subsequently imported into the metastatic colorectal cancer cells to generate ATP, promoting liver metastases⁷¹. Tumour-derived exosomes can also affect interactions between cancer cells and their microenvironment⁷²; breast cancer-derived vesicles, for example, can lead to preferential glucose uptake by metastatic breast cancer cells⁷³ (by suppressing glucose uptake by competitor cells in common metastatic sites).

Most of these instances of cooperation among cancer cells and between cancer and stromal cells, brought about by diffusible factors, are examples of what game theorists call ‘public goods games’^74,75: players (cells) can contribute (by secreting diffusible factors) to a public good. A public good is any good that leads to a benefit for a group — cooperators and defectors alike. In the case of cancer cells, the benefit is proliferation, protection against apoptosis or the immune system, acidification of the microenvironment or invasion and metastasis. The effect of the contributions can be direct or mediated by the stroma. A strategy, in this context, can be defined by the amount of diffusible factor produced by the cell.

A situation analogous to mutualism in ecology⁷⁶ can arise if two or more different subclones produce one type (or more) of diffusible factor each and rely on each other for the provision of the other factor(s)^2,4. But there are often cases in which there is no interdependence, that is, one subclone produces one or more diffusible factors and another subclone does not produce any or a lower amount — the defector cells have a free-ride on the diffusible factors provided by cooperative cells³. What prevents defector cells from spreading within the tumour? This is the essence of the problem we need to explain.

Direct interactions.

Other types of interactions occur via transmembrane molecules, such as cell–cell adhesion molecules, where fitness depends on a cell’s own phenotype, as well as the phenotype of the immediate one-step neighbours (the cells that are in direct contact). Cooperating for the production of cell–cell adhesion molecules enables cells to stick together, and even if one cell stops producing adhesion molecules, it is kept in place by adjacent cells. Multi-cell interactions represent a public goods game, in which a cell interacts with only its immediate neighbours, rather than with other cells within a diffusion range, and a benefit (cell adhesion) is achieved if at least one cell cooperates, a game known as a Volunteer’s Dilemma^77,78 (if the adhesion molecules produced by one cell are enough to keep a non-cooperative cell in place; if more than one cooperator is required, the game is a threshold public goods game^74,75,77,78). While interactions in this case do not involve diffusible factors, the game is still a type of public goods game, in which a benefit is achieved with a threshold of one cooperator (or more). Here, however, intratumour cooperation is clinically desirable (because it prevents metastases), whereas in most other cases of public goods, cancer therapy should aim at impairing cooperation.

In other cases, interactions can take the form of a pairwise game (a game with only two players). However, this is rare, as cells within tumours do not normally interact in pairs simply because they are surrounded by more than one cell. Even in cell culture monolayers, the average number of neighbouring cells is six (fewer than four or more than nine neighbours occurs rarely⁵¹), and the number of neighbours increases in three dimensions. A special case in which interactions are actually pairwise, but among multiple players (interacting sequentially in pairs), may occur in cell–cell competition^79,80 and in cell-induced apoptosis promoted, for instance, by FAS ligand (FASL)⁸¹. It may seem reasonable to conclude that a higher ability to induce apoptosis (a higher level or efficiency of FASL production) always leads to an advantage in a direct competition against neighbouring cells and hence an advantage in proliferation. As cells do not compete in pairs, however, this is not necessarily the case: in competition between more than two players, the one with the lowest ability can end up having a higher fitness^82,83 (BOX 3).

Box 3 |. The truel.

The most general principle of evolution by natural selection, Darwin’s ‘survival of the fittest’, does not necessarily apply to interactions between more than two players. Consider a duel in which two individuals, A and B, shoot at each other with accuracies (probabilities to hit the opponent) a and b, respectively. If a > b, clearly A has a higher probability of winning the contest.

In duels between more players, however, this is not necessarily the case. Consider a three-person version of the duel (a ‘truel’⁸²). Three individuals, A, B and C, shoot at each other with accuracies a, b and c, respectively (with a > b > c) in a sequential, repeated truel. Who will be the most likely to win? The answer here is not so simple as in the two-person duel; one must make a strategic decision: whom to shoot at? It is easy to see that one should shoot at the opponent whom one prefers not to face in the two-person duel because facing a weaker opponent confers a higher payoff in a duel: A would prefer a two-person duel against C rather than against B, and hence, A should shoot at B; B would prefer a two-person duel against C rather than against A, and hence, B should shoot at A; C would prefer a two-person duel against B rather than against A, and hence, C should shoot at A. In synthesis, in a three-person duel, the best strategy is to shoot at the strongest opponent: if all three players are still in the game, both B and C will shoot at A; A will shoot at B; nobody will shoot at C.

Given these considerations, one can calculate the probability of ultimately winning the contest for the three types. Straightforward algebra shows that this probability is highest for C and lowest for A, unless the differences in skills are extremely large. For example, with a = 0.8, b = 0.6 and c = 0.4, the probabilities of winning for A, B and C are 30%, 33% and 37%, respectively. What seems paradoxical (the weakest type can have the highest fitness) is actually the result of rational, strategic considerations (it is better to shoot at the strongest opponent). The logic of the theory is indisputable, but the result is not intuitive – that is why game theory can help us understand complex strategic interactions.

Extensions of this game to evolving populations with clonal selection have shown⁸³ that three types (or more) can be maintained as a mixed population, potentially explaining stable heterogeneity in the absence of fluctuating selection for characteristics that directly affect competition.

The vast majority of the interactions we have discussed, however, are examples of multiplayer collective action problems for the production of public goods. How is cooperation possible here?

The logic of cooperation

Public goods games.

In a public goods game^74,75, individuals in a group can decide to cooperate or defect; all members of the group receive a benefit from the fact that the group (the tumour) does well, but only the cooperators pay a cost from contributing to the collective benefit, whereas defectors do not pay this cost (or pay less). One way to calculate how much each individual benefits from the enhanced group benefit is to sum all the contributions, multiply the result by an enhancement factor and then redistribute it equally to all players, including the defectors. In this game, which is called the N-person Prisoner’s Dilemma (NPD)^84,85, it is easy to see that free-riding on the contribution of other group members (that is, ‘defecting’) is the strategy most favoured by natural selection. Contributing cells do get their share of the group benefit, but defecting cells get their share plus the savings from not having contributed to the group benefit. Defecting cells thus enjoy a higher fitness and make up a larger proportion of the tumour in the next generation, resulting in fewer cells contributing to the group benefit until, eventually, only defecting cells are left, and nobody contributes to the group benefit. In short, the inexorable logic of the NPD is the extinction of cooperators — the tragedy of the commons¹⁵.

There is a vast literature^19–25 in evolutionary biology and economics about how, in spite of this prediction, cooperation can evolve. Explanations fall into two main categories: genetic relatedness or repeated interactions. Genetic relatedness enables cooperators to provide benefits to their own kin, hence helping their own genes; repeated interactions allow reciprocation (punishment of defectors or rewards for cooperators). Essentially, both are forms of positive assortment: cooperation can evolve when a cooperative type interacts preferentially with other cooperative types.

Some results from the evolutionary game theory literature have been applied to game theory of cancer. For instance, game theory predicts⁸⁶ that when cooperation affects the probability of reproduction, it evolves under less strict conditions than when it affects the probability of surviving death. In the context of cooperation among cancer cells, this would imply that cooperation for the production of diffusible factors that promote proliferation is more likely than cooperation for diffusible factors that promote resistance to apoptosis.

This and other existing results, however, are based on the NPD and make a crucial assumption that is not valid in cancer biology: linear effects. Diffusible factors in tumours have, in fact, nonlinear effects. In general, the effect of biological molecules, including growth factors, is a sigmoid function of their concentration⁸⁷: the effect of each contribution is not simply added in a linear way, but it has synergistic effects at first and then diminishing returns, as observed in a logistic curve. Nonlinear games are notoriously difficult to analyse, but using linear games like the NPD can lead to misleading results⁷⁴; hence, evolutionary game theory of linear public goods games cannot be simply applied to cancer biology. New methods^88,89 have been developed recently that enable analysis for many types of nonlinearities, including sigmoid benefit functions encompassing the effect of most types of growth factors.

Predictions and tests.

The theory of nonlinear public goods suggests that subclones that produce different amounts of growth factors can be maintained in a stable polymorphic equilibrium, even though defectors do not pay the cost of contributing to the public good. This is because at intermediate frequencies of producers within the cell population, owing to nonlinear effects, cooperating confers a higher fitness than defecting if the cost–benefit ratio of cooperation is low enough^3,50–53 (FIG. 2). It is important to notice that the maintenance of cooperation has nothing to do with the benefit of the tumour: players do not cooperate because cooperation improves the overall fitness of the group (indeed, the maximum benefit for the group is not at the achieved equilibrium but requires a higher fraction of producers³ — the equilibrium is inefficient).

Fig. 2 |. Nonlinear dynamics.

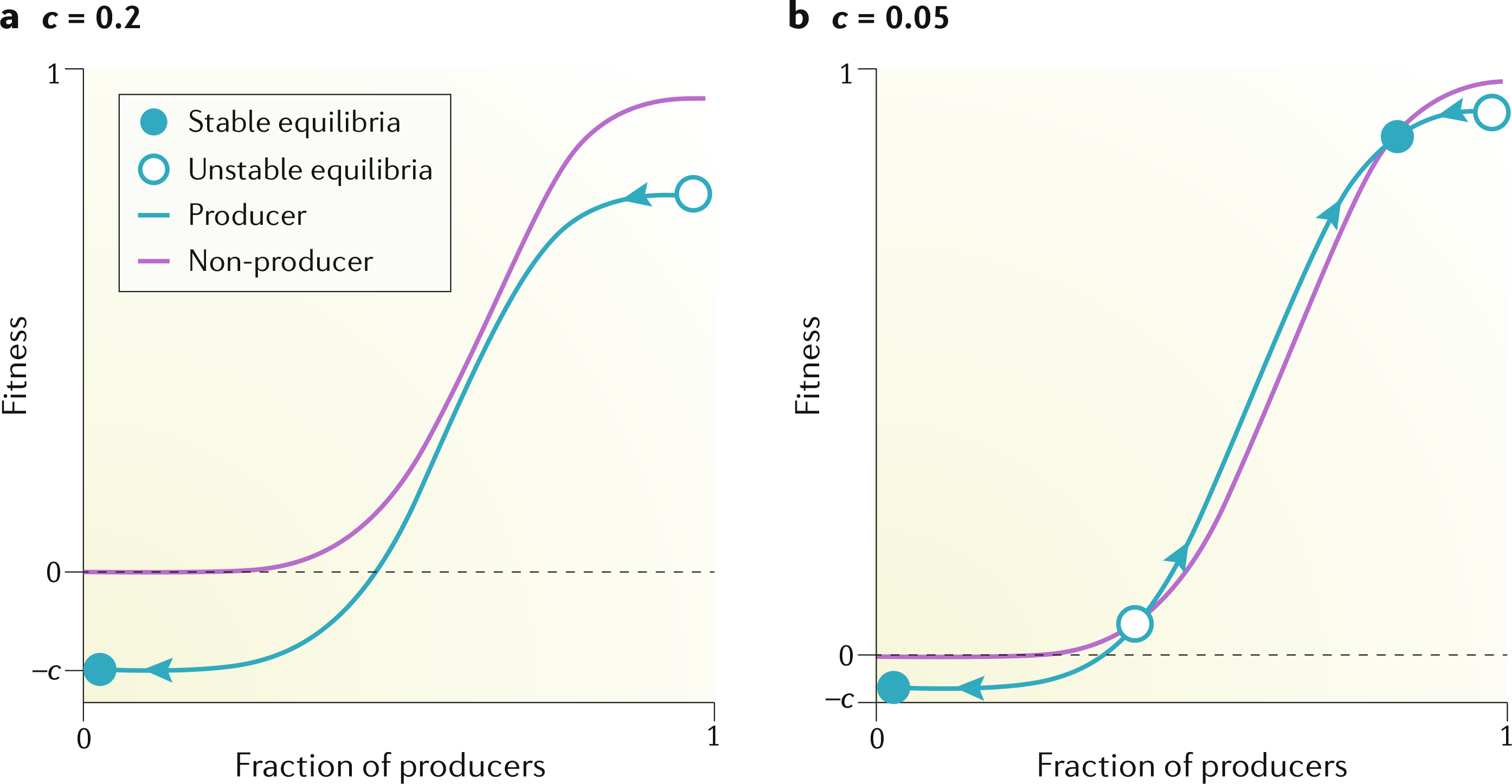
The fitness values of producer and non-producer cells as a function of the fraction of producer cells for different costs of growth factor production c are shown. Equilibria and the direction of the dynamics (arrows) are shown. a | When the cost–benefit ratio of growth factor production (c) is high (c = 0.2), non-producer cells have a fitness advantage for any fraction of the two types, and hence, their frequency increases over time until the producers are eliminated from the population. b | When the cost is low enough (c = 0.05), however, the small advantage of having an extra producer (itself) in the group can be enough to confer a net fitness advantage to producers when they are at intermediate frequencies within the population; in this case, the population can converge to a mixed equilibrium of the two cell types.

Note that, while a cooperative population can be invaded by defector mutants, a population of defector cells cannot be invaded by a cooperative mutant because the benefit of cooperation is shared among all players, but the cost a cooperator pays is a private cost. Hence, both pure defection and a mixture of cooperators and defectors are stable outcomes, and their occurrence also depends on the initial composition of the population⁷⁵. Well-known features of cancer, such as intratumour heterogeneity, the inefficiency of metastasis, the inefficiency of establishing cell lines from single clones and the low plating efficiency of single cells, are all compatible with such bistable dynamics.

The stable heterogeneous equilibrium can be achieved if the cost of producing the growth factor is low enough compared with the benefit it confers (FIG. 2b); if the cost is too high, no polymorphic equilibrium can exist (FIG. 2a). The critical cost–benefit ratio depends on the diffusion range of the secreted molecule and on the shape of the curve representing its effect as a function of its concentration^3,50–53. Not surprisingly, cooperation evolves more easily when the cost is low (and disappears entirely above the critical threshold). This prediction has been confirmed using experimental tests of the theory in pancreatic cancer cells³, where the cost–benefit ratio can be manipulated experimentally by titrating the amount of exogenous growth factors available to the cells. Interestingly, the collapse of cooperation may be happening naturally all the time within tumours because only a tiny minority of cancers actually develop enough to become clinically relevant^90,91. The few tumours that manage to develop stable cooperation may thus be the exception rather than the rule.

Cooperation also evolves more easily if the diffusion range is low and if the benefit function is steep (more specifically, a steep function enables cooperation for a higher value of the critical cost, but it also makes cooperation less robust to random fluctuations^52,88). These parameters can be estimated in cell populations, and the dynamics of the system — the number and types of equilibria and how the population changes in response to changes in these parameters — can be predicted. Other empirical results related to the theory, however, are still rare, and experiments done specifically to test the theory are even less common. The diffusion range of growth factors, a crucial parameter of the models, remains difficult to estimate. In addition, there is no comprehensive view of how important each growth factor is for each tumour type — information about these combinations is scattered through the literature. With the development of new technologies to engineer cells, it is now easier to produce non-cooperative subclones by knocking out genes for growth factors and use these cells in competition and cooperation experiments with their original producer cells³.

More interactions between theory and experiments are needed to link the large amount of data already existing in cancer research to models of evolutionary game theory. Such interactions should also improve the ability to manipulate and measure clonal selection in cancer cell populations. For example, a recent study showed interdependence between two subclones within a tumour⁴, which resembles mutualism for the exchange of diffusible goods between cells, while a model of essentially the same system (two types of players trading two different public goods)⁹² was published almost at the same time in evolutionary biology. In this and other cases, clearly a mutual awareness between theoretical results in game theory and empirical results in cancer research would be beneficial.

Evolution-proof therapies

Designing stable therapies.

Most therapies generally lead to resistance and eventual relapse. While therapies that target the stroma, like immunotherapies, may be less susceptible to the evolution of resistance because stromal cells are not genetically unstable like cancer cells^7,93, mutants that are not susceptible to a therapy can arise in the population of cancer cells and spread by clonal selection even when therapies seem effective in the short term. Evolution-proof therapies — therapies not prone to the evolution of resistant clones — are needed. Unfortunately, considerations on equilibria and dynamics are rarely, if ever, taken into account in the design of therapies⁹⁴.

Game theory deals with the core problem of the evolution of resistance: the stability of equilibria and the dynamics of perturbations. Mechanism design, or reverse game theory, in economics and ecology generally aims at devising ways to improve efficiency among rational self-interested individuals⁹⁵. In cancer research, the equivalent of mechanism design is the design of an effective therapy.

An example of the use of concepts from game theory in the design of therapies is the idea of changing the dosage of drugs in order to enable or promote cell–cell competition. Rather than targeting a tumour with the highest dose tolerated by the patient, it might be beneficial to reduce the dosage to enable competition between cancer subclones, which can prevent or slow down the development of resistance. This idea is termed ‘adaptive therapy’^96–99 and has parallels in the field of infectious diseases^100–104. Other ideas include changing the selection pressure in a tumour such that the more benign (or easier to treat) subclones within the tumour would be selected for (‘sucker’s gambit’¹⁰⁵) or to use two therapies with synergistic effects such that cancer cells evolving to elude one will become more susceptible to the other (‘double bind’^106–108).

Impairing cooperation.

While these approaches exploit the interactions between different subclones within the tumour (and highlight the importance of finding the right dosage and the right sequence of treatments), they do not specifically target cooperation. An example of the use of game theory of cooperation in the analysis of the stability of therapies is the case of tumour–stroma interactions in multiple myeloma, where osteoblasts, osteoclasts and malignant plasma cells are players in a public goods game^46,61,66. It has been shown that reducing the number of malignant plasma cells (the current approach to treating multiple myeloma) is not an evolutionarily stable strategy, whereas changing the parameters of the game, for instance, by targeting the growth factors produced by the stroma and by the tumour, could lead to the extinction of the malignant cells and re-establish a healthy osteoblast–osteoclast balance.

It has been suggested that, in general, therapies that target diffusible factors are a more evolutionarily robust approach (less susceptible to the evolution of resistance) than conventional cytotoxic therapy^109–112. Similarly, therapies that target growth factor receptors or their signalling pathways are also expected to be less evolutionarily robust because receptors confer a private advantage to a single cell, whereas growth factors benefit a larger number of cells (the cells within the diffusion range of the growth factor); hence, the benefit of resistance to therapies for growth factors is ‘diluted’ and must be greater than for receptors in order to evolve. Game theory shows^50,53, however, that an effective targeted therapy against a ligand must be extremely efficient in order to be evolutionarily stable. A therapy that reduces the amount of available growth factor increases the amount of growth factors that cells must produce to achieve the pretreatment fitness level (because some of the ligands are impaired by the therapy); in the short term, this makes tumour growth decline because there is not enough ligand available; but in the long term, the dynamics of the system change: unless the speed and efficacy of the initial reduction are high enough, the population will evolve to a new equilibrium with an even higher production of the growth factor^50,53.

Engineering defector cells.

Rather than targeting the ligands or receptors, one possible alternative, inspired by the logic of the dynamics of growth factor production, is to use a type of cell therapy: engineering tumour cells by knocking out the genes coding for essential growth factors. When re-inserted within the original tumour, these modified cells would have a proliferation advantage because they could free-ride on the growth factors produced by the original cells (‘autologous cell defection’^53,113) and would therefore spread by clonal selection like a tumour within the tumour. Eventually, a tumour made of all defector cells would collapse for lack of essential growth factors or at least reduce the deleterious effect of cytokine overproduction — which is among the immediate causes of death for a patient¹¹⁴.

This theoretical approach would harness clonal selection to our advantage: rather than leading to relapse, clonal selection would lead to the spread of the non-growth-factor-producing subclone, leading to the collapse of intratumour cooperation — as pointed out earlier, a tragedy of the commons at the cellular level. By harnessing the power of clonal selection, autologous cell defection would be self-promoting. By contrast, current forms of therapy have the opposite effect because they confer a proliferation advantage to subclones that are immune to the treatment and hence eventually enable the tumour to grow again and lead to relapse.

There would of course be difficulties to overcome. The constitutive activation of a downstream pathway could make a growth factor irrelevant (as with current targeted therapies), although this would be a problem only for diffusible factors that affect proliferation and not other hallmarks of cancer, and could be mitigated by knocking out multiple growth factors (hence multiple pathways). The cost of growth factor production must be high enough to drive producer cells to extinction, and the knockout subclone must expand quickly within the tumour. Game theory can be used to predict the critical costs and speed necessary to achieve the collapse of cooperation, and these predictions can already be tested in vitro³; similar tests in vivo must be developed.

In spite of all the incredibly challenging and inevitable technical difficulties, these are examples of how thinking in terms of dynamics and equilibria may lead to alternative approaches that have not been fully considered so far. There are certainly more.

Conclusion

Cooperation is a fundamental force in populations subject to natural selection, including clonal selection, and it has been noted¹¹⁵ that the major transitions in evolution are different ways of overcoming the problem of cooperation between self-interested entities, ranging from cells within a body to individuals in a society. Cooperation, however, is not inevitable — indeed, stable cooperation between selfish individuals is rare and fragile^14,15. Only a small minority of cancer cells develop into malignancies⁹⁶, and it stands to reason that these are the ones that have successfully managed to evolve cooperation. Using game theory to understand how to impair cooperation and harness clonal selection can provide insight into the design of evolution-proof therapies.

Glossary

Clonal selection

Natural selection (the preferential survival of the fitter phenotypes) within populations of cells

Cooperators

Players that pay a cost to produce a benefit for their opponents or contribute to a public good (for example, a growth factor producer)

Defectors

Players that do not produce a benefit for their opponents or do not contribute to a public good (for example, a growth factor non-producer)

Equilibrium

An evolutionarily stable state to which a population converges over time

Frequency-dependent

A type of natural (clonal) selection in which fitness depends on the frequency of other phenotypes in the population

Games

The formal description of strategic interactions; they include the definitions of the players, strategies and payoffs

Linear effects

The effects of cooperation on fitness when the sum of the contributions is additive (each contribution produces the same increment in benefit)

Multiplayer games

Games with multiple players (which can be made of multiple pairwise interactions or a single public goods game)

Nonlinear effects

The effects of cooperation on fitness when the sum of the contributions is not additive but has increasing and/or diminishing returns

Optimization

The choice of the best set of actions to maximize a payoff function

Pairwise game

A game with only two players

Payoff

The reward from the outcome of the interaction (in biology, this is evolutionary fitness)

Players

The individuals (or cells or other entities) that adopt strategies and obtain payoffs

Public goods games

Multiplayer games in which the payoff depends on the collective decision of multiple players rather than their pairwise interactions

Strategy

The decision or type adopted by a player (in biology, this is phenotype)

Warburg effect

The switch from aerobic energy production through oxidative phosphorylation to anaerobic energy production through glycolysis