Evaluation of automated pipelines for tree and plot metric estimation from TLS data in tropical forest areas

Abstract

Background and Aims

Terrestrial LiDAR scanning (TLS) data are of great interest in forest ecology and management because they provide detailed 3-D information on tree structure. Automated pipelines are increasingly used to process TLS data and extract various tree- and plot-level metrics. With these developments comes the risk of unknown reliability due to an absence of systematic output control. In the present study, we evaluated the estimation errors of various metrics, such as wood volume, at tree and plot levels for four automated pipelines.

Methods

We used TLS data collected from a 1-ha plot of tropical forest, from which 391 trees >10 cm in diameter were fully processed using human assistance to obtain control data for tree- and plot-level metrics.

Key Results

Our results showed that fully automated pipelines led to median relative errors in the quantitative structural model (QSM) volume ranging from 39 to 115 % at the tree level and 10 to 134 % at the 1-ha plot level. For tree-level metrics, the median error for the crown-projected area ranged from 46 to 59 % and that for the crown-hull volume varied from 72 to 88 %. This result suggests that the tree isolation step is the weak link in automated pipeline methods. We further analysed how human assistance with automated pipelines can help reduce the error in the final QSM volume. At the tree scale, we found that isolating trees using human assistance reduced the error in wood volume by a factor of 10. At the 1-ha plot scale, locating trees with human assistance reduced the error by a factor of 3.

Conclusions

Our results suggest that in complex tropical forests, fully automated pipelines may provide relatively unreliable metrics at the tree and plot levels, but limited human assistance inputs can significantly reduce errors.

Introduction

Terrestrial LiDAR scanning (TLS) data are increasingly used in forest ecology and management because they provide detailed information on 3-D tree structure. In temperate forest areas, TLS data can be routinely used in forest inventories to collect information on tree location, diameter at breast height (DBH), total height (Dassot et al., 2011; Hildebrandt and Iost, 2012) and, in some cases, crown dimensions (Srinivasan et al., 2015). These studies generally report low estimation errors and underline the potential of using TLS data to obtain traditional inventory metrics such as DBH and height using automated data processing approaches. The recent evolution of quantitative structural models (QSMs) has allowed researchers to entirely reconstruct the geometrical and topological branching systems of trees (Raumonen et al., 2013; Hackenberg et al., 2015; Bournez et al., 2017), thus providing a promising approach for understanding of the role of tree architecture in tree and forest functioning (Malhi et al., 2018; Verbeeck et al., 2019; Martin-Ducup et al., 2020). Moreover, QSMs allow the accurate quantification of the above-ground tree biovolume and therefore biomass (AGB) (Calders et al., 2015). Using destructive tree biomass data from tropical forests as a reference, Momo Takoudjou et al. (2017) and Gonzales de Tanago et al. (2018) showed that TLS-derived biomass estimations were subject to low estimation errors; however, data acquisition was time-consuming, and data were obtained and processed for individual selected trees. Momo Takoudjou et al. (2017) selected trees in areas with visibility from the ground to the canopy; low-level vegetation was cleared to limit TLS signal occlusion by the understorey and multiple scans of each targeted tree were obtained to increase the point cloud density. Gonzales de Tanago et al. (2018) used a plot-scanning design, and plots were established around the target tree positions. Moreover, semi-automated approaches based on visual inspections of algorithm outputs are often necessary to ensure the accuracy of the results by selecting the most reliable QSMs (Lau et al., 2019) or modifying QSMs to correct obvious reconstruction errors (Momo Takoudjou et al., 2017).

Upscaling this tree-centred analysis approach at large spatial scales, such as the scales of forest sample plots, which typically measure 1 ha in tropical forests, creates new challenges. Specific area-based scanning protocols involving many trees at a time have been proposed. Such methods consist of co-registering multiple scans obtained over a systematic sampling grid covering an entire plot (Wilkes et al., 2017). However, this approach generates additional uncertainties, such as large zones of occlusion and co-registration errors, which may result in unreliable tree biovolume estimations from QSM algorithms or other reconstruction approaches (Stovall et al., 2017). Moreover, point cloud processing steps upstream of tree reconstruction, which consist of identifying tree base locations, isolating individual trees (the trunk and crown) and separating wood from leaves, are not trivial tasks. These steps have been and remain the subjects of intensive research and development (Béland et al., 2011; Dassot et al., 2011; Li et al., 2013; Tao et al., 2015; Burt et al., 2019; Wang, 2020). Moreover, these steps remain particularly challenging in hyperdiverse natural tropical forests, where trees are very large and diversely shaped, the forest structure is multilayered and the understorey is dense.

As TLS data are becoming a reference for tree AGB estimation, we will soon have hundreds of forest sample plots scanned with TLS systems. For example, Chave et al. (2019) called for the establishment of forest monitoring ‘supersites’ featuring both traditional forest inventories and TLS surveys to generate reference sets of high-quality biomass estimations for the calibration and validation of upcoming remote sensing missions (e.g. BIOMASS mission; see Chave et al., 2019). TLS technology is also increasingly recognized as an essential tool for developing site- and species-specific AGB allometric models. Moreover, the size distribution of the sampled trees on which pantropical allometries are based can be improved (Stovall et al., 2018; Lau et al., 2019), and plot-level TLS data collection will likely intensify worldwide. These data sets will mainly be processed using automated pipelines that still need to be evaluated. Unfortunately, control data with sufficient accuracy related to tree- and plot-level metrics are lacking. For instance, tree height or crown dimensions cannot be as accurately measured with a clinometer from the ground in a crowded forest as accurately as they potentially can with TLS. However, posteriori human-assisted measurements of such variables from a point cloud displayed on a graphical user interface can help to evaluate the quality of automated pipeline outputs.

In the present study, we used a TLS survey of a 1-ha sampling plot located in an undisturbed tropical forest in central Africa. We evaluated the performance of four extraction pipelines in obtaining tree- and plot-level forestry metrics. Ground inventory data and data generated through human-assisted treatments of individual tree point clouds were used as control datasets to evaluate the pipeline outputs. The specific aims of this study were (1) to evaluate and compare the abilities of the four automated pipelines to extract ecologically relevant tree-level metrics, (2) to analyse how these pipelines performed in the extraction of plot-level metrics for different plot sizes, (3) to evaluate the potential of the pipelines to automatically extract direct measurements of wood volume for the calibration and validation of large-scale AGB estimations, and (5) to identify which parts of the pipelines should be improved and/or supervised and to provide recommendations based on the metrics and level of analysis considered.

MATERIALS AND METHODS

Study site

The study site is located in an undisturbed tropical forest in Eastern Cameroon near Bouamir Research Station (3°11′27″N, 12°48′41″E; 650–800 m elevation) within the Dja Faunal Reserve. A 1-ha plot on a flat ground surface was established in November 2018 by a field team. For all the trees with DBHs >10 cm, the species names were recorded, the DBHs were measured, and the approximate x,y tree locations were recorded using a measuring tape. In total, 391 trees with DBHs >10 cm were inventoried. The mean DBH of the plot was 24.36 cm, and the maximum DBH recorded was 122.9 cm for an Irvingia grandifolia specimen. Tree height was measured with a Trupulse 360S laser finder for 76 trees with a mean height of 20.45 m and minimum and maximum heights of 8.93 and 40.43 m, respectively. We recorded 103 different species in the plot, among which six were undetermined. The plot was dominated by the Uapaca genus, with 31 specimens of U. guineensis and 12 of U. paludosa, and by the species Tabernaemontana crassa and Strombosia pustulata, with 31 and 27 specimens, respectively.

Scanning design

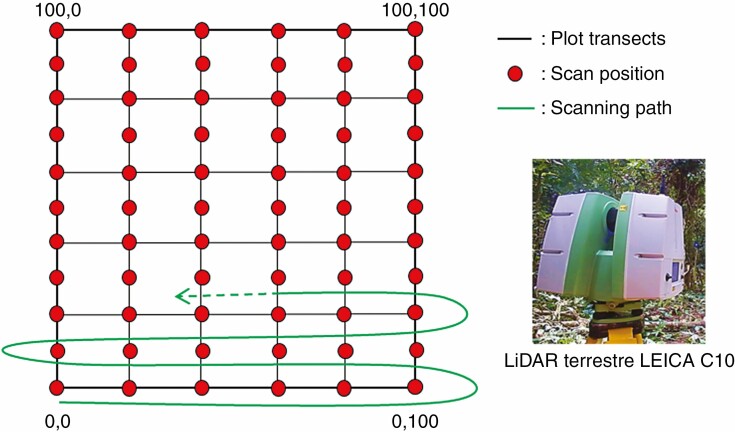
In December 2018, the plot was scanned with a Leica C10 terrestrial laser scanner following the design presented in Fig. 1. One scan position was established every 20 m following the x-axis of the plot and every 10 m following the y-axis of the plot, giving 66 scan positions in total. A path approach proposed by the Leica company was used to co-register the multiple scans in the same coordinate system. This approach consists of recording the previous and next positions of the scanner before launching the scanning process. These two positions are recorded using 6-inch circular targets that are accurately positioned with a surveying nail on the ground. At each position, the scanner is situated exactly above the surveying nail with a laser beam shot to the ground from below the scanner. The scanner height above the nail is recorded with a measuring tape. For the first scan, only the next position is recorded, and for the last scan the last position and another, previously measured, position are recorded to close the path. The final co-registration steps were automatically performed using Cyclone software from Leica.

Fig. 1.

Scanning design at the plot scale.

Automated pipelines

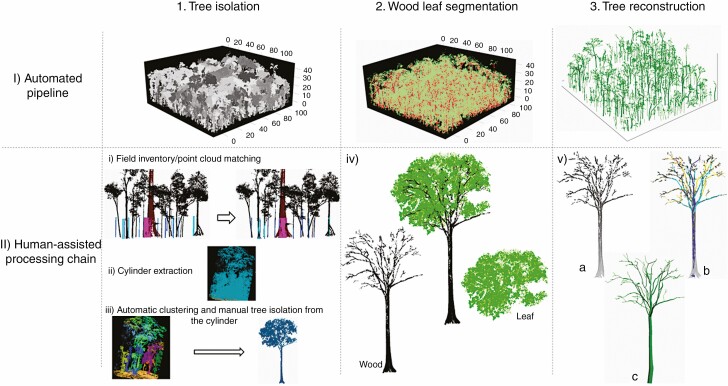
Four automated pipelines for tree- and plot-level forestry metric extraction were tested. A 10-m buffer zone was added to the 1-ha plot to avoid edge effects, i.e. only the trees with bases within the sampling plot were considered for analysis. The methods for the four automated pipelines (APs), hereafter referred to as AP1, AP2, AP3 and AP4, included three main steps: (1) tree localization and isolation; (2) segmentation of wood and leaves; and (3) tree QSM reconstruction (Fig. 2). The first and second steps are combined in a single algorithm (AP1) or separated (AP2, AP3 and AP4). Refined tree isolation is performed after the segmentation of wood and leaves for AP2 and AP3. AP4 is thus the only pipeline in which the three main steps are sequential, and the wood volume estimation error could be assessed for each step (see section Estimation of the reduction in error with human supervision in each step). All four pipelines use the same TreeQSM algorithm in the third step (reconstruction) (Raumonen et al., 2013; Calders et al., 2015). To optimize the selection of customizable parameters when running the TreeQSM algorithm, 32 reconstructions of each tree were generated using different parameter sets (Supplementary Data Table S1). The minimum distance between the raw point cloud and the reconstructed QSM was used as a selection criterion; this criterion is the default option in the select_optimum function in TreeQSM. Because point clustering is a random process in TreeQSM, it results in a slightly different QSM each time the algorithm is repeated with the same set of parameters. Therefore, we generated five different QSMs with the same optimal set of parameters for each tree and retained the mean wood volume as the final tree volume estimation.

Fig. 2.

Summary scheme representing the automated and human-assisted processing pipelines. The three columns represent the main steps of the pipelines: (1) tree isolation; (2) wood/leaf segmentation; and (3) tree reconstruction. The two rows represent (I) an automated pipeline and (II) the fully human-assisted pipeline. The tree isolation step in the human-assisted processing chain (II-1) is split into three steps (i, ii and iii).

Only the tree isolation and separation of wood and leaves steps differed among the four pipelines. In AP1, AP2 and AP3, tree isolation is based on first locating the stems and then determining the shortest paths on graphs. The only difference is in how the stems are located. Additionally, wood/leaf separation is performed by detecting linear structures based on point cloud segmentation. In AP4, tree isolation is based on first locating the stems based on their verticality and then segmenting branch sections that are later combined with the stems to form final trees. The methods are briefly detailed below, as the approaches have already been fully described in Tao et al. (2015), Wang et al. (2016, 2019) and Wang (2020) for AP1, AP2 and AP3, respectively. AP4 has not yet been published and is thus fully described in Supplementary Data Method S1.

AP1 simultaneously isolates trees and segments wood versus leaves based on superpoint graphs (Wang, 2020). Superpoints represent a small cluster of points with similar geometric properties. AP2 is similar to AP1 but uses a shortest path algorithm to locate each tree base (Wang, 2016, 2019), as implemented in the commercial software LiDAR360 (https://greenvalleyintl.com/software/lidar360/) from an algorithm proposed by Tao et al. (2015). AP3 is fully run with LiDAR360 and locates tree bases by Euclidean clustering at a certain height above ground. Several parameters, such as the minimum cluster size (i.e. 500 points in our study), minimum DBH (5 cm), maximum DBH (1.4 m) and minimum tree height (2 m), are applied to control the validity of clustered tree stems.

AP4 is based on stem and branch segmentation. This tree isolation method has not been previously published but is based on published approaches. Here, we present an overview of the method, and more details can be found in Supplementary Data Method S1. This method includes (1) filtering the point cloud and determining the heights of points, (2) covering the filtered point cloud with patches, (3) extracting stems as subsets of the patches, (4) segmenting the non-stem patches into branch sections, and (5) forming the final trees by combining the segments. The filtered point cloud is first covered with ‘surface patches’, as introduced by Raumonen et al. (2015). Then, using the patches, the aim is to extract the stems of all the large trees and as many small trees as possible without extracting information for non-stems. Potential stem sections are first located based on the concept that the patches on the stems have nearly horizontal surface normals. Next, the potential stem sections are iteratively expanded by adding neighbouring patches. The expansion first proceeds towards the ground and then moves towards the treetop to prevent side expansion. Finally, a subset of expanded stems not influenced by parts of branches or other trees is obtained. These stems do not need to be highly accurate but serve as starting points for the segmentation process, where everything in the point cloud, including the leaves and lianas, is segmented into branch sections (Raumonen et al., 2015). The final tree isolation step is based on the formation of trees by combining the segments into the final trees and comparing the estimated radii of the segments; in some cases the direction from one tree to others and the distance between trees are also determined. Following this step, the number of clusters can be very high (>40 000 in our case). A filtering step to remove clusters with a height <5.8 m was thus applied to limit the number of clusters and perform reconstruction using TreeQSM. A height of 5.8 m was set according to the lowest tree height in our plot but could be adjusted according to plot characteristics. Finally, wood and leaves were segmented for each isolated tree using LeWoS (Wang et al., 2019).

Human-assisted generation of control data

We generated reference (control) data by introducing human assistance in different steps of the processing chains (Fig. 2). The human-assisted tree localization and isolation step (step 1) starts by matching the tree bases in the TLS point cloud with tree x,y coordinates, as recorded in the field using Computree software (Othmani et al., 2011) and the ‘Matching point scenes and field tree positions’ function. Each tree in the field is represented as a cylinder that can be selected and moved independently to exact coordinates in the point cloud (Fig. 2-II-i). The tree ID was displayed in the point cloud by painting the tree stem during the field inventory. A cylindrical point cloud subset is then extracted around each tree base to isolate each individual (Fig. 2-II-ii). The diameter of the point cloud cylinder is determined based on the allometric relationship between tree DBH and crown diameter proposed by Martinez Cano et al. (2018). Trees are finally extracted from individual cylindrical point clouds using a semi-automatic approach based on a clustering step with 3D Forest software (Trochta et al., 2017) and a final visual ‘cleaning’ using the CloudCompare graphical interface (CloudCompare [GPL software], 2015) (Fig. 2-V-iii). The wood and leaf segmentation step (step 2) starts by applying the MATLAB iDSM algorithm to each tree point cloud (Wang et al., 2018). Outputs are then manually corrected to reallocate obvious poorly classified points to the correct class (wood or leaf) (Fig. 2-II-iv). TreeQSM is then applied to leaf-off individual point clouds, and the optimal QSM is selected based on the same approach as for the automated pipeline outputs (see section Automated pipelines) (Fig. 2-II-v-b). Manual editing of the QSMs is finally performed to correct for obvious adjustment errors using AMAPstudio-Scan, as suggested by Momo Takoudjou et al. (2017) (Fig. 2-II-v-c).

Matching pipeline outputs with control data

We evaluated the performance of the automated pipelines by comparing plot- and tree-level metrics derived from the automated pipeline outputs and the control data. To evaluate the tree-level metrics extracted from the point clouds generated from the automated pipelines (hereafter Auto_Trees), we needed to pair the generated point clouds with control point clouds generated for reference through a human-assisted processing chain (hereafter Man_Trees). For each Man_Tree and Auto_Tree, the barycentre of the points in a 20-cm slice 1.2–1.4 m from the ground was calculated. All Auto_Trees with barycentres falling in a 2-m diameter sphere around the barycentre of a specific Man_Tree were considered potential matching candidates. Among them, the Auto-Tree that shared the highest number of points with the Man_Tree was considered the true match, and both were paired. In some instances, a single Auto_Tree was classified as the true match of several Man_Trees and was kept as such in subsequent analyses. This case appeared when an Auto_Tree encompassed several Man_Trees. Finally, if no Auto_Tree barycentre was found in the 2-m sphere, the Man_Tree was not paired and therefore excluded from analyses. This entire matching step was coded in R.

Forestry metrics analysed

Tree-level metrics.

We compared the pipeline outputs with the paired reference control data generated with human assistance using five tree-level metrics:

• • tree DBH, as extracted by the TreeQSM algorithm;

• • tree height, taken as the 99th highest percentile of the distances from points to the ground;

• • crown-projected area (CPA), corresponding to the area of the convex hull of individual leaf-on point clouds (‘geometry’ R package);

• • volume of the tree hull computed as the sum of volumes of the 3-D convex hulls fitted based on 10-cm horizontal slices along the Z axis; and

• • total wood volume, as extracted by the TreeQSM algorithm.

For each metric, the relative error (RE) was calculated using the human-processed trees as a reference:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{R}\mathrm{E}=\frac{|{M_i}_{\mathrm{M}\mathrm{a}{\mathrm{n}}_t}-{M_i}_{\mathrm{A}\mathrm{u}\mathrm{t}{\mathrm{o}}_t}|}{{M_i}_{\mathrm{M}\mathrm{a}{\mathrm{n}}_t}}}\end{array}}$$

where ${M_i}_{\mathrm{M}\mathrm{a}{\mathrm{n}}_t}$ and ${M_i}_{\mathrm{A}\mathrm{u}\mathrm{t}{\mathrm{o}}_t}$ are the values of metric i for Man_tree and Auto_tree pair t, respectively. This error was calculated for each metric from the outputs of each of the four automated pipeline methods. The mean, median, and first and third quartiles of RE were further analysed.

The tree wood volume derived from the regional AGB allometry of Fayolle et al. (2018) was also estimated for comparison with control data generated with human assistance. The wood volume was estimated by dividing the AGB by the species’ wood density.

Plot-level metrics.

At the plot level, the five following metrics were obtained based on comparisons of pipeline outputs and the human-assisted reference control data:

• • number of trees (N);

• • basal area expressed in square metres (BA);

• • quadratic diameter in centimetres (QDBH), i.e. the DBH of trees with a BA close to the overall mean;

• • Lorey’s height in metres, which is the BA-weighted mean tree height; and

• • plot wood volume, which is taken as the sum of the volumes of all tree QSMs in cubic metres.

Three plot sizes were considered for the plot-level analyses: one 1-ha plot, four 0.25-ha plots and 25 0.04-ha plots. The 0.25- and 0.04-ha plots were obtained by dividing the 1-ha plot into 4 and 25 different subplots, respectively. The different plot sizes allowed us (1) to highlight the relationship between plot size and estimation error and (2) to characterize metric errors for different plot sizes commonly used in forest ecology and remote sensing. The 0.04-ha size approximately corresponds to the footprint level of Global Ecosystem Dynamics Investigation (GEDI) LiDAR satellite information for forest biomass estimation.

The RE formula above was also used to compare the plot-level metrics computed from the automated pipeline outputs and from the control data generated with human assistance. The mean RE was further obtained for the 0.25- and 0.04-ha plot results, and only one value was available for the 1-ha plot.

The plot wood volume was estimated by summing the volumes obtained for all trees using the allometry approach of Fayolle et al. (2018). The relative deviation was used to compare the plot wood volumes obtained from QSMs and from allometry:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{R}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{d}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}=\frac{|\mathrm{W}{\mathrm{V}}_{\mathrm{Q}\mathrm{S}{\mathrm{M}}_p}-\mathrm{W}{\mathrm{V}}_{\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{o}{\mathrm{m}}_p}|}{\mathrm{m}\mathrm{a}\mathrm{x}(\mathrm{W}{\mathrm{V}}_{\mathrm{Q}\mathrm{S}{\mathrm{M}}_p};\mathrm{W}{\mathrm{V}}_{\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{o}{\mathrm{m}}_p})}}\end{array}}$$

where $\mathrm{W}{\mathrm{V}}_{\mathrm{Q}\mathrm{S}{\mathrm{M}}_p}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{W}{\mathrm{V}}_{\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{o}{\mathrm{m}}_p}$ are the plot wood volumes derived from the QSM control data and from allometry, respectively. For the 0.25- and 0.04-ha plots, the mean relative deviation was used.

Estimation of the reduction in error with human supervision in each step

We analysed the error reduction in QSM volume estimation when each processing step (tree location, isolation, wood/leaf segmentation and tree reconstruction) was supervised. We performed this analysis with the AP4 pipeline, as each step is performed in sequence, and intermediate outputs are generated, unlike in the other tested pipeline methods. To conduct this analysis, we computed the RE between tree- and plot-level QSM volumes obtained from a fully human-assisted processing chain (our reference control data) and obtained based on different levels of human assistance with automated processing steps up to the final QSM reconstruction. In addition to the fully automated and fully human-assisted processing chain described above and in Fig. 2, we considered three intermediate levels of human assistance: (1) tree location; (2) tree location and isolation; and (3) tree location, isolation and segmentation. We finally analysed the reduction in RE for the intermediate levels of human assistance provided (considering the outputs of the fully human-assisted processing chain as references).

It should be noted that tree location and isolation are merged in a single processing step in the automated pipelines and are decomposed in several steps in the human-assisted processing chain (Fig. 2-II-1). Therefore, the first level of human assistance (i.e. tree location is human-assisted, and the rest of the pipeline is automatic for AP4) consists of selecting only the paired trees (i.e. matching trees; see section Matching pipeline outputs with control data) from the raw AP4 outputs.

RESULTS

Tree level

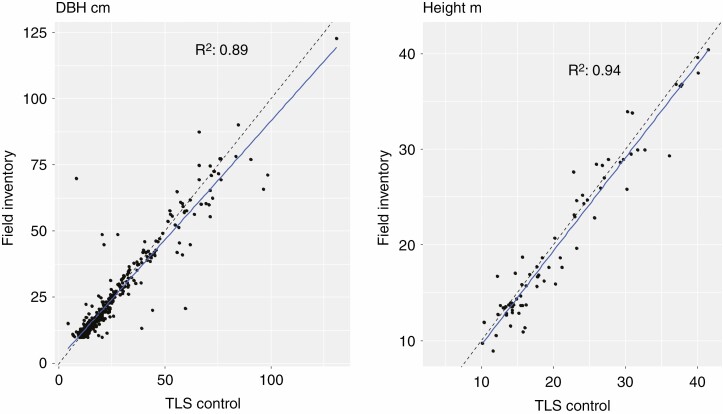
With human assistance, all 391 trees with DBHs >10 cm in the field inventory were retrieved from the point cloud. Good relationships between field inventory data and trees processed with human assistance were found for DBH (RE = 5 %) and height (RE = 4 %) (Fig. 3). At plot level, we obtained low errors for BA (RE = 8 %) and QDBH (RE = 4 %) (Table 1). The wood volumes derived from the regional allometry and from human processing were comparable (Supplementary Data Fig. S1 and Table S2).

Fig. 3.

DBH and height relationships between the field inventory and TLS control data. Blue lines are linear regressions and dashed black lines represent the 1:1 lines. Note that only 76 of the 391 field-inventoried trees had a field inventory height value.

Table 1.

Relative error in tree-level (DBH and height) and plot-level (N, BA and QDBH) metrics estimated from a human-processing chain based on the TLS point cloud. Here, the field inventory is the reference

	Field inventory	TLS human-assisted processed	Relative error (%)
Tree level
DBH (cm)	24.28 (17.41)	25.08 (18.26)	5 (20)
Height (m)	20.38 (8.49)	20.97 (8.4)	4 (12)
1-ha plot level
N	391	391	0
BA (m2)	27.1	29.22	8
QDBH (cm)	16.85	17.49	4

Field inventory height was available for 74 trees only. At tree level, the mean and standard deviation (in parentheses) are given.

Depending on the level of pipeline automation, between 207 and 388 trees were successfully paired out of 391 trees with DBHs >10 cm in the field inventory (Table 2). The four automated pipelines exhibited large REs for all metrics. Some outliers led to high mean RE values, especially for metrics such as tree hull volume (e.g. 1038 % for AP2), for which small errors in tree point cloud isolation can lead to large differences in hull volume. Because of these outliers, median values give a more realistic RE. AP3 is the automated pipeline that provided the best results for all metrics, with a median RE of 23 % for DBH, 7 % for height, 46 % for CPA, 72 % for tree hull volume and 39 % for QSM volume. Moreover, AP3 had the highest number of paired trees, with 388 paired trees among the 391 trees in the inventory data.

Table 2.

Error statistics for the four automated pipeline methods in tree metric estimation. A fully human-assisted processed point cloud is considered as the reference

	RE (%)				Mean absolute error (variable units)
	Quartile 1	Median	Quartile 3	Mean (s.d.)	Quartile 1	Median	Quartile 3	Mean (s.d.)
Paired trees AP1 (N = 207)
DBH (cm)	4	23	88	83 (145)	0.96	5.63	23.81	17.79 (24.88)
Height (m)	3	11	38	26 (35)	0.68	1.9	6.66	4.23 (4.96)
CPA (m2)	23	55	136	196 (685)	9.21	22.59	44.32	37.25 (44.76)
Tree hull volume (m3)	36	86	349	1038 (6182)	26.55	92.31	227.35	213.4 (331.05)
QSM volume (m3)	19	43	94	278 (1156)	0.06	0.25	1.16	1.15 (2.32)
Paired trees AP2 (N = 365)
DBH (cm)	28	125	320	221 (253)	5.64	27.26	68.11	39.64 (37.8)
Height (m)	2	8	28	22 (35)	0.3	1.22	4.36	3.23 (4.43)
CPA (m2)	21	51	120	155 (609)	5.31	12.63	30.53	26.69 (38.36)
Tree hull volume (m3)	39	88	308	612 (2325)	17.14	50.49	143.11	146.2 (262.78)
QSM volume (m3)	34	115	572	577 (1135)	0.14	0.63	1.87	1.37 (2.2)
Paired trees AP3 (N = 388)
DBH (cm)	7	23	83	79 (134)	1.39	5.4	19.39	14.23 (19.44)
Height (m)	2	7	24	19 (27)	0.25	0.95	3.62	2.83 (3.87)
CPA (m2)	22	46	88	151 (1271)	3.82	11.59	24.89	25.68 (47.82)
Tree hull volume (m3)	36	72	210	402 (1852)	12.44	37.76	110.62	136.19 (326.61)
QSM volume (m3)	18	39	95	183 (570)	0.04	0.15	0.61	0.8 (1.84)
Paired trees AP4 (N = 370)
DBH (cm)	9	37	118	95 (150)	1.6	8.13	24.16	18.81 (25.32)
Height (m)	4	14	33	22 (25)	0.58	1.9	5.19	3.89 (4.86)
CPA (m2)	26	59	97	127 (366)	5.39	12.87	30.35	31.13 (56.18)
Tree hull volume (m3)	36	81	198	419 (2456)	14.47	36.3	109.56	142.74 (353.93)
QSM volume (m3)	16	40	170	241 (701)	0.04	0.18	0.57	0.78 (2.24)

The total number of trees (N) in the control dataset is 391.

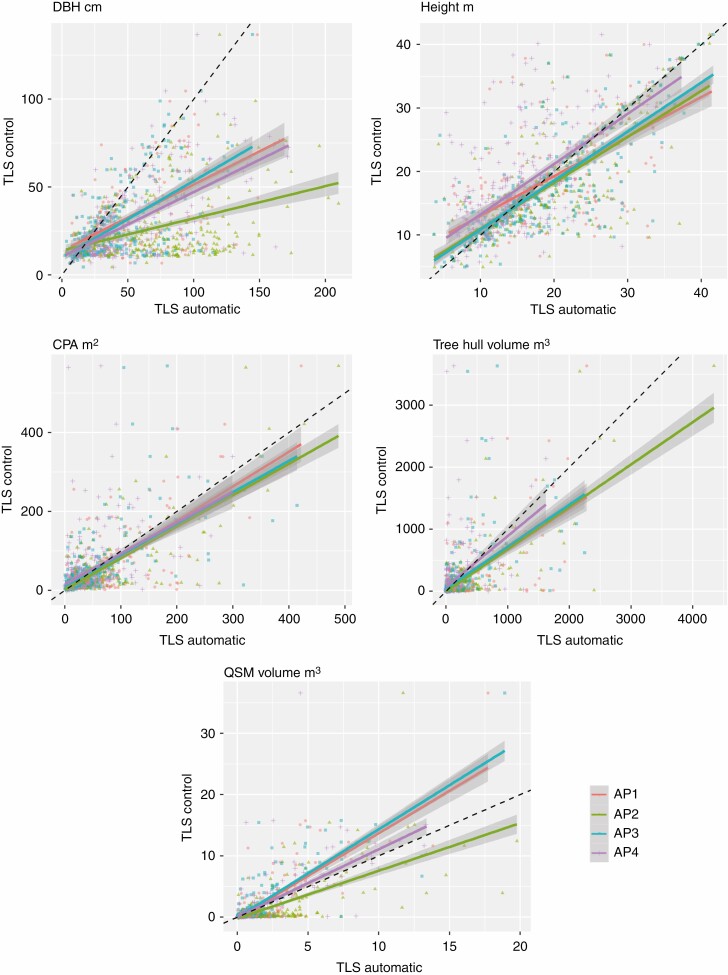
Figure 4 shows the relationships between tree-level metrics obtained using human assistance and automatically from the four automated pipelines. All the automated pipelines significantly overestimated CPA, hull volume and tree DBH. Height displayed low bias, with a general underestimation trend for small trees and overestimation tendency for large trees. The automated pipelines underestimated QSM volumes, but the AP2 results reflected overestimation. These results are surprising because the automatically detected trees are overall larger than manually assessed trees and have higher tree hull volume, CPA and height values for tall trees.

Fig. 4.

Tree-level metric relationships between automatically and human-assisted paired trees for the four automated pipelines. Plain coloured lines are linear regressions and dashed black lines represent the 1:1 lines.

Plot level

At the 1-ha plot level, the first remarkable result was the considerable overestimation of the number of trees with DBHs >10 cm detected by AP2, AP3 and AP4 (REs of 141, 311 and 136 %, respectively), which caused large overestimations of plot-level BA (881, 426 and 379 %, respectively) and QSM volume (134, 39 and 34 %, respectively) but underestimations of Lorey’s height (28, 39 and 40 %, respectively). AP1 underestimated the number of trees, with a relative error of 21 % (Table 3); this result had relatively little influence on Lorey’s height and QSM volume (underestimation of 3 and 10 %, respectively). However, strong overestimation of BA and QDBH was observed for AP1 due to the tree-level DBH overestimation reported in section Results-Tree level (Fig. 3). In contrast, AP3 yielded the lowest relative error for QDBH (13 %) due to its high accuracy in tree-level DBH estimation (section Results-Tree level and Fig. 4).

Table 3.

Mean (s.d.) values of plot characteristics and REs for the human-assisted processing chain and the four automated pipelines

		AP1		AP2		AP3		AP4
	Human-assisted	Automatic	RE (%)	Automatic	RE (%)	Automatic	RE (%)	Automatic	RE (%)
1-ha plot (N = 1)
N	379	298	21	914	141	1557	311	894	136
BA (m2)	30.37	82.17	171	297.87	881	159.79	426	145.3	379
QDBH (cm)	18.02	33.43	86	36.34	102	20.39	13	25.66	42
Lorey’s height (m)	26.39	25.63	3	19.01	28	16.11	39	15.74	40
QSM volume (m3)	538.31	485.8	10	1259.93	134	748.57	39	721.65	34
0.25-ha plot (N = 4)
N	94.75 (14.01)	74.5 (16.58)	20 (20)	228.5 (12.77)	145 (40)	389.25 (30.04)	316 (59)	223.5 (9)	139 (25)
BA (m2)	7.59 (1.26)	20.54 (4.39)	173 (56)	74.47 (5.47)	896 (129)	39.95 (2.05)	436 (80)	36.32 (4.79)	394 (138)
QDBH (cm)	18.12 (2.37)	33.53 (1.81)	87 (23)	36.34 (1.08)	103 (30)	20.42 (0.92)	16 (14)	25.61 (1.24)	44 (27)
Lorey’s height (m)	26.08 (2.52)	25.55 (2.66)	5 (2)	18.95 (1.3)	27 (4)	16.09 (1.62)	38 (6)	15.65 (1.72)	40 (7)
QSM volume (m3)	134.58 (34.04)	121.45 (26.28)	14 (9)	314.98 (37.25)	141 (40)	187.14 (17.76)	44 (29)	180.41 (28.06)	41 (49)
0.04-ha plot (N = 25)
N	15.16 (3.91)	11.92 (4.75)	29 (22)	36.56 (6.73)	155 (72)	62.28 (8.26)	340 (142)	35.76 (6.79)	148 (68)
BA (m2)	1.21 (0.61)	3.29 (2.27)	189 (165)	11.91 (2.97)	1216 (1047)	6.39 (1.59)	555 (338)	5.81 (1.9)	499 (425)
QDBH (cm)	17.75 (4.59)	30.72 (9.08)	77 (47)	36.32 (4.1)	120 (68)	20.32 (2.34)	31 (24)	25.43 (3.5)	52 (43)
Lorey’s height (m)	24.47 (4.81)	23.24 (5.72)	16 (13)	18.95 (2.53)	23 (12)	16.09 (2.57)	33 (12)	15.18 (3.06)	38 (11)
QSM volume (m3)	21.53 (12.97)	19.43 (15.24)	47 (38)	50.4 (14.7)	278 (387)	29.94 (8.8)	106 (159)	28.87 (11.02)	106 (176)

For RE the reference was human-assisted processed trees.

N, number of trees.

Decreasing the plot size from 1 to 0.25 ha led to an increase in estimation errors for all automated pipelines and almost all the metrics (but N for AP1 and Lorey’s height for AP2, AP3 and AP4 are counterexamples). Estimation errors further increased at the 0.04-ha scale, with QSM volumes 2–5 times greater than those for the 0.25- and 1-ha plots (47, 278, 106 and 106 % for AP1, AP2, AP3 and AP4, respectively).

Step-by-step evaluation of estimation error based on tree volume

The error associated with each level of human assistance for AP4 is presented in Table 4 (see section Estimation of the reduction in error with human supervision in each step for an overview of the approach). At tree level, after Auto_Trees and Man_Trees were paired we observed a strong mean error of 241 % in tree volume estimation with AP4 (Tables 2 and 4). Human assistance for tree isolation reduced this error by a factor of almost 10–26 %. Finally, assisting in wood/leaf segmentation reduced the mean error between raw TreeQSM reconstructions and human-assisted QSMs to 21 %.

Table 4.

Relative mean absolute error of wood volume estimation (%) for various levels of human supervision for AP4 at 1-, 0.25- and 0.04-ha plot scales and tree scale

Level of human assistance	1-ha plot	0.25-ha plot	0.04-ha plot	Tree
I	34	41 (49)	106 (176)	–
II	12	24 (16)	26 (20)	241 (701)
III	11	11 (13)	20 (15)	26 (36)
IV	12	12 (8)	24 (22)	21 (38)
V	0	0	0	0

I, fully automated pipeline (AP4) (Fig. 2-I); II, human-assisted tree location; Auto_Trees and Man_Trees are paired; III, human-assisted tree location and tree isolation; IV, human-assisted tree location, tree isolation and tree wood/leaf segmentation; V, fully human-assisted (control data) (Fig. 2-II).

Only 370 of the 894 trees generated with AP4 were paired with the 391 reference trees (Tables 2 and 3) and used to quantify the plot-level QSM volume (Table 4). At the 1-ha plot level, when the tree location step was human-assisted, the error in the plot-level QSM volume was reduced from 34 to 12 %. However, isolating trees and segmenting wood from leaves based on human assistance did not significantly reduce this error further (11 and 12 % for tree isolation and wood/leaf segmentation, respectively). At the 0.25-ha plot level, human assistance in tree location reduced the mean error from 41 to 24 %; moreover, human-assisted tree isolation led to a reduction to 11 %, but human assistance in wood/leaf segmentation did not reduce the error (12 %). At the 0.04-ha plot level, human assistance in tree location drastically reduced the mean error (from 106 to 26 %), while assisting with tree isolation and wood/leaf segmentation did not further improve the results (Table 4).

Discussion

During the past decade, improvements in TLS technology have led to the development of a plethora of new metrics related to 3-D tree structure used to study relations among trees (Seidel et al., 2015; Krůček et al., 2019), tree crown plasticity (Martin-Ducup et al., 2016; Barbeito et al., 2017), tree architecture (Lau et al., 2018; Martin-Ducup et al., 2020) and even tree crown dynamics (Martin-Ducup et al., 2017; Jackson et al., 2019). Moreover, with QSMs, TLS data sets now provide references for non-destructive field biomass estimations and were noted on the ‘good practice’ list for the validation of AGB map products by the Committee on Earth Observation Satellites (Calders et al., 2020). For all these reasons, an increasing number of automated pipelines implemented with dedicated freeware, such as Computree (Othmani et al., 2011) and 3D Forest (Trochta et al., 2017), or available in Python (Burt et al., 2019), R (Lecigne et al., 2018) or MATLAB (Raumonen et al., 2013; Wang, 2020) environments, have been developed. Validating these pipelines based on real data acquired under operational conditions is critical to pinpoint the most detrimental weaknesses, quantify estimation errors and orient research efforts. However, obtaining reference data in the field for detailed metrics, e.g. crown structure or wood volume, is at best highly laborious and often impossible over entire plots. We circumvented this limitation by using a human-assisted TLS point cloud processing chain to obtain reference data and evaluate four different automated pipelines. Though labour-intensive, human-assisted processing has allowed us to assemble an exceptional dataset in terms of tree number, tree size and the accuracy of architecture reconstruction. These data were used to thoroughly assess the successive steps in automated pipeline methods for stand-level metric extraction in a complex, natural tropical forest.

Assessment of tree detection and traditional forest inventory metrics

We used a 1-ha plot of undisturbed tropical forest in Cameroon as a reference. Tropical forests are at the centre of carbon sequestration, biodiversity and ecosystem functioning questions. The hyperdiverse and structurally complex characteristics of these forests make them very interesting but difficult to study. With TLS approaches, a high vegetation density in the understorey, large tree sizes and multilayered structures can result in large occlusion rates in the point cloud, leading to poor descriptions of some trees. Despite these limitations, when the point cloud was processed with human supervision, we were able to identify trees and match the results with the field inventory for all trees in the plot, with errors <5 % for DBH and height estimates. Thus, the point cloud collected with the scanning protocol in Fig. 1 was sufficiently dense, at least for these metrics. Moreover, the good relationship between the wood volume derived from allometry and from control QSMs strengthens the confidence in our TLS control data. These results are consistent with those of previous studies in tropical and temperate forests, where low errors were reported for DBH estimation using semi-automatic or automatic approaches (Dassot et al., 2011; Calders et al., 2015; Ravaglia et al., 2019). Dassot et al. (2011), summarizing four pioneering studies in temperate stands with low densities and clear understoreys, obtained very good results for tree detection rate, DBH and height estimates using automatic algorithms. In our tropical context, automatic tree base detection appeared to be a critical step. Without human assistance, three out of the four algorithms tested in this paper returned largely overestimated (141–310 %) densities of trees with DBHs >10 cm. There are two mutually non-exclusive explanations for these overestimations: (1) the point cloud is overclustered in the initial stage of automated pipeline creation, thus artificially inflating the tree detection rate, and (2) tree DBH is generally overestimated compared with the control data due to the inclusion of trees below the 10 cm DBH threshold. Large overestimations of tree DBH come from the important noise around tree bases due to the high density of understorey vegetation, which is difficult to identify and filter automatically, thus leading to QSM algorithms fitting much wider cylinders than the actual tree trunk diameters. Improving point cloud filtering for the understorey is thus a critical step in future methods.

Tree-level assessment

Obtaining detailed tree-level metrics from QSMs is highly challenging and requires, beyond precise delineations of the tree trunk and crown, good reconstructions of the topology and geometry of the branching system (Martin-Ducup et al., 2020). In this paper, we did not assess such detailed reconstructions but focused on simple metrics related to tree dimensions (crown-projected area, crown volume or tree height) and wood volume through QSMs. Among the four algorithms we tested, AP3 (Wang, 2020) performed the best in tree isolation. However, all four automated pipelines yielded poorly reliable results for CPA and tree hull volume, suggesting that, in general, tree boundaries were not well identified horizontally. The lower errors found for tree height (median between 7 % for AP3 and 14 % for AP4) suggest, however, that the uppermost vertical tree boundary of the trees was quite well captured.

Most errors detected in DBH and QSM volume estimations were a consequence of the tree isolation step. Indeed, the results showed that human assistance in tree isolation strongly reduced the mean error of QSM volume estimation (from 241 to 26 %), while assisting in wood/leaf segmentation reduced the error by only 5 %. The last 21 % of the error was due to reconstruction errors with the TreeQSM algorithm only. Although human supervision in tree isolation is quite time-consuming (7–10 min per tree; Table 5), we recommend such supervision when working at the tree level. There is, nonetheless, considerable room for improvement in this step in the future, especially with the improvement of deep learning approaches (Xi et al., 2018; Halupka et al., 2019; Morel et al., 2020) and the increasing availability of reference datasets for training.

Table 5.

Time estimation for each human-assisted step to produce reference data. The time estimate is for one person and does not consider the time needed to execute the automated part of the pipeline method

	Time per tree	Time for the 1-ha plot (391 trees)
1. Tree location	A few seconds to 2 min	1–2 d
2. Tree isolation	7–10 min	6–9 d
3. Wood/leaf segmentation	15–25 min	19–22 d
4. Tree reconstruction	15–30 min	21–24 d

Plot-level assessment

At the plot level, the considerable overestimation of the number of trees for AP2, AP3 and AP4 led to large errors in downstream plot-level metrics such as BA, QSM volume and Lorey’s height. This result was observed at all plot sizes, with particularly large errors for the 0.04-ha plot. AP1 returned the best results for the number of trees, with an underestimation of only 21 % because of the extensive filtering of the smallest and non-tree-shaped clusters before running the TreeQSM algorithm. Despite this tree density underestimation, plot BA was largely overestimated because of the general DBH overestimation at the tree level. However, we observed a low underestimation (10 %) of total tree QSM volume at the 1-ha plot size. This finding is surprising since, with the 207 trees paired to reference trees, the tendency was an underestimation of QSM volume at tree level. This result indicates that the 298 trees automatically detected with AP1 were mainly large trees. Moreover, the 91 clusters not paired to reference trees were probably very large, and individual errors at plot level were offset, leading to an apparent good estimate of plot-level wood volume (confirmed by the strong overestimation of BA and QDBH at plot level).

We analysed error reduction in tree and plot volume estimates when each processing step was sequentially manually assisted for AP4. The results revealed that manually matching tree locations with a field inventory in the initial step of pipeline creation sharply reduced the error for all plot-level volume estimates (up to a 4-fold reduction at the 0.04-ha plot size) and returned acceptable errors (12 and 26 % respectively). For a 1-ha plot, this manual step only requires 1–2 d of work (Table 5); therefore, we recommend implementing it. It should be noted that this estimated time only accounts for the time spent by an expert in front of a computer and does not account for the fieldwork required for tree mapping. Moreover, in our case, we used an objective tree-pairing approach based on reference tree point clouds to select the ‘best’ cluster within 2 m around the tree coordinates. However, without reference tree point clouds, this selection of the best cluster can be performed through a visual inspection of the candidate clusters by an expert. Finally, the downstream processing steps of the pipeline, which included tree isolation, wood/leaf segmentation and tree reconstruction, did not strongly impact the QSM volume estimation error at the plot level, except for the 0.25-ha plot. The relevance of human assistance is thus questionable for these steps in the context of biomass estimations at the plot level, considering the required manpower (Table 5). The trade-off between time invested and acceptable error is of course largely dependent on the level of analysis (e.g. 1-ha plot level versus tree level) and the precision required for a given study (e.g. biomass estimation for large-scale map product validation versus tree architecture and functional understanding). Finally, this study was performed for a single 1-ha plot of structurally complex tropical forest, so similar evaluations involving more plots in different forest types with different scanning protocols and automated pipelines are required to obtain more general conclusions.

Further considerations for AGB estimation

TLS data are becoming the reference for non-destructively estimating field-derived tree- and plot-level AGB used for the calibration and validation of large-scale AGB mapping models based on remote sensing data, such as those from airborne LiDAR or Earth observation satellite systems. It has been shown through destructive measurements that QSMs provide reasonably reliable estimates of tree AGB for tropical species (Momo Takoudjou et al., 2017; Lau et al., 2019). However, these studies focused on preselected trees using individual tree-centred scanning protocols. Assessments of the potential of using TLS data in AGB estimations at the plot scale by using a plot-centred scanning protocol, as in the present paper, has, to our knowledge, never been performed before in tropical forests. Here, we evaluate wood volume estimation by using a human-assisted processing chain to generate reference control data since collecting independent field data for testing the performance of automatic algorithms is almost impossible at the plot scale. Consequently, several factors have to be kept in mind: (1) we focused on wood volume estimation and not biomass per se; thus, all the potential sources of error, such as those related to intra- and inter-individual wood density variability (Lehnebach et al., 2019; Momo et al., 2020), were not considered; (2) the reference tree volumes we used were ‘the best we were able to do’ using human supervision with the point clouds collected; i.e. given the remaining biases due to occlusions and other factors, there was substantial uncertainty in some reference estimations. Only simulated TLS data for detailed tree/stand mock-ups (Antin et al., 2015) could truly provide independent testing data. For now, for structurally complex and dense forests such as the one studied in this paper, a reliable solution for plot-level biomass estimates could provide a hybrid approach that combines (1) QSM-derived volume estimates for all trees with high-quality QSMs, and (2) the calibration of these data based on local allometry for estimating the wood volume of the remaining trees in the plot, i.e. those with poor-quality QSMs. The use of methodological approaches based on objective criteria to rate the quality of individual tree point clouds and the resulting QSMs would thus be particularly helpful and should be considered in the future development of automated pipelines.

Conclusions

Using 1-ha plot-level TLS data collected in a complex tropical forest, we were able to assess the reliability of four automatic pipelines for extracting tree- and plot-level structural metrics, including wood volume, a key component of non-destructive above-ground biomass estimations. The results showed that all the pipelines returned poorly reliable results when performed fully automatically. This finding highlights the risk of blindly using these automated treatments at the plot scale. However, we demonstrated that providing human assistance, even limited assistance, in critical steps in the automated pipeline methods could greatly help in reducing estimation errors. Specifically, our results suggest that tree isolation is improved by human assistance when working at the tree level and that providing tree locations is highly valuable at the plot level. These findings allowed us to establish recommendations for key improvements to processing algorithms based on TLS data; these algorithms can be used in forest ecology studies and non-destructive AGB estimates. Our global recommendation is to perform systematic expert visual quality checks of automated pipeline outputs to ensure reliable data quality. Sharing high-quality data could also help computer scientists improve their algorithms.

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of the following. Method S1: AP4 description. Figure S1: wood volume relationships between allometry and TLS control data. Table S1: parameter values used to generate QSMs from the TreeQSM algorithm. Table S2: comparison of the wood volumes derived from regional allometry and from the reference TLS data.

FUNDING

This study is part of the 3DForMod project (ANR-17-EGAS-0002-01) funded by the framework of the JPI FACCE ERA-GAS call funded under the European Union’s Horizon 2020 research and innovation programme (grant agreement number 696356). We also thank the CNES (Centre National d’Etude Spatial) for funding through the BIOMASS project.