ParsVNN: parsimony visible neural networks for uncovering cancer-specific and drug-sensitive genes and pathways

Abstract

Prediction of cancer-specific drug responses as well as identification of the corresponding drug-sensitive genes and pathways remains a major biological and clinical challenge. Deep learning models hold immense promise for better drug response predictions, but most of them cannot provide biological and clinical interpretability. Visible neural network (VNN) models have emerged to solve the problem by giving neurons biological meanings and directly casting biological networks into the models. However, the biological networks used in VNNs are often redundant and contain components that are irrelevant to the downstream predictions. Therefore, the VNNs using these redundant biological networks are overparameterized, which significantly limits VNNs’ predictive and explanatory power. To overcome the problem, we treat the edges and nodes in biological networks used in VNNs as features and develop a sparse learning framework ParsVNN to learn parsimony VNNs with only edges and nodes that contribute the most to the prediction task. We applied ParsVNN to build cancer-specific VNN models to predict drug response for five different cancer types. We demonstrated that the parsimony VNNs built by ParsVNN are superior to other state-of-the-art methods in terms of prediction performance and identification of cancer driver genes. Furthermore, we found that the pathways selected by ParsVNN have great potential to predict clinical outcomes as well as recommend synergistic drug combinations.

INTRODUCTION

For decades of cancer study, one of the most striking findings has been the extreme genetic heterogeneity among cancer patients (1–4). The heterogeneity of tumor cells poses a fundamental challenge for predicting the clinical response to therapeutic agents (5–9). To address this problem, there has been great interest recently to apply deep learning to model the complexity of cancer mutations on various cancer types (10–13). Despite the improved performance, deep learning in cancer still faces a critical challenge that they are still ‘black box’ models and are fundamentally more difficult to interpret than classical statistical models (14–16). Although they are accurate, they provide no meaningful insights about how their decisions are made. Such models, while undoubtedly useful, are insufficient in cancer studies for which clinicians need to understand the mechanisms underlying the predictions.

To address this problem, a new type of interpretable deep learning model emerged that coupled the neural network architecture with the hierarchical structure of a cell. Ma et al. (17) first proposed a visible neural network (VNN), named Dcell, to accurately predict the impact of genetic mutations on cellular growth response by directly mapping the neurons of a deep neural network into a large hierarchy of known and putative molecular components and pathways. It has been demonstrated that the VNN model could gain better interpretability than the conventional deep learning model by assigning biological meanings to the neurons and edges in the neural networks. This seminal research has spurred the development of other VNN models that cast different types of biological networks into the architecture of deep learning models. For instance, Wang et al. (18) embedded the structure of the gene regulatory network derived from multi-omics data into a large multilevel deep learning model. The resulting model was adopted to impute intermediate phenotypes and provide forward predictions from genotypes to traits. DrugCell (19) was developed by combining a VNN model with a fully connected neural network model to simulate the response of cancer cells to therapeutic chemical compounds by guiding the neural network architecture with the hierarchical structure of a tumor cell. Very recently, another VNN model named P-NET (20) was designed to predict treatment resistance in prostate cancer patients using a biologically informed architecture that integrated mutation, copy number, methylation and gene expression information.

However, a major drawback of the VNN models is that the biological hierarchies used in VNN models might have redundant nodes and edges that are irrelevant to the downstream prediction tasks, which significantly limits the VNN models’ explanatory power. These uninformative nodes and edges also contribute to the ‘curse of dimensionality’ and overfitting associated with highly nonlinear models like deep neural networks. Specifically, in order to incorporate rich prior information, the VNN model typically utilizes a general biological hierarchy that is agnostic to the downstream prediction tasks, which implies that some functional components in the biological hierarchy might not involve in the biological process related to the prediction task. However, the conventional learning algorithm used by the VNN model cannot distinguish these redundant functional components and therefore enforces them to make contributions. Such a phenomenon would lead the VNN model to generate misleading interpretations since even uninformative network components still contribute to the prediction task. Postprocessing procedures have been proposed to alleviate the problem by ranking functional components by their numerical contributions to the prediction accuracy (17,19,20). However, they cannot fundamentally resolve the problem because functional components that do not make biological contributions might make great numerical contributions. Furthermore, the redundant functional components result in overparameterized neural network architectures and thus require a lot of training data to avoid overfitting.

To address the above problems in VNNs, here we introduce ParsVNN, a method to prune redundant components in the VNN model to make its biological hierarchy simple and specific to the prediction task. ParsVNN starts from a VNN model with a general biological hierarchy and uses the training data of a specific prediction task to guide the pruning procedure. As a result, redundant components in the general biological hierarchy used in the VNN model that are less important to the prediction task will be pruned and the VNN model will become a parsimonious model with greater explanatory predictive power. ParsVNN addresses important challenges in building biologically interpretable deep learning models. It can be used to elucidate the interpretability of deep learning models that utilize biological networks in their architectures.

We applied ParsVNN to build cancer-specific VNN models to help us better understand the biological mechanisms for five different cancers: stomach, breast, pancreatic, kidney and liver cancers. We use ParsVNN to prune the DrugCell model whose architecture mirrors the Gene Ontology (GO) hierarchy (21,22) of a human cell using the cancer-specific training samples collected from the Cancer Therapeutics Response Portal (CTRP) v2 and the Genomics of Drug Sensitivity in Cancer (GDSC) database (23,24). To validate the predictive power of models generated by ParsVNN, we evaluate their prediction performance on the test samples. We compared ParsVNN with several state-of-the-art methods and found that the models generated by ParsVNN have extremely simple architectures compared to the original DrugCell (19), and surprisingly, most of them achieve significantly better test accuracy. In addition, we examined the explanatory power of the models generated by ParsVNN. We found that the genes remaining in these ParsVNN models consist of more cancer driver genes (25), co-occurrence genes and mutually exclusive genes than the competing methods. Furthermore, we discovered that the functional modules in biological hierarchies recognized by ParsVNN can help predict clinical outcomes for different cancers. Finally, we demonstrated that we can analyze the subsystems identified by ParsVNN to suggest synergistic drug combinations.

MATERIALS AND METHODS

ParsVNN overview

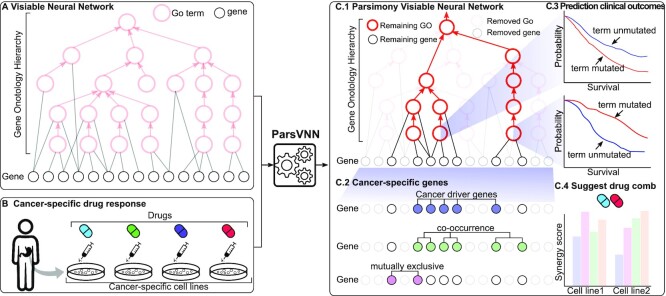
The main idea of ParsVNN is to use cancer-specific drug response data to prune the redundant components in the biological hierarchy used in a VNN model. The resulting biological network in the pruned model will be simple and important for explaining drug response in cancers. To accomplish this, ParsVNN requires three components: (i) a VNN model with the general biological hierarchy to begin with (Figure 1A); (ii) the cancer-specific drug response samples to guide the pruning process (Figure 1B); and (iii) an algorithmic technique guaranteeing convergence of the pruning procedure. Below we provide a basic explanation of these three components. The details of the method and its mathematical underpinning are described in this section.

Figure 1.

The overview of ParsVNN. (A) A VNN model using a specific biological network as its architecture. (B) Cancer-specific drug response data to guide the pruning in ParsVNN. (C.1) The resulting parsimony VNN model after applying ParsVNN. (C.2) Genes identified by ParsVNN are enriched in cancer driver genes, co-occurrence genes and mutually exclusive genes. (C.3) Mutation of the GO terms remaining in panel (C.1) leads to different patient survival. (C.4) New drug combinations could be suggested by panel (C.1).

As shown in Figure 1A, the VNN model uses a biological hierarchy as its architecture. Because the biological hierarchy is agnostic to the cancer type we aim to model, some of the nodes and edges in it might be redundant and irrelevant to the underlying mechanism. The drug response training samples for a specific cancer (Figure 1B) can help to guide ParsVNN to prune those redundant components. After applying ParsVNN, a parsimony VNN model will be obtained (Figure 1C.1). Then, we can further analyze the parsimony architecture to interpret the predictive power of the obtained model in Figure 1C.1. Specifically, we can identify the essential genes for the drug response (Figure 1C.2) and important pathways that lead to different patient survival rates (Figure 1C.3). Furthermore, by analyzing the parsimony architecture in Figure 1C.4, new drug combinations with synergistic effective would be suggested.

Overall, as shown in Figure 1, starting from a VNN model ParsVNN treats each edge weight as a feature of the VNN model and performs sparse learning to simultaneously enhance prediction accuracy as well as select important features/edges, the latter removing redundant features/edges and allowing better interpretability for the downstream analysis (Figure 1C.1–C.4). Computationally, ParsVNN is formulated as a sparse learning problem, where ℓ₀ norm regularization is used to prune edges between genes and subsystems, while group lasso regularization is applied to remove edges between subsystems. The novel combination of ℓ₀ norm regularization and group lasso regularization makes the corresponding training objective nonconvex and NP-hard. We addressed this computational challenge by using a new cutting-edge technique known as proximal alternative linearized minimization (PALM) (26) as described in this section. The source code of ParsVNN is available at https://github.com/EJIUB/ParsVNN.

Visible neural network model

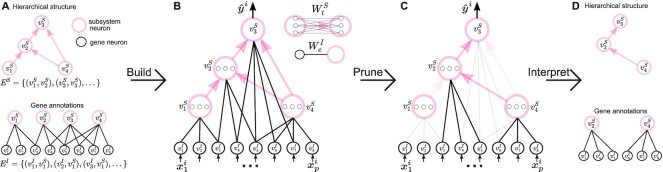
A visible neural network (VNN) model is a transparent deep learning model that aims to characterize the relationship between gene-level measurements and the corresponding phenotypic response in a cell. The architecture of the VNN model mirrors the hierarchical organization of molecular subsystems in a cell. Specifically, as shown in Figure 2, the VNN model consists of artificial neurons that represent genes (black color in Figure 2) and artificial neurons that represent molecular subsystems (pink color in Figure 2). As illustrated in Figure 2, we call the neurons that represent genes the ‘gene-neurons’ and the neurons that represent molecular subsystems the ‘subsystem-neurons’, respectively. We further use 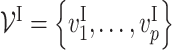to annotate all ‘gene-neurons’ and use 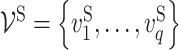to annotate all ‘subsystem-neurons’. Notably, as illustrated in Figure 2, each ‘gene-neuron’ is a single artificial neuron, but each ‘subsystem-neuron’ is a group of neurons. The use of multiple neurons to represent a subsystem acknowledges that molecular subsystems are often multifunctional, with states that are too complex to be described by a single neuron (19).

Figure 2.

The overview of ParsVNN. (A) Biological knowledge is encoded in networks. (B) A VNN model embeds the networks in its architecture. (C) ParsVNN prunes the VNN model by removing less important edges for a specific prediction task. The resulting network is essential for the prediction task. (D) We can further analyze the components in the resulting network to study how they related to the prediction task.

The wiring between ‘gene-neurons’ 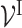and ‘subsystem-neurons’ 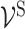and connectivity between ‘subsystem-neurons’ 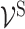are provided by biological prior knowledge. Specifically, if we know the gene annotation for each molecular subsystem, we can connect ‘gene-neurons’ to the corresponding ‘subsystem-neurons’. The black edges in Figure 2 represent such connectivity. Similarly, if we know the hierarchical organization of molecular subsystems, we are able to link ‘subsystem-neurons’. The pink edges in Figure 2 represent interactions between ‘subsystem-neurons’. Let E^I be the edge set including all edges between ‘gene-neurons’ 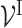and ‘subsystem-neurons’ 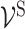and E^S be the edge set containing all interactions between ‘subsystem-neurons’ 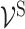. We further define 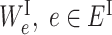, as the weight of the edge e in E^I and define 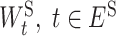, as the weight matrix associated with the edge t in E^S.

Given n training samples {(xⁱ, yⁱ); i = 1, …, n}, where 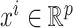is the ith input vector for the VNN model and its element 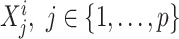, is the measurement from gene j, and yⁱ is the corresponding phenotypic output, the VNN model can be trained by solving the following empirical risk minimization:

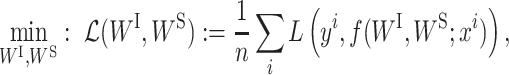(1)

where 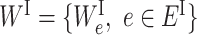and 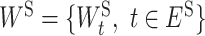. L is the loss function and f(W^I, W^S; xⁱ) yields the predicted phenotypic response 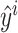for input xⁱ. We can use the off-the-shelf conventional optimization methods to minimize the loss function and learn the model parameters in W^I and W^S.

Learning a parsimony VNN model

We hypothesize that ‘gene-neurons’ and ‘subsystem-neurons’ do not contribute equally to the predictive power of the VNN model. There must be a small portion of ‘gene-neurons’ and ‘subsystem-neurons’ that are crucial to the VNN model. Therefore, we propose to learn a parsimony VNN model that only retains the key ‘gene-neurons’ and ‘subsystem-neurons’ as shown in Figure 2. Furthermore, because the ‘input neurons’ and ‘subsystem neurons’ all have specific biological meanings, the remaining ‘gene-neurons’ and ‘subsystem-neurons’ can help us to better interpret the VNN model.

We propose to learn the VNN model with parsimonious structures by pruning less important weights in W^I and W^S in the VNN model. The pruning of the VNN model can be achieved by solving the following optimization problem:

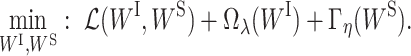(2)

Comparing to Equation (1), we add two sparse-inducing penalty terms Ω_λ(W^I) and Γ_η(W^S) to remove less important edges in E^I and E^S, respectively. Specifically, Ω_λ(W^I) is defined as

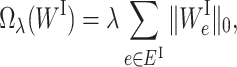(3)

where λ is the regularization parameter. For each edge e ∈ E^I, 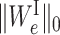is 1 when 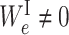and 0 otherwise. Minimizing Equation (3) tends to zero out the weight of the edge e ∈ E^I, which results in removing the edge between the corresponding ‘gene-neuron’ and ‘subsystem-neuron’. In other words, the penalty term in Equation (3) could help refine the gene annotation of each molecular subsystem as illustrated in Figure 2. We note that using ℓ₁ norm is also able to prune less important edges in the VNN model. We choose to use ℓ₀ norm because ℓ₀ norm has been proved to have better empirical performance on selecting sparse features (27,28). The other sparse-inducing penalty term Γ_η(W^S) is defined as follows:

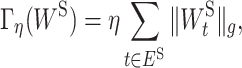(4)

where η is the regularization parameter that controls the strength of the penalty term. 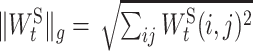[ 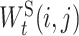is the element in 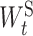] is the group lasso term that is applied to the groups of weights associated with the connection t ∈ E^S between ‘subsystem-neurons’. Minimizing Equation (4) tends to zero out all weights in 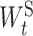resulting in the removal of the connection t ∈ E^S. Such removal can be interpreted as the interaction between the corresponding molecular subsystems is less important for the learning task in Equation (1).

The ParsVNN algorithm

The optimization problem in Equation (2) is challenging to solve. Both the sparse-inducing penalty terms are not differentiable; therefore, convectional optimization techniques for regular deep learning models cannot be applied. We employ proximal alternative linearized minimization (PALM) algorithm (29) to solve the proposed formulation in Equation (2). PALM is designed to solve a general optimization problem formulated as

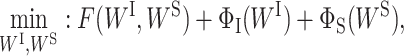(5)

where F(W^I, W^S) is a smooth function and Φ_I(W^I) and Φ_S(W^S) do not need to be convex or smooth but are only required to be lower semi-continuous. The PALM algorithm applies the proximal forward–backward algorithm (29) to optimize both W^I and W^S in an alternative manner. Specifically, at iteration k, the proximal forward–backward mappings of Φ_I(W^I) and Φ_S(W^S) for given (W^I)^k and (W^S)^k are the solutions of the following subproblems, respectively:

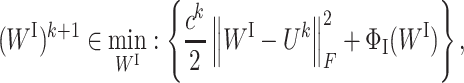(6a)

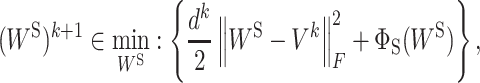(6b)

where 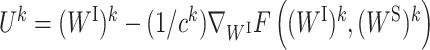and 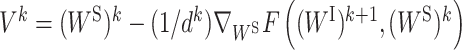. c^k and d^k are positive real numbers and 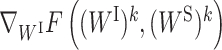is the derivative of F(W^I, (W^S)^k) with respect to W^I at point (W^I)^k for fixed (W^S)^k and 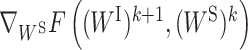is the derivative of F((W^I)^k+1, W^S) with respect to W^S at point (W^S)^k for fixed (W^I)^k+1. It has been proven that the sequence 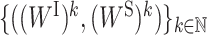generated by PALM converges to a critical point (29).

Casting our proposed optimization problem (2) into the PALM framework (5) introduced above, we have 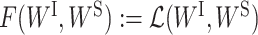, Φ_I(W^I) ≔ Ω_λ(W^I) and Φ_S(W^S) ≔ Γ_η(W^S). It is easy to verify that F(W^I, W^S), Φ_I(W^I) and Φ_S(W^S) satisfy the requirements of the PALM algorithm. Hence, we can apply the PALM algorithm to our problem as long as we can efficiently solve the proximal forward–backward mappings for our specific Φ_I(W^I) and Φ_S(W^S).

Putting Φ_I(W^I) ≔ Ω_λ(W^I) and Φ_S(W^S) ≔ Γ_η(W^S) into Equations (6a) and (6b), we have the specific subproblem for our formation (2):

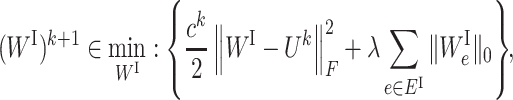(7a)

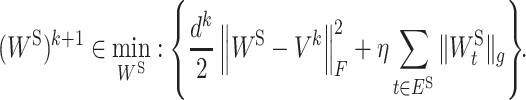(7b)

Both subproblems (7a) and (7b) have closed-form solutions as follows:

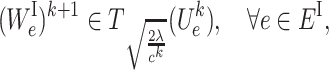(8a)

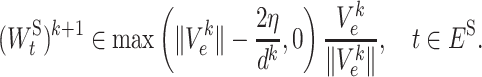(8b)

T _c(·) is the hard-thresholding operator (29). We skip the derivations of (8a) and (8b) because similar derivations can be found in (30).

We now have all the ingredients for our ParsVNN algorithm. Hence, we describe the VNN_Prune algorithm in Algorithm 1. The operations from line 3 to line 6 compute the solution for subproblem (7a), where line 4 and line 5 estimate the Lipschitz constant of 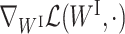. Similarly, the operations from line 7 to line 10 compute the solution for subproblem (7b), where line 8 and line 9 estimate the Lipschitz constant of .

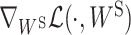Build cancer-specific ParsVNN models

We applied the ParsVNN algorithm to prune the DrugCell model to predict drug responses for specific cancer types.

Data

In order to build cancer-specific ParsVNN models, we collected cancer-specific data from the CTRP v2 and the GDSC database (23,24). We have collected data for five specific cancer types, which are stomach adenocarcinoma (STAD), breast invasive carcinoma (BRCA), pancreatic adenocarcinoma (PAAD), kidney chromophobe/kidney renal clear cell carcinoma/kidney renal papillary cell carcinoma (KICH/KIRC/KIRP) and liver hepatocellular carcinoma (LIHC). Table 1 provides an overview of each cancer dataset. For example, STAD-specific data include 17 964 cell line–drug pairs covering 42 stomach cancer cell lines and 684 drugs.

Table 1.

Details of the cancer-specific data

Cancer type	No. of samples	No. of cell types	No. of drugs
STAD	17 964	42	684
BRCA	24 928	57	684
PAAD	22 101	42	684
KICH/KIRC/KIRP	13 463	38	684
LIHC	12 550	26	684

The DrugCell model

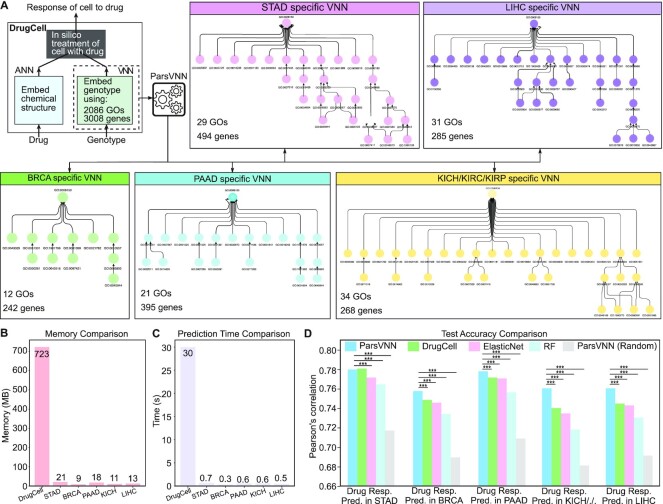
DrugCell is a VNN model that is built on the GO hierarchy and has been successfully applied to predict drug response and synergy (19). The architecture of DrugCell is shown in Figure 3A and has two main branches. The first branch is a conventional artificial neural network (ANN) that takes the Morgan fingerprint of a drug, a canonical vector representation of chemical structure (31), as the input. This branch intends to embed the chemical structure of drugs. The second branch is a VNN model, whose architecture is provided by the GO hierarchy of a cell. The GO hierarchy consists of 3008 GO terms (subsystems in Figure 1) and 2086 genes. There are 3176 interactions between GO terms, which represent the functional organization of the GO terms. There are 19 744 connections between GO terms and specific genes, which represent the gene annotation of each GO term (21,22). The VNN branch takes cancer cell-line genotype, which is represented by a binary vector registering the mutational status (1 = mutated, 0 = nonmutated) of each gene as input. The VNN branch aims to embed the genotype of different cancer cell lines. Overall, DrugCell integrates the embeddings of drug structures and genotypes and associates them with corresponding drug responses.

Figure 3.

The architectures of five cancer-specific ParsVNN models and their performance on test samples. (A) The architecture of DrugCell. The resulting architectures of ParsVNN models for STAD, BRCA, PAAD, KICH/KIRC/KIPR and LIHC cancer types after applying ParsVNN to the original DrugCell model using cancer-specific training samples. (B) Memory comparison of DrugCell and the pruned models. (C) Prediction time comparison of DrugCell and the pruned models. Prediction time is the average forward passing time of the deep learning models for 10 000 inputs over 10 times. (C) Performance comparison between ParsVNN and other competing methods on drug response prediction for five different cancer types. RF stands for random forest. We use the Pearson’s correlation between the predicted drug responses and the observed drug responses as the evaluation criterion. The asterisks (***) indicate the P-value <0.0001.

The ParsVNN model

The original architecture of a ParsVNN model is exactly the same as the DrugCell model as shown in Figure 3A, which has an ANN branch for drug embedding and a VNN branch for genotype embedding. We then apply the ParsVNN algorithm to train and prune the original ParsVNN model using cancer-specific training data. We train and prune edges in the VNN branch. For the ANN branch, we train the edge weights without pruning. After training, we obtained the cancer-specific ParsVNN model, where the VNN branch would have a cancer-specific architecture as shown in Figure 3A.

The competing models

We compared our cancer-specific ParsVNN models with models built by other methods. We first compared with the original DrugCell models that are trained on cancer-specific samples. We also compared with ParsVNN (random) models, where the biological meanings of each neuron are randomly assigned. We compared with the models generated from the elastic net (ElasticNet), a state-of-the-art sparse learning technique that could also yield parsimony models and has been used in many previous approaches to drug response prediction (19,32–34). Last but not least, we compared with the random forest (RF) model. For the ElasticNet and RF models, we build the input feature set by stacking the Morgan fingerprint of drugs and the genotypes of cells. All competing models take the same input data. The difference among them is the way they extract features.

Training and evaluation

We use 80% of the cancer-specific samples for training and 20% samples for testing for each competing model. The hyperparameters for each competing model are selected by 5-fold cross-validation on the training samples. We compared the competing models in terms of the prediction accuracy, which is estimated by Pearson’s correlation between predicted drug response and the observed area under the curve values provided in (31).

The final models

The final cancer-specific models are built by using the entire cancer-specific samples and the selected hyperparameters.

RESULTS

Cancer-specific ParsVNN models have parsimonious architectures and improved performance

Following the ‘Build cancer-specific ParsVNN models’ section, we built five cancer-specific ParsVNN models and benchmarked them with other cancer-specific competing models. First, we observed that the learned cancer-specific ParsVNN models are very compact as shown in Figure 3A. For example, the STAD-specific ParsVNN model has only 29 GO terms and 494 genes left, which indicates around 98% GO terms and 83% genes have been removed from the original DrugCell model. Similarly, all the remaining cancer-specific ParsVNN models have very few GO terms and genes left. Because the cancer-specific ParsVNN models are extremely compact, as shown in Figure 3B and C, the memory consumption of each model and the forward passing prediction time have been dramatically reduced.

We further found out that the obtained cancer-specific ParsVNN models although compact have better prediction performance. Specifically, we compared the performance of the cancer-specific ParsVNN models with other models (19,35) in terms of test accuracy. The test accuracy is measured by Pearson’s correlation between the predicted drug responses and the ground truth drug responses. As illustrated in Figure 3D, the cancer-specific ParsVNN models achieve higher Pearson’s correlation on all five cancer-specific datasets, except that DrugCell is slightly better than the ParsVNN model on the STAD dataset. We further tested whether the correlation achieved by ParsVNN is statistically better than others (36). It turns out that the correlation achieved by ParsVNN is significantly larger than the competing algorithms with P-values <0.0001 for BRCA, PAAD, KICH/KIRC/KIRP and LIHC cancer types (36). DrugCell achieves a slightly larger correlation than ParsVNN on STAD cancer type, but the difference is not significantly larger with a P-value of 0.68 (36), which indicates ParsVNN and DrugCell have similar test accuracy for STAD cancer data. The performance comparison indicates that the ParsVNN is able to prune redundant architectures of VNN models into compact ones and thus reduces the generalization error of the models.

Remarkably, the architectures in these five cancer-specific ParsVNN models (Figure 3A) are quite different, which confirms that drug responses are cancer type specific. In the following sections, we scrutinize these parsimonious architectures to see whether they can provide the biological insights to explain cancer-specific drug responses.

ParsVNN identifies cancer driver genes

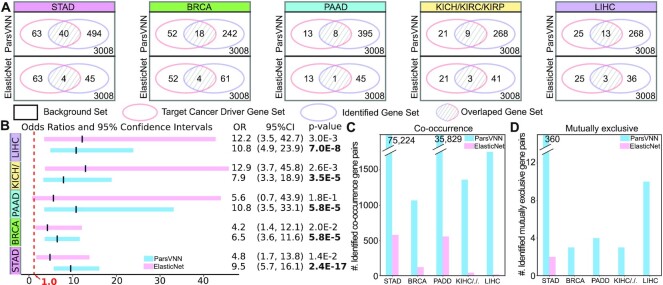
To demonstrate ParsVNN models have better explanatory power, we studied the genes that remained in the parsimonious architectures of the ParsVNN models. It has been shown that cancer driver genes are the key factor to influence cancer-specific drug response (37). Therefore, we measure the overlap between the genes in the ParsVNN models and the cancer-specific driver genes reported by IntOGen pipeline (25). As illustrate in Figure 4A, the Venn diagrams show the overlap between genes identified by ParsVNN and ElasticNet and the cancer driver genes reported by IntOGen pipeline (25) for five different cancer types. Clearly, ParsVNN selected more cancer driver genes than ElasticNet. We further computed the odds ratios, 95% confidence intervals and P-values (H0: the odds ratio is ≤1) for the gene lists identified by both methods. As shown in Figure 4B, the gene lists identified by ParsVNN for STAD, BRCA and PAAD attain higher odds ratios than ElasticNet and the gene lists identified by ElasticNet achieve higher odds ratios than ParsVNN. However, the gene lists identified by ParsVNN achieve narrower confidence intervals across all five cancer types, which suggests that we have more statistically precise odds ratios obtained by ParsVNN. Furthermore, the gene lists identified by ParsVNN also achieve lower P-values across all five cancer types, which indicates that ParsVNN provides stronger evidence to reject the null hypothesis (the odds ratio is ≤1). Furthermore, we studied the number of co-occurrence and mutually exclusive gene pairs within the selected gene set found by ParsVNN and ElasticNet. Co-occurrence and mutually exclusive are important mutational patterns that can help characterize specific cancers. For example, we use cBioPortal (38,39) to identify 75 224 and 360 co-occurrence and mutually exclusive gene pairs within the 494 genes found by ParsVNN for STAD cancer. However, there are only 578 and 2 co-occurrence and mutually exclusive gene pairs within the 45 genes found by ElasticNet. We have the same observation for the rest of the cancer types as shown in Figure 4C and D. Clearly, the genes selected by ParsVNN have richer mutational information than genes found by ElasticNet. The detailed numbers can be found in Supplementary Data.

Figure 4.

Comparison between genes selected by ParsVNN and ElasticNet. (A) Comparison of agreement with cancer driver genes using Venn diagrams. (B) Comparison of odds ratios, 95% confidence intervals and P-values (H0: the odds ratio is ≤1). OR stands for odds ratio and CI stands for confidence interval. (C) Comparison of the number of co-occurrence gene pairs in the selected gene sets of both methods. (D) Comparison of the number of mutually exclusive gene pairs in the selected gene sets of both methods.

These results indicate that ParsVNN has better explanatory power than ElasticNet, which is a state-of-the-art sparse learning technique used in many previous approaches to drug response prediction (19,32–34).

Cancer-specific subsystems identified by ParsVNN predict clinical outcomes

To illustrate that the subsystems identified by ParsVNN also have explanatory power, we explored the relationships between subsystems in ParsVNN models and clinical outcomes of cancer patients. We screened the leaf GO terms of each cancer-specific GO hierarchy and study the influence of the mutation of each leaf GO term with respect to cancer survival.

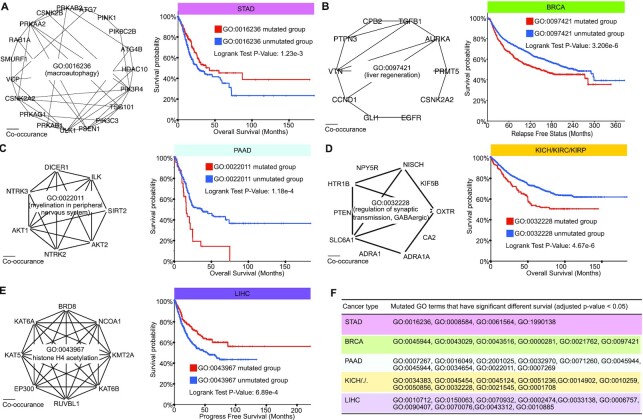
We first examined 15 leaf GO terms for GO hierarchy in the STAD-specific ParsVNN model. The cBioPortal’s survival analysis tool and all STAD samples (40–45) are used to analyze each leaf GO term. Specifically, for each GO term, we split all STAD samples into two groups, where one group contains the samples that do not have any genes mutated in the GO term and the other group includes all samples that have at least one gene mutated in the GO term. We found that the mutations of 4 GO terms out of 15 lead to significantly different survival rates (P-value <0.01). The details of these four GO terms are listed in Figure 5F and the genes annotated in those GO terms can be found in Supplementary Figure S1. For example, we scrutinize GO:0016235 shown in Figure 5A. We found that most of the genes in the term are co-occurrence genes. Surprisingly, as illustrated in Figure 5A, patients with the mutation of the GO term have better survival rates compared to those without the mutation, which indicates that the mutation of the GO term is beneficial.

Figure 5.

Examples of the GO terms identified by ParsVNN for the five cancer-specific models. (A) GO:0016236 is a GO term in the STAD-specific ParsVNN model. We study how the mutation of GO:001623 influences the survival in patients. (B) GO:0097421 is a GO term in the BRCA-specific ParsVNN model. We study how the mutation of GO:0097421 influences the survival in patients. (C) GO:0022011 is a GO term in the PAAD-specific ParsVNN model. We study how the mutation of GO:0022011 influences the survival in patients. (D) GO:0032228 is a GO term in the KICH/KIRC/KIRP-specific ParsVNN model. We study how the mutation of GO:0032228 influences the survival in patients. (E) GO:0043967 is a GO term in the LIHC-specific ParsVNN model. We study how the mutation of GO:0043967 influences the survival in patients. (F) All GO terms in the ParsVNN models lead to significantly different survival in patients (adjusted P-value <0.05) for five cancers.

We investigated the six leaf GO terms in the GO hierarchy identified by BRCA-specific ParsVNN model. For each GO term, we did survival analysis on samples with the term mutated and samples with the term unmutated using BRCA samples (45–48). We found that all six leaf GO terms showing the mutation of the GO terms would lead to significantly different survival times (P-value <0.01). The details of these six GO terms are shown in Figure 5F and the genes annotated in those GO terms can be found in Supplementary Figure S2. In addition, in Figure 5B, we show the genes in GO:0037421 term and the corresponding survival analysis. The survival analysis shows that the mutation of GO:0037421 would lead to poor survival in patients.

Similarly, we analyzed the 12 leaf GO terms in the GO hierarchy identified by PAAD-specific ParsVNN model. For each GO term, we did survival analysis on samples with the term mutated and samples with the term unmutated using PAAD samples (45,49–56). There are 10 out of 12 leaf GO terms showing that the mutation of the GO terms would lead to significantly different survival times (P-value <0.01). The details of these 10 GO terms are shown in Figure 5F and the genes annotated in those GO terms can be found in Supplementary Figure S3. We further illustrated the genes in GO:0022011 and the co-occurrence pattern between these genes in Figure 5C. We also show the survival analysis (Figure 5C) with respect to this GO term. The survival analysis demonstrates that the mutation of GO:0022011 would lead to poor survival in patients.

In the KICH/KIRC/KIPC-specific ParsVNN model, there are 24 leaf GO terms in the corresponding GO hierarchy. We discovered that the mutation of 10 out of 24 GO terms would lead to significantly different survival times in patients. The details of these nine GO terms are listed in Figure 5F and the genes annotated in those GO terms can be found in Supplementary Figure S4. We illustrated the genes in GO:0022011 and the co-occurrence pattern between these genes in Figure 5D. We also show the survival analysis (Figure 5D) with respect to this GO term (45,57–65). The survival analysis shows that the mutation of GO:0032228 would lead to poor survival in patients.

In the LIHC-specific ParsVNN model, there are 18 leaf GO terms in the corresponding GO hierarchy. We discovered that the mutation of 10 out of 18 GO terms would lead to significantly different survival times in patients. The details of these eight GO terms are listed in Figure 5F and the genes annotated in those GO terms can be found in Supplementary Figure S5. In Figure 5E, we listed the genes in GO:0043967 and the co-occurrence pattern between these genes and the survival analysis with respect to this GO term (45,66–71). The survival analysis shows that the mutation of GO:0043967 would benefit the survival of patients.

ParsVNN models suggest synergistic drug combination opportunities

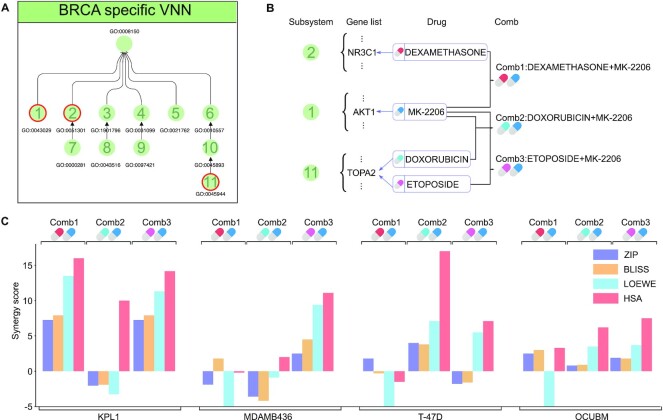
In this section, we investigated whether we can use the subsystems identified by ParsVNN to find synergistic drug combination opportunities. Suggested by the parallel pathway inhibition theory of drug synergy (72), two drugs will be synergistic if they inhibit different pathways that regulate the same essential function. Therefore, we look for drugs that target genes in different subsystems in the BRCA ParsVNN model as shown in Figure 6A. We found that dexamethasone targets NR3C1 in subsystem 2, MK-2206 targets AKT1 in subsystem 1, and doxorubicin and etoposide target TOPA2 in subsystem 11. These drugs suggest three different drug combinations as shown in Figure 6B. We further explored the DrugCombDB to check the drug synergy of these three different drug combinations. We listed four drug synergy scores: ZIP, BLISS, LOEWE and HSA. For these four scores, positive scores imply drug synergy and negative scores imply drug antagonism. We showed the average synergy scores in DrugCombDB in Figure 6C. We found that Comb1 has a synergistic effect on the KPL1 breast cancer cell line because all four synergy scores are positive. Similarly, Comb2 has a synergistic effect on T-47D and OCUBM breast cancer cell lines. Comb3 has a synergistic effect on KPL1, MDAMB436 and OCUBM breast cancer cell lines. This analysis indicates that we can analyze the subsystems identified by ParsVNN to find synergistic drug combinations.

Figure 6.

Drug combinations suggested by subsystems identified by ParsVNN. (A) Functional organization of subsystems in BRCA-specific ParsVNN model. (B) Genes in subsystems 1, 2 and 11 and the corresponding drugs targeting those genes. Three drug combinations are suggested by parallel pathway inhibition theory. (C) The average drug synergy scores of the three drug combinations on four different breast cancer cell lines extracted from DrugCombDB (73). Comb1 is synergistic on KPL1. Comb2 is synergistic on T-47D and OCUBM. Comb3 is synergistic on KPL1, MDAMB436 and OCUBM.

ParsVNN models for other cancer types also suggest novel drug combinations, which await experimental validation. We provide those novel drug combinations in Supplementary File TS1.

DISCUSSION

Deep learning models have raised unprecedented attention in the field of bioinformatics and computational biology, due to their outperformance of traditional models extracting inherently valuable information from biological networks. VNN models have been developed (17,19,20) to overcome the issue in modern ANNs that densely entangled layers are not based on human interpretable relationships such as known biological interactions. VNNs achieve this by explicitly utilizing a biological network as its architecture and assigning both artificial neurons and the edges between neurons specific biological meanings. However, VNN models are agnostic to the biological context and have limited abilities to grasp the most important, relevant and concise architecture in regard to a particular condition of interest, by including nodes and edges that are irrelevant to the downstream prediction tasks. Specifically, the training algorithm used by VNN models cannot distinguish those irrelevant nodes and edges. After training, those irrelevant edges always have nonzero weights indicating that they are making contributions to the VNN models. For example, DrugCell uses GO hierarchy as its architecture to predict drug responses. The GO hierarchy is very general and encodes all possible prior knowledge, but it might contain irrelevant GO terms when we want to build a DrugCell model that only predicts drug responses for a specific cancer type. If we cannot distinguish the essential GO terms from those irrelevant ones, a misleading interpretation could be generated. The training data provide specific information on the prediction task; therefore, it is important to be able to utilize the training data, along with the task-agnostic VNN model, for the construction of task-specific VNN models. To address this need, we introduced here a VNN learning algorithm—ParsVNN. The unique property of ParsVNN is that starting from a task-agnostic VNN model, it utilizes training data to remove redundant nodes and edges in the task-agnostic VNN model. We demonstrated that ParsVNN outperforms the original VNN models and other state-of-the-art methods to build task-specific VNN models in terms of test accuracy and interpretability (Figures 2 and 3).

We build interpretable ParsVNN models for five different cancer types and showed that the much simpler ParsVNN models contain many more cancer driver genes, co-occurrence genes and mutually exclusive genes than the competing methods (Figure 4). In addition, we discovered that most of the subsystems identified by ParsVNN have a significant impact on patient survival (Figure 5). Furthermore, we illustrated that we can analyze the subsystems identified by ParsVNN to find potential drug combinations with synergistic effects. All these aspects mentioned above demonstrated that ParsVNN models reveal insights specific to the learning task and are interpretable to bioinformaticians and clinicians alike.

Overall, our results show that ParsVNN is a very powerful method for building parsimonious VNN models that are predictive and explanatory. The explainability of our models solves one of the oldest and most challenging problems facing the biological application of deep learning. Furthermore, ParsVNN can be applied to all deep learning models that utilize biological networks in their architectures representing a broadly applicable advance in computational biology. ParsVNN can also be extended to answer a set of questions that puzzle many clinicians, biologists and researchers. One such question is how to identify unknown GO subsystems, regulatory links or pathways that are not annotated in the literature or ontologies but are very informative for specific tasks. This newly discovered ontology information could be used to guide novel studies of these previously unknown mechanisms. One of our future works will be to implement a ParsVNN variant to discover interactions and links not found in the given ontology knowledge database to better guide sensible experiments and inform more precise decisions.

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

This research was supported by the Indiana University Precision Health Initiative fund.

Conflict of interest statement. None declared.