Effective connectivity extracts clinically relevant prognostic information from resting state activity in stroke

Abstract

Recent resting-state functional MRI studies in stroke patients have identified two robust biomarkers of acute brain dysfunction: a reduction of inter-hemispheric functional connectivity between homotopic regions of the same network, and an abnormal increase of ipsi-lesional functional connectivity between task-negative and task-positive resting-state networks. Whole-brain computational modelling studies, at the individual subject level, using undirected effective connectivity derived from empirically measured functional connectivity, have shown a reduction of measures of integration and segregation in stroke as compared to healthy brains. Here we employ a novel method, first, to infer whole-brain directional effective connectivity from zero-lagged and lagged covariance matrices, then, to compare it to empirically measured functional connectivity for predicting stroke versus healthy status, and patient performance (zero, one, multiple deficits) across neuropsychological tests. We also investigated the accuracy of functional connectivity versus model effective connectivity in predicting the long-term outcome from acute measures. Both functional and effective connectivity predicted healthy from stroke individuals significantly better than the chance-level; however, accuracy for the effective connectivity was significantly higher than for functional connectivity at 1- to 2-week, 3-month and 1-year post-stroke. Predictive functional connections mainly included those reported in previous studies (within-network inter-hemispheric and between task-positive and -negative networks intra-hemispherically). Predictive effective connections included additional between-network links. Effective connectivity was a better predictor than functional connectivity of the number of behavioural domains in which patients suffered deficits, both at 2-week and 1-year post-onset of stroke. Interestingly, patient deficits at 1-year time-point were better predicted by effective connectivity values at 2 weeks rather than at 1-year time-point. Our results thus demonstrate that the second-order statistics of functional MRI resting-state activity at an early stage of stroke, derived from a whole-brain effective connectivity, estimated in a model fitted to reproduce the propagation of neuronal activity, has pertinent information for clinical prognosis.

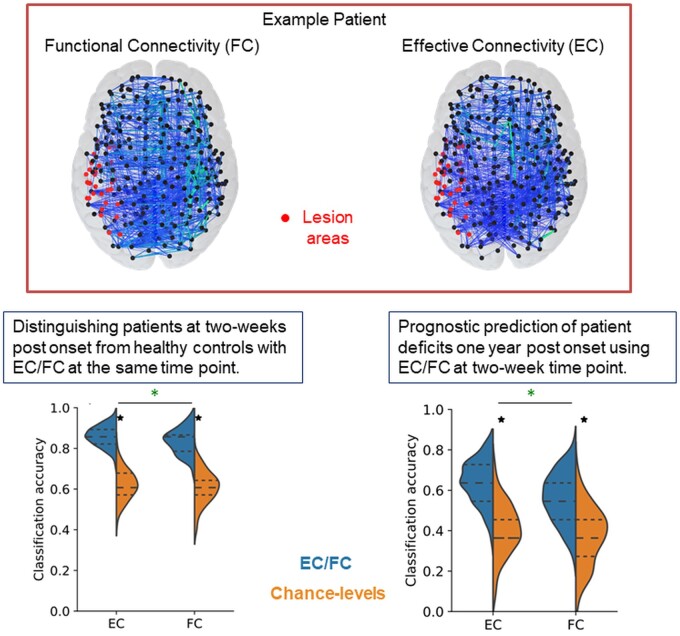
Focal stroke alters resting-state functional connectivity that measures inter-regional statistical associations but ignores directed, causal interactions captured by effective connectivity. Adhikari et al. find that a model-driven effective connectivity outperforms functional connectivity as a predictive biomarker for distinguishing patients from controls and, far more importantly, for prognostic prediction of patient behavioural deficits.

Graphical Abstract

Graphical Abstract.

Introduction

First-time stroke patients with heterogeneous lesion location show widespread alterations of resting-state (RS) functional connectivity (FC)—the temporal correlation of the functional MRI (fMRI) signals across brain regions and networks—in the acute stage,^1–4 what is now called ‘connectional diaschisis’.⁵ The most common abnormalities include a reduction of the inter-hemispheric (IH) FC between homotopic regions of the same networks, and an increase of intra-hemispheric FC between regions/networks that are typically not or negatively correlated (e.g. task-positive and task-negative networks).⁶ Abnormalities of FC are strongly correlated with acute behavioural deficits and their recovery.^6,7 The low dimensionality of FC alterations across brain regions has been proposed as an explanation for why behavioural deficits are also low dimensional and correlated across subjects, with three sets of deficit components accounting for ∼70% of the behavioural variance.^8,9

Whole-brain network models of sub-acute stroke have been used to characterize and understand the impact of stroke.^10,11 Adhikari et al. obtained a patient-specific, optimized whole-brain model before calculating an information theoretical measure of network segregation and a graph theoretical measure of integration for each patient and showed that they correlated with ipsilesional inter-resting-state network (RSN) FC and IH FC between homotopic regions, respectively. Starting with a group-average structural connectivity matrix, model optimization involved inference of a symmetric, undirected effective connectivity (EC) matrix from each patient’s own FC using a heuristic, gradient descent approach. The effect of lesions was modelled by weakening the structural edges to/from a damaged cortical region.

A weakness of this approach is that FC captures the levels of correlated activity between a pair of brain regions, but it does not describe the causal influence from one region to another or the simultaneous influence of a third region. A second weakness is that stroke lesions affect not only cortical parcels but also predominantly white matter pathways.⁸ Therefore, a better approach for estimating the effect of lesions would be to take in account the structural disconnection, between both damaged and non-damaged regions, caused by lesions.

In contrast to FC, EC measures directed interactions and indirectly, some form of causality. Partial correlations Smith et al¹² can be used to infer undirected EC, while methods such as dynamic causal modelling^13–15 can yield directed EC. Recently, Gilson et al.¹⁶ demonstrated a theoretically robust technique to infer whole-brain EC from zero-lagged and lagged RS-FC. Modelling each local brain region with an Ornstein–Uhlenbeck process, the inference procedure uses a mask of the putatively existing anatomical connections as a topological prior and since it also estimates non-symmetric lagged FC, the resulting EC is directional for every connection, edge or link. In the following, we will use link to connote a statistical or effective connection. EC changes were found to align with those known from electrophysiology in the visual field mapping between early visual cortices.¹⁷ Pallarés et al.¹⁸ showed that EC predicts in a cross-validated fashion the identity of individual healthy participants from fMRI sessions more accurately than FC.

In this study, we aimed to compare the predictive ability of EC vis-à-vis FC in (i) distinguishing patients from healthy controls, and (ii) predicting behavioural deficits of patients longitudinally. We first obtained the EC for healthy participants and first-time stroke patients, using the approach of Gilson et al., at 2-week, 3-month and 1-year post-onset of stroke. Critically, the disconnection effect of lesions was estimated embedding the volume of each lesion in an atlas of normal white matter connections,¹⁹ and estimating the severity of disconnection among cortical regions. Then we classified this cohort in multiple classifications using EC or FC values. The first classification diagnosed patients from healthy controls at each time-point. The second classification aimed to diagnose stroke individuals with different numbers of behavioural deficits (zero, one, many) across seven factors of behavioural impairments using EC and FC values of links at the same time-point. Besides, we tried EC and FC of links from previous time-points to predict future behavioural deficit status.

We hypothesized that EC would be a more sensitive biomarker than FC, especially for more dimensional behavioural predictions. This hypothesis is based on EC’s theoretical ability to infer directional interactions and its superiority (as compared to FC) in predicting individual scans.¹⁸ Moreover, we hypothesized that EC predictive topography will provide additional and complementary information to FC topography.

Materials and methods

Stroke cohort

A total of 172 patients were prospectively enrolled in this study, 132 of whom met the post-enrolment inclusion criteria. Female participants made up 45% of the study sample while 55% were male. Inclusion and exclusion criteria are described in detail in an earlier manuscript.⁸

Healthy controls

A healthy control group (n = 25; 52% female, 48% male) was matched with the study sample for age, gender and years of education.

Patients and controls provided written informed consent prior to participation in the study. Study procedures were performed in accordance with the Declaration of Helsinki ethical principles and approved by the Institutional Review Board at Washington University in St. Louis. The complete data collection protocol is described in full detail in a previous publication.⁸

Lesion identification

Each patient’s structural MRI scans were used to manually segment the lesions with the Analyze software package²⁰. Surrounding vasogenic oedema was included in the lesion definition for patients with haemorrhagic stroke. Two board-certified neurologists (Maurizio Corbetta and Alexandre Carter) reviewed all segmentations before they were converted into binary lesion masks. These masks, transformed to MNI atlas space, were used for subsequent processing and analysis.

Behavioural testing

Assessment of motor, language, attention, memory and visual function was done for each participant after each scanning session. Dimensionality of the behavioural performance data was reduced as described previously⁸ to identify a few factors that explained majority of across-subject variance. We summarize these factors and their loadings here for completeness. The ‘Motor’ score describes contralesional deficits that correlated across shoulder flexion, wrist extension/flexion, ankle flexion, hand dynamometer, nine hole peg, action research arm test, timed walk, functional independence measure and the lower extremity motricity index. The ‘Visual Field Attention’ score describes contra-lesional attention biases in Posner, Mesulam and BIT centre of cancellation tasks. A separate ‘Sustained Attention’ score loaded on non-spatial measures of overall performance, reaction time and accuracy on the same tests. A third ‘Shifting Attention’ score loaded on tests indexing attention shifts. The ‘Spatial Memory’ score loaded on the Brief Visuospatial Memory Test and spatial span. The ‘Verbal Memory’ score loaded on the Hopkins Verbal Learning Test. The ‘Language’ score loaded on both comprehension and production.

Factor scores for each patient were z-scored using mean and standard deviation of corresponding factor scores in age-matched healthy controls.K-nearest neigbour (KNN) imputation was employed to impute the scores for the missing domains in a patient using weighted average across five of its nearest-neighbours. A z-score of –2 or less was considered to be a deficit.

fMRI procedure and scanning

Patients were scanned at three time-points—2 weeks (mean = 13.4 days, SD = 4.8 days), 3 months (mean = 112.5 days, SD = 18.4 days) and 1 year (mean = 393.5 days, SD = 55.1 days) post-onset of stroke. Healthy controls were scanned at two time-points separated by a 3-month interval.

Scanning was performed with a Siemens 3T Tim-Trio scanner at the School of Medicine of the Washington University in St. Louis. Scanning parameters are described in detail in previous publications.^6,21 Six to eight resting state fMRI runs, each including 128 volumes (30 min total), were acquired.

fMRI data pre-processing

fMRI data underwent a preprocessing procedure consisting of the following steps: (i) asynchronous slice acquisition was compensated by sinc interpolation to align all slices; (ii) elimination of odd/even slice intensity differences resulting from interleaved acquisition; (iii) a whole brain normalization corrected for changes in signal intensity across scans; (iv) realignment within and across scans to correct for head movement and (v) co-registration of echo-planar imaging data to the subject’s T₂-weighted anatomical image, which in turn was co-registered with the T₁-weighted magnetization-prepared 180 degrees radio-frequency pulses and rapid gradient-echo (MP-RAGE).²² The MP-RAGE was then transformed to an atlas-space Talairach and Tournoux²³ representative target using a 12-parameter affine transformation. Data were passed through several additional preprocessing steps²⁴: spatial smoothing (6 mm full width at half maximum Gaussian blur), filtering in the 0.009–0.08 Hz band and removal, through linear regression, of (i) six parameters obtained by rigid body correction of head motion; (ii) the whole-brain signal averaged over a fixed region in atlas space; (iii) signal from a ventricular region of interest (ROI) and (iv) signal from a region centred in the white matter.

Quality control of RS data

For each frame of RS-fMRI scan, a DVARS (temporal derivative of timecourses of RMS variance over voxels) score was calculated.²⁵ Here, RS-fMRI scan corresponds to a time series, whereas frame corresponds to an image. DVARS spikes represent large spikes in brain-wide signal that are correlated very strongly with head movements.²⁶ The DVAR threshold for patients, calculated as mean plus 2 SD of DVARS values for all frames, excluding the first four frames, in the group of age-matched control subjects, was equal to 4.6. The threshold was chosen to optimize reliability of FC measurements. All frames with a DVARS value of 4.6 or higher were removed for the calculation of FC. However, they were linearly interpolated over in order to maintain the temporal continuity for the calculation of lagged covariances in each scan.

Exclusion criteria for FC quality included (i) < 180 usable frames, and (ii) severe haemodynamic lags (>500 ms IH difference) measured from RS-fMRI.²⁷ Large haemodynamic lags are confounds produced by altered neurovascular coupling that are known to substantially alter the relationships between neural activity and the blood oxygen level dependent (BOLD) timecourse. The large magnitude of these delays (relative to the homotopic region on the unaffected hemisphere) makes it possible to separate them from neural lags attributed to neural activity. The threshold was chosen to mitigate the contribution of neurovascular damage in FC.²⁸ After motion and lag exclusion, 98 patients were included at 2 weeks, 74 patients at 3 months, 53 patients at 1 year, 23 controls at time-point 1 and 22 controls at time-point 2.

Parcels and system assignments

FC and covariance matrices were obtained for all links between 324 cortical parcels from the Gordon333 cortical parcellation and RS network assignments (available at http://www.nil.wustl.edu/labs/petersen/Resources.html),²⁹ and consists of 333 cortical parcels associated with 13 RSNs. Owing to very low number of vertices, nine parcels were excluded as done in previous studies.^6,7,21 The remaining 324 cortical parcels were assigned to these 13 RSNs: visual (VIS), retro-splenial (RSP), somato-motor hand (SMH), somato-motor mouth (SMM), auditory (AUD), cingulo-opercular (COP), ventral attention network (VAN), salience (SAL), cingulo-parietal (CPL), dorsal attention network (DAN), frontal parietal network (FPN), default mode network (DMN) and none of the above (NON).

Mask of neuroanatomical structural links for EC estimation

The EC for each participant was estimated for a mask of strongest neuroanatomical links. This mask (EC_mask_Ctl), identical for each healthy control, included (i) all links stronger than 0.5% of the strongest link in the structural connectivity matrix (SC-Ctl) averaged across SCs of healthy controls from this study, obtained using diffusion weighted imaging (DWI) and probabilistic tractography, and (ii) links in the Human Connectome Project (HCP)-SCT—a structural connectome template created from a publicly available tractography atlas,¹⁹ constructed using DWI data from 842 HCP participants and deterministic tractography. The mask for each patient included all links in EC_mask_Ctl except, those from and to a ROI with 100% grey matter damage and all other completely damaged links in the patient’s structural disconnectome (SDC).

Due to the end-to-end nature of tractography used by Yeh et al., HCP-SCT links were too few (n = 4218) to obtain a robust estimate of EC that can produce sufficiently high fit between model and data.^16,30 Therefore it was necessary to include the strongest links in SC-Ctl (n = 28 256). However, HCP-SCT links were found to have stronger FC, on average, in both controls and patients than those not present in HCP-SCT.³¹ Thus the sparseness and reliability of HCP-SCT links allowed us to use only them for classification and biomarker identification, thus keeping the computational cost low without losing the prediction accuracy (Supplementary Fig. 1). A more clinically oriented reason is to seek the effect of stroke on the structural backbone of brain, independently of individual variability in SC as well as patient-specific stroke characteristics. Also, incorporating impact of lesions on white matter pathways through structural disconnections for each individual patient was possible only through the HCP-SCT.

Structural connectivity for healthy controls

DWI along with probabilistic tractography were used to obtain the SC for each healthy participant in this study. The complete methodological details are included in the supplementary material. Number of streamlines between every pair of ROIs in the Gordon parcellation divided by the total number of vertices in them was taken as a measure of SC strength between them. SC_Ctl was obtained by averaging SC matrices of all healthy participants.

HCP-SCT

HCP-SCT was constructed using the HCP-842 streamline tractography atlas¹⁹ as previously described.²¹ In brief, Yeh et al.¹⁹ performed deterministic fibre tracking³² on the high-angular resolution diffusion MRI data from 842 participants and extracted 550 000 streamline trajectories in MNI space. A 324 × 324 SC adjacency matrix A^S was constructed whose each entry ${\mathrm{A}}_{\text{ij}}^{\mathrm{S}}$ indexed the number of streamlines connecting regions i and j.

Structural lesion features and SDC

As described in detail in Griffis et al.,²¹ parcel-wise grey matter damage measure was obtained for each patient by computing the proportion of each grey matter parcel that overlapped with the lesion. Subsequently, the expected disconnection for each patient was obtained by intersecting their MNI-registered lesion and the HCP-SCT (A^S) normalized by A^S.²¹

EC estimation

The method^16,30 for EC estimation optimizes the effective weights of a mask of structural links (quantifying the causal interactions along them) using a multivariate Ornstein–Uhlenbeck (MOU) process model for each region and zero-lagged and lagged empirical covariances. Optimization is done using a gradient descent algorithm that minimizes the model error.

Estimation of lagged and zero-lagged covariances and FC

For every session of T time frames, we denote the BOLD time series by $s_i^t$ for each region $1\le i\le N$ whose mean signal over time is denoted by $\stackrel{-}{s_i}=\mathrm{ }\frac{1}{T}{\sum }_t{s}_i^t$. The empirical BOLD covariances to be optimized without and with time lag are then given by:

$${\widehat{Q}}_{ij}^0=\frac{1}{T-2}\sum _{1\le t\le T-1}(s_i^t-s_i)(s_j^t-s_j)$$ (1)

$${\widehat{Q}}_{ij}^1=\frac{1}{T-2}\sum _{1\le t\le T-1}(s_i^t-s_i)(s_j^{t+1}-s_j)$$ (2)

and the FC between region i and region j is given by:

$$F{C}_{ij}=\mathrm{ }\frac{{\widehat{Q}}_{ij}^0}{\sqrt{{\widehat{Q}}_{ii}^0{\widehat{Q}}_{jj}^0}}\mathrm{ }$$ (3)

MOU process to model whole-brain dynamics

The activity variable, $x_i$, for each region decays exponentially with a time constant, ${\tau }_x$ and evolves depending on the activity of other populations:

$$d{x}_i=\mathrm{ }\left(\frac{-x_i}{{\tau }_x}+\mathrm{ }\sum _{j\ne i}{C}_{ij}{x}_j\right)dt+d{B}_i\mathrm{ }$$ (4)

Here, the fluctuating inputs, $d{B}_i$, are independent and correspond to a diagonal covariance matrix $\mathrm{\Sigma }$. In the model, all variables, $x_i$, have zero mean. The spatio-temporal zero-lagged and lagged covariances are denoted by $Q_{ij}^0$ and $Q_{ij}^1$ and can be calculated by solving the following consistency equations:

$$J{Q}^0+\mathrm{ }{Q}^0{J}^{†}=\mathrm{ }-\mathrm{\Sigma }\mathrm{ }$$ (5)

$$Q^1=Q^0{e}^{J^{†}}\mathrm{ }$$ (6)

Here J is the Jacobian of the dynamical system; $J_{ij}=\mathrm{ }\frac{{-\delta }_{ij}}{{\tau }_x}+\mathrm{ }{C}_{ij}$, where, ${\delta }_{ij}$ is the Kronecker delta function and $†$ denotes matrix transpose. Lyapunov optimization is used to tune EC values $C_{ij}$ so that the model covariances $Q^0$ and $Q^1$ reproduce the emprical ${\widehat{Q}}^0$ and ${\widehat{Q}}^1$ (see supplementary material³⁰).

Classification

We used values of EC and FC as measures to classify the cohort at each time-point in two schemes: (i) healthy controls versus patients and (ii) patients without a deficit, those with deficit in a single factor, and those with multiple deficits. For the first classification, we pooled data from healthy controls at two time-points separated by 3 months to improve the balance between class frequencies.

We selected EC values of HCP-SCT links (n = 4218) and, due to symmetry, FC values of half of them (n = 2109) for each participant, z-scored and rearranged them as a vector. Participants were randomly split into stratified training (80% from each class) and test (20%) sets and a multinomial logistic regression (MLR) classifier was trained using EC/FC values of all links in the training set and tested on the test set. The procedure was repeated for 100 splits and the significance of mean accuracy was tested, at 0.05 level, against the null hypothesis of chance by comparing it with a chance-level accuracy distribution. Here, for each split, we randomly permuted class labels across individuals and obtained 100 chance-level accuracy values. We also calculated the confusion matrices that compares the true class labels with the predicted.³⁰ Identical splits were used to compare the accuracy of EC and FC for each classification.

Statistical comparison of classification accuracy

As we used identical train-test splits to calculate the classification accuracy of EC and FC as well as the chance-level, we used Wilcoxon signed rank test to test whether the median, across 100 splits, of paired difference in the accuracy was significantly different from zero. In case of comparison with the chance-level, we used the one-tailed test where the alternate hypothesis is that the median difference is positive.

We also calculated the variance explained by EC and FC for each classification. As our statistical model is not a linear but a logistic regression for prediction of discrete class-labels, the definition of variance explained or R² in this case is based on using maximum likelihood estimates as model fit.³³ Following Nagelkerke, R² in this case is defined as:

$$R^2=\mathrm{ }\frac{1-{\text{exp}}^{-2(\mathit{logL}\left(B\right)-\mathit{logL}(0\left)\right)/N}}{1-{\text{exp}}^{2\left(\mathit{logL}\left(0\right)\right)/N}}$$

where, Log L(B) and Log L(0) are the log likelihood of the fitted and null models, respectively, and n is the number of samples. The R² is normalized so that the maximum value is 1. When the fitted model performs worse than the null model, the R² values can be negative and unbounded.

Identification of important links for classification

We used recursive feature elimination (RFE) to identify the most predictive links. Here, we used 90% of participants in each class as the training set, ranked the links via RFE, trained the MLR using one link at a time, in the order of the ranking, and calculated its accuracy as a function of links, on the remaining 10% participants. We then identified, as the predictive links for that train-test split, a minimum number of highest ranked links for which the slope of the smoothed accuracy curve was less than a millionth (to locate saturation) and the accuracy was at least 90% of the mean accuracy obtained with all links considered. We repeated this procedure for 90 train-test splits and links that were part of the predictive set in at least 20% of all splits constituted the most-predictive set. This percentage threshold was used as the accuracy, using the most-predictive links, began to drop below 1 beyond it (Supplementary Figs 1 and 2). We also compared the size of the union of predictive links from all splits with the total number of links to test the stability of the ranking.

The rank of links in each training set was linearly transformed to a normalized rank so that the highest and lowest ranked links were rank-normalized to 1 and 0 respectively. Subsequently, the normalized ranking for each link was averaged across all train-test splits.

Data availability statement

The full set of neuroimaging and behavioural data are available at http://cnda.wustl.edu/app/template/Login.vm. Specific data and analysis scripts are available on request to the authors.

Results

EC estimation for individual participants

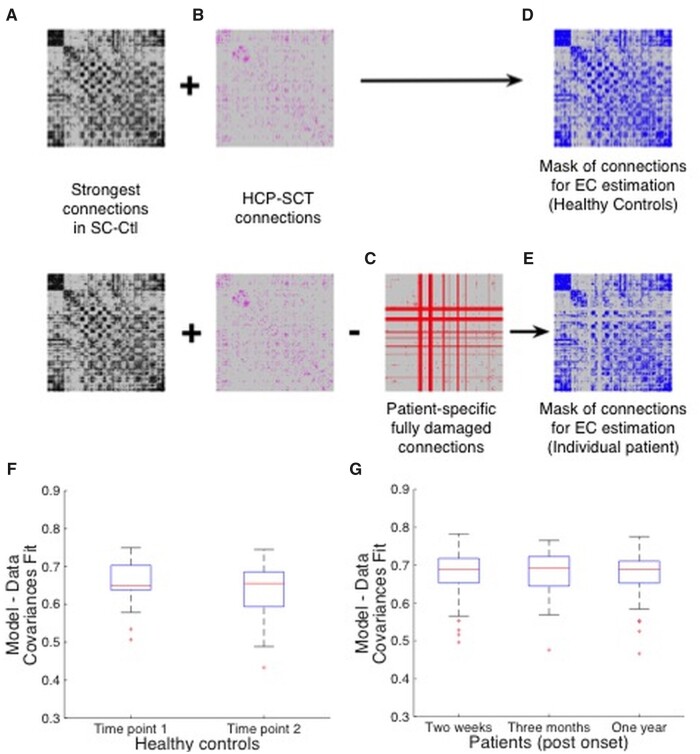
We first obtained FC matrices for each participant using zero-lagged Pearson’s correlation between BOLD signals of all 324 ROIs. Then we fit the model to reproduce the zero-lagged and lagged empirical BOLD covariances by estimating EC for a mask of plausible neuro-anatomical links. This mask, EC_mask_Ctl (Fig. 1D), was identical for each healthy participant. It included all links with value stronger than 0.5% of the strongest SC value in SC-Ctl (Fig. 1A), a SC averaged across all healthy individuals from this study, and all links in the HCP-SCT (Fig. 1B). For each patient, we built an individual mask (Fig. 1E), by excluding from EC_mask_Ctl, all completely damaged links (Fig. 1C).

Figure 1.

Masks of structural links used in estimating the effective connectivity. For healthy controls, the mask shown in D is the union of links stronger than 0.5% of the strongest value in the SC_Ctl, shown in A, matrix averaged across healthy control participants (SC_Ctl, see Materials and methods section), and existing links in the HCP-SCT, shown in B. From this mask, we remove all links that are completely damaged by the lesion in an individual patient, shown in C, to find an individualized mask for the patient, shown in E. (F and G) Box plots of Pearson correlation values between the empirical and model lagged and non-lagged co-variances for age- and education-matched healthy controls at two time-points, 3 months apart, shown in F and stroke patients at three time-points: 2 weeks, 3 months and 1 year post onset of stroke, shown in G.

Using the structural connections mask for each participant as a constraint on the model (akin to a topological prior), we inferred individual EC matrix that maximized the Pearson’s correlation between model and empirical lagged and non-lagged covariances. Average fit across healthy controls and patients was found to be 0.65 and 0.7 respectively (Fig. 1F and G).

Distinction of patients from healthy controls using EC and FC

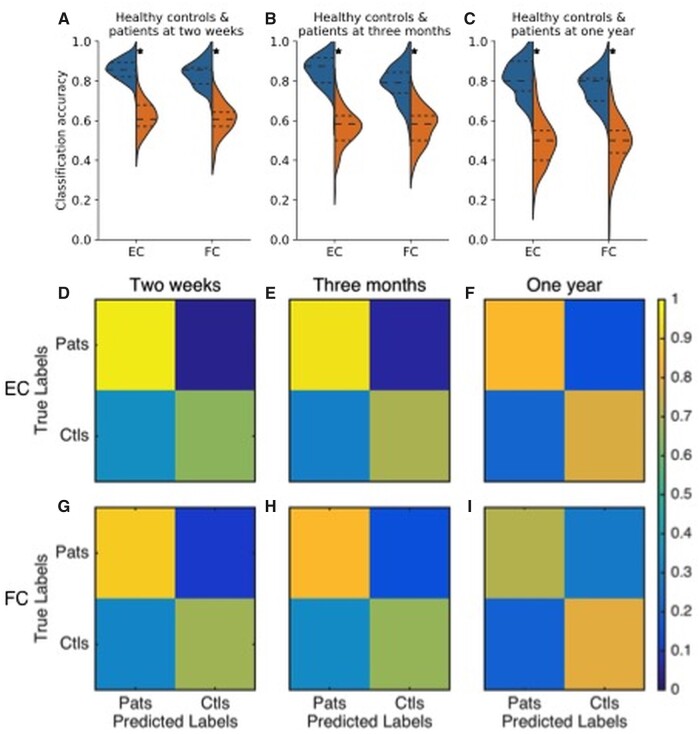
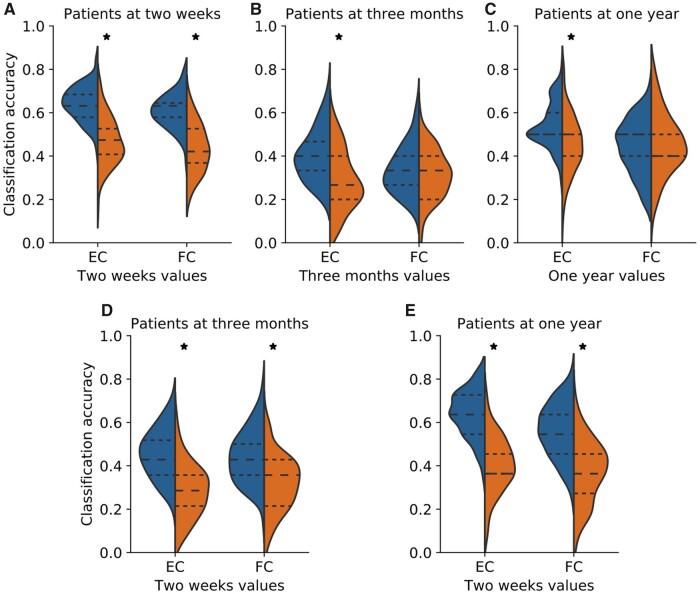
Statistical comparison of median EC values, between healthy control and patients groups, for all HCP-SCT links showed significant difference for only 14 and 5 links at the 2-week and 3-month time-points, respectively (P < 0.05, Mann–Whitney test, corrected for multiple comparisons using false discovery rate). No significant differences was found at the 1-year time-point. Next we assessed the predictive power of EC and FC using their values for HCP-SCT links. We had EC and FC values for 45 Control scans, and, 95, 73 and 53 patients at the 2-weeks, 3-month and 1-year time-points, respectively. Figure 2A–C show the distributions of accuracy of these measures in classifying healthy controls versus patients, along with chance-level distributions. At all three time-points, median accuracy values for EC (0.86, 0.88 and 0.8) and FC (0.85, 0.79 and 0.8) were significantly higher than chance (P < 1E-16; Wilcoxon signed-rank test, signed rank statistic: 4.94E + 3 for all three comparisons involving EC and 4.95E + 3, 4.83E + 3 and 4.47E + 3 for all comparisons involving FC). However, a statistically significant difference between EC and FC accuracy values was found (P < 1E-4; Wilcoxon signed-rank test, Bonferroni corrected; signed rank statistic: 2.17E + 3, 3.37E + 3 and 2.60E + 3 for three comparisons, respectively) at all three time-points.

Figure 2.

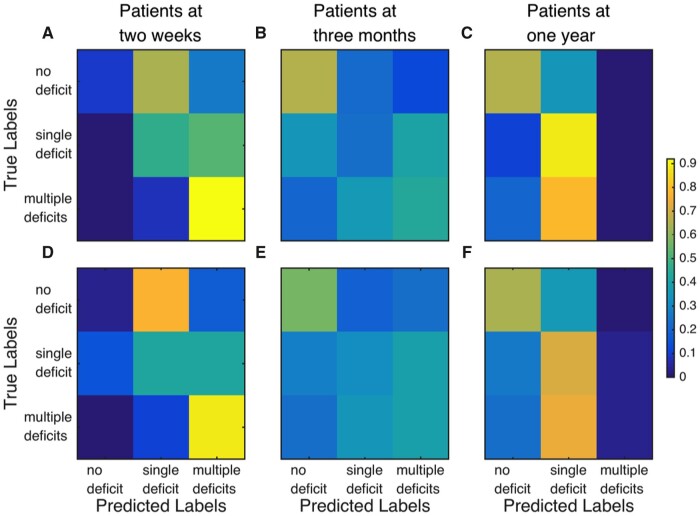
Performance of EC and FC in classification of patients and healthy controls. Distributions of accuracy in distinguishing healthy controls and patients using EC and FC values for all links in the HCP-SCT at 2-weeks, shown in A, 3-months, shown in B, and 1-year, shown in C, post onset of stroke. Orange violin displays chance-level accuracy distribution and asterix denotes significantly higher median accuracy than chance level (P < 1E-16 Wilcoxon signed rank test). Median EC accuracy was significantly greater than median FC accuracy at all three time-points (P < 1E-4, Wilcoxon signed rank test, Bonferroni corrected for three comparisons). D–I shows confusion matrices using EC, shown in D–F, and FC, shown in G–I, values for classifying healthy controls and patients at the 2 weeks, shown in D and G, 3 months, shown in E and H, and 1-year time-point, shown in F and I.

We calculated the explained variance, R² in a cross-validated fashion using the 80–20 train-test splits by comparing the fitted MLR classifier with a null model of uniform predictive probability for each of the two classifications we considered. Median R² values, across train-test splits, were found to be 0.65, 0.67 and 0.57 for EC and were significantly higher (P < 0.001; Wilcoxon signed rank test) than the values with FC—0.60, 0.49 and 0.44 for the controls versus stroke classification at all three time-points, respectively (Supplementary Fig. 3). There was a significant correlation between the R² and the accuracy values obtained by predicting the labels in each case (Supplementary Fig. 4). The R² values vary considerably across the splits as they are based on log likelihood estimates while accuracy values, obtained by predicting labels for test-set subjects, do not. However, the strong correlation between these two metrics shows that the accuracy can be used to interpret the variance explained.

Bottom panels of Fig. 2 display the confusion matrices for the three time-points using EC (D–F) and FC (G–I) values. The asymmetry of confusion matrices at the 2-week and 3-month time-points shows that classification error is mostly due to some patients being classified as controls. Mean accuracy using FC values for all links between 324 ROIs was not significantly different from that using FC values for only HCP-SCT links (Supplementary Fig. 5), confirming that HCP-SCT links were sufficiently informative for classification.

EC and FC biomarkers for distinguishing patients from controls

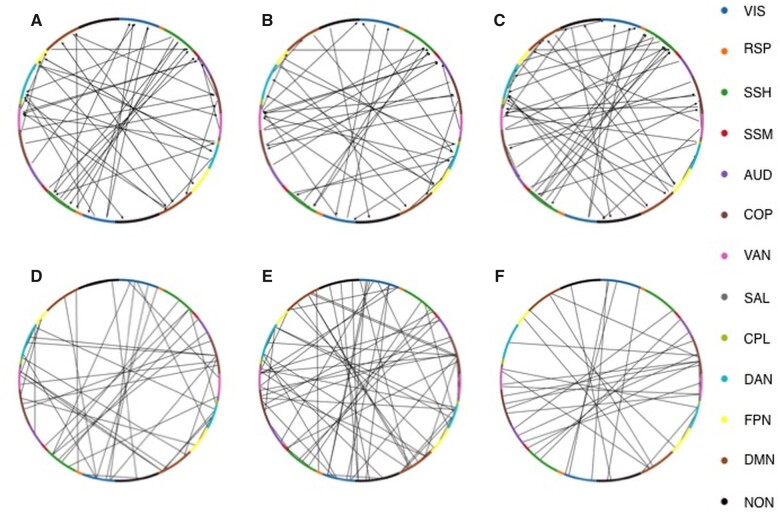
A biomarker, in this context, is a subset of all HCP-SCT links sufficient for an accurate classification. We found that the ranking was stable across different splits as the union of predictive links from at least two splits accounted for only a small fraction of all links—9.6%, 12.7% and 7.2%—, in case of EC, and—18.2%, 4.6% and 10.3%—in case of FC at the three time-points, respectively. Predictive links in at least 20% of all splits were identified as biomarkers.

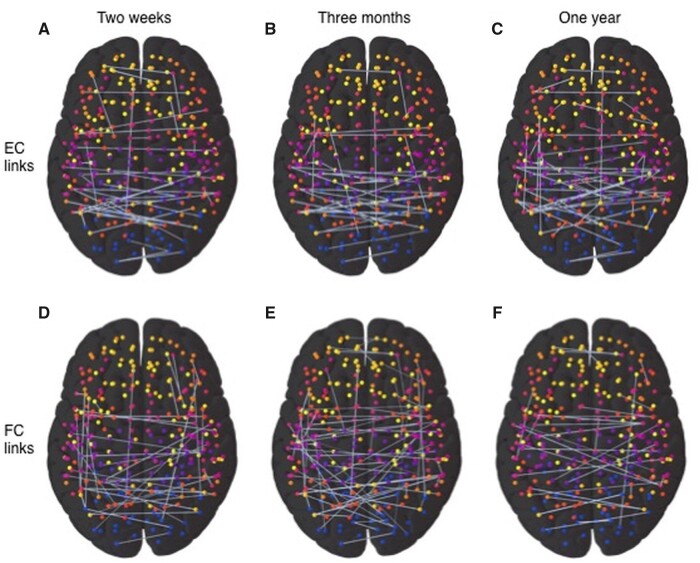
Figure 3A–C display the biomarker EC links for the three time-points, respectively, while Fig. 3D–F display the corresponding, most predictive FC links. Figure 4 demonstrates within- and IH predictive links according to RSNs, with EC (Fig. 4A–C) and FC (Fig. 4D–F) as measures, for the classification at the three time-points, respectively. Arrows in the top panels indicate the directionality of predictive EC links. Next, we compared, for each RSN, the average ranking weighted by the fraction of links in each of the four sub-groups, namely (i) efferent, IH; (ii) afferent, IH; (iii) efferent, intra- or within-hemispheric (WH) and (iv) afferent, WH, of predictive EC links. We also found average weighed ranking across all WH and IH predictive links for classifications involving FC. Supplementary Fig. 6 shows mean (±SEM) normalized rank across splits of these sub-groups of links. First, the IH links were relatively more important than the WH links for most RSNs. At the 2-week time-point, efferent WH links from DAN and VAN, IH links from DMN and SMH and afferent WH links to DMN and IH links to SMH were significantly more important than other groups for EC-based classification while for FC-based classification, WH links in VIS, VAN, DAN and DMN, and IH links in SMH and COP were most important. At the 3-month time-point, most relevant contributors to EC-based classification were efferent WH links from VAN and IH links from COP, SMH, VAN, DMN and VIS; afferent WH links to SAL, DMN and SMH and IH links to SMH while for FC-based classification, COP and DAN WH links and VIS and COP IH links were the most important. Finally for the 1-year EC-based classification, efferent WH links from SMM and VAN and IH links from DMN; afferent WH and IH links to SMH, and for the FC-based classification, WH COP links and IH links in COP, VIS, SMH, AUD and VAN were the most prominent contributors.

Figure 3.

Most predictive links for distinguishing patients from healthy controls. Predictive links using EC values (top panels) and FC values (bottom panels) for classification of healthy controls and patients at the 2 weeks, shown in A and D, 3-months B and E, and 1 year, shown in C and F, time-points, respectively. The node colours represent different RSNs.

Figure 4.

Distribution of predictive links for distinguishing patients from healthy control in terms of RSNs and hemispheres. Predictive links according to RSNs for EC (top panels) and FC (bottom panels) for the classification of healthy controls versus stroke patients at each time-point (2 weeks, A and D; 3 months B and E; 1 year C and F). Arrows in the top panel figures show the directionality of interaction in the predictive EC links.

Normalized ranking of all links, averaged across splits, was correlated across time-points for both EC and FC as well as between EC and FC at each time-point (Supplementary Fig. 7); however, sets of most predictive links in any two cases had few common members. This points to the fact that physiological changes caused by stroke are not static and while changes at earlier time-point could recover at later time-points, network re-organizations could happen at later time-points. Mean rankings of links were not related to their mean structural disconnections (Supplementary Fig. 8) or the frequency of disconnection at any time-point indicating that the average structural damage alone could not explain a link’s relevance for this classification.

Predicting number of behavioural deficits and prognosis

Next, we sought to predict the behavioural deficit severity in patients by classifying them into three classes: (i) patients without a deficit across all seven factors; (ii) patients with a deficit in one factor and (iii) patients with deficits in multiple factors across four behavioural domains. At time-point 1, 16, 30 and 49 patients, at time-point 2, 23, 22 and 25, and at time-point 3, 20, 25 and 9 were in these three classes, respectively. Then, we used EC and FC links to classify patients in these three classes. In the first analysis, EC and FC links at one time-point classified patients’ number of deficits at the same time-point. In a clinically more pertinent analysis from a prognostic point-of-view, we used links at the 2-week time-point to predict patients’ number of deficits at later time-points.

Figures 5A–C show the accuracy of same time-point EC and FC links in classifying patients’ number of deficits. Figures 5D and E show the prognostic accuracy of 2-week time-point EC and FC links in classifying patients at the 3-month and 1-year time-points, respectively. EC performed significantly better than the chance-level in all cases (P < 1E-6, Wilcoxon signed-rank test, Bonferroni corrected; signed rank statistic: 4E + 3, 3.4E + 3, 2.1E + 3, 3.9E + 3 and 4.4E + 3 for the five cases outlined in Fig. 5A–E) with the corresponding median accuracy values of 0.63, 0.4, 0.5, 0.43 and 0.64 respectively. Median accuracy of only the 2-week time-point FC, 0.63, 0.43 and 0.54, respectively, in predicting the patient deficits at all three time-points was significantly higher than chance (P < 1E-9, Wilcoxon signed rank test, Bonferroni corrected; signed rank statistic: 4.3E + 3, 3.4E + 3, 3.6E + 3 for the three cases outlined in Fig. 5A, D and E). Median accuracy of 2-week EC links in classification of 2-week and 1-year time-points patients was significantly higher than the accuracy of 2-week FC links (P < 1E-2, Wilcoxon signed-rank test, Bonferroni corrected; signed rank statistic: 2.5E + 3, and 2.3E + 3 respectively) while no significant difference in the performance of two-weeks EC and FC in classifying patients at the 3-month time-point was observed. Median R² for both EC and FC were close to 0 indicating a much worse model fit than the case of healthy controls versus stroke classification (Supplementary Fig. 9). This is also reflected in levels of accuracy seen (Fig. 5) in comparison to those found for the controls versus patients classification (Fig. 2).

Figure 5.

Performance of EC and FC in prediction of behavioural deficits in patients. Accuracy of classification of stroke patients according to the number of deficits using EC and FC values of all links in the HCP-SCT. Top panels: classification of patients at the 2-week, shown in A, 3-month, shown in B, and 1-year, shown in C, time-points using EC and FC values at the same respective time-points; bottom panels: prognostic accuracy of EC and FC—classification of patients at the 3-months, shown in D, and 1-year, shown in E, time-points using EC and FC values at the 2-week time-point. Orange violin displays chance-level accuracy distribution and asterix denotes significantly higher median accuracy than chance level (P < 1E-6, Wilcoxon signed rank test). Median classification accuracy using 2-weeks EC links for classifying patients at 2-weeks and 1-year time-points was significantly higher than that using corresponding FC values (P < 1E-2, Wilcoxon signed rank test, Bonferroni corrected for five comparisons).

Figure 6 displays the confusion matrices for classification of patients at all three time-points using 2-week EC (A–C) and FC (D–F) links. While both EC and FC predicted patients with multiple deficits at the 2-week time-point (Fig. 6A and D) well, both failed to predict participants without any deficit. At the 1-year time-point, since several patients with multiple deficits at the 2-week time-point have recovered, this is a very small class (nine participants) and both EC and FC fail to predict it well.

Figure 6.

Confusion matrices for the three-way classification of patients by number of behavioural deficits. Only 2-weeks EC (top row) and FC (bottom row) values for all links in the HCP-SCT are used for classifying patients at the 2 weeks, shown in A and D, 3 months, shown in B and E, and 1 year, shown in C and F, time-points.

Predictive 2-week EC links for number of behavioural deficits and prognosis

Next, we looked for the biomarker links whose 2-week EC values were most predictive of patient deficits at 2-week and 1-year time-points. Ranking of links across different training sets was robust as the fraction of all EC links that were predictive in at least 2 of the 90 realizations at the 2-week and 1-year time-point were 11% and 9.7%, respectively (Supplementary Fig. 10A and B). The normalized average ranking of all links was correlated across the two time-points (r = 0.32, Supplementary Fig. 10C); however, the most predictive links in the two cases had few common members. Finally, the average normalized ranking of all and predictive links did not correlate with their average structural disconnection (Supplementary Fig. 10D and E) or the frequency of disconnection.

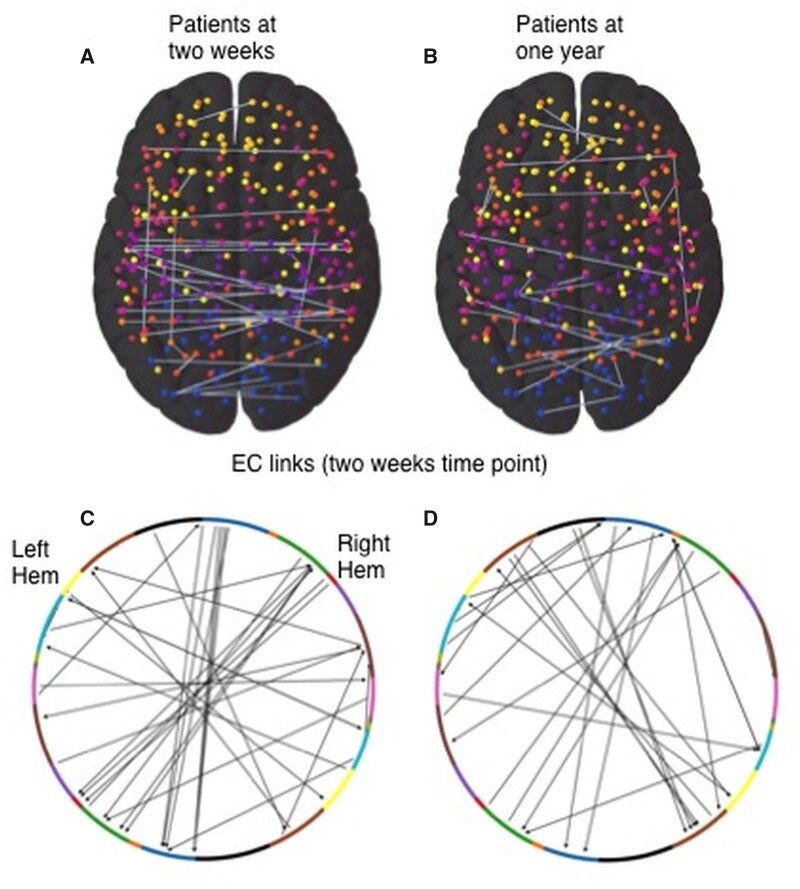
Figure 7A and B display these predictive EC links, while Fig. 7C and D display their distribution according to RSNs in each hemisphere. Bidirectional WH links in DAN and IH links from and to visual, SMH along with efferent, IH links from DAN and VAN and afferent, IH links to DMN stood out for the 2-week time-point classification. On the other hand, at the 1-year time-point, efferent WH links from SMH, FPN and DMN and IH links from SMH and DAN while afferent WH links to AUD, DAN and VAN and IH links to VIS, SMH and DMN found to be the most prominent contributors (Supplementary Fig. 11).

Figure 7.

Most predictive links for prediction of behavioural deficits in patients. A and B: Predictive links (top panels) and their distribution according to RSNs (bottom panels) from EC values at the 2-week time-point in classifying patients according to the number of behavioural deficits at the 2-week (A and C) and 1-year (B and D) time-points. Arrows in the bottom panel figures show the directionality of interaction in the predictive EC links.

Discussion

In this paper, we classified stroke patients using RS-FC and a linear model-based EC inferred from lagged and non-lagged second-order statistics of the RS-fMRI data. While both EC and FC performed significantly better than chance in distinguishing controls from patients’ 2-weeks, 3-month and 1-year post-onset, accuracy for EC was significantly higher than for FC at each time-point. More importantly, EC values at 2-week time-point were significantly more predictive than chance as well as FC values in classifying patients according to the number of behavioural deficits not only at the 2-week time-point but also at the 1-year time-point. Thus, the EC could extract information from RS neurophysiological signals at an early time-point that was relevant, not just for the diagnosis of patients but also their prognosis. We also identified biomarker sub-networks for stroke diagnosis and prognosis.

Estimation of EC is robust when a mask of neuro-anatomically plausible links is used as a prior in the inference.³⁰ In this study, we combined two SC masks to, (i) define the links for which EC was estimated in healthy controls and (ii) to define the corresponding links for each patient by excluding from the combined mask all completely damaged links in that individual’s brain. The first mask, consisting of strongest links in the SC averaged across controls obtained using DWI and probabilistic tractography, was necessary to have a reasonable minimum number of estimated links (27%), so that the fit between empirical and model covariances was sufficiently high (∼0.7 on average). The second mask, consisting of existing links in the HCP-SCT, found using end-to-end tractography with DWI scans in 842 HCP participants, was too sparse (4% edge density) but necessary as these were the only links used for classification; their sparseness ensuring low computation cost of biomarker identification. Second, and more importantly, FC, averaged across HCP-SCT links was found to be significantly stronger than the average across other links³¹ in both the healthy and the patients groups. Their importance for classification was evident from the comparison of mean accuracy with that using all links (Supplementary Fig. 1).

Our application of structural constraints to optimize the sparsity of our connectivity model is a key aspect of characterizing EC—in the current setting and more generally. The key difference between FC and EC is that functional connections can exist between all pairs of regions, even if there are only a sparse number of links. This follows from the fact that correlations can be induced through multi-link pathways (i.e. involving network effects). Technically, this becomes an important consideration as a manner to regularize the estimates of EC. In terms of model optimization, this corresponds to finding the model of EC with the greatest evidence or marginal likelihood. Crucially, the marginal likelihood can always be decomposed into accuracy minus complexity. Therefore, we minimize model complexity by imposing sparsity constraints on the parameters, thereby promoting models with the greatest evidence. This is important because models with a higher evidence are those that have the greatest predictive validity. In other words, they are the models that generalize to new data because they do not overfit. In our work, we used a heuristic proxy for model evidence via the cross-validation accuracy (i.e. classification patients versus controls, of cognitive deficits), beyond the ‘simple’ goodness of fit of the empirical BOLD data.

While both EC and FC were significantly more accurate than chance at distinguishing patients from healthy controls at all three time-points, EC’s performance was better than FC especially at the two later time-points as the confusion matrix in Fig. 2 also shows. Recent papers on recovery from stroke⁷ Ramsey et al³⁴ have shown that as patients recover from behavioural deficits, a corresponding recovery of FC alterations observed at the sub-acute stage (1–2 weeks post onset) takes place. Therefore, it is reasonable to expect that as patients recover, the magnitude of FC differences between healthy controls and patients at later time-points is reduced in comparison with the early time-point. Hence, making the distinction between patients and healthy individuals using FC, that only measures spatial correlation, would be less accurate at later time-points than at the earlier one. In contrast, the EC, that is inferred using both spatial and temporal correlations, continues to predict the two classes well at later time-points.

Prediction of stroke severity in terms of number of behavioural deficits was a significantly more complex task. Here, the class definitions were driven by a consideration to balance predictability with interpretability. Sufficient number of participants in each class and balanced class frequencies were required to ensure predictability. The notion of behavioural deficit was based on a clinical definition of a score 2 SD below the average control score. We did consider other class definitions—one, in particular, to assess recovery distinguished patients according to the change in either the within-domain deficit or in the number of deficits across domains. However, here, we did not have sufficient samples in each such class to ensure predictability. Also, some patients recovered from deficit in one factor while worsened in another making labelling such cases appropriately a challenge from the point of view of interpretation.

In this classification, EC at the 2-week time-point not only predicted patient classes at the same time-point with significantly higher accuracy than chance as well as FC, it did so at the 1-year time-point as well. Moreover, as the confusion matrices in Fig. 6 demonstrate, at the 1-year time-point, classes that included recovered patients—namely patients without deficit and with deficit in a single factor, were better predicted. Therefore, the temporal correlation structure found in an early stage RS-fMRI that is captured by the EC is an important contributor to predicting recovery and prognosis of patients.

The objective of this study, apart from comparing classification accuracies of two neurophysiological data-driven measures, was also to identify specific links as biomarkers. Most important FC-based signature of patients at all three time-points included IH links within several RSNs—namely visual, somato-motor, cingulo opercular, dorsal attention and default mode—and intra-hemispheric links between the dorsal attention, fronto-parietal and default mode networks. These observations are in line with the previous research of markers of stroke at the acute/sub-acute stage.^4,6 EC biomarkers for the classification at 2-week time-point included within-RSN IH links similar to the FC but links to a RSN were not necessarily equally important as links from that RSN. This distinction can be assessed in the case of EC due to its asymmetry. Thus, at 2-week time-point, while links in both directions were important for IH links from/to somato-motor, efferent links from DMN were more relevant than afferent ones. Afferent links from somato-motor network were more important at later time-points along with efferent links from cingulo-opercular networks (Supplementary Fig. 6).

Since they predicted the number of behavioural deficits in patients at 2-weeks and 1-year time-points accurately, we extracted biomarker networks for this classification using only the 2-week EC links. IH links from and to visual, somato-motor, efferent links from DAN and VAN, and afferent links to DMN were found to be most important for predicting patients’ deficit severity at 2-weeks post onset of stroke. At 1-year post onset, when a significant proportion of patients with initial deficit had recovered thus making the no-deficit class the largest, IH links from and to somato-motor along with afferent links to visual network and efferent links from the DAN were most predictive (Supplementary Fig. 11). In case of WH links, bidirectional links in DAN were most predictive of patients’ deficit severity at 2-week time-point while at the 1-year time-point, afferent links to DAN, VAN and AUD while efferent links from somato-motor, FPN and DMN were the two most predictive sets.

In conclusion, impact of focal stroke and recovery from it can be characterized in terms of low dimensional constructs consisting of patterns of FC as well as clinical concomitants. Going beyond the statistical associations measured by FC, EC captures directed and causal influences and has been found to be superior to FC in neuropsychiatric setting.³⁵ Our results confirm this finding and show that whole-brain model based EC inferred from second-order statistics of the resting state fMRI data in patients of stroke outperforms FC in extracting information relevant for clinical prognosis from early stages of the neurological condition.

Supplementary material

Supplementary material is available at Brain Communications online.

Funding

M.H.A. and M.C. were supported by National Institutes of Health grant R01 NS095741 to M.C. M.C. was also supported by Flag-Era joint transnational call 2017; Departments of Excellence Italian Ministry of Research (MIUR); Cariparo Foundation Excellence grants 2019; Ministry of Health Italy RF-2018–12366899. M.T.S. was supported by European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 818521). G.D. is supported by the Spanish Research Project (ref. PID2019-105772GB-I00 AEI FEDER EU), funded by the Spanish Ministry of Science, Innovation and Universities (MCIU), State Research Agency (AEI) and European Regional Development Funds (FEDER); and Human Brain Project Specific Grant Agreement 3 (grant agreement no. 945539), funded by the European Union Horizon 2020 Future and Emerging Technologies Flagship program and Research Support Group support (ref. 2017 SGR 1545), funded by the Catalan Agency for Management of University and Research Grants (AGAUR). A.I. was supported by the European Union Horizon 2020 Research and Innovation Programme Grant 785907 (Human Brain Project SGA2) and 945539 (Human Brain Project SGA3). M.G acknowledges funding from the German Excellence Strategy of the Federal Government and the L ¨ander (G:(DE-82)EXS-PF-JARA-SDS005) and the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 785907 (Human Brain Project SGA2).

Competing interests

The authors report no competing interests.

Glossary

AUD =

auditory network

BOLD =

blood oxygen level dependent

COP =

cingulo-opercular network

CPL =

cingulo-parietal network

DAN =

dorsal attention network

DMN =

default mode network

DWI =

diffusion weighted imaging

EC =

effective connectivity

EPI =

echo-planar imaging

FC =

functional connectivity

fMRI =

functional magnetic resonance imaging

FPN =

frontal parietal network

HCP =

Human Connectome Project

MOU =

multivariate Ornstein–Uhlenbeck

NON =

non-assigned to any resting-state networks

RS =

resting-state

RSN =

resting-state networks

RSP =

retro-splenial network

SAL =

salience network

SC =

structural connectivity

SC_Ctl =

structural connectivity for controls

SCT =

structural connectome template

SDC =

structural disconnectome

SMH =

somato-motor hand network

SMM =

somato-motor mouth network

VAN =

ventral attention network

VIS =

visual network