Abstract
Noise correlations (i.e. trial-to-trial covariations in neural activity for a given stimulus) limit the stimulus information encoded by neural populations, leading to the widely-held prediction that they impair perceptual discrimination behaviors. However, this prediction neglects the effects of correlations on information readout. We studied how correlations affect both encoding and readout of sensory information. We analyzed calcium imaging data from mouse posterior parietal cortex during two perceptual discrimination tasks. Correlations reduced the encoded stimulus information, but, seemingly paradoxically, were higher when mice made correct rather than incorrect choices. Single-trial behavioral choices depended not only on the stimulus information encoded by the whole population, but unexpectedly also on the consistency of information across neurons and time. Because correlations increased information consistency, they enhanced the conversion of sensory information into behavioral choices, overcoming their detrimental information-limiting effects. Thus, correlations in association cortex can benefit task performance even if they decrease sensory information.
Introduction
The collective activity of a population of neurons, beyond properties of individual cells, is critical for perceptual discrimination behaviors1,2. A fundamental question is how functional interactions in a population impact both the encoding of sensory information and how this information is read out to guide behavioral choices3. A commonly studied feature of population coding is noise correlations, the correlated trial-to-trial variability over repeated presentations of the same stimulus4,5. Noise correlations can take the form of “across-neuron” correlations between the time-averaged spike rates of different neurons or populations, or “across-time” correlations between the activity of the same neural population at different times.
The impact of correlations has been long debated. Much work has proposed that they limit the information encoding capacity of a neural population6–9. Based on the widely-held assumption that perceptual discrimination performance increases proportionally with the amount of sensory information encoded in neural activity10, this has been taken to imply that information-limiting correlations hinder the ability to discriminate sensory stimuli6,10. Specifically, across-time correlations have been proposed to limit the benefit of integrating noisy information over time for a speed-accuracy tradeoff11,12. Further, across-neuron correlations are thought to lessen the benefit of averaging noisy information across neural populations6,7,9.
However, the effect of noise correlations may be more nuanced, as indicated by a separate stream of biophysical studies showing that spatially and temporally correlated spiking can more strongly drive responses in postsynaptic neural populations13–17. It remains poorly tested if and how enhanced signal propagation may have a beneficial impact on behavioral discrimination performance.
We investigated how noise correlations shape behavioral performance in perceptual discrimination by studying together not only how correlations impact the encoding of sensory information, but critically also how they impact the readout of this information by downstream neural circuits to guide behavioral choices.
Correlations of PPC activity limit sensory coding
To examine how noise correlations affect both stimulus coding at the population level and behavioral discrimination performance, we focused on the mouse posterior parietal cortex (PPC). PPC participates in transforming multisensory signals into behavioral outputs, is essential for perceptual discrimination tasks during virtual-navigation18, and has stimulus information related to an animal’s choices19–23. It is thus a relevant area to study the impact of correlated neural activity on behavior.
We examined across-time and across-neuron correlations in PPC population activity using previously published datasets. To study across-time correlations, we used calcium imaging data from a sound localization task19 in which mice reported perceptual decisions about the location of an auditory stimulus by navigating through a visual virtual reality T-maze (Fig. 1a). As mice ran down the T-stem, a sound cue was played from one of eight possible locations in head-centered coordinates. Mice reported whether the sound originated from their left or right by turning in that direction at the T-intersection (78.0 ± 0.5% correct). During each session, the activity of ~50 layer 2/3 neurons was imaged simultaneously. Because the same sensory cue (sound location) was presented throughout the trial, this task is well-suited to study across-time correlations.
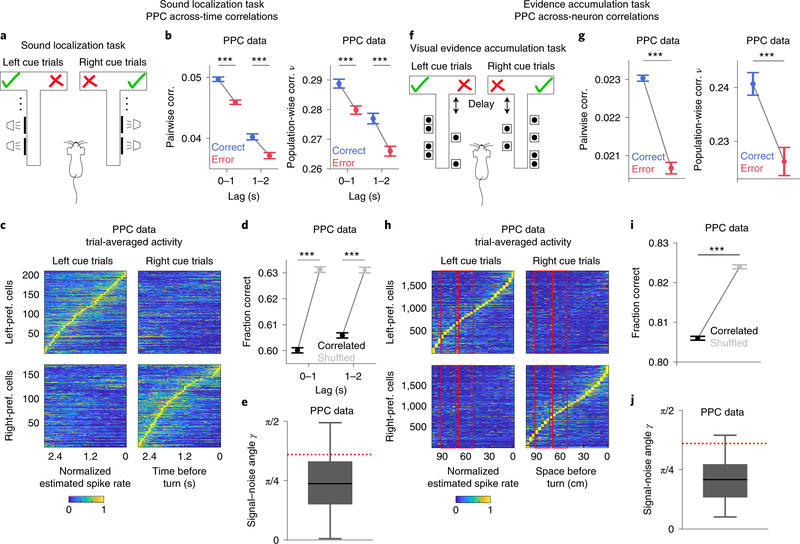
Figure 1: Response properties and across-time and across-neuron correlations in PPC during perceptual discrimination tasks.
Panels a-e refer to PPC data during the sound localization task. a, Schematic of the task. Left/right sound category (speaker symbols) indicate the rewarded side of the maze (checkmark). b, Pairwise (left) and population-wise (right) noise correlations in time-lagged activity, for correct and error trials. c, Trial-averaged estimated spike rate traces for PPC cells (left-preferring, n=212; right-preferring, n=172), aligned to the turn frame, normalized to each cell’s peak mean activity and sorted by peak time. d, Accuracy of a linear decoder of stimulus category applied to joint population activity, for real recorded (black) or trial-shuffled (gray) data. In b and d, errorbars report mean ± SEM across all cell pairs (b left, n_pairs = 133,860 and 119,562 for Lag 0–1s and 1–2s respectively) and all time point pairs within the specified lag range from n=6 sessions. For all comparisons, P=10−4, two-sided permutation test. e, Distribution of the signal-noise angle γ (over n=6 sessions and all time point pairs within a 2s lag). Boxplots show the median (line), quartiles (box) and whiskers extend to ±1.5*interquartile range. Red dotted line: analytically computed bound between the information-limiting and information-enhancing regime.
Panels f-j refer to PPC data during the evidence accumulation task. f, Schematic of the task. The rewarded side of the maze (checkmark) is the one identified by the most numerous visual cues (wall segments with black dots patterns). g, Pairwise (left) and population-wise (right) noise correlations in time-averaged activity, for correct and error trials. Errorbars report mean ± SEM across all cell pairs (left, n_pairs = 1,561,202) and Early and Late Delay epochs from n=11 sessions. For all comparisons, P=10−4, two-sided permutation test. h, As in c, for all PPC cells (left-preferring, n=1,840; right-preferring: n=2,000). Activity traces are averaged over spatial bins (about 200 ms). Red rectangles indicate the Early and Late Delay epochs. i, Accuracy of a linear decoder of stimulus applied to joint population activity, for real recorded (black) or within-pool trial-shuffled (gray) data. Errorbars report mean ± SEM across n=11 sessions, Early and Late Delay epochs and 100 pool splits. P=10−4, two-sided permutation test. j, As in e, for across-time correlations, using data from n=11 sessions.
To study across-neuron correlations, we used calcium imaging data from an evidence accumulation task21 in which ~350 layer 2/3 neurons were imaged simultaneously per session. During virtual navigation, mice were presented with six temporally separate visual cues on the left or right walls of a T-maze (Fig. 1f). Mice reported which side had more cues by turning in that direction at the T-intersection (84.5 ± 1.6% correct). We categorized the visual stimuli as having more total left or right cues. Because of the high number of simultaneously imaged neurons, this task is well-suited for studying across-neuron correlations.
For all analyses, we focused on the period toward the end of the T-stem before the mouse had reported its choice and after it had received sensory information. This is a window in which neural activity may carry sensory information used to inform choice.
We tested how noise correlations impacted the encoding of sensory information in population activity. We computed both pairwise (Pearson correlation between activities of two neurons) and population-wise correlations (the fraction of total population activity variance carried by the largest principal component1) for each stimulus category. Pair- and population-wise correlations were positively related and varied consistently across conditions in PPC data (Fig. 1b,g, Extended Data Fig. 1g–k,s–w) and in population encoding models (Supplementary Mathematical Notes S3, Extended Data Fig. 2a,b). PPC neurons had, on average, positive across-neuron and across-time pairwise and population-wise noise correlations (Fig. 1b,g, Extended Data Fig. 1g–j, s–v). Since many neurons exhibited activity selective for distinct trial types, with different neurons active at distinct time points in the trial (Fig. 1c,h), we could decode the stimulus category significantly above chance from pairs of temporally offset instantaneous population activity vectors (Fig. 1d) and from the population activity vector in one time window (Fig. 1i). Stimulus category decoding performance was higher in the sound localization dataset because of the larger number of recorded neurons. To evaluate how across-time correlations affected the encoding of stimulus category, we shuffled instantaneous population activity vectors across trials of the same stimulus category, independently at each time point. This shuffle destroyed within-trial temporal relationships while preserving instantaneous population activity. We disrupted across-neuron correlations by randomly splitting the neural population into two non-overlapping pools of neurons of equal size and shuffling the trial labels separately for each pool within the same stimulus category. Importantly, in both datasets stimulus decoding performance was higher when across-time or across-neuron correlations were disrupted by shuffling, indicating that both forms of correlations limited stimulus category information in population activity (Fig. 1d,i).
Whether noise correlations limit the information encoded by a neural population depends on how they relate to signal correlations (correlations between trial-averaged responses to individual stimuli4,5,24). We quantified their relationship using the angle25,26 between the axis of largest variation at fixed stimulus (noise correlations axis) and the axis of largest stimulus-related variation (signal correlations axis) in the high-dimensional space of population activity (see Fig. 2c for a sketch). Encoding models5,24 predict that the smaller the signal-noise angle, the more noise correlations impair stimulus discrimination due to larger overlap between the stimulus-specific response distributions to different stimuli (Fig. 2c, Fig. 3a). Supporting the observation above that correlations were information-limiting in our datasets, most signal-noise angles resided in the information-limiting regime, below the signal-noise angle critical value for the transition to the information-enhancing regime reported in previous work27,28 (Fig. 1e,j). Correlations were information-limiting both in “easy” and “hard” trials with high and low levels of sensory evidence, respectively (Extended Data Fig. 1a–b,d–e,m–n,p–q).
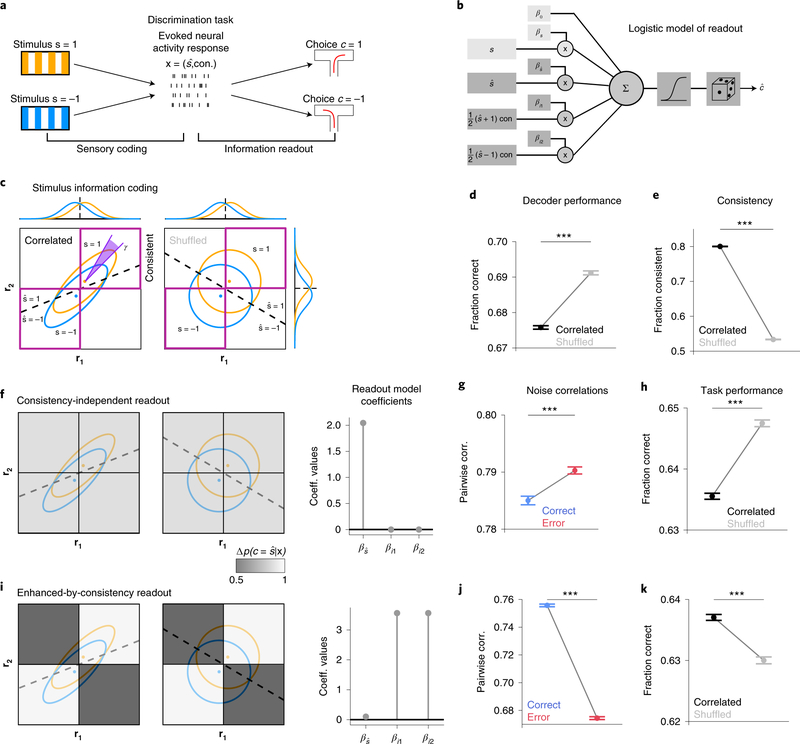
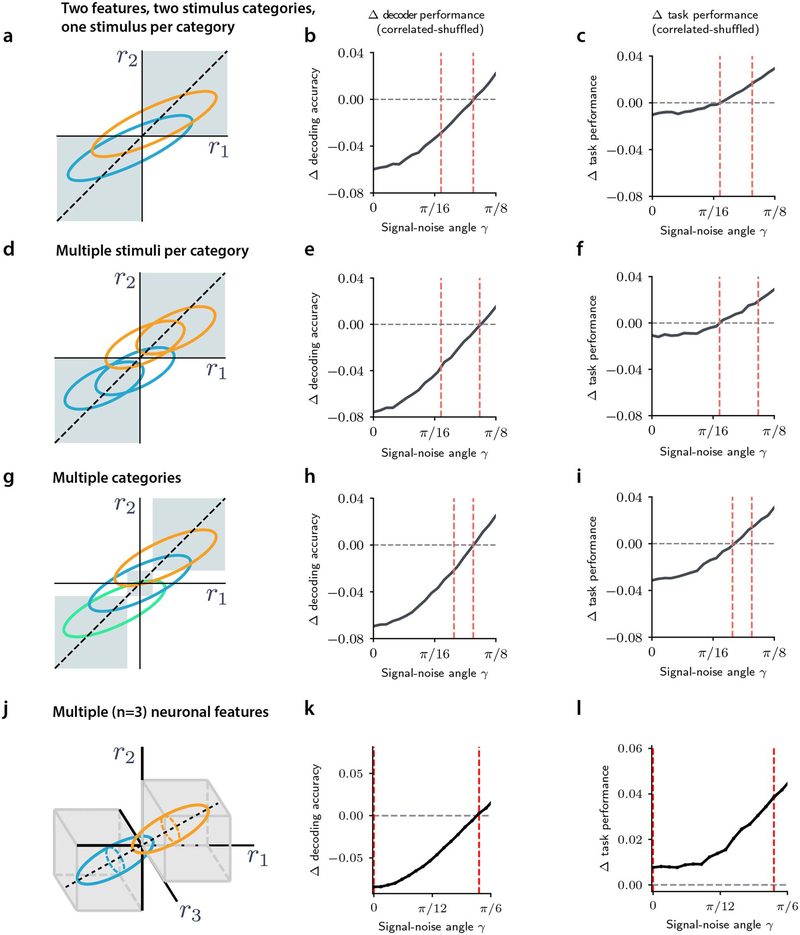
Figure 2: A simple encoding-readout model shows how different readouts determine the impact of correlations on task performance.
a, Schematic conceptualizing two fundamental information processing stages in sensory perception included in the model: sensory coding (mapping from sensory stimuli to neural activity) and information readout (mapping from neural activity to behavioral choice). Task-relevant neural activity is recapitulated by the stimulus predicted from population activity () and its consistency across features (con). b, Schematic of the readout model used to model choices. Non-neural predictors (bias and real stimulus, light gray boxes on the left; used only in real data analyses to account for the effect of non-recorded neurons) and neural predictors (stimulus predicted and consistency, dark gray boxes on the left; used both in simulations and data analyses) are weighted, summed and transformed through a sigmoid function that outputs the binomial probability of a binary choice.
c, Example of simulated response distributions of two one-dimensional neural features (r1, r2) to two stimuli (s=1, s=−1), modelled as bivariate Gaussians. For the correlated example, noise and signal axes are closely but not perfectly aligned (γ=0.08π). Ellipses: 95% confidence intervals of stimulus-specific activity distributions. Dashed black line: optimal stimulus decoding boundary. Purple squares: regions in which r1 and r2 encode consistently stimulus information, i.e. the same stimulus is decoded from both. Marginal response distributions and decoding boundaries are shown sideways. d, Accuracy of a linear decoder of stimulus applied to simulated responses is higher for uncorrelated responses (correlations limit the encoded stimulus information). e, The fraction of trials in which r1 and r2 encode consistent stimulus information is higher for correlated responses (correlations increase consistency).
Panels f-h refer to the consistency-independent readout. f, The readout is represented as a grayscale map in the r1-r2 response space. Orange and blue ellipses: stimulus-specific distributions. Shade of gray: readout efficacy (probability of transformation from encoded stimulus to choice), which for this readout is independent of consistency. The corresponding readout model regression coefficients are shown on the right ( for the predicted stimulus, and βi1 βi2 for the consistency-dependent interaction terms between predicted stimuli and neural consistency). g, Pairwise noise correlations are higher in error trials. h, Task performance computed using this readout model is higher for uncorrelated responses.
Panels i-k refer to the enhanced-by-consistency readout (consistency modulation index η = 0.9, see Methods). i, Same as f. The readout efficacy is higher for consistent trials. j, Same as g. Pairwise noise correlations are higher in correct trials. k, Same as h. Task performance is higher for correlated responses, indicating that this readout overcomes the information-limiting effect of correlations.
In panels d, e, g, h, j, k errorbars report mean ± SEM over 200 simulations with 5,000 trials each with N=1, γ = 0.08π, , σ = 0.2. Correlated: ρ=0.8, equivalent to ν=0.9. Uncorrelated: ρ=0, equivalent to ν=0.5. For all comparisons, P=10−4, two-sided permutation test. Model parameters were purely illustrative and did not match real data.
Figure 3: Exploration of the parameter space of the encoding readout model.
Data are simulated with the encoding-readout model with N=20 neurons in each pool. Panels represent the mean over 100 simulations with 300,000 trials each.
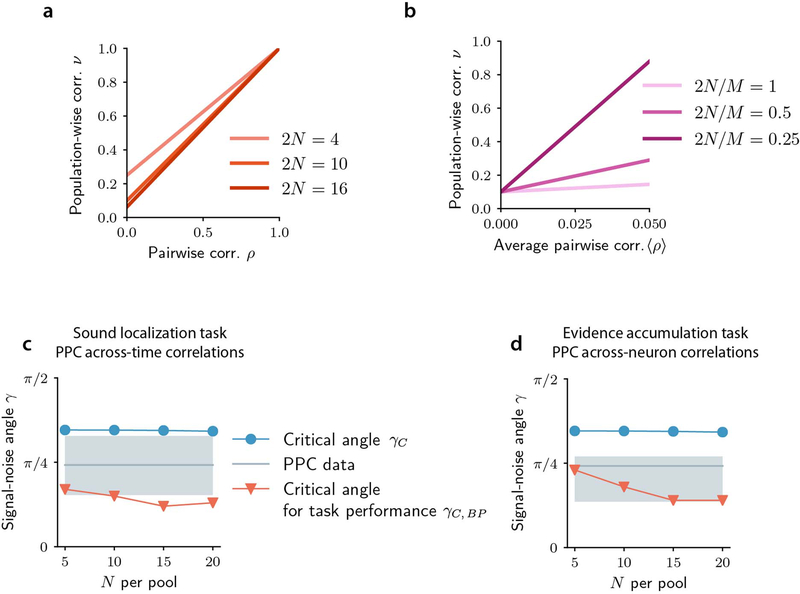
a, Difference in the accuracy of a linear decoder of stimulus applied to correlated and shuffled simulated neural activity for different values of the signal-noise angle (γ) and population-wise correlations (ν). For all panels, black solid line: boundary between a regime with information-limiting correlations and information-enhancing correlations. b, The difference between correlated and shuffled activity in the fraction of trials in which the two neural features encode consistent stimulus information is higher in the information-limiting regime and increases with the population-wise correlations strength.
Panels c-e refer to the consistency-independent readout. c-d, Difference in average pairwise correlations (c) and population-wise correlations (d) between trials with correct and incorrect predicted task performance for different combinations of model parameters. e, Difference in task performance predicted by applying the consistency-independent readout to correlated and shuffled simulated neural activity for different combinations of model parameters. For panels c-i, dashed black line: boundary between a regime where task performance is higher for correlated responses and a regime where performance is higher for shuffled responses. The overlap between the continuous and dashed black line indicates that information-limiting correlations are also detrimental for behavior.
Panel f-h refer to the enhanced-by-consistency readout (consistency modulation index η = 0.85). f-g, Same as in c-d. With the enhanced-by-consistency readout correlations are higher in correct trials. h, Same as in e. The area between the dashed and the continuous black lines indicates a regime where correlations are information-limiting but task performance is higher for correlated responses. In the parameter range between the two lines, this readout can overcome the negative impact of correlations. Dark and light gray dots and ellipses: mean values and range between the 25th and the 75th percentile of the signal-noise angles and population-wise correlations for PPC data from the sound localization task and evidence accumulation task, respectively.
i, Difference in task performance predicted by applying the enhanced-by-consistency readout or the consistency-independent readout (with matched readout efficacy) for different combinations of model parameters.
If correlations are detrimental to perceptual behaviors, one would expect noise correlations to be lower when animals make correct choices and higher when animals make errors. Contrary to this expectation, both across-time and across-neuron noise correlations were higher in correct trials than in error trials (Fig. 1b, g). Thus, although correlations limit information in population activity, including on correct trials (Extended Data Fig. 1c,f,o,r), they might not impair behavioral performance.
A model of how correlations affect task performance
The above findings lead to the paradoxical suggestion that correlations limit information encoded by a neural population but at the same time may be beneficial for making accurate choices. To reconcile these observations, we developed a simple mathematical model that incorporated both the encoding of stimulus information and the readout of this information to form a choice. We compared two alternative views of how information in population activity may be used to perform a stimulus discrimination task. In the traditional view, choice accuracy is proportional to the amount of information in a neural population, and thus information-limiting correlations constrain task performance. Alternatively, a choice could depend on both stimulus information and features of neural activity that emerge from correlations, in particular the consistency of information across time and neurons in a population.
We simulated a perceptual discrimination task with two possible stimuli that had to be converted into two possible corresponding choices (c = 1 for s = 1 and c = −1 for s = −1) (Fig. 2a). We simulated trials of two N-dimensional sets of neural activity features r1 and r2, which can alternatively represent neural activity of a pool of N neurons at different points in time (for across-time correlations) or activity of two different pools of N neurons each (for across-neuron correlations). Fig. 2 and Extended Data Fig. 3 illustrates the model using a case with unrealistically high noise correlations and one neuron per feature (N=1). We display results for N=20 (Fig. 3) and N=10 (Extended Data Fig. 4) neurons per feature, to show that these are largely independent of N, and to document how they depend on the two parameters that are key for model behavior and comparison with real data: the signal-noise angle and the strength of population-wise noise correlations (Supplementary Mathematical Notes S1–S2).
In the encoding model, for each feature, higher trial-averaged activity was associated with one sensory stimulus (s = 1), while lower mean activity corresponded to the opposite sensory stimulus (s = −1), meaning that the two features showed positive signal correlations (Fig. 2c). We simulated noise correlations between r1 and r2 (noise correlation strength intuitively corresponds to the elongation of the ellipses depicting the distributions of responses to stimuli), and we varied across simulations the signal-noise angle (in the example of Fig. 2c this angle is small, as signal and noise are closely but not perfectly aligned). When signal-noise angles were small, noise correlations increased the overlap between the stimulus-specific response distributions (cf. orange and blue ellipses in Fig. 2c, left panel vs right panel) and decreased the stimulus information encoded by the two features jointly (Fig. 2d, Fig. 3a). There was a critical signal-noise angle value below which correlations limited information and above which they enhanced information (Fig. 3a). This value depended mildly on the noise correlation strength (Fig. 3a), but was largely independent of the stimulus information level or the population size (Supplementary Mathematical Notes S1, Eq. (S3)).
We then considered the readout stage of the model. Commonly, the choice during a task trial is expected to follow the decoded stimulus. However, because of the apparent importance of correlations for accurate choices in our experimental data, we hypothesized that the readout of stimulus information might utilize aspects of population activity imposed by correlations. Intuitively, correlations imply that there is greater consistency in the neural population representations (Fig. 2e). In our model, we defined consistency as a single-trial measure of similarity between the stimuli that are decoded from features r1 and r2 separately. In our simulations, a stimulus representation in a trial was classified as consistent when features r1 and r2 both signaled the same stimulus (i.e. both features higher than average and thus both signaling s = 1, top right quadrant of panels in Fig. 2c, or both lower than average and thus both signaling s = −1, bottom left quadrant of panels in Fig. 2c).
We simulated choices for a binary task discrimination with two alternative readout models, formulated as logistic models of the dependence of choice on several features of stimulus encoding. In the first model, termed the consistency-independent readout, the simulated choice in each trial depended only on the stimulus decoded from the two features jointly (Fig. 2f, right panel). This case followed the traditional assumption29 that the choice reflects the stimulus decoded from the full population activity (Fig. 2f, readout map superimposed to left and middle panels). In our experimental data, we did not observe a perfect correspondence between the stimulus decoded from neural activity and the choice of the mouse (the mean ± SEM over sessions and trials of the fraction of times the mouse’s choice matched the decoded stimulus was 61.0% ± 0.2% in the sound localization dataset and 91.1% ± 0.1% in the evidence accumulation dataset). Therefore, in the model, we set the probability that in a given trial the choice matched the decoded stimulus (termed “readout efficacy”) to a value smaller than 100%.
In the second readout model, termed the enhanced-by-consistency readout, the choice in each trial depended not only on the stimulus decoded from both features jointly, but also on the consistency of the stimulus decoded from the features separately (Fig. 2i, left and middle panel). If r1 and r2 reported consistent information about the stimulus, this readout was more likely to use the stimulus encoded in neural activity to inform the choice. This effect was reflected in the positive coefficients assigned to the interaction terms between the decoded stimulus and consistency (Fig. 2i, right panel). In other words, the readout efficacy was higher when the two features were consistent (Fig. 2i, readout map superimposed to left and middle panel). Importantly, the average readout efficacy of this model was matched to the readout efficacy of the consistency-independent model.
For the consistency-independent readout, correlated activity resulted in worse task performance compared to activity in which correlations were absent, across the entire information-limiting regime of the model’s parameter space (Fig. 2h, Fig. 3e). This was expected because, with this readout, the task performance directly follows the level of stimulus information, with higher information resulting in higher performance. Further, in the information-limiting regime, noise correlations were higher on simulated error trials than on correct trials (Fig. 2g, Fig. 3c,d), which was notably inconsistent with our PPC data (Fig. 1b,g).
For the enhanced-by-consistency readout, larger noise correlations within the information-limiting region increased the fraction of trials with consistent information (Fig. 3b, Extended Data Fig. 4b). As a result, correlations generated a larger fraction of trials that were better read out by the enhanced-by-consistency readout. Because of this, this readout produced behavioral task performance as good or better with noise correlations than without correlations (Fig. 2k, Fig. 3h). When the signal-noise angle was not too small but still in the information-limiting region (so that the information decrease due to correlations was not too large), the enhanced-by-consistency readout compensated and even overcame the information-limiting effects of correlations (Fig. 3h). Interestingly, signal-noise angles and noise correlation values estimated from PPC data resided mostly in this specific parameter region (Fig. 3h).
Importantly, for the enhanced-by-consistency readout, noise correlations were higher in correct trials than error trials (Fig. 2j, Fig. 3f,g), matching our experimental PPC findings. Thus, the enhanced-by-consistency readout reconciled our experimental observations, providing a mechanism whereby correlations limit information but benefit task performance.
Correlations and consistency contribute to choices
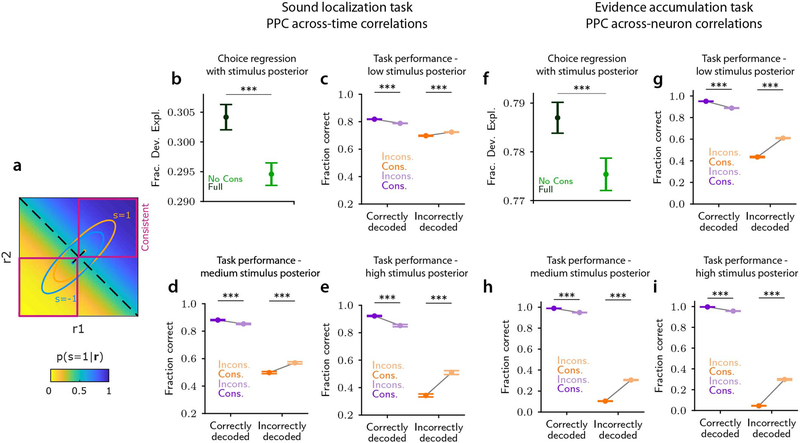
We then used our experimental measurements of PPC neural activity to test for signatures of an enhanced-by-consistency readout. A key prediction of this readout is that the mouse’s single-trial choices should depend not only on the correctness of stimulus encoding but also on the consistency of stimulus information. In our experimental data, we defined consistency as the single-trial similarity between the stimuli decoded from population activity at different points in time (across-time consistency) or between the stimuli decoded from separate neuronal pools in the same time window (across-neuron consistency). An example of across-time consistency is a trial in which population activity at time t1 signaled the same stimulus category as the population activity at time t2. We calculated the mouse’s performance for four subclasses of trials, defined by the correctness and consistency of the stimulus decoded from neural activity in a given trial. In both datasets, the mouse’s task performance was higher for trials with correctly decoded stimulus information than for incorrectly decoded trials, suggesting that the stimulus information carried by PPC neurons was used to inform behavioral choices (Fig. 4b,f). Also, the mouse’s task performance was higher for trials with consistent information across time or across neurons, suggesting that the consistency of neural population information was important for accurate choices (Fig. 4a,e). Critically, in trials with correctly decoded stimulus information, the mouse’s task performance was higher when information was consistent than when it was inconsistent, both across neurons and across time (Fig. 4b,f). Further, in trials with incorrectly decoded stimulus information, task performance was lower on consistent trials than on inconsistent trials (Fig. 4b,f). These findings indicate that the stimulus information in PPC was read out in a manner that, in consistent trials, amplified the effect of the decoded stimulus on the mouse’s choice, both when the decoded information was correct or incorrect.
Figure 4: Across-time and across-neuron correlations in PPC activity influence mouse’s choices.
Panels a-d refer to PPC data during the sound localization task. a, Task performance (fraction correct) is higher when neural population vectors encode the stimulus consistently across time. b, Task performance (fraction correct) is higher in trials with correct stimulus decoding, suggesting that stimulus information is used to inform behavior. Left. Task performance in trials with correctly decoded stimulus is higher when information is encoded consistently. Right. The opposite happens when information is decoded incorrectly. Thus, stimulus information in neural activity has a larger impact on choices when it is encoded consistently. c, Performance (fraction of deviance explained) in explaining single-trial choices of various readout models. Full model uses all predictors (neural and non-neural). The other models neglect information from selected predictors as follows. No Cons: neglects neural consistency; No Neural: neglects stimulus decoded from neural activity and neural consistency. Models indicated by abbreviations lin, quad, rbf use linear, quadratic or radial basis function Support Vector Machines (SVMs) respectively to decode stimulus from neural activity. If no such abbreviation is used, a linear SVM is intended d, Left: Best-fit coefficients of the Full readout model (β0 and βs are non-neural coefficients corresponding to bias and stimulus-related drive due to non-recorded neurons, is the coefficient of the predicted stimulus, and βi1, βi2 correspond to the consistency-dependent interaction terms between each predicted stimulus and the neural consistency, with positive values amplifying the predicted stimulus effect in consistent trials). Right: Readout efficacy estimated from the best-fit coefficients of the Full model, above the baseline-level due to non-neural predictors, for consistent and inconsistent population vectors, represented schematically as a readout map in the 2D response space similarly to Fig. 2. In panels a-c, for all comparisons, P=10−4, two-sided permutation test. In panels a-c, d left, errorbars report mean ± SEM across n=6 sessions and all time point pairs within a 1 s lag. In panel d-right, the gray levels represent mean over n=6 sessions and all time point pairs within a 1s lag.
Panels e-h refer to PPC data during the evidence accumulation task. e, Same as in a. f, Same as in b. g, Same as in c. h, Same as in d. In e-h, consistency and choices are computed from the activity of two neuronal pools. Also in the evidence accumulation task, stimulus information in neural activity has a larger impact on choices when it is encoded consistently, and choices depend critically on neural consistency across pools.
In panels e-g, for all comparisons, P=10−4, two-sided permutation test. In panels e-g, h left, errorbars report mean ± SEM across n=11 sessions, Early and Late Delay epochs, and n=100 random pool splits. In panel h-right, the gray levels represent mean over n=11 sessions, Early and Late Delay epochs, and n=100 random pool splits.
To rule out that differences in a mouse’s task performance between consistent and inconsistent trials were due to higher stimulus information in consistent trials, we sorted trials according to the stimulus information level and verified that performance in correctly (respectively incorrectly) decoded trials was still higher (respectively lower) when information was consistent across neurons or across time (Extended Data Fig. 5c–e,g–i).
We further examined the possibility of an enhanced-by-consistency readout by developing an analytical understanding of how single-trial choices were made by the mouse. We used logistic regression to relate PPC activity to the mouse’s choices. We expressed a mouse’s choice on a given trial as a function of features of the recorded neural activity: the stimulus decoded from the full PPC population activity and its interaction with the across-time or across-neuron consistency (Fig. 2b). In addition, we included a predictor for the experimenter-defined stimulus presented to the mouse and a bias term. These two terms captured the stimulus-related and stimulus-unrelated information carried by sources other than the recorded neurons, such as non-recorded neurons. The inclusion of these terms allowed us to test how much the stimulus information in the recorded neural activity explained the mouse’s choice after discounting what could be explained by other sources.
The regression coefficients for the stimulus decoded from neural activity were positive (Fig. 4d,h, left), indicating that the neural stimulus information impacted the mouse’s choice. The coefficients for the consistency-dependent terms were also positive, indicating that the readout of PPC activity performed similarly to the enhanced-by-consistency readout model from Fig. 2i,j. That is, the probability that the choice matched the stimulus decoded from neural activity was higher in consistent trials (Fig. 4d,h, right). We tested the specific contribution of the neural-based predictors in explaining the mouse’s choices by fitting the logistic regression after shuffling the values of these predictors across trials (Fig. 4c,g). Shuffling all neural-based predictors (Fig. 4c,g) made it harder to predict a mouse’s choice, again demonstrating that neural activity contributed to choices. Moreover, shuffling only the neural consistency values, while leaving intact the stimulus decoded from neural activity and the experimenter-determined stimulus, resulted in worse predictions of a mouse’s choices. Using readout models that non-linearly combined neural population activity to decode directly the stimulus regardless of consistency also failed to explain choices as well as the enhanced-by-consistency readout model (Fig. 4c,g) even though they decoded the stimulus well (Extended Data Fig. 1l,x). The specific non-linear interaction between neural consistency and decoded stimulus thus was key to form the mouse’s choice.
To rule out that the modulation of the readout by consistency might just reflect differences in overall stimulus information levels between consistent and inconsistent trials, we verified that consistency provided a similar contribution to predicting a mouse’s choices when we used a more sophisticated logistic model that included the magnitude of the stimulus information, instead of only the identity of the decoded stimulus (Extended Data Fig. 5b,f). Further, to control for and discount potential contributions from movement-related neural activity, we verified that neural consistency also contributed to predicting choices when adding to the regression the consistency of the mouse’s running speed and direction (Extended Data Fig. 6c–e).
An enhanced-by-consistency readout benefits task performance
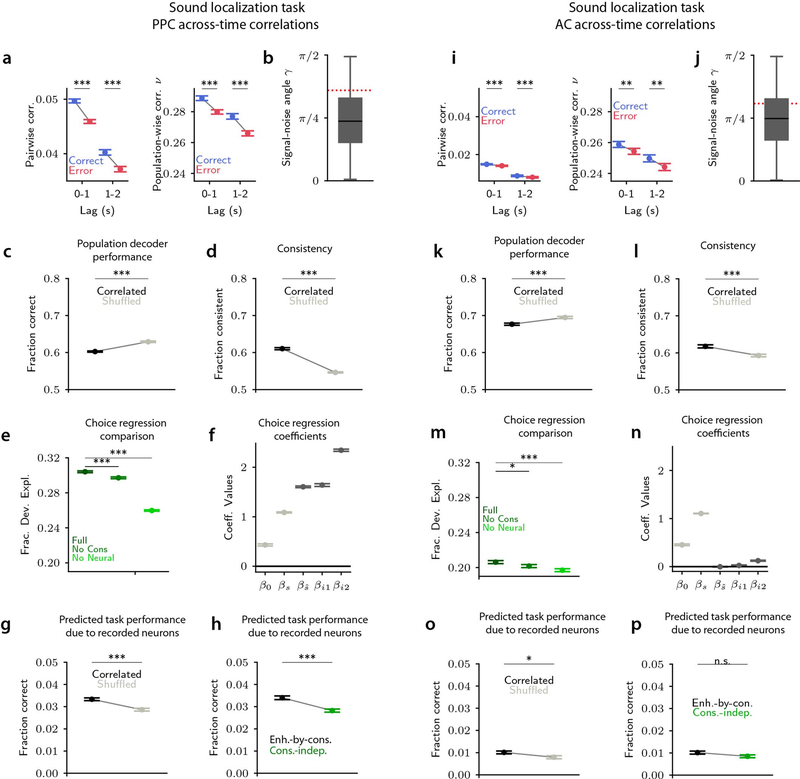
Our results show that across-time and across-neuron consistency in the experimental data impact a mouse’s choices. We examined the implications of this finding for mouse task performance, in the presence or absence of experimentally-measured information-limiting correlations. Because correlations cannot be removed experimentally, we instead created a set of simulated choices using the experimentally-fit logistic choice regression from Fig. 4. We used as input to the experimentally-fit choice regression either trials with simultaneously-recorded PPC neural activity or trials with neural activity shuffled to disrupt across-time or across-neuron correlations. We used these simulated choices to estimate how well the mouse would have performed on the task with and without correlations present (Fig. 5a).
Figure 5: Simulated mouse’s choices show that the best-fit enhanced-by-consistency readout improves task performance in the presence of information-limiting correlations in PPC.
a, Schematic of the method used to study the impact of correlations on task performance. The best-fit readout model was applied to the original correlated patterns of neural activity and to artificial patterns where correlations were removed by shuffling.
Panels b, c refer to PPC data during the sound localization task. b, Left. Fraction of trials with stimulus information encoded consistently across pairs of time points, for real recorded (black) or trial-shuffled (gray) population vectors. Right. Task performance due to the recorded neurons predicted by applying the best-fit readout model to real recorded (black) or trial-shuffled (gray) population vectors. c, Same as in b, computed after subsampling trials to equalize the encoded stimulus information between correlated and shuffled data.
d, Schematic of the method used to study the impact of the enhanced-by-consistency readout on task performance. Task performance was predicted by applying to the original correlated patterns of neural activity the best-fit enhanced-by-consistency model and a consistency-independent readout model with readout efficacy matched to the best-fit readout model.
Panels e, f refer to PPC data during the sound localization task. e, Left. Best-fit coefficients of the enhanced-by-consistency readout model. Right. Coefficients of the consistency-independent model with matched readout efficacy. f, Task performance due to the recorded neurons predicted by applying to the original correlated patterns of neural activity the best-fit enhanced-by-consistency (black) and the consistency-independent (green) readout model. In panels b-c, e-f errorbars represent mean ± SEM across n=6 sessions and all time point pairs within a 1 s lag. For all comparisons, P=10−4, two-sided permutation test.
Panels g-j refer to PPC data during the evidence accumulation task. g, Same as in b, for across-neuron correlations. Left: P=10−4. Right: P=0.1136. Two-sided permutation test. h, Same as in c, for across-neuron correlations. Left: P=10−4. Right: P=0.0105. Two-sided permutation test. i, Same as in e, for across-neuron correlations. j, Same as in f, for across-neuron correlations. P=10−4, two-sided permutation test. In panels g-j, errorbars represent mean ± SEM across n=11 sessions, Early and Late Delay epochs, and 100 splits in pairs of neuronal pools.
We focused only on the contribution of the recorded neural population, by computing task performance from choices simulated using all predictors extracted from experimental data and then subtracting the task performance computed from choices simulated after shuffling across trials the values of neural predictors. This calculation is more precise than the one obtained by simply mapping the session-averaged PPC parameters to the encoding-readout model (as we did in Fig. 3h), because it estimates the contribution of correlations to task performance using single trials recorded in each session and choice readout regression computed in the same session. In the sound localization dataset, the ~50 recorded neurons were estimated to increase task performance by ~3.5%, and in the evidence accumulation dataset, the ~350 neurons increased task performance by ~25% (Fig. 5b,g right). Strikingly, although the stimulus information in the recorded neurons was lower with correlations intact (Fig. 1d,i), the recorded neurons increased task performance to a greater extent when across-time correlations were intact than when they were removed by shuffling in the sound localization dataset (Fig. 5b right). Furthermore, in the evidence accumulation task, the recorded neurons contributed similarly to task performance with and without across-neuron correlations intact, despite lower information with correlations present (Fig. 5g right). Thus, the enhanced-by-consistency feature of the experimentally-fit readout could overcome, or at least offset, the information-limiting effect of correlations and benefit task performance.
These results incorporate the overall impact of correlations on task performance by combining the effects of the encoding and readout. To quantify the specific contribution of the readout, we again simulated choices from the experimentally-fit choice regression, except we equalized the stimulus information in the correlated and shuffled responses by selecting subsets of trials having the same fraction of correctly decoded stimuli. With this matching, the correlated and shuffled trials differed only in their neural consistency (Fig. 5c,h, left), with a proportion of consistent trials equal to those of the full data (Fig. 5b,g, left). For both datasets, the estimated contribution to task performance of the recorded neurons was higher when correlations were intact than when they were disrupted (Fig. 5c,h, right). This result shows that the readout of PPC activity was more efficient in extracting information from correlated than from uncorrelated data.
These results also indicate that the readout of stimulus information from PPC activity is suboptimal. From the ~50 neurons recorded in the sound localization task and ~350 neurons in the evidence accumulation task, we were able to decode the stimulus at ~60% and ~80% correct, respectively (Fig. 1d,i). These populations therefore could have increased task performance by ~10% and ~30% above chance, respectively, if stimulus information was read out optimally. However, these populations only increased task performance by ~3.5% and ~25%, respectively (Fig. 5b,g, right). Therefore, in both datasets, the recorded neurons apparently increased task performance by a smaller amount than would have been possible if all their stimulus information was converted into choice, indicating that PPC’s stimulus information is read out for behavior, but not optimally.
The theoretical analysis of the encoding-readout model (Fig. 3i) predicted that, when population activity is correlated, an enhanced-by-consistency readout leads to higher task performance than a consistency-independent readout with matched readout efficacy. To test this prediction on PPC data, we generated simulated choices by inputting real neural activity into the experimentally-fit regression that incorporated across-time and across-neuron consistency. We also generated simulated choices using an alternative choice regression that included only the decoded stimulus predictor, regardless of its consistency (Fig. 5d–f,i–j). For fairness of comparison and to match the experimental data, the coefficients for this second choice regression were selected to yield the same readout efficacy as for the experimentally-fit regression. The estimated contribution of the recorded neurons to task performance was higher with the experimentally-fit choice regression that used consistency than with the consistency-independent choice regression matched in readout efficacy (Fig. 5f,j). These experimental findings, in agreement with model predictions, suggest that the enhanced-by-consistency readout is well suited for forming behavioral choices in the presence of information-limiting noise correlations, such as those found in PPC.
In the sound localization experiments, we also had experimental data19 from auditory cortex (AC). Relative to PPC, in AC we observed similar signal-noise angles, but weaker noise correlations which led to smaller information-limiting effect of correlations, and a much lower impact of consistency on the readout (Extended Data Fig. 7). Therefore, an enhanced-by-consistency readout may be more beneficial for PPC activity than for AC activity.
A model of enhanced-by-consistency information transmission
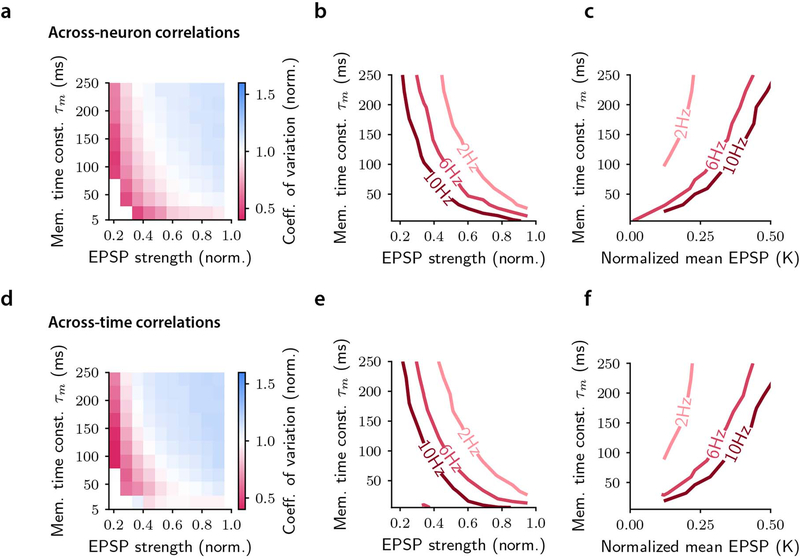
We developed a biophysical model for the downstream transmission of PPC’s stimulus information to understand potential mechanisms for the behavioral benefit of information consistency across neurons and time. Our model was based on previous observations that correlations in the presynaptic inputs to a neuron, either across neurons or time, elicit larger firing rates in postsynaptic neurons with a short integration time constant through a coincidence-detection mechanism16,29. In our model (Fig. 6a), two presynaptic input spike trains, representing the summed inputs from two neuronal pools, were integrated by a postsynaptic “readout” spiking neuron. The neural responses to two different stimuli were simulated (Fig. 6a). We assumed that the average response to the two stimuli was the same across the two input pools, leading to positive signal correlation, and we implemented positive noise correlations, both across input pools and across time (Fig. 6b,c,h). This ensured that noise and signal correlations were aligned and thus information-limiting. Therefore, and in agreement with our encoding models (Fig. 3), higher correlation strengths in the input pools, that is enhanced across-pool synchrony and/or across-time correlations (Fig. 6b,c,h), more strongly limited the information contained in the inputs (Fig. 6d,i).
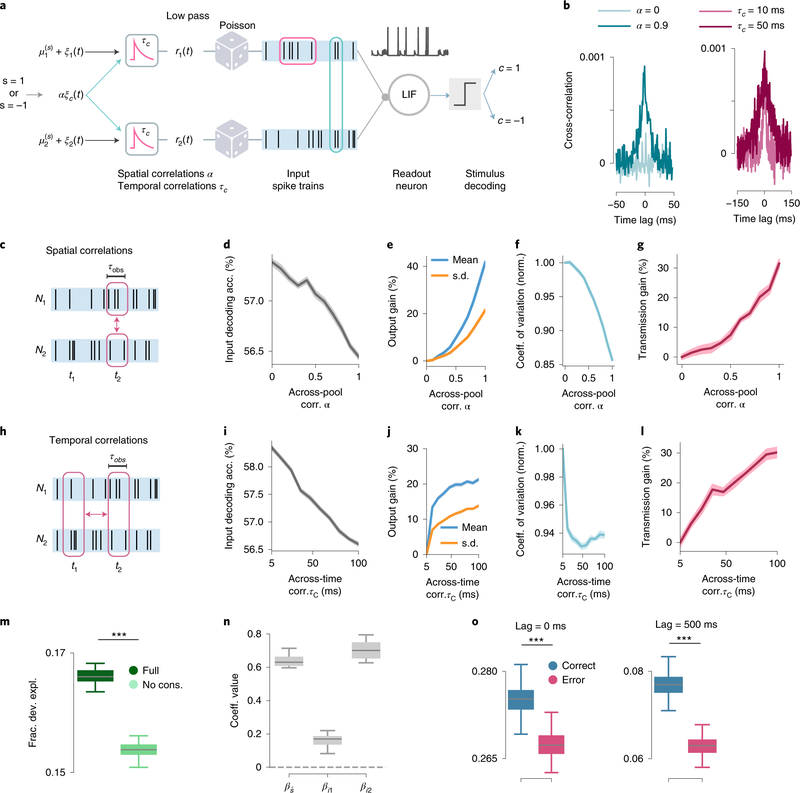
Figure 6: A biophysical model for the enhanced-by-consistency readout.
a, Schematic of the model. A leaky integrate-and-fire (LIF) readout neuron receives stimulus-modulated spike trains from two input pools. A linear stimulus classifier of the readout activity generates the transmitted output c. b, Cross-correlograms of the two input spike trains for different values of the across-pool (left) and across-time (right) correlation parameters α and τC (mean input rate Rin = 2Hz). c, Schematic illustrating across-pool correlations between the input activity. τobs is the length of each simulated trial. d, Input stimulus decoding accuracy as a function of the across-pool correlation strength α. e, Mean and standard deviation of the readout activity (normalized to their reference value in absence of correlations) as a function of α. f, Coefficient of variation (CV) of the readout activity as a function of α, normalized by its value in absence of input correlations. g, Gain in the stimulus information transmission from the input to the readout neuron (Eq. (S9), Supplementary Mathematical Note S5) as a function of α. In d-g τm = 5ms, Rin = 2Hz, τC = 100ms. All the quantities were computed on the input or output spike counts measured on time windows of length τobs h, Schematic illustrating across-time correlations between the input activity at two different time points t1 and t2. i-l, The quantities as in d-g showed similar trends when computed as a function of the across-time correlations τC. In i-l τm = 5ms, Rin = 2Hz, α = 0.9. In d-l data are presented as mean ± SEM over n=20 simulations. m, Time-lagged pairwise noise correlations computed separately on correctly-transmitted and incorrectly-transmitted simulated trials, across time lags of 500mmss. (for 0ms time lag P = 1.72 × 10−117, t=33.4, [−1.65,1.65], for 500ms time lag P = 1.24 × 10−195, t=57.8, [−1.65,1.65]; two-sided t-test, n=200 independent sets of equalized correct and error trials). n, Fraction of deviance explained for the model choices (output of the stimulus classifier on readout neuron’s activity) for the enhanced-by-consistency and the consistency-independent readout regressions (P = 4.58 × 10−23, t=21.8, [−1.69,1.69], two-sided t-test, n=20 independent sets of equalized correct and error trials). o, Values of the coefficients of the enhanced-by-consistency readout regressions. The coefficients , βi1 and βi2 correspond respectively to the stimulus decoded regressor and the two consistency regressor (Methods). In m-o boxplots show the median (line), first and third quartiles (box), and whiskers extend to ±1.5*interquartile range; in simulations τm = 5ms, Rin = 6Hz, α = 0.9, τC = 500ms.
We then considered how information-limiting correlations in the inputs to a readout neuron with a short but realistic29 integration time-constant (~5–10 ms) affected information transmission. First, input correlations enhanced information transmission by increasing the average firing rate of the readout neuron in response to each stimulus (Fig. 6e,j). However, correlations also limited information transmission by increasing the variance of the readout’s firing activity (Fig. 6e,j). To quantify the trade-off between these factors, we measured the coefficient of variation of the readout activity and the gain of transmitted information (accuracy of stimulus decoding from the readout neuron’s firing). The coefficient of variation decreased, and the transmitted information increased, when increasing correlations (Fig. 6f,g,k,l). Thus, correlations in inputs to a neuron have advantages in enhancing the neuron’s output rate that outweigh their disadvantages in increasing the neuron’s output noise.
By systematically varying the model parameters, we demonstrated that input correlations enhance readout information from a postsynaptic neuron, even when decreasing input information, when the readout integration time-constant is short enough so that the average amount of excitatory postsynaptic potentials received during an integration window is much smaller than the gap between the spiking threshold and resting potential of the readout neuron (Extended Data Fig. 8). In this regime, output firing is driven by input fluctuations. Correlated fluctuations on a short timescale increase the frequency with which the readout neuron reaches the firing threshold, thus enhancing the transmission of both neural activity and information (Supplementary Mathematical Note S5 and Extended Data Fig. 8).
Importantly, for biophysical parameters consistent with the coincidence-detection regime, the model predicted key features of PPC data. We divided the model’s simulated trials into correctly-transmitted and incorrectly-transmitted trials, namely trials in which the stimulus identity was correctly or incorrectly decoded from the activity of the readout neuron. We then analyzed the simulated data with the logistic readout regressions used for the analysis of PPC data. First, as in PPC data, the enhanced-by-consistency readout regression explained a larger fraction of the variance of the model choices (i.e. the outcome of the stimulus decoding algorithm applied on the readout activity) with respect to a consistency-independent readout (Fig. 6m). Also, the enhanced-by-consistency readout fitted on the model choices revealed that the transmission of stimulus information increased when the input activity carried consistent information across pools (Fig. 6n). Second, correlations in the input spike trains were stronger for correctly-transmitted trials than for incorrectly-transmitted trials (Fig. 6o), as in the PPC data (Fig. 1b,g).
Thus, a coincidence-detection information transmission model suggests how the enhanced-by-consistency readout may benefit behavior. Correlations in the inputs to a neuron can enhance the transmission of stimulus information from a neuron’s inputs to its output, even though these correlations limit the information contained in the inputs.
Discussion
Our results show that noise correlations limit information at the encoding stage, but they also enhance consistency in neural codes, which improves readout. The trade-off of these two effects defines the overall impact of correlations on task performance. Strikingly, we found that noise correlations can enhance task performance despite limiting the information capacity of a neural population.
Much work has emphasized that the information-limiting effect of correlations in sensory areas may be a bottleneck for behavioral performance1,6,7. A largely separate set of theoretical and biophysical work has alternatively proposed that correlations improve the propagation of neural activity13,14,16,17,30. However, whether the advantages of correlations for signal propagation can overcome their information-limiting effect has not been fully clarified. Theoretical work on signal propagation has seldom specified whether the transmitted activity is informative17, and its connection to behavior remains unclear. Recent work has proposed that information-limiting across-neuron correlations may benefit information propagation in the presence of output non-linearities17. Our models extend these results by identifying the biophysical conditions for which across-time and across-neuron correlations overcome their information-limiting effect by increasing the efficacy of information transmission. Experimental support for a role of correlations in facilitating the readout of population information to aid behavior has also been limited31,32. Although a recent study has suggested a beneficial role of correlations by reporting higher correlation levels during correct behaviors31, these effects have not been reported when correlations limit information encoding. Remarkably, in PPC data and in the biophysical model presented here, the advantages of correlations for signal readout were large enough to compensate and overcome their negative encoding effects. Moreover, both our experimental and modelling results revealed a key computation underlying this effect: the amplification of the readout of stimulus information when neural activity is consistent across neurons or time.
Here we developed a formalism to address how the information-limiting effects of correlations on encoding and their benefits for signal readout intersect. Our approach provides a generally applicable framework to dissect the contribution of correlated neural activity to perceptual behaviors. We anticipate that this approach can be applied to different tasks and brain areas. Sensory and association cortices differ in the magnitude of their correlations, with higher correlations in association areas19. This difference could relate to the potential functions of each area, and our initial observations between PPC and AC suggest that the best trade-off between the effect of correlations on encoding and readout may also vary across areas. In sensory cortices, a major function may be to encode rapidly changing and high-dimensional sensory features regardless of whether they are used for the immediate behavior at hand. In this case, weaker correlations may be advantageous to lessen information-limiting effects, and a readout sensitive to consistency for propagating the signals may be less critical. This view is compatible with reciprocal relationships between noise correlation levels and behavioral performance in sensory cortices1. In contrast, because association cortices are closer to behavioral output, they may only need to encode a moderate amount of behaviorally relevant sensory information, but this information should have a strong impact on behavior. In these areas, higher correlations could be beneficial because the consequence of reducing encoded information is small, whereas the ramifications of failing to propagate signals to drive behavior is higher. Thus, in association areas, the best tradeoff may involve some redundancy in the neural representation coupled with a readout mechanism that uses this redundancy to enhance signal propagation to inform choice, as we found here. We anticipate that our formalism will allow the design of causal tests of the actual readout used in the brain during perceptual discrimination tasks, such as with holographic perturbations33.
Noise correlations can reflect interactions between cells, shared covariations due to common inputs, general fluctuations in behavioral state or network excitability, or variations with stimuli within the same category2. Previous work and our simulations (Supplementary Mathematical Notes S6, Extended Data Fig. 9) show that positive information-limiting correlations (such as those observed in PPC) can be created by shared common inputs34–37 or stronger excitatory connectivity between neurons with similar stimulus tuning35,36, features which have been reported in cortical circuits38,39. Although our present data cannot disambiguate between these possibilities, this shared variability, regardless of its origin, acts as noise for decoding, because it cannot be reduced by integrating information over more cells or longer times, but it also helps signal propagation by generating more consistent neural representations. Thus, our conclusions are expected to hold regardless of the biophysical origins of the observed noise correlations.
Many studies of neural coding implicitly or explicitly assume that the readout of sensory information is optimal and interpret neural codes with higher sensory information as being more relevant for perception6,28,29. Part of the reason is that the presence and shape of non-optimality are unknown. If the readout is not optimal, then neural codes with higher information are not necessarily the most relevant ones for perception. Our data suggest that stimulus information in population activity is not used optimally to produce accurate behavioral choices. Our work provides a measure of both the nature of readout non-optimality and its implication for the behavioral relevance of a neural code. Previous work has shown that even simple stimulus decoders of population activity trained sub-optimally to decode separately single-cell activity and then joined together can decode stimulus information accurately40–42. Together with our results, this evidence suggests that correlations do not necessarily complicate the decoding of sensory information and may offer advantages for turning sensory information into appropriate behavioral choices.
Methods
No statistical methods were used to predetermine sample size of imaging experiments in mice. The experiments were not randomized. The investigators were not blinded to allocation during experiments and outcome assessment.
Subjects, behavioral task and two-photon imaging
This study represents an independent analysis of mouse calcium imaging experiments described previously19,21 and publicly available43,44. A brief summary of the experimental procedures is provided here. We refer to Refs 19,21 for full details. All experimental procedures were approved by the Harvard Medical School Institutional Animal Care and Use Committee.
Both experiments used a modified version of a previously described visual virtual reality system18. Head-restrained mice ran on a spherical treadmill, while images of a virtual maze were projected on a half-cylindrical screen. Forward/backward translation in the maze was controlled by treadmill changes in pitch. Rotation in the virtual environment was controlled by roll of the treadmill. The virtual maze was constructed using the Virtual Reality Mouse Engine (VirMEn) in MATLAB45.
Sound localization task dataset
Imaging data were acquired from five male C57BL/6J mice (The Jackson Laboratory), aged 6–8 weeks at the initiation of behavioral task training. Imaging began 4–6 weeks after viral injection and continued for 4–12 weeks.
Mice ran down the stem of the virtual T-maze, while sound stimuli were delivered from 8 possible locations (−90°, −60°, −30°, −15°, +15°, +30°, +60°, +90°) using four electrostatic speakers positioned in a semicircular array, centered on the mouse’s head. The sound stimulus was activated when the mouse passed an invisible spatial threshold at ~10 cm into the T-stem. The stimulus was repeated after a 100 ms gap; repeats continued until the mouse reached the T-stem. Task difficulty was modulated by the direction of the incoming stimulus. To receive a reward (4 μl water), mice had to judge the location of sound stimuli to be either on the left or right, and to report their decisions by turning left or right at the T-intersection. A “reward tone” was played as the water reward was delivered on correct trials (when the mouse had reached ~10 cm into the correct arm of the T-maze), and a “no reward tone” was played when the mouse reached ~10 cm into the incorrect arm on error trials. The inter-trial interval was 3 s on correct trials and 5 s on error trials. Mice performed ~200 trials (range, 125–251) per session.
Imaging was performed on alternating days from AC and PPC on the left hemisphere (PPC centered at 2 mm posterior and 1.75 mm lateral to bregma; AC centered at 3.0 mm posterior and 4.3 mm lateral to bregma). In each session, ~50 neurons (range, 37–69) were simultaneously imaged using a two-photon microscope (Sutter MOM) operating at 15.6 Hz frame rate and at 256 × 64 pixel resolution (~ 250 μm × 100 μm). ScanImage (version 3, Vidrio Technologies) was used to control the microscope. Imaging data were acquired at depths between 150 and 300 μm, corresponding to layers 2/3. Seven AC and seven PPC fields of view from five mice were analyzed.
Evidence accumulation task dataset
Imaging data were acquired from five male C57BL/6J mice (The Jackson Laboratory), aged 8–10 weeks at the initiation of behavioral task training. Imaging began at least 4 weeks after viral injection and was continued for up to 12 weeks.
Mice run down the stem of a virtual T-maze with predominantly gray walls, encountering six visual cues (white wall segments with black dots) at fixed locations. Each cue appeared on either the left or right wall, with only one cue visible at a time. To receive a reward (4 μl 10% sweetened condensed milk), mice had to determine whether more cues were presented on the left or the right and, after a short stretch of maze without additional cues (90 cm), turn at the T-intersection toward the direction with more cues (left for 6–0, 5–1, 4–2 trials; right for 2–4, 1–5, 0–6 trials). Task difficulty was modulated by varying the difference between the number of left and right cues (net evidence). The sequence of cues was determined randomly for each trial of a given net evidence. On trials having zero net evidence (3–3 trials), a random location was rewarded. Inter-trial interval duration was 2 s for correct choice and 4 s for incorrect choice. Mice performed ~300 trials (range, 231–414) in a typical session.
Imaging data were acquired from the left PPC (PPC centered at 2 mm posterior and 1.75 mm lateral to bregma). In a given session, ~350 neurons (range, 188–648) were simultaneously imaged using a custom-built two-photon microscope operating at ~30 Hz frame rate and at 512 × 512 pixel resolution (~700 μm × 700 μm). The microscope was controlled by ScanImage (version 5; Vidrio Technologies). Imaging data were acquired at depths between 100 and 200 μm below the dura. Eleven fields of view from five mice were analyzed.
Imaging data processing
After motion correction46, correlations in fluorescence time series between pixels within ~60 μm were calculated. Fluorescence sources (putative cells) were identified by applying a continuous-valued eigenvector-based approximation of the normalized cuts objective to the correlation matrix, followed by K-means clustering segmentation (see Refs19,21). To estimate potential neuropil contamination, the cell body fluorescence signal was regressed against the signal from surrounding pixels during the imaging frames when the cell of interest was not active, and then neuropil contamination was removed during the ΔF/F calculation by subtracting a scaled version of the neuropil signal from the cell body signal. All fluorescence traces were deconvolved to estimate the relative spike rate in each imaging frame47. The deconvolution alleviated the possible artificial lengthening of time scales of across-time correlations due to slow calcium transients. The time scales of single neuron activity of the deconvolved signal were ~200 ms19,21, much shorter than the time scales of across-time correlations (~> 1s), and were shorter in AC than in PPC19, suggesting that the deconvolution was effective at preventing major artificial inflations of across-time correlations time scales.
Data inclusion and task epoch selection for encoding and readout analyses
Sound localization task dataset
For the analysis of across-time correlations in PPC, population activity data were temporally aligned to the imaging time frame of the turn, defined as the frame in which the mouse entered the short arm of the maze. Since it is reasonable to assume that the animal computes its choice after the stimulus presentation but before the turn, the analysis focused on the 39 frames preceding the turn frame (this number of frames was chosen because it covered the maximum portion of the pre-turn period that was commonly available across all recording sessions). One of the seven PPC recording sessions used in our previous published work19 was excluded due to the large unbalance of left/right stimuli that were presented to the mouse across trials in that session, which would result in too few trials available for our analyses.
For the analysis of across-time correlations in AC, population activity data were temporally aligned to the imaging time frame of the first auditory stimulus presentation, and the analysis focused on the 50 frames after that frame (this number of frames was chosen because it covered the maximum portion of the post-stimulus period that was commonly available across all recording sessions). AC neural data aligned to the turn did not encode a sufficient amount of stimulus information for following analyses. One of the seven AC sessions used in our previous published work17 was excluded due to the large unbalance of left/right stimuli that were presented to the mouse across trials in that session.
Evidence accumulation task dataset
PPC population activity data were first grouped into spatial bins (3.75 cm/bin) covering the whole T-maze (long and short arm) by averaging population activity first in each bin (2 or 3 imaging frames per bin per trial) and then over epochs of 4 spatial bins each (about 200 ms). We used the same 10 epochs defined in Ref 21. We plotted results of population activity data recorded in the Early Delay and Late Delay epochs. During the delay epochs, the cue presentation was completed but the animal had not yet committed to a final turn (these epochs correspond to the four spatial bins beginning respectively 15 and 37.5 cm after the offset of the final cue). Therefore, it is reasonable to assume that the animal’s decision is formed in these epochs. All 11 sessions in the original work19 were used. We did not use trials with zero net evidence (<10% trials in 2/11 sessions).
Selectivity of single cells to stimulus category
For Fig. 1c, h, we computed the selectivity of single cells to stimulus category. For the sound localization task, stimulus category corresponds to the direction of incoming auditory stimuli. Each stimulus category comprises four different sound locations (left: −90°, −60°, −30°, −15°; right: +15°, +30°, +60°, +90°). For the evidence accumulation task, stimulus category corresponds to the side of the maze where the majority of the visual cues were presented (left: 6–0, 5–1, 4–2 trials; right: 2–4, 1–5, 0–6 trials).
The selectivity index18 (SI) was quantified as:
| (1) |
Cells with selectivity index greater (smaller) than zero were classified as right-preferring (left-preferring) cells.
Pairwise noise correlations
For each neuron pair and time points pair in the trial epoch selected for analyses, we quantified across-time pairwise correlations as the Pearson correlation between the activity of neuron 1 at time t1 and the activity of neuron 2 at time t2 across trials with the same stimulus category. Results were averaged across all neuron pairs, all time point pairs with the same time lag, across stimuli and across trials subsamples. We quantified across-neuron pairwise correlations as the Pearson correlation between neuron pairs recorded in a single session, across trials sharing the same stimulus category. Results were averaged across stimuli, across trials subsamples, and across Early Delay and Late Delay Epochs. We quantified noise correlations separately for correct and error trials. To control for differences in trial numerosity, we subsampled trials to equalize the number of correct and error trials in each recorded session. Results were averaged over 10 instantiations of random subsampling.
Population-wise noise correlations
We quantified the across-neuron population-wise correlations by performing PCA on the population response to all trials sharing the same stimulus category. The population-wise noise correlations ν was defined as the fraction of variance explained by the first PC of the whole population activity (concatenated population activity of the two pools for across-neuron correlations, concatenated activity of the two considered time points for across-time correlations). For across-neuron correlations, results were first averaged across stimuli, then across trials subsamples and eventually pooled across Early Delay and Late Delay Epochs. For across-time correlations, results were averaged first across all time point pairs sharing the same lag between each other, then across stimuli and finally across trials subsamples. We quantified across-time and across-neuron population-wise noise correlations1 separately for correct and error trials. To control for differences in trials numerosity, we randomly subsampled trials to equalize the number of correct and error trials in each recorded session. Results were averaged over 10 instantiations of random subsampling. Population-wise noise correlations, when computed on a small number of trials, suffered from finite-sampling bias. Since we equalized trials between correct and error choices, the comparison was not affected. However, to map the experimental data to the model, we corrected for the finite-sampling bias. We estimated the bias by computing the population-wise noise correlation index for randomly selected subsamples of trials with progressively increasing size (from 5 to the maximum number of available trials) and then using polynomial extrapolation.
Analysis of stimulus encoding and consistency
For encoding and consistency analyses, we considered information about stimulus category. Information about stimulus category carried by population activity was extracted by decoding the most likely stimulus category presented to the animal in each trial using a C-Support Vector Machine (C-SVM) classifier with a linear basis function kernel48, implemented using the libsvm library49. For each imaging session, we first subsampled trials randomly such that the left/right stimulus categories were equally represented in the data (sound localization task dataset: no more than 13% of removed trials per session; evidence accumulation task dataset: no more than 15% of removed trials per session). Then, we randomly split the remaining trials 10 times into 50/50 training/testing sets, such that left and right stimulus categories were equally represented in both training and testing sets. For each trial split, we trained the C-SVM on the training set and we tested on the test set, which was left out of the fitting procedure. The regularization hyperparameter (C) was selected by maximizing the 3-fold cross-validated decoding accuracy in the training set. For the analyses that required computing a posterior probability of the decoded stimulus given the observed population activity, we used Platt scaling to calibrate posterior probabilities on the binary outputs of the C-SVM50.
We decoded, again using the libsvm library49, stimulus category considering also non-linear classifiers: we decoded the most likely stimulus category using a C-SVM with radial and quadratic basis function kernels.
For the across-time correlations analysis, for any considered pair of time points, we defined the activity in trial as consistent if the stimulus decoded from the population activity at each of the two time points coincided. For the across-neuron correlations analysis, we first split the neuronal population recorded in each session into two randomly-selected, equally-sized pools of neurons. 100 random splits were performed. For each random split, we defined the activity in trial as consistent if the stimulus decoded from the population activity of each individual pool coincided.
Quantifying the angle γ between the signal and noise axes
We quantified the angle γ (∈ [0, π/2]) between the direction of maximum stimulus variation (signal correlations axis) and the direction of maximum noise variation (noise correlations axis)25,26 in the neural population response space. The signal correlations axis was defined as the vector connecting the mean responses to the two stimuli. The noise correlations axis was computed as the direction of the first PC obtained by applying PCA to all single-trial responses at fixed stimulus category. The angle between signal correlation and noise correlation axes was computed separately for each stimulus categories (γs=−1, γs=1) and then averaged as follows:
| (2) |
This weighted average of the stimulus-specific angles facilitates comparisons between data and model (Supplementary Mathematical Notes S4).
The computation of γ uses the population’s covariance matrix. Since in the accumulation evidence task the dimensionality of the dataset (~350 neurons) was larger than the number of trials per session (~200), we first performed a PCA to keep only those components that explained 95% of the total variance (the dimensionality of the dataset was reduced to 59 ± 18 components, mean ± sem across sessions). This did not change substantially the values of the angles (we obtained a median value of the signal noise angle of 0.21π in Fig. 1j with the 95% variance cutoff whereas we would have obtained a value of 0.25π had we used all neurons without variance cutoff, with both values inside the information-limiting region). However, we used the variance cutoff because it led to better stability of individual results when removing random fractions (10%, 20%,..) of data.
For across-time correlations, γ was computed in the space defined by the concatenated population activity at the two time points considered for the analysis. For across-neuron correlations, γ was computed in the full-dimensional space defined by the population responses, and did not depend on the random split in two pools.
Mathematical model of encoding and readout with two N-dimensional neural features
We developed a simple model of how two N-dimensional neural activity features r1 and r2 (each representing the firing rates of two different pools of N neurons each for across-neuron correlations, or the population activity of the same pool of N neurons at two different times for across-time correlations) encode information about a binary stimulus, and how this information is read out to inform choice in a simulated stimulus discrimination task.
Neural encoding (stimulus-response) model
The encoding (stimulus-response) models describes the neural activity of the two N-dimensional features (r1, r2) in response to two stimuli (s = −1, s = 1).
We chose a simple model accounting for the observation that average pairwise correlations in PPC neural population were positive (Fig. 1b,g). Distributions of stimulus-specific neural responses for each N-dimensional feature were modelled as N-dimensional multivariate Gaussians with mean and stimulus-independent covariance given by:
| (3) |
where s indexes the stimulus category and k the neural feature (k = 1,2), ρwithin parametrizes the strength of correlation between neurons within the same feature, and wsingnal,k represents the signal correlation direction in the N-dimensional space of each feature. For simplicity, we assumed equal variance σ for each neuron s and equal covariances for the two pools k=1,2. The signal-noise angle γ was the same across stimuli in this model.
The joint population activity was simulated as a 2N-dimensional multivariate Gaussian with mean and covariance given by:
| (4) |
wsingnal indicates the normalized signal correlation direction in the 2N-dimensional space, JN×N indicates the unit matrix and ρ determines the correlation between the two neural features. This correlation matrix allowed us to mimic the effect of real-data shuffling procedure of selectively removing correlations between the two N-dimensional features, while keeping intact single-features correlation structures, by simply setting ρ to zero. For simplicity we also set ρ = ρwithin for correlated activity. The means of the two response distributions were symmetrically located around the origin of the 2N-dimensional space, at distance . Together, the parameters and σ control the overlap between the two stimulus-specific response distributions.
The first eigenvector of the covariance matrix, representing the noise correlation axis direction, is given by , with eigenvalue λ1 = (Nρ + 1 − ρ)σ2. The other 2N − 1 eigenvectors form an orthonormal basis with the vector wnoise and the 2N − 1 corresponding eigenvalues are given by λi = (1 − ρ)σ2. The value of the largest eigenvalue λ1 normalized by the sum of all eigenvalues (total response variance) yields the population-wise noise correlation index ν as a function of the pairwise correlation index ρ:
| (5) |
We denote with
| (6) |
the angle between the signal correlations and the noise correlation axes in the 2N-dimensional space. The signal correlations axis orientation wsingal was randomly sampled across all vectors satisfying Eq. (6) for the fixed γ and wnoise.
We quantified the amount of stimulus information carried by the simulated responses (r1, r2) as the accuracy of a linear decoder of stimulus identity applied to the responses. We then applied the same classifier to the responses r1 and r2 of each pool separately. For the simulations in Fig. 2, Extended Data Fig. 3 we set N=1, , σ = 0.2, ρ = 0.8 and we performed 200 simulations with 5,000 trials per stimulus (Fig. 2) or 10 simulations with 50,000 trials per stimulus (Extended Data Fig. 3). For the simulations in Fig. 3 and Extended Data Fig. 4 we set N=20,10, , σ = 0.2 (consistent with the value found for both experimental datasets. Across-time: σ = 0.195 ± 0.005, mean±sem across n_t=39 time points and n=6 sessions; across-neuron: σ = 0.230 ± 0.012, mean±sem across Early and Late Delay Epoch and n=11 datasets), and we performed 100 simulations with 300,000 trials per stimulus each.
Model of choice generation in a simulated discrimination task
We simulated the process of generating a binary choice in each trial from neural activity through a logistic regression readout model:
| (7) |
Where indicates the stimulus decoded from the concatenated activity of the two N-dimensional neural features; con is a “consistency” binary variable that is 1 if the stimuli decoded individually from each neural feature are the same, and 0 otherwise; x indicates the entire set of predictors .
The model coefficients β0, , βi1 and βi2 control the relative impact of the different model predictors on the simulated choice. The values for the model coefficients were set as follows. We first defined a consistency modulation index η, ranging from 0 to 1, to control the relative strength of neural consistency in the readout. We then derived the readout efficacy, which we defined as the probability of conversion from to c, for each of the four possible combinations of predictors values, from the modulation index η and a reference readout efficacy as:
| (8) |
where takes values between .5 and 1. For the simulations in Fig. 2, Fig. 3, Extended Data Fig. 2, Extended Data Fig. 3 and Extended Data Fig. 4, we arbitrarily set (0) = (1) = 0.75. Given the readout efficacy values from Eq. (8), we used Eq. (7) to compute the model coefficients corresponding to the chosen modulation index η.
Logistic regression of the mouse’s choice
To study how features of recorded neural population activity related to the mouse’s choices, we fitted to the recorded neural activity a logistic regression of the choice (left/right turns) made in each trial.
Our readout model explicitly focuses on the part of the choice signal in neural population activity that relates to the encoded stimulus information (as opposite to the part of the choice signal that is independent of the stimulus information). It differs from other quantifications of choice signals (e.g. choice probability51,52) using either “zero-signal” trials containing no sensory evidence or pooling data across stimulus levels after corrections to remove the stimulus modulation, to infer specifically choice signals in neural activity beyond stimulus-related modulation. Our model also focuses on how the correlation-induced consistency of neural information affects choices, and differs from other models10 focusing only on how the total sensory evidence in neural activity influences choices.
Our logistic regression readout model was implemented as follows. For each trial, we considered the choice c made by the mouse (c = 1: left; c = −1: right), the presented stimulus s (s =1 left, s =−1 right), and the neural population activity for each pair of time points (across-time correlations analysis) or for each pair of randomly-selected neuronal pools (across-neuron correlations analysis). For each session, trial split, and pair of time points or neuronal pools, we fitted the following logistic regression:
| (9) |
where (: left, : right) represents the stimulus decoded from the concatenated activity of two time points or neuronal pools; con is a binary variable that is 1 if the stimuli decoded individually from each time point or neuronal pool are the same, and 0 otherwise; x indicates the combination of neural and non-neural (s) predictors.
Logistic regression fitting was implemented using statsmodel Python module53. The logistic regression was fit on the testing set using L1-regularized maximum likelihood. The regularization hyperparameter (λ) was selected by maximizing 3-fold cross-validated fraction of deviance explained.
For control analyses, we fitted mouse’s choices with more complex choice regressions that included other predictors on top of those described in Eq. (9).
To discern the genuine role of across-time neural consistency (con) in explaining the mouse’s choices from that of across-time behavioral consistency (conb), we fitted a logistic regression which included additional behavioral consistency-dependent predictors:
| (10) |
We performed this control analysis for three behavioral parameters of interest that were measured during the experiments: the lateral running velocity, lateral position and view angle of the mouse in the virtual environment (Extended Data Fig. 6). Two values of lateral running velocity or lateral position at two different time points were defined to be consistent whenever their sign was the same; two values of view angle at two different time points were defined to be consistent whenever they were both higher or both lower than 90°.
We also fitted mouse’s choices with a more sophisticated logistic regression where the discrete binary variable in Eq. (9) was replaced with the continuous value of the decoder stimulus posterior probability p(s = left|r). Because this model accounts also for the magnitude of stimulus information and not only for the identity of the decoded stimulus, we used it to account for possible confounders due to differences in overall stimulus information between consistent and inconsistent trials (Extended Data Figure 5).
Predictive performance was quantified as the fraction of deviance explained (FDE), evaluated with 3-fold cross validation. For each fold, we computed the log-likelihood l of the test data given the values of the β coefficients of the training data. To calculate a reference null value for the log-likelihood, we computed the log-likelihood l0 of the test data given the value of the coefficient β0 of an intercept-only regression fit on the training data. The FDE was then defined as:
| (11) |
Estimating the impact of across-time and across-neuron correlations on task performance
To estimate the impact of across-time and across-neuron correlations on mouse’s task performance, we generated synthetic choices using the experimentally-fit choice regression of Eq. (9). As input to the regression, we provided either predictors extracted from the real recorded neural data, which included across-time and across-neuron correlations, or predictors extracted from hypothetical neural data whose correlations were disrupted by shuffling. We used this analytical approach because current experimental methods cannot remove correlations during task performance, and thus we had to estimate effects with post-hoc removal of correlations.
Task performance p(c = s), the probability that the choice c matches the presented stimulus s, was estimated by computing (using the choice’s logistic regression) the probabilities p(x) of all possible combinations of predictors values X, multiplying them with the corresponding readout probabilities p(c = s|x) obtained from the logistic choice regression, and then summing over X:
| (12) |
The same readout probabilities p(c = s|x) were used for the computation of task performance from both real and shuffled neural data.
We isolated the part of task performance that can be attributed to the (correlated or shuffled) neural activity by subtracting from the total estimated task performance a baseline non-neural estimated task performance. The latter was computed by applying Eq. (12) after shuffling the values of neural predictors across trials, while keeping the relationship between non-neural predictors and mouse’s choices fixed.
Computation of readout efficacy of the transformation from stimulus information to choice
We termed “readout efficacy” the probability that in a given trial the choice c matched the stimulus decoded by neural activity. We computed this probability as:
| (13) |
where X represents the set of all possible combinations of predictors values and are obtained from the logistic choice regression.
To generate the readout maps in Fig. 4d, h we computed, separately for consistent and inconsistent trials, readout efficacy as deviation from the average probability of choice being left or right when the presented stimulus is left or right:
| (14) |
In Eq. (14), X represents the set of all possible combinations of predictors values and .
Matching enhanced-by-consistency and consistency-independent readouts in terms of efficacy
To quantify the impact on task performance of the enhanced-by-consistency experimentally-measured readout, we compared the task performance predicted by the experimentally-fit choice regression to the one predicted by a consistency-independent choice regression of the form:
| (15) |
For a fair comparison, the values of the coefficients , and were chosen so that the two readouts were matched in terms of readout efficacy (Eq. (13)). To compute the values of the coefficient of the consistency-independent choice regression in Eq. (15), we imposed the following conditions:
| (16a) (16b) (16c) |
then plugged Eq. (9) and Eq. (15) into Eq. (16a) and Eq. (16b), and solved for and .
Shuffling procedure to disrupt across-time or across-neuron noise correlations
Across-time correlations between population vectors at different time points were removed by shuffling trial identities independently for each of the two population vectors within trials with the same stimulus category. With this procedure across-time signal correlations were maintained, while across-time noise correlations were disrupted. Single-cell autocorrelations were also disrupted. Across-neuron correlations between two neuronal pools were disrupted by shuffling trial identities independently for each pool within trials with the same stimulus category. With this procedure signal correlations were maintained for all pairs of neurons, noise correlations between neurons pairs in two different pools were disrupted, and noise correlations of neuron pairs within the same pool were maintained. Shuffling was performed separately for the training and the testing set.
Biophysical model of consistency-modulated information transmission
We modelled biophysical signal propagation using a integrate-and-fire model neuron receiving inputs from a population of neurons exhibiting correlations across neurons or time.
Our model consisted of an input population, corresponding to PPC population activity in our data, projecting in a feed-forward manner to a single output (or “readout”) neuron. We simulated responses of the input population to two different external stimuli (corresponding to the stimulus categories in our data). Stimulus s = − 1 (s = + 1) was the one with the lowest (highest) mean rate. We simulated multiple trials for each stimulus. In each simulated trial, the activity of the readout neuron was decoded by an optimal linear classifier (readout neuron activity lower or higher than the optimal decoding boundary is decoded as stimulus −1 or +1 respectively), and the outcome of the decoding algorithm represents the result of the information transmission process through the synapses (which can be compared to the behavioral choice in our neural data) in each trial. We modelled the readout neuron as an input-driven leaky integrate-and-fire neuron with dynamics given by:
| (17) |
where τm represents the membrane time constant of the neuron and Vr is the resting value of its membrane potential V. The rightmost term of Eq. (17) describes the external drive to the readout neuron coming from two input units (corresponding to two different neural pools). denotes the set of spike times of each input unit. For each input spike received by the output unit, the output membrane voltage V instantaneously increases of a fixed amount w.
To examine the effect of across-pool (analogous to the across-neuron correlations in PPC data) and across-time correlations between the two input units on the activity of the output neuron, we generated correlated input spike trains and as follows. First, we generated stochastic input firing rates for the two pools and with across-pool correlations by modulating the amount of shared noise ξc between the two units according to
| (18) |
where is the mean activity of input pool i in response to stimulus s, is proportional to the derivative of the mean activity with respect to the stimulus, and σ equally modulates the variability of the input units. The values of ξ1, ξ2 (private noise) and ξc (shared noise) were independently drawn from Gaussian distributions with zero means and unit variance. The parameter α, ranging from 0 (fully uncorrelated activity) to 1 (fully correlated activity) modulates the amount of shared variability between the two input units. Eq. (18) generates correlations aligned with the derivative of the mean activity with respect to the stimulus Δμ, which are therefore information-limiting7. Additionally, Eq (18) ensured that varying α changed only the amount of across-pool correlation but not the variance of the activity of each individual input unit.
We created across-time input correlations by filtering the input activity with a low-pass filter with time constant τC:
| (19) |
We then generated the spike trains of the input units as inhomogeneous Poisson processes with firing rates given by and .
Data availability
The sound localization task data that support the findings of the current study can be downloaded at https://gin.g-node.org/MMoroni/PPC_AC_2p_sound_localization (see Ref44).
The evidence accumulation task data that support the findings of the current study can be downloaded at https://gin.g-node.org/MMoroni/PPC_2p_evidence_accumulation. (see Ref43).
Code availability
The code for the biophysical information transmission model (Fig. 6) is available for download at: https://github.com/gbondanelli/BiophysicalReadout.
The code for the encoding and readout model (Figs 2,3) is available for download at: https://github.com/moni90/encoding_readout_model.
The code for data analysis is available from the corresponding authors upon reasonable request.
Extended Data
Extended Data Figure 1: Response properties and across-time and across-neuron correlations in PPC during perceptual discrimination tasks for different trials categories.
Panels a-l refer to PPC data during the sound localization task and across-time correlations. a-c, Accuracy of a linear decoder of the stimulus applied to the joint population activity at two different time points, for recorded (black) or trial-shuffled (gray) population vectors, for “easy” trials with high level of sensory evidence (a, sound locations further from the midline than 45 deg), “difficult” trials with low level of sensory evidence (b, sound locations closer to the midline than 45 deg) and behaviorally correct trials only (c). Errorbars report mean ± SEM across n=6 sessions and all time point pairs within the specified lag range. For all comparisons, P=10−4, two-sided permutation test. d-f, Distribution of the signal-noise angle γ (over n=6 sessions and all time point pairs within a 2 s lag), for “easy” trials (d), “difficult” trials (e) and behaviorally correct trials only (f). Boxplots show the median (line), quartiles (box) and whiskers extend to ±1.5*interquartile range. Red dotted line: theoretical value of the critical angle γCC between the information-limiting and information-enhancing regime. g-h, Pairwise noise correlations in time-lagged activity, for correct and error trials, for “easy” (g) and “difficult” (h) trials. Errorbars report mean ± SEM across n=6 sessions, all time point pairs within the specified lag range and all cell pairs. For all comparisons, P=10−4, two-sided permutation test. i-j, Population-wise noise correlations in time-lagged activity, for correct and error trials, for “easy” (i) and “difficult” (j) trials. Errorbars report mean ± SEM across n=6 sessions and all time point pairs within the specified lag. In i, P=0.0380 for Lag 0–1s, n.s. P=0.1510 for Lag 1–2s, two-sided permutation test. In j, P=0.0480 for Lag 0–1s, P=0.001 for Lag 1–2s, two-sided permutation test. k, Relation between pairwise and population-wise noise correlations. Each dot represents the average across n=6 session and all time points with a given lag. The black line indicates the linear fit. l, Accuracy of a linear, quadratic and radial basis function SVM decoder of stimulus identity applied to joint population activity at two different time points for real recorded population vectors. Errorbars report mean ± SEM across n=6 sessions and all time point pairs within the specified lag range.
Panels m-x refer to PPC data during the evidence accumulation task and across-neuron correlations. m-o, Same as in a-c. p-r, Same as in d-f. s-t, Same as in g-h. u-v, Same as in i-j. For the evidence accumulation task, “easy” and “difficult” trials were defined as trials with net evidence ≥4 or <4 respectively. In panels m-v errorbars report mean ± SEM across n=11 sessions, Early and Late Delay epochs and 100 pairs of neuronal pools. In m-o, for all comparisons, P=10−4. In s, P=0.0120. In t, P=9×10−4. In u, P=0.001. In v, P=0.8641. For all comparisons, two-sided permutation test. w, Same as in k. Each dot represents the average across n=11 sessions for a given delay epoch. x, Same as in l, with errorbars reporting mean ± SEM across all n=11 sessions, Early and Late Delay epochs, and 100 pairs of randomly split neuronal pools.
Extended Data Figure 2: Parameter exploration of the two-pools encoding readout model and comparison with PPC data.
a, Population-wise noise correlations ν as a function of the pairwise noise correlations ρ, for different values of the active neurons 2N (N neurons per pool). Here we assumed that all neurons were active (M = 2N). For ρ = 0, the population-wise correlation is equal to ν = 1/(2N) b, Population-wise noise correlations ν as a function of the average over all pairs of pairwise noise correlations ⟨ρ⟩ (where ⟨⋅⟩ denotes the average over neuron pairs), for different fraction of active neurons 2N/M (total number of neurons given by M = 2N + K). By decreasing the fraction of active neurons, the constant of proportionality between ν and ⟨ρ⟩ increases. c, Blue line: critical signal-noise angle γC below which correlations are information-limiting in the model, as a function of the number of neurons per pool N, computed using the experimental value of the PPC across-time population-wise correlation for the sound localization task. Red line: critical value γC,BP for the angle above which the task performance in correlated data is higher than that in shuffled data. The experimental distribution of PPC signal-noise angles is reported for comparison (n=6 sessions and all time point pairs within a 2s lag). Horizontal gray line indicates the median. Box edges indicate the first and third quartile. d, Same as c for the evidence accumulation task and across-neuron PPC correlations.
Extended data Figure 3. Extension of the encoding readout model to multiple features, multiple stimuli per category and multiple categories.
a, Left: schematic of the encoding readout models with two neural features, two categories, two stimuli per category. Each axis represents the activity of a single feature. Colored ellipses: 95% confidence intervals for the simulated neural responses to two different stimuli (s=1, s=−1). Dashed black line: stimulus axis. Gray shaded areas: regions of the response space in which stimulus information is encoded consistently across pools and the behavioral readout efficacy is enhanced. b, Difference in stimulus classification accuracy between correlated and shuffled responses computed using a linear decoder applied to the joint population activity across the two features, as a function of the signal-noise angle γ. c, Difference in task performance between correlated and shuffled responses predicted by an enhanced-by-consistency readout of simulated neural activity, as a function of the signal-noise angle γ. In panel b-c, the red dashed lines delimit the parameter range where correlations are information-limiting but task performance is enhanced for correlated data. Data are mean ± SEM over n=10 simulations with 50,000 trials each, with , ρ = 0.8, σ = 0.2 η = 0.7. d-f, Same as in a-c, but for an encoding model with two neural features, two categories, and multiple (n=2) stimuli per category. Within each category, stimulus-specific distributions are symmetrically displaced on either side of the between-category signal axis. Within each category, the noise axes of the individual distributions are aligned to each other and aligned to the vector of differences of mean activity. Data are mean ± SEM over n=10 simulations with 50,000 trials each. We set half the distance between the centers of the distributions of the two categories to , and the distance between the centers of the distributions of individual stimuli within each category to d2 = 0.3. In simulations, we set ρ = 0.8, σ = 0.13 (for the distributions of individual stimuli within each category), η = 0.7. g-i, Same as in a-c, but for an encoding readout model with two pools and multiple (n=3) stimulus categories. Mean responses to the three stimulus categories are aligned along a unique signal axis, and the noise axes of individual distributions form an angle γ with the stimulus axis. Data are mean ± SEM over n=10 simulations with 50,000 trials each, with (distance between the distributions across individual categories), ρ = 0.8, σ = 0.2 (for individual distributions), η = 0.7. j-l, Same as in a-c, for a model with three one-dimensional neural features. Neural activity is considered consistent if the same stimulus is decoded from all three features. Data are mean ± SEM over n=10 simulations with 50,000 trials each, with , ρ = 0.8, σ = 0.2, η = 0.7.
Extended Data Figure 4: Exploration of the parameter space of the encoding readout model.
Same as in Fig. 3, for an encoding readout model with N=10 neurons in each pool. a, Difference in the accuracy of a linear decoder of stimulus applied to correlated and shuffled simulated neural activity for different values of the signal-noise angle (γ) and population-wise correlations (ν). For all panels, black solid line: boundary between a regime with information-limiting correlations and information-enhancing correlations. b, The difference between correlated and shuffled activity in the fraction of trials in which the two neural features encode consistent stimulus information is higher in the information-limiting regime and increases with population-wise correlations strength.
Panels c-e refer to the consistency-independent readout. c-d, Difference in average pairwise correlations (c) and population-wise correlations (d) between trials with correct and incorrect predicted task performance for different combinations of model parameters. e, Difference in task performance predicted by applying the consistency-independent readout to correlated and shuffled simulated neural activity for different combinations of model parameters. For panels c-i, dashed black line: boundary between a regime where task performance is higher for correlated responses and a regime where performance is higher for shuffled responses. The overlap between the continuous and dashed black line indicates that correlations that limits information are also detrimental for behavior.
Panel f-h refer to the enhanced-by-consistency readout (consistency modulation index η = 0.85). f-g, Same as in c-d. With the enhanced-by-consistency readout correlations are higher in correct trials. h, Same as in e. The area between the dashed and the continuous black line indicates a regime where correlations are information-limiting but task performance is higher for correlated responses. Thus, in the parameter range between the two lines, the readout is able overcoming the negative impact of correlations. Dark and light gray dots and ellipses: mean values and range between the 25th and the 75th percentile of the signal-noise angles and population-wise correlations for PPC data from the sound localization task and evidence accumulation task, respectively.
i, Difference in task performance predicted by applying the enhanced-by-consistency readout or the consistency-independent readout with matched readout efficacy for different combinations of model parameters. The enhanced-by-consistency readout yields increased task performance with respect to the consistency-independent readout.
Panels represent the mean over n=100 simulations with 300,000 trials each.
Extended Data Figure 5: The effect of neural correlations on the mouse’s single trial choices cannot be explained by higher stimulus information associated to consistent neural representations.
a, Schematic example showing response distributions along two neural features (r1, r2) to two stimuli (ss = −1: blue, ss = 1: orange). Black dashed line: optimal decoding boundary of a linear decoder trained on the simulated neural responses. The background color represents the linear decoder posterior probability that stimulus s=1 has occurred given the observation of the neural response r = (r1, r2). Intuitively, the farther neural response r is from the decoding boundary, the farther p(s = 1|r) is from 0.5, and the more “informative” r is about the stimulus. Note that, in the example shown, consistent trials have on average higher posterior probability than inconsistent trials, which might represent a confounder for the effect of consistency on mouse’s choices. To control for potential confounders due to differences in the levels of stimulus information between trials with consistent and inconsistent stimulus information, we fitted to the data a readout model that predicted choice using the posterior probability of the stimulus and posterior probabilities consistency given the neural responses, rather than just the decoded stimulus identity (b, f). We further repeated the analyses of Fig. 4 on trials partitioned into those with low (|p(s = 1|r) − 0.5| < 0.16), medium (|p(s = 1|r) − 0.5| > 0.16 ⋀|p(s = 1|r) − 0.5| < 0.32), or high (|p(s = 1|r) − 0.5| > 0.32) “stimulus information” (c-e, g-i).
Panels b-e refer to PPC data during the sound localization task. b, Performance (fraction of deviance explained) in explaining single-trial choice of models using neural predictors based on posterior probabilities. Full model includes all predictors values, comprising stimulus posterior probability and posterior probability consistency. No Cons model neglects neural consistency by shuffling consistency values across trials. c-e, Left (purple dots). Task performance in trials with correctly decoded stimulus is higher when information is encoded consistently than inconsistently. Right (orange dots). The opposite happens for trials with incorrectly decoded stimulus. Thus, stimulus information in neural activity has a larger impact on choices when it is encoded consistently across time, even when subsets of trials having approximately the same posterior are used. For all comparisons in b-e, P=10−4, two-sided permutation test. Errorbars represent mean ± SEM across n=6 sessions and all time point pairs within a 1 s lag.
Panels f-i refer to PPC data during the evidence accumulation task. f, Same as in b. P=6 × 10−4, two-sided permutation test g, Same as in c. h, Same as in d. i, Same as in j. In panels f-i, consistency and mouse choices are computed from the activity of two pools of neurons. For all comparisons in g-i, P=10−4,, two-sided permutation test. In f-i, errorbars represent mean ± SEM across n=11 sessions, Early and Late Delay epochs and 100 pairs of neuronal pools.
From b-i, the fact that information in neural activity informs choice more effectively when it is consistent cannot be explained by differences in overall stimulus information level. Rather, for a given amount of sensory information, more information can be extracted to guide behavioral choices if it is distributed redundantly across neurons or across time.
Extended Data Figure 6: The role of neural consistency in the readout of PPC activity is not due to the consistency of measured behavioral parameters.
Panels a-e refer to PPC neural activity during the sound localization task. To rule out the concern that the impact of across-time consistency of PPC activity on the mouse’s choice does not only reflect the effect of running related parameters (whose temporal consistency may correlate with both the mouse’s choice and the temporal consistency of neural activity), we developed and fit to PPC data a more sophisticated readout model that explicitly includes such contributions in predicting choices. a, The temporal evolution of the decoder posterior probability of left stimulus presentation given the recorded PPC population activity is shown along with the corresponding temporal evolution of a selection of three concurrently-measured behavioral parameters (lateral position, lateral velocity, view angle), for an example left (orange) and right (blue) cue trial. Colored dots indicate two example time point pairs with consistent (t1-t2, dark purple) or inconsistent (t3-t4, light purple) neural information. Colored dots in the first and third row show that neural consistency is not necessarily associated to behavioral consistency (when considering lateral running speed, t1-t2 are behaviorally inconsistent while t3-t4 are behaviorally consistent). b, Schematic representation of the virtual T-maze with corresponding x-y coordinates labelling and mouse’s view angle (for a mouse oriented along the y axis). c-e, Performance (fraction of deviance explained) in explaining (using two population vectors at different points) single-trial mouse choice of models that use both neural and behavioral consistency (c: lateral position, d: lateral velocity, e: view angle). Full model includes all predictors values, comprising neural and behavioral consistency. No Cons model neglects neural consistency by shuffling consistency values across trials. c, P=10−4. d, P=2×10−4. e, P=10−4, two-sided permutation test. Errorbars report mean ± SEM across n=6 sessions and all pairs of time point within a 1s lag.
Results in c-e show that neural consistency still contributed to predicting choices when we added the consistency of running-related variables to the choice regression. This suggests that consistency of the instantaneous PPC population activity across time genuinely influences the behavioral readout of the stimulus information, above and beyond what can be predicted about choice from the consistency of measured behavioral variables.
Extended Data Figure 7: Across-time correlations in AC do not benefit task performance as they do in PPC.
Panels a-h refer to PPC neural activity during the sound localization task. a-h, Summary of the main results of the analysis of across-time correlations in PPC activity (from Fig. 1, Fig. 4 and Fig. 5), useful for the comparison with AC data.
Panels i-p refer to AC neural activity during the sound localization task. i, Pairwise (left) and population-wise (right) noise correlations in time-lagged activity, for correct and error trials. Overall, noise correlations strength is lower in AC than in PPC. j, Distribution of the signal-noise angle γ (over n=6 sessions and all time point pairs within a 2s lag). Boxplots show the median (line), quartiles (box) and whiskers extend to ±1.5*interquartile range. Red dotted line: analytically computed bound between the information-limiting and information-enhancing regime. k, Accuracy of a linear decoder of the stimulus applied to joint population activity at two different time points, for real recorded (black) or trial-shuffled (gray) data. The decoder accuracy is higher in AC than in PPC (fraction correct: 0.676 ± 0.003 in AC, 0.602 ± 0.001 in PPC, P=10−4, two-sided permutation test), compatible with the view that AC is involved in the encoding of sound information. Across-time correlations limit the encoding of stimulus information also in AC, but with a smaller effect than in PPC (average increase in decoder accuracy by shuffling: 0.018 ± 0.001 in AC, 0.026 ± 0.001 in PPC. P=10−4, two-sided permutation test. Equivalent percentage increase of above-chance (i.e. above 50%) decoding performance: 10.5% in AC, 25.5% in PPC). l, Fraction of trials in which stimulus information is encoded consistently across time, for real recorded (black) or trial-shuffled (gray) data. The increase in consistency due to across-time correlations is smaller in AC than in PPC (−0.025 ± 0.001 in AC, −0.064 ± 0.01 in PPC, P < 10−4, two-sided permutation test). m, Performance (fraction of deviance explained) in explaining single-trial choices of several readout models (see Methods). Full model uses all predictors (neural and non-neural). “No Cons” model neglects neural consistency. “No Neural” model neglects stimulus decoded from neural activity and neural consistency. A linear SVM is used to decode the stimulus from neural activity. Across-time consistency in AC provides negligible improvements in behavioral choice predictions when compared to PPC (increase in fraction of deviance explained when comparing the Full with the “No Cons” model: 0.0045 ± 0.0001 in AC, 0.0083 ± 0.0012 in PPC, P=10−4, two-sided permutation test). n, Best-fit coefficients of the Full readout model. AC neural predictors are characterized by low weights. o, Task performance predicted by applying the best-fit readout model to real recorded (black) or trial-shuffled (gray) data. Task performance attributable to recorded neurons is much lower in AC than in PPC (~1% in AC, ~3.5% in PPC). Correlations in AC activity enhance task performance, but the effect is small. p, Task performance predicted by applying to real recorded population vectors the best-fit enhanced-by-consistency (black) and the consistency-independent readout model (green). Task performance attributable to the recorded AC neural activity would not be substantially different if the behavioral readout was consistency-independent. In i, k-p, errorbars report mean ± SEM across all cell pairs (only b-left) and all time point pairs within the specified lag range or within a 1s lag from n=6 sessions. For i, left, P=10−4 for all comparisons, right, P=0.0016 for lag 0–1s, P=0.001 for lag 1–2s. For k, l, P=10−4. For m, ***P=10−4, *P=0.0324. For o, P=0.0191. For p, P=0.0690. All comparisons, two-sided permutation test.
Extended Data Figure 8: Exploration of the parameters of the biophysical model for the enhanced-by-consistency readout.
a, Normalized coefficient of variation (CV) computed for different values of the membrane time constant τm of the readout neuron and EPSP strength w (connection strength from the input to the readout neuron). The mean input rate was set to Rin = 6 Hz. The red parameter region corresponds to the region where the standard deviation of the readout firing rate increases less than the readout mean firing rate with the value of spatial correlations. b, Contour lines corresponding to the parameter values (τm, w) where the normalized CV is equal to 1, for different values of the input firing rate. c, Contour lines for which the normalized CV is equal to unity, in the parameter space defined by the membrane time constant τm and the mean EPSP input in a window τm normalized by the voltage gap ΔV = Vthreshold − Vr, i.e. K = wRinτm/ΔV. Regions of parameters on the left of the contour lines correspond to the parameter values where the standard deviation of the readout neuron increases less than its mean with spatial correlations. d-f, Same as a-c for temporal correlations.
Extended Data Figure 9: Encoding model internally generating correlated activity through recurrent dynamics.
a, Schematic illustrating the basic setup of the encoding recurrent model. Two neurons receive stimulus-dependent feedforward input (which determines the signal correlations) and input noise, and are connected through recurrent synapses with strength w. b, Noise correlations are generated through recurrent connectivity, and depend on the sign of w (for w = 0 responses are uncorrelated). Top: for positive signal correlations, positive (resp. negative) values of the connectivity generate information-limiting (resp. information-enhancing) noise correlations. Bottom: for negative signal correlations, positive (resp. negative) values of the connectivity generate information-enhancing (resp. information-limiting) noise correlations. c-f, Average pairwise noise correlation (over n=10000 random pairs of neurons) (c), decoding accuracy for correlated and shuffled responses (d), difference in decoding accuracy between correlated and shuffled responses for different values of shared noise (e) and average consistency (f) as a function of connectivity strength w. In c,d,f the external input noise is uncorrelated across the two neurons. g, Schematic illustrating the 2N-dimensional encoding recurrent model. Two N-dimensional neuronal groups with opposite stimulus selectivity receive stimulus-dependent feedforward input and input noise. The connectivity strength is excitatory, sparse and takes the value w > 0 between neurons belonging to the same group, and η > 0 between neurons belonging to different groups. h, Example of a connectivity matrix adopted in these analyses. All matrix entries are positive (excitatory synapses) and sparse with connection probability p. i-l Same quantities computed in c-f as a function of the difference between the within-group connectivity and between-groups connectivity strength, w − η. We set N = 50, p = 0.5, η = 0.5. In c-f, i-l data are presented as mean ± SEM over n=50 simulations.
Supplementary Material
Acknowledgements
We thank E. Piasini for his early contribution, members of our laboratories for helpful discussions, G. Iurilli, C. Kayser, E. Piasini, C. Becchio and J. Drugowitsch for feedback, M. Libera for technical support. This work was supported by NIH grants from the NIMH BRAINS program R01 MH107620 (C.D.H.), NINDS R01 NS089521 (C.D.H.), the BRAIN Initiative R01 NS108410 (C.D.H. and S.P.) and U19 NS107464 (S.P.), and the Fondation Bertarelli (S.P).
Footnotes
Competing interests
The authors declare no competing interests.
References
- 1.Ni AM, Ruff DA, Alberts JJ, Symmonds J & Cohen MR Learning and attention reveal a general relationship between population activity and behavior. Science 359, 463–465, doi: 10.1126/science.aao0284 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kohn A, Coen-Cagli R, Kanitscheider I & Pouget A Correlations and Neuronal Population Information. Annu Rev Neurosci 39, 237–256, doi: 10.1146/annurev-neuro-070815-013851 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Panzeri S, Harvey CD, Piasini E, Latham PE & Fellin T Cracking the Neural Code for Sensory Perception by Combining Statistics, Intervention, and Behavior. Neuron 93, 491–507, doi: 10.1016/j.neuron.2016.12.036 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gawne TJ & Richmond BJ How independent are the messages carried by adjacent inferior temporal cortical neurons? J Neurosci 13, 2758–2771 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Averbeck BB, Latham PE & Pouget A Neural correlations, population coding and computation. Nat Rev Neurosci 7, 358–366, doi: 10.1038/nrn1888 (2006). [DOI] [PubMed] [Google Scholar]
- 6.Zohary E, Shadlen MN & Newsome WT Correlated neuronal discharge rate and its implications for psychophysical performance. Nature 370, 140–143, doi: 10.1038/370140a0 (1994). [DOI] [PubMed] [Google Scholar]
- 7.Moreno-Bote R et al. Information-limiting correlations. Nat Neurosci 17, 1410–1417, doi: 10.1038/nn.3807 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bartolo R, Saunders RC, Mitz AR & Averbeck BB Information-Limiting Correlations in Large Neural Populations. J Neurosci 40, 1668–1678, doi: 10.1523/JNEUROSCI.2072-19.2019 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rumyantsev OI et al. Fundamental bounds on the fidelity of sensory cortical coding. Nature 580, 100–105, doi: 10.1038/s41586-020-2130-2 (2020). [DOI] [PubMed] [Google Scholar]
- 10.Gold JI & Shadlen MN Neural computations that underlie decisions about sensory stimuli. Trends Cogn Sci 5, 10–16, doi: 10.1016/s1364-6613(00)01567-9 (2001). [DOI] [PubMed] [Google Scholar]
- 11.Zariwala HA, Kepecs A, Uchida N, Hirokawa J & Mainen ZF The limits of deliberation in a perceptual decision task. Neuron 78, 339–351, doi: 10.1016/j.neuron.2013.02.010 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mazurek ME & Shadlen MN Limits to the temporal fidelity of cortical spike rate signals. Nat Neurosci 5, 463–471, doi: 10.1038/nn836 (2002). [DOI] [PubMed] [Google Scholar]
- 13.Diesmann M, Gewaltig MO & Aertsen A Stable propagation of synchronous spiking in cortical neural networks. Nature 402, 529–533, doi: 10.1038/990101 (1999). [DOI] [PubMed] [Google Scholar]
- 14.Zandvakili A & Kohn A Coordinated Neuronal Activity Enhances Corticocortical Communication. Neuron 87, 827–839, doi: 10.1016/j.neuron.2015.07.026 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Alonso JM, Usrey WM & Reid RC Precisely correlated firing in cells of the lateral geniculate nucleus. Nature 383, 815–819, doi: 10.1038/383815a0 (1996). [DOI] [PubMed] [Google Scholar]
- 16.Salinas E & Sejnowski TJ Correlated neuronal activity and the flow of neural information. Nat Rev Neurosci 2, 539–550, doi: 10.1038/35086012 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zylberberg J, Pouget A, Latham PE & Shea-Brown E Robust information propagation through noisy neural circuits. PLoS Comput Biol 13, e1005497, doi: 10.1371/journal.pcbi.1005497 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Harvey CD, Coen P & Tank DW Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68, doi: 10.1038/nature10918 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Runyan CA, Piasini E, Panzeri S & Harvey CD Distinct timescales of population coding across cortex. Nature 548, 92–96, doi: 10.1038/nature23020 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hanks TD et al. Distinct relationships of parietal and prefrontal cortices to evidence accumulation. Nature 520, 220–223, doi: 10.1038/nature14066 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Morcos AS & Harvey CD History-dependent variability in population dynamics during evidence accumulation in cortex. Nat Neurosci 19, 1672–1681, doi: 10.1038/nn.4403 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Raposo D, Kaufman MT & Churchland AK A category-free neural population supports evolving demands during decision-making. Nat Neurosci 17, 1784–1792, doi: 10.1038/nn.3865 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pho GN, Goard MJ, Woodson J, Crawford B & Sur M Task-dependent representations of stimulus and choice in mouse parietal cortex. Nat Commun 9, 2596, doi: 10.1038/s41467-018-05012-y (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Panzeri S, Schultz SR, Treves A & Rolls ET Correlations and the encoding of information in the nervous system. Proc Biol Sci 266, 1001–1012, doi: 10.1098/rspb.1999.0736 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Averbeck BB & Lee D Effects of noise correlations on information encoding and decoding. J Neurophysiol 95, 3633–3644, doi: 10.1152/jn.00919.2005 (2006). [DOI] [PubMed] [Google Scholar]
- 26.Nogueira R et al. The Effects of Population Tuning and Trial-by-Trial Variability on Information Encoding and Behavior. J Neurosci 40, 1066–1083, doi: 10.1523/JNEUROSCI.0859-19.2019 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Romo R, Hernandez A, Zainos A & Salinas E Correlated neuronal discharges that increase coding efficiency during perceptual discrimination. Neuron 38, 649–657, doi: 10.1016/s0896-6273(03)00287-3 (2003). [DOI] [PubMed] [Google Scholar]
- 28.Reich DS, Mechler F & Victor JD Independent and redundant information in nearby cortical neurons. Science 294, 2566–2568, doi: 10.1126/science.1065839 (2001). [DOI] [PubMed] [Google Scholar]
- 29.Koch C, Rapp M & Segev I A brief history of time (constants). Cereb Cortex 6, 93–101, doi: 10.1093/cercor/6.2.93 (1996). [DOI] [PubMed] [Google Scholar]
- 30.Reyes AD Synchrony-dependent propagation of firing rate in iteratively constructed networks in vitro. Nat Neurosci 6, 593–599, doi: 10.1038/nn1056 (2003). [DOI] [PubMed] [Google Scholar]
- 31.Shahidi N, Andrei AR, Hu M & Dragoi V High-order coordination of cortical spiking activity modulates perceptual accuracy. Nat Neurosci 22, 1148–1158, doi: 10.1038/s41593-019-0406-3 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Histed MH & Maunsell JH Cortical neural populations can guide behavior by integrating inputs linearly, independent of synchrony. Proc Natl Acad Sci U S A 111, E178–187, doi: 10.1073/pnas.1318750111 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Emiliani V, Cohen AE, Deisseroth K & Hausser M All-Optical Interrogation of Neural Circuits. J Neurosci 35, 13917–13926, doi: 10.1523/JNEUROSCI.2916-15.2015 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shadlen MN & Newsome WT The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci 18, 3870–3896 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ostojic S, Brunel N & Hakim V How connectivity, background activity, and synaptic properties shape the cross-correlation between spike trains. J Neurosci 29, 10234–10253, doi: 10.1523/JNEUROSCI.1275-09.2009 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rosenbaum R, Smith MA, Kohn A, Rubin JE & Doiron B The spatial structure of correlated neuronal variability. Nat Neurosci 20, 107–114, doi: 10.1038/nn.4433 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.de la Rocha J, Doiron B, Shea-Brown E, Josic K & Reyes A Correlation between neural spike trains increases with firing rate. Nature 448, 802–806, doi: 10.1038/nature06028 (2007). [DOI] [PubMed] [Google Scholar]
- 38.Cossell L et al. Functional organization of excitatory synaptic strength in primary visual cortex. Nature 518, 399–403, doi: 10.1038/nature14182 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Marshel JH et al. Cortical layer-specific critical dynamics triggering perception. Science 365, doi: 10.1126/science.aaw5202 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pitkow X, Liu S, Angelaki DE, DeAngelis GC & Pouget A How Can Single Sensory Neurons Predict Behavior? Neuron 87, 411–423, doi: 10.1016/j.neuron.2015.06.033 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nirenberg S, Carcieri SM, Jacobs AL & Latham PE Retinal ganglion cells act largely as independent encoders. Nature 411, 698–701, doi: 10.1038/35079612 (2001). [DOI] [PubMed] [Google Scholar]
- 42.Karpas EM, O.; Kiani R; Schneidman E Strongly correlated spatiotemporal encoding and simple decoding in the prefrontal cortex. bioRxiv 693192 doi:doi: 10.1101/693192 (2019) [DOI] [Google Scholar]
Methods references
- 43.Morcos A et al. Dataset of ‘History-dependent variability in population dynamics during evidence accumulation in cortex’. G-Node, g1xyem, doi: 10.12751/g-node.g1xyem (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Runyan CA et al. Dataset of ‘Distinct timescales of population coding across cortex’. G-Node, tqbad8, doi: 10.12751/g-node.tqbad8 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Aronov D & Tank DW Engagement of neural circuits underlying 2D spatial navigation in a rodent virtual reality system. Neuron 84, 442–456, doi: 10.1016/j.neuron.2014.08.042 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Greenberg DS & Kerr JN Automated correction of fast motion artifacts for two-photon imaging of awake animals. J Neurosci Methods 176, 1–15, doi: 10.1016/j.jneumeth.2008.08.020 (2009). [DOI] [PubMed] [Google Scholar]
- 47.Vogelstein JT et al. Fast nonnegative deconvolution for spike train inference from population calcium imaging. J Neurophysiol 104, 3691–3704, doi: 10.1152/jn.01073.2009 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Boser BEG, I. M.; Vapnik VN. in Fifth annual workshop on Computational learning theory - COLT ‘ 92 (ACM Press; ). [Google Scholar]
- 49.Chang CCL, C.J. LIBSVM: a library for support vector machines. ACM Transactions on Intelligent Systems and Technology 2, 1–27 (2011). [Google Scholar]
- 50.Lin H-TL, C.-J; Weng RC A note on Platt’s probabilistic outputs for support vector machines. Mach. Learn 68, 267–276 (2007). [Google Scholar]
- 51.Britten KH, Newsome WT, Shadlen MN, Celebrini S & Movshon JA A relationship between behavioral choice and the visual responses of neurons in macaque MT. Vis Neurosci 13, 87–100, doi: 10.1017/s095252380000715x (1996). [DOI] [PubMed] [Google Scholar]
- 52.Kang I & Maunsell JH Potential confounds in estimating trial-to-trial correlations between neuronal response and behavior using choice probabilities. J Neurophysiol 108, 3403–3415, doi: 10.1152/jn.00471.2012 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Seabold SP, in J 9th Python in Science Conference. 92–96. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The sound localization task data that support the findings of the current study can be downloaded at https://gin.g-node.org/MMoroni/PPC_AC_2p_sound_localization (see Ref44).
The evidence accumulation task data that support the findings of the current study can be downloaded at https://gin.g-node.org/MMoroni/PPC_2p_evidence_accumulation. (see Ref43).