Variational inference using approximate likelihood under the coalescent with recombination

Abstract

Coalescent methods are proven and powerful tools for population genetics, phylogenetics, epidemiology, and other fields. A promising avenue for the analysis of large genomic alignments, which are increasingly common, is coalescent hidden Markov model (coalHMM) methods, but these methods have lacked general usability and flexibility. We introduce a novel method for automatically learning a coalHMM and inferring the posterior distributions of evolutionary parameters using black-box variational inference, with the transition rates between local genealogies derived empirically by simulation. This derivation enables our method to work directly with three or four taxa and through a divide-and-conquer approach with more taxa. Using a simulated data set resembling a human–chimp–gorilla scenario, we show that our method has comparable or better accuracy to previous coalHMM methods. Both species divergence times and population sizes were accurately inferred. The method also infers local genealogies, and we report on their accuracy. Furthermore, we discuss a potential direction for scaling the method to larger data sets through a divide-and-conquer approach. This accuracy means our method is useful now, and by deriving transition rates by simulation, it is flexible enough to enable future implementations of various population models.

A powerful and widely accepted and used mathematical framework for capturing the evolution of genomes and their individual loci is the theory of coalescence (Kingman 1982). This framework, applied to the increasingly available genomic data, has “turned theoretical population genetics on its head” (Hartl and Clark 2007) and propelled population and phylogenomic inferences to successful applications that span several fields of biology and biomedicine (Siepel 2009; Rogers and Gibbs 2014). Coalescent-based models allow for estimating the values of parameters, including population divergence times, mutation and recombination rates, ancestral population sizes, population structure, etc., from patterns of site frequencies and local genealogies (Hartl and Clark 2007; Nielsen and Slatkin 2013).

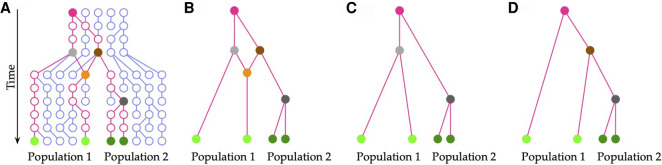
To account for varying levels of complexities in evolutionary histories, the standard coalescent has been extended in various directions to accommodate processes such as recombination, population structure and migration, and selection (Hudson 1990; Wakeley 2008). In this work, we focus on the coalescent with recombination, illustrated in Figure 1A.

Figure 1.

The multispecies coalescent with recombination. (A) The evolutionary history of a sample of four extant individuals in two divergent populations from their MRCA (solid magenta circle). The recombination node (solid orange circle) results in an ancestral recombination graph (ARG), shown in B. (C) The genealogy of genomic regions that traces their evolution back from the recombination node to the gray ancestral node. (D) The genealogy of genomic regions that traces their evolution back from the recombination node to the brown ancestral node.

As McVean and Cardin (2005) noted, the coalescent with recombination is very difficult to estimate likelihoods under owing to, at least, three important issues: (1) the state space of recombining genealogies (also known as ancestral recombination graphs (ARGs), illustrated in Fig. 1B) is huge; (2) the data are generally not very informative about the actual ARG; and (3) likelihood estimation is a missing-data problem with highly redundant augmentation.

The consequence of these issues is seen in BACTER (Vaughan et al. 2017), a Bayesian method that uses MCMC to infer the ARG posterior distribution down to the coalescent and recombination times and genomic boundaries of recombinant segments. Although this kind of joint inference yields the most detailed posterior distribution, calculating the likelihood of an ARG scales poorly as the number of recombinations increases, and BACTER is limited to analysis of an unstructured population (Vaughan et al. 2017).

Coalescent inference can be scaled up using multilocus methods that assume each locus is spaced far enough apart so that there is effectively no linkage between loci, and each locus is short enough so that no recombination has occurred within it. However, the assumption of no recombination within loci has been called into question (Springer and Gatesy 2016), although the issue is far from being settled, especially when it comes to robustness of species tree inference under the multispecies coalescent (MSC) model (Edwards et al. 2016).

To strike a balance between the scalability of multilocus methods and the power of ARG inference, the coalescent with recombination can be approximated as a sequential Markovian process operating across the genome, rather than operating in time along the branches of the phylogeny (Hein et al. 2005). Using this view, the coalescent hidden Markov model (coalHMM) was introduced (Hobolth et al. 2007). In this model, a hidden Markov model (HMM) is built such that every coalescent history (gene history) given the species tree is modeled by a state, the transition probabilities are derived based on the recombination rate and the given genealogies, and the emission probabilities are given by the likelihood of the gene trees (Felsenstein 1981). Figure 1, C and D, shows two gene histories that are embedded inside the ARG shown in Figure 1B.

In the work of Hobolth et al. (2007), the investigators determined the transition probabilities by careful inspection of recombination scenarios given the species tree. Later, Dutheil et al. (2009) provided a detailed mathematical derivation under the coalescent with recombination of the model of Hobolth et al. (2007). Such a manual approach to deriving transition probabilities has limited coalHMM-based inference of evolutionary parameters to three genomes. Several later works have attempted to automatically create coalHMMs for various demographic scenarios. For example, Mailund et al. (2012) used colored Petri nets to represent genetic models and gave an algorithm for translating such models into coalHMMs. However, there is no software associated with the method. Cheng and Mailund (2020) developed the Jocx tool for ancestral population genomics inference based on pairwise coalHMMs, but Jocx currently only supports a limited number of demographic models.

In this work, we present a new method, variational inference under the coalescent with recombination (VICAR) for approximate inference under the MSC with recombination. VICAR consists of two novel components. First, it implements a simulation-based technique for automatically deriving a coalHMM on which likelihood calculations are performed efficiently. More specifically, the likelihood of a candidate model (species tree, divergence times, and population sizes) is computed by simulating data under the coalescent with recombination using the candidate model, using these data to automatically construct an HMM, and then computing the likelihood by means of the forward algorithm (Chang and Hancock 1966; Baum et al. 1970, 1972). This way the method is able to automatically generate coalHMMs and learn their parameters for arbitrarily complex demographic scenarios. Leveraging those coalHMMs learned by simulation, VICAR also infers local genealogies for arbitrary demographic models using posterior decoding. Second, the parameter estimation in VICAR consists of a novel application of variational inference for Bayesian inference of demographic parameters using this approximate likelihood (the species tree topology is assumed to be known and fixed).

We show the utility and accuracy of VICAR on both simulated and biological data and compare it to diCal2 (Steinrücken et al. 2019), which is the current state-of-the-art coalHMM algorithm for inferring population histories. Furthermore, we discuss and provide preliminary results for how to scale the method to larger numbers of taxa using a divide-and-conquer approach in the Supplemental Material. The automated nature of our method provides a step toward wider applicability of the coalescent with recombination.

Results

Overview of VICAR

Given the topology of a species tree, we seek to estimate its continuous parameters from the genomic data under the (multispecies) coalescent with recombination. As we stated above, maximum likelihood estimation of the topology's parameters under the exact complex model of the coalescent with recombination is intractable. We introduce a novel variational Bayesian method, VICAR, for accomplishing this estimation by using a simulation-based likelihood kernel. The kernel automatically derives an empirical, simulation-based coalHMM and performs the likelihood computations on the HMM, which can be performed in polynomial time in the number of states (Durbin et al. 1998). This automated procedure of generating a coalHMM and computing the likelihood obviates the need for theoretical derivations based on the coalescent theory for every evolutionary scenario, as in most previous coalHMM methods, and thus can be applied to infer parameters of any demographic model. We now give a high-level description of how VICAR works and then give the full details in the Methods.

Let Ψ be a species tree on a set $\mathcal{X}$ of taxa, N be a vector of the effective population sizes associated with Ψ’s internal and root branches, and T be a vector of the divergence times, in unit of generations, of the internal nodes of Ψ. Let Θ = [N; T]. We fix the hyperparameters of the prior distributions on the parameters Θ. We also assume a fixed mutation rate μ, in units of the expected number of mutations per site per generation, and recombination rate ρ, in units of the expected number of recombinations per site per generation. Parameters μ and ρ are assumed to be constant across the species tree. VICAR assumes one sequence from each extant population so the posterior distribution of tip branch population sizes will be identical to the prior and, hence, not estimated by the method. VICAR seeks to estimate the posterior distribution over the model parameters, given by

$$p\left(\mathrm{\Theta }|\mathcal{S}\right)\propto P\left(\mathcal{S}|\mathrm{\Theta }\right)p\left(\mathrm{\Theta }\right),$$

where S is a genomic sequence alignment that is assumed to have evolved under the coalescent with recombination and a model of sequence evolution. VICAR estimates $p\left(\mathrm{\Theta }|\mathcal{S}\right)$ via a novel method of approximating the likelihood $P\left(\mathcal{S}|\mathrm{\Theta }\right)$ and a novel application of variational inference.

For approximating the likelihood, VICAR simulates a set of genealogies along a sequence under the coalescent with recombination. Using the simulated data, VICAR constructs an empirical HMM and applies an existing polynomial-time algorithm to compute the likelihood of the HMM. For approximating the posterior distribution, we introduce a novel application of black-box variational inference (BBVI) to this domain. VICAR produces estimates of the parameter values Θ along with measures of confidence.

Accuracy of parameter inference on data simulated under a human–chimp–gorilla-like scenario

In this section, we show the performance of VICAR on simulated data and compare it with that of diCal2 (Steinrücken et al. 2019). diCal2 is based on the sequentially Markov conditional sampling distribution framework (Paul et al. 2011; Sheehan et al. 2013; Steinrücken et al. 2013) with a combination of expectation–maximization (EM) and genetic algorithm to infer a maximum likelihood point estimate, which differs from our Bayesian approach.

We used the program msprime (Kelleher et al. 2016) as the simulator for coalescent with recombination process and used INDELible (Fletcher and Yang 2009) as the sequence evolution simulator. We simulated 100 data sets with 500,000 sites each, intended to resemble human–chimp–gorilla. We refer to the three extant species as human (H), chimp (C), and gorilla (G), and the ancestral species as the human–chimp ancestor (HC) and the human–chimp–gorilla ancestor (HCG). The simulation setup consists of two steps. In the first step, we took the demographic parameters of a species tree and simulated under the coalescent with recombination process. This step gave us a set of segments of the sequence, in which each segment had a corresponding coalescent tree. The second step used standard evolutionary simulators to generate sequence alignments at each segment at the given substitution rate under the coalescent tree at that segment. The result of the simulation was a sequence alignment for the set of taxa, in which different sites in the alignment had potentially different genealogies. The continuous parameters used in simulation are population sizes N_HC = N_HCG = 40,000 and N_H = N_C = N_G = 30,000, speciation time T_HC = 160,000 generations (or 4 Myr assuming a generation time of 25 yr), and speciation time T_HCG = 220,000 generations (or 5.5 Myr assuming a generation time of 25 yr). The recombination rate is r = 1.5 × 10⁻⁸ per site per generation, corresponding to a genetic recombination frequency of 1.5 cM/Mb. The mutation rate is 2.5 × 10⁻⁸ per site per generation, corresponding to 0.1% change per million years assuming a generation time of 25 yr. The parameters are the same as used in the other two human–chimp–gorilla simulation studies of coalescent HMM (Hobolth et al. 2007; Dutheil et al. 2009).

For each data set, VICAR was used to find the variational posterior of each continuous parameter. The configuration for constructing simulation-based coalHMM as in Algorithm 1 is nb = 2 and −r = 1000. The meaning of nb and −r will be introduced below. The simulation length ℓ is determined automatically using a scaling formula depending on the −r setting, as described below. For a stochastic variational inference search, we used 50 samples per iteration with 200 iterations. We used an improper uniform prior U(0, inf) on node heights and used a gamma prior on population sizes with a shape parameter of two and a scale parameter of 25,000. For diCal2, we used 70 samples for each generation of the genetic algorithm, each optimized for four EM iterations, and six parents for the next generation. To improve the accuracy of diCal2, we used 12 intervals for HMM state generation, compared with 10 intervals in the examples from the diCal2 manual. We ran the genetic algorithm for five generations (the same setting as used by Steinrücken et al. 2019) and reported the maximum likelihood parameters for each data set.

Figure 2A shows the maximum a posteriori (MAP) estimates obtained by VICAR and maximum likelihood estimates (MLEs) obtained by diCal2 as a violin plot. All parameters are estimated by VICAR with very high accuracy and little variance. Generally, population sizes are estimated with larger variance than node heights, which is true for both methods. VICAR produces more accurate estimates than diCal2 for all four parameters. Furthermore, diCal2's estimations have a large variance on the ancestral population size for human–chimp ancestor, whereas VICAR infers that parameter with much higher accuracy and less variability.

Figure 2.

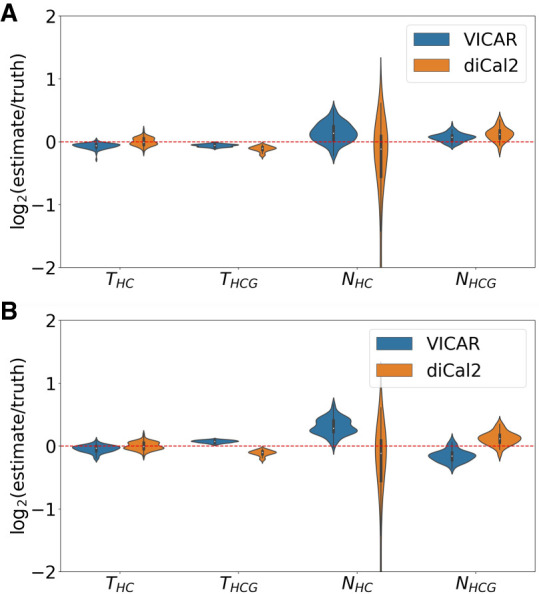
Accuracy results of VICAR (blue) and diCal2 (orange) on simulated human–chimp–gorilla data sets. The violin plot shows the base-2 logarithm of the relative error (estimate/truth) for the analysis of 100 data sets by VICAR and diCal2. A value of zero (the red dashed line) represents an exact estimate. The two panels show the results based on different values of the number of iterations of variational inference in VICAR (the parameter T in Algorithm 2 in Methods). (A) T = 200. (B) T = 20.

All the experiments reported above were run on a Macbook Pro with 2.4-GHz Intel Core i5 CPU. On average, the run-time of VICAR is ∼10.08 h for a data set. Building the coalHMM by simulation takes 3.93 h, and computing the likelihood using the forward algorithm takes 6.15 h. diCal2 takes less time, with only 0.7 h per data set. This can be partially explained by the fact that diCal2 makes further approximations to make the HMM more efficient and incorporates optimizations for speeding up the forward algorithm, whereas our current implementation of VICAR does not optimize the HMM and applies a vanilla implementation of the forward algorithm. To study how the two methods perform given comparable computational cost, we assessed the performance of VICAR based on the partial results obtained after the first 20 iterations of variational inference search, which take ∼1 h to run (comparable to the running time of diCal2). As the results in Figure 2B show, VICAR still achieves similar or better estimates for three of the four parameters and much more precise estimates for N_HC.

For a more general view of VICAR's performance as a function of the number of VI iterations in this scenario, Figure 3 shows the convergence plot of VICAR on one of the data sets. As the figure shows, the likelihood increases rapidly in the first few iterations and converges after only about 50 iterations.

Figure 3.

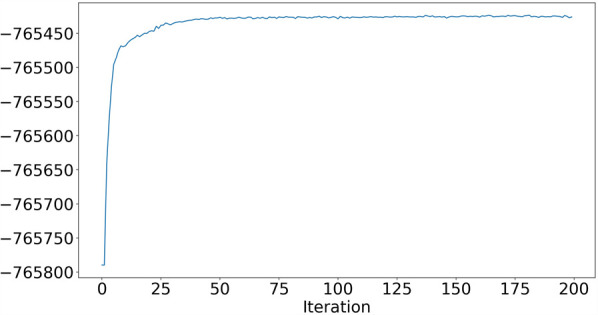
Convergence of VICAR. The x-axis is the number of iterations, and the y-axis is the log likelihood of the current estimation.

Another advantage of our method is that it is a Bayesian approach, with the ability to specify priors and provide posterior support for parameters. Once VICAR converges, the uncertainty associated with the inference is quantified by the Bayesian posterior, whereas for maximum likelihood approaches such as diCal2, running the algorithm multiple times for bootstrapping is required to infer confidence intervals, which increases the actual running time. To assess the quality of uncertainty estimates obtained by maximum likelihood, as implemented in diCal2, and the quality of uncertainty estimates obtained by VICAR, we used the diCal2 parameter estimates for one simulated data set from above to perform parametric bootstrapping. We simulated 20 bootstrap alignments and reran diCal2 on each of them. We then used the bootstrap samples to estimate a standard deviation for each parameter and reported the confidence intervals based on a normal approximation. The confidence intervals were computed in the log space and transformed back to the natural space to avoid falling outside the domain of each parameter. Table 1 shows the 95% credible intervals of VICAR and the 95% confidence intervals of diCal2 for each parameter.

Table 1.

Results of VICAR versus diCal2 with parametric bootstrapping

Although it is true that Bayesian credible intervals conceptually differ from frequentist confidence intervals, as the results show, the diCal2 confidence intervals exclude the true value for all parameters bar T_HC. In contrast, all VICAR credible intervals include the true parameter value. As we note in the Discussion section, the confidence measure obtained by the simple factorized Gaussian variational family used by VICAR could be further improved. It is also worth noting that diCal2 with bootstrapping took a total of 11.6 h (similar to VICAR).

Accuracy of local genealogy inference on data simulated under a human–chimp–gorilla-like scenario

Other than inferring continuous parameters, an important capability of VICAR is the inference of the local genealogy of each site along the genome. Because the hidden states of a coalHMM are coalescent histories (genealogies), local genealogy inference can be performed by posterior decoding of the HMM along the sequence data, which gives us the posterior probability of each genealogy at each site. In this section, we study the performance of VICAR in terms of local genealogy inference.

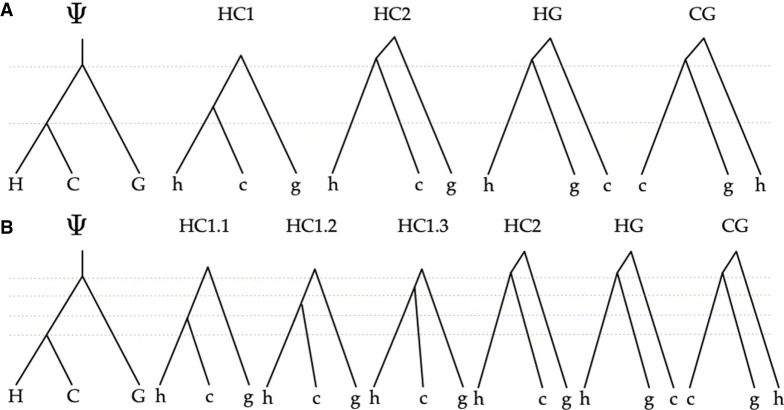
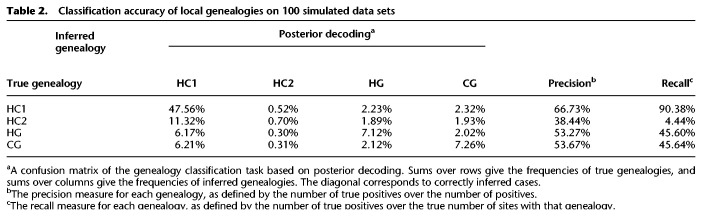
We used the same 100 simulated data sets as in the simulation study above. Because we used msprime to simulate under the coalescent with recombination process when generating data, we have the true coalescent tree of each site. We used nb = 2 and −r = 1000 to build our HMM by simulation. For the human–chimp–gorilla species tree, there are four types of genealogies: HC1, HC2, HG, and CG, as shown in Figure 9A, below. Because we fine-grained each branch into two sub-branches, our HMM has a higher granularity than four genealogies. The total number of states in our HMM is actually 13. However, for the purpose of local genealogy inference, we only consider the four basic types as they are the most meaningful categorization for determining the shared ancestry of molecular characters or traits. Therefore, after posterior decoding on the 13-state HMM, we merged hidden states of the same type together and took the type with the highest posterior probability as the inferred genealogy at each site. We also discretized the true coalescent tree at each site into one of the four genealogies. We then compared the inferred genealogy with the true one. Table 2 shows the confusion matrix of the classification task, as well as the precision and recall measures for each type of genealogy. Figure 4 shows a graphical comparison of the posterior probabilities of each genealogy at each site with the true genealogy along the sequence from a segment of 100,000 sites from one of the data sets.

Figure 9.

The coalHMM model. (A) The four states of a standard coalHMM that corresponds to the species tree Ψ. (B) The six states of a refined coalHMM that corresponds to the species tree Ψ when its internal branch is broken into three sub-branches.

Table 2.

Classification accuracy of local genealogies on 100 simulated data sets

Figure 4.

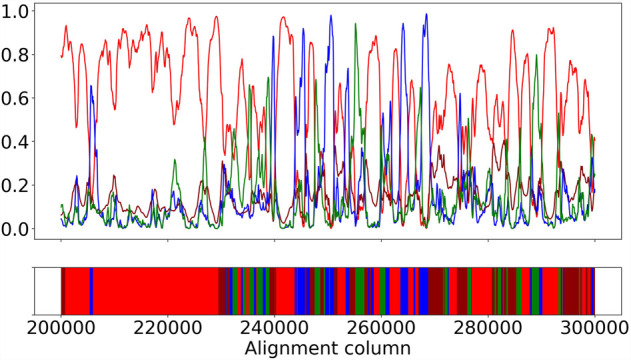
True genealogy and posterior distribution along the sequence. The upper panel shows posterior probability of each genealogy at each site. The lower panel shows the true genealogy of each site. Coloring corresponds to different genealogies: Genealogy HC1 is in red, HC2 is in dark red, HG is in blue, and CG is in green.

The results show that the accuracy of local genealogy inference is very good: 90% of true HC1 sites are inferred to have HC1 genealogy (Table 2). This number is 46% for HG and CG, with an overall classification accuracy of 63%. This number is significantly higher than random expectation (Dutheil et al. 2009). We observe the same good performance in Figure 4, where there is a good correspondence between true genealogy and posterior distribution. However, note that the recall measure of HC2 is only 4.44%, meaning only 4.44% of all true HC2 genealogies are actually estimated to be HC2. Dutheil et al. (2009) reported the same poor performance on HC2. Many sites with HC2 as true genealogy are assigned to another type, mostly HC1 (Dutheil et al. 2009). This is likely a model artifact of the HMM approximation to the coalescent with recombination process. We already know that the HMM approximation would underestimate the recombination rate (Dutheil et al. 2009; Mailund et al. 2011), which means it would underestimate state transitions, leading to a global underestimation of incomplete lineage sorting. For most of the true HC2 sites, it is unsurprising that these sites are misclassified as HC1, because the stationary frequency of HC1 is so much higher and because the site patterns of true HC1 sites and true HC2 sites should be similar.

Relationship between inference accuracy, number of sub-branches, simulation length, and branch lengths

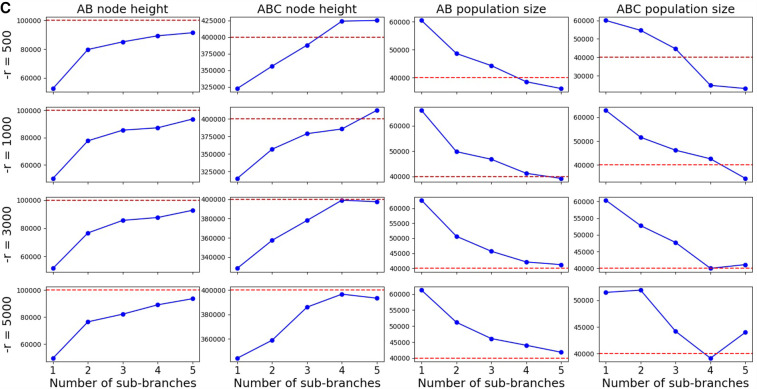
The accuracy of inferences depends on the quality of the approximate likelihood, which in turn depends on two aspects: the accuracy of the simulation-based coalHMM approximation of the coalescent with recombination process, and the quality of the trained coalHMM itself. The accuracy of the coalHMM approximation of the coalescent with recombination process is determined by the refinement of coalHMM state space, that is, the number of sub-branches on each branch of the species tree when building the HMM. If the number of sub-branches is small, the resulting coalHMM has a state space of coarse coalescent histories that is not enough to capture the detailed coalescent distribution, leading to biased likelihood (Dutheil et al. 2009; Mailund et al. 2011). The quality of the coalHMM itself (i.e., the quality of the transition matrix) is determined by the length of simulation used to derive the HMM because our coalHMM is trained directly from labeled sequence data. The more sub-branches we use to refine a branch, the more accurate approximation we obtain, but more sub-branches incur a larger state space, necessitating a longer simulation length in order to train a high-quality transition matrix. If we use a large number of sub-branches but a small simulation length, the resultant HMM will be unreliable because of limited training data. Moreover, depending on the branch length, we may not need a large number of sub-branches to approximate the coalescent process on that branch, but a too-small number of sub-branches may introduce bias. In this section, we study the relationship between accuracy of inference result, number of sub-branches used to refine HMM state space, length of simulation used to build HMM, and branch length of the species tree we do inference on. We derive some empirical suggestions on what number of sub-branches and simulation length to use for any specific inference problem.

There are two hyperparameters controlling the HMM building process in Algorithm 1: nb, the number of sub-branches on each branch of the species tree, and l, the length of simulated HMM training data. In our implementation, they are user-defined inputs NUM_BIN and CROSS_OVER_RATE. NUM_BIN is the number of sub-branches used to approximate each branch of the species tree. CROSS_OVER_RATE is the −r switch of ms (Hudson 2002), which is defined as 4N₀ r, where N₀ is a customized population size, and r is the probability of recombination per generation between the ends of the locus being simulated, which is the probability of recombination per site per generation times the number of sites to simulate. Our implementation assumes a value of 10,000 for N₀, and it can be changed according to the scale of population sizes. For example, if the recombination rate is 1.5 × 10⁻⁷/site/generation and we seek to simulate 500,000 sites, we use 4 × 10,000 × 1.5 × 10⁻⁷ × 500,000 = 3000 as the value for the −r option.

We simulated sequence alignments under three different evolutionary scenarios, the difference between which is the internal branch length. All three scenarios have the same three-taxon tree topology ((A, B), C);. Internal node height T_AB is fixed at 100,000 generations. The root node height varies across scenarios. Scenario 1 has a root node height of 150,000 generations. Scenario 2 has a root node height of 200,000 generations. Scenario 3 has a root node height of 400,000 generations. Population sizes of all branches are fixed at 40,000. Hence, the branch length of the internal branch for scenarios 1, 2, and 3 in coalescent units are 0.625, 1.25, and 3.75, respectively. The recombination rate is r = 1.5 × 10⁻⁷/site/generation. The mutation rate is 1.25 × 10⁻⁶/site/generation. The length of the sequence is 100,000 bp.

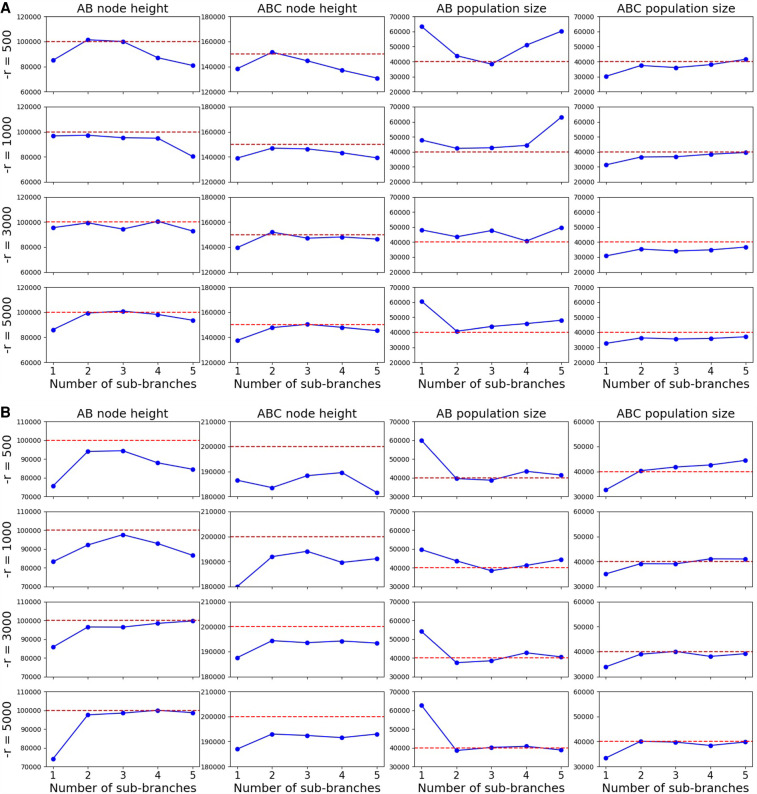
We inferred the continuous parameters of each scenario under various configurations of the hyperparameters. The number of sub-branches explored were one, two, three, four, and five. The values for the −r parameter explored were 500, 1000, 3000, and 5000, which correspond to simulation lengths of 83,333, 166,666, 500,000, and 833,333, respectively. For each combination of number of sub-branches and −r parameter value (simulation length), we conducted inference on each scenario using the combination for coalHMM construction to find the MAP solution and inspected the accuracy. In total, we conducted 3 × 4 × 5 = 60 inferences.

Figure 5, A through C, shows inference results for scenarios 1, 2, and 3, respectively. The message is clearest in Figure 5C. Looking at each individual plot, for a fixed simulation length, increasing the number of sub-branches increases the accuracy of inference until it flattens out. But Figure 5A suggests that the accuracy does not stay on a plateau after reaching a certain number of sub-branches. Rather, if the simulation length is not long enough, increasing the number of sub-branches might decrease inference accuracy. The reason is that the transition rate matrix of a large state space cannot be sufficiently trained from a short length of simulation. Each column of the plots shows that generally, for a fixed number of sub-branches, increasing the simulation length increases the accuracy, but the gain is smaller than increasing the number of sub-branches. Simulation length only determines how close the transition matrix of a coalHMM trained from simulated data is to the true transition rate matrix calculated from a strict mathematical model. However, the bias in approximate likelihood comes from a restricted state space, not a poor transition matrix. If the state space is restricted, increasing simulation length does not solve the bias problem because the bias still exists when the transition rate matrix is analytically derived (Dutheil et al. 2009; Mailund et al. 2011). Put simply, increasing the simulation length is not going to address any biases resulting from discretization the state space of coalescent histories, or from using a Markov chain to approximate the ARG.

Figure 5.

Results on the three scenarios, shown for internal branch lengths 0.625 (A), 1.25 (B), and 3.75 (C). Dashed red lines are true values. Blue lines are inferred MAP values. Rows correspond to different simulation lengths. Columns correspond to different continuous parameters. The x-axes are number of sub-branches ranging from one to five. (Figure continued on following page.)

The appropriate number of sub-branches and simulation length to use depends on the internal branch length of the species tree. For example, using two sub-branches and −r = 1000 infers a very good result on scenario 1 but does not work well on scenario 3. Based on the plot, for a short internal branch (about one coalescent unit), two or three sub-branches with a −r of around 1000 are sufficient. For a larger branch length (one to three coalescent units), three or four sub-branches with a −r of about 3000 would suffice. For branches longer than three coalescent units, more than four sub-branches and a −r value higher than 3000 would be needed.

Running time is also a consideration when choosing hyperparameters. We studied the relationship between time taken by the forward algorithm and the number of sub-branches for refining the species tree (Supplemental Fig. S2), the relationship between the running time and the length of simulation (Supplemental Fig. S3), the time taken by simulating a long region versus several short regions (Supplemental Fig. S4), and the relationship between the running time and the branch length of the species tree (Supplemental Fig. S5).

Analysis of an empirical human–chimp–gorilla genomic alignment

We reanalyzed the empirical human–chimp–gorilla sequences from Hobolth et al. (2007) for comparison with previous models. We reanalyzed target 106 (Chromosome 20) of Hobolth et al. (2007) using VICAR and diCal2 and compared the results with those reported by Hobolth et al. (2007) and Dutheil et al. (2009) on the same data. The VICAR settings were the same as in the simulation study above. We used a recombination rate r = 2 × 10⁻⁹ per site per generation and a mutation rate μ = 2.35 × 10⁻⁸ per site per generation, as they were estimated from pedigree data and reported by Dutheil et al. (2009) for this target. The result is shown in Figure 6. Generally, VICAR infers comparable results to those reported by Hobolth et al. (2007) and Dutheil et al. (2009), whereas diCal2 yields farther estimates for some parameters. For T_HC and N_HCG, all four methods infer about the same value. For T_HCG, VICAR's estimate is closer to that of Dutheil et al. (2009) than the other two.

Figure 6.

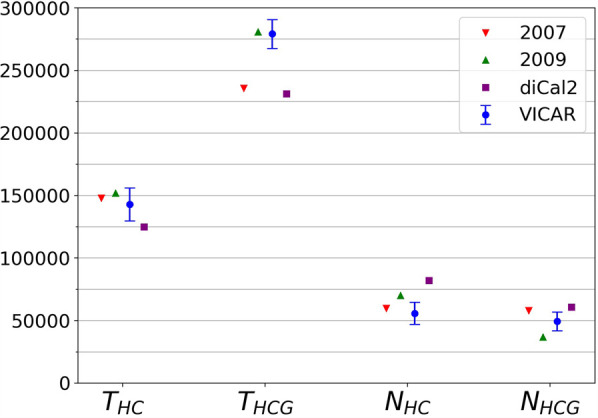
Inference results on target 106. The factorized normal variational posterior distribution of each parameter inferred by VICAR is shown in blue. The red triangle shows the maximum likelihood solution obtained by Hobolth et al. (2007). The green triangle shows the maximum likelihood solution obtained by Dutheil et al. (2009). For the 2009 model, we took the result after bias correction. The purple square shows the solution obtained by diCal2, and the blue circle is the VICAR solution. Given that VICAR uses Bayesian inference, it provides confidence measures; shown are standard deviations of the Gaussian posteriors.

Analysis of an empirical Heliconius genomic alignment

Additionally, we used VICAR to analyze the demographic history of three Heliconius butterfly species. Previous methods to construct the evolutionary history of the Heliconius butterflies include a genome-wide maximum likelihood tree constructed on the whole-genome alignment (Zhang et al. 2016) or reticulate phylogenetic networks constructed using random samples of 10-kb windows across the alignment (Edelman et al. 2019), but no previous work attempted to infer the phylogenetic relationships, including divergence times and population sizes, while accounting for recombination. Van Belleghem et al. (2018) used pairwise sequentially Markovian coalescent (PSMC) (Li and Durbin 2011; Schiffels and Durbin 2014) to infer the stepwise changes of the historical population sizes of the Heliconius erato and the Heliconius melpomene clades, but the results only reflect the population size changes that have occurred after the split of those populations. In this study, we analyze three taxa, Heliconius cydno, Heliconius timareta, and H. numata, from the melpomene clade and infer their ancestral divergence times and ancestral population sizes. We choose these three taxa because they do not show strong introgression and fit the three-taxon model. In future developments of our method, introgression can be simultaneously analyzed, and we can have a clearer picture of the demographic history of other taxa in the Heliconius butterflies.

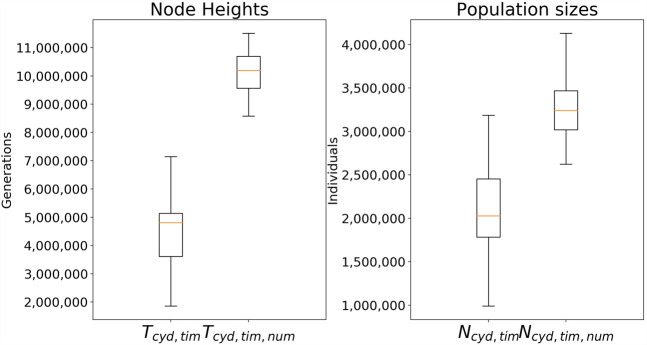
We took the whole-genome alignment from Edelman et al. (2019) and randomly extracted 17 1-Mb windows across the genome following the pipeline described in that paper. We used a recombination rate r = 5 × 10⁻⁸ per site per generation (Wilfert 2007) and a mutation rate of μ = 2 × 10⁻⁹ per site per generation (Van Belleghem et al. 2018). The settings for VICAR are nb = 4 and −r = 1000, and we used an N₀ population size of 2 million. For BBVI search, we used 50 samples per iteration to evaluate the gradient and 100 iterations of gradient update. We used an improper uniform prior U(0, inf) on node heights, gamma prior on population sizes with a shape parameter of two, and a scale parameter of 1 million. The results are shown in Figure 7.

Figure 7.

Inference results on 17 windows extracted from the Heliconius alignment for H. cydno, H. timareta, and H. numata. The MAP estimates for all windows are plotted in a box-and-whisker plot.

We observe a wide range of cydno–timareta divergence times across different chromosomes, with the median value at about 4.8 million generations ago. Assuming a generation time of 0.25 yr, the median value is 1.2 Myr, which corresponds well with the estimate of 1.1544 Myr from Zhang et al. (2016), as well as the previous estimate of 0.9–1.4 Myr for cydno–melpomene divergence (Kronforst et al. 2013; Lohse et al. 2016). We infer a median cydno–timareta–numata divergence time of 2.5 Myr. This number is higher than that inferred by a whole-genome maximum likelihood tree but the same as the Bayesian inference of Kronforst (2008). For the population sizes, we infer a larger root ancestral population size than the population size of the cydno–timareta ancestor. There was no previous estimate of this value, but the effective population size of H. melpomene was inferred to be about 2 million (Keightley et al. 2015).

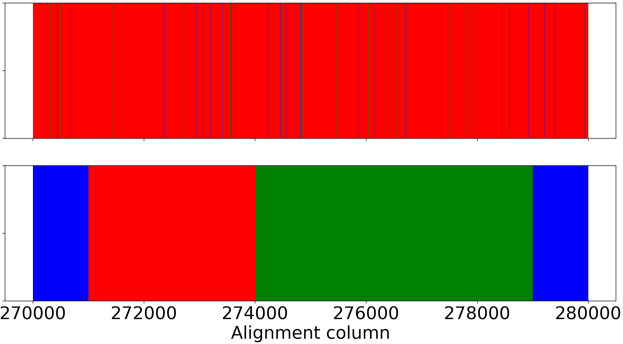
We inferred local genealogies on a region of 10,000 sites in one of the alignments analyzed above. We also divided the region into 1000-site nonoverlapping windows and inferred the topology of the maximum likelihood tree using RAxML (Stamatakis 2014) for each sliding window. The point of this analysis is to understand the frequency of alternating topologies along the alignment and to test the no-recombinaton assumption of common multilocus MSC methods. The results are shown in Figure 8.

Figure 8.

Comparison of VICAR local genealogy inference with RAxML trees. RAxML was run on nonoverlapping sliding windows each of 1000 sites. The upper panel shows the topology of the local genealogy at each site inferred by VICAR. The lower panel shows the topology inferred by RAxML at each window. Coloring corresponds to different topologies: red corresponds to ((H. cydno, H. timareta), H. numata), which is also the topology of the species tree; blue, ((H. cydno, H. numata), H. timareta); and green, ((H. numata, H. timareta), H. cydno).

We observe that window-based RAxML analyses give rise to much incongruence between the gene trees of individual loci and the species tree. This is reflected in the fact that for 70% of that genomic region, the local phylogeny differs from the species tree. VICAR, on the other hand, finds that most of the region supports the species tree with a few sites supporting the two alternative topologies. These sites could have a strong signal that potentially impacted the RAxML inferences.

This analysis further highlights the utility of our method, even in the context of multilocus MSC methods.

Discussion

Coalescent methods are a fundamental tool of population genetics and are increasingly standard in phylogenetics. In particular, the MSC has emerged as a central model underlying a wide array of methods for inferring species trees that account for the phenomenon of incomplete lineage sorting. However, inference under this model assumes that the data come from multiple loci such that there is free recombination between loci and no recombination within any locus. This assumption necessitates preprocessing the data carefully before using them as inputs to the methods. Although genomic regions are sampled far enough from each other so as to increase the likelihood of independence among loci, the assumption of no recombination within individual loci is much harder to satisfy when each locus is given by a sequence alignment, as those sequence alignments need to be long enough for phylogenetic signal.

As whole genomes become more affordable and widely available, an alternative approach to inference of evolutionary parameters is to use methods that account for recombination. The (multispecies) coalescent with recombination extends the MSC and allows for modeling the evolution of genomic regions in the presence of coalescent effects as well as recombination. However, inference under this model has thus far proven much more challenging computationally than inference under the MSC. The coalHMM framework was introduced for inferences under the MSC with recombination and has offered a promising approach for the analysis of large genomic alignments. In this framework, recombination is viewed as a spatial process operating along the genomic sequence, and an HMM whose states correspond to local genealogies captures the evolutionary dynamics.

However, coalHMM methods have been difficult to generalize beyond a simple three-taxon ultrametric tree. In the work of Dutheil et al. (2009), the investigators conducted detailed mathematical analysis in order to parameterize the transition probabilities of a four-state coalHMM. Such a manual approach of parameterizing coalHMMs for different species trees is not tenable, and more general inference methods were needed. Most recently, diCal2 (Steinrücken et al. 2019) was introduced for obtaining MLEs of evolutionary parameters under the coalescent (and MSC) with recombination given an arbitrary tree structure of the species or subpopulations. In this work, we presented the method VICAR, which uses a different approach from that of diCal2, for general inference under the MSC with recombination. VICAR uses variational inference for sampling the posterior distribution of the evolutionary parameters and uses simulations to derive an empirical coalHMM that is amenable to efficient likelihood computations. Furthermore, as VICAR explicitly builds a coalHMM, it can be used in a straightforward manner for obtaining local genealogies for the individual sites (or blocks of sites) in a genomic data set. We showed that VICAR obtains either comparable or more accurate inferences than diCal2 on a simulated three-taxon data set. We discussed the potential direction for scaling up the method to larger data sets (in terms of the number of genomes) in a divide-and-conquer fashion in the Supplemental Material (for the divide-and-conquer process, see Supplemental Fig. S1; for the results of a simulation study on a four-taxon data set, see Supplemental Tables S1–S3).

However, it is important to note that in their current implementations, diCal2 is much more optimized computationally than VICAR (e.g., implementing an algorithm for grouping neighboring sites into single large blocks). One limitation of the factorized Gaussian variational posterior used by VICAR is that the inferred variance of each individual factor will converge to the smallest variance of the true posterior (Bishop 2006). As a result, the standard deviations of the Gaussian posteriors inferred by VICAR may not be reliable. Another limitation of VICAR at this stage is the possibility of sampling illegal configurations during Monte Carlo gradient estimation. Because each node height and each population size have an independent Gaussian posterior, a configuration of child node having higher node height than parent node, or of a branch with negative population size, could be sampled during Monte Carlo samplings of the posterior for gradient estimation. To avoid this problem, VICAR currently needs to have an initialization that sets each node far enough from each other and sets each population size far from zero. Future methods that build on VICAR can explore whether different parameterizations and/or variational families can address these quirks.

The runtime scalability of our method depends primarily on the number of unique discretized coalescent histories simulated during variational inference. This is a consequence of the forward algorithm, which has a running time of O(k²n), where k is the number of states, n is the number of sites, and each state corresponds to an observed discretized coalescent history. Each rooted tree topology corresponds to at least one valid coalescent history, and because the number of topologies grows superexponentially with the number of taxa (Foulds and Robinson 1981), so must the number of possible coalescent histories. For each combination of species and gene topology, the number of coalescent histories is variable but can be very large (Rosenberg and Degnan 2010; Disanto and Rosenberg 2019). Having more than one bin per branch will further increase the possible number of coalescent histories for each topology.

However, the number of states may be far less than the number of valid coalescent histories for several reasons. First, it is bound by the number of loci (segmented by recombination breakpoints) in each simulated genome, which may be smaller than the size of the set of valid coalescent histories. Second, if branch lengths are long and/or population sizes are small, the frequency of coalescent histories more congruent with the species phylogeny will increase (and the frequency of less congruent histories will decrease). Therefore, to fully understand the scaling properties of our method in relation to parameters such as the number of taxa, branch lengths, population sizes, and species topology will require follow-up studies that make advances through theoretical or empirical analysis regarding the distribution of observed unique discretized coalescent histories.

Both diCal2 and VICAR assume that the demographic, or evolutionary, structure is known (the tree topology) and focus on estimating the (continuous) evolutionary parameters. Both methods can be coupled with a tree search procedure for a straightforward implementation of evolutionary history inference, including the topology, under the coalescent and MSC with recombination. However, such an implementation could face many of the challenges associated with phylogenetic inference in general owing to the discrete nature of the search space as well as the complexity of the likelihood surface and posterior distribution. Furthermore, although in this work we focused on tree-structured models, the approach underlying VICAR is extendible to network structures, thus allowing for modeling gene flow as well, which we identify as a direction for future research. In principle, all kinds of generalizations are possible as long as they can be simulated. Examples would include nonconstant demographic functions such as linear, stepwise, or exponential changes in population sizes, as well as ancient hybridization. Our new approach will be immediately useful to researchers working at the intersection of population genetics and phylogenetics but also represents an additional step forward in terms of applying coalHMMs to biological systems beyond the relatively simple human–chimp–gorilla tree.

Methods

Simulation-based likelihood approximation

For a fixed species tree topology Ψ, given a specific Θ and a sequence alignment $\mathcal{S}$, we seek to compute the likelihood of Θ given by $P\left(\mathcal{S}|\mathrm{\Theta }\right)$. Note that this likelihood marginalizes over the local genealogy at each site. Algorithm 1 gives the procedure for approximate likelihood computation.

Algorithm 1: Approximate likelihood —

Input: Species tree topology Ψ. Sequence alignment $\mathcal{S}$. Continuous parameters Θ. Number of sub-branches nb. Simulation length ℓ.

Output: Approximate likelihood $P\left(\mathcal{S}|\mathrm{\Theta }\right)$.

1. $\mathcal{G}=g_1,g_2,\dots ,g_k\leftarrow \mathbf{C}\mathbf{R}\left(\mathrm{\Psi },\mathrm{\Theta },\rho ,\ell \right)$;

2. $\mathcal{M}\leftarrow \mathbf{B}\mathbf{u}\mathbf{i}\mathbf{l}\mathbf{d}\mathbf{c}\mathbf{o}\mathbf{a}\mathbf{l}\mathbf{H}\mathbf{M}\mathbf{M}\left(\mathcal{G},nb,\mu \right)$;

3. $L\leftarrow \mathbf{F}\mathbf{o}\mathbf{r}\mathbf{w}\mathbf{a}\mathbf{r}\mathbf{d}\left(\mathcal{S},\mathcal{M}\right)$;

4. return L;

Coalescent with recombination (CR) runs a coalescent-with-recombination simulator to generate a sequence $\mathcal{G}$ of k local genealogies corresponding to ℓ sites under the model specified by Ψ and Θ. Here, each of the k genealogies correspond to a contiguous genomic region of one or more sites, the genomic regions of the genealogies are pairwise disjoint, and the concatenation of the k genomic regions yields a region of ℓ sites. Each of the k genomic regions is recombination-free, and every two consecutive regions are separated by at least one recombination event. In the implementation, we use msprime (Kelleher et al. 2016), a reimplementation of Hudson's classical ms simulator (Hudson 2002) for efficient coalescent simulations. There is clearly a trade-off between computational requirements and accuracy when setting the value of ℓ, which we discuss in the Results section.

After the sequence $\mathcal{G}$ of gene trees is produced, BuildcoalHMM empirically builds a coalHMM as follows. In its basic version, BuildcoalHMM builds a coalHMM with one state per coalescent history (Degnan and Salter 2005) given the species tree. The branch lengths of all the local gene trees simulated by msprime having the same coalescent history are averaged out to obtain the branch lengths of a representative tree for that hidden state. For example, for the species tree Ψ in Figure 9A, the basic coalHMM would have four states corresponding to the four coalescent histories HC1, HC2, HG, and CG. This is precisely the model used by Hobolth et al. (2007). However, as discussed elsewhere (Dutheil et al. 2009), having one state per coalescent history could result in unidentifiability of some of the parameters. To ameliorate this problem, BuildcoalHMM in our method can refine the states further by segmenting branches in the species tree into contiguous nonoverlapping sub-branches and refining individual coalescent histories based on this segmentation. This concept is illustrated in Figure 9B, where the internal branch separating (H,C) from the root of the tree is segmented into three sub-branches. Now, coalescent history HC1 of Figure 9A is refined into three coalescent histories, HC1.1, HC1.2, and HC1.3, each corresponding to a unique mapping of the coalescent history of h and c to a sub-branch. The number of sub-branches is controlled by the parameter nb in Algorithm 1. We explore the impact of nb on the accuracy and computational requirements in the Results section. By refining the hidden state space this way, we avoid the time-consuming debiasing procedure used by Dutheil et al. (2009), which involves conducting a large set of simulations to train linear models to predict the bias of each parameter. Finally, the transition probabilities are derived empirically from the simulated coalescent histories, estimating the rate of transition from one history to another by simple counting of the number of transitions in the simulation. By empirically constructing the coalHMM from simulated sequence, we also potentially reduce the state space explosion problem of dealing with many populations (Mailund et al. 2012; Cheng and Mailund 2020). Only coalescent histories that appear in the simulation are taken into account, and states that are not simulated are omitted without affecting the accuracy of the likelihood. The emission probabilities for each state at each alignment column of $\mathcal{S}$ are computed by Felsenstein's pruning algorithm (Felsenstein 1981) using the representative tree of each state. In the implementation, we use the BEAGLE library (Ayres et al. 2012) for efficient implementation of Felsenstein's algorithm.

Finally, once the coalHMM is built, Forward runs the forward algorithm (Durbin et al. 1998) to compute $p\left(\mathcal{S}\right)$ as an approximation of the likelihood $P\left(\mathcal{S}|\mathrm{\Theta }\right)$.

Bayesian formulation and variational inference

As noted above, the data in our case is a sequence alignment $\mathcal{S}$ on the set of taxa of the species tree. We are interested in the posterior $p\left(\mathrm{\Theta }|\mathcal{S}\right)\propto P\left(\mathcal{S}|\mathrm{\Theta }\right)p\left(\mathrm{\Theta }\right)$, where we assume a prior distribution on Θ. Exact computation of the posterior is intractable, so we use variational inference to find an approximate distribution to $p\left(\mathrm{\Theta }|\mathcal{S}\right)$. In variational inference, we posit a simple family of distributions over Θ and try to find the member of the family closest in terms of the Kullback–Leibler (KL) divergence to the true posterior $p\left(\mathrm{\Theta }|\mathcal{S}\right)$ (Bishop 2006). Denote the variational distribution we posit on Θ as Q(Θ|λ), governed by a set of free parameters λ; our goal is to approximate $p\left(\mathrm{\Theta }|\mathcal{S}\right)$ by optimizing λ to make Q(Θ|λ) as close in KL divergence to $p\left(\mathrm{\Theta }|\mathcal{S}\right)$ as possible. In variational inference, we optimize the evidence lower bound (ELBO), given by

$$\begin{array}{r}\mathcal{L}\left(\lambda \right):=E_{Q(\mathrm{\Theta }|\lambda )}[\log p(\mathcal{S},\mathrm{\Theta })-\log Q(\mathrm{\Theta }|\lambda )\left]=E_{Q(\mathrm{\Theta }|\lambda )}\right[\log P(\mathcal{S}|\mathrm{\Theta })\\ +\log p\left(\mathrm{\Theta }\right)-\log Q\left(\mathrm{\Theta }|\lambda \right)].\end{array}$$ (1)

Maximizing $\mathcal{L}\left(\lambda \right)$ amounts to minimizing the KL divergence from Q to p. To maintain the general nature of VICAR and minimize the burden on users, we use BBVI (Ranganath et al. 2014). BBVI is a stochastic optimization algorithm using noisy estimates of the gradient to maximize the ELBO, without the need for model-specific derivations (hence the “black box”). The gradient of the ELBO (Eq. 1) with respect to λ can be written (Ranganath et al. 2014) as

$${\mathrm{\nabla }}_{\lambda }\mathcal{L}=E_{Q(\mathrm{\Theta }|\lambda )}[{\mathrm{\nabla }}_{\lambda }\log Q(\mathrm{\Theta }|\lambda )\cdot (\log P\left(\mathcal{S}|\mathrm{\Theta }\right)+\log p\left(\mathrm{\Theta }\right)-\log Q\left(\mathrm{\Theta }|\lambda \right)\left)\right],$$ (2)

and its noisy unbiased Monte Carlo estimate is

$${\mathrm{\nabla }}_{\lambda }\mathcal{L}\approx \frac{1}{N}\sum _{n=1}^N[{\mathrm{\nabla }}_{\lambda }\log Q({\mathrm{\Theta }}^{(n)}|\lambda )\cdot (\log P(\mathcal{S}|{\mathrm{\Theta }}^{(n)})+\log p({\mathrm{\Theta }}^{(n)})-\log Q({\mathrm{\Theta }}^{(n)}|\lambda ))],$$ (3)

where ${\mathrm{\Theta }}^{\left(n\right)}\sim Q\left(\mathrm{\Theta }|\lambda \right)$ is the nth of N samples from the current variational distribution. All parts of the equations are known: ${\mathrm{\nabla }}_{\lambda }\log Q\left({\mathrm{\Theta }}^{\left(n\right)}|\lambda \right)$ is the score function (Cox and Hinkley 1979) of the current variational distribution, an approximation of $\log P(\mathcal{S}|{\mathrm{\Theta }}^{\left(n\right)})$ is computed by Algorithm 1 above; log p(Θ⁽ⁿ⁾) is the prior, and log Q(Θ ⁽ⁿ⁾|λ) is computation about the variational distribution itself. Using Equation 3, we can compute noisy gradients of $\mathcal{L}\left(\lambda \right)$ from samples of the variational posterior, and therefore, we are able to do stochastic gradient ascent in the space of $\mathcal{L}\left(\lambda \right)$ to optimize λ.

Factorized approximation

As the variational family of Q(Θ), we assume the variational distribution to be a factorized Gaussian. Each parameter in Θ has a univariate Gaussian with a mean and a standard deviation. That is, each population size and node height of the species tree that we are interested in is independent and has a Gaussian variational posterior with its own mean and standard deviation. We have

$$Q(\mathrm{\Theta }|\lambda )=\prod _{i=1}^M{Q}_i({\mathrm{\Theta }}_i|{\lambda }_i)=\prod _{i=1}^M\mathcal{N}({\mathrm{\Theta }}_i|{\mu }_i,{\sigma }_i),$$ (4)

where M = |Θ| is the number of continuous parameters (divergence times and population sizes) associated with Ψ.

The per-component gradient of the ELBO with respect to each component of λ then becomes

$${\mathrm{\nabla }}_{{\lambda }_d}\mathcal{L}=E_{Q(\mathrm{\Theta }|\lambda )}[{\mathrm{\nabla }}_{{\lambda }_d}\log Q_i({\mathrm{\Theta }}_i|{\lambda }_i)\cdot (\log P\left(\mathcal{S}|\mathrm{\Theta }\right)+\log p\left(\mathrm{\Theta }\right)-\log Q_i\left({\mathrm{\Theta }}_i|{\lambda }_i\right)\left)\right],$$ (5)

where λ_d belongs to the ith factor of the factorized variational distribution. For factorized Gaussian, each factor has two λ components, mean and standard deviation. Taking all together, Algorithm 2 gives the general framework of VICAR. We note that under the BBVI framework, other variational families can serve as a drop-in replacement of the factorized Gaussian. Our method is easily generalizable to many other forms of variational distributions. In future implementations, we plan to support additional variational distributions so that users can choose a more flexible variational family and, hence, better approximation posteriors.

Algorithm 2:

VICAR

Variance reduction and adaptive learning rate

Although Algorithm 2 gives the basic framework of the method, a few more challenges remain to be addressed to make it useful. In particular, the variance of the Monte Carlo estimator of the gradient given in Equation 3 can be too large to be useful. To reduce the variance of the sampled estimator, we use control variates (Ross 1997; Ranganath et al. 2014). Control variate estimators are a family of functions with equivalent expectation but smaller variance than the function being approximated by Monte Carlo. Details of the application of control variates to BBVI can be found in the work by Ranganath et al. (2014).

Another crucial challenge is setting the learning rate schedule. A large learning rate might overshoot the optimum, but a small learning rate might never converge. Moreover, the variational distribution in our problem has different scales (the scale of the population sizes and the node heights are different), so we would like our learning rate to be able to handle the smallest scale while not being too small for the largest scale. As a result, we implement the AdaGrad (Duchi et al. 2011) optimizer to adaptively set the learning rate. AdaGrad adapts each learning rate by scaling it inversely proportional to the square root of the sum of all the squared past values of the gradient, resulting in greater progress in the more smoothly sloped direction of the parameter space and smaller progress otherwise. AdaGrad is a per-parameter updater, meaning it has a different adaptive learning rate for each parameter, addressing the multiscale problem of our distribution. Other off-the-shelf optimizers like RMSProp (Tieleman and Hinton 2012) and Adam (Kingma and Ba 2015) can also be easily implemented within our framework.

Software availability

VICAR has been implemented in Java and is freely available as part of the software package PhyloNet (Than et al. 2008; Wen et al. 2018), available for download at https://github.com/NakhlehLab/PhyloNet and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.