Abstract
Coronavirus disease (COVID-19) is a unique worldwide pandemic. With new mutations of the virus with higher transmission rates, it is imperative to diagnose positive cases as quickly and accurately as possible. Therefore, a fast, accurate, and automatic system for COVID-19 diagnosis can be very useful for clinicians. In this study, seven machine learning and four deep learning models were presented to diagnose positive cases of COVID-19 from three routine laboratory blood tests datasets. Three correlation coefficient methods, i.e., Pearson, Spearman, and Kendall, were used to demonstrate the relevance among samples. A four-fold cross-validation method was used to train, validate, and test the proposed models. In all three datasets, the proposed deep neural network (DNN) model achieved the highest values of accuracy, precision, recall or sensitivity, specificity, F1-Score, AUC, and MCC. On average, accuracy 92.11%, specificity 84.56%, and AUC 92.20% values have been obtained in the first dataset. In the second dataset, on average, accuracy 93.16%, specificity 93.02%, and AUC 93.20% values have been obtained. Finally, in the third dataset, on average, the values of accuracy 92.5%, specificity 85%, and AUC 92.20% have been obtained. In this study, we used a statistical t-test to validate the results. Finally, using artificial intelligence interpretation methods, important and impactful features in the developed model were presented. The proposed DNN model can be used as a supplementary tool for diagnosing COVID-19, which can quickly provide clinicians with highly accurate diagnoses of positive cases in a timely manner.
Keywords: COVID-19, Blood tests, Diagnosis, Machine learning, Deep learning
1. Introduction
Following the December of 2019, the SARS-CoV-2 first reported in Wuhan, China [1], [4], [5], [6], [7], [9], [10] caused a pandemic (declared by World Health Organization (WHO) on March 11th, 2020) [1], [5], [9] by inducing respiratory infection (called COVID-19) with symptoms typical of fever, tiredness, and coughs [5], [7], [9]. While being highly contagious [1], in some cases, COVID-19 infection could be asymptomatic making it capable of spreading at an increasing pace [2], [6], [7]. This poses a challenge to most of the countries worldwide with a much more burden on developing and less-developed countries.
Currently, after more than a year of COVID-19 pandemic onset, multiple vaccines have been introduced, and the vaccination process is progressing at a promising but non-homogenous pace among different countries. Naturally, developed countries have faster and more comprehensive access to vaccines, while other countries are facing multiple hindrances progressing in vaccination course of action like shortage of sufficient vaccine doses for the vaccination of vulnerable groups. Moreover, there are still no confirmed medications to cure patients infected with COVID-19 [1]. Thus, the importance of screening patients suspected to be infected with the SARS-CoV-2 has not declined [1].
Multiple diagnostic methods have been adopted by physicians, including Reverse Transcription-Polymerase Chain Reaction (RT-PCR) [1], [5], [6], imaging solutions (i.e., Chest Radiography (Chest X-ray), and Chest Computed Tomography (Chest CT)), and blood tests. RT-PCR, which is the gold standard for the diagnosis of COVID-19 infection [6], suffers from a low sensitivity (60–71%), longer waiting time for the results [2], [3], [5], [6], and poses additional burdens on the healthcare system requiring costly equipment [1], [7]. Also, there might be a shortage of testing kits, reagents as well as trained personnel for the diagnosis process, especially in the less developed countries [2], [7]. For these reasons, scientists are looking for more accessible methods of diagnosis among which imaging methods have received special interest.
Chest X-ray and chest CT are the two mainstream imaging options available for detecting COVID-19 infection. Chest CT offers a better sensitivity [2], [10], even compared to RT-PCR [7], but on the other hand, raises multiple concerns like radiation safety, hospital-acquired infection, and lower access rates to CT devices [2], [6], [10], [11]. Chest X-ray, a less expensive imaging option, unlike CT, imposes a lower radiation dose to the patient and is available in almost every hospital and most of the clinics, thus effectively provides more access for the patients [2]. Similar to CT, Chest-X-ray provides doctors with imaging indications of SARS-CoV-2 infection including ground-glass opacity, etc. [5], but suffers from a high rate of false-negative results [2], [6].
Blood tests are widely available and cost less compared to RT-PCR and imaging tests. Since biochemical parameters included in routine blood tests such as lactate dehydrogenase (LDH), C-reactive protein (CRP), etc., change in the course of the COVID-19 infection, they may provide physicians with information about the diagnosis of COVID-19 [1], [7]. As a result, blood tests may provide a potentially valuable tool for the fast screening of infected patients and compensate for the shortage of RT-PCR and CT scan by providing a timely initial stage of detection.
From the very first days of the pandemic onset, efforts have been made by the artificial intelligence (AI) community to develop tools that could help clinicians with diagnostic procedures. Multiple machine learning and deep learning models have so far been introduced, which can detect SARS-CoV-2 infection using Chest X-ray [11], [12] and Chest CT images [7], [8] with promising results. Even the most skilled and experienced physicians cannot rely solely on routine blood tests results to differentiate COVID-19 from other sources of infection [1]. Therefore, another aspect of those efforts is directed to the use of the machine and deep learning models to detect the specific pattern of changes seen in routine blood tests and to identify patients with SARS-CoV-2 infection [1]. This approach can be of great help for clinicians because of the inherent advantage of blood tests and could be adopted as a complementary tool to other diagnostic procedures.
Different machine learning and deep learning models have so far been proposed in different publications to diagnose COVID-19 from routine blood tests [1], [2], [4], [6], [9], [13]. For example, in a study conducted by Kukar et al. [1], a machine learning model was developed based on a dataset containing routine blood test results of 160 COVID-19 positive patients and 5333 patients with other types of viral and bacterial infections. They could achieve a sensitivity of 81.9%, a specificity of 97.9%, and an Area under the Curve (AUC) of 0.97. Plante et al. [4] developed a machine learning model using data from 192,779 patients and achieved an area under the receiver operating characteristic (AUROC) of 0.91. Thell et al. [13] examined the effective parameters in diagnosing patients with COVID-19 using standard blood tests in their study. They examined 590 patient samples (ranging in age from 20 to 100 years, including 276 women and 314 men) from five hospitals in Vienna, Austria, 208 of whom had a positive PCR test. The AUC of their model was 0.915. The findings of this study suggest that leukopenia, eosinopenia, and increased hemoglobin are particularly useful for distinguishing between positive and negative COVID-19 patients.
Despite reporting promising results, the credibility of many of the models was questioned in literature [14]. A general issue that affected the publications in this field is poor or unclear reporting. In this study, we present the development and comparison of seven machine learning models and four deep learning models for diagnosing positive cases of COVID-19 using three datasets of routine laboratory blood tests. Our study differs from many similar studies in terms of the methodology we applied to reduce the risk of bias, the unique structure of the models, evaluating time efficiency of the proposed models, and since we used transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD) for reporting our results [15]. The remaining parts of this study are as follows: the materials and methods section (that describes the methods steps, source of data, outcome, predictors, sample size, statistical analysis and methods, and development vs. validation), the result section (including participants, and model performance), the discussion (which includes interpretation and limitations), and the conclusion (containing other information about and future of the study).
2. Materials and methods
First, the input data were preprocessed. Then, the relevance of the samples presented in datasets was investigated using three different correlation coefficient methods, namely Pearson, Spearman, and Kendall, and visualized subsequently. In the third step, to perform four-fold cross-validation, the datasets were divided into three sub-datasets: training, validation, and testing. In the fourth step, machine learning and deep learning models of this study are selected experimentally with the best parameters, and the proposed models started training, validation, and testing. Then, the important features were examined and displayed based on the SHAP method. Next, the results of the diagnosis of COVID-19 and non-COVID-19 cases were reviewed based on evaluation criteria in machine learning and deep learning models. In the seventh step, the results of the models were compared using a paired-sample t-test for a statistical significant difference. As the last step, features (based on their weight and classification effectiveness), which effectively identified and decided the best model proposed in this study, were reviewed and interpreted using three methods: SHAP, ELI5, and LIME.
2.1. Datasets
Three open access study datasets [2], [6], [9] containing routine blood tests data of COVID-19 and non-COVID-19 cases were used. The number of labels and the number of samples in each dataset are shown in Table 1 . Features of the datasets and the number of data items in each dataset are shown in Table 2 .
Table 1.
Characteristics of the three datasets.
Table 2.
The total number of features of each dataset.
| Dataset | Features | Number of features |
|---|---|---|
| First dataset [2] | Gender, Age, Leukocytes (WBC), Platelets, C-reactive Protein (CRP), Transaminases (AST), Transaminases (ALT), Gamma Glutamil Transferasi (GGT), Lactate dehydrogenase (LDH), Neutrophils, Lymphocytes, Monocytes, Eosinophils, Basophils | 15 |
| Second dataset (OSR dataset) [6] | White blood cells (WBC), Red blood cells (RBC), Hemoglobin (HGB), Hematocrit (HCT), Mean corpuscular volume (MCV), Mean Corpuscular hemoglobin (MCH), Mean Corpuscular hemoglobin concentration (MCHC), Erythrocyte distribution width (RDW), Platelets (PLT), Mean platelet volume (MPV), Neutrophils count (NE), Lymphocytes count (LY), Monocytes count (MO), Eosinophils count (EO), Basophils count (BA), Neutrophils count (NET), Lymphocytes count (LYT), Monocytes count (MOT), Eosinophils count (EOT), Basophils count (BAT), Prothrombin time (PTINR), Activated partial thromboplastin time (PPTR), Fibrinogen (FG), D-dimer (XDP), Glucose (GLU), Creatinine (CREA), Urea (UREA), Direct bilirubin (BILD), Indirect bilirubin (BILIN), Total bilirubin (BILT), Alanine aminotransferase (ALT), Aspartate aminotransferase (AST), Alkaline phosphatase (ALP), Gamma glutamyl transferase (GGT), Lactate dehydrogenase (LDH), Creatine kinase (CK), Sodium (NA), Potassium (K), Calcium (CA), C-reactive protein (CRP), NT-proB-type natriuretic peptide (PROBNP), Troponin T (TROPOT), Interleukin (IL), pH (PHPOC), Carbonic anhydride (CO POC), Oxygen (PO POC), Bicarbonates (BICPOC), Standard calculated bicarbonates(BISPOC), Base excess (BEPOC), Actual base excess (BEEPOC), Hematocrit (PHCTPOC), Total oxyhemoglobin (THBPOC), O saturation (SO POC), Oxyhemoglobin/Total hemoglobin (FO POC), Carboxyhemoglobin (FCOPOC), Methemoglobin (METPOC), Deoxyhemoglobin (HHBPOC), Bound O maximum concentration (BO POC), Total oxygen (CTOPOC), Inspired oxygen fraction (FIOPOC), Inspired O /O ratio (OFIPOC), Sodium (NAPOC), Potassium (KPOC), Chloride (CLPOC), Ionized calcium (CAPOC), Standard ionized calcium (CASPOC), Anion gap (ANGPOC), Glucose blood gas (GLUEMO), Lactate (LATPOC), Age (Age), Gender (Sex), COVID-suspect (patient suffers from COVID-specific symptoms at triage) (Suspect*) | 34 |
| Third dataset [9] | Patient age quantile, Hematocrit, Hemoglobin, Platelets, Red blood cells, Lymphocytes, Leukocytes, Basophils, eosinophils, Monocytes, Serum glucose, Neutrophils, Urea, C reactive protein, Creatinine, Potassium, Sodium, Alanine Transaminase, Aspartate transaminase | 19 |
This is not a laboratory feature, and due to the same conditions, it has been used to compare the results of the proposed models of this study with the study [6].
2.2. Data preprocessing
To balance and organize samples of the datasets, the Pandas library in the python programming language is used to fill in unspecified values with the average value of each feature. Also, the Sklearn library is used to normalize the datasets. Normalization is the process of scaling individual samples to have a unit scale. The Min-Max normalization method is used, which in addition to unifying the data scale, changes the boundaries in the range (0, 1). This method is as follows:
| (1) |
In Eq. (1), represents the maximum values and represents the minimum data values.
In all datasets, we labeled COVID-19 disease with the number 0 and non-COVID-19 disease with the number 1.
2.3. Investigate data relevancies
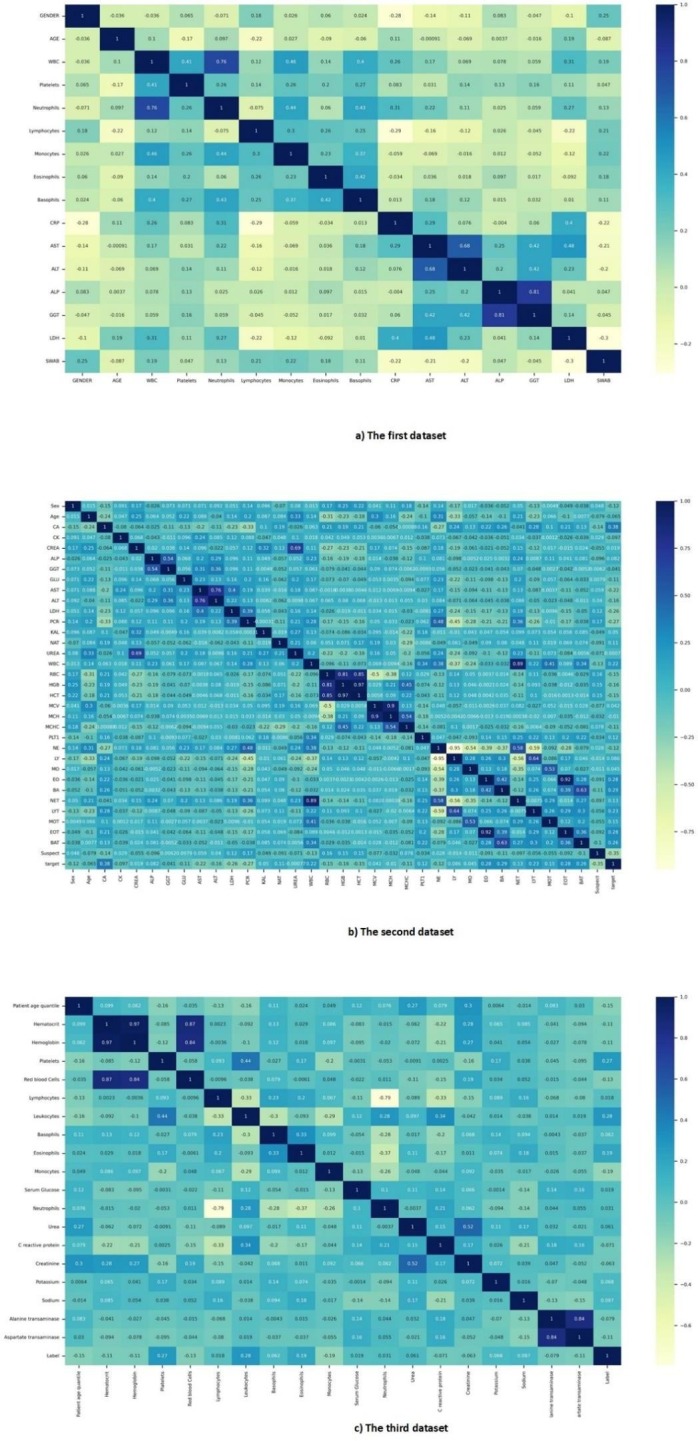
Three statistical methods were used to examine the correlation of samples of each dataset. Pearson, Spearman, and Kendall correlation coefficients were used in this study [16], [17], [18]. The result of Pearson correlation coefficient reflects the relevance of the features for the different datasets is shown in Fig. 1 . Also, the results of other correlation coefficients are given in Fig. AP-1, Fig. AP-2 in Appendix A.
Fig. 1.
Pearson correlation coefficient map of all datasets.
Fig. AP-1.
Spearman correlation coefficient map of all datasets.
Fig. AP-2.
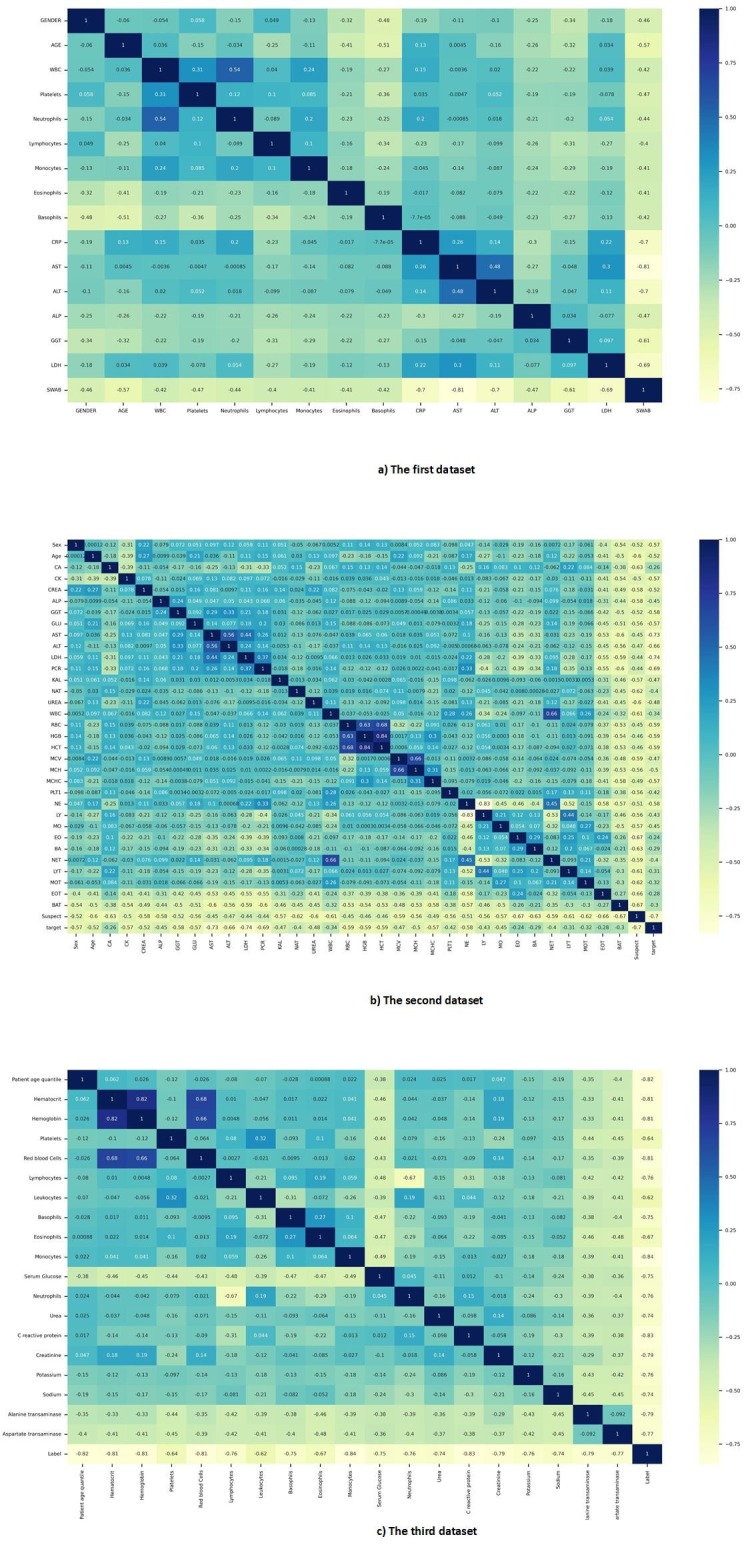
Kendall correlation coefficient map of all datasets.
2.4. Machine learning and deep learning models
Machine learning (ML) is a fast-growing branch of AI which is making its way into biomedicine [19], [21], [22]. This branch of AI attempts to use algorithms to design machines for learning and predicting without explicitly planning. In ML, instead of programming everything from the ground, the data is given to a general algorithm, and it is this algorithm that learns its logic based on the data provided to it. Deep learning (DL) is a type of machine learning, which mimics the way the human mind learns a particular subject [20]. DL provides a better understanding of realities and can identify different patterns at complicated tasks. This technique is used to automate predictions. Also, conventional machine learning algorithms are usually linear, but deep learning algorithms are generally nonlinear and learn complex concepts.
In this study, seven machine learning methods including Logistics Regression (LR), K Nearest Neighbors (KNN), Decision Tree (DT), Support Vector Machine (SVM), Naive Bayes (NB), Extremely Randomized Trees (ET), Random Forest (RF), and XGBoost [19], [23], [24], along with four deep learning methods including Deep Neural Network (DNN), Convolutional Neural network (CNN), Recurrent Neural Network (RNN), and Long Short-term Memory (LSTM) [20], have been developed and trained to evaluate the diagnosis of COVID-19 disease from routine blood tests. The routine blood tests used in this study are tests in which the number of white blood cells (WBC) or leukocytes is precisely determined [25]. The seven models of machine learning and four models of deep learning that have been proposed in this study are among the most popular and prevalent models. These prevailing models have been used after training to predict the two-state label, so in this study, these models have been used to diagnose COVID-19 disease from routine blood tests.
Logistic regression is a machine learning algorithm, which is used to predict the probability of a dichotomous target variable, meaning that only two classes may exist [19]. It is one of the simplest machine learning algorithms, which used to classify a variety of problems. K Nearest Neighbors is one of the simplest machine learning algorithms. In this algorithm, a sample is classified by a majority vote of its neighbors. K is a positive integer value and is generally small. K nearest neighbors is used for many problems because it is efficient, non-parametric, and easy to implement. The best value selected for k depends on each dataset [19]. Decision tree is a predictive modeling tool that is used in many fields. The decision tree can be created through an algorithmic solution that can differentiate data sets based on different conditions in different ways. It has two main elements, the decision nodes that split the data and the leaves that get the output [19].
Support vector machine is a machine learning algorithm used for prediction and classification problems [19]. Support Vector Machine (SVM) presents multiple classes in multidimensional space as a hyperplane. The closest data points to the hyperplane are called support vectors. With the help of these data points, the dividing line will be defined. A hyperplane is a plan or decision space, which divides a set of objects into different classes. The term boundary refers to how far two lines on the nearest data points with different classes are located. Support vector machine algorithm is practically implemented by a kernel. This kernel converts the input data space into a suitable format. The support vector machine uses a kernel trick that takes a small input space and turns it into a larger space [19]. The main purpose of a support vector machine is to partition datasets into several classes and find a hyperplane with a maximum margin [19].
Naive Bayes algorithm is a fast, easy-to-implement machine learning model used for classification and prediction [19]. The principles of this classification are based on Bayes' theorem, according to Eq. (2).
| (2) |
According to Eq. (2), the probability of occurrence of event A is considered in case B occurs. Here, B is the evidence, and A is the hypothesis.
Extremely randomized tree is a machine learning algorithm based on decision trees [23]. This algorithm generates a large number of decision trees from the training dataset. Using majority voting, predictions are made for classification [23]. Random forest is one of the traditional algorithms in machine learning [19]. First, the random forest makes trees on the data samples. Then, it predicts each of them, and in the last step, it chooses the best solution through voting [19]. This algorithm is a group decision method. It reduces over-fitting by averaging the result. Therefore, it is better than one single decision tree [19]. XGBoost is an algorithm that is used in machine learning [24]. XGBoost algorithm is an implementation of the decision tree gradient boosting designed for high speed and performance [24].
The deep neural network is a broader category of neural networks, that its calculations are inspired by the structure of complex brain neural networks. It included a large number of neurons, hidden layers, input, output, and activation functions [20]. The convolutional neural network consists of layers of convolution, pooling, fully connected, classification, and activation functions. The convolution layer can extract features, unlike other machine learning methods. The pooling layer is a prototype operation, usually applied after a convolution layer, which in part leads to spatial inversion. Maximum and average pooling are specific types of pooling that take the maximum and average values, respectively. Fully connected layers are usually found at the end of the convolutional neural network. The fully connected layer acts on a flattened input so that each input is connected to all neurons [20].
The recurrent neural network has a feedback layer that returns the network’s output to the network with the next input. The recurrent neural network can remember its previous input due to its internal memory and use this memory to process a sequence of inputs. In other words, the recurrent neural network consists of a recursive loop that prevents the information from the previous moments from being lost and keeps it in the network. The recurrent neural network has two main problems, vanishing and exploding gradient, which are solved in long short-term memory [20]. Long short-term memory can learn long-term attachments. The purpose of designing Long Short-Term Memory was to solve the problem of long-term dependencies. Memorizing information for long periods is the default and normal behavior of long short-term memory, and its structure is such that it learns very distant information well, a feature that lies in its structure [20].
2.5. Experimental implementation of models
Cross-validation is a common method for evaluating the performance of machine learning and deep learning models and a preventive measure against overfitting [26]. We used a four-fold cross-validation method to measure the performance of our proposed models in this study. According to Fig. 2 , in each iteration, a subset containing 75 percent of the data is used for training, and the remaining 25 percent is used for testing. Furthermore, we set aside another subset containing 25 percent of the training subset for validation.
Fig. 2.
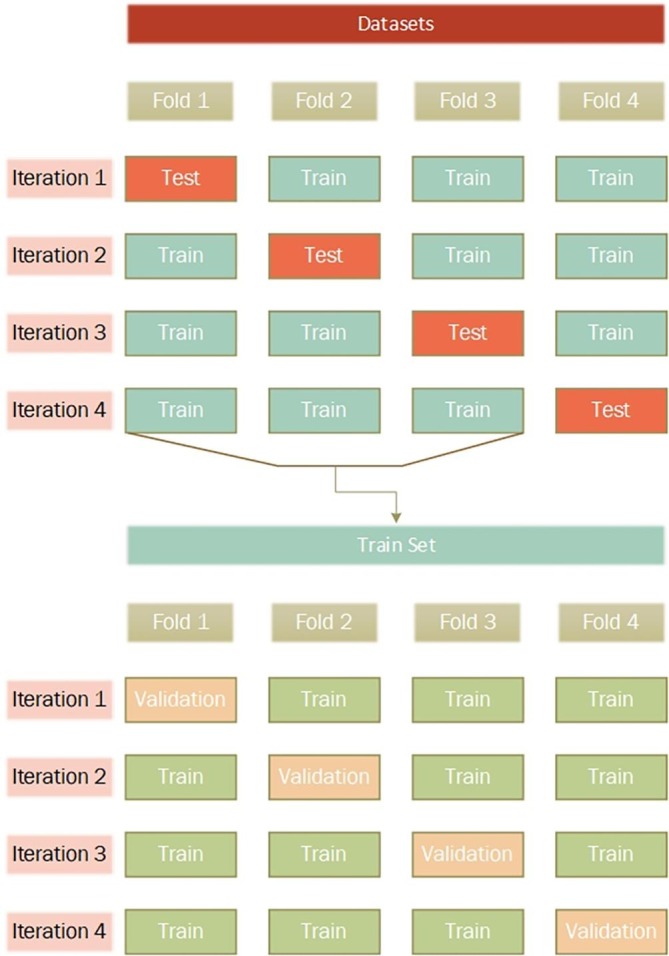
Train, Validation, and Test sections of datasets.
To implement our proposed models, we have used the Python programming language. We have used TensorFlow and Sklearn packages to create our models. The system we used included the Nvidia GTX 1650 graphics card with 4 GB of RAM and the Intel Core i7-9850h CPU. The machine learning and deep learning models proposed in this study were implemented experimentally with their various parameters. The parameters of all models were tested using the GridSearchCV method, and the range of their values was presented in detail in Appendix A, Table AP-1. The best parameters of the proposed models, which have yielded the best results, are shown in Table 3 and Table 4 . The reason for selecting these values was overfitting parameters with values greater than the selected value, and under-fitting for parameters with values less than the specified value. By implementing the proposed models with the best parameters, we were intended to predict COVID-19 positive cases using routine blood test results.
Table 3.
Description of best-selected parameters of machine learning models.
| Algorithm | Parameters |
|---|---|
| LR | penalty: l2, solver: lbfgs, max_iter: 100 |
| KNN | n_neighbors: 8, algoritgm: kd_tree, p: 2 |
| DT | criterion: gini, spliter: best, max_depth: none, max_features: none |
| SVM | C: 5, gamma: 1, kernel: rbf, decision_function_shape: ovr |
| NB | var_smoothing: 1e-1 |
| ET | n_estimators: 100, criterion: gini, max_depth: none, max_features: none |
| RF | n_estimators: 100, criterion: gini, max_depth: none, max_features: none |
| XGBOOST | booster: gbtree, eta: 0.3, max_depth: 6, sampling method: gradiant_based |
Table 4.
Description of best-selected parameters of deep learning models.
| Algorithm | Number of units | Number of layers | Number of full connected units | Number of fully connected layers | Learning rate | Number of epochs (in each fold) | Batch size | Optimizer | Loss function | Dropout | Activation function of layers | Last layer’s activation function |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DNN | – | – | 34, 68, 136, 272, 544, 1088, 544, 272, 136, 68, 34, 1 | 1–12 | 1e-4 | 50 | 21 | Binary cross-entropy | Adam | – | Tanh | Sigmoid |
| CNN | 128, 64 | 1, 2 | 32, 16, 1 | 1–3 | 1e-4 | 50 | 21 | Binary cross-entropy | Adam | 0.1 | Tanh | Sigmoid |
| RNN | 64 | 1 | 32, 16, 1 | 1–3 | 1e-4 | 50 | 21 | Binary cross-entropy | Adam | 0.1 | Tanh | Sigmoid |
| LSTM | 64 | 1 | 32, 16, 1 | 1–3 | 1e-4 | 50 | 21 | Binary cross-entropy | Adam | 0.1 | Tanh | Sigmoid |
2.6. Performance testing of the developed model
The paired sample t-test is a common statistical hypothesis test used to check the differences between the results of several models and their datasets [27]. The performance of the proposed models was tested using t-test at priory level of 0.05 (p-value < 0.05) [27], [28]. The random forest algorithm with the SHAP library in Python programming language was used to determine the importance of the features in the models. The value of the SHAP determines the importance of each feature, the high or low value of each feature, and its impact based on the model output [29]. To interpret the final model of this study, we used tools such as SHAP, ELI5, and LIME [29], [30], [31]. This way, we can understand the internal performance of the model and gain insight into the application. This insight can well demonstrate the importance, effectiveness, and rank of the features used by the model.
3. Results
3.1. Results of implemented models
The confusion matrix in Fig. 3 , is a table with two rows and two columns that describe the numbers of true positives, false positives, false negatives, and true negatives. This allows us to have a more accurate analysis of the correct prediction [32].
Fig. 3.
Confusion matrix. TP, FP, TN, and FN are True Positives, False Positives, True Negatives, and False Negatives, respectively.
In this study, TP is correctly indicated as COVID-19, FP is incorrectly indicated as COVID-19, TN is correctly indicated as non-COVID-19, and FN is incorrectly indicated as non-COVID-19 in the models. The criteria we used for evaluating our machine learning and deep learning models are as follows [33], [34], [35]:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
All laboratory features (tests) of all three datasets are given to the experimentally implemented models. Then, to evaluate the performance of the proposed models, the values of accuracy, precision, recall or sensitivity, specificity, F1-Score, area under the curve (AUC), and Matthews correlation coefficient (MCC) [33], [34], [35] were calculated for each of them. The average performances of four-fold cross-validation of machine learning models are shown in Table 5 , and the deep learning models are also given in Table 6 .
Table 5.
Average performance evaluation of machine learning models for all test datasets.
| Dataset | Model | Accuracy (%) | Precision (%) | Recall or Sensitivity (%) | Specificity (%) | F1-Score (%) | AUC (%) | MCC (%) |
|---|---|---|---|---|---|---|---|---|
| First Dataset [2] | LR | 67.14 | 97.50 | 63.93 | 88.89 | 77.23 | 62.10 | 35.73 |
| KNN | 67.14 | 92.50 | 64.91 | 76.92 | 76.29 | 62.90 | 32.87 | |
| DT | 78.57 | 85.00 | 79.07 | 77.78 | 81.93 | 77.50 | 55.92 | |
| SVM | 68.57 | 90.00 | 66.67 | 75.00 | 76.60 | 65.00 | 35.36 | |
| NB | 67.14 | 70.00 | 71.79 | 61.29 | 70.89 | 66.70 | 33.21 | |
| ET | 80.00 | 97.50 | 75.00 | 94.44 | 84.78 | 77.10 | 61.33 | |
| RF | 78.57 | 92.50 | 75.51 | 85.71 | 83.15 | 76.30 | 56.69 | |
| XGBOOST | 76.72 | 85.28 | 79.52 | 70.60 | 81.85 | 74.95 | 49.89 | |
| Second dataset (OSR Dataset) [6] | LR | 84.73 | 81.99 | 87.82 | 81.82 | 84.80 | 84.80 | 69.66 |
| KNN | 77.83 | 72.99 | 82.35 | 73.97 | 77.39 | 78.00 | 56.19 | |
| DT | 75.62 | 76.30 | 76.67 | 74.49 | 76.48 | 75.60 | 51.17 | |
| SVM | 83.25 | 81.52 | 85.57 | 80.98 | 83.50 | 83.30 | 66.60 | |
| NB | 79.80 | 83.89 | 78.67 | 81.22 | 81.19 | 79.60 | 59.58 | |
| ET | 84.98 | 82.46 | 87.88 | 82.21 | 85.09 | 85.10 | 70.12 | |
| RF | 83.99 | 81.04 | 87.24 | 80.95 | 84.03 | 84.10 | 68.21 | |
| XGBOOST | 81.09 | 81.37 | 80.07 | 82.15 | 80.62 | 81.12 | 62.24 | |
| Third dataset [9] | LR | 88.00 | 33.33 | 38.46 | 92.70 | 35.71 | 63.7 | 29.22 |
| KNN | 90.67 | 20.00 | 60.00 | 91.72 | 30.00 | 59.30 | 30.95 | |
| DT | 80.67 | 60.00 | 28.13 | 94.92 | 38.30 | 71.50 | 31.46 | |
| SVM | 90.67 | 46.67 | 53.85 | 94.16 | 50.00 | 71.10 | 45.02 | |
| NB | 83.33 | 60.00 | 32.14 | 95.08 | 41.86 | 73.00 | 35.36 | |
| ET | 92.00 | 33.33 | 71.43 | 93.01 | 45.45 | 65.90 | 45.30 | |
| RF | 90.67 | 46.67 | 53.85 | 94.16 | 50.00 | 71.10 | 45.02 | |
| XGBOOST | 88.64 | 44.96 | 61.19 | 91.77 | 50.03 | 69.92 | 45.70 |
Table 6.
Average performance evaluation of deep learning models for all test datasets.
| Dataset | Model | Accuracy (%) | Precision (%) | Recall or Sensitivity (%) | Specificity (%) | F1-Score (%) | AUC (%) | MCC (%) |
|---|---|---|---|---|---|---|---|---|
| First dataset [2] | DNN | 92.11 | 91.86 | 96.14 | 84.56 | 93.88 | 92.20 | 82.50 |
| CNN | 72.77 | 87.57 | 75.52 | 69.07 | 80.10 | 69.95 | 41.90 | |
| RNN | 76.01 | 84.90 | 78.63 | 70.34 | 81.22 | 73.97 | 48.34 | |
| LSTM | 68.49 | 84.92 | 73.07 | 69.10 | 77.02 | 65.77 | 34.45 | |
| Second dataset (OSR Dataset) [6] | DNN | 93.16 | 92.09 | 93.27 | 93.02 | 92.63 | 93.20 | 86.33 |
| CNN | 81.03 | 77.21 | 82.64 | 79.70 | 79.76 | 81.00 | 62.19 | |
| RNN | 81.52 | 76.89 | 83.72 | 80.06 | 80.00 | 81.17 | 63.05 | |
| LSTM | 76.23 | 81.88 | 72.83 | 80.72 | 76.93 | 76.20 | 52.96 | |
| Third dataset [9] | DNN | 93.33 | 69.07 | 77.05 | 95.47 | 72.49 | 85.97 | 69.04 |
| CNN | 88.49 | 41.51 | 76.89 | 91.45 | 48.84 | 68.65 | 48.49 | |
| RNN | 88.99 | 51.77 | 63.44 | 92.83 | 55.62 | 73.17 | 50.58 | |
| LSTM | 78.50 | 32.58 | 37.29 | 89.81 | 19.36 | 59.22 | 17.06 |
The ET model has the best performance in most evaluation criteria among the machine learning models in all test datasets. The ET model, in the first test dataset, was able to achieve 80%, 97.50%, 75%, 94.44%, 84.78%, 77.10%, and 61.33% as the average values of accuracy, precision, recall or sensitivity, specificity, F1-Score, AUC, and MCC, respectively. In the second test dataset, the ET model was able to obtain values of 84.98%, 82.46%, 87.88%, 82.21%, 85.09%, 85.10%, and 70.12% as the average for accuracy, precision, recall or sensitivity, specificity, F1-Score, AUC, and MCC. Also, in the third test dataset, the average values of accuracy, precision, recall or sensitivity, specificity, F1-Score, AUC, and MCC in the ET model were obtained 92%, 33.33%, 71.43%, 93.01%, 45.45%, 65.90%, and 45.30%, respectively.
Between the deep learning models presented in this study, the DNN model in all three datasets test sections was able to show the best performance in all performance evaluation criteria. Table 7 shows the full performance of the DNN model in all folds for all test datasets.
Table 7.
DNN model performance in all folds for all test datasets.
| Dataset | Folds | Accuracy (%) | Precision (%) | Recall or Sensitivity (%) | Specificity (%) | F1-Score (%) | AUC (%) | MCC (%) |
|---|---|---|---|---|---|---|---|---|
| First dataset [2] | Fold 1 | 88.57 | 93.75 | 90.00 | 85.00 | 91.84 | 85.50 | 72.98 |
| Fold 2 | 87.14 | 83.33 | 94.59 | 78.79 | 88.61 | 88.10 | 74.77 | |
| Fold 3 | 95.65 | 94.23 | 100 | 85.00 | 97.03 | 97.10 | 89.50 | |
| Fold 4 | 97.10 | 96.15 | 100 | 89.47 | 98.04 | 98.10 | 92.75 | |
| Average | 92.11 | 91.86 | 96.14 | 84.56 | 93.88 | 92.20 | 82.50 | |
| Second dataset (OSR Dataset) [6] | Fold 1 | 91.63 | 89.00 | 93.68 | 89.81 | 91.28 | 91.6 | 83.34 |
| Fold 2 | 92.61 | 89.50 | 95.21 | 90.37 | 92.27 | 92.60 | 85.36 | |
| Fold 3 | 94.09 | 94.38 | 92.31 | 95.54 | 93.33 | 94.10 | 88.04 | |
| Fold 4 | 94.33 | 95.51 | 91.89 | 96.38 | 93.66 | 94.50 | 88.60 | |
| Average | 93.16 | 92.09 | 93.27 | 93.02 | 92.63 | 93.20 | 86.33 | |
| Third dataset [9] | Fold 1 | 92.67 | 52.94 | 75.00 | 94.20 | 62.07 | 84.60 | 59.22 |
| Fold 2 | 92.00 | 63.16 | 70.59 | 94.74 | 66.67 | 82.30 | 62.26 | |
| Fold 3 | 95.33 | 84.21 | 80.00 | 97.69 | 82.05 | 90.20 | 79.41 | |
| Fold 4 | 93.33 | 76.00 | 82.61 | 95.28 | 79.17 | 86.80 | 75.30 | |
| Average | 93.33 | 69.07 | 77.05 | 95.47 | 72.49 | 85.97 | 69.04 |
In the first test dataset, the DNN model was able to obtain the average values of all folds, 92.11%, 91.86%, 96.14%, 84.56%, 93.88%, 92.20%, and 82.50%, respectively, for accuracy, precision, recall or sensitivity, specificity, F1-Score, AUC, and MCC. In the second test dataset, the DNN model was able to obtain the average of all folds values accuracy, precision, recall or sensitivity, specificity, F1-Score, AUC, and MCC equal to 93.16%, 92.09%, 93.27%, 93.02%, 92.63%, 93.20%, and 86.33%, respectively. Also, the DNN model was able to obtain the average values of accuracy, precision, recall or sensitivity, specificity, F1-Score, AUC, and MCC in all folds in the third test dataset equal to 93.33%, 69.07%, 77.05%, 95.47%, 72.49%, 85.97%, and 69.04%, respectively.
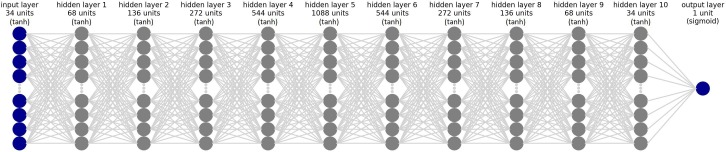
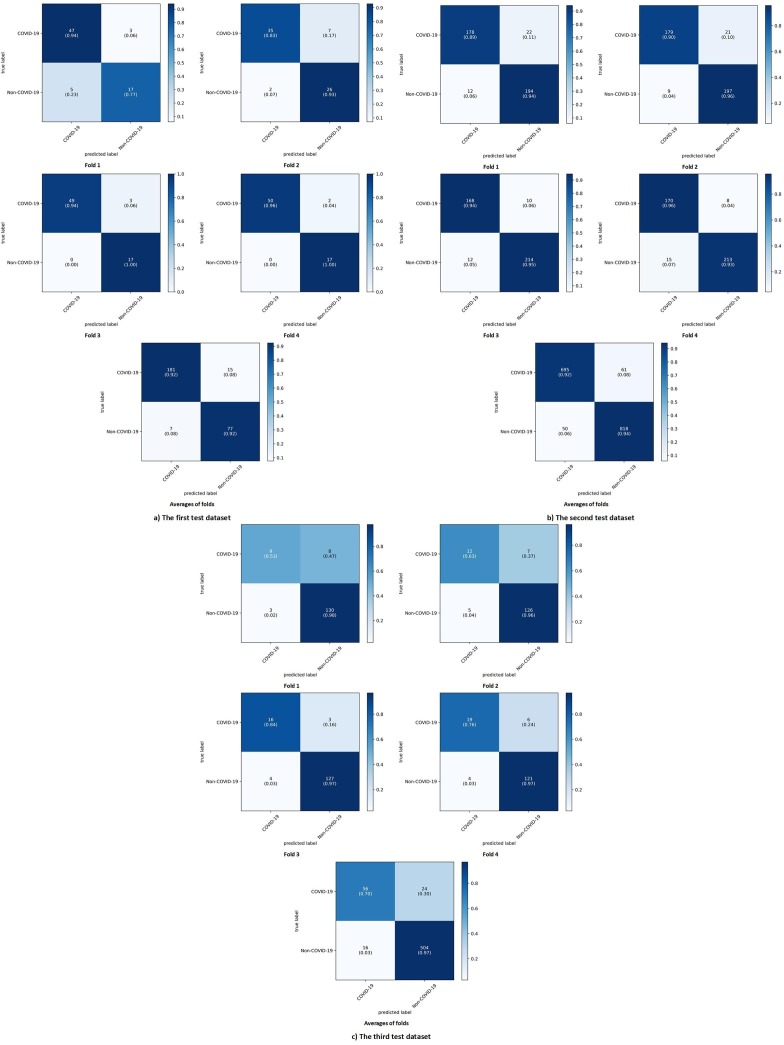
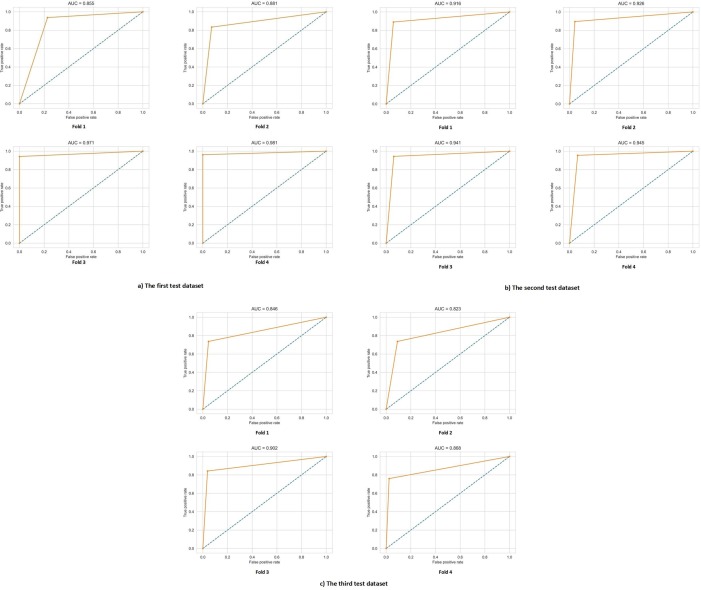
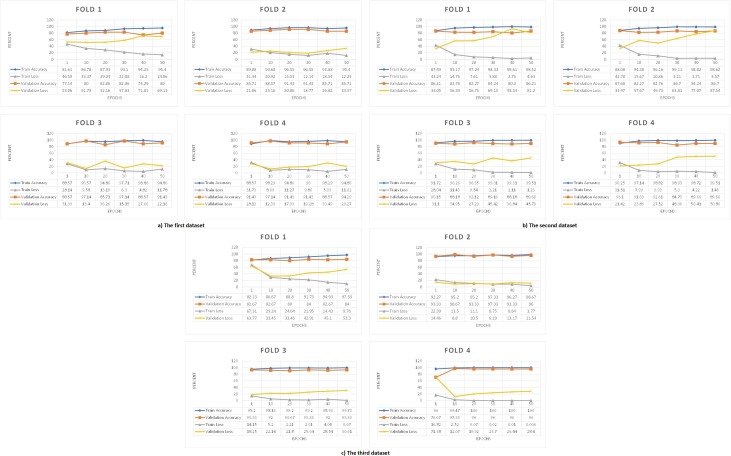
For better understanding the best model among the deep learning models, its architecture is shown in Fig. 4 . To illustrate the results and performance of the best model of this study in all three datasets test sections, their confusion matrix is shown in Fig. 5 . The AUC diagram of the best-proposed model in the test sections of all datasets in all folds is shown in Fig. 6 . Also, their accuracy and loss diagrams of train and validation are shown in Fig. 7 .
Fig. 4.
The architecture of deep neural network model (DNN).
Fig. 5.
Confusion matrix of DNN model at a) The first test dataset, b) The second test dataset, c) The third test dataset.
Fig. 6.
AUC diagram of DNN model at a) The first test dataset, b) The second test dataset, c) The third test dataset.
Fig. 7.
Accuracy and Loss diagram of DNN model train and validation sections of a) The first dataset, b) The second dataset, c) The third dataset.
3.2. Evaluating the best-implemented model
Overall, between the seven machine learning models and four deep learning models proposed in this study, the deep neural network model (DNN) in all assessment criteria in all three test datasets showed the best performance in diagnosing COVID-19 disease from routine blood tests. To better demonstrate the efficiency of the best model proposed in this study (i.e., DNN), we measured all proposed deep learning methods' training, validation, and testing time. The results of Table 8 show that the best-proposed model of this study (DNN) achieved the best time efficiency in each fold at all three datasets in the shortest possible time compared to other models.
Table 8.
Deep learning models training, validation, and testing computational times in each fold in each dataset.
Fig. 5-a and -b show correct label prediction of the first and second test datasets according to the confusion matrix results. The best model proposed in this study (DNN) was able to show very high performance in both datasets in the correct diagnosis of COVID-19 disease. The confusion matrix results of the best-proposed model for the third dataset are shown in Fig. 5-c. These results are indicative of a problem in the correct diagnosis of COVID-19 disease. Looking at Table 1, we realized the source of the problem was the imbalance between the number of COVID-19 samples and the number of non-COVID-19 samples. It is quite clear that due to the scanty of data related to the positive cases of COVID-19 in the third dataset, the number of these samples was less. The DNN model was mistaken in its diagnosis because of less observation of these samples. We randomly selected 80 non-COVID-19 samples and 80 COVID-19 samples from the third dataset to solve this problem. We re-trained, validated, and tested the models on the third balanced dataset for prediction using the four-fold cross-validation method. Table 9 shows the average evaluation results of the machine and deep learning models proposed in this paper on the third balanced dataset.
Table 9.
The performance evaluation results of machine and deep learning models on the third balanced dataset.
| Model | Accuracy (%) | Precision (%) | Recall or Sensitivity (%) | Specificity (%) | F1-Score (%) | AUC (%) | MCC (%) |
|---|---|---|---|---|---|---|---|
| LR | 85.00 | 84.62 | 91.67 | 75.00 | 88.00 | 85.20 | 68.47 |
| KNN | 70.00 | 65.38 | 85.00 | 55.00 | 73.91 | 72.00 | 41.93 |
| DT | 72.50 | 73.08 | 82.61 | 58.82 | 77.55 | 72.30 | 42.94 |
| SVM | 87.50 | 86.63 | 90.34 | 87.69 | 87.34 | 87.92 | 76.92 |
| NB | 85.00 | 88.46 | 88.46 | 78.57 | 88.46 | 83.50 | 67.03 |
| ET | 90.00 | 88.46 | 95.83 | 81.25 | 92.00 | 90.70 | 79.17 |
| RF | 85.00 | 80.77 | 95.45 | 72.22 | 87.50 | 86.80 | 70.59 |
| XGBOOST | 81.25 | 79.89 | 83.49 | 82.74 | 80.48 | 81.12 | 64.16 |
| DNN | 92.50 | 86.96 | 100 | 85.00 | 93.02 | 92.20 | 85.97 |
| CNN | 76.87 | 72.56 | 83.26 | 77.09 | 74.78 | 76.87 | 56.82 |
| RNN | 79.35 | 83.47 | 79.00 | 83.64 | 79.72 | 80.22 | 61.53 |
| LSTM | 51.25 | 100 | 50.59 | 25.00 | 67.05 | 51.12 | 5.18 |
As expected, the imbalance of the samples in the third dataset was the main reason for the wrong prediction of the models. According to Table 9, the DNN model obtained the best performance in most of the evaluation criteria in the third balanced dataset among the machine learning and deep learning models. In the third balanced dataset, on average, the DNN model was able to achieve 92.50%, 86.96%, 100%, 85.00%, 93.02%, 92.20%, and 85.97% in the criteria of accuracy, precision, recall or sensitivity, specificity, F1-Score, AUC, and MCC, respectively. The confusion matrix of the average of all folds for the DNN model in the third balanced dataset was presented in Fig. 8 .
Fig. 8.
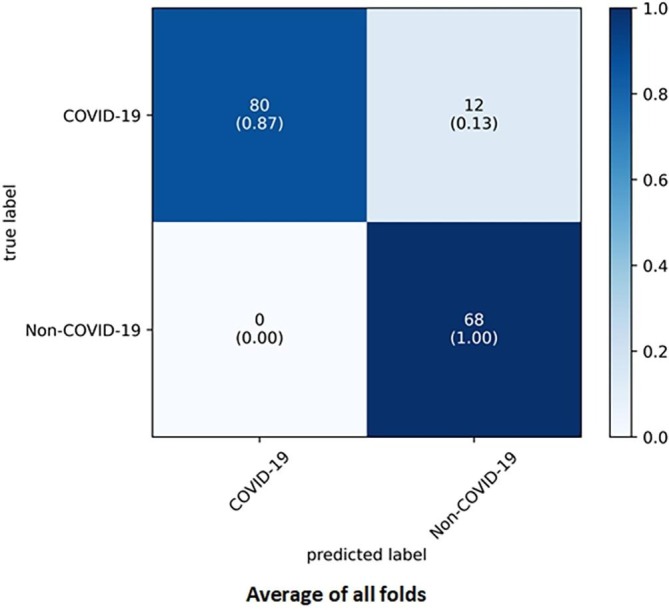
Average of all folds for DNN model in the third balanced dataset.
The p-values obtained from the paired-sample t-test based on the accuracy of our study models are shown in Table 10 . According to the results, it is ensured that the best model proposed in this study (DNN) has a significant difference in results obtained from other models.
Table 10.
Comparison of p-values of the proposed models of this study obtained from t-test.
| LR | KNN | DT | SVM | NB | ET | RF | XGB | DNN | CNN | RNN | LSTM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LR | – | 0.3106 | 0.4752 | 0.2746 | 0.1819 | 0.1282 | 0.3179 | 0.8357 | 0.0384 | 0.7429 | 0.9424 | 0.1899 |
| KNN | 0.3106 | – | 0.9296 | 0.2230 | 0.6398 | 0.0810 | 0.0881 | 0.1680 | 0.0467 | 0.1945 | 0.1454 | 0.1934 |
| DT | 0.4752 | 0.4752 | – | 0.3748 | 0.7164 | 0.0582 | 0.0651 | 0.1259 | 0.0026 | 0.3499 | 0.1550 | 0.1918 |
| SVM | 0.2746 | 0.2746 | 0.3748 | – | 0.1152 | 0.1757 | 0.5062 | 0.8639 | 0.0469 | 0.4612 | 0.7691 | 0.1755 |
| NB | 0.1819 | 0.6398 | 0.7146 | 0.1152 | – | 0.2342 | 0.0986 | 0.3553 | 0.0364 | 0.6269 | 0.4601 | 0.2900 |
| ET | 0.1282 | 0.0810 | 0.0582 | 0.1757 | 0.2342 | – | 0.1029 | 0.0353 | 0.0352 | 0.0964 | 0.0610 | 0.0796 |
| RF | 0.3179 | 0.0881 | 0.0651 | 0.5062 | 0.0986 | 0.1029 | – | 0.0091 | 0.0353 | 0.0233 | 0.0387 | 0.0766 |
| XGB | 0.8357 | 0.1680 | 0.1259 | 0.8639 | 0.3553 | 0.0353 | 0.0091 | – | 0.0167 | 0.1803 | 0.4640 | 0.1006 |
| DNN | 0.0384 | 0.0467 | 0.0026 | 0.0469 | 0.0364 | 0.0352 | 0.0353 | 0.0167 | – | 0.0248 | 0.0202 | 0.0275 |
| CNN | 0.7429 | 0.1945 | 0.3499 | 0.4612 | 0.6269 | 0.0964 | 0.0233 | 0.1803 | 0.0248 | – | 0.1853 | 0.1226 |
| RNN | 0.9424 | 0.1454 | 0.1550 | 0.7691 | 0.4601 | 0.0610 | 0.0387 | 0.4640 | 0.0202 | 0.1853 | – | 0.0897 |
| LSTM | 0.1899 | 0.1934 | 0.1918 | 0.1755 | 0.2900 | 0.0796 | 0.0766 | 0.1006 | 0.0275 | 0.1226 | 0.0897 | – |
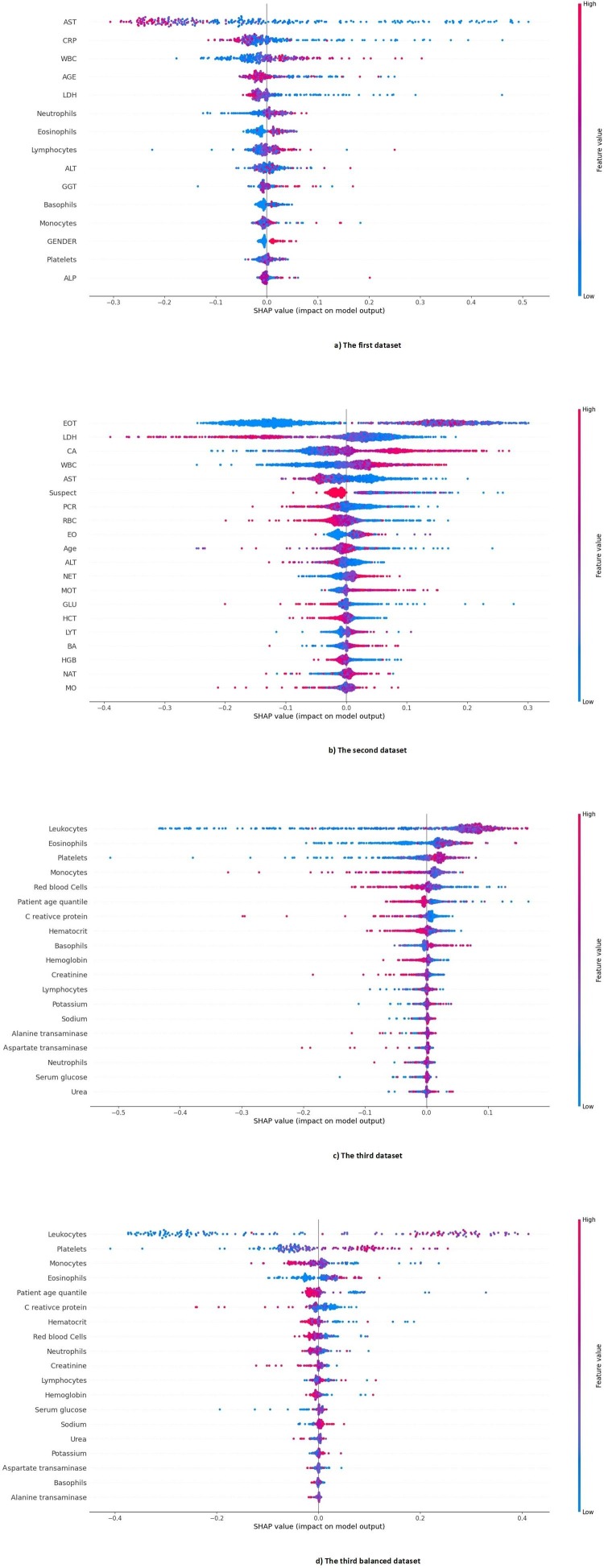
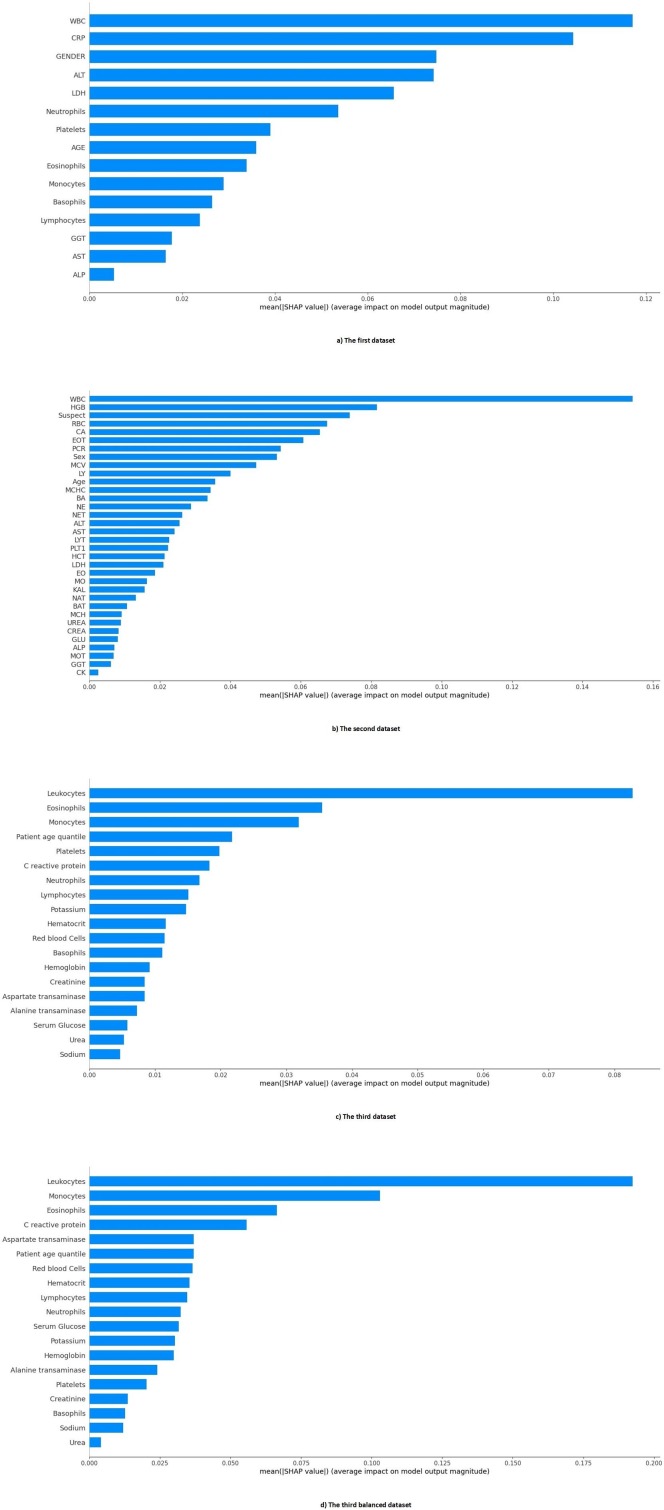
The importance of features in each dataset is presented in Fig. 9 . In the first dataset, Transaminases (AST), C-reactive Protein (CRP), Leukocytes (WBC), Age, and Lactate dehydrogenase (LDH) were the five most important features, respectively. In the second dataset, Eosinophils count (EOT), Lactate dehydrogenase (LDH), Calcium (CA), White blood cells (WBC), and Aspartate aminotransferase (AST) were the five most important features, respectively. Also, in the third dataset, Leukocytes (WBC), Eosinophils, Platelets, Monocytes, and Red Blood Cells (RBC) were the five most important features, respectively. Finally, in the third balance dataset, Leukocytes, Platelets, Monocytes, Eosinophils, and Patient age quantile were the five most important features. As it turns out, the most important common feature, that is one of the five most important features of all datasets, is the Leukocytes or White blood cells (WBC) feature.
Fig. 9.
The Importance of the features of all datasets.
Using the three methods of interpretation SHAP, ELI5 and LIME, we have ranked the features of all datasets in this study based on their importance and weight in the DNN model. Detailed information about the ranking of these features is shown in Table AP-2 in Appendix A. Also, Fig. 10 shows the average effect value of the features in our proposed DNN model in each dataset.
Fig 10.
The average effect size of the features of each dataset in our proposed DNN model.
4. Discussion
We used three open-access datasets of routine blood tests, which included cases with COVID-19 disease and non-COVID-19 disease. We trained, validated, and tested seven models of machine learning and four models of deep learning on these datasets in order to introduce a method for fast, reliable, and accurate diagnosis of COVID-19 cases. Our best proposed model was DNN, which had averaged 92.11%, 93.16%, 93.33% for accuracy, 91.86%, 92.09%, 69.07% for precision, 96.14%, 93.27%, 77.05% for recall or sensitivity, 84.56%, 93.02%, 95.27% for specificity, 93.88%, 92.62%, 72.49% for F1-Score, 92.20%, 93.20%, 85.97% for AUC in the first, second, and third datasets, respectively. When the third dataset was balanced (third balanced dataset) in terms of the number of COVID-19 cases and non-COVID-19 cases, our DNN model had averaged 92.50% for accuracy, 86.96% for precision, 100% for recall or sensitivity, 85% for specificity, 93.02% for F1-Score, 92.20% for AUC.
This study proposes multiple machine learning and deep learning methods to diagnose COVID-19 disease from routine blood tests. As far as we know, the structure of the best-proposed model of this study has not been used in similar studies [1], [2], [4], [6], [9], [13] and in any of the datasets used in this study. The best model we proposed, demonstrates the highest performance in each of the three datasets of routine blood tests based on the evaluation criteria of machine learning and deep learning models. It has achieved its high performance with the appropriate number of parameters, layers, learning rate, and the number of epochs with less time-consuming and complication. In the time comparison between the deep learning models proposed in our study, our proposed model achieved very high efficiency in the shortest possible time. Also, compared to other similar studies [2], [6], [9], our proposed model can diagnose patients with COVID-19 disease in the shortest time. As it can be seen from the results of the paired-sample t-test in Table 10, our DNN model was significantly different from the other models (p-value < 0.05). This significant difference is also evident in Table 5 and Table 6, the evaluation results obtained from all the proposed models. Moreover, according to Table 11 , when compared to other studies [2], [6], [9], our model has shown the best evaluation results, which confirms the soundness of our work.
Table 11.
Comparison of the best results of this study with the best results of related studies.
| study | Dataset | Method | Accuracy (%) | Precision (%) | Recall or Sensitivity (%) | Specificity (%) | F1-Score (%) | AUC (%) |
|---|---|---|---|---|---|---|---|---|
| Brinati et al. [2] | First dataset [2] | TWRF | 83–87 | – | – | – | – | – |
| Cabitza et al. [6] | Second dataset (OSR dataset) [6] | KNN | 86.00 | – | 80.00 | 92.00 | – | 87.00 |
| Alakus et al. [9] | Third dataset [9] | LSTM | 86.66 | 86.75 | 99.42 | – | 91.89 | 62.50 |
| Our study | First dataset [2] | DNN | 92.11 | 91.86 | 96.14 | 84.56 | 93.88 | 92.20 |
| Second dataset (OSR dataset) [6] | DNN | 93.16 | 92.09 | 93.27 | 93.02 | 92.63 | 93.20 | |
| Third dataset [9] | DNN | 93.33 | 69.07 | 77.05 | 95.47 | 72.49 | 85.97 | |
| Third balanced dataset | DNN | 92.50 | 86.96 | 100 | 85.00 | 93.02 | 92.20 |
–No information is available.
The relevance between the features was investigated based on three correlation coefficient methods, and the results are shown in Fig. 1, Fig. AP-1, Fig. AP-2. According to those figures, it can be said that some laboratory features moved in the same direction with each other. In other words, they moved in tandem. The confusion matrix of our DNN model in Fig. 5 and Fig. 8 shows that our DNN model correctly detected the highest true positive cases, that is, cases with COVID-19 disease. There is also a slight error in the false-negative cases, which means the cases with COVID-19 mistakenly recognized by the model as non-COVID-19. Finally, it can be said that our proposed model has shown the correct diagnosis in true negative and false positive cases as well. Using the evaluation criteria from the confusion matrix, according to Table 7 and Table 9, our DNN model has obtained the highest accuracy in all datasets. Fig. 7 shows that our proposed DNN model performed well after each training and validation epoch in all datasets. This history of training and validation supports the best performance with the best-selected parameters and not suffering from overfitting and under-fitting in general. It can be seen that the proposed model has achieved high accuracy and acceptable loss for each dataset. Also, according to Fig. 6, our DNN model was able to show the best performance in each fold of each dataset to recognize the classes. Therefore, because of such high performance, the proposed DNN model is potentially a good means to diagnose COVID-19 cases from routine blood tests.
Recently many studies have been conducted to diagnose COVID-19 from routine blood tests [1], [2], [4], [6], [9], [13]. We compared the results of our best-proposed model with the results of those studies that their datasets were accessible. Table 11 summarizes the differences between the results of our study and those of the recently published studies [2], [6], [9]. Brinati et al. [2] have proposed eight machine learning models to detect positive COVID-19 cases from routine blood tests in the data they collected (the first dataset in our study). Their best-proposed method, called TWRF, was achieved the highest accuracy in the range (0.87–0.83) with the five-fold cross-validation method. Cabitza et al. [6] compiled three datasets for routine blood tests to detect COVID-19. They proposed five machine learning models for this purpose. The KNN model obtained the best performance by a five-fold cross-validation method on the OSR database (the second dataset in our study). The model obtained 86%, 80%, 92%, and 87% for accuracy, recall or sensitivity, specificity, and AUC, respectively. Alakus and Turkoglu [9] proposed six deep learning models for predicting COVID-19 from their compiled blood tests datasets (the third dataset in our study). According to the results, their LSTM model showed the best performance with the ten-fold validation method. Their LSTM model obtained 0.8666, 0.9189, 0.8675, 0.9942, and 0.6250 for accuracy, F1-Score, precision, recovery, and AUC, respectively.
In our study, among all the proposed machine learning and deep learning models, the Deep Neural Network (DNN) model showed better results compared to the aforementioned studies [2], [6], [9]. As shown in Table 6, our DNN model performed much better in all criteria in the first and second datasets. The DNN model achieved 92.11% and 93.16% accuracy, 84.56% and 93.02% specificity, and 92.20% and 93.20 AUC in the first and second datasets. Moreover, our DNN model showed the highest performance with respect to the other evaluation criteria in the first and second datasets compared to similar studies [2], [6]. Surprisingly, we got completely different results in the third dataset, even though we used the same dataset and methodology as the study [9]. When all samples of the third dataset have been used, our DNN model has achieved accuracy, specificity, and AUC of 93.33%, 95.47%, and 85.97%, respectively. When we balanced the third dataset, our DNN model showed even the highest performance in most evaluation criteria among all proposed models. The DNN model achieved 92.50% accuracy, 86.96% specificity, and 92.20% AUC in the third balanced dataset. Our DNN model was made up of a sufficient number of parameters, layers, learning rates, and the number of epochs. It also showed outstanding performance in terms of processing time. The DNN model showed the highest speed of training, validation, and testing in all datasets. All in all, the DNN model showed the best performance in diagnosing COVID-19 disease from routine blood tests with better time efficiency.
With the emergence of the COVID-19 pandemic, we have witnessed many valuable efforts for introducing AI-based methods that could help fast, reliable, accurate diagnosis of COVID-19 [1], [2], [4], [6], [9], [13]. Based on the obtained results, it can be said that the DNN model proposed in this study is among the most accurate and fastest models introduced in the literature to date. Our proposed model is an automated tool that can help clinicians to diagnose the COVID-19 disease. Using AI-based models for COVID-19 diagnosis is more accurate than traditional methods that require experience and time to diagnose. However, clinicians have been skeptical of using these types of systems, mainly because of their black-box nature [36]. With the help of interpretable and feature selection methods, it is possible to explain which features of datasets have played a more important role in decision making. This can increase the acceptance rate and reliability of the AI-based systems for clinicians.
Using the random forest with the SHAP library in Python for determining important features, we realized that among the five most important features of all datasets, four features (i.e., WBC, Age, AST, LDH) were common at least between two of the three datasets. Leukocytes, or white blood cells (WBC) was common between the three datasets. This finding indicates the importance of WBC count in diagnosing COVID-19, which is in line with the findings of other studies [37], [38]. Also, using the SHAP, ELI5, and LIME interpretable methods, the DNN model decision-making procedure provides the most important and influential features for COVID-19 detection (the features of each dataset listed in Appendix A). As shown in Fig. 10, Leukocytes, or white blood cells (WBC) in all datasets, is the most influential laboratory feature in the decision of our proposed model. We can confidently conclude that Leukocytes, or white blood cells (WBC) count is the most important predictive feature for diagnosing COVID-19 disease in all datasets.
This study had many limitations which have to be taken into account when interpreting the results. First, the used datasets did not have homogenous types of blood tests, which made it difficult to interpret the performance of the models. Second, the COVID-19 and non-COVID-19 cases were not in the same proportions across the datasets. Third, the performance of the models could be better evaluated if the datasets had routine blood test results for non-COVID-19 viral infections, such as influenza, as well as for normal people.
5. Conclusion
RT-PCR test kits are a scarce resource in some parts of the world, especially in developing countries. On the other hand, this test also may result in a false negative error in some cases [3]. However, routine blood tests are more widely available worldwide, which are much less error-prone. Early and rapid detection of positive cases of COVID-19 through routine blood tests can help preventing the spread of this highly contagious disease. Therefore, mortality of the disease and the possibility of producing new mutations of the virus can be confined. Our study contributes to advancing of this objective with proposing a model that provides the potentiality of high accuracy and fast diagnosis of COVID-19, compared to previous methods and models.
The main strength of our study was using different datasets, which could be a compensation for any measurement error of the lab test. We used t-test to compare the performance results of different models. The results of this statistical test and measurements of the other performance indicators of prediction models showed that our proposed DNN model could outperform other models in all datasets. In this study, we also introduced the important and influential decision-making features of the proposed model, as well as the relevancy of the used features. We think this is a step forward to make AI-based systems more reliable for clinicians. In our proposed models, it was impossible to increase further the number of parameters or the range of parameters. The reason was the limited available resources, which we could not increased. Therefore, as a drawback for our study, it was not possible for us to further develop and improve the methods.
As for future work, we encourage further work on improving the performance of our proposed DNN model in diagnosing COVID-19 as well as using datasets of other readily accessible biomedical parameters. We also encourage trying AI methods for diagnosing different variants of the SARS-CoV-2 virus from clinical signs and blood tests data.
CRediT authorship contribution statement
Samin Babaei Rikan: Conceptualization, Methodology, Writing – original draft, Software. Amir Sorayaie Azar: Conceptualization, Methodology, Writing – original draft, Software. Ali Ghafari: Conceptualization, Writing – original draft, Data curation, Visualization. Jamshid Bagherzadeh Mohasefi: Supervision, Writing – review & editing. Habibollah Pirnejad: Supervision, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
This study is neither funded nor received a grant from any organization. However, we would like to thank the anonymous reviewers who greatly improved this study by providing helpful comments.
Appendix A
Table AP-1.
All parameters were examined for machine learning and deep learning models.
| Model | Parameters |
|---|---|
| LR | penalty: (l1, l2, None) |
| solver: (lbfgs, newtow-cg) | |
| max_iter: (100, 150, 200) | |
| other parameters: default | |
| KNN | n_neighbors: (2, 5, 8, 10) |
| algoritgm: (ball_tree, kd_tree) | |
| p: (1, 2) | |
| other parameters: default | |
| DT | criterion: (gini, entropy) |
| spliter: (best, random) | |
| max_depth: (5, 10, 15, None) | |
| max_features: (sqrt, log2, auto, None) | |
| other parameters: default | |
| SVM | C: (0.1, 0.5, 1, 5, 10, 25, 50) |
| gamma: (0.1, 0.5, 1, 5, 10, 25, 50, auto) | |
| kernel: (linear, poly, rbf) | |
| decision_function_shape: (ovo, ovr) | |
| other parameters: default | |
| NB | var_smoothing: (1e-5, 1e-7, 1e-9) |
| other parameters: default | |
| ET | n_estimators: (100, 150, 200) |
| criterion: (gini, entropy) | |
| max_depth: (5, 10, 15, None) | |
| max_features: (sqrt, log2, auto, None) | |
| other parameters: default | |
| RF | n_estimators: (100, 150, 200) |
| criterion: (gini, entropy) | |
| max_depth: (5, 10, 15, None) | |
| max_features: (sqrt, log2, auto, None) | |
| other parameters: default | |
| XGBoost | booster: (gbtree, gblinear, dart) |
| eta: (0.1, 0.3, 0.5, 0.7, 0.9) | |
| max_depth: (4, 5, 6) | |
| sampling method: (uniform, subsample, gradiant_based) | |
| other parameters: default | |
| DNN | number of fully connected layers: (1-4, 1-8, 1-12) |
| number of full connected units: ([34, 68, 34, 1], [34, 68, 126, 272, 126, 68, 34, 1], [34, 68, 136, 272, 544, 1088, 544, 272, 136, 68, 34, 1]) | |
| learning rate: (1e-3, 1e-4, 1e-5) | |
| number of epochs for each fold: (25, 50, 75) | |
| batch size: (7, 14, 21) | |
| loss function: (sgd, adam) | |
| number of drop out layers: (none, 1) | |
| drop out: (0.1, 0.2) | |
| activation function of layers: (relu, tanh) | |
| CNN | number of fully connected layers: (1-2, 1-3) |
| number of full connected units: ([64, 1], [32, 1], [16, 1], [8, 1], [64, 32, 1], [64, 16, 1], [32, 16, 1], [32, 8, 1]) | |
| number of layers: ([1, 2], [1,3]) | |
| number of units: ([256, 128], [128, 64], [64, 32], [32, 16], [256, 128, 64], [128, 64, 32], [64, 32, 16]) | |
| learning rate: (1e-3, 1e-4, 1e-5) | |
| number of epochs for each fold: (25, 50, 75) | |
| batch size: (7, 14, 21) | |
| loss function: (sgd, adam) | |
| number of drop out layers: (none, 1) | |
| drop out: (0.1, 0.2) | |
| activation function of layers: (relu, tanh) | |
| RNN | number of fully connected layers: (1-2, 1-3) |
| number of full connected units: ([64, 1], [32, 1], [16, 1], [8, 1], [64, 32, 1], [64, 16, 1], [32, 16, 1], [32, 8, 1]) | |
| number of layers: (1, 2) | |
| number of units: ([256], [128], [64], [32], [16], [256, 128], [128, 64], [64, 32], [32, 16]) | |
| learning rate: (1e-3, 1e-4, 1e-5) | |
| number of epochs for each fold: (25, 50, 75) | |
| batch size: (7, 14, 21) | |
| loss function: (sgd, adam) | |
| number of drop out layers: (none, 1) | |
| drop out: (0.1, 0.2) | |
| activation function of layers: (relu, tanh) | |
| LSTM | number of fully connected layers: (1-2, 1-3) |
| number of full connected units: ([64, 1], [32, 1], [16, 1], [8, 1], [64, 32, 1], [64, 16, 1], [32, 16, 1], [32, 8, 1]) | |
| number of layers: (1, 2) | |
| number of units: ([256], [128], [64], [32], [16], [256, 128], [128, 64], [64, 32], [32, 16]) | |
| learning rate: (1e-3, 1e-4, 1e-5) | |
| number of epochs for each fold: (25, 50, 75) | |
| batch size: (7, 14, 21) | |
| loss function: (sgd, adam) | |
| number of drop out layers: (none, 1) | |
| drop out: (0.1, 0.2) | |
| activation function of layers: (relu, tanh) |
Table AP-2.
Ranking the impact of each feature on the DNN model.
| Method | First dataset [2] | Second dataset (OSR dataset) [6] | Third dataset [9] | Third balanced dataset |
|---|---|---|---|---|
| ELI5 | 1. AST | 1. Suspect | 1. Leukocytes | 1. Leukocytes |
| 2. CRP | 2. LDH | 2. Platelets | 2. Platelets | |
| 3. AGE | 3. Age | 3. Eosinophils | 3. Monocytes | |
| 4. WBC | 4. PCR | 4. Monocytes | 4. Eosinophils | |
| 5. LDH | 5. BAT | 5. C reactive protein | 5. Patient age quantile | |
| 6. GENDER | 6. BA | 6. Patient age quantile | 6. C reactive protein | |
| 7. Eosinophils | 7. CA | 7. Red blood Cells | 7. Red blood Cells | |
| 8. ALT | 8. EO | 8. Neutrophils | 8. Hematocrit | |
| 9. Lymphocytes | 9. EOT | 9. Hematocrit | 9. Hemoglobin | |
| 10. Neutrophils | 10. WBC | 10. Lymphocytes | 10. Lymphocytes | |
| 11. Platelets | 11. LYT | 11. Basophils | 11. Basophils | |
| 12. Monocytes | 12. MOT | 12. Hemoglobin | 12. Creatinine | |
| 13. Basophils | 13. AST | 13. Creatinine | 13. Neutrophils | |
| 14. GGT | 14. NET | 14. Aspartate transaminase | 14. Potassium | |
| 15. ALP | 15. MO | 15. Potassium | 15. Urea | |
| 16. ALT | 16. Alanine transaminase | 16. Sodium | ||
| 17. RBC | 17. Urea | 17. Aspartate transaminase | ||
| 18. HGB | 18. Sodium | 18. Alanine transaminase | ||
| 19. NAT | 19. Serum Glucose | 19. Serum Glucose | ||
| 20. NE | ||||
| 21. HCT | ||||
| 22. LY | ||||
| 23. GLU | ||||
| 24. MCV | ||||
| 25. PLT1 | ||||
| 26. GGT | ||||
| 27. MCHC | ||||
| 28. CREA | ||||
| 29. UREA | ||||
| 30. MCH | ||||
| 31. ALP | ||||
| 32. KAL | ||||
| 33. CK | ||||
| 34. Sex | ||||
| LIME | 1. AST | 1. LDH | 1. Leukocytes | 1. Leukocytes |
| 2. LDH | 2. BAT | 2. Eosinophils | 2. Eosinophils | |
| 3. GENDER | 3. Suspect | 3. Platelets | 3. Monocytes | |
| 4. Lymphocytes | 4. CA | 4. Patient age quantile | 4. Platelets | |
| 5. WBC | 5. AST | 5. Creatinine | 5. Patient age quantile | |
| 6. CRP | 6. PCR | 6. Basophils | 6. Creatinine | |
| 7. Neutrophils | 7. WBC | 7. Alanine transaminase | 7. Red blood Cells | |
| 8. Eosinophils | 8. EOT | 8. Lymphocytes | 8. Hemoglobin | |
| 9. Basophils | 9. BA | 9. Potassium | 9. Sodium | |
| 10. ALT | 10. EO | 10. Serum Glucose | 10. C reactive protein | |
| 11. Platelets | 11. RBC | 11. Monocytes | 11. Basophils | |
| 12. AGE | 12. NET | 12. Hemoglobin | 12. Hematocrit | |
| 13. GGT | 13. HCT | 13. Hematocrit | 13. Potassium | |
| 14. Monocytes | 14. LYT | 14. Aspartate transaminase | 14. Urea | |
| 15. ALP | 15. MOT | 15. Red blood Cells | 15. Neutrophils | |
| 16. HGB | 16. Sodium | 16. Serum Glucose | ||
| 17. CK | 17. Urea | 17. Lymphocytes | ||
| 18. ALT | 18. C reactive protein | 18. Aspartate transaminase | ||
| 19. GGT | 19. Neutrophils | 19. Alanine transaminase | ||
| 20. Age | ||||
| 21. Sex | ||||
| 22. NAT | ||||
| 23. GLU | ||||
| 24. NE | ||||
| 25. KAL | ||||
| 26. PLT1 | ||||
| 27. MO | ||||
| 28. MCH | ||||
| 29. UREA | ||||
| 30. ALP | ||||
| 31. MCV | ||||
| 32. MCHC | ||||
| 33. CREA | ||||
| 34. LY | ||||
| SHAP | 1. WBC | 1. WBC | 1. Leukocytes | 1. Leukocytes |
| 2. CRP | 2. HGB | 2. Eosinophils | 2. Monocytes | |
| 3. GENDER | 3. Suspect | 3. Monocytes | 3. Eosinophils | |
| 4. ALT | 4. RBC | 4. Patient age quantile | 4. C reactive protein | |
| 5. LDH | 5. CA | 5. Platelets | 5. Aspartate transaminase | |
| 6. Neutrophils | 6. EOT | 6. C reactive protein | 6. Patient age quantile | |
| 7. Platelets | 7. PCR | 7. Neutrophils | 7. Red blood Cells | |
| 8. AGE | 8. Sex | 8. Lymphocytes | 8. Hematocrit | |
| 9. Eosinophils | 9. MCV | 9. Potassium | 9. Lymphocytes | |
| 10. Monocytes | 10. LY | 10. Hematocrit | 10. Neutrophils | |
| 11. Basophils | 11. Age | 11. Red blood Cells | 11. Serum Glucose | |
| 12. Lymphocytes | 12. MCHC | 12. Basophils | 12. Potassium | |
| 13. GGT | 13. BA | 13. Hemoglobin | 13. Hemoglobin | |
| 14. AST | 14. NE | 14. Creatinine | 14. Alanine transaminase | |
| 15. ALP | 15. NET | 15. Aspartate transaminase | 15. Platelets | |
| 16. ALT | 16. Alanine transaminase | 16. Creatinine | ||
| 17. AST | 17. Serum Glucose | 17. Basophils | ||
| 18. LYT | 18. Urea | 18. Sodium | ||
| 19. PLT1 | 19. Sodium | 19. Urea | ||
| 20. HCT | ||||
| 21. LDH | ||||
| 22. EO | ||||
| 23. MO | ||||
| 24. KAL | ||||
| 25. NAT | ||||
| 26. BAT | ||||
| 27. MCH | ||||
| 28. UREA | ||||
| 29. CREA | ||||
| 30. GLU | ||||
| 31. ALP | ||||
| 32. MOT | ||||
| 33. GGT | ||||
| 34. CK |
References
- 1.Kukar M., Gunčar G., Vovko T., Podnar S., Černelč P., Brvar M., Zalaznik M., Notar M., Moškon S., Notar M. COVID-19 diagnosis by routine blood tests using machine learning. Sci. Rep. 2021;11(1):10738. doi: 10.1038/s41598-021-90265-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brinati D., Campagner A., Ferrari D., Locatelli M., Banfi G., Cabitza F. Detection of COVID-19 infection from routine blood exams with machine learning: a feasibility study. J. Med. Syst. 2020;44(8):135. doi: 10.1007/s10916-020-01597-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alsharif W., Qurashi A. Effectiveness of COVID-19 diagnosis and management tools: a review. Radiography (Lond). 2021;27(2):682–687. doi: 10.1016/j.radi.2020.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Plante T.B., Blau A.M., Berg A.N., Weinberg A.S., Jun I.C., Tapson V.F., Kanigan T.S., Adib A.B. Development and external validation of a machine learning tool to rule out COVID-19 among adults in the emergency department using routine blood tests: a large, multicenter, real-world study. J. Med. Internet Res. 2020;22(12):e24048. doi: 10.2196/24048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.J. Wu, P. Zhang, L. Zhang, W. Meng, J. Li, C. Tong et al. Rapid and accurate identification of COVID-19 infection through machine learning based on clinical available blood test results [Internet]. bioRxiv. 2020. doi:10.1101/2020.04.02.20051136.
- 6.Cabitza F., Campagner A., Ferrari D., Di Resta C., Ceriotti D., Sabetta E., et al. Development, evaluation, and validation of machine learning models for COVID-19 detection based on routine blood tests. Clin. Chem. Lab. Med. 2020;59(2):421–431. doi: 10.1515/cclm-2020-1294. [DOI] [PubMed] [Google Scholar]
- 7.Kalane P., Patil S., Patil B.P., Sharma D.P. Automatic detection of COVID-19 disease using U-Net architecture based fully convolutional network. Biomed. Signal Process. Control. 2021;67:102518. doi: 10.1016/j.bspc.2021.102518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Thakur S., Kumar A. X-ray and CT-scan-based automated detection and classification of covid-19 using convolutional neural networks (CNN) Biomed. Signal Process. Control. 2021;69:102920. doi: 10.1016/j.bspc.2021.102920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Alakus T.B., Turkoglu I. Comparison of deep learning approaches to predict COVID-19 infection. Chaos, Solitons Fractals. 2020;140(110120):110120. doi: 10.1016/j.chaos.2020.110120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Arpaci I., Huang S., Al-Emran M., Al-Kabi M.N., Peng M. Predicting the COVID-19 infection with fourteen clinical features using machine learning classification algorithms. Multimed Tools Appl. 2021;80(8):11943–11957. doi: 10.1007/s11042-020-10340-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.A. Sorayaie Azar, A. Ghafari, M. Ostadi Najar, S. Babaei Rikan, R. Ghafari, M. Farajpouri Khamene, et al. Covidense: Providing a suitable solution for diagnosing Covid-19 lung infection based on Deep Learning from chest X-ray images of patients. fbt [Internet]. 2021; doi:10.18502/fbt.v8i2.6517.
- 12.Nayak S.R., Nayak D.R., Sinha U., Arora V., Pachori R.B. Application of deep learning techniques for detection of COVID-19 cases using chest X-ray images: a comprehensive study. Biomed. Signal Process. Control. 2021;64:102365. doi: 10.1016/j.bspc.2020.102365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thell R., Zimmermann J., Szell M., Tomez S., Eisenburger P., Haugk M., Kreil A., Spiel A., Blaschke A., Klicpera A., Janata O., Krugluger W., Sebesta C., Herkner H., Laky B. Standard blood laboratory values as a clinical support tool to distinguish between SARS-CoV-2 positive and negative patients. Sci. Rep. 2021;11(1) doi: 10.1038/s41598-021-88844-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wynants L., Van Calster B., Collins G.S., Riley R.D., Heinze G., Schuit E., et al. Prediction models for diagnosis and prognosis of covid-19: systematic review and critical appraisal. BMJ. 2020;369 doi: 10.1136/bmj.m1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Collins G.S., Reitsma J.B., Altman D.G., Moons K. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD Statement. BMC Med. 2015;13(1):1. doi: 10.1186/s12916-014-0241-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhu H., You X., Liu S. Multiple ant colony optimization based on Pearson correlation coefficient. IEEE Access. 2019;7:61628–61638. [Google Scholar]
- 17.Sedgwick P. Spearman’s rank correlation coefficient. BMJ. 2014;349(v28 1) doi: 10.1136/bmj.g7327. g7327. [DOI] [PubMed] [Google Scholar]
- 18.van Doorn J., Ly A., Marsman M., Wagenmakers E.-J. Bayesian inference for Kendall’s rank correlation coefficient. Am. Stat. 2018;72(4):303–308. [Google Scholar]
- 19.Shalev-Shwartz S., Ben-David S. Cambridge University Press; Cambridge, England: 2014. Understanding Machine Learning: From Theory to Algorithms. [Google Scholar]
- 20.LeCun Y., Bengio Y., Hinton G. Deep learning. Nature. 2015;521(7553):436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 21.Shastry K.A., Sanjay H.A. Statistical Modelling and Machine Learning Principles for Bioinformatics Techniques, Tools, and Applications. Springer Singapore; Singapore: 2020. Machine Learning for Bioinformatics; pp. 25–39. [Google Scholar]
- 22.Li Y.u., Huang C., Ding L., Li Z., Pan Y., Gao X. Deep learning in bioinformatics: introduction, application, and perspective in the big data era. Methods. 2019;166:4–21. doi: 10.1016/j.ymeth.2019.04.008. [DOI] [PubMed] [Google Scholar]
- 23.Geurts P., Ernst D., Wehenkel L. Extremely randomized trees. Mach Learn. 2006;63(1):3–42. [Google Scholar]
- 24.Torlay L., Perrone-Bertolotti M., Thomas E., Baciu M. Machine learning–XGBoost analysis of language networks to classify patients with epilepsy. Brain Inform. 2017;4(3):159–169. doi: 10.1007/s40708-017-0065-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ferrari D., Motta A., Strollo M., Banfi G., Locatelli M. Routine blood tests as a potential diagnostic tool for COVID-19. Clin. Chem. Lab. Med. 2020;58(7):1095–1099. doi: 10.1515/cclm-2020-0398. [DOI] [PubMed] [Google Scholar]
- 26.Refaeilzadeh P., Tang L., Liu H. Encyclopedia of Database Systems. Springer US; Boston, MA: 2009. Cross-Validation; pp. 532–538. [Google Scholar]
- 27.Kuzlu M., Cali U., Sharma V., Guler O. Gaining insight into solar photovoltaic power generation forecasting utilizing explainable artificial intelligence tools. IEEE Access. 2020;8:187814–187823. [Google Scholar]
- 28.Toğaçar M., Muzoğlu N., Ergen B., Yarman B.S.B., Halefoğlu A.M. Detection of COVID-19 findings by the local interpretable model-agnostic explanations method of types-based activations extracted from CNNs. Biomed. Signal Process. Control. 2022;71:103128. doi: 10.1016/j.bspc.2021.103128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rinderknecht M.D., Klopfenstein Y. Predicting critical state after COVID-19 diagnosis: model development using a large US electronic health record dataset. NPJ Digit Med. 2021;4(1):113. doi: 10.1038/s41746-021-00482-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ergen B., Baykara M., Polat C. Determination of the relationship between internal auditory canal nerves and tinnitus based on the findings of brain magnetic resonance imaging. Biomed. Signal Process. Control. 2018;40:214–219. [Google Scholar]
- 31.Gao J. P-values - a chronic conundrum. BMC Med. Res. Method. 2020;20(1):167. doi: 10.1186/s12874-020-01051-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Deng X., Liu Q.i., Deng Y., Mahadevan S. An improved method to construct basic probability assignment based on the confusion matrix for classification problem. Inf. Sci. (Ny). 2016;340-341:250–261. [Google Scholar]
- 33.Parikh R., Mathai A., Parikh S., Chandra Sekhar G., Thomas R. Understanding and using sensitivity, specificity and predictive values. Indian J. Ophthalmol. 2008;56(1):45–50. doi: 10.4103/0301-4738.37595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Huang J., Ling C.X. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans. Knowl. Data Eng. 2005;17(3):299–310. [Google Scholar]
- 35.Boughorbel S., Jarray F., El-Anbari M., Zou Q. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE. 2017;12(6):e0177678. doi: 10.1371/journal.pone.0177678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kiener M. Artificial intelligence in medicine and the disclosure of risks. AI Soc. 2021;36(3):705–713. doi: 10.1007/s00146-020-01085-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhu B., Feng X., Jiang C., Mi S., Yang L., Zhao Z., Zhang Y., Zhang L. Correlation between white blood cell count at admission and mortality in COVID-19 patients: a retrospective study. BMC Infect. Dis. 2021;21(1):574. doi: 10.1186/s12879-021-06277-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Vafadar Moradi E., Teimouri A., Rezaee R., Morovatdar N., Foroughian M., Layegh P., Rezvani Kakhki B., Ahmadi Koupaei S.R., Ghorani V. Increased age, neutrophil-to-lymphocyte ratio (NLR) and white blood cells count are associated with higher COVID-19 mortality. Am. J. Emerg. Med. 2021;40:11–14. doi: 10.1016/j.ajem.2020.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]