Summary
Two useful strategies to speed up drug development are to increase the patient accrual rate and use novel adaptive designs. Unfortunately, these two strategies often conflict when the evaluation of the outcome cannot keep pace with the patient accrual rate and thus the interim data cannot be observed in time to make adaptive decisions. A similar logistic difficulty arises when the outcome is late-onset. Based on a novel formulation and approximation of the likelihood of the observed data, we propose a general methodology for model-assisted designs to handle toxicity data that are pending due to fast accrual or late-onset toxicity and facilitate seamless decision making in phase I dose-finding trials. The proposed time-to-event model-assisted designs consider each dose separately and the dose-escalation/de-escalation rules can be tabulated before the trial begins, which greatly simplifies trial conduct in practice compared to that under existing methods. We show that the proposed designs have desirable finite and large-sample properties and yield performance that is comparable to that of more complicated model-based designs. We provide user-friendly software for implementing the designs.
Keywords: Adaptive design, Dose finding, Late-onset toxicity, Maximum tolerated dose, Model-assisted designs
1. Introduction
Drug development enterprises are struggling because of unsustainably long development cycle and high costs. The pharmaceutical industry and regulatory agencies both recognize the urgency and necessity of speeding up drug development. Toward that goal, two common strategies are to increase the accrual rate to shorten the trial duration (Dilts and others, 2008) and to use novel adaptive designs for more efficient decision making (Kairalla and others, 2012). These two strategies, unfortunately, often conflict. The majority of adaptive designs require that the endpoint is quickly ascertainable, such that by the time interim decisions to be made, the outcomes of patients already enrolled in the trial have been fully ascertained. When the accrual rate is fast, some enrolled patients may not have completed their outcome assessment by the interim decision making time, which causes a major logistic difficulty for implementing adaptive trial designs. This is particularly true for phase I trials, where adaptive decisions of dose escalation and de-escalation are mandated after each patient or patient cohort is treated. For example, in a trial where the dose limiting toxicity (DLT) takes up to 28 days to evaluate and patients are treated in cohorts of three patients, if the accrual rate is two patients per week, an average of five new patients will be accrued while the investigators wait to evaluate the outcomes of the three previously enrolled patients. The question is then: How can new patients receive timely treatment when the previous patients’ outcomes are pending?
The same difficulty arises when the DLT is late-onset and requires a long assessment window to be ascertained. For example, if the DLT assessment window of a new agent is 3 months, given the accrual rate of three patients per month, then an average of six new patients will be accrued while investigators wait to evaluate the DLT outcomes of the three previously enrolled patients. Still the investigators must determine how to provide the new patients with timely treatment. The problem of late-onset toxicity is particularly common and important in the era of targeted therapy and immunotherapy. A recent study reported that in 36 clinical trials of molecularly targeted agents, more than half of the grade 3 or 4 toxicity events occurred after the first treatment cycle (Postel-Vinay, 2011). Immune-related toxicity is often of late onset, for instance, endocrinopathies have been observed between post-treatment weeks 12 and 24 (Weber and others, 2015; June and others, 2017).
The fundamental issue associated with fast accrual and late-onset toxicity is that at the interim decision time, some patients’ DLT data are pending (i.e., unknown), which causes difficulty in making adaptive decisions. A number of model-based designs and algorithm-based designs have been proposed to address this issue. Cheung and Chappell (2000) proposed the time-to-event continual reassessment method (TITE-CRM), a model-based design, where the likelihood of each patient is weighted by his/her follow-up proportion. Taking a different perspective, Yuan and Yin (2011) and Liu and others (2013) treated the pending DLT data as a missing data problem, and proposed the expectation–maximization algorithm and Bayesian data augmentation method to facilitate real-time decision making. These model-based designs yield excellent operating characteristics, but their use in practice has been limited because they are often perceived by practitioners as difficult to understand, due to the blackbox-style of decision making, and complicated to implement, because of the requirement of repeated model fitting and estimation. Thus, in practice, the rolling six (R6) design (Skolnik and others, 2008), an algorithm-based design, is often used. To implement R6, investigators only need to count the number of patients with DLTs, the number of patients without DLTs and the number of patients with pending outcomes, and then use the prespecified decision table to determine the dose for the next new cohort, in a fashion similar to the 3+3 design. However, the performance of the R6 design is substantially inferior to that of the model-based designs (Zhao and others, 2011) in identifying and allocating patients to the maximum tolerated dose (MTD).
The goal of this article is to develop new model-assisted phase I designs that combine the simplicity of the algorithm-based design and the superior performance of the model-based design. The proposed designs are transparent and can be implemented in a simple way like the algorithm-based design (e.g., the R6 design), but they have desirable statistical properties and yield performance that is comparable to that of the model-based designs (e.g., TITE-CRM). The proposed designs allow users to tabulate the dose-escalation and de-escalation rules before the trial begins. To conduct the trial, there is no complicated model fitting and calculation, investigators only need to look up the decision table to make the dose-assignment decisions. Simulation studies show that albeit simplistic, the proposed design yields excellent operating characteristics compared to those of the more complicated model-based design.
Our approach is built upon the framework of model-assisted designs (Yan and others, 2017; Zhou and others, 2018a), which use a probability model for efficient decision making like model-based designs, while their dose-escalation and de-escalation rules can be pre-tabulated before the onset of a trial, as with algorithm-based designs. Ivanova and others (2007) developed the cumulative cohort design based on the asymptotic distribution of patient allocation of the up-and-down design using the Markov chain theory. Ji and others (2010) proposed the modified toxicity probability interval (mTPI) design that utilizes unit probability mass (UPM) to guide the dose assignment. Liu and Yuan (2015) developed the Bayesian optimal interval (BOIN) design that makes the decision of dose escalation and de-escalation by simply comparing the observed toxicity rate at the current dose with two prespecified boundaries that are optimized to minimize the incorrect decision of dose assignment. Yan and others (2017) noted the overdosing issue of the mTPI design due to the use of UPM and proposed the keyboard design as a seamless improvement of the mTPI to achieve higher accuracy of identification of the MTD and better overdose control. The model-assisted designs have been extended to drug-combination trials (Zhang and Yuan, 2016; Lin and Yin, 2017a), to account for toxicity grades (Mu and others, 2018), and for phase I–II trials (Lin and Yin, 2017b). For overviews and comparison of model-assisted designs, see Zhou and others (2018a) and Zhou and others (2018b). Because of their simplicity and good performance, model-assisted designs have been increasingly used in practice. For example, the BOIN design has been widely used in variety of oncology trials, including solid tumors (Wu, 2016; Phan, 2017), liquid tumors (Al-Atrash, 2018; Leonard and others, 2017), and various treatment agents (Wu, 2016; Phan, 2017; Al-Atrash, 2018). However, these designs cannot handle the issue of fast accrual or late-onset toxicity, and they all require that accrued patients have completed DLT assessment before treating the next patients.
Recently, Yuan and others (2018) proposed the time-to-event BOIN (TITE-BOIN) design to accommodate late-onset toxicity by imputing the unobserved pending toxicity outcome using the single mean imputation method. That approach, however, is only applicable to the BOIN design, whose decisions of dose escalation/de-escalation involve only the point (or maximum likelihood) estimate of the toxicity probability of the current dose. It cannot be used with other model-assisted designs (e.g., mTPI and keyboard designs) because these designs require the calculation of the posterior distribution of the toxicity probability to determine dose escalation/de-escalation. We herein proposed a general methodology that is applicable to all model-assisted designs. The new methodology is built upon a novel approximation of the likelihood of the observed data that transfers the complicated observed likelihood into a standard binomial likelihood, which is fundamentally different from the missing data/imputation approach used in the TITE-BOIN. As a result, the proposed method is more general and can be used with all existing model-assisted designs to handle the late-onset toxicity or fast accrual issue.
Our study is motivated by a phase I trial planned at MD Anderson Cancer Center. The objective is to find the MTD of a mitogen-activated protein kinase kinase (MEK) inhibitor combined with 200 mg pembrolizumab for treating patients with advanced melanoma. Four doses, 100, 125, 150, and 175 mg, of the MEK inhibitor will be studied, administered orally twice daily on a schedule of 3 days on, 4 days off. The maximum sample size is 21 patients, treated in cohort sizes of 3. As the DLT of the treatment is expected to be of late onset, the clinical investigator set the DLT assessment window at 3 months. The DLT will be scored using the NCI common Terminology Criteria for Adverse Events, version 4.0. The accrual rate is expected to be two patients per month.
The remainder of this article is organized as follows. In Section 2, we formulate a new likelihood-based approach to account for both observed and pending DLT data and develop the TITE-keyboard design and study its theoretical properties. We also briefly discuss the development of other model-assisted designs. As an illustration, we apply the TITE-keyboard design to a phase I dose-finding trial in Section 3. In Section 4, we examine the performance of the new design based on simulation studies and make extensive comparisons with existing methods. Section 5 concludes with some remarks. The Supplementary material contains proofs of the theorems.
2. Methodology
Consider a phase I dose-finding trial with  prespecified doses and
maximum sample size
prespecified doses and
maximum sample size  . Let
. Let  denote the toxicity
probability of dose level
denote the toxicity
probability of dose level  ,
,  , with
, with
 , and
, and
 denote the target DLT rate. The objective
is to find the MTD, defined as the dose that has the DLT probability closest to
denote the target DLT rate. The objective
is to find the MTD, defined as the dose that has the DLT probability closest to
 . Patients are sequentially enrolled, and
each patient is followed for a fixed period of time, say
. Patients are sequentially enrolled, and
each patient is followed for a fixed period of time, say  , to assess
the binary DLT outcome
, to assess
the binary DLT outcome  . If DLT is observed within the assessment
window
. If DLT is observed within the assessment
window  ,
,  ; otherwise,
; otherwise,
 . Let
. Let  denote the time to DLT
for patients with
denote the time to DLT
for patients with  , where
, where  . The DLT assessment window
. The DLT assessment window
 is prespecified by clinicians such that it
is expected to capture all DLTs relevant for the MTD determination. For many chemotherapies,
is prespecified by clinicians such that it
is expected to capture all DLTs relevant for the MTD determination. For many chemotherapies,
 is often taken as the first cycle of 28
days; whereas for agents expected to induce late-onset toxicity, e.g., some targeted or
immunotherapy agents,
is often taken as the first cycle of 28
days; whereas for agents expected to induce late-onset toxicity, e.g., some targeted or
immunotherapy agents,  can be several (e.g., 3–6) months or
longer.
can be several (e.g., 3–6) months or
longer.
2.1. Keyboard design
The proposed methodology to deal with fast accrual and late-onset toxicity is general and
applies to all model-assisted designs, including keyboard, mTPI, and BOIN. For ease of
exposition, we illustrate our approach using the keyboard design, reviewed briefly as
follows. The keyboard design starts by specifying a proper dosing interval
 ,
referred to as the “target key,” which represents the range of toxicity probabilities that
are close enough to the target
,
referred to as the “target key,” which represents the range of toxicity probabilities that
are close enough to the target  so that they are regarded as
acceptable in practice, where
so that they are regarded as
acceptable in practice, where  and
and  are
small constants, such as
are
small constants, such as  . The keyboard design
populates the interval toward both sides of the target key, forming a series of keys of
equal width that span the range of 0 to 1. For example, given the target key of (0.25,
0.35), on its left side, we form two keys of width 0.1, i.e., (0.15, 0.25] and (0.05,
0.15]; and on its right side, we form six keys of width 0.1, i.e.,
. The keyboard design
populates the interval toward both sides of the target key, forming a series of keys of
equal width that span the range of 0 to 1. For example, given the target key of (0.25,
0.35), on its left side, we form two keys of width 0.1, i.e., (0.15, 0.25] and (0.05,
0.15]; and on its right side, we form six keys of width 0.1, i.e.,
 . To
cover the whole toxicity probability domain, we can include two “incompleted” keys
[0,0.05] and [0.95,1], which are shorter than the target key. Yan and others (2017) showed that including or
excluding these two “incompleted” keys has no impact on the performance of the design. We
denote the resulting intervals/keys as
. To
cover the whole toxicity probability domain, we can include two “incompleted” keys
[0,0.05] and [0.95,1], which are shorter than the target key. Yan and others (2017) showed that including or
excluding these two “incompleted” keys has no impact on the performance of the design. We
denote the resulting intervals/keys as  , and
assume that the
, and
assume that the  th interval is the target key, i.e.,
th interval is the target key, i.e.,
 .
.
Suppose that at a particular point during the trial,  patients have been
treated at dose level
patients have been
treated at dose level  , and among them
, and among them  patients
experienced DLT. The keyboard design assumes a beta-binomial model
patients
experienced DLT. The keyboard design assumes a beta-binomial model
 |
Given data  observed at dose level
observed at dose level
 , the posterior distribution arises as
, the posterior distribution arises as
 |
(2.1) |
In contrast to model-based designs (e.g., the CRM), which model toxicity across doses
using a dose–toxicity curve model (e.g., a power or logistic model), the keyboard design
models toxicity at each dose independently, which simplifies the design and renders it
possible to pre-tabulate the decision rules of dose escalation and de-escalation. Modeling
toxicity at each dose independently is an essential feature of the model-assisted designs:
mTPI assumes the same beta-binomial model as above and BOIN only assumes the binomial
model for 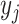 .
.
To make the decisions of dose escalation and de-escalation, where
 is the current dose level, the keyboard
design identifies the interval that has the largest posterior probability (referred to as
the “strongest” key), i.e.,
is the current dose level, the keyboard
design identifies the interval that has the largest posterior probability (referred to as
the “strongest” key), i.e.,  which can easily be evaluated based on the posterior distribution of
which can easily be evaluated based on the posterior distribution of
 given by equation (2.1). The keyboard design determines the
next dose as follows: If
given by equation (2.1). The keyboard design determines the
next dose as follows: If  , escalate the dose to level
, escalate the dose to level
 ; if
; if  , retain the
current dose level
, retain the
current dose level  ; if
; if  , de-escalate
the dose to level
, de-escalate
the dose to level  . This dose-escalation/de-escalation
process continues until the prespecified sample size
. This dose-escalation/de-escalation
process continues until the prespecified sample size  is exhausted, and the MTD
is selected as the dose for which the isotonic estimate (Barlow and Brunk, 1972) of the toxicity rate is closest to the target
is exhausted, and the MTD
is selected as the dose for which the isotonic estimate (Barlow and Brunk, 1972) of the toxicity rate is closest to the target
 .
.
The most appealing feature of the keyboard design is that its decision rule can be
tabulated before the trial begins, which greatly simplifies the practical implementation
of the design. This is possible because given the maximum sample size
 , the possible outcome
, the possible outcome
 is finite for
is finite for
 and
and
 , and given each of the
possible outcomes, the strongest key and thus the dose-escalation/de-escalation rule can
be easily determined based on (2.1).
, and given each of the
possible outcomes, the strongest key and thus the dose-escalation/de-escalation rule can
be easily determined based on (2.1).
2.2. Likelihood with pending DLT data
When the accrual is fast or when there is late onset of DLT, the fundamental difficulty
that cripples the keyboard and other model-assisted designs is that by the time of
decision making, say time  , the
, the  ’s may not be
observed for patients who have not completed their DLT assessment. The data actually
observed are indicator variables
’s may not be
observed for patients who have not completed their DLT assessment. The data actually
observed are indicator variables  ,
,  , which indicate that the
patient has experienced DLT (
, which indicate that the
patient has experienced DLT ( ) or not yet
(
) or not yet
( ) by time
) by time
 . Clearly,
. Clearly,  implies
implies  , but when
, but when  ,
,
 can equal 0 or 1.
can equal 0 or 1.
Let  indicate that the toxicity outcome
indicate that the toxicity outcome
 has been ascertained (i.e.,
has been ascertained (i.e.,
 ) or is still pending (i.e.,
) or is still pending (i.e.,
 ) by the decision time
) by the decision time
 , and
, and 
 ) denote the
actual follow-up time for patient
) denote the
actual follow-up time for patient  up to that moment. For a patient with
up to that moment. For a patient with
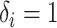 , we have
, we have
 , thus the likelihood is
given by
, thus the likelihood is
given by
 |
(2.2) |
For a patient with  ,
,  has not been
ascertained yet and his/her DLT outcome is pending. These patients with pending outcome
data are a mixture of two subgroups: patients who will not experience DLT (i.e.,
has not been
ascertained yet and his/her DLT outcome is pending. These patients with pending outcome
data are a mixture of two subgroups: patients who will not experience DLT (i.e.,
 ), and patients who will experience DLT
(i.e.,
), and patients who will experience DLT
(i.e.,  ) but have not experienced it yet by
the interim decision time (i.e.,
) but have not experienced it yet by
the interim decision time (i.e.,  ). Note that
). Note that
 only takes a value of 0 because
once
only takes a value of 0 because
once  (i.e., the patient
experiences DLT),
(i.e., the patient
experiences DLT),  becomes observable and
becomes observable and
 . Therefore, for a patient with
pending data with
. Therefore, for a patient with
pending data with  , the likelihood is given by
, the likelihood is given by
 |
where  can
be interpreted as a weight, adjusting for the fact that the DLT outcome has not been
ascertained yet. We discuss how to specify
can
be interpreted as a weight, adjusting for the fact that the DLT outcome has not been
ascertained yet. We discuss how to specify  later.
later.
Given the observed interim data  at the current dose level
at the current dose level  , the joint likelihood function is given
by
, the joint likelihood function is given
by
 |
(2.3) |
where  is
the number of patients who experienced DLT by the interim time
is
the number of patients who experienced DLT by the interim time  , and
, and
 is the
number of patients who have completed the assessment without experiencing DLT.
is the
number of patients who have completed the assessment without experiencing DLT.
Let  denote the prior distribution for
denote the prior distribution for
 , e.g.,
, e.g.,  . The posterior
distribution
. The posterior
distribution  is given by
is given by
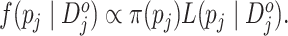 Although this posterior distribution can be routinely sampled by the Markov chain Monte
Carlo method and the strongest key thus can be identified to determine dose assignment,
the issue is that now it is impossible to enumerate the dose-escalation and de-escalation
rules before the trial begins. This is because the posterior depends on individual-level
continuous variable
Although this posterior distribution can be routinely sampled by the Markov chain Monte
Carlo method and the strongest key thus can be identified to determine dose assignment,
the issue is that now it is impossible to enumerate the dose-escalation and de-escalation
rules before the trial begins. This is because the posterior depends on individual-level
continuous variable  and there is an infinite number of
possible outcomes, prohibiting the enumeration of the decision rule. As a result, the
keyboard design with pending DLT data loses its most appealing advantage. This issue also
occurs for the other model-assisted designs.
and there is an infinite number of
possible outcomes, prohibiting the enumeration of the decision rule. As a result, the
keyboard design with pending DLT data loses its most appealing advantage. This issue also
occurs for the other model-assisted designs.
To circumvent the aforementioned issue and maintain the simplicity of the keyboard design, we approximate the last term in (2.3) as follows:
 |
(2.4) |
When  ,
,  ; when
; when
 , we perform Taylor expansion of
, we perform Taylor expansion of
 at
at
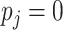 , resulting in
, resulting in  Ignoring the second-order and higher terms, we obtain the approximation (2.4). Thus, the likelihood (2.3) is approximated as
Ignoring the second-order and higher terms, we obtain the approximation (2.4). Thus, the likelihood (2.3) is approximated as
 |
(2.5) |
where  This approximation is simple but powerful. It converts the non-regular likelihood (2.3) into a binomial likelihood arising
from “effective” binomial data
This approximation is simple but powerful. It converts the non-regular likelihood (2.3) into a binomial likelihood arising
from “effective” binomial data  ,
where
,
where  is
the “effective” sample size (ESS) at dose level
is
the “effective” sample size (ESS) at dose level  , and
, and
 is the “effective” number of
patients who have not experienced DLT. As all model-assisted designs are based on the
binomial likelihood, this means that these designs can be seamlessly extended to
accommodate pending DLT data using the approximated likelihood (2.5), as demonstrated in Section 2.4. In addition, because the approximated
likelihood (2.5) depends on the
aggregated value of the
is the “effective” number of
patients who have not experienced DLT. As all model-assisted designs are based on the
binomial likelihood, this means that these designs can be seamlessly extended to
accommodate pending DLT data using the approximated likelihood (2.5), as demonstrated in Section 2.4. In addition, because the approximated
likelihood (2.5) depends on the
aggregated value of the  ’s, rather than the individual value of
’s, rather than the individual value of
 , the approximation renders it possible to
enumerate the decision rules for the resulting design, maintaining the most important
feature of the model-assisted designs. Lastly, the following theorem indicates that (2.5) provides a very accurate
approximation of the exact likelihood (2.3).
, the approximation renders it possible to
enumerate the decision rules for the resulting design, maintaining the most important
feature of the model-assisted designs. Lastly, the following theorem indicates that (2.5) provides a very accurate
approximation of the exact likelihood (2.3).
Theorem 2.1
Let
and
. The approximation error is bounded by
where
. Specifically, for any
, the approximation error
.
The Proof of Theorem 2.1 is provided in the supplementary material available at Biostatistics online. Figure 1 provides two data examples to illustrate the high accuracy of the approximation.
Fig. 1.
The exact and approximated posterior functions based on the observed data: (a)
 patients have been treated and
only
patients have been treated and
only  patients have finished the
assessment without any DLT, and the weights for the remaining three patients are 0.3,
0.4, and 0.5; (b)
patients have finished the
assessment without any DLT, and the weights for the remaining three patients are 0.3,
0.4, and 0.5; (b)  patients have been treated,
patients have been treated,
 DLT has been observed,
DLT has been observed,
 patients have finished the
assessment without any DLT, and the weights for the remaining seven patients are
patients have finished the
assessment without any DLT, and the weights for the remaining seven patients are
 . The prior
distribution of
. The prior
distribution of 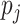 is
is  ;
;
 and
and
 , respectively, represent
the number of patients with DLT and effective sample size by the interim time
, respectively, represent
the number of patients with DLT and effective sample size by the interim time
 ;
; 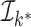 represents the target
key.
represents the target
key.
2.3. Specifying the weight
Following the TITE-CRM, one way for specifying the weight  is to assume
that the time-to-toxicity outcome is uniformly distributed over the assessment period
is to assume
that the time-to-toxicity outcome is uniformly distributed over the assessment period
 . Thus,
. Thus,  As a result,
As a result, 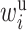 can be interpreted as the
follow-up proportion that patient
can be interpreted as the
follow-up proportion that patient  has finished, and the ESS can be easily
calculated as
has finished, and the ESS can be easily
calculated as
 |
As shown later in simulation, although the uniform scheme seems very restrictive, it
yields remarkably robust performance. This was also observed by Cheung and Chappell (2000) in the TITE-CRM and based on that they
recommended the uniform weight as the default for general use. We consider two alternative
weighting schemes that allow incorporating prior information on  in the Supplementary material available at
Biostatistics online.
in the Supplementary material available at
Biostatistics online.
2.4. TITE-keyboard design
Application of the proposed methodology to the keyboard design is straightforward. We
refer to the resulting design as the TITE-keyboard design. The decision rule of the
TITE-keyboard design is almost the same as that of the keyboard design. The only change is
that to make decisions of dose escalation and de-escalation, we replace the complete data
 , which are not observable
when some DLT data are pending, with the “effective” binomial data
, which are not observable
when some DLT data are pending, with the “effective” binomial data
 for
calculating the posterior distribution of
for
calculating the posterior distribution of  and identifying the
strongest key. Once the strongest key is identified, the same
dose-escalation/de-escalation rule is used to guide the dose transition.
and identifying the
strongest key. Once the strongest key is identified, the same
dose-escalation/de-escalation rule is used to guide the dose transition.
Compared to the model-based TITE-CRM, the most appealing feature of TITE-keyboard is that
its dose transition rule can be tabulated before the trial begins; see Table 1 as the decision table with the target DLT rate
 . To conduct the trial, there is no
need for real-time model fitting, investigators only need to count the number of patients
with DLTs (i.e.,
. To conduct the trial, there is no
need for real-time model fitting, investigators only need to count the number of patients
with DLTs (i.e.,  ), the number of patients with
data pending (i.e.,
), the number of patients with
data pending (i.e., 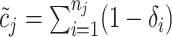 ),
the ESS at dose level
),
the ESS at dose level  (i.e., ESS
(i.e., ESS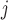 ), and then
use the decision table to determine the dose assignment for the next new cohort. Another
feature of the TITE-keyboard design is that its decision table does not depend on the
weighting scheme or the length of the DLT assessment window. Table 1 applies no matter which of the aforementioned three weighting
schemes is used and no matter the length of the assessment window. This is because the
likelihood (2.5) only depends on
ESS
), and then
use the decision table to determine the dose assignment for the next new cohort. Another
feature of the TITE-keyboard design is that its decision table does not depend on the
weighting scheme or the length of the DLT assessment window. Table 1 applies no matter which of the aforementioned three weighting
schemes is used and no matter the length of the assessment window. This is because the
likelihood (2.5) only depends on
ESS and
and  . Moreover, when
all the pending DLT data become available, i.e.,
. Moreover, when
all the pending DLT data become available, i.e., 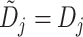 , the
TITE-keyboard design reduces to the standard keyboard design in a seamless way.
, the
TITE-keyboard design reduces to the standard keyboard design in a seamless way.
Table 1.
Dose-escalation and de-escalation boundaries for TITE-keyboard with a target DLT rate of 0.3 and cohort size of 3, up to 12 patients
| Num. patients | Num. DLTs | Num. pending | Escalation patients | Stay DLTs | De-escalation pending |
|---|---|---|---|---|---|
| 3 | 0 |
 1
1 |
Y | ||
| 3 | 0 |
 2
2 |
Suspend accrual | ||
| 3 | 1 | 0 | Y | ||
| 3 | 1 | 1–2 |

|

|
|
| 3 |
|
 1
1 |
Y | ||
| 3 |

|

|
Y&Eliminate | ||
| 6 | 0 |
 4
4 |
Y | ||
| 6 | 1 |
 1
1 |
Y | ||
| 6 | 1 | 2–3 |

|

|
|
| 6 | 1 | 4–5 |

|

|

|
| 6 | 2 | 0 | Y | ||
| 6 | 2 | 1–4 |

|

|
|
| 6 |

|
 3
3 |
Y | ||
| 6 |
 4
4 |
 2
2 |
Y&Eliminate | ||
| 9 | 0 |
 7
7 |
Y | ||
| 9 | 1 |
 4
4 |
Y | ||
| 9 | 1 | 5–6 |

|

|
|
| 9 | 1 | 7–8 |

|

|

|
| 9 | 2 | 0 | Y | ||
| 9 | 2 | 1–3 |

|

|
|
| 9 | 2 | 4–7 |

|

|

|
| 9 | 3 | 0 | Y | ||
| 9 | 3 | 1–6 |

|

|
|
| 9 |

|
 5
5 |
Y | ||
| 9 |
 5
5 |
 4
4 |
Y&Eliminate | ||
| 12 | 0 |
 10
10 |
Y | ||
| 12 | 1 |
 7
7 |
Y | ||
| 12 | 1 | 8–9 |

|

|
|
| 12 | 1 | 10–11 |

|

|

|
| 12 | 2 |
 3
3 |
Y | ||
| 12 | 2 | 4–6 |

|

|
|
| 12 | 2 | 7–10 |

|

|

|
| 12 | 3 |
 3
3 |
Y | ||
| 12 | 3 | 4–9 |

|

|
|
| 12 | 4 | 0 | Y | ||
| 12 | 4 | 1–8 |
|

|
|
| 12 | 5,6 |
 7
7 |
Y | ||
| 12 |
 7
7 |
 5
5 |
Y&Eliminate | ||
 , which is the effective sample size. Dose escalation is not
allowed if fewer than two patients at dose level
, which is the effective sample size. Dose escalation is not
allowed if fewer than two patients at dose level  have
finished the assessment. “Y” means Yes. At each time for decision making, the
observed data should be updated before using the table to determine the dose for the
next patient.
have
finished the assessment. “Y” means Yes. At each time for decision making, the
observed data should be updated before using the table to determine the dose for the
next patient.
For patient safety, we require that dose escalation is not allowed until at least two
patients have completed the DLT assessment at the current dose level. In addition, we
impose an overdose control/stopping rule: at any time during the trial, if any dose
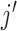 satisfies
satisfies
 ,
then that dose and any higher doses are regarded as overly toxic and should be eliminated
from the trial, and the dose is de-escalated to level
,
then that dose and any higher doses are regarded as overly toxic and should be eliminated
from the trial, and the dose is de-escalated to level 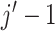 for the next
patients, where
for the next
patients, where  is the prespecified elimination
cutoff, say
is the prespecified elimination
cutoff, say  . If the lowest dose level is
eliminated, the trial should be early terminated. Table
1 also reflects such safety and overdose control rules.
. If the lowest dose level is
eliminated, the trial should be early terminated. Table
1 also reflects such safety and overdose control rules.
When the trial is completed, various approaches can be used to make the final inference on the toxicity probability of the doses based on the observed data, including the nonparametric approach (e.g., isotonic estimate (Barlow and Brunk, 1972)), parametric approach (e.g. fitting a logistic model to the final data), or semiparametric approach (e.g., Yuan and Yin, 2011). In the TITE-keyboard design, the final inference procedure at the end of the trial does not have to be bundled with the dose-escalation procedure, and they are relatively independent components. In other words, we can take different approaches for dose transition and final inference. In our design, we use the isotonic estimate for final toxicity estimation because of its robustness and good performance.
When dealing with fast accrual or late-onset toxicities, the top concern is patient
safety as the patients with pending outcome data who have not experienced DLT at the
interim decision time may yet experience DLT late in the follow-up period. Any reasonable
design that handles late-onset toxicity should take that fact into account in its decision
making, which can be described by the monotonicity property. Let  denote the
“cross-sectional” interim data obtained by setting
denote the
“cross-sectional” interim data obtained by setting  , i.e.,
treating the patients’ temporary DLT outcomes at the interim time as their final DLT
outcomes at the end of the assessment window. In other words,
, i.e.,
treating the patients’ temporary DLT outcomes at the interim time as their final DLT
outcomes at the end of the assessment window. In other words,  . Let
. Let
 and 1, respectively denote
the decisions of dose de-escalation, retaining the current dose and dose escalation based
on the data
and 1, respectively denote
the decisions of dose de-escalation, retaining the current dose and dose escalation based
on the data  .
.
Definition (Monotonicity) A
dose-finding design is monotonic if  for
for
 .
.
Monotonicity indicates that the decision of dose transition based on the observed data
 should be less aggressive than that
based on
should be less aggressive than that
based on  . This is a property that any
reasonable design should obey to reflect that patients who have not experienced DLT by the
interim decision time may yet experience DLT late in the follow-up period. As shown in the
Supplementary material
available at Biostatistics online, the TITE-keyboard design has this
property.
. This is a property that any
reasonable design should obey to reflect that patients who have not experienced DLT by the
interim decision time may yet experience DLT late in the follow-up period. As shown in the
Supplementary material
available at Biostatistics online, the TITE-keyboard design has this
property.
Theorem 2.2
The TITE-keyboard design is monotonic.
Another finite-sample design property of practical importance is coherence. Cheung (2005) originally defined coherence as a design
property by which dose escalation (or de-escalation) is prohibited when the most recently
treated patient experiences (or does not experience) toxicity. Liu and Yuan (2015) extended that concept and defined two different
types of coherence: short-memory coherence and long-memory coherence. They referred to the
coherence proposed by Cheung (2005) as short-memory
coherence because it concerns the observation from only the most recently treated patient,
ignoring the observations from the patients who were previously treated. Long-memory
coherence is defined as a design property by which dose escalation (or de-escalation) is
prohibited when the observed toxicity rate among all accumulative patients treated at the
current dose is larger (or smaller) than the target toxicity rate. From a practical
viewpoint, long-memory coherence is more relevant because when clinicians determine
whether a dose assignment is practically plausible, they almost always base their decision
on the toxicity data that have accumulated from all patients, rather than only the single
patient most recently treated at that dose. In practice, patients in phase I trials are
very heterogeneous, therefore, the toxicity outcome from a single patient can be spurious.
For example, suppose the target DLT rate  and at the current
dose, the most recently treated patient experienced DLT but none of the seven patients
previously treated at the same dose had DLT. As the overall observed DLT rate at the
current dose is 1/8, escalating the dose should not be regarded as an inappropriate
action, although it violates short-memory coherence. It can be shown that the keyboard
design is long-memory coherent. The Proof of Theorem 2.3 is given in the supplementary material available at
Biostatistics online.
and at the current
dose, the most recently treated patient experienced DLT but none of the seven patients
previously treated at the same dose had DLT. As the overall observed DLT rate at the
current dose is 1/8, escalating the dose should not be regarded as an inappropriate
action, although it violates short-memory coherence. It can be shown that the keyboard
design is long-memory coherent. The Proof of Theorem 2.3 is given in the supplementary material available at
Biostatistics online.
Theorem 2.3
The TITE-keyboard design is long-memory coherent in the sense that if the empirical toxicity rate
at the current dose is greater (or less) than the target toxicity rate, the design will not escalate (or de-escalate) the dose.
In addition to monotonicity and coherence, the TITE-keyboard design also possesses a desirable large-sample convergence property. The proof is provided in the Supplementary material available at Biostatistics online.
Theorem 2.4
Suppose the number of treated patients goes to infinity and no overdose control rule is imposed, the dose assignment of the TITE-keyboard design converges almost surely to the dose level
with
. If multiple dose levels are inside the proper dosing interval, the TITE-keyboard design converges almost surely to one of these levels. If no dose level has
, the TITE-keyboard design will eventually oscillate almost surely between the two dose levels whose toxicity rates straddle the proper dosing interval.
2.5. Extension to mTPI and BOIN designs
The proposed methodology can be directly applied to mTPI, another model-assisted design.
The mTPI design specifies three dosing intervals: the proper dosing interval
 ,
underdosing interval
,
underdosing interval  and
overdosing interval
and
overdosing interval  . The
dose-escalation/de-escalation decision is based on the UPM of the three intervals:
. The
dose-escalation/de-escalation decision is based on the UPM of the three intervals:
 |
(2.6) |
The mTPI design assumes the same beta-binomial model and calculates the
UPM ’s based on the posterior of
’s based on the posterior of
 given by (2.1). The dose-assignment
decision of mTPI is then
given by (2.1). The dose-assignment
decision of mTPI is then  ;
that is, making the decision that corresponds to the largest UPM.
;
that is, making the decision that corresponds to the largest UPM.
To apply the proposed methodology, the only change needed is to replace the complete data
 , potentially unobserved due to late-onset
toxicity or fast accrual, by the “effective” data
, potentially unobserved due to late-onset
toxicity or fast accrual, by the “effective” data  in (2.6) when calculating the UPMs. Once the
UPMs are determined, the decision rules remain the same. We refer to the resulting design
as the TITE-mTPI. Table S1 in the supplementary material available at Biostatistics online shows
the dose-escalation/de-escalation rule for the TITE-mTPI design.
in (2.6) when calculating the UPMs. Once the
UPMs are determined, the decision rules remain the same. We refer to the resulting design
as the TITE-mTPI. Table S1 in the supplementary material available at Biostatistics online shows
the dose-escalation/de-escalation rule for the TITE-mTPI design.
Last, we briefly discuss how to apply our methodology to the BOIN design. The BOIN design
has a simpler and more transparent decision rule than the mTPI and keyboard designs. It
does not require calculating the posterior distribution of  and
enumerating all possible outcomes for
and
enumerating all possible outcomes for  . BOIN makes the
decision of dose escalation/de-escalation by comparing the observed DLT rate
. BOIN makes the
decision of dose escalation/de-escalation by comparing the observed DLT rate
 with a pair of
dose-escalation and de-escalation boundaries
with a pair of
dose-escalation and de-escalation boundaries  that
are optimized to minimize the probability of incorrect dose-assignment decisions, assuming
that
are optimized to minimize the probability of incorrect dose-assignment decisions, assuming
 . If
. If
 , escalate the dose;
if
, escalate the dose;
if  , de-escalate the
dose; otherwise, i.e.,
, de-escalate the
dose; otherwise, i.e.,  , stay at
the same dose. Liu and Yuan (2015) provided a
closed-form formula for
, stay at
the same dose. Liu and Yuan (2015) provided a
closed-form formula for  , and showed that the
dose-escalation/de-escalation rule of the BOIN is equivalent to using the frequentist
likelihood ratio test statistic, or Bayesian factor, to guide the dose transition. That
is, BOIN has both frequentist and Bayesian interpretations.
, and showed that the
dose-escalation/de-escalation rule of the BOIN is equivalent to using the frequentist
likelihood ratio test statistic, or Bayesian factor, to guide the dose transition. That
is, BOIN has both frequentist and Bayesian interpretations.
In the presence of pending DLT data due to fast accrual or late-onset toxicity, BOIN
cannot be used because  is not available as
is not available as
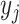 is unknown. To address this issue,
utilizing our approximation with the “effective” binomial data
is unknown. To address this issue,
utilizing our approximation with the “effective” binomial data  , we can simply use
, we can simply use
 to
replace
to
replace  as the maximum likelihood
estimate of
as the maximum likelihood
estimate of  , and then make the decision of dose
escalation/de-escalation in the same way as in the original BOIN. Our numerical study
showed that the resulting design has very similar performance as the TITE-BOIN proposed by
Yuan and others (2018) based on
the imputation method (results are not shown due to space limitation), further confirming
the approximation accuracy of the approximated likelihood function (2.5).
, and then make the decision of dose
escalation/de-escalation in the same way as in the original BOIN. Our numerical study
showed that the resulting design has very similar performance as the TITE-BOIN proposed by
Yuan and others (2018) based on
the imputation method (results are not shown due to space limitation), further confirming
the approximation accuracy of the approximated likelihood function (2.5).
2.6. Software
The R codes for implementation of the proposed methods are available on Github (https://github.com/ruitaolin/TITE-MAD). To facilitate the use of the TITE-keyboard design, we have developed graphical user interface-based software that allows users to generate the dose-assignment decision table, conduct simulations, obtain the operating characteristics of the design, and generate a trial design template for protocol preparation. The software will be freely available at http://www.trialdesign.org.
3. Trial illustration
We apply the proposed TITE-keyboard design to the melanoma trial described in the Section
1. The target toxicity probability  , assessment window
, assessment window
 months, and patients are enrolled at the
rate of two patients per month. The maximum sample size is 21 patients. Patients are treated
in cohorts of three, starting from the lowest dose level.
months, and patients are enrolled at the
rate of two patients per month. The maximum sample size is 21 patients. Patients are treated
in cohorts of three, starting from the lowest dose level.
Given the target toxicity rate of 0.3, Table 1 shows
the TITE-keyboard decision rule with a cohort size of 3. Figure 2 displays the whole trial procedure using the TITE-keyboard design and the
uniform scheme  . Patients in the first cohort
were treated at the lowest dose level. Since no DLT was observed and the TITE-keyboard
design requires at least two finished patients before dose escalation, the trial was
suspended until day 120 when the first two patients had completed the assessment. Following
the TITE-keyboard decision rule, the second cohort was treated at dose level 2. On the
arrival of the third cohort (day 165), one DLT had occurred on day 145 among the second
cohort, and the follow-up proportions for patients 5 and 6 were 1/3 and 1/6, respectively,
leading to
. Patients in the first cohort
were treated at the lowest dose level. Since no DLT was observed and the TITE-keyboard
design requires at least two finished patients before dose escalation, the trial was
suspended until day 120 when the first two patients had completed the assessment. Following
the TITE-keyboard decision rule, the second cohort was treated at dose level 2. On the
arrival of the third cohort (day 165), one DLT had occurred on day 145 among the second
cohort, and the follow-up proportions for patients 5 and 6 were 1/3 and 1/6, respectively,
leading to  . According to Table 1, dose de-escalation was needed. Had we treated
the two pending outcomes as non-DLTs, the keyboard design based on
. According to Table 1, dose de-escalation was needed. Had we treated
the two pending outcomes as non-DLTs, the keyboard design based on  would have recommended retaining the current dose for the next cohort of patients. However,
since the two patients with pending outcome data had been followed for only a short period,
there was greater uncertainty regarding the toxicity probabilities of dose level 2 and it
was preferable to be conservative. The TITE-keyboard automatically took into account such
uncertainty and de-escalated the dose to the first level for treating the third cohort. When
patient 10 arrived, no DLT was observed among the six patients at that dose level, thus the
fourth cohort received dose level 2. On day 255, six patients had been treated at level 2,
with three finished patients. The observed data at level 2 were
would have recommended retaining the current dose for the next cohort of patients. However,
since the two patients with pending outcome data had been followed for only a short period,
there was greater uncertainty regarding the toxicity probabilities of dose level 2 and it
was preferable to be conservative. The TITE-keyboard automatically took into account such
uncertainty and de-escalated the dose to the first level for treating the third cohort. When
patient 10 arrived, no DLT was observed among the six patients at that dose level, thus the
fourth cohort received dose level 2. On day 255, six patients had been treated at level 2,
with three finished patients. The observed data at level 2 were 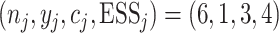 , which
were less than the dose-escalation boundary. As a result, the fifth cohort was still treated
at dose level 2. On day 300, the observed data at that level were updated to be
, which
were less than the dose-escalation boundary. As a result, the fifth cohort was still treated
at dose level 2. On day 300, the observed data at that level were updated to be
 , and
the dose for patients 15 to 18 was escalated to level 3. As one DLT was observed at level 3
before the arrival of patient 19, patients in the last cohort were assigned to dose level 2.
Based on TITE-keyboard, the total trial duration was 14 months. In contrast, the trial would
have run about 31.5 months if we had applied standard adaptive designs that require full DLT
assessment before enrolling each new cohort. At the end of the trial, a total of 12 patients
had been treated at dose level 2, and three DLTs were observed. The final isotonic estimates
of the toxicity rates for the four doses were
, and
the dose for patients 15 to 18 was escalated to level 3. As one DLT was observed at level 3
before the arrival of patient 19, patients in the last cohort were assigned to dose level 2.
Based on TITE-keyboard, the total trial duration was 14 months. In contrast, the trial would
have run about 31.5 months if we had applied standard adaptive designs that require full DLT
assessment before enrolling each new cohort. At the end of the trial, a total of 12 patients
had been treated at dose level 2, and three DLTs were observed. The final isotonic estimates
of the toxicity rates for the four doses were 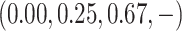 , where
“
, where
“ ” indicates that no data are available at dose
level 4. Therefore, dose level 2 was selected as the MTD.
” indicates that no data are available at dose
level 4. Therefore, dose level 2 was selected as the MTD.
Fig. 2.
Hypothetical phase I clinical trial using the TITE-Keyboard design. The target toxicity rate is 0.3, and the toxicity assessment window is 3 months. Patients are treated in cohort sizes of 3, and the accrual rate is one patient every 15 days. The number above the “x” indicates the time when DLT occurs.
To assess the accuracy of the approximated likelihood function (2.5), we provide the decisions by the TITE-keyboard design respectively with the exact likelihood (2.3) and the approximated likelihood (2.5) in Table S2 in the supplementary material available at Biostatistics online. As expected, the posterior model probabilities calculated based on the exact and approximated likelihoods are almost identical, thus, the decisions made based on the approximated likelihood are consistent with those based on the exact likelihood.
4. Numerical studies
4.1. Fixed scenarios
We perform simulation studies to examine the operating characteristics of the proposed
TITE-keyboard and TITE-mTPI designs. We consider six dose levels, with the target toxicity
probability  . The toxicity assessment window
is
. The toxicity assessment window
is 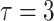 months. A maximum of 36 patients will
be recruited in cohorts of three, with the accrual rate of two patients per month. Six
toxicity scenarios with different locations of the MTD and various shapes of dose–toxicity
curves are considered; see Table 2. We delegate the
detailed data generating process and the configurations of the considered methods in Supplementary material available at
Biostatistics online. Table 2
summarizes the simulation results, including the dose selection percentage; the percentage
of patients treated at each dose; the mean squared error (MSE) of the MTD estimation; the
average trial duration; the early stopping percentage; the risk of poor allocation,
defined as the percentage of simulated trials allocating fewer than six patients to the
MTD; and the risk of overdosing, defined as the percentage of simulated trials that treat
more than half of the patients at doses above the MTD. In terms of MTD selection and
patient allocation, the TITE-CRM, TITE-mTPI, and TITE-keyboard designs yield performances
generally comparable to those of the CRM, while the R6 design performs the worst as it
inherits the drawbacks of the 3+3 design. For MTD estimation, the R6 design has the
largest MSE, and the proposed TITE-keyboard design yields similar MSE as the TITE-CRM,
indicating that TITE-keyboard is as efficient as model-based TITE-CRM. Compared to the
CRM, the TITE-CRM, TITE-mTPI, and TITE-keyboard designs dramatically shorten the trial
duration by approximately 22 months. In Scenarios 1 and 2, TITE-CRM requires a slightly
shorter trial duration than TITE-keyboard because it is more likely to stop the trial
early. R6 requires repeated suspension of accrual until six patients have been treated at
the current dose level. As a result, it generally has a longer trial duration than the
other three TITE methods.
months. A maximum of 36 patients will
be recruited in cohorts of three, with the accrual rate of two patients per month. Six
toxicity scenarios with different locations of the MTD and various shapes of dose–toxicity
curves are considered; see Table 2. We delegate the
detailed data generating process and the configurations of the considered methods in Supplementary material available at
Biostatistics online. Table 2
summarizes the simulation results, including the dose selection percentage; the percentage
of patients treated at each dose; the mean squared error (MSE) of the MTD estimation; the
average trial duration; the early stopping percentage; the risk of poor allocation,
defined as the percentage of simulated trials allocating fewer than six patients to the
MTD; and the risk of overdosing, defined as the percentage of simulated trials that treat
more than half of the patients at doses above the MTD. In terms of MTD selection and
patient allocation, the TITE-CRM, TITE-mTPI, and TITE-keyboard designs yield performances
generally comparable to those of the CRM, while the R6 design performs the worst as it
inherits the drawbacks of the 3+3 design. For MTD estimation, the R6 design has the
largest MSE, and the proposed TITE-keyboard design yields similar MSE as the TITE-CRM,
indicating that TITE-keyboard is as efficient as model-based TITE-CRM. Compared to the
CRM, the TITE-CRM, TITE-mTPI, and TITE-keyboard designs dramatically shorten the trial
duration by approximately 22 months. In Scenarios 1 and 2, TITE-CRM requires a slightly
shorter trial duration than TITE-keyboard because it is more likely to stop the trial
early. R6 requires repeated suspension of accrual until six patients have been treated at
the current dose level. As a result, it generally has a longer trial duration than the
other three TITE methods.
Table 2.
Simulation results with sample size of 36 and cohort size of 3
| Methods | Dose level | MSE | Duration | Stop | Poor | Overdose | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | (in months) | (%) | (%) | (%) | |||
| Scenario 1 | Pr(tox) | 0.13 | 0.28 | 0.41 | 0.50 | 0.60 | 0.70 | |||||
| R6 | Sel% | 43.2 | 30.5 | 7.8 | 0.8 | 0.0 | 0.0 | 1.3 | 35.9 | 17.7 | 83.5 | 10.0 |
| Pts% | 45.6 | 29.0 | 9.0 | 1.5 | 0.1 | 0.0 | ||||||
| TITE-CRM | Sel% | 8.4 | 58.7 | 29.2 | 2.7 | 0.1 | 0.0 | 0.5 | 24.6 | 0.9 | 15.6 | 27.1 |
| Pts% | 25.2 | 42.6 | 25.1 | 5.7 | 0.7 | 0.0 | ||||||
| TITE-mTPI | Sel% | 14.7 | 58.8 | 22.8 | 3.2 | 0.2 | 0.0 | 0.5 | 24.8 | 0.3 | 20.8 | 21.8 |
| Pts% | 29.4 | 46.0 | 20.0 | 3.9 | 0.4 | 0.0 | ||||||
| TITE-keyboard | Sel% | 13.9 | 58.2 | 23.2 | 4.0 | 0.4 | 0.0 | 0.6 | 25.2 | 0.3 | 8.4 | 15.7 |
| Pts% | 33.3 | 41.9 | 19.3 | 4.5 | 0.7 | 0.1 | ||||||
TITE-keyboard
|
Sel% | 14.4 | 58.1 | 23.1 | 3.6 | 0.3 | 0.0 | 0.6 | 25.2 | 0.4 | 8.3 | 14.6 |
| Pts% | 34.2 | 42.0 | 18.7 | 4.1 | 0.6 | 0.1 | ||||||
| CRM | Sel% | 7.9 | 58.9 | 29.8 | 2.6 | 0.1 | 0.0 | 0.5 | 49.4 | 0.7 | 17.4 | 30.0 |
| Pts% | 22.9 | 42.1 | 27.2 | 6.4 | 0.8 | 0.1 | ||||||
| Scenario 2 | Pr(tox) | 0.08 | 0.15 | 0.29 | 0.43 | 0.50 | 0.57 | |||||
| R6 | Sel% | 20.3 | 40.2 | 25.9 | 5.4 | 0.6 | 0.0 | 2.0 | 38.0 | 7.5 | 94.2 | 0.0 |
| Pts% | 30.3 | 35.6 | 20.6 | 6.1 | 1.0 | 0.1 | ||||||
| TITE-CRM | Sel% | 0.2 | 14.1 | 61.7 | 21.9 | 1.9 | 0.1 | 0.5 | 26.6 | 0.2 | 17.1 | 18.2 |
| Pts% | 14.0 | 23.1 | 39.5 | 19.3 | 3.6 | 0.3 | ||||||
| TITE-mTPI | Sel% | 1.0 | 21.8 | 56.4 | 17.7 | 2.7 | 0.3 | 0.6 | 26.9 | 0.0 | 26.5 | 12.7 |
| Pts% | 16.4 | 29.6 | 37.0 | 14.3 | 2.3 | 0.3 | ||||||
| TITE-keyboard | Sel% | 1.1 | 20.8 | 55.5 | 19.9 | 3.3 | 0.4 | 0.6 | 27.2 | 0.0 | 15.4 | 7.5 |
| Pts% | 17.8 | 31.5 | 33.3 | 13.8 | 3.0 | 0.4 | ||||||
TITE-keyboard
|
Sel% | 1.0 | 21.1 | 55.9 | 18.5 | 3.1 | 0.4 | 0.6 | 27.2 | 0.0 | 15.8 | 6.7 |
| Pts% | 18.1 | 32.1 | 33.2 | 13.5 | 2.7 | 0.4 | ||||||
| CRM | Sel% | 0.1 | 13.1 | 62.8 | 22.4 | 2.1 | 0.1 | 0.5 | 49.8 | 0.0 | 16.2 | 19.4 |
| Pts% | 12.3 | 20.8 | 42.5 | 20.6 | 3.8 | 0.5 | ||||||
| Scenario 3 | Pr(tox) | 0.28 | 0.42 | 0.49 | 0.61 | 0.76 | 0.87 | |||||
| R6 | Sel% | 36.2 | 8.8 | 1.1 | 0.0 | 0.0 | 0.0 | 0.8 | 23.3 | 53.9 | 70.8 | 9.9 |
| Pts% | 40.8 | 11.9 | 2.0 | 0.2 | 0.0 | 0.0 | ||||||
| TITE-CRM | Sel% | 54.0 | 25.2 | 2.6 | 0.1 | 0.0 | 0.0 | 0.6 | 20.5 | 18.1 | 10.4 | 28.3 |
| Pts% | 56.8 | 25.7 | 6.2 | 1.0 | 0.1 | 0.0 | ||||||
| TITE-mTPI | Sel% | 67.8 | 21.8 | 3.3 | 0.2 | 0.0 | 0.0 | 0.4 | 22.2 | 6.9 | 13.2 | 30.4 |
| Pts% | 65.0 | 25.7 | 5.1 | 0.5 | 0.0 | 0.0 | ||||||
| TITE-keyboard | Sel% | 61.1 | 23.9 | 3.6 | 0.3 | 0.0 | 0.0 | 0.5 | 22.9 | 11.1 | 5.3 | 25.0 |
| Pts% | 61.4 | 25.7 | 6.0 | 1.0 | 0.1 | 0.0 | ||||||
TITE-keyboard
|
Sel% | 62.4 | 22.7 | 3.3 | 0.3 | 0.0 | 0.0 | 0.5 | 22.8 | 11.4 | 4.6 | 22.9 |
| Pts% | 63.1 | 23.7 | 5.4 | 0.8 | 0.1 | 0.0 | ||||||
| CRM | Sel% | 52.5 | 25.8 | 3.0 | 0.1 | 0.0 | 0.0 | 0.6 | 43.6 | 18.6 | 11.0 | 29.6 |
| Pts% | 54.5 | 24.9 | 7.7 | 1.1 | 0.1 | 0.0 | ||||||
| Scenario 4 | Pr(tox) | 0.05 | 0.10 | 0.20 | 0.31 | 0.50 | 0.70 | |||||
| R6 | Sel% | 10.9 | 29.9 | 33.8 | 19.8 | 2.5 | 0.0 | 3.0 | 38.3 | 3.2 | 99.7 | 0.0 |
| Pts% | 24.0 | 31.2 | 25.6 | 12.6 | 3.6 | 0.4 | ||||||
| TITE-CRM | Sel% | 0.0 | 1.5 | 29.5 | 58.9 | 9.9 | 0.1 | 0.5 | 28.3 | 0.1 | 23.7 | 5.7 |
| Pts% | 11.3 | 14.1 | 29.1 | 33.3 | 11.2 | 0.9 | ||||||
| TITE-mTPI | Sel% | 0.2 | 5.2 | 35.3 | 49.5 | 9.7 | 0.3 | 0.7 | 28.5 | 0.0 | 38.9 | 3.4 |
| Pts% | 12.7 | 19.7 | 31.5 | 27.1 | 8.3 | 0.7 | ||||||
| TITE-keyboard | Sel% | 0.2 | 4.3 | 33.2 | 49.8 | 12.0 | 0.4 | 0.7 | 28.8 | 0.0 | 28.1 | 1.7 |
| Pts% | 13.5 | 21.2 | 30.4 | 25.0 | 8.9 | 1.1 | ||||||
TITE-keyboard
|
Sel% | 0.2 | 4.5 | 35.4 | 49.1 | 10.5 | 0.3 | 0.7 | 28.7 | 0.0 | 30.6 | 1.3 |
| Pts% | 13.7 | 22.1 | 31.1 | 24.3 | 7.9 | 0.9 | ||||||
| CRM | Sel% | 0.1 | 1.4 | 29.7 | 58.9 | 9.9 | 0.1 | 0.5 | 50.0 | 0.0 | 20.7 | 5.5 |
| Pts% | 10.3 | 11.8 | 28.7 | 36.9 | 11.3 | 1.0 | ||||||
| Scenario 5 | Pr(tox) | 0.06 | 0.08 | 0.12 | 0.18 | 0.30 | 0.41 | |||||
| R6 | Sel% | 7.6 | 13.6 | 21.9 | 30.7 | 17.1 | 4.8 | 5.0 | 36.4 | 4.4 | 100.0 | 0.0 |
| Pts% | 21.8 | 22.7 | 22.0 | 17.6 | 8.7 | 3.6 | ||||||
| TITE-CRM | Sel% | 0.0 | 0.4 | 5.7 | 32.2 | 47.4 | 14.2 | 0.8 | 30.0 | 0.1 | 42.1 | 6.5 |
| Pts% | 11.8 | 12.2 | 17.3 | 25.4 | 23.7 | 9.6 | ||||||
| TITE-mTPI | Sel% | 0.2 | 1.5 | 8.9 | 32.9 | 40.7 | 15.9 | 1.0 | 30.6 | 0.0 | 50.4 | 3.5 |
| Pts% | 13.2 | 15.5 | 20.1 | 23.9 | 19.2 | 8.2 | ||||||
| TITE-keyboard | Sel% | 0.1 | 0.8 | 7.5 | 30.3 | 43.3 | 18.0 | 0.9 | 31.0 | 0.0 | 37.4 | 0.9 |
| Pts% | 13.4 | 15.6 | 19.8 | 23.8 | 18.7 | 8.6 | ||||||
TITE-keyboard
|
Sel% | 0.1 | 1.3 | 7.9 | 32.5 | 42.0 | 16.2 | 0.9 | 30.8 | 0.0 | 41.3 | 0.9 |
| Pts% | 13.7 | 16.2 | 20.6 | 24.2 | 17.9 | 7.5 | ||||||
| CRM | Sel% | 0.0 | 0.4 | 4.6 | 30.7 | 49.4 | 15.0 | 0.7 | 50.4 | 0.0 | 37.0 | 7.3 |
| Pts% | 10.5 | 9.9 | 15.0 | 27.2 | 26.5 | 10.8 | ||||||
| Scenario 6 | Pr(tox) | 0.05 | 0.06 | 0.08 | 0.11 | 0.19 | 0.32 | |||||
| R6 | Sel% | 4.3 | 7.1 | 12.1 | 23.7 | 31.4 | 18.4 | 6.0 | 36.0 | 3.1 | 100.0 | 0.0 |
| Pts% | 19.6 | 19.7 | 19.5 | 18.2 | 12.3 | 8.2 | ||||||
| TITE-CRM | Sel% | 0.0 | 0.1 | 2.1 | 10.9 | 38.0 | 48.8 | 1.1 | 32.0 | 0.1 | 49.7 | 0.0 |
| Pts% | 11.2 | 11.0 | 13.7 | 17.8 | 23.5 | 22.9 | ||||||
| TITE-mTPI | Sel% | 0.1 | 0.5 | 2.6 | 11.2 | 38.0 | 47.7 | 1.2 | 32.6 | 0.0 | 48.9 | 0.0 |
| Pts% | 12.1 | 13.2 | 15.2 | 17.6 | 21.8 | 20.1 | ||||||
| TITE-keyboard | Sel% | 0.1 | 0.3 | 1.7 | 9.9 | 38.5 | 49.5 | 1.0 | 32.8 | 0.0 | 45.0 | 0.0 |
| Pts% | 12.2 | 13.1 | 15.2 | 18.8 | 21.7 | 18.9 | ||||||
TITE-keyboard
|
Sel% | 0.0 | 0.2 | 1.8 | 10.4 | 38.9 | 48.7 | 1.0 | 32.7 | 0.0 | 47.4 | 0.0 |
| Pts% | 12.2 | 13.2 | 15.5 | 19.1 | 21.7 | 18.3 | ||||||
| CRM | Sel% | 0.0 | 0.1 | 1.1 | 8.6 | 40.7 | 49.5 | 0.9 | 50.6 | 0.0 | 42.7 | 0.0 |
| Pts% | 10.0 | 9.2 | 11.4 | 17.6 | 25.8 | 26.0 |
The assessment window is 3 months and the accrual rate is two patients per month.
The MTD is in boldface. R6 is the rolling six design; TITE-CRM is the time-to-event
CRM; TITE-keyboard and TITE-mTPI are the proposed time-to-event versions of keyboard
and mTPI designs, respectively. TITE-keyboard is the
design that utilizes the exact likelihood function (2.3). CRM is the continual reassessment method based on
the complete data. “MSE” is the mean squared error of the MTD estimation; “Stop%” is
the early stopping percentage; “Poor%” is the risk of poor allocation, which is the
percentage of simulated trials allocating fewer than six patients to the MTD;
“Overdose%” is the risk of overdosing, which is the percentage of simulated trials
that treat more than half of the patients at doses above the MTD.
is the
design that utilizes the exact likelihood function (2.3). CRM is the continual reassessment method based on
the complete data. “MSE” is the mean squared error of the MTD estimation; “Stop%” is
the early stopping percentage; “Poor%” is the risk of poor allocation, which is the
percentage of simulated trials allocating fewer than six patients to the MTD;
“Overdose%” is the risk of overdosing, which is the percentage of simulated trials
that treat more than half of the patients at doses above the MTD.
When dealing with late-onset toxicities, it is not desirable to be overly conservative and retain low doses too long because that allocates too many patients to subtherapeutic doses. This early-settlement problem is quantified by the risk of poor allocation. Among the considered designs, the TITE-keyboard and TITE-CRM have the lowest risk of poor allocation, indicating that these two designs can quickly recover from the false settlement and allocate patients to the appropriate doses. TITE-mTPI is more likely to become stuck at incorrect doses than TITE-keyboard and TITE-CRM, with a higher risk of poor allocation. The R6 design performs the worst since it is excessively conservative and would not escalate the dose until six patients have been treated at the current dose level. When handling late-onset toxicities, it is also not desirable to be overly aggressive and treat a large percentage of patients at overly toxic doses. We measure this design behavior using the risk of overdosing. According to Table 2, the TITE-keyboard design is safer than the TITE-CRM and TITE-mTPI designs, demonstrating the lowest risk of overdosing patients among the three designs.
To investigate the accuracy of our proposed approximation procedure, we implement the
TITE-keyboard design that is based on the exact
likelihood function (2.3), where the
superscript “
design that is based on the exact
likelihood function (2.3), where the
superscript “ ” represents the exact likelihood.
As shown in Table 2, the operating characteristics
of the TITE-keyboard design are essentially identical to those of the
TITE-keyboard
” represents the exact likelihood.
As shown in Table 2, the operating characteristics
of the TITE-keyboard design are essentially identical to those of the
TITE-keyboard design. To gain more insight, we
record the percentage of discrepancy in dose assignment between the two designs across 10
000 simulated trials, which is merely about 1.3% on average for the considered scenarios.
These results verify the high accuracy of the approximated likelihood function. In Supplementary material available at
Biostatistics online, we also show the robustness of TITE-keyboard to
different weighting schemes for
design. To gain more insight, we
record the percentage of discrepancy in dose assignment between the two designs across 10
000 simulated trials, which is merely about 1.3% on average for the considered scenarios.
These results verify the high accuracy of the approximated likelihood function. In Supplementary material available at
Biostatistics online, we also show the robustness of TITE-keyboard to
different weighting schemes for  based on a sensitivity analysis.
based on a sensitivity analysis.
4.2. Random scenarios
To ensure that the simulation results represent the general performance of the designs,
we conducted a large-scale simulation study to compare the proposed TITE-keyboard,
TITE-mTPI designs with R6 and TITE-CRM based on randomly generated dose–toxicity
scenarios. We considered 12 configurations that cover various target toxicity rates,
numbers of cohorts, cohort sizes, distributions of time-to-toxicity outcomes, percentages
of toxicity occurring in the latter half of the assessment window
 , and accrual rates. Details
of the configurations are provided in Table S3 in the Supplementary material available at
Biostatistics online. Under each configuration, we randomly generated
50 000 random dose–toxicity scenarios based on the procedure described in Zhou and others (2018a). The setup of
the comparative designs is the same as that described in Section 4.1.
, and accrual rates. Details
of the configurations are provided in Table S3 in the Supplementary material available at
Biostatistics online. Under each configuration, we randomly generated
50 000 random dose–toxicity scenarios based on the procedure described in Zhou and others (2018a). The setup of
the comparative designs is the same as that described in Section 4.1.
Figure 3 shows the simulation results, which are generally consistent with those obtained in the fixed scenarios. TITE-keyboard, TITE-mTPI, and TITE-CRM have similar accuracy when identifying the MTD, and they uniformly outperform the R6 design. TITE-keyboard is safer and easier to implement than TITE-CRM. In terms of the risk of underdosing, the two model-assisted designs perform similarly as the TITE-CRM, while the R6 design is more likely to underdose patients by allocating more patients to the doses that are below the MTD and potentially subtherapeutic.
Fig. 3.
Simulation results based on 50 000 randomly generated scenarios. The target toxicity probability in scenarios 1–6 is 0.2, while that in scenarios 7–12 is 0.3. Six metrics are summarized: (a) percentage of correct MTD selection; (b) percentage of patients allocated to correct MTD; (c) percentage of patients allocated to overdoses; (d) percentage of patients allocated to underdoses; (e) risk of poor allocation, defined as the percentage of simulated trials allocating fewer than six patients to the MTD; and (f) average trial duration (in months).
Between the two model-assisted designs, TITE-keyboard is preferable because it has substantially lower risk of overdosing patients and poor allocation than TITE-mTPI. By comparing the operating characteristics of TITE-keyboard across the 12 simulation configurations, we additionally found that the performance of TITE-keyboard is robust to the late-onset toxicity profile, including the ratio of the assessment window and the patient inter-arrival time as well as the distribution of time-to-toxicity outcomes.
5. Concluding remarks
We have proposed general methodology to allow model-assisted trial designs to handle late-onset toxicity and fast accrual. We have formulated a new likelihood-based approach to account for pending DLT data and have derived a novel approximation of the observed likelihood that enables all existing model-assisted designs to accommodate pending data in a seamless way without destroying their simplicity. In particular, we have proposed the TITE-keyboard design, which has been demonstrated to possess desirable finite-sample and large-sample properties: monotonicity, coherence, and consistency. The TITE-keyboard design is simple and easy to implement yet has superior performance that is comparable to that of the more complicated TITE-CRM design.
Supplementary Material
Acknowledgments
We thank the associate editor, the two referees, and the editor for their many constructive and insightful comments that have led to significant improvements in the article. Conflict of Interest: None declared.
Funding
The National Cancer Institute (Award Number P50CA098258 and P50CA217685 to Y.Y.), in part.
References
- Al-Atrash G. (2018). Nivolumab and Ipilimumab After Donor Stem Cell Transplant in Treating Participants With High Risk Refractory or Relapsed Acute Myeloid Leukemia. ClinicalTrials.gov Identifier: NCT03600155. [Google Scholar]
- Barlow R. E. and Brunk H. D. (1972). The isotonic regression problem and its dual. Journal of the American Statistical Association 67, 140–147. [Google Scholar]
- Cheung Y. K. (2005). Coherence principles in dose-finding studies. Biometrika 92, 863–873. [Google Scholar]
- Cheung Y. K. and Chappell R. (2000). Sequential designs for phase I clinical trials with late-onset toxicities. Biometrics 56, 1177–1182. [DOI] [PubMed] [Google Scholar]
- Dilts D. M., Sandler A. B., Cheng S., Crites J., Ferranti L., Wu A., Bookman M. A., Thomas J. P. and Ostroff J. (2008). Accrual to clinical trials at selected comprehensive cancer centers. Journal of Clinical Oncology 26, 6543–6543. [Google Scholar]
- Ivanova Flournoy and Ivanova A., Flournoy N., and Chung Y. (2007). Cumulative cohort design for dose finding. Journal of Statistical Planning and Inference 137, 2316–2327. [Google Scholar]
- Ji Y., Liu P., Li Y., and Nebiyou Bekele B. (2010). A modified toxicity probability interval method for dose-finding trials. Clinical Trials 7, 653–663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- June C. H., Warshauer J. T., Bluestone J. A. (2017). Is autoimmunity the Achilles’ heel of cancer immunotherapy? Nature Medicine 23, 540–547. [DOI] [PubMed] [Google Scholar]
- Kairalla J. A., Coffey C. S., Thomann M. A., and Muller K. E. (2012). Adaptive trial designs: a review of barriers and opportunities. Trials 13, 145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leonard J. P., Abramson J. S. and Rutherford S. (2017). Study of Venetoclax Plus DA-EPOCH-R for the Treatment of Aggressive B-Cell Lymphomas (V+DA-EPOCH-R). ClinicalTrials.gov Identifier: NCT03036904. [Google Scholar]
- Lin R. and Yin G. (2017a). Bayesian optimal interval design for dose finding in drug-combination trials. Statistical Methods in Medical Research 26, 2155–2167. [DOI] [PubMed] [Google Scholar]
- Lin R. and Yin G. (2017b). STEIN: A simple toxicity and efficacy interval design for seamless phase I/II clinical trials. Statistics in Medicine 36, 4106–4120. [DOI] [PubMed] [Google Scholar]
- Liu S., Yin G., and Yuan Y. (2013). Bayesian data augmentation dose finding with continual reassessment method and delayed toxicity. The Annals of Applied Statistics 7, 2138–2156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu S. and Yuan Y. (2015). Bayesian optimal interval designs for phase I clinical trials. Journal of Royal Statistical Society: Series C (Applied Statistics) 64, 507–523. [Google Scholar]
- Mu R., Yuan Y., Xu J., Mandrekar S. J. and Yin J. (2018). gBOIN: a unified model-assisted phase I trial design accounting for toxicity grades, binary or continuous endpoint. Journal of the Royal Statistical Society: Series C (Applied Statistics) 68, 289–308. [Google Scholar]
- O’Quigley J., Pepe M., and Fisher L. (1990). Continual reassessment method: a practical design for phase 1 clinical trials in cancer. Biometrics 46, 33–48. [PubMed] [Google Scholar]
- Phan J. (2017). Trial of Stereotactic HYpofractionateD RadioAblative (HYDRA) Treatment of Laryngeal Cancer. ClinicalTrials.gov Identifier: NCT03114462. [Google Scholar]
- Postel-Vinay S., Gomez-Roca C., Molife L. R., Anghan B., Levy A., Judson I., De Bono J., Soria J. C., Kaye S. and Paoletti X. (2011). Phase I trials of molecularly targeted agents: should we pay more attention to late toxicities? Journal of Clinical Oncology 29, 1728–1735. [DOI] [PubMed] [Google Scholar]
- Skolnik J. M., Barrett J. S., Jayaraman B., Patel D. and Adamson P. C. (2008). Shortening the timeline of pediatric phase I trials: the rolling six design. Journal of Clinical Oncology 26, 190–195. [DOI] [PubMed] [Google Scholar]
- Storer B. E. (1989). Design and analysis of phase I clinical trials. Biometrics 45, 925–937. [PubMed] [Google Scholar]
- Weber J. S., Yang J. C., Atkins M. B., and Disis M. L. (2015). Toxicities of immunotherapy for the practitioner. Journal of Clinical Oncology 33, 2092–2099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J. (2016). TG02 Plus Dose-Dense or Metronomic Temozolomide Followed by Randomized Phase II Trial of TG02 Plus Temozolomide Versus Temozolomide Alone in Adults With Recurrent Anaplastic Astrocytoma and Glioblastoma. ClinicalTrials.gov Identifier: NCT02942264. [Google Scholar]
- Yan F., Mandrekar S. J., and Yuan Y. (2017). Keyboard: a novel Bayesian toxicity probability interval design for phase I clinical trials. Clinical Cancer Research 23, 3994–4003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan Y. and Yin G. (2009). Bayesian dose finding by jointly modelling toxicity and efficacy as time-to-event outcomes. Journal of the Royal Statistical Society: Series C (Applied Statistics) 58, 719–736. [Google Scholar]
- Yuan Y. and Yin G. (2011). Robust EM continual reassessment method in oncology dose finding. Journal of the American Statistical Association 106, 818–831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan Y. and Yin G. (2011). Dose-response curve estimation: a semiparametric mixture approach. Biometrics 67, 1543–1554. [DOI] [PubMed] [Google Scholar]
- Yuan Y., Hess K. R., Hilsenbeck S. G., and Gilbert M. R. (2016). Bayesian optimal interval design: a simple and well-performing design for phase I oncology trials. Clinical Cancer Research 22, 4291–4301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan Y., Lin R., Li D., Nie L., and Warren K. E. (2018). Time-to-event Bayesian optimal interval design to accelerate phase I trials. Clinical Cancer Research 24, 4921–4930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L. and Yuan Y. (2016). A practical Bayesian design to identify the maximum tolerated dose contour for drug combination trials. Statistics in Medicine 35, 4924–4936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao L., Lee J., Mody R., and Braun T. M. (2011). The superiority of the time-to-event continual reassessment method to the rolling six design in pediatric oncology phase I trials. Clinical Trials 8, 361–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H., Murray T., Pan H., and Yuan Y. (2018a). Comparative review of model-assisted designs for phase I clinical trials. Statistics in Medicine 37, 2208–2222. [DOI] [PubMed] [Google Scholar]
- Zhou H., Yuan Y., and Nie L. (2018b). Accuracy, safety and reliability of novel Bayesian phase I trial designs. Clinical Cancer Research 24, 4357–4364. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.





