Abstract
The goal of long term research on age assessment is to focus on the strengths and weaknesses of existing reliable methods of age estimation. In cases of age estimation when all teeth are present, maximum accuracy can be obtained using a 7 tooth model. Demirjian’s system and Willems models require all seven mandibular teeth in the lower left quadrant for age assessment. Unfortunately, these methods cannot be applied in children with hypodontia. In 2019, Bedek et al., from Croatia, developed new models of age estimation based on a combination of one to seven mandibular teeth. In the present study, we tested the accuracy of the newly developed models for age estimation in South Indian children. Tested in parallel with Willems models, the accuracy of the new models was tested in terms of mean difference, mean absolute error (MAE) and percentage of correct estimations within intervals of +0.5 and +1 years. In terms of mean difference between chronological age (CA) and estimated dental age (DA), all models along with Willems models have underestimated the CA except Bedek et al’s 6 tooth model where overestimation of CA was seen in boys. For MAE and percentage of correct estimations, the new models performed better than Willems models. With regards to our results, it can be concluded that the new models for dental age calculation are accurate and suitable. Therefore, we may encourage their use for age estimation in South Indian children, particularly in individuals with hypodontia or when multiple teeth are missing.
Keywords: Forensic Odontology;
Introduction
The need for accurate age estimation exists when the chronological age (CA) of the individual who is in conflict with the law and who was not known or could not be documented. (1) In the majority of countries, court officials rely either on forensic practitioners or health authorities (in UAE) to provide specific age estimations in an attempt to reduce inappropriate judicial ruling and to carry out age-dependent legal procedures in accordance with the law. (1- 3) Adapting an appropriate and accurate age assessment method for any population group in need is vital in forensic practice. Many methods which are accepted all over the world are based on the analyses of Europeans and North Americans, pointing out the scarcity and underrepresentation of literature for scientific standards for the populations most in need. (4) Owing to the changes in modern population such as global migrations, increased number of intermarriages and other environmental factors,
there is a need to set new contemporary global standards, as a large proportion of available methods were formulated several generations ago.
In 1973, Demirjian and co-workers derived dental maturity scores by evaluating the dental development of children of French-Canadian origin. (5) Three years later (1976), the same authors updated their work by increasing the sample size to incorporate dental maturity scores for additional tooth development stages. They also presented scoring systems and percentile standards for two different sets of four teeth. (6) To date, Demirjian’s method is considered to be the oldest and most frequently used method for dental age estimation in children. Later, a multitude of validation studies exploring the reliability and accuracy of Demirjian’s system in populations foreign to the original reference sample, resulted in an overestimation of CA. (7- 9) In their original work, Demirjian et al., reported a possibility that their method may not be valid in other populations and perhaps adaptations should be made. Considering this, Willems et al, in 2001, presented a modified scoring system based on a Belgian Caucasian sample, which is a relatively simple system. Using these models, dental age (DA) is calculated by summing scores assigned to each stage of a single tooth. (10) When its accuracy was tested in different comparative studies, it revealed greater accuracy consistently in estimating CA. (11- 13)
The most significant disadvantage of Demirjian’s system and Willems models, is that neither of these methods can be used in children with multiple missing teeth or those with mandibular hypodontia. To date, no method in the literature was put forward to assess CA in living individuals or incomplete human remains with multiple missing mandibular teeth. Bedek et al., highlighted the absolute necessity of age estimation methods, particularly in cases where there is an absence of several teeth as in hypodontia or incomplete human remains with multiple missing teeth. (14) They developed and tested new models for dental age estimation based on a combination of one to seven mandibular teeth using univariate regression and regression with forward and backward elimination.
In the same study, Bedek et al., also tested new age estimation models by comparing their performance in parallel with Willems models. Results showed that the newly developed models significantly surpass the accuracy of Willems models. (14) To the best of our knowledge, no studies are available in the dental literature that tested the accuracy of Bedek et al’s new models of age estimation. Therefore, this study was aimed to evaluate the accuracy of Bedek et al’s new models (gender specific scores) for age estimation of 7 to 15 year old South Indian children and to compare their accuracy with Willems models.
MATERIAL AND METHODS
Materials
Six hundred and fifty orthopantomographs (OPGs) of children (275 boys and 375 girls) aged between 7 and 15 years were collected retrospectively from four different states of Southern India: Telangana, Andhra Pradesh, Chennai and Bangalore. Table 1 shows the age and gender distribution of the sample. All the OPGs were obtained from private clinical practitioners, taken for the purpose of radiological diagnosis. No OPG was taken for the sole purpose of this investigation. Ethics approval to undertake this investigation was granted by the Institutional ethics committee. OPGs from individuals of South Indian origin, aged between 7 to 15 years, with no apparent dental pathology on the left side of the mandible, all permanent teeth present in the lower left quadrant (except third molars) were included. Exclusion criteria were OPGs with incomplete details, dental pathology of permanent teeth, low quality radiographs, history of systemic diseases and congenital anomalies.
Table 1. Age and Gender distribution of the sample (n=650).
| Age groups | Boys | Girls | Total |
|---|---|---|---|
| 7- 7.9 | 7 | 10 | 17 |
| 8- 8.9 | 14 | 16 | 30 |
| 9- 9.9 | 24 | 22 | 46 |
| 10- 10.9 | 28 | 37 | 65 |
| 11- 11.9 | 36 | 94 | 130 |
| 12- 12.9 | 49 | 79 | 128 |
| 13- 13.9 | 53 | 53 | 106 |
| 14- 14.9 | 64 | 64 | 128 |
| Total | 275 | 375 | 650 |
All OPGs were digitalised and each OPG was coded with unique identification, with relevant information about date of birth (DOB) and date of exposure (DOE). Chronological age (CA) for each individual was then calculated by subtracting DOB from DOE of the radiograph, which was then converted into decimal points (years and months) as a fraction of twelve months.
Methods
The developmental stages of seven permanent mandibular teeth on the left side of the jaw were evaluated using Demirjian’s method. (5) Details of the combination of mandibular teeth to derive new models of age estimation for both genders were presented in table 2. Coefficients were assigned gender wise based on the developmental stages of the teeth. The coefficients of individual teeth were summed up. The age of each individual was calculated by the formula:
Table 2. Combination of one to seven mandibular teeth used to derive new models of dental age estimation by Bedek et al., in both genders.
| Bedek et al., New models of dental age estimation | Combination of teeth† | |
|---|---|---|
| Boys | Girls | |
| Seven-teeth model | 31-37 | 31-37 |
| Six-teeth model | 31 33 34 35 36 37 | 32 33 34 35 36 37 |
| Five-teeth model | 31 33 34 36 37 | 32 33 34 36 37 |
| Four-teeth model | 31 33 34 37 | 32 33 34 37 |
| Three-teeth model | 33 34 37 | 32 34 37 |
| Two-teeth model | 34 37 | 34 37 |
| One-tooth model | 34 | 37 |
†FDI notation
Dental age= Intercept + coefficients assigned to the tooth stages in the model.
Table 3 show the details of the formulae for different tooth models for boys and girls separately.
Table 3. Calculation of dental age (DA) using newly developed models in Boys and Girls, separately.
| Model | Formula |
|---|---|
| Boys | |
| 31-37 (Seven- teeth) | DA= 4.396 + Sum of coefficients assigned to the stages of teeth in the model |
| 31 33 34 35 36 37 (Six- teeth) | DA= 4.544 + Sum of coefficients assigned to the stages of teeth in the model |
| 31 33 34 36 37 (Five- teeth) | DA= 4.664 + Sum of coefficients assigned to the stages of teeth in the model |
| 31 33 34 37 (Four- teeth) | DA= 5.451 + Sum of coefficients assigned to the stages of teeth in the model |
| 33 34 37 (Three- teeth) | DA= 6.069 + Sum of coefficients assigned to the stages of teeth in the model |
| 34 37 (Two- teeth) | DA= 5.370 + Sum of coefficients assigned to the stages of teeth in the model |
| 34 (One- tooth) | DA= 5.828 + Sum of coefficients assigned to the stages of teeth in the model |
| Girls | |
| 31-37 (Seven- teeth) | DA= 5.095 + Sum of coefficients assigned to the stages of teeth in the model |
| 32 33 34 35 36 37 (Six- teeth) | DA= 5.077 + Sum of coefficients assigned to the stages of teeth in the model |
| 32 33 34 36 37 (Five- teeth) | DA= 5.079 + Sum of coefficients assigned to the stages of teeth in the model |
| 32 33 34 37 (Four- teeth) | DA= 5.122 + Sum of coefficients assigned to the stages of teeth in the model |
| 32 34 37 (Three- teeth) | DA= 5.350 + Sum of coefficients assigned to the stages of teeth in the model |
| 34 37 (Two- teeth) | DA= 5.350 + Sum of coefficients assigned to the stages of teeth in the model |
| 37 (One- tooth) | DA= 5.771 + Sum of coefficients assigned to the stages of teeth in the model |
All the OPGs were examined for staging by a single examiner (single blind approach), a forensic odontologist (SB Balla), who had six years of experience in evaluating radiographic images and age estimation. The second examiner was a dentist with a Master’s degree in orthodontics (SA Ankisetti). To test intra- and inter- examiner agreement, 100 OPGs were selected randomly and re-assessed after an interval of one month.
Statistical analysis
Statistical and mathematical analyses were carried out using SPSS software version 20.0 for Windows (SPSS Inc, Chicago, IL, USA). Kappa statistics were applied to determine intra- and inter-examiner agreement. A Paired sample t-test was performed to quantify statistical significance of the difference between the CA and estimated dental age (DA) among all age groups in each sex for all models. For all tested models, differences at the individual level were evaluated by subtracting CA from DA, expressed in mean error (ME), that indicates the direction of the error (over- vs. underestimation). (15) We also calculated absolute mean difference or mean absolute error (MAE), which expresses the magnitude of the error for all models in each sex. The results of Bedek et al’s new models were compared with Willems models, and their accuracy was determined by the percentage of correct estimations within specified intervals i.e., +0.5 years and +1 year. If the obtained p-value was less than 0.05, the results were considered statistically significant.
RESULTS
Kappa statistics revealed that there were no statistically significant differences between intra- and inter-examiner agreement. Kappa values of intra-examiner agreement varied from 0.76 for first molar to 0.91 for first premolar, while inter-examiner agreement varied from 0.73 for second premolar to 0.9 for the central incisor (Table 4).
Table 4. Intraexaminer and Interexaminer agreement of Demirjian’s stages of tooth development.
| Tooth | 31 | 32 | 33 | 34 | 35 | 36 | 37 | Mean |
|---|---|---|---|---|---|---|---|---|
| Intra | 0.84 | 0.87 | 0.89 | 0.91 | 0.83 | 0.76 | 0.79 | 0.84 |
| Inter | 0.9 | 0.88 | 0.78 | 0.82 | 0.73 | 0.78 | 0.85 | 0.82 |
Boys
Group differences
Tables (Tables 5-12) showed the results of mean comparisons of estimated DA with CA for each age group for both Willems models and Bedek et al’s newly developed models. When the mean differences between DA and CA for individual age groups were evaluated, it shows that Willems models have the least number of significantly different age groups (i.e., 4 out of 8). Among the new models of Bedek et al’s 3 to 7 tooth models have 7 out 8 significantly different age groups, whereas 1 and 2 tooth models have all significantly different age groups.
Table 5. Comparison between chronological age and dental age estimated using Willems gender specific scores in boys and girls.
|
Age
Groups (n) |
Mean (SD) | 95% CI of age difference | t statistics (df) | p-value | ||
|---|---|---|---|---|---|---|
| Chronological Age (CA) |
Dental
Age (DA) |
DA-CA
(SE) |
||||
| Boys | ||||||
| 7- 7.9 (7) | 7.35 (0.29) | 7.24 (0.46) | -0.11 (0.46) | -0.54 to 0.31 | -0.66 (6) | 0.530 |
| 8- 8.9 (14) | 8.51 (0.29) | 7.99 (0.57) | -0.52 (0.64) | -0.89 to -0.15 | -3.05 (13) | 0.009* |
| 9- 9.9 (24) | 9.37 (0.26) | 8.86 (1.04) | -0.51 (1.08) | -0.96 to -0.05 | -2.03 (23) | 0.030* |
| 10- 10.9 (28) | 10.39 (0.26) | 9.73 (0.72) | -0.65 (0.63) | -0.91 to -0.41 | -5.44 (27) | 0.000* |
| 11- 11.9 (36) | 11.4 (0.29) | 11.49 (1.25) | 0.09 (1.19) | -0.31 to 0.49 | 0.47 (35) | 0.641 |
| 12- 12.9 (49) | 12.47 (0.27) | 12.29 (1.64) | -0.17 (1.6) | -0.63 to 0.28 | -0.77 (48) | 0.444 |
| 13- 13.9 (53) | 13.51 (0.29) | 13.74 (1.61) | 0.23 (1.49) | -0.17 to 0.65 | 1.17 (52) | 0.247 |
| 14- 14.9 (64) | 14.44 (0.29) | 14.77 (1.32) | 0.33 (1.27) | 0.01 to 0.64 | 2.08 (63) | 0.041* |
| 7- 14.9 (275) | 12.17 (2.01) | 12.13 (2.63) | -0.03 (0.07) | -0.19 to 0.11 | -0.46 (274) | 0.640 |
| Girls | ||||||
| 7- 7.9 (10) | 7.52 (0.31) | 7.71 (1.27) | 0.18 (0.36) | -0.63 to 1.01 | 0.51 (9) | 0.617 |
| 8- 8.9 (16) | 8.34 (0.25) | 7.6 (0.9) | -0.74 (0.96) | -1.25 to -0.22 | -3.07 (15) | 0.008* |
| 9- 9.9 (22) | 9.45 (0.25) | 8.89 (2.07) | -0.56 (2.07) | -1.48 to0.35 | -1.27 (21) | 0.218 |
| 10- 10.9 (37) | 10.42 (0.25) | 9.55 (1.52) | -0.87 (1.46) | -1.36 to -0.38 | -3.63 (36) | 0.001* |
| 11- 11.9 (94) | 11.41 (0.28) | 10.58 (1.43) | -0.82 (1.43) | -1.11 to -0.52 | -5.54 (93) | 0.000* |
| 12- 12.9 (79) | 12.43 (0.28) | 12.06 (1.51) | -0.36 (1.49) | -0.71 to -0.03 | -2.18 (78) | 0.032* |
| 13- 13.9 (53) | 13.46 (0.29) | 13.73 (1.52) | 0.26 (1.5) | -0.14 to 0.68 | 1.30 (52) | 0.198 |
| 14- 14.9 (64) | 14.46 (0.23) | 15.16 (1.06) | 0.71 (1.02) | 0.44 to 0.96 | 5.15 (63) | 0.000* |
| 7- 14.9 (375) | 11.99 (1.8) | 11.72 (2.66) | -0.27 (0.07) | -0.42 to -0.11 | -3.43 (374) | 0.001* |
*Statistically significant (p<0.05); SD Standard deviation; SE Standard error; df degree of freedom
Table 6. Comparison between chronological age and dental age estimated using Bedek et al., 7- teeth formulae in boys and girls.
|
Age
Groups (n) |
Mean (SD) | 95% CI of age difference | t statistics (df) | p-value | ||
|---|---|---|---|---|---|---|
| Chronological Age (CA) |
Dental
Age (DA) |
DA- CA
(SE) |
||||
| Boys | ||||||
| 7- 7.9 (7) | 7.35 (0.29) | 6.58 (0.35) | -0.77 (0.13) | -1.11 to -0.43 | -5.57 (6) | 0.001* |
| 8- 8.9 (14) | 8.51 (0.29) | 7.17 (0.69) | -1.33 (0.21) | -1.77 to -0.89 | -6.6 (13) | 0.000* |
| 9- 9.9 (24) | 9.37 (0.26) | 8.5 (1.38) | -0.87 (0.28) | -1.46 to -0.27 | -3.01 (23) | 0.006* |
| 10- 10.9 (28) | 10.39 (0.26) | 9.72 (0.93) | -0.66 (0.87) | -1.01 to -0.32 | -4.01 (27) | 0.000* |
| 11- 11.9 (36) | 11.4 (0.29) | 11.31 (1.01) | -0.08 (0.16) | -0.41 to 0.23 | -0.55 (35) | 0.582 |
| 12- 12.9 (49) | 12.47 (0.27) | 11.9 (0.19) | -0.56 (0.18) | -0.94 to -0.18 | -3.01 (48) | 0.004* |
| 13- 13.9 (53) | 13.51 (0.29) | 13.07 (1.24) | -0.43 (0.15) | -0.74 to -0.11 | -2.77 (52) | 0.008* |
| 14- 14.9 (64) | 14.44 (0.29) | 13.88 (0.9) | -0.55 (0.11) | -0.77 to -0.34 | -5.13 (63) | 0.000* |
| 7- 14.9 (275) | 12.17 (2.01) | 11.61 (2.38) | -0.55 (0.06) | -0.68 to -0.42 | -8.47 (274) | 0.000* |
| Girls | ||||||
| 7- 7.9 (10) | 7.52 (0.31) | 7.93 (1.49) | 0.41 (0.45) | -0.61 to 1.43 | 0.91 (9) | 0.389 |
| 8- 8.9 (16) | 8.34 (0.25) | 7.86 (0.91) | -0.48 (0.25) | -1.02 to 0.06 | -1.89 (15) | 0.078 |
| 9- 9.9 (22) | 9.45 (0.25) | 9.22 (1.86) | -0.22 (0.39) | -1.05 to 0.59 | -0.57 (21) | 0.570 |
| 10- 10.9 (37) | 10.42 (0.25) | 10.01 (1.17) | -0.41 (0.18) | -0.78 to -0.04 | -2.26 (36) | 0.030* |
| 11- 11.9 (94) | 11.41 (0.28) | 10.88 (1.12) | -0.52 (0.11) | -0.75 to -0.29 | -4.50 (93) | 0.000* |
| 12- 12.9 (79) | 12.43 (0.28) | 12.01 (1.16) | -0.42 (0.12) | -0.67 to -0.16 | -3.29 (78) | 0.001* |
| 13- 13.9 (53) | 13.46 (0.29) | 13.23 (1.06) | -0.22 (0.14) | -0.51 to 0.06 | -1.59 (52) | 0 118 |
| 14- 14.9 (64) | 14.46 (0.23) | 14.16 (0.75) | -0.29 (0.09) | -0.47 to -0.11 | -3.24 (63) | 0.002* |
| 7- 14.9 (375) | 11.99 (1.8) | 11.62 (2.11) | -0.36 (0.05) | -0.48 to -0.25 | -6.32 (374) | 0.000* |
*Statistically significant (p<0.05); SD Standard deviation; SE Standard error; df degree of freedom
Table 7. Comparison between chronological age and dental age estimated using Bedek et al., 6- teeth formulae in boys and girls.
|
Age
Groups (n) |
Mean (SD) | 95% CI of age difference | t statistics (df) | p-value | ||
|---|---|---|---|---|---|---|
| Chronological Age (CA) |
Dental
Age (DA) |
DA-CA
(SE) |
||||
| Boys | ||||||
| 7- 7.9 (7) | 7.35 (0.29) | 8.51 (0.36) | 1.15 (0.16) | 0.75 to 1.55 | 7.08 (6) | 0.000* |
| 8- 8.9 (14) | 8.51 (0.29) | 9.14 (0.61) | 0.63 (0.18) | 0.23 to 1.03 | 3.43 (13) | 0.004* |
| 9- 9.9 (24) | 9.37 (0.26) | 10.36 (1.26) | 0.98 (0.26) | 0.43 to 1.53 | 3.72 (23) | 0.001* |
| 10- 10.9 (28) | 10.39 (0.26) | 11.48 (0.96) | 1.09 (0.17) | 0.73 to 1.45 | 6.29 (27) | 0.000* |
| 11- 11.9 (36) | 11.4 (0.29) | 12.88 (0.81) | 1.47 (0.13) | 1.2 to 1.74 | 11.51 (35) | 0.000* |
| 12- 12.9 (49) | 12.47 (0.27) | 13.35 (1.1) | 0.88 (0.15) | 0.56 to 1.19 | 5.64 (48) | 0.000* |
| 13- 13.9 (53) | 13.51 (0.29) | 14.12 (0.82) | 0.62 (0.11) | 0.42 to 0.82 | 6.16 (52) | 0.000* |
| 14- 14.9 (64) | 14.44 (0.29) | 14.56 (0.47) | 0.12 (0.06) | -0.01 to 0.25 | 1.81 (63) | 0.075 |
| 7- 14.9 (275) | 12.17 (2.01) | 12.93 (1.91) | 0.75 (0.05) | 0.64 to 0.87 | 13.24 (274) | 0.000* |
| Girls | ||||||
| 7- 7.9 (10) | 7.52 (0.31) | 7.63 (1.79) | 0.11 (0.54) | -1.11 to 1.33 | 0.19 (9) | 0.848 |
| 8- 8.9 (16) | 8.34 (0.25) | 7.65 (1.27) | -0.68 (0.33) | -1.39 to 0.02 | -2.06 (15) | 0.057 |
| 9- 9.9 (22) | 9.45 (0.25) | 9.17 (1.96) | -0.28 (0.41) | -1.14 to 0.58 | -0.67 (21) | 0.508 |
| 10- 10.9 (37) | 10.42 (0.25) | 10.01 (1.17) | -0.41 (0.18) | -0.78 to -0.04 | -2.25 (36) | 0.030* |
| 11- 11.9 (94) | 11.41 (0.28) | 10.88 (1.12) | -0.52 (0.11) | -0.75 to -0.29 | -4.49 (93) | 0.000* |
| 12- 12.9 (79) | 12.43 (0.28) | 12.01 (1.16) | -0.41 (0.12) | -0.67 to -0.16 | -3.29 (78) | 0.001* |
| 13- 13.9 (53) | 13.46 (0.29) | 13.23 (1.06) | -0.22 (0.14) | -0.51 to 0.06 | -1.59 (52) | 0.118 |
| 14- 14.9 (64) | 14.46 (0.23) | 14.16 (0.75) | -0.29 (0.09) | -0.47 to -0.11 | -3.24 (63) | 0.002* |
| 7- 14.9 (375) | 11.99 (1.8) | 11.6 (2.16) | -0.38 (0.05) | -0.5 to -0.26 | -6.49 (374) | 0.000* |
*Statistically significant (p<0.05); SD Standard deviation; SE Standard error; df degree of freedom
Table 8. Comparison between chronological age and dental age estimated using Bedek et al., 5- teeth formulae in boys and girls.
|
Age
Groups (n) |
Mean (SD) | 95% CI of age difference | t statistics (df) | p-value | ||
|---|---|---|---|---|---|---|
| Chronological Age (CA) |
Dental
Age (DA) |
DA-CA
(SE) |
||||
| Boys | ||||||
| 7- 7.9 (7) | 7.35 (0.29) | 6.5 (0.41) | -0.85 (0.16) | -1.26 to -0.44 | -5.12 (6) | 0.002* |
| 8- 8.9 (14) | 8.51 (0.29) | 7.24 (0.77) | -1.27 (0.22) | -1.75 to -0.78 | -5.7 (13) | 0.000* |
| 9- 9.9 (24) | 9.37 (0.26) | 8.46 (1.37) | -0.91 (0.28) | -1.49 to -0.31 | -3.18 (23) | 0.004* |
| 10- 10.9 (28) | 10.39 (0.26) | 9.72 (0.93) | -0.67 (0.16) | -1.02 to -0.32 | -4.03 (27) | 0.000* |
| 11- 11.9 (36) | 11.4 (0.29) | 11.25 (1.02) | -0.14 (0.16) | -0.48 to 0.18 | -0.89 (35) | 0.379 |
| 12- 12.9 (49) | 12.47 (0.27) | 11.85 (1.35) | -0.61 (0.18) | -0.99 to -0.23 | -3.26 (48) | 0.002* |
| 13- 13.9 (53) | 13.51 (0.29) | 13.03 (1.25) | -0.46 (0.15) | -0.78 to -0.15 | -2.99 (52) | 0.004* |
| 14- 14.9 (64) | 14.44 (0.29) | 13.84 (0.93) | -0.59 (0.11) | -0.81 to -0.37 | -5.31 (63) | 0.000* |
| 7- 14.9 (275) | 12.17 (2.01) | 11.58 (2.38) | -0.59 (0.06) | - 0.72 to -0.46 | -8.94 (274) | 0.000* |
| Girls | ||||||
| 7- 7.9 (10) | 7.52 (0.31) | 7.65 (1.71) | 0.13 (0.51) | -1.02 to 1.3 | 0.26 (9) | 0.798 |
| 8- 8.9 (16) | 8.34 (0.25) | 7.67 (1.19) | -0.66 (0.31) | -1.33 to 0.01 | -2.13 (15) | 0.050 |
| 9- 9.9 (22) | 9.45 (0.25) | 9.11 (1.92) | -0.34 (0.41) | -1.19 to 0.51 | -0.83 (21) | 0.415 |
| 10- 10.9 (37) | 10.42 (0.25) | 9.83 (1.25) | -0.59 (0.19) | -0.99 to -0.19 | -3.03 (36) | 0.004* |
| 11- 11.9 (94) | 11.41 (0.28) | 10.79 (1.21) | -0.61 (0.12) | -0.86 to -0.36 | -4.86 (93) | 0.000* |
| 12- 12.9 (79) | 12.43 (0.28) | 12.01 (1.19) | -0.43 (0.13) | -0.69 to -0.17 | -3.3 (78) | 0.001* |
| 13- 13.9 (53) | 13.46 (0.29) | 13.26 (1.04) | -0.21 (0.14) | -0.48 to 0.07 | -1.47 (52) | 0.147 |
| 14- 14.9 (64) | 14.46 (0.23) | 14.11 (0.81) | -0.34 (0.09) | -0.54 to -0.15 | -3.56 (63) | 0.001* |
| 7- 14.9 (375) | 11.99 (1.8) | 11.55 (2.19) | -0.43 (1.18) | -0.55 to -0.31 | -7.14 (374) | 0.000* |
*Statistically significant (p<0.05); SD Standard deviation; SE Standard error; df degree of freedom
Table 9. Comparison between chronological age and dental age estimated using Bedek et al., 4- teeth formulae in boys and girls.
|
Age
Groups (n) |
Mean (SD) | 95% CI of age difference | t statistics (df) | p-value | ||
|---|---|---|---|---|---|---|
| Chronological Age (CA) |
Dental
Age (DA) |
DA-CA
(SE) |
||||
| Boys | ||||||
| 7- 7.9 (7) | 7.35 (0.29) | 6.54 (0.41) | -0.81 (0.17) | -1.24 to -0.38 | -4.63 (6) | 0.004* |
| 8- 8.9 (14) | 8.51 (0.29) | 7.26 (0.82) | -1.25 (0.24) | -1.77 to -0.72 | -5.15 (13) | 0.000* |
| 9- 9.9 (24) | 9.37 (0.26) | 8.48 (1.44) | -0.88 (0.3) | -1.51 to -0.26 | -2.94 (23) | 0.007* |
| 10- 10.9 (28) | 10.39 (0.26) | 9.69 (0.9) | -0.7 (0.16) | -1.03 to -0.37 | -4 35 (27) | 0.000* |
| 11- 11.9 (36) | 11.4 (0.29) | 11.22 (1.07) | -0.17 (0.17) | -0.52 to 0.17 | -1.01 (35) | 0.319 |
| 12- 12.9 (49) | 12.47 (0.27) | 11.84 (1.36) | -0.62 (0.19) | -1.01 to -0.24 | -3.27 (48) | 0.002* |
| 13- 13.9 (53) | 13.51 (0.29) | 13.03 (1.25) | -0.46 (0.15) | -0.78 to -0.15 | -3.01 (52) | 0.004* |
| 14- 14.9 (64) | 14.44 (0.29) | 13.84 (0.93) | -0.59 (0.11) | -0.82 to -0.37 | -5.33 (63) | 0.000* |
| 7- 14.9 (275) | 12.17 (2.01) | 11.57 (2.38) | -0.59 (0.06) | -0.72 to -0.46 | -8.90 (274) | 0.000* |
| Girls | ||||||
| 7- 7.9 (10) | 7.52 (0.31) | 8.06 (1.31) | 0.54 (0.39) | -0.34 to 1.43 | 1.37 (9) | 0.201 |
| 8- 8.9 (16) | 8.34 (0.25) | 7.96 (0.78) | -0.37 (0.22) | -0.86 to 0.11 | -1.67 (15) | 0.116 |
| 9- 9.9 (22) | 9.45 (0.25) | 9.17 (1.8) | -0.27 (0.38) | -1.07 to 0.51 | -0.72 (21) | 0.474 |
| 10- 10.9 (37) | 10.42 (0.25) | 9.82 (1.26) | -0.6 (0.19) | -1.01 to -0.19 | -3.02 (36) | 0.005* |
| 11- 11.9 (94) | 11.41 (0.28) | 10.72 (1.23) | -0.62 (0.12) | -0.88 to -0.37 | -4.89 (93) | 0.000* |
| 12- 12.9 (79) | 12.43 (0.28) | 12.01 (1.19) | -0.43 (0.12) | -0.68 to -0.17 | -3.31 (78) | 0.001* |
| 13- 13.9 (53) | 13.46 (0.29) | 13.25 (1.03) | -0.21 (0.14) | -0.49 to 0.07 | -1.49 (52) | 0.142 |
| 14- 14.9 (64) | 14.46 (0.23) | 14.11 (0.81) | -0.34 (0.09) | -0.54 to -0.15 | -3.59 (63) | 0.001* |
| 7- 14.9 (375) | 11.99 (1.8) | 11.57 (2.13) | -0.41 (0.05) | -0.53 to -0.29 | -6.91 (374) | 0.000* |
*Statistically significant (p<0.05); SD Standard deviation; SE Standard error; df degree of freedom
Table 10. Comparison between chronological age and dental age estimated using Bedek et al., 3- teeth formulae in boys and girls.
|
Age
Groups (n) |
Mean (SD) | 95% CI of age difference | t statistics (df) | p-value | ||
|---|---|---|---|---|---|---|
| Chronological age (CA) |
Dental
Age (DA) |
DA-CA
(SE) |
||||
| Boys | ||||||
| 7- 7.9 (7) | 7.35 (0.29) | 6.11 (0.1) | -1.23 (0.09) | -1.46 to -1.01 | -13.27 (6) | 0.000* |
| 8- 8.9 (14) | 8.51 (0.29) | 7.04 (0.89) | -1.46 (0.26) | -2.04 to -0.89 | -5.49 (13) | 0.000* |
| 9- 9.9 (24) | 9.37 (0.26) | 8.01 (1.78) | -1.36 (0.37) | -2.13 to -0.59 | -3.68 (23) | 0.001* |
| 10- 10.9 (28) | 10.39 (0.26) | 9.53 (1.14) | -0.86 (0.2) | -1.28 to -0.43 | -4.18 (27) | 0.000* |
| 11- 11.9 (36) | 11.4 (0.29) | 11.22 (1.1) | -0.18 (0.17) | -0.54 to 0.17 | -1.01 (35) | 0.316 |
| 12- 12.9 (49) | 12.47 (0.27) | 11.83 (1.41) | -0.63 (0.19) | -1.03 to -0.23 | -3.19 (48) | 0.002* |
| 13- 13.9 (53) | 13.51 (0.29) | 13.03 (1.25) | -0.46 (0.15) | -0.77 to -0.15 | -2.98 (52) | 0.004* |
| 14- 14.9 (64) | 14.44 (0.29) | 13.84 (0.93) | -0.59 (0.11) | -0.82 to -0.37 | -5.33 (63) | 0.000* |
| 7- 14.9 (275) | 12.17 (2.01) | 11.49 (2.53) | -0.67 (0.07) | -0.82 to -0.53 | -9.24 (274) | 0.000* |
| Girls | ||||||
| 7- 7.9 (10) | 7.52 (0.31) | 8.02 (1.45) | 0.49 (0.42) | -0.47 to 1.46 | 1.15 (9) | 0.277 |
| 8- 8.9 (16) | 8.34 (0.25) | 7.86 (0.8) | -0.48 (0.22) | -0.96 to 0.001 | -2.11 (15) | 0.052 |
| 9- 9.9 (22) | 9.45 (0.25) | 9.02 (1 74) | -0.43 (0.37) | -1.2 to 0.33 | -1.16 (21) | 0.256 |
| 10- 10.9 (37) | 10.42 (0.25) | 9.75 (1.26) | -0.66 (0.19) | -1.07 to -0.26 | -3.36 (36) | 0.002* |
| 11- 11.9 (94) | 11.41 (0.28) | 10.65 (1.14) | -0.74 (0.11) | -0.98 to -0.51 | -6.22 (93) | 0.000* |
| 12- 12.9 (79) | 12.43 (0.28) | 11.83 (1.19) | -0.59 (0.13) | -0.85 to -0.33 | -4.54 (78) | 0.000* |
| 13- 13.9 (53) | 13.46 (0.29) | 13.14 (1.12) | -0.31 (0.15) | -0.62 to -0.01 | -2.1 (52) | 0.040* |
| 14- 14.9 (64) | 14.46 (0.23) | 14.08 (0.84) | -0.37 (0.1) | -0.57 to -0.17 | -3.67 (63) | 0.000* |
| 7- 14.9 (375) | 11.99 (1.8) | 11.47 (2.14) | -0.51 (0.05) | -0.63 to -0.4 | -8.69 (374) | 0.000* |
*Statistically significant (p<0.05); SD Standard deviation; SE Standard error; df degree of freedom
Table 11. Comparison between chronological age and dental age estimated using Bedek et al., 2- teeth formulae in boys and girls.
|
Age
Groups (n) |
Mean (SD) | 95% CI of age difference | t statistics (df) | p-value | ||
|---|---|---|---|---|---|---|
| Chronological Age (CA) |
Dental
Age (DA) |
DA-CA
(SE) |
||||
| Boys | ||||||
| 7- 7.9 (7) | 7.35 (0.29) | 6.22 (0.09) | -1.13 (0.11) | -1.39 to -0.86 | -10.52 (6) | 0.000* |
| 8- 8.9 (14) | 8.51 (0.29) | 6.96 (0.87) | -1.54 (0.25) | -2.1 to -0.98 | -5.98 (13) | 0.000* |
| 9- 9.9 (24) | 9.37 (0.26) | 7.72 (1.56) | -1.64 (0.32) | -2.32 to -0.97 | -5.04 (23) | 0.000* |
| 10- 10.9 (28) | 10.39 (0.26) | 8.99 (1.25) | -1.39 (0.21) | -1.84 to -0.94 | -6.36 (27) | 0.000* |
| 11- 11.9 (36) | 11.4 (0.29) | 10.96 (1.16) | -0.43 (0.18) | -0.82 to -0.04 | -2.29 (35) | 0.028* |
| 12- 12.9 (49) | 12.47 (0.27) | 11.54 (1.42) | -0.93 (0.19) | -1.32 to -0.53 | -4.73 (48) | 0.000* |
| 13- 13.9 (53) | 13.51 (0.29) | 12.83 (1.25) | -0.67 (0.15) | -0.98 to -0.35 | -4.27 (52) | 0.000* |
| 14- 14.9 (64) | 14.44 (0.29) | 13.66 (1.02) | -0.77 (0.12) | -1.01 to -0.52 | -6.33 (63) | 0.000* |
| 7- 14.9 (275) | 12.17 (2.01) | 11.24 (2.55) | -0.92 (0.07) | -1.07 to -0.78 | -12.54 (274) | 0.000* |
| Girls | ||||||
| 7- 7.9 (10) | 7.52 (0.31) | 7.62 (1.61) | 0.09 (0.46) | -0.95 to 1.15 | 0.21 (9) | 0.840 |
| 8- 8.9 (16) | 8.34 (0.25) | 7.24 (1.04) | -1.09 (0.27) | -1.68 to -0.5 | -3.96 (15) | 0.001* |
| 9- 9.9 (22) | 9.45 (0.25) | 8.52 (2.04) | -0.93 (0.43) | -1.83 to -0.02 | -2.13 (21) | 0.044* |
| 10- 10.9 (37) | 10.42 (0.25) | 9.42 (1.58) | -1.01 (0.25) | -1.51 to -0.48 | -3.95 (36) | 0.000* |
| 11- 11.9 (94) | 11.41 (0.28) | 10.54 (1.33) | -0.87 (0.13) | -1.14 to -0.59 | -6.24 (93) | 0.000* |
| 12- 12.9 (79) | 12.43 (0.28) | 11.83 (1.19) | -0.59 (0.13) | -0.85 to -0.33 | -4.55 (78) | 0.000* |
| 13- 13.9 (53) | 13.46 (0.29) | 13.14 (1.12) | -0.31 (0.15) | -0.62 to -0.01 | -2.1 (52) | 0.040* |
| 14- 14.9 (64) | 14.46 (0.23) | 14.08 (0.85) | -0.37 (0.1) | -0.57 to -0.17 | -3.67 (63) | 0.000* |
| 7- 14.9 (375) | 11.99 (1.8) | 11.33 (2.34) | -0.65 (0.06) | -0.78 to -0.51 | -9.76 (374) | 0.000* |
*Statistically significant (p<0.05); SD Standard deviation; SE Standard error; df degree of freedom
Table 12. Comparison between chronological age and dental age estimated using Bedek et al., 1- tooth formulae in boys and girls.
|
Age
Groups (n) |
Mean (SD) | 95% CI of age difference | t statistics (df) | p-value | ||
|---|---|---|---|---|---|---|
| Chronological Age (CA) |
Dental
Age (DA) |
DA-CA
(SE) |
||||
| Boys | ||||||
| 7- 7.9 (7) | 7.35 (0.29) | 6.43 (0.0) | -0.92 (0.11) | -1.19 to -0.65 | -8.32 (6) | 0.000* |
| 8- 8.9 (14) | 8.51 (0.29) | 7.2 (0.91) | -1.31 (0.26) | -1.89 to -0.72 | -4.86 (13) | 0.000* |
| 9- 9.9 (24) | 9.37 (0.26) | 7.7 (1.41) | -1.67 (0.29) | -2.29 to -1.05 | -5.57 (23) | 0.000* |
| 10- 10.9 (28) | 10.39 (0.26) | 8.8 (1.39) | -1.58 (1.32) | -2.1 to -1.07 | -6.34 (27) | 0.000* |
| 11- 11.9 (36) | 11.4 (0.29) | 10.92 (1.35) | -0.47 (0.22) | -0.92 to -0.02 | -2.13 (35) | 0.040* |
| 12- 12.9 (49) | 12.47 (0.27) | 11.65 (1.78) | -0.81 (0.24) | -1.31 to -0.31 | -3.28 (48) | 0.002* |
| 13- 13.9 (53) | 13.51 (0.29) | 13.03 (1.32) | -0.46 (0.16) | -0.8 to -0.12 | -2.77 (52) | 0.008* |
| 14- 14.9 (64) | 14.44 (0.29) | 13.72 (0.8) | -0.71 (0.1) | -0.92 to -0.51 | -6.89 (63) | 0.000* |
| 7- 14.9 (275) | 12.17 (2.01) | 11.31 (2.62) | -0.86 (0.08) | -1.02 to -0.7 | -10.71 (274) | 0.000* |
| Girls | ||||||
| 7- 7.9 (10) | 7.52 (0.31) | 8.07 (1.61) | 0.55 (0.46) | -0.48 to 1.6 | 1.02 (9) | 0.260 |
| 8- 8.9 (16) | 8.34 (0.25) | 7.76 (1.07) | -0.57 (0.28) | -1.18 to 0.02 | -2.03 (15) | 0.060 |
| 9- 9.9 (22) | 9.45 (0.25) | 9.04 (1.85) | -0.41 (1.87) | -1.24 to 0.41 | -1.03 (21) | 0.312 |
| 10- 10.9 (37) | 10.42 (0.25) | 9.88 (1.53) | -0.54 (0.23) | -1.02 to -0.05 | -2.26 (36) | 0.030* |
| 11- 11.9 (94) | 11.41 (0.28) | 10.69 (1.34) | -0.71 (0.13) | -0.99 to -0.44 | -5.16 (93) | 0.000* |
| 12- 12.9 (79) | 12.43 (0.28) | 11.74 (1.14) | -0.68 (0.12) | -0.93 to -0.43 | -5.37 (78) | 0.000* |
| 13- 13.9 (53) | 13.46 (0.29) | 13.05 (1.13) | -0.41 (0.15) | -0.71 to -0.11 | -2.72 (52) | 0.009* |
| 14- 14.9 (64) | 14.46 (0.23) | 14.05 (0.86) | -0.41 (0.1) | -0.61 to -0.2 | -4.01 (63) | 0.000* |
| 7- 14.9 (375) | 11.99 (1.8) | 11.45 (2.17) | -0.53 (0.06) | -0.66 to -0.41 | -8.38 (374) | 0.000* |
*Statistically significant (p<0.05); SD Standard deviation; SE Standard error; df degree of freedom
When the mean data of all age groups was calculated, except Willems models, all newly developed models showed statistically significant differences between the DA and CA; Willems models (t=-0.468; p=0.640), Bedek et al’s 7 tooth model (t=-8.476; p=0.000), 6 tooth model (t=13.249; p=0.000), 5 tooth model (t=-8.941; p=0.000), 4 tooth model (t=-8.900; p=0.000), 3 tooth model (t=-9.249; p=0.000), 2 tooth model (t=-12.542; p=0.000) and 1 tooth model (t=-10.709; p=0.000). When the overall mean age deviations were calculated, Willems models had the smallest mean error of -0.03 years, for Bedek et al’s 7 tooth model (-0.55 years), 6 tooth model (0.75 years), 5 tooth model (-0.59 years), 4 tooth model (-0.59 years), 3 tooth model (-0.67 years), 2 tooth model (-0.92 years) and 1 tooth model (-0.86 years).
Individual differences
The maximum and minimum deviations and their frequency were presented for all models in Figure 1. The individual difference between the DA and CA was found to be more frequent within 0 to +0.5 years (overestimation) for Bedek et al’s 7 tooth, 5 tooth and 2 tooth models, within 0 to -0.5 years (underestimation) for Willems models, within 0.5 to 1 years (overestimation) for Bedek et al’s 4 tooth, 3 tooth and 1 tooth models, within -0.5 to -1 year (underestimation) for Bedek et al’s 6 tooth model.
Figure 1.
Individual differences for South Indian sample of boys using Willems model (GS) and Bedek et al., age estimation models
Mean absolute error
Table 13 shows the output for gender as well as overall mean absolute error (MAE) for each tested model. The smallest MAE for boys was obtained for Bedek et al’s 6 tooth model, 0.75 years, while the greatest MAE was for Bedek et al’s 1 tooth model, 1.05 years. For the remaining models, MAE ranged from 0.85 to 1.02 years.
Table 13. Mean absolute error (MAE) for all tested methods in boys and girls respectively.
| Methods | Mean Absolute error/ deviation | ||
|---|---|---|---|
| Boys | Girls | Total | |
| Willems | 1.02 | 1.25 | 1.16 |
| Bedek’s seven teeth | 0.85 | 0.88 | 0.86 |
| Bedek’s six teeth | 0.75 | 0.9 | 0.94 |
| Bedek’s five teeth | 0.85 | 0.94 | 0.9 |
| Bedek’s four teeth | 0.86 | 0.92 | 0.89 |
| Bedek’s three teeth | 0.95 | 0.91 | 0.93 |
| Bedek’s two teeth | 0.96 | 1.01 | 0.99 |
| Bedek’s one tooth | 1.05 | 0.98 | 1.01 |
Girls
Group differences
Comparisons of mean estimated DA and CA for all the tested models for girls were shown in tables 5 - 12. When the mean differences DA and CA for individual age groups were evaluated, Bedek et al’s 7 to 4 tooth models have the least number of statistically significant different age groups (i.e., 4 out of 8). For Willems models, Bedek et al’s 3 and 1 tooth models, statistically significant differences were seen in 5 out of 8 age groups, while the 2 tooth model has 7 out of 8 statistically significant age groups.
With respect to the mean data of all age groups, it is evident that all models significantly underestimated CA in girls; Willems models (t=-3.437; p=0.001), Bedek et al’s 7 tooth model (t=-6.322; p=0.000), 6 tooth model (t=-6.497; p=0.000), 5 tooth model (t=-7.144; p=0.000), 4 tooth model (t=-6.913; p=0.000), 3 tooth model (t=-8.694; p=0.000), 2 tooth model (t=-9.767; p=0.000) and 1 tooth model (t=-8.380; p=0.000). Overall mean age deviations are larger for Bedek et al’s 2 tooth model (-0.65 years) and the smallest deviation for Willems model (-0.27 years). For the remaining models, the mean age deviations are as follows; Bedek 7 tooth (-0.36 years), 6 tooth (-0.38 years), 5 tooth (-0.43 years), 4 tooth (-0.41 years), 3 tooth (-0.51 years), and 1 tooth (-0.53 years).
Individual differences
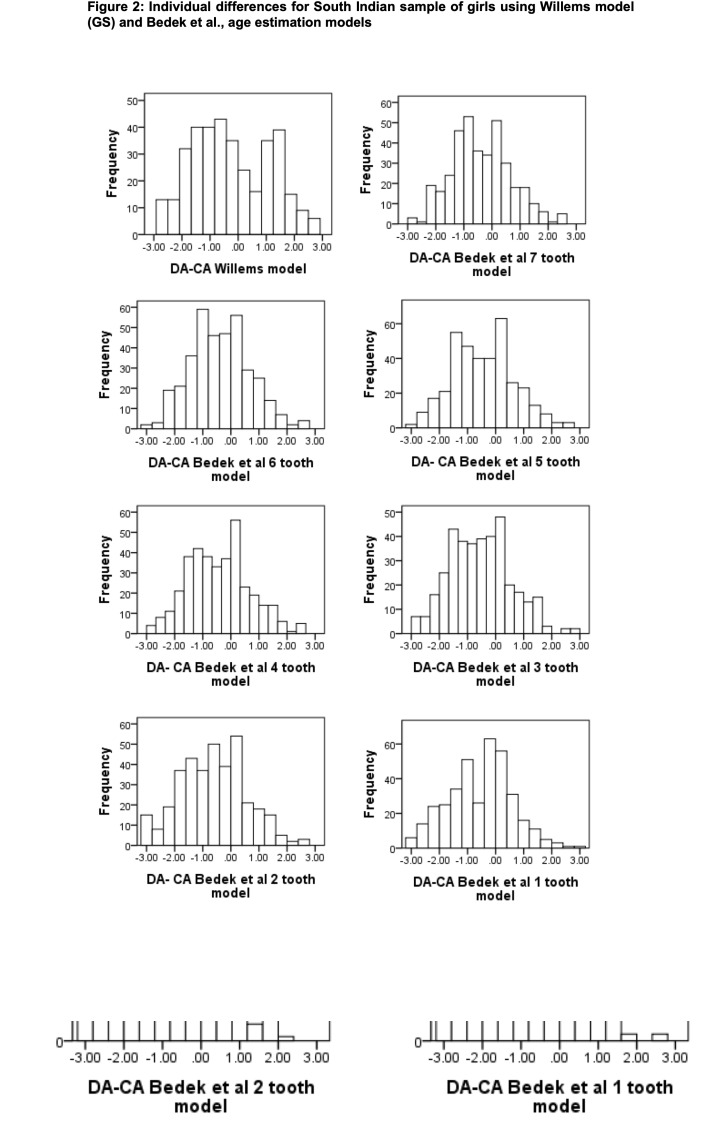
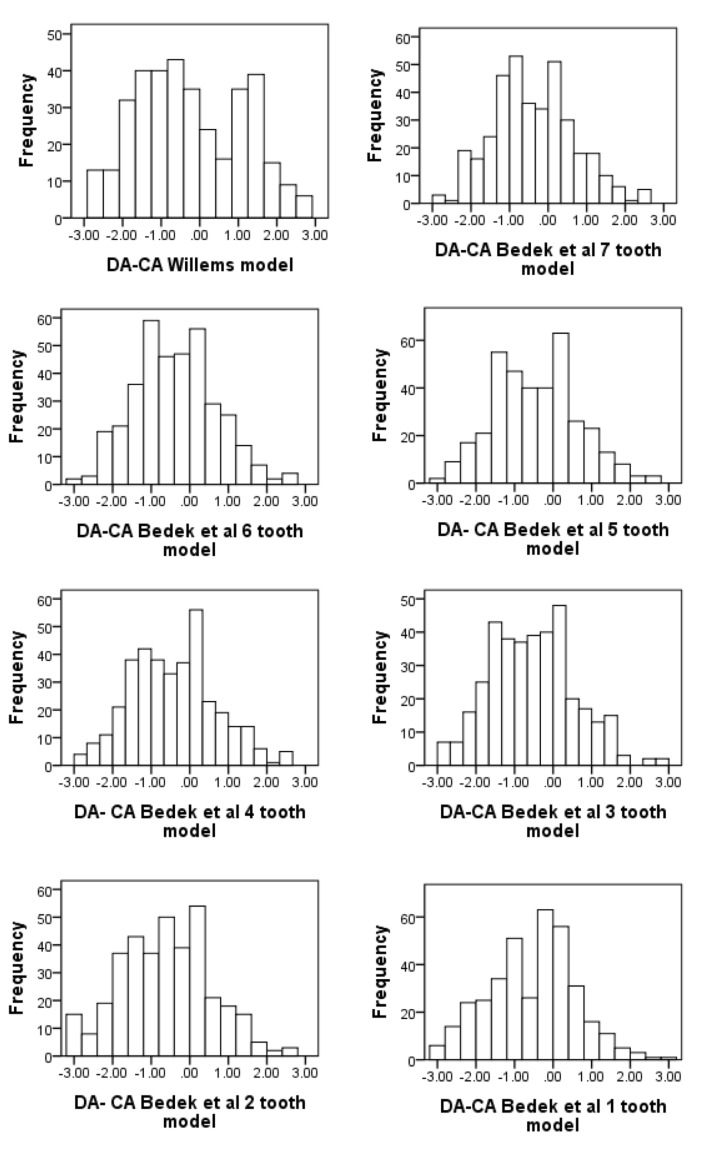
The maximum and minimum deviations and their frequency were presented for all models in Figure 2.
Figure 2.
Individual differences for South Indian sample of girls using Willems model (GS) and Bedek et al., age estimation models
The individual difference between the CA and estimated DA was found to be more frequently within 0 to +0.5 years (overestimation) for Bedek et al’s 1 tooth model, within 0 to -0.5 years (underestimation) for Bedek et al’s 5 to 2 tooth models, within 0.5 to 1 years (overestimation) for Bedek et al’s 7 and 6 tooth models, within -0.5 to -1 year (underestimation) for Willems models.
Mean absolute error
Results of MAE in girls shows that Bedek et al’s 7 tooth model has the smallest value i.e., 0.88 years, while the greatest MAE was for Willems models, 1.25 years. And for remaining models of Bedek et al., MAE ranged between 0.9 to 1.01 years (Table 13).
Percentage of correct estimations
Table 14 presents the accuracy of dental age estimation for different models as a percentage of correct estimations within +0.5 years and +1 year interval. Our results show that Bedek et al’s 7 tooth model has outperformed remaining models, 33.8% (220 out of 650) of age estimates fell within +0.5 years from CA, whereas 60.1% (391 out of 650) of age estimates were found to be within +1 year. For Willems models, 24.1% of age estimates were within +0.5 years and 45.3% were within +1 year, which is markedly less when compared to the remaining models of Bedek et al.
Table 14. Accuracy of age estimation using Willems method and Bedek et al., newly developed models based on 1 to 7 teeth for overall (percentage of correct estimations within interval).
| Methods | Percentage of correct estimations | |||
|---|---|---|---|---|
| Boys | Girls | |||
|
+0.5 years
n (%) |
+1 year
n (%) |
+0.5 years
n (%) |
+1 year
n (%) |
|
| Willems | 90 (32.7) | 144 (52.3) | 67 (17.8) | 151 (40.2) |
| Bedek’s seven teeth | 102 (37.1) | 171 (62.1) | 118 (31.4) | 220 (58.6) |
| Bedek’s six teeth | 91 (33.1) | 164 (59.6) | 121 (32.2) | 217 (57.8) |
| Bedek’s five teeth | 98 (35.6) | 170 (61.8) | 122 (32.5) | 202 (53.8) |
| Bedek’s four teeth | 95 (34.5) | 174 (63.2) | 124 (33.1) | 204 (54.4) |
| Bedek’s three teeth | 94 (34.1) | 165 (60) | 113 (30.1) | 200 (53.3) |
| Bedek’s two teeth | 71 (25.8) | 135 (49.1) | 110 (29.3) | 190 (50.6) |
| Bedek’s one tooth | 84 (30.5) | 149 (54.1) | 132 (35.2) | 205 (54.6) |
DISCUSSION
Traditionally, Demirjian’s system and Willems method require all seven mandibular teeth in the lower left quadrant to make an assessment. If any tooth/teeth is/are missing in the examining quadrant, the authors have suggested substituting an assessment of the matching tooth from the contralateral side, as there is high degree of lateral symmetry. If the same tooth from the contralateral side was also missing, then estimations may be obtained by inserting an average score of the remaining six teeth. (5) Assigning score zero for all non- appearance teeth or calculating the average from the remaining teeth (less than seven) could result in a biased estimate at any particular age. This is a marked limitation for the use of maturity scores in Demirjian’s system, and no allowance is made for missing data. (16)
Each case is specific in a forensic incident. Conducting age assessments in individuals with multiple missing teeth is a challenge for forensic experts. According to the reports from the survey by Endo et al., the most common symmetrical missing tooth could be the mandibular second premolars. (17, 18) Wide variations in incidence and prevalence of hypodontia were reported in different studies conducted in various populations; 11.2% in Korea, (19) 3% to 5.9% in Germany, (20) 6.3% in Brazil, (21) 3.31% in Spain, (22) 11.01% in India. (23) Rakhshan in their systematic review and meta-analysis reported that congenitally missing teeth can range from 0.15% to 16.18% among different populations worldwide. (24) Badrov et al., indicated that age assessment methods may not be implemented in subjects with congenitally missing teeth, as lower permanent teeth are most likely to be affected with agenesis. (25) They also believed that hypodontia can impact results of dental age estimation, therefore researchers must account for the difference in the dental development of children with hypodontia when calculating DA. (25)
Most of the studies published so far mentioned “radiographs that showed hypodontia or subjects with hypodontia were excluded” suggesting the unavailability of methods to assess dental age in such individuals. In 1976, Demirjian proposed two 4 tooth methods for age estimation, when tested in other populations, both 4 tooth methods were found to be relatively inaccurate, less frequently overestimate age and are not suitable. (15, 26) As congenitally missing teeth are prevalent and methods to assess dental age are indispensable, Bedek et al., provided models for dental age estimation for forensic and clinical purposes in such subjects. (14)
Willems method
In the present study, Willems method underestimated CA by 0.03 years in boys and 0.27 years in girls. Consistent results were reported by various studies in the literature i.e., in British Caucasian and Bangladeshi, Korean and Brazilian children. (27- 29) On the other hand, many researchers have reported overestimations with Willems method. (26, 30, 31) Similar to our findings, Hedge et al., also reported smaller underestimations of age when tested in Indian children. (32) The MAE was 1.02 years, 1.25 years and 1.16 years for boys, girls and the total sample using Willems method.
Bedek et al’s new models
When considering the suitability of Bedek et al’s new models, generalised underestimation of age was seen in all age groups (Tables 8-12) for both sexes except the 6 tooth model, where overestimation of CA was seen in boys.
In forensic anthropology, the mean difference between DA and CA is considered accurate if it falls within the range of +0.5 years, and a difference of +1.0 year is considered acceptable. (33, 34) In the present study, in boys the 7 tooth model produced 37.1% cases within the +0.5 year interval, while the 4 tooth model produced 63.2% cases within the +1.0-year interval. These findings were less when compared to the original Bedek et al models where they observed 43.5% cases within +0.5 year interval and 72.2% cases within +1.0-year interval, both for the 7 tooth model respectively. (14) In girls, the 7 tooth model produced 33.1% cases within +0.5 year interval, while the 7 tooth model had 58.6% cases falling within +1.0-year interval. Similar to boys, observations in girls were also less compared to original Bedek et al’s models where they observed 40.7% cases within +0.5 year (5 tooth model) and 71.6% cases within +1.0-year interval (7 tooth model) respectively. (14)
As the phrase goes “Time is of the essence” and in forensic cases time is one important factor that needs to be considered seriously. During criminal or civil investigations, the method of choice for forensic examiners will be the one that gives accurate results in a tested population within a short period of time. A method that quickly gives accurate results and is user-friendly satisfies judicial requirements. (35) It can be inferred from our results that Bedek et al’s models of age estimation are simple, accurate, produce maximum accuracy with a smaller number of teeth.
CONCLUSIONS
In cases of age estimation in children, maximum accuracy is usually obtained and prediction of DA is higher when all seven lower left mandibular teeth are available. Similarly, an equally effective and accurate method is needed when an individual has less than seven teeth. Our study results show that Bedek et al’s new models of age assessment could be valid for the tested population. The following are some advantages:
These new models are simple, reliable, accurate and easily applicable in cases of multiple missing teeth.
They can be used for simple clinical purposes (assessing age in individuals with hypodontia) as well as for complex forensic scenarios (incomplete human remains).
In the original study, it has been determined that models with two teeth are significantly more accurate than Willems models. When tested in the studied population, the 1 tooth model produced a higher percentage of correct estimations (+0.5 and 1 year) than Willems models.
Maximum accuracy was also obtained using the models with less than seven teeth.
Footnotes
The authors declare that they have no conflict of interest.
References
- 1.Altalie S, Thevissen P, Fieuws S, Willems G. Optimal dental age estimation practice in United Arab Emirates’ children. J Forensic Sci. 2014;59(2):383–5. 10.1111/1556-4029.12351 [DOI] [PubMed] [Google Scholar]
- 2.Vermylen Y. Guidelines in forensic odontology: legal aspects. Forensic Sci Int. 2006;159 Suppl 1:S6–8. 10.1016/j.forsciint.2006.02.002 [DOI] [PubMed] [Google Scholar]
- 3.Schmeling A, Dettmeyer R, Rudolf E, Vieth V, Geserick G. Forensic Age Estimation. Dtsch Arztebl Int. 2016;113(4):44–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Franklin D, Flavel A, Noble J, Swift L, Karkhanis S. Forensic age estimation in living individuals: methodological considerations in the context of medico-legal practice. 2015;2015(5):53-66.
- 5.Demirjian A, Goldstein H, Tanner JM. A new system of dental age assessment. Hum Biol. 1973;45(2):211–27. [PubMed] [Google Scholar]
- 6.Demirjian A, Goldstein H. New systems for dental maturity based on seven and four teeth. Ann Hum Biol. 1976;3(5):411–21. 10.1080/03014467600001671 [DOI] [PubMed] [Google Scholar]
- 7.Blenkin MR, Evans W. Age estimation from the teeth using a modified Demirjian system. J Forensic Sci. 2010;55(6):1504–8. 10.1111/j.1556-4029.2010.01491.x [DOI] [PubMed] [Google Scholar]
- 8.Tunc ES, Koyuturk AE. Dental age assessment using Demirjian’s method on northern Turkish children. Forensic Sci Int. 2008;175(1):23–6. 10.1016/j.forsciint.2007.04.228 [DOI] [PubMed] [Google Scholar]
- 9.Koshy S, Tandon S. Dental age assessment: the applicability of Demirjian’s method in south Indian children. Forensic Sci Int. 1998;94(1-2):73–85. 10.1016/S0379-0738(98)00034-6 [DOI] [PubMed] [Google Scholar]
- 10.Willems G, Van Olmen A, Spiessens B, Carels C. Dental age estimation in Belgian children: Demirjian’s technique revisited. J Forensic Sci. 2001;46(4):893–5. 10.1520/JFS15064J [DOI] [PubMed] [Google Scholar]
- 11.Akkaya N, Yilanci HO, Goksuluk D. Applicability of Demirjian’s four methods and Willems method for age estimation in a sample of Turkish children. Leg Med (Tokyo). 2015;17(5):355–9. 10.1016/j.legalmed.2015.04.003 [DOI] [PubMed] [Google Scholar]
- 12.Balla SB, Venkat Baghirath P, Hari Vinay B, Vijay Kumar J, Babu DBG. Accuracy of methods of age estimation in predicting dental age of preadolescents in South Indian children. J Forensic Leg Med. 2016;43:21–5. 10.1016/j.jflm.2016.07.004 [DOI] [PubMed] [Google Scholar]
- 13.Kelmendi J, Vodanovic M, Kocani F, Bimbashi V, Mehmeti B, Galic I. Dental age estimation using four Demirjian’s, Chaillet’s and Willems’ methods in Kosovar children. Leg Med (Tokyo). 2018;33:23–31. 10.1016/j.legalmed.2018.04.006 [DOI] [PubMed] [Google Scholar]
- 14.Bedek I, Dumancic J. New model for dental age estimation: Willems method applied on fewer than seven mandibular teeth. International Journal of Legal Medicine. 2019. (Ahead of Print) [DOI] [PubMed]
- 15.Flood SJ, Franklin D, Turlach BA, McGeachie J. A comparison of Demirjian’s four dental development methods for forensic age estimation in South Australian sub-adults. J Forensic Leg Med. 2013;20(7):875–83. 10.1016/j.jflm.2013.07.002 [DOI] [PubMed] [Google Scholar]
- 16.Smith BH. Standards of human tooth formation and dental age assessment. In: Kelley MA, Larsen CS, editors. Advances in dental anthropology. New York: Wiley-Liss; 1991. P. 143-68. [Google Scholar]
- 17.Endo T, Ozoe R, Kubota M, Akiyama M, Shimooka S. A survey of hypodontia in Japanese orthodontic patients. American journal of orthodontics and dentofacial orthopedics: official publication of the American Association of Orthodontists, its constituent societies, and the American Board of Orthodontics. 2006;129(1):29-35. [DOI] [PubMed]
- 18.Rakhshan V. Congenitally missing teeth (hypodontia): A review of the literature concerning the etiology, prevalence, risk factors, patterns and treatment. Dent Res J (Isfahan). 2015;12(1):1–13. 10.4103/1735-3327.150286 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chung CJ, Han JH, Kim KH. The pattern and prevalence of hypodontia in Koreans. Oral Dis. 2008;14:620–5. 10.1111/j.1601-0825.2007.01434.x [DOI] [PubMed] [Google Scholar]
- 20.Behr M, Proff P, Leitzmann M, Pretzel M, Handel G, Schmalz G, et al. Survey of congenitally missing teeth in orthodontic patients in Eastern Bavaria. Eur J Orthod. 2011;33(1):32–6. 10.1093/ejo/cjq021 [DOI] [PubMed] [Google Scholar]
- 21.Gomes RR, da Fonseca JA, Paula LM, Faber J, Acevedo AC. Prevalence of hypodontia in orthodontic patients in Brasilia, Brazil. Eur J Orthod. 2010;32(3):302–6. 10.1093/ejo/cjp107 [DOI] [PubMed] [Google Scholar]
- 22.Sola RA, Sola PA, Perez JC, Sanchez IN, Renovales ID. Prevalence of Hypodontia in a Sample of Spanish Dental Patients. Acta Stomatol Croat. 2018;52(1):18–23. 10.15644/asc52/1/3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Soni HK, Joshi M, Desai H, Vasavada M. An orthopantomographic study of prevalence of hypodontia and hyperdontia in permanent dentition in Vadodara, Gujarat. Indian J Dent Res. 2018;29(4):529–33. 10.4103/ijdr.IJDR_215_16 [DOI] [PubMed] [Google Scholar]
- 24.Rakhshan V, Rakhshan A. Systematic review and meta-analysis of congenitally missing permanent dentition: Sex dimorphism, occurrence patterns, associated factors and biasing factors. Int Orthod. 2016;14(3):273–94. 10.1016/j.ortho.2016.07.016 [DOI] [PubMed] [Google Scholar]
- 25.Badrov J, Lauc T, Nakas E, Galic I, et al. Dental Age and Tooth Development in Orthodontic Patients with Agenesis of Permanent Teeth. BioMed Res Int. 2017;2017:8683970. 10.1155/2017/8683970 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ambarkova V, Galic I, Vodanovic M, Biocina-Lukenda D, Brkic H. Dental age estimation using Demirjian and Willems methods: cross sectional study on children from the Former Yugoslav Republic of Macedonia. Forensic Sci Int. 2014;234:187.e1–7. 10.1016/j.forsciint.2013.10.024 [DOI] [PubMed] [Google Scholar]
- 27.Maber M, Liversidge HM, Hector MP. Accuracy of age estimation of radiographic methods using developing teeth. Forensic Sci Int. 2006;159 Suppl 1:S68–73. 10.1016/j.forsciint.2006.02.019 [DOI] [PubMed] [Google Scholar]
- 28.Lee SS, Kim D, Lee S, Lee UY, Seo JS, Ahn YW, et al. Validity of Demirjian’s and modified Demirjian’s methods in age estimation for Korean juveniles and adolescents. Forensic Sci Int. 2011;211(1-3):41–6. 10.1016/j.forsciint.2011.04.011 [DOI] [PubMed] [Google Scholar]
- 29.Franco A, Thevissen P, Fieuws S, Souza PH, Willems G. Applicability of Willems model for dental age estimations in Brazilian children. Forensic science international. 2013;231(1-3):401 e1-4. [DOI] [PubMed]
- 30.El-Bakary AA, Hammad SM, Mohammed F. Dental age estimation in Egyptian children, comparison between two methods. J Forensic Leg Med. 2010;17(7):363–7. 10.1016/j.jflm.2010.05.008 [DOI] [PubMed] [Google Scholar]
- 31.Medina AC, Blanco L. Accuracy of dental age estimation in Venezuelan children: comparison of Demirjian and Willems methods. Acta odontologica latinoamericana. AOL. 2014;27(1):34–41. [PubMed] [Google Scholar]
- 32.Hegde S, Patodia A, Dixit U. A comparison of the validity of the Demirjian, Willems, Nolla and Haavikko methods in determination of chronological age of 5-15-year-old Indian children. J Forensic Leg Med. 2017;50:49–57. 10.1016/j.jflm.2017.07.007 [DOI] [PubMed] [Google Scholar]
- 33.Flood SJ, Mitchell WJ, Oxnard CE, Turlach BA, McGeachie J. A comparison of Demirjian’s four dental development methods for forensic age assessment. J Forensic Sci. 2011;56(6):1610–5. 10.1111/j.1556-4029.2011.01883.x [DOI] [PubMed] [Google Scholar]
- 34.Chaillet N, Nystrom M, Kataja M, Demirjian A. Dental maturity curves in Finnish children: Demirjian’s method revisited and polynomial functions for age estimation. J Forensic Sci. 2004;49(6):1324–31. 10.1520/JFS2004211 [DOI] [PubMed] [Google Scholar]
- 35.Namene J, Doggalli N. Challenges in forensic odontology age estimation methods. International Journal of Forensic Odontology. 2018;3(2):46–9. 10.4103/ijfo.ijfo_16_18 [DOI] [Google Scholar]