Abstract
When quasiparticles move in condensed matters, the texture of their internal quantum structure as a function of position and momentum can give rise to Berry phases that have profound effects on the material’s properties. Seminal examples include the anomalous Hall and spin Hall effects from the momentum-space Berry phases in homogeneous crystals. Here, we explore a conjugate form of the electron Berry phase arising from the moiré pattern: the texture of atomic configurations in real space. In homobilayer transition metal dichalcogenides, we show that the real-space Berry phase from moiré patterns manifests as a periodic magnetic field with magnitudes of up to hundreds of Tesla. This quantity distinguishes moiré patterns from different origins, which can have an identical potential landscape, but opposite quantized magnetic flux per supercell. For low-energy carriers, the homobilayer moirés realize topological flux lattices for the quantum-spin Hall effect. An interlayer bias can continuously tune the spatial profile of the moiré magnetic field, whereas the flux per supercell is a topological quantity that can only have a quantized jump observable at a moderate bias. We also reveal the important role of the non-Abelian Berry phase in shaping the energy landscape in small moiré patterns. Our work points to new possibilities to access ultra-high magnetic fields that can be tailored to the nanoscale by electrical and mechanical controls.
Keywords: two-dimensional materials, transition metal dichalcogenides, moiré pattern, Berry phase, quantum Hall effect
INTRODUCTION
In van der Waals layered structures, the creation of long-period moiré patterns (via a small lattice mismatch between the layers) has become a powerful method for engineering superlattice electronic, optical and topological properties. Experiments have discovered emergent electron phenomena from graphene moiré superlattices, including the fractal quantum Hall effect [1–3], gate-tunable Mott insulators [4,5] and superconductivity [6–11]. In heterostructures of 2D semiconductors, the moiré pattern leads to nanoscale patterning in the energy and emission features of optical excitations and thereby significantly changes the heterostructure optical responses [12–17]. Furthermore, theories have predicted the emergence of novel topological insulating states in transition metal dichalcogenides (TMD) heterobilayer moiré [18] and twisted homobilayers [19].
The nature of the moiré pattern as a spatial texture of atomic configurations suggests that the Berry-phase effect can be an indispensable part of moiré superlattice physics. In a smoothly varying crystalline environment like a long-period moiré, the Berry phase has several important manifestations in the electron’s equations of motion [20]:  ,
, 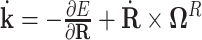 , where
, where 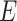 ,
,  and
and 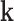 are the energy, position and momentum of an electron wavepacket.
are the energy, position and momentum of an electron wavepacket.  and
and  are Berry curvatures from the momentum-space and real-space textures, respectively, in the electron’s spin and pseudospin wavefunction
are Berry curvatures from the momentum-space and real-space textures, respectively, in the electron’s spin and pseudospin wavefunction 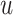 . Homogeneous crystals can only have the momentum-space curvature
. Homogeneous crystals can only have the momentum-space curvature  and the resultant anomalous velocity
and the resultant anomalous velocity 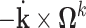 is responsible for the various Hall effects [20]. Spatial inhomogeneity can give rise to the real-space curvature
is responsible for the various Hall effects [20]. Spatial inhomogeneity can give rise to the real-space curvature  that plays the same role as a magnetic field. Such an emergent magnetic field also generates a Hall current, which has attracted remarkable interest in explorations of magnetization skyrmions and domains [21–23].
that plays the same role as a magnetic field. Such an emergent magnetic field also generates a Hall current, which has attracted remarkable interest in explorations of magnetization skyrmions and domains [21–23].
Here, we show that the real-space Berry phase from moiré patterns realizes a nanoscale patterned magnetic field for the massive Dirac fermions in TMD homobilayers. The field is normal to the plane, with the full symmetry of the moiré pattern. The magnetic flux per moiré supercell has a quantized value, while its sign distinguishes moirés introduced by a uniaxial strain from those by a twisting or biaxial strain, although they have the same potential landscape. For low-energy carriers, the complex hopping in the moiré potential as determined by the Berry phase realizes the topological flux lattices hosting the quantum-spin Hall effect. Strain control of the moiré period (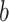 ) can dramatically tune the moiré magnetic field with the
) can dramatically tune the moiré magnetic field with the  scaling, while preserving the flux per supercell. The field magnitude can reach hundreds of Tesla at a moiré size of
scaling, while preserving the flux per supercell. The field magnitude can reach hundreds of Tesla at a moiré size of  nm. The profile of the moiré magnetic field can also be electrically tuned through an interlayer bias and a topological transition occurs at a moderate bias where the magnetic flux per supercell has a quantized jump. We also reveal that the geometric scalar potential due to the non-Abelian nature of the Berry phase can qualitatively change the potential landscape in a small moiré.
nm. The profile of the moiré magnetic field can also be electrically tuned through an interlayer bias and a topological transition occurs at a moderate bias where the magnetic flux per supercell has a quantized jump. We also reveal that the geometric scalar potential due to the non-Abelian nature of the Berry phase can qualitatively change the potential landscape in a small moiré.
RESULTS
TMD monolayers have their spin-valley locked conduction and valence band edges at the 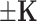 corners of the Brillouin zone, which are described by the massive Dirac model [24]. We focus here on the physics at these band edges in a homobilayer moiré, formed by a small twisting or strain applied to one layer in R-stacking [25] (cf. Fig. 1 and Table 1). The interlayer hopping of the valley electron is sensitive to the atomic registry between the layers [18,26]. The smooth variation of the interlayer registry in a long-period moiré thus leads to the dependence of the hopping on the position
corners of the Brillouin zone, which are described by the massive Dirac model [24]. We focus here on the physics at these band edges in a homobilayer moiré, formed by a small twisting or strain applied to one layer in R-stacking [25] (cf. Fig. 1 and Table 1). The interlayer hopping of the valley electron is sensitive to the atomic registry between the layers [18,26]. The smooth variation of the interlayer registry in a long-period moiré thus leads to the dependence of the hopping on the position  [27,28]. In the basis of
[27,28]. In the basis of  , denoting conduction (c) and valence (v) band-edge states from the top (t) and bottom (b) layers, respectively, the Hamiltonian for the two coupled massive Dirac cones reads:
, denoting conduction (c) and valence (v) band-edge states from the top (t) and bottom (b) layers, respectively, the Hamiltonian for the two coupled massive Dirac cones reads:
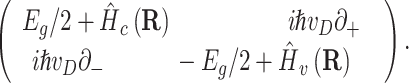 |
(1) |
Figure 1.

Moiré pattern as a real-space texture for the Berry phase. (a) Schematic of a homobilayer moiré and periodic magnetic flux (green arrows) from the real-space Berry phase. The dashed rhombus denotes a supercell. (b) Upper panel: atomic registries at three high-symmetry locales A, B and C. Lower panel: corresponding layer distributions of conduction (c) and valence (v) band-edge carriers (yellow isosurfaces), with the arrows indicating the layer-pseudospin orientations. (c) A schematic of the coupled massive Dirac cones from the two layers. The interlayer-coupling parameters (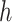 ,
, 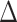 ) depend on the interlayer registry characterized by the displacement r between a near-neighbor pair of atoms from two layers (inset); in a moiré, they are functions of location R.
) depend on the interlayer registry characterized by the displacement r between a near-neighbor pair of atoms from two layers (inset); in a moiré, they are functions of location R.
Table 1.
Comparison of flux superlattices in three types of homobilayer moiré. One monolayer has the primitive lattice vectors  ,
, 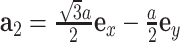 and the other layer is rotated by a twisting angle
and the other layer is rotated by a twisting angle  or subject to a biaxial or uniaxial tensile strain, respectively. The uniaxial strain is applied along the armchair or zigzag direction, with the area of the strained unit cell conserved. The magnetic flux per moiré supercell is given for the spin-up carrier (−K-valley). The local registry is parameterized by the in-plane displacement
or subject to a biaxial or uniaxial tensile strain, respectively. The uniaxial strain is applied along the armchair or zigzag direction, with the area of the strained unit cell conserved. The magnetic flux per moiré supercell is given for the spin-up carrier (−K-valley). The local registry is parameterized by the in-plane displacement  between a near-neighbor pair of atoms from the opposite layers (cf. Fig. 1 inset).
between a near-neighbor pair of atoms from the opposite layers (cf. Fig. 1 inset). 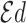 is the interlayer electric bias and its critical value
is the interlayer electric bias and its critical value  .
.
Twisting (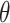 ) ) |
Biaxial strain (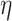 ) ) |
Uniaxial strain (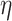 ) ) |
||
|---|---|---|---|---|
Moiré period ( ) ) |
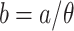
|

|
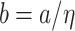
|
|
| Supercell primitive vectors |
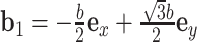
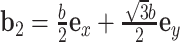
|


|

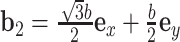
|
|
Local registry ( ) as a function of position ( ) as a function of position (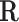 ) ) |


|
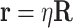
|


|
|
| Magnetic flux per |

|
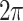
|
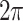
|

|
| supercell |

|
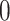
|
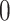
|

|
The 2 × 2 block  describes the spatially varying interlayer-coupling effects in valence bands.
describes the spatially varying interlayer-coupling effects in valence bands.  is the layer pseudospin.
is the layer pseudospin.  is the hopping matrix element between the valence band edges from the two layers. The interlayer coupling also leads to energy shifts of the band edges accounted for by
is the hopping matrix element between the valence band edges from the two layers. The interlayer coupling also leads to energy shifts of the band edges accounted for by  and
and 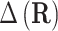 [19,26].
[19,26]. 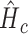 describes similar interlayer-coupling effects in the conduction bands. The
describes similar interlayer-coupling effects in the conduction bands. The 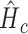 and
and 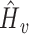 blocks are coupled through the
blocks are coupled through the  term of the monolayer Dirac Hamiltonian. Equation (1) is for the
term of the monolayer Dirac Hamiltonian. Equation (1) is for the 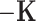 valley, which has spin-up states only at the band edge, and the
valley, which has spin-up states only at the band edge, and the 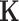 valley is its time reversal.
valley is its time reversal.
Non-Abelian Berry connection in real space
We derive an effective Hamiltonian for holes in the bilayer moiré, whereas that for the electron is similar. It is convenient to go to the basis spanned by the eigenstates of interlayer coupling  :
: 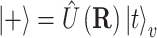 and
and 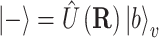 , where
, where  . Through a unitary transformation by
. Through a unitary transformation by  , the bilayer Hamiltonian in Equation (1) becomes:
, the bilayer Hamiltonian in Equation (1) becomes:
| (2) |
In the off-diagonal block, the matrix 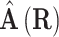 is the non-Abelian real-space Berry connection on the basis of the layer-pseudospin eigenstates:
is the non-Abelian real-space Berry connection on the basis of the layer-pseudospin eigenstates:
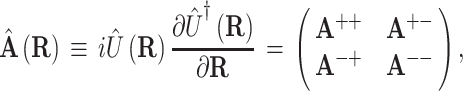 |
(3) |
where  and
and  .
.  ,
,  and
and  are the unit vectors along the x and y directions.
are the unit vectors along the x and y directions.
At the three high-symmetry locales in the moiré (Fig. 1a and b), rotational symmetry dictates that 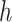 vanishes at B and C, while
vanishes at B and C, while  vanishes at A and takes opposite values at B and C (Fig. 2b). These determine a real-space texture in the two branches of layer-pseudospin eigenstates. For example, in the
vanishes at A and takes opposite values at B and C (Fig. 2b). These determine a real-space texture in the two branches of layer-pseudospin eigenstates. For example, in the 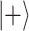 state,
state,  is in-plane at A and points out-of-plane in opposite directions at B and C, as illustrated in Fig. 1b. Such a spatial texture of the layer pseudospin gives rise to a non-trivial Berry connection.
is in-plane at A and points out-of-plane in opposite directions at B and C, as illustrated in Fig. 1b. Such a spatial texture of the layer pseudospin gives rise to a non-trivial Berry connection.
Figure 2.
Layer-pseudospin texture and moiré magnetic field. (a) The symbols are from the ab initio calculations of the split valence band edges 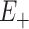 and
and  in MoSe2 homobilayers of various interlayer registries. The curves are fitted using Equation (5) with the parameters
in MoSe2 homobilayers of various interlayer registries. The curves are fitted using Equation (5) with the parameters  ,
, 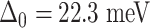 ,
,  and
and 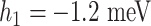 . (b) The corresponding interlayer-coupling parameters as functions of position
. (b) The corresponding interlayer-coupling parameters as functions of position  in the moiré.
in the moiré. 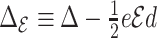 at the critical bias value
at the critical bias value  is shown as the dotted curve. (c) Color map showing the scalar potential landscape
is shown as the dotted curve. (c) Color map showing the scalar potential landscape 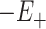 in a moiré supercell, where the high-symmetry locales A, B and C are energy minima. (d, e) Upper panel: layer-pseudospin texture in the lower-energy pseudospin branch
in a moiré supercell, where the high-symmetry locales A, B and C are energy minima. (d, e) Upper panel: layer-pseudospin texture in the lower-energy pseudospin branch  . The arrows show
. The arrows show  at different positions and the color codes its z-component. Lower panel: magnetic field
at different positions and the color codes its z-component. Lower panel: magnetic field 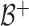 in a moiré of period
in a moiré of period 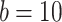 nm. The peak value reaches 200 T. (d) is for a moiré induced by a twisting or biaxial strain and (e) is for a moiré induced by a uniaxial strain (cf. Table 1).
nm. The peak value reaches 200 T. (d) is for a moiré induced by a twisting or biaxial strain and (e) is for a moiré induced by a uniaxial strain (cf. Table 1).
With the large gap 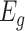 , the coupling to the conduction states can be perturbatively eliminated and the hole Hamiltonian keeping its leading effects becomes:
, the coupling to the conduction states can be perturbatively eliminated and the hole Hamiltonian keeping its leading effects becomes:
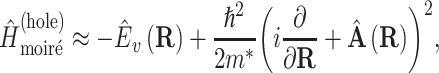 |
(4) |
where the dropped terms are  .
.  is the Dirac mass.
is the Dirac mass.
Periodic magnetic fields in different types of moiré
We focus first on the diagonal Berry connection  . The main effect of off-diagonal connection
. The main effect of off-diagonal connection  is a correction to the scalar potential landscape that is negligible in a sufficiently large moiré, which we will revisit later. If
is a correction to the scalar potential landscape that is negligible in a sufficiently large moiré, which we will revisit later. If  is simply dropped in Equation (4), the two branches of layer-pseudospin eigenstates are decoupled, each described by an effective Hamiltonian:
is simply dropped in Equation (4), the two branches of layer-pseudospin eigenstates are decoupled, each described by an effective Hamiltonian:  . The moiré effects manifest as the scalar superlattice potential
. The moiré effects manifest as the scalar superlattice potential 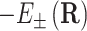 and, more intriguingly, the vector potential
and, more intriguingly, the vector potential  that generates a real-space magnetic field:
that generates a real-space magnetic field: 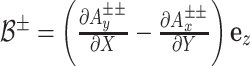 .
.
We establish below the quantitative forms of the superlattice potential  and the periodic magnetic field
and the periodic magnetic field 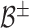 . In a long-period moiré, the interlayer-coupling parameters at location
. In a long-period moiré, the interlayer-coupling parameters at location  are determined by the local atomic registry, which can be parameterized by the in-plane displacement
are determined by the local atomic registry, which can be parameterized by the in-plane displacement  between a near-neighbor pair of atoms from opposite layers (Fig. 1, inset). Under the two-center-approximation and keeping only the leading Fourier components [26], we find the dependences of
between a near-neighbor pair of atoms from opposite layers (Fig. 1, inset). Under the two-center-approximation and keeping only the leading Fourier components [26], we find the dependences of 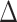 ,
, 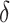 and
and 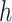 on the registry
on the registry 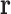 :
:
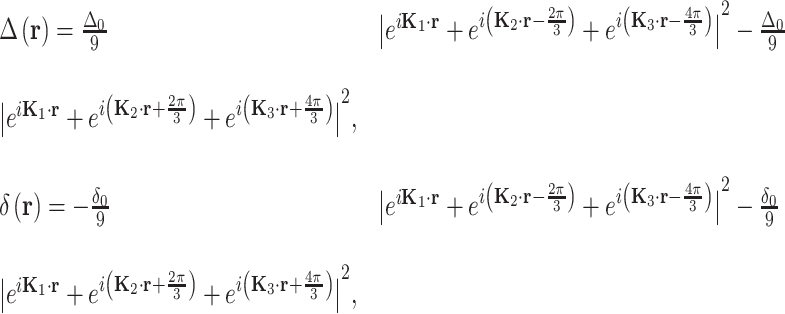 |
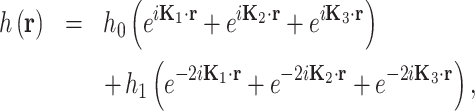 |
(5) |
where 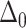 ,
,  ,
,  and
and  are real constants.
are real constants. 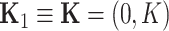 ,
, 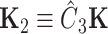 ,
,  are, respectively, the three corners of the monolayer Brillouin zone related by
are, respectively, the three corners of the monolayer Brillouin zone related by 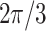 -rotations. On the other hand, the split valence band edges
-rotations. On the other hand, the split valence band edges 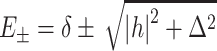 can be obtained from ab initio band structures of lattice-matched bilayers of various registry
can be obtained from ab initio band structures of lattice-matched bilayers of various registry  . In Fig. 2a, the ab initio calculated
. In Fig. 2a, the ab initio calculated  as functions of
as functions of 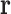 are shown as the symbols, which are remarkably well fitted by the solid curves from Equation (5), with
are shown as the symbols, which are remarkably well fitted by the solid curves from Equation (5), with  ,
,  ,
, 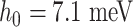 and
and  .
.
The registry 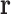 is a function of position
is a function of position 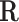 in the moiré. The mapping
in the moiré. The mapping 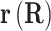 , together with Equation (5), gives the position dependences of the interlayer-coupling parameters in
, together with Equation (5), gives the position dependences of the interlayer-coupling parameters in 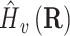 , i.e.
, i.e. 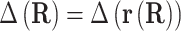 , etc. The resultant spatial texture of layer-pseudospin eigenstates, the scalar potential
, etc. The resultant spatial texture of layer-pseudospin eigenstates, the scalar potential  and the moiré magnetic field
and the moiré magnetic field 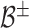 can then be determined. Table 1 summarizes the mapping function
can then be determined. Table 1 summarizes the mapping function 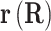 for three different types of moiré pattern formed, respectively, by applying a twisting, a biaxial strain and an area-conserving uniaxial strain to one layer. All three moiré patterns realize hexagonal superlattices, with the identical scalar potential landscape
for three different types of moiré pattern formed, respectively, by applying a twisting, a biaxial strain and an area-conserving uniaxial strain to one layer. All three moiré patterns realize hexagonal superlattices, with the identical scalar potential landscape 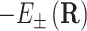 (except for a 90o rotation of the superlattice in the twisting case, cf. Table 1).
(except for a 90o rotation of the superlattice in the twisting case, cf. Table 1).
Figure 2d and e shows the spatial profile of layer-pseudospin vector 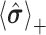 and a moiré magnetic field
and a moiré magnetic field  in a moiré supercell in the lower-energy hole branch. Remarkably, while the twisting moiré and biaxial moiré have identical pseudospin textures and magnetic-field distribution, the uniaxial moiré is of a distinct texture that leads to an opposite magnetic-field distribution. The magnetic flux per supercell
in a moiré supercell in the lower-energy hole branch. Remarkably, while the twisting moiré and biaxial moiré have identical pseudospin textures and magnetic-field distribution, the uniaxial moiré is of a distinct texture that leads to an opposite magnetic-field distribution. The magnetic flux per supercell 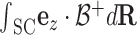 is a quantized value:
is a quantized value:  for the twisting moiré and biaxial moiré and
for the twisting moiré and biaxial moiré and  for the uniaxial moiré, corresponding to the fact that the pseudospin texture is of a skyrmion [19] and anti-skyrmion configuration, respectively. Thus, the three different origins give rise to two topologically distinct types of moiré patterns. The moiré magnetic field
for the uniaxial moiré, corresponding to the fact that the pseudospin texture is of a skyrmion [19] and anti-skyrmion configuration, respectively. Thus, the three different origins give rise to two topologically distinct types of moiré patterns. The moiré magnetic field 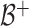 is peaked between the B and C points (Fig. 2d and e). In a moiré of period
is peaked between the B and C points (Fig. 2d and e). In a moiré of period 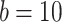 nm, this magnetic field reaches a peak value of 200 Tesla, comparable in size to the giant pseudo magnetic field from an inhomogeneous strain in a graphene nano-bubble [29–31].
nm, this magnetic field reaches a peak value of 200 Tesla, comparable in size to the giant pseudo magnetic field from an inhomogeneous strain in a graphene nano-bubble [29–31].
Topological flux lattice and quantum-spin Hall effect
The periodic scalar potential and magnetic field generated by the moiré together define a flux superlattice. Some remarkable features include: (i) the flux per supercell is quantized and independent of the moiré period; (ii) the two layer-pseudospin branches 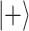 and
and  have opposite magnetic fields
have opposite magnetic fields 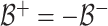 and distinct trapping locations in their potentials
and distinct trapping locations in their potentials  and
and 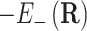 (Fig. 2a); (iii) spin-up and -down carriers experience opposite magnetic fields as required by the presence of time-reversal symmetry.
(Fig. 2a); (iii) spin-up and -down carriers experience opposite magnetic fields as required by the presence of time-reversal symmetry.
Holes can be trapped in the low-energy pseudospin branch  at the three high-symmetry locales A, B and C in a moiré supercell (cf. Fig. 2c). Low-energy holes hopping between these trapping sites can then be described by a three-orbital tight-binding model (Fig. 3a):
at the three high-symmetry locales A, B and C in a moiré supercell (cf. Fig. 2c). Low-energy holes hopping between these trapping sites can then be described by a three-orbital tight-binding model (Fig. 3a):
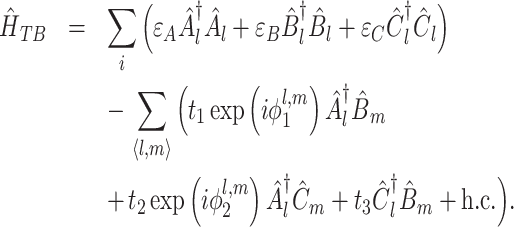 |
(6) |
Figure 3.

Flux superlattice for quantum-spin Hall effect. (a) The color map shows the moiré magnetic field  . The lines illustrate hopping between trapping sites A, B and C. The phases for the hopping direction indicated by the dashed arrows are shown. (b) The effective two-orbital model in a long-period moiré where the high-energy trapping sites A are perturbatively eliminated. The positive phase directions of the next-nearest-neighbor hopping are indicated by the arrows. (c, d) Band dispersions and momentum-space Berry curvature
. The lines illustrate hopping between trapping sites A, B and C. The phases for the hopping direction indicated by the dashed arrows are shown. (b) The effective two-orbital model in a long-period moiré where the high-energy trapping sites A are perturbatively eliminated. The positive phase directions of the next-nearest-neighbor hopping are indicated by the arrows. (c, d) Band dispersions and momentum-space Berry curvature  of the mini-bands calculated using the three-orbital model in (a). For (c), the parameters are
of the mini-bands calculated using the three-orbital model in (a). For (c), the parameters are  ,
, 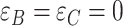 ,
,  and
and  and the three mini-bands have the Chern numbers of
and the three mini-bands have the Chern numbers of 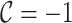 ,
,  and
and 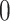 , respectively. For (d),
, respectively. For (d), 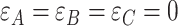 ,
, 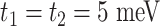 and
and  and the band Chern numbers become
and the band Chern numbers become  ,
,  and
and 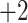 , respectively.
, respectively.
Here,  ,
,  and
and 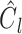 are annihilation operators for the hole trapped at A, B and C sites in lth supercell, and
are annihilation operators for the hole trapped at A, B and C sites in lth supercell, and 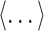 runs over nearest-neighbor pairs of sites. The sum of hopping phases
runs over nearest-neighbor pairs of sites. The sum of hopping phases 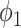 and
and 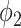 around any closed loop equals the magnetic flux enclosed. The equilateral triangle A-B-C-A loop in Fig. 3a encloses a flux of
around any closed loop equals the magnetic flux enclosed. The equilateral triangle A-B-C-A loop in Fig. 3a encloses a flux of  (
(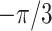 ) for the spin-up (-down) hole, for the example of a twisting moiré or a biaxial moiré.
) for the spin-up (-down) hole, for the example of a twisting moiré or a biaxial moiré.
The out-of-plane mirror symmetry dictates that 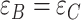 and
and  . Because of the higher barrier between B and C,
. Because of the higher barrier between B and C, 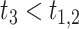 . The onsite energy
. The onsite energy  is larger than
is larger than  in the scalar potential shown in Fig. 2a. In a sufficiently large moiré, where the hopping becomes exponentially small,
in the scalar potential shown in Fig. 2a. In a sufficiently large moiré, where the hopping becomes exponentially small, 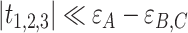 , we can adiabatically eliminate the A sites. The resultant two-orbital tight-binding model consisting of the B and C sites becomes (Fig. 3b):
, we can adiabatically eliminate the A sites. The resultant two-orbital tight-binding model consisting of the B and C sites becomes (Fig. 3b):
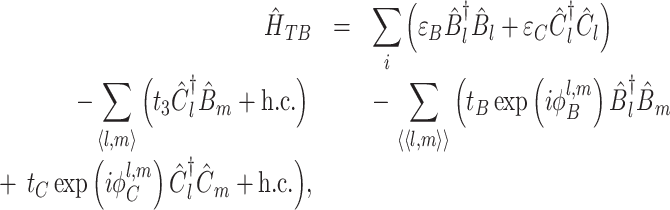 |
where 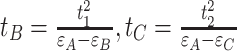 , and
, and  runs over next-nearest-neighbor pairs.
runs over next-nearest-neighbor pairs.  and the positive phase hopping directions are indicated by the arrows shown in Fig. 3b. This realizes the Kane-Mele model [32] and the Haldane model in each spin subspace [33], which explains the quantized spin Hall conductance found in mini-band calculations in the TMD homobilayer moiré [19,25].
and the positive phase hopping directions are indicated by the arrows shown in Fig. 3b. This realizes the Kane-Mele model [32] and the Haldane model in each spin subspace [33], which explains the quantized spin Hall conductance found in mini-band calculations in the TMD homobilayer moiré [19,25].
Figure 3c shows the dispersions and the momentum-space Berry curvatures  of the three mini-bands, calculated with the parameters
of the three mini-bands, calculated with the parameters 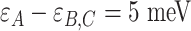 ,
, 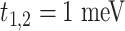 and
and  . The topological numbers of the three bands are
. The topological numbers of the three bands are 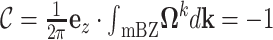 ,
,  and
and 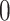 . This three-band tight-binding model reproduces well the band dispersions, the
. This three-band tight-binding model reproduces well the band dispersions, the 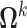 distributions and topological numbers from the direct mini-band calculations in the twisted MoTe2 bilayer [19].
distributions and topological numbers from the direct mini-band calculations in the twisted MoTe2 bilayer [19].
Geometric scalar potential
The off-diagonal Berry connection can become increasingly important with the decrease in the moiré period  . In the Hamiltonian in Equation (4),
. In the Hamiltonian in Equation (4),  plays two roles. First, it contributes
plays two roles. First, it contributes  to the diagonal element of Hamiltonian. As a result, the scalar superlattice potential is corrected from
to the diagonal element of Hamiltonian. As a result, the scalar superlattice potential is corrected from  to
to 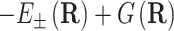 . Second, it introduces a residue coupling between the layer-pseudospin branches
. Second, it introduces a residue coupling between the layer-pseudospin branches  and
and 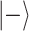 , with the coupling form
, with the coupling form 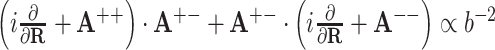 . However, in the lower branch
. However, in the lower branch 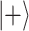 , low-energy states are detuned from the branch
, low-energy states are detuned from the branch  by a gap independently of
by a gap independently of  (cf. Fig. 2a), which quenches the off-diagonal effect except for a very small moiré (
(cf. Fig. 2a), which quenches the off-diagonal effect except for a very small moiré (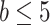 nm). Therefore, the low-energy holes are well described by the effective Hamiltonian:
nm). Therefore, the low-energy holes are well described by the effective Hamiltonian:
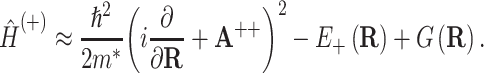 |
(7) |
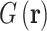 here is an additional energy due to the precession of the layer pseudospin in the adiabatic transport [34], which repels electrons (holes) from the position where the pseudospin changes quickly. This effective potential of the geometric origin is known as the geometric scalar potential. In a homobilayer moiré,
here is an additional energy due to the precession of the layer pseudospin in the adiabatic transport [34], which repels electrons (holes) from the position where the pseudospin changes quickly. This effective potential of the geometric origin is known as the geometric scalar potential. In a homobilayer moiré,  , increasing rapidly with the decrease in the moiré period
, increasing rapidly with the decrease in the moiré period  and peaking between the B and C points of the supercell (Fig. 4a).
and peaking between the B and C points of the supercell (Fig. 4a).
Figure 4.

Geometric scalar potential from the non-Abelian Berry connection. (a) The geometric scalar potential  for a moiré of period
for a moiré of period 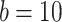 nm. (b) The Zeeman energy
nm. (b) The Zeeman energy  , where
, where  is the orbital magnetic moment of massive Dirac fermion from the momentum-space Berry phase. (c) The overall scalar potential
is the orbital magnetic moment of massive Dirac fermion from the momentum-space Berry phase. (c) The overall scalar potential 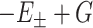 in the two pseudospin branches at different moiré periods. (d) The schematic-level scheme for the non-Abelian Berry-phase effect in a homobilayer moiré.
in the two pseudospin branches at different moiré periods. (d) The schematic-level scheme for the non-Abelian Berry-phase effect in a homobilayer moiré.  is coupled to the conduction state of the same pseudospin
is coupled to the conduction state of the same pseudospin 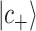 and the second-order perturbative correction
and the second-order perturbative correction  accounts for the moiré magnetic field
accounts for the moiré magnetic field  effects, including the Zeeman energy shown in (b). The coupling of
effects, including the Zeeman energy shown in (b). The coupling of 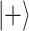 to the conduction state of the opposite pseudospin
to the conduction state of the opposite pseudospin 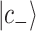 leads to another correction
leads to another correction 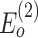 and its sum with the Zeeman energy term is the overall geometric scalar potential
and its sum with the Zeeman energy term is the overall geometric scalar potential 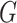 shown in (a).
shown in (a).
Figure 4c plots the overall scalar potential at different moiré periods b. The correction by the geometric contribution becomes significant at 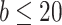 nm. The local out-of-plane mirror symmetry at A dictates that
nm. The local out-of-plane mirror symmetry at A dictates that  vanishes at this location. The geometric scalar potential therefore pushes
vanishes at this location. The geometric scalar potential therefore pushes  towards
towards 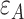 (see Fig. 4c), so the A orbital can no longer be perturbatively eliminated in a small moiré. From the three-orbital tight-binding calculation using Equation (6), we find that a topological phase transition occurs when
(see Fig. 4c), so the A orbital can no longer be perturbatively eliminated in a small moiré. From the three-orbital tight-binding calculation using Equation (6), we find that a topological phase transition occurs when  is increased to
is increased to 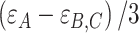 . In Fig. 3d, we show the results with parameters
. In Fig. 3d, we show the results with parameters 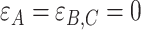 ,
, 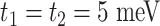 and
and  , where the topological numbers of the three bands become
, where the topological numbers of the three bands become  ,
, 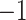 and
and 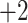 , respectively. The tight-binding calculations shown in Fig. 3c and d reproduce the distinct moiré band dispersions and topologies in MoTe2 bilayers at twist angles 1.2° and 2°, respectively. The change in the energy landscape caused by the geometric scalar potential accounts for the topological phase transition as a function of the twist angle.
, respectively. The tight-binding calculations shown in Fig. 3c and d reproduce the distinct moiré band dispersions and topologies in MoTe2 bilayers at twist angles 1.2° and 2°, respectively. The change in the energy landscape caused by the geometric scalar potential accounts for the topological phase transition as a function of the twist angle.
Quantized switch of magnetic flux by interlayer electric bias
An interlayer bias can add a tunable term  to
to  , where
, where  is the interlayer distance and
is the interlayer distance and 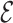 is the perpendicular electric field. The effect is to replace
is the perpendicular electric field. The effect is to replace  by
by 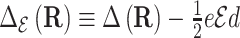 , which changes the profiles of both the potential landscape
, which changes the profiles of both the potential landscape  and the magnetic field
and the magnetic field 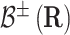 . The electric bias can thus be exploited to continuously tune the moiré magnetic field and the flux superlattice.
. The electric bias can thus be exploited to continuously tune the moiré magnetic field and the flux superlattice.
The lower panel of Fig. 5a shows the magnetic-field distribution in the pseudospin branch  under an interlayer bias
under an interlayer bias 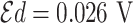 in the twisting moiré. The magnetic-field distribution is significantly changed compared to the zero-bias distribution shown in Fig. 5a upper panel, having been pushed from the B–C center towards the C point, where the difference between
in the twisting moiré. The magnetic-field distribution is significantly changed compared to the zero-bias distribution shown in Fig. 5a upper panel, having been pushed from the B–C center towards the C point, where the difference between 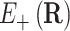 and
and  is minimal. The magnetic flux per supercell remains
is minimal. The magnetic flux per supercell remains 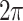 . With a further increase in bias to the critical value
. With a further increase in bias to the critical value  ,
, 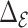 crosses
crosses 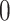 at C point, where
at C point, where 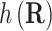 also vanishes (cf. Fig. 2b). Therefore, the gap between
also vanishes (cf. Fig. 2b). Therefore, the gap between 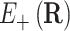 and
and  closes, whereupon a topological transition of the layer-pseudospin texture occurs (Fig. 5b). Figure 5c shows the magnetic-field distribution after this transition (
closes, whereupon a topological transition of the layer-pseudospin texture occurs (Fig. 5b). Figure 5c shows the magnetic-field distribution after this transition (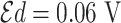 ), where the magnetic flux per supercell becomes
), where the magnetic flux per supercell becomes 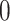 .
.
Figure 5.

Tuning of magnetic-field profile and quantized change of magnetic flux by interlayer bias. (a) The magnetic-field profile and energy contour in the lower pseudospin branch  under an interlayer bias
under an interlayer bias 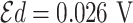 (lower panel) compared to the zero-bias profile (upper panel). The moiré period
(lower panel) compared to the zero-bias profile (upper panel). The moiré period  nm. The flux per supercell is
nm. The flux per supercell is  in both cases. (b) Scalar superlattice potentials in the two pseudospin branches at three bias values. At the critical bias
in both cases. (b) Scalar superlattice potentials in the two pseudospin branches at three bias values. At the critical bias  ,
, 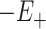 and
and  touch at C, whereupon a topological transition of the layer-pseudospin texture occurs. (c) The magnetic-field distribution has a bias of
touch at C, whereupon a topological transition of the layer-pseudospin texture occurs. (c) The magnetic-field distribution has a bias of  , where the flux per supercell is 0.
, where the flux per supercell is 0.
DISCUSSION
Massive Dirac fermion features an orbital magnetic moment 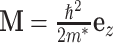 arising from the momentum-space Berry-phase effect [35], which leads to Zeeman shifts in the band edges of the monolayer TMDs in an external magnetic field [36–38]. It is interesting to ask whether the emergent moiré magnetic field
arising from the momentum-space Berry-phase effect [35], which leads to Zeeman shifts in the band edges of the monolayer TMDs in an external magnetic field [36–38]. It is interesting to ask whether the emergent moiré magnetic field  , as a manifestation of the real-space Berry phase, can couple to the orbital magnetic moment as well. In the perturbative expansion from Equation (2) to Equation (7), we can separate two contributions in the second-order perturbative correction:
, as a manifestation of the real-space Berry phase, can couple to the orbital magnetic moment as well. In the perturbative expansion from Equation (2) to Equation (7), we can separate two contributions in the second-order perturbative correction:  ,
,
 |
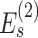 is from the coupling between
is from the coupling between 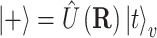 and the conduction state of the same pseudospin orientation
and the conduction state of the same pseudospin orientation  (see Fig. 4d), which can be rewritten as:
(see Fig. 4d), which can be rewritten as: 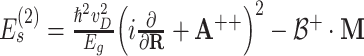 . In addition to the kinetic-energy term, it does contain the coupling of the orbital magnetic moment to the moiré magnetic field
. In addition to the kinetic-energy term, it does contain the coupling of the orbital magnetic moment to the moiré magnetic field 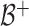 , which contributes to the scalar potential landscape (Fig. 4b). Because of the non-Abelian nature of the Berry-phase effect here, there is also a contribution
, which contributes to the scalar potential landscape (Fig. 4b). Because of the non-Abelian nature of the Berry-phase effect here, there is also a contribution  from the coupling between
from the coupling between 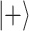 and the conduction state of opposite pseudospin
and the conduction state of opposite pseudospin  . The Zeeman energy partially cancels with
. The Zeeman energy partially cancels with  , with the net effect being the geometric scalar potential
, with the net effect being the geometric scalar potential  .
.
In contrast to the twisting moiré, the moiré introduced by a biaxial or uniaxial strain allows engineering a moiré magnetic field and flux superlattice through mechanical controls. In a rotationally aligned homobilayer, the application of a relative strain 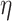 between the two layers, e.g. through the substrate, can create a moiré pattern with period
between the two layers, e.g. through the substrate, can create a moiré pattern with period 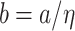 . A modest tensile strain can thus tune
. A modest tensile strain can thus tune  over several orders of magnitude, where the magnetic-field scales as
over several orders of magnitude, where the magnetic-field scales as 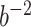 . This homobilayer moiré points to unprecedented opportunities to explore physics in an ultra-high magnetic field that can be tailored on the nanoscale by both electrical and mechanical means.
. This homobilayer moiré points to unprecedented opportunities to explore physics in an ultra-high magnetic field that can be tailored on the nanoscale by both electrical and mechanical means.
It is also interesting to compare with twisted bilayer graphene, where the interplay of a sublattice pseudospin and a layer pseudospin leads to a more complex gauge structure for the massless Dirac fermion [28,39]. Only at the AA stacking locales [39] can the gauge structure in a graphene moiré be simplified to a form equivalent to that of a magnetic field  (in contrast to the
(in contrast to the 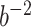 scaling underlying the
scaling underlying the  -independent flux quantization here). This gives rise to pseudo Landau levels of the massless Dirac fermion at the AA locales, which can be connected to the flat mini-bands in the bilayer graphene at the magic twist angle [28,39]. For massive particles here, the strongly inhomogeneous magnetic-field profile in a moiré supercell of exactly quantized flux points to manifestations of ultra-high magnetic fields that are remarkably different from the well-studied Landau-level physics.
-independent flux quantization here). This gives rise to pseudo Landau levels of the massless Dirac fermion at the AA locales, which can be connected to the flat mini-bands in the bilayer graphene at the magic twist angle [28,39]. For massive particles here, the strongly inhomogeneous magnetic-field profile in a moiré supercell of exactly quantized flux points to manifestations of ultra-high magnetic fields that are remarkably different from the well-studied Landau-level physics.
The flux lattices and quantum-spin Hall effects need to be explored at low doping in a relatively small moiré, since the topological gap (determined by hopping integrals between superlattice sites) decreases exponentially with 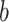 . The other limit, i.e. relatively high doping in a large moiré, is equally interesting to explore, where the nanoscale patterned magnetic field in the associated potential landscape (Fig. 5) points to a new realm of magneto transport. Electrostatic doping and interlayer bias control of the moiré magnetic flux can both be exploited to tune the magnetic field experienced by an electron gas of a periodically varying density. With the valley-spin-dependent sign, the moiré magnetic field also leads to the valley and spin Hall effects in such a metallic regime. Remarkable gate tunability of the valley-spin Hall conductance can be expected from both the bias dependence and the carrier-density dependence of moiré magnetic flux experienced by the carriers. The non-local transport measurement in Hall bar geometry can be used to detect such effects. We also expect other important manifestations of the moiré magnetic field when an external magnetic field is applied. With carriers experiencing the sum or difference of the moiré and applied magnetic fields at the two valleys, their response quantified with respect to the external magnetic field, e.g. magnetoresistance, can be significantly changed by the moiré field.
. The other limit, i.e. relatively high doping in a large moiré, is equally interesting to explore, where the nanoscale patterned magnetic field in the associated potential landscape (Fig. 5) points to a new realm of magneto transport. Electrostatic doping and interlayer bias control of the moiré magnetic flux can both be exploited to tune the magnetic field experienced by an electron gas of a periodically varying density. With the valley-spin-dependent sign, the moiré magnetic field also leads to the valley and spin Hall effects in such a metallic regime. Remarkable gate tunability of the valley-spin Hall conductance can be expected from both the bias dependence and the carrier-density dependence of moiré magnetic flux experienced by the carriers. The non-local transport measurement in Hall bar geometry can be used to detect such effects. We also expect other important manifestations of the moiré magnetic field when an external magnetic field is applied. With carriers experiencing the sum or difference of the moiré and applied magnetic fields at the two valleys, their response quantified with respect to the external magnetic field, e.g. magnetoresistance, can be significantly changed by the moiré field.
Our study here focuses on 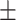 K-valley carriers only. In certain TMD homobilayers, the
K-valley carriers only. In certain TMD homobilayers, the  K-valley is still the band edge: e.g. the valence band edge of bilayer WSe2
[40] and conduction and valence band edges of bilayer MoTe2 [41]. In other compounds,
K-valley is still the band edge: e.g. the valence band edge of bilayer WSe2
[40] and conduction and valence band edges of bilayer MoTe2 [41]. In other compounds, 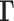 pocket of holes and/or
pocket of holes and/or 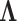 pockets of electrons become relevant. In such cases, the quantum-spin Hall effect may not be possible to observe, as the topological gap overlaps with the Fermi sea at
pockets of electrons become relevant. In such cases, the quantum-spin Hall effect may not be possible to observe, as the topological gap overlaps with the Fermi sea at  or
or 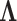 . Nevertheless, other important manifestations of the moiré magnetic field (like the valley-spin Hall effect in the metallic regime) can still be explored for the carriers at
. Nevertheless, other important manifestations of the moiré magnetic field (like the valley-spin Hall effect in the metallic regime) can still be explored for the carriers at 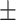 K-valleys, even if they are not the band edge.
K-valleys, even if they are not the band edge.
METHODS
DFT calculations of the bilayer MoSe2 structure, which is modeled by a slab, were performed using the Vienna ab initio Simulation Package [42]. To avoid artificial interactions between the polar slabs when the bilayer deviates from the AA stacking, two such slabs, oppositely oriented with mirror symmetry, are placed in each cell, which is separated from its periodic images by 20-Å vacuum regions [43]. The cutoff energies for the plane-wave basis set used to expand the Kohn-Sham orbitals are 400 eV for all calculations. The exchange correlation functional is approximated by the generalized gradient approximation as parametrized by Perdew, Burke and Ernzerhof [44]. The 2D Brillouin zone is sampled by a 30 × 30 × 1 Monkhorst-Pack mesh. Van der Waals dispersion forces between the adsorbate and the substrate were accounted for through the optB88-vdW functional by using the vdW-DF method developed by Klimeš et al. [45].
Funding
This work was supported by the Research Grants Council of Hong Kong (17306819), Croucher Foundation and Seed Funding for Strategic Interdisciplinary Research Scheme of HKU.
Conflict of interest statement. None declared.
REFERENCES
- 1. Dean CR, Wang L, Maher Pet al.. Hofstadter's butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 2013; 497: 598–602. [DOI] [PubMed] [Google Scholar]
- 2. Hunt B, Sanchez-Yamagishi JD, Young AFet al.. Massive dirac fermions and Hofstadter butterfly in a van der Waals heterostructure. Science 2013; 340: 1427–30. [DOI] [PubMed] [Google Scholar]
- 3. Ponomarenko LA, Gorbachev RV, Yu GLet al.. Cloning of Dirac fermions in graphene superlattices. Nature 2013; 497: 594–7. [DOI] [PubMed] [Google Scholar]
- 4. Cao Y, Fatemi V, Demir Aet al.. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 2018; 556: 80–4. [DOI] [PubMed] [Google Scholar]
- 5. Chen G, Jiang L, Wu Set al.. Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice. Nat Phys 2019; 15: 237–41. [Google Scholar]
- 6. Cao Y, Fatemi V, Fang Set al.. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018; 556: 43–50. [DOI] [PubMed] [Google Scholar]
- 7. Yankowitz M, Chen S, Polshyn Het al.. Tuning superconductivity in twisted bilayer graphene. Science 2019; 363: 1059–64. [DOI] [PubMed] [Google Scholar]
- 8. Chen G, Sharpe AL, Gallagher Pet al.. Signatures of tunable superconductivity in a trilayer graphene moiré superlattice. Nature 2019; 572: 215–9. [DOI] [PubMed] [Google Scholar]
- 9. Liu X, Hao Z, Khalaf Eet al.. Spin-polarized correlated insulator and superconductor in twisted double bilayer graphene. arXiv:190308130.
- 10. Shen C, Li N, Wang Set al.. Observation of superconductivity with Tc onset at 12K in electrically tunable twisted double bilayer graphene. arXiv:190306952.
- 11. Cao Y, Rodan-Legrain D, Rubies-Bigorda Oet al.. Electric field tunable correlated states and magnetic phase transitions in twisted bilayer-bilayer graphene. arXiv:190308596.
- 12. Yu H, Liu G-B, Tang Jet al.. Moiré excitons: from programmable quantum emitter arrays to spin-orbit-coupled artificial lattices. Sci Adv 2017; 3: e1701696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Yu H, Liu G-B, Yao W. Brightened spin-triplet interlayer excitons and optical selection rules in van der Waals heterobilayers. 2D Mater 2018; 5: 035021. [Google Scholar]
- 14. Wu F, Lovorn T, MacDonald AH. Theory of optical absorption by interlayer excitons in transition metal dichalcogenide heterobilayers. Phys Rev B 2018; 97: 035306. [Google Scholar]
- 15. Seyler KL, Rivera P, Yu Het al.. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 2019; 567: 66–70. [DOI] [PubMed] [Google Scholar]
- 16. Tran K, Moody G, Wu Fet al.. Evidence for moiré excitons in van der Waals heterostructures. Nature 2019; 567: 71–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Jin C, Regan EC, Yan Aet al.. Observation of moiré excitons in WSe2/WS2 heterostructure superlattices. Nature 2019; 567: 76–80. [DOI] [PubMed] [Google Scholar]
- 18. Tong Q, Yu H, Zhu Qet al.. Topological mosaics in moiré superlattices of van der Waals heterobilayers. Nat Phys 2017; 13: 356–62. [Google Scholar]
- 19. Wu F, Lovorn T, Tutuc Eet al.. Topological insulators in twisted transition metal dichalcogenide homobilayers. Phys Rev Lett 2019; 122: 086402. [DOI] [PubMed] [Google Scholar]
- 20. Xiao D, Chang M-C, Niu Q. Berry phase effects on electronic properties. Rev Mod Phys 2010; 82: 1959–2007. [Google Scholar]
- 21. Ye J, Kim YB, Millis AJet al.. Berry phase theory of the anomalous Hall effect: application to colossal magnetoresistance manganites. Phys Rev Lett 1999; 83: 3737–40. [Google Scholar]
- 22. Bruno P, Dugaev VK, Taillefumier M. Topological Hall effect and Berry phase in magnetic nanostructures. Phys Rev Lett 2004; 93: 096806. [DOI] [PubMed] [Google Scholar]
- 23. Nagaosa N, Tokura Y. Topological properties and dynamics of magnetic skyrmions. Nat Nanotechnol 2013; 8: 899–911. [DOI] [PubMed] [Google Scholar]
- 24. Xiao D, Liu G-B, Feng Wet al.. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys Rev Lett 2012; 108: 196802. [DOI] [PubMed] [Google Scholar]
- 25. Bi Z, Yuan NFQ, Fu L. Designing flat band by strain. Phys Rev B 2019; 100: 035448. [Google Scholar]
- 26. Wang Y, Wang Z, Yao Wet al.. Interlayer coupling in commensurate and incommensurate bilayer structures of transition metal dichalcogenides. Phys Rev B 2017; 95: 115429. [Google Scholar]
- 27. Bistritzer R, MacDonald AH. Moiré bands in twisted double-layer graphene. Proc Natl Acad Sci USA 2011; 108: 12233–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. San-Jose P, González J, Guinea F. Non-Abelian gauge potentials in graphene bilayers. Phys Rev Lett 2012; 108: 216802. [DOI] [PubMed] [Google Scholar]
- 29. Guinea F, Katsnelson MI, Geim AK. Energy gaps and a zero-field quantum Hall effect in graphene by strain engineering. Nat Phys 2010; 6: 30–3. [Google Scholar]
- 30. Levy N, Burke SA, Meaker KLet al.. Strain-induced pseudo-magnetic fields greater than 300 Tesla in graphene nanobubbles. Science 2010; 329: 544–7. [DOI] [PubMed] [Google Scholar]
- 31. Liu Y, Rodrigues JNB, Luo YZet al.. Tailoring sample-wide pseudo-magnetic fields on a graphene-black phosphorus heterostructure. Nat Nanotechnol 2018; 13: 828–34. [DOI] [PubMed] [Google Scholar]
- 32. Kane CL, Mele EJ. Quantum spin Hall effect in graphene. Phys Rev Lett 2005; 95: 226801. [DOI] [PubMed] [Google Scholar]
- 33. Haldane FDM. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the ‘parity anomaly’. Phys Rev Lett 1988; 61: 2015–8. [DOI] [PubMed] [Google Scholar]
- 34. Aharonov Y, Stern A. Origin of the geometric forces accompanying Berry's geometric potentials. Phys Rev Lett 1992; 69: 3593–7. [DOI] [PubMed] [Google Scholar]
- 35. Xiao D, Yao W, Niu Q. Valley-contrasting physics in graphene: magnetic moment and topological transport. Phys Rev Lett 2007; 99: 236809. [DOI] [PubMed] [Google Scholar]
- 36. Srivastava A, Sidler M, Allain AVet al.. Valley Zeeman effect in elementary optical excitations of a monolayer WSe2. Nat Phys 2015; 11: 141–7. [Google Scholar]
- 37. Aivazian G, Gong Z, Jones AMet al.. Magnetic control of valley pseudospin in monolayer WSe2. Nat Phys 2015; 11: 148–52. [Google Scholar]
- 38. Li Y, Ludwig J, Low Tet al.. Valley splitting and polarization by the Zeeman effect in monolayer MoSe2. Phys Rev Lett 2014; 113: 266804. [DOI] [PubMed] [Google Scholar]
- 39. Liu J, Liu J, Dai X. Pseudo Landau level representation of twisted bilayer graphene: band topology and implications on the correlated insulating phase. Phys Rev B 2019; 99: 155415. [Google Scholar]
- 40. Wilson NR, Nguyen PV, Seyler KLet al.. Determination of band offsets, hybridization, and exciton binding in 2D semiconductor heterostructures. Sci Adv 2017; 3: e1601832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Froehlicher G, Lorchat E, Berciaud S. Direct versus indirect band gap emission and exciton-exciton annihilation in atomically thin molybdenum ditelluride (MoTe2). Phys Rev B 2016; 94: 085429. [Google Scholar]
- 42. Kresse G, Furthmuller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci 1996; 6: 15–50. [DOI] [PubMed] [Google Scholar]
- 43. Chen M, Weinert M. Layer k-projection and unfolding electronic bands at interfaces. Phys Rev B 2018; 98: 245421. [Google Scholar]
- 44. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett 1996; 77: 3865–8. [DOI] [PubMed] [Google Scholar]
- 45. Klimeš J, Bowler DR, Michaelides A. Van der Waals density functionals applied to solids. Phys Rev B 2011; 83: 195131. [Google Scholar]



