Fast and accurate bootstrap confidence limits on genome-scale phylogenies using little bootstraps

Abstract

Felsenstein’s bootstrap approach is widely used to assess confidence in species relationships inferred from multiple sequence alignments. It resamples sites randomly with replacement to build alignment replicates of the same size as the original alignment and infers a phylogeny from each replicate dataset. The proportion of phylogenies recovering the same grouping of species is its bootstrap confidence limit. But, standard bootstrap imposes a high computational burden in applications involving long sequence alignments. Here, we introduce the bag of little bootstraps approach to phylogenetics, bootstrapping only a few little samples, each containing a small subset of sites. We report that the median bagging of bootstrap confidence limits from little samples produces confidence in inferred species relationships similar to standard bootstrap but in a fraction of computational time and memory. Therefore, the little bootstraps approach can potentially enhance the rigor, efficiency, and parallelization of big data phylogenomic analyses.

Editor summary:

The authors show that accurate bootstrap confidence limits on inferred evolutionary relationships of species can be estimated by bootstrapping a collection of little samples of very long sequence alignments. Little bootstraps take a fraction of computer time and memory compared to the standard bootstrap, enabling big data analytics on personal computers.

Main text

Felsenstein’s bootstrap resampling approach¹ (standard BS) is being applied to increasingly larger datasets in molecular phylogenetics due to the widespread accessibility of genome sequence databases and the assembly of multispecies and multigene alignments containing hundreds of thousands of bases^2–4. These large datasets have the power to reconstruct hard-to-resolve evolutionary relationships with high confidence^4–14. But, they impose onerous computational demands because the computational complexity of phylogenomic analyses using the maximum likelihood (ML) method increases exponentially with the number of sequences and linearly with sequence length¹⁵ (Fig. 1b). Consequently, standard BS can require a large amount of computer memory and take days to complete for big datasets^4,15. Many heuristics moderate the escalation due to the increasing number of sequences^15,16, but none focus on relieving the onerous computational burden imposed by an increase in sequence length due to the widespread adoption of next-generation sequencing methods.

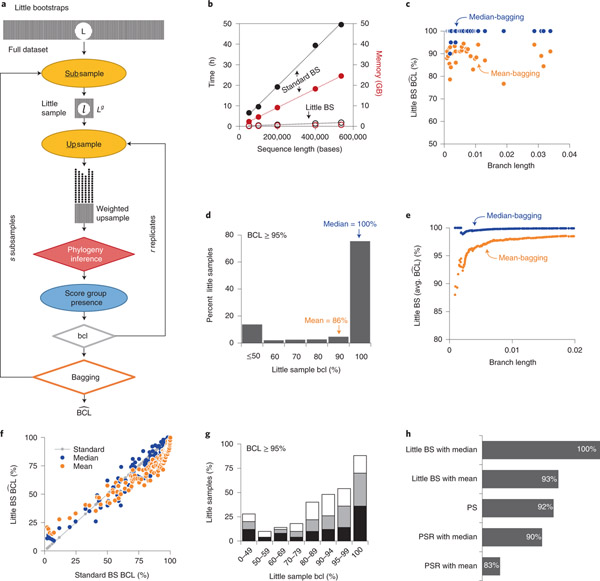
Figure 1. The little BS approach and analyses of simulated and empirical phylogenomic datasets |.

(a) Steps in the little bootstrap (BS) approach. Shaded boxes represent sequence alignments, with width representing the sequence length; see main text for a detailed description and Extended Data Fig. 1 for a comparison with Felsentein’s standard BS approach. (b) Time and memory savings per replicate of little bootstrap (open circles) compared to the standard bootstrap (closed circles) for a large simulated dataset containing 446 sequences of 50,000 to 536,534 bases. (c) The relationship of branch lengths and $\widehat{BCL}$ produced by little BS with mean-bagging (orange) and median-bagging (blue) for l = L^0.7. The x-axis is restricted to the branch length of 0.04 because $\widehat{BCL}=100\%$ for longer branches. (d) The distribution of bcl_is for 53 species groups that received $\widehat{BCL}<100\%$ in the little BS analysis with mean-bagging of the large dataset. (e) The average $\widehat{BCL}$ for all the species groups connected to the phylogeny with a given cutoff branch length (x-axis). The x-axis is restricted to 0.02 because the performance does not change any further. (f) The relationship of standard BS (BCL) and little BS ($\widehat{BCL}$) with mean-bagging and median-bagging for datasets smaller than 10,000 sites (l = L^0.9). The gray line shows the 1:1 relationship with the standard BS. The linear regression slope is 0.97 (R² = 0.93) for median-bagging and 0.89 (R² = 0.89) for the mean-bagging. (g) The distribution of little sample bcls for species groups in smaller datasets for which standard BS BCL ≥ 95% (black bars = 9,359 sites, gray bars = 7,002 sites, and white bars = 4,070 sites). (h) The true positive rates (TPR) for little BS with mean- and median-bagging compared to other phylogenomic subsampling approaches (PS and PSR with Mean and with Median) in which upsampling was not applied (see Methods).

The little bootstraps (BS) approach for phylogenomics.

Here, we introduce the bag of little bootstraps¹⁷ to place confidence limits on molecular phylogenies. In the little bootstraps approach, bootstrapping is performed independently on s little samples, each containing l sites sampled randomly (with or without replacement) from the full dataset consisting of L sites (l ≪ L). Bootstrap confidence limit for a group of sequences (bcl_i) is estimated for each little dataset i by generating r bootstrap phylogenies. Each bootstrap phylogeny is inferred from the bootstrap replicate dataset that contains L sites sampled with replacement from little subsamples (Fig. 1a). Because l ≪ L, the same site is selected many times (upsampling) to build the bootstrap replicate dataset in the little BS approach (Fig. 1a, see Extended Data Fig. 1). Then, the bootstrap confidence limit ($\widehat{BCL}$) for a given group of species is derived from s little sample bcl values, a procedure referred to as bagging. The average of s little sample bcl values, called mean-bagging ($\widehat{BCL}=\frac{1}{s}{\sum }_{i=1}^{s}bc{l}_i$), was found to work well¹⁷.

In the little BS approach, every site of the little sample is included L/l times, on average, in a bootstrap replicate dataset, so they have the same number of sites as the full dataset. The upsampling has desirable asymptotic theoretical properties¹⁷ and obviates ad hoc corrections needed in other divide-and-conquer approaches¹⁸. As the computational burden of ML phylogeny estimation is proportional to the number of distinct site configurations, time and memory requirements for analyzing a little BS replicate dataset is of order O(L/l) needed for a standard BS replicate (Fig. 1b). Kleiner et al.¹⁷ have suggested the use of little samples of size l = L^g (0.5 < g < 1.0), which can reduce time and memory by orders of magnitude. In phylogenomics, these savings can be substantial and remain low as the length of the sequence alignment increases from thousands to millions of sites (Fig. 1b, Extended Data Fig. 2).

Results

We first present ML phylogenetic analysis of a computer-simulated alignment containing 446 species and 134,131 sites (see Methods). We conducted 100 standard BS replicates, an ad hoc convention adopted in many studies to make calculations feasible¹⁹. It required 6.1 GB of memory and 13.1 CPU hours per replicate (54 CPU days of total computation). These analyses established all the true evolutionary relationships among sequences with very high confidence (BCL ≥ 95%). For this dataset, we generated ten little samples (s = 10) containing l = L^0.7 sites (3,884 sites) and analyzed ten bootstrap datasets for each little sample (r = 10). ML phylogeny inference of each little dataset required ~0.3 GB RAM and ~0.6 hours, a 95% reduction in memory and time compared to the standard BS. Now, several little BS datasets could be run concurrently on a multicore desktop with 8 GB of RAM, unlike the standard BS analyses that took up almost all the memory for estimating the ML phylogeny for one replicate dataset.

However, little BS with mean-bagging did not produce $\widehat{BCL}\ge 95\%$ for 32 species groups (7.2% false negatives). These 32 species groups were connected with relatively short branches, and their confidence limits were underestimated by as much as 24% (Fig. 1c). We found that the distribution of little sample bcls was skewed (Fig. 1d), making the mean unsuitable for measuring the central tendency. We explored the use of median because it is more resilient to outliers²⁰, and median-bagging is expected to have the same statistical properties as those established for mean-bagging¹⁷. However, median bagging seems to be not previously applied for the bag of little BS.

Median-bagging eliminated 31 false negatives, and the remaining species group received $\widehat{BCL}=90\%$ (Fig. 1c). The average $\widehat{BCL}$ at every branch length threshold was greater than 95% for median-bagging, but not for mean-bagging (Fig. 1e). We confirmed the improvement offered by median-bagging for a greater range of BCL values by analyzing three gene-specific sequence alignments (4,000 < L < 10,000; 446 species; Fig. 1f). Median-bagging performed much better because the distribution of bcls was skewed and contained many outliers for each dataset (Fig. 1g). Also, false-negative rates of phylogenomic subsampling approaches were higher when upsampling or median-bagging were not used (Fig. 1h). We found that little BS needed smaller samples of sites for empirical datasets with larger numbers of unique site configurations per sequence (C/S; Table 1; see Extended Data Fig. 3). Therefore, little BS with median-bagging achieves higher accuracy by overcoming the deficiency of mean-bagging and traditional divide- and-conquer approaches.

Table 1 |.

Performance of little bootstraps analysis for empirical datasets.

	Full Dataset			Little BS samples						Little BS Results				Little BS Resources
Species	No. of Sites (L)	No. of Seqs (S)	Unique Sites/Seq. (C/S)	Power factor (g)	s × r	Sites (l)	Uniq. Sites (c)	Uniq. Sites/Seq. (c/S)	Total Uniq. Sites (U)	Avg. $\widehat{BCL}$	ΔBCL	TPR (≥70%)	TPR (≥95%)	Time (Hours)	Memory (GB)	Total Time (Hours)
Butterflies	5,267,461	61	61,684	0.700	4×10	50,714	1.3%	793	5%	100%	0.0%	100%	100%	1.37	0.38	54.8
Plants A	4,246,454	16	11,897	0.700	4×5	43,614	3.3%	389	9%	100%	0.0%	100%	100%	0.08	0.01	1.6
Insects A	3,011,544	174	11,758	0.700	6×8	34,289	1.6%	188	8%	97%	−1.8%	98%	98%	3.80	0.74	182.0
Insects B	2,938,039	48	29,092	0.747	10×12	67,401	3.8%	1,103	25%	91%	4.5%	100%	94%	3.80	0.33	546.0
Insects C	1,719,036	193	7,346	0.748	5×7	46,331	3.2%	236	15%	97%	1.1%	96%	99%	5.80	1.14	548.0
Mammals	1,391,742	37	20,962	0.700	7×9	19,976	2.3%	485	13%	98%	0.0%	97%	100%	0.32	0.11	18.9
Spiders A	137,170	27	3,071	0.800	4×8	12,877	13.4%	411	39%	94%	0.0%	96%	90%	0.08	0.04	2.5
Plants B	135,243	30	795	0.800	7×9	12,732	14.2%	113	56%	99%	−1.0%	100%	96%	0.03	0.01	1.9
Spiders B	89,212	34	1,296	0.800	9×15	9,128	14.4%	186	66%	97%	0.0%	93%	90%	0.06	0.03	14.9
Birds	61,794	39	750	0.863	6×10	13,633	26.7%	201	80%	90%	−3.3%	97%	93%	0.11	0.04	17.4

Empirical sequence alignments from a variety of speci es were analyzed (see Methods). The L and S are the total number of sites and sequences, respectively, in the full dataset. C the number of unique site configurations in the full sequence alignment. The power factor (g), the number of little samples (s), and the number of replicates per little sample (r), and were selected using the automatic procedure. l = L^g, which is the number of sites in little samples. c is the number of unique site configurations in a little sample. U is the number of unique site configurations found in all the little samples used for a given dataset. Avg. $\widehat{BCL}$ is the average of $\widehat{BCL}$ values produced by little BS for all species groupings in a phylogeny. ΔBCL is the difference between average bootstrap supports produced by the standard and little BS approaches. The true positive rate (TPR) is the percentage of species groups statistically supported by standard BS ($\widehat{BCL}$) at the given cutoff value, which were also supported in the by little BS analysis ($\widehat{BCL}$) at that cutoff value. The time and memory estimates are for one little BS dataset. The total time is for the completion of all little bootstrap replicates in a single computing thread.

For practical applications of little BS, we developed a simple, automated protocol to tune key parameters (g, s, and r; Methods). Its application to the 446×134,131 dataset confirmed all correct species groups ($\widehat{BCL}=100\%$; g = 0.8, s = 4, and r = 6). We applied the automated protocol to analyze empirical sequence alignments (Table 1). Also, we generated standard errors (SEs) of $\widehat{BCL}$ estimates during the little BS analysis in which little samples and replicate phylogenies were resampled with replacement (see Methods). High precision (low SEs) for $\widehat{BCL}$ was achieved even when using small s and r because $\widehat{BCL}$ values were generally high for most of the species groupings in long sequence alignments (Table 1; Extended Data Fig. 4).

Next, we evalulaed the performance of little BS for empirical datasets. The accuracy of little BS with median bagging was excellent in these analyses (Table 1). The true positive rate (TPR) at $\widehat{BCL}\ge 95\%$ was greater than 95% for six datasets and 90% for the other four (Table 1). Phylogeny-wide average $\widehat{BCL}$ was close to that from standard BS BCL, as the average difference was only 0.1% achieved by analyzing little samples containing only a fraction of sites and memory (Table 1). The computation time was in minutes to hours per little dataset (Table 1). For example, the little BS analysis of the mammalian dataset required 0.1 GB per replicate, on average, rather than 3.1 GB RAM (~29-fold memory savings) and 0.32 CPU hours rather than 9.8 CPU hours per bootstrap replicate (31-fold time efficiency). These savings enabled multiple concurrent little BS replicates on a standard multicore personal desktop equipped with a modest memory (8 GB). A similar pattern was seen for the other nine empirical datasets (Table 1).

We also evaluated little BS (LBS) performance by combining it with Ultrafast bootstrap¹⁶ (UFB). UFB makes standard bootstrapping faster for a large number of sequences. For the mammalian dataset, LBS+UFB required only 50 minutes (0.2 GB RAM) on a computer with 5 cores when using ten little samples (r = 1,000, default in IQTREE^16,21). This was much faster and leaner than using only one of the optimizations: UFB alone required 4.5 hours and 7.1 GB of RAM, whereas LBS alone needed 19.8 hours and 0.1 GB of RAM. Therefore, plugging in the UFB optimization for generating sample-wise bcl’’s further increases memory and time savings. In the future, we expect LBS to be used along with other efficient heuristics developed to speed up bootstrap calculations^15,16. One may also use Transfer Bootstrap²² when estimating confidence limits.

However, users need to ensure that sufficiently large little samples are utilized in the little BS approach. We recommend using the automatic pipeline to selecting key parameters for little BS analysis (g, s, and r). In addition, it will be prudent to inspect SEs reported and reconfirm high $\widehat{BCL}s$ associated with large SEs (low precision) by conducting additional little BS analysis with a larger number of sites in little samples as well as more little samples and number of bootstrap replicates.

In conclusion, the little BS approach can help break the bottleneck created by the rise of large genomic datasets assembled from burgeoning sequence databases. It can enable parallelization even with modest computational resources and promote greater reproducibility and scientific rigor in building the tree of life that requires assessing the robustness of inferences to selecting biologically distinct subsets of data, choice of substitution models and strategies, and application of a myriad of ways of combining multigene datasets.

METHODS

Simulated and empirical sequence data assembly.

We analyzed multigene alignments assembled from a collection of simulated datasets analyzed previously^23,24. They were generated using an evolutionary tree of 446 species and a wide range of biologically realistic parameter values derived from hundreds of empirical gene sequence alignments, including sequence length (445 – 4,439 bases), G+C content (39 – 82%), transition/transversion rate ratio (1.9 – 6.0), and gene-wise evolutionary rates (1.35 – 2.60×10⁻⁶ per site per billion years)²³. Evolutionary rates were also heterogeneous across lineages, simulated for each gene independently under autocorrelated and uncorrelated rate models^23,24. Simulated alignments of 100 genes that evolved with the autocorrelated rate model were concatenated to form the 446×134,131 (species x bases) dataset. A bigger 446×536,524 sequence alignment was generated by concatenating sequence alignments generated by concatenating 100 randomly selected gene alignments from each of the four different lineage rate variation models simulated²⁴. Three smaller datasets were analyzed, corresponding to individual simulated genes: 446×4,070, 446×7,002, and 446×9,359 bases.

Ten empirical datasets were also analyzed. These DNA alignments consisted of sequences from eutherian mammals¹⁴, butterflies⁷, plants (A⁶ and B¹⁰), insects (A¹¹, B¹², and C⁵), spiders (A⁹ and B⁸), and birds¹³ (Table 1). The number of species ranged from 16 to 193, and the number of sites ranging from 61,794 to 5,267,461. We used the phylogenetic trees (ML trees) presented in the original studies as the reference trees for empirical datasets. The ground truth for little BS confidence limits were the standard BS confidence limits reported in the published articles.

Standard and little BS analyses.

We used the IQTREE software²¹ with a general time-reversible nucleotide substitution model with gamma-distributed rate variation (GTR+Γ) and default ML search parameters. One hundred replicates of standard bootstrap analyses were conducted to generate BCLs, all of which were very high for large datasets analyzed. For three single-gene datasets, 1,000 bootstrap replicates were used to generate stable BCLs. The confidence limits obtained using the standard bootstrap analyses were the ground truth in our analyses, as the bag of little bootstraps is being investigated as a computationally efficient alternative. The true tree used in computer simulations was the reference in the analysis of simulated datasets. The bootstrap confidence limits presented in the published phylogenies were used as references for the empirical datasets analyzed. The parameters of little BS analyses for these datasets were selected using the protocol presented below. We also applied the Ultrafast bootstrap (UFB)¹⁶ on the mammal dataset using the (GTR+Γ) model in IQTREE with the default option of 1,000 replicates. For little bootstrap analysis, the UFB with the same options was carried out for each little dataset directly to estimate the required time and memory. These are approximate estimates because IQTREE does not have a provision for upsampling when generating bootstrap replicate datasets. The reported estimates are expected to be very close to the actual time estimates because IQTREE compresses identical site configurations during ML calculations, and upsampling only alters site configurations’ frequencies.

Automatic selection of the little BS parameters.

Our procedure automatically determines the size of the sample (g), the number of samples (s), and the number of bootstrap replicates (r). The procedure starts with g = 0.7 if the sequence alignment contains ≥ 100,000 unique site configuration (such that l < 50,000), otherwise we set g = 0.8. One may set any starting or fixed value of g. In step 1, we conduct little BS with s = 3 and r = 3 to generate initial $\widehat{BCL}$ for all the nodes in the given phylogeny (if provided) or from a majority rule bootstrap consensus tree. Using these values, we generate average $\widehat{BCL}$ (Av) and the fraction of inferred tree partitions with $\widehat{BCL}\ge 95\%$ (Nv). Through an iterative process, we stabilize and maximize both Av and Nv, as follows. In step 2, we add one little BS replicate to each subsample (i.e., r increases by 1) and then compute Av. We repeat steps 2 and 3 by increasing r until the difference in successive Av values is less than 0.1% (or a user-specified threshold, δr). In step 4, we increase s by one and generate r additional replicate datasets and phylogenies, and compute Av and Nv. If the difference between Av for the current (s) and the previous (s-1) set of subsamples is greater than 1% (or user-specified δs), then we repeat step 4. In step 5, we check and see if Nv is less than 100% or the SE of estimated $\widehat{BCL}\ge 95\%$ is too high (>5%). If so, we increase the little subsample size by l and restart the analysis from step 2. In step 6, we go to step 4 if the user-specified precision (SE) has not been achieved.

Estimating standard errors of $\widehat{BCL}s$.

Given r bootstrap replicate-phylogenies for s samples, we employ a bootstrap procedure to generate SE of $\widehat{BCL}$. We use already computed phylogenies of r × s little BS replicates and derive $\widehat{BCL}$ for all the nodes from collections of phylogenies by resampling s samples with replacement and r replicates with replacement every time a subsample is selected. This process is repeated 100 times, and the standard deviation of each tree partition’s $\widehat{BCL}$ is generated to estimate its SE. This process is extremely fast because precomputed phylogenies are used.

Phylogenomic subsampling approaches without upsampling.

We also generated $\widehat{BCL}$ values by a little BS procedure in which upsampling was replaced by the standard BS resampling such that the replicate datasets contained only l sites rather than L sites. We refer to this as the Phylogenomic Subsampling with Resampling (PSR) approach. For PSR, one may use either mean- or median-bagging. We also generated $\widehat{BCL}s$ without any resampling or upsampling (i.e., r = 0) such that the ML phylogenies were inferred from s subsample datasets containing l sites each. We call it the Phylogenomic Subsampling (PS) approach. We compared the true positive rates ($\widehat{BCL}\ge 95\%$) of little BS, PSR, and PS approaches for the computer-simulated 446×134,131 dataset (g = 0.7) For all analyses, 100 replicate phylogenies were generated by using s = 10 and r =10 for little BS and PSR, and s = 100 for the PS approach.

Analysis pipeline for little BS.

We developed an R²⁵ pipeline to conduct little bootstraps analysis by using IQTREE. In this case, we used the Biostrings²⁶ package to generate little datasets of the specified lengths (l) and then bootstrap replicate datasets in which L sites were resampled with replacement from l sites. The resulting datasets were used to obtain ML phylogenies that were summarized by using the function plotBS from the phangorn²⁷ library that produced the bcl for each of the phylogenetic groups in the standard bootstrap phylogeny. Mean and median-bagging estimates were obtained from sample-wise bcls from s little samples using a customized function in R. We used ten samples and ten bootstrap replicates for little bootstraps analysis for concatenated gene datasets, and 50 little samples and 20 bootstrap replicates for single-gene datasets. We applied the automated protocol using a customized R function. We also developed a customized R function for estimating SEs of $\widehat{BCL}s$.

Data availability:

All simulated DNA sequence alignments containing 446 taxa were obtained from published research articles^23,24. Ten empirical datasets from a variety of species have been analyzed. These DNA sequence alignments consisted of sequences from eutherian mammals¹⁴, butterflies⁷, plants (A⁶ and B¹⁰), insects (A¹¹, B¹², and C⁵), spiders (A⁹ and B⁸), and birds¹³. All empirical and simulated datasets analyzed in this article are available in an online repository³⁰.

Code availability:

R codes are available from https://github.com/ssharma2712/Little-Bootstraps. A capsule containing source codes and datasets for our analyses is available on the CodeOcean service²⁸. Users can replicate the little bootstraps sampling and bagging steps in this capsule.

Extended Data

Extended Data Fig. 1. A comparison of the standard and little bootstrap approaches.

Steps of (a) the standard phylogeny bootstrap and (b) the little bootstraps (BS) approach. Shaded boxes represent sequence alignments, with width representing sequence length. In standard BS, L sites are randomly sampled with replacement from the original dataset containing L sites. In this resampling process, ~63.2% of the data points^17,29 are expected to be represented in a bootstrap replicate dataset. Each replicate dataset is compressed into weighted resamples that contain only distinct site configurations and a vector of their counts (represented by stacks of dots). An ML tree is inferred from each replicate dataset, and the BCL for a species group is the proportion of times that appeared in bootstrap replicate phylogenies. In little BS, L sites are randomly sampled with replacement from the little dataset consisting of only l = L^g sites, which produces bootstrap replicate datasets. Because l ≪ L, each site will be represented many times in the little bootstraps replicate datasets, which we refer to as upsampling that changes the frequency of unique site configurations. Stacks of dots are much higher for little BS due to upsampling than standard BS that involves only resampling. The number of distinct site configurations in the upsampled dataset is smaller than in the standard bootstrap replicate dataset because of l ≪ L.

Extended Data Fig. 2. The number of sites used in little and standard bootstrap replicates.

The proportion of sites included in the little bootstrap replicates for little datasets with l = L^0.7 (open circles) and standard bootstrap (closed circles). The choice of l = L^0.7 offers increasingly greater computational savings for longer sequences because of a decreasing proportion of sites included in the little samples. For example, the standard bootstrap replicates always contain approximately 63%²⁹ of the site configurations from the full datasets. But, the little dataset size is ~3.1% of the original alignment for L = 100,000 bases, but it decreases to ~1.6% when L increases 10-fold (1,000,000 bases).

Extended Data Fig. 3. Patterns of unique site configurations per sequence and little sample size.

The relationship of the number of unique site configurations per sequence (C/S, log-transformed) and little sample size selected (power parameter, g) (R² = 0.76).

Extended Data Fig. 4. Precision of little bootstrap confidence limits.

The relationship between little $\widehat{BCL}s$ and their precision (standard errors, SEs) for the selected little BS parameters. The SEs are inversely related to little bootstrap confidence limits (R² = 0.59).