Modeling Direct and Bystander Effects that cause Growth Delay of Breast Cancer Xenografts in Bone Marrow of Mice Treated with Radium-223

Abstract

Rationale.

The role of radiation-induced bystander effects in cancer therapy with alpha-particle emitting radiopharmaceuticals remains unclear. With renewed interest in using alpha-particle emitters to sterilize disseminated tumor cells, micrometastases, and tumors, a better understanding of the direct effects of alpha particles and the contribution of the bystander responses they induce is needed to refine dosimetric models that help predict clinical benefit. Accordingly, this work models and quantifies the relative importance of direct effects (DE) and bystander effects (BE) in the growth delay of human breast cancer xenografts observed previously in the tibiae of mice treated with ²²³RaCl₂.

Methods.

A computational model of the MDA-MB-231 and MCF-7 human breast cancer xenografts in the tibial bone marrow of mice administered ²²³RaCl₂ was created. A Monte Carlo radiation transport simulation was performed to assess individual cell absorbed doses. The responses of the breast cancer cells to direct alpha particle irradiation and gamma irradiation were needed as input data for the model and were thus determined experimentally using a colony forming assay and compared to the responses of preosteoblast MC3T3-E1 and osteocyte-like MLO-Y4 bone cells. Using these data, a scheme was devised to simulate the dynamic proliferation of the tumors in vivo, including DE as well as BE propagated from the irradiated cells. The parameters of the scheme were estimated semi-empirically to fit experimental tumor growth.

Results.

A robust BE component, in addition to a much smaller DE component, was required to simulate the in vivo tumor proliferation. We also found that the relative biological effectiveness (RBE) for cell killing by alpha particle radiation was greater for the bone cells than the tumor cells.

Conclusion.

This modeling study demonstrates that direct effects of radiation alone cannot explain experimental observations of ²²³RaCl₂-induced growth delay of human breast cancer xenografts. Furthermore, while the mechanisms underlying BE remain unclear, the addition of a BE component to the model is necessary to provide an accurate prediction of the growth delay. More complex models are needed to further comprehend the extent and complexity of ²²³RaCl₂-induced BE.

INTRODUCTION

Since the FDA approval of Xofigo^® (²²³RaCl₂) for palliative treatment of metastatic castration-resistant prostate cancer, there has been renewed interest in alpha-particle-emitting radiopharmaceuticals. The benefit of ²²³RaCl₂ includes a decrease in bone pain as well as an increase in overall survival when compared to previous therapies for bone metastases (Parker 2013). Consequently, other cancers that metastasize to bone, such as breast cancer, are being investigated. A difficulty in successfully treating breast cancer is the prevention of metastases (Brewster 2008). Circulating tumor cells shed from the primary tumor can be eliminated but a small number survive and disseminate to various niches where they can develop into metastases. In one third of patients with Stage I-III breast cancer, disseminated tumor cells (DTC) are found in bone marrow biopsies (Braun 2005). While the overall breast cancer 5-year survival rate is ~89%, patients who develop bone-metastatic tumors have a median survival of 19–25 months after diagnosis (Selvaggi 2005). A goal of radionuclide therapy is therefore to develop new strategies to eliminate DTC.

One of the advantages of using ²²³Ra is that each decay deposits 27.5 MeV, of which ~90% is by alpha particles from ²²³Ra and three of its daughters. The remaining 10% emanates from beta-emitting daughters, X-rays, and Auger electrons. High linear energy transfer (LET) alpha particles cause cell death with only a few traversals across the cell nuclei (Howell 1990). Furthermore, because ²²³RaCl₂ localizes in cortical bone, it affords better sparing of bone marrow due to the alpha particles’ short range. Several studies have investigated the proliferation of bone metastases under ²²³Ra treatment and its consequences for bone toxicity (Hobbs 2012; Moreira 2019). However, DTC localized in bone marrow more than 70 μm away from the bone surface are less likely to be traversed by an alpha particle and there is no significant dose capable of deterministic effect in the deepest part of the bone marrow from radium-223 therapy (Dondossola 2019; Pinto 2020). Therefore, the understanding of additional mechanisms might help to better explain the observed clinical benefits. One such mechanism is radiation-induced bystander effects (BE): cells beyond the range of the alpha particles may be affected by signals sent by alpha particle-irradiated cells (Azzam 2001; Gaillard 2009; Bishayee 1999; Belyakov 2005). However, it is unclear how BE impact the therapeutic efficacy of alpha particles as the underlying mechanisms remain unclear (Brady 2013; Suominen 2013; Henriksen 2002). Using a mouse tibia model of breast cancer DTC, we have recently shown experimentally that BE play an important role in the response of DTC to ²²³RaCl₂ (Leung 2019). There, we used recently developed approaches for Monte Carlo radiation track-structure simulations at the cellular level (Rajon 2011; Howell 2012; Rajon 2013) to facilitate dosimetry calculations to show that the bystander region of the marrow was at distances greater than ~ 70 μm from the bone surface where the ²²³Ra localized (Leung 2019).

In this study, we extended our dosimetric approach by modeling the dynamic proliferation of breast cancer DTC in the tibial marrow of mice treated with ²²³Ra. The goals were: 1) to determine the response of breast cancer cells and bone cells to alpha particles and gamma rays, and 2) to use these data to model the experimental growth delay data from Leung et al. (2019) for MDA-MB-231 and for MCF-7 human breast cancer cells. The direct effect (DE) of radiation on the tumor cells, as well as BE from all irradiated cells were included in our model. This model establishes the groundwork necessary for modeling responses of DTC to radiopharmaceutical therapy.

MATERIALS AND METHODS

Measurement of Tumor and Bone Cell Response to Alpha Particles and Gamma Rays In Vitro

Cell culture

MCF-7-luc-F5 (estrogen receptor positive (ER+)) and MDA-MB-231-luc-D3H1 (estrogen receptor negative (ER−), progesterone receptor negative (PR−)), human epidermal growth factor receptor 2 negative (HER2/neu−)) human breast cancer cells were the same as those we used to obtain the Leung et al. data on tumor growth delay that is being modeled in this study (Leung 2019). The cells were cultured at 37°C in Leibovitz L-15 medium (Sigma-Aldrich) supplemented with 2 mM L-glutamine (Gibco), 100 IU/mL penicillin and 100 μg/mL streptomycin (Corning), and 10% (vol/vol) fetal bovine serum (Gibco). MLO-Y4, an immortalized representative osteocyte cell line was acquired from ATCC. MC3T3-E1, a preosteoblast cell line was a gift from Dr. Christopher Fritton (co-author of this study). The MC3T3E-1 were cultured in L-15 media supplemented as described above, whereas the serum for MLO-Y4 was replaced with 5% fetal bovine serum (Sigma) and 5% bovine calf serum (BCS). Cells were passaged 2–3 times per week upon reaching 80–95% confluency for no more than 1.5 months.

Cell cultures were prepared for alpha particle irradiation using the technique described by Neti et al. (Neti 2004). Briefly, cells were seeded in Mylar-bottomed stainless-steel dishes with a circular 36-mm-diameter growing surface that consists of 1.5 μm-thick Mylar. To facilitate cell attachment, the Mylar was precoated with FNC solution comprising fibronectin and collagen (AthenaES^™), overlaid with 2 mL of growth medium and incubated at 37°C. After 30 min, the medium was aspirated, and the cells were seeded at a density of 1.7 ×10⁵ or 4.1×10⁵ cells for MLO-Y4 cells and 3.4×10⁵ or 3.9×10⁵ cells for MC3T3-E1. MDA-MB-231 cells were seeded at a density of 5.0×10⁵ cells while MCF-7 cells were seeded at a density of 7.0×10⁵ cells.

Cell cultures were prepared for gamma ray irradiation by seeding into T-25 flasks at a density of 3.5 ×10⁵ or 5.0×10⁵ cells for MLO-Y4 cells and 3.1×10⁵ or 5.0×10⁵ cells for MC3T3-E1 cells. MDA-MB-231 cells were seeded at a density 5.1 ×10⁵ cells while MCF-7 cells were seeded at a density of 5.0 ×10⁵ cells. Irradiations were carried out within 1–3 days following cell seeding.

Alpha particle irradiation

The alpha particle irradiator is the one used by Neti et al. (2004). Cells were exposed at 37°C to alpha particles emitted by a ²⁴¹Am collimated source contained in a helium filled Plexiglas box at a dose rate of 8.0 cGy/min. The source is located below the Mylar^® -bottomed dish, and the alpha particles pass through the Mylar^® growing surface at an average energy of 2.9 MeV when hitting the cells. A photographic shutter is placed on the source window facilitating accurate delivery of a pre-set radiation dose, allowing different fluence conditions. Control cells were handled similarly by placing them on a shutter with no radioactive source below. Mean absorbed doses used in experiments were 0, 0.9, 1.7, 2.5, 3.4, 4.2, and 5.0 Gy.

Gamma irradiation

A calibrated cesium-137 irradiator (JL Shepherd Mark I) was used to perform irradiations with 662 keV gamma rays. The irradiator produced a dose rate of 99.6 cGy/min when the 5X lead attenuator was used.

Clonogenic cell survival

Cell survival was assayed by assessing colony formation. Immediately following irradiation, cells were harvested by trypsinization with 0.5 mL trypsin at 0.25% concentration (Sigma). A 2.5 mL aliquot of L-15 was added to neutralize the trypsin resulting in a 3 mL cell suspension from an individual Mylar dish (alpha particle irradiation) or T-25 flask (gamma irradiation). This 3 mL volume was syringed using a 21-gauge needle 5 times to disrupt clumps. A Z Series Coulter Counter (Beckman Coulter) was used to determine the cell counts which were used in turn to calculate the concentration of cells. Subsequently, cell suspensions were serially diluted 10-fold, 100-fold, and 1000-fold. These serial dilutions were plated into T-25 flasks in triplicate. Colonies were allowed 1–2 weeks to form depending on cell line doubling time. Once colonies had formed, flasks were washed 3 times with saline, fixed with 90% ethanol, and stained with 1% crystal violet. Colonies consisting of at least 50 cells were counted and surviving fraction relative to control calculated. Data from 1–3 independent experiments were averaged for each radiation type and cell line and SigmaPlot V14 was used to least-squares fit the data with the linear quadratic (LQ) model:

$$S=e^{-\alpha D-\beta D^2},$$ (Eq. 1)

where S is the fraction of cells surviving absorbed dose D. The α and β are the linear and quadratic parameters of the dose-response relationship. The absorbed dose required to achieve 37% survival, D₃₇, was determined for each cell line and radiation type.

The traditional relative biological effectiveness (RBE) of the alpha particles compared to gamma rays was calculated at 37% survival for each cell line. RBE was calculated as follows:

$$\text{RBE}=\frac{D_{37}\left(\text{gamma rays}\right)}{D_{37}\left(\text{alpha particles}\right)}$$ (Eq. 2)

Modeling Response of Tumor Cells in Vivo to Direct Effects and Bystander Effects

The overall strategy to model tumor proliferation under the ²²³Ra treatment conditions in Leung et al. (2019) was to use the Monte Carlo simulation toolkit Geant4 (Agostinelli 2003) (version 10.1 with patch 02) to compute individual cell absorbed doses within a three-dimensional (3D) model of a mouse tibia and to use this information to construct the proliferation curve. A solution would have been to simulate the ²²³Ra decays one by one and re-evaluate the number and position of the cells after each decay by assessing the duplication or killing of each individual cell. Such solution would have required an unacceptable amount of computing time. Instead, we dissociated the Monte Carlo transport from the construction of the proliferation curve. We first created a series of static Monte Carlo models with different tumor sizes, covering the range we observed in Leung et al. (2019) and measured microscopically in this work. Then, a dynamic proliferation scheme of the tumor was developed using data interpolated from the results of the static models as the tumor size varies over time.

Constructing a model of a section of a mouse tibia

A series of micro-Computed Tomography (μCT) images of a mouse tibia were acquired to produce a 3D volume with 5.0 μm voxel size (Bruker Skyscan 1172). A 3D rendering compiled from three thousand transverse images is shown in Figure 1(A). The high resolution allows delineating the bone trabeculae (Figure 1(B)). Only the region of interest (ROI) delimited by the two green lines on Figure 1(A) was modeled because only the proximal end of the mouse bone received tumor cells during in-vivo inoculations (Leung 2019).

Figure 1.

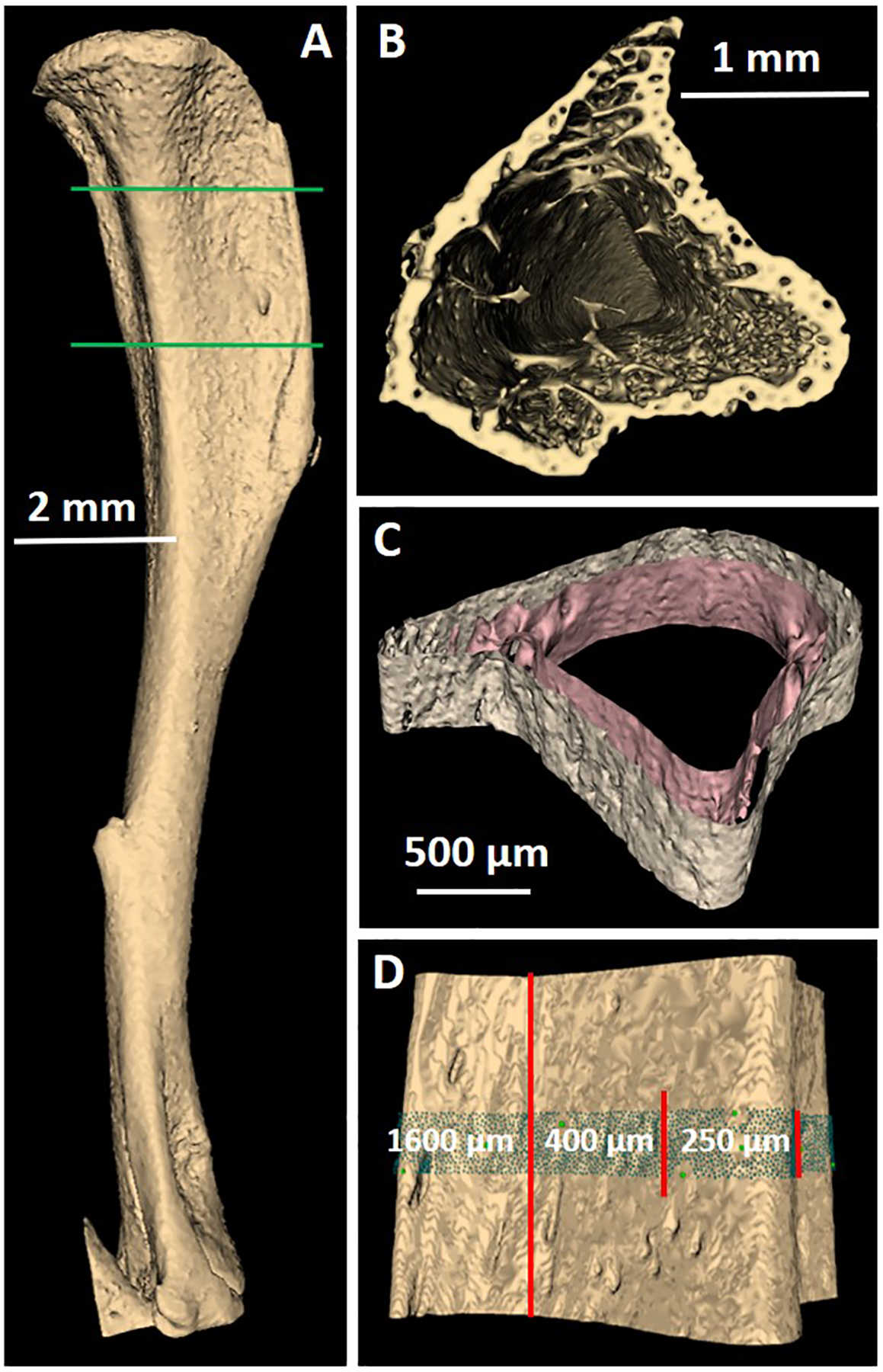
Model of a mouse tibia constructed from a series of μCT images. A) 3D rendering of the tibia. B) Cut showing the trabeculae near the proximal end. C) Section of the tibia showing the periosteal (outer) and endosteal (inner) surfaces. D) 3D rendering of the periosteal surface showing the 250-μm central region that contains the cells, the 400-μm radioactive region, and the 1600-μm ROI (between the green lines on A).

The ROI was then segmented to produce two surfaces, the periosteum surface between the periosteum and cortical bone and the endosteum surface between the endosteum and cortical bone. The two surfaces separate the ROI into three regions: medullary cavity (including endosteum cells), cortical bone, and remainder tissue (including periosteum cells). The best μCT-number threshold value for segmenting the regions, determined by using the technique described by Rajon et al. (2006), was 130 for both surfaces on an 8-bit-depth image dataset. One requirement for particle transport is that all surfaces must be closed. For that reason, both the proximal and distal ends of the ROI were padded with extra bone voxels before segmentation. Another requirement is that all surfaces must not intersect with one another. Because the segmentation was unable to differentiate between blood, marrow, and soft tissues, the voxels that belonged to blood vessels traveling through the cortical bone were changed to bone tissue to disconnect the two surfaces. These voxel changes will have very little effect on the results as they represent a small fraction of the cortical bone region. After segmentation, the ROI was contoured to obtain both surfaces (see Figure 1(C)). The surfaces were then converted into tessellated solids suitable for transport by Geant4.

Incorporating cell nuclei into the model

Eight groups of cells were introduced into the bone model (see Table 1). For computational optimization, only the central 250-μm region of the ROI, measured along the longitudinal axis of the tibia, was filled with cells. To ensure that all cells satisfy particle equilibrium from the alpha radiation, the central 400-μm region of the ROI was similarly loaded with ²²³Ra. To ensure that any point within the medullary cavity had its closest endosteum surface in the transverse plane of the bone, the artificial closure of the endosteum and periosteum surfaces were extended longitudinally 600 μm on both sides of the radioactive region. The total length of the ROI was thus 1600 μm. The different regions are shown in Figure 1(D).

Table 1.

Characteristics of the types of cell nuclei modeled within the ROI. When the number of nuclei depends on the static model, only the range is shown.

Cell type	Compartment	Number of nuclei	Radius of nucleus (μm)	Minimum radial extent (μm)
Periosteal Osteoclast	Surrounding tissue	15	12.0±1.2	45.0
Periosteal Osteoblast	Surrounding tissue	3,954	4.0±0.4	8.0
Osteocyte	Cortical bone	9,800	3.0±0.3	12.0
Endosteal Osteoclast	Medullary cavity	12	12.0±1.2	45.0
Endosteal Osteoblast	Medullary cavity	2,866	4.0±0.4	8.0
Tumor cell	Medullary cavity	MDA: 1,000 → 51,186 MCF: 400 → 6,163	MDA: 4.4±1.0 MCF: 6.1±1.4	MDA: 5.8 MCF: 7.5
Yellow fat Cell	Medullary cavity	MDA: 22 → 1 MCF: 22 → 18	8.0±0.8	35.0
Red marrow Cell	Medullary cavity	MDA: 83,972 → 38,583 MCF: 84,272 →75,039	4.0±0.4	6.0

Cells were modeled as follows. The cell nuclei were taken as spheres. The cytoplasm was not modeled explicitly, rather nuclei were positioned to maintain a separation between their centers of at least 90% of the measured diameter (see below) of the cells to account for cell compaction. Importantly, cell diameter does not change due to fixation (Fox 1985). A computer program was created to add the cells into the model by randomly selecting a position and rejecting the cell if it failed the separation distance requirement. The geometrical characteristics of the cells (Table 1) were based on a compilation from descriptions by various authors (Travlos 2006; Hiddemann 1982; Florencio-Silva 2015; Brown 2012; Gruber 1986; Lundberg 2007; Sandkühler 1956; Secondini 2011; Yang 2007) and from our measurements of tumor cells labeled with CellTracker^™ Green (Thermo Fisher). For tumor cell measurements, transverse sections of tibiae, prepared as described previously (Leung 2019), were stained with DAPI and imaged with a Nikon A1R confocal microscope with 60X oil objective. Tumor cell nuclear diameters were quantified using ImageJ and published measurement methods (Mouton 2002). Values, given in Table 1, were averaged from 200 nuclei distributed across 3 animals for each of the two cell types. The different cells were added in the following order: 1) osteoclasts outside the periosteal surface and inside the endosteal surface to cover 10% of both surfaces; 2) osteoblasts covering the remaining 90% of both surfaces; 3) osteocytes within the cortical bone region; 4) tumor cells as a cluster within the medullary cavity; 5) yellow fat cells within the medullary cavity until they fill 5% of the volume (95% cellularity); 6) red marrow cells filling the rest of the medullary cavity with possible inclusions between tumor cells.

While the number and positions of osteoclasts, osteoblasts, and osteocytes were kept the same for all static models, tumor, yellow fat, and red marrow cells depended on the size of the tumor. A total of 16 static models of different sizes spanning from smallest to largest were created for both MDA-MB-231 and MCF-7 cells. The tumor was modeled as a 250-μm-long cylinder with its axis parallel to the bone shaft. Because of the importance of being within or outside the bystander region, the distance of the tumor axis to the endosteal bone surface was measured by estimating the midpoint of the tumor from the confocal microscopic images using ImageJ. The midpoint was determined by traversing the CellTracker^™ Green-labeled tumor with 6 distinct diameters and finding the closest point to their intersection. This length of the closest point to the inner endosteal surface of the bone was averaged from 3 different lengths. This distance represented the distance of the tumor axis to the endosteal bone surface. Seven different animals inoculated with either MDA-MB-231 or MCF-7 cells were used for this calculation. Eight distinct sections from each animal were used to calculate an average midpoint for a given animal. The values found were 84 ± 29 μm for MDA-MB-231 and 100 ± 63 μm for MCF-7 cells. Each static tumor size was set by varying the diameter of the cylinder while keeping the tumor within the limit of the medullary cavity. The number of cells within each static tumor was then determined by using a cell number density computed by deriving the estimated tumor volume and tumor cell number from the same 8 sections from each of the 7 animals for each cell line. ImageJ and published stereological models were used to derive the estimated tumor volume. First, a uniformly spaced point grid was overlayed onto each transverse tibial section. The number of points falling within the tumor area was noted and multiplied by the area represented by each point, 2000 μm², and the thickness of each section, 5 μm. This product was multiplied by the sampling interval for a given animal resulting in the estimated volume of the interval. This process was repeated for each interval and then summed to obtain the tumor volume. An average tumor volume value for MDA-MB-231 and MCF-7 cells was calculated similarly to the distance between the tumor axis and the endosteal bone surface. The number of tumor cells in each of the 8 sections were also counted individually before being summed for each animal. The average tumor volume and cell number was 4.27 × 10⁶ ± 4.16 × 10⁶ μm³ and 822 ± 353 cells for MDA-MB-231, and 2.73 × 10⁶ ± 3.38×10⁶ μm³ and 431 ± 274 cells for MCF-7. From these values we computed the following densities: 1.92 × 10⁵ ± 2.05 × 10⁵ cells/mm³ for MDA-MB-231 and 1.58 × 10⁵ ± 2.19 × 10⁵ cells/mm³ for MCF-7. The characteristics of the tumors for the static models are reported in Supplemental Table 1. The locations of the different types of cells for two MCF-7 static models are shown in Figures 2(A) and 2(B).

Figure 2.

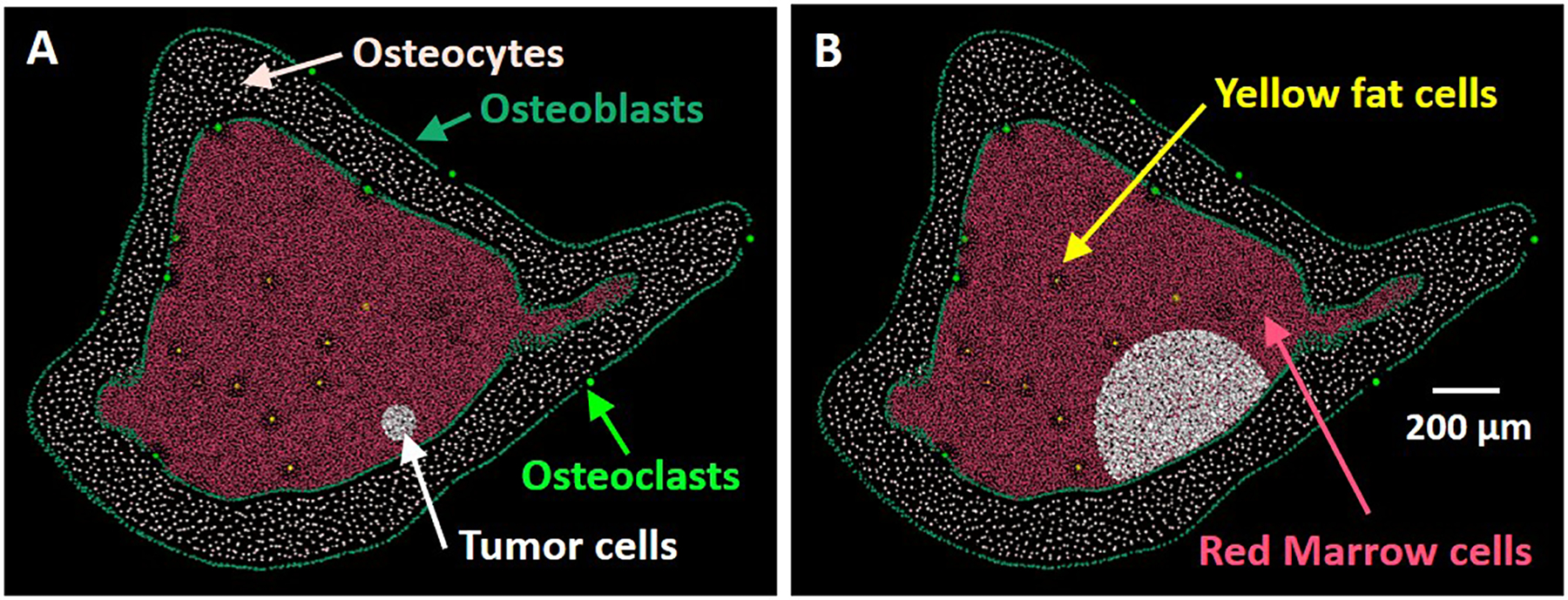
Rendering of the cell nuclei along the central cross section of the ROI for two MCF-7 static models. Number of tumor cells are A): 400 (model 1) and B): 6,163 (model 16).

Dynamic proliferation scheme

To build a proliferation curve, we first divided the entire radioactive decay of ²²³Ra into N = 40 time-steps. Each time-step is characterized by a time interval and a number of decays, with the last time-step extending until the last ²²³Ra decay (i.e. infinity). At the end of each time-step, we interpolated the surviving fraction S caused by direct irradiation and the surviving fraction B caused by radiation-induced BE from the two static models for which the tumor size is closest to the tumor size at the beginning of the time-step. The tumor size at the end of the time-step was then computed with the iterative proliferation equation:

$$C_j=C_{j-1}*G_j*S_j*B_j,$$ (Eq. 3)

where j is the time-step id, C_j the number of tumor cells at the end of time-step j, G_j the natural growth fraction of the unirradiated tumor during time-step j, and S_j and B_j the two fractions just discussed. How the three parameters G_j, S_j, and B_j were computed will be explained later in this text. The initial number of cells at day 0, C₀, was extrapolated from the day 1 values (derived from measurements as described above) using the natural growth equation (Eq. 5) defined in the next section, and finally adjusted to the 250-μm limitation of our bone model. We found C₀ = 2,966 for MDA-MB-231 and 1,283 for MCF-7.

Each of the N time-steps was set a different time interval, chosen to compensate for the exponential decline of the activity over time. A constant number of decays per time-step was acceptable at the beginning of the curve, but near the end, a reduction in the number of decays was needed to avoid long time intervals that would affect the time resolution needed for the natural growth of the cells. A simple function that was found to be acceptable is:

$$\widetilde{A_j}=\tilde{A}\text{sin}\frac{\pi j}{2N},$$ (Eq. 4)

where $\widetilde{A_j}$ and $\tilde{A}$ are the time integrated activity at the end of time-step j and for complete decay, respectively. The intervals were computed based on an effective clearance half-time of 9.93 days. The numbers of decays were computed from an initial activity of 2.3 Bq within our irradiation region. Both the effective half-time and the initial activity were based on the activity per gram in the diaphysis (i.e. sans epiphyses) of the tibia (Leung 2019). Supplemental Table 2 lists the characteristics of each time-step.

Computing the natural growth fractions G_j

The unirradiated proliferation curve from Leung et al. (2019) (see Figures 3–5) was used to derive a semi-empirical natural growth model made of two exponential functions that account for an early shrinkage of the tumor and a later growth. At time t, the size n(t) of the unirradiated tumor is thus given by:

$$n\left(t\right)=n_0\left(f{e}^{-dt}+\left(1-f\right)e^{gt}\right),$$ (Eq. 5)

where n₀ is the initial tumor size at day 0, and f, d, and g are three parameters that are adjusted to fit the experimental data. The natural growth fraction G_j during time-step j is simply the ratio between the values of (Eq. 5) at the end and at the beginning of time-step j. Because our bone model only allows the tumor size to vary along the radius of the tumor (i.e. in two dimensions), the growth fraction G_j obtained from (Eq. 5) was raised to the power 2/3 before it was used in (Eq. 3). Then, the C_j values of the 40 time-steps were raised to the power 3/2 (i.e. back to three dimensions) before they could be compared with the experimental data from Leung et al. (2019).

Figure 3.

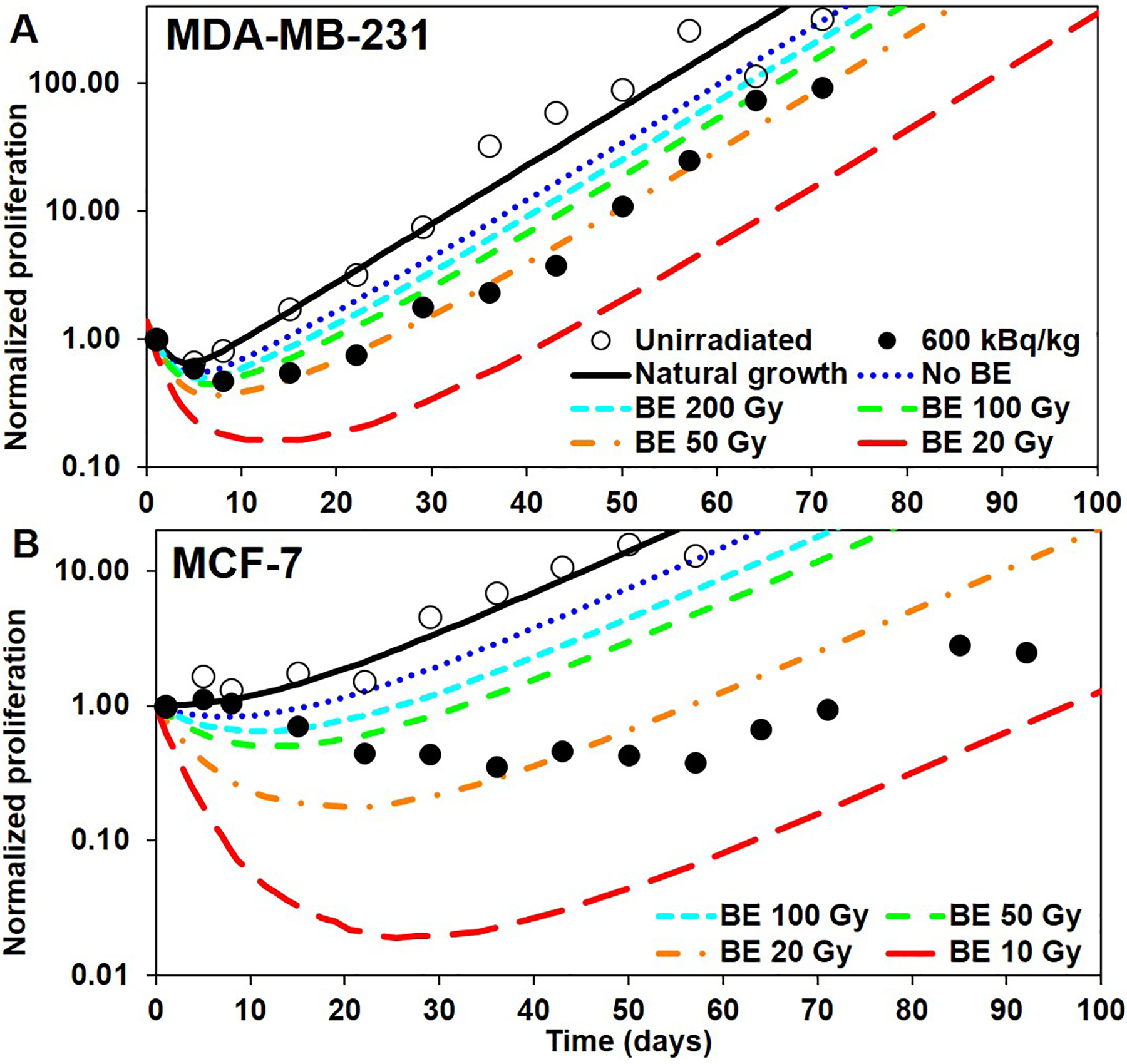
Tumor proliferation curves constructed by applying the direct effects (DE) and bystander effects (BE) at the end of each time step: A) MDA-MB-231 and B) MCF-7. Open and closed circles: unirradiated controls and 600 kBq/kg experimental data, respectively, from Leung et al. (2019). Black curve: best fit of the unirradiated experimental data, using (Eq. 3). Blue curve: only DE, no BE considered. Colored curves from cyan to red: include DE and BE with varying B₃₇ (values shown in legend).

Figure 5.

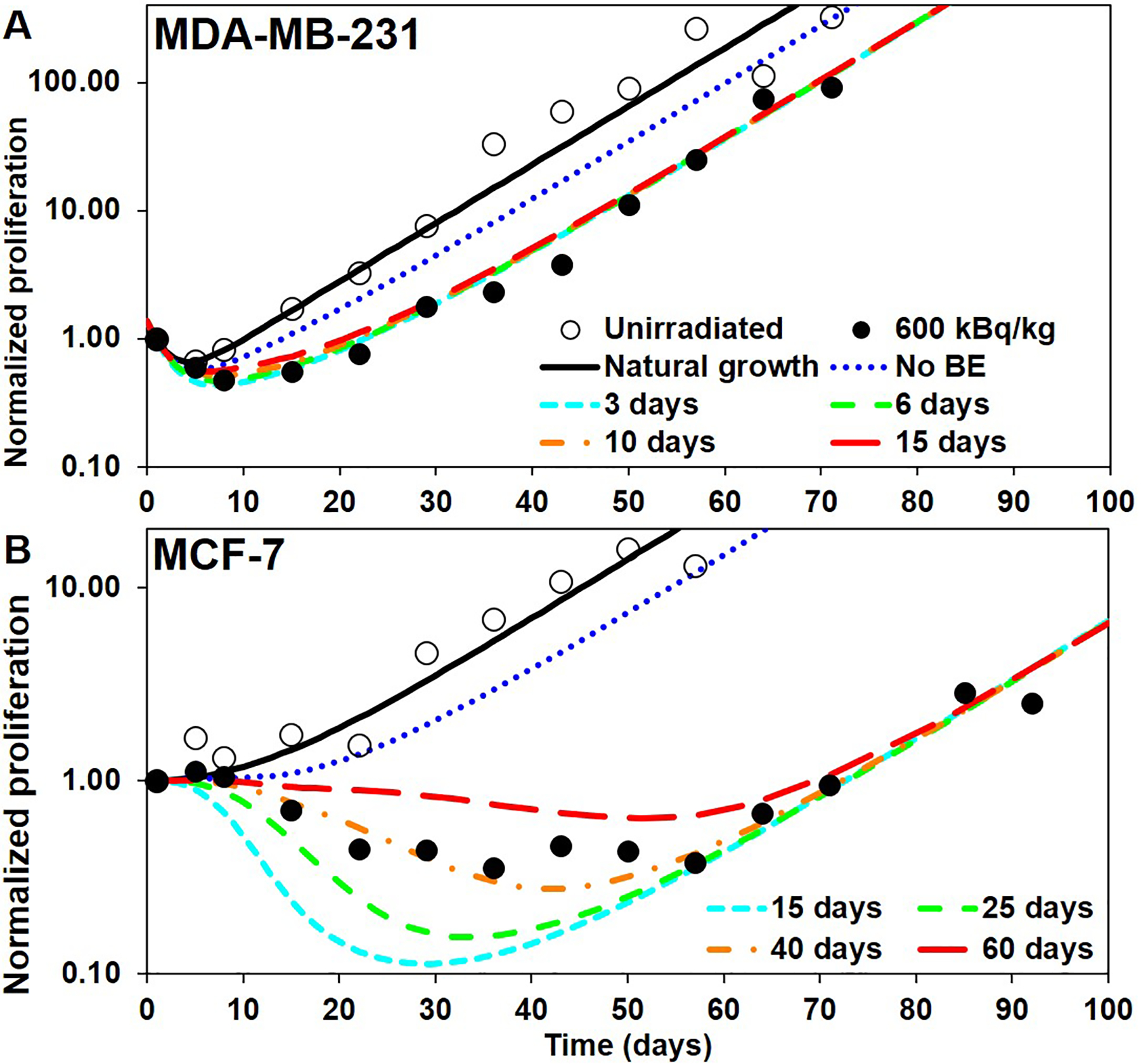
Tumor proliferation curves constructed by applying a temporal distribution on both direct effects (DE) and bystander effects (BE): A) MDA-MB-231 (with T_S = 6 d) and B) MCF-7 (with T_S = 15 d). Open and closed circles: unirradiated controls and 600 kBq/kg experimental data, respectively, from Leung et al. (2019). Blue curves: built with no BE (same as curve with T_S = 3 d (MDA-MB-231) and T_S = 15 d (MCF-7) of Figure 4). Colored curves from cyan to red: built with B₃₇ = 60 Gy (MDA-MB-231) and B₃₇ = 15 Gy (MCF-7) and an increasing T_s (values shown in legend).

Monte Carlo transport simulations

Geant4 was used to assess the dosimetric data within the 16 static models for both types of cells. For each simulation, the number of ²²³Ra decays for the 40 time-steps (see Supplemental Table 2) were simulated including all radiations (i.e. alpha, beta, Auger electrons, X- and γ-rays) emitted by ²²³Ra and its daughters (~27.5 MeV per decay), using the G4RadioactiveDecayPhysics module from Geant4. Because redistribution of the daughters is < 1% (Henriksen 2003), daughter decays were simulated at the ²²³Ra parent decay sites. Decays were simulated within the 400-μm central region of the ROI, as explained earlier. The radial distribution was determined as follows: Based on activity measurements reported by Leung et al. (2019), 99.2% of decays were in the cortical bone and only 0.8% in the marrow cavity. Exponential activity distributions based on activity quantitation measurements with an alpha camera and HpGe detector (see ref. (Leung 2019)) were used to assign the activity concentration as one moves radially away from the bone surfaces. A half-distance of 75 μm was determined within the bone tissue as one moves into the bone from either the endosteal or periosteal surfaces, and 37 μm within the marrow tissue as one moves away from the endosteal surface into the marrow.

The physics used during transport was provided by the G4EmLowEPPhysics module from Geant4. The ICRP tissue composition for cortical bone and soft tissue were used for the bone and marrow compartments, respectively (ICRP 1994). Geant4 parameters used during this study are reported in Supplemental Table 3. At the end of each time-step, the individual cell absorbed doses received during the time-step were computed.

Surviving fractions S_j caused by direct irradiation

For each time-step j and for each static model i, a surviving fraction S_j,i was computed as follows. Each individual tumor cell is determined to die or to survive based on its probability p of surviving a radiation insult, calculated as:

$$p=e^{-\frac{D_{\text{alpha}}}{D_{37,\text{alpha}}}}{e}^{-\frac{D_{\text{beta}}}{D_{37,\text{beta}}}}.$$ (Eq. 6)

In (Eq. 6), D_alpha and D_beta are the absorbed doses received by the cell during time-step j of the Monte Carlo transport simulation from alpha particles and beta particles, respectively. As described above, D_37,alpha and D_37,beta are the respective absorbed doses that achieve 37% survival for a particular type of cell. The probability function in Eq. 6 is a reasonable approximation given that the linear term in the LQ model drives the response to alpha particles at all absorbed doses (Table 2), and the D_37,beta is a good approximation of the response to beta particles at the relatively low absorbed doses from beta particles encountered in this work. A random number is then generated and compared with the probability p to determine whether the cell survives or dies (Vaziri 2014; Rajon 2011). The surviving fraction S_j,i is determined from the number of tumor cells that have survived this process. The surviving fraction S_j was then interpolated from the S_j,i based on the tumor size at the beginning of time-step j.

Table 2.

Mean lethal absorbed doses, RBE, and linear quadratic fit parameters derived from cell survival curves for breast cancer and bone cells.

Cell line	Cell type	Radiation type	D37 (Gy)	RBE*	α** (Gy−1)	β** (Gy−2)
MDA-MB-231	Triple neg human breast cancer	Alpha	0.73	3.0	1.4±0.26	(2.3±0.08)×10−17
MDA-MB-231	Triple neg human breast cancer	Gamma	2.2		0.42±0.092	0.018±0.0094
MCF-7	ER+, PR+, HER2+ human breast cancer	Alpha	0.77	2.9	1.3±0.50	(6.1±0.19)×10−17
MCF-7	ER+, PR+, HER2+ human breast cancer	Gamma	2.2		0.38±0.077	0.04±0.0088
MLO-Y4	Osteocyte-like cell from mice	Alpha	0.71	4.9	1.4±0.24	0.014±0.070
MLO-Y4	Osteocyte-like cell from mice	Gamma	3.5		0.19±0.043	0.025±0.0042
MC3T3-E1	Preosteoblast cell from mice	Alpha	0.58	4.3	1.7±0.25	(2.3±0.078)×10−17
MC3T3-E1	Preosteoblast cell from mice	Gamma	2.5		0.37±0.048	0.010±0.0047

^*RBE = relative biological effectiveness compared to 662 keV gamma rays.

^**Values presented include standard error of estimate

Surviving fractions B_j caused by radiation-induced bystander effect

For each time-step j and for each static model i, a surviving fraction due to radiation-induced BE B_j,i was computed as follows. We first defined B_37,c as being the mean absorbed dose received by a particular type of cell c (i.e. osteocytes, osteoclasts, osteoblasts, red marrow cells, fat cells, tumor cells) that would cause 37% survival of the tumor cells because of bystander mechanisms. Each type of cell can have a different B_37,c value, based on its mean distance to the tumor, its capability to send signals to the tumor, or other unknown mechanism(s). Then, B_j,i is computed as the product:

$$B_{j,i}=\prod _c{e}^{-\frac{{\overline{D}}_{c,j,i}}{B_{37,c}}},$$ (Eq. 7)

where ${\overline{D}}_{c,j,i}$ is the mean absorbed dose received by all cells of type c, during time-step j, and within static model i. The surviving fraction B_j (Eq. 3) caused by BE is then interpolated from the B_j,i values based on the tumor size at the beginning of time-step j.

Building the proliferation curves

In a first attempt to build a proliferation curve, we assumed: 1) that the direct radiation effects S and the bystander effects B computed from absorbed doses received during time-step j were applied to the tumor at the end of time-step j, and 2) that all types of cells were assigned the same B_37,c value, which only depends on the type of tumor being targeted. The proliferation scheme is thus only dependent on one unknown parameter B₃₇. We selected several values for B₃₇ from infinity (no BE) down to a value that delays the proliferation beyond what is seen on the experimental data from Leung et al. (2019). Then, we interpolated the B₃₇ value that provided a proliferation curve that best fitted the data.

As will be shown from the results of this first attempt, applying the effect entirely at the end of the time-step does not reproduce the experimental tumor growth curves adequately. While the end of the curve can be easily fitted, providing a good estimation for the overall (late) growth of the tumor, the early part of the curve suggested that this first attempt was too aggressive during the early stage of the proliferation. Therefore, we tried to delay the early effect by distributing the overall effect of a time-step j during several subsequent time-steps (instead of just at the end of time-step j), based on a distribution function f(t) that shapes the effect over a period of time T. We used a sine squared function between 0 and π, because it has many advantages (i.e. over a Gaussian function): a known primitive function, no infinite tails, and only one parameter T. The effect distribution was thus:

$$f\left(t\right)=\frac{2}{T}si{n}^2\left(\frac{\pi }{T}t\right)\text{ between }t=0\text{ and }t=T,$$ (Eq. 8)

where t = 0 at the beginning of each time-step j. Such a distribution has mean $\mu =\frac{T}{2}$, standard deviation $\sigma =T\sqrt{\frac{1}{12}-\frac{1}{2{\pi }^2}}$, and is normalized. Both DE and BE have their own distribution period: T_S and T_B respectively. The parameter T is thus a characterization of how long the growth of the tumor remains affected by the amount of radiation received during a time-step of our model.

Because the distribution of the effect of time-step j overlaps with several subsequent time-steps, the iterative proliferation equation (Eq. 3) was modified to reflect the dependency of time-step j on the effect generated during several previous time-steps, including time-step j itself:

$$C_j=C_{j-1}*G_j*\prod _{k=1}^j{S}_k{}^{f_{S,k\to j}}*\prod _{k=1}^j{B}_k{}^{f_{B,k\to j}}.$$ (Eq. 9)

In (Eq. 9), f_S,k→j and f_B,k→j are the fractions of effect generated during time-step k and applied during time-step j, for DE and BE, respectively. They are computed by integrating (Eq. 6) over the time interval corresponding to time-step j.

This new scheme has three parameters that can be adjusted: B₃₇, T_S, and T_B. We kept the value of B₃₇ that gave the best result during the first attempt as it provided a good estimate of the late part of the experimental proliferation curve. We then investigated T_S alone by assuming no BE. Trying different values for T_S allowed selecting the value that best reproduced the very start of the experimental proliferation curve. Finally, we investigated T_S by adding BE. Once again, trying different values for T_B allowed selecting the value that best reproduced the intermediate part of the experimental proliferation curve.

RESULTS AND DISCUSSION

Response of Tumor and Bone Cells to Alpha Particles and Gamma Rays In Vitro

The response of the four cell lines to alpha and gamma rays is shown in Figure 6. The LQ parameters for the least squares fits to the cell survival data are given in Table 2 along with the D₃₇ values. As expected, all cell lines were more sensitive to alpha particles than gamma rays. Both breast cancer cell lines had a D_37,gamma value of 2.2 Gy following gamma ray irradiation. The D_37,gamma values for MDA-MB-231 and MCF-7 are similar to the 2.2 Gy, ~2.5 Gy, and ~2.5 Gy values reported by Svetličič et al., Duangmano et al., and Sun et al. respectively (Svetličič 2020; Duangmano 2012; Sun 2015). Following alpha particle irradiation, our D_37,alpha value was 0.73 Gy and 0.77 Gy for MDA-MB-231 and MCF-7 cells, respectively. These values are somewhat higher than the ~0.25 Gy and ~0.6 Gy observed by Svetličič et al. (Svetličič 2020). Our RBE₃₇ for alpha particles was 3.0 for MDA-MB-231 and 2.9 for MCF-7.

Figure 6.

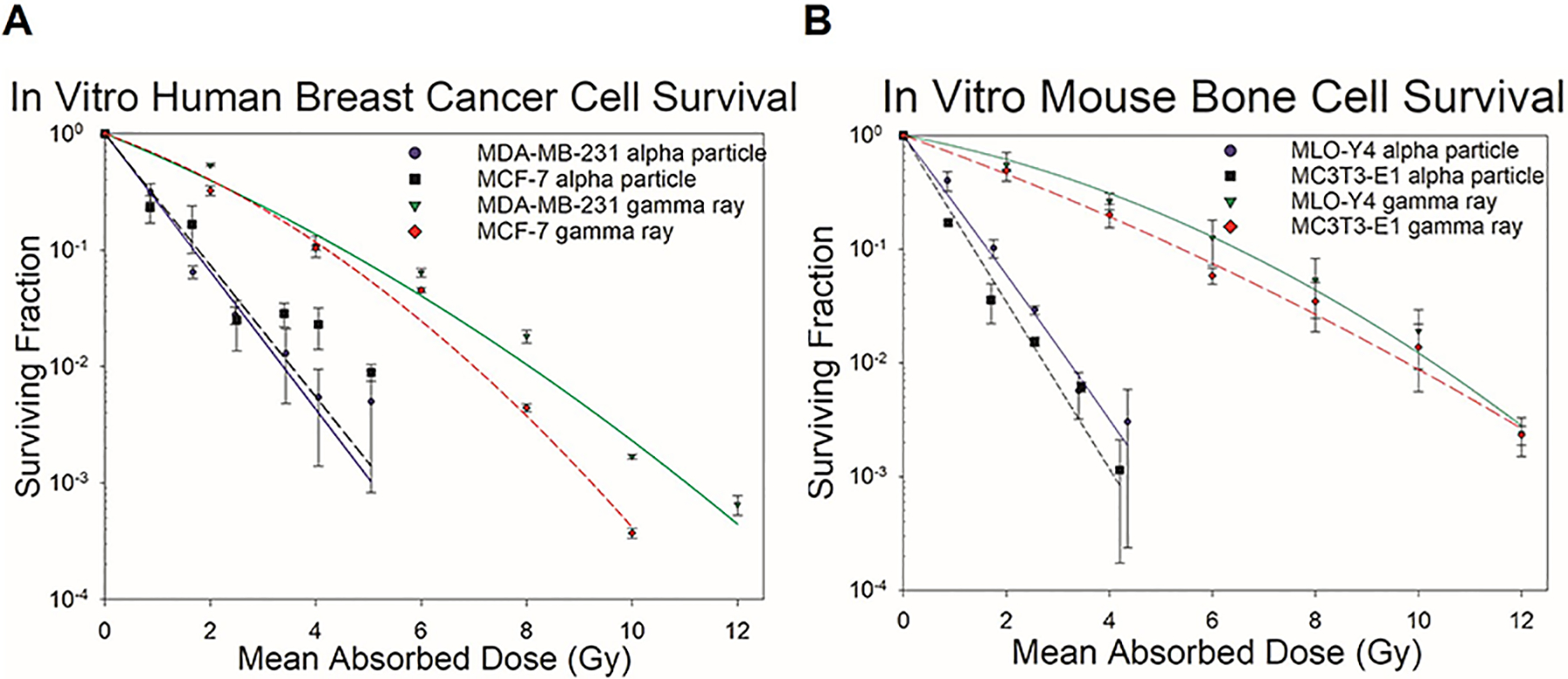
Clonogenic survival of alpha- or gamma-irradiated MDA-MB-231 and MCF-7 human breast cancer cells and MLO-Y4 and MC3T3-E1 mouse bone cells exposed to alpha particles or gamma rays. MDA-MB-231 cells displayed a 37% surviving fraction value of 0.73 Gy following alpha particle irradiation and 2.2 Gy following gamma ray irradiation. MCF-7 cells displayed a 37% surviving fraction value of 0.77 Gy following alpha particle irradiation and 2.2 Gy following gamma ray irradiation. Error bars corresponded to standard error of the mean. Surviving fraction is plotted on a log scale. All curves represent 1–3 experiments and are fits of the data to the LQ model. MLO-Y4 cells displayed a 37% surviving fraction value of 0.71 Gy following alpha particle irradiation and 3.5 Gy following gamma ray irradiation. MC3T3-E1 cells displayed a 37% surviving fraction value of 0.58 Gy following alpha particle irradiation and 2.5 Gy following gamma ray irradiation. Error bars corresponded to standard error of the mean while surviving fraction is plotted on a log scale. All curves represent 2–3 experiments and are fitted for the LQ model.

The D_37,gamma was 3.5 Gy for MLO-Y4 cells and 2.5 Gy for MC3T3-E1 cells, whereas the D_37,alpha was 0.71 Gy and 0.58 Gy, respectively. The D_37,gamma value for MC3T3-E1 cells was similar to the value reported by Gevorgyan et al. (2008). Our RBE₃₇ values for alpha particles were 4.9 for MLO-Y4 and 4.3 for MC3T3-E1. We were unable to find similar dose response data for MLO-Y4 cells in the literature. Our results, summarized in Table 2, indicate that the RBE values are higher for the bone cells thans the tumor cells.

These cell survival results are used for the modeling conducted with Eq. 6. As given in Table 2, the quadratic term of the LQ model is insignificant for alpha irradiation (except for the MLO-Y4 cells), thereby justifying the use of the linear term only in our simulation study. The D_37,beta were taken to be the same as D_37,gamma in view of the low-LET nature of the two radiation types. We recognize that these data were obtained for acute irradiation in vitro, while the cells in the mouse tibia were irradiated chronically by the radiations emitted by ²²³Ra. Given that responses to alpha particle irradiation generally do not have a significant dose-rate effect, and that the absorbed doses to the tumor cells from the beta particles are very small in our in vivo mouse tibia model (< 0.2 Gy, see Table 1 in Leung et al. (2019)), these assumptions are reasonable.

Natural growth curves

The parameters for the natural growth equation (Eq. 5) were adjusted to fit the experimental data (reproduced as “unirradiated” data on Figures 3–5). The following values were found: f = 75%, d = 0.5 d⁻¹, and g = 0.105 d⁻¹ for MDA-MB-231 and f = 60%, d = 0.05 d⁻¹, and g = 0.071 d⁻¹ for MCF-7. The resulting curves are the “Natural Growth”, black solid curves of Figures 3–5.

Proliferation curves when the effect is applied at the end of the time-steps

When applying DE and BE at the end of the time-step during which the irradiation has occurred, the proliferation scheme produces the five colored, dashed curves of Figures 3(A) and 3(B). The blue (dotted) curves are for B₃₇ = ∞ (i.e. no BE), thereby corresponding to the effect of direct irradiation (DE) only. The other 4 curves from cyan to red (small-dashed to large dashed) are for decreasing values of B₃₇ (i.e. increasing strength of BE). All curves are to be compared with the 600 kBq/kg experimental data points in Leung et al. (2019).

For both types of cells, the “No BE”, blue (dotted) curves show that 1) the killing effect is too strong at the beginning of the curve, and 2) DE alone does not produce enough delay before the tumor starts growing again after most of the ²²³Ra has decayed. The latter point is particularly noticeable for MCF-7 which appears to be subjected to a stronger BE than MDA-MB-231. The same finding was observed from in vitro studies with these two cell lines (Akudugu 2012). When BE is added to the scheme, corresponding to the curves from cyan to red (small-dashed to large-dashed), it provides an additional delay to the tumor regrowth, whereas the end of the curves remains parallel to the “Natural growth” curve as most of the ²²³Ra has decayed. Interpolating between the curves of Figure 3 allows selecting the value of B₃₇ that provides a delay matching the experimental data. We found that 60 Gy and 15 Gy were suitable values of B₃₇ for MDA-MB-231 and MCF-7, respectively. Nevertheless, two discrepancies remain when compared with experimental data: 1) the sharp killing effect of the beginning of the “No BE” curve has been amplified by the additional BE, and 2) the nadir of the curve still occurs too early (mainly for MCF-7).

Proliferation curves with distributed direct effect and no bystander effect

One solution to bring the nadir of the curve closer to the experimental data was to delay the killing by distributing both DE and BE over time, as described earlier. We first ignored BE to assess an optimal value for T_S. The results are shown in Figures 4(A) and 4(B). The blue (dotted) curves correspond to T_S = 0 (no distribution) and are the same as the blue (dotted) curves of Figures 3(A) and 3(B). The other curves, from cyan to red (small-dashed to large-dashed) have an increasing value of T_S.

Figure 4.

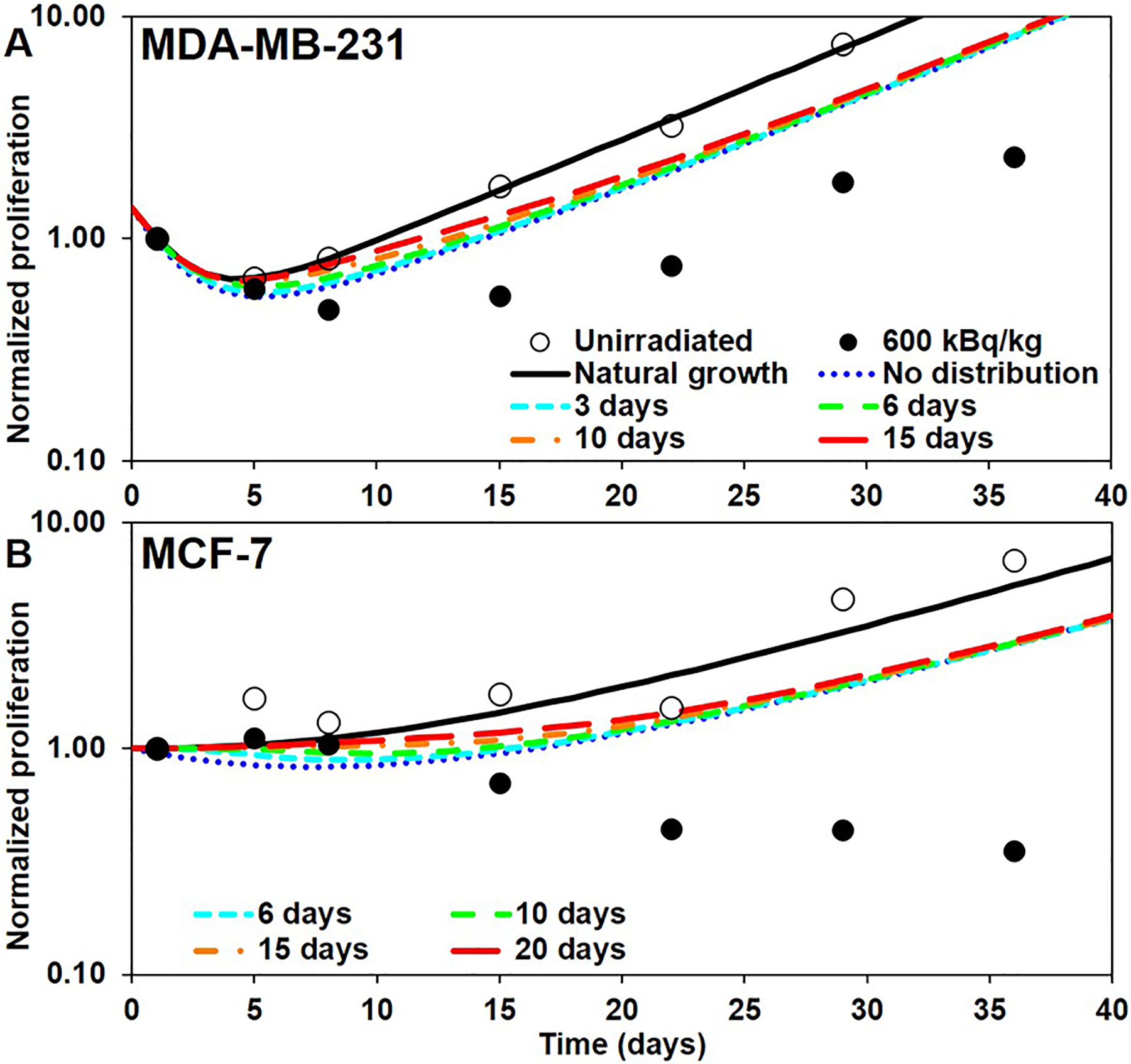
Tumor proliferation curves constructed by applying a temporal distribution of direct effects (DE) and without considering bystander effects (BE): A) MDA-MB-231 and B) MCF-7. Open and closed circles: unirradiated controls and 600 kBq/kg experimental data, respectively, from Leung et al. (2019). Blue curve: built with no distribution of DE over time (same as blue curve of Figure 3). Colored curves from cyan to red: built with an increasing T_s (values shown in legend). Only the start of the curves is shown for clarity.

Distributing the effect over time helps eliminate the sharp initial drop of the curve and matches the early time points of the experimental data. One interesting finding is that distributing the effect over time does not have much effect on the end of the curve: all colored (dashed) curves in Figures 4(A) and 4(B) converge to the “No distribution” curve. This was somewhat expected because of the normalization of (Eq. 8). The slight shift of the end of the curve is due to the fact that the values of S_j are interpolated between different static models, as the tumor at the beginning of each time-step has a different size depending on the importance of the effect applied before the step.

The values of T_S that best approximate the beginning of the experimental data were found to be 3 days and 15 days for MDA-MB-231 and MCF-7, respectively. This corresponds to spreading the effect over a time distribution with mean μ_S = 1.50 days and standard deviation σ_S = 0.54 days for MDA-MB-231 and μ_S = 7.50 days and σ_S = 2.71 days for MCF-7. These values were left unchanged when adding BE to the model.

Proliferation curves with distributed direct effect and bystander effect

When adding BE and varying the value of T_B, the resulting proliferation curves are shown in Figures 5(A) and 5(B). The blue (dotted) curves are the same as the curves of Figure 4 with the chosen values for T_S and no BE. The other curves, from cyan to red (small-dashed to large-dashed) have an increasing value of T_B.

For MDA-MB-231, distributing BE has little effect because, as we already indicated, DE is much stronger than BE. But for MCF-7, the distribution of effect on both DE and BE produces an important shift of the re-growth of the tumor that allows matching the experimental curves by selecting an appropriate value for T_B. From Figure 5, we found T_B = 6 d for MDA-MB-231 and T_B = 40 d for MCF-7 to be the best values. This corresponds to delaying the effect over a time distribution with mean μ_B = 3.00 days and standard deviation σ_B = 1.09 days for MDA-MB-231 and μ_B = 20.00 days and σ_B = 7.23 days for MCF-7. The final model is shown on Figures 7(A) and 6(B). The larger values of T_B compared to T_S for both types of tumor cells suggests that there is a delay between irradiation of tissues and the BE that they generate. Importantly, the model indicates that direct effects play little role in the initial drop in tumor volume and can be explained largely by radiation-induced bystander effects.

Figure 7.

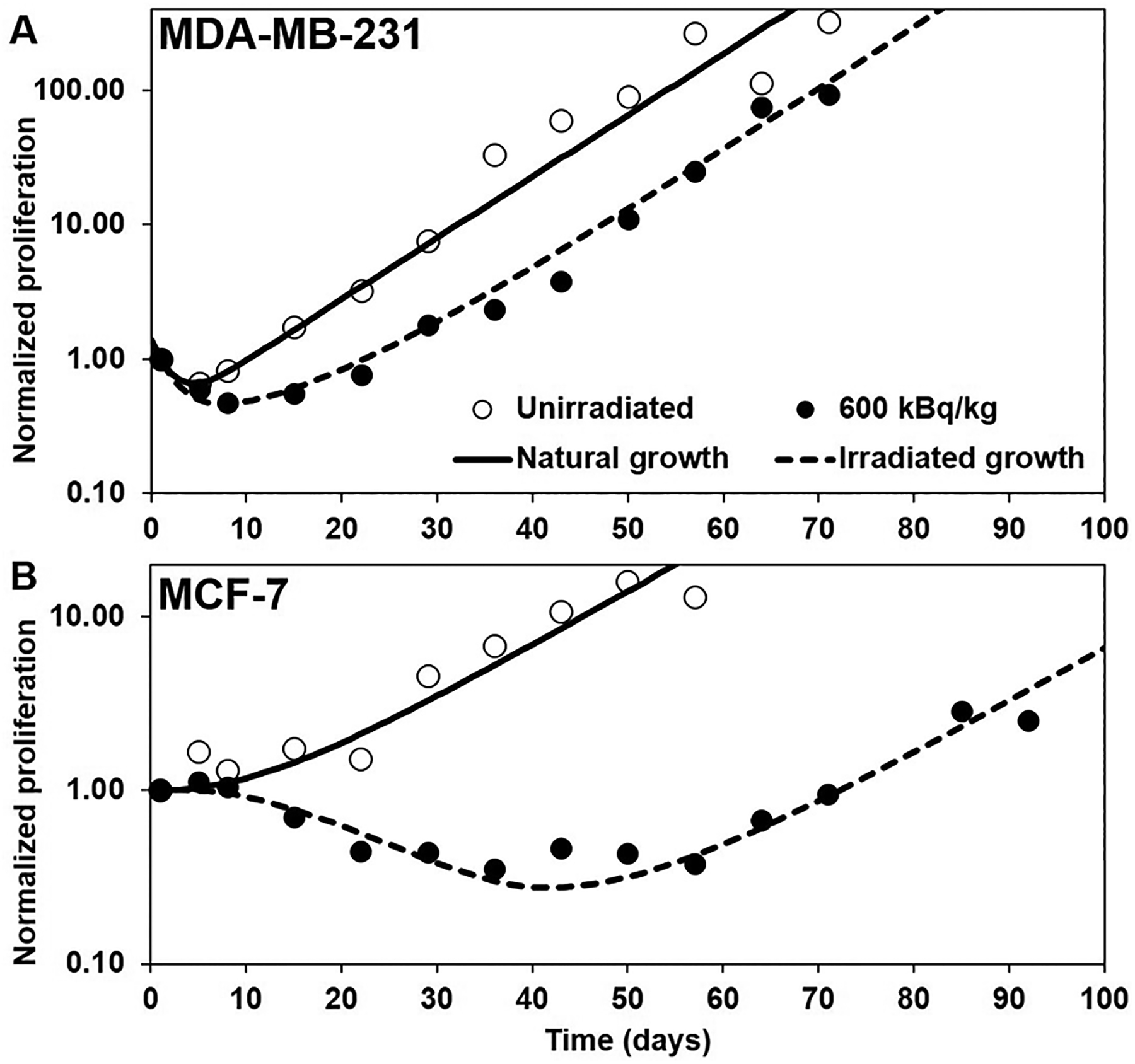
Tumor proliferation curves constructed using our model of direct effects (DE) and bystander effects (BE): A) MDA-MB-231 and B) MCF-7. Open and closed circles: unirradiated controls and 600 kBq/kg experimental data, respectively, from Leung et al. (2019). Dashed black curve: best empirical fit of the irradiated 600 kBq/kg experimental data.

Sensitivity to D₃₇

In the modeling described above, we used values of D_37,alpha for each cell line (0.73 Gy for MDA-MB-231 and 0.77 Gy for MCF-7) that were determined experimentally in our laboratory. However, published values vary; therefore, we conducted modeling with lower D₃₇ values to increase the contribution of DE (0.43 Gy for MDA-MB-231 and 0.46 Gy for MCF-7). The bystander parameters that allow a best fit of the experimental data when these D₃₇ values were used were B₃₇ = 80 Gy, T_S = 6 d, and T_B = 10 d for MDA-MB-231 and B₃₇ = 16 Gy, T_S = 15 d, and T_B = 40 d for MCF-7. When compared with the results presented above, the main trend was that the determination of the BE parameters was more sensitive to a change in the value of D_37,alpha for MDA-MB-231 than for MCF-7. This supports our previous finding that the response of MDA-MB-231 cells is driven primarily by DE and less subject to BE than MCF-7 cells.

Limitations of the current model

The current study only models the cells within a thin cross-section (250 μm) of the mouse tibia. Although we have been careful to place the cells both within and beyond the reach of the alpha particles, 10% of the energy deposited by ²²³Ra comes from non-alpha particles and some edge effects are anticipated from the limit of the model size. This factor is not likely to be significant because the 10% is principally from beta particles and conversion electrons which are of a low-LET nature that makes them much less effective than alpha particles at inducing DE and BE.

The tumor was modeled as a growing cylinder with a homogeneous, constant over time, cell density. The outside of the tumor may grow less compact and further from its original center in vivo than it does in our model. It may also grow faster towards the center of the medullary cavity than towards the bone surface. We expect theses discrepancies to make a difference for the position of the tumor relative to the source of the alpha particles, which in turn affects DE.

Caution should be exercised when applying this model to other animal models or humans. This model is based on experimentally measured growth of human breast cancer xenografts in the proximal tibia of nude mice, and only the small segment of the tibia where the tumor cells were inoculated was modeled. Placing these same tumor cells in other regions of the tibia or at other locations in the body would lead to different absorbed doses and perhaps different magnitudes of radiation-induced BE. Had the tumor cells been inoculated into the distal region of the tibia, presumably the balance between direct radiation effects and BE may be different in this scenario as well as in the bone marrow of individual patients. Although, it is possible, and even likely, that the signals that cause the BE may be produced by ²²³Ra throughout the entire skeleton and circulated systemically to affect tumor growth. Nevertheless, different tumor cell types will likely require different D₃₇ and B₃₇ values. However, given that the ER⁺ MCF-7 cells are more strongly affected by BE than the triple negative MDA-MB-231, it is possible that the bystander signals are hormone related which may ultimately lead to strategies to predict B₃₇ values for various classes of tumor cells. As discussed in our recent article (Canter et al. 2021), the large difference in growth delay caused by ²²³RaCl₂ radiation-induced bystander effects between MDA-MB-231 and MCF-7 cells may be caused by differences in their ER statuses. Prior work by others found that bystander MCF-7 cells formed more micronuclei than the bystander MDA-MB-231 cells (Shao 2008). Further experimental work may discern the effect of ER status on the radiation-induced bystander DNA damage observed in this study. Also discussed in depth by (Canter et al. 2021), the different bystander responses between MDA-MB-231 and MCF-7 cells may be related to differences in p53. MDA-MB-231 cells have a mutant copy of p53 while MCF-7 cells have wildtype p53 (Neve 2006). Future studies may investigate whether p53 contributes to the radiation-induced bystander DNA damage observed in this study.

CONCLUSION

The use of our 3D simulation model demonstrated that it is possible to empirically reproduce the tumor proliferation curve obtained from experimental data. First, we confirmed that the effects of direct irradiation of the tumor cells are not sufficient to explain the tumor growth profiles seen in vivo and that BE must play a role. Second, we introduced a parameter B₃₇ that quantifies the strength of the radiation-induced BE in terms of the mean absorbed dose received by the different populations of cells. Finally, we also introduced two distribution parameters T_S and T_B that account for the delays in the onset of DE and BE, respectively, after cells receive radiation hits. The empirical selection of these 3 parameters permitted a reasonable reproduction of the experimental tumor proliferation curves of Leung et al. (2019).

The empirical method of this study does not explain the mechanism of BE that are experienced by the two types of human breast cancer cells that were used. Further work needs to be done to extend the method to more types of cells. There is also need for more experimental data to identify the irradiated cell populations that are producing a BE and determine the B₃₇ value for each cell type. Finally, further work is needed to extend this model to observations in the clinic where it may be useful for predicting patient responses to ²²³Ra dichloride and other therapeutic radiopharmaceuticals.

Biographical Note

Didier A. Rajon is an Associate Scientist at the Department of Neurosurgery, University of Florida, Gainesville, Florida, USA

Brian S. Canter completed a PhD in the Department of Radiology, New Jersey Medical School, Rutgers University, Newark, New-Jersey, USA

Calvin N. Leung is a Doctoral Student at the Department of Radiology, New Jersey Medical School, Rutgers University, Newark, New-Jersey, USA

Tom A. Bäck is a Researcher at the Department of Radiation Physics, The Sahlgrenska Academy, University of Gothenburg, Gothenburg, Sweden

J. Christopher Fritton is an Associate Professor in the Departments of Mechanical and Biomedical Engineering, The City College of New York, New York, USA

Edouard I. Azzam is a retired Professor Emeritus of Radiology, New Jersey Medical School, Rutgers University, Newark, New-Jersey, USA; currently, Radiobiology Scientific Lead, Radiobiology and Health Branch, Canadian Nuclear Laboratories, Chalk River, Ontario, Canada

Roger W. Howell is a Professor at the Department of Radiology, New Jersey Medical School, Rutgers University, Newark, New-Jersey, USA