Modeling aging and its impact on cellular function and organismal behavior

Abstract

Aging is a complex phenomenon of functional decay in a biological organism. Although the effects of aging are readily recognizable in a wide range of organisms, the cause(s) of aging are ill defined and poorly understood. Experimental methods on model organisms have driven significant insight into aging as a process, but have not provided a complete model of aging. Computational biology offers a unique opportunity to resolve this gap in our knowledge by generating extensive and testable models that can help us understand the fundamental nature of aging, identify the presence and characteristics of unaccounted aging factor(s), demonstrate the mechanics of particular factor(s) in driving aging, and understand the secondary effects of aging on biological function. In this review, we will address each of the above roles for computational biology in aging research. Concurrently, we will explore the different applications of computational biology to aging in single-celled versus multicellular organisms. Given the long history of computational biogerontological research on lower eukaryotes, we emphasize the key future goals of gradually integrating prior models into a holistic map of aging and translating successful models to higher-complexity organisms.

1. A brief Introduction to modeling in aging biology

The field of modern aging research is considered by many to have started with the work of Benjamin Gompertz. Gompertz was an actuary with a keen interest in refining the calculation of human survival probabilities (reviewed in Miller, 2004), performed at that time through the use of complicated charts and tables. His passion for studying trends in human mortality led to a startling insight – that a simple exponential formula could accurately capture human mortality risk from young adulthood through old age. Initially proposed in 1825, the Gompertz function is capable of fitting mortality curves from a wide range of biological organisms by predicting risk of death μ at time t as: μ(t)=αe^βt (Gompertz, 1825). This can be rewritten as a function of survival: $S(t)=e^{\left(\frac{\alpha }{\beta }\right)\left(1-e^{\beta t}\right)}$ (Figure 1). This function operates on a simple but surprisingly effective assumption that the risk of mortality exponentially increases with age. Thus, the birth of modern aging research came about through the insightful application of mathematical models to otherwise uninterpretable data.

Figure 1:

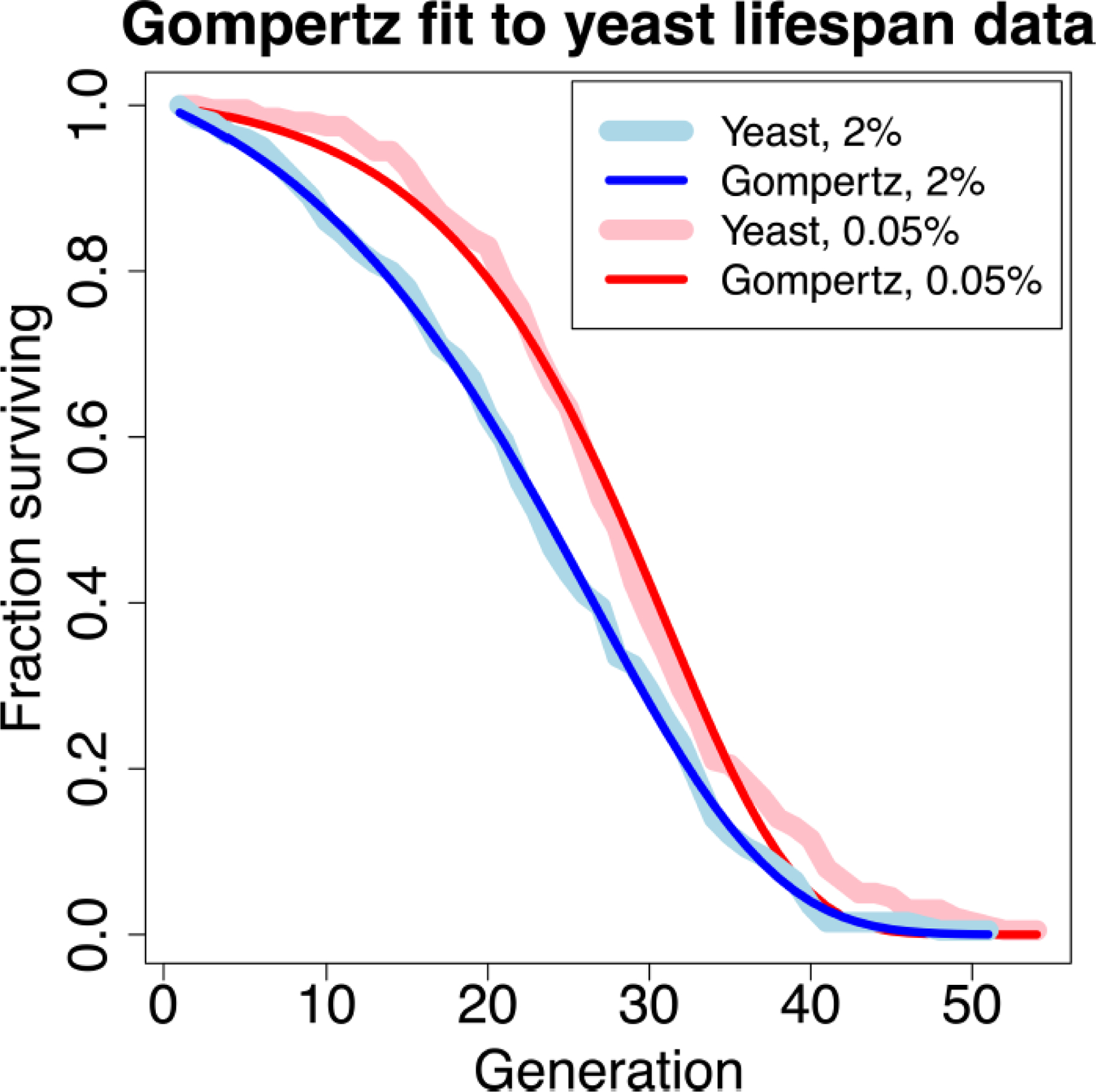
Yeast replicative lifespan data from a representative experiment. n=200 cells, media with 2% or 0.05% Glucose, Replicator microfluidic chip (Liu et. al. 2015). Gompertz fit: For 2% glucose: α=0.008597, β=0.088187, R²=0.999. For 0.05% glucose: α=0.002691, β=0.123122, R²=0.994

It is of interest to note that the Gompertz function assumes that risk of death is exponentially accumulative within certain bounds. Aging can be viewed as a cyclical process, in which certain aging factors drive an aging phenotype, which in turn exacerbates the aging factors, further accelerating the aging phenotype (Figure 2). An output from this feedback loop is the impact of aging on non-feedback processes. In the following sections, we will refer to aging models as “black-box” or “factor-driven”. A “black-box” model is one in which the factors driving aging are unspecified or implicit (e.g. human frailty index), while a “factor-driven” model is one in which an explicit factor is identified (e.g. DNA damage accumulation).

Figure 2:

Generalized theory of aging where factors accumulating during aging reinforce the aging phenotype through a positive feedback loop.

The breadth of aging research has grown exponentially since Gompertz, and it would be foolhardy to attempt a full summary of all aging research. Instead, we offer here a tailored selection of papers focused on the mathematical and computational modeling of aging, intended to offer a thorough yet accessible portfolio of the available methods and some insight into the directions ripe for future research.

2. Fundamental theories of aging

Why do we age? While this question has a rich philosophical history, it can also be interpreted literally in both an evolutionary and a mechanistic sense. Traditional aging research broadly attributes aging to a decline in the force of natural selection with time. A naive explanation is that the overrepresentation of young, fecund, organisms in any population will make them the predominant “unit” of selection, although many revisions and refinements to this idea have emerged (reviewed in Flatt and Partridge, 2018). However, translating the evolutionary motivations of aging into a mechanistic understanding has proven difficult at best. Currently, the complexity of even single-celled organisms has prevented a satisfactory experimental explanation of aging. Computational biology offers the unique opportunity to focus on the relevant complexity inherent in biological systems, potentially yielding a clear picture of the critical components in the aging process (López-Otín et al., 2013; Song et al., 2018). Given the difficulty of picking out a handful of theories from a rich and variegated history, we have given preference to those theories that are either organism-agnostic or that can be adapted to improve understanding in our later discussions on black-box / factor-specific theories of aging.

Vural and colleagues provide an excellent demonstration of the use of computational biology to explore the fundamental mechanisms driving aging (Vural et al., 2014). Their approach centers around the use of network theory to explore the “reliability theory of aging” (outlined in Gavrilov and Gavrilova, 2001) in an organism-agnostic setting. In brief, the “reliability theory of aging” proposes that biological organisms are 1) intrinsically defective in some capacity and 2) possess high levels of redundancy for irreplaceable components. High levels of redundancy explain the initial period of high viability for all organisms. Variation in intrinsic defects paired with a constant failure rate lead to a period of high failure. In the final stage of the mortality curve, only individuals with very high redundancy levels and minimal intrinsic defects remain, leading to a final period of minimal mortality. Vural and colleagues treated organisms as networks, with some set of nodes whose interdependencies are represented by directed edges. Nodes and dependencies could be genes within a regulatory network, or cells within an organism, rendering the model both scale- and organism-agnostic (Vural et al., 2014). Network structures were “evolved” via stepwise modification following a simple set of rules. Completed networks were subjected to an aging process: at each time step, individual nodes have a chance of failing at rate γ₀, failed nodes have a chance of being repaired at rate γ₁, and healthy nodes fail if a majority of their dependencies have failed. Additional parameters include the number of nodes in the network N, and the initial number of damaged nodes d.

Stochastic simulations of this model found that sufficiently large networks become highly interdependent, leading to a very strong tendency towards slow damage accumulation ending in sudden network collapse. Mortality curves generated using the model of Vural and colleagues generally replicated the Gompertz-Makeham curve (μ(t)=αe^βt + λ, where λ is an age-independent death risk component). Modifying the four parameters outlined above enabled tight fitting of available mortality data for six model organisms (C. elegans, D. melanogaster, Ceratitis capitate, Callosobruchus maculatus, Mus musculus, Hemitragus jemlahicus). To demonstrate directed use of the model for insight-generation, the mortality curve for a long-lived C. elegans mutant was fitted by single-parameter modification. The mutant lifespan data could only be fitted by increasing the node repair rate γ₁, suggesting that the mutation increases repair rate instead of reducing the rate of damage. Thus, an entirely abstracted representation of the aging process generated a testable hypothesis about a specific biological phenomenon. This can be viewed as an extremely abstracted version of the black-box models discussed in Section 3.

In turn, Boonekamp and colleagues implemented a stochastic model for the reliability theory of aging, placing a special emphasis on exploring the role of specific parameters and on using their model to make predictions about the biological mechanisms in D. melanogaster aging interventions (Boonekamp et al., 2015). Their approach centers around the reliability-theory derived mortality rate formula:

$$\mu (x)=m{\gamma }_{0}Ndc{e}^{-Nd}{e}^{-{\gamma }_{0}x}\sum \frac{N{d}^{i-1}{\left(1-e^{-{\gamma }_{0}x}\right)}^{i-1}}{(i-1)!\left(1-{\left(1-e^{-{\gamma }_{0}x}\right)}^i\right)}$$

This formula is very similar to the network-theory implementation of Vural and colleagues, with some key differences. Here, an organism can have multiple independent “blocks” of nodes m; each block is essential to life and thus the failure of any one block leads to death. Vural and colleagues only treated the case where m=1, the “block” being the entire network and network failure resulting in organism death. c is a normalizing factor. All other factors have the same meaning as defined above, with the notable absence of a factor representing the repair probability for a damaged node γ₁. This equation was fitted to mortality data for 1.2 million medflies (Ceratitis capitate), far outperforming the Gompertz curve ability to fit the data. Exploration of parameter space revealed that: 1) initial mortality rate is primarily driven by Nd and m, 2) rate of increase in mortality rate is driven primarily by γ₀, 3) the height of the mortality rate plateau seen with advanced aging is determined by γ₀m. The impact of two aging abstracted interventions, reducing γ₀ and restoring a single damaged node, were tested via stochastic simulations of individual “organisms”. Note that these interventions were applied part-way through the simulated lifespan, and the impact on age-dependent mortality rate and remaining lifespan were observed. Reducing the node failure rate γ₀ led to an immediate reduction in age-specific mortality rate, and a lifelong dampening of the overall mortality rate curve (degree of dampening dependent on age of intervention, with earlier interventions being more effective). Alternatively, restoring a single damaged node led to a sharp short-term reduction in mortality rate, followed by a gradual convergence of the long-term mortality rate curves. Mortality rate convergence occurs because the number of nodes damaged per time step, D(x), is proportional to the total number of nodes D(x) = N(x)d (N(x) is the number of remaining nodes at time x). Repairing a node directly increases N(x), thus leading to a higher average D(x) and a higher increase in mortality rate over time.

Having sufficiently established the model’s properties, it was used to model and make predictions about the mechanisms behind different aging interventions in D. melanogaster. First, the model was applied to a temperature change intervention. D. melanogaster exhibit a higher mortality rate at 27°C than 18°C. Initially, the model was fitted to data for mortality rates under continuous exposure to 27°C and 18°C, with all parameters held constant between the two conditions except the rate of node damage γ₀. Next individual lifespan simulations were carried out, during which γ₀ would be swapped from the 27°C value to the 18°C value or vice-versa. Model results for the temperature change interventions closely replicated experimental results, strongly suggesting that temperature intervention modulates mortality rate by decreasing the rate of node failure γ₀ (this could be biologically interpreted as reducing the rate of cell death, genetic damage, etc.). Next, the model was applied to a calorie restriction intervention. Calorie restriction involves a deliberate reduction in the amount of available food (or other energy source) provided to an organism. Calorie restriction has been proven to reliably extend lifespan and/or healthspan in a myriad of organisms including S. cerevisiae, C. elegans, mice, rats, and monkeys. The mechanism(s) behind calorie-restriction induced lifespan extension are poorly understood and an area of highly active research.

As discussed above, calorie restriction is known to extend lifespan in D. melanogaster, but the mechanism behind this is poorly understood. Following the protocol used for temperature interventions, the model was fitted to control and calorie restricted mortality rate data. Initially, the model was fitted with only γ₀ as a free parameter. Although these models were able to fit the continuous-exposure data with reasonable efficacy, they could not reproduce the experimental data in control organisms to calorie restriction interventions (or vice-versa). Next, it was proposed that calorie restriction may lead to a reallocation of resources from reproduction to survival, and that this reallocation would eliminate the risk of damage to reproductive systems. “Turning off” the reproductive system can be modeled by reducing the number of active blocks by reducing γ₀ ≈ 0 for all nodes in certain blocks. This fitted the control groups and was able to fit the control-calorie restriction intervention, but completely failed to fit the calorie restriction-control intervention. Finally, a reallocation step was added in which some nodes from “inactivated” blocks (γ₀ ≈ 0) were transferred to active blocks. This model was capable of tightly fitting the continuous exposure and bidirectional control-calorie restriction interventions. Thus, a highly abstracted, organism and process-agnostic aging model based on stochastic simulation was capable of providing a potential high-level explanation of the benefits of calorie restriction in D. melanogaster. It is interesting to note that this re-allocation hypothesis matches with the predictions of the “Disposable Soma” theory of aging under calorie restricting conditions (Kirkwood, 1977; Shanley and Kirkwood, 2000). However, recent work has challenged the ‘Disposable Soma’ hypothesis as a paradigm for explaining caloric restriction-induced life extension (McCracken et al., 2020; Regan et al., 2020). As detailed in Section 3, Qin and colleagues used an alternative implementation of reliability theory applying the aging failure rate, γ₀, to the connections between nodes, and applies this model to both known lifespan-influencing mutations and yeast natural isolates (Qin, 2019).

To close this section, we turn to work focused on developing models of the changes induced by lifespan-extending interventions. The driving question is not “Why do we age?” but rather “How can we model and measure aging?”. Stroustrup reviews the theoretical framework for identifying the impact of aging interventions on a variety of aging-models. Four common parametric models of aging (two Gompertz variants, Weibull, Inverse Gaussian) are subjected to parameter analysis to identify how changes in key parameters manipulate aging outcomes (Stroustrup, 2018). Take the Gompertz Equation as an example:

$$\mu (t)=\alpha e^{\beta t}$$

The α parameter in a traditional Gompertz equation was shown to translate the predicted mortality rate curve without altering curve shape, while the β parameter is shown to control the steepness of the increase in mortality rate with age. Although each of the four parametric models is capable of fitting a variety of aging data, this overlap in performance is argued to be disadvantageous, as it prevents a clear interpretation of the biological processes that produced this aging data. For example, consider a dataset that is fit by the Gompertz and the Gompertz-Makeham models equally well; it would be difficult to confidently predict whether an age-independent mortality risk is actually present.

Semi-parametric models are proposed as a potential resolution to this issue. Semi-parametric models fit only the impact of the aging intervention itself, avoiding unjustifiable assumptions about whole-lifetime mortality risk. Common semi-parametric models include proportional hazard (PH) and accelerated failure time (AFT). Frailty models attempt to capture intrinsic population heterogeneity in aging by adding a random variable Z(σ).

$$\begin{array}{lll}\text{ PH: }{\mu }_1(t)=\lambda {\mu }_0(t)\hfill & \text{ AFT: }{\mu }_1(t)={\mu }_0(\lambda t)\hfill & \text{ Frailty: }{\mu }_1(t)=Z(\sigma ){\mu }_0(t)\hfill \end{array}$$

An expansion on the motivation behind frailty models, competing risk models are based on the theory that multiple distinct causes of death exist. Although ultimately only one will cause death, the organism is at risk for multiple causes of death until death occurs. The Standard Competing Risk (SCR) model implements this as a sum of mortality rates per-cause of death. An alternative approach referred to as mixture models assumes that set sub-populations are exposed to differences in risk. An experimental-computational exploration of this approach is discussed in Section 3 in unicellular (Jin et al., 2019; Li et al., 2020) and multi-cellular (Zhao et al., 2017) systems. The final model discussed is the biphasic model, which contains a static switch between two distinct mortality models at a set time-point.

$$\begin{array}{ll}\text{ SCR: }\mu (t)=\sum {\mu }_i(t)\hfill & \text{ Biphasic: }\mu (t)=\{\begin{array}{l}{\mu }_0(t)\text{ for }t<t_{\mathit{\text{switch }}}\hfill \\ {\mu }_1(t)\text{ for }t\ge t_{\mathit{\text{switch }}}\hfill \end{array}\hfill \end{array}$$

Finally, we turn to the work by Petrascheck and Miller for an exploration of the experimental detectability of aging interventions. Using lifespan data generated from over 5000 C. elegans, the ability to statistically significantly distinguish an aging intervention from noise was examined under a variety of measurement conditions. A standard Gompertz curve was used for simplicity. Conditions explored included granularity of aging data (the size of Δt during data collection, e.g. minutes vs hours vs days), the real effect size of the aging intervention (as a % change from expected lifespan), and the sample size used. They found that with a sample size of n=100, it was difficult to reliably detect a lifespan extension of less that 20%, regardless of the granularity of data collection (Petrascheck and Miller, 2017). Note that even a well-characterized lifespan extending intervention such as calorie restriction in yeast is susceptible to similar issues of sample size, as highlighted by Huberts and colleagues (Huberts et al., 2014). Interestingly, lifespan interventions that altered α or β had similar probability-of-detection profiles. Although the symmetric detectability of α and β interventions is desirable, the inability to reliably detect small changes in mortality after an aging intervention at common experimental sample sizes raises serious concerns. High-throughput research in single cell organisms offers potential resolution to this issue, such as the use of the microfluidic technologies developed by a handful of research groups (Crane et al., 2014; Fehrmann et al., 2013; Goulev et al., 2017; Jin et al., 2019; Jo et al., 2015; Lee et al., 2012; Liu et al., 2015; Sarnoski et al., 2018; Zhang et al., 2012).

Alternative approaches include integrating other data such as cause of death or measurements of vitality; these have shown promise in experiments on primate response to calorie restriction (Pifferi et al., 2018) and work on modeling human aging (Redman et al., 2018); see also discussion of Frailty indices and associated papers in Section 3.

3. Black-box theories of aging

A black-box theory of aging is one that attempts to explain a set of observational data for which the true causative factor(s) is (are) not known or specified. This definition is necessarily amorphous and wide-reaching, as black-box models can range from simple predictions of a single causative factor to explain a phenomenon to collective modeling of many phenotypic phenomena to directly predict mortality. Black-box theories of aging occupy a unique place in the aging literature. Given the complex nature of aging, it is often exceedingly difficult to identify and experimentally validate clear causative factors. Black-box models can be used to evade this issue as follows: the causative factors of aging in a specific organism are treated as unknown, and a model is developed that attempts to account for a set of known data about aging in that organism. The resultant model must make certain assumptions about the causative factors in aging to match the data. The model directly informs our understanding of the aging process in the target organism, while the model assumptions about aging factors guide future experimental work by setting clear requirements that a proposed factor must satisfy. Thus, black box models can better our understanding of a particular aging phenomenon and guide us towards the biological factors responsible without forcing an extensive initial search for causative factors.

The discovery of extrachromosomal ribosomal DNA circles (ERCs) as a key aging factor in yeast offers a striking demonstration of the utility of black-box models in guiding experimental work. The black-box “cytoplasmic senescence factor” theory set certain requirements for the behavior of a predicted aging factor (exponential accumulation, asymmetrically portioned during cell division, leakage leading to premature aging and death). By experimentally demonstrating that ERCs fulfilled these requirements, Sinclair and Guarente were able to confidently identify ERCs as a primary causative aging factor in yeast (Sinclair and Guarente, 1997).

3.1. Phenotypic Observation and Aging Theory

Recent work from the Hao lab offers a striking modern demonstration of the power of black-box theory in guiding future experimental work. It was noted that aging S. cerevisiae tend to produce daughters that are either oblong (Path 1) or circular but undersized (Path 2) (healthy daughter cells are circular and of moderate size). Using single-cell imaging and microfluidic technology, Jin and colleagues tracked these parameters for 205 wild-type cells from birth to death. The authors found that cells diverge to one of these two phenotypes relatively early in life, and that once diverged tend to stick to their “path” (Jin et al., 2019). The two phenotypic “paths” resulted in extremely different aging outcomes: Path 1 mothers survived through approximately 33% more cell divisions than Path 2 mothers. Additionally, Path 1 mothers exhibited a faster cell cycle with a smaller standard deviation. It is interesting to note that this appears to be a variant of the mixture models mentioned in Section 2 as discussed by Stroustrup. Based on this data, the authors developed a four-state stochastic model that was capable of tightly fitting the observed data. To demonstrate the robustness of this four-state model, the authors turned to classical lifespan-altering mutants in yeast. The model was able to accurately fit lifespan curves for the lifespan-shortening mutant Δsir2, the lifespan-extending mutant Δsgf73, the lifespan-extending intervention calorie restriction, and the Δsir2-mimicking chemical intervention consisting of nicotinamide administration. Although the authors were unable to clearly define the biological processes underpinning the four-state model, the model was capable of reproducing a wide range of known aging behavior using a limited range of phenotypic cues. Later work by the same laboratory would go on to fill-in this black-box by identifying the exact biological processes responsible (Li et al., 2020); see Section 4 for details.

Zhao and colleagues offer a multicellular implementation of the phenotypic observation approach used by Jin and colleagues. Extensive handling of aging and dead C. elegans led to the observation that dying nematodes tend to have either an over-enlarged pharyngeal bulb, referred to as P or an atrophied pharyngeal bulb, referred to as p (Zhao et al., 2017). Note that C. elegans eat by pumping a mixture of bacteria and plate media through their grinder, which crushes the bacteria into a digestible state. Combining lifespan data with pharyngeal bulb phenotypic readout enabled a deconvolution of the mortality data, revealing that P-type worms tend to die far sooner than mean lifespan, while p-type worms outlive mean lifespan. All worms observed were either P or p. This suggests that what was traditionally considered wild-type or mean lifespan in C. elegans was actually a composition of two distinct aging pathways. P-status was discernible at an early life stage with strong predicting power. Thus, P-status represents a simple 2-state black-box model for predicting aging outcomes. Based on existing data on pharyngeal bulb abnormalities, the authors suspected that P was due to a bacterial infection of the bulb and surrounding tissue.

Use of red fluorescent E. coli quickly confirmed that P worms were subject to widespread infection of the bulb, while p worms appeared relatively uninfected. In support of this, antibiotic treatment eliminated P worms from the population, shifting the lifespan data accordingly. The effects of different mutations related to pharyngeal pumping were tested for impact on P/p ratio, revealing that the rate of pharyngeal pumping correlates to the amount of P worms. This led to the hypothesis that P state emerged later in life due to an early life injury from aggressive pharyngeal pumping. E. coli colonize this injured site and the surrounding tissue, eventually leading to death. The effects of various lifespan-extending mutations were tested for impact on P/p ratio, revealing that many traditional aging-mutants can be accounted for within the P/p 2-state model. This study demonstrates the power of black-box models paired with close phenotypic observation to enable the identification of relevant aging-related mortality factors. We find this study particularly valuable for its concise demonstration of the utility of mortality curve deconvolution in “un-black-boxing” a model. While it is unclear if P status, e.g. early pharyngeal damage leading to infection in later life, is technically an “aging” phenomenon (it is better termed an aging-dependent pathology that limits maximal lifespan), this process exhibits quite clearly the potential for early organismal “decisions” to impact long-term health and survival outcomes.

To close this subsection, we will review a selection of papers exploring the evolutionary benefits of asymmetric cell division and the resultant impact on cellular aging. Many single-celled organisms engage in asymmetric cell division, where some subset of cellular material is preferentially retained in one of the two cells resulting from cell division. At least some of the specially allocated materials are considered “damaging”, e.g. ERCs in S. cerevisiae are known to cause aging and death and are retained in the larger “mother” cell during cell division. Cells with high concentrations of these damaging factors exhibit an increased risk of death, making these damaging factors a primary cause of aging. Thus, asymmetric division can be considered a potential contributor to aging, motivating exploration of its evolutionary origin. The following are considered black-box models due to their generic definitions of “damage factors” without resorting to specific biological entities such as ERCs or damaged proteins.

Ali and colleagues offer a theoretical exploration of the balancing act required by cells undergoing asymmetric division. They attempt to account for the ability of cells to adjust the level of asymmetry in cell division. It is well known that extreme conditions can lead to a breakdown of the asymmetric allocation of damage factors: heat shock in aging yeast often leads to a symmetric division of damage factors as evidenced by the premature death of the resultant daughter cells (Baldi et al., 2017). Additionally, severely aged yeast tends to leak a portion of their damage factors into their daughter cells, as evidenced by the premature aging and death of these cells, although less extreme than under heat shock conditions (Kennedy et al., 1994; Sinclair et al., 1998). Note that the model of Ali and colleagues accounts for the accumulation of both functional proteins (termed the intact component: I) and damaged proteins (termed the damaged component: D), and motivates cell division and death based on their respective accumulations. Two distinct damage retention strategies are used to model the decrease in damage retention efficiency R with age. These strategies are termed division and distance:

$$\begin{array}{c}\hfill \mathit{\text{Divisionstrategy}}:\hfill \\ \hfill R{E}_{\text{div}}(g+1)=1-\frac{g^n}{g^n-{\alpha }^n}\hfill \\ \hfill \mathit{\text{Distancestrategy}}:\hfill \\ \hfill R{E}_{\text{dist }}(g+1)=1-\frac{R_t^n(g)}{R_t^n(g)-{\alpha }^n}\hfill \end{array}$$

where g is the replicative age of the cell, and α > 0 and n ≥ 1 are constant parameters. For the distance strategy, R_t is the ratio between the amount of time required for I to reach the division threshold and D to reach the threshold for cell death:

$$R_t=\frac{{\tau }_I}{{\tau }_D}$$

As the cell ages, the accumulation rate of D increases, causing τ_D →0 and thus $\frac{R_t^n(g)}{R_t^n(g)-{\alpha }^n}\to 1$ such that RE_dist → 0. Cells are forced to retain less and less of their damage factors if they hope to stay alive until their next division. Ultimately, the rate of damage accumulation overtakes the rate of division and the cell dies.

In addition to the above two strategies, which determine the rate at which retention efficiency declines with aging, the authors included a parameter to model intentional modification of the retention efficiency by the cell, termed the altruistic factor, A, 0 ≤ A ≤ 1. The effective retention efficiency (R(A, g)) is set to a renormalized form of the difference between R and A such that:

$$\begin{array}{c}A=1\Rightarrow R(A,g)=1\\ A=0.5\Rightarrow R(A,g)=R(g)\\ A=0\Rightarrow R(A,g)=0\end{array}$$

Thus A < 0.5 corresponds to “selfish behavior” via releasing more damage than is ‘necessary’, A > 0.5 to “altruistic behavior” by retaining more damage than is ‘necessary’, and A = 0.5 corresponds to strictly neutral behavior.

With all of this established, Ali and colleagues ran a series of simulations of cell populations testing a range of values for the flexible parameters (α, n, A). Cost functions were defined to score a given parameter set based on the resultant populations’ ability to minimize damage and maximize the number of cells in the population. Later simulations involved the periodic calculation of the cost function for a given parameter set, and allowed for A to be either deterministically or stochastically modified to attempt to minimize future cost. Although the division and distance strategies performed similarly to some degree, the division strategy imparted a higher proportion of damage to daughter cells in early generations, disproportionately damping future population growth. Thus, the distance strategy was moderately favored. High altruism was found to reduce total population size but greatly increased population health (note that the distance strategies’ emphasis on minimal damage transition to early-born daughters works synergistically with high altruism towards this high-health low-population size outcome). Low altruism reduced overall population health but did increase individual cells’ replicative lifespans. Finally, it is interesting to note that the stochastic simulations revealed an evolutionary trap for distance-strategy cell division. The cost function for distance-strategy dividing cells exhibited a local (but not absolute) minima at A = 1 such that cell populations initialized between 0.5 < A < 1 frequently became trapped at this partially adapted but not ideal value (Ali et al., 2019). This captures the frequent theme in evolutionary biology that certain biological processes are not representative of a state of maximal fitness, and suggests that some aspects of aging may be the result of highly accessible but ultimately local fitness minima (for a generalized review of rugged fitness landscapes, see de Visser and Krug, 2014).

Song and Acar argued that although the use of differential equations in modeling damage segregation was plausible, it failed to capture the stochasticity intrinsic to biological processes. They proposed a stochastic black-box model of aging for S. cerevisiae centered around the accumulation of cellular damage and its reduction through repair and cell division (Song and Acar, 2019). Stochasticity was implemented through cell-to-cell variations in various parameter values, and in the level of inheritance for these parameter values. Cells were modeled as accumulating damage D at a constant rate r_dmg. This damage was repaired at a damage-dependent rate by a Michaelis-Menten kinetic process:

$$r_{\mathit{\text{repair}}}(D)=\frac{v_{max}D}{k_m+D}$$

Cell growth was inversely proportional to the level of damage:

$$\frac{dV}{dT}=\frac{r_{\mathit{\text{growth}}}V}{1+D^{\alpha }}$$

Overall damage accumulation was a linear combination of the above factors:

$$\frac{dD}{dt}=r_{dmg}-r_{\mathit{\text{repair}}}(D)-\frac{D}{V}\frac{dV}{dt}$$

Parameters r_growth, V_i (initial volume), V_crit (critical volume) were derived from biological data. For each progenitor cell in the simulation, a parameter for r_dmg, ν_max and k_m was selected from a biologically-derived range of values. To simulate the effects of cellular noise, the parameters (p) for r_dmg, ν_max and k_m were resampled from a normal distribution scaled by the noise in damage and repair factor n_d : N(μ = p, σ = n_dp). Similarly, the mother/daughter volume ratio at cell division R was resampled based on the noise in cell volume control factor n_ν : N(μ = p, σ = n_νp). Other parameters were assigned to progenitor cells at simulation start from a biologically-derived range of values. Cell division occurred once the critical volume V_crit was reached. Cells derived from these progenitor cells would inherit a stochastic proportion of their mother’s parameter values based on c (level of inheritance of all variable parameters): p_new = cp_mother + (1 − c)p_fresh where p_fresh is a novel parameter value sampled from the normal distribution of possible values for a given parameter. Using this model, senescence outcomes were simulated for all possible parameter value combinations. A population of cells was considered senescent if it exhibited an average doubling time greater than 1000 minutes (10 times the expected doubling time of 100 minutes) during the simulation.

As expected, changes in the rate of damage r_dmg and the repair rate ν_max controlled population senescence outcomes in the vast majority of cases. Other parameters were far less likely to alter senescence outcomes. Interestingly, when noise in damage and repair (n_d) did alter senescence outcomes (~2% of all cases), the largest value of n_d was always the best fit. This can be understood as offering a benefit analogous to that of damage segregation; although mean fitness remains unchanged, the fitness of one subset of the population is sacrificed (e.g. sampling a high damage rate from the normal distribution, or preferentially retaining cellular damage) to maximize the fitness of the other (e.g. sampling a low damage rate from the normal distribution, or preferentially retaining cellular damage). Of note is that damage segregation (equal volume partitioning but one cell retains more damage) and division asymmetry (unequal volume partitioning, damage is distributed proportionally to volume) only determined clonal senescence in a fraction of parameter-sets (1.6%, 0.4% respectively). However, damage segregation was essential in cases where it was capable of altering senescence outcomes. By contrast, division asymmetry was found to be neutral or mildly detrimental in most cases. This evidence suggests that asymmetric damage partitioning during cell division was not evolutionarily motivated by a need to avoid clonal senescence.

Note that asymmetric damage partitioning could still be evolutionarily beneficial. Asymmetric division and aging may confer additional benefits beyond avoiding clonal senescence(Knorre et al., 2018). By de-homogenizing the cellular population, asymmetric damage partitioning increases resilience to fitness challenges. For example young S. cerevisiae exhibit an increased resilience to heat shock and oxidative stress (Knorre et al., 2018), while UV stress resistance increases during the first few generations and later decreases, peaking at the 8^th generation (Kale and Jazwinski, 1996). This line of reasoning was explored by Chao and colleagues using black-box models of cell division and aging in E. coli. Chao seeks to define a new conceptual and mathematical framework for understanding how damage accumulates and moves within populations (Chao, 2010). Proposed as a natural foil to “mutation load”, “damage load” is the accumulation of harmful non-heritable changes to phenotype (e.g. oxidized proteins, protein aggregates, torn muscles, broken bones). While mutation load is thought to be a dominant cause of aging and senescence in metazoans (Vijg and Montagna, 2017), it likely has a negligible impact on single celled organisms like yeast (Kaya et al., 2015). Inspired by this idea, Chao posits that damage load may drive aging in organisms with a low mutation load. Assuming symmetric division of damage load, a single-cell organism can theoretically be immortal so long as the rate of damage is below the threshold of dilution. Asymmetric division of damage load renders the population mortal, but increases fitness variance by rendering a subset of the population resilient against higher rates of damage. Chao develops a concise mathematical model to validate this reasoning. Comparison with available E. coli data reveals that they exhibit weakly asymmetric division, enabling immortality at typical experimental damage levels while still incrementally increasing fitness variance. Interestingly, fitness benefit from asymmetric division of damage load tapers as asymmetry increases, suggesting that for each given damage rate there is an optimal level of asymmetry (Chao, 2010), potentially explaining why damage load division in E. coli is only weakly asymmetric. Following this, Chao and colleagues sought to model the respective benefits of deterministic asymmetry vs. stochasticity in damage load partitioning, with an eye towards understanding how non-genetic phenotypic variation is motivated towards genetic integration. Modeling the respective damage partitioning techniques reveals that although stochastic damage partitioning is beneficial, deterministic partitioning offers similar benefits and allows for better adaptation in response to environmental demands (Chao et al., 2016).

Borgqvist and colleagues achieved similar results using a series of ordinary differential equations by directly tracking a damage resilience factor, Q, that is proportional to the amount of damage a cell can tolerate prior to cell death (Borgqvist et al., 2020). Of note is that Q can be accurately estimated for the model by the difference in size between young and old yeast cells (as yeast age, they increase in cell volume (Mortimer and Jonhston, 1959)). Using this alongside a handful of other biologically-derived aging parameters, they modeled the conditions required for replicative aging without leading to either immortality or immediate death. Asymmetric cell division and a higher Q were found to enable cells to survive higher damage rates and thus achieve longer replicative lifespans.

Thus we are faced with strong arguments that the contribution of asymmetric damage partitioning to aging is a classic case of species fitness maximization at cost to the individual. It is important to note that the force of natural selection on an organism typically diminishes after a reproductive maxima has been achieved, in large part because younger organisms generally make up the bulk of a population (Medawar, 1952). A typical yeast population under exponential growth conditions has a mean age of ~1 (½ cells at age 0, ¼ at age 1, ⅛ at age 2, and so on…), and is almost immediately at a reproductive maxima, meaning the average “unit” on which natural selection can act must be young. This feeds into the “selection shadow” theory in which the early life fitness offered by a novel mutation overshadows the late-life deleterious effects, eventually leading to aging and senescence (reviewed in Flatt and Schmidt, 2009; Rose et al., 2007). Asymmetric damage partitioning fits neatly into this theoretical landscape by offering a tantalizing increase to early-life fitness (increased stress resistance and fecundity) in exchange for a decrease in late-life fitness that is masked by a population that is overwhelmingly young.

3.2. Lifespan data and aging theory

Next, we will discuss a pair of papers that extend fundamental theories of aging with direct application to experimental data, yielding novel black-box models of aging with strong theoretical ties. Qin utilized the reliability theory of aging to model aging in S. cerevisiae. A cell was treated as a network of nodes and edges, where each node represented a gene and each edge represented interactions between genes (Qin, 2019). All edges are subject to a constant mortality chance per time-step, γ₀. Lost edges cannot be recovered in this model. Once a node has lost all edges, it is deleted from the network permanently. Certain nodes are considered “essential” and others “nonessential”. The loss of nonessential nodes has no impact on network survival. If any essential node is lost, the network is considered “dead” (Qin, 2019). Note that edges are assigned randomly at network creation with probability p for a given edge to exist between any two nodes (this is analogous to initial damage load in a fully connected network signified by d in Boonekamp and colleagues’ work reviewed above (Boonekamp et al., 2015)). n signifies the number of edges for a given node, equivalent to the number of lifespan-influencing interactions per node. This network model can be treated as a circuit block with n parallel components. When t ≪ 1/γ₀, this enables the mortality rate of the entire network to be calculated as:

$${\mu }_{net}(t)\approx m{\gamma }_{0}ncp\sum \left(\begin{array}{c}n-1\\ i-1\end{array}\right){\left(p{\gamma }_{0}t\right)}^{i-1}{(1-p)}^{(n-1)-(i-1)}$$

Note similarities between this equation and the formulation used by Boonekamp and colleagues.

This in turn can be reduced to the binomial equation:

$${\mu }_{net}(t)\approx R{\left(1+t/t_0\right)}^{N-1}$$

where:

$$\begin{gathered} t_0=\frac{1-p}{p{\gamma }_0} \\ R=cmN{\left(p{\gamma }_0\right)}^N{t}_0^{N-1} \end{gathered}$$

The parameter t₀ is considered the “initial virtual age of the system” and is representative of the degree of “age” present at network creation. The parameter R represents the initial mortality rate. The above binomial was shown to accurately fit lifespan data for a collection of yeast strains with known lifespan-altering mutations. Interestingly, the model best fit available data for Δsir2, Δhxk2, and Δfob1 yeast by altering the parameter t₀. This suggests that these mutations work by influencing the “initial age” or reliability of certain gene interactions, and not by altering the initial mortality rate (R) or structure of the network (n). It is interesting to note that Sir2 and Fob1 are thought to exert opposite effects on rDNA recombination, which in turn alters the rate of extrachromosomal ribosomal DNA circle (ERC) excision. ERC excision and subsequent accumulation is a known contributor to aging and mortality in S. cerevisiae. Thus, direct biological evidence exists to support the model-proposed theory that Sir2 and Fob1 function by altering the reliability of genetic interactions (biologically manifested as probability of rDNA recombination/ERC excision). Application of this model to other aging-implicated genes with unknown function could prove fruitful in guiding future research.

Generally speaking, it is possible to imagine aging as being either integrated or disparate. In an integrated aging system, some number of distinct biological factors are integrated by the cell to form an overarching “aging” state. Altering any one factor will smoothly transition the cell along a predetermined aging output function. In a disparate system, multiple distinct aging factors are competing to drive aging in the cell, potentially leading to discontinuities in the aging output function as one factor overtakes the others. To identify which of these models more accurately represents aging in S. cerevisiae, Liu and Acar utilized a microfluidic chip (Liu et al., 2015) to collect large amounts of single-cell resolution whole-lifespan data for a variety of lifespan-altering mutants. They predicted that a disparate aging system should yield fundamentally different mortality curves as different aging factors are given precedence (changing the aging “equation”). Alternatively, an integrated aging system would smoothly alter the existing mortality curve (changing the aging “parameters”).

Consider the following illustrative examples:

A simplified mortality risk equation for a disparate aging system, based on the level of aging factor F:

For simplicity, suppose there are only two aging factors F₁ and F₂, and two genetic backgrounds denoted by subscript ‘a’ and ‘b’. In a disparate aging system, these two aging factors would contribute independently to net mortality. The mortality risk equations for these two genetic backgrounds in a disparate aging system can be described as:

$$\begin{gathered} {\mu }_a(t)=F_{a,1}{\mu }_1(t)+F_{a,2}{\mu }_2(t) \\ {\mu }_b(t)=F_{b,1}{\mu }_1(t)+F_{b,2}{\mu }_2(t) \end{gathered}$$

Alternatively, the mortality risk equations for these same genetic backgrounds in an integrated aging system could be described as:

$$\begin{gathered} {\mu }_a(t)=\left(F_{a,1}{F}_{a,2}\right){\mu }_1(t){\mu }_2(t) \\ {\mu }_b(t)=\left(F_{b,1}{F}_{b,2}\right){\mu }_1(t){\mu }_2(t) \end{gathered}$$

which can be rewritten as:

$$\begin{gathered} {\mu }_a(t)=F_{a,12}{\mu }_{12}(t) \\ {\mu }_b(t)=F_{b,12}{\mu }_{12}(t) \end{gathered}$$

In the integrated system, despite the different parameter values for various aging factors, the aging process for different genetic backgrounds is governed by a common ‘knob’ (μ₁₂(t) in the above illustrative system).

Note that combinations of the two arrangements are also plausible, such that some subset of aging factors are integrated by the cell while another factor can disparately drive aging.

Liu and Acar found that all of the lifespan-altering mutants exhibited a conserved lifespan curve shape (Liu and Acar, 2018). To validate this observation, they applied the semi-parametric accelerated failure time model (discussed by Stroustrup, as we have seen in Section 2):

$${\mu }_1(t)={\mu }_0(\lambda t)$$

The observed lifespan curves could be cleanly rescaled to reproduce one another by varying λ, confirming that they were generated by a single integrated aging system. This finding is striking given the variety of lifespan-altering mutants tested. As further evidence of an integrated aging system, a simple linear equation was capable of tightly fitting the pairs of λ and mean replicative lifespans observed for the various curves. Gamma, Gompertz, and Weibull models were all capable of reproducing the lifespan data, with Weibull offering the best fit. The Weibull model was capable of accurately fitting the data even when reduced to a single parameter (α = 3.28, leaving r as a free parameter):

$$\frac{S(t)}{S_0}=e^{{(-rt)}^{3.28}}$$

where S(t) is the survival distribution at time t. This strongly reinforces the idea of a single fundamental aging output that is rescaled based on integrated aging factors. Next, three stochastic models (Semi-infinite random walk, drift diffusion with drift heterogeneity, Strehler-Mildvan) of cellular aging were tested for their ability to fit the data. Of note is that all three models were capable of fitting the observed lifespan curve scaling behavior. Ultimately, the Strehler-Mildvan model offered the best fit. Finally, they characterized the mean generation time for two lifespan-altering mutants and wild-type yeast. Interestingly, the resultant data were well-fitted by a power law that could be rescaled linearly to fit any of the data. This persistence of scaling from survival curves to phenotypic curves reinforces the evidence for an integrated aging system in S. cerevisiae (Liu and Acar, 2018).

Similar to the work of Liu and Acar on S. cerevisiae, Stroustrup and colleagues examined how lifespan distributions are altered by aging interventions in C. elegans. Using a unique device, the C. elegans aging machine (Stroustrup et al., 2013), they found that, for a wide range of interventions including calorie restriction, temperature manipulation, oxidative stress, and gene mutants, the resultant lifespan distributions were merely rescaled from the wild-type distribution (Stroustrup et al., 2016). Curve rescaling was tested via the semi-parametric accelerated failure time regression model. Even the effects of transient interventions applied in early life could be well-modeled by a temporary shift in theoretical scaling factor λ. This evidence strongly reinforces the theory that aging, or at least mortality risk, is somehow integrated in C. elegans, providing a multicellular counterpart for the findings of Liu and Acar at the unicellular level. It is important to note that only lifespan was measured and quantified by Liu & Acar and by Stroustrup and colleagues, meaning that the length of life (lifespan) appears to be driven by some integrative processes, but the quality of life (healthspan) need not follow this trend. Obtaining a clear understanding of the scalability of quality of life measurements, and of the pairing or potential mismatch of the length and quality of life, represents a logical next step in aging research.

3.3. Health as a (semi)-independent predictor of mortality

Two papers from the Rutenberg lab (Farrell et al., 2016; Taneja et al., 2016) are representative examples of recent work to develop models based on aging-associated trends in quality of life for humans. The “Frailty Index”, F, is a clinical measure of health obtained by averaging scores for a wide range of age-associated deficits. Possible scores per deficits are 0 (healthy) or 1 (damaged). Prior work has shown that in aged populations F is as powerful as chronological age in predicting mortality. The distribution of F becomes significantly wider with age, reflecting the high variability intrinsic to human aging. Taneja and colleagues turned to network theory to model the dynamics of F. Taneja and colleagues treat an individual as an undirected network of nodes, where each node is a deficit. Each node tracks a 2-state value corresponding to the healthy and damaged states typically used by Frailty Indices. To capture both mortality dynamics and frailty dynamics, mortality is defined as the damaging of one of the most connected nodes, while frailty is defined by the average damage state of nodes that are not mortality nodes. Nodes are capable of stochastically transitioning between healthy and damaged state based on damage and repair rates. Damage and repair rates are determined based on local frailty relative to the node in question. Unlike in the model by Vural and colleagues, all nodes start out in the healthy state. This model was found to tightly fit the existing Frailty Index data for individuals with ages from 20 to 90 years (Taneja et al., 2016). It is interesting to note that this model is capable of recapitulating the Gompertz-guided increase in mortality for ages over 50. Mortality was consistently strongly influenced by F, whereas F was only loosely correlated to chronological age. Scaling damage and repair to local frailty eliminates the need for an explicit time-dependence of these values, demonstrating that network dynamics alone can recapitulate the majority of the observed aging behaviors (frailty and mortality risk).

Directly building on the work of Taneja and colleagues, Farrell and colleagues sought to alter the network model such that the maximum observed value of F was less than the maximum possible value. In human data, the maximum observed value of F, F_max, is always less than the maximum possible value of 1, and frequently F_max ≈ 0.7 (Mitnitski et al., 2013). However, the model of Taneja and colleagues frequently resulted in F_max = 1, even when mean F matched human data. To resolve this disparity, Farrell and colleagues hypothesized that the observed gap between F_max and 1 in human data was the result of the limited sensitivity of clinical diagnosis of deficits (Farrell et al., 2016). This hypothesis is compatible with the observed regional variations in F_max. To implement this in their network model, a false-negative rate q was added. In addition to q, several other model parameters were simplified for simulation efficiency or otherwise altered. The resultant network model was able to tightly fit observed mortality rate data for ages ~40+ and frailty index data for ages 20+. A false-negative rate of q = 0.3 resulted in an F_max ≈ 0.78 at the 99^th percentile of aged networks, demonstrating that the false-negative hypothesis is capable of reproducing observed phenomenon. Testing an alternative hypothesis, that human-observed F_max is the result of F_max directly inducing death, led to discontinuities in model outputs inconsistent with observed human aging data. Thus, the false-negative hypothesis is reasonably supported by the model and available human data. The authors next turned to the use of information theory to determine how chronological age and F can be used to predict mortality. Their model predicts that the value of knowing an individual’s F is maximized at approximately 80 years old. Additionally, F is more predictive at higher values; this increase correlates with higher age but is not strictly dependent on it. Thus, a network model of a collection of aging-associated deficits is capable of capturing the majority of both mortality and health characteristics observed in actual human data (Farrell et al., 2016). This model reinforces the argument of Vural and colleagues that aging itself may be an emergent property of highly connected biological networks (Vural et al., 2014).

Extending this work on Frailty Indices, Schultz and colleagues employed machine-learning techniques to develop the FRIGHT and AFRAID, which use various non-invasive metrics (e.g. presence of gait disorders, corneal capacity, etc.) to predict chronological age and life expectancy in mice (Schultz et al., 2020). Frailty Index scores (F) were taken every ~6 weeks for a cohort of male mice from 21 months of age until all individuals were deceased. Linear regression on raw F was capable of predicting chronological age with a median error of 1.8 months, mean error of 1.9 months. The authors hypothesized that error was representative of a mismatch between biological age and chronological age, and termed the mismatch delta age (ΔA = Age_Biological − Age_{Chronological}). Thus, if ΔA < 0 for a given individual, that individual would be expected to live longer than average individuals of an equivalent chronological age. This expectation was met for certain age groups, supporting the idea that organisms have a biological aging clock that is at least partially distinguishable from chronological age alone. To improve model predictions, the authors calculated correlations between all Frailty Index items and chronological age. Certain items exhibited strong correlations with chronological mouse age (Tail Stiffening, Breathing Rate/Depth, and Gait Disorders had the strongest correlations), while others exhibited no correlation (e.g. Cataracts, Corneal Capacity, Nasal Discharge). Note that the presence of uncorrelated factors in frailty indices could represent a source of error when using these indices to predict age and mortality outcomes (all uncorrelated factors found present would be false-positive for actual aging-associated deficit). This ties in nicely with the work of Farrell and colleagues reviewed above. Multivariate regressions of the frailty scores were generated using multiple methods, with a random forest regression yielding the highest accuracy. The resultant model, termed FRIGHT, had a median error of 1.3 months (38% reduction) and a mean error of 1.6 months (18.75% reduction), making FRIGHT a good predictor of chronological age. Note that although FRIGHT was able to strongly predict chronological age, it was a poor predictor of mortality for all but the oldest of mice.

To predict life expectancy, the authors regenerated the correlation values for all frailty items, this time against life expectancy instead of chronological age. Note that chronological age data was added as a value to fit against in addition to the frailty index items. Although many items that correlated with chronological age also correlated with life expectancy, there were significant shifts in correlation weights (strongest correlations were Chronological Age, Tremor, and Body Condition Score, weakest/uncorrelated were Corneal Capacity, Loss of Whiskers, Nasal Discharge). Multiple multivariate regression models were tried, with a random forest regression again yielding the highest accuracy. The resultant model, termed AFRAID, had a median error of 1.7 months and a mean error of 2.3 months. Exchanging true chronological age for FRIGHT age did not significantly decrease model performance, indicating that frailty index scores alone can yield good predictions of life expectancy.

Of interest is the ability for aging models to preemptively predict the long-term outcomes of aging interventions. FRIGHT and AFRAID were used to quantify mouse data for several interventions. For example, treating mice with enalapril improves health but not maximum lifespan in mice. In concert with the experimental results, FRIGHT consistently under-estimated the chronological age of enalapril-treated mice (an indicator of excess health) and AFRAID did not predict lifespan extension in enalapril-treated mice. In turn, FRIGHT/AFRAID appropriately predicted both healthspan and lifespan extension in methionine-restricted mice (a known health+lifespan extending intervention). Thus, a pair of models processing only auxiliary (phenomenological) aging information was capable of accurately determining biological age and future lifespan, and of detecting and predicting the impact of attempted aging-interventions. FRIGHT offers a valuable tool for accessing otherwise hidden information about biological aging state, and when paired with AFRAID it allows researchers to decouple the effects of aging interventions on healthspan vs. lifespan. Similar results can be achieved utilizing biomarkers such as the CpG methylation-based aging clock that correlates epigenetic changes with chronological age (Horvath, 2013). Extension of these models to other organisms could prove highly valuable in guiding our understanding of the interactions between healthspan and lifespan.

One potential dilemma when attempting to extend the work of Schultz and colleagues is the lack of predefined frailty indices for the vast majority of organisms. Although extensive experimental experience with an organism can lead to observation of traits that appear to predict aging, this process is time consuming and potentially highly inaccurate (as suggested by the large number of uncorrelated or very weakly age-correlated items in the mouse frailty index). Recent advances in neural networks may provide alternatives as they have profoundly changed the way many kinds of data are processed. Convolutional neural networks (CNNs) in particular have rendered image analysis and classification relatively facile (O’Shea and Nash, 2015), and they have been used widely in biology (Angermueller et al., 2016). Lin and colleagues capitalized on this by developing a pair of CNNs for predicting the chronological age of a C. elegans based on a given single brightfield microscopy image (similar brightfield processing CNNs have been used for labelling components of tissue samples (Ounkomol et al., 2018)). CNNs allow the tracking of health and aging without having to predict which features may actually be relevant to these processes. Instead, relevant features are identified by the network without human interference, enabling the use of features indiscernible to human vision or that would be too difficult to define manually (e.g. degree of stippling in the midbody). 913 worm images were taken for nematodes with ages from 1–14 days. 70% of these images were used to train a pair of CNNs for continuous or discrete chronological age prediction, 20% were used for validation, 10% for testing network performance. Various CNN components were tested for integration with the final neural network; InceptionResNetV2 was chosen as the best performing CNN component. To improve network performance, the researchers did artificially specify a network component to detect worm whole-body curvature. Thus, inputs to the final model were: 1) a binary value representing whether the worm body was “curved” or “straight”, and 2) the brightfield image of the worm. The continuous-output network (with 1 floating point output signifying age in days, e.g. 10.73) achieved a minimum mean average error of 0.94 days on the test dataset. The discrete-output network (with 14 floating point outputs matching age 1–14 days, highest value output is the assigned age class) achieved 84.78% accuracy with an error tolerance of 1-day (Lin et al., 2020). This technology represents a sizable advance in automated age-detection tools available for C. elegans. From an applications standpoint, technologies such as this are highly valuable for streamlining future aging research. Unfortunately, neural networks tend to obscure insight into the meaningful features of the data being analyzed. Future work on extracting meaningful feature-targets of these networks could help guide experimental investigation of various aging features; Zeiler and Fergus demonstrate one such technique for visualizing CNN feature layers (Zeiler and Fergus, 2013).

The use of health as a predictor for mortality offers a two-fold benefit in aging research. The obvious advantage is its accessibility and accuracy as a phenotypic readout of aging state. The more subtle advantage is the emphasis it places on healthspan. By using health as a predictor of aging and mortality, we force ourselves to confront the ominous gap that often emerges between measurements of healthspan and lifespan. The current dilemmas faced in human healthcare illustrate this disparity with uncomfortable clarity. Following our success in extending mean lifespan via reductions in infant mortality and elderly mortality alike, the world is now faced with an unprecedented increase in our aged population (Rouzet et al., 2019). Although this demographic shift was once limited to first-world industrialized nations, it has begun to appear in many other countries; for a detailed review of changes in the US, see Cutler and Meara, 2004. The resultant disease burden is immense, and is a strong motivator for future research into methods for reducing or eliminating the healthspan/lifespan gap (for a brief review of this topic, see Crimmins, 2015).

4. Factor-specific theories of aging

A factor-specific theory of aging is one that attempts to explain a set of observational data by identifying one or more causative factor(s). This definition is broad by necessity, as aging factors range from the simple accumulation of a single protein to multi-level hybrid systems that seek to combine molecular and cellular data. Factor-specific theories of aging contain both the highlights and pitfalls of aging research. The pursuit of a crisp, comprehensive factor(s)-driven theory that explains all aspects of aging in a given organism is akin to the quest for the mythical holy grail. Although factor-specific theories often offer unique insights into the real biological mechanisms driving aspects of aging, integrating these theories effectively is often difficult at best. Given the wide range of aging characteristics that have been investigated, the task of integrating this knowledge is one of the most important challenges in aging research in the near future. Many advances in aging research have come from the pursuit of biological mechanisms that can cleanly explain the missing portions of a given black-box model. We note that there are not many factor-specific theories of aging in multicellular organisms. We suspect that the increased complexity renders precise mathematical treatment of biological processes highly challenging, although we contend that it is precisely this mathematical treatment that will ultimately demonstrate the foundations of multicellular aging. Thus, we highlight this as a critical area for future research.

We open with a discussion of papers that have attempted to apply particular aging factors to the theories surrounding damage retention dynamics in unicellular organisms such as E. coli, S. pombe and S. cerevisiae. The more abstracted theoretical foundations for this work are reviewed in Section 2. Erjavec and colleagues constructed a series of ordinary differential equations to calculate the effects of asymmetric damage partitioning, where damage is based on the production and degradation of oxidatively carbonylated proteins, in S. pombe (Erjavec et al., 2008). In brief, it was argued that symmetric damage partitioning led to a homogenous cellular population. No cell was “aged”, but no cell could be considered “young” either. At sufficiently high rates of damage accumulation, this left the simulated population susceptible to clonal senescence. Alternatively, asymmetric damage partitioning ensured that a subset of the population was always in a low-damage state, although at the cost of other cells accumulating damage repeatedly until death. Experimental work confirmed that oxidatively carbonylated proteins asymmetrically partitioned during cell division in S. pombe, and that the recipient of these proteins experiences an extended doubling time and reduced mean lifespan. Additional work implicated SIR2 and TEA1 in the successful segregation of oxidatively carbonylated proteins, as deletion of either of those genes eliminates asymmetric allocation of oxidatively carbonylated proteins. Of particular note was that while Δsir2 cells matched the fitness (e.g. cell division rate) of wild-type cells in standard growth conditions, under stressful growth conditions (e.g. with the addition of hydrogen peroxide) Δsir2 exhibited a marked reduction in fitness relative to wild-type cells (Erjavec et al., 2008). This result strongly supports the hypothesis that asymmetric cell-division is a bet-hedging mechanism to ensure fitness in the face of adversity by demonstrating that this strategy is successful (e.g. capable of outcompeting symmetrically dividing cells) under certain conditions.

Andrade-Restrepo tested whether passive diffusion alone was sufficient to model the behavior of damaged protein aggregates during cell division in S. cerevisiae (Andrade-Restrepo, 2017). Prior experimental work has identified stable aggregates of damaged proteins that are preferentially retained in the aging mother cell during division in S. cerevisiae (Aguilaniu et al., 2003). Although it has been frequently assumed that some form of active partitioning mechanism is required for this, a theoretical need for this had not been clearly demonstrated. Andrade-Restrepo developed a stochastic model that tracked aggregate motion within aging and dividing cells over time. Several versions of aggregate motion were tested including purely random motion and three active variants (a bias towards the mother cell, aggregate confinement at the nucleus or vacuoles, cell membrane adherence and trapping). The model design was heavily influenced by extensive experimental observation. The passive-only model was capable of capturing the major features of aggregate motion and asymmetric allocation during cell division (Andrade-Restrepo, 2017), similar to the findings of Song and Acar that showed that stochastic events alone are sufficient to drive asymmetric division (Song and Acar, 2019). However, the passive-only model of Andrade-Restrepo was not able to reproduce all experimental observations. The average number of mother ↔ daughter boundary crossings was much higher than experimentally observed in the well-fit passive model. Addition of any of the three active mechanisms outlined above greatly reduced the number of boundary crossings and generally improved the model’s ability to replicate experimental observations, suggesting that some forms of active transport are utilized to promote asymmetric allocation of protein aggregates. Andrade-Restrepo also carried out long-term simulations of aging cells with a passive aggregate allocation strategy. He found that high rates of aggregation can induce damage accumulation and thus aging in mother cells. However, low rates of aggregate formation combined with sufficient rates of aggregate clearance can lead to non-aggregate-aging cells under passive allocation regime, suggesting that active allocation may be a requirement for aggregate-dependent aging to occur. This resembles the findings of Erjavec and colleagues, wherein a lack of asymmetric aggregate allocation led to a population of non-aging but less than ideally fit cells (Erjavec et al., 2008). The evolution of active mechanisms for allocating damage during cell division may represent a bet-hedging strategy to increase the fitness of a subset of the population.

Moreno and colleagues observed that aging yeast cells have a strong tendency to arrest in the G1 phase of the cell cycle. Cell cycle phase was quantified by tracking Whi5-GFP localization (Whi5 migrates between the nucleus and cytosol regularly during the cell cycle) in living yeast trapped in a microfluidic chip (Moreno et al., 2019). Of note was that nuclear Whi5 increased 3-fold immediately prior to the final arrest in G1. Whi5 regulatory cyclin Cln3 displayed similar defects in localization in aging cells. Further investigation revealed that protein chaperone function is greatly reduced in aging cells, and Cln3 is heavily dependent on chaperone activity for its proper functioning (Aldea et al., 2007; Moreno et al., 2019; Vergés et al., 2007). The rate of misfolded protein aggregation also increases greatly prior to the final cell cycle and cell death. Based on these findings, they propose a stochastic model of yeast aging centered on the role of asymmetric aggregate inheritance in driving proteostasis failure and death. Asymmetric aging drives an exponential accumulation of protein aggregates, which sap the available pool of protein chaperones. This leads to a loss of functional Cln3, deregulating Whi5 and leading to cell cycle lockup and death. Although chaperone knockdown or knockout was predicted to stunt maximal lifespan, chaperone overexpression was predicted by their model and experimentally confirmed to have no impact on lifespan, as the extent of the chaperone overexpression cannot compete with the exponential nature of the aggregate accumulation in the aging cell. Additionally, the model predicted that increasing available Cln3 via overexpression would increase lifespan in a chaperone-dependent manner, as the higher levels of Cln3 required the presence of the Ydj1 chaperone to extend the lifespan fully (although the Cln3 overexpression was able to almost restore the lifespan in the ydj1 mutant). Finally, it was experimentally demonstrated that premature induction of protein aggregation in young cells led to a recapitulation of the effects observed in old yeast (delayed cell cycle progression, reduced Cln3 function), and that chaperone protein or Cln3 overexpression were sufficient to partially or fully rescue this premature aging effect. Thus, Moreno and colleagues cleanly demonstrates a role for protein aggregation and asymmetric cell division in driving proteostasis collapse, aging, and cell death. This work grounds the plethora of black-box models surrounding asymmetric cell division and aggregate accumulation in concrete biological processes.

Fehrmann and colleagues offer another striking demonstration of the utility of modeling in guiding aging research. Following the development of a specialized microfluidic chip for tracking aging in yeast, they noted the unexpectedly sudden onset of senescence in aging yeast, termed the senescence entry point, or SEP. By most metrics, aging yeast appear generally healthy until a few generations prior to death, at which point they begin to rapidly deteriorate. Some prior work had suggested that mitochondrial failure may be a driving factor of aging in yeast (Hughes and Gottschling, 2012; Veatch et al., 2009). Observation of mitochondrial membrane potential, ΔΨ, as a measure of mitochondrial function revealed no clear relationship between the SEP and loss of mitochondrial function. Instead, loss of ΔΨ appeared to correspond to a shift in metabolism, not in aging process (Fehrmann et al., 2013). A stochastic model of cell aging and death was developed to check whether the available data supported an aging-dependent or aging-independent mechanism driving the loss of ΔΨ. The aging-dependent model could not fit the available data, confirming that loss of ΔΨ is an aging-independent process. Further experimental work revealed that loss of ΔΨ is symmetrically inherited during cell division, leading eventually to clonal senescence among descendants of cells that have lost ΔΨ. Although some associations were found between mitochondrial allocation during cell division and aging, changes in mitochondrial function do not appear to drive the onset of the SEP. This paper demonstrates the utility of modeling to help dissect the complex results common in aging research and the all-too-common outcome of discovering a new and difficult to explain aspect of aging biology.

Expanding on the discovery and characterization of extrachromosomal ribosomal DNA circles (ERCs) in S. cerevisiae (Sinclair and Guarente, 1997), Gillespie and colleagues created a stochastic model of ERC accumulation and impact on aging yeast (Gillespie et al., 2004). This model is driven by three central processes: 1) ERC acquisition (either via excision from rDNA or inheritance) 2) ERC replication 3) ERC redistribution during cell division. Since little was known about the rate of ERC formation, this is treated as a stochastic event with probability:

$$P_{\mathit{\text{excision}}}(t)=min\left(\alpha t^i,1\right)\text{ for i=0,1,2 }$$

where α was a fittable constant and t represented the age of the yeast cell in generations. Although use of discrete values for i limited goodness-of-fit to experimental data, it forced a clear delineation of whether ERC formation probability was uncorrelated with age, increased linearly with age, or increased quadratically with age. Existing ERCs replicate with a constant probability P_rep per-ERC per-generation.

Note that ERCs are known to be asymmetrically retained in the mother yeast cell during cell division. Two schemes of ERC redistribution during cell division were tested: 1) each ERC had a constant probability of being retained in the mother cell, 2) the first N ERCs were always retained in the mother, overflow ERCs were distributed equally between mother and daughter. Mortality was arbitrarily defined as occurring once a cell reached 1000 ERCs. Note that since this model accounts for mother-daughter transmission of ERCs, it must be run across multiple successive generations in a population to accurately replicate actual biological phenomenon. This model was able to reliably reproduce experimentally observed aging curves for wild-type yeast. The best model fit was found using a quadratic increase in ERC-excision probability relative to age (i = 2) and the second scheme of ERC redistribution during cell division (all retained to threshold, then evenly split). Note that model fit is highly sensitive to i, with i = 0 leading to an aging curve shape that is incompatible with experimental data, strongly suggesting that ERC formation is influenced by cellular age. Prior experimental work had shown that overexpression of Sir2 extended lifespan in yeast, purportedly by repressing recombination in rDNA. Best fit to existing Sir2 lifespan data was obtained via halving the probability of ERC excision, suggesting that Sir2 overexpression extends lifespan in yeast by reducing the excision rate for ERCs. Gillespie and colleagues demonstrate how simple stochastic models can be used to capture complex aging factor dynamics (ERC excision, allocation, and mutant gene impact) and identify clear biological consequences (excision rate is strongly age-dependent, allocation is non-stochastic up to a threshold, Sir2 overexpression extends lifespan by reducing excision rate).

Morlot and colleagues follow up on the SEP black-box aging model of Fehrmann and colleagues. Prior work had established that ERCs accumulate exponentially in aging yeast (Gillespie et al., 2004; Sinclair and Guarente, 1997), leading the authors to suspect ERC accumulation may be a driver of the SEP. Fluorescence tracking of rDNA in aging yeast revealed that rDNA accumulation strongly predicted senescence progression and the SEP. Additionally, both pre-rRNAs and rDNA-specific polymerase Pol I were found to accumulate exponentially prior to SEP, suggesting that ERC accumulation leads to excessive rDNA transcription (Morlot et al., 2019). However, net ribosome production was found to be relatively constant throughout cell lifespans, suggesting that a key component of the SEP is a loss of synchronization between rDNA transcription and ribosome production. Thus, exponential ERC accumulation drives excessive rDNA transcription, resulting in the breakdown of nuclear homeostasis, rapidly accelerated senescence, and death. Δfob1 mutants (which have reduced rates of ERC excision from the rDNA) were found to have delayed SEP, with the majority of cells not undergoing SEP at all. These cells exhibited an extended lifespan, and eventually died from an unknown (non-SEP associated) cause. The vast majority of Δsir2 mutants (which accumulate high levels of ERCs) experienced a SEP prior to death. To integrate all these findings, the authors developed a stochastic model of ERC excision, accumulation, SEP, and cell death, heavily based on the prior ERC model developed by Gillespie and colleagues. In brief, this model simulates an individual cell starting from the following parameters:

$$\begin{gathered} Age=0 \\ \mathit{\text{ERCs}}=0 \end{gathered}$$

At each age step, the cell has a k_e chance of accidentally excising an ERC, incrementing ERCs by 1. All ERCs in the cell double every 1.5 generations (derived from experimental data). After accumulating at least 360 ERCs (derived from experimental data), the cells undergo the SEP. Post-SEP cells have a random death rate of 1/5 each generation (derived from experimental data). Choice of k_e was the only free parameter in the model. With a reasonable choice of k_e, this model was capable of tightly fitting the experimental data for SEP-undergoing WT cells. The data for Δsir2 cells was well-fit by merely increasing the k_e , strongly suggesting that Δsir2 reduces lifespan and increases ERC load by increasing the rate of ERC excision in cells. SEP-experiencing Δfob1 cells were accurately modeled by merely reducing k_e , matching prior knowledge that Δfob1 reduces the ERC excision rate. The fit for both WT and Δfob1 non-SEP experiencing cells was improved by the addition of an ERC-independent Gompertz mortality risk, λ:

$$\lambda (age)={\lambda }_0{e}^{\alpha age}$$

This matches the experimental finding that some WT cells and the majority of Δfob1 cells do not experience SEP and thus should not be dying from ERC-associated aging processes. This work, and the resultant model, cleanly fills in the black-box surrounding the role of the SEP in yeast aging left by Fehrmann and colleagues. In doing so, these papers integrate several previously established aging phenomena into a coherent overarching theory of aging in yeast. These integrative theories are essential to progress towards a single, cohesive theory of aging in yeast.

Li and colleagues offer a striking demonstration of the value of black-box models in guiding future research with their crisp biological explanation of the black-box model developed by Jin and colleagues. As an additional bonus, their proposed biological mechanism synthesizes two previously disparate aging processes: chromatin instability and mitochondrial decline (Li et al., 2020). Previous work from the Hao group had developed a 4-state model of aging in S. cerevisiae to accommodate marked phenotypic differences in daughter cell shape and size between aging yeast mother cells. The four states were:

$$\begin{array}{c}{S}_0\to \mathit{\text{healthy}}\\ S_1^{\prime },S_1\to \mathit{\text{elongated}} +\mathit{\text{enlarged}}{}_{\mathit{\text{buds}}}\\ S_2\to \mathit{\text{small}}+\mathit{\text{circular}}{}_{\mathit{\text{buds}}}\end{array}$$

Their model found that one set of states (S₁′, S₁) was associated with a decreased mortality risk and increased overall lifespan, and that state-assignment occurred early in life (see Section 3 for details). Further examination of aging yeast revealed that S₁′, S₁ yeast exhibited nucleolar decline, while S₂ yeast exhibited mitochondrial decline. Integration of a GFP reporter of rDNA silencing revealed that S₁′, S₁ yeast lose rDNA silencing as they age (S₂ yeast do not). Exposure to nicotinamide (a targeted inhibitor of rDNA silencer Sir2) forced the majority of yeast into S₁′, S₁. Tracking levels of heme (an iron-containing compound with a role in mitochondrial maintenance) via two fluorescent reporters revealed a marked decline of heme in S₂ cells. Artificial depletion of heme forced the majority of cells into S₂. Dual-reporter observation revealed that isogenic yeast subdivided between S₁′, S₁ and S₂ early in life with an approximately even split, and that the decision was largely irreversible. Gene deletion lifespan assays revealed that this decision appears to be controlled by SIR2 and HAP4 (heme activator protein, related to mitochondrial function), where SIR2 expression inhibits HAP4 and vice versa. This scheme can be represented as a basic toggle switch, a motif that has been deeply explored in systems biology: first demonstration of a synthetic genetic toggle switch (Gardner et al., 2000); adaptation to glucose-sensing (Bothfeld et al., 2017); growth-rate toggle switch (Jaruszewicz-Błońska and Lipniacki, 2017). Following established methods for modeling toggle switches, a pair of ordinary differential equations were used to model the SIR2 / HAP4 balance. The model predicted that over-expression of SIR2 should enable an escape from HAP4 repression, yielding an additional stable point. Experimental work confirmed that 2x over-expression of SIR2 enabled an escape from the toggle switch, resulting in a third aging state, S₃. S₃ yeast retained both high heme levels and efficient rDNA silencing, exhibiting highly extended lifespans as a result. However, only a small proportion of the population successfully entered S₃ (due to SIR2 over-expression, the majority ended up in the short-lived high SIR2 low HAP4 state S₂). The model predicted that over-expression of HAP4 alongside SIR2 would further bias cells towards S₃, and experimental work confirmed this prediction. This model provides a framework for reducing cellular aging in S. cerevisiae to a simple fate-decision process, where cells stochastically choose which side of a toggle-switch they are locked into for the remainder of their lifespan. The ability of this model to cleanly integrate previously disparate theories of aging (chromatin dysregulation and mitochondrial failure) via both theoretical foundations and experimental validation demonstrates the power of integrative approaches in decoding aging biology.

Hoffman and colleagues offer an innovative approach to modeling aging dynamics in a multicellular organism through the use of multi-level hybrid models. Often a target system will encompass multiple layers of complexity (e.g. biochemical reactions, organelle function, cellular survival); applying a one-size-fits-all model to such a system is either inadvisable or impossible (Anderson, 1972). Multi-level models attempt to integrate two or more “layers” of modeling to achieve a more holistic view of the target system. Hybrid models attempt to wed stochastic and deterministic components to better capture system dynamics. Given the complex, multi-scale nature of aging even in simple organisms such as S. cerevisiae (biochemical adjustments to metabolism and respiration, accumulation of ERCs, mitochondrial failure), multi-level hybrid models can play a unique role in attempting to coherently synthesize the available information. For example, to investigate how the cellular response to heat-shock is optimized: a model accounting for discrete biochemical steps in cell metabolism may be paired with a model of variable cellular response to heat-shock, which in turn could be plugged into a model of many cells competing in a dynamic environment. Mitochondrial failure has long been considered a key symptom and potential cause of aging. A reasonable body of research has explored the role of mitochondrial free radical (over)production in aging C. elegans (Balaban et al., 2005; Harman, 1956). However, this theory cannot fully explain many unusual observations, such as a temporary improvement in fitness following low levels to oxidative stress in C. elegans (this is thought to result from the temporarily protective effects of the activation of the mitochondrial unfolded protein response and represents a subset of the dose-response phenomena known as hormesis). In an attempt to clarify how mitochondrial mechanisms interact with cellular processes with regard to aging, Hoffman and colleagues constructed a multi-level hybrid model. The foundation is a collection of differential equations representing the biochemical and biological dynamics present within a single mitochondrion. Multiple mitochondria were simulated per cell, in addition to a collection of equations controlling cell-scale aging processes. Finally, a population of these cells were simulated to sample the breadth of possible outcomes (Hoffman et al., 2017). On top of this hierarchical collection of differential equations is a stochastic agent-based framework controlling multiple cellular decisions that are difficult to model via traditional means. For example, the “decision” for a healthy cell to become compromised was made based on the proportion of damaged mitochondria in a given cell relative to a stochastically selected threshold value:

$$\mathit{\text{CellStatus}}=\{\begin{array}{c} \mathit{\text{Healthy}}\text{for }\frac{\mathit{\text{mito}}{ }_{\mathit{\text{damaged}}}}{\mathit{\text{mito}}{ }_{\mathit{\text{total}}}}<\mathit{\text{threshold}}\\ \mathit{\text{Compromised}}\text{for }\frac{\mathit{\text{mito}}{ }_{\mathit{\text{damaged}}}}{\mathit{\text{mito}}{ }_{\mathit{\text{total}}}}\ge \mathit{\text{threshold}}\end{array}$$

Note the similarities between this method of simulating aging state transitions and the switch-like shift in mortality in a hypothetical disparate aging system as outlined in Section 3.2 above. In combination, these tools enabled Hoffman and colleagues to fully model mitochondrial and aging dynamics in populations of single cells. Parameters and reaction schemes were derived from available experimental data, and free parameters were individually optimized to fit model outputs to experimental data. The resultant model was capable of capturing small-scale aging processes such as declining NAD⁺ levels, O₂ consumption, and ATP concentration with age (Hoffman et al., 2017). Analysis of broader trends at the cellular level revealed that multiple aging fates were readily observed, matching available experimental data. Some cells exhibited a steady decline towards death, whereas others exhibited an initial period of high stress followed by a recovery of some functionality (the latter case was representative of the experimentally observed instances where low levels of oxidative stress trigger protective mechanisms that increase fitness; similar outcomes have been observed in aging yeast (Swieciło et al., 2000).

Having demonstrated the model’s ability to capture micro- and macro-scale mitochondrial dynamics in aging C. elegans, the authors turned to simulated perturbations of aging based on drug administration and genetic mutation. Based on available data for the mechanism behind a variety of drugs (rapamycin, bafilomycin, pterostilbene, low and high-dose paraquat), simulations were run exploring the impact of variable dosing regimens on micro- and macro-scale outcomes. Detailed analysis revealed that rapamycin and pterostilbene excelled at reducing the damage caused by aging mitochondria. Of note was the ability of the model to distinguish pterostilbene’s ability to delay severe ROS accumulation from rapamycin’s ability to both delay severe ROS accumulation and reduce the proportion of cells that ever reach a severe ROS state. Finally, the model was used to explicitly simulate aging and death with the addition of a probabilistic mortality rate based on cell parameters. The impact of drug and genetic interventions on aging was explored, with rapamycin and pterostilbene again having the greatest ability to extend lifespan.

Through the use of a multi-level hybrid model, Hoffman and colleagues were able to integrate a wide range of known aging phenomena and biological mechanisms to produce a holistic understanding of mitochondrial function and aging in C. elegans. Multi-level hybrid approaches such as this offer real promise for integrating the wealth of available information surrounding aging factors in a variety of model organisms. Although daunting, the use of a multi-level model that accounts for multiple (or all known) aging factors in a given organism could yield the first truly integrative aging model. This would allow us to directly probe whole-organism aging dynamics, and immediately identify if a disconnect exists between current aging theories and real-world aging dynamics. Ultimately, these multi-level hybrid models (with extensive experimental validation) may pave the way towards a complete understanding of aging in a given organism.

5. Modeling the impact of aging on cellular function and organismal behavior

Although the majority of this review (and much of aging research) is devoted to understanding the biological mechanisms driving aging, it is important to acknowledge a secondary aspect of aging research: how aging fundamentally alters cellular function and organismal behavior, for better or for worse. As mentioned in Section 2 above, it is interesting to consider aging not just as a downward spiral towards functional collapse and death, but as a mechanism for generating population heterogeneity and ensuring high fitness against a wide range of possible challenges. The case of the human-pathogenic yeast C. neoformans offers an excellent demonstration of this idea. Aged C. neoformans acquire an unusually thick cell wall, lending them a unique resistance to anti-fungals (reviewed in Bouklas and Fries, 2015). These aged, resilient yeast are capable of forming a persistent sub-population leading to chronic infections.

Although much attention has been paid to the molecular mechanisms governing bud formation and cell division in S. cerevisiae, Wang and colleagues pursued the novel question of how budding preferences govern yeast colony formation. Haploid yeast prefer to bud in an axial manner (next bud site tends to be adjacent to prior site), diploid yeast prefer to bud in a bipolar manner (Freifelder, 1960). Aging haploid yeast are known to lose their axial budding preference (Jazwinski et al., 1998). Combing this and other prior knowledge, Wang and colleagues constructed an agent-based model of yeast colony formation and expansion in a 2-dimensional dynamic nutrient field. Yeast were considered to be circular in shape and were distributed in a grid-free system. Biophysical (e.g. cell-cell adhesion and repulsion) and biochemical (e.g. cell cycle length, aging, damage inheritance) properties were stochastically simulated based on experimental data. Although their findings ultimately revealed that aging plays only an auxiliary role in yeast colony formation, it is interesting to note several results. Colonies spawned from a single aged haploid progenitor cell tended to grow much more slowly and mate much less frequently vs. young-haploid-progenitor colonies. Colonies derived from four aged diploid progenitor cells tended to exhibit a larger colony radius and sparser cell density vs. young-diploid-progenitors (Wang et al., 2017). This work highlights the relative strength of agent-based models in integrating multiple complex processes (aging, budding, mating choice, nutrient consumption) to generate a holistic picture of organismal and population behavior.

Liu and colleagues attempted to probe the often-neglected and difficult to capture phenomenon of gene expression noise in aging cells. Although long recognized as a potent source for heterogeneity, accurately measuring and dissecting noise in gene expression is a challenging task (we recommend Raser and O’Shea, 2005 for a review of this topic). Traditional micro-manipulation assays allow for good access to noise information in morphological features of single yeast cells, but are incompatible with simultaneous lifespan and gene expression measurements. To work around this issue, Liu and colleagues used a microfluidic platform to track individual yeast cells from birth to death. This microfluidic platform was combined with a microscope with a programmable stage to enable automatic tracking of fluorescence in aging cells throughout their lifespans. Noise in gene expression was measured by tracking the variations in fluorescence intensity of YFP driven by the GAL1 promotor, P_GAL1 (the HHF2 promotor was also tested to confirm generalizability of results). Fluorescence measurements were taken every 10 minutes. To calculate variation over time in a reliable manner, fluorescence readings were binned every two generations, yielding ~14 readings per bin. For each bin, coefficient of variation (CV, standard deviation divided by the mean $CV=\frac{\sigma }{\mu }$) and the Fano factor $\left(F=\frac{{\sigma }^2}{\mu }\right)$ were calculated. CV decreased by ~35% with age, while the Fano factor decreased by ~57% with age. To confirm that this reduction in expression noise was driven by aging-induced changes specifically at P_GAL1 and not at the upstream controllers of P_GAL1 activity, P_GAL1 activity was excised from the upstream GAL network by deletion of the GAL80 gene, leading to a constitutively active promoter. The resultant cells still exhibited an aging-dependent decrease in CV and Fano factor, confirming that the aging-associated decrease in noise must act directly at P_GAL1 (Liu et al., 2017).

Based on this data and prior work characterizing the ability of chromatin state to alter eukaryotic gene expression noise (Blake et al., 2003; Raser and O’Shea, 2004), Liu and colleagues expanded on prior work by the Acar lab (Peng et al., 2016; Song et al., 2015, 2014) to develop a stochastic model of chromatin state controlling P_GAL1 →YFP expression. In brief, each promotor in a gene network is assigned a chromatin-base ON and OFF state, where the ON state corresponds to rapid transcription and the OFF state corresponds to basal transcription. The switching rate from OFF to ON is determined by r = r_ONF^η where r_ON is a fittable parameter, η is a promotor-specific nonlinearity constant to account for the number of GAL4 binding sites on the promotors (GAL4 is a transcriptional activator), and F corresponds to the activity of the overall gene network. This model was paired with a prior model of cell volume changes during cell cycle (Ferrezuelo et al., 2012). Parameters were derived from experimental data or fit as appropriate. The model predicted that r_ON and r_OFF both increased with aging; this finding was partially validated by the secondary prediction that YFP expression should remain constant with age, which was confirmed experimentally (Liu et al., 2017). This model strongly predicted that promotor-dynamics were necessary to explain the observed decrease in noise with aging, as changes in transcription rate and mRNA degradation could not accurately reproduce this phenomenon. Deletion of RPD3, a histone deactylase, extended lifespan and significantly reduced noise change with age and constant YFP expression level, suggesting a symmetric protection of r_ON and r_OFF from aging effects. A constitutively active synthetic P_GAL1 was created by combining nucleosome disfavoring sequences in the promotor with the deletion of transcriptional repressor GAL80. This substantially reduced noise in YFP expression, supporting their model of chromatin modification driving the decrease in transcriptional noise with aging. Thus, a combination of experimental and modeling work demonstrated that, at least in S. cerevisiae, noise in gene expression decreases with age, likely as a result of chromatin modification. Moreno and Acar followed up on this work with a comprehensive investigation of the impact of various chromatin regulatory genes on gene expression, noise, and fitness (Moreno and Acar, 2021).

Sarnoski and colleagues investigated the intracellular noise dynamics during the aging of diploid yeast. Using a strain expressing a short-lived protein under a constitutive promotor, they saw that variability in diploid yeast was relatively stable as cells age. Interestingly, the highest level of variability observed in diploid cells was similar to the lowest level observed in haploid cells. The authors attributed the absence of noise reduction in diploids to a few potential factors including the difference in ploidy and the differential abundances of cellular machineries and housekeeping proteins between haploids and diploids; the higher abundance in diploids potentially provides a buffer reducing the observed variability (Sarnoski et al., 2018).

We now turn to an analysis of the role of epigenetics in modulating age-related phenotypes (ARPs) in stem cells. Note that modeling the role of epigenetics in aging is a highly active area of research (Busto-Moner et al., 2020; Chen et al., 2021; Zagkos et al., 2019; reviewed in Mc Auley et al., 2016). Przybilla and colleagues applied a multi-level computational model developed in their previous paper (Przybilla et al., 2012) to explore the relationship between epigenetics and aging in stem cells. Specifically, the authors were interested in the relationship between aging-associated progressive alterations of the epigenome, “epigenetic drift”, and age-related phenotypes experimentally observed in aging stem cells (Przybilla et al., 2014).

To model transcriptional regulation (and the corresponding role of epigenetic modification on transcription), Przybilla and colleagues first constructed an artificial gene interaction network from an “artificial genome”. In brief, the “artificial genome” was a string of length 10⁵ consisting exclusively of the digits 0,1,2,3 (akin to the four-letter code of DNA). A random promotor sequence of 5 digits was used to define all “genes” in the “artificial genome” (yielding ~98 genes, $97.65\approx \frac{{10}^5}{4^5}$). The coding region for each gene was defined as the first seven digits following the end of the promotor, which defined a “transcription factor” (randomly assigned as activating/repressing) capable of binding at: Binding Site = Coding Value[mod4]. The regulatory region for each gene was defined as the entire upstream sequence prior to the next gene. A subset of genes were chosen to control age-related phenotypes (ARPs) for the network.

Transcription of each gene in this network is governed by a differential equation integrating promotor occupancy (dependent on transcription factors) and the binding probability of the protein complex responsible for H3K4 histone methyltransferase at the gene. A series of differential equations governs histone methylation and DNA methylation along with their associated dynamics (H3K4me3 histone methylation leads to upregulated local H3K4me3 in a positive feedback loop, H3K4me3 also blocks local DNA methylation). The combination of positive feedback and nonlinear response mean that H3K4me3 activity can be modeled as a bistable system (Przybilla et al., 2014). The use of bistable systems for modeling certain gene networks are widespread in the literature (Acar et al., 2005; Ferrell, 2008).

Cells, defined in this model as an instance of the artificial genome with associated interaction network, are subjected to environments promoting an active (Ω), or inactive (α) cellular state with defined switching rates between the two states. Active environment cells can proliferate and eventually differentiate (differentiated cells are removed from the model). At start, cells have all available H3K4me3 sites methylated and no DNA methylation. Initial simulations defined no ARPs and did not allow exchange between environments. The authors identified four classes of genes that emerged within this system, genes that are: α stably locked in the high-nucleasome-H3K4me3 state, Ω bistable (can switch between DNA methylation and high-H3K4me3 state), unstable fixed point (stable at H3K4me3 state, but once silenced via DNA methylation, they are “locked-in”); genes less than 200bp in length are too short for nucleosome association and were considered null. Thus, although some gene classes are aging-resilient, certain aging-sensitive classes immediately emerge as a result of the interplay between H3K4me3 / DNA methylation. As the rate of exchange between α and Ω is raised above zero, the regulatory states of α-cells and Ω-cells converge.

Next, a subset of genes in the artificial genome were chosen as ARP-associated genes, whose silencing lead to either a decrease in differentiation or a decrease in proliferation (simulated separately). To maximize age-responsiveness, only bistable genes were selected for controlling the ARP. An ARP-associated decrease in differentiation leads to an overtake of the population by the progeny of aged cells, as they tend to silence bistable genes and thus avoid differentiation (which is equivalent to “senescence” for this model) (Przybilla et al., 2014).

Finally, their model is applied to hematopoietic stem cells (HSC). Recent experimental work revealed that HSCs paradoxically both maintain a pool of young cells for an unusually long time-frame and have young cells that disproportionately contribute to the differentiated cell population. Model simulations revealed that this is likely achieved by assigning the ARP to an increased probability of shifting from Ω to α, P_Ω→α, and a decreased probability of the reverse motion P_α→Ω. Aged cells become enriched in the non-differentiating, non-replicating α state, while young cells can escape to the active Ω state. Simulations based on this setup predicted that it would take ~1 year for the ARP to overtake the system. Thus, a highly abstracted model of a genetic network with a simple pair of regulatory interactions (H3K4me3 vs DNA silencing) paired with an abstracted cell-state simulation was capable of predicting the mechanism behind an unusual observation in aging HSC (Przybilla et al., 2014). This work demonstrates the flexibility of multi-level models in exploring aging beyond causative factors in senescence, and emphasizes their ability to capture unusual and complex phenotypes with relatively simple fundamentals.

Work from the Heinemann lab (Janssens et al., 2015; Leupold et al., 2019) offer an extensive investigation of the effects of aging on the proteome, transcriptome, and metabolism in S. cerevisiae. Note that traditional *omics work in yeast has been limited by a lack of high-throughput methods to isolate aged yeast. Since budding yeast population grows exponentially, the proportion of an unfiltered population of a given replicative age, $P_{age}(n),\text{ is }{P}_{age}(n)\approx \frac{1}{2^n}$. Since aged yeast cells are generally considered to have a replicative age > 15 at a minimum, $P_{age}(15+)\le \frac{1}{32768}$, far below the detection threshold for any bulk assay. To enable *omics work in aging yeast, Janssens and colleagues developed a novel tool for isolating aged yeast cells. This relies on using biotinylation to bind streptavidin-bound iron beads to a population of young yeast. These yeast are flowed through a magnetized column where some of them are captured by the magnet. Fresh media is flowed continuously over the column. Newborn yeast lack the biotin-streptavidin-iron beads, allowing them to flow out of the column, leaving only the old yeast from the initial population in the column. Once the desired time point is reached (prior measurement of doubling time enables estimation of age of cells on the column, verifiable via bud-scar staining of a sample of cells post-column harvest), the column is de-magnetized and the aged cells are harvested for further experiments. Very similar principles were used by another group to develop the Miniature chemostat Aging Device (MAD) (Hendrickson et al., 2018). Note that the harvested cell populations are enriched for aged cells, but the samples also contain a fraction of young cells and dead cells. Isolating the aged cell “signal” requires mathematical deconvolution taking into account the proportions of aged, young and dead cells (measured by cytometry) and the resultant phenotypic values (e.g. proteomic, transcriptomic, metabolic) obtained from three different fractions of a sample (the column effluent, containing mostly daughter cells; the wash fraction, also enriched in daughter cells; and the mother-enriched fraction, with dead and alive aged cells). Janssens and colleagues used this tool to explore the proteome and transcriptome of aging cells, finding a steady de-coupling of the proteome from the transcriptome with age. It is interesting to note that proteins associated with translation regulation were severely over-represented in the proteome relative to the transcriptome in aged cells (Janssens et al., 2015). Later, the same group used LC-MS/MS to measure 18 key metabolites in aged samples generated using the above method. HPLC was used to track extra-cellular metabolites in the wash media (Leupold et al., 2019). Flow cytometry was used to track cell concentrations. A Respiration Activity Monitoring System (RAMOS) was used to track CO₂ production and O₂ consumption by yeast in the aging column. These data were integrated with a system of ordinary differential equations to determine several key parameters, which were then fed to a complex thermodynamic and stochiometric network model of cell function. Regression on this network model to fit the available data yielded the intracellular metabolic flux distribution (Niebel et al., 2019). Advanced age was associated with a drastic decrease in cellular growth rate. Aging yeast were found to switch from a fermentation-dominated metabolism to a respiration-dominated metabolism. Interestingly, this age-induced respiratory metabolism included an unusually high rate of acetate and glycerol excretion, indicative of apoptosis and stress response, respectively. Redox-factor turnover rate was elevated in aged yeast, likely to combat increased production of reactive oxygen species. When paired with the aging-proteome and aging-transcriptome data from Janssens and colleagues, this aging-metabolism dataset and analysis represents a significant step towards a full enumeration of the effects of aging in S. cerevisiae. Although these efforts do not extensively address causality (are the observed effects aging-derived or driving aging?), these deep observations play an essential role in guiding future work towards understanding the causal factors driving aging in S. cerevisiae.

To close this section, we will discuss the use of computational modeling by Augustin and colleagues to investigate the aging-associated decline in function of a fly neural circuit. Common to dipteran insects, the giant fiber system (GFS) is a simple neural circuit dedicated to generating an escape action in response to certain threatening visual stimuli. A pair of giant fiber (GF) neurons in the fly brain initiates this response by activating first the TTMn neurons (which in turn activate the TTM muscles leading to a jump response) and then by activating the DLMn neurons and thus the DLM muscles, which mediate flight (Figure 3A). Prior experimental work by the same lab demonstrated an aging-dependent increase in response to latency of the GFS (Augustin et al., 2017). Augustin and colleagues propose a computational model of the GFS is used to investigate the different circuit properties to identify the cause of this aging-dependent increase in GFS response time. The model was constructed using the NEURON simulation environment (Hines et al., 2009; Hines and Carnevale, 1997), designed for fine-grain simulations of neuronal firing dynamics. In this model, the GFS consisted of four neurons (only accounted for one “side” of the symmetric biological GFS): GF neuron, PSI neuron, TTMn neuron and DLM neuron. NEURON allows for the encoding of simple 2-dimensional structural information for neurons. Given the relatively simple layout of the GFS, encoding it via NEURON was a straightforward process (Figure 3B). Anatomical and physiological parameters were sourced from available data or estimated as necessary. Prior experimental work strongly suggested that a decrease in gap junction conductance (g_gap) was responsible for the increased response latency observed in aging flies (Augustin et al., 2017). Initial simulations with the model revealed that modification of g_gap alone was sufficient to reproduce the observed increase in response time in old flies (Figure 3C). To further validate this, the authors checked whether modification of any other single biophysical parameter could also capture the disparity in response time between young and aged flies. No other single biophysical parameter could capture the experimentally observed data, strongly supporting the hypothesis that a decrease in g_gap is the driving force behind the age-associated increase in GFS response latency. Next, the authors investigated whether modification of anatomical parameters could recover the young phenotype in a fly with the aged g_gap parameter. Strikingly, a ~5-fold decrease in the diameter of the connective neuron PSI reverted DLM latency to the young phenotype. No equivalent anatomical parameter was found for the TTM latency. Overall, changes in anatomical parameters had a larger impact on response latency than biophysical parameters. Finally, the authors demonstrated the utility of their model as a tool for investigating the relationship between arbitrary pairs of parameters as a guide to experimental work (Augustin et al., 2018). These analyses enabled a more holistic understanding of how the GFS is constructed, highlighting the interplay between sodium and potassium reversal potentials, synapse locations vs. weight, and axon length vs. diameter. This work offers an interesting demonstration of the adaptation of specialized non-aging models to aging research, and the potential for these models to offer both aging-specific and generalizable insight into system function. Given the difficulty of generating de novo aging models for multicellular systems, repurposing existing models for aging research offers exciting new inroads to understanding aging in these systems.

Figure 3:

The giant fiber system (GFS) shows an age-dependent increase in response time latency. A. Diagram of GFS anatomy. B. NEURON model of GFS. Arrows indicate where output readings were taken. C. Membrane potential recorded from simulations of the model in (B). Figure adapted from Augustin et al., 2018.

6. Conclusion

Aging is a highly complex phenomenon, outmatched only by the myriad approaches to understanding its causes and effects. Computational and mathematical modeling have played an essential role in the efforts to unravel aging. Here we have tried to present a tailored selection of papers, intended as an introduction to the available methods and as a means for highlighting the current questions in aging research.

Fundamental models of aging suggest profound connections between how aging proceeds across a wide number of organisms, and offer an essential theoretical basis for more applied work. Black-box models in turn enable researchers to map out potential mechanisms driving aging when the experimental techniques to map a causative agent are unavailable (or invisible to the human eye, a novel possibility resulting from the revolution in machine learning). These models play an essential role in guiding future research, contributing strongly to the plethora of factor-specific aging models available for many organisms. Of particular interest is the future role of multi-scale models in integrating these disparate aging models to form a holistic picture of aging in a given organism. Integrating our understanding of lifespan and healthspan, and working to close the lingering gap between them, presents a critical issue in aging research. One exciting possibility is that healthspan could be modeled separately from lifespan, yielding a pair of connected but ultimately independent systems. Finally, we note that mapping and modeling ancillary effects of aging (alterations to metabolism, stress resistance, reaction time) can offer valuable insight into the potential evolutionary benefits of aging and bolster our understanding of how and why healthspan fails long-prior to actual mortality in many organisms. Given the extensive body of work on modeling aging in unicellular organisms such as S. cerevisiae, we believe that the critical next step is an integration of existing models yielding a holistic map of all known aging processes. Although this is a daunting proposition that will require incremental progress, the requisite experimental and theoretical foundations have already been more than fulfilled.

The path towards progress in multi-cellular organisms is less clear. The ability of fundamental models to capture aging dynamics in unicellular and multicellular organisms alike suggests that many of the techniques developed to understand aging in unicellular organisms can be adapted. Future work on multi-cellular aging will likely benefit from the adaptation of multi-scale unicellular and non-aging multicellular models to establish a stronger fundamental understanding of aging at the multicellular level.