A Novel Imputation Approach for Sharing Protected Public Health Data

Abstract

Objectives. To develop an imputation method to produce estimates for suppressed values within a shared government administrative data set to facilitate accurate data sharing and statistical and spatial analyses.

Methods. We developed an imputation approach that incorporated known features of suppressed Massachusetts surveillance data from 2011 to 2017 to predict missing values more precisely. Our methods for 35 de-identified opioid prescription data sets combined modified previous or next substitution followed by mean imputation and a count adjustment to estimate suppressed values before sharing. We modeled 4 methods and compared the results to baseline mean imputation.

Results. We assessed performance by comparing root mean squared error (RMSE), mean absolute error (MAE), and proportional variance between imputed and suppressed values. Our method outperformed mean imputation; we retained 46% of the suppressed value’s proportional variance with better precision (22% lower RMSE and 26% lower MAE) than simple mean imputation.

Conclusions. Our easy-to-implement imputation technique largely overcomes the adverse effects of low count value suppression with superior results to simple mean imputation. This novel method is generalizable to researchers sharing protected public health surveillance data. (Am J Public Health. 2021; 111(10):1830–1838. https://doi.org/10.2105/AJPH.2021.306432)

In this information age, increasing availability of public health surveillance data is catalyzing groundbreaking research while presenting new challenges related to data privacy and completeness. For example, protected government surveillance data cannot be shared without suppressing small values to protect the confidentiality of individuals,¹ which may adversely affect the subsequent analyses. Inference from the analytical results using suppressed data may be subject to bias because of the removal of small count values, yielding potential loss of statistical power because of the reduced sample size. Analyses using data with suppressed values may not produce reliable results for areas with low population counts, for minority population groups, or for rare outcomes.² Suppression is particularly troublesome for geomapping and spatial analytic methods that rely upon joined data across multiple data sets. Suppressed small cell data disproportionately affect rural and small population areas, may discourage research comparing smaller subsets of the population, and leave large spatial areas with unknown or unreportable risk.² We describe a novel and practical method that can provide imputed values for protected government data that would otherwise have limited analytic utility because of cell suppression.

Our imputation approach was motivated by a public health study using administrative surveillance data that employed geographic information systems and spatial epidemiological analyses to investigate spatial and temporal patterns of opioid overdoses in Massachusetts. For this purpose, surveillance data provided researchers the opportunity to evaluate unknown or lesser-known determinants of opioid overdose, misuse, and other adverse outcomes of inappropriate opioid prescribing.³ However, because of required data suppression, as much as 39% of our zip code‒level data were missing for some measures, which had the potential to hamper a precise characterization of the breadth and complexity of these data.² In Massachusetts, the recent availability of enhanced administrative public health data has spurred innovative analysis techniques,^3,4 which have highlighted the need to incorporate small cell values. To overcome this issue, we developed an approach to create a “complete” data set by imputing the missing cells before sharing, so that the subsequent spatial analysis could use an imputed but complete data set.

Our goal was to develop an imputation approach that produced unbiased, reliable, and replicable estimates for suppressed values within an aggregated de-identified opioid prescription data set from the Massachusetts Prescription Monitoring Program. The standard in public health research has been complete case deletion,⁵ or use of basic single imputation methods such as mean imputation (i.e., substituting the suppressed observations with the mean value of the nonsuppressed observations) and last value carried forward (i.e., substituting the suppressed observations with the value from last time point when unsuppressed value was available),^5–8 which have been found to introduce bias and reduce statistical power. More sophisticated imputation methods, including Bayesian spatiotemporal modeling⁸ and multiple imputation,^9–12 are known to produce superior results to simple methods but are not routinely used in epidemiological research, in part because of their steep learning curve and lack of tools and expertise required to conduct them.^8,13 In addition, left-censored data like ours are the most difficult to model^5,7 because assumptions are made on unverifiable observations. Most multiple imputation methods assume missingness is not related to the observed values and incorporate characteristics of the full data set. For our data, the imputation method must include assumptions and adjustments for the suppressed value range to allow precision and minimize bias.^5,7

We tested and compared combinations of several strategies developed from simple imputation methods^8,9,14 and a modified multiple imputation. We developed an imputation method that gleaned information from the zip code of residence, including previous- and future-year values in the zip code as well as the population size, to predict missing values more precisely. A unique attribute of this imputation process is that, as the owner of the data, we knew the characteristics of the suppressed values and we were able to accurately assess the performance of our modeling methods. We incorporated the sum and mean of the suppressed values in our process to improve imputation precision. The method does not require advanced statistical knowledge or programming skills, paving the way for our approach to be applied with protected public health data in various settings, including those with limited resources. Our analysis enables innovative and insightful approaches to better understand key components of prescription opioid misuse in Massachusetts.

METHODS

We employed 35 statewide data sets in the Massachusetts Prescription Monitoring Program that identify individuals with possible opioid prescription misuse through records of all controlled substances dispensed by Massachusetts pharmacies or delivered to a Massachusetts resident by mail to individuals aged 18 years or older. We evaluated these data within a larger analysis that required all nonzero values less than 11 to be suppressed when the data were shared. The data sets included 5 categories of prescriptions that identified individuals with potential opioid prescription misuse, aggregated by year and by zip code. The 35 data sets included variables representing 5 types of potential opioid misuse with 1 annual summary count per 538 zip codes, across 7 years, 2011 to 2017. These 5 types, defined in previous analyses as potentially inappropriate prescribing (PIP),³ were

• PIP1: high-dose opioid prescrip- tions—receipt of opioid prescriptions greater than 100 morphine milligram equivalents per day in 3 separate months;

• PIP2: receipt of opioid and benzodiazepine prescriptions that overlapped by at least 1 day in at least 3 months;

• PIP3: receipt of opioid prescriptions from 4 or more prescribers in any quarter;

• PIP4: receipt of opioid prescriptions from 4 or more pharmacies in any quarter; and

• PIP5: cash payments for opioid prescriptions on 3 or more separate occasions in any quarter.

Imputation Process

For these protected government data, observed counts from zip codes with values between 1 and 10 must be suppressed before sharing. We incorporated the mean, sum, and the standard deviation of the redacted values in our imputation technique to more precisely estimate values to use in the suppressed cells. In addition, we capitalized upon the longitudinal structure of our data to compare previous and future-year results in the same zip codes as the missing values. We considered that social, demographic, and physical characteristics within communities that are likely to contribute to prescription opioid misuse among residents remain similar from year to year during the study period. We inferred that we could more accurately predict the missing values by using values from the previous and next year in the same zip code and by incorporating the zip code population size in the method.

We developed and tested a 3-step imputation process for longitudinal variables (Figure 1). We used SAS version 9.3 (SAS Institute, Cary, NC) to conduct the statistical analyses, model the process, and produce the final imputed results. The steps included a modified previous or next substitution using the suppressed data, followed by mean imputation, and finally a count adjustment based on the actual values. The input was a suppressed data table with each row i representing zip code (i = 538) and column t consecutive years of data (t = 7).

FIGURE 1—

Three-Step Imputation Method Decision Process

Note. The decision process was as follows: (1) data were compared with previous and next year’s value in the same zip code and an imputed value was assigned; (2) if cell value was still missing, the mean of the suppressed values for that year was imputed; and (3) the difference between the sum of the imputed values and the suppressed values was computed; each imputed value was then modified using a population-based modifier to match the sums of suppressed values. The result is the final imputed value.

• 1.Compare previous and next values (modified previous or next substitution). Let xi,t denote a suppressed value x for year t at zip code i. We assumed that previous (xi,t‒1) and future (xi,t+1) values in zip code i would be related to the missing suppressed value and could be used to predict the range of the imputed value. When both xi,t‒1 and xi,t+1 were available (not suppressed), we assumed the suppressed value (xi,t) would be close to the suppression limit, and we assigned it a value of 10; where either xi,t‒1 or xi,t+1 was present but the other suppressed or a zero, we assigned xi,t = 1/2(xi,t‒1 + xi,t+1; i.e., half of the available value); and when the previous and next values were missing or zero (i.e., [xi,t‒1] and [xi,t+1] = 0), we would assume the missing value close to zero and hence assigned xi,t = 1. This imputation procedure aims to simulate the dispersion of the suppressed values. The downside with this method is errors up to a value of 9 can result (i.e., a 1 is used as the imputed value when the true value was 10).
• 2.Mean imputation. Following step 1, for the remaining missing values, we took advantage of the longitudinal structure of the data and substituted the mean of the suppressed values by year. In this case, we assigned all missing xi,t with value $\overline{x}$ t where $\overline{x}$ t was the average for all n zip codes of the suppressed values for year t.
• 3.Population-based adjustment to refine impute values. Following step 2, the sum of the imputed values did not match the original suppressed values. We then developed a zip code‒level population-based modifier using American Community Survey¹⁵ population counts to adjust all the imputed values, so the sum matched the sum of the suppressed values. To adjust the sum, we chose an auxiliary variable, the population count per zip code. The correlation between the population counts by zip code and the test data set values by zip code was 0.75, indicating a strong relationship between zip code population size and the test data values.

We calculated the population modifier for each zip code as the ratio of the total population (on log scale) and the average of the statewide zip code log population, shown in formula 1. The resulting population modifier summed to 1 across the 538 zip codes and ranged from 0.26 for the lowest zip code population count of 10 to 1.27 for the largest zip code population of 60 725.

$$\begin{array}{l}\mathrm{Population}\mathrm{ }\mathrm{modifier}\left[t\right]\\ =\frac{\log \left(\mathrm{zip}\mathrm{ }\mathrm{code}\mathrm{ }\mathrm{population}\mathrm{ }\mathrm{count}\left[t\right]\right)}{\mathrm{mean}(\log (\sum \mathrm{zip}\mathrm{ }\mathrm{code}\mathrm{ }\mathrm{population}\mathrm{ }\mathrm{count}\left[t]\right))}\\ \mathrm{Count}\mathrm{ }\mathrm{adjustment}\left[\mathrm{t}\right]\\ =\mathrm{ }\left(\mathrm{population}\mathrm{ }\mathrm{modifier}\left[\mathrm{t}\right]\right)\mathrm{*}\frac{\mathrm{count}\mathrm{ }\mathrm{difference}\mathrm{ }\left[\mathrm{t}\right]}{\mathrm{n}\mathrm{ }\mathrm{imputed}\mathrm{ }\mathrm{values}\mathrm{ }\left[\mathrm{t}\right]}\end{array}$$ (1)

Modeling

To assess the performance of our approach, we implemented 4 imputation methods using a single year, 2016, within a longitudinal data set of high-dose opioid prescriptions, of which 19% of 538 zip codes were suppressed values. We chose this test variable because it represented the average missing amount (19%) for these data. We created 5 models to compare combinations of the imputation methods. Examples are provided in Table A (available as supplement to the online version of this article at http://www.ajph.org).

• Model 0 – baseline: mean imputation (M0). The mean of each year’s suppressed values was imputed where missing values existed. This method was intended to create an analysis baseline employing a frequently used and simple imputation method.

• Model 1 – mean minus 1 standard deviation imputation (M1). The mean of each year’s suppressed value minus 1 standard deviation of the mean was imputed where missing values existed.

• Model 2 – 2-step imputation (M2). A 2-step imputation approach was employed. A longitudinal previous and next comparison was used to substitute either a 10, half of the existing value, or a 1 in the missing cell. For the remaining missing values, we imputed the mean of the suppressed values for that year.

• Model 3 – 3-step imputation (M3). Model 3 adds a third step to model 2, a population-based count modifier. In this final step, the difference between the original values and suppressed values was calculated. Then the imputed values were multiplied by a ratio of the zip code‒based population modifier and the difference so that the sum of the imputed values closely matches the sum of the suppressed data set by year.

• Model 4 – modified multiple imputation (M4). This was a 3-step process using multiple imputation instead of the longitudinal previous and next approach. We started with the multiple imputation model using SAS statistical software and the previous and next year’s data as parameters and a minimum of 1 and maximum output of 10 to create 5 imputed data sets. For the remaining missing cells, we imputed the mean of the suppressed values for the year and added the population modifier to adjust the imputed sum to closely match the actual suppressed values.

We compared the modeling results to the original unsuppressed values, which are available within the Massachusetts Department of Public Health but cannot be shared externally because of legal suppression requirements. To evaluate the performance of the imputation models, we calculated the root mean squared error (RMSE), the mean absolute error (MAE), and the proportional variance (PV) where

$$\mathit{RMSE=}\frac{\sqrt{{\displaystyle \sum {\mathit{(imputed-actual)}}^2}}}{n\hspace{0.17em}\mathit{imputed}}\mathit{MAE=\sum }\frac{\mathit{|imputed-actual|}}{n\hspace{0.17em}\mathit{imputed}}\mathit{PV=}\frac{\mathit{variance}\hspace{0.17em}\mathit{imputed}}{\mathit{variance}\hspace{0.17em}\mathit{suppressed}}$$ (2)

RMSE and MAE summarize the differences between the imputed and actual values and provide measures of the precision of the imputation; MAE gives equal weight to all errors while RMSE gives extra weight to large errors. For MAE and RMSE, a smaller value indicates smaller errors and, hence, better imputation performance. PV compares the variance between the imputed and suppressed values and is a measure of how well the variance is preserved. A PV of 1 is the goal, less than 1 implies the imputed values are underdispersed, and greater than 1 implies that they are overdispersed.

To further analyze the model result and suitability for spatial analysis, we created maps visualizing the original data including suppressed cells, the imputed values for each model’s suppressed cells, and the final “complete” data set showing the original data with the imputed values. We subjectively evaluated whether the maps incorporating the imputed values preserved the spatial patterns and range in the actual suppressed values.

RESULTS

We compared results for the 4 models, M1 through M4, with the baseline M0, and present them in Table B (available as a supplement to the online version of this article at http://www.ajph.org). We observed that the PV differed considerably among the 4 models. M0 and M1 modeled results were underdispersed with a PV near zero; while they provide a “complete” data set, the imputed values tell us little about the nuances between the zip codes they represent. M2, the 2-step method, had lower RMSE and MAE than M0 and retained 29% of the variance of the data, yet the sum of the opioid prescription imputed values in model M2 was 18.26 lower than the actual suppressed values. M3, the 3-step method, had the best results, with 22% lower RMSE (2.27 vs 2.92) and 27% lower MAE (1.88 vs 2.56) than the baseline M0. Model M3 nearly matched the sum of the actual suppressed values (‒1.44 less) and retained 34% of the variance of the suppressed values. Of the 5 multiple imputation‒based results, we selected multiple imputation 1, which had the lowest errors and highest proportional variance as the values to be used in M4. The results showed model M4 was less dispersed than M2 and M3, retaining only 17% of the variance, and had slightly higher errors than M3 (2.65 RMSE vs 2.27 and 2.26 MAE vs 1.88). Ultimately, we used M3, the 3-step method, to impute values for all our study variables.

After choosing the 3-step imputation approach as our final imputation model, we performed it on all 35 variables (i.e., 5 opioid prescription misuse variables across 7 years). The method produced similar errors as the modeled result (RMSE of 2.34; 95% confidence interval [CI] = 2.28, 2.40 vs 2.27 and MAE of 1.91; 95% CI = 1.85, 1.97 vs 1.88) with slightly improved PV over the test results (0.46 [95% CI = 0.37, 0.55]) vs 0.34 PV). The stratified results summarized in Table 1 show that as the percentage of imputed values increased, the errors decreased (from 2.37 [95% CI = 2.26, 2.48] to 2.20 [95% CI = 2.13, 2.27] RMSE and 1.95 [95% CI = 1.83, 2.07] to 1.76 [95% CI = 1.70, 1.64] MAE), while the PV increased (from 0.46 [95% CI = 0.36, 0.56] to 0.52 [95% CI = 0.43, 0.61]). The variables with 30% to 39% of values imputed had the best results. Precision, of which dispersion is a measure, is particularly important for spatial analysis, in which differences between small cells can be used to identify areas with emerging and subsiding risks, known as hot and cold spots.

TABLE 1—

Modeled Results for High-Dose Opioid Prescriptions, 2016, and Imputed Statistical Results for 35 Suppressed Opioid Prescription Variables: Massachusetts, 2011–2017

	% Imputed	RMSE	MAE	PV
Model results
M0: mean imputation	19	2.92	2.56	0.00
M1: mean‒1 SD	19	4.06	3.17	0.00
M2: 2-step	19	2.53	2.11	0.29
M3: 3-step	19	2.27	1.88	0.34
M4: mean imputation plus 2-step	19	2.65	2.26	0.17
Imputed resultsa
17 data sets	10–15	2.37 (2.26, 2.48)	1.95 (1.83, 2.07)	0.46 (0.36, 0.56)
11 data sets	16–20	2.37 (2.30, 2.44)	1.93 (1.82, 2.04)	0.43 (0.34, 0.52)
7 data sets	30–39	2.20 (2.13, 2.27)	1.76 (1.70, 1.82)	0.52 (0.43, 0.61)
All 35 data sets, mean	19	2.34 (2.28, 2.40)	1.91 (1.85, 1.97)	0.46 (0.37, 0.55)

Note. MAE = mean absolute error; PV = proportional variance; RMSE = root mean squared error.

^aIncludes 95% confidence interval.

Table 1 compares the modeled and the overall imputed values and statistical results. We stratified the imputed data by the percentage of the data imputed (10%–15%, 16%–20%, and 30%–39%) and provided the overall results and 95% CIs for the imputed results. The full results are provided in Table C (available as a supplement to the online version of this article at http://www.ajph.org).

Figures 2a through 2c present the statistical measures of the imputed values categorized by percentage of values imputed. The charts illustrate that errors (RMSE and MAE) converge at lower values as the percentage imputed increases, and as the imputed proportion increases, the values become less dispersed (PV). This clustering as the proportion of imputed values increases results from more instances in which the mean value is inserted in the imputation algorithm. As the percentage missing increased, the variability in errors and the variance decreased, showing that, with up to 39% missing values, this method maintains similar precision and variance preservation as data missingness increases.

FIGURE 2—

Error Results for Imputed Values in 35 Potentially Inappropri- ate Opioid Prescription Variables for (a) Root Mean Squared Error, (b) Mean Absolute Error, and (c) Proportional Variance of Imputed Values: Massachusetts, 2011–2017

DISCUSSION

We developed an imputation approach for longitudinal data that largely overcame the adverse effects of the suppression of small cell sizes. The imputed data set can then improve the subsequent statistical and spatial analyses conducted with public health surveillance data.

Our imputed variables retained the mean and sum of the suppressed values and, on average, preserved nearly half (46%) of the variance. In addition, we found that the 3-step imputation method produced lower errors than mean imputation (19% lower RMSE and 25% lower MAE). This technique allows inclusion of variables at lower aggregation levels enhancing analytic precision for rare outcomes, particularly in rural areas, while preserving data confidentiality. This novel imputation method is generalizable to public health practitioners and researchers using protected data with design features similar to ours. We also suggest that researchers can modify multiple imputation results by adding mean imputation and a population modifier to produce useable data.

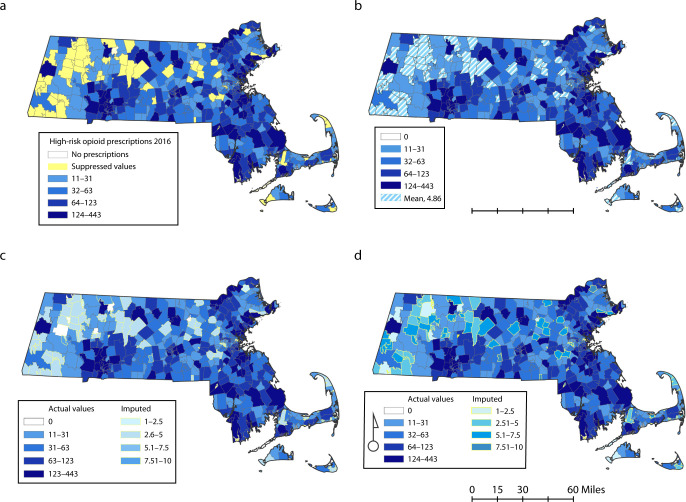
The value of spatial analyses that utilize data from an imputed and complete data set, free of suppressed area-level measures (or “holes” in the map), cannot be understated. As demonstrated in Figure 3a (with yellow suppressed polygons), nearly 1 in 5 (19%) low-count areas (i.e., zip codes) would be “omitted” from standard maps that rely on suppressed data, leaving most of the western part of the state mapped with a lack of heterogeneity. Although the data visualized in Figures 3b and 3c allow analysis of the full data set, they do little to draw out the nuances between small areas and may not produce adequate precision for small cells and areas. Meanwhile, Figure 3d (with imputed polygons) presents a more comprehensive range of values, allowing for a closer approximation of the spatial distributions of the outcome in small cells while distinguishing the imputed values from the true values. As the data visualized in Figures 3a and 3d are very different, the imputed values will allow an examination of the small cell data, up to 39% of the values in these data.^9,13 Recently, Bayesian spatiotemporal modeling has gained popularity in analyzing synthetic data for public use.¹² However, the complex statistical expertise^8,9 to conduct these models may exceed the benefit compared with this straightforward method. Our proposed approach, admittedly less sophisticated, is easy to carry out, and can be utilized by a wide range of researchers with nonstatistical background and without geospatial software.

FIGURE 3—

Illustrative Example of Thematic Maps of a Test Data Set “High-Dose Opioid Prescription” Count by Zip Code for (a) Initial Data With 19% Values Missing Because of Suppression, as Denoted by Yellow Shading; (b) Mean Imputation Shown With Original Values; (c) Modified Multiple Imputation Results Shown With Original Values; and (d) “Complete” Final Data Showing Original Data With Imputed Results Together: Massachusetts, 2016

Limitations

Our findings should be considered in light of several limitations. We conducted our test approaches on a single outcome variable, high-dose opioid prescriptions, and our method might produce different results with other longitudinal outcomes depending on the characteristics of the data set. For example, our imputation method resulted in an average of 24% of values imputed in the first step and 76% in the second step, mean imputation. Another data set may result in a different proportion of cells imputed in each step, hypothetically producing much different variance and errors in the imputed values. In addition, our results required that summary statistics for the complete and unsuppressed data be available; the method is best performed by the data sharer, or a researcher who has access to summary statistics of the suppressed values. Third, we used these data for a geospatial analysis project and had the benefit of reviewing the results in geographic information systems maps. Researchers should include a method to assess the imputation results such as mapping the data or comparing the unimputed analysis findings to the imputed analysis results.

Public Health Implications

This novel multistep imputation approach provides a method to obtain reliable measures for key opioid prescribing measures, which had up to 39% suppressed cells. Our computationally efficient approach enhances precision of small area estimates for rare events and less populated areas, facilitating more accurate risk mapping, spatial epidemiological, and statistical modeling approaches while preserving confidentiality. These results warrant further application of the imputation method to refine the approach, to assess whether this approach can function accurately when used with more diverse longitudinal data, and to compare the results with more sophisticated modeling methods.