An isotropic EPI database and analytical pipelines for rat brain resting-state fMRI

Abstract

Resting-state functional magnetic resonance imaging (fMRI) has drastically expanded the scope of brain research by advancing our knowledge about the topologies, dynamics, and interspecies translatability of functional brain networks. Several databases have been developed and shared in accordance with recent key initiatives in the rodent fMRI community to enhance the transparency, reproducibility, and interpretability of data acquired at various sites. Despite these pioneering efforts, one notable challenge preventing efficient standardization in the field is the customary choice of anisotropic echo planar imaging (EPI) schemes with limited spatial coverage. Imaging with anisotropic resolution and/or reduced brain coverage has significant shortcomings including reduced registration accuracy and increased deviation in brain feature detection. Here we proposed a high-spatial-resolution (0.4 mm), isotropic, whole-brain EPI protocol for the rat brain using a horizontal slicing scheme that can maintain a functionally relevant repetition time (TR), avoid high gradient duty cycles, and offer unequivocal whole-brain coverage. Using this protocol, we acquired resting-state EPI fMRI data from 87 healthy rats under the widely used dexmedetomidine sedation supplemented with low-dose isoflurane on a 9.4 T MRI system. We developed an EPI template that closely approximates the Paxinos and Watson’s rat brain coordinate system and demonstrated its ability to improve the accuracy of group-level approaches and streamline fMRI data pre-processing. Using this database, we employed a multi-scale dictionary-learning approach to identify reliable spatiotemporal features representing rat brain intrinsic activity. Subsequently, we performed k-means clustering on those features to obtain spatially discrete, functional regions of interest (ROIs). Using Euclidean-based hierarchical clustering and modularity-based partitioning, we identified the topological organizations of the rat brain. Additionally, the identified group-level FC network appeared robust across strains and sexes. The “triple-network” commonly adapted in human fMRI were resembled in the rat brain. Through this work, we disseminate raw and pre-processed isotropic EPI data, a rat brain EPI template, as well as identified functional ROIs and networks in standardized rat brain coordinates. We also make our analytical pipelines and scripts publicly available, with the hope of facilitating rat brain resting-state fMRI study standardization.

1. Introduction

Resting-state functional magnetic resonance imaging (fMRI) provides a non-invasive means to measure brain-wide functional connectivity (FC) without assigned tasks or stimuli (Biswal, 2012). This translational approach has drastically expanded the scope of neuroimaging research in both humans (Menon, 2011; Sadaghiani and Wirsich, 2020; Smith et al., 2013) and animals (Chuang and Nasrallah, 2017; Coletta et al., 2020; Grandjean et al., 2020; Liska et al., 2015; Liu et al., 2020; Ma and Zhang, 2018; Pais-Roldan et al., 2018; Pan et al., 2015; Schwarz et al., 2009) by advancing our knowledge about the topologies and dynamics of functional brain networks (He et al., 2018; Keilholz et al., 2016; Ma and Zhang, 2018; Sobczak et al., 2021). Several pioneering efforts have been made in the human fMRI community to minimize data variability arising from diverse implementation of data acquisition (Casey et al., 2018; Van Essen et al., 2012; Yan et al., 2013), pre-processing (Adhikari et al., 2019; Alfaro-Almagro et al., 2018; Benhajali et al., 2020; Esteban et al., 2019), and post-processing methodologies (Smith et al., 2013; Wyman et al., 2013). As a result, several databases and processing pipelines have been disseminated (Casey et al., 2018; Glasser et al., 2016; Howell et al., 2019; Mueller et al., 2005; Sudlow et al., 2015; Van Essen et al., 2013; Yan et al., 2013), making significant contributions to data standardization and reproducibility. Similarly, several key initiatives have been led by researchers in the rodent fMRI community to develop and share databases (Grandjean et al., 2020; Liu et al., 2020). Despite these efforts, progress has been hampered by challenges in the acquisition and analysis of rodent resting-state fMRI data using echo planar imaging (EPI).

EPI rapidly encodes signals with robust T2* sensitivity to blood oxygenation, and is the standard imaging sequence used to acquire fMRI data (Ogawa et al., 1990). In humans, EPI data is commonly acquired with isotropic spatial resolution and whole-brain coverage (Smith et al., 2013; Van Essen et al., 2012). In rodents, however, EPI is predominantly acquired with anisotropic resolution (Aedo-Jury et al., 2020; Albaugh et al., 2016; Broadwater et al., 2018; Hsu et al., 2016; Liang et al., 2018; Liu et al., 2020; Lu et al., 2012; Mandino et al., 2019; Pan et al., 2018; Tsai et al., 2020; Van Den Berge et al., 2017). This setting is inherited from the traditional coronal slicing used to view rodent brains in histological sections (Paxinos and Watson, 2014; Paxinos et al., 2015). As the rostral-caudal axis is the longest axis in the rodent brain, coronal imaging requires either many imaging slices or thick slices in order to achieve sufficient spatial coverage. In a conventional setting, the number of slices is limited by the repetition time (TR) that dictates the fMRI temporal resolution. This has led to anisotropic voxels with high in-plane resolution and low through-plane resolution (i.e., “French fry” shaped voxels). It remains common to image rodent brains at 2–3 times lower through-plane than in-plane resolution, and in many cases, slices covering the olfactory bulb and cerebellum are omitted due to temporal resolution requirements, gradient duty cycle limitations, or field inhomogeneity-related distortion over these areas (Broadwater et al., 2018; Coletta et al., 2020; Grandjean et al., 2020; Liang et al., 2018; Liu et al., 2020; Lu et al., 2012; Paasonen et al., 2018; Pan et al., 2018).

Imaging with anisotropic voxels and/or reduced brain coverage to achieve desired temporal resolutions comes with significant trade-offs for data standardization and processing pipeline development. For example, in comparison to isotropic voxels, anisotropic voxels increase deviation in brain feature detection (Mulder et al., 2019), reducing registration accuracy to template space. Additionally, incomplete brain coverage requires either additional resampling or truncation of the brain template to match the imaging volume, making it difficult to compare results across studies. These shortcomings prompted us to implement an imaging protocol with isotropic spatial resolution and whole-brain coverage in rodents. Our strategy was to simply reduce the total number of slices required for whole-brain coverage by acquiring images in the short dorsal-ventral axis rather than the long rostral-caudal axis.

We expected that an isotropic EPI protocol with whole-brain coverage would benefit the standardization of rodent resting-state fMRI data as it facilitates spatial normalization with minimal data modifications. In this study, we evaluated a high-spatial-resolution (0.4 mm), isotropic, whole-brain EPI protocol with TR of 2 s for the rat brain and disseminated an 87-subject database with a total of 74,200 volumes acquired on a 9.4 T MRI system. All rat subjects were ventilated and sedated with a widely used protocol of dexmedetomidine supplemented with low dose isoflurane (Fukuda et al., 2013). We documented quality control profiles and demonstrated superior registration results that more accurately localized brain anatomical features compared to data with anisotropic resolution. We generated an isotropic EPI template of the rat brain to streamline the preprocessing steps and used a multi-scale dictionary-learning approach and k-means clustering to identify reliable functional regions of interest (ROIs) from this dataset. We reported several key topological properties of the rat brain intrinsic functional network and demonstrated that the group-level FC network exhibited high spatial similarities across rat strains and sexes. Through dissemination of the raw and processed data, we seek to join forces with existing rodent resting-state fMRI databases, to promote open science, and to overcome standardization barriers.

2. Materials and methods

2.1. Animal subjects and preparation

This database includes rats aged P80–210 weighing 300–450 g across cohorts of three different rat strains: Sprague-Dawley (n = 41), Long-Evans (n = 13), and Wistar (n = 33); and both sexes: male (n = 65) and female (n = 22). Detailed information about each cohort is summarized in supplementary Table S1. All animals were housed in a temperature- and humidity-controlled vivarium on a 12:12 h light:dark cycle with ad libitum access to food and water. All experiments were in accordance with the Guide for the Care and Use of Laboratory Animals established by the National Institutes of Health, using protocols approved by the Institutional Animal Care and Use Committee at the University of North Carolina (UNC) at Chapel Hill. In preparation for MRI, rats were initially anesthetized with 4% isoflurane (Vaporizer #911103, VetEquip Inc., Livermore, CA, USA) mixed with medical air and endotracheally intubated using a 14G × 2″(> 400 g) or 16G × 2″(< 400 g) intravenous (i.v.) catheter (Surflash Polyurethane Catheter, TERUMO, Somerset, NJ, USA). Respiration was maintained by an MRI compatible ventilator (MRI-1, CWE Inc, Ardmore, PA, USA) set at 60 breaths/min and an inspiration time ratio of 40%. Next, the isoflurane concentration was adjusted to 2% and the animals were secured to a custom-built, MR-compatible rat cradle. A rectal probe was used to monitor core body temperature (OAKTON Temp9500, Cole-Parmer, Vernon Hills, IL, USA) and a capnometer was used to monitor heart rate, peripheral blood oxygen saturation, and end-tidal CO₂ (SURGIVET® V90041LF, Smith Medical, Dublin, OH, USA). Body temperature was maintained at 37 ± 0.5 °C using a circulating water blanket connected to a temperature adjustable water bath (Haake S13, Thermo Fisher Scientific, Waltham, MA, USA). Ventilation tidal volume was adjusted to keep the heart rate at 300 ± 50 beats per minute, peripheral blood oxygen saturation above 96%, and end-tidal CO₂ between 2.8 and 3.2%. End-tidal CO₂ values from this capnometer system were previously calibrated against invasive sampling of arterial blood gas, reflecting a partial pressure of carbon dioxide (pCO₂₎ level of 30–40 mm Hg (Shih et al., 2012; Shih et al., 2013). Upon stabilizing the animals, a cocktail of dexmedetomidine (0.05 mg/kg/h) and pancuronium bromide (0.5 mg/kg/hr) was continuously infused via the intraperitoneal cavity (i.p.) (Albaugh et al., 2016; Broadwater et al., 2018; Van Den Berge et al., 2017) and isoflurane was reduced to 0.5% (Fukuda et al., 2013). The infusion was started 30 min prior to the resting-state fMRI scans (Lu et al., 2012).

2.2. MRI acquisition

All MR images were collected through the UNC Center for Animal MRI (CAMRI) service on a Bruker BioSpec 9.4-Tesla, 30 cm bore system (Bruker BioSpin Corp., Billerica, MA) with ParaVision 5.1 or 6.0.1 on an AVANCE II console. Two combinations of hardware were used: 1) a 72 mm volume coil as the radio frequency (RF) transmitter (Bruker BioSpin Corp., Billerica, MA) with an RRI BFG 150/90 gradient insert (up to 740 mT/m gradient strength; Resonance Research, Inc, Billerica, MA) paired with a Copley C700 gradient amplifier (up to 300 A and 700 V; Copley Controls Corp., Canton, MA) or 2) an 86 mm volume coil as the RF transmitter (Bruker BioSpin Corp., Billerica, MA) with an RRI BFG 240/120 gradient insert (up to 1000 mT/m gradient strength; Resonance Research, Inc, Billerica, MA) paired with a Prodrive BNG-500/1000 gradient amplifier (up to 500 A and 1000 V; Resonance Research, Inc, Billerica, MA). The difference of hardware versions was investigated by comparing tSNR between two similar subject groups (cohort ID WT-M between P80-P90 and P193–200 groups, see Table S1) using permutation-based one-way ANOVA. We did not find any significant difference (p < 0.05, voxel size > 10, multiple comparison corrected). All data used a 4-channel, rat brain array coil as the receiver (Bruker Biospin Corp., Billerica, MA). Magnetic field homogeneity was first optimized by global shimming, followed by local second-order shims using a MAP-SHIM protocol. For each subject, we acquired a total of 20 or 30 min of blood oxygenation level-dependent (BOLD) resting-state fMRI data using a 2D multi-slice, single-shot, gradient-echo EPI sequence: TR = 2000 ms, echo time (TE) = 14 or 15 ms, bandwidth = 250 kHz, flip angle = 70°, field of view (FOV) = 28.8 × 28.8 mm, matrix size = 72 × 72, slice number = 32, and slice thickness = 0.4 mm, resulting in an isotropic voxel resolution of 0.4 mm. These parameters were set originally using the hardware combination #1 stated above and were kept the same after an instrument upgrade. Detailed information related to the specific hardware combination used for each subject group is summarized in Table S1.

To evaluate preprocessing performance, we compared isotropic EPI data against an anisotropic EPI dataset obtained via the UNC CAMRI service using hardware combination #1 stated above. These data were acquired with a 2D multi-slice, single-shot, gradient-echo EPI sequence: TR = 1000 ms, TE = 12.6 ms, bandwidth = 250 kHz, flip angle = 70 degrees, FOV = 25.6 × 25.6 mm, matrix size = 80 × 80, slice number = 12, slice thickness = 1 mm (Broadwater et al., 2018).

2.3. EPI template and coordinate system

To minimize the number of spatial normalization steps, we developed an EPI template and proposed a coordinate system using anterior commissure (AC) and posterior commissure (PC) landmarks that can best match the standard, histology-based, coordinate system from the Paxinos and Watson’s rat brain atlas (Paxinos and Watson, 2014). We employed a high-resolution structural rat brain MRI template (Paxinos et al., 2015) to guide EPI template reorientation. We used the AC as the center point and then aligned the PC to the following coordinates with respect to AC: −4.6 mm anterior-posterior (AP), 1.6 mm dorsal-ventral (DV), and 0 mm left-right (LR) according to the Paxinos and Watson’s rat brain coordinate system (Paxinos and Watson, 2014). Next, using the EPI data from a cohort with fluorinated-paste ear-filling (Sprague-Dawley rats, male, n = 10), we performed motion correction and manual skull stripping followed by the Advanced Normalization Tools (ANTs) ‘buildtemplateparallel.sh’ script (Avants et al., 2010) for Symetric Normalization (SyN) non-linear co-registration to generate a population-averaged EPI as our template. Finally, the initial template was co-registered to the anatomical template with affine transformation. The detailed pipeline is presented in Fig. 1. The high-resolution structural template and resulting EPI template are shown in Fig. S1.

Fig. 1.

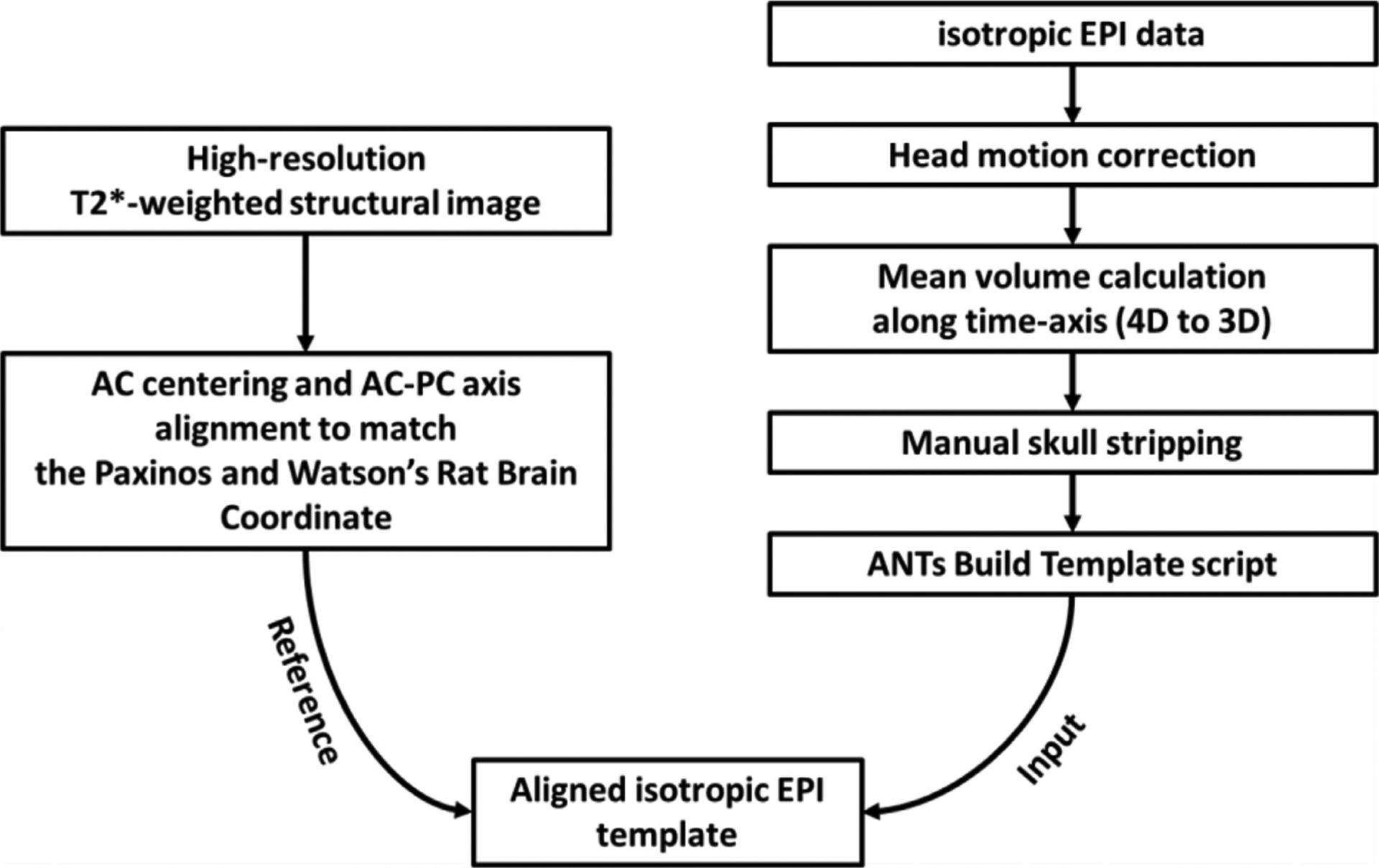
Rat brain EPI template development pipeline which uses an EPI dataset with 0.4 mm isotropic spatial resolution and high-resolution T2*-weighted structural images.

2.4. Comparison of registration performance between isotropic and anisotropic EPI data

To demonstrate whether our proposed isotropic EPI protocol improved image registration performance compared to a conventional anisotropic EPI protocol, we compared the accuracy of estimated rigid-body motion parameters and outcomes of non-linear spatial normalization. Due to the challenge of reproducing identical motion across conditions, we evaluated rigid-body motion parameters by computer simulation. First, we acquired a single volume of reference brain-wide EPI data at a higher 0.3 mm isotropic resolution. Random sub-voxel-level motion with six degrees of freedom (three transpositions and three rotations for each axis) was generated from continuous uniform distribution and added to 100 replicates of the reference brain-wide EPI data. The 3rd order polynomial curves are also applied to produce drift motion. This process was repeated 100 times to generate 100 time-series datasets with 100 volumes each. Subsequently, random gaussian-distributed spatial noise with amplitudes up to one standard deviation of the reference image’s background was added to each volume. We then down-sampled the data to 1) 0.4 mm isotropic resolution and 2) 0.32 mm in-plane resolution with 1 mm slice thickness (i.e., anisotropic resolution). The anisotropic data were also cropped to cover 5 mm anterior to AC and 7 mm posterior to AC, mimicking the anisotropic EPI data referenced in Section 2.2 MRI Acquisition. Motion parameters were then estimated by using 3dvolreg command in Analysis of Functional Neuro Images (AFNI) (Cox, 1996). The root mean square error (RMS) of each motion axis was calculated and compared against ground-truth data. For the non-linear registration, we performed SyN diffeomorphic registration (Avants et al., 2008) on both isotropic and anisotropic data. As the issues related to this non-linear registration process are hard to demonstrate with parametric measurements, visual inspection of the outcome is still recommended in practice. Therefore, in this study, we performed a subjective visual comparison of registration outcomes to demonstrate the representative issues on non-linear registration.

2.5. Data preprocessing, and quality profiling

All EPI data were first corrected for slice timing, followed by motion correction using AFNI (Cox, 1996). Each 4D dataset was then averaged across time to improve signal-to-noise ratios (SNR) for subsequent skull stripping. The brain mask for each time-averaged EPI image was manually drawn using ITK-snap (Yushkevich et al., 2006) by an experienced, rodent brain MRI data-analyst (W.B.) (Hsu et al., 2020) and was subsequently applied to the corresponding 4D EPI data to remove non-brain components. The skull-stripped data were then spatially normalized to the EPI template using ANTs SyN diffeomorphic registration (Avants et al., 2008) before further group-level analysis. For nuisance signal removal, third-degree polynomial curves representing baseline trend and the six motion parameters estimated from motion correction were regressed out, after which a 0.01 – 0.1 Hz band-pass filter was applied. Of note, because recent studies showed that signals with a neural origin may be embedded within the global signal (Gutierrez-Barragan et al., 2019; Ma et al., 2020), we opted for not regressing out global signal. We also did not regress the white matter (Li et al. 2020) and the cerebral spinal fluid signals (Fultz et al., 2019) to maintain data integrity and avoid partial volume confounds. The filtered data were then smoothed with a gaussian kernel with full width half maximum (FWHM) at 0.5 mm. To evaluate the effect of nuisance removal, we performed quality control using metrics including framewise displacement (FD), temporal SNR (tSNR), and DVARS. The FD is defined as the sum of the absolute derivatives of the six realignment parameters and for calculation. For the calculations, rotational displacements were converted from angular degrees into millimeters by calculating displacement on the surface of a 9 mm radius sphere (Power et al., 2012). This radius is selected as it is approximately the distance from the cortex to the center of interaural line, representing the rotational axis of head motion with ear-bar fixation. Regarding the DVARS, D refers to temporal derivative of time-courses and VARS refers to root mean squared variance over voxels (Power et al., 2012). A lower DVARS value indicates fewer intensity changes with respect to the previous time point as opposed to the global signal. Note that the mode value of brain voxels was normalized to 1000 before and after nuisance removal for DVARS (Power et al., 2012) calculations, while the tSNR was calculated without intensity normalization for both conditions.

2.6. Amplitude of low frequency oscillation, regional homogeneity, and functional connectivity strength

Amplitude of low frequency oscillation (ALFF), regional homogeneity (ReHo), and FC strength were computed from the isotropic EPI dataset at the voxel level. ALFF measures the strength of low frequency power at the voxel level and is the summation of power spectrum amplitudes in the frequency range of 0.01–0.1 Hz (Yang et al., 2007). ReHo measures the synchrony between a voxel and its neighboring voxels using Kendall’s coefficient of concordance (Zang et al., 2004). We used 27 neighboring voxels for ReHo calculation in this study. FC strength measures the FC of each voxel to the entire brain (Rubinov and Sporns, 2010), and is the summation of the Pearson’s correlation coefficients between a given voxel and all other voxels in the brain. We used positive FC values to calculate connectivity strength because our FC results are predominantly positive (Fig. S2). Also, it has been reported that negative FC is not robust under anesthesia, and the interpretation of the negative FC under anesthetized condition remains controversial (Liang et al., 2012). Each metric was calculated first at the subject-level, then at the group-level using permutation-based one-sample t-tests (see Section 2.12 for statistical details).

2.7. Specificity of functional connectivity

The seeds of primary sensory (S1) and retrosplenial cortices (RSC) were used to extract FC values. We calculate connectivity map using left S1 seed, then estimated Z-scores by combining standardized individual seed-based connectivity maps after Fisher transformation (r – Z(r) – Z) to determine specificity thresholds. Such processing is needed to make non-gaussian distribution to gaussian-like distribution, Z(r), after which standardization (Z) can be performed by subtracting the mean followed by dividing standard deviation. The threshold of specific FC (i.e., S1–S1) was determined where the Z(r) is significant at p < 0.01 (non-corrected) based on the a priori assumption that significant positive FC exists between the bilateral sensory cortex. The threshold of non-specific FC (i.e., S1-RSC) was determined where the Z(r) at the center of distribution (p = 0.5) subtracted by one standard deviation of group Z(r). This is chosen because very weak or negative correlation is expected between the S1 and RSC due to their roles in functionally distinct brain networks.

2.8. Data-driven functional parcellation

Functional parcellation partitions the brain into functionally specialized subregions by clustering the voxels based on similarities and differences in FC profiles (Ma et al., 2018). In this study, we first performed multi-scale decomposition to extract reproducible and reliable spatiotemporal features of intrinsic FC. Instead of using canonical independent component analysis (ICA), we chose the dictionary-learning sparse decomposition algorithm from the nilearn Python package (Abraham et al., 2014) for its ability to better identify spatial features relevant to anatomical structures (Ge et al., 2018). This approach applies L1 regularization, allowing high sparsity and compact components to be extracted without subsequent thresholding compares to the ICA approach (Varoquaux et al., 2011). To minimize the bias associated with parameter selection, we used a total of 20 scales to decompose our data, starting from 5 with an increment of 5, until 100 (decomposed into 5, 10, 15, 20, 25, …. 100 features), resulting in a total of 1,050 features. We calculated a Pearson’s correlation coefficient matrix and Jaccard similarity coefficient matrix (Jaccard, 1912) between features and applied a threshold of 0.7 to each matrix. Of note, the Jaccard similarity coefficient matrix is defined as the size of the intersection divided by the size of the union of the finite sample sets. The correlation and Jaccard similarity matrices were then multiplied to generate a similarity matrix that considers both correlation and interception. Next, we performed Louvain community detection (Blondel et al., 2008) to group features with high-spatial similarity. We iterated this process 5000 times to generate a normalized occurrence matrix of clustering, and Louvain community detection was used again on this occurrence matrix. Clusters with 4 or more members were considered for further analysis, as they are reproducible across multiple decomposition scales. For each of the survived clusters, we performed a parametric, one-sample t-test with a two-sided unadjusted p-value of 0.05 thresholding across the cluster components and estimated the averaged spatial pattern of each cluster as a representative feature.

We then performed dual regression analysis (Nickerson et al., 2017) on each representative feature (Fig. S3) and derived subject-level features from three randomly selected 150-volume segments. To examine the reliability, we employed intra-class correlation (ICC) among segments by calculating the ratio of the variance between-subjects over the total variance. We also reported reproducibility by tabulating the spatial correlation between the representative features identified from the multiscale decomposition method and group-averaged subject-level features that were estimated via dual regression. Features with an ICC higher than 0.6 and Pearson’s correlation higher than 0.6 were considered to be reliable and reproducible. Finally, we performed voxel-wise k-means clustering on identified representative features to partition the voxels into spatially discrete ROIs under the assumption that these features can be considered as spatiotemporal fingerprints for intrinsic FC interpretation. The optimal number of clusters was determined via the automated elbow method using the Kneedle algorithm (Satopaa et al., 2011). The identified ROIs were labelled based on the Paxinos and Watson’s rat brain atlas (Paxinos and Watson, 2014). A detailed diagram of the functional parcellation pipeline is described in Fig. 2.

Fig. 2.

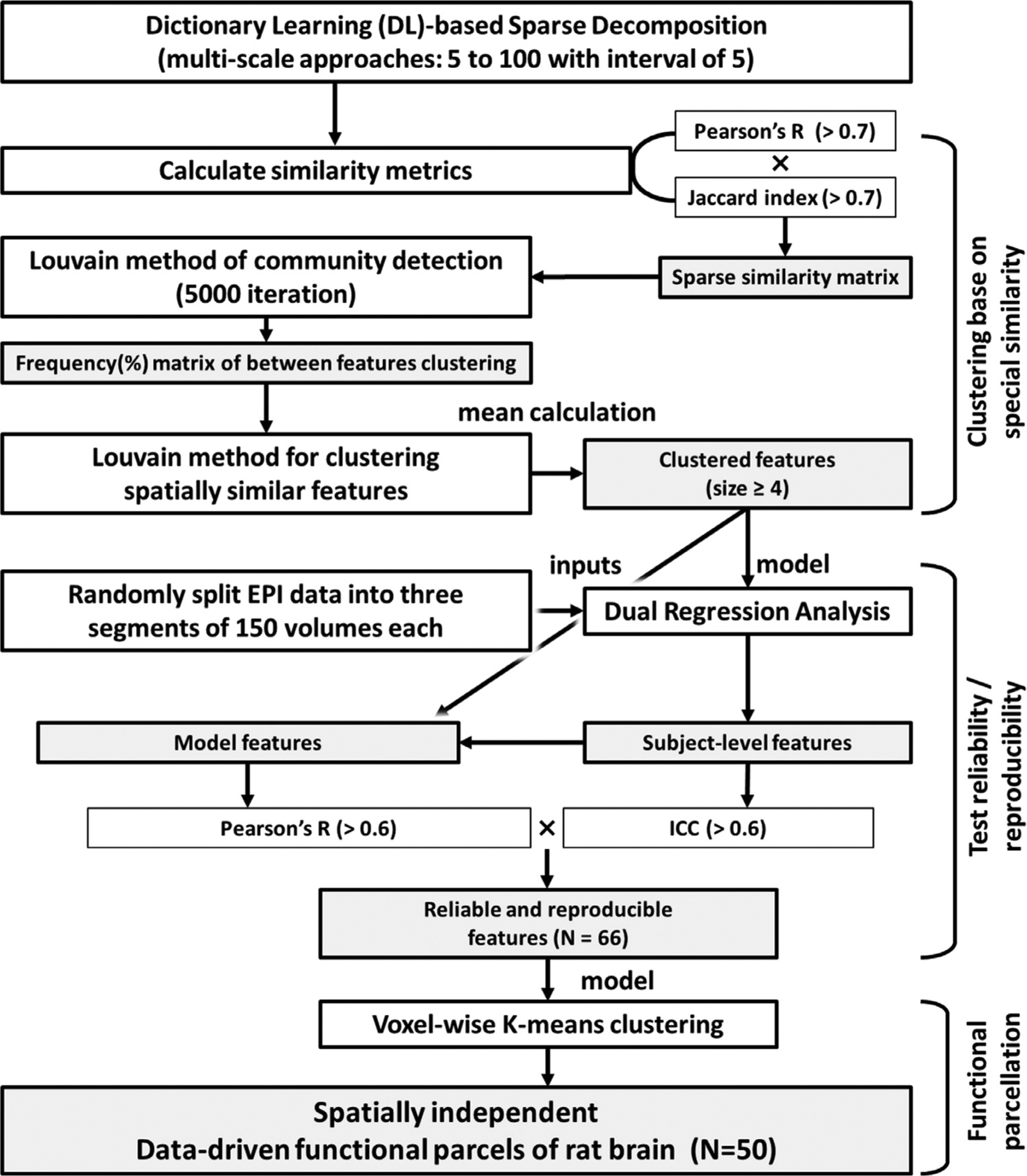
Schematic diagram of the data-driven functional parcellation pipeline.

2.9. Determination of intrinsic functional network topological organization

Time-course data were averaged within the identified ROIs and extracted from each subject. The three sets of time-series data with 150 volumes each were used to calculate a Pearson’s correlation coefficient matrix to match the degrees of freedom between cohorts (Table S2). The resulting three correlation matrices were averaged within each subject. The group-averaged correlation matrix was generated using a permutation-based, one-sample t-test (see Section 2.12 for statistical details). The correlation matrix was then converted to a weighted graph to facilitate network analysis. To characterize the FC network across different topological scales, we performed two analyses on the identified ROIs: 1) Euclidean-based hierarchical clustering and 2) modularity-based partitioning. For the Euclidean-based hierarchical clustering, we performed hierarchical agglomerative clustering to generate a dendrogram that grouped the clusters according to minimum Euclidian distance using Ward’s minimum variance method (Ward, 1963). A threshold of 1.83 was applied to the node height of the resultant dendrogram to extract clusters (Zingg et al., 2014). For the modularity-based partitioning, we employed Louvain community detection (Blondel et al., 2008) with 5000 iterations and determined the community structure by the partitions showing maximum modularity among the iterations (Bota et al., 2015). To test the impact of SNR on identified FC network structures, we applied different levels of Gaussian noise to the dataset. To determine the amplitude of the noise signal, we calculated the average power of the dataset followed by decibel (DB) conversion. We set the SNR of our original dataset as the 100% and computationally reduced it to 75%, 50%, 25%, 10%, and 1%. The noise amplitude of each condition was estimated by subtracting DB-converted SNR and subsequent inverse conversion to amplitude values. Finally, each estimated noise amplitude was used to generate a Gaussian noise signal and added. The same permutation-based one-sample t-test was applied to identify group-level network features. For comparison, we visualized results to present its topological organization based on our identified network structure and calculated averaged connectivity and number of edges that survived from significant test.

2.10. Graph theoretical analysis and identification of network hubs

Functional brain networks exhibit topological features of efficient organization including small-worldness and prominent hubs of connectivity (Bullmore and Sporns, 2009). To validate whether our proposed functional parcellation scheme generates data with well-established network properties and intrinsic FC organization in rats, we calculated sigma small-worldness coefficient (Humphries and Gurney, 2008), global efficiency, modularity, connection diversity (Coletta et al., 2020), betweenness centrality (Brandes, 2008), closeness centrality (Freeman, 1979), and strength centrality (Liska et al., 2015) on weighted connectivity matrices (Rubinov and Sporns, 2011). A network hub represents a node that densely connects with others and is involved in functional integration (Sporns, 2013). Hubs can be identified by measuring nodal centrality that quantifies how important nodes are within a network. To identify hubs in our dataset, the hubness index for each ROI was scored was calculated as follows: 1) For each centrality/connection diversity metric, the high-ranked ROIs were iteratively identified at increasing percentile thresholds ranging between 10% and 50%. 2) Percent occurrence (%) was calculated by plotting the number of times an ROI was counted as the hub across varying percentile thresholds. 3) The ROIs classified as high-ranked (at least 90% of the time for any of centrality metrics) were considered as hubs. In addition, a collection of highly inter-connected hubs, known as a “rich club” was identified by summing the FC strength of the existing connections for each node. The rich club coefficient was computed as described previously (Bota et al., 2015; Colizza et al., 2006; Liang et al., 2018).

2.11. Individual variability analysis of network-level connectivity

We derived group consistency (Φ) and differential power (DP) for measuring individual variability by employing the method described by Bergmann et al. (2020) and Finn et al. (2015). Randomly segmented 4D data used for ICC analysis was also utilized here to generate connectivity matrices based on 50 ROIs and standardized to Z score. The edgewise product was calculated for each edge of all ROI pairs of connectivity matrices. Φ values are the average edgewise products of two connectivity matrices generated from randomly sampled time-segments within subject. DP represents the empirical probability where the edgewise product of two within-subject connectivity matrices is higher than the edgewise product of two between-subject connectivity matrices. The top 1% of DP and Φ were presented in network-level heatmap plots based on modularity-based partitioning.

2.12. Statistics

To test the group-level significant consistency of each metric, we employed a non-parametric, permutation-based, one-sample t-test. A parametric one-sample t-test was performed to calculate T values based on the population average. Subsequently, the null distribution was generated by randomly assigning the subjects into two groups followed by a two-sample t-test for each iteration. A total of 5000 iterations was applied for all permutation-based testing in this study. To control the family-wise error rate, we employed the min P/max T procedure (Westfall and Young, 1993), which counts the maximal T value or minimal p-value among the values generated at each iteration to form the null distribution. The significance of the test was defined as where T values from the one-sample t-test surpassed those of the null distribution at p-value < 0.05.

3. Results

3.1. Isotropic EPI and EPI-based brain template

Our specific strategy for EPI acquisition relies on the fact that the dorsal-ventral axis of rat brain is the shortest, and thus performing slice selection along this direction is most efficient from the gradient duty-cycle perspective (Fig. 3 A&B). This encoding scheme facilitates true whole-brain coverage with the least number of slices. In data with isotropic resolution, 2D images can be extracted with any slice orientation while maintaining consistent in-plane resolution (Fig. 3C). Fig. 3C and D compare isotropic EPI data to anisotropic EPI data with limited spatial coverage. Using the isotropic EPI data, we built an EPI template using AC and PC as the key landmarks (Fig. 3 E). Specifically, we centered at AC and aligned PC at AP = −4.6 mm, DV = 1.6 mm, and LR = 0 mm with respect to AC. This template is built to best approximate the widely used Paxinos and Watson’s rat brain coordinate system (Paxinos and Watson, 2014), but centers at AC instead of bregma, which cannot be reliably identified by conventional MRI. If necessary, our template coordinate system can be readily converted to the bregma-centered coordinate system used in the Paxinos and Watson’s rat brain atlas by adding the distance between AC and bregma (AP = −0.36 mm, DV = 6.9 mm LR = 0 mm). This template is also similar to the Waxholm coordinate system (Papp et al., 2014) but circumvents the challenge of horizontally aligning bregma to lambda using MRI. Alignment of the population-averaged EPI template and the structural MRI template (Johnson et al., 2012) is shown in Figs. 3 F, and S1.

Fig. 3.

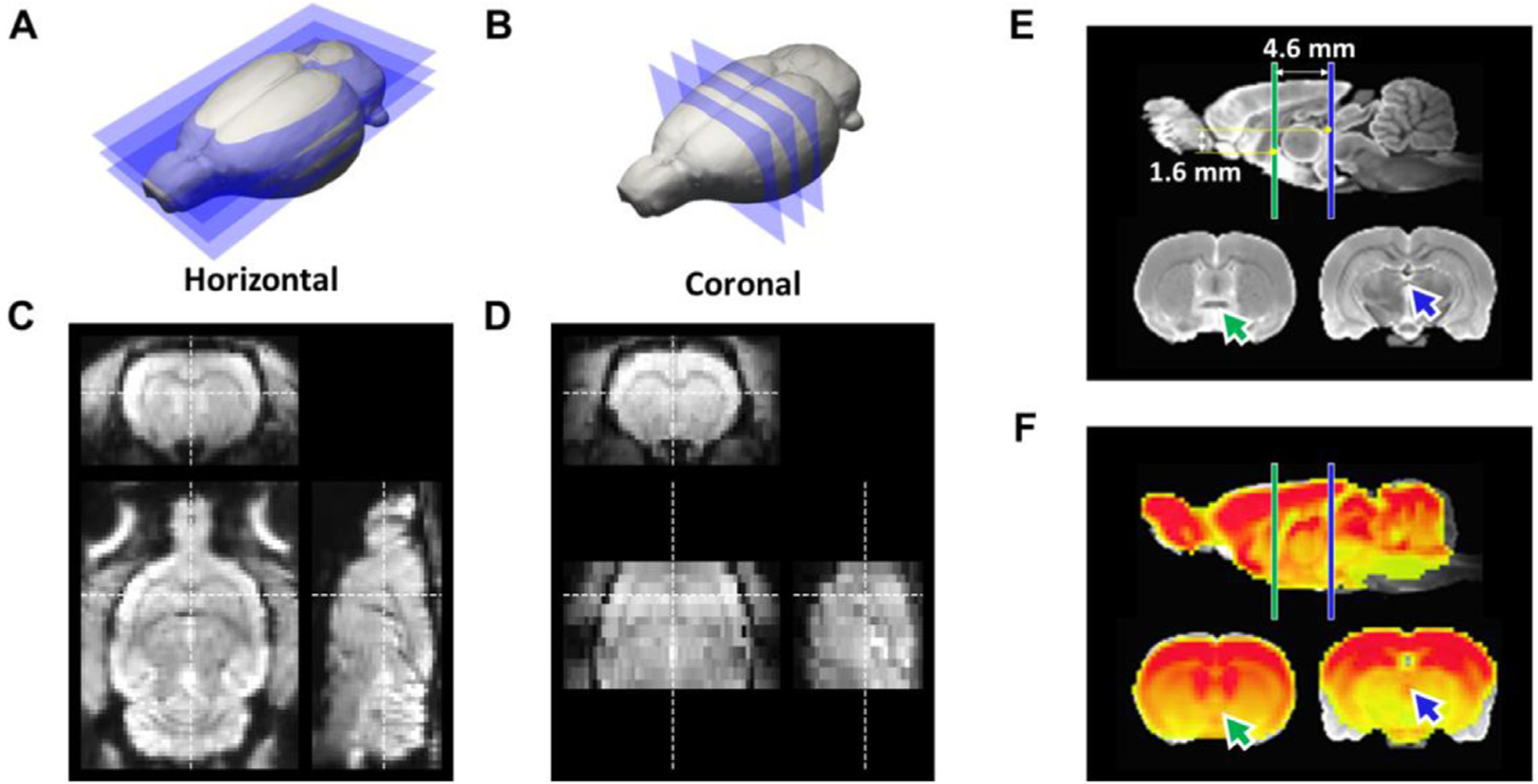
Comparison of two EPI protocols and the proposed coordinate system. (A) The proposed horizontal slicing scheme. (B) Conventional coronal slicing scheme. (C) Representative EPI images at 0.4 mm isotropic resolution acquired from horizontal slicing. (D) Representative EPI images with 0.32 × 0.32 × 1 mm anisotropic resolution acquired from coronal slicing. (E) A coordinate system centering at AC, with AC-PC axis alignment identical to the Paxinos and Watson’s (7th edition) rat brain atlas. (F) Co-registered isotropic EPI template on structural MRI template, showing high concordance except the areas prone to susceptibility artifacts, such as amygdala. Green arrow: AC; Blue arrow: PC.

3.2. Spatial normalization

Conventionally, co-registration between a subject’s structural image and the structural MRI template is essential as the same transformation would subsequently be applied to the subject’s EPI data. Our development of a rat brain EPI template facilitates image registration during fMRI preprocessing and streamlines the spatial normalization process by enabling direct co-registration between subject-level EPI data and the EPI template (Fig. 4 A). Additionally, registration accuracy may be improved by using data with isotropic voxels (Papp et al., 2014). Our results using isotropic EPI data with volumetric non-linear registration demonstrated superior registration performance (Fig. 4 B) compared to anisotropic EPI data without whole brain coverage. The latter showed low accuracy with volumetric non-linear registration, particularly along the slice axis (Fig. 4C, red rectangle), and truncated data around boundaries with linear registration (Fig. 4C, red arrow). We also simulated motion-parameter-estimation performance by resampling high resolution isotropic data and demonstrated inferior results when using anisotropic EPI with limited brain coverage (Fig. S4). Collectively, these data highlight that whole-brain coverage is an important factor to consider for rodent fMRI standardization in order to optimize spatial normalization accuracy, motion correction estimation accuracy, and preprocessing efficiency.

Fig. 4.

Preprocessing pipeline using EPI-based template. (A) Schematic diagram of the pipeline. (B) Representative nonlinear registration results using isotropic EPI data with whole brain coverage. (C) Representative linear and nonlinear registration results using anisotropic EPI data with limited brain coverage. Red outline: outline of EPI-based template; Red arrow: missing data due to registration mismatch; Red rectangle: mis-localization of brain slices.

3.3. Preprocessing and quality profiling

FD, DVARS, and tSNR were calculated pre- and post-nuisance removal to evaluate data quality and the regression process efficiency. The distribution of accumulated FD (mean: 0.0048 mm, median: 0.0057 mm) across all 87-subject time-courses is presented in Fig. 5 A. The population FD distribution suggested that FD beyond 0.012 mm can be considered outliers according to Tukey’s rule (multiply the interquartile range by 1.5 followed by adding the third quartile). DVARS distributions of pre- (mean: 2.97, median: 2.91) and post- (mean: 2.25, median: 2.16) nuisance removal are presented in Fig. 5 B. The effect of nuisance removal on reducing head-motion related signal changes is shown in Fig. 5C. The group-level tSNR map was estimated with a permutation-based one-sample t-test for pre- (Fig. 5 D) and post- (Fig. 5 E) nuisance removal. An increase in brain volume with significant tSNR at the group-level was observed (Fig. 5 D and E; pre: 897.02 mm 3 vs post: 976.06 mm 3). The data also showed an overall increase in tSNR after nuisance removal (Fig. 5 F).

Fig. 5.

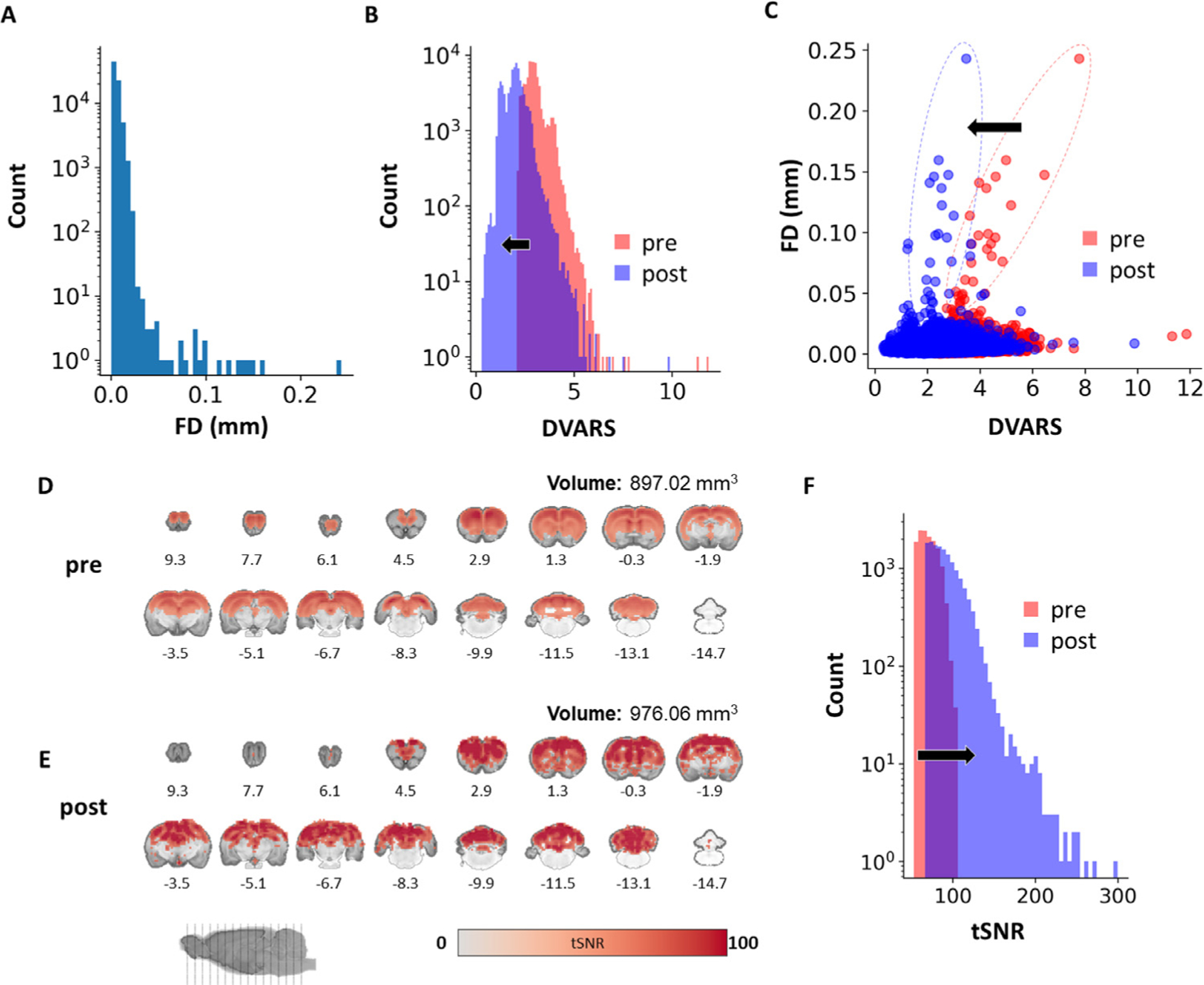
Quality profile of whole-brain isotropic EPI data (n = 87). (A) FD histogram of all subject time-courses. (B) DVARS histograms of all subject time-courses. (C) Scatterplot between framewise displacement and DVARS of all subjects. (D) Group-level voxel-wise tSNR map before nuisance removal (p < 0.05). (E) Group-level voxel-wise tSNR map after nuisance removal (p < 0.05), showing an overall increase in tSNR value and brain volume with significant tSNR on the group-level. (F) Histogram of all subject time-courses showing the effect of nuisance removal on tSNR. FD: framewise displacement; DVAR: brain image intensity changes with respect to the previous time point as opposed to the global signal; pre: without nuisance removal; post: with nuisance removal.

3.4. Voxel level resting-state functional metrics

To characterize common intrinsic FC metrics in the 87-subject EPI data, we extracted local (ALFF, ReHo) and global (FC strength) voxel-level profiles. Across these three metrics, voxels with group-level significance were located predominately in cortical regions (Fig. 6 A). Using these metrics as features, we performed k-means++ clustering among the voxels that survived permutation-based one-sample t-tests with all metrics thresholded at p < 0.05. Interestingly, the three identified clusters (Fig. 6 B) were distinct based on their ALFF, ReHO, and FC strength profiles: 1) a cluster that consists of the anterior cingulate and orbitofrontal cortices and features high ALFF, high ReHo, and high FC strength (Fig. 6C–E, red), 2) The blue cluster that includes the fontal association cortex and has high ReHo, but low FC strength (Fig. 6C–E, blue), and 3) a cluster that consists of motor and sensory areas and is characterized by low ALFF, low ReHo, and low FC strength (Fig. 6C–E, cyan). These results highlight that the frontal association cortex of the rat brain exhibit relatively low brain-wide FC while the limbic cortices show strong linear correlation between brain-wide FC and local metrics, in agreement with a characteristic of putative task-positive network in rodents (Belloy et al., 2018; Coletta et al., 2020).

Fig. 6.

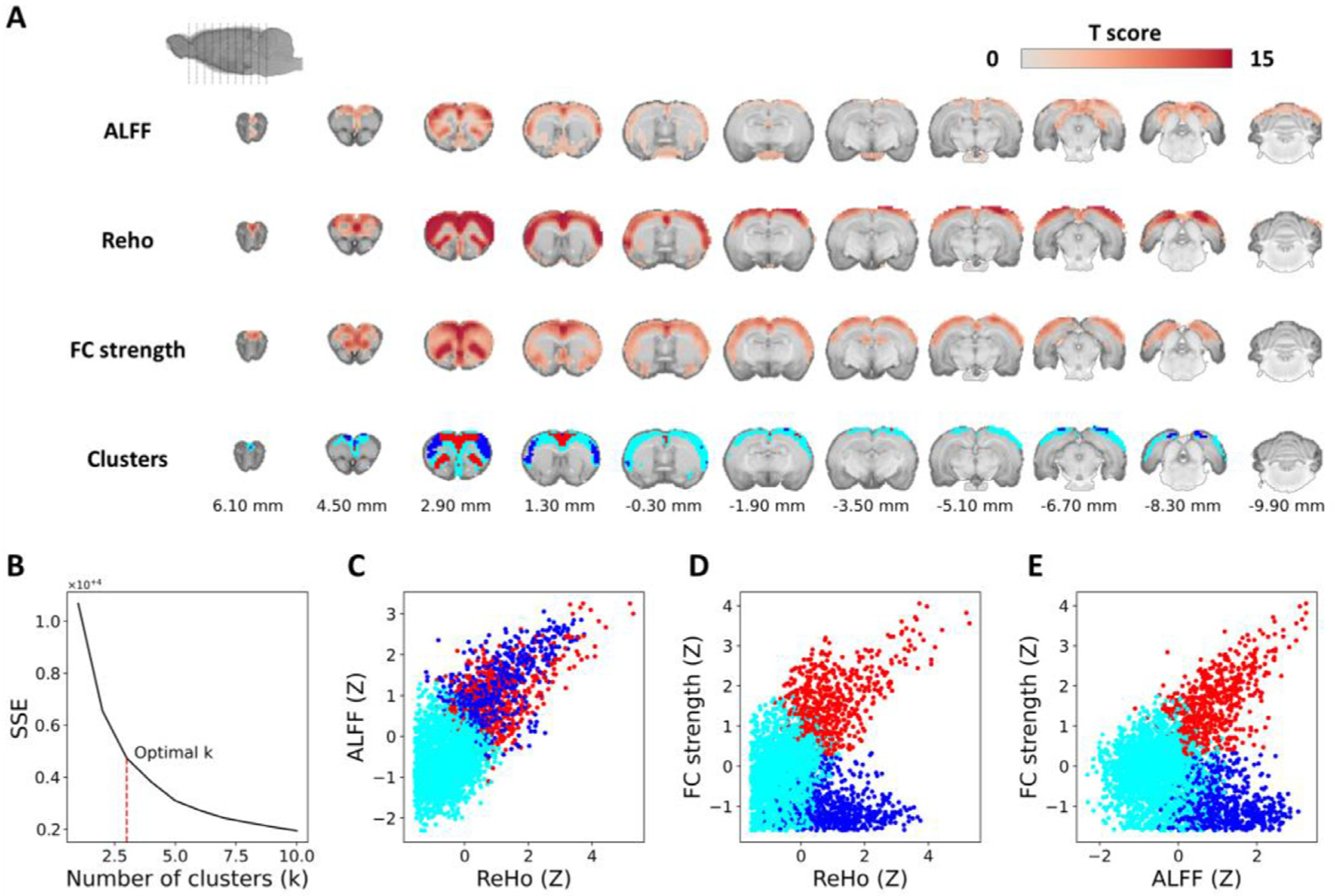
Voxel-level resting-state FC metrics. (A) Group-level significance maps of ALFF, ReHo, and FC strength and the three clusters identified using voxel-level k-means clustering in the Paxinos and Watson’s rat brain coordinates (0 mm indicates bregma location). (B) Elbow method to identify an optimal k-value. (C–E) Scatter plots comparing ReHo, ALFF, and FC strength.

3.5. Brain functional parcellation

Using dictionary-learning, we identified 66 spatiotemporal features (Fig. S5) that survived reliability and reproducibility tests (Table S2, see Section 2.8 for details). While it is suggested that resting-state BOLD fluctuation would go up to 0.2 Hz under medetomidine (Grandjean et al, 2014), we chose 0.01–0.1 Hz bandpass filtering based on the reliability and reproducibility of our feature detection. Fig. S6 shows that a bandpass filter cutoff at 0.2 Hz reduces total number of features as well as the features that passes the criteria of ICC > 0.6 and Spatial similarity > 0.6. It also indicates that the ICC of overall features decrease with a 0.2 Hz filter cutoff.

Our identified spatiotemporal features exhibited good sparsity and symmetricity, and contain a variety of cortical, subcortical, and vascular structures including major sinuses located at the mediodorsal region of the brain (Fig. S7). These vascular structures are segregated from the brain parenchyma, including the superficial sagittal sinus, transverse sinus, pineal gland, and straight sinus. Due to the location of these vascular structures, they may confound activity from cingulate cortex and RSC. To identify functionally meaningful and spatially discrete ROIs, we performed k-means clustering and subsequent scrubbing of the ROIs positioned on top of vascular components and the features with no meaningful spatial distribution. As a result, we identified a total of 50 spatially discrete ROIs. Fig.s S8 and 7A show all k-value estimations and identified ROIs after scrubbing, respectively. Of note, thalamic and midbrain areas were clustered as a single non-specific parcel (Fig. 7 B) that contained brain boundaries as well as the area prone to susceptibility artifacts (e.g., around ear-cannel). Such clustering could be due to inter-related thalamus/midbrain nuclei function, relatively low SNR, or use of anesthesia. Overall, our analysis suggested that these regions might be less reliable and reproducible compared to other classified regions. Thus, the parcel was discarded from subsequent analysis in the present study. Each ROI was then anatomically labelled according to the Paxinos and Watson’s rat brain coordinate system (Paxinos and Watson, 2014) (Table 1). Most of the ROIs represented meso-scale circuits which could be comprised of multiple distinct regions.

Fig. 7.

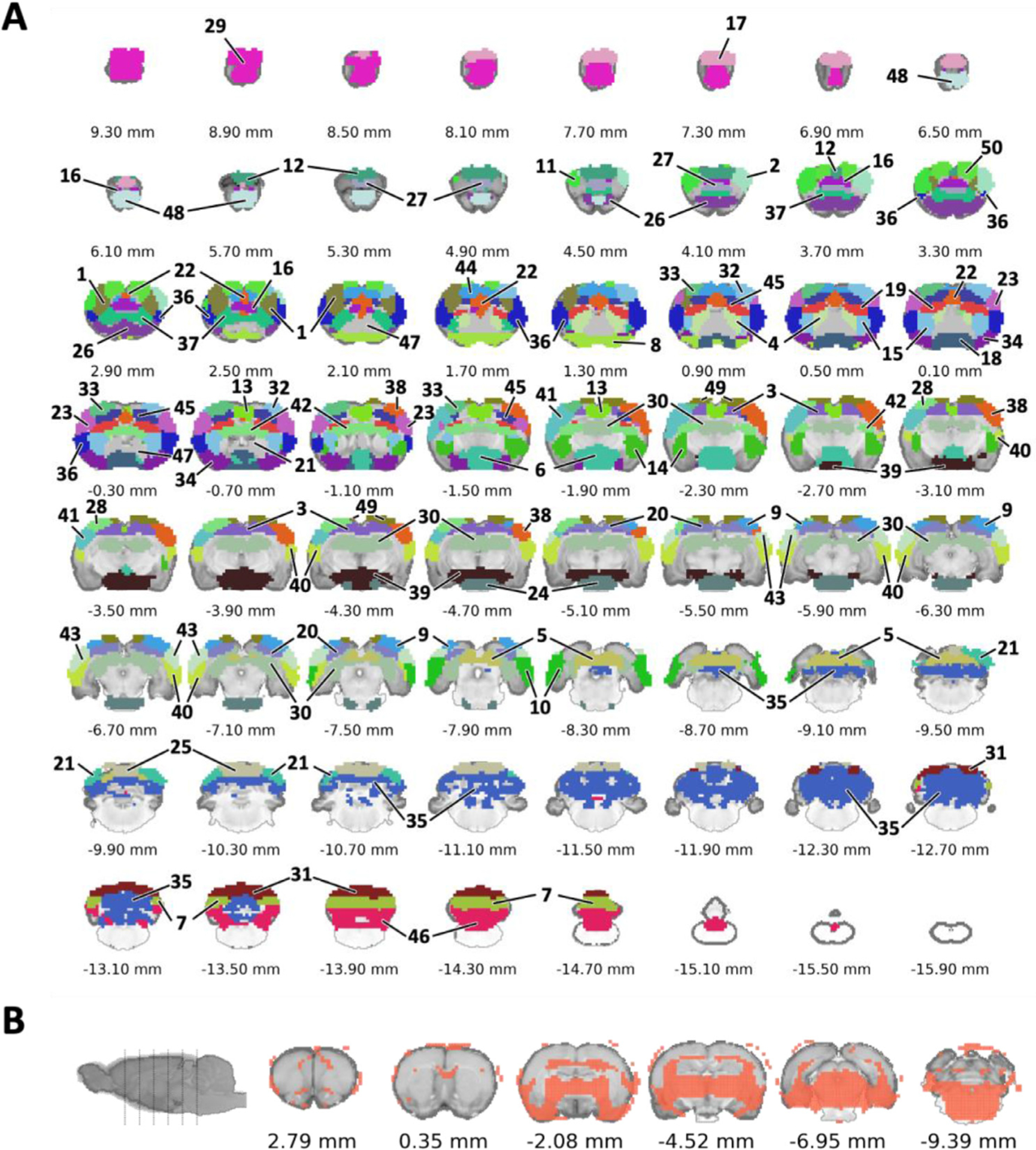
Functional parcellation. (A) Representation of spatially discrete ROIs in the proposed AC-centered space approximating Paxinos and Watson’s (7th edition) rat brain coordinates. (B) Representation of a single non-specific parcel that excluded from the ROIs.

Table 1.

Summary of spatially discrete ROIs with module, cluster, hub, and rich club labels. The full name of each abbreviation is provided in Table S3. C1–6: identified subnetworks with Euclidean-based hierarchical clustering; M1–5: identified subnetworks with modularity-based partitioning.

3.6. Functional connectivity specificity of the dataset

To benchmark overall FC specificity of this dataset, we implemented methods to evaluate individual specificity metric similar to that described previously (Grandjean et al., 2020, Liu et al., 2020). In this study, a higher FC between matching bilateral S1 and a lower FC between S1 and RSC within the same subject is considered specific. Our approach leveraged the parcellated spatiotemporal features for determining seed coordinates. Specifically, we selected the most robust feature, F01, to make the sensory cortex seed, and F47 to make the RSC seed (Fig. S5). Using the thresholds of Z(r) > 0.297 for S1–S1 and Z(r) < 0.061 for S1-RSC, we identified 73.6% specificity from this dataset (Fig. 8).

Fig. 8.

Functional connectivity specificity of the dataset. (A) seed-ROIs that was used for specificity analysis. (B) group statistical result of voxel-wise connectivity with the seed at left sensory cortex. (C) the scatter plot presenting the distribution of individual data among the criteria of specific FC (73.6%), unspecific FC (12.6%), spurious FC (10.3%), and no FC (3.4%).

3.7. Graph properties and intrinsic network organizations

It has been well documented that the brain network exhibits small-worldness, modular organization (Bullmore and Sporns, 2009; Liao et al., 2017) and comparatively resilience (Rubinov and Sporns, 2010). A small-world network is described by a high local clustering level while maintaining a low minimum path length. It can be characterized by a sigma coefficient, calculated with a mean clustering coefficient divided by characteristic path length that normalizes with matching null random networks (Rubinov and Sporns, 2010; Wang et al., 2010). Of note, a sigma coefficient larger than 1 indicates small-world classification of a network. In this study, we used non-parametric, permutation-based statistics to identify consistent group-level FC networks without arbitrary thresholds, allowing us to map the common topological organization of rat brain intrinsic networks. Our results demonstrated an average degree of 12.48% and a sigma coefficient of 1.19 indicating the identified group-level FC network showed small worldness therefore it has balanced regional segregation and global integration in general agreement with those reported in the literature (Ma et al., 2018). Group-level FC network also demonstrated assortativity coefficient of 0.22, where a positive value suggests that the network exhibited good resilience property indicating that the network has a comparatively resilient core of mutually interconnected high-degree hubs (Rubinov and Sporns, 2010). Our results also demonstrated that the group-level FC networks were spatially correlated across different rat strains and sexes (Fig. 9).

Fig. 9.

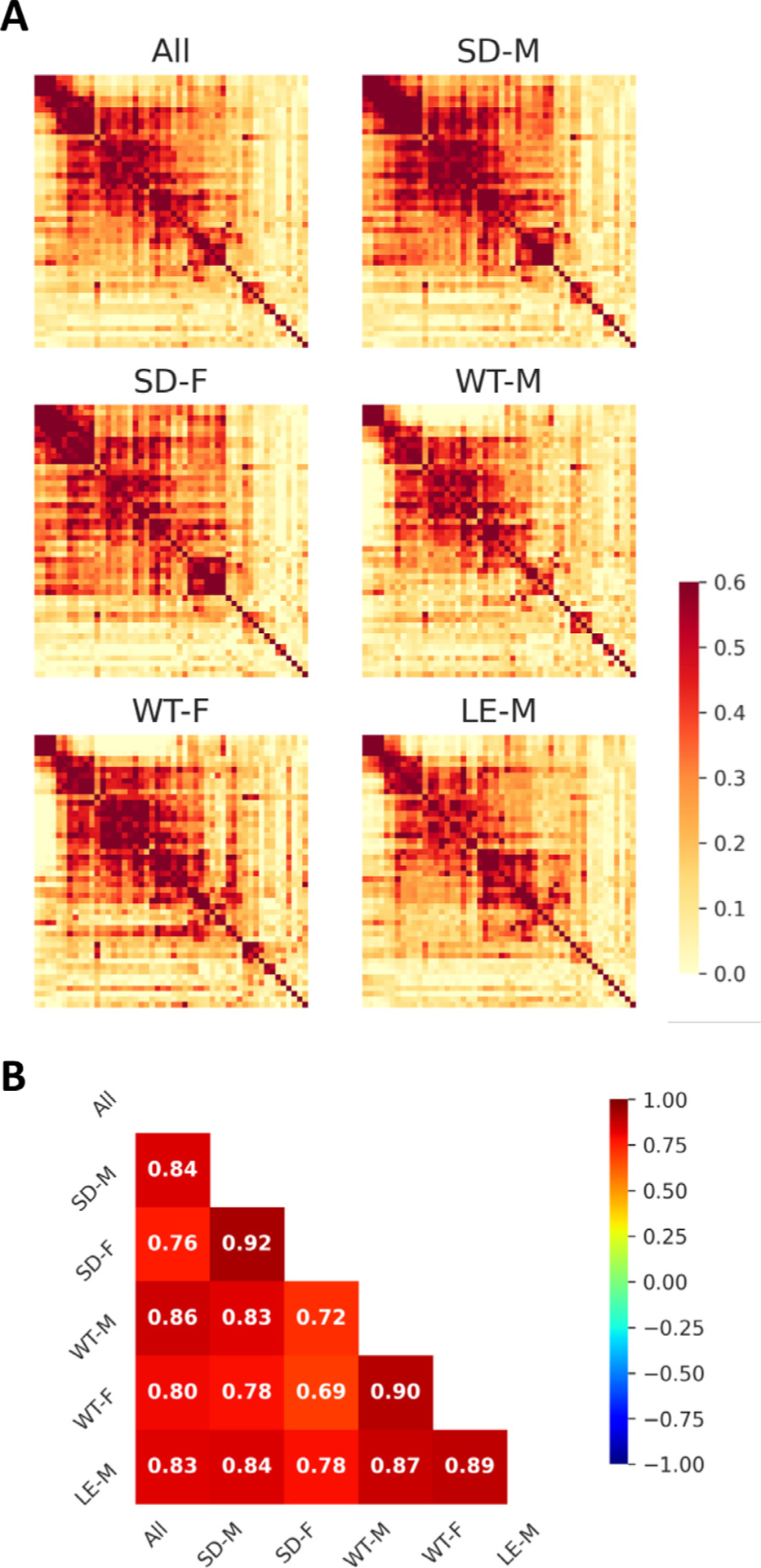
Robust group-level FC networks group-level FC networks across rat strains and sexes. (A) Group-level FC matrices of all subjects and specific strain and sex sub-groups. (B) Matrix showing spatial correlation between all subjects and each strain and sex sub-groups. Color bars represent Pearson’s correlation coefficient. SD: Sprague Dawley; WT: Wistar; LE: Long-Evans; M: male; F: female.

To further characterize the rodent intrinsic FC network across different topological scales, we performed two subsequent analyses on the 50 functional ROIs identified previously: 1) Euclidean-based hierarchical clustering and 2) modularity-based partitioning. While Euclidean-based hierarchical clustering identifies brain clusters with similar FC patterns and minimal Euclidian distance (Ward, 1963), modularity-based partitioning reveals any brain clusters exhibiting dense intra-connection and sparse inter-connection (Blondel et al., 2008).

Euclidean-based hierarchical clustering results (Figs. S9, 10 and Table 1) showed several clusters previously identified as interconnected subnetworks in a seminal neural tracing study (Zingg et al., 2014). Specifically, the C1 and C2 clusters including orofaciopharyngeal, upper limb, lower limb/trunk, and whisker cortices highly resemble the “somatic sensorimotor subnetwork”. The C3 cluster including anterior cingulate, retrosplenial, parietal association, visual, and auditory cortices highly resembles the “medial subnetwork”. The C4 cluster including insula and temporal association cortices highly resembles the “lateral subnetwork”. In addition, to these well-established cortical subnetworks, we also found subcortical subnetworks. The C5 cluster including limbic-related amygdala complex and ventral striatum. The C6 cluster including four sub-regions of dorsal striatum (ventrolateral, anteromedial, dorsal, and dorsomedial). Given the use of Euclidian distance in hierarchical clustering, most of the brain regions showing weak global FC strength would exhibit short distance and thus be grouped into a single cluster; accordingly, we did not attempt to identify these regions as a functional cluster.

Modularity-based partitioning results (Fig. 10 and Table 1) revealed several large-scale, functional brain networks documented in the rodent resting-state fMRI literature (Coletta et al., 2020; Grandjean et al., 2020; Lu et al., 2012; Tsai et al., 2020). Specifically, the M1, M2, and M3 modules include areas associated with the central executive network (CEN) (Coletta et al., 2020; Thompson et al., 2014), the DMN (Grandjean et al., 2020; Lu et al., 2012), and the salience network (SN) (Tsai et al., 2020), respectively. Interestingly, the basal forebrain, limbic system, and striatum are included in M3. The M4 module composed with cerebellum and superior/inferior colliculus. The M5 module includes the main and accessory olfactory bulbs, superior/inferior colliculus, bed nucleus of the stria terminalis, thalamus, periaqueductal gray, and brainstem. Interestingly, C2 and C4 were distributed between M1–M2 and M2–M3, respectively, indicating that brain clusters with similar FC patterns do not necessarily represent large-scale, intrinsic, functional brain networks.

Fig. 10.

Topologically organized FC matrix (permutation-based one-sample t-test, p < 0.05). Lower-left: weighted FC matrix; Upper-right: binary FC matrix. The numbers by the axes represent ROI ID (see Table 1). Colorbar represents Pearson’s correlation coefficient. C1–6: identified subnetworks with Euclidean-based hierarchical clustering; M1–5: identified subnetworks with modularity-based partitioning.

3.8. Individual variability among the rat brain intrinsic functional networks

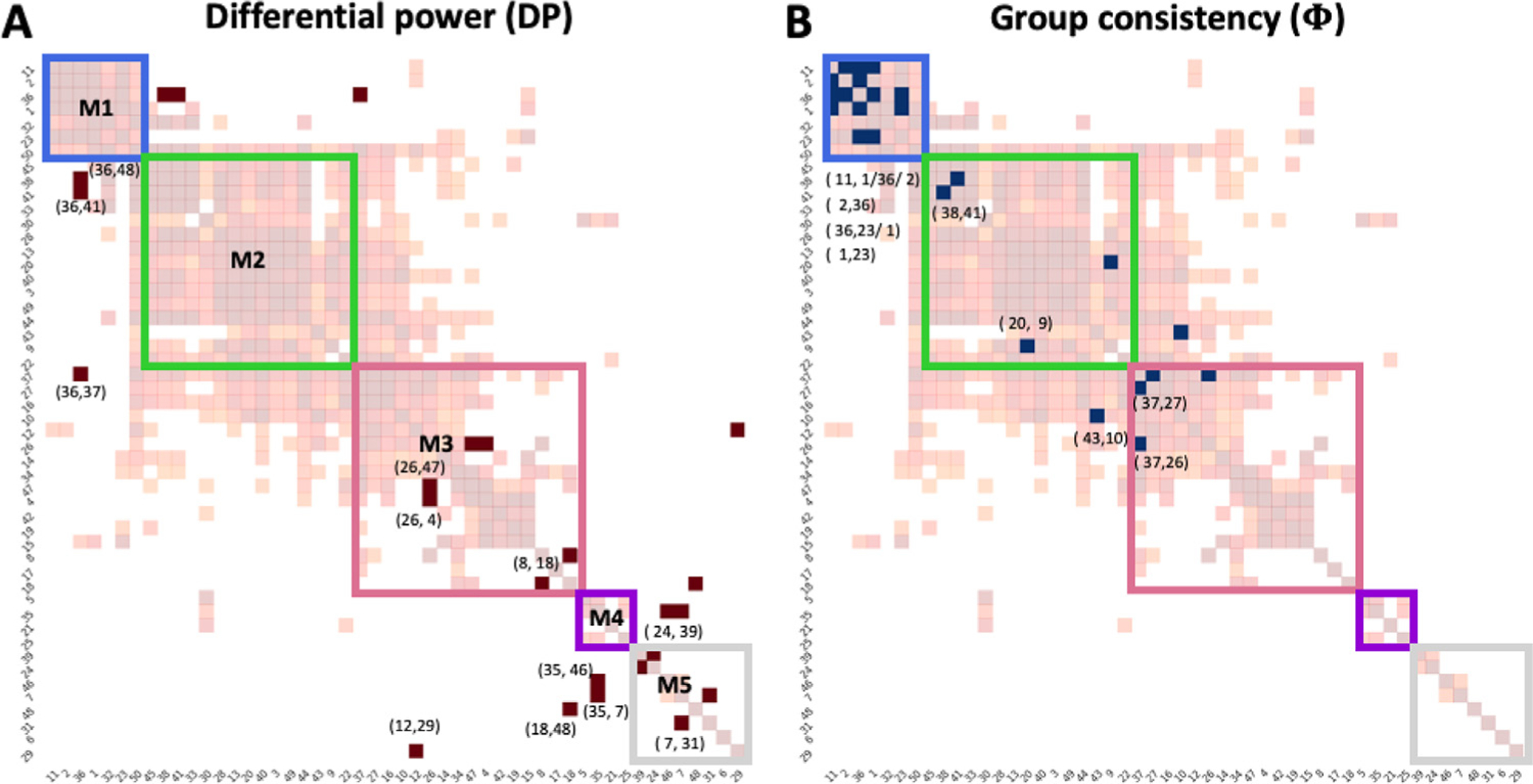
Individual variability analysis examines which connections contribute to distinguish an individual subject (Bergmann et al., 2020; Finn et al., 2015). After establishing intrinsic functional networks, we used Φ to probe group consistency, followed by computing DP to probe individual variability. The results were converted to the binary ROI-based matrix (Fig. 11) and a fraction of edges were calculated on the network-level (Fig. 12). We found that the edges in the top 1% of DP are associated with inter-sensory, prefrontal to sensory, frontal association, and olfactory areas that are mainly inter-network edges between M1 and M2 or between M1 and M3. These findings suggested that the subject variance is mostly presented in inter-network connectivity, in agreement with previous studies (Finn et al., 2015; Bergmann et al., 2020). However, the regions involved with individual variability are less consistent, showing high DP in the connectivity of olfactory areas with infralimbic and caudate putamen, in contrast to frontoparietal cortices in humans shown by Finn et al. and posterior parts of brain including visual, medial, and auditory systems in mice shown Bergmann et al. Additionally, we found the edges in the top 1% of Φ are related to the intra-network connections, including sensorimotor, visual, auditory, and prefrontal cortex. These findings are in agreement with previous studies (Finn et al., 2015; Bergmann et al., 2020).

Fig. 11.

Matrix representations of unique (A) and consistent (B) edges at the subject-level. M1–5: identified subnetworks with modularity-based partitioning. The light background network presenting group-level significant FC matrix as reference (see Fig. 10). Numbers pointed to individual brain areas represent ROI ID to indicate the high ranked edges (1%) (see Table 1)

Fig. 12.

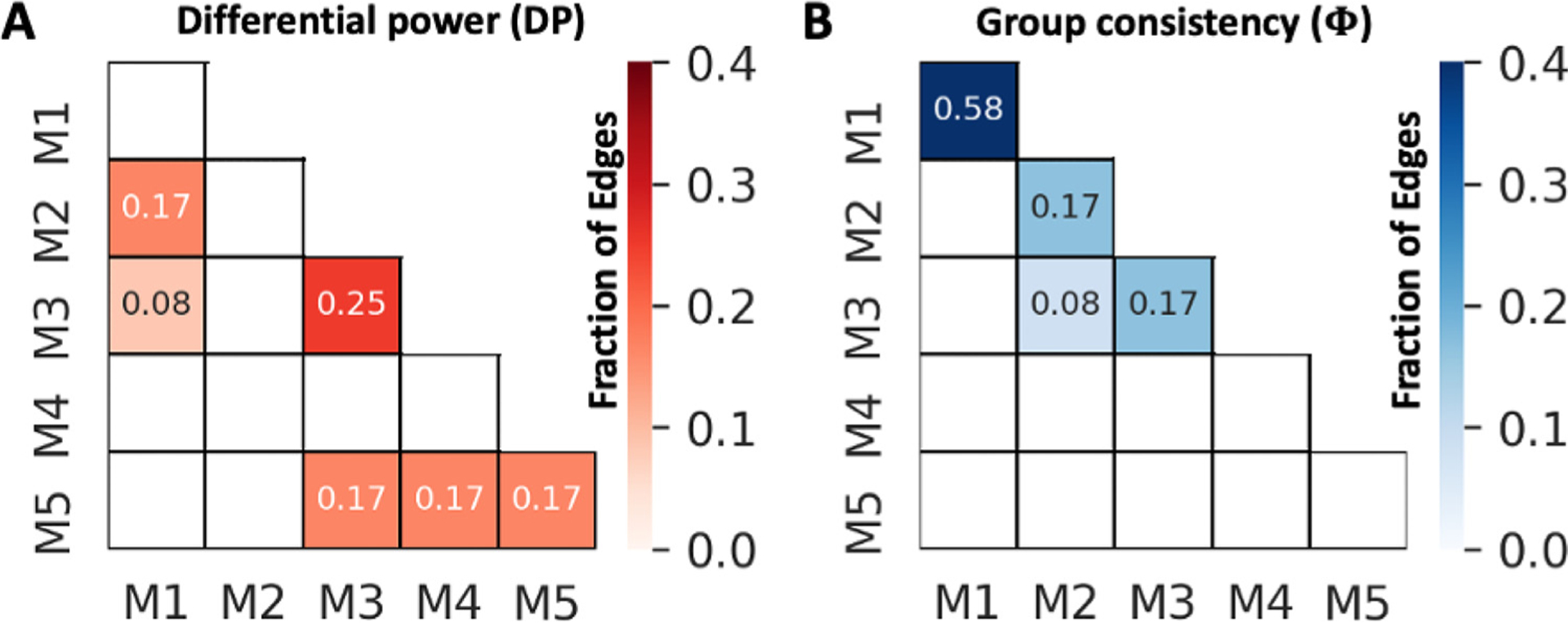
Matrix representations of unique (A) and consistent (B) edges intra- and inter-networks at the subject-level. M1–5: identified subnetworks with modularity-based partitioning.

3.9. Hubs, rich club structure, and their distributions among the rat brain intrinsic functional networks

A hub structure of the brain indicates a region with a higher number of connections, which usually facilitates functional integration and plays a key role in network resilience (Rubinov and Sporns, 2010). A rich club structure represents a set of densely inter-connected hubs (Colizza et al., 2006), and plays a crucial role in promoting global communication and information integration (Colizza et al., 2006; Liang et al., 2018). In this study, we identify hubs using connection diversity (Coletta et al., 2020) and three different measures of nodal centrality: strength centrality (Liska et al., 2015), closeness centrality (Freeman, 1979), and betweenness centrality (Brandes, 2008) (see section 2.10). We identified the following hub structures in our database: several cortical areas, including frontal association, medial prefrontal, anterior cingulate, insula, primary sensory of orofaciopharyngeal area, secondary sensory, primary and secondary motor, parietal association, temporal association, superior/inferior colliculus, and dorsal hippocampus (Fig. 13). Among these hubs, we identified the following rich club structures: anterior cingulate, primary and secondary motor, primary sensory, prelimbic, orbitofrontal cortex, anterior insula, temporal associative (Fig. 13) in agreement with previous DTI (Bota et al., 2015) and resting-state fMRI (Liang et al., 2018) studies. All 50 functional ROIs are shown in Table 1 with anatomical, hub, and rich club structure labels. Notably, major portions of hub and rich club structures hub structures were distributed within M1, M2, and M3. As evident by the isolation of hub structures within a few modules, our results facilitate the representation of three putative brain networks (Fig. 14) that are homologues to the triple-networks in the human brain (Menon, 2019; Menon, 2011).

Fig. 13.

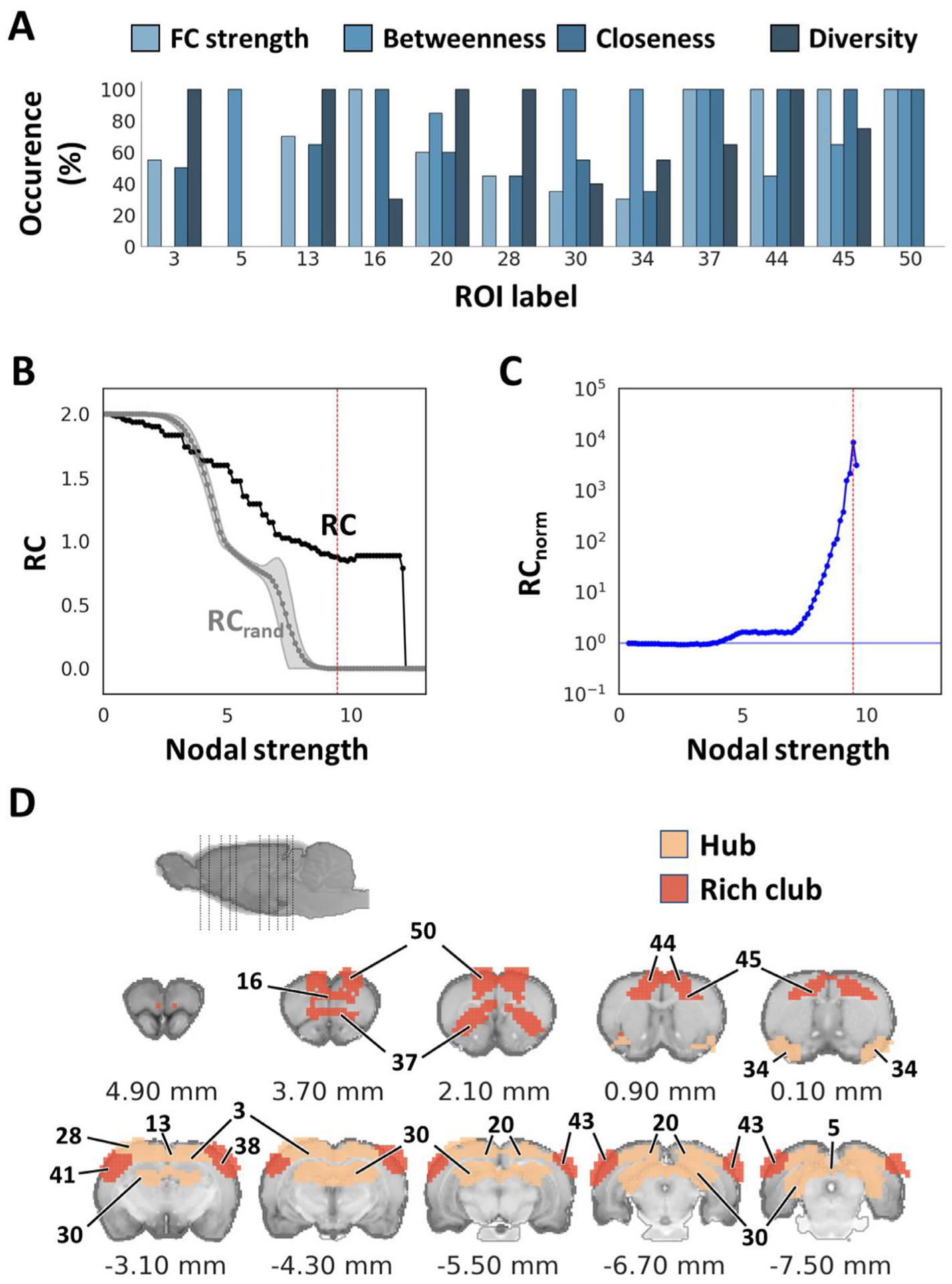
Identification of hub and rich club structures. (A) Percent occurrence of centrality metrics for each hub ROI. The ROIs that ranked at a high score of more than 90% on any of the centrality metrics among the thresholds throughout 5th to 25th among 50 ROIs, were determined as hubs. (B) Weighted rich club coefficient was calculated on the identified 50 ROIs. Black and gray curves compare the rich club coefficient at various nodal strengths between empirical and an average of 1,000 simulated random networks, respectively. (C) Normalized rich club coefficient calculated by RC/RC _rand. Red vertical lines indicate the significant nodal strength used to identify rich club structures (p < 1.96 × 10⁻¹¹⁰). (D) Illustration of hub and rich club structures in the Paxinos and Watson’s (7th edition) rat brain coordinates (0 mm indicate bregma location). RC: rich club coefficient.

Fig. 14.

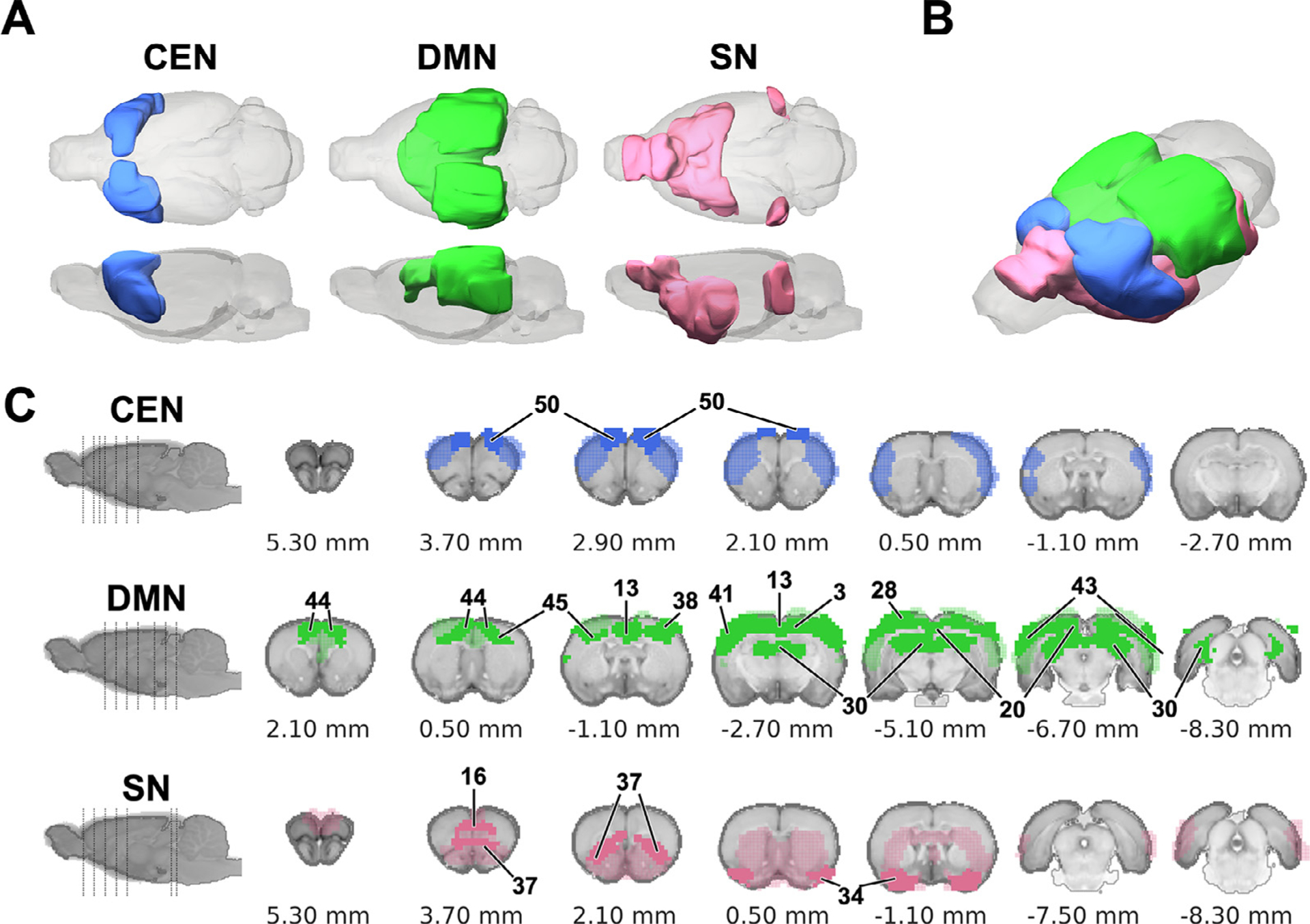
Distribution of hub structures among three intrinsic functional networks of the rat brain. (A&B) 3D-rendered CEN, DMN, and SN. (C) Coronal sections showing the contributing regions (light color) and hub structures (solid color) of each network in the Paxinos and Watson’s (7th edition) rat brain coordinates (0 mm indicates bregma location). Numbers pointed to individual brain areas represent ROI ID to indicate hub structure (see Table 1).

4. Discussion

This study demonstrates an EPI protocol capable of providing whole-brain coverage at 0.4 mm isotropic spatial resolution. Such an isotropic resolution was achieved by using a horizontal slicing scheme, which minimizes the number of slices needed to cover the entire brain. As a result, a TR of 2 s can be achieved without approaching the gradient duty-cycle limitation (e.g., with hardware combination #1 stated in Section 2.2). While the use of 0.4 mm slice thickness comes with a 2.5-fold SNR penalty (as compared to conventional 1 mm), higher voxel resolution reduces susceptibility-related BOLD signal loss (Feinberg et al., 2018; Volz et al., 2019; Iranpour at al., 2015; Goense et al., 2016; Chen et al., 2003) and the use of a relatively longer TR mitigates some SNR penalty. As a result, we observed comparable tSNR profile (Fig. 5 D) with other rodent resting-state fMRI reports in the literature (Liu et al., 2020; Grandjean., 2020). A TR of 2 s encodes up to 0.25 Hz Nyquist frequency which is well beyond the prominent 0.01 – 0.1 Hz frequency band typically used to filter FC-related hemodynamic signals. The results presented herein collectively demonstrate the utility of a 2-s TR for functional parcellation and brain-network metric identification in rats, which is supported by a recent human fMRI study showing consistent resting-state brain-network metrics when using 0.1 – 3 s TRs (Huotari et al., 2019). To achieve 0.4 mm isotropic resolution and whole-brain coverage with coronal brain sections, the number of required imaging slices would increase from 32 to 72, creating an excessive burden on the gradients and rendering a 2-s TR unachievable. It should be noted that acquisitions with a TR of 2 s are prone to cardiorespiratory aliasing (Pais-Roldan et al., 2018) and are too long to perform some dynamic analyses such as identification of quasi-periodic patterns (QPPs) (Thompson et al., 2014). We showed data with a 1 s TR can be acquired with a more up-to-date gradient and amplifier hardware (Fig. S12; e.g., hardware combination #2 stated in Section 2.2). Nevertheless, the gradient and amplifier combinations employed in this study (Table S1) may not be readily available at all rodent MRI laboratories. It is expected that the advent of hardware will make the proposed isotropic protocol or its variant at slightly lower resolution (e.g., 0.45 or 0.5 mm isotropic) more universally applicable. Alternatively, simultaneous multi-slice EPI may be employed to reduce gradient burden (Lee et al., 2019).

We documented the use of this high-spatial-resolution isotropic EPI protocol in building an EPI brain template, enabling spatial normalization of EPI-fMRI data into template space in one step. Aside from the clear benefit of improved acquisition and pre-processing efficiencies, the use of an EPI template could improve data accuracy as co-registration between structural and functional MRI data has been shown to be a potential cause of misalignment (Grabner et al., 2014). Additionally, compared to using a structural MRI template for spatial normalization, using an EPI-based template in humans reduces inter-subject variability and more efficiently estimates optimal parameters for inter-subject registration (Calhoun et al., 2017; Grabner et al., 2014; Huang et al., 2010).

A recent review article summarized that many rodent fMRI studies relied on custom-made pre-processing scripts, likely because well-disseminated functions designed for human fMRI pre-processing are not readily applicable to rodent fMRI data (Mandino et al., 2019a). Unlike human fMRI databases (Casey et al., 2018; Petersen et al., 2010; Sudlow et al., 2015; Van Essen et al., 2012) where isotropic EPI is the field-standard, nearly all published rodent fMRI studies (Aedo-Jury et al., 2020; Grandjean et al., 2020; Hsu et al., 2016; Liang et al., 2018; Liu et al., 2020; Lu et al., 2012; Mandino et al., 2019a; Pan et al., 2018; Tsai et al., 2020), including many of our own (Albaugh et al., 2016; Broadwater et al., 2018; Shih et al., 2012; Shih et al., 2013; Van Den Berge et al., 2017), used anisotropic EPI. When co-registering anisotropic EPI data to a template, it is practical to manually match slices and perform co-registration slice-by-slice to avoid slice misalignment or data truncation around boundaries; however, this represents a significant problem in rigor and reproducibility due to experimenter subjectivity. Our proposed isotropic EPI protocol and template provide an opportunity for superior registration performance as 3D non-linear registration tools (Avants et al., 2008; Avants et al., 2010) can be seamlessly applied without human bias.

Notably, the use of isotropic EPI also benefits the correction of subject motion as all six motion parameters can be measured with identical resolution, avoiding unbalanced weighting along the slice axis. While a pioneering study suggested that motion parameter regression could be a relatively insignificant nuisance factor in rodent resting-state fMRI (Chuang et al., 2019), our simulation results demonstrated that the impact of motion parameter regression might be underestimated for certain EPI protocols (Fig. S4). Moreover, with the field moving towards imaging rodents in the awake condition (Becerra et al., 2011; Dopfel and Zhang, 2018; Febo, 2011; Febo et al., 2005; Ferris et al., 2011; Liu et al., 2020; Ma et al., 2020, 2018; Paasonen et al., 2020; Paasonen et al., 2018; Stenroos et al., 2018; Tu et al., 2021a) where motion regression is crucial, using high-resolution isotropic EPI protocols may prove itself useful for nuisance removal.

Our proposed EPI template was aligned to coordinate-space centered at the AC, similar to the Waxholm rat brain coordinate system (Papp et al., 2014). However, the Waxholm coordinate system aligns bregma and lambda horizontally (Papp et al., 2014), and we instead aligned the PC at 4.6 mm posterior and 1.6 mm superior to the AC to match the AC-PC axis in the most widely used Paxinos and Watson’s rat brain coordinate system (Paxinos and Watson, 2014). Therefore, our proposed EPI template, ROIs, and all analyzed results can be converted to the bregma-centered, Paxinos and Watson’s rat brain coordinate system by applying the following spatial shift: AP −0.36 mm and DV + 6.9 mm. Bregma and lambda are difficult to discern in conventional MRI, but the AC in EPI is easy to locate. By using our proposed AC-centered coordinate system, registration outputs are readily benchmarked by verifying that the AC is centered. As AC-PC alignment is used, one can minimize slice-angle-mismatch and deep-brain-nuclei-mismatch with the Paxinos and Watson’s rat brain coordinate system, thus bridging a critical gap between the rodent MRI imaging field and neuroscience disciplines that rely on the use of Paxinos and Watson’s rat brain coordinate systems.

The effects of the nuisance removal and the source of physiological noise in the rodent brain have been examined in several studies (Pais-Roldan at al., 2018; Chuang et al., 2019; Drew at al., 2020; Grandjean at al. 2020; Ma et al., 2020) and remain to be an active field of research. While the present study aimed to present raw data quality of the disseminated rat brain resting-state database and avoid deletion of meaningful information in the global signal (Gutierrez-Barragan et al., 2019; Ma et al., 2020) or white matter/cerebral spinal fluid owing to partial volume effect (Dukart and Bertolino, 2014) or related spatiotemporal dynamics (Li et al., 2020; Fultz et al., 2019), we provided supplemental data showing the impact of global signal regression for further transparency. Fig. S11 shows significantly reduced overall connectivity values as well as inter-network connectivity when global signal regression is applied. These results are not surprising and consistent with literature (Grandjean et al., 2014; Belloy et al., 2018; Aedo-Jury et al., 2020). Instead of presenting our main outcomes with regression, we chose to discard the parcels associated with dorsal venous structure, pineal gland (Fig. S7), and those in proximity to broader areas and/or prone to susceptibility artifacts (Fig. 7 B). With this approach, we demonstrated resilience of the identified FC network structure to SNR reduction down to 10% (Fig. S10B) as well as high-order motion parameter regression (Fig. S11). Our individual variability analysis also showed reasonable group consistency among in putative intrinsic networks including CEN (M1), DMN (M2), and SN (M3) (Fig. 14), suggesting the robustness of our finding. We suspect this is due to sufficiently large number of subjects and the use of non-parametric permutation-based statistics. It should be noted that our approach may not be sufficient for removing all physiological noise in the data and could cause some false-positive findings during higher-level network analysis. Recording of physiological parameters such as heart rate and respiration for retrospective noise removal (Glover et al., 2000; Pais-Roldan et al, 2018) or using a multi-echo sequence for T2* fitting (Kundu at al., 2014, Ma et al., 2020) may help address these confounds. We trust that dissemination of this database will provide a useful resource for researchers to further develop and evaluate methods removing unwanted signal in resting-state data.

Grandjean et al. pioneered specificity metric that is proven useful to evaluate the quality of a multi-center mouse resting-state fMRI database. This approach was recently utilized by an awake rat resting-state fMRI database and derived similar results (Liu et al., 2020). The metric was built on robust cingulate and RSC FC, as both are considered to be key nodes of the DMN (Tu et al., 2021a; Tu et al., 2021b; Peeters at al., 2020; Belloy et al., 2021; Coletta et al., 2020; Grandjean et al., 2020; Paasonen et al., 2018; Lu et al., 2012), whereas the cingulate and somatosensory FC is usually low (Gozzi and Schwarz, 2016), or often in opposing states (Belloy et al., 2018; Gutierrez-Barragan et al., 2019). Nevertheless, emerging studies have shown dichotomous involvement of cingulate cortex in both the DMN and the SN (Tsai et al., 2020; Mandino et al., 2019b). It is likely that the specific duration by which anterior cingulate cortex engages in these two functionally antagonistic networks (Sridharan et al., 2008) in the rodent brain may vary across subject conditions and brain states, thus adding variability to serve as a straightforward quality control metric. Inspired by the contribution made by Grandjean et al., we modified the specificity metric by comparing S1-S1 FC against S1-RSC FC and showed 73.6% in our disseminated database (Fig. 8).

Additionally, we examined the impact of filter cutoff on spatiotemporal feature detection as previous study showed that dexmedetomidine may potentially shift the cortical fMRI signal fluctuation frequency up to 0.2 Hz (Grandjean et al, 2014; Paasonen et al., 2019). We found that ICC values of overall identified spatiotemporal features were reduced by using 0.2 Hz cutoff, resulting in significant reduction of the number of features compared to using 0.1 Hz cutoff. This finding suggests that using a wider bandwidth could increase variability of within-subject results, possibly due to remaining physiological noise in our data. Additional studies are warranted to elucidate the underlying mechanisms.

Common spatial decomposition methods such as ICA and dictionary-learning have contributed significantly toward isolating meaningful brain signals from physiological noise and identifying spatiotemporal features that can describe the spontaneous activity of the brain as measured via resting-state fMRI (Beckmann et al., 2009; Varoquaux et al., 2011). In this study, we clustered voxels into spatially discrete ROIs by using spatiotemporal features as the multivariable classifier. The resulting ROIs were subsequently used to identify the intrinsic functional networks, extract network properties including small-worldness, modularity, and resilience, and identify hubs and rich club structures, all of which are in general agreement with previous studies performed under lower voxel resolution in rats (Aedo-Jury et al., 2020; Liang et al., 2018; Ma et al., 2018) as well as in mice (Coletta et al., 2020; Grandjean et al., 2020; Gutierrez-Barragan et al., 2019; Liska et al., 2015). We observed similar FC architecture across strains and sexes, suggesting highly robust representations of these data-driven ROIs in the rat brain. Of note, this is likely because our approach preferentially extracted ROIs representing common features across strains and sexes, which does not necessarily indicate the lack of strain and sex differences in the rat brain FC networks.

We demonstrated the use of identified ROIs in characterizing putative intrinsic functional brain networks including the CEN (Coletta et al., 2020; Thompson et al., 2014), DMN (Grandjean et al., 2020; Lu et al., 2012), and SN (Tsai et al., 2020) (Fig. 14), recapitulating the triple-network model (Menon, 2011). As these networks are widely adapted to characterize human brain function and dysfunction (Bullmore and Sporns, 2009; Menon, 2019; Menon, 2011; Rubinov and Sporns, 2010, 2011; Sporns, 2013), the identified rat brain networks may prove useful when translating research findings. The CEN and DMN described in this work are in agreement with previous rodent rs-fMRI findings using correlation-based static connectivity approaches (Coletta et al., 2020; Grandjean et al., 2020; Liska et al., 2015; Lu et al., 2012) and non-correlation-based approaches (Gutierrez-Barragan et al., 2019). While DMN and CEN have been characterized by these data-driven approaches in rodents, the SN remains less-frequently identified. Nonetheless, the SN described here is supported by a recent study which utilized a systematic approach to evaluate the existence of SN in the rat brain (Tsai et al., 2020).

Anticorrelation between DMN and CEN or DMN and SN was not robust in our data, likely due to the absent of task. Perhaps results in Fig. 8 may indicate a trend toward such anticorrelation, where seed-based connectivity of S1 – a CEN node, showed slightly more negative correlation with RSC – a DMN node (range: −0.3 < r < 0.2). The individual variability showed that intra-network connectivity of CEN, DMN, and SN present high group consistency, in agreement with a previous human study (Finn et al., 2015) and suggest the network structures are stable across healthy rat subjects. The inter-networks connectivity between DMN and CEN contained edges with high DP, indicating the connectivity between these two networks may contribute to subject-specific connectivity pattern (Fig. 12 A). Our findings also indicate that intra-network connectivity of SN might contribute to individual variability. However, this was not observed in previous mouse (Bregmann et al., 2020) and human (Finn et al., 2015) studies. It is possible that species and subject condition might affect this metric. In addition, since our dataset contains multiple strains, sexes, and ages, further studies using a more restricted design is needed to validate specific network contribution to the individual variability differences.

While the inclusion of hippocampus in rodent DMN is increasingly controversial due to a lack of direct anatomical connections (Whitesell et al., 2021), our modularity-based partitioning and graph analysis classified the hippocampus as a DMN hub. Similarly, the hippocampus has been considered part of the DMN in rodents across anesthetized and awake conditions (Hsu et al., 2016; Lu et al., 2012; Tu et al., 2021) as well as in humans (Buckner and DiNicola, 2019; Raichle, 2015). However, this classification could still be subject to the physiological states under which the rs-fMRI data were acquired. For example, a non-human primate study demonstrated that hippocampal sharp-wave ripple activity triggers DMN activation. Intriguingly, such sharp-wave ripples occur during the awake state or rapid-eye-movement (REM) sleep, but not during deep non-REM sleep (Kaplan et al., 2016; Walker and Robertson, 2016). These data suggest the possible involvement of hippocampus in DMN under certain physiological conditions. We believe it is crucial for future studies to present behaviorally relevant events during brain-wide imaging for a thorough topological mapping of large-scale brain networks.

In summary, we demonstrated the performance of a 0.4 mm isotropic EPI protocol with whole-brain coverage. This protocol has potential to achieve superior motion parameter estimation compared to anisotropic EPI protocol with limited brain coverage. We acquired a rat brain rs-fMRI database (n = 87) and developed an EPI-based brain template leveraging the Paxinos and Watson’s rat brain coordinate system which could help streamline the image registration process. We also performed data-driven parcellation and identified spatially discrete ROIs and networks. It is our goal to continually expand this database and disseminate additional data through the same links provided in this manuscript. Importantly, the identified ROIs and networks are robust across different rat strains and sexes, and are thus suitable to investigate subject-level activity changes in response to various manipulations and treatments. We expect our approaches and findings to strengthen the foundation for future translational brain circuit/network studies. Echoing pioneering efforts to promote open science in the human (Casey et al., 2018; Glasser et al., 2016; Howell et al., 2019; Mueller et al., 2005; Sudlow et al., 2015; Van Essen et al., 2013; Yan et al., 2013) and rodent fMRI fields (Grandjean et al., 2020; Liu et al., 2020), we disseminated the raw and processed data, as well as the analytical tools used in this study, with the goal to facilitate standardization of rat brain resting-state fMRI studies.