Revisiting Performance Metrics for Prediction with Rare Outcomes

Abstract

Machine learning algorithms are increasingly used in the clinical literature, claiming advantages over logistic regression. However, they are generally designed to maximize area under the receiver operating characteristic curve (AUC). While AUC and other measures of accuracy are commonly reported for evaluating binary prediction problems, these metrics can be misleading. We aim to give clinical and machine learning researchers a realistic medical example of the dangers in relying on a single measure of discriminatory performance to evaluate binary prediction questions. Prediction of medical complications after surgery is a frequent but challenging task because many post-surgery outcomes are rare. We predicted post-surgery mortality among patients in a clinical registry who received at least one aortic valve replacement. Estimation incorporated multiple evaluation metrics and algorithms typically regarded as performing well with rare outcomes, as well as an ensemble and a new extension of the lasso for multiple unordered treatments. Results demonstrated high accuracy for all algorithms with moderate measures of cross-validated AUC. False positive rates were less than 1%, however, true positive rates were less than 7%, even when when paired with a 100% positive predictive value, and graphical representations of calibration were poor. Similar results were seen in simulations, with the addition of high AUC (>90%) accompanying low true positive rates. Clinical studies should not primarily report AUC or accuracy.

1. Introduction

Prediction with various types of electronic health data has become increasingly common in the clinical literature.¹ Data sources include medical claims, electronic health records, registries, and surveys. While each class of data has benefits and limitations, the growth in data collection and its availability to researchers has provided opportunities to study rare outcomes, such as mortality, in different populations that were previously difficult to examine in smaller epidemiologic studies. Creating mortality risk score functions has evolved in recent years to include both electronic health data and modern machine learning techniques. These machine learning methods claim advantages over logistic regression in terms of out-of-sample performance.² Previous studies have examined mortality in older adults,^3;4 intensive care units,^5;6, individuals with cardiovascular disease,^7;8 and other settings^9;10 using machine learning.

Machine learning algorithms for binary outcomes are generally designed to minimize prediction error or maximize the area under the receiver operating characteristic curve (AUC). This AUC value, also referred to as the c-index or AUROC, is a summary metric of the predictive discrimination of an algorithm, specifically measuring the ranking performance for random discordant pairs. However, when the outcome of interest is rare, or more generally, when there is class imbalance in the outcome, benchmarking the performance of such algorithms is not straightforward, although AUC and accuracy (i.e., the number of correct classifications over sample size) are the standard measures reported.^11–13

Assessing prediction performance primarily using AUC or accuracy can be misleading and is “ill-advised,”¹² especially for rare outcomes.^13;14 High accuracy can be achieved with a simple rule predicting the majority class for all observations, but this will not preform well for metrics centered on true positives. Previous work has also highlighted that when the outcome is rare, other measures, such as the percentage of true positives among all predicted positives (i.e., positive predictive value)¹⁵ and related precision-recall curves (i.e., plots of positive predictive value vs. true positive rate),^13;14 can be more informative. These earlier articles featured hypothetical settings with no real data,¹³ simulations only,¹⁵ and a lack of cross-validated metrics.¹⁴ There are also many arguments that measures of calibration (i.e., alignment of predicted probabilities with observed risk) for general classification problems are both more interpretable and better assess future performance.^16;17

Despite these published warnings, many machine learning competitions assign their leaderboard and winners solely on a single metric, typically AUC for binary outcomes. Work published in machine learning conference proceedings, even those events specifically focused on health care, often only consider AUC to compare methods.^18–20 This also occurs in the medical literature.^10;21 The lack of penetrance of the cautions against using a single metric, especially AUC, may be driven by a relative paucity of attention to this issue in translational papers, particularly work demonstrating these problems in real health data analyses. This is a major concern for the biomedical literature given the growing volume of papers applying machine learning to binary prediction problems in health outcomes.

This article provides a more comprehensive, clinically focused study evaluating prediction performance for rare outcomes incorporating (i) analyses in registry data, (ii) simulations, (iii) multiple metrics, (iv) multiple algorithms, and (v) cross-validated measures. It was motivated by the prediction of medical complications after major surgery. Examples of such complications in cardiac surgeries include in-hospital mortality after a percutaneous coronary intervention²² and reoperation after valve surgery.²³ Accurate and timely identification of patients who could have complications post-surgery, using characteristics collected prior to the surgery, has the potential to save lives and health care resources. However, many post-surgery outcomes are rare, making prediction a challenging task.

Aortic valve replacement (AVR) is necessary for many patients with symptomatic aortic valve disease,^24;25 and more than 64,000 AVR procedures were performed in the United States in 2010.²⁶ Mortality is a major risk factor following AVR surgery. Mechanical prosthetic valves are composed of synthetic material requiring anticoagulants following AVR, whereas bioprosthetic valves use natural (animal) cells as a primary material.²³ There are multiple manufacturers for each valve type and manufacturers introduce new generations of earlier valves over time. In addition to demographic features, comorbidities, medication history, and surgical urgency, the specific valve used is an important predictor of mortality following AVR.²⁶ However, earlier work predicting mortality outcomes following AVR has been limited to comparing mechanical vs. bioprosthetic values as valve-specific information is typically unavailable.²⁶ Recent work also demonstrated that bioprosthetic valves had increased mortality for some age groups.²⁷

We predicted 30-day and 1-year mortality among patients from a state-mandated clinical registry in Massachusetts who received at least one AVR between 2002 and 2014. Estimation incorporated multiple algorithms typically regarded as performing well with rare outcomes, as well as an ensemble and a new straightforward extension of the lasso for multiple unordered treatments developed here. Our application also expands on earlier applied work by additionally using manufacturer and generation specific subtypes of mechanical and bioprosthetic valves as predictors of mortality. We include wide-ranging simulation studies designed based on our AVR cohort. Our results demonstrate more extreme findings with respect to discordance along performance metrics than seen previously,¹⁴ and algorithms generally performed poorly on measures focused on true positives. Our goal with this work is to provide machine learning practitioners in clinical research with a clear demonstration of the pitfalls of relying on a single metric, and contribute to the body of literature that articulates the need to declare multiple measures.

2. The Statistical Estimation Problem

Baseline predictors are given by vector X of length p and Y is a post-surgery death outcome such that

$$Y=\{\begin{array}{ll}1& \text{if event occurred by time}t\\ 0& \text{otherwise}\end{array}$$

with t ∈ {30 days, 1 year}. X contains a vector V of binary treatment variables representing the distinct aortic valves. The observational unit is U = (Y, X) in nonparametric model M. The goal is to estimate ${\psi }_0=E(Y\mid X)=\mathrm{Pr}(Y=1\mid X)$, where the subscript 0 indicates the unknown true parameter, as a minimizer of an objective function:

$${\psi }_0={\mathrm{arg\; min}}_{\psi }E(L(U,\psi )),$$

with candidate algorithm ψ. We consider the rank loss function, $L(U,\psi )=1-\text{AUC}$, as the primary global loss function.²⁸ For a fixed ψ, let ${\widehat{Y}}_1^z,\dots ,{\widehat{Y}}_s^z$ be the predicted probabilities for s outcomes where Y = 1 and ${\widehat{Y}}_1^w,\dots ,{\widehat{Y}}_q^w$ be the predicted probabilities for q outcomes where Y = 0. Then the AUC associated with ψ is written as: $AUC={\sum }_{o=1}^s{\sum }_{r=1}^q\mathbb{I}\left({\widehat{Y}}_o^z>{\widehat{Y}}_r^w\right)/(sq)$, where $\mathbb{I}$ is an indicator function.²⁹ As a secondary global loss function, we use the negative log-likelihood function: $L(U,\psi )=-\log \left[{(\psi )}^Y{(1-\psi )}^{1-Y}\right]$.

2.1. Estimation Methods

We consider multiple candidate algorithms ψ typically regarded as performing well with rare outcomes, as well as an extension of the lasso for multiple unordered treatments and an ensemble³⁰ of these algorithms that optimizes with respect to a global loss function. The global loss function optimized for the ensemble can be different than the loss function optimized within each candidate algorithm. Existing methods for rare outcomes used in our data analysis include lasso,³¹ logistic regression with Firth’s bias reduction,^32;33 group lasso,³⁴ sparse group lasso,³⁵ random forest,^36;37, and logistic regression. These algorithms plus gradient boosted trees,^38;39 Bayesian additive regression trees (BART),⁴⁰ neural networks,^41;42 and support vector machines (SVMs)⁴³ were implemented in our simulations studies to expand the set of candidate algorithms to reflect additional widely used tools. Our extension of the lasso, used in both the data analysis and simulations, involves excluding the covariates for treatment from the penalty term, and is described in further detail below. Thus, the ensemble averaged over seven algorithms in our data analysis and eleven in our simulations.

The super learner creates an optimal weighted average of learners that will perform as well as or better than all individual algorithms with respect to a global loss function, and has various optimality properties discussed elsewhere.³⁰ We note that while we consider the rank and negative log-likelihood loss as global loss functions, we could alternatively have chosen to optimize our super super with respect to classification criteria.⁴⁴ As is common in the applied literature, our goal is instead to obtain the best estimator of Pr(Y = 1|X) while still being interested in evaluating performance by mapping the predicted probability into a classifier.

Five of the individual techniques, including our extension, are forms of penalized regression, which have gained traction in the clinical literature for their potentially beneficial performance for rare outcomes.⁴⁵ In penalized regression methods, a penalty function P(β) with preceding multiplicative tuning parameter λ is introduced in the objective function for coefficients β to reduce bias at the cost of increased variance: $L(U,\psi )+\lambda P(\beta )$. Lasso regression has a penalty function $P(\beta )=\parallel \beta {\parallel }_1={\sum }_{j=1}^p\left|{\beta }_j\right|$ with l₁ norm ∥.∥₁, such that some βs may be shrunk to exactly zero as the value of the tuning parameter λ increases.³¹ Previous work targeting causal parameters in comparative effectiveness research for multiple unordered treatments demonstrated that penalized regression methods may shrink all treatment variables V to zero or near zero.⁴⁶ Thus, although we target a different parameter, in our extension of the lasso the coefficients for the binary indicators for the multiple treatments V are excluded from the penalty function. Suppose these treatment coefficients within j = {1,..., p} are from k to p, we can then write this penalty as: $P(\beta )={\sum }_{j=1}^{k-1}\left|{\beta }_j\right|$. We refer to the procedure as the treatment-specific lasso regression.

Of course, logistic regression is a well-known parametric tool for predicting binary outcomes. Logistic regression with Firth’s bias correction is a method that can reduce the bias of regression estimates due to separation in small samples with unbalanced classes (e.g., a rare outcome). It produces finite parameter estimates by means of penalization with the Fisher information matrix I(β).³² We can translate this into the above framework with penalty $P(\beta )=\log |I(\beta )|$ and fixed λ = 1/2. To account for the categorical variables (i.e., sets of binary indicators for the levels in each category of a predictor) found in our application, we also consider group lasso regression³⁴ and sparse group lasso regression.³⁵ Group lasso regression enforces regularization on sets of variables (i.e., groups) rather than individual predictors. Let G be the total number of groups in X and p_g be the number of covariates in each group g. The penalty function for the group lasso regression can then be written as $P(\beta )={\sum }_{g=1}^G\sqrt{p_g}{\Vert {\beta }_g\Vert }_2$, where ∥.∥₂ denotes an l₂ norm of a vector. For sparse group lasso regression, regularization is enforced both on the entire group of predictors as well as within each group. The penalty term for the sparse group lasso regression is given as $P(\beta )=(1-\alpha ){\sum }_{g=1}^G\sqrt{p_g}{\Vert {\beta }_g\Vert }_2+\alpha \parallel \beta {\parallel }_1$, where α ∈ [0, 1].

Three of the other techniques are ensembles of classification trees. Classification trees generally rely on recursive binary partitioning of the predictor space to create bins that are highly homogenous for the outcome. A key benefit of tree-based methods comes from their ability to identify nonlinear relationships between the outcome variable and predictors.² Random forests aggregates multiple classification trees, each with a random selection of input predictors. Whereas in gradient boosted trees, multiple trees are trained in an additive and sequential manner based on residuals to improve outcome classification.^38;39 BART is a Bayesian approach leveraging regularization priors and posterior inference to estimate ensembles of trees.⁴⁰ The set of priors for the tree structure and leaves prevent any single tree from dominating the overall fit and a probit likelihood is used in the terminal nodes.

The last two algorithms considered are feed-forward neural networks and SVMs, originally called support vector networks. Neural networks follow an iterative procedure to estimate the relationships between variables with layers of nodes, where number of units in the hidden layer is a hyperparameter that needs to be specified.⁴¹ SVMs aim to find optimal partitions of the data across a decision surface using a hinge loss and a pre-specified kernel function.⁴³ These two algorithms, along with gradient boosted trees and BART described directly above, are applied in our simulation studies only.

Our implementation of these candidate algorithms ψ relies on the R packages glmnet⁴⁷ (lasso and treatment-specific lasso), brglm⁴⁸ (logistic regression with Firth’s bias correction), gglasso⁴⁹ (group lasso), msgl⁵⁰ (sparse group lasso), randomForest³⁷ (random forests), xgboost⁵¹ (gradient boosted trees), bartMachine⁵² (BART), nnet⁵³ (neural networks), kernlab⁵⁴(SVM), and SuperLearner⁵⁵ (ensemble). Internal tuning parameters for each algorithm were selected using nested cross-validation.⁵⁶ Additional details regarding the hyperparameter tuning are included in the supplemental material. As a benchmark for thresholding these prediction algorithms, a naive prediction rule that assigns every patient to the majority class is also considered. In our application, the majority class is surviving up to time t ∈ {30 days, 1 year}. We provide code to implement these estimators in a public GitHub repository github.com/SamAdhikari/PredictionWithRareOutcomes.

2.2. Evaluation Measures

We consider a suite of metrics for evaluating algorithms with out-of-sample prediction probabilities in stratified 5-fold nested cross-validation. The stratification refers to distributing our rare outcomes across the cross-validation folds to ensure that a roughly equal number of events occur in each fold. These measures have been previously identified in the literature as capturing differing aspects of algorithm performance. We extend the common approach where a fixed probability threshold is used to assign patients into different outcome classes by building a flexible thresholding rule. For a set of candidate thresholds between 0 and 1, accuracy is computed at each threshold. The threshold at which overall accuracy is maximized is then selected as the threshold for assigning a patient to an outcome class for that particular algorithm. If there are multiple thresholds that maximize the accuracy, the minimum of those thresholds is used.

The threshold selected is used to compute multiple evaluation metrics. In Figure 1, we use the notation in the 2 × 2 contingency table to formally define five of the evaluation metrics, where $\hat{Y}$ is the predicted outcome. Positive predictive value (PPV) is the proportion of true positive outcomes over the number of predicted positive outcomes and accuracy is the overall proportion of true positives and true negatives for n total observations. The true positive rate (TPR) is the proportion of true positive outcomes over the number of observed positive outcomes and the false positive rate (FPR) is the proportion of false positive outcomes over the number of observed negative outcomes. Finally, F₁ score is computed as the harmonic mean of TPR and PPV giving equal weight to precision and recall. We note that our naive prediction rule discussed in Section 2.1 will have high accuracy, but a TPR of zero. (We also consider a threshold where TPR is maximized in sensitivity analyses.) At the specified threshold, we present the mean evaluation metrics averaged over the cross-validation folds as well as the 95% confidence interval around the mean estimates computed using the standard error.

Figure 1.

Summary of Several Evaluation Measures under Simple Random Sampling. Not displayed: area under the receiver operator characteristic curve (also known as c-index), precision-recall plots, and plots of the percentage of true positive outcomes across risk percentiles

As discussed earlier, many medical machine learning applications claim a good prediction tool will have high AUC and accuracy. However, these results can be misleading, especially for rare outcomes, and it has been argued that use of PPV and precision-recall curves might be more informative.¹⁴ We do consider AUC given its pervasiveness in the literature, as presented in Section 1, but also precision-recall curves, which plot PPV versus TPR. Precision-recall curves are favored in some previous literature due to their focus on true positive classifications among the overall positive classifications, which may lead to better insights into future predictive performance.¹⁴ Assessing calibration is also important in projecting future predictive performance. We consider one variation of a graphical representation of calibration^16;57 with bar plots of the percentage of true positive outcomes across estimated risk percentiles, however alternative model-based approaches also exist.⁵⁸ Our set of evaluation measures is not exhaustive and debates regarding the best metrics continue in the scientific discourse. However, this collection represents an entry point for illustrating the perils of relying on AUC and accuracy.

3. Predicting Mortality After AVR

Our study data are from a state-mandated clinical registry coordinated by the Massachusetts Data Analysis Center.⁵⁹ The data included all AVRs performed between 2002 and 2014 in all nonfederal acute care Massachusetts hospitals for patients at least 18 years of age, regardless of health insurance status. We considered patients with AVR procedures only as well as other cohorts that included combination procedures. This resulted in four different cohorts: isolated AVR, patients who had either isolated AVR or a combination of AVR and mitral valve replacement procedures, patients who had either isolated AVR or a combination of AVR and coronary bypass surgery procedures, and patients in all of the previous cohorts combined. The endpoints of interest in the analysis are short-term (within 30 days) and long-term (within 1 year) mortality outcomes following AVR, recorded between 2002 and 2015, including patients who had at least one year of follow-up. Loss to follow-up was minimal across the cohorts (i.e., 2–6%) and noninformative (e.g., included patients who had moved out of state).

We focus on the isolated AVR cohort in the main text with the three other cohorts presented in the supplemental material. Table 1 displays the mortality rates overall in the isolated AVR cohort as well as subgroups for mechanical and bioprosthetic valves. These groupings were constructed based on the features of the devices, such as manufacturer and generation-specific information, and clinical expertise. They also serve as the binary indicator variables for our multiple treatments. We note that our overall 30-day and 1-year mortality rates of 1.8% and 5.3%, respectively, may or may not be deemed ‘rare’ depending on the definition considered, which can range from well under 1% to over 10%. As discussed in Section 1, the broader setting of imbalanced outcome classes clearly applies here.

Table 1.

Observed Mortality Rates in Isolated AVR Cohort. Cells with < 10 events were suppressed and replaced with *.

	Mortality Rate (%)
	30 Day	1 Year
Overall Cohort (n)
Isolated AVR (6472)	1.8	5.3
Mechanical (n)
Group 1 (34)	5.9	11.7
Group 2 (67)	1.5	2.9
Group 3 (27)	3.7	3.7
Group 4 (685)	1.3	3.8
Group 5 (107)	0.9	2.3
Group 6 (248)	1.6	4.4
Bioprosthetic (n)
Group 7 (361)	1.7	6.9
Group 8 (*)	*	*
Group 9 (299)	1.7	5.0
Group 10 (505)	1.4	3.9
Group 11 (149)	2.0	4.7
Group 12 (2308)	2.2	6.6
Group 13 (381)	0.5	4.2
Group 14 (1304)	1.8	5.1

Baseline predictors included demographic information (e.g., age, sex, race/ethinicity, and type of health insurance); comorbidities; family history of cardiac problems; cardiac presentation prior to the AVR (e.g., ejection fraction, cardiac shock, and acute coronary syndrome status); procedure-specific information (e.g., type of procedure performed); hospital; and medication history. Key baseline covariates measured prior to the valve replacement surgery are summarized in Table 2 with the complete list of covariates for all four cohorts presented in the supplemental material. We note that use of race and ethnicity in risk prediction algorithms should include thoughtful consideration regarding what these variables represent (e.g., structural racism) and how they may perpetuate health inequities if an algorithm is deployed.⁶⁰ Our algorithms had poor performance and we do not recommend them; this issue was important to raise as these variables were included. Continuous covariates were standardized to have mean zero and a standard deviation of one. Covariates with > 10% missingness were deemed unreliable and excluded from the analyses. For covariates with < 10% missingness, we introduced a missingness indicator variable.⁶¹

Table 2.

Key Baseline Predictors Measured Prior to Surgery in Isolated AVR Cohort.

Predictors	30-Day Mortality		1-Year Mortality
	Y = 1	Y = 0	Y = 1	Y = 0
Demographic
Age (mean, years)	73	68	73	68
Height (mean, cm)	166	168	168	169
Weight (mean, kg)	80	83	80	84
Male (%)	52	58	56	58
Race/Ethnicity (%)
White	89	92	92	92
Black	4	2	3	2
Hispanic	4	3	2	3
Comorbidities (%)
Diabetes	39	26	37	26
Hypertension	84	73	78	73
Left main disease	7	2	4	2
Previous cardiovascular	34	23	32	22
Intervention
Medication (%)
Betablocker
Yes	61	42	51	47
Contraindicated	2	6	5	6
Anticoagulation
Yes	17	12	23	12
Contraindicated	0	2	1	2

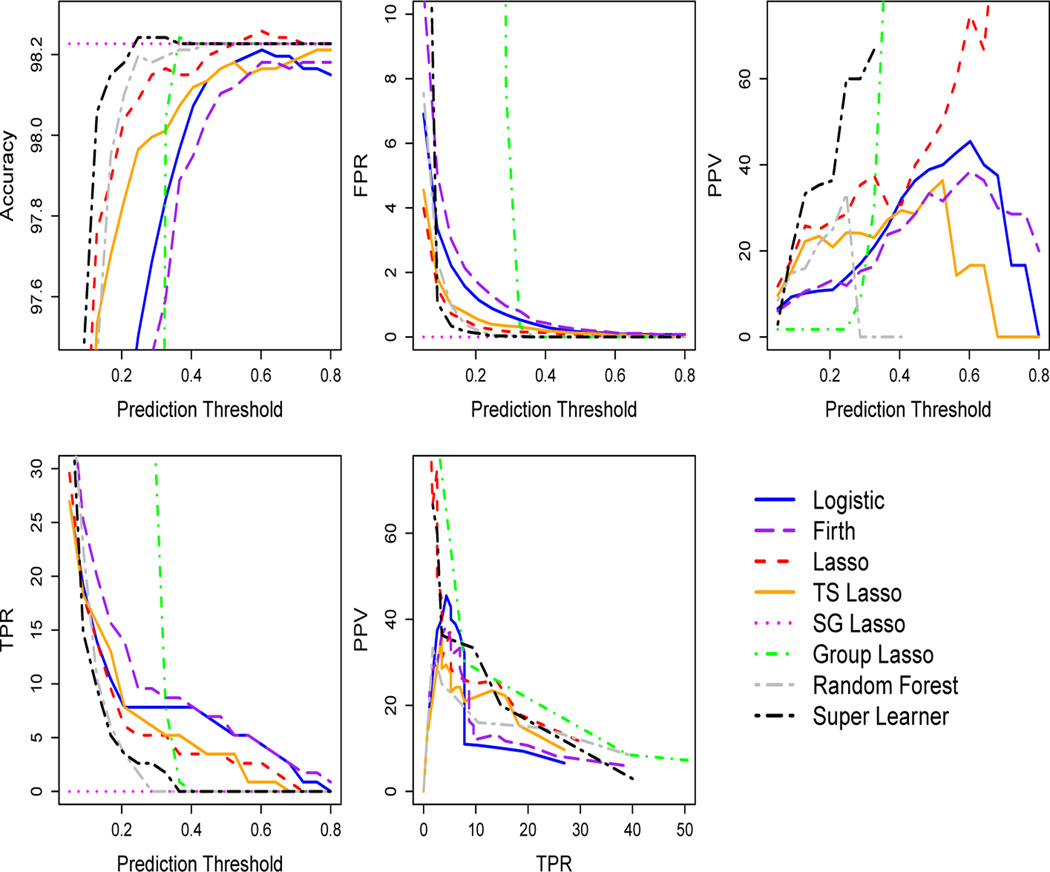
As described in Section 2.1, the out-of-sample cross-validated predicted probabilities were first deployed to select a prediction threshold that maximizes the accuracy for each algorithm in each fold, with sensitivity analyses in the supplemental material maximizing TPR. Analyses using the rank loss function and negative log-likelihood loss function were performed separately, with negative log-likelihood loss function performance reported in the supplementary material (results were similar). The top row and first panel of the second row in Figure 2 presents the accuracy, FPR, PPV, and TPR evaluation metrics for 20 prediction thresholds between 0 and 1 for the 30-day mortality outcome. We observe that three algorithms underperformed the naive prediction rule with respect to accuracy: logistic regression, logistic regression with Firth’s bias correction, and the treatment-specific lasso. FPR values quickly converged toward zero as the prediction threshold increased for all algorithms except group lasso. PPV performance varied by algorithm, although multiple algorithms did not exceed a mean of 50% for any threshold. (See supplementary material for 1-year mortality outcome figure.)

Figure 2.

Data Analysis: Cross-Validated Algorithm Performance by Prediction Threshold and Precision-Recall Plot for 30-Day Mortality in Isolated AVR Cohort. Prediction threshold chosen to maximize accuracy. Plots display the mean over 5-folds at each threshold value. For algorithms with TPR equal to zero, PPV is undefined and not plotted. In this isolated AVR cohort, the naive prediction rule accuracy is the same as the sparse group (SG) lasso. TS is an abbreviation for treatment-specific.

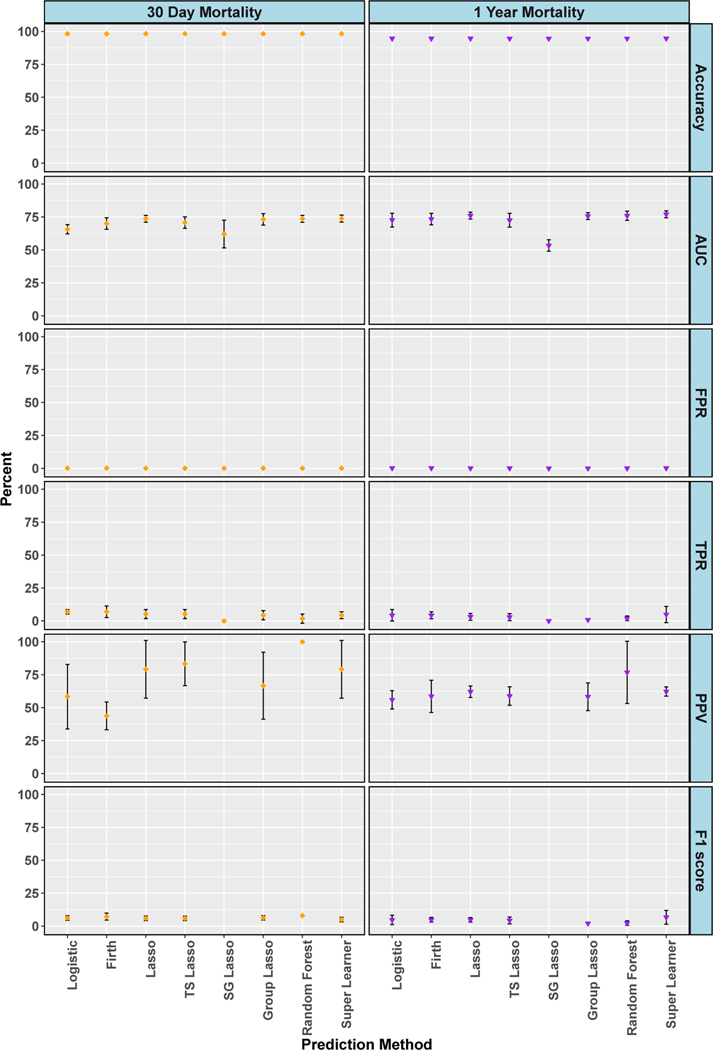
Figure 3 displays results at the selected threshold in the isolated AVR cohort for accuracy, AUC, FPR, TPR, PPV and F₁ score. Accuracies were high for both outcomes and flat across all algorithms: 98% for 30-day mortality and 95% for 1-year mortality. AUC ranged from 57 to 74% for 30-day mortality and 73 to 76% (except sparse group lasso at 53%) for 1-year mortality. AUC values in the 70s are often reported in published clinical analyses.^{10;18–20;62} The FPRs were desirably low; less than or equal to 0.1% for all algorithms and both outcomes. However, Figure 3 also shows extremely poor TPR, with all algorithms less than 7% and sparse group lasso at exactly zero. We found moderate PPVs (only defined for algorithms where the number of predicted positive values was nonzero), with random forests an outlier at 100% PPV for 30-day mortality. This 100% PPV could easily be misinterpreted, however, if not additionally noted that it was paired with a 2% TPR. The precision-recall plot in Figure 2 for 30-day mortality also highlights poor TPR and weak PPV performance. Many algorithms did not have a mean of at least 50% PPV (precision) for any level of TPR (recall). F₁ scores (when not undefined due to undefined PPV) were poor with all values less than 7%. Plots of the percentage of true positive outcomes across risk percentiles show less than 12% of true positive outcomes in the top ventile for 30-day mortality and less than 25% for 1-year mortality (see supplementary material for figures). Thus, overall we found that all algorithms demonstrated poor performance for predicting two mortality outcomes after AVR surgery, despite high accuracy values and moderate measures of AUC.

Figure 3.

Data Analysis: Cross-Validated Algorithm Performance in Isolated AVR Cohort. For algorithms with zero predicted positive values, PPV is undefined and not plotted, and therefore F₁ score is also undefined and not plotted. 95% confidence intervals for estimates with standard errors less than 1% are not shown. TS is an abbreviation for treatment-specific and SG is for sparse group.

4. Simulations

A large set of simulation studies for the two mortality outcomes and all four cohorts was designed to evaluate our findings in the context of a known data generating distribution, while also exploring additional settings and algorithms. These simulations were based on the real data from Section 3. For each cohort, a matrix of predictors X_sim was simulated to resemble the observed data. Nine positive continuous predictors, representing age, height, and weight, among others, were simulated from a truncated Normal distribution, such that for each continuous covariate h, $X_{\text{sim}}^h\sim N\left({\mu }_h,{\sigma }_h^2\right)$ with X ∈ [a_h, b_h]. The means μ_h and variances ${\sigma }_h^2$ were estimated as the empirical means and variances within the observed cohorts, while the lower limits a_h and the upper limits b_h were estimated as the minimums and maximums for each variable in the observed data.

Thirty-six binary predictors were simulated using Bernoulli distributions: $X_{\text{sim}}^d\sim \text{Bern}\left(e_d\right)$, where e_d is the observed proportion of events for each binary covariate d. Seven categorical predictors with multiple levels, including the valve types, were simulated from multinomial distributions using the observed proportions as the probabilities for each category. These categorical variables were converted into binary predictors, resulting in 72 total predictors. Finally, simulated outcomes were generated for each of the two endpoints such that $Y_{\text{sim}}\sim \text{Bern}\left(e_y\right)$ and $\text{logit}\left(e_y\right)=X_{\text{sim}}\beta$, where e_y is the proportion of events and βs were assigned using estimated coefficients from the observed AVR cohorts.

We explored three distinct settings with increasing complexities in data generation and covariate selection choices. In simulation setting 1, we used the same set of predictors for both data generation and prediction, assuming the analyst had access to all the predictors that generated the data. Specifically, all main effects of the available predictors X_sim were used to generate the outcome and to estimate ψ₀. In simulation setting 2, complex nonlinear functions of predictors, including interaction terms and quadratic forms, were used for data generation. However, this nonlinearity in predictors was essentially ignored while estimating ψ₀; these specifications were not explicitly provided to algorithms with a strict functional form although the random forests were not restricted from discovering interactions.

In simulation setting 3, we omitted a portion of predictors while generating the data, such that only a subset of X_sim was used to create Y_sim. The predictors that were omitted (i.e., did not contribute information to the generation of Y_sim) were intentionally introduced into the estimation of ψ₀, whereas a separate subset of predictors that were used for data generation were omitted from the estimation step. Estimation in this setting also did involve variables from X_sim that were part of both data generation and available for inclusion in the algorithms. This last setting represents the realistic scenario where important true predictors are not available for building a prediction function and uninformative ‘noise’ variables are included instead.

Further details on the construction of the simulations are available on our companion GitHub page with R code github.com/SamAdhikari/PredictionWithRareOutcomes as well as in our supplementary material. Mirroring the data analyses in Section 3, simulation results based on the isolated AVR cohort are discussed here with the additional results included in the supplemental material. We also present true conditional risk estimates based on the AUC loss function using the true data-generating probabilities and the simulated outcomes to compare with the cross-validated AUC estimates.

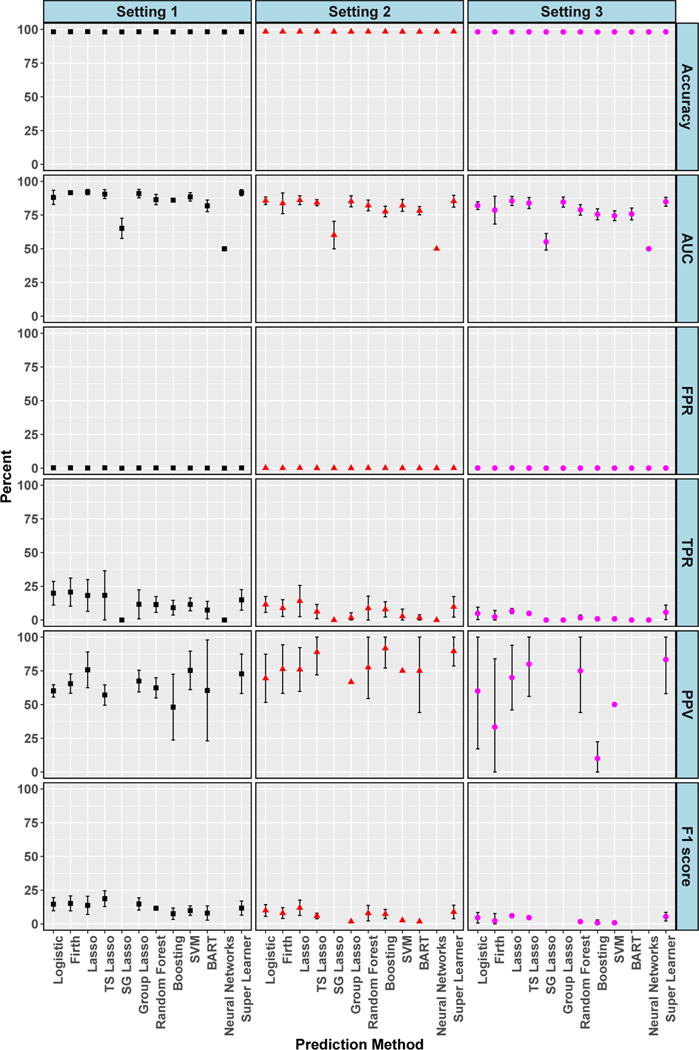
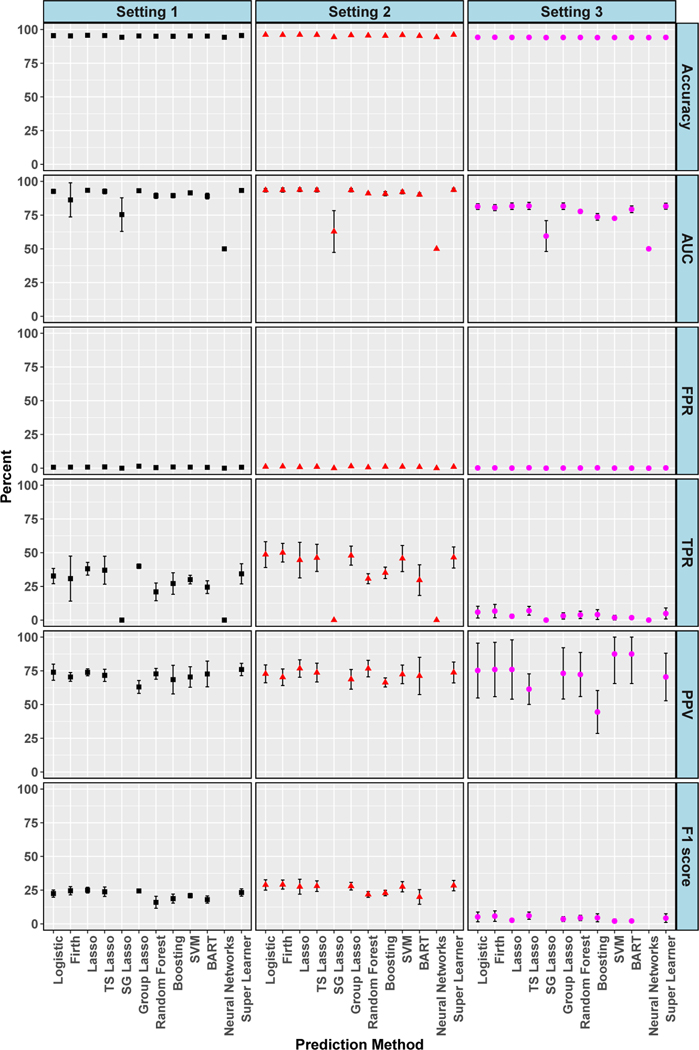
Figures 4 and 5 display evaluation metrics for 30-day and 1-year mortality outcomes, respectively, across the three simulation settings. These metrics were computed at the best threshold for each algorithm, as in the data analyses. High accuracies and near zero or zero FPRs were seen in all settings and both outcomes. Setting 3, reflecting the realistic scenario with missing predictors and ‘noise’ variables, had the worst performance for both outcomes with near zero or zero TPR and near zero F₁ scores. Broadly, setting 3 was the most similar to the results found in our data analyses. In settings 1 and 2 for 1-year mortality, AUC hovered around 90% for most algorithms, PPV was about 75%, and F₁ score approximately 25%. TPRs even reached the improved level of 40% in setting 1 and 50% in setting 2. The four additional algorithms added to our simulations did not appreciably improve performance, with gradient boosted trees, BART and SVMs having similar metrics to other algorithms. Neural networks was particularly poor, achieving the worst AUC values paired with 0% TPRs across settings and for both outcomes. In sensitivity analyses (see supplemental material) considering thresholds where TPR is maximized rather than accuracy, we saw improvements in TPR, although all values were less than 75% when considering those with low FPR. Values of 100% TPR were achieved, but only paired with 100% FPR. However, in the realistic setting 3, most TPR values were less than 50%, with two exactly zero. There was also a massive drop in PPV for every algorithm across each setting with all below 25%.

Figure 4.

Simulation: Cross-Validated Algorithm Performance for 30-Day Mortality in Isolated AVR Cohort. For algorithms with zero predicted positive values, PPV is undefined and not plotted, and therefore F₁ score is also undefined and not plotted. 95% confidence intervals for estimates with standard errors less than 1% are not shown. True conditional risk estimate based on AUC loss is 94% for setting 1, 89% for setting 2 and 95% for setting 3. TS is an abbreviation for treatment-specific and SG is for sparse group.

Figure 5.

Simulation: Cross-Validated Algorithm Performance for 1-Year Mortality in Isolated AVR Cohort. For algorithms with zero predicted positive values, PPV is undefined and not plotted, and therefore F₁ score is also undefined and not plotted. 95% confidence intervals for estimates with standard errors less than 1% are not shown. True conditional risk estimate based on AUC loss is 94% for settings 1 and 2 and 95% for setting 3. TS is an abbreviation for treatment-specific and SG for sparse group.

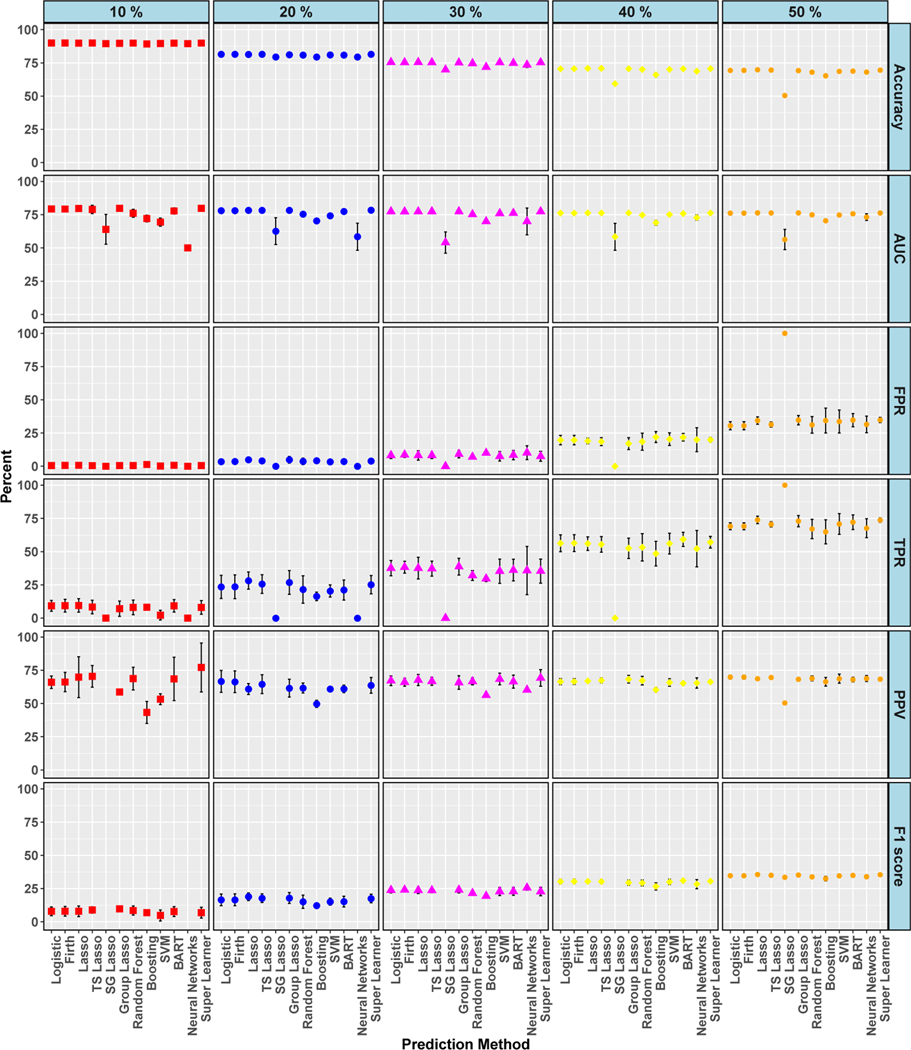
Lastly, for the isolated AVR cohort, we made modifications to the generation of the outcome in each of the three simulation settings to investigate whether performance improved as class imbalance for the outcome decreased. Simulated data were created with five different mortality rates ranging from 10 to 50%, with 50% representing no class imbalance. For simulation setting 3, shown in Figure 6, TPR was always less than 75% when the mortality rate ≤ 40% and less than 50% when the mortality rate ≤ 30%. With only one exception (10% rate with super learner algorithm), PPV was also less than 75% for all mortality rates, even with no class imbalance. Further graphical results are displayed in the supplementary material and we summarize several additional key findings from those results here. In simulation settings 1 and 2, TPRs improved with increasing mortality rate and were even around 75% for mortality rates ≥ 40% for the majority of the algorithms, although still paired with low F₁ scores. Plots of the percentage of true positive outcomes across risk percentiles for setting 1 showed improved calibration as mortality rate increased. At 10% mortality, most algorithms approached 80% of true positive outcomes in the top ventile and, at 50% mortality, these values approached 100%. We also explored the impact of the number of cross-validation folds (5, 10, or 15) and found that the results were similar across fold choice.

Figure 6.

Simulation: Cross-Validated Algorithm Performance for Varied Class Balance in Simulation Setting 3. For algorithms with zero predicted positive values, PPV is undefined and not plotted, and therefore F₁ score is also undefined and not plotted. 95% confidence intervals for estimates with standard errors less than 1% are not shown. True conditional risk estimate based on AUC loss is 94% (for 10% event rate), 92% (for 20%, 30%, and 50% event rates), and 91% (for 40% event rate). TS is an abbreviation for treatment-specific and SG is for sparse group.

5. Discussion

AUC and accuracy measures are commonly reported in medical and machine learning applications to assess prediction functions for binary outcomes. However, when the outcome of interest is rare, prediction performance with these metrics can be misleading; evaluations using one or two metrics will not be sufficient. Even when both AUC and accuracy are high, we found that TPR, PPV, F₁ score or graphical presentations of the percentage of true positive outcomes across risk percentiles can be poor. The TPR, F₁ score, precision-recall curves, and percentile plots were the most consistent metrics for correctly identifying the poor performance in our data analyses and simulations. Although it should be noted that F₁ score may still be low with no class imbalance, low FPR, and high TPR, PPV, AUC, and accuracy. We found that PPV (i.e., not paired with TPR in a precision-recall curve) was sometimes misleading (e.g., 100% when TPR was near zero) and not necessarily more informative than AUC and accuracy, which further distinguishes our work from some previous studies.¹⁵ Overall, our results are also more extreme with respect to discordance between measures (e.g., near perfect accuracy paired with near-zero TPR) compared to earlier works.

As one might imagine, this endeavor began as a study to design new prediction functions for 30-day and 1-year mortality in four AVR cohorts created from registry data. We aimed to build a tool leveraging the best existing algorithm options for rare outcomes while also proposing a new methodological extension of our own that was specific to multiple unordered treatments. What we found was unexpected – none of the methods yielded a usable prediction function, and far from it. Futhermore, this was only discovered because we considered a large suite of evaluation metrics. Had we been functioning in the common scenario where only AUC or accuracy were measured, we would have declared strong performance, and perhaps suggested that our tools had practical relevance for applied settings. As our data analyses and simulations demonstrated, high AUC and accuracy can be accompanied by extremely low TPR for predicting both short-term and long-term mortality following AVR.

One of the “strengths” of registry data, often touted as an advantage over claims databases, is the availability of detailed clinical information. We had access to dozens of relevant variables for prediction of mortality following AVR and were unable to develop a prediction function we could recommend. The prediction of medical complications after major surgery is a critical need, as accurate identification of patients at risk for serious complications post-surgery could save lives and preserve health care resources. Thus, it is regrettable we do not offer tools to contribute to this crucial area. However, it is always important to recognize that all data sources will not be appropriate for solving all research questions; this registry and other registries have proven valuable for many other settings.

Where our contribution does lie is in providing a more comprehensive, clinically focused evaluation of prediction performance with rare outcomes featuring (i) a relevant AVR data set, (ii) an array of simulations, (iii) multiple varied evaluation measures, (iv) parametric and machine learning algorithms, and (v) cross-validated metrics. We aimed to give clinical and machine learning researchers a realistic medical example of the dangers in relying on a single measure of discriminatory performance to evaluate performance. Additionally, we provide reproducible R code for our simulation study algorithms and evaluation measures on a companion GitHub page.

Another way the machine learning literature has dealt with class imbalance is by resampling the original dataset, either oversampling the minority (i.e., rare) outcome class or undersampling the majority class.^63–66 The synthetic minority oversampling technique (SMOTE) is one popular approach among these methods, relying on k-nearest neighbors to oversample observations with the rare outcome.⁶³ However, the feasibility of SMOTE and similar techniques in high-dimensional data is not clear, which is why we did not consider them here.⁶⁵ Other considerations include the lack of practical guidelines or procedures to select the rates of oversampling, especially when the outcome is extremely rare.

We also only explored global fit measures. Particularly when making claims that a tool is ready to be deployed in practice, developers must evaluate whether the algorithm has the potential to cause harm, especially to marginalized groups. Additionally calculating group fit measures is a critical (but not sufficient) step in assessing algorithms for fairness.⁶⁷ Constrained and penalty regression methods have been developed in this literature that aim to balance more than one metric, such as an overall fit metric and a group fit metric.^68–70 These techniques have largely been applied in other fields, such as criminal justice, with limited use in health care.⁷¹ Related work in constrained binary classification is highly relevant, where algorithms can be designed to optimize TPR subject to a maximum level of positive predictions, for example.⁴⁴ Partial AUC methods can also restrict to a range of acceptable values of TPR or FPR.⁷²

We recommend that medical studies focused on prediction, particularly with rare outcomes, should not report AUC or accuracy as a primary metric and minimally report a suite of metrics to have a more complete understanding of algorithm performance. Our simulation studies varying the level of class imbalance in the outcome indicate that any class imbalance can lead to problematic performance. Finally, methodological development of additional algorithms for rare outcomes targeting constrained loss functions optimizing multiple metrics as well as resampling-based approaches are promising future directions.