Abstract
The sudden advent of COVID-19 pandemic left educational institutions in a difficult situation for the semester evaluation of students; especially where the online participation was difficult for the students. Such a situation may also happen during a similar disaster in the future. Through this work, we want to study the question: can the deep learning methods be leveraged to predict student grades based on the available performance of students. To this end, this paper presents an in-depth analysis of deep learning and machine learning approaches for the formulation of an automated students’ performance estimation system that works on partially available students’ academic records. Our main contributions are: (a) a large dataset with 15 courses (shared publicly for academic research); (b) statistical analysis and ablations on the estimation problem for this dataset; (c) predictive analysis through deep learning approaches and comparison with other arts and machine learning algorithms. Unlike previous approaches that rely on feature engineering or logical function deduction, our approach is fully data-driven and thus highly generic with better performance across different prediction tasks. The main takeaways from this study are: (a) for better prediction rates, it is desirable to have multiple low weightage tests than few very high weightage exams; (b) the latent space models are better estimators than sequential models; (c) deep learning models have the potential to very accurately estimate the student performance and their accuracy only improves as the training data are increased.
Keywords: Deep neural network, COVID-19, Variational auto-encoder, Educational institutions
Introduction
This work explores the problem of students’ performance assessment under partial completion of their semester studies. During the starting of lock-downs, faced by the educational institutions in developing countries like India, students’ semester assessment emerged as a challenging and important problem [14]. Students were sent home; they were forced to study through online lectures and tutorials. During this period, many of the students did not have good Internet connections which lead to inculcation bias due to unequal participation by students. Furthermore, it was hard to conduct online examinations owing to unavailability of good infrastructures at home and challenges pertaining to curbing of unfair means during exams. This made many of the faculties adopt a binary (satisfactory/unsatisfactory) grading scheme. This situation may also happen during other uncalled for disasters or pandemics. This situation led the authors to ponder as to how modern computational intelligence (CI) technologies can be leveraged to alleviate the adverse effect of COVID-19 on education.
Course completion, organization of different exams, grades, admissions, and student psychology have been severely affected by this pandemic [3, 13]. Students worldwide were under tremendous stress due to uncertainty about their final grades. On the other hand, it has been very challenging for faculties to grade their students based on partial semester completion with little-to-no means for assigning grades. We propose to solve this problem by leveraging deep learning for automatic prediction of students’ grades. To this end, different partial course-completion durations were experimented with. Furthermore, due to unavailability of a good large-scale public dataset, a student academic performance dataset was also created and shared in the public interest.
Technology has played vital role in fighting against the COVID pandemic; however, educational plight has received little-to-no attention. This work is a humble attempt on leveraging CI methods for automatic students’ performance assessment through predictive analysis. Such an automated system has numerous applications in the education sector. It is not only useful for the present pandemic situation but can also assist in admission decisions; non-completion; dropout and retention; profiling and prediction for student’s feedback and guidance [5, 15].
Previously, operational-research based approaches have existed for solving this kind of problem. One example is the Duckworth/Lewis method for predicting adjusted target scores when the Cricket game is interrupted by rain [6]. Duckworth et al. studied thousands of Cricket match data and came out with a unique exponential function that tries to model the predicted score as a function of remaining resources. The problem of predictive performance assessment is challenging due to several reasons, and a Duckworth/Lewis approach seems naive, since, due to the complexity of the problem, finding a model analytically is not possible. Estimation of marks requires modeling different kinds of correlations. Due to the uncertainty of human behavior, it is hard to conceptualize all relations needed for assessment, for example, missing dependencies such as previous scores in a subject, previous records of a student, etc. Although absolute predictions cannot be made, and there is always room for unforeseeable events, we have worked with a basic setting that considers the available marks. The proposed model tries to intelligently capture the latent correlations in students’ performance and the complexity of subjects and other parameters.
Unprecedented pandemic circumstances and its adverse effect on education have propelled the relevance and need for a predictive assessment system based on available students’ academic data. CI algorithms are a useful tool for addressing this. So far, very little work has happened on this problem. The scope of previous approaches is limited for experimenting through classical machine learning on smaller datasets with less number of courses. Most of them have focused on predicting categorical grades. There has been little-to-no study with deep learning. Previously, researchers have used evolutionary algorithms, multi-layer perceptrons, fuzzy clustering, SVM, and random forests for the predictive analysis of students’ grades [1, 4, 7, 9, 10, 12]. A summary of the related work on performance assessment methods is presented in Table 1. For a broader literature overview, we would suggest going through [8].
Table 1.
Literature review on approaches for academic performance assessment or prediction
| References | Method | Contribution | Dataset | # of courses | Deep learning | Machine learning | Data analysis | Prediction range | Metric | Score |
|---|---|---|---|---|---|---|---|---|---|---|
| Chen et al. [4] | Multi-layer perceptron with evolutionary algorithms, for predictive analysis of academic performance | Comparison between Cuckoo and Gravitational search algorithms | Small | 3 | ✗ | ✔ | ✗ | Continuous (0–10) | MAE, RMSE, MSE, R | 0.72 (R2) |
| Livieris et al. [10] | Multi-layer perceptron, SVM, machine learning algorithms | A machine learning algorithm interface (tool) | Small | 1 | ✗ | ✔ | ✗ | Categorical (4 class) | Accuracy | 0.86 |
| Li et al. [9] | Fuzzy clustering and linear regression with Random Forest and SVM | Fuzzy c-means clustering implementation | Large | 3 | ✗ | ✔ | ✗ | Categorical (20 class) | Accuracy | 0.79 |
| Al-Shehri et al. [1] | Academic performance prediction using SVM and k-NN | Comparison between machine learning algorithms | Small | 2 | ✗ | ✔ | ✗ | Categorical (20 class) | MAE, RMSE, MSE, R | 0.82 (R2) |
| Patil et al. [12] | LSTM-based sequential modeling of grades | Comparison of deep and non-deep methods | Large | 5 | ✔ | ✔ | ✗ | Categorical (7 class) | RMSE, accuracy | 0.92 |
| Harvey et al. [7] | Machine learning for feature analysis and prediction in K-12 | Predictive study of K-12 education dataset | Large | 1 | ✔ | ✗ | ✔ | Continuous (0–100) | Accuracy | 0.71 |
| Proposed approach | Deep learning methods (LSTM, GRU, VAE) with multiple machine learning algorithms | Integration of generative and temporal deep learning approaches with machine learning algorithms and statistical study of the features of the dataset | Large | 15 | ✔ | ✔ | ✔ | Continuous (0–100) | MAE, RMSE, MSE, R2 | 0.94 (R2) |
Note that our work covers a large number of courses with much finer prediction range and better R2-score
Although there have been previous works with classical machine learning; however, through this paper, we present refreshing ideas into the field, leveraging deep learning. We show how deep learning can be used for students’ academic score estimation; particularly, the latent space models and their ability to model the correlation between student performance through different tests. Unlike evolutionary algorithms employed by [4], our emphasis is on gradient-based optimization algorithms, since we get better generalizations, faster training, and less computing resource requirement, and these algorithms can virtually scale to any size of the dataset. In our experiments, deep algorithms were found to perform better in comparison to machine learning approaches. Our dataset consists of 15 courses. We have shown the integration of generative and temporal deep learning approaches with machine learning algorithms, and the statistical study of the features of the dataset.
The proposed approach takes the partial academic performance as input and passes it through a neural network encoder to estimate the distribution of marks in a latent space. Once the training is complete, the estimated distribution has the potential to capture the correlation between the partial academic performance and the true grades. After the training of neural network encoder–decoder, the parameters estimated by the latent distribution are passed through machine learning regressors to predict the final marks. The detailed proposed approach is explained in Sect. 4. The proposed approach estimates final scores in a continuous range between (0, 100) rather than doing a grade-based categorical estimation. The main contributions of this work are:
We formulate a CI-based solution for the problem of academic performance estimation (APE). We have experimented with different machine or deep learning approaches and proposed a variational approach using machine learning regressors for solving this problem.
The APE problem requires a suitable dataset to experiment under different settings. To address the unavailability of such a dataset in the public domain, a new dataset was created and released in the public interest for benchmarking the future research.
We have extensively experimented and compared the proposed approach under different settings on this dataset. Including statistical assessment of the released dataset.
The rest of the paper is organized as follows. The next section describes the dataset details and attributes. The proposed approach is presented after this in Sect. 4. After this, the evaluation criteria are discussed in Sect. 5. The results and conclusion are presented under the last two sections.
Dataset
The data were collected at IIT Roorkee, India, for over 1000 students in 15 under-graduate and graduate-level courses between 2006 and 2017. It has been anonymized to protect the identities of individual students. Students’ academic performance is generally evaluated based on a set of individual parameters assessed across the comprehensive course of the evaluation. The dataset is called ‘IITR-APE dataset’, and is made available at https://www.hbachchas.github.io/data.html.
Institutions use distinct sets of exams, like end-term evaluation and multiple in-course examinations, supplemented with an estimation of the class performance of the students. Some courses also involve laboratory work with hands-on experience over real-life applications. In the wake of COVID-19, almost every educational institution is facing the problem of deferred evaluation and staggering students’ careers. This dataset is a humble effort toward the viability of recent developments in computational intelligence for the automatic assessment of students’ performance.
Let X be the set of all parameters used by the institutions for evaluation. The evaluation system customarily composites a weighted average of the collection of all parameters in X, which can be defined by the equation below
| 1 |
In Eq. (1), is the individual weight for each feature , where is the subset of feature-set X. The total score received by a student is represented by Y. The features used in our dataset include marks obtained in two tests and , assessment based on students classroom performance , a mid-term evaluation , and end-term evaluation . Three datasets used for experimentation and evaluation consist of a subset of above-mentioned features with specific weights for a given dataset as explained below.
Dataset consists of three basic features, which are two class-test based evaluations and one assessment based on the student’s class performance. Hence, feature-set can be defined as, . To establish an experimental setup for deferred evaluation for a given academic session, the mid-term marks and end-term evaluation scores were dropped, and the remaining features were used to estimate the final score . This analysis helps us understand how features with small weightage, in score calculations, can affect the final score.
Dataset consists of three features, viz., student’s class performance, mid-term evaluation, and end-term evaluation. Hence, feature-set can be defined as, . represents a weighted sum of features in . Two distinct analyses were conducted over to predict the final scores. First, using and , and later with and . Complementing with , helped us to analyze if deferred evaluation effects the total score estimation. On the other hand, utilizing helps to understand its effect on the overall score.
Preliminaries
In this section, we discuss about popular deep learning and machine learning techniques to evaluate the datasets. For temporal evaluation, recurrent neural network (RNN) variants such as long short-term memory and gated recurrent unit (GRU) were used along with discrete machine learning classifiers, [2]. Also, we employed Variational Bayes’ encoding for extensive feature extraction with machine learning classifier to evaluate the dataset.
Long Short-Term Memory (LSTM)
Long short-term memory is a state-of-the-art neural architecture used for modeling complex long- or short-term temporal relations in sequence translation/recognition tasks. LSTM is incipiently an enhanced variant of the recurrent neural networks. LSTM structures are known for handling not only the hidden state of an RNN, but also the cell-state of each recurring block. The mathematical description of a single LSTM cell is given by Eq. (2)–(7)
| 2 |
| 3 |
| 4 |
The above equations represent the three different gates in the LSTM structure. represents the sigmoid function in these equations. The symbol and represent bias and weight matrices, respectively, in each gate equation. represents the hidden state of the LSTM cell from the previous time step, whereas represents the input to the LSTM cell at the current time step. Equations (2)–(4) represent the input gate, forget gate, and the output gate, respectively. The input gate helps to capture the new information, to be stored in the cell-state. The forget gate tells about the information; one needs to remove from the cell-state. The output gate deduces the information that we need to emit as the final output from the LSTM cell. The outcomes of these three gates are used to find the LSTM’s cell-state and hidden state, as shown in the following equations
| 5 |
| 6 |
| 7 |
In the above equations, represents the cell-state memory for a given LSTM cell at timestamp j. represents the hidden state, at timestamp j, for the LSTM cell.
LSTM has become a popular structure of choice, as it overcomes the problem of vanishing and exploding gradients in comparison to simple RNNs. In our analysis, the LSTM cells were joined with fully connected neural network layers to make predictions.
Gated Recurrent Unit (GRU)
Gated recurrent unit is a modified version of recurrent neural networks. GRU resolves the problem of vanishing gradient, which dominates in standard RNN models. It is quite similar to the LSTM structure and sometimes even gives better performance. The working of GRU cells can be understood through the equations explained below
| 8 |
Equation (8) represents the update gate inside a GRU cell. This gate helps to learn the amount of information the GRU cell needs to pass from the previous th time step. and represent the weights of the new input, , and the information from the previous time steps, , respectively
| 9 |
The above equation represents the reset gate. This gate helps the network to understand, how much of the information from the past time steps, need to be forgotten
| 10 |
Equation (10) helps in calculation of the current memory-state. This uses the input information— and , along with from the reset gate, to store equivalent information from the past and the current time step
| 11 |
The above equation helps in the evaluation of the final hidden state information, , for the current time step to pass it on to a future time step. In our experiments, the GRU units were integrated with two fully connected layers to make the grade prediction pipeline for students.
Variational Auto-encoder (VAE)
Variational auto-encoder is a common method used for feature extraction. The major difference between a simple Auto-encoder (AE) and a variational auto-encoder is that it learns the latent space variable Z in the form of a prior distribution (usually a Gaussian).
In a VAE, the distribution of latent space is mapped with a presumed distribution. This distribution is learned in the format of mean and logarithmic variance . To enforce this distribution to a prior distribution, we use KL divergence loss which is defined as
| 12 |
The KL divergence for two mapping Normal distributions is represented by Eq. (12). Here, is our prior distribution and is the distribution upon which we want to enforce the prior distribution. The and for the calculation are obtained from the latent space, Z, of the VAE. In our model, we have assumed the prior distribution to be N(0, 1), i.e., a Gaussian distribution with and values of 0 and 1, respectively
| 13 |
Equation (13) represents the KL divergence loss for, N(0, 1), prior distribution used in our model. The VAE model was trained on X and the latent space Z was extracted and further used to train the machine learning classifiers to make a final prediction of students’ grades.
Machine Learning Regressors
The modeling of input data, X, to predict the students’ grades, Y, was done using machine learning-based regressors. The regressors used during our experiments are: Multi-layer Perceptron (MLP), Linear Regression (LR), Extra Tree Regressor (ET), Random Forest Regressor (RF), XGBoost Regressor (XGB), and k-Nearest Neighbour Regressor (kNN).
The variations in results were analyzed using fivefold shuffle split cross-validation. For all our experiments, the dataset was randomly shuffled five times, and each time, a test set was drawn to estimate the performance in terms of the metric results. The mean and standard deviation of these results are reported later under the section on Results and Discussion.
Approach
The datasets mentioned in Sect. 2 include a set of different evaluation features for students’ final score estimation. In this section, we discuss about experimental approach in final grade estimation. For temporal evaluation, recurrent neural network (RNN) variants such as long short-term memory and gated recurrent unit (GRU) were used considering incoming grades a sequential data [2]. For further evaluation, we employed Variational Bayes’ encoding for extensive feature extraction with machine learning classifiers to evaluate the datasets.
Proposed Method
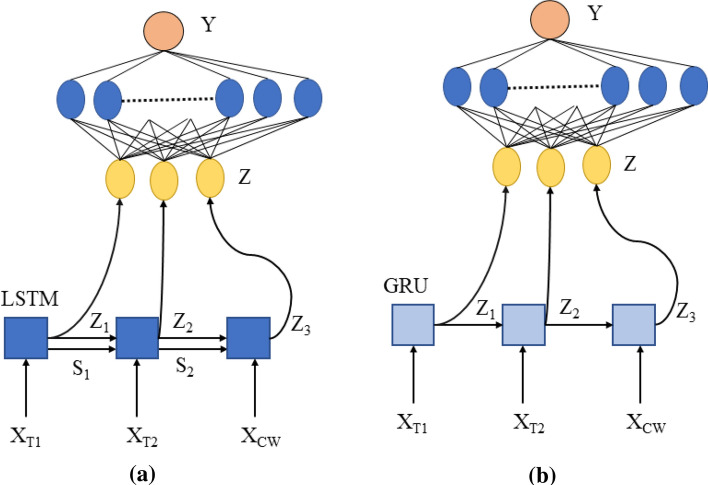
Initially, we perform experiments on dataset using feature set containing . We first evaluate a sequential approach using LSTM and GRU units followed by a fully connected neural network. For LSTM-based model, as shown in Fig. 1a, at every step, we take the hidden state , and , and concat them to make a final feature space Z
| 14 |
| 15 |
Finally, we pass these features Z through a fully connected neural network that maps feature space Z to predicted performance
| 16 |
In the above equation, p(Z) is the probability distribution of feature space Z which is mapped to predicted performance . Similarly, we apply GRU model, as shown in Fig. 1b, to estimate hidden state at input time stamps and and and concat them to make a final feature space Z
| 17 |
Finally, we send the concatenated feature space to a fully connected neural network to map it to predicted performance .
Fig. 1.
a Performance estimation using LSTM-based model. b Performance estimation using GRU-based model
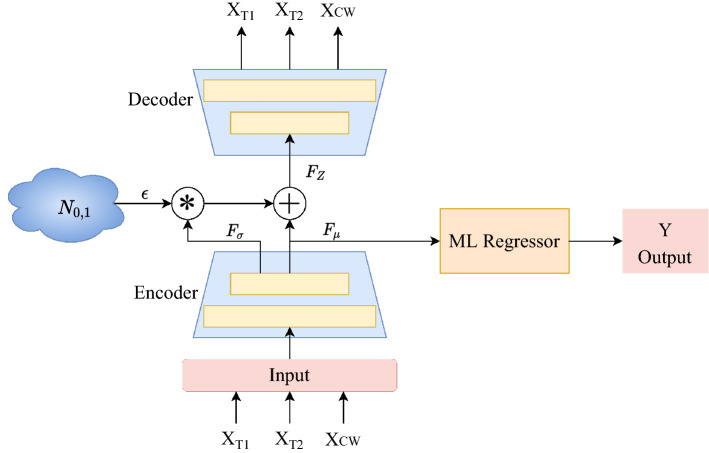
We also experiment a latent space-based approach using a variational auto-encoder (VAE) and then finally pass it through a machine learning regressor. To train a VAE architecture on features to get feature vectors in the form of mean and variance as
| 18 |
while training the variational auto-encoder assembly, the output mean and standard deviation is used to sample from a Gaussian space as
| 19 |
In the above equation, is the sampled feature space and epsilon is sampled from a normal distribution with mean 0 and variance 1. This feature space is passed through the decoder to reconstruct the original input features.
Finally, we use feature-set to train a machine learning regressors, namely: Multi-layer Perceptron (MLP), Linear Regression (LR), Extra Tree Regressor (ET), Random Forest Regressor (RF), XGBoost Regressor (XGB), and k-Nearest Neighbour Regressor (kNN).
We perform similar experiments on dataset using two different feature spaces including: and . While using LSTM and GRU, we forward pass for two time stamps generating feature space and only. We also evaluate this dataset using variational auto-encoder and machine learning regressor assembly.
The final approach to calculate predicted performance can be explained in a step by step manner as follows:
First, we utilize the dataset , , or to train a VAE.
Then, the dataset is passed through trained encoder to get features in term of and .
Feature-set is selected as a set of variationally conditioned features.
is then passed through the machine learning regressor to get output predicted performance .
Evaluation Criteria
The models were evaluated using various evaluation criteria, which include R2-score, mean absolute error (MAE), mean squared error (MSE), and root-mean-squared error (RMSE). Calculation of all these metrics ensures a better evaluation of our regression models. The calculation involves true performance score Y, predicted performance score , and the mean score
| 20 |
| 21 |
| 22 |
| 23 |
R2-score helps in deduction of the variation in the points along the regression line. These evaluation criteria metrics give an estimate of the effective predictions above the mean of the predicted label. MAE, MSE, and RMSE help us to infer the error in predicting students’ performance.
Results and Discussion
The datasets mentioned previously, in dataset description section, can be analyzed based on two methods: one, using exploratory analysis, and other using methods discussed in the section—Approach (Fig. 2).
Fig. 2.
Performance estimation using variational auto-encoder with ML regressors
Exploratory Data Analysis
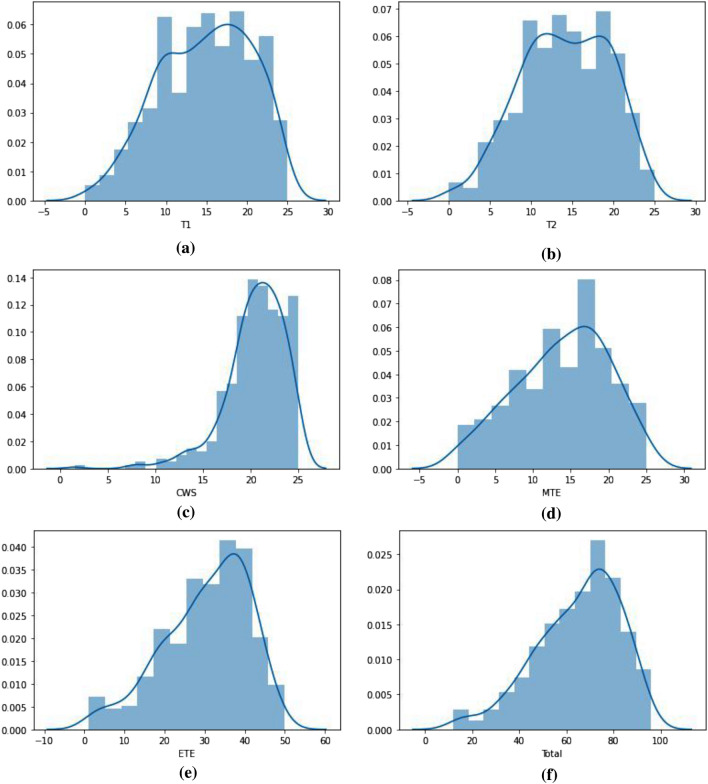
Exploratory analysis of the datasets can be done using gradient maps, correlation matrix, and distribution of data points. Figure 3 shows the distribution of various features of the datasets. It is clearly visible that and have a similar distribution to the actual students’ scores. However, the distribution of , , and are quite different from the distribution of overall performance. Visual analysis of these plots suggests some correlation between the features and final prediction score.
Fig. 3.
Distribution of data points for and datasets a test 1 (), b test 2 (), c class assessment (), d mid-term evaluation marks (), e end-term evaluation marks (), and f total performance of student (Y)
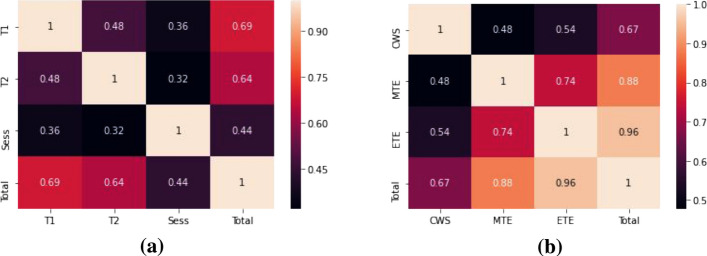
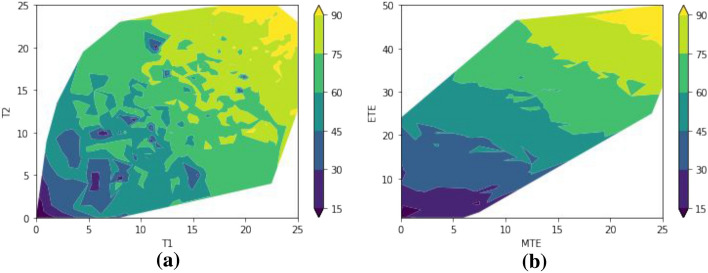
Moreover, the correlation matrix, in Fig. 4 shows similar results with high correlation values of 0.88 and 0.96 for and , respectively. Unlike that, and have a lower correlation score of 0.69 and 0.64 with respect to the total performance score of students’. The correlations can further be verified with the gradient maps, as shown in Fig. 5. It clearly demonstrates that vs. has an evident trend of possible marks in comparison to vs. .
Fig. 4.
Correlation matrix for a dataset ; b dataset
Fig. 5.
Gradient maps of students’ performance for a vs. ; b vs.
Prediction Results
The results of predictive modeling using various approaches described under the section—Approach—are given in Tables 2, 3, and 4. For dataset , the results using VAE with machine learning classifiers along with GRU and LSTM are reported. It is evident that minimum error was acquired by VAE in conjunction with Extra Tree Regressor classifier with R2-score, MAE, MSE, and RMSE of 0.720, 5.943, 77.709, and 8.781, respectively. The results show sufficient utility of and for students’ performance prediction. Also, almost similar R2-score is obtained for VAE in conjunction with Random Forest Regressor with R2-score, MAE, MSE, and RMSE of 0.720, 6.264, 78.595, and 8.815, respectively.
Table 2.
Results for dataset using features—, , and ; evaluation performed using—R2-score, MAE, MSE, RMSE
| R2 score | MAE | MSE | RMSE | |
|---|---|---|---|---|
| VAE + MLP | 0.561 | 7.601 | 124.679 | 11.129 |
| VAE + LR | 0.585 | 7.191 | 116.077 | 10.744 |
| VAE + ET | 0.720 | 5.943 | 77.709 | 8.781 |
| VAE + RF | 0.720 | 6.264 | 78.595 | 8.815 |
| VAE + XGB | 0.714 | 6.211 | 80.053 | 8.922 |
| VAE + KNN | 0.584 | 7.342 | 115.858 | 10.755 |
| LSTM | 0.587 | 138.230 | 11.757 | 7.356 |
| GRU | 0.672 | 77.214 | 8.787 | 6.431 |
Table 3.
Results for dataset using features— and ; evaluation performed using—R2-score, MAE, MSE, and RMSE
| R2 Score | MAE | MSE | RMSE | |
|---|---|---|---|---|
| VAE + MLP | 0.867 | 5.293 | 43.595 | 6.590 |
| VAE + LR | 0.866 | 5.325 | 44.142 | 6.633 |
| VAE + ET | 0.796 | 6.352 | 67.329 | 8.173 |
| VAE + RF | 0.823 | 5.975 | 58.386 | 7.621 |
| VAE + XGB | 0.808 | 6.139 | 63.157 | 7.918 |
| VAE + KNN | 0.842 | 5.727 | 52.204 | 7.203 |
| LSTM | 0.845 | 5.180 | 43.748 | 6.614 |
| GRU | 0.850 | 4.954 | 42.362 | 6.508 |
Table 4.
Results for dataset using features— and ; evaluation performed using—R2-score, MAE, MSE, and RMSE
| R2 score | MAE | MSE | RMSE | |
|---|---|---|---|---|
| VAE + MLP | 0.943 | 3.495 | 17.171 | 4.141 |
| VAE + LR | 0.947 | 3.385 | 17.279 | 4.154 |
| VAE + ET | 0.918 | 4.104 | 26.646 | 5.144 |
| VAE + RF | 0.928 | 3.901 | 23.430 | 4.829 |
| VAE + XGB | 0.929 | 3.881 | 22.976 | 4.788 |
| VAE + KNN | 0.933 | 3.798 | 21.706 | 4.649 |
| LSTM | 0.926 | 4.263 | 19.078 | 4.367 |
| GRU | 0.927 | 3.949 | 18.885 | 4.345 |
For dataset , the results using two different experiments are shown. In Table 3, using and , it is evident that minimum error was acquired by VAE with Multi-layer Perceptron Regressor with R2-score, MAE, MSE, and RMSE values of 0.867, 5.293 43.595, and 6.590, respectively. Also, almost similar R2-score is obtained for VAE in conjunction with Linear Regressor with R2-score, MAE, MSE, and RMSE of0.866, 5.3254, 44.142, and 6.633, respectively. TThe results establish the utility of and for predicting students’ performance in case of a deferred evaluation of an ongoing academic session.
In Table 4, for and , it is evident that minimum error was acquired using VAE in conjunction with Linear Regressor with with a R2-score, MAE, MSE, and RMSE of 0.947, 3.385, 17.279, and 4.154, respectively. Also, almost similar R2-score is obtained for VAE in conjunction with multi-layer perceptron with R2-score, MAE, MSE, and RMSE of 0.947, 3.385, 17.279, and 4.154, respectively. The results show that due to substantial weightage and maximum efforts given by the students, has the highest impact on the evaluation of a student’s collective performance.
Analysis and Discussion
The above results show that the final performance of the student is impacted most by the , followed by , and and . This is evident from the maximum weightage of in the final evaluation. This is also due to maximum concern of students on end-term evaluation due to maximum weightage. Similarly, in case of a deferred evaluation of an academic performance, we can suggest from the results that using along with is a better option for evaluation than , and .
Also, of all the models tested by us, the best results were obtained by VAE-based models methods, as shown in Table 5. This shows superiority of latent space models above sequential models for performance estimation. Our models attained fairly large R2-score, in comparison to other previous works, which shows how good deep learning techniques are for evaluation and prediction purposes. It should be noted that there is significant scope of increment in the size of our dataset, and it should only add to further improvement of the proposed deep learning approaches.
Table 5.
Comparison of the proposed approach with other related works
| Method | Metric | Score |
|---|---|---|
| Chen et al. (2014) [4] | R2 | 0.72 |
| Al-Shehri et al. (2017) [1] | R2 | 0.82 |
| Olive et al. (2019) [11] | Acc. | 0.77 |
| Proposed approach | R2 | 0.94 |
R2 and accuracy metrics are used. It can be noted that the proposed method has a significant improvement in R2 score
Conclusion
This study features the role of CI in alleviation of challenges and impact of COVID pandemic on education. Application of deep learning methods for academic performance estimation is shown. State of the current arts is explained with conclusive-related work. For the purpose of evaluation and benchmarking, an anonymized students’ academic performance dataset, called IITR-APE, was created and will be released in the public domain. The promising performance of the proposed approach explains the suitability of modern-day CI methods for modeling students’ academic patterns. However, we feel that availability of larger datasets would further allow the system to be more accurate. For this, we are building a larger pubic version of the current dataset. It was observed through the performance stats and gradient maps that better prediction happens when all components of final grade have equal weightage. It is thus suggested to have a continual evaluation strategy, i.e., there should be many equally weighted tests or assignments, conducted regularly with short frequency, rather than conducting two or three high weightage exams.
This work is an attempt in the direction of enabling CI-based methods for handling adverse effects of COVID like pandemics on education. It is expected that this study may pave the path for future research in the direction of CI enabled predictive assessment of students’ marks.
Acknowledgements
This work was supported by the Ministry of Electronics and Information Technology, Gov. of India, under Grant number MIT1100CSE. The dataset was contributed by Indian Institute of Technology, Roorkee.
Author Contributions
VB and HB have contributed equally to the experiments and manuscript preparation. BR reviewed and provided supervision to the research.
Funding
Not applicable.
Availability of data and materials
The dataset generated and analyzed during this study is available in the public domain for research purpose at: https://www.hbachchas.github.io/data.html.
Declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Vipul Bansal and Himanshu Buckchash have contributed equally to this work.
Contributor Information
Vipul Bansal, Email: vbansal@me.iitr.ac.in.
Himanshu Buckchash, Email: hbuckchash@cs.iitr.ac.in.
Balasubramanian Raman, Email: bala@cs.iitr.ac.in.
References
- 1.Al-Shehri H, Al-Qarni A, Al-Saati L, Batoaq A, Badukhen H, Alrashed S, Alhiyafi J, Olatunji SO. Student performance prediction using support vector machine and k-nearest neighbor. In: 2017 IEEE 30th Canadian conference on electrical and computer engineering (CCECE). IEEE; 2017, p. 1–4.
- 2.Buckchash H, Raman B. Variational conditioning of deep recurrent networks for modeling complex motion dynamics. IEEE Access. 2020;8:67822–67834. doi: 10.1109/ACCESS.2020.2985318. [DOI] [Google Scholar]
- 3.Cao W, Fang Z, Hou G, Han M, Xu X, Dong J, Zheng J. The psychological impact of the Covid-19 epidemic on college students in China. Psychiatry Res. 2020;5:112934. doi: 10.1016/j.psychres.2020.112934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chen JF, Do QH. Training neural networks to predict student academic performance: a comparison of cuckoo search and gravitational search algorithms. Int J Comput Intell Appl. 2014;13(01):1450005. doi: 10.1142/S1469026814500059. [DOI] [Google Scholar]
- 5.Delnoij LE, Dirkx KJ, Janssen JP, Martens RL. Predicting and resolving non-completion in higher (online) education—a literature review. Educ Res Rev. 2020;29:100313. doi: 10.1016/j.edurev.2020.100313. [DOI] [Google Scholar]
- 6.Duckworth F, Lewis A. A successful operational research intervention in one-day cricket. J Oper Res Soc. 2004;55(7):749–759. doi: 10.1057/palgrave.jors.2601717. [DOI] [Google Scholar]
- 7.Harvey JL, Kumar SA. A practical model for educators to predict student performance in k-12 education using machine learning. In: 2019 IEEE symposium series on computational intelligence (SSCI). IEEE; 2019. p. 3004–11.
- 8.Hellas A, Ihantola P, Petersen A, Ajanovski VV, Gutica M, Hynninen T, Knutas A, Leinonen J, Messom C, Liao SN. Predicting academic performance: a systematic literature review. In: Proceedings companion of the 23rd annual ACM conference on innovation and technology in computer science education. 2018. p. 175–99.
- 9.Li Z, Shang C, Shen Q. Fuzzy-clustering embedded regression for predicting student academic performance. In: 2016 IEEE international conference on fuzzy systems (FUZZ-IEEE). IEEE; 2016. p. 344–51.
- 10.Livieris I, Mikropoulos T, Pintelas P. A decision support system for predicting students’ performance. Themes Sci Technol Educ. 2016;9(1):43–57. [Google Scholar]
- 11.Olive DM, Huynh DQ, Reynolds M, Dougiamas M, Wiese D. A quest for a one-size-fits-all neural network: early prediction of students at risk in online courses. IEEE Transa LearnTechnol. 2019;12(2):171–183. [Google Scholar]
- 12.Patil AP, Ganesan K, Kanavalli A. Effective deep learning model to predict student grade point averages. In: 2017 IEEE international conference on computational intelligence and computing research (ICCIC). IEEE; 2017. p. 1–6.
- 13.Sahu P. Closure of universities due to coronavirus disease 2019 (Covid-19): impact on education and mental health of students and academic staff. Cureus. 2020;12(4). 10.7759/cureus.7541. [DOI] [PMC free article] [PubMed]
- 14.Spinelli A, Pellino G. Covid-19 pandemic: perspectives on an unfolding crisis. The British journal of surgery. 2020; 107(7):785–787. [DOI] [PMC free article] [PubMed]
- 15.Zawacki-Richter O, Marín VI, Bond M, Gouverneur F. Systematic review of research on artificial intelligence applications in higher education—where are the educators? Int J Educ Technol Higher Educ. 2019;16(1):39. doi: 10.1186/s41239-019-0171-0. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The dataset generated and analyzed during this study is available in the public domain for research purpose at: https://www.hbachchas.github.io/data.html.