Abstract
We develop a Bayesian method for inferring the species phylogeny under the multispecies coalescent (MSC) model. To improve the mixing properties of the Markov chain Monte Carlo (MCMC) algorithm that traverses the space of species trees, we implement two efficient MCMC proposals: the first is based on the Subtree Pruning and Regrafting (SPR) algorithm and the second is based on a node-slider algorithm. Like the Nearest-Neighbor Interchange (NNI) algorithm we implemented previously, both new algorithms propose changes to the species tree, while simultaneously altering the gene trees at multiple genetic loci to automatically avoid conflicts with the newly proposed species tree. The method integrates over gene trees, naturally taking account of the uncertainty of gene tree topology and branch lengths given the sequence data. A simulation study was performed to examine the statistical properties of the new method. The method was found to show excellent statistical performance, inferring the correct species tree with near certainty when 10 loci were included in the dataset. The prior on species trees has some impact, particularly for small numbers of loci. We analyzed several previously published datasets (both real and simulated) for rattlesnakes and Philippine shrews, in comparison with alternative methods. The results suggest that the Bayesian coalescent-based method is statistically more efficient than heuristic methods based on summary statistics, and that our implementation is computationally more efficient than alternative full-likelihood methods under the MSC. Parameter estimates for the rattlesnake data suggest drastically different evolutionary dynamics between the nuclear and mitochondrial loci, even though they support largely consistent species trees. We discuss the different challenges facing the marginal likelihood calculation and transmodel MCMC as alternative strategies for estimating posterior probabilities for species trees. [Bayes factor; Bayesian inference; MCMC; multispecies coalescent; nodeslider; species tree; SPR.]
Multilocus genetic sequence data have gained importance in inferring species trees in recent years and several inference methods have been proposed for this purpose (Edwards et al. 2016; Xu and Yang 2016, for recent reviews). As noted by Maddison (1997) several processes can cause the species tree to differ from gene trees underlying particular loci. Some of these processes, such as introgression between species and horizontal gene transfer, involve reticulations in the species tree, whereas others, such as incomplete lineage sorting and gene duplications, occur within the context of a nonreticulate (and typically binary) species tree. An important potential source of gene-tree versus species-tree conflicts among genetically isolated species is incomplete lineage sorting, which is typically modeled using a coalescence process.
A simple widely used method for multilocus species tree inference concatenates sequences from different loci, assuming that a single tree (treated as the species tree) underlies all the loci (reviewed in Rannala and Yang 2008; Edwards 2009). This approach can lead to strongly supported incorrect phylogenetic trees when incomplete lineage sorting occurs (see e.g., Leaché and Rannala 2011), and has been shown to be inconsistent (Kubatko and Degnan 2007). Another heuristic approach is to infer separate gene trees and then attempt to reconcile the differences among gene trees to obtain an estimate of the species tree (Page and Charleston 1997). The majority-vote method, which uses the most frequent gene tree among loci as the estimate of the species tree, can be inconsistent when the species tree and parameters are in the so-called “anomaly zone” (Degnan and Salter 2005; Degnan and Rosenberg 2006).
Maddison (1997) and Maddison and Knowles (2006) proposed a parsimony-inspired method for inferring the species tree, called minimizing deep coalescence (MDC) events for gene trees. Other examples include species tree estimation by minimizing coalescence times across genes (the Global LAteSt Split, GLASS; Mossel and Roch 2010), by using the average ranks of coalescences (STAR, Liu et al. 2009) or average gene-tree internode distances (NJst, Liu and Yu 2011), by using average coalescence times (STEAC, Liu et al. 2009), by using maximum likelihood for gene trees under coalescence (STEM, Kubatko et al. 2009), and by maximum pseudo-likelihood (MP-EST, Liu et al. 2010). Similarly ASTRAL (Mirarab and Warnow 2015) finds the species tree that agrees with the largest number of quartet trees induced by the collection of unrooted gene trees. All those methods treat the estimated gene trees (including either the gene tree topology alone or both the gene tree topology and branch lengths) as data, ignoring phylogenetic uncertainties. Such approximations can lead to systematic biases as well as underestimation of the uncertainty of inferred species trees (Leaché and Rannala 2011). The heuristic methods are computationally efficient and can be applied to genome-scale datasets, but they are not statistically efficient (Leaché and Rannala 2011; Liu et al. 2015; Ogilvie et al. 2016).
A parametric statistical method for inferring the species tree using multilocus sequence data
should integrate over the unobserved gene trees (both the tree topology and branch lengths).
For the case of three species, with one sequence from each species at each locus, a maximum
likelihood method used numerical integration to integrate out the two coalescent times in each
gene tree (Yang 2002; Dalquen et al. 2016). For larger problems with more species or more sequences,
maximum likelihood is not computationally feasible. Instead the Bayesian method is used, with
Markov chain Monte Carlo (MCMC) used for the computation. A few MCMC implementations now exist
to estimate species trees under the MSC, including BEST (Edwards et al. 2007; Ronquist et al. 2012),
*BEAST (Heled and Drummond 2010), BPP (Yang and Rannala 2014), and revBayes (Hohna et al. 2016), although they are limited to a small number of species
and loci, and suffer from mixing problems when there are  loci, say, in the
dataset.
loci, say, in the
dataset.
Under the MSC, the gene trees and the species tree impose constraints on each other, which
become a serious challenge for designing efficient MCMC algorithms under the model. The
divergence time ( ) between two sequences from species
) between two sequences from species
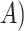 and
and 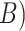 at any locus must be greater
than the divergence time (
at any locus must be greater
than the divergence time (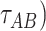 ) between species
) between species
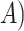 and
and 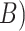 , with
, with
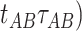 : in other words,
sequences split before species (see Fig.
1). Such constraints can cause serious difficulties in analysis of large datasets,
leading to poor MCMC mixing, when one attempts to change the species tree topology or species
divergence times if the gene trees at the mutliple loci are fixed. Two solutions are possible
to this difficulty: (i) integrating out the gene trees analytically without the need for MCMC
and (ii) developing efficient MCMC proposals to modify the species tree and the gene trees
jointly, maintaining the constraint. Recent methods for inferring species trees from single
nucleotide polymorphism (SNP) data follow the first strategy (Bryant et al. 2012). The simplicity of these data allow the gene trees to be
integrated out of the model analytically. However, a drawback of such methods is that SNPs
provide little information about branch lengths in the gene trees and the power may be reduced
in comparison with sequence-based methods. The SVDquartets method recently developed by Chifman and Kubatko (2014) takes a similar approach,
assuming independence among all sites given the species tree, and calculates the site-pattern
probabilities for quartets by integrating out the gene tree topologies and coalescent times
analytically.
: in other words,
sequences split before species (see Fig.
1). Such constraints can cause serious difficulties in analysis of large datasets,
leading to poor MCMC mixing, when one attempts to change the species tree topology or species
divergence times if the gene trees at the mutliple loci are fixed. Two solutions are possible
to this difficulty: (i) integrating out the gene trees analytically without the need for MCMC
and (ii) developing efficient MCMC proposals to modify the species tree and the gene trees
jointly, maintaining the constraint. Recent methods for inferring species trees from single
nucleotide polymorphism (SNP) data follow the first strategy (Bryant et al. 2012). The simplicity of these data allow the gene trees to be
integrated out of the model analytically. However, a drawback of such methods is that SNPs
provide little information about branch lengths in the gene trees and the power may be reduced
in comparison with sequence-based methods. The SVDquartets method recently developed by Chifman and Kubatko (2014) takes a similar approach,
assuming independence among all sites given the species tree, and calculates the site-pattern
probabilities for quartets by integrating out the gene tree topologies and coalescent times
analytically.
Figure 1.
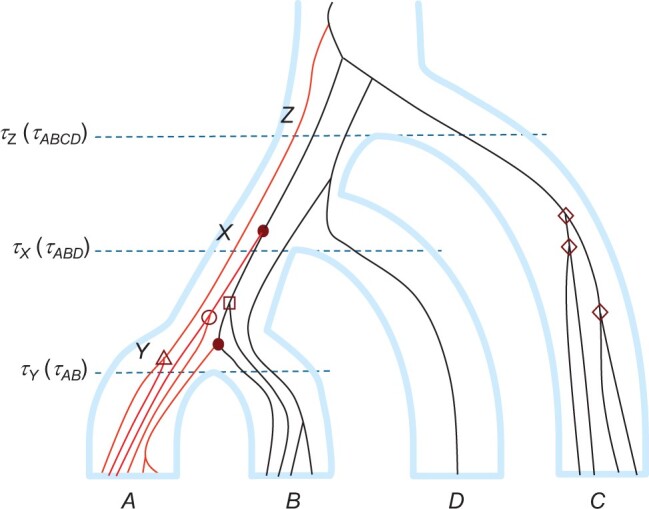
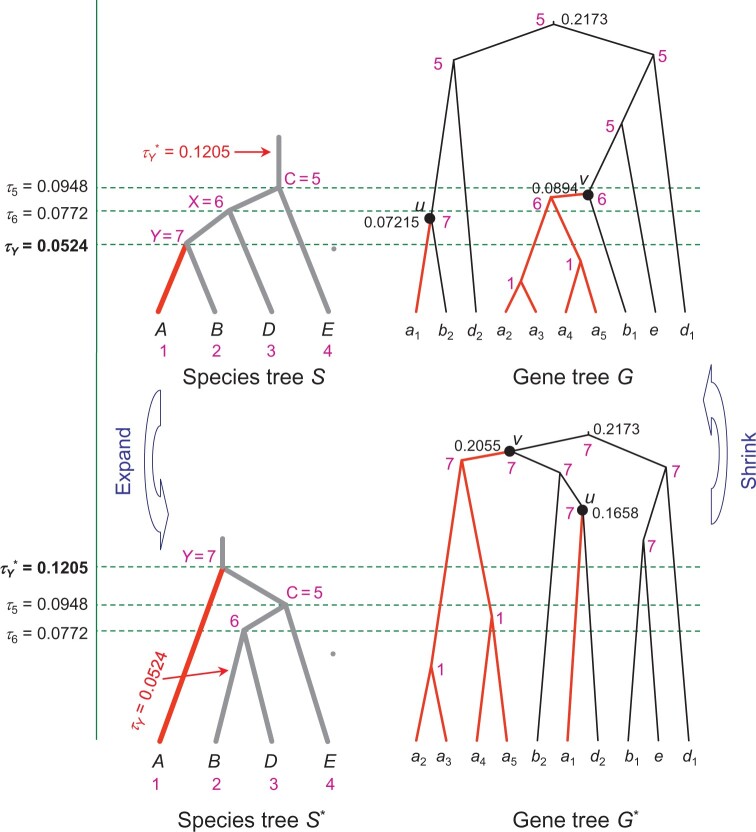
The SPR move makes coordinated changes to the species tree and the gene trees to avoid
conflicts between the proposed species tree and the gene trees. The species tree is
represented by the light blue boundary pipes while the gene tree is represented by lines
running inside the species-tree branches. The SPR move prunes off branch
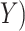 -
-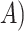 on the species tree
(including clade
on the species tree
(including clade 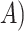 ) and reattaches it to a randomly-chosen
target branch
) and reattaches it to a randomly-chosen
target branch 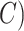 , while changing the gene trees through
similar SPR moves to avoid conflict. Moved nodes on the gene tree reside in species
, while changing the gene trees through
similar SPR moves to avoid conflict. Moved nodes on the gene tree reside in species
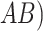 (
(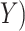 ) or in a species on the
path from
) or in a species on the
path from 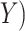 to
to 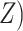 (the common ancestor of
(the common ancestor of
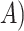 and
and 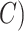 ), and have exactly one
daughter node with descendents in
), and have exactly one
daughter node with descendents in 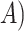 only. They are marked by
only. They are marked by
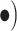 , and are pruned off and regrafted
to a randomly chosen branch on the gene tree that resides in a species on the path from
, and are pruned off and regrafted
to a randomly chosen branch on the gene tree that resides in a species on the path from
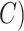 to
to 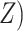 . Other affected nodes,
marked by
. Other affected nodes,
marked by  ,
, 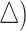 or
or
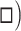 , have their population IDs changed by
the move.
, have their population IDs changed by
the move.
Here, we follow the second approach and develop a Bayesian inference procedure for the
analysis of multilocus sequence data that jointly infers the species tree and gene trees as
well as other relevant parameters such as species divergence times and ancestral population
sizes (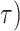 s and
s and 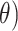 s). We extend our
program BPP (for Bayesian Phylogenetics and Phylogeography) (Yang and Rannala 2010; Rannala and Yang 2013;
Yang and Rannala 2014) to allow this joint inference.
We develop two novel MCMC proposals that change the species tree, at the same time modifying
the gene trees to avoid conflicts between the gene trees and newly proposed species tree. The
first move is based on the Subtree Pruning and Regrafting (SPR) algorithm for rooted trees.
This changes the species tree topology whereas preserving the node ages in the species tree as
well as in the gene trees. The second move is based on a node-slider algorithm, which changes
the topology as well as the node ages in the species tree and gene trees. Note that the NNI,
SPR, and nodeslider moves considered here make coordinated changes to the species tree and to
the gene trees at multiple loci. They are far more complex than similar MCMC moves in standard
Bayesian phylogenetics programs such as MrBayes or BEAST (Lakner et al. 2008; Hohna et al. 2008; Yang 2014). The two new proposal algorithms lead to
considerably improved mixing behavior of the MCMC in comparison with the simple NNI algorithm
implemented in our previous work (Yang and Rannala
2014). We also explore the calculation of the marginal likelihood for a given species
tree as an approach to comparing alternative species trees under the MSC. We apply our newly
developed method to two sets of empirical data, for rattlesnakes and Philippine shrews,
respectively.
s). We extend our
program BPP (for Bayesian Phylogenetics and Phylogeography) (Yang and Rannala 2010; Rannala and Yang 2013;
Yang and Rannala 2014) to allow this joint inference.
We develop two novel MCMC proposals that change the species tree, at the same time modifying
the gene trees to avoid conflicts between the gene trees and newly proposed species tree. The
first move is based on the Subtree Pruning and Regrafting (SPR) algorithm for rooted trees.
This changes the species tree topology whereas preserving the node ages in the species tree as
well as in the gene trees. The second move is based on a node-slider algorithm, which changes
the topology as well as the node ages in the species tree and gene trees. Note that the NNI,
SPR, and nodeslider moves considered here make coordinated changes to the species tree and to
the gene trees at multiple loci. They are far more complex than similar MCMC moves in standard
Bayesian phylogenetics programs such as MrBayes or BEAST (Lakner et al. 2008; Hohna et al. 2008; Yang 2014). The two new proposal algorithms lead to
considerably improved mixing behavior of the MCMC in comparison with the simple NNI algorithm
implemented in our previous work (Yang and Rannala
2014). We also explore the calculation of the marginal likelihood for a given species
tree as an approach to comparing alternative species trees under the MSC. We apply our newly
developed method to two sets of empirical data, for rattlesnakes and Philippine shrews,
respectively.
Theory
Here we review the formulation of the species tree inference problem in a Bayesian
framework and then describe our new MCMC algorithms. Let 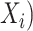 be the
sequence alignment for locus
be the
sequence alignment for locus 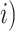 . The number of sequences per species may
vary for each locus and some species may not be sampled for a particular locus. Our
requirement is that every locus should have at least two sequences. Let there be
. The number of sequences per species may
vary for each locus and some species may not be sampled for a particular locus. Our
requirement is that every locus should have at least two sequences. Let there be
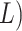 loci and define
loci and define 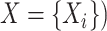 to
be the full dataset. Let
to
be the full dataset. Let 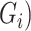 be the gene tree for the sequences
sampled at locus
be the gene tree for the sequences
sampled at locus 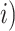 (including both the gene tree topology and
branch lengths or coalescent times). Let
(including both the gene tree topology and
branch lengths or coalescent times). Let 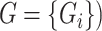 . We assume the
loci are independent so that
. We assume the
loci are independent so that
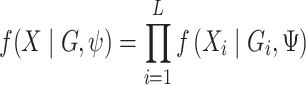 |
(1) |
where 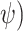 is a vector of parameters in the
mutation/substitution model, and
is a vector of parameters in the
mutation/substitution model, and 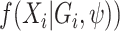 is the phylogenetic
likelihood for locus
is the phylogenetic
likelihood for locus 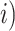 , calculated according to the usual pruning
algorithm (Felsenstein 1981). The posterior
probability of the species tree (
, calculated according to the usual pruning
algorithm (Felsenstein 1981). The posterior
probability of the species tree (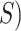 ) and the parameters is given by
) and the parameters is given by
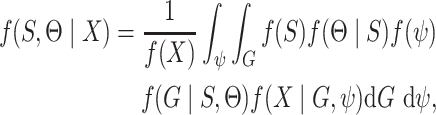 |
(2) |
where 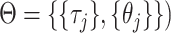 is
the set of parameters (
is
the set of parameters ( s and
s and 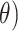 s)
associated with the species tree
s)
associated with the species tree 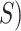 . Note that
. Note that 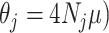 , where
, where
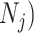 is the effective population size of
(ancestral or contemporary) species
is the effective population size of
(ancestral or contemporary) species 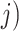 and
and 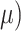 is the mutation rate per
generation, while
is the mutation rate per
generation, while 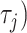 is the age of node
is the age of node
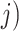 in the species tree. Both
in the species tree. Both
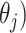 and
and 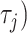 are
measured by sequence distance or the expected number of mutations per site, as are branch
lengths or coalecent times in the gene trees (Yang
2002; Rannala and Yang 2003). The term
are
measured by sequence distance or the expected number of mutations per site, as are branch
lengths or coalecent times in the gene trees (Yang
2002; Rannala and Yang 2003). The term
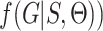 is the MSC density of gene
trees (topology and coalescent times) given the species tree
is the MSC density of gene
trees (topology and coalescent times) given the species tree 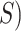 and parameters
and parameters
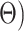 (Rannala and Yang 2003). We use MCMC to generate a sample from the joint posterior
density of the species tree
(Rannala and Yang 2003). We use MCMC to generate a sample from the joint posterior
density of the species tree 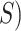 , parameters
, parameters 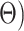 and
and
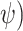 , and gene trees
, and gene trees 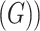 :
:
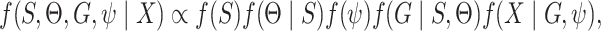 |
(3) |
The marginal posterior 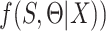 is obtained by simply ignoring
the gene trees and substitution parameters
is obtained by simply ignoring
the gene trees and substitution parameters 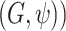 in the MCMC
sample. Here we focus on two new MCMC proposals that efficiently propose changes to the
species tree topology (
in the MCMC
sample. Here we focus on two new MCMC proposals that efficiently propose changes to the
species tree topology (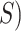 ). The moves that do not alter the species
tree topology are identical to those described in Rannala
and Yang (2003, 2013). The first move, based
on the SPR algorithm, is a direct extension of the Nearest-Neighbor Interchange (NNI)
algorithm implemented in Yang and Rannala (2014). The
second move, based on a node-slider algorithm, changes the topology as well as a node age in
the species tree.
). The moves that do not alter the species
tree topology are identical to those described in Rannala
and Yang (2003, 2013). The first move, based
on the SPR algorithm, is a direct extension of the Nearest-Neighbor Interchange (NNI)
algorithm implemented in Yang and Rannala (2014). The
second move, based on a node-slider algorithm, changes the topology as well as a node age in
the species tree.
The SPR Algorithm for Updating the Species Tree
Let anc(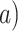 ) be the mother node of node
) be the mother node of node
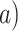 . We refer to the branch
anc(
. We refer to the branch
anc(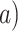 )-
)-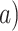 as branch
as branch
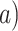 . We define clade or subtree
. We define clade or subtree
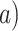 to include
to include 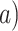 , all its
descendents, and branch
, all its
descendents, and branch 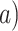 . Nodes on the species tree are
represented by capital letters, such as
. Nodes on the species tree are
represented by capital letters, such as 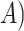 , and their ages are
denoted by
, and their ages are
denoted by 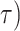 s (such as
s (such as 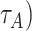 ). Nodes
on gene trees are labeled using small-case letters, and their ages are denoted by
). Nodes
on gene trees are labeled using small-case letters, and their ages are denoted by
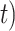 s.
s.
Our SPR move prunes off branch 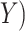 -
-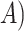 (including clade
(including clade
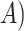 ) and reattaches it to a target branch
) and reattaches it to a target branch
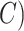 , retaining the same age
, retaining the same age
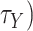 at reattachment (Fig. 1). Our algorithm does not change species divergence times in the
species tree (
at reattachment (Fig. 1). Our algorithm does not change species divergence times in the
species tree (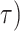 s) or node ages in the gene trees
(
s) or node ages in the gene trees
(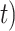 s). We preferentially propose changes to
the species tree topology around short (rather than long) internal branches. We sample an
internal branch
s). We preferentially propose changes to
the species tree topology around short (rather than long) internal branches. We sample an
internal branch 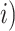 (out of
(out of 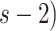 internal
branches for a species tree of
internal
branches for a species tree of 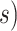 species) according to the following
probabilities
species) according to the following
probabilities
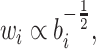 |
(4) |
where 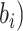 is the length of the internal branch.
The sampled branch is branch
is the length of the internal branch.
The sampled branch is branch 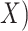 -
-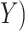 . Node
. Node
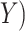 has two daughter branches. We sample one
at random and let it be
has two daughter branches. We sample one
at random and let it be 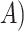 ; the other will be
; the other will be
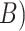 . We then prune off branch
. We then prune off branch
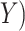 -
-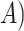 (including clade
(including clade
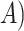 ) and reattach it to branch
) and reattach it to branch
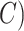 in the species tree. Let
in the species tree. Let
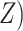 be the most recent common ancestor of
be the most recent common ancestor of
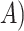 and
and 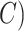 , with age
, with age
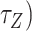 . The move affects species on the path
. The move affects species on the path
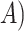 -
-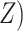 -
-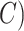 . For the SPR move
illustrated in Figure 1,
. For the SPR move
illustrated in Figure 1, 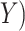 is species
is species
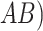 ,
, 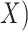 is
is
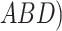 , and
, and 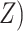 is
is
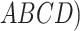 .
.
Among the feasible target branches of the species tree for reattachment, we sample one
using a probability distribution that favors small changes to the species tree topology. A
feasible target branch is a branch that remains after branch 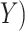 -
-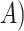 is pruned off (exclusive
of branch
is pruned off (exclusive
of branch 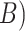 ) and that covers the age
) and that covers the age
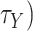 (see Fig. 1). In choosing a target branch, we use probabilities
(see Fig. 1). In choosing a target branch, we use probabilities
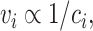 |
(5) |
where 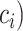 is the number of nodes on the path
is the number of nodes on the path
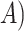 -
-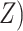 -
-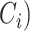 for potential target
branch
for potential target
branch 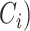 . The minimum for
. The minimum for
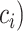 is 4, in which case node
is 4, in which case node
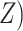 coincides with node
coincides with node
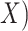 , and the SPR move reduces to the NNI move
(Yang and Rannala 2014). Our proposal using
Equation (5) thus favours small
changes to the species tree topology.
, and the SPR move reduces to the NNI move
(Yang and Rannala 2014). Our proposal using
Equation (5) thus favours small
changes to the species tree topology.
The move affects nodes on the gene trees that have age 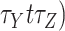 . A
moved node (marked with
. A
moved node (marked with 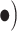 in Fig. 1) lies in species
in Fig. 1) lies in species  (
( ) or another ancestral species on the path
from
) or another ancestral species on the path
from 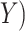 to
to 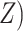 (excluding
(excluding
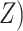 itself) and has exactly one daughter node
with descendants in
itself) and has exactly one daughter node
with descendants in 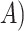 only. The other daughter node has
descendants in one or more non-
only. The other daughter node has
descendants in one or more non-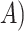 descendent populations as well. The
moved node (and the descendant clade) is pruned and regrafted to a randomly chosen
contemporary branch of the gene tree residing in a species on the path from
descendent populations as well. The
moved node (and the descendant clade) is pruned and regrafted to a randomly chosen
contemporary branch of the gene tree residing in a species on the path from
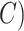 to
to 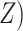 . In addition, four other
kinds of affected nodes have their population IDs changed. Any node
marked with
. In addition, four other
kinds of affected nodes have their population IDs changed. Any node
marked with  or
or 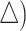 has descendents in species
has descendents in species 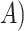 only and changes its population ID from
only and changes its population ID from
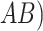 (
(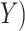 ) to
) to
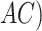 . Any node marked with
. Any node marked with
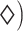 is in species
is in species
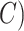 with age between
with age between 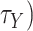 and
and
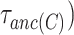 and changes its population
ID from
and changes its population
ID from 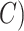 to
to 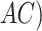 . Any node marked with
. Any node marked with
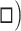 is in species
is in species
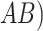 with both daughter nodes having
descendants in species
with both daughter nodes having
descendants in species 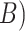 , and changes its population ID from
, and changes its population ID from
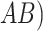 to
to 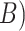 . The proposal ratio
incurred by the move can easily be derived using a procedure similar to that used for the
NNI move (Yang and Rannala 2014).
. The proposal ratio
incurred by the move can easily be derived using a procedure similar to that used for the
NNI move (Yang and Rannala 2014).
Nodeslider Algorithm for Updating the Species Tree
Overview of the algorithm.
The nodeslider move prunes off branch 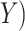 -
-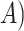 (including clade
(including clade
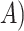 ) in the species tree, changes
) in the species tree, changes
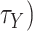 and rescales the ages inside
clade
and rescales the ages inside
clade 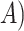 proportionally, and then reattaches the
branch (and clade
proportionally, and then reattaches the
branch (and clade 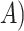 ) to a target branch in the remaining
species tree. This proposal consists of a pair of opposite steps, referred to as the
“Expand” and “Shrink” steps (Fig. 2). In the Expand
step (toward the root),
) to a target branch in the remaining
species tree. This proposal consists of a pair of opposite steps, referred to as the
“Expand” and “Shrink” steps (Fig. 2). In the Expand
step (toward the root), 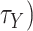 increases, and the target branch
is ancestral to node
increases, and the target branch
is ancestral to node 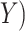 . In the Shrink step (toward the tips),
. In the Shrink step (toward the tips),
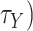 decreases, and the target branch
is a descendent of the sibling node of
decreases, and the target branch
is a descendent of the sibling node of 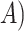 . Thus the move slides
node
. Thus the move slides
node 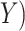 and the attached clade
and the attached clade
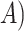 either toward the root, with the node
ages in clade
either toward the root, with the node
ages in clade 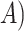 expanded (the Expand step), or to a
descendent branch of the sibling species of
expanded (the Expand step), or to a
descendent branch of the sibling species of 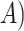 , with the node ages in
clade
, with the node ages in
clade 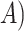 shrunk (the Shrink step). Figure 2 (from top to bottom) illustrates the changes
to the species tree (
shrunk (the Shrink step). Figure 2 (from top to bottom) illustrates the changes
to the species tree (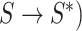 ) and to an example
gene tree (
) and to an example
gene tree (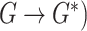 ) in the Expand step.
The reverse changes from bottom to top (
) in the Expand step.
The reverse changes from bottom to top (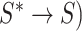 and
and
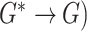 ) constitute the Shrink
step. Note that the sibling and target branches are reversed in the two steps: in the
Expand step,
) constitute the Shrink
step. Note that the sibling and target branches are reversed in the two steps: in the
Expand step, 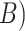 is the sibling node of
is the sibling node of
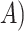 , and
, and 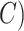 is the
target branch for reattachment, while in the Shrink step,
is the
target branch for reattachment, while in the Shrink step, 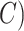 is the
sibling node and
is the
sibling node and 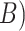 is the target branch.
is the target branch.
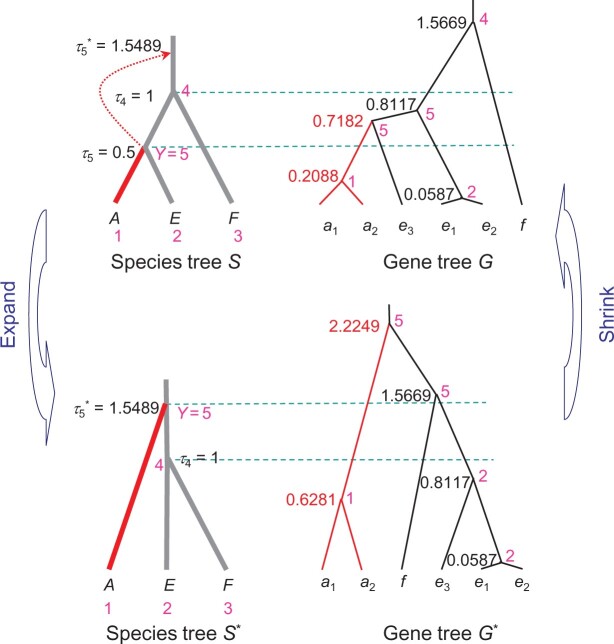
Figure 2.
The nodeslider/Expand move (top to bottom) prunes off branch
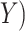 -
-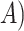 on the
species tree
on the
species tree 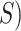 (including clade
(including clade
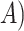 ), generates a new age for node
), generates a new age for node
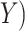 , with
, with 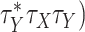 [Equation (6)], rescales the
node ages inside clade
[Equation (6)], rescales the
node ages inside clade  by
by 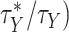 , and reattaches branch
, and reattaches branch
 -
-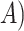 back to
the species tree at the ancestral branch
back to
the species tree at the ancestral branch 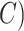 at age
at age
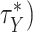 (indicated by the arrow).
Affected nodes in the gene tree (
(indicated by the arrow).
Affected nodes in the gene tree (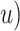 and
and
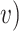 , marked by
, marked by
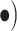 ) are pruned and regrafted,
with node ages inside the clades scaled by
) are pruned and regrafted,
with node ages inside the clades scaled by 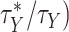 . In
the reverse Shrink step (from bottom to top), branch
. In
the reverse Shrink step (from bottom to top), branch 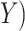 -
-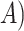 in
in
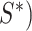 is pruned off and reattached to
a descendent branch (
is pruned off and reattached to
a descendent branch (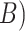 ) of the sibling node
(
) of the sibling node
(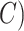 ), at the new age
), at the new age
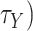 , generated from Equation
(7). Numeral labels on the
interior nodes in the gene trees are the population IDs.
, generated from Equation
(7). Numeral labels on the
interior nodes in the gene trees are the population IDs.
Changes to the species tree.
We describe the changes to the species tree first. A uniform random variable
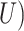 on
on 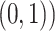 is generated to
decide whether to expand (if
is generated to
decide whether to expand (if 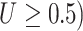 ) or to shrink (if
) or to shrink (if
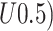 ).
).
In the Expand step (from 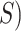 to
to 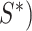 in Fig. 2), we use Equation (4) to sample an internal branch (out of
in Fig. 2), we use Equation (4) to sample an internal branch (out of
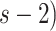 ) on the species tree and let it be
) on the species tree and let it be
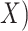 -
-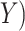 . Node
. Node
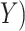 has two daughter nodes. We sample one at
random and let it be
has two daughter nodes. We sample one at
random and let it be 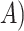 ; the other will be
; the other will be
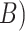 . We then propose a new age
. We then propose a new age
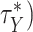 for node
for node
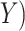 using an exponential density,
using an exponential density,
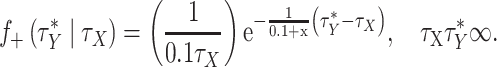 |
(6) |
In other words, the excess 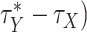 has mean
has mean
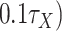 . The value
. The value
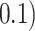 is the “Expand ratio” and is
adjustable; we suspect small values close to zero are preferable. We prune off branch
is the “Expand ratio” and is
adjustable; we suspect small values close to zero are preferable. We prune off branch
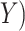 -
-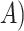 (including clade
(including clade
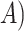 ), rescale the ages of all daughter nodes
of
), rescale the ages of all daughter nodes
of 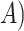 by the factor
by the factor 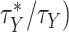 , and then re-attach the
branch to the remaining species tree at age
, and then re-attach the
branch to the remaining species tree at age 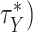 . There will be
only one ancestral branch (called
. There will be
only one ancestral branch (called  ) which covers the new age
) which covers the new age
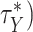 . If this is the root, node
. If this is the root, node
 will become the new root (as in Fig. 2).
will become the new root (as in Fig. 2).
The Shrink step is illustrated as the changes from bottom to top in Figure 2. We use Equation (4) to sample an internal branch on the
species tree (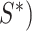 ) and let it be
) and let it be
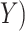 -
-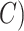 . The other daughter of
node
. The other daughter of
node 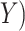 will be
will be 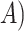 (i.e.,
(i.e.,
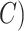 is the sibling of
is the sibling of
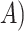 ). We prune off branch
). We prune off branch
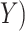 -
-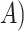 (including clade
(including clade
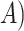 ), propose a new age
), propose a new age
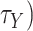 for node
for node
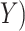 , rescale all node ages inside clade
, rescale all node ages inside clade
 by
by  , and
reattach branch
, and
reattach branch  -
- to a branch
(
to a branch
(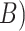 ) that is a descendent of the sibling
node (
) that is a descendent of the sibling
node (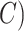 ). Let
). Let 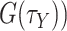 be
the number of descendent branches of
be
the number of descendent branches of 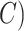 that exist at time
point
that exist at time
point 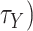 ; in the example of Figure 2,
; in the example of Figure 2, 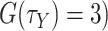 (for
branches
(for
branches 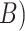 ,
, 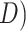 , and
, and
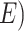 ). One of them is sampled at random to be
the target branch (
). One of them is sampled at random to be
the target branch (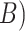 ). The new age
). The new age
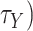 is proposed using a power density
is proposed using a power density
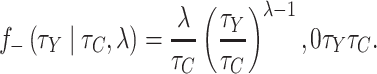 |
(7) |
To simulate from the power density we use the inverse transformation method. Generate a
uniform random variable 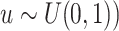 and set
and set
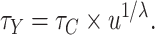 |
(8) |
Note that Equation (7) becomes the
uniform density on 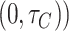 if
if 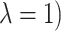 .
We choose
.
We choose 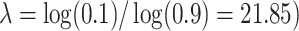 so
that 90% of the density is within 10% of
so
that 90% of the density is within 10% of 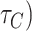 (with
(with
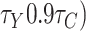 ). Here the value
10% is called the “Shrink ratio.” We favor small values like 0.1 so that the new age
). Here the value
10% is called the “Shrink ratio.” We favor small values like 0.1 so that the new age
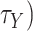 , smaller than
, smaller than
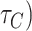 , tends to be close to it.
, tends to be close to it.
We now consider the factor in the acceptance ratio incurred by changes to the species tree. For the Expand step, this is given as
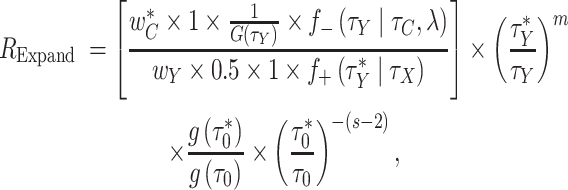 |
(9) |
where 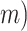 is the
number of node ages inside clade
is the
number of node ages inside clade 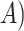 that are rescaled,
that are rescaled,
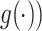 is the gamma prior density for
the root age
is the gamma prior density for
the root age 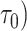 , and
, and 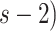 is the
number of nonroot interior nodes on the species tree. The denominator in the square
brackets is for the Expand step, and is the probability (
is the
number of nonroot interior nodes on the species tree. The denominator in the square
brackets is for the Expand step, and is the probability (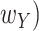 ) of
sampling branch
) of
sampling branch 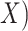 -
-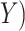 in
in
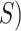 [Equation (4)], times the probability (0.5) of sampling the daughter
[Equation (4)], times the probability (0.5) of sampling the daughter
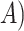 of node
of node 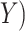 , times the
probability (1) of choosing target branch (
, times the
probability (1) of choosing target branch (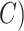 ), times the
probability density for the new age
), times the
probability density for the new age 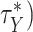 [Equation
(6)]. The numerator in the square
brackets is for the reverse Shrink step (from
[Equation
(6)]. The numerator in the square
brackets is for the reverse Shrink step (from 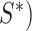 to
to
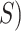 ) and reads as follows: we sample branch
) and reads as follows: we sample branch
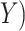 -
-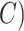 in
in
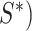 with probability
with probability
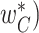 , choose node
, choose node
 as the sibling of
as the sibling of
 with probability 1, choose the target
branch (
with probability 1, choose the target
branch ( ) at age
) at age 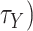 with
probability
with
probability 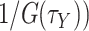 , whereas the new age
, whereas the new age
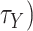 is generated from Equation (7). The factor
is generated from Equation (7). The factor 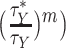 is due to
rescaling
is due to
rescaling 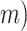 node ages (see Yang 2014 pp. 225–256). Furthermore, if the move changes the root age
(
node ages (see Yang 2014 pp. 225–256). Furthermore, if the move changes the root age
(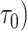 ) on the species tree, the prior
on the node ages in the species tree (the
) on the species tree, the prior
on the node ages in the species tree (the 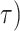 s) has to be
considered, which explains the terms involving
s) has to be
considered, which explains the terms involving 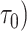 in Equation
(9) (see Yang and Rannala 2010, Equation (2)). Finally, for the reverse Shrink step, the factor in the
acceptance ratio is
in Equation
(9) (see Yang and Rannala 2010, Equation (2)). Finally, for the reverse Shrink step, the factor in the
acceptance ratio is 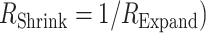 .
.
Changes to the gene trees.
The gene trees are modified to avoid conflicts with the newly proposed species tree,
similarly to the SPR algorithm. Some nodes are pruned off the gene tree and regrafted
back and some nodes have their population IDs changed due to the disappearance and
appearance of populations. We scan the gene tree at each locus to identify the moved
nodes. A moved node (marked with 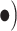 in Fig. 2) has exactly one daughter node with descendents in
in Fig. 2) has exactly one daughter node with descendents in
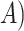 only. We prune off each moved node (and
its
only. We prune off each moved node (and
its 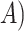 descendents), rescale the node ages
inside the subtree by the scale factor (
descendents), rescale the node ages
inside the subtree by the scale factor (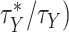 for
the Expand step) and re-graft the node back to a randomly-chosen branch that exists at
the new time
for
the Expand step) and re-graft the node back to a randomly-chosen branch that exists at
the new time 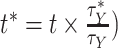 .
Note that target branches for reattachment must be in a population that is either node
.
Note that target branches for reattachment must be in a population that is either node
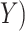 or its ancestor in the new species tree
(
or its ancestor in the new species tree
(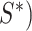 for the Expand step or
for the Expand step or
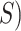 for the Shrink step, Fig. 2). There may be multiple target branches for
reattachment, from which one is chosen at random. For example, in the Shrink move of
Figure 2, the new age (
for the Shrink step, Fig. 2). There may be multiple target branches for
reattachment, from which one is chosen at random. For example, in the Shrink move of
Figure 2, the new age (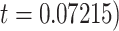 )
for the affected node
)
for the affected node 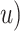 will be in population
will be in population
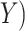 (
(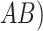 ) in the new gene tree
) in the new gene tree
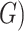 , and two branches
(
, and two branches
(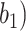 and
and 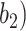 ) exist in
that population and are feasible targets for reattaching the subtree (or branch
) exist in
that population and are feasible targets for reattaching the subtree (or branch
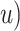 -
-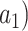 ). Similarly affected
node
). Similarly affected
node 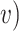 will be in population
will be in population
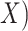 in
in 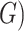 , and four branches
(
, and four branches
(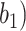 ,
, 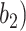 ,
,
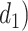 , and
, and 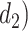 ) are
feasible targets for reattaching the subtree.
) are
feasible targets for reattaching the subtree.
At every locus, there may be multiple moved nodes and thus multiple subtree pruning and
regrafting operations on the gene trees. These are conducted in a disciplined manner, as
follows. We prune off all moved nodes (and the subtrees of
pure-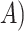 descendents, highlighted in red in
Fig. 2), and “lay them on the ground.” For each
moved node we then determine the new age after the scaling, sample the target branch for
reattachment and mark the reattachment point. The remaining part of the gene tree after
pruning off all moved nodes (black branches in the gene trees of Fig. 2), called the skeleton, is not changed except that gene tree
nodes in population
descendents, highlighted in red in
Fig. 2), and “lay them on the ground.” For each
moved node we then determine the new age after the scaling, sample the target branch for
reattachment and mark the reattachment point. The remaining part of the gene tree after
pruning off all moved nodes (black branches in the gene trees of Fig. 2), called the skeleton, is not changed except that gene tree
nodes in population 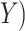 or in the target population (e.g.,
or in the target population (e.g.,
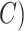 in the Expand step) may have their
population IDs changed. In short, we prune off the red subtrees and reattach them to the
black branches on the skeleton (Fig. 2).
in the Expand step) may have their
population IDs changed. In short, we prune off the red subtrees and reattach them to the
black branches on the skeleton (Fig. 2).
The order of pruning and reattachment of the affected nodes is thus inconsequential. In this way, we do not allow regrafting of one pruned branch onto another pruned branch, but it may be possible for multiple pruned subtrees to be reattached to the same branch on the skeleton (at different time points). It is also possible for a pruned branch to be regrafted to the same branch on the skeleton, so that the operation may change the node ages without changing the gene tree topology.
If all sequences at a locus are from populations inside clade 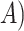 on the
species tree, all node ages on the gene tree are rescaled (in the same way as the moved
node), while their population IDs remain unchanged. This rescaling is necessary as
otherwise the gene tree may be in conflict with the proposed new species tree.
on the
species tree, all node ages on the gene tree are rescaled (in the same way as the moved
node), while their population IDs remain unchanged. This rescaling is necessary as
otherwise the gene tree may be in conflict with the proposed new species tree.
The changes to the gene trees will incur a factor in the acceptance ratio, because the
following components may not be the same in the forward and reverse moves: the number of
target branches for reattaching each moved node, the probability density of the gene
tree given the species tree topology and parameters (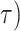 s and
s and
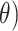 s in the MSC density), the
rescaling of gene-tree node ages, as well as the probability of the sequence alignment
given the gene tree at each locus (the phylogenetic likelihood).
s in the MSC density), the
rescaling of gene-tree node ages, as well as the probability of the sequence alignment
given the gene tree at each locus (the phylogenetic likelihood).
The case of three species.
In the case of only three species, the nodeslider move reduces to a variant of the
general NNI algorithm for rooted trees (Yang
2014, p. 293), although it differs from the NNI algorithm implemented by Yang and Rannala (2014) or the SPR move described
above. The move changes both the species tree topology and a species divergence time
(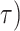 ), and always changes the root of
the species tree (Fig. 3). In the Expand step
(Fig. 3,
), and always changes the root of
the species tree (Fig. 3). In the Expand step
(Fig. 3, 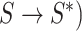 ),
branch
),
branch 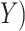 -
-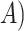 is pruned off, the age
is pruned off, the age
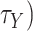 is increased to
is increased to
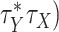 , and the branch is
reattached to the species tree, with node
, and the branch is
reattached to the species tree, with node 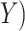 becoming the new root.
The reverse Shrink step (Fig. 3,
becoming the new root.
The reverse Shrink step (Fig. 3,
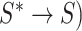 ) slides the root of
the species tree towards the tips so that the younger interior node becomes the new
root.
) slides the root of
the species tree towards the tips so that the younger interior node becomes the new
root.
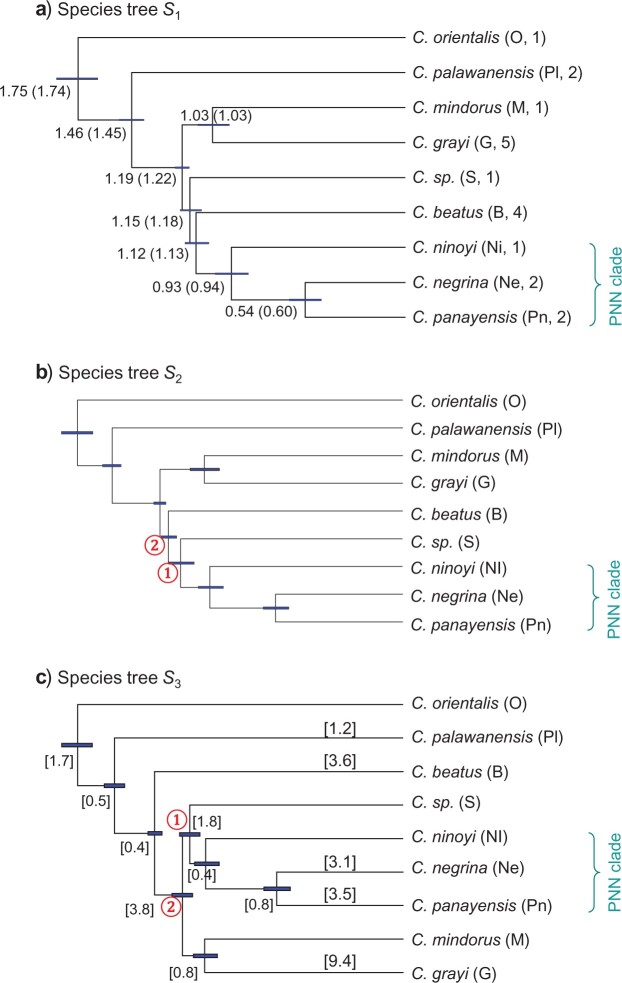
Figure 3.
The nodeslider move for three species is a variant of the NNI rearrangement for
rooted trees, and changes both the species tree topology and a species divergence
time (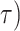 ), and always changes the root
of the species tree. The move prunes off branch
), and always changes the root
of the species tree. The move prunes off branch 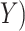 -
-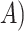 on the
species tree, changes
on the
species tree, changes 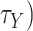 , and reattaches the branch to
target branch
, and reattaches the branch to
target branch 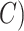 on the species tree. In the Expand
step, the target branch in the species tree
on the species tree. In the Expand
step, the target branch in the species tree 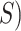 is
is
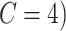 (the root), whereas in the
Split step, the target branch in the species tree
(the root), whereas in the
Split step, the target branch in the species tree 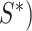 is
is
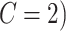 , a descendent of the sibling
branch
, a descendent of the sibling
branch 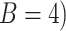 .
.
Validation of the Theory and Implementation
The new SPR and nodeslider moves are implemented in BPP. Our algorithms are complex and
extensive testing has been conducted to confirm the correctness of the theory and the
implementation. Because our new moves do not affect the calculation of the phylogenetic
likelihood our tests have focused mainly on generating the prior for the species trees and
parameters of the MSC model (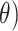 s and
s and 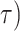 s) via MCMC
when the sequence likelihood is fixed at 1. Note that each of the three moves to change
the species tree topology that we have implemented, including the NNI of Yang and Rannala (2014) and the SPR and nodeslider
moves of this paper, is sufficient to allow the MCMC to traverse the whole space of the
species trees. In BPP, we use SPR (which includes NNI as a special case) and nodeslider
moves with pre-assigned probabilities (such as 0.6 for SPR and 0.4 for nodeslider). We
confirmed that the SPR and nodeslider algorithms, used either alone or in combination,
sampled the species trees correctly according to the prior, which is analytically
available for four different priors described by Yang and
Rannala (2014) and Yang (2015) for the
cases of 3, 4, and 5 species.
s) via MCMC
when the sequence likelihood is fixed at 1. Note that each of the three moves to change
the species tree topology that we have implemented, including the NNI of Yang and Rannala (2014) and the SPR and nodeslider
moves of this paper, is sufficient to allow the MCMC to traverse the whole space of the
species trees. In BPP, we use SPR (which includes NNI as a special case) and nodeslider
moves with pre-assigned probabilities (such as 0.6 for SPR and 0.4 for nodeslider). We
confirmed that the SPR and nodeslider algorithms, used either alone or in combination,
sampled the species trees correctly according to the prior, which is analytically
available for four different priors described by Yang and
Rannala (2014) and Yang (2015) for the
cases of 3, 4, and 5 species.
Summary of the Posterior
The BPP program generates an MCMC sample from the posterior probability distribution of
species trees and the posterior distribution of parameters (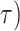 s and
s and
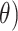 s) given each species tree. Here we
focus on summaries of the species trees. The species tree with the highest posterior
probability, called the maximum a posteriori (MAP) species tree, is the
best point estimate. The MCMC sample can also be used to calculate the support values for
clades on the MAP tree. The program also generates posterior probabilities for individual
clades as well as the majority-rule consensus tree, with support values. The posterior of
model parameters (
s) given each species tree. Here we
focus on summaries of the species trees. The species tree with the highest posterior
probability, called the maximum a posteriori (MAP) species tree, is the
best point estimate. The MCMC sample can also be used to calculate the support values for
clades on the MAP tree. The program also generates posterior probabilities for individual
clades as well as the majority-rule consensus tree, with support values. The posterior of
model parameters (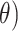 s and
s and 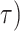 s) on the
MAP tree can be generated by using the subset of the MCMC sample in which the species tree
is the MAP tree. However, if the model parameters are of interest, one can run the program
a second time with the species tree fixed at the MAP tree (analysis A00, Yang 2015). This approach is used to generate the
posterior distribution of parameters on the MAP tree in our analysis of the empirical
datasets; see Figures 6 and 8.
s) on the
MAP tree can be generated by using the subset of the MCMC sample in which the species tree
is the MAP tree. However, if the model parameters are of interest, one can run the program
a second time with the species tree fixed at the MAP tree (analysis A00, Yang 2015). This approach is used to generate the
posterior distribution of parameters on the MAP tree in our analysis of the empirical
datasets; see Figures 6 and 8.
Figure 6.

The MAP trees for the six subspecies of Sistrurus rattlesnakes and
the outgroups in three analyses of the nuclear (18 loci) and mitochondrial datasets.
The three S. catenatus subspecies are S. c.
catenatus (C), S. c. tergeminus (T), and S. c.
edwardsii (E), whereas the three S. miliarius subspecies
are S. m. miliarius (M), S. m. barbouri (B), and
S. m. streckeri (S). Posterior probabilities for clades in the
species tree in the A01 analysis are shown next to the nodes as percentages (not
shown if 100%). The branch lengths are drawn to represent the posterior means of the
divergence times (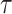 s) in the A00 analysis with the
phylogeny fixed, whereas the node bars represent the 95% HPD interval. The posterior
means of
s) in the A00 analysis with the
phylogeny fixed, whereas the node bars represent the 95% HPD interval. The posterior
means of 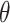 s for the extant and extinct
species from the A00 analysis are shown next to the nodes in brackets.
s for the extant and extinct
species from the A00 analysis are shown next to the nodes in brackets.
Figure 8.
a) The MAP species tree (also the majority-rule consensus species tree) produced in
the BPP analysis of the simulated dataset Sim1-Matching of Giarla and Esselstyn (2015). Posterior probabilities for nodes are
shown as percentages, whereas those not shown are 100%. Branches are drawn to reflect
the posterior means of the node ages (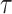 s), which are shown
next to the nodes (with the true values in parentheses,
s), which are shown
next to the nodes (with the true values in parentheses, 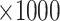 ), whereas the node bars
indicate the 95% highest posterior density (HPD) intervals. The number of sequences
per species per locus is in the parentheses after each species name. This tree is also
the species tree that Giarla and Esselstyn
(2015) inferred from the UCE data and is the true species tree used to
generate the three simulated datasets (Sim1, Sim2, and Sim3x). b) and c) Two
alternative species trees (
), whereas the node bars
indicate the 95% highest posterior density (HPD) intervals. The number of sequences
per species per locus is in the parentheses after each species name. This tree is also
the species tree that Giarla and Esselstyn
(2015) inferred from the UCE data and is the true species tree used to
generate the three simulated datasets (Sim1, Sim2, and Sim3x). b) and c) Two
alternative species trees (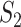 and
and 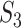 ) with
high posterior probabilities in the BPP analysis of the UCE dataset.
) with
high posterior probabilities in the BPP analysis of the UCE dataset.
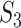 appears to be the MAP tree, and the
posterior means of
appears to be the MAP tree, and the
posterior means of 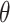 s for modern and ancestral
populations on
s for modern and ancestral
populations on 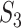 are shown in square brackets
(
are shown in square brackets
(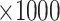 ). The 95% HPD intervals of
node ages in
). The 95% HPD intervals of
node ages in 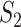 and
and 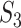 , shown
as node bars, are shorter than those in
, shown
as node bars, are shorter than those in  , probably because
there are 919 loci in the UCE dataset and 500 in Sim1. Note that
, probably because
there are 919 loci in the UCE dataset and 500 in Sim1. Note that
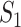 and
and 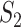 differ
by an NNI move around node 1, whereas
differ
by an NNI move around node 1, whereas 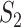 and
and
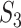 differ by another NNI move around
node 2.
differ by another NNI move around
node 2.
Marginal Likelihood Calculation for Fixed Species Trees
Alternative to the transmodel MCMC algorithms we implemented (NNI, SPR, and nodeslider), the posterior probabilities of species trees can easily be calculated if the marginal likelihood under the MSC given the species tree is available:
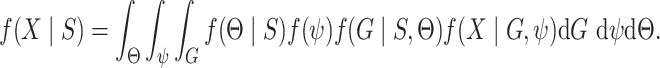 |
(10) |
As 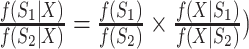 for any two alternative species trees
for any two alternative species trees 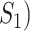 and
and
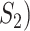 , the posterior probabilities for rooted
species trees are proportional to their marginal likelihood values under the uniform prior
on species trees (with
, the posterior probabilities for rooted
species trees are proportional to their marginal likelihood values under the uniform prior
on species trees (with 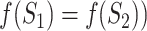 , Prior 1 in BPP, Yang and Rannala 2014), while under the uniform prior
on labeled histories (Prior 0, Yang and Rannala
2014), the posterior is proportional to the product of the marginal likelihood
and the number of compatible labeled histories. Note that the ratio of marginal likelihood
values,
, Prior 1 in BPP, Yang and Rannala 2014), while under the uniform prior
on labeled histories (Prior 0, Yang and Rannala
2014), the posterior is proportional to the product of the marginal likelihood
and the number of compatible labeled histories. Note that the ratio of marginal likelihood
values, 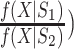 , is the Bayes
factor.
, is the Bayes
factor.
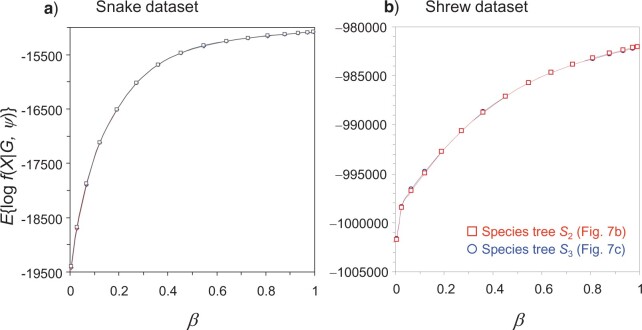
Here we implement the path-sampling or thermodynamic integration approach to marginal
likelihood calculation under the MSC, with the species tree fixed (Gelman and Meng 1998; Lartillot and
Philippe 2006). For a simple likelihood model with parameters
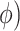 and data
and data 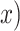 , the
path-sampling method makes use of the so-called power posterior, defined as
, the
path-sampling method makes use of the so-called power posterior, defined as
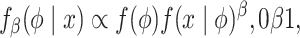 |
(11) |
which becomes the prior if 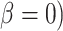 or the posterior if
or the posterior if
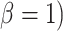 , so that different values of
, so that different values of
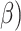 form a path from the prior to the
posterior. The logarithm of the marginal likelihood,
form a path from the prior to the
posterior. The logarithm of the marginal likelihood, 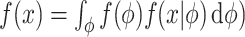 ,
is then given by
,
is then given by
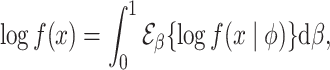 |
(12) |
where the expectation is taken over the power posterior 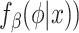 . We run multiple MCMC
algorithms to sample from the power posterior for different values of
. We run multiple MCMC
algorithms to sample from the power posterior for different values of
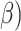 to approximate the expectation of the
log likelihood,
to approximate the expectation of the
log likelihood, 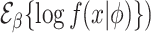 , by
the MCMC average, and then use numerical integration to calculate the integral of Equation
(12).
, by
the MCMC average, and then use numerical integration to calculate the integral of Equation
(12).
In our problem, the likelihood function for the species tree and parameters,
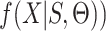 , averages over the gene
tree topologies and branch lengths (coalescent times), and is not directly calculable.
Instead we treat the latent variables (i.e., the gene tree topologies and coalescent
times) as parameters, and define the power posterior as
, averages over the gene
tree topologies and branch lengths (coalescent times), and is not directly calculable.
Instead we treat the latent variables (i.e., the gene tree topologies and coalescent
times) as parameters, and define the power posterior as
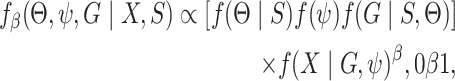 |
(13) |
so that 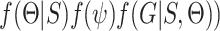 becomes
the joint prior while
becomes
the joint prior while 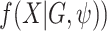 is the likelihood. The general
procedure of Equation (12) then
applies, with
is the likelihood. The general
procedure of Equation (12) then
applies, with
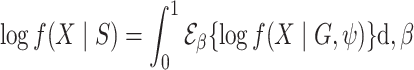 |
(14) |
where the expectation 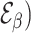 in the integrand is
over the power posterior of Equation (13). Calculation based on Equation (14) then shares all the statistical properties of calculation
based on Equation (12), such as
consistency and unbiasedness (Gelman and Meng
1998). This algorithm has the same structure as the algorithms for calculating the
Bayes factors for two substitution models, averaging over different phylogenetic trees,
discussed by Wu et al. (2014). Those authors
provided a mathematical proof that such algorithms are statistically consistent even
though the phylogeny varies in the MCMC. The argument above treating latent variables
(gene trees or phylogenies) as parameters appears to be simpler.
in the integrand is
over the power posterior of Equation (13). Calculation based on Equation (14) then shares all the statistical properties of calculation
based on Equation (12), such as
consistency and unbiasedness (Gelman and Meng
1998). This algorithm has the same structure as the algorithms for calculating the
Bayes factors for two substitution models, averaging over different phylogenetic trees,
discussed by Wu et al. (2014). Those authors
provided a mathematical proof that such algorithms are statistically consistent even
though the phylogeny varies in the MCMC. The argument above treating latent variables
(gene trees or phylogenies) as parameters appears to be simpler.
We use Gaussian quadrature to approximate the one-dimensional integral over
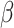 , using
, using 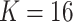 points in
the Gauss-Legendre rule. The
points in
the Gauss-Legendre rule. The 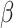 values are given as
values are given as
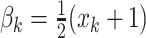 , for
, for
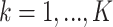 , where
, where
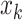 , with
, with 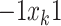 , are the Gauss–Legendre
points. This samples
, are the Gauss–Legendre
points. This samples 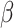 values more densely close to 0 and 1,
in comparison with the trapezoid or Simpson methods which use equally spaced points. For
each
values more densely close to 0 and 1,
in comparison with the trapezoid or Simpson methods which use equally spaced points. For
each 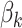 , we run an MCMC algorithm to
generate a sample from the power posterior distribution, and then calculate the average of
, we run an MCMC algorithm to
generate a sample from the power posterior distribution, and then calculate the average of
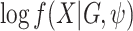 over the MCMC sample as an
approximate to the expectation
over the MCMC sample as an
approximate to the expectation 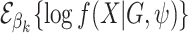 .
The integral or the log marginal likelihood is then approximated by
.
The integral or the log marginal likelihood is then approximated by
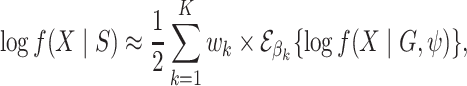 |
(15) |
where 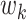 are the Gauss–Legendre weights.
are the Gauss–Legendre weights.
Two factors may affect the accuracy of the approximation. First the integrand or the
expected log likelihood 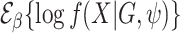 is not calculated exactly but approximated by the average over the MCMC sample from the
power posterior. Second, the number of quadrature points
is not calculated exactly but approximated by the average over the MCMC sample from the
power posterior. Second, the number of quadrature points  is finite. The
first factor appears to be much more important. In particular, for small values of
is finite. The
first factor appears to be much more important. In particular, for small values of
 and for large datasets, the power
posterior may differ substantially from the likelihood. As a result the log likelihood is
very small for most values of
and for large datasets, the power
posterior may differ substantially from the likelihood. As a result the log likelihood is
very small for most values of  sampled from the power
posterior, but is huge occasionally, making it difficult to estimate its average. Note
that the posterior probability ratio between two species trees is related to the
difference in log marginal likelihood (
sampled from the power
posterior, but is huge occasionally, making it difficult to estimate its average. Note
that the posterior probability ratio between two species trees is related to the
difference in log marginal likelihood (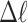 ) by
) by
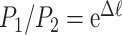 . As
. As
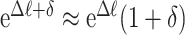 ,
where
,
where 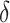 is the small error, we need the log
marginal likelihood difference or the expected log likelihood to be accurate at the 1st
(or 2nd) decimal point for the relative error in the posterior probability to be 10% (or
1%). This level of precision may require very long chains to simulate the power posterior.
In contrast, the second factor may not be important and
is the small error, we need the log
marginal likelihood difference or the expected log likelihood to be accurate at the 1st
(or 2nd) decimal point for the relative error in the posterior probability to be 10% (or
1%). This level of precision may require very long chains to simulate the power posterior.
In contrast, the second factor may not be important and 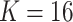 may be
large enough as in previous applications of the quadrature method, with exact calculation
of the integrand, use of 8 or 16 points provided excellent approximations to
one-dimensional integrals (Zhu and Yang 2012; Yang 2014 p. 206–209).
may be
large enough as in previous applications of the quadrature method, with exact calculation
of the integrand, use of 8 or 16 points provided excellent approximations to
one-dimensional integrals (Zhu and Yang 2012; Yang 2014 p. 206–209).
Thus although the challenge of the transmodel MCMC algorithms (the NNI, SPR, and
nodeslider) lies in the difficulty of moving from one species tree to another, the
challenge of the path-sampling approach to marginal likelihood calculation appears to lie
mainly in the reliable estimation of the expectation of the log likelihood over the power
posterior. In addition the algorithm of Equation (15) requires 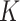 MCMC runs. The algorithm
may be useful for evaluating a few alternative species trees.
MCMC runs. The algorithm
may be useful for evaluating a few alternative species trees.
Results
Simulation to Evaluate the Statistical Performance of the Method
Simulations were used to examine the influence on the posterior probabilities of species
trees of the number of loci, the mutation rate (sequence divergence level), and the prior
on topology. We simulated data under the MSC using either a completely symmetrical or
asymmetrical tree of 16 species, with two sequences sampled per species per locus (see
Fig. 4). For simplicity, we assumed equal
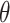 s among ancestral and contemporary
species with either
s among ancestral and contemporary
species with either 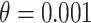 (low mutation rate) or
(low mutation rate) or
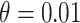 (high mutation rate). We set
all internal branch lengths equal to
(high mutation rate). We set
all internal branch lengths equal to 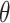 , so that
, so that 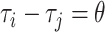 where node
where node
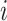 is the mother of node
is the mother of node
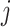 . Thus, the height of the root was
. Thus, the height of the root was
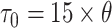 for the
asymmetrical tree and
for the
asymmetrical tree and 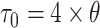 for the
symmetrical tree. For each of the
for the
symmetrical tree. For each of the 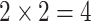 parameter/topology
combinations 50 datasets were simulated of either
parameter/topology
combinations 50 datasets were simulated of either 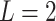 or
or
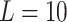 unlinked loci, each with
unlinked loci, each with
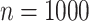 sites. Thus,
sites. Thus, 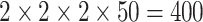 datasets were simulated in total. The MCcoal program which is part of the BPP package was
used to generate gene trees under the MSC and to simulate sequence alignments on the trees
under the JC69 model.
datasets were simulated in total. The MCcoal program which is part of the BPP package was
used to generate gene trees under the MSC and to simulate sequence alignments on the trees
under the JC69 model.
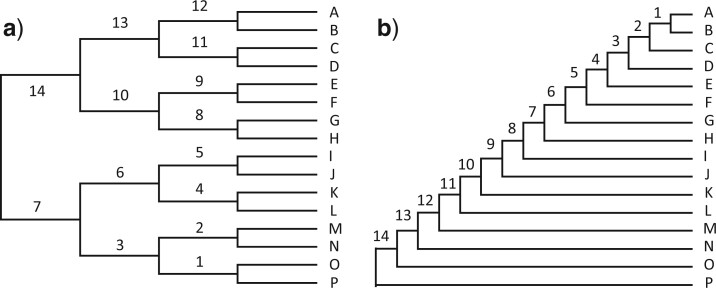
Figure 4.
Symmetrical a) and asymmetrical b) species trees used in computer simulation to
evaluate the performance of the BPP program. The branches are drawn to represent their
lengths (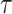 s) and the 14 nodes are labeled in
each tree.
s) and the 14 nodes are labeled in
each tree.
The simulated datasets were analyzed using the BPP 3.2 program with a
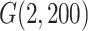 prior for
prior for
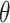 when the true
when the true
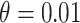 and a
and a 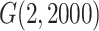 prior
for
prior
for 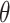 when the true
when the true
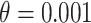 . Although the prior means
match the true values, the gamma distribution with shape parameter 2 is diffuse
(uninformative). Similarly, a gamma prior with shape parameter 2 and with mean equal to
the true value was assigned to
. Although the prior means
match the true values, the gamma distribution with shape parameter 2 is diffuse
(uninformative). Similarly, a gamma prior with shape parameter 2 and with mean equal to
the true value was assigned to 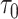 , the age of the root of the species
tree. In other words, the prior on
, the age of the root of the species
tree. In other words, the prior on 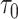 was
was 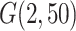 for
datasets simulated under a symmetrical tree with
for
datasets simulated under a symmetrical tree with 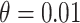 ,
,
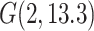 for the asymmetrical tree with
for the asymmetrical tree with
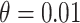 ,
, 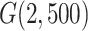 for
the symmetrical tree with
for
the symmetrical tree with 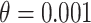 , and
, and 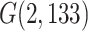 for
datasets simulated under an asymmetrical tree with
for
datasets simulated under an asymmetrical tree with 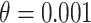 . Two analyses
were carried out for each dataset using different priors on the tree topology: a uniform
prior on labeled histories (Prior 0, Yang and Rannala
2014) and a uniform prior on rooted trees (Prior 1). Each of the simulated
datasets (and prior combinations) was analyzed using two independent MCMC runs with either
a good starting species tree (the true species tree) or a poor starting species tree to
check for consistency between runs. Thus
. Two analyses
were carried out for each dataset using different priors on the tree topology: a uniform
prior on labeled histories (Prior 0, Yang and Rannala
2014) and a uniform prior on rooted trees (Prior 1). Each of the simulated
datasets (and prior combinations) was analyzed using two independent MCMC runs with either
a good starting species tree (the true species tree) or a poor starting species tree to
check for consistency between runs. Thus 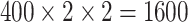 MCMC runs were
carried out in total. Each MCMC analysis was run for 200,000 iterations, sampling every
second iteration and discarding the first 50,000 iterations as burn-in.
MCMC runs were
carried out in total. Each MCMC analysis was run for 200,000 iterations, sampling every
second iteration and discarding the first 50,000 iterations as burn-in.
To examine the statistical performance of the method we calculated the proportion of
datasets (among 50 replicate simulations) in which each of the 14 nodes in the true
species tree is found in the consensus tree; note that a node of the true tree is in the
consensus tree if its posterior probability is 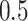 . This is a measure
of power. We also examined the empirical coverage of the
. This is a measure
of power. We also examined the empirical coverage of the 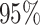 and
and
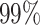 Credible Set of Trees (CST). Coverage is
defined as the proportion of credible sets that contain the true tree. The results are
summarized in Table 1. The method performs very
well in identifying the true clades, even with only 2 loci. With the exception of nodes 12
to 14 at the base of the tree (see Fig. 4) all nodes
of the true tree are present in the consensus tree with frequencies of 0.76 or greater.
The empirical coverage of the credible set of trees provides a measure of the accuracy of
the method. The accuracy is very high, with the true tree contained in both the 95% and 99
% credible sets in all cases (with the realized coverage to be 100%) except two: (i) trees
inferred using Prior 0 from data simulated on an asymmetrical tree with 2 loci and with
Credible Set of Trees (CST). Coverage is
defined as the proportion of credible sets that contain the true tree. The results are
summarized in Table 1. The method performs very
well in identifying the true clades, even with only 2 loci. With the exception of nodes 12
to 14 at the base of the tree (see Fig. 4) all nodes
of the true tree are present in the consensus tree with frequencies of 0.76 or greater.
The empirical coverage of the credible set of trees provides a measure of the accuracy of
the method. The accuracy is very high, with the true tree contained in both the 95% and 99
% credible sets in all cases (with the realized coverage to be 100%) except two: (i) trees
inferred using Prior 0 from data simulated on an asymmetrical tree with 2 loci and with
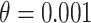 — the coverage is 0.92 for the
— the coverage is 0.92 for the
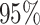 and
and 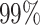 CSTs; and (ii) trees
inferred using Prior 1 from the data simulated on a symmetrical tree with 2 loci and with
CSTs; and (ii) trees
inferred using Prior 1 from the data simulated on a symmetrical tree with 2 loci and with
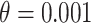 — the coverage is 0.98 for the
— the coverage is 0.98 for the
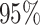 CST and 1.0 for the
CST and 1.0 for the
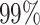 CST. In other words, in all but one case
the coverage is greater than the nominal value of either
CST. In other words, in all but one case
the coverage is greater than the nominal value of either 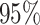 or
or
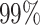 .
.
Table 1.
Summary of results for simulation analyses
| Number of loci: 2 | Number of loci: 10 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetrical tree | Asymmetrical tree | Symmetrical tree | Asymmetrical tree | |||||||||||||
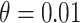
|
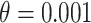
|
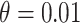
|
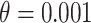
|
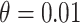
|
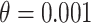
|
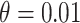
|
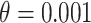
|
|||||||||
| Prior | LH | T | LH | T | LH | T | LH | T | LH | T | LH | T | LH | T | LH | T |
| Node | Proportion of datasets with true node present in consensus tree | |||||||||||||||
| 1 | 0.98 | 0.98 | 0.80 | 0.76 | 0.98 | 1.0 | 0.88 | 0.86 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 2 | 1.0 | 0.98 | 0.90 | 0.84 | 0.94 | 0.96 | 0.88 | 0.90 | 1.0 | 1.0 | 1.0 | 0.98 | 1.0 | 1.0 | 1.0 | 1.0 |
| 3 | 1.0 | 1.0 | 0.88 | 0.74 | 0.98 | 1.0 | 0.84 | 0.86 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 4 | 0.98 | 0.94 | 0.92 | 0.92 | 0.96 | 1.0 | 0.82 | 0.84 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 5 | 0.96 | 0.92 | 0.90 | 0.88 | 0.94 | 0.98 | 0.76 | 0.80 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 6 | 1.0 | 1.0 | 0.90 | 0.80 | 0.96 | 0.98 | 0.78 | 0.84 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 7 | 0.96 | 0.96 | 0.76 | 0.64 | 0.96 | 0.98 | 0.76 | 0.80 | 1.0 | 1.0 | 0.98 | 0.98 | 1.0 | 1.0 | 1.0 | 1.0 |
| 8 | 1.0 | 0.98 | 0.88 | 0.82 | 0.96 | 1.0 | 0.84 | 0.86 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0.98 | 1.0 |
| 9 | 0.98 | 0.98 | 0.90 | 0.90 | 0.94 | 0.98 | 0.86 | 0.88 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 10 | 0.96 | 0.96 | 0.80 | 0.78 | 0.98 | 1.0 | 0.86 | 0.90 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 11 | 0.98 | 0.94 | 0.80 | 0.76 | 0.96 | 1.0 | 0.76 | 0.80 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 12 | 0.98 | 0.96 | 0.92 | 0.88 | 0.90 | 0.96 | 0.68 | 0.80 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 13 | 0.96 | 0.96 | 0.76 | 0.68 | 0.86 | 0.94 | 0.36 | 0.64 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0.98 | 1.0 |
| 14 | 0.96 | 0.94 | 0.78 | 0.74 | 0.66 | 0.80 | 0.13 | 0.46 | 1.0 | 1.0 | 1.0 | 1.0 | 0.94 | 0.98 | 0.58 | 0.80 |
| CST | Empirical coverage | |||||||||||||||
| 95% | 1.0 | 1.0 | 1.0 | 0.98 | 1.0 | 1.0 | 0.92 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 99% | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0.92 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| CST | Mean number of trees in 99% CST | |||||||||||||||
| 243.5 | 372.8 | 4375.7 | 6297.3 | 443.9 | 200.9 | 6205.8 | 2711.7 | 1.1 | 1.1 | 15.6 | 19.1 | 3.7 | 3.0 | 46.9 | 26.3 | |
Notes: The upper matrix shows the proportion of simulated datasets for which each node of the true species tree is present in consensus tree. The empirical coverage of the 95% and 99% credible sets of trees (CSTs) tabulates the proportion of simulated datasets (across 50 simulated datasets for each set of simulation conditions) for which the true tree is contained within the credible set. The mean number of trees in the CST is the average number of trees in the 99% CST (averaging across 50 simulated datasets for each set of simulation conditions). Each dataset is analyzed using 2 species tree priors: the uniform prior for labeled histories (LH) and the uniform prior for rooted trees (T). Node numbers are shown in Figure 4.
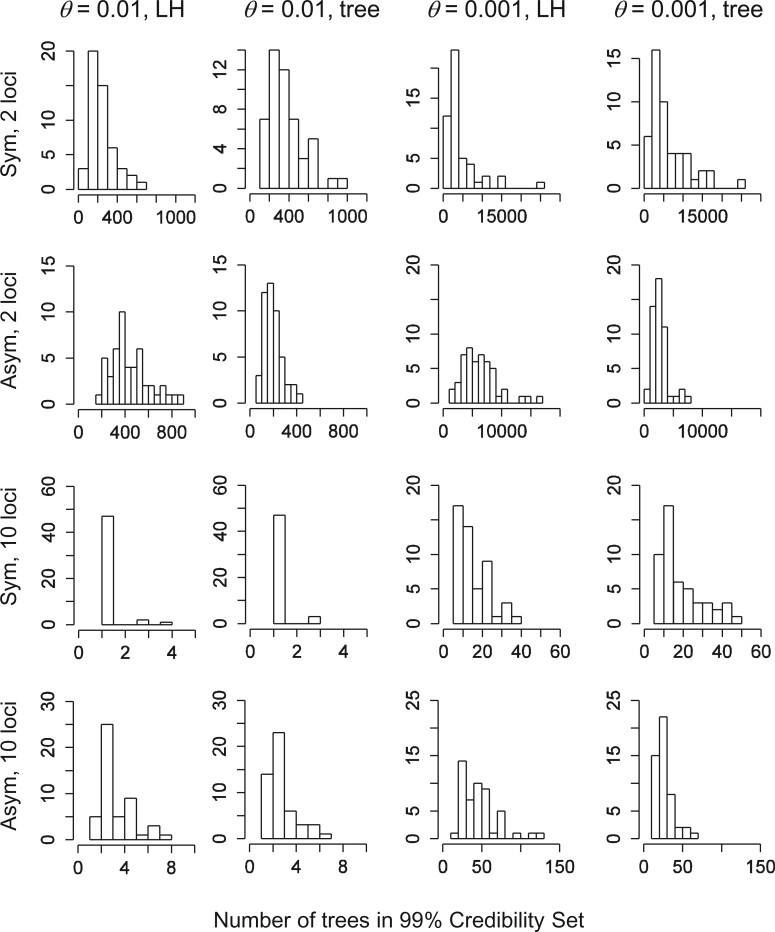
The mean number of trees contained in the 99% CST provides a measure of the precision of
the estimator of species tree topology (Fig. 5 and
Table 1). The mean number of trees ranged from a
minimum of  (for 10 loci,
(for 10 loci, 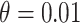 and
a symmetrical true tree with Prior 0) to a maximum of
and
a symmetrical true tree with Prior 0) to a maximum of 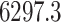 (for 2 loci,
(for 2 loci,
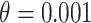 and a symmetrical true tree
with Prior 1). The prior on species trees can have a large effect on the precision of the
method (Fig. 5 and Table 1). Prior 0 favors symmetrical trees whereas Prior 1 favors asymmetrical
trees, and when the prior favors the shape of the true tree, the estimates are more
precise with a smaller CST. When the true tree is symmetrical (Fig. 5, rows 1 and 3), there are fewer trees in the 99% CST under Prior
0 than under Prior 1, whereas the opposite is true when the true tree is asymmetrical
(Fig. 5, rows 2 and 4). The impact of the prior is
less important when the number of loci increases from 2 to 10 and is negligible for the
informative data simulated using
and a symmetrical true tree
with Prior 1). The prior on species trees can have a large effect on the precision of the
method (Fig. 5 and Table 1). Prior 0 favors symmetrical trees whereas Prior 1 favors asymmetrical
trees, and when the prior favors the shape of the true tree, the estimates are more
precise with a smaller CST. When the true tree is symmetrical (Fig. 5, rows 1 and 3), there are fewer trees in the 99% CST under Prior
0 than under Prior 1, whereas the opposite is true when the true tree is asymmetrical
(Fig. 5, rows 2 and 4). The impact of the prior is
less important when the number of loci increases from 2 to 10 and is negligible for the
informative data simulated using 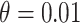 (see Table 1 and Fig. 5).
(see Table 1 and Fig. 5).
Figure 5.
Histograms of the number of species trees in the 99% credible set from analyses of 50
simulated datasets for each of 8 combinations of simulation conditions and two
different species tree priors: Prior 0 (LH) which assigns equal probabilities to
labeled histories (columns 1 and 3), and prior 1 (tree) which assigns equal
probabilities to rooted species trees (columns 2 and 4). The upper two rows show
results for two loci and and the lower two rows results for 10 loci. Rows 1 and 3 are
results for data simulated on symmetrical (Sym) trees and rows 2 and 4 for
asymmetrical (Asym) trees. The two columns to the left are simulations using
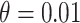 and the two columns on the
right are those using
and the two columns on the
right are those using 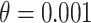 .
.
Analysis of the Rattlesnake Data
We analyze here the dataset of 18 nuclear loci from six subspecies of Sistrurus rattlesnakes, generated and analyzed by Kubatko et al. (2011). Rattlesnakes are venomous snakes of the New World, with species falling into two genera: Crotalus which contains more than 20 species and Sistrurus which contains three named species: catenatus, miliarius, and ravus. However, mtDNA suggests that ravus in fact belongs to the genus Crotalus (Murphy et al. 2002; Parkinson et al. 2002). The data analyzed here are from S. catenatus and S. miliarius only. Within each of these two species, three subspecies are formally described on the basis of morphological variation in scale characters, body size and coloration, and geographic distribution. The three S. catenatus subspecies are S. c. catenatus (C), S. c. tergeminus (T), and S. c. edwardsii (E), whereas the three S. miliarius subspecies are S. m. miliarius (M), S. m. barbouri (B), and S. m. streckeri (S). The data also include sequences from two outgroup species: Agkistrodon contortrix (Ac) and A. piscivorus (Ap). Although the BPP analysis does not require outgroups and those two outgroup species appear quite distant from the ingroup species, we use them as well for easy comparison with the results of Kubatko et al. (2011). We analyze the 18 nuclear loci and the single mitochondrial locus separately, since they have very different characteristics, including different mutation rates and effective population sizes.
The nuclear loci.
Among the 18 loci, the number of sequences per locus ranges from 48 to 52, and the
sequence length ranges from 194 to 849 (Kubatko et al.
2011, table 2). We use the uniform prior
for rooted species trees (Prior 1, Yang and Rannala
2014). For the parameters on the species tree, we use the gamma prior
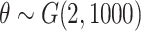 with the prior
mean 0.002 (2 differences per kb), and
with the prior
mean 0.002 (2 differences per kb), and 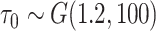 with the prior mean for the age of the root to be 0.012. Those parameters of the shape
parameter (2 and 1.2) specify diffuse gamma priors, while the means are chosen to be
plausible for the data, based on preliminary runs of the A00 analysis
(speciesdelimitation = 0, speciestree = 0) under a reasonable
tree (Yang 2015). We use 8000 iterations for the
burnin, after which we take
with the prior mean for the age of the root to be 0.012. Those parameters of the shape
parameter (2 and 1.2) specify diffuse gamma priors, while the means are chosen to be
plausible for the data, based on preliminary runs of the A00 analysis
(speciesdelimitation = 0, speciestree = 0) under a reasonable
tree (Yang 2015). We use 8000 iterations for the
burnin, after which we take 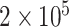 samples, sampling every 4
iterations. We run each analysis twice, with different starting models (species
delimitations and/or species trees), to check for consistency between runs and then
merge the samples to produce posterior summaries. Each run took about 10 hours on one
CPU core. Kubatko et al. (2011) reported running
times of
samples, sampling every 4
iterations. We run each analysis twice, with different starting models (species
delimitations and/or species trees), to check for consistency between runs and then
merge the samples to produce posterior summaries. Each run took about 10 hours on one
CPU core. Kubatko et al. (2011) reported running
times of  10 days using *BEAST in previous
analyses of those data.
10 days using *BEAST in previous
analyses of those data.
Table 2.
Summary of results obtained from BPP analysis of the rattlesnake datasets
| 28 nuc loci, one rate | 28 nuc loci, gamma rate G(2) | ATP (665 bp) | |
|---|---|---|---|
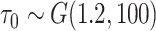
|
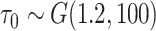
|
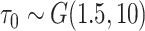
|
|
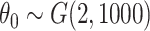
|
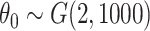
|
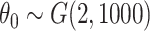
|
|
| A00 estimates | |||
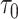 (root) (root) |
0.0125 (0.0097, 0.0154) | 0.0139 (0.0100, 0.0172) | 0.145 (0.127, 0.164) |
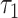 (CET-SMB) (CET-SMB) |
0.0042 (0.0033, 0.0052) | 0.0044 (0.0034, 0.0054) | 0.106 (0.088, 0.124) |
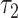 outgroup outgroup |
0.0026 (0.0013, 0.0039) | 0.0026 (0.0014, 0.0039) | 0.062 (0.047, 0.077) |
| A11 analysis | |||
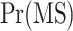
|
0.000 | 0.000 | 0.968 |
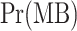
|
0.020 | 0.015 | 0.000 |
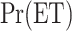
|
0.000 | 0.000 | 0.335 |
|
0.000 | 0.000 | 0.330 |
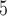
|
0.020 | 0.015 | 0.652 |
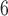
|
0.980 | 0.985 | 0.018 |
| A01 analysis | |||
|
0.696 | 0.608 | 0.013 |
|
0.232 | 0.313 | 0.977 |
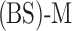
|
0.061 | 0.071 | 0.011 |
We conducted two analyses. In the first, we inferred both the species delimitation and species phylogeny (A11: speciesdelimitation = 1, speciestree = 1). The posterior probability is 98.0% that all the six subspecies are distinct species, with 2% probability that M and B are one species. The best supported phylogeny is shown in Figure 6, and this has posterior probability 69.2%. The next two trees have different relationships for the three subspecies of S. miliarius (B, M, and S) from the MAP 3 of Figure 6, with posterior probability 21.8% for (B, (M, S)), and 6.3% for (M, (B, S)). Together the three trees have a cumulative posterior probability of 97.3% and constitute the 97.3% credible set of the species-delimitation and species-tree models.
In the second analysis (A01: speciesdelimitation = 0, speciestree = 1), we treated the 8 species/subspecies as distinct to infer the species tree. As in the first analysis, the top 3 trees differ concerning the relationships among B, M, and S, with posterior probability 71.0% for ((M, B), S) (the MAP 3 of Fig. 6), 22.4% for (B, (M, S), and 6.1% for (M, (B, S)), with the total posterior for all 3 trees to be 99.5%. Because the A01 analysis evaluates a subset of the models considered in the A11 analysis, the posterior probabilities for the shared models in the two analyses should be proportional.
We applied the algorithm of Equation (15) to calculate the log marginal likelihood values for the top three species
trees, in comparison with the transmodel MCMC analysis (A01). We use
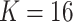 quadrature points, and run 16 MCMC
analyses to generate MCMC samples from the power posteriors. The average log likelihood
for given
quadrature points, and run 16 MCMC
analyses to generate MCMC samples from the power posteriors. The average log likelihood
for given 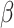 is calculated by averaging over the
MCMC sample. Each MCMC run is an A00 analysis. We use 16,000 iterations for the burnin,
after which we take
is calculated by averaging over the
MCMC sample. Each MCMC run is an A00 analysis. We use 16,000 iterations for the burnin,
after which we take 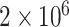 samples, sampling every 4
iterations. Each run used one core and took 2–4 days. The average log likelihood is
plotted in Figure 7a against
samples, sampling every 4
iterations. Each run used one core and took 2–4 days. The average log likelihood is
plotted in Figure 7a against
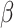 for each species tree. The log
marginal likelihood is then the area under the curve over the interval
for each species tree. The log
marginal likelihood is then the area under the curve over the interval
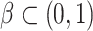 . Equation (15) then gives the log marginal
likelihood values as
. Equation (15) then gives the log marginal
likelihood values as  , and
, and
 for the 3 species trees. With
Prior 1, those species trees have the same prior probability, so that their posterior
probabilities are proportional to their marginal likelihood values. Thus the posterior
probability ratios are
for the 3 species trees. With
Prior 1, those species trees have the same prior probability, so that their posterior
probabilities are proportional to their marginal likelihood values. Thus the posterior
probability ratios are 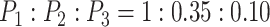 , in
comparison with
, in
comparison with 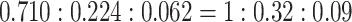 ,
obtained from the transmodel MCMC results in the A01 analysis above. The two approaches
are largely consistent. The discrepancies appear to be due to the inaccuracies in the
marginal likelihood calculation, or in the expectation of the log likelihood across the
MCMC sample from the power posterior.
,
obtained from the transmodel MCMC results in the A01 analysis above. The two approaches
are largely consistent. The discrepancies appear to be due to the inaccuracies in the
marginal likelihood calculation, or in the expectation of the log likelihood across the
MCMC sample from the power posterior.
Figure 7.
Calculation of the marginal likelihood for fixed species trees. The average log
likelihood over the MCMC sample from the power posterior is plotted against the
given 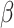 for each fixed species tree. In
a) the 3 alternative species trees for the rattlesnake dataset are compared: MB-S
(which is the MAP tree), MS-B, and BS-M (Fig.
6). The three curves are indistinguishable. In b), the 2 curves are for the
species trees
for each fixed species tree. In
a) the 3 alternative species trees for the rattlesnake dataset are compared: MB-S
(which is the MAP tree), MS-B, and BS-M (Fig.
6). The three curves are indistinguishable. In b), the 2 curves are for the
species trees 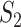 and
and 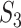 of
Philippine shrews for the UCE dataset (Fig.
8).
of
Philippine shrews for the UCE dataset (Fig.
8).
As the 18 nuclear loci show considerable rate variation (Kubatko et al. 2011, Table 2),
we repeated the analysis using a Gamma-Dirichlet model to account for the mutation rate
variation among loci (Burgess and Yang 2008). The
gamma parameter in the model is fixed at 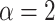 . This has a
small effect on the parameter estimates in the A00 analysis and on the posterior
probabilities on the A11 and A01 analyses. The results are summarized in Table 2.
. This has a
small effect on the parameter estimates in the A00 analysis and on the posterior
probabilities on the A11 and A01 analyses. The results are summarized in Table 2.
We used this dataset to examine the impact of the priors on parameters in the MSC model
(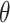 s and
s and 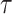 s) on the
posterior probabilities of species trees in the A01 analysis
(speciesdelimitation = 0, speciestree = 1). We treated the
analysis of Table 2 with the priors
s) on the
posterior probabilities of species trees in the A01 analysis
(speciesdelimitation = 0, speciestree = 1). We treated the
analysis of Table 2 with the priors
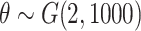 and
and
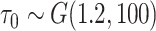 as the “standard”
analysis and changed either the mean or the shape parameter of the gamma prior for
either
as the “standard”
analysis and changed either the mean or the shape parameter of the gamma prior for
either 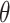 or
or 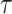 (table 3). In all those analyses, the MAP species tree
and indeed the top three species trees remained the same (table 3). Changes to the prior on
(table 3). In all those analyses, the MAP species tree
and indeed the top three species trees remained the same (table 3). Changes to the prior on 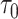 had virtually no
effect on the posterior probabilities of the species trees. In contrast, the
had virtually no
effect on the posterior probabilities of the species trees. In contrast, the
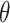 prior had considerable impact.
When the shape parameter for the
prior had considerable impact.
When the shape parameter for the 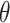 prior is fixed, the prior mean had
a complex effect, with both small and large
prior is fixed, the prior mean had
a complex effect, with both small and large 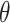 s leading to
reduced support for the MAP species tree. When the prior mean for
s leading to
reduced support for the MAP species tree. When the prior mean for
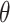 is fixed, larger shape parameters
(or highly concentrated priors) led to increased posterior for the MAP tree. Previously
Leaché and Rannala (2011) highlighted the
impact of the
is fixed, larger shape parameters
(or highly concentrated priors) led to increased posterior for the MAP tree. Previously
Leaché and Rannala (2011) highlighted the
impact of the 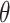 prior on species tree inference by
the Bayesian method BEST (Liu 2008), finding that
misspecified priors produced inflated posterior probabilities for species trees.
prior on species tree inference by
the Bayesian method BEST (Liu 2008), finding that
misspecified priors produced inflated posterior probabilities for species trees.
Table 3.
The impact of the priors for parameters in the MSC model on posterior probabilities of species trees in the BPP analysis of the rattlesnake dataset (18 nuclear loci)
| Species tree (Fig. 6a) | (MB)-S | (MS)-B | (BS)-M |
|---|---|---|---|
Prior mean for 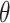 , with , with
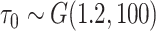
|
|||
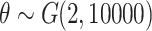 ,
with mean 0.0002 ,
with mean 0.0002 |
0.57 | 0.31 | 0.10 |
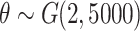 ,
with mean 0.0004 ,
with mean 0.0004
|
0.42 | 0.50 | 0.08 |
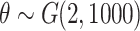 ,
with mean 0.002 ,
with mean 0.002 |
0.70 | 0.23 | 0.06 |
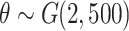 ,
with mean 0.004 ,
with mean 0.004 |
0.69 | 0.22 | 0.08 |
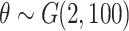 ,
with mean 0.02 ,
with mean 0.02 |
0.51 | 0.30 | 0.20 |
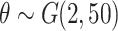 , with
mean 0.04 , with
mean 0.04 |
0.42 | 0.33 | 0.24 |
Prior shape for 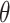 , with , with
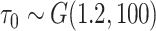
|
|||
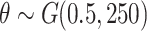 ,
with mean 0.002 ,
with mean 0.002 |
0.65 | 0.27 | 0.08 |
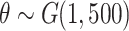 ,
with mean 0.002 ,
with mean 0.002 |
0.69 | 0.24 | 0.06 |
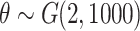 ,
with mean 0.002 ,
with mean 0.002 |
0.70 | 0.23 | 0.06 |
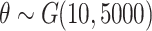 ,
with mean 0.002 ,
with mean 0.002 |
0.82 | 0.12 | 0.05 |
Prior mean for  , with , with
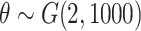
|
|||
 ,
with mean 0.0012 ,
with mean 0.0012 |
0.71 | 0.22 | 0.06 |
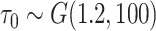 ,
with mean 0.012 ,
with mean 0.012 |
0.71 | 0.22 | 0.06 |
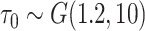 ,
with mean 0.12 ,
with mean 0.12 |
0.70 | 0.23 | 0.06 |
Prior shape for  , with , with
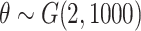
|
|||
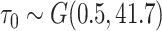 ,
with mean 0.012 ,
with mean 0.012 |
0.71 | 0.23 | 0.06 |
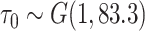 ,
with mean 0.012 ,
with mean 0.012 |
0.71 | 0.22 | 0.06 |
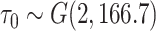 ,
with mean 0.012 ,
with mean 0.012 |
0.70 | 0.23 | 0.06 |
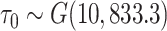 ,
with mean 0.012 ,
with mean 0.012 |
0.70 | 0.23 | 0.06 |
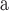 In the analysis using the priors
In the analysis using the priors 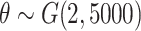 and
and
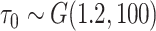 , there is
posterior uncertainty concerning the relationships of E, T, and C, as well as
uncertainties concerning M, B, and S. The 95% HPD set consists of 7 species
trees: (B(MS))-(C(ET)), with posterior 36%, (S(MB))-(C(ET)) with 30%,
(B(MS))-(E(CT)) with 10%, (S(MB))-(E(CT)) with 8%, (M(BS))-(C(ET)) with 6%,
(B(MS))-(T(CE)) with 5%, and (S(MB))-(T(CE)) with 4%. In all other analyses
listed in the table, only the 3 species trees that correspond to the different
resolutions of M, B, and C have substantial probabilities.
, there is
posterior uncertainty concerning the relationships of E, T, and C, as well as
uncertainties concerning M, B, and S. The 95% HPD set consists of 7 species
trees: (B(MS))-(C(ET)), with posterior 36%, (S(MB))-(C(ET)) with 30%,
(B(MS))-(E(CT)) with 10%, (S(MB))-(E(CT)) with 8%, (M(BS))-(C(ET)) with 6%,
(B(MS))-(T(CE)) with 5%, and (S(MB))-(T(CE)) with 4%. In all other analyses
listed in the table, only the 3 species trees that correspond to the different
resolutions of M, B, and C have substantial probabilities.
The mitochondrial locus (ATP, 665 bp).
The parameters on the species tree are assigned the following priors:
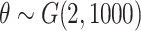 with the prior
mean 0.002 and
with the prior
mean 0.002 and 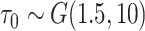 with the prior
mean 0.15. All other settings are the same as for the analysis of the nuclear loci. The
mitochondrial locus favored 5 species, with M and S grouped into one species in all
analyses, in contrast to the nuclear loci, which supported the distinct species status
of all the 6 subspecies (Table 2). Similarly, the
A01 analysis groups M and S together with posterior probability 97.7%. The A00 estimates
of species divergence times (
with the prior
mean 0.15. All other settings are the same as for the analysis of the nuclear loci. The
mitochondrial locus favored 5 species, with M and S grouped into one species in all
analyses, in contrast to the nuclear loci, which supported the distinct species status
of all the 6 subspecies (Table 2). Similarly, the
A01 analysis groups M and S together with posterior probability 97.7%. The A00 estimates
of species divergence times ( ) are shown in Figure 6c. The branches in the mitochondrial species tree are much
longer than for the nuclear loci, indicating that the mitochondrial locus has a much
higher mutation rate. As a result, the single mitochondrial locus appears to be at least
as informative as the 18 nuclear loci.
) are shown in Figure 6c. The branches in the mitochondrial species tree are much
longer than for the nuclear loci, indicating that the mitochondrial locus has a much
higher mutation rate. As a result, the single mitochondrial locus appears to be at least
as informative as the 18 nuclear loci.
The estimated species trees from the nuclear and mitochondrial data have strikingly
different shapes. Relative to the root of the tree, the mitochondrial species tree has
much older nodes for separation of S. catenatus and S.
miliarius, and for the separation of the the 2 outgroup species: A.
contortrix and A. piscivorus. In the simplistic model of
random mating and neutral evolution of both nuclear and mitochondrial loci, the species
divergence time parameters ( s) should be proportional for the
nuclear and mitochondrial loci. The ratio of the posterior means of the species
divergence times (
s) should be proportional for the
nuclear and mitochondrial loci. The ratio of the posterior means of the species
divergence times ( s) between the mitochondrial locus
and the nuclear loci is 12 for the root of the species tree, 25 for the common ancestor
of S. catenatus and S. miliarius, and 24 for the
divergence of the 2 outgroup species: A. contortrix and A.
piscivorus. If the absolute species divergence times are the same for the
nuclear and mitochondrial genomes, those estimates indicate that the mitochondrial
mutation rate is 12–25 times as high as the nuclear mutation rate. With such mutation
rate differences and if the mitochondrial population size is
s) between the mitochondrial locus
and the nuclear loci is 12 for the root of the species tree, 25 for the common ancestor
of S. catenatus and S. miliarius, and 24 for the
divergence of the 2 outgroup species: A. contortrix and A.
piscivorus. If the absolute species divergence times are the same for the
nuclear and mitochondrial genomes, those estimates indicate that the mitochondrial
mutation rate is 12–25 times as high as the nuclear mutation rate. With such mutation
rate differences and if the mitochondrial population size is 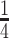 that for the nuclear loci, we would expect the population size parameters on the species
tree (
that for the nuclear loci, we would expect the population size parameters on the species
tree (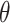 s) for the mitochondrial locus to
be 3–6 times as large as those for the nuclear loci. Yet, the average of the posterior
means for
s) for the mitochondrial locus to
be 3–6 times as large as those for the nuclear loci. Yet, the average of the posterior
means for 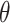 s over the populations on the
species tree is 0.0019 for the mitochondrial locus and 0.0037 for the nuclear genes,
with a ratio of 0.51 (Fig. 6), whereas the average
of the ratios is 0.81. Thus the mitochondrial
s over the populations on the
species tree is 0.0019 for the mitochondrial locus and 0.0037 for the nuclear genes,
with a ratio of 0.51 (Fig. 6), whereas the average
of the ratios is 0.81. Thus the mitochondrial 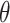 s are far smaller
than expected from the simple neutral model. In summary, both the fact that the
s are far smaller
than expected from the simple neutral model. In summary, both the fact that the
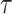 estimates are not proportional between
the nuclear and mitochondrial loci and the fact that the
estimates are not proportional between
the nuclear and mitochondrial loci and the fact that the 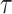 and
and
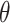 estimates are not proportional
suggest that the differences between the nuclear and mitochondrial loci cannot be
entirely explained by differences in mutation rates and population sizes alone, and the
idealized model does not fit the data. We suggest that extending the mitochondrial locus
and sequencing more nuclear loci may be useful for understanding the major factors
causing the conflicting signals.
estimates are not proportional
suggest that the differences between the nuclear and mitochondrial loci cannot be
entirely explained by differences in mutation rates and population sizes alone, and the
idealized model does not fit the data. We suggest that extending the mitochondrial locus
and sequencing more nuclear loci may be useful for understanding the major factors
causing the conflicting signals.
Kubatko et al. (2011) conducted a number of phylogenetic and coalescent-based analyses of the same data. The coalescent-based analyses used the heuristic method STEM (Kubatko et al. 2009) and the Bayesian MCMC method *BEAST (Heled and Drummond 2010). The 18 nuclear loci and the mitochondrial locus were analyzed as one single dataset. The species tree inferred in the *BEAST analysis is the tree shown in Figure 6c, with a posterior probability 0.93 for the M-S grouping. This may be explained by the fact that the mitochondrial locus has a much higher mutation rate so that the signal from the single mitochondrial locus has dominated the analysis when the nuclear and mitochondrial loci are analyzed together. Note that in our BPP analysis, the relationships among B, M, and S are uncertain, and the mitochondrial locus favors the M-S grouping (Fig. 6c and Table 2). Overall our results are largely consistent with those of Kubatko et al. (2011).
Analysis of Philippine Shrew Datasets
We used BPP to analyze one real and three simulated datasets for Philippine shrews (genus
Crocidura), published and analyzed previously by Giarla and Esselstyn (2015). Those authors sequenced ultra-conserved
elements (UCEs) from 19 individuals representing 7 species of Philippine shrews:
C. palawanensis (Pl), C. beatus (B), C.
mindorus (M), C. grayi (G), C. panayensis
(Pn), C. negrina (Ne), and C. ninoyi (Ni), as well as an
Indonesian outgroup species, C. orientalis (O) (Fig. 8). They generated 1112 UCEs, but 193 of them contained no
parsimony-informative sites and were excluded, leaving 919 loci in the dataset. There are
up to 19 sequences at each locus, the alignment length ranges from 232 to 1069 sites among
loci (with median 706), and the number of parsimony-informative sites ranges from 1 to 17
(with median 2). The authors’ phylogenetic analysis suggested that a specimen from
C. ninoyi represented a new species and is treated as a distinct
species in the analysis, C. sp (S). To evaluate the reliability of
species tree estimation, Giarla and Esselstyn
(2015) simulated 3 datasets by using parameter estimates under the MSC
(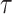 s and
s and 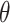 s)
obtained from the UCE data. These are referred to as Sim1-Matching, Sim2-Multi, and Sim3x,
each having 500 loci and 700 bp in the alignment per locus. Sim1-Matching matches the
characteristics of the UCE dataset, with 19 sequences per locus. Sim2-Multi includes five
sequences per species (with 45 sequences per locus) and was used to assess the effect of
increased sequence sampling. Sim3x was generated by increasing the
s)
obtained from the UCE data. These are referred to as Sim1-Matching, Sim2-Multi, and Sim3x,
each having 500 loci and 700 bp in the alignment per locus. Sim1-Matching matches the
characteristics of the UCE dataset, with 19 sequences per locus. Sim2-Multi includes five
sequences per species (with 45 sequences per locus) and was used to assess the effect of
increased sequence sampling. Sim3x was generated by increasing the
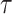 s by 3-fold while keeping the
s by 3-fold while keeping the
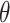 s unchanged, and was used to examine
the impact of increased mutation rate and increased phylogenetic information per locus.
Giarla and Esselstyn (2015) used 4 methods of
species tree estimation to analyze each of the 4 datasets (UCE and 3 simulated datasets):
(i) concatenation with MrBayes, two summary coalescent-based methods: (ii) MulRF (Chaudhary et al. 2013) and (iii) ASTRAL (Mirarab and Warnow 2015), and (iv) the Bayesian
coalescent method *BEAST (Heled and Drummond 2010).
For *BEAST, Giarla and Esselstyn (2015) divided
each of the four datasets into subsets of 50 loci, as they observed “little evidence of
convergence in analyses of more than 50 loci in *BEAST, even after billions of MCMC
generations.”
s unchanged, and was used to examine
the impact of increased mutation rate and increased phylogenetic information per locus.
Giarla and Esselstyn (2015) used 4 methods of
species tree estimation to analyze each of the 4 datasets (UCE and 3 simulated datasets):
(i) concatenation with MrBayes, two summary coalescent-based methods: (ii) MulRF (Chaudhary et al. 2013) and (iii) ASTRAL (Mirarab and Warnow 2015), and (iv) the Bayesian
coalescent method *BEAST (Heled and Drummond 2010).
For *BEAST, Giarla and Esselstyn (2015) divided
each of the four datasets into subsets of 50 loci, as they observed “little evidence of
convergence in analyses of more than 50 loci in *BEAST, even after billions of MCMC
generations.”
Here we analyze the 4 datasets using the new version of BPP. Giarla and Esselstyn (2015) used model testing to identify the
appropriate substitution model for every locus and encountered numerical problems as the
data lack information to estimate the rate parameters in the parameter-rich models such as
the GTR (Tavare 1986; Yang 1994). We bypassed this mechanical process of model selection and
used JC69 (Jukes and Cantor 1969) throughout. The
main role of the mutation/substitution model in such analysis is to correct for multiple
changes at the same site to extract information about the gene tree topology and branch
lengths at every locus. For such highly similar sequences, JC69 should be adequate (Satta et al. 2004; Burgess and Yang 2008). For datasests Sim1, Sim2, and UCE, we assign the gamma
prior  , with mean 0.002
(two mutations per kb) for the age of the root of the species tree (Yang and Rannala 2010, Equation 2), and
, with mean 0.002
(two mutations per kb) for the age of the root of the species tree (Yang and Rannala 2010, Equation 2), and 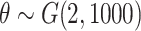 for all
for all
 parameters. For Sim3x, we used
parameters. For Sim3x, we used
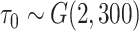 and
and
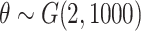 . We used a burn-in
of 32,000 iterations, and took
. We used a burn-in
of 32,000 iterations, and took 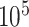 samples, sampling every 4 iterations.
For each analysis of the simulated datasets, the program was run 3 times using different
starting species trees. Each run (on a single core) took about 1 day for Sim1 and Sim3,
and 3–4 days for Sim2. Longer chains were run for the UCE dataset, as reported below.
samples, sampling every 4 iterations.
For each analysis of the simulated datasets, the program was run 3 times using different
starting species trees. Each run (on a single core) took about 1 day for Sim1 and Sim3,
and 3–4 days for Sim2. Longer chains were run for the UCE dataset, as reported below.
Dataset Sim1-Matching (500 loci).
The three BPP runs using different starting species trees produced the same MAP tree
(Fig. 8a), with the posterior probability varying
from 0.42 to 0.46 among the runs, indicating that the 3 chains have converged to the
equilibrium distribution. The 3 MCMC samples were then merged and summarized. The MAP
tree from the combined sample, which is also the majority-rule consensus tree, had the
posterior 45% (Fig. 8a). This is also the true
species tree used to simulate the dataset by Giarla and
Esselstyn (2015). The posterior for the nodes are shown in Figure 8a. The top 3 species trees are different resolutions of the 3
clades, S, B, and PNN, where PNN stands for the ((Pn, Ne), Ni) clade. Their posterior
probabilities are 45% for (S, (B, PNN)) (i.e., the true species tree
 of Fig.
8a), 22% for ((B, S), PNN), and 19% for ((S, PNN), B), so that those 3 trees
constitute the 85% credible set. In the analysis of the same data by Giarla and Esselstyn (2015, Figs. 3–6), all the 4 methods the
authors used, including concatenation/MrBayes, MulRF, ASTRAL, and *BEAST, inferred at
least one incorrect node, whereas concatenation produced the posterior 100% for the
wrong tree. Thus BPP is the only method that recovered the true species tree for this
dataset, although the support for two nodes is low. The posterior means and 95% highest
posterior density (HPD) intervals for the node ages (
of Fig.
8a), 22% for ((B, S), PNN), and 19% for ((S, PNN), B), so that those 3 trees
constitute the 85% credible set. In the analysis of the same data by Giarla and Esselstyn (2015, Figs. 3–6), all the 4 methods the
authors used, including concatenation/MrBayes, MulRF, ASTRAL, and *BEAST, inferred at
least one incorrect node, whereas concatenation produced the posterior 100% for the
wrong tree. Thus BPP is the only method that recovered the true species tree for this
dataset, although the support for two nodes is low. The posterior means and 95% highest
posterior density (HPD) intervals for the node ages ( s)
obtained from the BPP analysis are shown in Figure
8a. The posterior means are close to the true values used in the
simulation.
s)
obtained from the BPP analysis are shown in Figure
8a. The posterior means are close to the true values used in the
simulation.
Dataset Sim2-Multi (500 loci).
The 3 BPP runs using different starting species trees converged to the same
neighborhood of the species tree space, visiting 3 species trees that correspond to
different relationships among the 3 clades, S, B, and PNN in species tree
 (Fig.
8a). The posteriors for the 3 resolutions were about 40% for (S, (B, PNN)),
which is the true tree
(Fig.
8a). The posteriors for the 3 resolutions were about 40% for (S, (B, PNN)),
which is the true tree 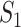 , 40% for (B, (S, PNN)), and 20% for
((B, S), PNN). In other words, node 1 in the true tree
, 40% for (B, (S, PNN)), and 20% for
((B, S), PNN). In other words, node 1 in the true tree  is not
well-resolved, whereas all other nodes are recovered with posterior probability
is not
well-resolved, whereas all other nodes are recovered with posterior probability
 . Compared with Sim1, for which
the MAP tree has two uncertain nodes, the increased sequence sampling (to five sequences
per species) in Sim2 helped to resolve one of the two uncertain nodes, but the other
remains unresolved. We note that all 4 methods used by Giarla and Esselstyn (2015, Figs. 3–6), including concatenation, MulRF, ASTRAL, and *BEAST,
inferred at least one incorrect node for this dataset, with concatenation to be the only
method that gave a 100% support for the wrong tree. In the BPP analysis, the true
species tree is one of the top two nearly equally good trees.
. Compared with Sim1, for which
the MAP tree has two uncertain nodes, the increased sequence sampling (to five sequences
per species) in Sim2 helped to resolve one of the two uncertain nodes, but the other
remains unresolved. We note that all 4 methods used by Giarla and Esselstyn (2015, Figs. 3–6), including concatenation, MulRF, ASTRAL, and *BEAST,
inferred at least one incorrect node for this dataset, with concatenation to be the only
method that gave a 100% support for the wrong tree. In the BPP analysis, the true
species tree is one of the top two nearly equally good trees.
Dataset Sim3x (500 loci).
The 3 runs using different starting species trees converged to the same MAP tree, which
is the true tree  (Fig.
8a). The posterior ranged from 0.996 to 0.999 among the 3 runs, and was 0.997
in the combined sample. In this dataset, all 4 methods used by Giarla and Esselstyn (2015) produced the true tree as the estimate.
By increasing the node ages by three folds and keeping the population sizes unchanged,
the impact of ancestral polymorphism and incomplete lineage sorting is reduced while the
sequences at every locus are more divergent and contain more phylogenetic information.
As a result Sim3x is far more informative than Sim1.
(Fig.
8a). The posterior ranged from 0.996 to 0.999 among the 3 runs, and was 0.997
in the combined sample. In this dataset, all 4 methods used by Giarla and Esselstyn (2015) produced the true tree as the estimate.
By increasing the node ages by three folds and keeping the population sizes unchanged,
the impact of ancestral polymorphism and incomplete lineage sorting is reduced while the
sequences at every locus are more divergent and contain more phylogenetic information.
As a result Sim3x is far more informative than Sim1.
The real UCE dataset (919 loci).
With 919 loci and with many ambiguity characters in the sequence alignments, the UCE
dataset was found to be more challenging to analyze than the 3 simulated datasets.
Indeed our analysis of this dataset using BPP was not entirely successful, and the
program showed mixing problems. We report our analysis of this dataset nevertheless,
partly to illustrate the computational difficulties encountered and the techniques for
their diagnosis. We conducted 6 initial runs with different (and poor) starting species
trees, with a burn-in of 32,000 iterations, and took 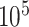 samples,
sampling every 10 iterations. Those runs suggested that 6 species trees had substantial
posterior probabilities. Three of them were different resolutions around node 1 in
species tree
samples,
sampling every 10 iterations. Those runs suggested that 6 species trees had substantial
posterior probabilities. Three of them were different resolutions around node 1 in
species tree  (Fig.
8b) concerning the relationships among the clades B, S, and PNN, whereas the
other three were different resolutions around node 1 in species tree
(Fig.
8b) concerning the relationships among the clades B, S, and PNN, whereas the
other three were different resolutions around node 1 in species tree
 (Fig.
8c) concerning the relationships among the clades S, PNN, and MG, where MG
stands for the (M, G) clade. We then conducted 6 further runs, using those 6 (good)
species trees as the starting tree, and the same settings otherwise. Each run (on a
single core) took 6–10 days.
(Fig.
8c) concerning the relationships among the clades S, PNN, and MG, where MG
stands for the (M, G) clade. We then conducted 6 further runs, using those 6 (good)
species trees as the starting tree, and the same settings otherwise. Each run (on a
single core) took 6–10 days.
The 3 runs that started using the different relationships of S, B, and PNN in
 (Fig.
8b) produced similar results, visiting the 3 species trees that correspond to
different resolutions of node 1 in
(Fig.
8b) produced similar results, visiting the 3 species trees that correspond to
different resolutions of node 1 in 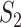 . The MAP tree was
. The MAP tree was
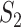 : (B, (S, PNN)), and the posterior
ranged from 70–77% among the three runs. The three samples combined gave the relative
proportions 73% for
: (B, (S, PNN)), and the posterior
ranged from 70–77% among the three runs. The three samples combined gave the relative
proportions 73% for 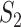 : (B, (S, PNN)), 24% for
: (B, (S, PNN)), 24% for
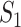 : (S, (B, PNN)), and 3% for ((S, B),
PNN).
: (S, (B, PNN)), and 3% for ((S, B),
PNN).
The 3 runs that started with the different relationships among S, PNN, and MG in
species tree 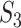 (Fig.
8c) produced similar results among them, visiting the 3 species trees that are
different resolutions of node 1 in
(Fig.
8c) produced similar results among them, visiting the 3 species trees that are
different resolutions of node 1 in 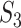 . The MAP tree had the relationship
. The MAP tree had the relationship
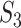 (Fig.
8c): (MG, (S, PNN)), and the posterior ranged from 71–80% among the runs. The 3
samples combined gave the relative posteriors 76% for
(Fig.
8c): (MG, (S, PNN)), and the posterior ranged from 71–80% among the runs. The 3
samples combined gave the relative posteriors 76% for 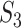 : (MG, (S,
PNN)), 21% for
: (MG, (S,
PNN)), 21% for 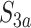 : (PNN, (S, MG)), and 3% for
: (PNN, (S, MG)), and 3% for
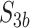 : (S, (MG, PNN)).
: (S, (MG, PNN)).
However, BPP had difficulty moving between the two sets of species trees. Note that
species trees 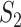 and
and 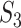 differ by
a single NNI move (around node 2 in either tree, Fig.
8b and c), and should be reachable by both SPR and NodeSlider moves. We leave
it to future research to investigate the precise reasons for the failure of the chains
to move between the two sets of trees and to design improved algorithms. The mixing
problem means that the MCMC runs reported here cannot be used to estimate the posterior
probabilities for the 6 species trees, or to decide whether
differ by
a single NNI move (around node 2 in either tree, Fig.
8b and c), and should be reachable by both SPR and NodeSlider moves. We leave
it to future research to investigate the precise reasons for the failure of the chains
to move between the two sets of trees and to design improved algorithms. The mixing
problem means that the MCMC runs reported here cannot be used to estimate the posterior
probabilities for the 6 species trees, or to decide whether 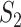 or
or
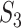 has the highest posterior and is the
MAP tree.
has the highest posterior and is the
MAP tree.
We applied the algorithm of Equation (15) to calculate the log marginal likelihood values for species trees
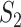 and
and 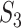 , using
, using
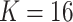 Gauss–Legendre points. For each of
the 16 MCMC runs to approximate the power posteriors, we use 8000 iterations for the
burnin, after which we take
Gauss–Legendre points. For each of
the 16 MCMC runs to approximate the power posteriors, we use 8000 iterations for the
burnin, after which we take 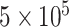 samples, sampling every 2
iterations. Each run took 4–6 days on a single core. The average log likelihood over the
MCMC sample is plotted in Figure 7. This
calculation gave the log marginal likelihood ratio
samples, sampling every 2
iterations. Each run took 4–6 days on a single core. The average log likelihood over the
MCMC sample is plotted in Figure 7. This
calculation gave the log marginal likelihood ratio 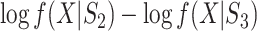 or log Bayes
factor to be
or log Bayes
factor to be 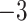 , which translates to the posterior
probability ratio
, which translates to the posterior
probability ratio 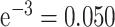 . This posterior
probability ratio can be used to convert the relative posteriors calculated from the
MCMC runs discussed above into (absolute) posterior probabilities for the 2 sets of
species trees. The posteriors for the top 4 species trees were then
. This posterior
probability ratio can be used to convert the relative posteriors calculated from the
MCMC runs discussed above into (absolute) posterior probabilities for the 2 sets of
species trees. The posteriors for the top 4 species trees were then
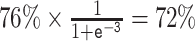 for
for 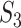 : (MG, (S, PNN)), 20% for
: (MG, (S, PNN)), 20% for
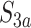 : (PNN, (S, MG)), 3% for
: (PNN, (S, MG)), 3% for
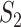 (Fig.
8b) and 3% for
(Fig.
8b) and 3% for 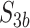 : (S, (MG, PNN)).
: (S, (MG, PNN)).
However, we note that the average log likelihood of Figure 7 was poorly estimated by the MCMC sample for the 2 smallest values of
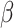 (0.0053 and 0.0271), when the power
posterior is close to the prior. Our conclusion that species tree
(0.0053 and 0.0271), when the power
posterior is close to the prior. Our conclusion that species tree
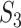 is the MAP tree is thus a tentative
one. We note that node 2 in
is the MAP tree is thus a tentative
one. We note that node 2 in 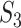 has a longer branch than node 2 in
has a longer branch than node 2 in
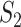 (Fig.
8), which supports the notion that
(Fig.
8), which supports the notion that 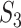 is more probable than
is more probable than
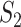 .
.
Certain phylogenetic relationships are supported in all BPP runs, with 100% posterior,
and they were also found in the analyses of (Giarla and
Esselstyn 2015). First, among all the species endemic to Philippine, C.
palawanensis (Pl) diverged the earliest. Second, C. mindorus
(M), C. grayi (G) form a clade. Third, C. panayensis
(Pn), C. negrina (Ne), and C. ninoyi (Ni) form a
clade, with the relationship ((Pn, Ne), Ni) inside the clade. It is also certain that
the MAP tree found in the BPP analysis is different from the best estimate that Giarla and Esselstyn (2015) obtained using
alternative methods. As mentioned earlier, the best species tree found by Giarla and
Esselstyn was 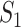 . This had a lower posterior
probability than
. This had a lower posterior
probability than 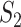 in the BPP analysis, while
in the BPP analysis, while
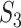 appeared to be the MAP tree.
appeared to be the MAP tree.
We also note that the posterior estimates of parameters under the MSC (the
 s and
s and 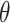 s)
suggest short internal branches in the species trees (Fig.
8a–c) and small effective population sizes for the ancestors (Fig. 8c; see also Giarla and Esselstyn 2015, Appendix 3). These indicate several radiative
speciation events following the colonization of Philippines, with the new species
founded by very small populations.
s)
suggest short internal branches in the species trees (Fig.
8a–c) and small effective population sizes for the ancestors (Fig. 8c; see also Giarla and Esselstyn 2015, Appendix 3). These indicate several radiative
speciation events following the colonization of Philippines, with the new species
founded by very small populations.
Discussion
Statistical Performance of BPP
Our simulation results suggest that the likelihood-based species tree inference method under the MSC, implemented in BPP, has both high precision (as indicated by the small credible set) and high accuracy (as indicated by the high coverage probability of the credible set). For the parameter combinations examined in our simulations, the correct species tree is recovered with high posterior probabilities when 10 loci are included in the dataset. The high power of the method is in contrast to the heuristic coalescent methods which use reconstructed gene tree topologies to infer the species tree, ignoring both random and systematic errors in tree reconstruction and ignoring information in the gene-tree branch lengths, leading to loss of power. Our results are consistent with several previous studies, which suggest that heuristic methods based on summary statistics such as estimated gene tree topologies can be much less efficient than full likelihood methods (Leaché and Rannala 2011; Liu et al. 2015; Ogilvie et al. 2016).
This conclusion is also apparent in the comparison of our BPP analysis of the three
simulated datasets of Giarla and Esselstyn (2015)
with those authors’ analysis of the same data using four competing methods. Concatenation
produced 100% support for every node in the species tree in each dataset, but one of the
inferred nodes was incorrect in Sim1 and Sim2 (Giarla and
Esselstyn 2015, Fig. 3), so that the high
confidence is spurious. Previous simulation and analysis of Kubatko and Degnan (2007) and Roch and
Steel (2015) suggest that in certain areas of the parameter space (certain
species trees and values of 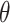 s and
s and 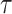 s),
concatenation may be statistically inconsistent, converging to an incorrect species tree
when the number of loci approaches infinity. The two heuristic coalescent methods, MulRF
(Chaudhary et al. 2013) and ASTRAL (Mirarab and Warnow 2015), inferred more nodes
incorrectly or produced lower support values for true nodes on the species tree than BPP
(Giarla and Esselstyn 2015, Figs. 4 and 5). The *BEAST analysis
of Giarla and Esselstyn (2015) used small data
subsets of 50 loci, producing many unresolved or uncertain nodes, whereas our BPP analysis
used the full datasets, so that the results cannot be used to make a sensible comparison
of the statistical performance of the two programs.
s),
concatenation may be statistically inconsistent, converging to an incorrect species tree
when the number of loci approaches infinity. The two heuristic coalescent methods, MulRF
(Chaudhary et al. 2013) and ASTRAL (Mirarab and Warnow 2015), inferred more nodes
incorrectly or produced lower support values for true nodes on the species tree than BPP
(Giarla and Esselstyn 2015, Figs. 4 and 5). The *BEAST analysis
of Giarla and Esselstyn (2015) used small data
subsets of 50 loci, producing many unresolved or uncertain nodes, whereas our BPP analysis
used the full datasets, so that the results cannot be used to make a sensible comparison
of the statistical performance of the two programs.
Computational Challenges and MCMC Diagnostics
The computational requirement of Bayesian MCMC methods tends to increase with the
increase in the number of species/populations, the number of loci, the number of sequences
per locus, and the number of sites per sequence. The number of species may have the
greatest impact, because more species mean many more species trees with a much expanded
parameter space, whereas the number of sites is the least important. The increased
computational effort may manifest itself in two ways. First, with more data, each
iteration of the MCMC algorithm takes more computation, mainly because the phylogenetic
likelihood (the probability of observing the sequence alignment at the locus given the
gene tree and coalescent times) is more expensive. In typical data analysis, the
likelihood calculation accounts for most (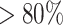 ) of the CPU time.
The likelihood calculation on a gene tree grows roughly linearly with the number of
sequences, and less than linearly with the number of sites in the sequence, although more
sequences at each locus also imply more gene trees and branch lengths to average over.
Second, with more data, the posterior distribution of the parameters
(
) of the CPU time.
The likelihood calculation on a gene tree grows roughly linearly with the number of
sequences, and less than linearly with the number of sites in the sequence, although more
sequences at each locus also imply more gene trees and branch lengths to average over.
Second, with more data, the posterior distribution of the parameters
(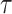 s and
s and 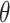 s) under
each species tree becomes more highly concentrated, and as a result it becomes more
difficult to move from one species tree to another in the transmodel MCMC algorithm, and
many more iterations will be necessary to allow adequate sampling of the posterior. If the
proposed parameter values for the new species tree are not good, the proposal will be
rejected even if the new species tree has a higher posterior probability than the current
species tree. This second problem of poor mixing is a far greater challenge than the first
problem of more expensive likelihood calculation per MCMC iteration. This article
continues our effort in designing smart transmodel moves to improve the mixing efficiency
of the MCMC. The superiority of the SPR and nodeslider moves over NNI is that they allow
the transition between species trees that were not direct neighbors by the NNI algorithm,
which is important especially during the early stage of the MCMC algorithm or when the
starting species trees is poor. The empirical rattlesnake and shrew datasets analyzed in
this article were found to be beyond the limit of the NNI algorithm we implemented earlier
(Yang and Rannala 2014). Roughly speaking, the
improvements made in this study appear to have increased the limit of the program from
about 20–100 loci (with
s) under
each species tree becomes more highly concentrated, and as a result it becomes more
difficult to move from one species tree to another in the transmodel MCMC algorithm, and
many more iterations will be necessary to allow adequate sampling of the posterior. If the
proposed parameter values for the new species tree are not good, the proposal will be
rejected even if the new species tree has a higher posterior probability than the current
species tree. This second problem of poor mixing is a far greater challenge than the first
problem of more expensive likelihood calculation per MCMC iteration. This article
continues our effort in designing smart transmodel moves to improve the mixing efficiency
of the MCMC. The superiority of the SPR and nodeslider moves over NNI is that they allow
the transition between species trees that were not direct neighbors by the NNI algorithm,
which is important especially during the early stage of the MCMC algorithm or when the
starting species trees is poor. The empirical rattlesnake and shrew datasets analyzed in
this article were found to be beyond the limit of the NNI algorithm we implemented earlier
(Yang and Rannala 2014). Roughly speaking, the
improvements made in this study appear to have increased the limit of the program from
about 20–100 loci (with  sequences per locus) to about
200–1000 loci.
sequences per locus) to about
200–1000 loci.
One caveat to this discussion is the effect of the data size on the posterior
probabilities of species trees. If we simulate datasets with the species tree (and the
number of species) fixed, increasing the number of loci or the number of sequences per
locus (and, to a lesser extent, the number of sites per sequence) will increase the
probability of recovering the true tree, so that a single species tree may dominate the
MCMC algorithm, with posterior about  in every dataset. In such a scenario,
multiple runs that start from different species trees may converge quickly to the same
species tree, and the computation may be even less problematic than in smaller datasets in
which many species trees have substantial posterior probabilities.
in every dataset. In such a scenario,
multiple runs that start from different species trees may converge quickly to the same
species tree, and the computation may be even less problematic than in smaller datasets in
which many species trees have substantial posterior probabilities.
Note that the acceptance proportion of cross-tree moves is not a reliable indicator of
the mixing performance of the transmodel MCMC algorithm, and an acceptance proportion of
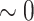 may not necessarily imply a mixing
problem. If the MAP tree has posterior near 100%, the chain should stay in that species
tree nearly 100% of the time and all proposals to change the species tree should be
rejected. Although a poorly mixing chain may be stuck in one species tree, leading to an
acceptance proportion of
may not necessarily imply a mixing
problem. If the MAP tree has posterior near 100%, the chain should stay in that species
tree nearly 100% of the time and all proposals to change the species tree should be
rejected. Although a poorly mixing chain may be stuck in one species tree, leading to an
acceptance proportion of 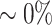 as well, the two scenarios can
easily be distinguished by running multiple chains with different starting species trees.
Indeed we have found that the most effective way of diagnosing a transmodel MCMC algorithm
is to run the same analysis multiple times, starting with different species trees and
parameter values.
as well, the two scenarios can
easily be distinguished by running multiple chains with different starting species trees.
Indeed we have found that the most effective way of diagnosing a transmodel MCMC algorithm
is to run the same analysis multiple times, starting with different species trees and
parameter values.
Similarly we suggest that the consistency among multiple runs starting with different species trees and parameter values be used as the major criterion for determining the length of the MCMC run, including the burn-in, the sampling frequency, and the number of samples. If the starting species trees are poor (e.g., a random species tree), it will take a long time for the MCMC algorithm to converge to the posterior distribution, so that a long burn-in is required. Good starting species trees—for example, those generated by concatenation or heuristic species tree methods such as MP-EST (Liu et al. 2010) or ASTRAL (Mirarab and Warnow 2015)—may be used to shorten the burn-in, but one should be aware of the risk of missing species trees with high posterior probabilities. We suggest that in the initial stage of exploratory analysis, very different starting species trees including poor ones should be used with long burn-ins to explore the posterior space. Later analysis may use good starting species trees with relatively short burn-ins to sample extensively from the posterior. This is the strategy taken in our analysis of the rattlesnake and Philippine shrew datasets in this article.
Note that MCMC iterations in different programs are not comparable. For example, MRBAYES
and BEAST sample one parameter to update in each iteration, whereas BPP updates all
parameters in the model one by one in each iteration, so that one iteration in BPP may be
worth 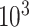 iterations in MRBAYES or BEAST. Note
also that the effective sample size (ESS) calculated using the log likelihood value is not
useful for diagnosing transmodel MCMC algorithms for species tree inference.
iterations in MRBAYES or BEAST. Note
also that the effective sample size (ESS) calculated using the log likelihood value is not
useful for diagnosing transmodel MCMC algorithms for species tree inference.
Limitations and Future Work
Besides the computational challenges in handling large datasets, we note two further limitations of our current implementation in BPP. The first is the use of the Jukes and Cantor (1969) mutation/substitution model. Although this appears to be adequate when closely related species are analyzed so that the sequences are highly similar and multiple hits at the same site are rare, the model may not be suitable for analysis of distant species such as different orders of mammals or land plants. It should be straightforward to implement more sophisticated substitution models. The second is the assumption of the molecular clock, which is expected to be seriously violated in comparisons of distantly related species. It is well-known that molecular clock rooting of phylogenetic trees is unreliable when the clock is seriously violated. We note that the relaxed-clock models developed for dating species divergences are designed for species data and should not be used directly to account for rate variation among branches of the gene tree. However, it appears to be straightforward to modify the model for use under the MSC. Instead of assigning a rate for each branch on the gene tree for the locus, we assign a rate for each branch on the species tree for every locus, so that different gene-tree branches residing in the same species should have the same rate.
Software Availability
The algorithms described in this article are implemented in the program BPP version 3.3, which may be downloaded from http://abacus.gene.ucl.ac.uk/software/. A small C program called BFdriver is written to generate the control files and job submission scripts for the multiple BPP MCMC runs to sample from the power posteriors for calculation of the marginal likelihood (or the Bayes factor). This is included in the release as well, with a tutorial using the frogs dataset of Yang (2015) as an example.
Acknowledgements
We thank Adam Leache, Thomas Giarla, the Associate Editor, and two anonymous reviewers for a number of constructive comments.
Funding
This work was supported by a Biotechnological and Biological Sciences Research Council (UK) grant (to Z.Y.).
References
- Bryant D., Bouckaert R., Felsenstein J., Rosenberg N.A., RoyChoudhury A. 2012. Inferring species trees directly from biallelic genetic markers: bypassing gene trees in a full coalescent analysis. Mol. Biol. Evol. 29(8):1917–1932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess R., Yang Z. 2008. Estimation of hominoid ancestral population sizes under Bayesian coalescent models incorporating mutation rate variation and sequencing errors. Mol. Biol. Evol. 25(9):1979–1994. [DOI] [PubMed] [Google Scholar]
- Chaudhary R., Fernandez-Baca D., Burleigh J.G. 2013. MulRF: a software package for phylogenetic analysis using multi-copy gene trees. Bioinformatics 31(3):432–433. [DOI] [PubMed] [Google Scholar]
- Chifman J., Kubatko L. 2014. Quartet inference from SNP data under the coalescent model. Bioinformatics 30(23):3317–3324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dalquen D., Zhu T., Yang Z. 2016. Maximum likelihood implementation of an isolation-with-migration model for three species. Syst. Biol. [DOI] [PubMed] [Google Scholar]
- Degnan J.H., Rosenberg N.A. 2006. Discordance of species trees with their most likely gene trees. PLoS Genet. 2(5):e68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degnan J.H., Salter L.A. 2005. Gene tree distributions under the coalescent process. Evolution 59(1):24–37. [PubMed] [Google Scholar]
- Edwards S.V. 2009. Is a new and general theory of molecular systematics emerging? Evolution 63(1):1–19. [DOI] [PubMed] [Google Scholar]
- Edwards S.V., Liu L., Pearl D.K. 2007. High-resolution species trees without concatenation. Proc. Natl. Acad. Sci. USA, 104(14):5936–5941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards S.V., Xi Z., Janke A., Faircloth B.C., McCormack J.E., Glenn T.C., Zhong B., Wu S., Lemmon E.M., Lemmon A.R., Leache A.D., Liu L., Davis C.C. 2016. Implementing and testing the multispecies coalescent model: a valuable paradigm for phylogenomics. Mol. Phylogenet. Evol. 94(Pt A): 447–462. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. 1981. Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol. 17(6):368–376. [DOI] [PubMed] [Google Scholar]
- Gelman A., Meng X. 1998. Simulating normalizing constants: from importance sampling to bridge sampling to path sampling. Stat. Sci. 13:163–185. [Google Scholar]
- Giarla T.C., Esselstyn J.A. 2015. The challenges of resolving a rapid, recent radiation: empirical and simulated phylogenomics of Philippine shrews. Syst. Biol. 64:727–740. [DOI] [PubMed] [Google Scholar]
- Heled J., Drummond A.J. 2010. Bayesian inference of species trees from multilocus data. Mol. Biol. Evol. 27(3):570–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hohna S., Defoin-Platel M., Drummond A.J. 2008. Clock-constrained tree proposal operators in Bayesian phylogenetic inference. 8th IEEE International Conference on BioInformatics and BioEngineering. Athens (Greece): BIBE, p. 7. [Google Scholar]
- Hohna S., Landis M.J., Heath T.A., Boussau B., Lartillot N., Moore B.R., Huelsenbeck J.P., Ronquist F. 2016. RevBayes: Bayesian phylogenetic inference using graphical models and an interactive model-specification language. Syst. Biol. 65(4):726–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jukes T., Cantor C. 1969. Evolution of protein molecules. In: Munro H., editor, Mammalian protein metabolism. New York: Academic Press, p. 21–123. [Google Scholar]
- Kubatko L.S., Degnan J.H. 2007. Inconsistency of phylogenetic estimates from concatenated data under coalescence. Syst. Biol. 56(1):17–24. [DOI] [PubMed] [Google Scholar]
- Kubatko L.S., Carstens B.C., Knowles L.L. 2009. STEM: species tree estimation using maximum likelihood for gene trees under coalescence. Bioinformatics 25(7):971–973. [DOI] [PubMed] [Google Scholar]
- Kubatko L.S., Gibbs H.L., Bloomquist E.W. 2011. Inferring species-level phylogenies and taxonomic distinctiveness using multilocus data in Sistrurus rattlesnakes. Syst. Biol. 60(4):393–409. [DOI] [PubMed] [Google Scholar]
- Lakner C., van der Mark P., Huelsenbeck J.P., Larget B., Ronquist F. 2008. Efficiency of Markov chain Monte Carlo tree proposals in Bayesian phylogenetics. Syst. Biol. 57:86–103. [DOI] [PubMed] [Google Scholar]
- Lartillot N., Philippe H. 2006. Computing Bayes factors using thermodynamic integration. Syst. Biol. 55:195–207. [DOI] [PubMed] [Google Scholar]
- Leaché A.D., Rannala B. 2011. The accuracy of species tree estimation under simulation: a comparison of methods. Syst. Biol. 60(2):126–137. [DOI] [PubMed] [Google Scholar]
- Liu L. 2008. BEST: Bayesian estimation of species trees under the coalescent model. Bioinformatics 24:2542–2543. [DOI] [PubMed] [Google Scholar]
- Liu L., Yu L. 2011. Estimating species trees from unrooted gene trees. Syst. Biol. 60:661–667. [DOI] [PubMed] [Google Scholar]
- Liu L., Yu L., Pearl D.K., Edwards S.V. 2009. Estimating species phylogenies using coalescence times among sequences. Syst. Biol. 58:468–477. [DOI] [PubMed] [Google Scholar]
- Liu L., Yu L., V., E.S. 2010. A maximum pseudo-likelihood approach for estimating species trees under the coalescent model. BMC Evol. Biol. 10(3):302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu L., Xi Z., Wu S., Davis C., Edwards S.V. 2015. Estimating phylogenetic trees from genome-scale data. Ann. NY. Acad. Sci. 10.1111/nyas.12747. [DOI] [PubMed] [Google Scholar]
- Maddison W.P. 1997. Gene trees in species trees. Syst. Biol. 46:523–536. [Google Scholar]
- Maddison W.P., Knowles L.L. 2006. Inferring phylogeny despite incomplete lineage sorting. Syst. Biol. 55(1):21–30. [DOI] [PubMed] [Google Scholar]
- Mirarab S., Warnow T. 2015. ASTRAL-II: coalescent-based species tree estimation with many hundreds of taxa and thousands of genes. Bioinformatics 31(12):i44–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mossel E., Roch S. 2010. Incomplete lineage sorting: consistent phylogeny estimation from multiple loci. IEEE/ACM Trans. Computat. Biol. Bioinfor. (TCBB) 7(1):166–171. [DOI] [PubMed] [Google Scholar]
- Murphy R.W., Fu J., Lathrop A., Feltham J.V., Kovac V. 2002. Phylogeny of the rattlesnakes (Crotalus and Sistrurus) inferred from sequences of five mitochondrial DNA genes. In: Schuett G.W., Hoggren M., Douglas M.E., Greene H.W., editors, Biology of the vipers. Eagle Mountain, UT: Eagle Mountain Publishing, p. 69–92. [Google Scholar]
- Ogilvie H.A., Heled J., Xie D., Drummond A.J. 2016. Computational performance and statistical accuracy of *BEAST and comparisons with other methods. Syst. Biol. 65:381–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Page R.D., Charleston M.A. 1997. From gene to organismal phylogeny: reconciled trees and the gene tree/species tree problem. Mol. Phylogenet. Evol. 7:231–240. [DOI] [PubMed] [Google Scholar]
- Parkinson C.L., Campbell J.A., Chippindale P.T., Schuett G. 2002. Multigene analyses of pitviper phylogeny with comments on their biogeographical history. In Schuett, G.W. Hoggren, M. Douglas, M.E. Greene, H.W. editors, Biology of the vipers. Eagle Mountain, Eagle Mountain Publishing, UT: p. 93–110. [Google Scholar]
- Rannala B., Yang Z. 2003. Bayes estimation of species divergence times and ancestral population sizes using DNA sequences from multiple loci. Genetics, 164(4): 1645–1656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala B., Yang Z. 2008. Phylogenetic inference using whole genomes. Annu. Rev. Genomics Hum. Genet. 9:217–231. [DOI] [PubMed] [Google Scholar]
- Rannala B., Yang Z. 2013. Improved reversible jump algorithms for Bayesian species delimitation. Genetics 194:245–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roch S., Steel M. 2015. Likelihood-based tree reconstruction on a concatenation of aligned sequence data sets can be statistically inconsistent. Theor. Popul. Biol. 100:56–62. [DOI] [PubMed] [Google Scholar]
- Ronquist F., Teslenko M., van der Mark P., Ayres D.L., Darling A., Höhna S., Larget B., Liu L., Suchard M.A., Huelsenbeck J.P. 2012. MrBayes 3.2: Efficient Bayesian phylogenetic inference and model choice across a large model space. Syst. Biol. 61(3): 539–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satta Y., Hickerson M., Watanabe H., O’hUigin C., Klein J. 2004. Ancestral population sizes and species divergence times in the primate lineage on the basis of intron and BAC end sequences. J. Mol. Evol. 59:478–487. [DOI] [PubMed] [Google Scholar]
- Tavare S. 1986. Some probabilistic and statistical problems on the analysis of DNA sequences. Lect. Math. Life Sci. 17:57–86. [Google Scholar]
- Wu R., Chen M.-H., Kuo L., Lewis P. 2014. Consistency of marginal likelihood estimation when topology varies. In: Chen M.-H., Kuo L., Lewis P., editors, Bayesian Phylogenetics: Methods, Algorithms, and Applications, London: Chapman and Hall/CRC, p. 113–127. [Google Scholar]
- Xu B., Yang Z. 2016. Challenges in species tree estimation under the multispecies coalescent model. Genetics. 10.1534/genetics.116.190173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z. 1994. Estimating the pattern of nucleotide substitution. J. Mol. Evol. 39:105–111. [DOI] [PubMed] [Google Scholar]
- Yang Z. 2002. Likelihood and Bayes estimation of ancestral population sizes in hominoids using data from multiple loci. Genetics 162(4):1811–1823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z. 2014. Molecular evolution: a statistical approach. Oxford, England: Oxford University Press. [Google Scholar]
- Yang Z. 2015. The BPP program for species tree estimation and species delimitation. Curr. Zool. 61:854–865. [Google Scholar]
- Yang Z., Rannala B. 2010. Bayesian species delimitation using multilocus sequence data. Proc. Natl. Acad. Sci. USA: 107:9264–9269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z., Rannala B. 2014. Unguided species delimitation using DNA sequence data from multiple loci. Mol. Biol. Evol. 31(12):3125–3135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu T., Yang Z. 2012. Maximum likelihood implementation of an isolation-with-migration model with three species for testing speciation with gene flow. Mol. Biol. Evol. 29:3131–3142. [DOI] [PubMed] [Google Scholar]