Measurement in Intensive Longitudinal Data

Abstract

Technological advances have increased the prevalence of intensive longitudinal data as well as statistical techniques appropriate for these data, such as dynamic structural equation modeling (DSEM). Intensive longitudinal designs often investigate constructs related to affect or mood and do so with multiple item scales. However, applications of intensive longitudinal methods often rely on simple sums or averages of the administered items rather than considering a proper measurement model. This paper demonstrates how to incorporate measurement models into DSEM to (1) provide more rigorous measurement of constructs used in intensive longitudinal studies and (2) assess whether scales are invariant across time and across people, which is not possible when item responses are summed or averaged. We provide an example from an ecological momentary assessment study on self-regulation in adults with binge eating disorder and walkthrough how to fit the model in Mplus and how to interpret the results.

As technological developments continue, data collection methods such as experience sampling (Scollon, Kim-Prieto, & Diener, 2003), ambulatory assessment (Fahrenberg, Myrek, Pawlik, & Perrez, 2007), daily diaries (Bolger, Davis & Rafaeli, 2003), and ecological momentary assessment (Smyth & Stone, 2003) permit data to be collected more intensively, more frequently, more naturally, and less invasively (Baraldi et al., 2016; Conner & Barrett, 2012; Hamaker & Wichers, 2017; Mehl & Conner, 2012; Trull & Ebner-Priemer, 2014). Because data are collected in real time through mobile or wearable devices, there is reduced burden to collect data and an increase in the ecological validity because data collection does not need to occur in a laboratory setting and responses can be given in real time rather than recalled after the fact (de Haan-Rietdijk, Voelkle, Keijsers, & Hamaker, 2017). As a result, these types of research designs have become popular in behavioral and health sciences, especially when studying moods, affect, and interpersonal behaviors (Moskowitz & Young, 2006).

Longitudinal designs employing intensive data collection yield a large amount of data per person, especially compared to traditional longitudinal designs for panel data where each person is measured only a few times over a much longer timeframe (e.g., Curran, Obeidat, & Losardo, 2010). More observations per person increases the ability to ask research questions that focus on within- and between-person variability and provides opportunities to study how within-person processes unfold moment to moment, rather than focusing on mean changes as is common with panel data (e.g., Hamaker & Wichers, 2017; Ram & Gertsoff, 2009; Wang, Hamaker, & Bergeman, 2012). To address these changes in data structure and the ability of richer data to support different research questions, novel statistical approaches have been advanced for this intensive longitudinal data (e.g., Asparouhov, Hamaker, & Muthén, 2018; Boker et al., 2011; Driver, Oud, & Voelkle, 2017; Hamaker & Wichers, 2017; Hamaker, Asparouhov, Brose, Schmiedek, & Muthén, 2018; Hedeker, Mermelstein, & Demirtas, 2008; Ou, Hunter, & Chow, 2018).

As similarly observed in applications of models for panel data (Bauer & Curran, 2015), approaches for modeling intensive longitudinal data often relegate or omit measurement models for the variables included in the model. Intensive longitudinal designs are often used to investigate constructs such as affect or mood, which are often formed by Likert responses to short multiple item scales to measure the underlying reflective construct (e.g., Lang, Lievens, de Fruyt, Zettler, & Tackett, 2019). Despite an extensive psychometrics literature discussing the benefits of proper measurement, applications of intensive longitudinal models and the methodological literature advancing them often rely on simple sums or averages of the administered items (Gorter, Fox, & Twisk, 2015; Hamaker, Ceulemans, Grasman, & Tuerlinckx, 2015; Hardt, Hecht, Oud, & Voelkle, 2019).

Sum or average scores serve as a rough approximation that are sometimes justifiable, but there are noted weaknesses with sum or average scores for reflective constructs, especially with longitudinal data (e.g., Braun & Mislevy, 2005; McNeish & Wolf, 2020). For instance, Kuhfeld and Soland (2020) noted that omitting the measurement model for outcome variables in longitudinal data has adverse effects on the parameter estimates. Similarly, Neale, Lubke, Aggen, and Dolan (2005) showed that sum scores can bias variance components when measurement non-invariance is present. Further, Edwards and Wirth (2009) note that the reflective latent variable model corresponding to sum or average scores does not easily permit invariance testing because summing or averaging implicitly assumes invariance, a sentiment echoed by Slof-Op’t Landt et al. (2009).

The difficulty of assessing measurement invariance with sum or average scores in intensive longitudinal data is particularly problematic because there are two sources of invariance that are important to consider. First is invariance across time to ensure that the items continue to relate to the construct in the same way at all measurement occasions (Millsap, 2010). Without demonstrating longitudinal invariance, potential changes in the underlying construct can be confounded with changes in the measurement instrument (Widaman, Ferrer, & Conger, 2010). That is, an observed change in the outcome could be due to a change in the construct (e.g., depression is increasing), but it could also occur if there is no change in the construct but the item responses carry different meaning at different measurement occasions (Rutter & Sroufe, 2000). Actively demonstrating that the measurement model is invariant over time strengthens conclusions because it can reasonably rule out the possibility that the change is due to the measurement instrument rather than the underlying construct.

Second, invariance across people ensures that the items are being interpreted and responded to similarly across people (Adolf, Schuurman, Borkenau, Borsboom, & Dolan, 2014; Borsboom & Dolan, 2007). If the items are non-invariant across people, then between-person differences may be attributable to different response behavior to the items rather than to a true difference in the underlying construct (Vandenberg & Lance, 2000). Many multiple item scales used to assess mood and affect have been noted to be susceptible to non-invariance over either time or people (e.g., Fried et al., 2016; Fried & Nesse, 2015; Hussey & Hughes, 2020), potentially leaving analyses of intensive longitudinal data vulnerable to adverse effects of measurement non-invariance when measurement is not considered and sum or average scores are used instead.

Conventional methods of assessing measurement invariance compare the fit of nested models with certain parameters constrained or freed (e.g., Meredith, 1993). However, this approach becomes infeasible rather quickly in intensive longitudinal studies with many measurement occasions and many participants because the number of possible model permutations and comparisons becomes unreasonable very quickly (Muthén & Asparouhov, 2018). For such situations, approximate invariance testing is more viable whereby random effects are used rather than fit comparisons to assess invariance (e.g., Asparouhov & Muthén, 2015; de Jong, Steenkamp, & Fox, 2007; Jak, Oort, & Dolan, 2013, 2014). With this method, between-person and between-time random effects can be placed on item parameters to quantify how much variability exists across people and measurement occasions. If the variance is reasonably small, then one can conclude that the item parameters are approximately invariant and measurement properties are stable. If the variability is large, this can indicate that non-invariance may exist.

The goal of this paper is to demonstrate how to assess measurement invariance with intensive longitudinal data – both across time and across people – and to serve as a reminder that measurement is critical for intensive longitudinal data. To outline the structure of the paper, we first overview basics of models for intensive longitudinal data. A short overview of cross-classification is also provided with a brief discussion of how measurement invariance in intensive longitudinal studies fits into a cross-classified framework. Then, we adapt the general framework described by Asparouhov and Muthén (2015) on cross-classified factor analysis to intensive longitudinal data to allow simultaneous assessment of variability in item parameters across time and people. We demonstrate with an application of this model to data from an ecological momentary assessment study on self-regulation behavior of adults who meet criteria for binge eating disorder and discuss how the model is fit in the dynamic structural equation modeling (DSEM) framework in Mplus (Asparouhov, Hamaker, & Muthén, 2018). We then show how measurement models can be embedded into broader intensive longitudinal models such that researchers can more rigorously consider measurement of their variables along with their focal hypotheses rather than relying on sum or average scores.

Modeling Intensive Longitudinal Data

Though the frequency of intensive longitudinal data (roughly defined as data with 20 or more measurement occasions per person; Collins, 2006; Walls & Schafer, 2006) is rapidly increasing in behavioral sciences as technology makes such data easier to collect, there is a long history of this data structure in other scientific fields like physics, economics, and meteorology where data are collected from inanimate sources (in these disciplines, intensive longitudinal data is more commonly referred to as a time-series; Box & Jenkins, 1970). Though not universal, a common underlying goal of time-series models is to model how the preceding state of the system affects the subsequent state (Hamaker, Asparouhov, Brose, Schmiedek, & Muthen, 2018).

A common way to accomplish this goal is through autoregressive models where the outcome variable of interest is predicted from itself at one or more earlier measurement occasions. The number of previous measurement occasions used is referred to as a lag; a lag-1 model uses the immediately preceding measurement occasion as a predictor, a lag-2 model uses the two immediately preceding measurement occasions. In its simplest form, a lag-1 autoregressive model – often abbreviated as AR(1) – can be written as

$$y_{{}_t}=\alpha +\phi y_{{}_{t-1}}+e_{{}_t}$$ (1)

where y_t is the outcome variable at time t, α the intercept of the time series, φ is a regression coefficient capturing the effect from the first lag of the outcome y_t−1, and e_t is the residual at time t that is normally distributed with a mean of 0 and constant variance σ². Autoregressive models of the form in Equation 1 require an assumption of stationarity such that the mean, variance, and autocorrelations of the outcome do not systematically change over time. This implies that the time-series is mean-reverting (Stroe-Kunold, Gruber, Stadnytska, Werner, & Brosig, 2012), meaning that the outcome variable may be higher or lower than the mean at particular measurement occasions, but the expected value does not systematically change from the first measurement occasion to the last. This basic AR(1) model can be generalized to other conditions in which there is a trend in the mean over time, there is a moving average component, the variance is heteroskedastic or a function of other predictor variables (e.g., location-scale models), the outcome is discrete, more lags are included (e.g., an AR(2) model) or there are multiple outcomes of interest (e.g., vector autoregressive models).

The challenge in adapting autoregressive methods to behavioral sciences has been the incidence of clustered data structures. That is, fields with a longer history of time-series analysis are concerned with a single entity that is followed intensively; however, in behavioral sciences, the interest is in following multiple people over time, resulting in measurement occasions being clustered within people. Extending the model to multiple people can be done with either bottom-up or top-down approaches (Liu, 2017). Bottom-up approaches first fit models to the data of each person separately and afterwards seek similarities between the dynamics of different people. This can be done by constraining parameters across people (e.g., Hamaker, Dolan, & Molenaar, 2003) or can be done with automatic searches for similarities (e.g., group iterative multiple model estimation, GIMME; Gates & Molenaar, 2012). Bottom-up approaches are more purely idiographic and allow for unique characteristics to emerge across people.

On the other hand, top-down approaches fit a model with the same functional form to all people but allow for variability in the parameters that regulate the dynamics for each person. Different dynamics across people are often accomplished with random effects such that the distribution of the parameter is modeled with a fixed effect (the average across all people) and a variance (the spread of the person-specific parameter values across people). The top-down approach combines aspects of idiographic and nomothetic perspectives because models estimate the average parameter value across all data (a nomothetic quantity) but also permit person-specific dynamics under the assumption that the functional form is constant across all people (e.g., Nesselroade & Molenaar, 1999).

Top-down models have historically been fit as multilevel or mixed effect models (e.g., Bolger & Laurenceau, 2013; Walls & Schafer, 2006), but multilevel models possess weaknesses for intensive longitudinal data in some contexts. As noted in McNeish and Hamaker (2020), multilevel models applied to intensive longitudinal data are challenged by unequal intervals between measurement occasions (which are a feature rather than a bug of some research designs to prevent participants from anticipating the next measurement occasion), Nickell’s bias (Nickell, 1981) and Lüdtke’s bias (Lüdtke et al., 2008) attributable to centering with the observed mean to disaggregate within-person and between-person effects, difficulties with models for multivariate outcomes, and the requirement that variables in the model are observed rather than latent.

To combat these weaknesses of multilevel models, the DSEM framework was recently introduced and incorporated into the Mplus software program (Asparouhov, Hamaker, & Muthén, 2017; 2018). DSEM integrates time-series analysis, multilevel models, and structural equation models into one unified framework, which allows users to mix and match aspects of the three approaches to meet the demands of the intended model, which can help address some of the aforementioned issues with the traditional multilevel modeling approach to intensive longitudinal data. DSEM applies a Kalman filter to address unequal intervals, can use latent centering from structural equation modeling to avoid Nickell’s bias and Ludtke’s bias, can combine multilevel and structural equation models to model multivariate outcomes, and can apply factor analysis within a multilevel model to permit modeling with latent variables.

The focus on this paper is on this last point – intensive longitudinal studies often administer a small number of items that indicate a reflective latent variable, but sum or average scores are created from item responses rather than employing a measurement model, possibly to adhere to the traditional restriction in multilevel models that the outcome be an observed variable. As noted in the introduction, a limitation of sum or average scores is that the ability to consider invariance – either over people or over time – is compromised, even though invariance is central to interpreting models fit to data with several dozen measurement occasions. We discuss how measurement invariance in intensive longitudinal data can be assessed with a cross-classified factor analysis model, but first overview the basics of cross classification.

Hierarchical vs. Cross-Classified Clustering

When observations are clustered within multiple organizational units, the clustering can be either hierarchical or cross-classified. The distinction is often clear to see in educational research (Goldstein, 1994). As a hypothetical hierarchical example, consider data from schools during a single academic year – students are clustered within schools and the schools are then clustered within towns. Each student attends one school and each school is located in one town. This nesting is hierarchical, meaning that knowing the school that a student attends will also necessarily indicate the town where they attend school because there is a one-to-one mapping of schools to towns. On the other hand, cross-classification occurs when one of the organizational units is not purely nested in another (Rasbash & Goldstein, 1994). This could occur if students are clustered within both schools and neighborhoods (e.g., Barker et al., 2020; Dunn, Richmond, Milliren, & Subramanian, 2015). Children who attend the same school do not necessarily live in the same neighborhood and children who live in the same neighborhood do not necessarily attend the same school (e.g., private versus public schools, magnet schools, school of choice options in the US). In cross-classified data, knowing which school a child attends will not necessarily identify the neighborhood in which the child lives and vice versa because there is not a strict one-to-one mapping of schools and neighborhoods and it is important to model both possible sources of variation (Luo & Kwok, 2009; Meyers & Beretvas, 2006).

Intensive Longitudinal Data as Cross-Classified

Data from intensive longitudinal studies can similarly be considered cross-classified. Responses are clustered within two higher level units – time and people – but those higher-level units are not nested within each other. Knowing from which time a response came will not necessarily identify the person from whom it came; conversely, knowing which person provided the response will not identify at which time it was collected.

Consider a hypothetical data structure showing three observations for three people. Each column corresponds to a different person, each row corresponds to a different time, and the values in the matrix represent outcome variable values.

	ID=1	ID=2	ID=3
T=1	Y11	Y12	Y13
T=2	Y21	Y22	Y23
T=3	Y31	Y32	Y33

The data are clustered within people such that all observations within a person are clustered together (vertically, down the columns). If clustering data this way, models can assess variability within a person (variance of values within a single column) and between people (variance across columns).

	ID=1	ID=2	ID=3
T=1	Y11	Y12	Y13
T=2	Y21	Y22	Y23
T=3	Y31	Y32	Y33

However, the data are also clustered within time such that the observations within the same measurement occasion are grouped together (horizontally, across the rows). If clustering data this way, models could assess the variability of the variable within a measurement occasion (variance of values in the same row) and between measurement occasions (variance of across rows).

	ID=1	ID=2	ID=3
T=1	Y11	Y12	Y13
T=2	Y21	Y22	Y23
T=3	Y31	Y32	Y33

Most intensive longitudinal studies consider a two-level structure where observations are clustered within people because this is logically consistent with the intended research questions. Nonetheless, although clustering by time may not address specific research questions, clustering by both time and people with a cross-classified model can be helpful to assess invariance over both levels of clustering. That is, whether the outcome variable is invariant across time remains relevant even if the research questions only concern between-person differences.

The next section discusses a cross-classified factor analysis model for assessing measurement invariance of intensive longitudinal items and applies the model to data on self-regulation in people with binge eating disorder. We subsequently discuss how this type of measurement model can be embedded into broader models for intensive longitudinal data in the DSEM framework to include more rigorous measurement in models testing research hypotheses.

Cross-Classified Factor Analysis

A cross-classified model to assess invariance across people and across time is,

$${\mathbf{y}}_{{}_{it}}={\mathit{v}}_{{}_{it}}+{\Lambda }_{{}_{it}}{\eta }_{{}_{it}}+{\mathbf{e}}_{{}_{it}}$$ (2)

Equation 2 shows that the vector of observed item responses from person i at time t (y_it) are equal to a vector of item intercepts (ν_it) plus a matrix of factor loadings (Λ_it) times a vector of latent variables (η_it) plus a vector of normally distributed residuals (e_it ~ MVN(0, Θ)). This first expression is standard matrix notation for a confirmatory factor analysis model with the exception that there are additional subscripts on the vectors and matrices to indicate that the parameters they contain vary across different levels of the data structure. The item intercepts ν_it, the factor loading matrix Λ_it, and the latent variables η_it are subscripted by both i and t to indicate that we are interested in the variance across people (denoted by i) and across time (denoted by t).

The decomposition of variance in the item intercepts, item factor loadings, and the latent variables across time and people can then be expressed as

$$\begin{gathered} {\eta }_{{}_{it}}={\pi }_{{}_{i\eta }}+{\tau }_{{}_{t\eta }} \\ {\mathit{v}}_{{}_{it}}={\alpha }_{{}_v}+{\pi }_{{}_{iv}}+{\tau }_{{}_{tv}} \\ {\Lambda }_{{}_{it}}={\alpha }_{{}_{\Lambda }}+{\pi }_{{}_{i\Lambda }}+{\tau }_{{}_{t\Lambda }} \end{gathered}$$ (3)

The first expression shows that the vector of latent variables for person i at time t (η_it) is equal to a vector of person-level random effects (π_iη) plus a vector of time-level random effects (τ_tη). A vector of latent variable means could also be added but is omitted here under the assumption that it is set to 0 for identification. The second expression shows that the vector of item intercepts (ν_it) is equal to a vector of item intercept fixed effects (α_ν) representing the average item scores when the latent variable equals 0, aggregated over both time and people plus a vector of person-level random effects (π_iν) that captures how the item scores differ from the average for person i plus a vector time-level random effects (τ_tν) that captures how the item scores differ from the average at time t. The third expression shows that the matrix of factor loadings is equal to the factor loadings fixed effects (α_Λ) representing the loadings aggregated over both people and time plus person-level random effects (π_iΛ) capturing how the loadings differ from the average for person i plus a time-level random effects (τ_tΛ) capturing how the loadings differ from the average at time t. The person-level random effects are assumed to follow a multivariate normal distribution, π_i ~ MVN(0, Ω), and the time-level random effects are assumed to follow a different multivariate normal distribution, τ_t ~ MVN(0, Ψ) and the random effects at different levels are independent, π_i ⊥ τ_t.

This variance decomposition will allow assessment of how the item properties change over time and over people – if there is large variance at one of the levels, this can be taken as evidence of non-invariance for this level. That is, the model allows researchers to assess whether the intercept or loading of each item varies across people or across time, which can help identify whether items have constant meaning over time or whether items have constant meaning across people in the data. The next section applies this model to data from an ecological momentary assessment study of binge eaters to show how invariance can be assessed with intensive longitudinal data.

Perseverance Binge Eating EMA

The data for the illustration are from an ecological momentary assessment study of 50 overweight/obese adults (27 ≤ BMI ≤ 45 kg/m2) who met DSM-5 criteria for a binge eating disorder. Specific details regarding data collection and aspects of the sample are reported on the study’s dedicated page on ClinicalTrials.gov.¹ These data were collected as part of a larger study of the ontology of self-regulation as described in Eisenberg et al. (2018).

Each participant was measured for 28 days, 4 times per day at random intervals within a 4-hour block for a maximum of 112 measures per participant. Three items related to perseverance were included at each measurement occasion; these items were selected based on a factor analysis of a large number of measures of self-regulation from a sample of 522 Mturk participants (Eisenberg et al., 2019; Mazza et al., 2020). The items, rephrased for the momentary context were: (a) “Since the last prompt, I've worked on what I planned until I succeeded”, (b) “Since the last prompt, I have set goals and kept track of my progress toward goals”, and (c) “Since the last prompt, I've been able to finish projects I started.”

The original items from which these three items were derived were the “I finish whatever I begin” item from the Short Grit Scale (Duckworth & Quinn, 2009), “I keep working on what I have planned until I succeed” from the Selection Optimization Compensation Scale (Freund & Baltes, 1998), “I set goals for myself and keep track of my progress” from the Short Self-Regulation Questionnaire (Carey, Neal, & Collins, 2004), and “I finish what I start” from the perseverance subscale of the UPPS-Impulsive Behavior scale (Cyders et al., 2007).

Model and Path Diagram

Each measurement occasion contains responses to each of the three items on a 1 (not at all) to 5 (very much) Likert scale. The distribution of the item responses is shown in Table 1 and approximately mirrored threshold values imposed to a symmetric normal distribution. Based on simulation evidence from Rhemtulla et al. (2012), this type of pattern with 5 response options can defensibly be treated as continuous. The three items are unidimensional and measure a single construct whose factor variance is constrained to 1 for identification.

Table 1.

Distribution of item responses for three Perseverance items across all people and measurement occasions

Response	Item 1	Item 2	Item 3
1	15.9%	17.1%	12.9%
2	16.7%	16.3%	15.0%
3	33.7%	33.2%	33.2%
4	24.8%	24.4%	26.4%
5	8.8%	9.0%	12.5%

The within-level model of a cross-classified factor analysis for these data would be

$$\begin{gathered} y_{{}_{1it}}=v_{{}_{1it}}+{\lambda }_{{}_{1it}}{\eta }_{{}_{1it}}+e_{{}_{1it}} \\ {y}_{{}_{2it}}=v_{{}_{2it}}+{\lambda }_{{}_{2it}}{\eta }_{{}_{1it}}+e_{{}_{2it}} \\ {y}_{{}_{3it}}=v_{{}_{3it}}+{\lambda }_{{}_{3it}}{\eta }_{{}_{1it}}+e_{{}_{3it}} \\ {\mathbf{e}}_{{}_{it}}\sim MVN\left(0_3,diag\left[{\theta }_{{}_{y1}},{\theta }_{{}_{y2}},{\theta }_{{}_{y3}}\right]\right) \\ {\eta }_{{}_{1it}}\sim N(0,1) \end{gathered}$$ (4)

“Within-level” is used here to indicate that this model corresponds to data that are nested within other units. In this case, the within-level model is nested within both people and time. The within-level model corresponds to the path diagram in Figure 1. There is a circle placed over the factor loading and intercept for each item to indicate that the parameters will be modeled as latent variables. These latent variables are subscripted by both i and t to indicate that their variance will be estimated at both the person and time levels. The within-level residuals (e_it) for the items also have variances but are not shown in the path diagram to make the path diagram as readable as possible.

Figure 1.

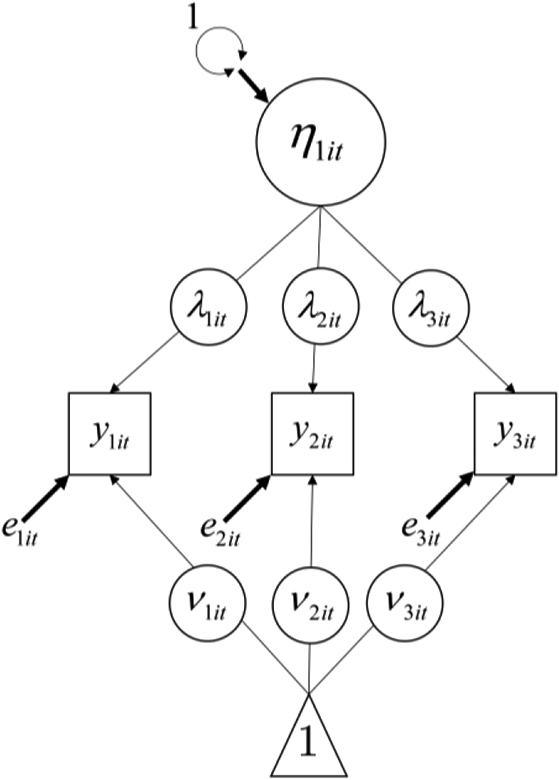
Within-level path diagram for cross-classified factor analysis model of Perseverance scale from binge eating EMA data. Residual variances for the items are included in the model but are not shown in the figure.

Next, we can model how parameters in the within-level model may vary across time in the between-time model, which can be written as

$$\begin{gathered} {\eta }_{{}_{1it}}={\tau }_{{}_{\eta 1t}} \\ {v}_{{}_{1it}}={\alpha }_{{}_{v1}}+{\tau }_{{}_{v1t}} \\ {v}_{{}_{2it}}={\alpha }_{{}_{v2}}+{\tau }_{{}_{v2t}} \\ {v}_{{}_{3it}}={\alpha }_{{}_{v3}}+{\tau }_{{}_{v3t}} \\ {\lambda }_{{}_{1it}}={\alpha }_{{}_{\lambda 1}}+{\tau }_{{}_{\lambda 1t}} \\ {\lambda }_{{}_{2it}}={\alpha }_{{}_{\lambda 2}}+{\tau }_{{}_{\lambda 2t}} \\ {\lambda }_{{}_{3it}}={\alpha }_{{}_{\lambda 3}}+{\tau }_{{}_{\lambda 3t}} \\ {\tau }_{{}_t}\sim MVN\left(0_{{}_7},diag\left[{\psi }_{{}_{\eta 1}},{\psi }_{{}_{v1}},{\psi }_{{}_{v2}},{\psi }_{{}_{v3}},{\psi }_{{}_{\lambda 1}},{\psi }_{{}_{\lambda 2}},{\psi }_{{}_{\lambda 3}}\right]\right) \end{gathered}$$ (5)

Which corresponds to the path diagram in Figure 2.

Figure 2.

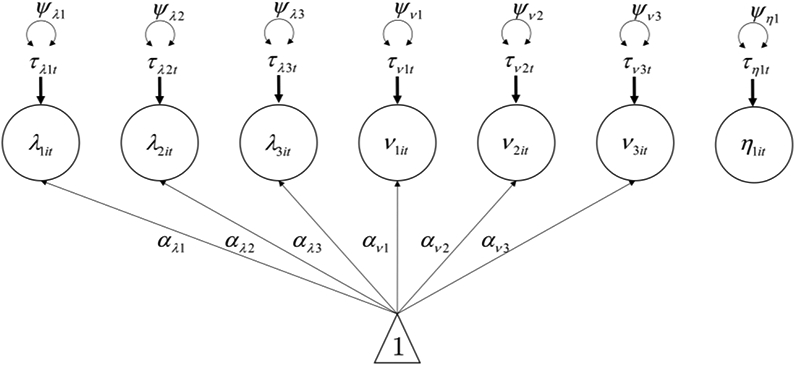
Between-time path diagram for cross-classified factor analysis model of Perseverance scale from binge eating EMA data

Each of the latent variables with a t subscript from the within-level model becomes an outcome of an equation at the between-time model. The fixed effects are captured by the α parameters and the variances of the latent variable at this level quantify the differences in the parameter across different values of time. It is possible to include structural relations between these latent variables as well (e.g., one latent variable predicts another) or to include covariances between latent variables (e.g., to test if measurement occasions with higher intercepts also have higher loadings).

Because the data are nested within multiple units, we can also model how the within-level model parameters vary across people with the between-person model, which can be written,

$$\begin{gathered} {\eta }_{{}_{1it}}={\pi }_{{}_{\eta 1i}} \\ {v}_{{}_{1it}}={\alpha }_{{}_{v1}}+{\pi }_{{}_{v1i}} \\ {v}_{{}_{2it}}={\alpha }_{{}_{v2}}+{\pi }_{{}_{v2i}} \\ {v}_{{}_{3it}}={\alpha }_{{}_{v3}}+{\pi }_{{}_{v3i}} \\ {\lambda }_{{}_{1it}}={\alpha }_{{}_{\lambda 1}}+{\pi }_{{}_{\lambda 1i}} \\ {\lambda }_{{}_{2it}}={\alpha }_{{}_{\lambda 2}}+{\pi }_{{}_{\lambda 2i}} \\ {\lambda }_{{}_{3it}}={\alpha }_{{}_{\lambda 3}}+{\pi }_{{}_{\lambda 3i}} \\ {\pi }_{{}_i}\sim MVN\left(0_{{}_7},diag\left[{\omega }_{{}_{\eta 1}},{\omega }_{{}_{v1}},{\omega }_{{}_{v2}},{\omega }_{{}_{v3}},{\omega }_{{}_{\lambda 1}},{\omega }_{{}_{\lambda 2}},{\omega }_{{}_{\lambda 3}}\right]\right) \end{gathered}$$ (6)

Which corresponds to the path diagram in Figure 3.

Figure 3.

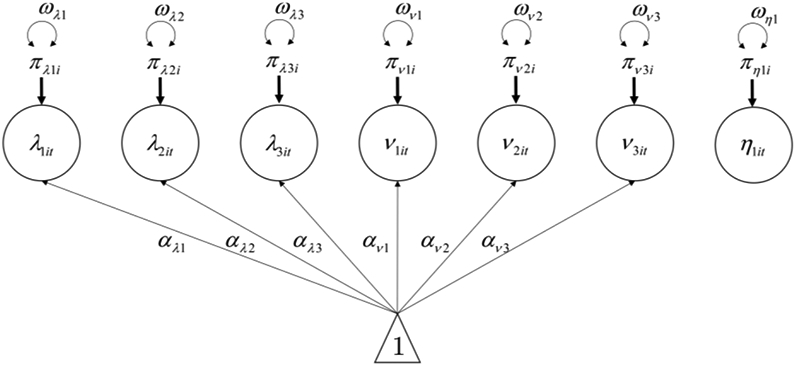
Between-person path diagram for cross-classified factor analysis model of Perseverance scale from binge eating EMA data

Figure 3 models each latent variable with an i subscript from the within-level as an outcome at the person-level. Figure 3 is similar to the between-time path diagram in Figure 2 because all latent variables were doubly subscripted by i and t, but all parameters do not necessarily need to vary at each level. Therefore, the latent variables and the fixed effects for the item intercepts and factor loadings are the same in Figure 3 as in Figure 2, but the random effects (π) and random effects variances (ω) in Figure 3 are at the person-level rather than the time-level and will capture the variability attributable to a different source. Combining the within-level model in Equation 4, the between-time model in Equation 5, and the person-person model in Equation 6 yields the overall cross-classified factor analysis presented in matrix form in Equations 3 and 4. The results and interpretation of the model are shown in the next section.

Results

We fit the cross-classified factor analysis model described in the previous subsection in Mplus Version 8.3 with Bayesian Markov Chain Monte Carlo estimation with two chains using the potential scale reduction method (Gelman & Rubin, 1992) with a stringent threshold of $\widehat{R}\le 1.10$ for all parameters (Brooks & Gelman, 1998, p. 442) to determine convergence after a minimum of 2,500 iterations and a maximum of 50,000 iterations. By default, Mplus discards the first half of iterations as burn-in and posteriors are based on the second half of iterations. Prior distributions were set to the Mplus defaults, which are improper uninformative distributions for all parameters. Annotated Mplus scripts and output are provided on the first author’s Open Science Framework page for this project.²

Bayesian estimation is preferred for these types of models for computational purposes because maximum likelihood and other frequentist methods often encounter convergence issues or are intractable with many random effects (Asparouhov et al., 2018). Because the motivation for Bayesian methods is computationally rather than philosophically motivated, the interpretation of the results minimally deviates from a model estimated with frequentist methods and the Mplus output changes little when the estimation method is changed. The parameter estimates³ are shown in Table 2.

Table 2.

Results from a cross-classified factor analysis of Perseverance items from binge eating data

Parameter	Notation	Item 1		Item 2		Item 3
		Est.	CI	Est.	CI	Est.	CI
Intercept Fixed Effect	α ν	3.087	[2.920, 3.331]	3.078	[2.881, 3.353]	3.258	[3.070, 3.479]
Intercept Person Variance	ω ν	0.040	[0.015, 0.082]	0.138	[0.080, 0.239]	0.221	[0.138, 0.364]
Intercept Time Variance	ψ ν	0.002	[0.000, 0.006]	0.001	[0.000, 0.004]	0.002	[0.000, 0.007]
Loading Fixed Effect	αλ	0.734	[0.649, 0.795]	0.768	[0.699, 0.844]	0.564	[0.489, 0.629]
Loading Person Variance	ω λ	0.083	[0.054, 0.132]	0.070	[0.045, 0.113]	0.074	[0.047, 0.119]
Loading Time Variance	ψ λ	0.000	[0.000, 0.001]	0.000	[0.000, 0.001]	0.001	[0.000, 0.002]

Note: Est. = Estimate and is taken from the median of the posterior distribution, CI = 95% symmetric credible interval

Item intercept estimates.

The fixed effects for the item intercepts are shown in the first row, all three of which are slightly above 3 and reflect that the average response to these items – averaged over people and time – is near the center of the Likert scale. This is consistent with the descriptive statistics for these items because they are Likert items scored on a 1 to 5 scale whose distribution was essentially symmetric.

The second row shows the between-person variance of the item intercepts (averaged over measurement occasions). Item 1 shows the smallest between-person variance of ω_ν1 = 0.040, meaning that the average response of this item was about the same across people when averaged over measurement occasions. Assuming normality, the 95% interval of person intercepts for Item 1 would be $3.087\pm 1.96(\sqrt{.040})=[2.70,3.48]$. Item 2 demonstrated larger variance across people with a between-person variance of ω_ν2 = 0.138, meaning that there was more variability in different people’s time-averaged response to this item. Assuming normality, the 95% interval of the Item 2 intercepts across people would be [2.35, 3.81]. Item 3 showed the most variability across people with a between-person variance of ω_ν3 = 0.221, which corresponds to a 95% interval of [2.34, 4.18], assuming normality.

The third row shows the between-time variance of the item intercepts (averaged over people). All three items have very small between-time variances for the item intercepts, suggesting that the between-time standard deviation of the item intercepts is at most about 0.05. This suggests the item intercepts are stable over time and there does not appear to be any systematic increase or decrease in the average item responses over time on any of the items. In other words, there appears to be evidence for the invariance for the item intercepts across time.

Factor loading estimates.

The fourth row of Table 2 shows the fixed effects for the unstandardized factor loadings (averaged over people and time), which are 0.734, 0.768, and 0.564 for Items 1 through 3, respectively. The metric of each item is the same, so the unstandardized factor loading can be used for relative comparisons between items. Because there are multiple sources of variance in a cross-classified factor analysis model, it is difficult to calculate standardized estimates and Mplus does not yet offer standardized factor loadings for this model as of Version 8.3. If attempting to approximate the standardized loading by dividing the unstandardized loading of each item by the descriptive standard deviation, the ‘standardized’ loadings would be 0.62, 0.64, and 0.47, respectively. Notably, the Item 3 factor loading appears to be weaker than the loadings associated with Items 1 and 2, possibly suggesting that a non-weighted sum of these items to form a composite score may not be warranted and the contribution of Item 3 to such a Perseverance score would be over-weighted.

The fifth row of Table 2 shows the between-person variance in the unstandardized factor loadings, which is non-zero and 0.083, 0.070, and 0.074 for Items 1 through 3, respectively. For Item 1, this translates to a 95% interval for the loadings across people of [0.17, 1.30] for Item 1, [0.25, 1.29] for Item 2, and [0.03, 1.10] for Item 3. This indicates that the factor loadings associated with these items vary across people and that the items reflect Perseverance to a varying degree across the people. In other words, the loadings do not appear to be invariant across people and person-specific loadings seem necessary. The variability of item loadings across persons is representative of the individual differences factor analysis idea mentioned in Asparouhov and Muthén (2015, p. 181) such that the parameters of the measurement model are person-specific, which still allows latent variables to be compared across people but refines the measurement model. Sum or average scores assume invariance across people and would fail to capture that the items reflect Perseverance differently across people.

The last row of Table 2 shows the between-time variance in the factor loadings. This variance is essentially zero for all three items, indicating that the factor loadings of the items are stable across time and that items reflect Perseverance to a similar degree across the observation window (e.g., Item 1 contributes as much to Perseverance at the beginning of the study as it does at the end of the study). These low between-time variances make sense given that the study lasts only four weeks and large changes in response behavior or drift in the parameters for Perseverance would not unlikely during such a short duration. Nonetheless, the model can verify this intuition empirically.

If non-invariance is detected, the model can also be used to investigate potential sources of non-invariance. The between-level models can feature predictors for the latent variables to condition measurement model parameters on relevant covariates. For instance, if sex were thought to be a reason why the intercepts vary across people, sex could be added as a covariate for ν_1it, ν_2it, and ν_3it in Figure 3. If sex differences were responsible for differences between item intercepts across people, the ω_ν parameters would be smaller because the variance would become a residual variance that captures how much variability remains after accounting for sex differences. We do not demonstrate this type of specification here, but we do wish to note it as a possibility because the DSEM framework gives researchers complete flexibility in the structural model, meaning that any variable can serve as a predictor or outcome in the model (e.g., McNeish & Hamaker, 2020).

Conclusion

When comparing many groups simultaneously with random effects rather than traditional binary hypothesis tests, the decision about how much variance can be tolerated while still feeling comfortable with labeling the items as meeting “approximate invariance” is up for debate. The cross-classified factor analysis for the Perseverance items administered to people with binge eating disorder had extremely low between-time variance in the item parameters and measurement invariance across time seems to be upheld rather unambiguously. That is, the latent variable retains its meaning across the window of observation and changes in the latent variable over time would indicate changes in the underlying construct, not changes in the measurement instrument.

The item parameters did show between-person variance in both item intercepts and factor loadings, suggesting that the items function differently across people. This indicates that the item parameters should be modeled as person-specific to most accurately compare the Perseverance latent variable across people (Asparouhov & Muthén, 2015). Additionally, the magnitude of the factor loading fixed effects were somewhat discrepant such that Item 3 appearing to be less relevant to Perseverance than Items 1 and 2. The discrepant factor loadings together with the non-negligible between-person variance in item parameters suggest that measuring Perseverance with an equally weighted sum or average across items is likely inappropriate.

Of course, the goal of intensive longitudinal studies is not often solely to inspect measurement properties of items but ultimately to explore how dynamic processes unfold. The next section shows how to incorporate the information from the cross-classified factor analysis for Perseverance into a broader intensive longitudinal model.

Embedding the Measurement Model into a Broader Model

With knowledge that there is invariance in the Perseverance scale across measurement occasions but not necessarily across people and person-specific measurement model parameters may be needed, we can incorporate this into the broader focal model to test hypotheses about how within-person dynamics unfold over time. In this data, in addition to the self-regulation items, there was another question at each measurement occasion that asked about people’s restraint to eat (On a scale of 1 to 10, where 1 means "no restraint in eating" and 10 means “total restraint”, what number would you give yourself at this moment?).

The focal question of interest is how Restraint and Perseverance interact across the window of observation. That is, how Perseverance at time t – 1 affects both Perseverance and Restraint at time t and how Restraint at time t – 1 affects both Perseverance and Restraint at time t. In the time-series literature, this is referred to as a vector autoregressive model (VAR). In this section, we will fit a two-level random intercepts VAR model with Perseverance scored with either (a) a sum of item responses at each measurement occasion or (b) a factor model for the three item responses at each measurement occasion with between-person random effects as found in the measurement invariance study in the previous section. Because the variance of the between-time random effects was essentially 0 for all item parameters in the cross-classified factor analysis, this model will remove the between-time random effects and the model will not be cross-classified.

Both models were fit in Mplus Version 8.3 with Bayesian Markov Chain Monte Carlo estimation with two chains using the potential scale reduction method (Gelman & Rubin, 1992) with a stringent threshold of $\widehat{R}\le 1.10$ for all parameters (Brooks & Gelman, 1998) to determine convergence after a minimum of 2,500 iterations with a maximum of 50,000 iterations. By default, Mplus discards the first half of iterations as burn-in and posteriors are based on the second half of the iterations. Ecological momentary assessments, by design, have unequal spacing between responses to prevent participants from anticipating the next response. To accommodate unequal spacing of responses in the model and the possibility of omitted responses, we coded time on an hourly scale and used a Kalman filter with 4-hour intervals (i.e., the TINTERVAL option in Mplus). The Mplus default prior distributions are again used. All code and output are provided from the previously provided Open Science Framework project page.

Sum Score for Perseverance

The within-person model of the two-level VAR model that treats Perseverance as a sum score can be written

$$\begin{gathered} Restrain{t}_{{}_{it}}={\alpha }_{{}_{1i}}+{\phi }_{{}_1}Restrain{t}_{{}_{i(t-1)}}^{{}^{(c)}}+{\phi }_{{}_3}Perseveranc{e}_{{}_{i(t-1)}}^{{}^{(c)}}+e_{{}_{1it}} \\ Perseveranc{e}_{{}_{it}}={\alpha }_{{}_{2i}}+{\phi }_{{}_2}Perseveranc{e}_{{}_{i(t-1)}}^{{}^{(c)}}+{\phi }_{{}_4}Restrain{t}_{{}_{i(t-1)}}^{{}^{(c)}}+e_{{}_{2it}} \\ {e}_{{}_{1it}}\sim N\left(0,{\sigma }_1^2\right) \\ {e}_{{}_{2it}}\sim N\left(0,{\sigma }_2^2\right) \end{gathered}$$ (7)

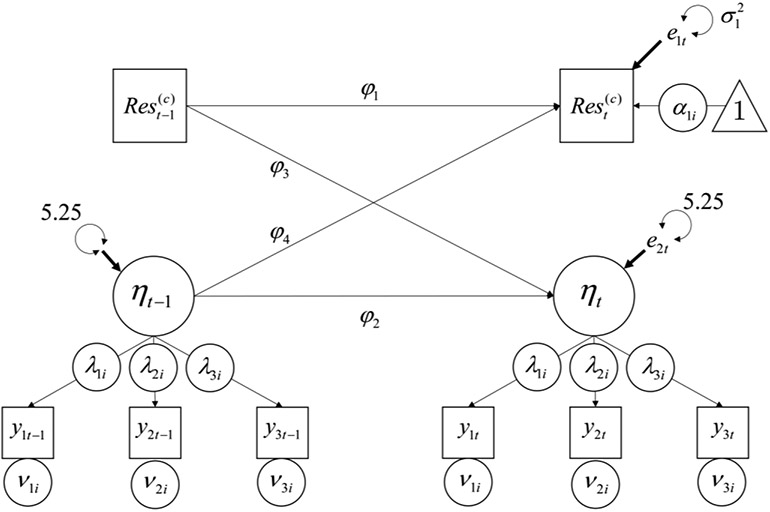
The model shows the Restraint at time t for person i is equal to the person-specific mean α_1i (which is the horizontal line to which the series will revert over time), plus the autoregressive effect of latent-centered Restraint at the previous measurement occasion (${\phi }_{1}Restrain{t}_{i(t-1)}^{(c)}$), plus the effect of latent-centered Perseverance at the previous measurement occasion (${\phi }_{3}Perseveranc{e}_{i(t-1)}^{(c)}$), plus a normally distributed residual for person i at time t $e_{1it}\sim N(0,{\sigma }_1^2)$. As alluded to earlier, DSEM allows users to latent-center within-person variables by subtracting the latent mean from each value rather than the observed mean as is common in multilevel models. That is, $Restrain{t}_{(t-1)i}^c=(Restrain{t}_{(t-1)i}-{\alpha }_{1i})$ and $Perseveranc{e}_{(t-1)i}^c=(Perseveranc{e}_{(t-1)i}-{\alpha }_{2i})$; the latent means α_1i and α_2i are subtracted instead of the observed means $\overline{Restraint}$ and $\overline{Perseverance}$. The conceptual idea is the same, but the latent means can account for measurement error and are less susceptible to biases that can affect intensive longitudinal data (Asparouhov et al., 2018). The second expression in the within-person model is similar except that the outcome is Perseverance instead of Restraint. The path diagram corresponding to the within-person model is shown in Figure 4.

Figure 4.

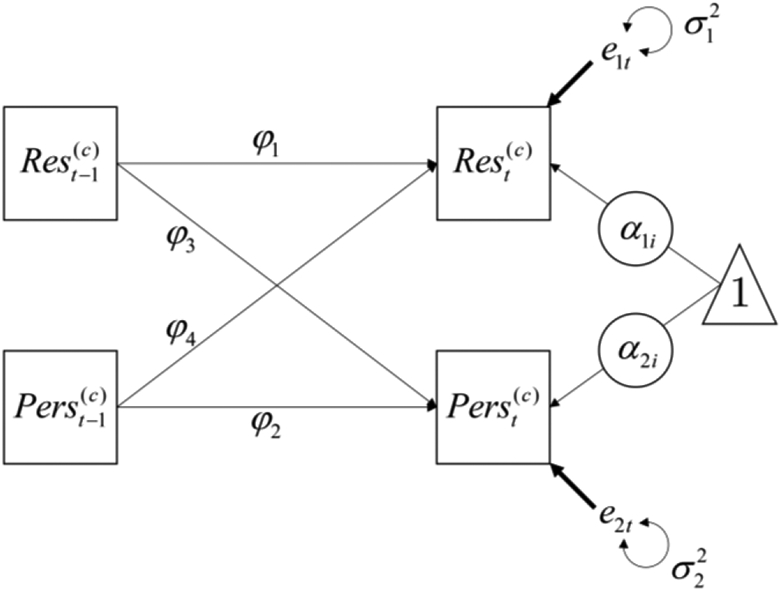
Within-person model of two-level VAR for Restraint and Perseverance. Perseverance is sum scored in this model and is represented by a square to indicate that it is an observed variable.

Figure 4 shows that the intercepts of Restraint and Perseverance are allowed to vary across people and that the previous occasion of Restraint and Perseverance predict the subsequent values of each variable (a Kalman filter is used to address difference in the timing from which the last occasion came; see Hamaker & Grasman, 2012 for additional details about Kalman filters in time-series models).

The between-person model then contains the fixed and random effects for the Restraint and Perseverance intercepts and assumes that the between-person random effects are multivariate normal with the random intercepts permitted to covary.

$$\begin{gathered} {\alpha }_{{}_{1i}}={\alpha }_{{}_{\alpha 1}}+{\pi }_{{}_{\alpha 1i}} \\ {\alpha }_{{}_{2i}}={\alpha }_{{}_{\alpha 2}}+{\pi }_{\alpha 2i} \\ \left[\begin{array}{c}\hfill {\pi }_{\alpha 1i}\hfill \\ \hfill {\pi }_{\alpha 2i}\hfill \end{array}\right]\sim MVN\left(\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],\left[\begin{array}{cc}\hfill {\omega }_{\alpha 1}\hfill & \hfill \hfill \\ \hfill {\omega }_{\alpha 2\alpha 1}\hfill & \hfill {\omega }_{\alpha 2}\hfill \end{array}\right]\right) \end{gathered}$$ (8)

The path diagram for the between-person model is shown in Figure 5.

Figure 5.

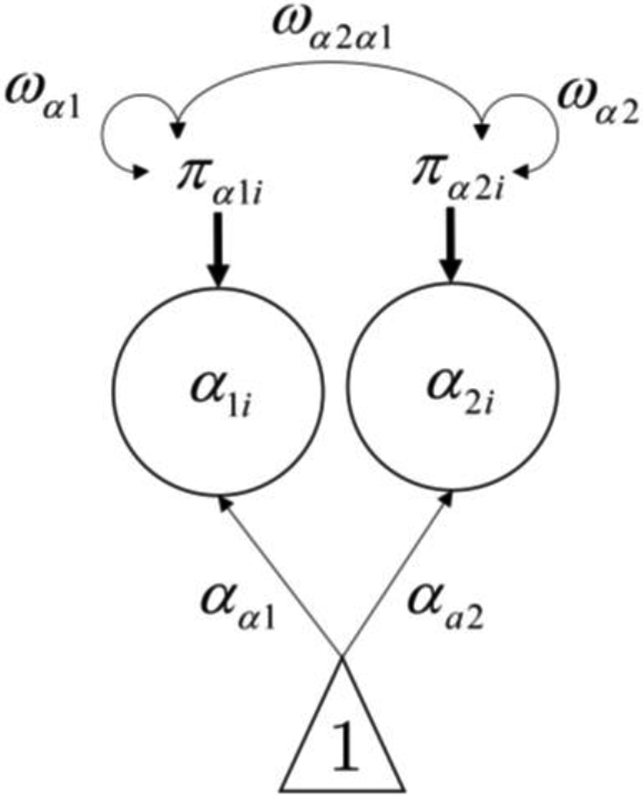
Between-person model for two-level VAR model when Perseverance is sum scored.

Latent Variable for Perseverance

The same two-level random intercepts VAR model can be fit featuring a measurement model for Perseverance rather than taking a sum across item responses. This will combine Equation 4 featuring the measurement model for Perseverance with the within-person VAR model in Equation 7 such that

$$\begin{gathered} y_{{}_{1it}}=v_{{}_{1i}}+{\lambda }_{{}_{1i}}{\eta }_{{}_{it}}+e_{{}_{y1it}} \\ {y}_{{}_{2it}}=v_{{}_{2i}}+{\lambda }_{{}_{2i}}{\eta }_{{}_{it}}+e_{{}_{y2it}} \\ {y}_{{}_{3it}}=v_{{}_{3i}}+{\lambda }_{{}_{3i}}{\eta }_{{}_{it}}+e_{{}_{y3it}} \\ Restrain{t}_{{}_{it}}={\alpha }_{{}_{1i}}+{\phi }_{{}_1}Restrain{t}_{{}_{i(t-1)}}^{{}^{(c)}}+{\phi }_{{}_3}{\eta }_{{}_{i(t-1)}}+e_{{}_{1it}} \\ {\eta }_{{}_{it}}={\phi }_{{}_2}{\eta }_{{}_{i(t-1)}}+{\phi }_{{}_4}Restrain{t}_{{}_{i(t-1)}}^{{}^{(c)}}+e_{{}_{2it}} \\ {\mathbf{e}}_{{}_{yit}}\sim MVN\left(0_{{}_3},diag\left[{\theta }_{{}_{y1}},{\theta }_{{}_{y2}},{\theta }_{{}_{y3}}\right]\right) \\ {e}_{{}_{1it}}\sim N\left(0,{\sigma }^2\right) \\ {e}_{{}_{2it}}\sim N\left(0,5.25\right) \end{gathered}$$ (9)

The first three expressions show that the item responses for person i at time t are modeled with a person-specific intercept (ν_i), a person-specific loading times the latent variable value for person i at time t (λ_i), and a residual for person i at time t (e_it). The fourth and fifth expressions are then the same regression equations as in Equation 7 except that Perseverance is replaced by the latent variable η_i.

The latent variable does not need to be latent centered because its mean is arbitrary and can be fixed to 0 and the variance of the latent variable is fixed for identification. The latent variable variance is conventionally fixed to 1, but we fix it to 5.25 because this is the variance of the Perseverance sum scores, which will allow us to directly compare the coefficients in the within-person models because the sum score and latent variable will be on the same scale. This rescaling will result in the unstandardized loadings and their variances to be smaller than those presented in Table 2, although the standardized loadings will be similar. The latent variable mean is not constrained to the mean of the sum scores because the sum scores are latent centered and will have a mean of 0 in the within-person model.

The path diagram corresponding to Equation 9 is shown in Figure 6. The conceptual idea is the same as in Figure 4, but Perseverance is replaced by a latent variable for the three Perseverance items. Based on the invariance assessment conducted earlier, the item intercepts and factor loadings are modeled with between-person random effects.

Figure 6.

Within-person model of two-level VAR for Restraint and Perseverance. Perseverance is modeled as a latent variable (η) in this model and is represented by a circle to indicate that it is a latent variable. All factor loadings and item intercepts are also modeled as random effects and vary across people.

All of the latent variables in the within-person model become outcomes in the between-person model, meaning that the between-person model will be much larger when treating Perseverance as a latent variable than the between-person model when treating Perseverance as a sum score in Equation 8. Specifically, the between-person model when Perseverance is latent would be

$$\begin{gathered} {\eta }_i={\pi }_{\eta i} \\ {\alpha }_{1i}={\alpha }_{\alpha 1}+{\pi }_{\alpha 1i} \\ {v}_{1i}={\alpha }_{v1}+{\pi }_{v1i} \\ {v}_{2i}={\alpha }_{v2}+{\pi }_{v2i} \\ {v}_{3i}={\alpha }_{v3}+{\pi }_{v3i} \\ {\lambda }_{1i}={\alpha }_{\lambda 1}+{\pi }_{\lambda 1i} \\ {\lambda }_{2i}={\alpha }_{\lambda 2}+{\pi }_{\lambda 2i} \\ {\lambda }_{3i}={\alpha }_{\lambda 3}+{\pi }_{\lambda 3i} \\ {\pi }_i\sim MVN\left(0_8,\begin{array}{cccccccc}\hfill {\omega }_{\eta }\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill {\omega }_{\alpha 1\eta }\hfill & \hfill {\omega }_{\alpha 1}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_{v1}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill {\omega }_{v2}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill {\omega }_{v3}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill {\omega }_{\lambda 1}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill {\omega }_{\lambda 2}\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\omega }_{\lambda 3}\hfill \end{array}\right) \end{gathered}$$ (10)

This is similar to the between-person model in Equation 6 except that Equation 10 includes the random intercept for Restraint and there are no t subscripts because the invariance assessment showed that it was not necessary to let parameters vary across time. As in the model using sum scores, the random intercepts of Perseverance and Restraint are allowed to covary. To keep the results comparable across models, no other random effect covariances are included in the model. Figure 7 shows the path diagram corresponding the between-person model in Equation 10. A comparison of results for these different models is shown in the next subsection.

Figure 7.

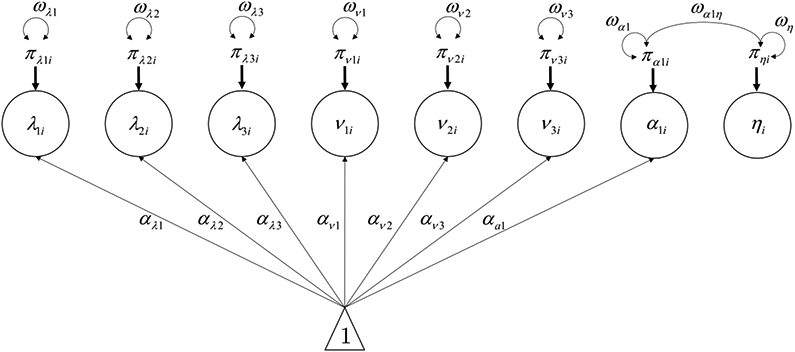
Between-person model for two-level VAR model when Perseverance is modeled a as a latent variable.

Results

A comparison of the two-level random intercepts VAR models with different scoring methods for Perseverance is shown in Table 3. Bayesian estimation is used, so the “estimates” are taken from the median of the posterior distribution for each parameter. Similarly, there are no p-values or confidence intervals but rather credible intervals, which are taken from the 2.5^th and 97.5^th percentile of the posterior distribution. To approximate frequentist inference, if 0 is outside the credible interval, this would be analogous to significance at the 5% level in a frequentist setting.

Table 3.

Comparison of posterior medians and 95% credible intervals for two-level random intercepts VAR model applied to binge eating data

		Sum Score		Latent Variable
Effect	Notation	Est.	CI	Est.	CI
Restraint_t on Restraint_t-1	φ 1	0.178	[0.137, 0.217]	0.178	[0.141, 0.216]
Perservance_t on Perservance_t-1	φ 2	0.358	[0.322, 0.395]	0.436	[0.391, 0.487]
Perservance_t on Restraint_t-1	φ 3	0.063	[0.016, 0.113]	0.079	[0.024, 0.133]
Restraint_t on Perservance_t-1	φ 4	0.026	[−0.003, 0.053]	0.040	[0.010, 0.068]
Res. Var. (Restraint)	${\sigma }_1^2$	3.112	[2.979, 3.256]	3.101	[2.972, 3.238]
Res. Var. (Perseverance)	${\sigma }_2^2$	5.250	[5.018, 5.503]	5.250	---
Intercept (Restraint)	α a1	6.835	[6.424, 7.256]	6.861	[6.450, 7.260]
Intercept (Perseverance)	α a2	8.779	[8.113, 9.403]	0.000	---
Var (Restraint)	ω α1	2.141	[1.425, 3.308]	2.091	[1.372, 3.321]
Var (Perseverance)	ω α2	4.814	[3.243, 7.549]	---	---
Cov (Restraint, Perseverance)	ω α1α2	0.131	[−0.920, 1.196]	0.016	[−0.608, 0.716]
Intercept (Item 1)	α ν1	---	---	2.964	[2.840, 3.108]
Intercept (Item 2)	α ν2	---	---	2.944	[2.781, 3.126]
Intercept (Item 3)	α ν3	---	---	3.155	[2.983, 3.325]
Intercept (Item 1 Loading)	α λ1	---	---	0.288	[0.252, 0.324]
Intercept (Item 2 Loading)	α λ2	---	---	0.310	[0.277, 0.343]
Intercept (Item 3 Loading)	α λ3	---	---	0.229	[0.198, 0.262]
Var (Item 1)	ω ν1	---	---	0.049	[0.019, 0.105]
Var (Item 2)	ω ν2	---	---	0.143	[0.089, 0.250]
Var (Item 3)	ω ν3	---	---	0.225	[0.145, 0.365]
Var (Item 1 Loading)	ω λ1	---	---	0.013	[0.009, 0.022]
Var (Item 2 Loading)	ω λ2	---	---	0.011	[0.007, 0.018]
Var (Item 3 Loading)	ω λ3	---	---	0.012	[0.007, 0.019]
Person Var (Perseverance)	ω η	---	---	1.704	[1.065, 2.984]
Res Var. (Item 1)	θ 1	---	---	0.351	[0.329, 0.376]
Res Var. (Item 2)	θ 2	---	---	0.226	[0.204, 0.253]
Res Var. (Item 3)	θ 3	---	---	0.443	[0.420, 0.469]

Note: Var = Variance, Res. Var. = Residual Variance, Est. = Median of the Posterior Distribution, CI = 95% Credible Interval Within-level factor variance constrained to the variance of the sum scores rather than the conventional value of 1 so that the autoregressive coefficients are on the same scale and directly comparable. The unstandardized loadings in Table 3 are noticeably different from those reported in Table 2 because the Perseverance variance is constrained to 5.25 in Table 3 rather than 1.00 as in Table 2. Because a one-unit difference in the latent variable has a different meaning in Table 3, the loadings are consequently smaller. Multiplying the loadings by $\sqrt{5.25}$ puts the loadings back on the metric used in Table 2.

First, φ₁ – which captures the lag-1 effect of Restraint – is identical with an almost identical credible interval across models because it is unaffected by how Perseverance is scored. φ₂ captures the lag-1 effect of Perseverance, which is stronger when Perseverance is modeled as a latent variable (i.e., the carryover effect of Perseverance from one measurement occasion to the next is greater when Perseverance is latent). φ₃ captures the cross-lagged effect of lag-1 Restraint on Perseverance and the estimated effect is stronger when Perseverance is modeled as a latent variable. φ₄ captures the cross-lagged effect of lag-1 Perseverance on Restraint and the estimated effect is stronger when Perseverance is modeled as a latent variable. Estimated effects for φ₂, φ₃, and φ₄ are all larger in magnitude for the model when Perseverance is modeled as a latent variable than when a sum score is used. Presumably, this occurs because the latent variable more heavily weights Items 1 and 2 because they are more construct-relevant than Item 3 based on the estimated factor loadings in the measurement. Additionally, the latent variable model also allows the item parameters to be person-specific so that the measurement model is better tailored to each person rather than assuming an invariant sum score applies equally to all people. Do note that a more rigorous measurement model will not necessarily lead to effects with larger magnitudes. Depending on the context, it is quite possible that a more rigorous measurement model or accounting for non-invariance could lead to smaller estimates or that non-invariance on different parameters could cancel each other out and have no net effect on estimates.

This difference in magnitude notably affects conclusions for φ₄. In the sum score model, the credible interval for φ₄ barely includes 0 and the effect would be considered null and the conclusion would be that lag-1 Perseverance does not affect Restraint at the subsequent measurement occasion. However, the credible interval for φ₄ in the measurement model is above 0 and would be considered non-null such that that lag-1 Perseverance positively affects Restraint at the subsequent measurement occasion. Granted, the lower bound of the credible interval for φ₄ in the sum score model is very close to 0 and the conclusion is borderline regardless of the decision.

Also note that the credible intervals for all φ parameters tend to be wider than those obtained using sum scores because the latent variable incorporates measurement error whereas the sum score model assumes that the sum scores for Perseverance are error free. Additionally, though the latent variable model is much larger and includes many more random effects than the sum score model, estimation was still very manageable and converged in 15 seconds compared to 3 seconds for the sum score model.

Embedding Measurement Models with Between-Time Variance

In the empirical data examined in this paper, the item intercepts and loadings of the Perseverance scale were reasonably invariant over time. Consequently, the measurement model embedded with VAR(1) time-series model was a two-level hierarchical model with the measurement parameters only having between-person variance. A reasonable extension revolves around how to proceed if the intercepts or loadings were non-invariant over time and demonstrated non-ignorable between-time variance in the cross-classified factor analysis. In cross-classified factor analysis in Mplus as of Version 8.6, all measurement model parameters (i.e., item intercepts, loadings, and factor variances) can have both between-time and between-person variance. However, when embedding measurement models into broader DSEM, only item intercepts and factor variances are permitted to have both between-person and between-time variance, but loadings can only have between-person variance and may not have between-time variance.

This means that researchers can incorporate shifts in average item responses over time or changes in the variability of the construct over time (akin to metric invariance in the traditional measurement invariance literature), but the relation of the items to the construct should be constant over time (though they may vary across people). A cross-classified DSEM with between-time variance is identified, but the posterior distribution of the latent variable would change at each time-point, which presents computational challenges. Between-time variance in the loadings could still be incorporated with a two-stage approach whereby a cross-classified factor analysis is fit in the first stage, the plausible values of the latent variables are extracted, and then a DSEM is fit in the second stage using the first stage plausible values in place of the latent variable. DSEM with plausible values is available in Mplus Version 8.6.⁴

Beyond the question of if a model with between-time variance in the loadings could be fit, researchers should consider whether they should fit such a model. If the loadings from the latent variable to the items have large between-time variance, it may be ambiguous if moment-to-moment dynamics can be meaningfully interpreted because the latent variable might have a different meaning by the end of the observation window. For instance, there is an emerging literature on measurement reactivity in intensive longitudinal data whereby the process of being measured repeatedly changes how people respond to items over time (e.g., Barta, Tennen, & Litt, 2012). Between-person variance in the loadings does not create this same issue because allowing a unique measurement model for every person does not affect the ability to investigate momentary dynamics so long as those relations are constant across time.

Currently, studies that use sum or average scores evade this issue entirely because summing or averaging item responses embeds assumptions about invariance into the scoring process. We are hopeful that the approach we propose can provide researchers with at least one option to assess and quantify invariance over time or over people and ultimately strengthen conclusions made from intensive longitudinal data.

Discussion

Despite the central of role of psychometrics in behavioral science research, the presence of rigorous psychometrics is often inversely related to the complexity of the intended model. Though the rationale for avoiding measurement models within complex models is understandable, a complex model does not negate that accurate measurement of variables is the foundation of any analysis. Models for intensive longitudinal data have the ability to provide unique insights into moment-to-moment dynamics of within-person processes, but the value and generalizability of these insights can depend on aspects of the variables involved. Using sum or average scores in the model is convenient but may not always represent the construct of interest and may overstate invariance across time or people. As outlined in this paper, modeling multiple-item scales with a measurement model rather than a sum or average score can help assess assumptions of sum scores (i.e., unit-weighting of items and invariance over time and people) and can more flexibly model item responses when these assumptions are not upheld.

Limitations and Extensions

Cross-classified factor analysis is not an answer to all measurement related problems for intensive longitudinal data and there are limitations that are important to note, many of which carryover from general issues with random effects models (e.g., Muthén & Asparouhov, 2018; Table 10). For instance, the method can be susceptible to both a small number of people or a small number of measurement occasions where “small” is usually defined near 30 (Schultzberg & Muthén, 2018), although sample size requirements for the number of people increase with model complexity. This makes the default implementation we demonstrated less appropriate for designs with a single observation per day and a relatively short window of observation (e.g., two-week daily diary studies). Estimation issues with a small number of people can be ameliorated by using informative priors within Bayesian estimation (McNeish, 2019; van de Schoot et al., 2015). Though not systematically explored yet in the literature, a similar approach could be instated to address a small number of measurement occasions. Cross-classified factor analysis also uses random effects to capture invariance which requires distributional assumptions, typically normality.

The number of response options and the distribution of the response options permitted our analyses to treat the items as continuous, but this may not always be the case. In the event that the items would be more appropriately treated as categorical, Mplus currently supports this option via a probit link where the thresholds for each possible response category are estimated rather than just a single item intercept as when items are treated as continuous. Estimation time will increase compared to what we present in our analysis when treating items categorically and the number of parameters in the model will also increase given that there are multiple thresholds per item need to be estimated.

Concluding Remarks

New models for intensive longitudinal data present exciting opportunities to study dynamics of within-person processes. A fundamental component of these analyses should be to ensure that the dynamics of the variables studied are accurately representing the constructs of interest and that those constructs mean the same thing across time and across people. Otherwise, models for intensive longitudinal models may be comparing apples to oranges either across time or across people and may misrepresent the true underlying dynamics. Cross-classified factor analysis is one method to assess measurement properties of items that are collected intensively over time, but opportunities to extend principles of measurement to the new environment of intensive longitudinal data are ample.